1 Introduction

The Frisch-grid ionization chamber (FGIC) is a type of pulse electron-collection ionization chamber that has been proven to be an effective tool for charged particle spectroscopy owing to its radiation hardness, approximately 100% detection efficiency, and nearly 2\(\uppi \) detection solid angle [1,2,3]. The FGIC was first developed by Frisch and Bunemann [4]. A grid electrode (parallel wire or mesh type) is used to shield the electron-collecting anode from the effects of the motion of primary electrons. In such a design, the pulse height of the anode signal is proportional to the energy deposited in the counting gas. However, the grid shielding is insufficient, which is generally referred to as grid inefficiency [5,6,7]. The anode signal is also slightly angular-dependent. Thus, in the physical design of an FGIC and relative measurements, it is necessary to consider the effects of grid inefficiency and its correction.

A theoretical approximation of the grid inefficiency in a parallel wire-type FGIC was performed by Bunemann [4], and the calculated grid inefficiency factor was in good agreement with the measured value. In 2011, based on the Shockley–Ramo theorem, Göök et al. investigated the grid inefficiency of an FGIC in a two-dimensional calculation model using a numerical computation method. The experimental and calculated grid inefficiency factors showed good agreement [8]. In contrast to the parallel wire-type FGIC (two-dimensional model), the study of the mesh-type FGIC requires a three-dimensional calculation model, which leads to the high cost of batch computation. To date, less investigation has been conducted on the calculation of grid inefficiency of mesh-type FGICs.

In this work, using the finite element method (FEM) and the Monte Carlo method [9, 10], a grid inefficiency \(\sigma \) evaluation model is developed for a mesh-type FGIC based on the Shockley–Ramo theorem for the first time [11, 12]. The relationship between the physical parameters of the detector and the grid inefficiency can be described by the developed model. A trained artificial neural network (ANN) [13] is applied to describe and predict the grid inefficiency factor \(\sigma \) with different physical parameters for the mesh-type FGIC. With the ANN method, a precise function \(\sigma \)(d, r, p) can be obtained for evaluating the grid inefficiency. This method avoids the complex calculation and provides a precise value of \(\sigma \). In the future, it can serve as a reference for the development of mesh-type FGICs and be used to correct for grid inefficiencies in measurements

Fig. 1
figure 1

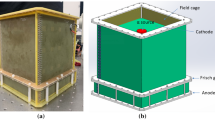
A schematic illustration of the mesh-type FGIC. p is the distance between anode and grid; D is the distance between grid and cathode; r is the grid wire radius; and d is the grid wire spacing. The xyz coordinate system is established with the origin at the center of the grid. The right inset shows the \(x-y\) plane of a mesh unit

Full size image

2 Theory and method

The Shockley–Ramo theorem states that the instantaneous current i induced on conductor A (investigated conductor) comes from the motion of a charge carrier. The i can be expressed as [11, 12]

$$\begin{aligned} i=qvE_{\mathrm{A}} \end{aligned}$$
(1)

where q is the charge carrier, v is the instantaneous velocity of the charge carrier, and \(E_{\mathrm{A}}\) is the weighting field at the position of the charge carrier when the charge carrier is removed. Conductor A is kept at unit potential, while all other conductors are grounded. The charge induced on conductorA can be calculated from the integration of current i

$$\begin{aligned} Q=-\int {idt=} q[\varphi _{\mathrm{A}} (r_{1} )-\varphi _{\mathrm{A}} (r_{0} )] \end{aligned}$$
(2)

where \(\varphi _{\mathrm{A}}\) is the potential distribution when the charge carrier is removed. \(r_{0}\) and \(r_{1}\) are the origin and current position of the charge carrier, respectively. \(\varphi _{\mathrm{A}} (r_{1} )\) and \(\varphi _{\mathrm{A}} (r_{0} )\) are the values of the weighting potential at \(r_{0}\) and \(r_{1}\). Unlike the actual electric potential, the weighting potential is not related to the applied voltages, and is only dependent on the geometric characteristics. It can be calculated by solving the Laplace equation under the boundary conditions \(\varphi _{\mathrm{A}} = 1\, {\mathrm{V}}\) for conductor A and \(\varphi _{\mathrm{A}} = 0\, {\mathrm{V}}\) for all other conductors. In this study, the weighting potential and electric field distributions in the mesh-type FGIC were calculated using the FEM. The solutions to the Laplace equation by the FEM were obtained by dividing the domain into a mesh of geometric shapes (elements) and iteratively finding the solution inside each element. This was implemented by the computer code COMSOL Multiphysics [14]. Coupled with the Monte Carlo method, the FEM results were read as the inputs of Garfield\(++\) to simulate the interaction of the charged particle with the counting gas, the electron drifting behavior, and the induced signals on the electrodes. In Garfield\(++\) code [9, 15], the signals were calculated using the Shockley–Ramo theorem and Eqs. (1) and (2).

The geometry of the mesh-type FGIC is shown in Fig. 1. The two regions, the interaction region (\(z <0\)) and collection region (\(z > 0\)), are separated by a mesh grid. In the interaction region, the charged particle energy was deposited in the gas. In the collection region, all electrons drifted toward the anode and were collected. The parameter D denotes the distance between the cathode and grid, while p denotes the distance between the anode and grid. As shown by the inset on the right, the grid consists of stainless-steel crossed wires. The parameter r is the grid wire radius, and d is the grid wire spacing.

In our model, the mesh-type FGIC is considered as an array consisting of multiple instances of the same cell. A schematic illustration of a cell is shown in Fig. 2a. Its whole shape is a cuboid which is filled with the gas. The upper part of the Fig. 2a is an anode element, while the bottom one is a cathode element. A grid element consists of four half-cylindrical and is placed between the anode and cathode element. By using COMSOL software, the field map of the cell, including the electric field and weighting potential distributions, were calculated. Figure 2b shows its electric field distribution. The field map of the entire FGIC, can be obtained from the periodic mirror transformation of the field map of the cell. With the well-justified symmetry simplification, any border effect will not be considered which reduces the computation cost and makes the calculations more reliable.

Fig. 2
figure 2

a A schematic illustration of a cell. It consists of anode, grid and cathode elements. b The calculated result of the field distribution in the cell

Full size image
Fig. 3
figure 3

The calculation of the electric field distribution for the mesh-type FGIC when r = 0.025 mm, d = 1 mm, p = 6 mm, and D = 31 mm. a the electric field map of the \(x-y\) plane when \(z = 0, |{x}|<\) 0.21 cm, and \(|{y}|<0.21\) cm. b The electric field map of \(x-z\) plane when y = 0.05 cm, \(|{x}|<0.21\) cm, and \(|{z}|<0.2\) cm. The color contour scale denotes the value of the field strength (V/cm)

Full size image

In the field map calculation, a high voltage was applied to the electrodes, i.e., 1000 V on the anode, − 1000 V on the cathode, while the grid was grounded. Figure 3 shows the calculation of the electric field distribution around the grid for r = 0.025 mm, d = 1 mm, p = 5.5 mm, and D = 31 mm. It consists of the field maps of multiple cells (the figure only shows 4 \(\times \) 4 cells). The electric field map of the \(x-y\) plane for z = 0 is shown in Fig. 3a. Near the surface of the grid wires, the maximum field strength reached approximately 5000 V/cm. Away from the grid wires and close to the center of the cell, the field strength gradually decreased. Figure 3b shows the electric field map of the \(x-z\) plane when y = 0.05 cm (the middle of two wires). Two uniform electric fields, \(E_{\mathrm{A-G}}\) and \(E_{\mathrm{G-C}}\), are separated by the grid. In this configuration, the strengths are |\(E_{\mathrm{A-G}}\)|= 1818 V/cm and |\(E_{\mathrm{G-C}}\)|= 323 V/cm. Similarly, the weighting potentials for the mesh grids were also calculated over the \(x-z\) plane. For the anode electrode, the boundary conditions are unity at z = 0 and zero at \(z = -D\) as well as at the grid mesh wires. The weighting potentials obtained by solving the Laplace equation are shown in Fig. 4a, when the anode electrode is selected as the investigated conductor. The same procedure was applied to the grid and cathode. Their weighting potential distributions are shown in Fig. 4b and c, respectively.

Fig. 4
figure 4

The calculation of the weighting potential distribution of the mesh-type FGIC for the a anode electrode, b grid electrode, and c cathode electrode. The color contour scale denotes the value of weighting potential (V)

Full size image

Garfield\(++\) is a toolkit for the detailed simulation of particle detectors based on ionization measurements in gases and semiconductors. Its main applications are currently in micropattern gaseous and silicon detectors [15, 16]. In this work, the calculated results of the field maps in Figs. 3 and 4 are the input parameters of the Garfield\(++\) code to investigate the ionization process in the FGIC. In the Garfield\(++\) simulation, the detector geometric model and material dielectric properties are given by the FEM mesh to ensure consistency with the field map. The chamber was operated with a medium P-10 gas at a gas pressure of 1 atm and temperature of 293.15 K. As a 3 MeV alpha particle leaves the origin position (0.05 cm, 0.05 cm, − 3.1 cm) and enters the gas, it ionizes the gas atoms and liberates the electrons. The ionization process was implemented by the TrackSrim package and microscopic tracking class [15]. Under the electric field, the electrons drift toward the anode. Owing to the three orders of magnitude difference in weight, the positive ions are practically motionless during the short time-scale of electron collection [8]. Figure 5 shows the simulated results of the ionization and transportation of an alpha particle and electrons. The green line denotes an alpha trace and the red lines are the electron traces. The electron cloud drifts along the electric field between the electrodes and induces charge signals on the anode, grid, and cathode.

Fig. 5
figure 5

Transportation process of an alpha particle and electrons in the mesh-type FGIC. The green line denotes the alpha trace and the red lines denotes the electrons traces

Full size image
Fig. 6
figure 6

a The signal waveforms. The black line denotes the negative signal on the anode -\(Q_{\mathrm{A}}(t)\), while the red line denotes the signal on the cathode \(Q_{\mathrm{C}}(t)\). The blue line is the \(\sigma Q_{\mathrm{C}}(t)\) cathode signal scaled with \(\sigma \). b The plot of \(Q_{\mathrm{C}}(t)\) vs -\(Q_{\mathrm{A}}(t)\) in Fig. 5a. The straight red line is the result of a linear fit to the data

Full size image

Figure 6a shows the calculation of the induced signal on the anode and cathode. The black line denotes the negative charge signal on the anode -\(Q_{\mathrm{A}}(t)\), while the red line denotes the charge signal on the cathode\( Q_{\mathrm{C}}(t)\). As the particle enters the gas (t = 0), the electrons start to drift away from the cathode, and the \(Q_{\mathrm{C}}(t)\) increases from zero. For the negative anode signal -\(Q_{\mathrm{A}}(t)\), because of the imperfect shielding of the anode by the grid, the anode detects the motion of the electrons even before they pass the grid, which is shown as the small slope in the inset in Fig. 6a when 0 < t < \(T_{\mathrm{G}}\) (At time \(T_{\mathrm{G}}\), the first electron reaches the grid). This leads to the slight angular-dependence of the charge signal on the anode (The anode signal is related to the angle of the alpha particle with respect to the drift field). The effect of imperfect shielding is generally referred to as grid inefficiency. It can be calculated from the signals -\(Q_{\mathrm{A}}(t)\) and \(Q_{\mathrm{C}}(t)\):

$$\begin{aligned} Q_{\mathrm{A}} (t)=-\sigma Q_{\mathrm{C}} (t) \qquad {(0<t<T_{\mathrm{G}} )} \end{aligned}$$
(3)

where \(\sigma \) is the grid inefficiency factor. Figure 6b shows a plot of the -\(Q_{\mathrm{A}}(t)\) and \(Q_{\mathrm{C}}(t)\) in the time interval from t = 0 to \(t = T_{\mathrm{G}}\). Each point in the plot represents a point in time, and its position is determined from -\(Q_{\mathrm{A}}(t)\) and \(Q_{\mathrm{C}}(t)\). Using the linear function fit of the plot, the slope of this line is \(\sigma \). The result is shown in Fig. 6a by the cathode signal scaled with the obtained \(\sigma \). As a function of time, this scaled cathode signal represents the fraction of the charge induced on the anode by electrons moving in the interaction region.

3 Results and discussion

According to the calculation method for the grid inefficiency \(\sigma \) discussed above, four sets of calculated results with different geometric properties are compared with the experimental data [6, 8], which are summarized in Table 1. The \(\sigma \) values calculated at the anode-grid distance p that were much larger than grid wires spacing d are in good agreement with the measured values. When the p was comparable to that of the grid wires, the calculation was slightly different from that of the experiment. A similar conclusion was reported in Ref. [8] for the parallel wire-type FGIC. This can be explained by nonuniformity of the field between grid and anode. Uniformity of the field is assumed to determining \(\sigma \), the calculated results is not reliable when the initial assumption is no longer valid [17]. Overall, the calculated results show good agreement with the measured results.

Table 1 The comparison of calculated and measured \(\sigma \)[6, 8]
Full size table
Fig. 7
figure 7

The grid inefficiency factor \(\sigma \) as a function of the electric filed strength ratio R between the interaction and collection regions

Full size image

For the parallel wire-type FGIC [4], its grid inefficiency factor is independent on the electric field strength and dependent on the anode-grid distance p, grid wire radius r, and grid wire spacing d. To verify whether this conclusion is the same as that for the mesh-type FGIC, the relationship between the physical parameters of the detector and grid inefficiency \(\sigma \) was investigated. The grid was always grounded in all calculations.

Fig. 8
figure 8

The grid inefficiency factor \(\sigma \) as a function of parameters d, r, p and D with all other conditions unchanged: a \(\sigma \) as a function of parameter d, b \(\sigma \) as a function of parameter r, c \(\sigma \) as a function of parameter p, and d \(\sigma \) as a function of parameter D

Full size image
Fig. 9
figure 9

Comparison of the grid inefficiency factor \(\sigma \) of the parallel wire and mesh-type FGIC: a \(\sigma \) as a function of parameter d, b \(\sigma \) as a function of parameter r, and c \(\sigma \) as a function of parameter p

Full size image
Fig. 10
figure 10

The training dataset for ANN. The three-dimensional distribution of the d, p, and \(\sigma \) values with different r values. The cases of a r = 0.015 mm, b r = 0.025 mm, c r = 0.035 mm, d r = 0.045 mm, e r = 0.055 mm, f r = 0.065 mm, g r = 0.075 mm, h r = 0.085 mm, i r = 0.095 mm, and j r = 0.105 mm

Full size image

The parameters were fixed at r = 0.025 mm, d = 1 mm, p = 5.5 mm, and D = 31 mm. The voltages on the anode \(V_{\mathrm{A}}\) and cathode \(V_{\mathrm{C}}\) were varied to investigate the influence of the electric field on \(\sigma \). The \(V_{\mathrm{A}}\) ranged from 100 to 1000 V. The \(V_{\mathrm{C}}\) was selected as − 600 V, − 800 V, and − 1000 V. Figure 7 shows the grid inefficiency factor \(\sigma \) as a function of the electric field strength ratio R(|\(E_{\mathrm{A-G}}\)|/|\(E_{\mathrm{G-C}}\)|) between the interaction and collection regions. When R changed from 0.5 to 10, \(\sigma \) remained unchanged. Thus, for the mesh-type FGIC, the grid inefficiency factor \(\sigma \) is not affected by the electric field strength in the chamber.

Figure 8 shows the grid inefficiency factor \(\sigma \)as a function of the parameters d, r, p, and D, when all other conditions are unchanged. When p = 5.5 mm, r = 0.025 mm, and D = 31 mm, \(\sigma \) increased with d, as shown in Fig. 8a. When d, p, and D are fixed, \(\sigma \) decreased as d increased, as shown in Fig. 8b. This can be attributed to the mesh wire density. The use of dense grid wires increases the shielding efficiency of the grid [18]. Figure 8c shows the increase in \(\sigma \)as a function of p. It is approximately an exponential decrease. For small p-values, a slight change in p results in a significant change in \(\sigma \). When p = 5.5 mm, r = 0.025 mm, and d = 1 mm, the influence of the grid-cathode distance D on \(\sigma \) is shown in Fig. 8d. A change in the value ofD, does not change the value of \(\sigma \). Thus, according to Figs. 7 and 8, the grid inefficiency factor \(\sigma \) of the mesh-type FGIC is only affected by the parameters d, r, and p, similar that of to the parallel wire-type FGIC.

A comparison of the grid inefficiency factor \(\sigma \) of the parallel wire and mesh-type FGIC under the same conditions is shown in Fig. 9. The \(\sigma \) of the parallel wire-type was calculated by an empirical formula [4], while that of the mesh-type FGIC was obtained using our method. The mesh-type FGIC grid proved better shielding than the parallel wire-type with the same r, d, and p. Thus, the use of a mesh instead of the usual parallel wires provides better signal quality and resolution [4, 19]. Unlike the parallel wire-type (two-dimensional model), the study of the mesh-type FGIC requires the use of a three-dimensional calculation model, which leads to the high cost of batch computation for \(\sigma \). It leads to less investigation on the calculation of the \(\sigma \) of the mesh-type FGIC from an accurate empirical formula.

In this work, in order to obtain an empirical expression for fast calculation on the \(\sigma \) of mesh-type FGIC, the relationship between \(\sigma \) and d, r, and p; and the empirical prediction of \(\sigma \) were investigated by the ANN. ANN has a significant advantage in solving nonlinear pattern classification and regression problems [20]. Theoretically, it has been proven that a backpropagation (BP) neural network with a three-layer structure (input, hidden, and output layers) can approximate any continuous function using a sigmoid function [21]. The BP learning algorithm is a powerful approach. Despite its slow convergence, it is one of the most popular and effective algorithms for pattern recognition.

According to the method in Sect. 2, 1700 sets of \(\sigma \) with different d, r, and p values were obtained as the database. The data was split into two groups: a training dataset and testing dataset containing 1000 and 700 samples, respectively. The training dataset was used to develop the logistic regression and multilayer perceptron models, while the testing dataset was used to evaluate the network. The training data, as the input of the ANN, are shown in Fig. 10. The p value changed from 1.5 to 10.5 mm in a 1 mm step; the d changed from 0.4 to 2.2 mm in a 0.2 mm step and the r changed from 0.015 to 0.105 mm in a 0.01 mm step.

After a data set has been created, the neural network was optimized to determine the appropriate number of layers and the neurons per layer. The usual approach is to test the neural network with different training times from simple structure to the complex one, so as to find a network with small error between the predicted and expected value and relatively stable with the increase of training times.

Fig. 11
figure 11

For different neural network structures, the relationship between the mean absolute error \(\overline{\vert \sigma _{\mathrm{ANN}} -\sigma _{\mathrm{truth}} \vert }\) and the number of training times

Full size image
Fig. 12
figure 12

The training result of the ANN. The blue circles denote neurons. Each black line connects two neurons. The left side of the figure is the input layer with three neurons, the middle part is the hidden layer with three layers (5:8:10), and the right side is the output layer for the evaluated values. The thickness of each line represents the level of correlation (or weight value) between two neurons

Full size image

Figure 11 shows the relationship between the mean absolute error \(\overline{\vert \sigma _{\mathrm{ANN}} -\sigma _{\mathrm{truth}} \vert }\) and the training times for different neural network structures. \(\sigma _{\mathrm{ANN}}\) is the predicted value from ANN, and \(\sigma _{\mathrm{truth}}\) is the value from the testing dataset. With the increasing of the training times, the \(\overline{\vert \sigma _{\mathrm{ANN}} -\sigma _{\mathrm{truth}} \vert }\) of network gradually become smaller and then tend to be stable. The \(\overline{\vert \sigma _{\mathrm{ANN}} -\sigma _{\mathrm{truth}} \vert }\) with the three-layer structure 5:8:10 is relatively small and its trend is relatively stable as training times changes. Thus, the neural network with 5:8:10 hidden layer was used in this work.

Figure 12 shows the results of the ANN after training. The left side is the input layer with three neurons, the middle part is the hidden layer with three layers (5:8:10), and the right side is the output layer for the evaluated value \(\sigma \). Each black line connects two neurons. The thickness represents the level of correlation (weight value) between the two neurons. The purpose of training is to update this weight value to reduce the error between the actual and predicted values.

Figure 13 shows the errors between the predicted value \(\sigma _{\mathrm{ANN}}\) and the actual value \(\sigma _{\mathrm{truth}}\) from the testing dataset. As shown in Fig. 13a, the fluctuation of errors increased with the increase in \(\sigma _{\mathrm{truth}}\). It is caused by statistical errors since there are few data points with large \(\sigma \). Overall, the relative error between the actual value and ANN predictions was less than 1%. Figure 13b shows the relationship between the errors \(\sigma _{\mathrm{ANN}}-\sigma _{\mathrm{truth}}\) and the input values of d, r, and p. These inputs contributed to the low errors. These results show that the ANN after training in this work is capable of describing and predicting the relationship between \(\sigma \) and d, r, and p.

Fig. 13
figure 13

The difference in \(\sigma \) between the ANN output and actual values. a The relationship between the errors \(\sigma _{\mathrm{ANN}}-\sigma _{\mathrm{truth}}\) and \(\sigma _{\mathrm{truth}}\). b The relationship between errors \(\sigma _{\mathrm{ANN}}-\sigma _{\mathrm{truth}}\) and input values of d, r, and p

Full size image

4 Conclusions

In this study, a new grid inefficiency \(\sigma \) evaluation model was developed for a mesh-type FGIC based on the FEM and Monte Carlo method for the first time. The relationship between the physical parameters of the detector and the grid inefficiency can be described by the developed grid inefficiency \(\sigma \) evaluation model. The calculated grid inefficiency \(\sigma \) at the anode-grid distance p that were much larger than grid wires spacing d are in good agreement with the measured values. It indicates that the model is reasonable reliable for determining the grid inefficiency factor \(\sigma \).

According to the developed model, the relationship between the physical parameters of the detector and the grid inefficiency was described with reasonable accuracy. This indicates that the grid inefficiency \(\sigma \) of the mesh-type FGIC is only affected by the parameters d, r, and p, similar to that of the parallel wire-type FGIC.

An ANN was applied as empirical expression to predict the grid inefficiency factor \(\sigma \) of the mesh-type FGIC. Based on a backpropagation algorithm, the trained ANN can well describe and predict the grid inefficiency factor with different physical parameters (d, r, and p). The relative error between the actual value and ANN prediction was less than 1%. Thus, the developed grid inefficiency \(\sigma \) evaluation model can serve as a reference for the development of mesh-type FGICs and be used to correct for grid inefficiencies in measurements.