Local one-dimensional reggeon model of the interaction of several pomerons

Abstract

We consider the one-dimensional local reggeon theory describing the leading pomeron with the conformal spin $l=0$ and two subdominant pomerons with $l=\pm 2$. The dependence of the propagators of pomerons and the hA amplitude on rapidity are found numerically by integrating the evolution equation.

1 Introduction

In the framework of the quantum chromodynamics (QCD) in the kinematic region where energy is much greater than the transferred momenta (“the Regge kinematics”), the strong interactions can be described by the exchange of pomerons, which can be interpreted as bound states of pairs of so-called reggeized gluons. In the quasi-classical approximation, which neglects pomeron loops, this leads to the well-known Balitsky–Kovchegov equation [1, 2] and its generalizations in the form of the JIMWLK equations [3,4,5,6,7,8], widely used for describing high-energy scattering. However, it was recognized from the start that at sufficiently high energies, the formation of pomeron loops would change the picture radically. In the QCD, going beyond the quasi-classical approximation and taking account of loops presents an almost insurmountable problem, which has not been solved until now. However, this problem can be investigated in simplified models in which the pomeron is local and interacts with phenomenologically introduced vertices and coupling constants, the Regge–Gribov model [9,10,11]. Further simplifying the model to zero transverse dimension (“toy model”), one can study the influence of loops and find that they indeed cardinally change the behaviour at very large energies [12,13,14,15,16,17].

It is remarkable that in the QCD the pomeron appears as a set of multiple states, which differ in their energies $\mu$ (intercepts minus unity) and conformal spins. Transformed to the one-dimensional transverse world, they appear as a set of pomerons corresponding to the rising spin l (angular momentum in the full transverse world). The leading pomeron with $l=0$ may be phenomenologically identified with a local pomeron with $\mu \simeq 0.12$. In QCD language, this will correspond to quite a low value of the coupling constant $\bar{\alpha }=0.0433$. Subdominant pomerons with $l>0$ will have negative values $\mu$. Of these, the pomeron with $l=\pm 2$ will have the largest $\mu =-0.0531$. It is of some interest to see how the presence of higher pomerons will influence the behaviour of observables in the limit of high energies.

In this note, we generalize the Regge–Gribov model in a zero-dimensional transverse world to include a pair of subdominant pomerons with $l=\pm 2$. The resulting model includes three types of fields $\Phi _0$, $\Phi _2$ and $\Phi _{-2}$ corresponding to projections of conformal spins 0 and 2. It turns out that, similarly to the model with only one field, it permits numerical study of evolution in energy. As a result, we find that loops generated by the additional pomerons act in the same direction as the main pomeron loops: they diminish both propagators and amplitudes.

2 Model

The Hamiltonian of the one-dimensional Regge–Gribov model with only the pomerons is

$$\begin{aligned} {H}= - \mu _P \Phi ^{+} \Phi + i \lambda \Phi ^{+} ( \Phi + \Phi ^{+} ) \Phi , \end{aligned}$$

(1)

where $\Phi ,\Phi ^{+}$ are the complex pomeron field and its conjugate: these fields are functions of the rapidity y only. The mass parameter $\mu _P=\alpha (0)-1$ is defined by the intercept of the pomeron Regge trajectory, and $\lambda$ is the effective coupling constant.

Our aim is to generalize this model for the case when there are several pomeron states which interact with a similar triple pomeron interaction. As a guiding model, we use the Balitsky–Kovchegov equation [1, 2], which sums fan diagrams with the standard BFKL pomeron and triple pomeron vertices:

$$\begin{aligned} \frac{\partial \Phi (\varvec{k},y)}{\partial y} = {\bar{\alpha }}_{s}\, (K\otimes \Phi )(\varvec{k},y) - {\bar{\alpha }}_{s}\Phi ^2(\varvec{k},y). \end{aligned}$$

(2)

Here, the linear terms describe the standard BFKL evolution in the forward direction

$$\begin{aligned} (K\otimes \Phi )(\varvec{k},y)= & {} \frac{1}{\pi }\int \frac{ d^2 \varvec{k}'}{(\varvec{k}- \varvec{k}')^2} \nonumber \\&\times \left[ \Phi (\varvec{k}',y) - \frac{k^2\Phi (\varvec{k},y)}{\varvec{k}'^2 + (\varvec{k}- \varvec{k}')^2} \right] \end{aligned}$$

(3)

and $\Phi (\varvec{k},y)=\Phi (-\varvec{k},y)$.

We develop $\Phi$ in angular momenta l, which are actually conformal spins in the conformally invariant BFKL dynamics.

$$\begin{aligned} \Phi (\varvec{k},y) = \sum _{l, even}\Phi _l(k,y)e^{il\varphi }. \end{aligned}$$

(4)

Here, $\varphi$ is the angle between $\varvec{k}$ and the fixed direction in the transverse plane. The conformal spin l goes from $-\infty$ to $+\infty$, namely $l=\cdots -4,-2,0,2,4 \ldots$ (the parity condition requires even conformal spins).

In the absence of interaction, the evolution of each angular component is given by the solution of the BFKL equation. For each l the spectrum is continuous and is characterized by the conformal parameter $\nu$ with the intercept minus unity given by

$$\begin{aligned} \mu (l,\nu )&={\bar{\alpha }}_{s}\left[ 2\psi (1)-\psi \left( \frac{1+|l|}{2}+i\nu \right) \right. \nonumber \\&\quad \left. - \psi \left( \frac{1+|l|}{2}-i\nu \right) \right] ,\ \ {\bar{\alpha }}_{s}=\frac{N_c\alpha _s}{\pi }. \end{aligned}$$

(5)

It goes down with |l| and $\nu$. For $l=0,\pm 2,\pm 4$ at $\nu =0$ one gets

$$\begin{aligned}&\mu (0,0)=4{\bar{\alpha }}_{s}\,\ln 2,\ \ \mu (2,0)=4{\bar{\alpha }}_{s}\,(\ln 2-1),\ \ \nonumber \\&\quad \mu (4,0)=4{\bar{\alpha }}_{s}\, (\ln 2-4/3). \end{aligned}$$

(6)

In units $4{\bar{\alpha }}_{s}$, the values are respectively $+0.693$, $-0.307$ and $-0.640$. Thus, only the leading pomeron with $l=0$ gives increasing amplitudes. Higher pomerons with $|l|\ge 2$ give contributions which increasingly diminish with energy as |l| increases. Still, one cannot exclude their significant contribution once the interaction is turned on and loops are taken into account.

We aim to include the first of a series of pomerons with $l=\pm 2$ in a local model in which the dependence on the momenta is neglected altogether. This is a good approximation for fans in which the momentum is dictated by the nuclear ones which are much smaller than the typical momenta in the BFKL chain. But of course this is a poor approximation for loops, so the loops we will study serve only to find and estimate their influence on fans. To build a tractable model we also neglect the continuum in the conformal parameter $\nu$ and consider only $\nu =0$. Our pomerons then include three discrete states corresponding to $l=0,\pm 2$, which we denote as $\Phi _0,\Phi _{\pm 2}$, and the free Hamiltonian is

$$\begin{aligned} H_0=-\mu _0{\Phi }^{\dagger }_0\Phi _0-\mu _2({\Phi }^{\dagger }_{-2}\Phi _2+{\Phi }^{\dagger }_{2}\Phi _{-2}). \end{aligned}$$

(7)

Here we use the notation of the conjugate momentum

$$\begin{aligned} (\Phi _2)^\dagger =\Phi ^\dagger _{-2}, \quad (\Phi _{-2})^\dagger =\Phi ^\dagger _{2}, \end{aligned}$$

which implies that the subindex $\pm 2$ actually shows the angular momentum transferred by the operator, and each term in (7) is independent of the angle. The energies $-\mu _0$ and $-\mu _2$ are taken from (6).

Now we look at the interaction. From the fan equation (2) we conclude that it has the form

$$\begin{aligned} {\bar{\alpha }}_{s}\int \frac{d^2k}{4\pi ^2}\Big (\Phi ^\dagger (\varvec{k})\Phi ^2(\varvec{k})+h.c.\Big ) , \end{aligned}$$

where h.c. is the Hermitian conjugation. For the local reggeons it passes into

$$\begin{aligned} V={\bar{\alpha }}_{s}\Big (\Phi ^\dagger \Phi ^2+\Phi {\Phi ^\dagger }^2\Big ). \end{aligned}$$

(8)

Taking

$$\begin{aligned} \Phi =\Phi _0+\Phi _2+\Phi _{-2} \end{aligned}$$

and leaving only terms with the total angular momentum zero we get (suppressing coefficient ${\bar{\alpha }}_{s}$)

$$\begin{aligned} V= & {} \Big (\Phi _0^\dagger +\Phi ^\dagger _2+\Phi ^\dagger _{-2}\Big ) \Big (\Phi _0+\Phi _2+\Phi _{-2}\Big )^2+h.c.\nonumber \\= & {} \Big (\Phi _0^\dagger +\Phi ^\dagger _2+\Phi ^\dagger _{-2}\Big ) \Big (\Phi _0^2+2\Phi _0(\Phi _2+\Phi _{-2})\nonumber \\&\qquad +2\Phi _2\Phi _{-2}\Big )+h.c.\nonumber \\= & {} \Phi _0^\dagger (\Phi _0^2+2\Phi _2\Phi _{-2})+2\Phi ^\dagger _2\Phi _{-2} \Phi _0\nonumber \\&\qquad +2\Phi ^\dagger _{-2}\Phi _2\Phi _0+h.c. \end{aligned}$$

(9)

Together with the standard nonzero commutation relations

$$\begin{aligned}{}[\Phi _0,\Phi _0^\dagger ]=[\Phi _2,\Phi ^\dagger _{-2}]=[\Phi _{-2},\Phi ^\dagger _2]=1 \end{aligned}$$

(10)

the Hamiltonian $H_0+V$ defines a local pomeron model with three pomerons having conformal spins $l=0,\pm 2$. To preserve the absorptive character of the triple interaction, we have to change the real ${\bar{\alpha }}_{s}$ to the imaginary coupling ${\bar{\alpha }}_{s}\rightarrow i\lambda$ in accordance with (1).

3 The Hamiltonian

3.1 Passage to real fields

Our Hamiltonian is the sum of the free Hamiltonian

$$\begin{aligned} H_0=-\mu _0{\Phi }^{\dagger }_0\Phi _0-\mu _2({\Phi }^{\dagger }_{-2}\Phi _2+{\Phi }^{\dagger }_{2}\Phi _{-2}) \end{aligned}$$

(11)

and the interaction

$$\begin{aligned} V= & {} \lambda \Big [\Phi _0^\dagger \Phi _0^2+2{\Phi }^{\dagger }_0\Phi _2\Phi _{-2}+2\Phi ^\dagger _2\Phi _{-2}\Phi _0+2\Phi ^\dagger _{-2}\Phi _2\Phi _0 \nonumber \\&+{{\Phi }^{\dagger }_0}^2\Phi _0+2{\Phi }^{\dagger }_2{\Phi }^{\dagger }_{-2}\Phi _0+2{\Phi }^{\dagger }_0{\Phi }^{\dagger }_2\Phi _{-2} +2{\Phi }^{\dagger }_0{\Phi }^{\dagger }_{-2}\Phi _2\Big ].\nonumber \\ \end{aligned}$$

(12)

To pass to real fields we put

$$\begin{aligned} {\Phi }^{\dagger }_0=-iu,\ \ {\Phi }^{\dagger }_2=-iw,\ \ {\Phi }^{\dagger }_{-2}=-iq,\end{aligned}$$

$$\begin{aligned} \Phi _0=-iv,\ \ \Phi _{-2}=-ix,\ \ \Phi _2=-it \end{aligned}$$

(13)

with abnormal nonzero commutation relations

$$\begin{aligned}{}[v,u]=[x,w]=[t,q]=-1 . \end{aligned}$$

(14)

In terms of these fields, the Hamiltonian becomes real

$$\begin{aligned} H_0= & {} \mu _0 uv+\mu _2(wx+qt), \end{aligned}$$

(15)

$$\begin{aligned} V= & {} -\lambda \Big [uv^2+u^2v+2uxt+2wqv+2wxv\nonumber \\&\quad +2uwx+2qtv+2uqt\Big .] \end{aligned}$$

(16)

We take the uwq representation in which the state vector is a function of u, w and q, namely F(u, w, q), and the operators v, x and t are the derivatives

$$\begin{aligned}v=-\frac{\partial }{\partial u},\ \ x=-\frac{\partial }{\partial w},\ \ t=-\frac{\partial }{\partial q} . \end{aligned}$$

Then the Hamiltonian takes the form

$$\begin{aligned} H_0= & {} -\mu _0u\frac{\partial }{\partial u}-\mu _2\Big (w\frac{\partial }{\partial w}+q\frac{\partial }{\partial q}\Big ) , \end{aligned}$$

(17)

$$\begin{aligned} V= & {} -\lambda \Big [u\frac{\partial ^2}{\partial u^2}-u^2\frac{\partial }{\partial u}+2u\frac{\partial ^2}{\partial w\partial q}-2wq\frac{\partial }{\partial u}\nonumber \\&+2w\frac{\partial ^2}{\partial w\partial u}-2uw\frac{\partial }{\partial w}+2q\frac{\partial ^2}{\partial q\partial u}-2uq\frac{\partial }{\partial q}\Big ] . \end{aligned}$$

(18)

This form can be used for the power-like or the point-like evolution.

3.2 Transition to two fields

The full Hamiltonian obviously commutes with the operator of spin

$$\begin{aligned} l=2 \left( \Phi _{2}^{+}\Phi _{-2} - \Phi _{-2}^{+}\Phi _{2} \right) . \end{aligned}$$

(19)

The conservation of angular momentum allows one to split the solution into parts with a definite value of l, each reducible to only two fields. Consider a sector with $l=2n\ge 0$. The complete basis of this sector consists of the Fock basis elements $u^k w^m q^p$ with $m-p=n$. If we introduce the new zero-spin variable $z=wq$, the basis element becomes $u^k w^n z^p$, and it is sufficient to consider the action of derivatives in w and q in the Hamiltonian on it and to express them via the derivatives in z. In particular, we evidently find

$$\begin{aligned} w\frac{\partial }{\partial w} \left( u^k w^n (wq)^p\right)= & {} (p+n)\,\left( u^k w^n (wq)^p\right) \\= & {} \left( z\frac{\partial }{\partial z} + \frac{l}{2}\right) \left( u^k w^n z^p\right) ,\\ q\frac{\partial }{\partial q} \left( u^k w^n (wq)^p\right)= & {} p\,\left( u^k w^n (wq)^p\right) = z\frac{\partial }{\partial z} \left( u^k w^n z^p\right) \\ \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2}{\partial w \partial q} \left( u^k w^n (wq)^p\right)= & {} (p+n)p\,\left( u^k w^n (wq)^{p-1}\right) \nonumber \\= & {} \left( z\frac{\partial ^2}{\partial z^2} + \frac{l+2}{2}\frac{\partial }{\partial z}\right) \left( u^k w^n z^p\right) .\nonumber \\ \end{aligned}$$

(20)

Using these formulas, we can rewrite our Hamiltonian in terms of fields u and z.

$$\begin{aligned} H_0= & {} -\mu _0 u\frac{\partial }{\partial u}-2\mu _2 z\frac{\partial }{\partial z} -\frac{l\mu _2}{2}, \end{aligned}$$

(21)

$$\begin{aligned} V= & {} -\lambda \left[ u\frac{\partial ^2}{\partial u^2}-u^2\frac{\partial }{\partial u} +l\left( \frac{\partial }{\partial u} - u\right) \right. \nonumber \\&+(l+2)u\frac{\partial }{\partial z} -2z\frac{\partial }{\partial u}+2uz\frac{\partial ^2}{\partial z^2}\nonumber \\&\left. \quad +4z\frac{\partial ^2}{\partial z\partial u}-4uz\frac{\partial }{\partial z}\right] . \end{aligned}$$

(22)

As compared to our original Hamiltonian, the term $2uz\partial ^2/\partial z^2$ appears, corresponding to the quadruple interaction absent in the original formulation.

For $l=-2n<0$, the general basis element is $u^k z^m q^n$ and the analogous consideration shows that the resulting Hamiltonians are (21) and (22), where l is substituted with $-l=|l|$. Thus the evolution proceeds similarly in the sectors $\pm l$.

One can further simplify the Hamiltonian expressing

$$\begin{aligned}z=\xi ^2.\end{aligned}$$

Then we find

$$\begin{aligned}\frac{\partial }{\partial z}=\frac{1}{2\xi }\,\frac{\partial }{\partial \xi }, \ \ z\frac{\partial }{\partial z}=\frac{1}{2}\xi \frac{\partial }{\partial \xi }\end{aligned}$$

and

$$\begin{aligned} \Big (z\frac{\partial ^2}{\partial z^2}\Big ) =\xi ^2 \frac{1}{2\xi }\frac{\partial }{\partial \xi } \Big (\frac{1}{2\xi }\frac{\partial }{\partial \xi }\Big ) =-\frac{1}{4\xi }\frac{\partial }{\partial \xi }+\frac{1}{4}\frac{\partial ^2}{\partial \xi ^2}. \end{aligned}$$

(23)

With these formulas we get

$$\begin{aligned} H_0=-\mu _0 u\frac{\partial }{\partial u}-\mu _2\xi \frac{\partial }{\partial \xi } -\frac{l\mu _2}{2} \end{aligned}$$

(24)

and

$$\begin{aligned} V= & {} -\lambda \left[ u\frac{\partial ^2}{\partial u^2}-u^2\frac{\partial }{\partial u} +l\left( \frac{\partial }{\partial u} - u\right) +\frac{(l+1)u}{2\xi }\,\frac{\partial }{\partial \xi }\right. \nonumber \\&\left. + \frac{1}{2}u\frac{\partial ^2}{\partial \xi ^2}-2\xi ^2\frac{\partial }{\partial u} +2\xi \frac{\partial ^2}{\partial u \partial \xi }-2u\xi \frac{\partial }{\partial \xi }\right] . \end{aligned}$$

(25)

Rescaling

$$\begin{aligned} \xi \rightarrow \frac{\xi }{\sqrt{2}} \end{aligned}$$

(26)

we finally get (24) for $H_0$ and

$$\begin{aligned} V= & {} -\lambda \left[ u\frac{\partial ^2}{\partial u^2}-u^2\frac{\partial }{\partial u} +l\left( \frac{\partial }{\partial u} - u\right) +\frac{(l+1)u}{\xi }\,\frac{\partial }{\partial \xi }\right. \nonumber \\&\left. + u\frac{\partial ^2}{\partial \xi ^2}-\xi ^2\frac{\partial }{\partial u} +2\xi \frac{\partial ^2}{\partial u\partial \xi }-2u\xi \frac{\partial }{\partial \xi }\right] . \end{aligned}$$

(27)

This Hamiltonian is a polynomial in variables and derivatives with the total degree not greater than three except for the term

$$\begin{aligned} V_1=-\lambda \frac{(l+1)u}{\xi }\frac{\partial }{\partial \xi } . \end{aligned}$$

(28)

Most importantly, it permits the linear transformation of fields, which eliminates the mixed second derivative.

3.3 Composite fields

The Hamiltonian (27) with fields u and $\xi$ in principle can be used for numerical studies. However, calculations based on it have a very small region of applicability. Both methods discussed in Sect. 4, the power expansion and point-like evolution, have a rather narrow region of convergence, and for the point-like evolution with the blow-up starting already at rapidities 8-9. The reason for this behaviour can be traced to the presence of the mixed second derivative $\frac{\partial ^2}{\partial u\partial \xi }$ in the Hamiltonian (27). It turns out that by suitably introducing certain linear combinations of fields u and $\xi$ (“composite operators”), one can exclude this mixed second derivative and substantially enhance the region of convergence of our numerical procedure.

We re-denote

$$\begin{aligned} u\rightarrow U,\ \frac{\partial }{\partial u}\rightarrow -V,\ \ \xi \rightarrow W,\ \ \frac{\partial }{\partial \xi }\rightarrow -Z\end{aligned}$$

with the anomalous commutators

$$\begin{aligned}=[Z,W]=-1.\end{aligned}$$

In terms of these operators,

$$\begin{aligned} H_0=\mu _0UV+\mu _2WZ-\frac{l\mu _2}{2} \end{aligned}$$

(29)

and

$$\begin{aligned} V= & {} -\lambda \Bigg [-l(U+V) +UV^2+U^2V-(l+1)\frac{U}{W}Z \Bigg .\nonumber \\&\Bigg . + UZ^2+W^2V+2WZV+2UWZ\Bigg ]. \end{aligned}$$

(30)

Now we will use the composite field operators to eliminate the mixed second derivative. We define the new operators as

$$\begin{aligned} u=\frac{U+W}{\sqrt{2}},\ \ v=\frac{V+Z}{\sqrt{2}},\ \ w=\frac{U-W}{\sqrt{2}},\ \ z=\frac{V-Z}{\sqrt{2}}.\nonumber \\ \end{aligned}$$

(31)

With (31) we get

$$\begin{aligned} V=-\sqrt{2}\lambda \Big [uv^2+u^2v+wz^2+w^2z\Big ]+V_1+V_2 \end{aligned}$$

(32)

with

$$\begin{aligned} V_1=\frac{l+1}{\sqrt{2}}\lambda \frac{u+w}{u-w}(v-z), \quad V_2=\frac{l}{\sqrt{2}}\lambda (u+w+v+z) .\nonumber \\ \end{aligned}$$

(33)

The free Hamiltonian becomes

$$\begin{aligned} H_0=\frac{1}{2}\mu _0(u+w)(v+z)+\frac{1}{2}\mu _2(u-w)(v-z) -\frac{l\mu _2}{2}.\nonumber \\ \end{aligned}$$

(34)

Here, in the (uw) representation,

$$\begin{aligned} v=-\frac{\partial }{\partial u},\ \ z=-\frac{\partial }{\partial w}\ .\end{aligned}$$

Thus, the Hamiltonian is now explicitly a sum of four terms

$$\begin{aligned} H_0= & {} -\frac{1}{2}\mu _0(u+w)\Big (\frac{\partial }{\partial u}+\frac{\partial }{\partial w}\Big )\nonumber \\&-\frac{1}{2}\mu _2(u-w) \Big (\frac{\partial }{\partial u}-\frac{\partial }{\partial w}\Big ) -\frac{l\mu _2}{2}, \end{aligned}$$

(35)

$$\begin{aligned} V_I= & {} -\sqrt{2}\lambda \left[ u\frac{\partial ^2}{\partial u^2} -u^2\frac{\partial }{\partial u}+w\frac{\partial ^2}{\partial w^2}-w^2\frac{\partial }{\partial w}\right] , \end{aligned}$$

(36)

$$\begin{aligned} V_1= & {} -\frac{l+1}{\sqrt{2}}\lambda \frac{u+w}{u-w}\Big (\frac{\partial }{\partial u}-\frac{\partial }{\partial w}\Big ) \end{aligned}$$

(37)

and

$$\begin{aligned} V_2=\frac{l}{\sqrt{2}}\lambda \left[ (u+w)-\Big (\frac{\partial }{\partial u}+\frac{\partial }{\partial w}\Big )\right] . \end{aligned}$$

(38)

We expect that in the new form the evolution becomes more stable: the mixed second derivative is absent. These expressions in the cases $l=0$ and $l=2$ will be used for the point-like evolution.

3.4 Power expansion

We present

$$\begin{aligned} F(u,w,q;y)=\sum u^iw^jq^k g_{ijk}(y),\ \ i,j,k=0,1,\ldots .\nonumber \\ \end{aligned}$$

(39)

Consider the action of different terms in the Hamiltonian $H=H_0+V$ from (17), (18) on F. We write out only the polynomials in u, w, q, omitting the common $g_{ijk}$ and the sign of summation:

$$\begin{aligned} -\mu _0u\frac{\partial }{\partial u}= & {} -\mu _0 iu^iw^jq^k,\ \ -\mu _2\Big (w\frac{\partial }{\partial w}+q\frac{\partial }{\partial q}\Big )\nonumber \\= & {} -\mu _2(j+k)u^iw^jq^k,\nonumber \\ -\lambda u\frac{\partial ^2}{\partial u^2}= & {} -\lambda i(i-1)u^{i-1}w^jq^k,\ \ +\lambda u^2\frac{\partial }{\partial u}\nonumber \\= & {} +\lambda iu^{i+1}w^jq^k,\nonumber \\ -2\lambda u\frac{\partial ^2}{\partial w\partial q}= & {} -2\lambda jk u^{i+1}w^{j-1}q^{k-1},\ \ +2\lambda wq\frac{\partial }{\partial u}\nonumber \\= & {} +2\lambda iu^{i-1}w^{j+1}q^{k+1},\nonumber \\ -2\lambda w\frac{\partial ^2}{\partial w\partial u}= & {} -2\lambda iju^{i-1}w^jq^k,\ \ +2\lambda uw\frac{\partial }{\partial w}\nonumber \\= & {} +2\lambda j u^{i+1}w^jq^k ,\nonumber \\ -2\lambda q\frac{\partial ^2}{\partial q\partial u}= & {} -2\lambda iku^{i-1}iw^jq^k,\ \ +2\lambda uq\frac{\partial }{\partial q}\nonumber \\= & {} +2\lambda k u^{i+1}w^jq^k. \end{aligned}$$

(40)

Using these results we present

$$\begin{aligned} HF(u,w,q;y)=\sum u^{i'}w^{j'}q^{k'} f_{i'j'k'}(y) . \end{aligned}$$

(41)

Our task is only to relate i, j, k with $i',j'k'$. For 10 terms in (40) we subsequently write out only these relations and the following $f_{i'j'k'}$

$$\begin{aligned} i'= & {} i,\ \ j'=j,\ \ k'=k:\ \ -\mu _0i'g_{i'j'k'},\\ i'= & {} i,\ \ j'=j,\ \ k'=k;\ \ -\mu _2(j'+k')g_{i'j'k'},\\ i'= & {} i-1,\ \ i=i'+1,\ \ j'=j,\ \ k'=k:\ \ \\&-\lambda i'(i'+1)g_{(i'+1)j'k'},\\ i'= & {} i+1,\ \ i=i'-1,\ \ j'=j,\ \ k'=k:\ \ \\&+\lambda (i'-1)g_{(i'-1)j'k'},\\ i'= & {} i+1,j'=j-1,\ \ k'=k-1,\ \ i=i'-1,\ \ \\&j=j'+1,\ \ k=k'+1:\\&-2\lambda (j'+1)(k'+1)g_{(i'-1)(j'+1)(k'+1)},\\ i'= & {} i-1,\ \ j'=j+1,\ \ k'=k+1,\ \ i=i'+1,\ \\&j=j'-1,\ \ k=k'-1:\\&+2\lambda (i'-1)g_{(i'+1)(j'-1)(k'-1)},\\ i'= & {} i-1,\ \ i=i'+1,\ \ j'=j,\ \ k'=k:\ \ \\&-2\lambda (i'+1)j'g_{(i'+1)j'k'},\\ i'= & {} i+1,\ \ i=i'-1,\ \ j'=j,\ \ k'=k:\ \ \\&+2\lambda j' g_{(i'-1)j'k'},\\ i'= & {} i-1,\ \ i=i'+1,\ \ j'=j,\ \ k'=k:\ \ \\&-2\lambda (i'+1)k'g_{(i'+1)kj'k'},\\ i'= & {} i+1,\ \ i=i'+1,\ j'=j,\ \ k'=k:\ \ \\&+2\lambda k'g_{(i'-1)j'k'}. \end{aligned}$$

Thus, in the $g_{ijk}$ representation we find $Hg=f$, where

$$\begin{aligned} f_{ijk}= & {} -\mu _0ig_{ijk}-\mu _2(j+k)g_{ijk} -\lambda i(i+1)g_{(i+1)jk}\nonumber \\&\quad +\lambda (i-1)g_{(i-1)jk}\nonumber \\&-2\lambda (j+1)(k+1)g_{(i-1)(j+1)(k+1)}\nonumber \\&\quad +2\lambda (i+1)g_{(i+1)(j-1)(k-1)}\nonumber \\&-2\lambda (i+1)jg_{(i+1)jk}+2\lambda jg_{(i-1)jk}\nonumber \\&\quad -2\lambda (i+1)kg_{(i+1)jk}+2\lambda kg_{(i-1)jk}. \end{aligned}$$

(42)

This expression is the basis for the power-like evolution.

4 Numerical results

Our numerical calculations of the propagators and amplitudes consist in solving the evolution equations in rapidity by the Runge–Kutta method starting from their values at $y=0$

$$\begin{aligned} \frac{\partial F(y)}{\partial y}=-HF(y) , \end{aligned}$$

(43)

where F(y) is the wave function at rapidity y. In fact it is a function of field variables. For instance, in variables u, w and q we have the wave function F(u, w, q; y), and the Hamiltonian is given by (17) and (18). For the point-like approach, we introduce a lattice for all field variables with N points in each variable and consider the wave function evolution on this lattice, treating all derivatives in the Hamiltonian as discretized. For power expansion, the evolving quantities are defined by (39) and the corresponding Hamiltonian determined by (42).

For the propagators, the initial values of the wave function are given by $F=u$, $F=w$ or $F=q$ for pomerons with spins 0, $+2$ and $-2$, respectively. The amplitudes are found from the same initial condition by projecting on the relevant final states as explained in [17, 19].

4.1 Propagators

With three fields $\Phi _0$, $\Phi _{+2}$ and $\Phi _{-2}$ numerical evolution both by power expansion and by points turns out to be possible only for a limited interval of rapidities $0<y<y_{max}$, beyond which evolution breaks down. In our power expansion we limited the powers of u, w and q by the maximal number 20 to perform evolution in a reasonable amount of time. The resulting maximal rapidity turned out to lie in the region 14-15. Remarkably, this restriction is the same as with the pure Gribov model without any extra field. This is clearly seen in Fig. 1, where we show the results found by power expansion both with three fields (the lower curve) and with only the main pomeron $l=0$ (the upper curve). As expected, the extra loops with pomerons $l=\pm 2$ bring the propagator further down, the drop growing with rapidity.

Fig. 1

The propagator of the pomeron $l=0$ at different rapidities found by power expansion with three pomerons $l=0,\pm 2$ (lower curve) and without subdominant pomerons of $l=\pm 2$ (upper curve). $\mu _0=0.12$, $\mu _2=-0.0531$, ${\bar{\alpha }}_{s}= 0.0433$

Fig. 2

The propagator of the pomeron $l=0$ at different rapidities with three pomerons $l=0,\pm 2$ obtained by power expansion (middle curve), direct point-like evolution (lower curve) and two-field point-like evolution with composite fields (upper curve). $\mu _0=0.12$, $\mu _2=-0.0531$, ${\bar{\alpha }}_{s}= 0.0433$

The point-like evolution of course gives practically identical results with the Hamiltonians (17) and (18) with three fields and (21) and (22) for $l=0$ with two fields (using $N=400$ points), although the processor time is naturally much shorter with two fields. In both cases for the point-like evolution, convergence is the same and considerably worse than for the power-like expansion. The maximal rapidity goes down to 8-9, above which the evolution breaks down. This is a new phenomenon, absent for a single pomeron, where evolution is possible to very high rapidities. Presumably this effect is due to the presence of the mixed second derivatives in the Hamiltonians. Numerically, the propagator obtained by the point-like evolution is somewhat smaller (in the convergence interval) than the one obtained by power expansion. This is illustrated in the bottom curve in Fig. 2 in comparison with the power-like evolution shown by the middle curve.

Passage to composite fields, and thus elimination of the mixed derivative, improves evolution dramatically and makes it possible in a wide interval of rapidity up to very large rapidities. The results found for the main pomeron propagator by this method are shown in the same Fig. 2 by the upper curve and separately in Fig. 3 for a wider interval of y together with the results found without the subdominant pomerons.

Fig. 3

The propagator of the pomeron $l=0$ at different rapidities with three pomerons $l=0,\pm 2$ obtained by two-field point-like evolution with composite fields (lower curve) and without the subdominant pomerons (middle curve). $\mu _0=0.12$, $\mu _2=-0.0531$, ${\bar{\alpha }}_{s}= 0.0433$. The upper curve corresponds to the free propagator $\exp (0.12 y)$

In relation to Figs. 1 and 2, we have to note that the precision of the power expansion decreases with the increase in $\lambda$. From our previous experience [19], the value $\lambda =0.0433$ used in our calculations lies quite close to the convergence border $\lambda =0.04$. To illustrate this point, in Fig. 4 we compare the results found by power expansion and point-like evolution with composite fields at a considerably smaller value ${\bar{\alpha }}_{s}=0.01$. One can observe nearly complete agreement.

Fig. 4

The propagator of the pomeron $l=0$ at different rapidities with three pomerons $l=0,\pm 2$ obtained by power expansion (upper curve) and two-field point-like evolution with composite fields (lower curve) with a smaller coupling constant ${\bar{\alpha }}_{s}=0.01$ and the same $\mu _0=0.12$ and $\mu _2=-0.0531$

Fig. 5

The propagator of the subdominant pomeron $l=2$ at different rapidities with three pomerons $l=0,\pm 2$ obtained by power evolution (middle curve) and two-field point-like evolution with composite fields (lower curve). $\mu _0=0.12$, $\mu _2=-0.0531$, ${\bar{\alpha }}_{s}= 0.0433$. The upper curve corresponds to the free propagator $\exp (-0.0531 y)$

For the subdominant pomerons, we are met with certain problems. For $l=2$, the power expansion works as for the main pomeron, but the point-like evolution with composite fields converges only when the number of variable points does not exceed $N=260$. For larger N, evolution breaks down already at $y=3$. In the region of convergence, the power expansion and point-like evolution with composite field give practically identical results up to $y\sim 12$, starting from which point the power expansion blows up, which apparently shows the breakdown of convergence. This is illustrated in Fig. 5. Note that loops diminish the propagator with $l=2$ in the same way as with $l=0$, as follows compared with the upper curve in Fig. 5.

4.2 Amplitude

Our amplitude depends on the initial and final coupling constants for the pomerons. To couple the pomeron with $l=\pm 2$ to hadrons, one should assume that they possess some quadrupole moment. For spherical hadrons the quadrupole moment is absent, and for any hadrons it should be very small. Thus we neglect the coupling of pomerons with $l=\pm 2$ to nucleons, and our amplitude will take them into account only in the loops.

To calculate the amplitude we have to know the two coupling constants of the principal pomeron with $l=0$, $g_{ini}$ for the incoming hadron (proton) and $g_{fin}$ for the final amplitude. The latter corresponds to the coupling to the nucleon inside the nucleus. The corresponding fan diagram describes the amplitude at fixed impact parameter b and is equal to [18]

$$\begin{aligned} {{\mathcal {A}}}_A(y,b)=\frac{g_{ini}g_{fin}(A,b)e^{\mu y}}{1+\lambda g_{fin}(A,b)\frac{e^{\mu y}-1}{\mu }}. \end{aligned}$$

(44)

The final coupling constant depends on the atomic number A and impact parameter b. For simplicity we assume that the nucleus is a sphere of radius $R_A=A^{1/3}R_0$. Therefore, for collisions with the nucleus, $g_{fin}\propto \theta (R_A-b)$ and does not depend on b as soon as $b<R_A$. As to A dependence, it is natural to assume (see also [18]) that $g_{fin}\propto A^{1/3}$. So in the end we take

$$\begin{aligned} g_{fin}=A^{1/3}g_{ini}\theta (R_A-b). \end{aligned}$$

(45)

The fan amplitude of hA interaction obtained after integration over b becomes

$$\begin{aligned} {{\mathcal {A}}}_A(y)=\pi A R_0^2\frac{g_{ini}^2 e^{\mu y}}{1+\lambda A^{1/3}g_{ini}\frac{e^{\mu y}-1}{\mu }}. \end{aligned}$$

(46)

With a small $\lambda$ at comparatively low energies $\mu y\sim 1$, we find for the scattering on the nucleus

$$\begin{aligned} {{\mathcal {A}}}_A(y)=\pi A R_0^2g_{ini}^2 e^{\mu y},\ \ \lambda e^{\mu y}\ll 1 \end{aligned}$$

(47)

(single pomeron exchange). For the scattering on the proton we assume that one has to put $A=1$ and change the nuclear radius $R_A$ to the proton radius $R_p$. In this way, at comparatively low energies with the proton target one gets

$$\begin{aligned} {{\mathcal {A}}}_{pp}(y)=\pi R_p^2g_{ini}^2 e^{\mu y},\ \ \lambda e^{\mu y}\ll 1. \end{aligned}$$

(48)

We can use this formula to fix the value of $g_{ini}$. At $s=100$ $\hbox {GeV}^2$, the cross-section (which is just ${{\mathcal {A}}}$ in our normalization) is approximately equal 40 mbn = 4 fm$^2$. At this energy, $y_0=\ln (s/s_0)=4.6$, where we take $s_0=1$ Gev$^2$. We also take $R_p=0.8$ fm. With these values and taking $\mu =0.12$

$$\begin{aligned} g_{ini}^2&=\frac{{{\mathcal {A}}}_{pp}(4.6)e^{-\mu y_0}}{\pi R_p^2}\nonumber \\&=\frac{4*e^{-0.12*4.6}}{\pi *0.64}=1.144,\ \ g_{ini}=1.069. \end{aligned}$$

(49)

From the fan diagrams we can conclude that the effective coupling constant in the interaction with nuclei is actually given by $\lambda g_{ini}A^{1/3}$ and so grows with A. Thus, passing to the diagrams with loops we expect that in the power expansion, convergence will be poorer with the growth of A. Calculations show that this is indeed the case. In Fig. 6 we show the cross-sections for the scattering on beryllium ($A=9$) found by the power expansion and point-like evolution with composite operators. The two curves corresponding to the power expansion refer to direct expansion and expansion of the inverse amplitude. In both cases we observe a breakdown of convergence at $y\sim 7.7$ (slightly higher for the expansion of the inverse amplitude). The situation for heavier nuclear targets shows even worse convergence for the power expansion.

Fig. 6

The hBe cross-sections calculated by power expansion (the leftmost curve), power expansion of the inverse amplitude (the curve shifted slightly to the right) and point-like evolution with composite operators (the smooth upper curve). $\mu _0=0.12$, $\mu _2=-0.0531$, ${\bar{\alpha }}_{s}= 0.0433$

Fig. 7

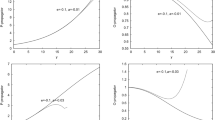
The y-dependence of the hA cross-sections calculated by point-like evolution with composite operators (the lower curves), without the subdominant pomerons $l=\pm 2$ (the middle curves) and without loops (fan diagrams, the upper curves). Panels correspond to the scattering on aluminium (upper left), copper (upper right), silver (bottom left) and gold (bottom right). In all cases $\mu _0=0.12$, $\mu _2=-0.0531$, ${\bar{\alpha }}_{s}= 0.0433$

Because of this, our results for the hA cross-sections presented in the following figure refer to constructive calculations by the point-like evolution with composite operators. We separate dimensionful factor $\sigma _A(y=0)=\pi R_0^2 A$ carrying the bulk of the A dependence and present the ratio

$$\begin{aligned} R(y)=\frac{\sigma _A(y)}{\sigma _A(y=0)} \end{aligned}$$

(50)

showing the energy dependence of the cross-sections. To illustrate the influence of the subdominant pomerons and loops in general, we also present the results obtained with only the dominant pomeron $l=0$ and without loops (fan diagrams). As we see in all cases, the loops diminish the amplitude, and the effect of the subdominant pomerons acts in the same direction as that of the dominant one (Fig. 7).

5 Conclusions

We constructed a local pomeron model in the one-dimensional transverse world with three interacting pomerons of conformal spins 0 and 2 and phenomenological intercepts and coupling. Evolution in rapidity was studied numerically. It was found that direct evolution from the Hamiltonian of the three fields is only possible in a restricted interval of rapidities below $y\sim 6-12$ due to divergence. This obstacle was overcome by passage to two effective fields separately for sectors with $l=0$ and $l=2$. Transition to composite fields then allows evolution in a wider interval, up to $y=20$ considered in the calculations.

The resulting propagators and hA amplitudes were found to be smaller than without subdominant pomerons with $l=2$ and, as expected, without any loops at all. Thus the subdominant loops were found to act in the same direction as the dominant ones corresponding to $l=0$. This result shows the difference between the pomeron with signature $+1$ and the odderon with signature $-1$. The odderon loops in contrast act in the opposite direction and enhance both the propagators and amplitudes [19].