Abstract
We consider higher-order QCD corrections to the production of high-mass systems in hadron collisions within the transverse-momentum (\(q_T\)) subtraction formalism. We present a method to consistently remove the linear power corrections in \(q_T\) which appears when fiducial kinematical cuts are applied on the final state system. We consider explicitly the case of fiducial cross sections for Drell–Yan lepton pair production at the Large Hadron Collider up to next-to-next-to-next-to-leading order (N\(^3\)LO) in QCD. We have implemented our method within the DYTurbo numerical program and we have obtained perturbative predictions which are in agreement at the permille level with those obtained with local subtraction formalisms up to the next-to-next-to-leading order (NNLO). At the N\(^3\)LO we are able to provide predictions for fiducial cross sections with numerical accuracy at the permille level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Hard scattering processes at high-energy colliders, such as the Large Hadron Collider (LHC), characterized by large scales of energy (M) transferred, allows us to probe the dynamics of fundamental interactions at short distances. In this regime, theoretical predictions for cross sections can be evaluated with perturbative techniques. In particular accurate results require the inclusion of the dominant effects from strong interactions through the calculation of the higher-order terms in Quantum Chromodynamics (QCD) as a series expansion in the coupling \(\alpha _S(M)\). In order to match the experimental kinematical cuts on the measured final states, it is essential to obtain predictions for fiducial cross sections and corresponding differential distributions.
The computation of higher-order QCD corrections at fully-differential level is complicated by the presence of infrared singularities at intermediate stage of the calculation which prevents a direct implementation of numerical techniques and enforce the use of an hybrid analytic and numerical approach. At the next-to-leading order (NLO) general subtraction algorithms, which exploit the universality properties of soft and collinear emissions in QCD, have been developed [1,2,3,4]. These methods have been successfully implemented in general purpose Monte Carlo programs which satisfy the needs for the analysis of experimental data. Beyond the NLO, a widely used extension of the subtraction method is the so called transverse-momentum (\(q_T\)) subtraction formalism originally proposed in Ref. [5]. In fact, thanks to its relative simplicity and generality, the method has been successfully applied to fully differential QCD calculations for several hard-scattering processes at the next-to-next-to-leading order (NNLO) (see Ref. [6] and references therein) and, more recently, also at the next-to-next-to-next-to-leading order N\(^3\)LO [7,8,9].
In the case of the \(q_T\) subtraction formalism, a source of numerical uncertainty which is particularly difficult to quantify in a robust way is due to the unphysical power corrections of the type \({\mathcal {O}}(q_T^{\mathrm{cut}}/M)\), where \(q_T^{\mathrm{cut}}\) is the technical parameter necessary to separate the \(q_T\) resolved and unresolved parton emissions. Power corrections ambiguities are particularly severe in the case of fiducial selection cuts which yield an acceptance that has a linear dependence on \(q_T^{\mathrm{cut}}\) [10,11,12]. In principle the effect of these perturbative power corrections can be reduced setting the value of the technical parameter \(q_T^{\mathrm{cut}}\) sufficiently small. However, very small values of \(q_T^{\mathrm{cut}}\) require an extremely precise numerical control of cross sections in the infrared region \(q_T\rightarrow 0\) which are typically very challenging and time consuming.
In the case of the production of colourless high mass systems, sufficiently inclusive cross sections (such as total cross section in absence of fiducial selection cuts) computed within the \(q_T\) subtraction method have a residual dependence on \(q_T^{\mathrm{cut}}\) of order \({\mathcal {O}}((q_T^{\mathrm{cut}}/M)^2)\) originated from the integration of the corresponding scattering amplitudes over the final state kinematics in the small \(q_T\) region [13, 14]. In the case of the production of coloured systems the residual dependence on \(q_T^{\mathrm{cut}}\) is linear even in absence of fiducial cuts [15,16,17]. In this case, in order to remove the linear power corrections in \(q_T^{\mathrm{cut}}\), it is necessary to take care of both the dependence related to the fiducial selection cuts and the dependence which is present at the inclusive level.
Linear fiducial power corrections have been connected with alternating sign factorial growth of the perturbative expansion in Ref. [18] and modifications of the selection cuts typically used in experimental analysis have been proposed in order to eliminate the linear dependence of the acceptance. In Ref. [19], an experimental procedure has been proposed to remove from cross section measurements the effect of selection cuts which are responsible for linear fiducial power corrections. In Ref. [11] it has been shown that linear fiducial power corrections can be consistently removed through the \(q_T\) resummation formalism, if the \(q_T\) recoil due to multi-parton emission is correctly taken into account. Nevertheless fixed-order calculations have a great relevance in precision physics at colliders: they can be computed (in principle) in a definite and unambiguous way, and they are an essential ingredient for all-order resummed predictions. Therefore the goal of having at disposal fixed-order calculations at high numerical accuracy is very relevant, regardless of the effective physical precision of such predictions.
In this paper we consider standard fixed-order calculations and we discuss a method to remove linear fiducial power corrections (FPC) within the \(q_T\) subtraction formalism. Our method, which is equivalent to the one proposed in Ref. [11] based on a Lorentz decomposition for hadronic and leptonic tensors, introduces an additional subtraction exploiting the recoil procedure of Ref. [20] and it allows us to obtain fiducial fixed-order predictions with a residual uncertainty of the type \({\mathcal {O}}((q_T^{\mathrm{cut}}/M)^2)\) which can be brought down at sub-permille level. We stress that in this paper we are dealing with the linear power corrections to the \(q_T\) subtraction formalism [5] by using the subtraction counterterms related to the specific \(q_T\) resummation formalism of Refs. [21, 22] and to the use of the class of recoil prescriptions which were introduced in Ref. [20]. Therefore the strict validity of our results and the novelty with respect to the previous results in the literature [8, 11] are related to the particular implementation of the subtraction procedure within the formalism of Refs. [20,21,22].
Our results turn out to be crucial in the case of the N\(^3\)LO extension of the \(q_T\) subtraction formalism [7, 9] where it is particularly challenging to obtain precise perturbative predictions for very small values of \(q_T^{\mathrm{cut}}\).
We consider explicitly the case of fiducial cross sections for Drell–Yan lepton pair production at the Large Hadron Collider up to the N\(^3\)LO in QCD. We have implemented our method within the DYTurbo [23] numerical program and we have obtained perturbative predictions which are in agreement at permille level with those obtained with local subtraction formalism at NLO and NNLO.
We consider the hard-scattering process
where \(F_i\) denotes the (colourless) final states with momenta \(q_i\) produced by the colliding hadrons \(h_1\) and \(h_2\) which we collectively identify as the system F(q), with momentum \(q=\sum _i q_i\), invariant mass \(M=\sqrt{q^2}\) and transverse momentum \(q_T\).
We start from the master formula of the \(q_T\) subtraction formalism for the hadronic cross section [5]
where \(\sigma ^{F}_{LO}\) is the Born level cross section, \({\mathcal {H}}^F(\alpha _S)\) is the process-dependent hard-collinear function [24, 25] with the following perturbative expansion
\(d\sigma ^{\mathrm{CT}}\) is the subtraction counter-term [21]
and the symbol \(\otimes \) stands for convolutions over momentum fractions and sum over flavour indices of the partons. The second term in the r.h.s. of Eq. (2), \(d\sigma ^{{\mathrm{F}}+{\mathrm{jets}}}\), is the differential cross section for the production of F(q) in association with jets and it has to be evaluated at the previous perturbative order with respect to \(d\sigma ^{\mathrm{F}}\). The subtraction counter-term \(d\sigma ^{\mathrm{CT}}\) has the same singular behaviour of \(d\sigma ^{{\mathrm{F}}+{\mathrm{jets}}}\) in the limit \(q_T \rightarrow 0\) which functional form is known from the \(q_T\) resummation formalism [21, 22].
The terms \(d\sigma ^{{\mathrm{F}}+{\mathrm{jets}}}\) and \(d\sigma ^{\mathrm{CT}}\) in Eq. (2) are separately divergent due to infrared singularities at \(q_T=0\) and a technical parameter \(q_T^{\mathrm{cut}}\) has to be introduced. For \(q_T^{\mathrm{cut}}>0\) the sum of the terms in the square bracket of Eq. (2) is IR finite (or, more precisely, integrable over \(q_T\)) and it should be evaluated in the limit \(q_T^{\mathrm{cut}}\rightarrow 0\) to obtain the “exact” (free form residual \(q_T^{\mathrm{cut}}\) dependence) value of the cross section. However for finite value of \(q_T^{\mathrm{cut}}\) the cross section in Eq. (2) contains power corrections \({\mathcal {O}}((q_T^{\mathrm{cut}}/M)^p)\), with \(p>0\) [10]. The exact value of the exponent p depends by the cuts on the final states which define the fiducial cross section
we thus have
In Ref. [12] has been shown that, in the case of Drell–Yan lepton pair production, typical cuts on the transverse momenta and rapidities of the final state particles \(F_i(q_i)\) leads to linear power corrections (\(p=1\)), which corresponding systematic uncertainty may spoil the accuracy of fixed-order calculations within the \(q_T\) subtraction formalism.
Clearly the effect of perturbative power corrections \({\mathcal {O}}((q_T^{\mathrm{cut}}/M)^p)\) can be reduced setting the value of the technical parameter \(q_T^{\mathrm{cut}}\) sufficiently small. However, very small values of \(q_T^{\mathrm{cut}}\) lead to large cancellations among the terms in the square bracket of the r.h.s. of Eq. (2), which in turns give rise to larger numerical integration uncertainties. These cancellations are particularly challenging at NNLO and N\(^3\)LO where the precise knowledge of the fully differential calculations of F in association with jets at NLO and NNLO is respectively required. Eventually a trade-off between the systematical and statistical uncertainties of the computation have to be found and, more importantly, a robust systematic uncertainty to the missing perturbative power corrections has to be computed. The systematic uncertainty can be estimated by evaluating the cross section at different values of \(q_T^{\mathrm{cut}}\) and carrying out a \(q_T^{\mathrm{cut}}\rightarrow 0\) extrapolation [6]. This is not a trivial task due to the large numerical uncertainties associated to the \(q_T^{\mathrm{cut}}\rightarrow 0\) limit.
We now discuss the method which enable us to consistently remove the FPC within the \(q_T\) subtraction formalism thus leaving a quadratic residual uncertainty \({\mathcal {O}}(({q_T^{\mathrm{cut}}}/M)^2\)). The starting point is the observation that the FPC have a kinematical origin [10,11,12]. They are generated by the selection cuts on the final state particles and they are indeed absent in fixed-order [10, 14, 26, 27] or \(q_T\) resummed calculations inclusive over the final state F decay products [28] and also in the case of \(q_T\) resummation with fiducial cuts when the \(q_T\) recoil due to multi-parton emission is correctly taken into account [11]. According to the \(q_T\) resummation formalism of Refs. [21, 22] the fiducial cross section in Eq. (6) can be schematically written in the following form:
where
and
The first term on the r.h.s. of Eq. (9) is the resummed component of the cross section which collects in the generalized form factor \(\exp {({\mathcal {G}}(\alpha _S))}\) and resums to all orders (in the Fourier–Bessel conjugated impact-parameter b space) the enhanced logarithmic corrections of the type \(\alpha _S^n\ln ^m (M^2/q_T^2)\) which are present in the transverse momentum distribution at small \(q_T\) [21]. The second term on the r.h.s. of Eq. (9) is the fixed-order finite component of the cross section and \(q_T^{\mathrm{cut}}\) represents the minimum value of \(q_T\) used to compute such term. In the resummed formula in Eq. (7) the underlying amplitude of the Born level cross-section \(d{\widetilde{\sigma }}^F_{LO}\), which enters also in the term \(d\widetilde{\sigma }^{\mathrm{CT}}\), differs from the corresponding quantity \(d{\hat{\sigma }}^{(0)}\) in Eqs. (2) and (4) for the fact that it is not evaluated with the leading order (LO) kinematics but following the prescription introduced in Appendix A of Ref. [20], which takes into account the \(q_T\) recoil originated from the multiple radiation of soft and collinear partons in a kinematically consistent way.
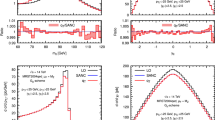
Fiducial cross section for the production of \(l^+ l^-\) pairs from \(Z/\gamma ^*\) decay at the LHC (\(\sqrt{s}=13\) TeV). NLO results with the \(q_T\) subtraction method (blue squared points) and \(q_T\) subtraction method without FPC (red circled points) at various values of \(q_T^{\mathrm{cut}}\), and with a local subtraction method (black line). Error bars indicate the statistical uncertainties from Monte Carlo numerical integration
Exploiting the resummation formula in Eq. (7) we are thus able to construct the following modified \(q_T\) subtraction formula which is free from linear fiducial power corrections [8, 11]:
where
The inclusion of the additional term \(d\sigma ^{\mathrm{FPC}}\) for \(q_T<q_T^{\mathrm{cut}}\) allows us to produce the correct behavior of the fiducial cross section up to quadratic power corrections in \(q_T^{\mathrm{cut}}\). The terms \(d\sigma ^{{CT}}\) and \(d\widetilde{\sigma }^{{CT}}\) differ for the fact that they are respectively evaluated with the LO (\(q_T = 0\)) and with the recoil (\(q_T \ne 0\)) kinematics. We note that the term \(d\sigma ^{\mathrm{FPC}}\) is universal (i.e. process independent) and it is IR finite (albeit the two terms on the r.h.s. of Eq. (11) are separately divergent). Furthermore the contribution of \(d\sigma ^{\mathrm{FPC}}\) can be treated as a local subtraction: the difference of the terms in Eq. (11) is evaluated pointwise at integrand level and therefore the integration for \(q_T<q_T^{\mathrm{cut}}\) can be extended up to (virtually) arbitrary small value of \(q_T\). In the current numerical implementation [29] we extended the \(q_T\) integration of the term \(d\sigma ^{\mathrm{FPC}}\) down to \(q_T/M \sim 10^{-6}\) GeV (this value is comparable with the typical technical cuts used in local subtraction methods).
We have encoded the formula in Eq. (10), by using the recoil prescription of Ref. [20],Footnote 1 in the public numerical program DYTurbo [23] which implements the \(q_T\) subtraction formalism for Drell–Yan processes. We stress that within our method we are able to correctly remove the linear fiducial power corrections which originates from a mismatch between the real and the counterterm (Born-like) kinematics in the standard implementation of the \(q_T\) subtraction method. In this way the inclusion of fiducial selection cuts does not introduce additional linear power corrections in \(q_T^{\mathrm{cut}}\) with respect to the ones present at inclusive level. Moreover, within our numerical implementation in DYTurbo, we are able to confirm numerically, up to the N\(^3\)LO, that our method correctly removes the linear power corrections and to quantify the residual systematic uncertainty from the \(q_T^{\mathrm{cut}}\) technical parameter in the Drell–Yan fiducial cross section.
We consider the production of \(l^+ l^-\) pairs from \(Z/\gamma ^*\) decay at the LHC (\(\sqrt{s}=13\) TeV) with the following fiducial cuts [31]: the leptons are required to have transverse momentum \(p_T>25\) GeV, pseudo-rapidity \(|\eta |<2.5\) while the lepton pair system is required to have invariant mass \(66<M<116\) GeV and transverse momentum \(q_T < 100\) GeV. We use parton densities functions (PDFs) from the NNPDF3.1 set [32] at NNLO with \(\alpha _S(m_Z^2)=0.118\), and we have evaluated \(\alpha _S(\mu _R^2)\) at \((n+1)\)-loop order at N\(^n\)LO accuracy. Factorization and renormalization scales have been set to \(\mu _F=\mu _R= \sqrt{M^2+q_T^2}\). We use the so called \(G_\mu \) scheme for EW couplings with input parameters \(G_F = 1.1663787\times 10^{-5}\) GeV\(^{-2}\), \(m_Z = 91.1876\) GeV, \(\Gamma _Z=2.4952\) GeV, \(m_W = 80.379\) GeV [31]. We then computed the fiducial cross section for the Drell–Yan process at the LHC with the original \(q_T\) subtraction formula Eq. (2) and with the improved formula Eq. (10).
Fiducial cross section for the production of \(l^+ l^-\) pairs from \(Z/\gamma ^*\) decay at the LHC (\(\sqrt{s}=13\) TeV). NLO results with the \(q_T\) subtraction method (blue squared points) and the \(q_T\) subtraction without FPC (red circled points) at various values of \(q_T^{\mathrm{cut}}\), and with a local subtraction method (black line). Error bars indicate the statistical uncertainties from Monte Carlo numerical integration
The results presented in this paper have been obtained by including the hard-collinear functions (see Eq. (3)) from Refs. [24, 33,34,35,36] while the \(\mathrm{Z+jets}\) results have been obtained from Refs. [31, 37, 38]. The counter-term in Eq. (4) have been obtained by analytic expansion of the resummation formula of Ref. [21] using the coefficients calculated in Refs. [39, 40]
In Fig. 1 we show the NLO fiducial cross section calculated for different values of the \(q_T^{\mathrm{cut}}\) technical parameter with the original \(q_T\) subtraction method (blue squared points) and with the modified formula in Eq. (10) (labeled as recoil \(q_T\) subtraction, red circled points). As a reference, we also show the result obtained with a local subtraction formalism (black line) which represents the exact (free from significant systematic uncertainties) prediction. The local result is obtained independently with the dipole subtraction formalism [1, 2] as implemented in MCFM [41,42,43]. Error bars in Fig. 1 indicate the statistical uncertainties from Monte Carlo numerical integration which turns out to be completely negligible. From Fig. 1 we observe that the systematic uncertainty (defined as the deviation from the local subtraction result) of the original \(q_T\) subtraction results increase linearly with \(q_T^{\mathrm{cut}}\) and it is around \(0.3\%\) at \(q_T^{\mathrm{cut}}=0.5\) GeV, \(0.6\%\) at \(q_T^{\mathrm{cut}}=1\) GeV, \(1\%\) at \(q_T^{\mathrm{cut}}=2\) GeV and \(2\%\) at \(q_T^{\mathrm{cut}}=4\) GeV. In order to obtain a systematic uncertainty below \(0.1\%\) level a calculation with \(q_T^{\mathrm{cut}}\lesssim 0.1\) GeV is necessary. Conversely the results obtained with the \(q_T\) subtraction without FPC have a systematic uncertainty for \(q_T^{\mathrm{cut}}=1\) GeV which is smaller than the statistical uncertainty of the local-subtraction result, which is \(0.01\%\). In Fig. 1 an interpolation of the \(q_T^{\mathrm{cut}}\) dependence of the modified (original) \(q_T\)-subtraction obtained with quadratic (linear and quadratic) terms is represented by the red dashed (blue solid) line.
In Fig. 2 we show the fiducial cross section at NNLO with the original \(q_T\) subtraction method (blue squared points) and with the modified formula in Eq. (10) (red circled points) together with the result obtained with a local subtraction formalism (black line). The local result is obtained with the sector improved subtraction formalism [44, 45] as implemented in FEWZ [46, 47]. Error bars in Fig. 2 indicate the statistical uncertainties from Monte Carlo numerical integration. Statistical uncertainties are at the level of \(0.1\%\) for the local subtraction results and at the level of \(0.1\%\) or larger (smaller) for the \(q_T\) subtraction results with \(q_T^{\mathrm{cut}}\lesssim 0.1\) GeV (\(q_T^{\mathrm{cut}} > rsim 0.1\) GeV). The \(q_T^{\mathrm{cut}}\) systematic uncertainty of the \(q_T\) subtraction results is around \(0.3\%\) at \(q_T^{\mathrm{cut}}=0.5\) GeV, \(0.6\%\) at \(q_T^{\mathrm{cut}}=1\) GeV and \(0.7\%\) at \(q_T^{\mathrm{cut}}=2\) GeV and \(0.2\%\) at \(q_T^{\mathrm{cut}}=4\) GeV. As in the case of the NLO results, in order to obtain a systematic uncertainty below \(0.1\%\) level a calculation with \(q_T^{\mathrm{cut}}\lesssim 0.1\) GeV is necessary. However this is exactly the IR region where large cancellations give rise to sizable statistical uncertainties due to numerical integration. Conversely the results obtained with the \(q_T\) subtraction without FPC have a systematic uncertainty which is smaller than \(0.04\%\) for \(q_T^{\mathrm{cut}}=1\) GeV. As in Fig. 1 also in Fig. 2 we have shown an interpolation of the \(q_T^{\mathrm{cut}}\) dependence of the results.
Finally, in Fig. 3 we show the fiducial cross section at N\(^3\)LO with the original \(q_T\) subtraction method (blue squared points) and with the modified formula in Eq. (10) (red circled points) for different values of \(q_T^{\mathrm{cut}}\) with the interpolation of the results as in Figs. 1 and 2. No local subtraction results are available at this perturbative order. Moreover in this case we are not able to show results for \(q_T^{\mathrm{cut}}< 4\) GeV. In fact we have checked that our analytic expression for the counter-term \(d\widetilde{\sigma }^{\mathrm{CT}}\) agrees with the small-\(q_T\) limit of the NNLO fixed-order results for the production of a \(Z/\gamma ^*\) boson in association with jets reported in Ref. [31] at permille level down to \(q_T\sim 4\) GeV while below that threshold such agreement deteriorates.
We observe, in the case of the \(q_T\) subtraction without FPC, a strong reduction of the dependence from \(q_T^{\mathrm{cut}}\) also at the N\(^3\)LO and we have quantified the residual \(q_T^{\mathrm{cut}}\) dependence by performing an extrapolation fit of the subleading power corrections at NLO, NNLO and N\(^3\)LO. We performed an interpolation fit for \(q_T>q_T^{\mathrm{cut}}\) of the known structure of subleading power corrections [8, 14, 26] and we estimated the uncertainty on the extrapolated cross section for \(q_T^{\mathrm{cut}} \rightarrow 0\). The interpolation curves have been shown in Figs. 1, 2 and 3. The uncertainty on the extrapolated results is below \(0.01\%\) level at the NLO and NNLO (interpolation range \(0.05 \le q_T^{\mathrm{cut}} \le 20 \) GeV) and of \(0.18\%\) at the N\(^3\)LO (interpolation range \(4 \le q_T^{\mathrm{cut}} \le 20 \) GeV).Footnote 2 At the NLO and NNLO, this uncertainty is smaller than statistical errors of our results, which is consistent with the agreement between our predictions and the local results reported in Table 1. In the N\(^3\)LO case the interpolation convergence is less good and we obtain an uncertainty on the extrapolated cross section which is of the same order of the statistical error quoted in Table 2.
In order to quantify the impact of the calculated fiducial power corrections, we show in Fig. 4 the contribution of the FPC (Eq. (10)) as a function of \(q_T^{\mathrm{cut}}\). First of all we observe that the sign of the FPC contribution changes from \({\mathcal {O}}(\alpha _S)\) to \({\mathcal {O}}(\alpha _S^2)\) and from \({\mathcal {O}}(\alpha _S^2)\) to \({\mathcal {O}}(\alpha _S^3)\). This behaviour is consistent with the observation that linear power corrections in the small \(q_T\) region (produced by the fiducial cuts) results in an alternating-sign factorial growth of the fixed-order perturbative series [18]. The second observation is that the impact of the FPC is not numerically reduced at higher orders and it turn out to be particularly sizable at N\(^3\)LO up to very small value of \(q_T^{\mathrm{cut}}\): for \(q_T^{\mathrm{cut}}= 0.05\) GeV the impact of the N\(^3\)LO FPC is about \(-0.4\%\) and it is the result of a \(+0.3\%\) contribution at \({\mathcal {O}}(\alpha _S^2)\) and a \(-0.7\%\) at \({\mathcal {O}}(\alpha _S^3)\) (the \({\mathcal {O}}(\alpha _S)\) FPC contribution turns out to be negligible at \(q_T^{\mathrm{cut}}= 0.05\) GeV). This means that when standard selection cuts are implemented within the original \(q_T\) subtraction, a permille level systematic accuracy for NNLO and N\(^3\)LO fiducial cross sections cannot be easily reached even with extremely low values of \(q_T^{\mathrm{cut}}\).
In Table 1 we report the predictions for the cross section in the fiducial region at NLO and NNLO with the \(q_T\) subtraction method for \(q_T^{\mathrm{cut}}= 0.5\) GeV and \(q_T^{\mathrm{cut}}= 1\) GeV, with the recoil \(q_T\) subtraction for \(q_T^{\mathrm{cut}}= 1\) GeV and we compare with the local subtraction results.Footnote 3 Errors indicate the statistical uncertainties from Monte Carlo numerical integration. In the case of the recoil \(q_T\) subtraction the results are nearly independent by \(q_T^{\mathrm{cut}}\) for \(q_T^{\mathrm{cut}}\lesssim {\mathcal {O}}\)(GeV).
From the results of Table 1 we observe that the differences between the recoil \(q_T\) subtraction results and the local subtraction results are of \({\mathcal {O}}(0.01\%)\). Thus the modified \(q_T\) subtraction formula in Eq. (10) allows us to obtain accurate permille level predictions for fiducial cross section with values of \(q_T^{\mathrm{cut}}\sim {\mathcal {O}}\)(GeV).
In Table 2 we report the predictions for the cross section in the fiducial region at N\(^3\)LO with the \(q_T\) subtraction method and with the recoil \(q_T\) subtraction for \(q_T^{\mathrm{cut}}= 4\) GeV. Local subtraction results are not available at this order.
From the results shown in Fig. 4 we could expect that a value of \(q_T^{\mathrm{cut}}\sim 4\) GeV is associated with a systematic uncertainty due to the FPC of around \(2\%\), which is of the same order of the size of the \(\alpha _S^3\) corrections and thus challenge the reliability of the \(q_T\) subtraction results.Footnote 4 However the cancellation of the alternating sign linear fiducial power corrections shown Fig. 4 makes the impact of the N\(^3\)LO FPC for the particular value of \(q_T^{\mathrm{cut}}= 4\) GeV to be around \(0.2\%\) which is indeed the difference between the \(q_T\) subtraction and recoil \(q_T\) subtraction results reported in Table 2.
We finally note that any numerical implementation of the subtraction method, including the local versions, contains and depends on various technical parameters necessary to avoid the numerical evaluation of singular points. These parameters cannot be arbitrarily large and their actual value has to be chosen in order to make the numerical result independent (within the required numerical accuracy) from their actual value. From this viewpoint the independence by \(q_T^{\mathrm{cut}}\) observed within our method is similar to the one observed in the local version of the subtraction method.
In this paper we have considered higher-order QCD corrections to the production of high-mass systems in hadron collisions within the \(q_T\) subtraction formalism. We have presented a method to consistently remove the linear power corrections in \(q_T\) of the type \({\mathcal {O}}(q_T^{\mathrm{cut}}/M)\), where \(q_T^{\mathrm{cut}}\) is the technical parameter necessary to separate resolved and unresolved parton emission regions, which appears when fiducial kinematical cuts are applied on the final state system. As a first application we have implemented our method within the DYTurbo numerical program and we have considered explicitly the case of fiducial cross sections for \(Z/\gamma ^*\) boson production at the LHC up to N\(^3\)LO in QCD. We have obtained perturbative predictions which are in excellent (permille level) agreement with those obtained with local subtraction formalism at NLO and NNLO and we have computed N\(^3\)LO predictions with a residual \(q_T^{\mathrm{cut}}\) systematic uncertainty at the permille level.
Our results can be helpful in increasing the numerical precision of the existing numerical codes based on the \(q_T\) subtraction formalism and also on improving their time performances. In particular we were able to remove the source of systematic uncertainty at the origin of the discrepancies observed in Ref. [12]. Moreover our method is particularly important in the cases where fully local perturbative calculations for cross section are not available or when large numerical integration uncertainties are associated to the \(q_T\rightarrow 0\) limit such as in the case of N\(^3\)LO predictions in hadron collisions.
Finally, we make some observations about some consequences of our findings on resummed calculations. Our results show that resummed fiducial cross sections calculated by correctly taking into account the \(q_T\) recoil effects [20] (e.g. the resummed cross sections calculated in Ref. [9]) are free from significant numerical systematic uncertainties due to the minimum value of \(q_T\) used to compute the finite component of the cross section in Eq. (9). Moreover our results show that the matching between the resummed and finite (fixed-order) calculations in the small \(q_T\) region has an impact of \({\mathcal {O}}((q_T/M)^2)\) and it is expected to have a very small (negligible) effect for \(q_T/M\lesssim {\mathcal {O}}(10^{-1})\) (\(q_T/M\lesssim {\mathcal {O}}(10^{-2})\)).
DataAvailability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and has no associated experimental data.]
Notes
In particular within the class of \(q_T\)-recoil prescriptions introduced in Ref. [20] we use the choice defined by setting the transverse momentum of the colliding partons equal to \(q_{T}/2\), which corresponds to evaluate the Born level cross-section in Eq. (9) in the Collins–Soper rest frame [30].
We note that at N\(^3\)LO the difference between the cross section with \(q_T^{\mathrm{cut}} = 4\) GeV and the cross section extrapolated for \(q_T^{\mathrm{cut}} = 0\) is smaller than the uncertainty on the extrapolated result.
Since the numerical code FEWZ does not allow to set \(\mu _F=\mu _R= \sqrt{M^2+q_T^2}\) the NNLO local result has been obtained with \(\mu _F=\mu _R= M\). We have estimated the effect of the different scales with DYTurbo and it turn out to be at the level of 0.5 pb. This effect has been included in the numerical uncertainty.
To reduce such uncertainty at the few permille level in Ref. [9] the value of \(q_T^{\mathrm{cut}}\sim 4\) GeV have been used for the \(\alpha _S^3\) terms only with a lower value of \(q_T^{\mathrm{cut}}\sim 0.5\) GeV for the \(\alpha _S\) and \(\alpha _S^2\) contributions.
References
S. Catani, M.H. Seymour, Phys. Lett. B 378, 287–301 (1996). https://doi.org/10.1016/0370-2693(96)00425-XarXiv:hep-ph/9602277
S. Catani , M.H. Seymour, Nucl. Phys. B 485, 291–419 (1997). [Erratum: Nucl. Phys. B 510, 503–504 (1998)] https://doi.org/10.1016/S0550-3213(96)00589-5. arXiv:hep-ph/9605323
S. Frixione, Z. Kunszt, A. Signer, Nucl. Phys. B 467, 399–442 (1996). https://doi.org/10.1016/0550-3213(96)00110-1arXiv:hep-ph/9512328
S. Frixione, Nucl. Phys. B 507, 295–314 (1997). https://doi.org/10.1016/S0550-3213(97)00574-9arXiv:hep-ph/9706545
S. Catani, M. Grazzini, Phys. Rev. Lett. 98, 222002 (2007). https://doi.org/10.1103/PhysRevLett.98.222002arXiv:hep-ph/0703012
M. Grazzini, S. Kallweit, M. Wiesemann, Eur. Phys. J. C 78(7), 537 (2018). https://doi.org/10.1140/epjc/s10052-018-5771-7arXiv:1711.06631 [hep-ph]
L. Cieri, X. Chen, T. Gehrmann, E.W.N. Glover, A. Huss, JHEP 02, 096 (2019). https://doi.org/10.1007/JHEP02(2019)096arXiv:1807.11501 [hep-ph]
G. Billis, B. Dehnadi, M.A. Ebert, J.K.L. Michel, F.J. Tackmann, Phys. Rev. Lett. 127(7), 072001 (2021). https://doi.org/10.1103/PhysRevLett.127.072001arXiv:2102.08039 [hep-ph]
S. Camarda, L. Cieri, G. Ferrera, Phys. Rev. D 104(11), L111503 (2021). https://doi.org/10.1103/PhysRevD.104.L111503arXiv:2103.04974 [hep-ph]
M.A. Ebert, F.J. Tackmann, JHEP 03, 158 (2020). https://doi.org/10.1007/JHEP03(2020)158arXiv:1911.08486 [hep-ph]
M.A. Ebert, J.K.L. Michel, I.W. Stewart, F.J. Tackmann, JHEP 04, 102 (2021). https://doi.org/10.1007/JHEP04(2021)102arXiv:2006.11382 [hep-ph]
S. Alekhin, A. Kardos, S. Moch, Z. Trócsányi, Eur. Phys. J. C 81(7), 573 (2021). https://doi.org/10.1140/epjc/s10052-021-09361-9arXiv:2104.02400 [hep-ph]
I. Moult, L. Rothen, I.W. Stewart, F.J. Tackmann, H.X. Zhu, Phys. Rev. D 95(7), 074023 (2017). https://doi.org/10.1103/PhysRevD.95.074023arXiv:1612.00450 [hep-ph]
L. Cieri, C. Oleari, M. Rocco, Eur. Phys. J. C 79(10), 852 (2019). https://doi.org/10.1140/epjc/s10052-019-7361-8arXiv:1906.09044 [hep-ph]
S. Catani, M. Grazzini, A. Torre, Nucl. Phys. B 890, 518–538 (2014). https://doi.org/10.1016/j.nuclphysb.2014.11.019arXiv:1408.4564 [hep-ph]
R. Bonciani, S. Catani, M. Grazzini, H. Sargsyan, A. Torre, Eur. Phys. J. C 75(12), 581 (2015). https://doi.org/10.1140/epjc/s10052-015-3793-yarXiv:1508.03585 [hep-ph]
L. Buonocore, M. Grazzini, F. Tramontano, Eur. Phys. J. C 80(3), 254 (2020). https://doi.org/10.1140/epjc/s10052-020-7815-zarXiv:1911.10166 [hep-ph]
G.P. Salam, E. Slade, JHEP 11, 220 (2021). https://doi.org/10.1007/JHEP11(2021)220arXiv:2106.08329 [hep-ph]
A. Glazov, Eur. Phys. J. C 80(9), 875 (2020). https://doi.org/10.1140/epjc/s10052-020-08435-4arXiv:2001.02933 [hep-ex]
S. Catani, D. de Florian, G. Ferrera, M. Grazzini, JHEP 12, 047 (2015). https://doi.org/10.1007/JHEP12(2015)047arXiv:1507.06937 [hep-ph]
G. Bozzi, S. Catani, D. de Florian, M. Grazzini, Nucl. Phys. B 737, 73–120 (2006). https://doi.org/10.1016/j.nuclphysb.2005.12.022arXiv:hep-ph/0508068
S. Catani, D. de Florian, M. Grazzini, Nucl. Phys. B 596, 299–312 (2001). https://doi.org/10.1016/S0550-3213(00)00617-9arXiv:hep-ph/0008184
S. Camarda, M. Boonekamp, G. Bozzi, S. Catani, L. Cieri, J. Cuth, G. Ferrera, D. de Florian, A. Glazov , M. Grazzini et al., Eur. Phys. J. C 80(3), 251 (2020). https://doi.org/10.1140/epjc/s10052-020-7757-5. arXiv:1910.07049 [hep-ph] [Erratum: Eur. Phys. J. C 80(5), 440 (2020)]
S. Catani, L. Cieri, D. de Florian, G. Ferrera, M. Grazzini, Eur. Phys. J. C 72, 2195 (2012). https://doi.org/10.1140/epjc/s10052-012-2195-7arXiv:1209.0158 [hep-ph]
S. Catani, L. Cieri, D. de Florian, G. Ferrera, M. Grazzini, Nucl. Phys. B 881, 414–443 (2014). https://doi.org/10.1016/j.nuclphysb.2014.02.011
M.A. Ebert, I. Moult, I.W. Stewart, F.J. Tackmann, G. Vita, H.X. Zhu, JHEP 04, 123 (2019). https://doi.org/10.1007/JHEP04(2019)123arXiv:1812.08189 [hep-ph]
C. Oleari, M. Rocco, Eur. Phys. J. C 81(2), 183 (2021). https://doi.org/10.1140/epjc/s10052-021-08878-3arXiv:2012.10538 [hep-ph]
I. Balitsky, A. Tarasov, JHEP 05, 150 (2018). https://doi.org/10.1007/JHEP05(2018)150arXiv:1712.09389 [hep-ph]
J. Ablinger, J. Blümlein, M. Round, C. Schneider, Comput. Phys. Commun. 240, 189–201 (2019). https://doi.org/10.1016/j.cpc.2019.02.005arXiv:1809.07084 [hep-ph]
J.C. Collins, D.E. Soper, Phys. Rev. D 16, 2219 (1977). https://doi.org/10.1103/PhysRevD.16.2219
W. Bizon, A. Gehrmann-De Ridder, T. Gehrmann, N. Glover, A. Huss, P.F. Monni, E. Re, L. Rottoli, D.M. Walker, Eur. Phys. J. C 79(10), 868 (2019). https://doi.org/10.1140/epjc/s10052-019-7324-0arXiv:1905.05171 [hep-ph]
R.D. Ball et al. (NNPDF), Eur. Phys. J. C 77(10), 663 (2017). https://doi.org/10.1140/epjc/s10052-017-5199-5. arXiv:1706.00428 [hep-ph]
T. Gehrmann, T. Lubbert, L.L. Yang, Phys. Rev. Lett. 109, 242003 (2012). https://doi.org/10.1103/PhysRevLett.109.242003arXiv:1209.0682 [hep-ph]
M.X. Luo, T.Z. Yang, H.X. Zhu , Y.J. Zhu, Phys. Rev. Lett. 124(9), 092001 (2020). https://doi.org/10.1103/PhysRevLett.124.092001. arXiv:1912.05778 [hep-ph]
M.A. Ebert, B. Mistlberger, G. Vita, JHEP 09, 146 (2020). https://doi.org/10.1007/JHEP09(2020)146arXiv:2006.05329 [hep-ph]
G. Billis, M.A. Ebert, J.K.L. Michel, F.J. Tackmann, Eur. Phys. J. Plus 136(2), 214 (2021). https://doi.org/10.1140/epjp/s13360-021-01155-yarXiv:1909.00811 [hep-ph]
J.M. Campbell, R.K. Ellis, Nucl. Phys. B Proc. Suppl. 205–206, 10–15 (2010). https://doi.org/10.1016/j.nuclphysbps.2010.08.011. arXiv:1007.3492 [hep-ph]
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, A. Huss, D.M. Walker, Phys. Rev. Lett. 120)(12), 122001 (2018). https://doi.org/10.1103/PhysRevLett.120.122001. arXiv:1712.07543 [hep-ph]
Y. Li, H.X. Zhu, Phys. Rev. Lett. 118(2), 022004 (2017). https://doi.org/10.1103/PhysRevLett.118.022004arXiv:1604.01404 [hep-ph]
A.A. Vladimirov, Phys. Rev. Lett. 118(6), 062001 (2017). https://doi.org/10.1103/PhysRevLett.118.062001arXiv:1610.05791 [hep-ph]
J.M. Campbell, R.K. Ellis, Phys. Rev. D 60, 113006 (1999). https://doi.org/10.1103/PhysRevD.60.113006arXiv:hep-ph/9905386
J.M. Campbell, R.K. Ellis, C. Williams, JHEP 07, 018 (2011). https://doi.org/10.1007/JHEP07(2011)018arXiv:1105.0020 [hep-ph]
J.M. Campbell, R.K. Ellis, W.T. Giele, Eur. Phys. J. C 75(6), 246 (2015). https://doi.org/10.1140/epjc/s10052-015-3461-2arXiv:1503.06182 [physics.comp-ph]
C. Anastasiou, K. Melnikov, F. Petriello, Phys. Rev. D 69, 076010 (2004). https://doi.org/10.1103/PhysRevD.69.076010arXiv:hep-ph/0311311
C. Anastasiou, L.J. Dixon, K. Melnikov, F. Petriello, Phys. Rev. D 69, 094008 (2004). https://doi.org/10.1103/PhysRevD.69.094008arXiv:hep-ph/0312266
K. Melnikov, F. Petriello, Phys. Rev. D 74, 114017 (2006). https://doi.org/10.1103/PhysRevD.74.114017arXiv:hep-ph/0609070
Y. Li, F. Petriello, Phys. Rev. D 86, 094034 (2012). https://doi.org/10.1103/PhysRevD.86.094034arXiv:1208.5967 [hep-ph]
L. Buonocore, S. Kallweit, L. Rottoli, M. Wiesemann, Phys. Lett. B 829, 137118 (2022). https://doi.org/10.1016/j.physletb.2022.137118arXiv:2111.13661 [hep-ph]
Acknowledgements
We gratefully acknowledge Stefano Catani and Massimiliano Grazzini for useful discussions and comments on the manuscript and Alessandro Guida and Simone Amoroso for extensive tests of the numerical code. LC is supported by the Generalitat Valenciana (Spain) through the plan GenT program (CIDEGENT/2020/011) and his work is supported by the Spanish Government (Agencia Estatal de Investigación) and ERDF funds from European Commission (Grant no. PID2020-114473GB-I00 funded by MCIN/AEI/10.13039/ 501100011033). Note added: An equivalent method to include linear fiducial power corrections in the \(q_T\) subtraction formalism has been contemporarily presented in Ref. [48].
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Camarda, S., Cieri, L. & Ferrera, G. Fiducial perturbative power corrections within the \(\mathbf{q}_T\) subtraction formalism. Eur. Phys. J. C 82, 575 (2022). https://doi.org/10.1140/epjc/s10052-022-10510-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10510-x