1 Introduction

The Bekenstein–Hawking [2, 3] black hole entropy formula in conjunction with the holographic principle [4, 5] suggest that a region of space surrounded by a boundary surface of finite area, should be described by a finite dimensional Hilbert space. It is not known how such an holographic description works, except then in few notable cases. In the context of AdS/CFT [6], despite a large amounts of results, several relevant questions related to black holes cannot be cast in quantitative terms, due to the complexity of the boundary theory at finite temperature.

A manifestation of the black hole information problem in holographic models [7] appears in the behavior of correlation functions of boundary operators at very large separation times. Finiteness of the entropy demands that a correlation function cannot decay to zero at large times, since this would violate quantum mechanics in the form of quantum information loss. For the sake of illustration, let us consider a thermal two point function for a boundary operator \({\hat{O}}(t)\)

$$\begin{aligned} G_{\beta }(t)= & {} \frac{1}{Z(\beta )} Tr \left( e^{-\frac{\beta }{2} H} {\hat{O}}(t) e^{-\frac{\beta }{2} H} {\hat{O}}(0)\right) \nonumber \\= & {} \frac{1}{Z(\beta )} \sum _{m, n} e^{- \left( \frac{\beta }{2} - it\right) E_{n}} e^{- \left( \frac{\beta }{2} + it\right) E_{m}} | \langle n | {\hat{O}} | m \rangle |^{2}, \end{aligned}$$
(1)

where \(Z(\beta )\) is the thermal partition function, the dimension of the Hilbert space is finite and exponentially large in the entropy and we omit to denote dependence of \({\hat{O}}\) on spacial coordinates. At early times \(G_{\beta }(t)\) decays exponentially in time as the effect of thermalization, which in the bulk corresponds to the black hole quasi-normal modes relaxation. However, the finite sum in (1) cannot not go to zero at large times, instead it keeps oscillating with an amplitude exponentially small in the entropy [8,9,10]. On the other hand, the above requirement is not satisfied by a semiclassical bulk theory. The reflection coefficient for an incoming wavepacket scattered from the black hole classical horizon diminishes with boundary time, because of the increasing blueshift of the scattered particle, with an increasing penetrating power beyond the horizon of its wave function. From this intuitive argument, one expects the two point function to go to zero in the separation time infinite limit, which is indeed the case. This process is described by black hole quasi normal modes [11]. On the other hand, one expects a departure from classical dynamics for the black hole horizon at times exponentially large in the entropy, when discreteness of the spectrum of the black hole microstates becomes relevant. This effect should conspire to reproduce the expected erratic fluctuations in the two point function. This is a non perturbative quantum gravity effect that is hard to be reproduced. It is interesting to study this problem in the SYK model, as its collective mode describes the dynamics of a boundary graviton in a nearly two dimensional anti de Sitter spacetime (\(nAdS_2\)), which accounts for the dynamics of the horizon of a low temperature nearly extremal black hole in four dimensions.

The above formulation of the black hole information paradox in an holographic setup can be rephrased in terms of a somehow simpler and more universal correlation function then (1), which does not contain matrix elements of specific boundary operators \(| \langle n | {\hat{O}} | m \rangle |^{2}\) but still exhibits the same phenomenon [12]. This is the so called spectral form factor

$$\begin{aligned} |Z(\beta , t)|^2= & {} Z(\beta -it)Z(\beta + it) \nonumber \\= & {} \sum _{m,n} e^{-\beta (E_n + E_m )} e^{it (E_n - E_m ) }. \end{aligned}$$
(2)

While at short times \(|Z(\beta , t)|^2\) is of the order of the square of the thermal partition function \(Z(\beta )^{2}\), at very long times, of the order of the inverse of the mean energy level spacing, the spectral form factor reaches a limiting value \(Z(2 \beta )\) usually called the plateau, due to a cancellation between the off diagonal contributions in the sum (2). A direct computation at large times of the spectral form factor in theories with a well defined gravity dual such as super Yang Mills is currently impossible. However, the Sachdev–Ye-Kitaev model (SYK) [13,14,15,16,17,18,19] offers both a numerical and an analytic handle for studying the spectral form factor. An accurate numerical analysis of the SYK spectral form factor was done in [20], (see also [21] for earlier related work), while a subsequent work [1] explains part of the observed behavior in terms of a large N collective fields description.

SYK is a statistical mechanics model over an ensemble of quantum mechanical many body systems of Majorana fermions, with random couplings of even order \(q \ge 4\) all to all interactions. A statistical average over an ensemble of quantum systems is not equivalent to a single quantum mechanical model, a fact that may cast doubts upon using SYK for discussing delicate issues like unitarity in a black hole holographic description. Yet, there are qualitative and quantitative features that survive the ensemble disorder average that make SYK an interesting playground for discussing certain quantum gravity issues related to black holes.Footnote 1

SYK has a collective fields description that in the large N limit at low temperatures/strong coupling exhibits an interesting quasi conformal behavior, with aspects of a gravity dual. In particular, as an holographic model for nearly extremal black holes it provides an interesting arena for testing various ideas and proposals and sharpen open problems. One of its attractive features is a dominant soft mode dynamics at low temperatures [13, 14, 23, 24], that from a bulk perspective encodes the full black hole gravitational backreaction [25,26,27,28], and, under certain circumstances, allows for a quantum mechanical description of a black hole interior [28,29,30,31,32,33]. One of the exciting recent results, that is understood also from the SYK perspective, is a gravitational description of the quantum teleportation protocol [28, 34, 35]. This is based on recent observations on how certain double trace deformations that violate the average null energy condition make a wormhole temporarily traversable [36]. In the teleportation protocol those double trace deformations implement the transmission of classical instruction for the quantum protocol between the two boundaries through external space-time and make the wormhole connecting them temporarily traversable.

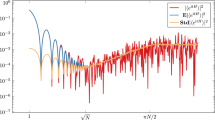
Another interesting feature is that SYK exhibits quantum chaotic behavior both at short and long times scales. At short times scales, out of time ordered (OTO) four point thermal correlators involving a perturbation on a typical operator saturate [13, 14, 37] a universal chaos bound [38] for their Liapunov exponent. In AdS/CFT, saturation of the chaos bound in the boundary is understood [39] by a corresponding bulk near horizon scattering dynamics that involves Dray and ’t Hooft shock waves [40]. The requirement for the boundary theory to be a fast scrambler [41] avoids black hole quantum cloning in certain gedanken experiments [5, 42]. The fast scrambler property is satisfied by boundary theories that are q-local quantum many body systems with all to all interactions [41]. In the SYK case there are no shock waves in the two dimensional bulk and the only bulk gravitational degrees of freedom are boundary modes that undergo classical chaotic dynamics by moving in hyperbolic space [25, 28, 43, 44]. On the other hand, SYK exhibits also chaotic behavior at large time scales,Footnote 2 related to the fine details of correlations among its energy eighenvalues. The connected part of the two point correlation function for the SYK spectral density controls the large time behavior of the spectral form factor, a quantity of interest to diagnose the existence of quantum information loss. Numerics on the SYK spectral form factor exhibit the emergence at long time scalesFootnote 3 of typical behaviour of quantum chaotic systems, in particular random matrix theory (RMT) universality. We refer to [20] for relevant numerical plots and typical values of the SYK spectral form factor, here we would like to mention the main qualitative features of the time behavior of the spectral form factor. The plot in Fig. 1, starts at early times with a decaying phase from its initial value \(Z(\beta )^2\) with a characteristic decreasing power law up to a minimum value. This decaying part of the plot is called the slope and the minimum value is called the dip, which occurs at \(t_{dip} \sim e^{N / 2}\). After the dip, the SFF starts a linear rising behavior called the ramp. The ramp occurs up to a saturation time \(t_{plateu} \sim e^{N}\) where \(|Z(\beta , T)|^2\) reaches the limiting value \(Z(2\beta )\). The ramp and the plateau are typical of quantum chaotic systems in particular in random matrix theory(RMT). The emergence of RMT universality in itself is not surprising from a Hilbert space perspective, the interest, motivated by the black hole information problem, is to understand the behavior of the spectral form factor by using a large N collective fields description. This problem was discussed in [1] for the SYK model and by the same authors in [45] for Jackiw Teitelboim (JT) gravity [46, 47], where a non perturbative completion of JT gravity in terms of RMT is proposed. In [48] the relations between JT gravity and RMT are extended to the case where the boundary theory has time-reversal symmetry and have fermions with or without supersymmetry.

Fig. 1
figure 1

A log–log plot [20] of the SYK spectral form factor for \(q = 4\), \(N = 34\), \(\beta J = 5\). In red the time plot for a single realization of the disorder, wild erratic oscillations are quite visible in the ramp and the plateau parts of the plot. Oscillations are washed out by disorder average over a large enough number of samples without tough throwing away the main trend. Statistical average (in black) still exhibits an interested lack of information loss in the form of a random matrix universality. The black plot refers to numerics from an ensemble of 90 samples [20]

Full size image

An interesting point that emerges from the numerics on the SYK spectral form factor is that for a single realization of the disorder, the time plot exhibits erratic oscillations in its ramp and plateau regions, (Fig. 1). Oscillations are washed out either by averaging SYK over a large enough ensemble or by taking a suitable time average of the spectral form factor. Although part of the information that corresponds to the erratic wild oscillations is washed out by the disorder average, the main trend that does not exhibit information loss is still present after ensemble average. This provides an interest for a quantitative study of the SYK spectral form factor in terms of large N collective fields, in relation to the black hole information paradox.

It is easy to check that the connected part of the disorder averaged two point function for the analytically continued thermal partition function

$$\begin{aligned} \langle Z(\beta + iT) Z(\beta - iT) \rangle _{c}\equiv & {} \langle Z(\beta + iT) Z(\beta - iT) \rangle \nonumber \\&- \langle Z(\beta + iT) \rangle \langle Z(\beta - iT) \rangle \nonumber \\= & {} \int dE dE' \, \langle \rho (E) \rho (E') \rangle _{c} \, \nonumber \\&\times e^{- \beta (E + E')} e^{iT(E -E')} \end{aligned}$$
(3)

exhibits a linear ramp for a contribution of the form \(\langle \rho (E) \rho (E') \rangle _{c} \sim \frac{1}{(E - E')^{2}} \) in the connected component of the two point correlator for the spectral density of states \(\rho (E)\). In the above expression brackets in the l.h.s. denote disorder average, while brackets in the r.h.s. denotes statistical correlation. It is indeed the disorder average over a statistical ensemble that provides a non zero connected component \(\langle Z(\beta + iT) Z(\beta - iT) \rangle _{c}\) to the analytically continued partition function. In a single quantum mechanical model the partition function is just a number and there would be no two points connected contributions whatsoever. The above relation indicates that in order to study the connected component of the spectral form factor, in terms of a functional integral in collective fields, one should look to a two replica system. In fact, disorder average creates interactions between distinct replica, which leads to a connected component for the spectral form factor. Another indication that the non decaying contributions for the SYK spectral form factor may be understood by a two replica systems may come from the ER = EPR conjecture [7, 49, 50]. Indeed, it turns out [1] that the family of off replica diagonal saddle points responsible for the SYK ramp are obtained with good approximation from a sum over images of SYK correlators on the thermofield double state. On the other hand, from the JT gravity side, the ramp is reproduced by a JT double trumpet instanton [45], a connected Euclidean baby universe that connects two identical Euclidean black holes at the same temperature.

In this paper we derive a time reparametrization soft modes effective action that corrects the SYK critical (replica non-diagonal) saddles of the spectral form factor (3). This effective action governs the late times dynamics for the spectral form factor. We follow a method inspired by [26] to study enhanced responses to the conformal breaking kinetic operator in SYK. This two sides Schwarzian effective action that we obtain, appear also in [1]. In that work, the form of the effective action was guessed by indirect reasoning, supported by numerical evidence [51]. On the other hand, we carry on a constructive analysis by outlining the dominant quantum effects that correct the spectral form factor correlation functions at late times. Our results as a byproduct allow to obtain an explicit derivation of the late times effective action. A point of interest of the analysis carried here is a direct observation of when and how non Schwarzian contributions to the effective action become ineffective for the spectral form factor. This kind of analysis has also some interesting points of contact with the recently appeared work [52].

The organization of the paper is the following, in Sect. 2 we go through the construction of a two replica functional integral for the SYK spectral form factor, by going into details in the derivation of the replica non-diagonal conformal saddles. In Sect. 3 we compute a large N approximation for the spectral form factor by steepest descent method, around conformal replica non-diagonal saddles. We then analyse the effects of a smeared version of the two replica kinetic operator and single out that a specific projection of the kinetic operator dominates the late dynamics of the spectral form factor. In section 4 we compute the soft modes effective action for the spectral form factor that governs the late times dynamics. In appendix, we review the method presented in [26] for the case of regular SYK.

2 Two replica path integral representation for the connected part of the spectral form factor

The Sachdev–Ye-Kitaev model (SYK) [13,14,15,16,17,18,19] is a statistical mechanics model over an ensemble of many body systems given by N (even) Majorana fermions \(\psi _i = \psi _i ^{\dag }\)

$$\begin{aligned} \{ \psi _i , \psi _j \} = \delta _{ij}, \end{aligned}$$
(4)

on a complete hypergraph of even order \(q \ge 4\). Each system of the ensemble has Hamiltonian

$$\begin{aligned} H = \frac{(i)^{\frac{q}{2}}}{q!} \sum _{i_1 \dots i_q} J_{i_1 \dots i_q} \psi _{i_1} \dots \psi _{i_q}, \end{aligned}$$
(5)

where the couplings \(J_{i_1, \dots , i_q}\) are random variables, independently taken from a Gaussian probability distribution with zero mean \( \langle J_{i_1, \dots , i_q} \rangle = 0\) and variance \( \langle J_{i_1, \dots , i_q}^2 \rangle = J^2/ N^{q-1}\). The parameter J fixes the characteristic energy scales of the model. In the large N limit, at high temperatures/weak coupling \(\beta J<< 1\), the model is asymptotically free, while at low temperatures/strong coupling \(\beta J>> 1\), SYK develops an interesting quasi-conformal dynamics. Conformal symmetry is slightly explicitly broken by a dominant \(O\left( \frac{\beta J}{N}\right) \) corrections, with leading contribution coming from a local Schwarzian effective action. The same pattern of symmetry breaking and a Schwarzian effective action occur in a certain limit of two dimensional Jackiw–Teitelboim (JT) gravity. Moreover, JT gravity describes the classical dynamics of the near horizon region of a low temperature nearly extremal black hole. In the following we mainly focus on the \(q=4\) case, extensions of the results for generic even q are usually straightforward.Footnote 4

We consider the following connected contribution to the SYK disorder averaged analytically continued thermal partition function two point correlator

$$\begin{aligned} \langle Z(\beta - iT )Z(\beta + iT) \rangle _{c}\equiv & {} \langle Z(\beta - iT )Z(\beta + iT) \rangle \nonumber \\&\quad - \langle Z(\beta - iT ) \rangle \langle Z(\beta + iT) \rangle , \nonumber \\ \end{aligned}$$
(6)

where brackets denote disorder average. As already remarked in the introduction, in order to have a non vanishing connected component we shall look for a system of two replicas on which to perform disorder average. In fact, disorder average creates an interaction among non interacting replica. By following [1] we construct a functional integral representation for \(\langle Z(\beta - iT )Z(\beta + iT) \rangle _{c}\) in terms of two copies or replica of SYK, \(SYK_{L}\) and \(SYK_{R}\). We consider the following two replica representation for the spectral form factor for one particular realization of the disorder

$$\begin{aligned} Z(\beta - iT)Z(\beta + iT)= & {} Tr \left( e^{- (\beta - iT)H_L } e^{- (\beta + iT)H_R } \right) \nonumber \\= & {} Tr \left( e^{-T \left( J_L H_L + J_R H_R \right) } \right) \end{aligned}$$
(7)

where

$$\begin{aligned} H_{I} = - \frac{1}{4!} \sum _{i,j,k,l} J_{ijkl} \psi _{i}^{I}\psi _{j}^{I} \psi _{k}^{I}\psi _{l}^{I}, \qquad I=L,R \end{aligned}$$
(8)

and

$$\begin{aligned} J_L = \frac{\beta }{T} - i, \qquad J_R = \frac{\beta }{T} + i = J_{L}^{*}. \end{aligned}$$
(9)

The parametrization employed in Eq. (7) requires Euclidean time with fermions antiperiodic by T.

By disorder averaging (7) one finds the following path integral representation

$$\begin{aligned}&\langle Z(\beta + iT) Z(\beta - iT) \rangle _{c} \nonumber \\&\quad = \int {\mathcal {D}} \psi _i^{I} \exp \left( - \int _{0}^{T} d \tau \psi _{i}^{I} (\tau ) \partial _{\tau } \psi _{i}^{I} (\tau ) \right. \nonumber \\&\qquad \left. + \frac{N J^2 J_{I}J_{J}}{8} \int _{0}^{T} d \tau d \tau ' \left( \frac{1}{N} \psi _{i}^{I}(\tau ) \psi _{i}^{J}(\tau ')\right) ^{4} \right) , \end{aligned}$$
(10)

where replica indexes \(I,J = L,R \) are summed up.

The above connected component has to be contrasted with the disconnected part of the two point function \(\langle Z_{SYK}(\beta - iT ) \rangle \langle Z_{SYK}(\beta + iT) \rangle \), obtained by the standard SYK disorder averaged thermal partition function \(\langle Z_{SYK}(\beta ) \rangle \) by analytic continuation \(\beta \rightarrow \beta \pm iT\). \(\langle Z_{SYK}(\beta ) \rangle \) can be computed at full quantum level in the Schwarzian approximation, since the Schwarzian path integral over soft modes is one loop exact [54]. This same result for \(\langle Z_{SYK}(\beta ) \rangle \) can also be obtained by solving a quantum mechanical problem for a particle scattered by a Liouville potential [55, 56]. Accurate methods for computing Schwarzian amplitudes at full quantum level are developed in [57, 58]. The full quantum answer is given by

$$\begin{aligned} \langle Z_{SYK}(\beta ) \rangle \sim \frac{e^{+ \frac{\alpha _{S}}{{\mathcal {J}}} \frac{2\pi ^2}{\beta }}}{({\mathcal {J}}\beta )^{3/2}}, \end{aligned}$$
(11)

which gives the following disconnected contribution to the spectral form factor

$$\begin{aligned} \langle Z_{SYK}(\beta + iT ) \rangle \langle Z_{SYK}(\beta - iT) \rangle \sim \frac{e^{\frac{\alpha _{S}}{{\mathcal {J}}} \frac{4\pi ^2 \beta }{\beta ^2 + T^2 }}}{({\mathcal {J}}^{3/2} (\beta ^{2} + T^{2})^{3/2}}. \nonumber \\ \end{aligned}$$
(12)

This disconnected contribution reproduces accurately the decaying slope of the spectral form factor in Fig. 1. It is not surprising that this contribution manifests information loss, since it is given by a product of analytic continuations of the SYK thermal partition function. From the two replica system perspective, it is the result of a replica diagonal saddle plus the one loop determinant from fluctuations, that together give the full quantum answer. In contrast, the connected contribution from off diagonal replica saddle is somehow related to a purification of the thermal density matrix, obtained by doubling the system. Indeed it turns out that the connected saddles can be written in terms of an antisymmetrized version of the thermofield double correlators [1], (see Eq. (35) and related discussion).

Concerning the functional integral in (10), before switching from the representation in terms of Majorana fermions to a more convenient description in terms of O(N) singlets collective fields, let us notice that in any regime where the effects of the bilocal kinetic operator in (10)

$$\begin{aligned} {\hat{\sigma }}_{IJ}(\tau , \tau ') \equiv \delta _{IJ} \delta (\tau - \tau ') \partial _{\tau } \end{aligned}$$
(13)

can be neglected, the eight fermions interaction vertex in (10) is invariant under the following transformation

$$\begin{aligned}&\varPsi _{i}^{I}(\tau _{I}) \rightarrow \left( f_{I}'(\tau _{I})\right) ^{\varDelta }\varPsi _{i}^{I}(f_{I}(\tau _{I})),\nonumber \\&\qquad \varDelta = \frac{1}{4}, \qquad I=L,R, \end{aligned}$$
(14)

for two independent time reparametrization diffeomorphisms, (aka left and right soft modes), \(f_{I}(\tau _{I})\), \(I=L,R\). In fact, it can be checked easily that this transformation corresponds to a change of integration variables in the double integral interaction term in (10). Therefore in any regime where \({\hat{\sigma }}_{IJ}(\tau , \tau ')\) (13) can be neglected, the system develops the time reparametrization symmetry (14), where fermions are primary fields of weight \(\varDelta = \frac{1}{4}\). Let us notice also that fermions appear in the interaction term in (10) as the following O(N) singlet collective field

$$\begin{aligned} G_{IJ}(\tau ,\tau ') = \frac{1}{N}\sum _{i=1}^{N} \psi _{i}^{I}(\tau ) \psi _{i}^{J}(\tau '). \end{aligned}$$
(15)

As a consequence of (14), in any regime where the kinetic operator \({\hat{\sigma }}_{IJ}(\tau , \tau ')\) (13) can be ignored, the action is invariant under the following reparametrization of the bilocal field

$$\begin{aligned}&G_{IJ}(\tau _{I},\tau _{J}) \rightarrow \left( f_{I}'(\tau _{I}) f_{J}'(\tau _{J})\right) ^{\varDelta } G_{IJ}( f_{I}(\tau _{I}) f_{J}(\tau _{J})), \nonumber \\&\qquad \varDelta = \frac{1}{4}, \qquad I=L,R. \end{aligned}$$
(16)

In order to study \(\langle Z(\beta + iT) Z(\beta - iT) \rangle _{c}\) in the large N limit, it is convenient to recast the functional integral (10) in terms of the collective field \(G_{IJ}(\tau ,\tau ')\) (15) and a corresponding Lagrangian multiplier \(\varSigma _{IJ}(\tau ,\tau ')\), by integrating out the Majorana fermion fields. This is achieved by inserting in the path integral (10) the identity

$$\begin{aligned} 1= & {} \int {\mathcal {D}}G_{IJ} \, \, \delta \left( G_{IJ}(\tau ,\tau ') - \frac{1}{N}\sum _{i=1}^{N} \varPsi _{i}^{I}(\tau ) \varPsi _{i}^{J}(\tau ') \right) \nonumber \\= & {} \int {\mathcal {D}}G_{IJ} \nonumber \\&\times \int {\mathcal {D}}\varSigma _{IJ} e^{\varSigma _{IJ}(\tau , \tau ') \left( G_{IJ}(\tau , \tau ') - \frac{1}{N}\sum _{i=1}^{N} \varPsi _{i}^{I}(\tau ) \varPsi _{i}^{J}(\tau ') \right) },\nonumber \\ \end{aligned}$$
(17)

where integration over \(\varSigma _{IJ}\) is performed along an imaginary direction in field space. By integrating out fermions one finds

$$\begin{aligned} \langle Z(\beta - iT) Z(\beta + iT) \rangle _{c}= & {} \int {\mathcal {D}}G_{ij}(\tau , \tau ') {\mathcal {D}} \nonumber \\&\times \varSigma _{ij}(\tau , \tau ') e^{- I(G_{ij},\varSigma _{ij})}, \end{aligned}$$
(18)

where

$$\begin{aligned} \frac{I(G_{ij},\varSigma _{ij}) }{N}= & {} - \frac{1}{2} \log \det \nonumber \\&\times \left( \delta (\tau - \tau ') \delta _{ij} \partial _{\tau } - \varSigma _{ij}(\tau , \tau ') \right) \nonumber \\&+ \frac{1}{2} \sum _{i,j} \int _{0}^{T} d \tau d \tau ' \left( \varSigma _{ij}(\tau , \tau ' ) G_{ij}(\tau , \tau ') \right. \nonumber \\&\left. - \frac{J^2 J_{ij} }{4} G_{ij}(\tau , \tau ')^4 \right) . \end{aligned}$$
(19)

Notice that for notational convenience from now on we use lowercase indexes to denote left and right replicas entries, by switching our previous notation \(I =L,R\) to \(i= L,R\). This should not be source of confusion, since fermions have been integrated out. We also use the notation \(J_{ij} = J_{i}J_{i}\) where

$$\begin{aligned} J_{ij} = \begin{pmatrix} J_{L}J_{L} &{} J_{L}J_{R} \\ J_{R}J_{L} &{} J_{R}J_{R} \end{pmatrix} = \begin{pmatrix} \left( \frac{\beta }{T} + i \right) ^2 &{} \frac{\beta ^2}{T^2} + 1 \\ \frac{\beta ^2}{T^2} + 1 &{} \left( \frac{\beta }{T} - i \right) ^2 \end{pmatrix}, \end{aligned}$$
(20)

which follows from the definitions (9).

The two replica action (19) gives the following saddle point equations. A variation with respect to \(\varSigma _{ij}\)

$$\begin{aligned} \frac{\delta I}{ \delta \varSigma _{ij}} = 0, \end{aligned}$$
(21)

gives

$$\begin{aligned} \left( \delta (\tau {-} \tau '') \delta _{ik} \partial _{\tau } {-} \varSigma _{ik}(\tau , \tau '')\right) * G_{kj}(\tau '' , \tau ' ) = {-} \delta _{ij}\delta (\tau {-} \tau '), \nonumber \\ \end{aligned}$$
(22)

where \(*\) is the convolution product

$$\begin{aligned} f * g (x) \equiv \int d y f(x - y)g(y). \end{aligned}$$
(23)

While a variation with respect to \(G_{ij}\)

$$\begin{aligned} \frac{\delta I}{ \delta G_{ij}} = 0, \end{aligned}$$
(24)

gives

$$\begin{aligned} \varSigma _{ij}(\tau , \tau ') = J^{2}J_{ij} G_{ij}^3(\tau , \tau '). \end{aligned}$$
(25)

We now show that in the large time T regime, for large enough time separation intervals \(\varDelta \tau \), an almost conformal regime emerges. Let us consider the Fourier transform of the saddle equation (22)

$$\begin{aligned} \left( - i \omega \delta _{ik} - \varSigma _{ik}(\omega ) \right) G_{kj}(\omega ) = - \delta _{ij}. \end{aligned}$$
(26)

We look at the regime where the \(i \omega \delta _{ij}\) term can be neglected, and the equation simplifies to

$$\begin{aligned} \varSigma _{ik}(\omega ) G_{kj}(\omega ) \sim \delta _{ij}. \end{aligned}$$
(27)

The following ansatz for the self energy

$$\begin{aligned} \varSigma _{ij}(\omega ) = \varPhi _{ij} \sqrt{ J \omega }, \end{aligned}$$
(28)

does the job in (26) for small enough \(\omega \), because of the square root. The square root ansatz (28), solves also (25) for a suitable constant invertible matrix \(\varPhi _{ij}\), if one take also

$$\begin{aligned} G_{ij}(\omega ) = \frac{\varPhi _{ij}^{-1}}{\sqrt{J \omega }}. \end{aligned}$$
(29)

By plugging (28) and (29) into (25), one has the following equation for \(\varPhi _{ij}\)

$$\begin{aligned} \varPhi _{ij} = J_{ij} (\varPhi _{ij}^{-1})^{3}, \end{aligned}$$
(30)

which is solved by

$$\begin{aligned} \varPhi _{ij}^{-1} = \frac{1}{2^{1/ {5}}} \begin{pmatrix} \left( \frac{\beta }{T} + i \right) ^{- 1/2} &{} i \left( \frac{\beta ^2}{T^2} + 1 \right) ^{- 1/4} \\ i \left( \frac{\beta ^2}{T^2} + 1 \right) ^{- 1/4} &{} \left( \frac{\beta }{T} - i \right) ^{- 1/2} \end{pmatrix}. \end{aligned}$$
(31)

The conformal solution (28), (29), with \(\varPhi _{ij}\) given by (31) is valid in the regime

$$\begin{aligned} |\varDelta \tau |>> \frac{1}{J} \frac{1}{\sqrt{1 + \frac{\beta ^2}{T^2}}}, \end{aligned}$$
(32)

which corresponds to a negligible \(i \omega \delta _{ij}\) term in Eq. (26).

In order to have a quasi conformal regime (32) it is therefore necessary that

$$\begin{aligned} J T>> \frac{1}{\sqrt{1 + \frac{\beta ^2}{T^2}}}. \end{aligned}$$
(33)

Whenever \(T>> \beta \), the above condition simplifies further to \(JT>> 1\).

Let us summarize what we have just discussed: for large time argument T, the SYK spectral form factor saddle is well approximated by a conformal replica-non-diagonal complex saddle. This approximation breaks down for short enough time separation intervals \(|\tau - \tau ' |\), according to (32).

By taking the conformal complex saddle we just calculated, make it periodical by T, and analytically continue it to real time, one finds

$$\begin{aligned} G_{LL}(t, t')= & {} \frac{1}{(4\pi )^{1/4}\sqrt{J}} \frac{1}{\left( \frac{\beta }{T} + i \right) ^{1/2}} \frac{ \text {sgn}(t - t')}{\left[ \frac{T}{\pi } \sinh \left( \frac{\pi |t - t'|}{T}\right) \right] ^{1/2}}, \nonumber \\ G_{LR}(t,t')= & {} G_{RL}(t,t') \nonumber \\= & {} \frac{1}{(4\pi )^{1/4}\sqrt{J}} \frac{1}{\left( \frac{\beta ^2}{T^2} + 1 \right) ^{ 1/4}}\nonumber \\&\quad \times \frac{i}{\left[ \frac{T }{\pi } \cosh \left( \frac{\pi ( t - t' + \varDelta )}{T} \right) \right] ^{1/2}}, \nonumber \\ G_{RR}(t, t')= & {} (G_{LL}(t, t'))^{*}. \end{aligned}$$
(34)

Let us pause for a moment, in order to comment on how Eq. (34) relates to Ref. [1]. Here we have computed the conformal complex saddle directly from the two replica (conformal) action, (Eq. (19) without the derivative term). On the other hand Ref. [1] makes a broader analysis on the SYK spectral form factor and, for his purpose, employs an auxiliary SYK thermal system at inverse temperature \(\beta _{aux}\). The introduction of the auxiliary system follows from the observation that in the infinite temperature limit (\(\beta \rightarrow 0\)) and large time T, the Keldysh contour in the path integral for the SYK spectral form factor is similar to the one for an auxiliary thermal system, the difference being the way the two contours are closed. Saad et al. [1] claims that the spectral form factor and the auxiliary thermal system have similar saddle point equations, since saddle point equations are insensitive to boundary conditions. On the other hand, since the spectral form factor does not depend on \(\beta _{aux}\), for consistency the SFF action needs to vanish on the auxiliary system saddle, a fact that [1] checks explicitly.

For non vanishing \(\beta \) [1] provides the following approximated saddle point for the spectral form factor

$$\begin{aligned} G_{LL}^{\beta _{aux}}(t)= & {} \frac{1}{(4\pi )^{1/4}\sqrt{J}} \left( \frac{\beta - iT}{\beta + iT} \right) ^{1/4} \nonumber \\&\quad \times \frac{ \text {sgn}(t)}{\left[ \frac{\beta _{aux}}{\pi }\left| \sinh \left( \frac{\pi t}{\beta _{aux}} \sqrt{1 + \frac{\beta ^2}{T^2}} \right) \right| \right] ^{1/2}}, \nonumber \\ G_{LR}^{\beta _{aux}}(t)= & {} G_{RL}^{\beta _{aux}}(t) = \frac{1}{(4\pi )^{1/4}\sqrt{J}} \nonumber \\&\quad \times \frac{i}{\left[ \frac{\beta _{aux}}{\pi } \cosh \left( \frac{\pi (t + \varDelta )}{\beta _{aux}} \sqrt{1 + \frac{\beta ^2}{T^2}} \right) \right] ^{1/2}}, \nonumber \\ G_{RL}^{\beta _{aux}}(t)= & {} (G_{LR}^{\beta _{aux}}(t))^{*}, \end{aligned}$$
(35)

where the above correlators need to be made periodic by period T, by summing over images. In the \(\beta > 0\) case, however the spectral form factor action is no longer vanishing on the saddle (35) and a runaway in the \(\beta _{aux}\) parameter appears [1].

One can check that Eq. (35) is recovered by taking the saddle solution obtained here (28) and (29) and make it periodic by the following rescaled auxiliary thermal system inverse temperature

$$\begin{aligned} {\tilde{\beta }}_{aux} = \frac{\beta _{aux}}{ \sqrt{1 + \frac{\beta ^2}{T^2}}}. \end{aligned}$$
(36)

For illustrative purposes, let us pause for a moment in order to recall the meaning of the parameters \(\beta _{aux}\) and \(\varDelta \). According to [1], \(\beta _{aux}\) and \(\varDelta \) come from phase space considerations. By using the correspondence with JT gravity in the bulk, [1] expects the phase space for the spectral form factor backgrounds to be two dimensional. Two possible parameters to describe the phase space, are the auxiliary \(\beta _{aux} > 0\) and the compact coordinate \(\varDelta \in [-T, T]\). \(\varDelta \) is a relative time shift between the two holographic boundaries clocks. On the other hand, \(\beta _{aux}\) is a uv cutoff for the boundary theory, arising by holographic renormalization.

Let us notice that the saddle (35) corresponds to a complex version of SYK correlators on the auxiliary thermal system at inverse temperature \({\tilde{\beta }}_{aux}\) (36), computed on the double field thermal state

$$\begin{aligned} | TFD \rangle = \frac{1}{\sqrt{Z(\beta )}} \sum _{n = 1}^{2^{\frac{N}{2}}} e^{- \frac{\beta }{2}E_n } | E_n \rangle _{L} \otimes | E_n \rangle _{R}. \end{aligned}$$
(37)

From a bulk gravity perspective, the auxiliary thermal system inverse temperature \(\beta _{aux}\) fixes the uv energy cutoff of the two holographic boundaries in \(nAdS_2\). In the \(nAdS_2\) wormhole, described holographically by the double field thermal state (37), on each of the two thermal Rindler pathces, the metric and the dilaton have the following form

$$\begin{aligned} ds^2 = - \sinh (\rho )^2 d{\tilde{t}}^2 + d \rho ^2, \qquad \varPhi = \varPhi _h \cosh (\rho ). \end{aligned}$$
(38)

In the bulk solution argued to be relevant for the spectral form factor [1], there is a Rindler time periodic identification \({\tilde{t}}_{R} \sim {\tilde{t}}_{R} + {\tilde{T}}\) and \({\tilde{t}}_L \sim {\tilde{t}}_L - {\tilde{T}}\). This is compatible with the asymmetric analytic continuation in the spectral form factor \(\langle Z(\beta - iT) Z(\beta + iT) \rangle _{c} \). This Rindler time identifications give rise to a Lorentzian manifold with the topology of a double cone with closed time curves [1]. \(\beta _{aux}\) arises in relating Rindler time \({\tilde{t}}\) to boundary time t in the following way. By using an holographic renormalization parameter \(\epsilon \) one can relate the boundary proper time t to the bulk Rindler time \({\tilde{t}}\) from the bulk metric (38) at a large fixed \(\rho = \pm \rho _c\)

$$\begin{aligned} d t^2 = \epsilon d s^2 |_{\rho = \pm \rho _c }. \end{aligned}$$
(39)

This gives the following relation between SYK boundary time t and bulk Rindler time \({\tilde{t}}\)

$$\begin{aligned} t = \epsilon \frac{e^{\rho _c}}{2} {\tilde{t}} = \frac{\beta _{aux}}{ 2\pi } {\tilde{t}}. \end{aligned}$$
(40)

Given, that \(\beta _{aux}\) provides a uv cutoff for the boundary theory, it plays a somehow similar role to the time argument T in the spectral form factor. In fact, T fixes the uv coarse graining energy scale at which correlation between pairs of energy eigenvalues of SYK are probed

$$\begin{aligned} \langle Z(\beta - iT) Z(\beta + iT) \rangle= & {} \int dE dE' \langle \rho (E) \rho (E') \rangle \nonumber \\&\quad \times e^{- \beta (E + E' ) + iT (E - E' )}. \end{aligned}$$
(41)

Saad et al. [1] points out in their analysis that for non vanishing \(\beta \), there is an instability in the parameter \(\beta _{aux}\), which appears as a runaway direction. They suggest that such instability can be cured by going at fixed total energy, in a microcanonical description.

In Ref. [1], the form of the correlarators in (35) was also checked numerically, by computing geodesics distances from boundaries points in a \(AdS_2\) wormhole geometry. The idea is that in the large N limit the bulk theory classicizes and boundary CFT two points correlators reduce to simple functions of the length of the geodesic connecting the pair of points on which the two point function is evaluated.

As we already mentioned, besides \(\beta _{aux}\), there is at least a second phase space parameter, since phase space is always even dimensional. In the case of pure JT gravity the dimension of phase space is two, (see for example [59] for a detailed account). This missing phase space parameter is the compact parameter \(\varDelta \in [- T, T]\) that appears in the off diagonals saddle correlator \(G_{LR}^{\beta _{aux}} = G_{RL}^{\beta _{aux}}\) in (35) and it is responsible for the linear ramp behavior in the SYK spectral form factor [1]. \(\varDelta \) corresponds to a relative shift between the time coordinate origins on the right and left boundary. It is not a surprise that it appears only on the left-right diagonal correlator in (35), since only there a relative shift on the origins of times coordinates is relevant. The fact that \(\varDelta \) is responsible for the ramp goes as follows [1]. It turns out that the conformal saddles (35) have zero action. In order to compute the functional integral in the large N limit, one has to still integrate over the phase space parameters \(\beta _{aux}\) and \(\varDelta \). Integration over \(\beta _{aux}\) gives just a constant overall constant to the spectral form factor. On the other hand, \(\varDelta \) integration on \([-T, T]\) gives a linear T factor which reproduces the ramp. The above discussion was at the conformal level, for the spectral form factor family of conformal saddle points of the critical action. When effects of the two replica bilocal kinetic operator \({\hat{\sigma }}_{ij}(\tau , \tau ')\) (13) are taken into account, at lowest order in the perturbative expansion an effective action for the left and right time reparametrization soft modes \(f_{L}(\tau )\), \(f_{R}(\tau )\) occurs. This effective action at the saddle point level turns out to be independent on T, consistently with the existence of a linear ramp. However, the value of the action in the saddle point is non zero and a runaway direction for the functional integral representation of the spectral form factor arises, toward large \(\beta _{aux}\). The \(\beta _{aux}\) instability can be cured in the microcanonical ensemble [1], this is a consequence of \(\beta _{aux}\) being actually related to the energy of the Schwarzian modes. On the other hand, \(\beta _{aux}\) might be stabilized in the canonical ensemble, at the price of slightly changing the model, by adding a small non local coupling between left and right soft modes \(f_{L}(\tau )\) and \(f_{R}(\tau )\) [1]. This is an interesting possibility that deserves further studies. The two boundaries non local coupling term that stabilizes \(\beta _{aux}\) has some formal analogy to non-local double trace interaction terms that make a wormhole temporarily traversable [28, 36]. Analysis related to this discussion from the perspective of two boundaries JT gravity is found in [60]. Beyond the Schwarzian saddle point approximation, the one loop determinant receives contributions both from the two time reparametrization soft modes \(f_{L}(\tau )\), \(f_{R}(\tau )\), and from fluctuations of the phase space parameters \(\delta \beta _{aux}(t)\), and \(\delta \varDelta (t)\) [1]. These latter fluctuations are controlled by an hydrodynamic action and computation of the one loop determinant consistently reproduces the ramp [1].

3 A large N, large T, approximation for the spectral form factor path integral

The breaking of conformal invariance is due to the presence of the kinetic operator \({\hat{\sigma }}_{ij} = \delta _{ij}\delta (t -t')\partial _{t}\) in the action (19). The action can be recast in the form (42) below, where in the last term \({\hat{\sigma }}_{ij}(t,t')\) appears as a source coupled to \(G_{ij}(t,t')\). This term breaks conformal invariance explicitly, while the previous three terms in (42) are conformal invariant. As it was discussed in the previous section in the part leading to Eq. (34), for large enough T, the spectral form factor saddle is well approximated by the conformal one given in (34), for sufficiently large time separations \(|\varDelta t| = |t - t'|\). The breaking of conformal invariance induced by the source term in the action (42) is therefore a uv effect. In the large N limit and large T regime a steepest descent approximation for the spectral form factor path integral can be taken through the conformal saddle. We take a regularized version of the source \({\hat{\sigma }}_{ij} = \delta _{ij}\delta (t -t')\partial _{t}\), by replacing the Dirac delta by a smearing function that cuts off time intervals below the scale 1/J. On the other hand, we replace the linear derivative operator \(\partial _{\tau }\) by a more generic combination of terms with different scalings, in order to account for non linear effects. By steepest descent, the approximated action depends on the regularized source, in particular, through a term where the four point function two replica ladder kernel emerges, (see Eq. (50) below). By looking at Eq. (50) one expects an enhanced effect along the four point kernel invariant eigenfunction in functional space. Due to the vanishing of the denominator it seems that a divergence occurs. However, the divergence is cured by the regularization of the source. We provide an argument that shows how for large enough T, all eigenfunctions terms in the expansion for the source does not contribute, except that the invariant eigenfunction of the ladder kernel. This argument provides an explicit form for the regularized source in the large T regime. By plugging this form in the last source term in (42), we are finally able to compute the large T effective action for the spectral form factor in the \(f_{L}(t)\), \(f_{R}(t)\) time reparametrization modes.

We start by performing a translation in field space \(\varSigma _{ij}(t, t') \rightarrow \varSigma _{ij}(t, t') + {\hat{\sigma }}_{ij}(t, t')\), where \({\hat{\sigma }}_{ij}(t, t') = \delta _{ij} \delta (t - t' ) \partial _{t}\). The action (19) turns into

$$\begin{aligned}&\frac{I(G_{ij},\varSigma _{ij}) }{N} = - \frac{1}{2} \log \det \left( - \varSigma _{ij}(t, t') \right) \nonumber \\&\quad + \frac{1}{2}\sum _{i,j} \int _{0}^{T} d t d t' \left( \varSigma _{ij}(t, t' ) G_{ij}(t, t') - \frac{J^2 J_{ij} }{4} G_{ij}(t, t')^4 \right) \nonumber \\&\quad + \frac{1}{2}\sum _{i,j} \int _{0}^{T} d t d t' {\hat{\sigma }}_{ij}(t, t' ) G_{ij}(t, t'). \end{aligned}$$
(42)

As it was remarked in the previous section, (see the discussion that leads to Eq. (16)), the first three terms of the above action are invariant under the simultaneous time reparametrization \(t \rightarrow f_{1}(t)\), \(t' \rightarrow f_{2}(t')\), where \(G_{ij}(t_1, t_2)\) transforms as a primary bilocal field with weights \( \frac{1}{4}\) and \(\varSigma _{ij}(t_1, t_2)\) transforms with weights \(\frac{3}{4}\). The spectral form factor conformal saddle (34) breaks spontaneously the twofold conformal invariance down to the diagonal \(SL_{diag}(2,{\mathbb {R}})\) subgroup of \(SL_{L}(2) \times SL_{R}(2)\). On the other hand, the source term in (42) breaks explicitly conformal invariance. In order to study the effects of the kinetic operator \({\hat{\sigma }}_{ij}(t, t')\), we will regularize it, by smearing the singular Dirac delta kernel on the account that times shorter than the time scale 1/J cannot be resolved.

In the large N limit, at strong coupling, the path integral for the spectral form factor can be approximated by using the steepest descent method through the conformal saddle (34) \((G_{ij}^{c}, \varSigma _{ij}^{c})\)

$$\begin{aligned} G_{ij}= & {} G_{ij}^c + \frac{1}{J_{ij}^{1/2} |G_{ij}^c|} \delta G_{ij} \nonumber \\ \varSigma _{ij}= & {} \varSigma _{ij}^c + J_{ij}^{1/2} |G_{ij}^c| \delta \varSigma _{ij}, \end{aligned}$$
(43)

where the normalization in front of the fluctuations is chosen for convenience.

In the large N limit, the path integral is well approximated by evaluating the action in the saddle points in the complex plane and by Gaussian integrating fluctuations along the steepest descent direction through the saddle point.

An expansion of the action up to quadratic order in the fluctuations gives

$$\begin{aligned} \frac{I}{N}\sim & {} \frac{I_{c}}{N} - \frac{1}{12J^2 }\langle \delta \varSigma _{ij} | {\tilde{K}}_{ij,kl}^{c} | \delta \varSigma _{kl} \rangle + \frac{1}{2} \langle \delta \varSigma _{ij} |\delta G_{ij} \rangle \nonumber \\&- \frac{3}{4}J^2 \langle \delta G_{ij} | \delta G_{ij} \rangle \nonumber \\&+ \frac{1}{2} \left\langle \sigma _{ij} | G_{ij}^{c} + \frac{\delta G_{ij}}{J_{ij}^{1/2}|G_{ij}^c|} \right\rangle , \end{aligned}$$
(44)

where \(I_{c}\) is the action evaluated in the conformal saddle, replica indexes \(i,j = R,L\) are summed over and \(\langle f | g \rangle \) denotes the following scalar product in the space of bilocal functions

$$\begin{aligned} \langle f | g \rangle \equiv \int d t d t' f^{*}(t, t') g(t, t'). \end{aligned}$$
(45)

The four indexes integral kernel appearing in (44)

$$\begin{aligned} {\tilde{K}}^{c}_{ij, kl}(t_1, t_2 ; t_3, t_4)= & {} 3 J^2 J_{ij}^{1/2}J_{kl}^{1/2} |G_{ij}^{c}(t_{12})|\nonumber \\&G_{ik}^{c}(t_{13})G_{jl}^{c}(t_{24})|G_{kl}^{c}(t_{34})|, \nonumber \\ t_{pq}= & {} t_p - t_q \end{aligned}$$
(46)

is the two replica version of the four point function symmetrized ladder kernel in regular SYK [23]. The latter for generic even coupling \(q \ge 4\) has the form

$$\begin{aligned} {\tilde{K}}(t_1, t_2 ; t_3, t_4)= & {} J^2 (q - 1) |G^{\frac{q-2}{2}}(t_{12})|\nonumber \\&\quad \times G(t_{13})G(t_{24})|G^{\frac{q-2}{2}}(t_{34})|. \end{aligned}$$
(47)

We now introduce a convenient alternative indexing for the replica entries. We define \(\alpha = 1,2,3,4\) such that \(\alpha = 1 = LL\), \(\alpha = 2 = RR\), \(\alpha = 3 = LR\), \(\alpha = 4 = RL\). The action (44) in this new indexing reads

$$\begin{aligned} \frac{I}{N}= & {} \frac{I_{c}}{N} - \frac{1}{12J^2 }\langle \delta \varSigma _{\alpha } | {\tilde{K}}_{\alpha \beta }^{c} | \delta \varSigma _{\beta } \rangle \nonumber \\&+ \frac{1}{2} \langle \delta \varSigma _{\alpha } |\delta G_{\alpha } \rangle - \frac{3}{4}J^2 \langle \delta G_{\alpha } | \delta G_{\alpha } \rangle \nonumber \\&+ \frac{1}{2} \left\langle \sigma _{\alpha } | G_{\alpha }^{c} + \frac{\delta G_{\alpha }}{J_{\alpha }^{1/2} |G_{\alpha }^c|} \right\rangle . \end{aligned}$$
(48)

Since fluctuations are of order \(1 / \sqrt{N}\), in the large N limit, one can extend the integration contour on the complex plane along the steepest direction to make a full Gaussian integral. By \(\delta \varSigma _{\alpha }\) integration on finds

$$\begin{aligned} \frac{{\tilde{I}}}{N}= & {} \frac{I}{N} - \frac{I_c}{N} \nonumber \\= & {} \frac{3}{4}J^2 \left\langle \delta G_{\alpha } | \left( ({\tilde{K}}_{c}^{-1})_{\alpha \beta } - \delta _{\alpha \beta } \right) | \delta G_{\beta } \right\rangle \nonumber \\&+ \frac{1}{2} \left\langle \sigma _{\alpha } | \frac{\delta G_{\alpha }}{J_{\alpha }^{1/2} |G_{\alpha }^c|} \right\rangle + \frac{1}{2} \langle \sigma _{\alpha } | G_{\alpha }^{c} \rangle . \end{aligned}$$
(49)

By then integrating along the steepest descent contour in the \(\delta G_{\alpha }\) complex plane through the saddle \(G_{\alpha }^{c}\), one finds the following approximation at large N for the action of the spectral form factor

$$\begin{aligned} \frac{{\tilde{I}}}{N} = \frac{1}{12 J^2} \bigg \langle s_{\alpha } | \left( \delta _{\alpha \gamma } - {\tilde{K}}_{\alpha \gamma }^{c} \right) ^{-1} {\tilde{K}}^{c}_{\gamma \beta } | s_{\beta }\rangle + \frac{J_{\alpha }^{1/2}}{2}\langle s_{\alpha } | |G_{\alpha }^{c}|^2 \bigg \rangle , \nonumber \\ \end{aligned}$$
(50)

where \(s_{\alpha }(t, t)\)

$$\begin{aligned} s_{\alpha }(t, t') \equiv \frac{\sigma _{\alpha }(t, t')}{J_{\alpha }^{1/2} |G_{\alpha }^{c}(t, t')|}, \end{aligned}$$
(51)

is a rescaled version of the regularized source.

So far, by steepest descent method, we obtained the following large N approximation for the spectral form factor

$$\begin{aligned}&Z(\beta + iT)Z(\beta - iT) \sim \nonumber \\&\quad \times e^{ \frac{N}{12 J^2} \langle s_{\alpha } | \left( \delta _{\alpha \gamma } - {\tilde{K}}_{\alpha \gamma }^{c} \right) ^{-1} {\tilde{K}}^{c}_{\gamma \beta } | s_{\beta }\rangle + \frac{N}{2}\langle s_{\alpha } | J_{\alpha }^{1/2}|G_{\alpha }^{c}|^2 \rangle }. \end{aligned}$$
(52)

Equation (52) allows to compute various correlators by functional deriving w.r.t. regularized source \(\sigma _{\alpha }\). In particular, the two point function is given by

$$\begin{aligned} \langle G_{\alpha } \rangle= & {} \frac{1}{N} \frac{\delta |Z|^2}{\delta \sigma _{\alpha } } = \frac{1}{N}\frac{1}{J_{\alpha }^{1/2}|G_{\alpha }^{c}|} \frac{\delta |Z|^2}{\delta s_{\alpha } } \nonumber \\\sim & {} \left[ \frac{1}{2} G_{\alpha }^{c} + \frac{1}{12 J^2 J_{\alpha }^{1/2}|G_{\alpha }^{c}| } \right. \nonumber \\&\quad \times \left. \left( \delta _{\alpha \gamma } - {\tilde{K}}_{\alpha \gamma }^{c} \right) ^{-1} {\tilde{K}}^{c}_{\gamma \beta } | s_{\beta }\rangle \right] e^{N I}. \end{aligned}$$
(53)

We now discuss the form of the regularized source. Let us start by considering the eigenvalues problem for the four points conformal ladder Kernel

$$\begin{aligned} {\tilde{K}}^{c}_{\alpha \beta }(t_1, t_2 ; t,t')\psi _{\beta }^{h}(t,t') = {\tilde{k}}_{SFF}(h)\psi _{\alpha }^{h}(t_1 ,t_2). \end{aligned}$$
(54)

Where, h labels the eigenvalues of the Carimir \({\mathcal {C}}_{diag}\) of \(SL_{diag}(2)\), the diagonal subgroup of \(SL_{L}(2) \times S_{R}(2)\) which is the symmetry group that survives the spontaneous breaking induced by the conformal replica non-diagonal saddle (34). The h dependence on the eigenvalues \({\tilde{k}}_{SFF}(h)\) is due to the fact that \({\tilde{K}}^{c}_{\alpha \beta }(t_1, t_2 ; t,t')\) commutes with \({\mathcal {C}}_{diag}\).

Let us expand the source in terms of the ladder kernel eigenfunctions

$$\begin{aligned} s_{\alpha }(t,t') = \sum _{h} C_{h} \psi _{\alpha }^{h}(t,t') U(\log \zeta _{\alpha }(|t - t'|)), \end{aligned}$$
(55)

where \(U(\xi )\) is a smooth smearing function of \(\xi _{\alpha } = \log ( \zeta _{\alpha }(| t - t'|)) \) that regularizes the singular Dirac kernel \(\delta (t - t')\) in the two replica kinetic operator \({\hat{\sigma }}_{ij} = \delta _{ij}\delta (t - t')\partial _{t}\). U cuts off the short times intervals region, below the scale related to the SYK energy scale 1/J. It works as follows, \(U(\xi )\) is demanded to vanish for \(\xi < 0\), and for \(|t - t'| > 2T\). \(\zeta _{\alpha }(|t - t'|)\) is defined to be the denominator of the \(\alpha \) component of the weight h eigenfunction of the two replica four point kernel

$$\begin{aligned} \psi _{\alpha }^{h}(t,t') \propto \frac{1}{\zeta _{\alpha }(|t - t'|)^{h}}. \end{aligned}$$
(56)

Since \(\psi _{\alpha }^{h}(t,t')\) is also an eighenfunction of the \(SL_{diag}(2)\) Casimir \({\mathcal {C}}_{diag}\), \(\zeta _{\alpha }(|t - t'|)\) is typically an hyperbolic sine or cosine. One has \(0 < \zeta _{\alpha }(|t - t'|) \le 1\) for \(|t - t'| < \frac{1}{J}\) , which makes \(\xi _{\alpha } < 0\) because of the logarithm and the smearing function U vanishes correspondingly. This implements the impossibility to resolve time intervals below 1/J. On the other hand, for large enough \(|t - t'|\), \(\zeta _{\alpha }(|t - t'|)\) grows exponentially in the separation time. This makes the support of the smearing function \(U(\log ( \zeta _{\alpha }(| t - t'|)))\) to be of order O(T).

The smearing function is normilized as folllow

$$\begin{aligned} \int d \xi \, U(\xi ) = 1. \end{aligned}$$
(57)

Let us write the smearing function as a Fourier integral

$$\begin{aligned} U(\xi ) = \int \frac{d \eta }{ 2 \pi } e^{- i \xi \eta } {\tilde{U}}(\eta ). \end{aligned}$$
(58)

Since \( U(\xi )\) has support \(\varDelta \xi \sim O(T) \), \({\tilde{U}}(\eta )\) has support \(\varDelta \eta \sim O\left( \frac{1}{T}\right) \). Therefore, in the large T limit, the Fourier transform \({\tilde{U}}(\eta )\) becomes very narrow.

By inserting (55) and (58) into (53), one finds

$$\begin{aligned} \langle G_{\alpha }(t,t') \rangle\sim & {} \left[ \frac{1}{2} G_{\alpha }^{c} + \frac{1}{12 J^2 J_{\alpha }^{1/2}|G_{\alpha }^{c}| } \sum _{h} c_{h} \right. \nonumber \\&\times \left. \int \frac{d \eta }{ 2\pi } \frac{{\tilde{k}}_{SFF}(h + i\eta )}{1 - {\tilde{k}}_{SFF}(h + i \eta )} \psi _{\alpha }^{h + i \eta }(t,t') {{\tilde{U}}}(\eta ) \right] e^{N I}, \nonumber \\ \end{aligned}$$
(59)

where we used both

$$\begin{aligned} e^{- i \eta \xi } = \frac{1}{ \left( \zeta _{\alpha }(|t - t'|)^{h} \right) ^{i\eta }}, \end{aligned}$$
(60)

and Eq. (56).

Since \({\tilde{U}}(\eta )\) has support \(\varDelta \eta = O\left( \frac{1}{T} \right) \), in the large T limit, one can expand \({\tilde{k}}_{SFF}(h + i\eta )\) up to the first order in eta \({\tilde{k}}_{SFF}(h + i\eta ) \sim {\tilde{k}}_{SFF}(h) + i \eta \, {\tilde{k}}_{SFF}'(h)\). By residues theorem on the \(\eta \) integral, one finds

$$\begin{aligned} \langle G_{\alpha }(t,t') \rangle\sim & {} \left[ \frac{1}{2} G_{\alpha }^{c} + \frac{i}{12 J^2 J_{\alpha }^{1/2}|G_{\alpha }^{c}| } \right. \nonumber \\&\times \left. \sum _{h} c_{h} \psi _{\alpha }^{h + i \eta _h }(t,t') {{\tilde{U}}}_{h}(\eta _h ) \right] e^{N I}, \end{aligned}$$
(61)

with

$$\begin{aligned} \eta _h = i \frac{{\tilde{k}}_{SFF}(h) - 1}{{\tilde{k}}_{SFF}'(h)}. \end{aligned}$$
(62)

Since the support of \({\tilde{U}}(\eta )\) is \(\varDelta \eta \sim O\left( \frac{1}{T}\right) \), for large enough T, the only non vanishing term in (61) is the \(\eta _{h} = 0\) one. We have \({\tilde{U}}(0) = 1\) and by Eq. (62), \(\eta _{h} = 0\) iff \({\tilde{k}}_{SFF}(h_{*}) = 1\).

To summarize, we have shown that in the large N limit, for T large enough, the effects of breaking of conformal invariance in the spectral form factor are fully determined by the regularized source along the invariant direction under the four point ladder kernel. In particular, the large T limit of the two point function is given by

$$\begin{aligned} \langle G_{\alpha }(t,t') \rangle \sim \left[ \frac{1}{2} G_{\alpha }^{c} + \frac{i}{12 J^2 J_{\alpha }^{1/2}|G_{\alpha }^{c}| } \psi _{\alpha }^{h_{*}}(t,t') \right] e^{N I},\nonumber \\ \end{aligned}$$
(63)

for \(\psi _{\alpha }^{h_{*}}(t_1 ,t_2)\)

$$\begin{aligned} {\tilde{K}}^{c}_{\alpha \beta }(t_1, t_2 ; t,t')\psi _{\beta }^{h_{*}}(t,t') = \psi _{\alpha }^{h_{*}}(t_1 ,t_2). \end{aligned}$$
(64)

It follows that at large T, the regularized source that encodes the explicit breaking of conformal invariance has the following short separation times \(|t - t'| \rightarrow 0\) behavior

$$\begin{aligned} s_{\alpha }(t,t') \sim {\mathcal {P}} \left( \psi _{\alpha }^{h_{*}}(t,t') \right) U\left( \log \left( J |t - t'| \right) \right) , \end{aligned}$$
(65)

where \({\mathcal {P}}\) is the projector over the two diagonal directions \(\alpha = 1 = LL\) and \(\alpha = 2 = RR\) in replica indexes. This projection is required, since the source is diagonal in replica indexes. As already remarked, the breaking of conformal invariance is a \(| t -t' | \rightarrow 0\) effect, that’s why we focus on the short time separation uv behavior of the quantities of interest.

Since \(s_{1}(t,t') = s_{LL}(t,t')\) is expected to have the same form as \(s_{2}(t,t') = s_{RR}(t,t')\), it follows that the source that dominates the large T dynamics needs to be invariant under the operator \({\mathcal {P}}^{-1} {\tilde{K}}^{c}_{\alpha \beta } {\mathcal {P}} = {\tilde{K}}^{c}_{11}\).

By using (34) in (46) one finds that \({\tilde{K}}^{c}_{11} ={\tilde{K}}^{c}_{LLLL} = {\tilde{K}}^{c}_{22} = {\tilde{K}}^{c}_{RRRR} = {\tilde{K}}_{c}\), where \({\tilde{K}}_{c}\) is the regular SYK, \(q = 4\), four point function symmetrized ladder kernel (47)

$$\begin{aligned} {\tilde{K}}^{c}_{11}(t_1, t_2 ; t,t')= & {} 3J^2 J_{LL} |G_{LL}(t_1,t_2)| G_{LL}(t_1,t) \nonumber \\&\quad G_{LL}(t_2, t') |G_{LL}(t,t')| \nonumber \\= & {} 3J^{2}|G_{c}(t_1,t_2)| G_{c}(t_1, t) \nonumber \\&\quad G_{c} (t_2, t') |G_{c}(t,t')| \nonumber \\= & {} {\tilde{K}}_{c}(t_1, t_2; t, t') \end{aligned}$$
(66)

with

$$\begin{aligned} G_{c}(t,t') \sim \frac{1}{(4\pi )^{1/4}\sqrt{J}} \frac{sgn(t-t')}{\left| t - t' \right| ^{1/2}}, \quad |t - t'| \rightarrow 0. \end{aligned}$$
(67)

Therefore, the regularized source whose effects dominate the non conformal dynamics for the spectral form factor at large T can be obtained by looking for the invariant function under the four point ladder conformal kernel in regular SYK

$$\begin{aligned} {\tilde{K}}_{c}(t_1, t_2; t,t') \psi _{h_{*}}(t,t') = \psi _{h_{*}}(t,t'). \end{aligned}$$
(68)

The spectrum of eigenvalues and eigenfunctions of of \({\tilde{K}}_{c}\) is known

$$\begin{aligned} {\tilde{K}}_{c}(t_1, t_2; t,t') \psi _{h}(t,t') = {\tilde{k}}_{c}(h) \psi _{h}(t,t'), \end{aligned}$$
(69)

in the following we recall some of their properties [23].

Since the SL(2) Casimir operator \({\mathcal {C}}\) commutes with the four points ladder conformal kernel \( {\tilde{K}}_{c}\), \({\mathcal {C}}\) eigenfunctions

$$\begin{aligned} {\mathcal {C}}(t_1, t_2 ; t, t' ) \psi _{h} (t,t') = h(h - 1) \psi _{h}(t_1 ,t_2 ). \end{aligned}$$
(70)

are also \( {\tilde{K}}_{c}\) eigenfunctions. \({\mathcal {C}}\) has a spectrum with both a continuum and a discrete component [23]. The continuum component is given by the points on the critical line \(h_s = \frac{1}{2} + is\), \(s \in {\mathbb {R}}\), while the discrete component is given by \(h_{n} = 2n\), \(n \in {\mathbb {N}}_{> 0}\). The Casimir \({\mathcal {C}}\) eigenfunctions have the following form [23]

$$\begin{aligned} \psi _{h}(t_0, t_1, t_2) = \int d t_0 g_{h}(t_0) \frac{\text {sgn}(t_{12})}{ |t_{01}|^{h} |t_{02}|^{h} | t_{12}|^{1- h}}. \end{aligned}$$
(71)

Notice that in the \(t_0\) large limit

$$\begin{aligned} \psi _{h}(t_0, t_1, t_2) \sim \frac{sgn(t_{12})}{| t_{12}|^{1- h}}, \qquad t_0 \rightarrow \infty \end{aligned}$$
(72)

In the eigenvalue equation

$$\begin{aligned} {\tilde{K}}_{c}(t_1 , t_2 ; t, t' ) \psi _{h}(t_0, t , t' ) = {\tilde{k}}_c (h) \, \psi _{h}(t_0, t_1 , t_2 ), \end{aligned}$$
(73)

by SL(2) symmetry, one can fix \(t_0 = \infty \), \(t_1 = 1\) and \(t_2 = 0\) and compute explicitly \({\tilde{k}}_{c}(h)\) by the a double integral

$$\begin{aligned} {\tilde{k}}_{c}(h) = {\tilde{K}}_{c}(1 , 0 ; t, t' ) \psi _{h}(\infty , t , t' ). \end{aligned}$$
(74)

For the four order coupling \(q=4\), the result is

$$\begin{aligned} {\tilde{k}}_{c}(h) = - \frac{3}{2} \frac{\tan \left( \frac{\pi }{2} \left( h - \frac{1}{2} \right) \right) }{ h - \frac{1}{2}}. \end{aligned}$$
(75)

The discrete component of the spectrum \(Spec({\mathcal {C}})\) thus is given

$$\begin{aligned} {\tilde{k}}_c (2n) = \frac{3}{4n - 1} \quad n =1,2,\dots \end{aligned}$$
(76)

We are looking for invariant functions under the action of \({\tilde{K}}_c\). From the above results on the spectrum, we have that \({\tilde{k}}_{c}(2) = 1\).

On the other hand, the continuous component of the spectrum

$$\begin{aligned} k_{c}(h_{s}) = i \frac{3}{2} \tanh \left( \frac{\pi }{2} s \right) , \quad s \in {\mathbb {R}}, \end{aligned}$$
(77)

does not provide any further invariant eigenfunction, besides.

To summarize, we have found that in the large T regime, the source that induces the breaking of conformal invariance for the spectral form factor has the following form

$$\begin{aligned} s_{LL}(t, t')= & {} s_{RR}(t, t') = a_0 \frac{\text {sgn}(t - t')}{ J |t - t' |^{2}} U\left( 2 \log J |t - t'|\right) , \nonumber \\&\quad \times |t - t'| \rightarrow 0, \end{aligned}$$
(78)

where \(a_0\) is a coefficient to be fitted numerically,

3.1 Effective action for the time reparametrization soft modes

By using the \(| t - t'| \rightarrow 0\) behavior of the source (78), we are finally able to compute the effective action for the breaking of conformal invariance in the large T regime, by the last term in (42)

$$\begin{aligned} \frac{I_{s}}{N}= & {} \int _{0}^{T} d t d t' \left( G_{LL}(t, t') \sigma _{LL}(t, t') \right. \nonumber \\&\quad \left. + G_{RR}(t, t') \sigma _{RR}(t,t')\right) . \end{aligned}$$
(79)

The \(| t - t' | \rightarrow 0\) behavior of the \(T \rightarrow \infty \) dominant source is given by

$$\begin{aligned} \sigma _{LL}(t, t') \sim \frac{a_0}{J_{LL}^{1/4}} \frac{\text {sgn}(t - t')}{\left[ J |t - t' | \right] ^{5/2}} U\left( \log \left( J |t - t'| \right) \right) . \end{aligned}$$
(80)

On the other hand, \(\sigma _{RR}(t, t')\) has the same form (80) but with \(J_{RR}\) replacing \(J_{LL}\).

The components of the Green function by the two times reparametrization \(t_{i} \rightarrow f_{i}(t_i)\) transform as

$$\begin{aligned} G_{ii}(t, t')= & {} \frac{1}{(J_{ii})^{1/4}}G_{\beta = \infty }(f_{i}(t), f_{i}(t')) f_{i}'(t)^{\varDelta } f_{i}'(t')^{\varDelta },\nonumber \\ \varDelta= & {} \frac{1}{4} i=L,R, \end{aligned}$$
(81)

where

$$\begin{aligned} G_{\beta = \infty }(t, t' ) = \frac{1}{(4\pi )^{1/4}\sqrt{J}} \frac{\text {sgn}(t - t')}{ |t - t'|^{1/2} }. \end{aligned}$$
(82)

As already remarked in various occasions, the breaking of conformal invariance in the SYK model is due to a uv short-time effect, as the conformal forms for the correlators describe accurately the low energy ir dynamics. We find a local effective local action, by going from \((t, t')\) to \((t_{+}, t_{-})\), slow average time \(t_{+} = \frac{t + t'}{2}\), and \(t_{-} = t - t'\). We expand the fields up to lowest order in \(t_{-}\) and then we integrate out \(t_{-}\). This gives a local effective action in \(t_{+}\) in the two time reparametrization soft modes \(f_{i}(t^{+}_{i})\), \(i = L,R\).

A Taylor expansion in \(t_{-}\) gives

$$\begin{aligned} G_{ii}(t_{+}, t_{-})= & {} \frac{1}{(J_{ii})^{1/4}} G_{\beta = \infty }(i t_{-}) \nonumber \\&\quad \times \left( 1 + \frac{\varDelta }{6} \text {Sch} (f_{i}(t_{+}), t_{+}) t_{-}^2 + O\left( t_{-}^4 \right) \right) . \nonumber \\ \end{aligned}$$
(83)

On the other hand, the diagonal components (34) of spectral form factor Green functions have the short time separation form

$$\begin{aligned} G^{c}_{ii}(t, t') \sim \frac{1}{ (J_{ii})^{1/4} (4 \pi )^{1/4} \sqrt{J}} \frac{\text {sgn}(t - t')}{|t - t' |^{1/2}}, \qquad i=L,R.\nonumber \\ \end{aligned}$$
(84)

By inserting in Eq. (79) the short time \(t_{-}\) expansions (83), the rescaled source along the enhanced direction (80) and the conformal Green function (84) one finds

$$\begin{aligned} - \frac{I_{s}}{N}= & {} \frac{a_{0} (4\pi )^{-1/4}}{24 \sqrt{J J_{LL}}} \int _{0}^{T} d t_{+} \text {Sch} (f_{L}(t_{+}), t_{+})\nonumber \\&\times \int _{- T}^{T} d t_{-} G_{\beta = \infty } ( i t_{-})t_{-}^{2} \frac{\text {sgn}(t_{-})}{ \left| J t_{-} \right| ^{2 + 1/2}}U\left( \xi (|t_{-}|) \right) \nonumber \\&+ L \leftrightarrow R \nonumber \\\sim & {} \frac{\alpha _{S}}{{\mathcal {J}}} \left( \frac{1}{\sqrt{J_{LL}}} \int _{0}^{T} d t_{+} \text {Sch} (f_{L}(t_{+}), t_{+}) \right. \nonumber \\&\left. + \frac{1}{\sqrt{J_{RR}}} \int _{0}^{T} d t_{+} \text {Sch} (f_{R}(t_{+}), t_{+}) \right) \nonumber \\&\times \int _{-T}^{T} \frac{ d t_{-}}{ J|t_{-}| }U\left( \log \left( J|t_{-}| \right) \right) \nonumber \\= & {} \frac{\alpha _{S}}{{\mathcal {J}} } \left( \frac{1}{\sqrt{J_{LL}}} \int _{0}^{T} d t_{+} \text {Sch} (f_{L}(t_{+}), t_{+}) \right. \nonumber \\&\left. + \frac{1}{\sqrt{J_{RR}}} \int _{0}^{T} d t_{+} \text {Sch} (f_{R}(t_{+}), t_{+}) \right) \nonumber \\= & {} \frac{\alpha _{S}}{{\mathcal {J}}\left( \frac{\beta }{T} + i\right) } \int _{0}^{T} d t \, \, \text {Sch} (f_{L}(t), t) \nonumber \\&+ \frac{\alpha _{S}}{{\mathcal {J}}\left( \frac{\beta }{T} - i\right) } \int _{0}^{T} d t \, \, \text {Sch} (f_{R}(t), t). \end{aligned}$$
(85)

In the above expression \(\alpha _{S}\) is found by numerical fitting.

4 Conclusions

In this work we obtain a large N, late times T, steepest descent approximation for the SYK spectral form factor. We worked out a regularization for the replica diagonal kinetic operator and find explicitly its dominant form for the large T regime. By those results, we derive the effective action in the two time reparametrization soft modes, for the large time T regime. Our work puts on a stronger ground [1], where the form of the two Schwarzian effective action was heuristically guessed by indirect arguments, supported by numerical evidences [51].