1 Introduction

The theory of strongly interacting matter, quantum chromodynamics (QCD), predicts hadrons to quarks and gluons deconfinement transition at high density and/or temperature [1]. The deconfinement transition at high temperature has been observed in heavy-ion collisions [2, 3] but the presence of quarks at high density remains unsolved. One of the naturally occurring laboratories of the dense matter is the cores of neutron stars (NSs). However, the cores are not directly visible, and to have any information, we have to model NSs from the core to the surface and then match them with observations [4, 5].

The properties of matter, in particular, the equation of state (EoS) that relates energy density and pressure at two extreme density limits at zero temperature, are known with a certain degree of accuracy [6]. At the low-density regime till nuclear saturation density, the matter is in the hadronic (HAD) phase, and the modern nuclear theory (like chiral effective field theory) is quite accurate [7] in describing it. In the very high-density limit perturbative-QCD (pQCD) techniques with quarks and gluons as their degrees of freedom become reliable. This points to the fact that there is a deconfinement phase transition (PT) from hadrons to quarks happening at densities between these two limits. The cores of NSs at their heart bears these intermediate densities where PT can occur [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].

Various astrophysical observations in the last two decades have given much hope to establishing the properties of matter at NS cores. A big breakthrough came with the precise measurements of masses of three massive pulsars [23,24,25]. However, mass measurement alone is not sufficient to eliminate the uncertainties in the EoS; subsequent accurate knowledge of NS radius is also needed. NS Interior Composition Explorer (NICER) was recently launched, which is estimated to measure the NS radius with \(5\%\) accuracy. It recently measured the mass-radius of a pulsar PSR J0030+0451 (R=\(12.71^{+1.14}_{-1.19}\) and M=\(1.34^{+0.15}_{-0.16}\)) [26, 27]. A few months ago, a joint NICER/XMM-Newton Collaboration measured the radius of the most massive pulsar PSR J0740+6620 [28, 29].

Another significant milestone was reached with the detection of gravitational waves (GW) from binary NS merger event GW170817 [30]. During the inspiral phase, both the NSs induce a strong tidal deformation on the other due to their strong gravitational fields [31]. The tidal deformability of an NS is governed by its compactness (compactness \(C=M/R\)), and its information gets imprinted on the GW signal, which puts an additional constraint on the EoS [32,33,34,35,36]. GW170817 gave tidal deformability (\(\varLambda \)) bound of \(\varLambda _{1.4} \le 580\) for a 1.4 solar mass NS [37], which constrains the radius of the same to be in the range of \(11.9^{+1.4}_{-1.4}\) km.

Even with these new stringent constraints, it is not possible to conclude whether an NS core can shelter quark matter or not [32, 38]. It would be important if some general relations capable of distinguishing between pure HAD NS and NS with quark core could be obtained. Also, it would be very significant if one could quantitatively deduce the amount of quark matter present in a star. In the present article, we investigate whether one can define some semi-empirical relations towards the fact.

2 Formalism

In this study we consider both non-rotating and rotating NSs. For rotating NS, we have used the publicly available RNS code [39] that solves Einstein equations for axisymmetric stars. The metric used for the rotating star is [40] is given by

$$\begin{aligned} ds^2=&-e^{2\nu }dt^2+e^{2\alpha }(dr^2+r^2d\theta ^2)\nonumber \\&+e^{2\beta }r^2\sin ^2\theta \left( d\phi -\omega dt\right) ^2 \end{aligned}$$
(1)

where \(\nu \), \(\alpha \) and \(\beta \) are unknown functions of r and \(\theta \) and \(\omega \) is the frame dragging term which is also function of r and \(\theta \). The stress energy tensor is taken to be

$$\begin{aligned} T_{\mu \nu }=(\rho +P)u_{\mu }u_{\nu }+Pg_{\mu \nu } \end{aligned}$$
(2)

where \(\rho \) and P are density and pressure of the star. For a rotating star, the fluid velocity \(u^{\mu }\) can be written as

$$\begin{aligned} u^\mu =\frac{dx^\mu }{d\tau }=\frac{dx^\mu }{dt}\frac{dt}{d\tau }=\frac{dx^\mu /dt}{\sqrt{1-v^2}}e^{-\nu } \end{aligned}$$
(3)

where \(v=(\varOmega -\omega )r\sin \theta e^{\beta -\nu }\) and \(\varOmega \) is the angular velocity of the star measured by an observer at infinity. For a static non-rotating star (\(\varOmega =\omega =0\)), we use the Tolman–Oppenheimer–Volkoff (TOV) equations to calculate P, \(\rho \), mass \(M^s\) and radius \(R^s\) of the static star respectively using,

$$\begin{aligned}&\frac{dP(r)}{dr}=\frac{(\rho (r)+P(r))(4\pi r^3P(r)+m(r))}{r^2(1-2m(r)/r)} \end{aligned}$$
(4)
$$\begin{aligned}&\frac{dm(r)}{dr}=4\pi r^2\rho (r) \end{aligned}$$
(5)

where due to spherical symmetry, all the quantities are functions of r only. \(M^s\) and \(R^s\) is calculated by numerically solving Eqs. (4) and (5) till the condition \(P(r=R^s)\rightarrow 0\) and \(\rho (r=R^s)\rightarrow 0\) is reached at the surface of the star. However for a rotating star (\(\varOmega \ne 0\) and \(\omega \ne 0\)), the star loses its spherical symmetry due to centrifugal distortions but retains axisymmetric. The pressure equation for such a system in differential form is

$$\begin{aligned} dP-(\rho +P)\left[ d\ln u^t+u^tu_\phi d\varOmega \right] =0 \end{aligned}$$
(6)

where the quantity \(u^tu_\phi \) arises due to the differential rotation of the NS and is taken to be zero as the rotational velocity at the center of the coordinate system \(\varOmega _c\) is equal to the rotational velocity of the star \(\varOmega \). Equation (6) is solved in order to calculate \(R_e\) and \(r_p/r_e\) which is the equatorial radius and the axes ratio of the star respectively by solving for pressure and density as a function of radius. The gravitational mass of the star is calculated by solving the integral,

$$\begin{aligned} M&=2\pi \int _0^{R_e}\int _0^{\pi } drd\theta r^2\sin \theta e^{2\alpha +\beta }\Bigg [e^\nu \Bigg (\frac{(\rho +P)(1+v^2)}{1-v^2}\nonumber \\&\quad +2P\Bigg )+2r\sin \theta \omega e^\beta \frac{\rho +P}{1-v^2}v\Bigg ]. \end{aligned}$$
(7)

However, the final ingredient needed to obtain the stellar structure in both cases is the EoS. To construct a NS, one needs a HAD EoS. In our study, we have used 18 different EoS, and their details are given in Table I of Supplementary. To construct a hybrid star (HS), we need a hybrid (HYB) EoS. We construct the HYB EoS such that it has HAD matter (HM) at low density, mixed-phase (quarks and hadrons) at intermediate density range, and pure quark matter at high density. For the EoS of the HM, we consider several relativistic mean-field (RMF) models (details are in Supplemental Material). The EoS of the quark part is constructed by adopting the modified MIT Bag model consisting of up (u), down (d), and strange (s) quarks and electrons [41]. The strong interaction correction and the non-perturbative QCD effects are included via two effective parameters \(a_4\) and \(B_\mathrm{eff}\) [42, 43]. The EOS of the mixed-phase region is obtained via Gibbs construction [44, 45] as can be seen from Fig. 1. The \(B_\mathrm{eff}\) and \(a_4\) are chosen in such a way so that the hybrid star (HS) formed by such hybrid (HYB) EoS satisfies all the present nuclear and astrophysical bounds. If the mixed-phase region extends to very high densities, the NS constructed with these EoS will have a mixed-phase at their core, and pure quark matter will not appear in these stars. However, the mixed-phase occurs at relatively lower densities; therefore, massive stars constructed with these EoS are likely to have a pure quark core followed by a mixed-phase region in the intermediate region and a pure HAD outer surface. In the rest of the paper, our quark core implies a mixed-phase and/or pure quark core with radius \(R^q\) (\(R_e^q\) and \(R_p^q\) for equatorial and polar radius, respectively, in the case of the rotating star), which can be calculated by numerically solving the change in density of the star’s interior as a function of r. For a static star, the r at which we reach \(\rho _\mathrm{crit}^\mathrm{mix/pure}\) is the \(R^q\), where \(\rho _\mathrm{crit}^\mathrm{mix/pure}\) is the starting density of the mixed-phase, and we get an inner spherical core of mixed-phase inside the HS. For a rotating star the \(\rho _\mathrm{crit}^\mathrm{mix/pure}\) along different direction (\(\theta \)) is reached at different r. Along the equator (\(\theta =\frac{\pi }{2}\)) it is at \({R_e^q}\) and along the pole (\(\theta =0\)) it is at \({R_p^q}\), where \(R_p^q<R_e^q<R_e\).

The volume for the quark content inside the star is calculated by integrating the star over the proper radius of the quark core \(R_e^q\) and taking the ratio of the volume of the quark core with the volume of the star. Thus we define the volume fraction (VF) as

$$\begin{aligned} VF=\frac{\int _{0}^{R_{e}^q}\int _{0}^{\pi /2}\sqrt{-g}r^2(\theta )\sin \theta d\theta dr}{\int _{0}^{R_{e}}\int _{0}^{\pi /2}\sqrt{-g}r^2(\theta )\sin \theta d\theta dr} \end{aligned}$$
(8)

whereas mass fraction (MF) of the quark content inside the star is calculated by taking the ratio of the mass of the quark core with the total mass of the star (M)

$$\begin{aligned} MF=\frac{4\pi }{M}\int _{0}^{R_{e}^q}\int _{0}^{\pi /2}\rho (r,\theta )r^2(\theta )\sin \theta d\theta dr. \end{aligned}$$
(9)

The radial integration can be done up to \(R_e^q\) for all values of \(\theta \) and is simple for a static star. For a rotating star as \(R_p^q<R_e^q\) we do the integration but assume \(\rho =0\) for those \(\theta \) where \(r > R_p^q\).

Fig. 1
figure 1

Plot of pressure P as a function of the density \(\rho \) for 18 EoS using Gibbs construction. The change in slope in the Plot indicates the presence of a mixed-phase having quark and HM. The beginning of the constant slope shows the presence of pure quark matter

Full size image

3 Results

In Fig. 2, we plot the mass-radius sequences for pure HAD stars using S271v2 (shortened as S27) and DD2 EoS [46, 47]. It also shows sequences for HSs (with HYB EoS). The \(M{-}R\) curves are clustered into two distinct regions, one for the static stars and the other for stars rotating with Kepler frequency. The clustering of the curves happens because the Keplerian stars have the rotational energy to support more massive stars compared to the static stars having the same central energy density. Moreover, due to centrifugal distortion (Keplerian star), the equatorial radius \(R_e\) of the star is greater than that of the static star radius, resulting in the shift of the \(M{-}R\) curve to the right. The HYB EoS are softer than HAD EoS because of extra degrees of freedom. Thus HAD EoS supports more massive stars than the HYB EoS, as seen from the \(M{-}R\) curves. By calculating the ratio \(M^k_\mathrm{max}/M^s_\mathrm{max}\), where \(M^k_\mathrm{max}\) and \(M^s_\mathrm{max}\) are the maximum masses of static and Keplerian sequences, respectively, we find that it remains in the range \(\simeq 1.19-1.28\) (see Table II in Supplementary Materials) across the EoS and thereby showing a semi-universal behavior. An earlier study [48] done with purely HAD EoS found \(M^k_\mathrm{max}/M^s_\mathrm{max}=1.203\pm 0.022\). Therefore, we can conclude that the inclusion of HYB EoS does not break the universality of the ratio \(M^k_\mathrm{max}/M^s_\mathrm{max}\) obtained for pure HAD EoS, although the range gets a little wider.

Fig. 2
figure 2

\(M{-}R\) has been plotted for S27 EoS. The Plot shows two main clusters, the static model (Stat) and Keplerian model (Kep), where each of the models has hadronic (HAD) and Hybrid (HYB) EoS. The maximum mass and its corresponding radius and central density are obtained from the Plot. The hadronic EoS supports more massive stars than the quark EoS (as the EoS is softer)

Full size image
Fig. 3
figure 3

Plot of \(C^s/C^k\) as a function of \(j/j^{k}\) for NSs and HSs constructed from 18 HYB EoS are shown in the figure. Gray dots represent the NSs, and the HSs are red dots

Full size image

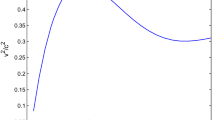
Next, we calculate the compactness of non-rotating and uniformly rotating NS for both HAD and HYB EoS as a function of angular momentum (J). In the Fig. 3 we have plotted the ratio \(C^j/C^s\) as a function of dimensionless angular momentum \(j/j^k\), where \(j=J/(M^j_\mathrm{max})^2\), \(j^k=J^k/(M^k_\mathrm{max})^2\), \(J^k\) is the Keplerian angular momentum, i.e., the maximum angular momentum that a uniformly rotating NS can sustain for a given EOS and \(M_\mathrm{max}^j\) is the maximum mass of a sequence for a given J. Interestingly, the values of \(C^j/C^s\) lie in a narrow band for the whole range of \(j/j^k\). The compactness does not change much with rotation till \(j/j^k\sim 0.6\). However, for larger values of \(j/j^k\), compactness decreases fast, producing a knee-region and getting reduced by \(\sim 10\%\) at \(j=j^k\). Careful observation reveals that \(C^j\) drops a little faster for HYB EoS in comparison to the HAD EoS. We obtain fits for both the cases with a function of the form:

$$\begin{aligned} \frac{C^j}{C^s} = a + b\, \left( \frac{j}{j^k} \right) ^c . \end{aligned}$$
(10)

The coefficients of the fits are given in Table 1.

Table 1 Coefficients and error of fit given in Eq. (10) for the data shown in Fig. 3
Full size table

A relation between the compactness of the Keplerian stars and static stars can be obtained by setting \(j=j^k\) in Eq. (10). It gives \(C^k=0.911\,C^s\) for HAD fit and \(C^k=0.913\,C^s\) for HYB fit. There is no significant difference between the two sets of EoS. It necessarily means that the ratio \(C^k/C^s\) is not only independent of the EoS but also does not depend on whether an NS contains quarks or not. However, there is some difference in the knee region (see Fig. 3). For example, putting \(j=0.8\,j^k\) in Eq. (10) we get \(C^j=0.974\, C^s\) and \(0.990\,C^s\) for HAD and HYB EoS, respectively. It seems like if the angular momentum and the compactness of an NS are estimated from astrophysical observation and if \(j/j^k\) lies around 0.8, within the calculated \(\chi _{red}^2\) error, one may possibly differentiate whether the star has a quarks core. However, from the scattered nature of the plot, this would require an unrealistically high observational accuracy which is difficult to achieve with present detectors. In Fig. 3 we, therefore, include a fit obtained with all the HAD and HYB EOS. The corresponding data are shown in the last row of Table 1.

Fig. 4
figure 4

(Left panel) The plot shows relation between the volume fraction and mass fraction with the critical density \(\rho ^{mix}_{crit}\) of appearance of quark matter and shows a decreasing pattern with increase in density. (Right panel) Volume fraction has been plotted with mass fraction of quark matter in the interior of the star showing linear relation among them. The calculation has been done for \(1.4\;M_{\odot }\) hybrid stars constructed from 18 different hybrid EoSs

Full size image
Fig. 5
figure 5

(Left panel) The plot shows volume fraction VF as a function of the tidal deformability \(\varLambda _{1.4}\). (Right panel) The plot of the quark content MF as a function of the tidal deformability \(\varLambda _{1.4}\) for a \(1.4\; M_{\odot }\) static star constructed from 18 different EoS in the red hollow dots. The nonlinear relation of the quark content and the tidal deformation depicts the dependency of both the quark content of the star and the stiffness of the EoS in giving the final tidal deformability value. The \(Z=\left( MF\times \frac{M}{R^k}\right) _{1.4}\) has been plotted along with the quark content and is shifted by 0.73 for comparison. The Z shows a constant behavior independent of the \(\varLambda _{1.4}\) value

Full size image

The quark core further warrants the analysis of the quark content of the star, which is quantified by the volume fraction and mass fraction. This, in turn, depends on the critical density of the star \(\rho _{crit}^{mix}\) from where quark matter starts to appear. Figure 4 (left panel) shows that as the critical density increases, the volume and mass fraction decreases. It is primarily because the QM appears at a much higher density as the critical density increases. Therefore, the region of quark matter at the core of the HS shrinks, decreasing the star’s VF or MF as the star’s overall volume and mass do not alter much. There is also a minimum limit for the VF and MF as there exists a maximum mass for each EoS corresponding to a particular central density. The distribution of VF and MF is fitted by the linear relation, \(VF=1.028-0.189\left[ \rho _{crit}^{mix}\right] \) and \(MF=1.207-0.136\left[ \rho _{crit}^{mix}\right] \) with \(\chi _{red}^2=5.807\times 10^{-4}\) and \(\chi _{red}^2=9.442\times 10^{-4}\) respectively.

In Fig. 4 (right panel), we have plotted the quark content of the star, where the mass fraction of the quark core is seen to be related to the volume fraction as

$$\begin{aligned} MF=a_1+b_1\left[ VF\right] \end{aligned}$$
(11)

where \(a_1=0.465\) and \(b_1=0.725\) with a reduced chi-squared value of \(\chi _{red}^2=4.909\times 10^{-4}\). Although a linear relationship between the VF and MF exists, there is no such relationship between the actual volume and masses of the star. Thus knowing one (either VF or MF), the information of the other can be easily obtained from Eq. (11). The two relations (fitting function) are consistent, as are the figures.

The tidal deformability \(\varLambda \) is the measure of the quadrupole (\(Q_{ij}\)) response of the star in presence of an external tidal field \(\epsilon _{ij}\) (\(Q_{ij}=-\lambda \epsilon _{ij}\)) and \(\varLambda \) is defined as \(\varLambda =\lambda M^{-5}\) [31]. The tidal deformability of a star depends on its compactness, which thereby depends on the EoS. Universal relations (known as I-Love-Q relations) between the moment of inertia (I), \(\varLambda \) and Q that are independent of the neutron and quark star’s internal structure were found to exist [49]. Recently, it has been shown that even hybrid stars resulting from a strong first-order PT satisfy I-Love-Q relations for both static and rotating stars [50].

In our calculation, the presence of quark matter softens the EoS; hence the tidal deformability of a star also depends on the amount of quark content at the star’s core, which can be quantified by either MF and VF. The quark fraction of each HYB EoS is different; therefore, the tidal deformation is not a linear function of the quark content (VF or MF), as shown by the red hollow circle in Fig. 5 (left and right panel). Both the quark fraction and stiffness of the EoS play a part in determining the effective compactness of the star. The Keplerian compactness \(\left( M/R^k\right) _{1.4}\) gives a good measure of the stiffness of the EoS of the star as it depicts the maximum deformation of the star before it starts to shed mass. We thus define \(Z\equiv \left( MF\times \frac{M}{R^k}\right) _{1.4}\) and plot it as a function of \(\varLambda _{1.4}\). Interestingly, we find that the value of Z does not change much with \(\varLambda _{1.4}\) and can be fitted by a linear function as \(Z= 0.783-0.00003\varLambda _{1.4}\) (\(\chi ^2_{\mathrm{red}}=5.850\times 10^{-5}\)), which has been shown by a dotted line in Fig. 5 (right panel). A constant factor of 0.730 has shifted the value of Z to compare it with the variation of MF. A similar analysis can be done for VF, which, however, produces the same qualitative result due to its linear relationship with MF. Z carries the information of both the quark content and stiffness of the EoS of a \(1.4\; M_{\odot }\) star and is independent of the EoS. The particular analysis is done for a star of 1.4 solar mass; however, the linear relationship of VF and MF holds for other masses.

Fig. 6
figure 6

The plot of Q is a function of the mass has been shown. The mass is in the units of solar mass \(M_{\odot }\) and has been plotted for mass ranging from \(1.0\; M_{\odot }\) to \(2.79\; M_{\odot }\) constructed with 18 HYB EoS. The Q for stars having a particular rotational velocity lies in a band, and its width increases with an increase in rotational velocity

Full size image
Fig. 7
figure 7

Plot of gravitational mass as a function of the radius of the star. The Plot has been done for static and Keplerian stars constructed from S27 EoS. The Plot shows PT from NSs to HSs indicated by arrows (keeping the baryonic mass conserved). The mass and radius change can be seen from the plots where the mass loss is most prominent for the highest masses in each case

Full size image

The change in the quark content of a rotating star \(VF^{\varOmega }\) to that of the static star of the same mass and can be compared by the relation \(Q\equiv \frac{VF^{\varOmega }}{VF^s}\). The Q measures the loss of quark content by a rotating star compared to a static star of the same mass. We have plotted Q for stars with four different masses and angular velocities in Fig. 6. As the rotational velocity increases, its quark content reduces (due to the reduction of central density). For a specific rotational value, it lies in a range (shaded region in the figure). The range increases with the increase in rotational velocity. It can be seen from Fig. 6 that, for \(\varOmega =0.20\) and \(\varOmega =0.35\), the Q value is almost identical and close to unity for most of the EoS. This is because as the rotational velocity is significantly less than \(\varOmega =0.50\) and the Keplerian velocity, the quark content does not differ much from the static case. Thus the low velocity Q values overlap. For a star rotating with Keplerian velocity, the quark content is minimum, and the Q value lies in a patch having the bound of \(0.224\le Q\le 0.514\), as can be seen from the figure. The value of Q shows that the quark content of a rotating star reduces (by an amount bounded by this range) for the star to be stable. An HS with a quark core must lie within the Q bound to be stable and not start shedding mass or collapse into a black hole (BH).

Also, for each equation of state, we have defined \(Q^{\#}\), the ratio of the quark content between the maximum static mass star and the maximum Keplerian mass star constructed from a given EoS. It is interesting to find that the \(Q^{\#}\) lies in a narrow range between \(\sim 0.506{-}0.623\) universally across the EoS (Table IV in Supplementary). \(Q^\#\) thus contains the information of the shift in quark content between the maximum static star mass and the maximum Keplerian star mass, which lies on the maxima of the respective \(M{-}R\) curves. The values of \(Q^\#\) lie in a narrow range indicating a constant shift of the volume fraction independent of the EoS. This behavior is similar to the \(M{-}R\) curve shift between Keplerian and static stars due to the clustering as previously discussed for Fig. 2 (see Table II in Supplementary).

If an HS is to be formed via PT from an NS and there is no mass loss during a PT, the baryonic mass of a star remains conserved. However, the star’s gravitational mass, a combination of the baryonic mass and the negative binding energy of the star, changes. Figure 7 shows how the gravitational mass and radius of the star change after PT for S27 EoS. The change in the gravitational mass is relatively small; however, the radius shrinks considerably. Therefore, as PT occurs and a quark core is formed inside a star, the star becomes more compact. The figure also shows the mass and radius change due to the PT increases with the star’s mass. These results are consistent with previous results regarding the PT of hadronic matter at the core of NS to a new phase. The new degree of freedom or entirely new phase that appears at the center of the star can be in the form of Kaon-condensate [51], heavier baryons like hyperons and \(\varDelta \)-resonances [52], or even can be a quark matter phase [53, 54]. In almost every study, the new phase softens the EoS, and therefore the mass of the phase-transformed star decreases and can even collapse to a black-hole [54].

Fig. 8
figure 8

(Left panel) Figure shows the ratio of \(M_\mathrm{crit}/R_\mathrm{crit}\) as a function of \(M_\mathrm{had}\) and the corresponding band of critical compactness (gray region), the unstable region (black region) and the stable region (white region). Each black hollow dot denotes a given EoS. (Right panel) Plot shows the variation of \(\varDelta (M/R)\) as a function of \(M_\mathrm{crit}/R_\mathrm{crit}\) for different EoS and the obtained fit for PT from NS to HS

Full size image

In our present study, we also find that massive NS after PT becomes unstable and probably collapses to a BH as relatively softer HYB EoS (due to the presence of quark after PT) can no longer balance inward gravitational pull. There is an upper bound on the initial NS mass \(M_\mathrm{crit}\) and its corresponding radius \(R_{crit}\) beyond which if an NS undergoes PT, it becomes unstable (beyond the Q bound), which either shreds mass or collapses to a BH.

We plot the critical compactness (\(M_\mathrm{crit}/R_\mathrm{crit}\)) of the initial NS with \(M_\mathrm{had}\), which denotes the maximum hadronic mass of a static star for different EoS, and is shown in Fig. 8 (left panel). The critical compactness of the hadronic star undergoing phase transition lies in a band (gray region). Therefore, given an initial mass of an NS undergoing PT, we can infer that it will surely result in a stable NS if it lies below the band (white zone) and will shed mass or collapse to a BH if it stays above the band (black region). Once this is deduced, the right panel of Fig. 8 then gives the change in the compactness of the star (the difference between the parent NS and daughter HS compactness). Although the points corresponding to different EoS are a bit scattered, we can draw a linear curve for the scattered points. With the approximate linear curve one can find that the compactness varies linearly with \(M_\mathrm{crit}/R_\mathrm{crit}\) having a fit value of \(\varDelta (M/R)=0.053-0.245 M_\mathrm{crit}/R_\mathrm{crit}\) and with \(\chi ^2_{red}=1.54\times 10^{-6}\). The change in compactness (and thereby the mass) due to PT is related to the energy released during PT. Therefore, one can approximately determine the amount of energy that will be emitted during the PT.

It is seen from Table I of Supplementary Material that the onset density of the mixed-phase as well as the quark core is confined within a given range. This is because we have chosen the EOS to be consistent with all the current nuclear physics and astrophysical bounds. In practice, we have scanned all the RMF parameter sets available in the literature and the full parameter space of the MIT Bag model (different values of \(B_\mathrm{eff}\) and \(a_4\)) and found only a few combinations that are used here, are consistent with all the bounds. Furthermore, we have considered phase transition from hadronic matter to quark matter via Gibbs construction, characterized by the appearance of the mixed-phase. In such a scenario, an HS is always less massive than the corresponding hadronic star. This is in contrast to the case of Ref. [32], where the EOS of the high-density phase (e.g., quark) can be stiffer than the hadronic EOS. Moreover, the stiffer the quark EOS earlier the mixed-phase starts, and we do not consider quark EOS for which the mixed-phase starts at densities much smaller than the saturation density. This further restricts the number of EOS in our study. We, therefore, can not rule out the possible model dependence of our results. However, to compare our findings, we have also checked our results with a very different quark matter EoS, the quark hadron crossover 2018 (QHC18) [55]. Although the EoS is very different (fig 2 of the Supplementary File), the findings are consistent with our results for the MIT Bag model EoS (fig 2 and Table VI, VII, and VIII in Supplementary).

4 Summary and conclusion

Recently, there has been considerable development in astrophysical observation from pulsars and binary NS mergers, which can throw light on the presence of exotic matter at NS cores. It would be incredibly beneficial if one could develop an empirical relation that can distinguish between NS and HS. We find that the ratio \(C^j/C^s\) shows different behavior for fast rotating NSs compared to fast-rotating HSs and is independent of EoS. However, there is also quite a scatter in the data, therefore, even if we measure fast-rotating newly born pulsars, it would require unnaturally precise measurement to infer the occurrence of a quark core at the center of the star. It is consistent with the earlier findings that HYB stars can masquerade NS [56].

If pulsars shelter quark matter at their cores, the next question would be the amount of quark matter in them. We have shown that the amount of QM depends on both stiffness of the EoS and density where the PT from HM to QM takes place (the critical density). Both the volume fraction and mass fraction depend linearly on the critical density. We have also shown that Z, which carries the information of both quark content and stiffness of the EoS of a 1.4 static solar mass star, is independent of the EoS. Although Z is defined for static stars, the quark content change for rotating stars is obtained from the bound on the Q value. Therefore, given a quark content of a star rotating with some velocity, one can deduce the amount (within a range) of quark content of stars of the same mass having different rotational velocities.

We have also discussed the critical mass of an NS, which after PT results in a stable HS. The critical compactness of the initial NS as a function of the maximum mass lies on the band. Therefore, assuming that two NSs are undergoing a merger and forming a hyper-massive NS which harbors a quark core at their center, our calculation tells whether the hyper-massive star would result in a stable NS or collapse to a BH. Our study can also deduce the approximate energy released during the PT process.

In this study, we have employed a limited number of hadronic and hybrid EOS. Moreover, all the hadronic EOS considered are from RMF theory and the QM EoS are modeled with MIT bag model having effective quark interactions. To make our analysis model-independent and more robust, we plan to explore a more extensive set of EOS in a future study.