1 Introduction

In astronomy, polytropic equation of state (EoS) is used extensively in the study of stellar structure of compact objects (CO) [1, 2]. The idea of polytropes is crucial because of the availability of a simple EoS and the resulting Lane–Emden equation (LEe), which helped us in understanding a variety of phenomena related to CO. Chandrasekhar [1] explained how Newtonian polytropes emerge from the principles of thermodynamics for polytropic spheres. Tooper [3, 4] developed the fundamental formalism of polytropes for compressible fluids. He extended his discoveries to an adiabatic process and set up the basic structure for the development of relativistic polytropes.

Polytropes are widely used for different kinds of analysis in general relativity (GR) by utilizing the LEe, which is obtained from hydrostatic equilibrium configuration of stars. Herrera et al. [5] examined anisotropic polytropes with a conformally flat condition obtained relativistic LEe. Cracking of anisotropic polytropes is discussed by Herrera et al. [6, 7]. The existence of charge plays very significant role in understanding the dynamics of celestial objects. Azam et al. [8,9,10,11] studied the existence of cracking points in charged CO models. The electromagnetic field, as well as the EoS, chosen, are found to have an impact on the stability of these objects. Noureen et al. [12] examined the impact of charge and anisotropy with the help of generalized polytropic equation of state (GPEoS) in CO.

The GPEoS depends is a combination of linear EoS and regular polytropic EoS and can be written as

$$\begin{aligned} P=\alpha _{1}\rho _{1}+\kappa \rho _{1}^{\varrho } =\alpha _{1}\rho _{1}+\kappa \rho _{1}^{1+\frac{1}{a_{r}}} , \end{aligned}$$
(1)

where the isotropic pressure, mass (baryonic) density are denoted by P and \(\rho _{1}\), the polytropic constants, polytropic exponents, and polytropic index are referred to as \(\kappa \), \(\varrho \), and \(a_{r}\), respectively.

The existence of pressure anisotropy is a very common issue in CO (see [13,14,15] and references therein) as it occurs due to unbalance pressure stresses. Furthermore, system variables such as dissipation, energy density inhomogeneity, and shear cause the isotropic pressure state to become unstable, as demonstrated recently in [16]. We propose to use the same approach as in [13, 17], expecting that both radial and tangential pressure fulfill GPEoS as

$$\begin{aligned} P_{r}= & {} \alpha _{2}\rho +\kappa _{r}\rho ^{\varrho _{r}}=\alpha _{2}\rho +\kappa _{r}\rho ^{1+\frac{1}{a_{r}}}, \end{aligned}$$
(2)
$$\begin{aligned} P_{\perp }= & {} \alpha _{2}\rho +\kappa _{\perp }\rho ^{\varrho _\perp }=\alpha _{2}\rho +\kappa _{\perp }\rho ^{1+\frac{1}{a_{\perp }}}, \end{aligned}$$
(3)

where energy density is represented by \(\rho \). This plan of this work is as follows: Sect. 2 is devoted for the derivation of Einstein–Maxwell field equations and development of hydrostatic equilibrium condition. In Sect. 3, two different cases of relativistic polytropes will be discussed. We will examine the theory of relativistic double polytropes in Sect. 4. In Sect. 5, we will conclude our results and discussion.

2 Einstein–Maxwell field equations

A static spherically symmetric charged anisotropic fluid distribution is considered and the line element is given by

$$\begin{aligned} ds^2=e^{\nu (r)} dt^2-e^{\lambda (r)} dr^2 - r^2 (d\theta ^2 + \sin ^2 d\phi ^2), \end{aligned}$$
(4)

where \(\nu \) and \(\lambda \) are function of r only. The energy momentum tensor for anisotropic fluid is given by

$$\begin{aligned} T_{k l}=(\rho +P_\perp )u_{k}u_{l}-P_\perp g_{k l}+(P_{r}-P_\perp )s_{k}s_{l}, \end{aligned}$$
(5)

where, \(u^{k}=(e^{-\frac{\nu }{2}}, 0, 0, 0)\) and \(S^k =(0,e^{-\frac{\lambda }{2}},0,0)\) are defined as the four-velocity and four-vectors respectively having the properties \(s^{k}u_{k}=0\), \(s^{k}s_{k}=-1\). The electromagnetic part of energy–momentum tensor is defined as

$$\begin{aligned} T_{k l}=\frac{1}{4\pi }\Big (F_{k}^{f}F_{l f}-\frac{1}{4}F^{f g}F_{f g}g_{k l}\Big ), \end{aligned}$$
(6)

where \(F_{k l}=\varphi _{l,k}-\varphi _{k,l}\) , is the Maxwell field tensor and it satisfy the following relations

$$\begin{aligned} F^{k l}_{;l}=c_{1}J^{k},~~~F_{[kl,m]}=0, \end{aligned}$$
(7)

with four potentials is denoted by \(\varphi _{k}\), four current is represented by \(J^{k}\) and magnetic permeability is \(c_{1}\). In comoving coordinates, following identities must be satisfied

$$\begin{aligned} \varphi _{k}=\varphi (r)\delta _{k}^{0}~~,~~J^{k}=\sigma u^{k}~~,~~k=0, 1, 2, 3. \end{aligned}$$
(8)

In the above relations \(\varphi \) is scalar potential and the charge density is denoted by \(\sigma \). Then from Eq. (7)

$$\begin{aligned} \varphi ^{\prime \prime }+\Big (\frac{2}{r}-\frac{\nu ^{\prime }}{2}-\frac{\lambda ^{\prime }}{2}\Big )\varphi ^{\prime }=4\sigma \pi e^{\frac{\nu +\lambda }{2}}~~, \end{aligned}$$
(9)

where the prime denotes derivative with respect to r and

$$\begin{aligned} \varphi ^{\prime }=\frac{q(r)}{r^{2}}e^{\frac{\nu +\lambda }{2}}. \end{aligned}$$
(10)

The entire charge inside the sphere is represented by \(q(r)=4\pi \int _{0}^{r}\mu e^{\frac{\lambda }{2}}r^{2}dr\) and Einstein-Maxwell field equations for the line element given in Eq. (4) are given by

$$\begin{aligned}&\lambda ^{\prime } r e^{-\lambda }+(1-e^{-\lambda })=8\pi r^2 \rho -q^2 r^{-2}, \end{aligned}$$
(11)
$$\begin{aligned}&\nu ^{\prime } r e^{-\lambda }-(1-e^{-\lambda })=8\pi r^2 P_r-q^2 r^{-2}, \end{aligned}$$
(12)
$$\begin{aligned}&r^4 e^{-\lambda }\Big [-\frac{\nu ^{\prime }\lambda ^{\prime }}{4}+\frac{\nu ^{\prime \prime }}{2}+\frac{\nu ^{\prime ^2}}{4}+\frac{\lambda ^{\prime }-\nu ^{\prime }}{2r}\Big ]=8 \pi r^{4} P_\perp + q^{2} , \nonumber \\ \end{aligned}$$
(13)

The external metric is considered as Reissner–Nordström metric. Also for smooth matching of interior and exterior regions, following conditions must be satisfied [18,19,20,21]

$$\begin{aligned}&e^{\nu _{\sum }}=\bigg (1-\frac{2M}{r_{\sum }}+\frac{Q^{2}}{r_{\sum }^{2}}\bigg )=e^{-\lambda _{\sum }},\nonumber \\&\quad q(r)=Q \quad m(r)=M, \quad P_{r_{\sum }}=0. \end{aligned}$$
(14)

where M is total mass, \(r_{\sum }\) total radius and Q is the charge on sphere. Now using \(\nu ^{\prime }=\frac{8\pi P_{r}r^{4}-2q^{2}+2mr}{r(r^{2}-2m+q^{2})},\) with mass function \(e^{-\lambda }=1-\frac{2m}{r}+\frac{q^{2}}{r^{2}},\) the conservation law’s \(\nabla _{k}T^{k l}=0\), leads to modified Tolman–Oppenheimer–Volkoff equation

$$\begin{aligned} P^\prime _{r}-\frac{2}{r}\bigg (\Delta +\frac{qq^{\prime }}{8\pi r^{3}}\bigg )=-\frac{4\pi r^{4}P_{r}-q^{2}+mr}{r(r^{2}-2mr+q^{2})}(\rho +P_{r}), \nonumber \\ \end{aligned}$$
(15)

with boundary conditions

$$\begin{aligned} m(0)=0, \quad m\Big (r_{\sum } \Big )=M, \quad P_{r}\Big (r_{\sum }\Big )=0. \end{aligned}$$
(16)

In the above equation \(\Delta =(P_{\perp }-P_{r})\), is the anisotropy factor. In the next section, the development of LEe will be discussed with the help of GPEoS.

3 Generalized relativistic polytopes

In this section, we will briefly describe the theory generalized polytropes for two different cases of GPEoS.

3.1 Case 1

For case 1, the GPEoS is written is

$$\begin{aligned} P_{r}=\alpha _{2}\rho +\kappa \rho ^{\varrho _{r}}, \end{aligned}$$
(17)

and we define a variable \(\chi \) as

$$\begin{aligned} \rho =\rho _{c}\chi ^{a_{r}}, \end{aligned}$$
(18)

where \(\rho _{c}\) shows the central energy density, then \(P_{r}\) can be written as

$$\begin{aligned} P_{r}=\alpha _{2}\rho _{c}\chi ^{a_{r}}+\kappa \rho ^{\varrho _{r}}_{c}\chi ^{1+a_{r}}=\alpha _{2}\rho _{c}\chi ^{a_{r}}+h_{rc}\chi ^{1+a_{r}}, \end{aligned}$$
(19)

with \(h_{rc}=\kappa \rho ^{\varrho _{r}}_{c}\), Also the derivative \(P_{r}\) is given by

$$\begin{aligned} P^\prime _{r}=\alpha _{2}\rho _{c}a_{r}\chi ^{a_{r}-1}\chi ^\prime +h_{rc}(1+a_{r})\chi ^{a_{r}}\chi ^\prime , \end{aligned}$$
(20)

and as a result of which Eq. (15) can be written as

$$\begin{aligned}&2a_{r}\rho _{c}\alpha _{2}\frac{\chi ^\prime }{\chi }+2h_{rc}(1+a_{r})\chi ^\prime \nonumber \\&\quad -\frac{4}{r\chi ^{a_{r}}}\bigg (\Delta +\frac{qq^\prime }{8\pi r^{3}}\bigg )+ \nu ^\prime (\rho _{c}+\alpha _{2}\rho _{c}+h_{rc}\chi )=0, \nonumber \\ \end{aligned}$$
(21)

we define \(j_{c}=\frac{h_{rc}}{\rho _{c}}\), which implies

$$\begin{aligned}&2a_{r}\alpha _{2}\frac{\chi ^\prime }{\chi }+2j_{c}(1+a_{r})\chi ^\prime \nonumber \\&\quad -\frac{4}{r\rho _{c}\chi ^{a_{r}}}(\Delta +\frac{qq^\prime }{8\pi r^{3}})+ \nu ^\prime (1+\alpha _{2}+j_{c}\chi )=0, \end{aligned}$$
(22)

and \(\nu ^\prime \) can be calculated as

$$\begin{aligned} \nu ^\prime= & {} \frac{4(\Delta +\frac{qq^\prime }{8\pi r^{3}})}{r\rho _{c}\chi ^{a_{r}}(1+\alpha _{2}+j_{c}\chi )}\nonumber \\&\quad -2j_{c}\Bigg (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Bigg )\frac{\chi ^\prime }{1+\alpha _{2}+j_{c}\chi }, \end{aligned}$$
(23)

The integration of Eq. (23) results in following expression

$$\begin{aligned} \nu= & {} \nu _{c}+\frac{4}{\rho _{c}}\int _{0}^{r}\frac{(\Delta +\frac{qq^\prime }{8\pi r^{3}})dr}{r\chi ^{a_{r}}(1+\alpha _{2}+j_{c}\chi )}\nonumber \\&-2\Bigg (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\log \bigg (\frac{1+\alpha _{2}+j_{c}\chi }{1+\alpha _{2}+j_{c}}\bigg )\Bigg ), \end{aligned}$$
(24)

also the boundary conditions from Eq. (14) can be used to obtain \(\nu _{c}\) as

$$\begin{aligned} \nu _{c}= & {} \log \Bigg (\frac{1-\frac{2M}{r_{\sum }}+\frac{Q^{2}}{r^{2}}}{(1+\alpha _{2}+j_{c})^{2\big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\big )}}\Bigg )\nonumber \\&- \frac{4}{\rho _{c}}\int _{0}^{r_{\sum }}\frac{(\Delta +\frac{qq^\prime }{8\pi r^{3}})dr}{r\chi ^{a_{r}}(1+\alpha _{2}+j_{c}\chi )}, \end{aligned}$$
(25)

now by using Eq. (25) into Eq. (24), we obtain

$$\begin{aligned} \nu= & {} \log \Bigg (\frac{1-\frac{2M}{r_{\sum }}+\frac{Q^{2}}{r^{2}}}{(1+\alpha _{2}+j_{c}\chi )^{2\big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\big )}}\Bigg )\nonumber \\&- \frac{4}{\rho _{c}}\int _{0}^{r_{\sum }}\frac{(\Delta +\frac{qq^\prime }{8\pi r^{3}})dr}{r\chi ^{a_{r}}(1+\alpha _{2}+j_{c}\chi )}. \end{aligned}$$
(26)

Also by using mass function and Eq. (23) into Eq. (12) yields

$$\begin{aligned}&\frac{d m}{dr}(\alpha _{2}+j_{c}\chi )+\frac{m}{r}-\frac{q^{2}}{r^{2}}\nonumber \\&\quad + \frac{r\frac{d\chi }{dr} \left( j_{c}\left( \frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\right) \right) (1-\frac{2m}{r}+\frac{q^{2}}{r^{2}})}{(1+\alpha _{2}+j_{c}\chi )} \nonumber \\&\quad - \frac{2\left( \Delta +\frac{qq^\prime }{8\pi r^{3}}\right) \left( 1-\frac{2m}{r}+\frac{q^{2}}{r^{2}}\right) }{\rho _{c}\chi ^{a_{r}}(1+\alpha _{2}+j_{c}\chi )}=0. \end{aligned}$$
(27)

Now we define dimensionless variables as

$$\begin{aligned} \psi= & {} \frac{m}{4\pi \rho _{c}(\alpha _{3})^{3}},~~~r=\alpha _{3}x,~~~\nonumber \\ (\alpha _{3})^{2}= & {} \frac{\epsilon (1+a_{r})j_{c}}{4\pi \rho _{c}}, \end{aligned}$$
(28)

then Eq. (27) can be written as

$$\begin{aligned}&\psi ^\prime x(\alpha _{2}+j_{c}\chi )+\psi -\frac{q^{2}}{4\pi \rho _{c} x} +\Big (x\chi ^\prime \nonumber \\&\quad -\frac{2(\Delta +\frac{qq^\prime }{8\pi r^{3}})}{j_{c}\rho _{c}\chi ^{a_{r}}\big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+ (1+a_{r})\big )}\Big )\Big (\frac{1}{1+\alpha _{2}+j_{c}\chi }\Big )\nonumber \\&\quad \times \Big (\frac{x a_{r}\alpha _{2}}{4\pi \rho _{c}\chi }+\epsilon x-\frac{2m a_{r}\alpha _{2}}{4\pi \rho _{c}\chi }-2j_{c}(1+a_{r})\psi \nonumber \\&\quad +\frac{q^{2}}{x}\Big (\frac{j_{c}}{4\pi \rho _{c}}\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )\Big )\Big )=0, \end{aligned}$$
(29)

where \(\psi ^{\prime } = x^{2}\chi ^{a_{r}}\) and either \(\epsilon =+1\) for \(a_{r}>-1\) or \(\epsilon =-1\) for \(a_{r}<-1\).

From this point onward prime ”\(\prime \)” represents the derivative with respect to variable x. Also by taking \(j_{c}=\frac{q_{c}}{\rho _{c}c^{2}}\), we obtain

$$\begin{aligned}&\psi ^\prime x \alpha _{2}+\psi -\frac{q^{2}}{4\pi \rho _{c} x}\nonumber \\&\quad +\frac{1}{1+\alpha _{2}} \Big (x \chi ^\prime -\frac{2(\Delta +\frac{qq^\prime }{8\pi r^{3}})}{h_{rc}\chi ^{a_{r}}\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )}\Big )\nonumber \\&\quad \times \Big (x+\frac{x a_{r} \alpha _{2}}{4 \pi \rho _{c} \chi } -\frac{2 \alpha _{2} \psi a_{r}}{\chi }+\frac{q^{2}a_{r}\alpha _{2}}{4\pi \rho _{c} x \chi }\Big )=0. \end{aligned}$$
(30)

Now using \(\psi ^{\prime } = x^{2}\chi ^{a_{r}}\), we get

$$\begin{aligned}&\chi ^{a_{r}} + \frac{q^{2}}{4\pi \rho _{c} x^{4}}+3\alpha _{2}\chi ^{a_{r}}+\Big (\frac{1}{1+\alpha _{2}}\Big ) \Big [\chi ^{\prime \prime } \nonumber \\&\quad + \frac{2\chi ^\prime }{x} - \frac{2}{h_{rc} x \chi ^{a_{r}}(1+a_{r})} \nonumber \\&\quad \times \Big (\frac{\Delta }{x}+\Delta ^\prime -\frac{a_{r}\Delta \chi ^\prime }{\chi } +\frac{qq^\prime }{8\pi r^{3}}\Big (\frac{1}{x}-\frac{a_{r}\chi ^\prime }{\chi x}\Big )\Big )\nonumber \\&\quad + \frac{\alpha _{2} a_{r}}{4\pi \rho _{c}x^{2}}(2 x \chi \chi ^\prime +x^{2} \chi ^{\prime \prime } \chi ^{-1} \nonumber \\&\quad -x^{2}(\chi ^\prime )^{2}\chi ^{-2}) -\frac{2 a_{r}\alpha _{2}}{(1+a_{r})4\pi \rho _{c}h_{rc}x^{2}}\nonumber \\&\quad \times \Big (x \chi ^{-a_{r}-1}\Delta ^{\prime }+\Delta \chi ^{-a_{r}-1} \nonumber \\&\quad +x\Delta \chi ^{-a_{r}-2}(-a_{r}-1)\chi ^{\prime }+\frac{qq^\prime }{8\pi r^{3}}\nonumber \\&\quad \times (\chi ^{-a_{r}-1}+x(-a_{r}-1)\chi ^{-a_{r}-2}\chi ^\prime )\Big ) \nonumber \\&\quad -\frac{2}{3}\frac{\alpha _{2} a_{r}}{x^{2}}\Big (4 x^{3}\chi ^{\prime } \chi ^{a_{r}-1}+x^{4}\chi ^{\prime \prime }\chi ^{a_{r}-1}\nonumber \\&\quad +x^{4}(\chi ^\prime )^{2}(a_{r}-1)\chi ^{a_{r}-2}\Big ) \nonumber \\&\quad + \frac{4\alpha _{2} a_{r}}{3 h_{rc}(1+a_{r})}\Big (3 x^{2}\chi ^{-1}\Delta +x^{3}\Delta ^\prime \chi ^{-1}\nonumber \\&\quad +x^{3}\Delta (-1)\chi ^{-2}\chi ^{\prime }+\frac{qq^\prime }{8\pi r^{3}} \nonumber \\&\quad \times (3x^{2}\chi ^{-1}+x^{3}(-1)\chi ^{-2}\chi ^{\prime })\Big )+\frac{q^{2}a_{r}\alpha _{2}}{4\pi \rho _{c}}\Big (\chi ^{\prime \prime }\chi ^{-1}\nonumber \\&\quad +(\chi ^\prime )^2(-1)\chi ^{-2}\Big ) \nonumber \\&\quad -2 \Big (\frac{a_{r}\alpha _{2} q^{2}}{h_{rc}(1+a_{r})}\Big )\Big (-x^{-2}\Delta \chi ^{-a_{r}-1}+x^{-1}\Delta ^\prime \chi ^{-a_{r}-1}\nonumber \\&\quad + x^{-1}\Delta (-a_{r}-1)\chi ^{-a_{r}-2}\chi ^\prime \nonumber \\&\quad +\frac{qq^\prime }{8\pi r^{3}}(-x^{-2}\chi ^{-a_{r}-1}+x^{-1}(-a_{r}-1)\chi ^{-a_{r}-2}\chi ^\prime )\Big )\Big ]=0, \nonumber \\ \end{aligned}$$
(31)

which is the required results [13].

3.2 Case 2

In this section, we will discuss the isothermal case: \(a=\pm \infty \), \(\varrho =1\), we define

$$\begin{aligned} \rho =\rho _{c}e^{-\chi }, \end{aligned}$$
(32)

then, we may rewrite (32) as

$$\begin{aligned} p_{r}=\alpha _{2}\rho _{c}e^{-\chi }+h_{rc}e^{-\chi }, \end{aligned}$$
(33)

with \(\kappa _{r}\rho _{c}=h_{rc}\). Also from Eq. (15), we get

$$\begin{aligned} \frac{d\nu }{dr}= & {} \frac{4(\Delta +\frac{qq^\prime }{8\pi r^3})}{r e^{-\chi }(\rho _{c}+\alpha _{2}\rho _{c}+h_{rc})}\nonumber \\&+\frac{2(\alpha _{2}\rho _{c}+h_{rc})\frac{d\chi }{dr}}{(\rho _{c}+\alpha _{2}\rho _{c}+h_{rc})}, \end{aligned}$$
(34)

now by using Eqs. (12) and mass function, with \(j_{c}=\frac{h_{rc}}{\rho _{c}}\), we obtain

$$\begin{aligned}&\frac{2 e^\chi (\Delta +\frac{qq^{\prime }}{8\pi r^{3}})(1-\frac{2m}{r}+\frac{q^{2}}{r^{2}})}{\rho _{c}(1+\alpha _{2}+j_{c})}\nonumber \\&\quad + \frac{r (\alpha _{2}+j_{c})}{1+\alpha _{2}+j_{c}}\Big (1-\frac{2m}{r}+\frac{q^{2}}{r^{2}}\Big )\frac{d\chi }{dr}\nonumber \\&\quad +\frac{q^{2}}{r^{2}}-\frac{m}{r}-\frac{d m}{dr}(\alpha _{2}+j_{c})=0, \end{aligned}$$
(35)

which leads to generalized LEe as

$$\begin{aligned}&\Big [x \chi ^{\prime }+\frac{2 e^{\chi }(\Delta +\frac{qq^{\prime }}{8\pi r^{3}})}{\alpha _{2} \rho _{c}+h_{rc}}\Big ]\Big [\frac{x\alpha _{2}}{4\pi \rho _{c}(1+\alpha _{2}+j_{c})}\nonumber \\&\quad +\frac{x}{(1+\alpha _{2}+j_{c})}-\frac{2m\alpha _{2}}{4\pi \rho _{c}(1+\alpha _{2}+j_{c})} \nonumber \\&\quad - \frac{2\psi j_{c}}{(1+\alpha _{2}+j_{c})}+\frac{x(\alpha _{2}+j_{c})}{4\pi \rho _{c}(1+\alpha _{2}+j_{c})}\frac{q^{2}}{r^{2}}\Big ]\nonumber \\&\quad -\psi -\psi ^{\prime }x(\alpha _{2}+j_{c}) +\frac{q^{2}}{4\pi \rho _{c}x}=0, \end{aligned}$$
(36)

with \(\psi ^\prime =x^2e^{-\chi }\)

$$\begin{aligned}&\frac{1}{1+\alpha _{2}}\Big [\frac{\alpha _{2}}{4\pi \rho _{c}x^{2}}\Big (2x\chi ^{\prime }+x^{2}\chi ^{\prime \prime }\Big )\nonumber \\&\quad +\frac{2\alpha _{2} e^{\chi }}{4\pi \rho _{c}x^{2}(\alpha _{2}\rho _{c}+h_{rc})}\Big (\Delta +x\Delta \chi ^{\prime }+x\Delta ^{\prime }\nonumber \\&\quad +\frac{qq^{\prime }}{8\pi r^{3}}(1+x\chi ^{\prime })\Big )+2\frac{\chi ^{\prime }}{x}+\chi ^{\prime \prime }+\frac{2 e^{\chi }}{x(\alpha _{2}\rho _{c}+h_{rc})}\Big (\Delta ^{\prime }\nonumber \\&\quad +\frac{\Delta }{x}+\Delta \chi ^{\prime }+\frac{qq^{\prime }}{8\pi r^{3}}\Big (\frac{1}{x}+\chi ^{\prime }\Big )\Big )\nonumber \\&\quad -2\alpha _{2}\Big (\frac{x e^{-\chi }\chi ^{\prime }}{3}+x e^{-\chi }\chi ^{\prime }+\frac{x^{2}}{3}e^{-\chi }\chi ^{\prime \prime }\Big )\nonumber \\&\quad -\frac{4\alpha _{2}}{(\alpha _{2}\rho _{c}+h_{rc})}\Big (\Delta + \frac{x}{3}\chi ^{\prime }\Delta +\frac{x}{3}\Delta ^{\prime }+\frac{qq^{\prime }}{8\pi r^{3}}\nonumber \\&\quad \times \Big (1+\frac{x}{3}\chi ^{\prime }\Big )\Big )+ \frac{q^{2}\chi ^{\prime \prime }}{4\pi \rho _{c}x^{2}}+\frac{2q^{2}e^{\chi }}{4\pi \rho _{c}x^{2}(\alpha _{2}\rho _{c+}h_{rc})}\nonumber \\&\quad \times \Big (-\frac{\Delta }{x^{2}}+ \frac{\Delta \chi ^{\prime }}{x}+\frac{\Delta ^{\prime }}{x}+\frac{qq^{\prime }}{8\pi r^{3}}\Big (\frac{-1}{x^{2}}\nonumber \\&\quad +\frac{\chi ^{\prime }}{x}\Big )\Big )\Big ]-\alpha _{2}(3e^{-\chi })-\frac{q^{2}}{4\pi \rho _{c}x^{4}}=e^{-\chi }, \end{aligned}$$
(37)

4 Double polytrope

In this section, we will discuss the theory of double generalized polytropes for different cases of GPEoS.

4.1 Case 1: double polytrope with \(\varrho \ne 1\)

Here, we will discuss the case \(\varrho _{r}\ne 1\), \(\varrho _\perp \ne 1\), the GPEoS is fulfilled by radial and tangential pressure

$$\begin{aligned} P_{r}=\alpha _{2}\rho _{r}+\kappa _{r}\rho ^{\varrho _{r}}, \end{aligned}$$
(38)

and

$$\begin{aligned} P_{\perp }=\alpha _{2}\rho _{\perp }+\kappa _{\perp }\rho ^{\varrho _{\perp }}, \end{aligned}$$
(39)

then, by the definition of anisotropy factor, we obtain

$$\begin{aligned} \Delta =\alpha _{2}\rho _{\perp }+\kappa _{\perp }\rho ^{\varrho _{\perp }}-\alpha _{2}\rho _{r}-\kappa _{r}\rho ^{\varrho _{r}}. \end{aligned}$$
(40)

We introduce \(\chi \) by

$$\begin{aligned} \rho =\rho _{c}\chi ^{a_{r}}, \end{aligned}$$
(41)

and substituting (41) in (40), we may write

$$\begin{aligned} \Delta =\alpha _{2}(\rho _{\perp }-\rho _{r})+\rho _{c}j_{c}\chi ^{a_{r}}(\chi ^{\vartheta }-\chi ), \end{aligned}$$
(42)

where \(\vartheta =\frac{a_{r}}{a^{\perp }}\). Inside this model, the Lane-Emden condition gives

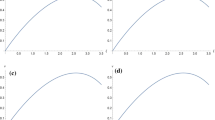
$$\begin{aligned}&\psi ^\prime x(\alpha _{2}+j_{c}\chi )+\psi -\frac{q^{2}}{4\pi \rho _{c} x}\nonumber \\&\quad +\Big (x\chi ^\prime -\frac{2(\alpha _{2}(\rho _{\perp }-\rho _{r})+\rho _{c}j_{c}\chi ^{a_{r}}(\chi ^{\vartheta }-\chi )+\frac{qq^\prime }{8\pi r^{3}})}{j_{c}\rho _{c}\chi ^{a_{r}}\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+ (1+a_{r})\Big )}\Big )\nonumber \\&\quad \times \Big (\frac{1}{1+\alpha _{2}+j_{c}\chi }\Big )\nonumber \\&\quad \times \Big (\frac{x a_{r}\alpha _{2}}{4\pi \rho _{c}\chi }+\epsilon x-\frac{2m a_{r}\alpha _{2}}{4\pi \rho _{c}\chi }-2j_{c}(1+a_{r})\psi +\frac{q^{2}}{x}\nonumber \\&\quad \times \Big (\frac{j_{c}}{4\pi \rho _{c}}\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )\Big )\Big )=0, \end{aligned}$$
(43)

with \(\psi ^{\prime }=x^{2}\chi ^{a_{r}}\). The integration of Eq. (43) is illustrated in Fig. 1. The upsides of the boundaries displayed in the subtitle of the figure. It is significant to observe that \(\chi \) is continuous function with no singularities.

Fig. 1
figure 1

Case 1. plot \(\chi \) is function of x. For \(a_{r}=3\), \(j_{c}=0.1\) and \(\vartheta =0.5\) (blue line),  \(\vartheta =2\) (orange line),  \(\vartheta =4\) (green line)

Full size image

Now we will calculate Tolman mass, which is a the measure of active gravitational mass [22] in order to discuss the stability of our framework, which is defined as

$$\begin{aligned} m_{T}=\frac{1}{2}r^{2}e^{\frac{\nu -\lambda }{2}}\nu ^{\prime }, \end{aligned}$$
(44)

and Tolman mass expression is given by [15]

$$\begin{aligned} m_{T}=e^{\frac{\nu +\lambda }{2}}\Big (m-\frac{q^{2}}{r^{2}}+4\pi r^{3} P_{r}\Big ). \end{aligned}$$
(45)

Now the hydrostatic equilibrium equation can written as

$$\begin{aligned}&h_{rc}\chi ^{\prime }\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )=\frac{-\nu ^{\prime }\rho _{c}}{2}\Big (1+\alpha _{2}+j_{c}\chi \Big )\nonumber \\&\quad +\frac{2}{r\chi ^{a_{r}}}\Big (\alpha _{2}(\rho _{\perp }-\rho _{r}) \nonumber \\&\quad + \rho _{c}j_{c}\chi ^{a_{r}}(\chi ^{\vartheta }-\chi )+\frac{qq^\prime }{8\pi r^{3}}\Big ), \end{aligned}$$
(46)

from which we obtain

$$\begin{aligned}&\int _{\chi (r)}^{\chi (r_{\sum })}\frac{d\chi }{1+\alpha _{2}+j_{c}\chi }\nonumber \\&\quad =-\frac{\rho _{c}}{2j_{rc}(\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})})\int _{\nu _{(r)}}^{\nu (r_{\sum })}d\nu \nonumber \\&\quad + \frac{2}{\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )}\int _{r}^{r_{\sum }}\Big (\frac{(\alpha _{2}(\rho _{\perp }-\rho _{r})+\frac{qq^{\prime }}{8\pi r^{3}})}{\chi ^{a_{r}}h_{rc}(1+\alpha _{2}+j_{c}\chi )}\nonumber \\&\quad + \frac{\chi ^{\vartheta }-\chi }{1+\alpha _{2}+j_{c}\chi }\Big )\frac{dr}{r}. \end{aligned}$$
(47)

Next, characterize G(r) as

$$\begin{aligned} G(r)= & {} \int _{r}^{r_{\sum }}\Big (\frac{(\alpha _{2}(\rho _{\perp }-\rho _{r})+\frac{qq^{\prime }}{8\pi r^{3}})}{\chi ^{a_{r}}h_{rc}(1+\alpha _{2}+j_{c}\chi )}+ \frac{\chi ^{\vartheta }-\chi }{1+\alpha _{2}+j_{c}\chi }\Big )\frac{dr}{r}, \nonumber \\ \end{aligned}$$
(48)

from Eq. (47), we have

$$\begin{aligned}&-2\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )\log (1+\alpha _{2}+j_{c}\chi )\nonumber \\&\quad =\nu (r)-\nu (r_{\sum })+4 j_{c}G(r), \end{aligned}$$
(49)

and the value of metric potential \(e^{\nu }\) is derived as

$$\begin{aligned}&e^{\nu }=\frac{1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}}{(1+\alpha _{2}+j_{c}\chi )^{2\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )}e^{4j_{c}G(r)}}. \end{aligned}$$
(50)

Eventually, after some simple calculation the \(\psi _{T}\) becomes

$$\begin{aligned} \psi _{T}= & {} \Big (\frac{1-2p+\frac{Q^{2}}{r^{2}}}{1-2\epsilon (1+a_{r})j_{c}\frac{\psi }{x_{\sum }q}+\frac{q^{2}}{r^{2}}}\Big )^{\frac{1}{2}}\nonumber \\&\times \Big (\frac{\chi ^{a_{r}}x^{3}_{\sum }q^{3}(\alpha _{2}+p_{c}\chi )-\frac{q^{2}}{4\pi \rho _{c}x_{\sum }q}+\psi }{(1+\alpha _{2}+j_{c}\chi )^{\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )}e^{2j_{c}G(q)}}\Big ), \end{aligned}$$
(51)

where

$$\begin{aligned} \psi _{T}=\frac{mT}{4\pi \rho _{c}\alpha _{3}}, \quad p=\frac{M}{r_{\sum }}, \quad q=\frac{x}{x_{\sum }}, \end{aligned}$$
(52)

and

$$\begin{aligned} G(q)= & {} \int _{q}^{1}\Bigg (\frac{\Big (\alpha _{2}(\rho _{\perp }-\rho _{r})+\frac{qq^{\prime }}{8\pi r^{3}}\Big )}{\chi ^{a_{r}}h_{rc}(1+\alpha _{2}+j_{c}\chi )}\nonumber \\&\quad + \frac{\chi ^{\vartheta }-\chi }{1+\alpha _{2}+j_{c}\chi }\Bigg )\frac{d q^{\prime }}{q^{\prime }}, \end{aligned}$$
(53)
Fig. 2
figure 2

Case 1. Surface potential p for a pair \((j_{c},a_{r})\) is function of the anisotropy parameter \(\vartheta \). Blue line (0.1, 1.0), Orange line (0.1, 2.0), green line (1.0, 1.0), red line (1.0, 2.0)

Full size image
Fig. 3
figure 3

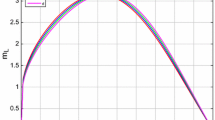
case 1. Plot \(\frac{\psi _{T}}{(\psi _{T})_\Sigma }\) as a function of q for \(a_{r} = 2.0\),\(j_{c}=1.0\), and various \(p(\vartheta )\) values. 0.4790(0.1) (blue line),  0.2350(0.5) (orange line),  0.2249(1.0) (green line),  0.2142(1.5) (red line). The value of p is taken from the graph in the Fig. 2

Full size image

We take Tolman mass as an function of metric potentials. The curves are qualitatively consistent over a wide range of parametric values and it ensure the stability of the model.

4.2 Case 2: \(\varrho _{r}=1\) and \(\varrho _{\perp }\ne 1\)

In this case, the radial pressure is \(P_{r}=\alpha _{2}\rho _{r}+\kappa _{r}\rho \) and tangential pressure \(P_{\perp }=\alpha _{2}\rho _{\perp }+\kappa _{\perp }\rho ^{\varrho _{\perp }}\) with \(\rho =\rho _{c}e^{-\chi }\), then

$$\begin{aligned} P_{r}= & {} \alpha _{2}\rho _{r}+\kappa _{r}\rho _{c}e^{-\chi } \end{aligned}$$
(54)
$$\begin{aligned} P_{\perp }= & {} \alpha _{2}\rho _{\perp }+\kappa _{\perp }\rho _{c}^{\varrho _{\perp }}e^{-\chi \varrho _{\perp }} \end{aligned}$$
(55)

From above equation

$$\begin{aligned} \Delta =\alpha _{2}(\rho _{\perp }-\rho _{r})+h_{rc}e^{-\chi }(e^{\frac{-\chi }{a_{\perp }}}-1) \end{aligned}$$
(56)

then Eq. (36) becomes

$$\begin{aligned}&\Big [x \chi ^{\prime }+\frac{2 e^{\chi }(\alpha _{2}(\rho _{\perp }-\rho _{r})+h_{rc}e^{-\chi }(e^{\frac{-\chi }{a_{\perp }}}-1)+\frac{qq^{\prime }}{8\pi r^{3}})}{\alpha _{2} \rho _{c}+h_{rc}}\Big ]\nonumber \\&\quad \times \Big [\frac{x\alpha _{2}}{4\pi \rho _{c}(1+\alpha _{2}+j_{c})}\nonumber \\&\quad +\frac{x}{(1+\alpha _{2}+j_{c})}-\frac{2m\alpha _{2}}{4\pi \rho _{c}(1+\alpha _{2}+j_{c})}- \frac{2\psi j_{c}}{(1+\alpha _{2}+j_{c})}\nonumber \\&\quad +\frac{x(\alpha _{2}+j_{c})}{4\pi \rho _{c}(1+\alpha _{2}+j_{c})}\frac{q^{2}}{r^{2}}\Big ]\nonumber \\&\quad -\psi -\psi ^{\prime }x(\alpha _{2}+j_{c}) +\frac{q^{2}}{4\pi \rho _{c}x}=0, \end{aligned}$$
(57)

with \(\psi ^{\prime }=x^{2}e^{-\chi }\). The integration of Eq. (57) is illustrated in Fig. 4 for the parameters stated in the figure caption values.

Fig. 4
figure 4

Case 2. Plot \(\chi \) as a function of x. For \(j_{c}=0.1\) and \(a_{\perp }=1\) (orange line), \(a_{\perp }=2\) (green line) and \(a_{\perp }=3\) (blue line)

Full size image

4.3 Case 3: \(\varrho _{r}\ne 1\) and \(\varrho _{\perp }=1\)

We consider \( P_{r}=\alpha _{2} \rho _{r}+\kappa _{r}\rho ^{\varrho _{r}}\) with \(\rho =\rho _{c}\chi ^{a_{r}}\),  \(\varrho _{r}=1+\frac{1}{a_{r}}\) and \( P_{\perp }=\alpha _{2}\rho _{\perp }+\kappa _{\perp }\rho ,\) then anisotropy of the system is written as

$$\begin{aligned} \Delta =\alpha _{2}(\rho _{\perp }-\rho _{r})+h_{rc}\chi ^{a_{r}}(1-\chi ), \end{aligned}$$
(58)

Then Eq. (29) becomes,

$$\begin{aligned}&\psi ^\prime x(\alpha _{2}+j_{c}\chi )+\psi -\frac{q^{2}}{4\pi \rho _{c} x}\nonumber \\&\quad +\Bigg (x\chi ^\prime -\frac{2(\alpha _{2}(\rho _{\perp }-\rho _{r})+h_{rc}\chi ^{a_{r}}(1-\chi )+\frac{qq^\prime }{8\pi r^{3}})}{j_{c}\rho _{c}\chi ^{a_{r}}\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+ (1+a_{r})\Big )}\Bigg )\nonumber \\&\quad \times \Big (\frac{1}{1+\alpha _{2}+j_{c}\chi }\Big )\nonumber \\&\quad \times \Bigg (\frac{x a_{r}\alpha _{2}}{4\pi \rho _{c}\chi }+\epsilon x-\frac{2m a_{r}\alpha _{2}}{4\pi \rho _{c}\chi }-2j_{c}(1+a_{r})\psi +\frac{q^{2}}{x}\nonumber \\&\quad \times \Big (\frac{j_{c}}{4\pi \rho _{c}}\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )\Big )\Bigg )=0, \end{aligned}$$
(59)

with \(\psi ^{\prime }=x^{2}\chi ^{a_{r}}\). Figure 5 is the integration of Eq. (59) for the values of the parameters given in the caption.

Fig. 5
figure 5

Case 3. \(\chi \) as a function of x for \(j_{c}=0.1\) and \(a_{r}=1\) (orange line), \(a_{r}=2\) (green line), \(a_{r}=3\) (blue line)

Full size image
Fig. 6
figure 6

Case 3. For varying \(j_{c}\) values, the surface potential p is a function of the polytropic index \(a_{r}\). \(j_{c}=0.10\) (blue line),  \(j_{c}=0.18\) (orange line), \(j_{c}=0.24\) (green line), \(j_{c}=0.30\) (red line)

Full size image

In this case, then hydrostatic equation is written as

$$\begin{aligned}&h_{rc}\chi ^{\prime }\Big (\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})\Big )=\frac{-\nu ^{\prime }\rho _{c}}{2}\Big (1+\alpha _{2}+j_{c}\chi \Big )\nonumber \\&\quad +\frac{2}{r\chi ^{a_{r}}}\Big (\alpha _{2}(\rho _{\perp }-\rho _{r})\nonumber \\&\quad +h_{rc}\chi ^{a_{r}}(1-\chi )+\frac{qq^\prime }{8\pi r^{3}}\Big ), \end{aligned}$$
(60)

and from integration of above equation, we obtain

$$\begin{aligned}&\int _{\chi (r)}^{\chi (r_{\sum })}\frac{d\chi }{1+\alpha _{2}+j_{c}\chi }=-\frac{\rho _{c}}{2h_{rc}(\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r})})\int _{\nu _{(r)}}^{\nu (r_{\sum })}d\nu \nonumber \\&\quad + \frac{2}{(\frac{a_{r}\alpha _{2}}{\chi j_{c}}+(1+a_{r}))}\int _{r}^{r_{\sum }}\Bigg (\frac{(\alpha _{2}(\rho _{\perp }-\rho _{r})+\frac{qq^{\prime }}{8\pi r^{3}})}{\chi ^{a_{r}}h_{rc}(1+\alpha _{2}+j_{c}\chi )}\nonumber \\&\quad + \frac{1-\chi }{1+\alpha _{2}+j_{c}\chi }\Bigg )\frac{dr}{r}, \end{aligned}$$
(61)

G(r) for case 3 is calculated as

$$\begin{aligned} G(r)=\int _{r}^{r_{\sum }}\Bigg (\frac{(\alpha _{2}(\rho _{\perp }-\rho _{r})+\frac{qq^{\prime }}{8\pi r^{3}})}{\chi ^{a_{r}}h_{rc}(1+\alpha _{2}+j_{c}\chi )}+ \frac{1-\chi }{1+\alpha _{2}+j_{c}\chi }\Bigg )\frac{dr}{r}, \nonumber \\ \end{aligned}$$
(62)
Fig. 7
figure 7

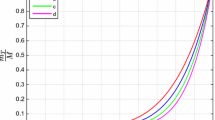
Case 3. \(\frac{\psi _{T}}{(\psi _{T})_\Sigma }\) as a function of q for \(j_{c}=0.3\), and various \(p(a_{r})\) values. 0.3729(0.1) (blue line),  0.3887(0.5) (orange line),  0.2897(1.0) (green line). Figure 6 provides the p values

Full size image

The surface potential and the normalized Tolman mass, for an assurance of potential gains of the boundaries, are plotting in Figs. 6 and 7 separately.

5 Conclusion

The GPEoS is used in this investigation to discuss relativistic anisotropic double polytropes. GPEoS is the result of combining linear and polytropic EoS. Accordingly, this investigation might be seen as a characteristic augmentation of the methodology portrayed in [13] to the relativistic circumstance. Since pressure anisotropy present in the system provides the opportunity of in depth analysis. It is worth noticing that, whether we utilize energy density or baryonic mass density, there are two polytropic conditions of state for each polytrope. So we have four possible cases for two polytropes in this work.

Depending on \(\varrho =1\) or \(\varrho \ne 1\), we may distinguish between two alternative scenarios. Since the framework’s subjective conduct does not change much across a wide scope of boundary, because the situation \(\varrho _{r}=\varrho _{\perp }\) prompts the isotropic pressing factor case \(p_{r}=p_{\perp }\), there are just three prospects. We have developed the LEe for these occurrences over a genuinely wide scope of boundary values, regardless of whether just a little set for each case is given. The system’s qualitative behavior does not change much over a wide range of parameter values. The protocol presented here, on the other hand, is useful for dealing with a range of events that result in anisotropic polytropes, with a focus on the physics of CO and other related phenomena. The resulting models also revealed several intriguing aspects that ought to be discussed.

As shown in Fig. 1, limited configurations occur for a range of parameter values, whereas unbounded configurations exist for the rest of the parameter values. There are more elements in the later situation than in the isotropic example, the criterion for the existence of finite radius distributions is more complicated. The same is true for Case 3, as seen in Fig. 5. On the other hand, all configurations are unbounded, as seen in Fig. 4. This example corresponds to an isothermal gas, this is an anticipated outcome. Figures 3 and 7 delineate the technique embraced by the liquid conveyance to keep the balance; it attempts to focus the Tolman mass in the external areas. The conduct of Tolman mass was at that point noticed for various groups of anisotropic polytopes examined in [23].

The chance of utilizing the strategies given here to the investigation of super Chandrasekhar white dwarfs, which have massed on the quest for \(2.8M_{\bigodot }\) and are addressed utilizing a polytropic condition of state (see [24] and references in that). The relativistic effects, charge and pressure anisotropy are vital in the study of such systems.