Abstract
Using a data sample of \(\sqrt{s}=13\,\text {TeV}\) proton-proton collisions collected by the CMS experiment at the LHC in 2017 and 2018 with an integrated luminosity of \(103\text {~fb}^{-1}\), the \(\text {B}^{0}_{\mathrm{s}} \rightarrow \uppsi (\text {2S})\text {K}_\mathrm{S}^{0}\) and \(\text {B}^{0} \rightarrow \uppsi (\text {2S})\text {K}_\mathrm{S}^{0} \uppi ^+\uppi ^-\) decays are observed with significances exceeding 5 standard deviations. The resulting branching fraction ratios, measured for the first time, correspond to \({\mathcal {B}}(\text {B}^{0}_{\mathrm{s}} \rightarrow \uppsi (\text {2S})K_\mathrm{S}^{0})/{\mathcal {B}}(\text {B}^{0}\rightarrow \uppsi (\text {2S})K_\mathrm{S}^{0}) = (3.33 \pm 0.69 (\text {stat})\, \pm 0.11\,(\text {syst}) \pm 0.34\,(f_{\mathrm{s}}/f_{\mathrm{d}})) \times 10^{-2}\) and \({\mathcal {B}}(\text {B}^{0} \rightarrow \uppsi (\text {2S})\text {K}_\mathrm{S}^{0} \uppi ^{+} \uppi ^{-})/ {\mathcal {B}}(\text {B}^{0} \rightarrow \uppsi (\text {2S})\text {K}^{0}_{\mathrm{S}}) = 0.480 \pm 0.013\,(\text {stat}) \pm 0.032\,(\text {syst})\), where the last uncertainty in the first ratio is related to the uncertainty in the ratio of production cross sections of \(\hbox {B}^{0}_{\mathrm{s}}\) and \(\hbox {B}^{0}\) mesons, \(f_{\mathrm{s}}/f_{\mathrm{d}}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Decays of neutral  mesons into charmonium resonances (
mesons into charmonium resonances ( , etc.) are well suited to study the flavour sector of the standard model (SM) and to search for indications of new physics beyond the SM. In the last decade, interest in
, etc.) are well suited to study the flavour sector of the standard model (SM) and to search for indications of new physics beyond the SM. In the last decade, interest in  hadron decays to final states containing a charmonium resonance has increased after several exotic hadrons have been observed as intermediate resonances in multibody decays. Starting from the observation of X(3872) [1], many new charmonium-like states have been observed, such as X(4140) [2,3,4,5], Y(4260) [6, 7], and others, with properties (mass, width and decay pattern) not fitting into the landscape of traditional charmonium states. The first charged tetraquark candidate, \(Z(4430)^{+}\) was discovered in the
hadron decays to final states containing a charmonium resonance has increased after several exotic hadrons have been observed as intermediate resonances in multibody decays. Starting from the observation of X(3872) [1], many new charmonium-like states have been observed, such as X(4140) [2,3,4,5], Y(4260) [6, 7], and others, with properties (mass, width and decay pattern) not fitting into the landscape of traditional charmonium states. The first charged tetraquark candidate, \(Z(4430)^{+}\) was discovered in the  decay as a peak in the
decay as a peak in the  mass spectrum [8,9,10,11]. Many other exotic hadrons have been observed in the last 15 years [12, 13], and the nature of most of them is still unclear. Moreover, channels whose final state is accessible both from
mass spectrum [8,9,10,11]. Many other exotic hadrons have been observed in the last 15 years [12, 13], and the nature of most of them is still unclear. Moreover, channels whose final state is accessible both from  and
and  can be used to measure time-dependent CP asymmetry [14,15,16,17,18,19,20,21,22,23,24,25,26,27] as well.
can be used to measure time-dependent CP asymmetry [14,15,16,17,18,19,20,21,22,23,24,25,26,27] as well.
This paper presents the first measurement of the  and
and  decays, using a data sample of proton-proton collisions at \(\sqrt{s}=13\,\text {TeV}\) collected by the CMS experiment at the CERN LHC in 2017 and 2018 with an integrated luminosity of 103
decays, using a data sample of proton-proton collisions at \(\sqrt{s}=13\,\text {TeV}\) collected by the CMS experiment at the CERN LHC in 2017 and 2018 with an integrated luminosity of 103 [28, 29]. Both decays can potentially be used for CP asymmetry measurements, and, in addition, the second one can also be used to search for intermediate exotic resonances. The
[28, 29]. Both decays can potentially be used for CP asymmetry measurements, and, in addition, the second one can also be used to search for intermediate exotic resonances. The  and
and  mesons are reconstructed using their decays into
mesons are reconstructed using their decays into  and
and  , respectively. The
, respectively. The  decay is chosen as the normalization channel for the measurement of the branching fractions, since its probability is precisely known [13], and its topology and kinematic properties are similar to those of the
decay is chosen as the normalization channel for the measurement of the branching fractions, since its probability is precisely known [13], and its topology and kinematic properties are similar to those of the  or
or  decays. Therefore, using this normalization reduces the systematic uncertainties related to muon and track reconstruction. The relative branching fractions are measured using the relations
decays. Therefore, using this normalization reduces the systematic uncertainties related to muon and track reconstruction. The relative branching fractions are measured using the relations

where  is the branching fraction, N is the number of reconstructed events in data, \(\epsilon \) is the total reconstruction efficiency, and \({f_\mathrm {d}/f_\mathrm {s}}\) is the ratio of production cross sections of \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) mesons (also called fragmentation fraction ratio). Charge-conjugate states are implied to be included throughout the paper.
is the branching fraction, N is the number of reconstructed events in data, \(\epsilon \) is the total reconstruction efficiency, and \({f_\mathrm {d}/f_\mathrm {s}}\) is the ratio of production cross sections of \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) mesons (also called fragmentation fraction ratio). Charge-conjugate states are implied to be included throughout the paper.
Tabulated results are provided in the HEPData record for this analysis [30].
2 The CMS detector and simulated event samples
The central feature of the CMS apparatus [31] is a superconducting solenoid of \(6\,{\mathrm{m}}\) internal diameter, providing a magnetic field of \(3.8\,{\mathrm{T}}\). Within the solenoid volume are a silicon pixel and strip tracker, a lead tungstate crystal electromagnetic calorimeter, and a brass and scintillator hadron calorimeter. Muons are measured in gas-ionization detectors embedded in the steel flux-return yoke outside the solenoid.
Events of interest are selected using a two-tiered trigger system [32]. The first level, composed of custom hardware processors, uses information from the calorimeters and muon detectors to select events at a rate of around \(100\,{\mathrm{kHz}}\) within a time interval of less than \(4\,\upmu \mathrm{s}\) [33]. The first-level trigger used in this analysis requires at least two muons. The second level, known as the high-level trigger, consists of a farm of processors running a version of the full event reconstruction software optimized for fast processing that reduces the event rate to around \(1\,{\mathrm{kHz}}\) before data storage. The high-level trigger algorithm used in the analysis requires two opposite-sign muons compatible with the dimuon decay of a  meson with transverse momentum (
meson with transverse momentum ( ) larger than \(18\,\mathrm{GeV}\).
) larger than \(18\,\mathrm{GeV}\).
Simulated Monte Carlo samples for the decays of interest are generated for the analysis. The  8.230 package [34] with the CP5 tune [35] is used to simulate the production of the \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) mesons, whose subsequent decays are performed by
8.230 package [34] with the CP5 tune [35] is used to simulate the production of the \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) mesons, whose subsequent decays are performed by  1.6.0 [36], where final-state photon radiation is included using
1.6.0 [36], where final-state photon radiation is included using  3.61 [37, 38]. The lifetimes of \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) mesons used in the generation are 1.52 and \(1.47\,{\mathrm{ps}}\), respectively. The generated events are passed to a detailed GEANT4-based simulation [39] of the CMS detector, and are then processed using the same trigger and reconstruction as used for the collision data. The simulation includes effects from multiple proton-proton interactions in the same or nearby bunch crossings (pileup) with the multiplicity distribution tuned to match those of the data.
3.61 [37, 38]. The lifetimes of \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) mesons used in the generation are 1.52 and \(1.47\,{\mathrm{ps}}\), respectively. The generated events are passed to a detailed GEANT4-based simulation [39] of the CMS detector, and are then processed using the same trigger and reconstruction as used for the collision data. The simulation includes effects from multiple proton-proton interactions in the same or nearby bunch crossings (pileup) with the multiplicity distribution tuned to match those of the data.
3 Event reconstruction and selection
The reconstruction procedure starts with finding two muons of opposite charges, that must match those that triggered the event readout. The muon candidates are required to have  , a pseudorapidity
, a pseudorapidity  , and to satisfy general identification (soft-muon) criteria [40]. The two muons with a two-prong vertex fit probability
, and to satisfy general identification (soft-muon) criteria [40]. The two muons with a two-prong vertex fit probability  are paired to form the
are paired to form the  candidate, which must have
candidate, which must have  and an invariant mass
and an invariant mass  (the world average
(the world average  meson mass is
meson mass is  [13]).
[13]).
The  candidates are formed from displaced two-prong vertices, as described in Ref. [41]. The
candidates are formed from displaced two-prong vertices, as described in Ref. [41]. The  invariant mass is required to be within \(\pm 20\,\text {MeV}\) of the world average value
invariant mass is required to be within \(\pm 20\,\text {MeV}\) of the world average value  [13], which corresponds to approximately three times the mass resolution. Selected
[13], which corresponds to approximately three times the mass resolution. Selected  and
and  tracks are then refitted with their invariant mass constrained to
tracks are then refitted with their invariant mass constrained to  , and the obtained
, and the obtained  candidate is required to have
candidate is required to have  .
.
The  candidates are obtained through a kinematic vertex fit on the
candidates are obtained through a kinematic vertex fit on the  system which constrains the dimuon mass to
system which constrains the dimuon mass to  . The
. The  candidates are required to have
candidates are required to have  , a 3D pointing angle between
, a 3D pointing angle between  and
and  to satisfy
to satisfy  , and a transverse displacement significance for
, and a transverse displacement significance for  of
of  . Here
. Here  denotes the vector from the
denotes the vector from the  production vertex to the
production vertex to the  decay vertex, while
decay vertex, while  and
and  correspond to the length of
correspond to the length of  , the transverse component of \(\vec {D}\), and its uncertainty. To suppress the combinatorial background, additional requirements are applied:
, the transverse component of \(\vec {D}\), and its uncertainty. To suppress the combinatorial background, additional requirements are applied:  ,
,  , and
, and  , where the
, where the  meson transverse displacement
meson transverse displacement  is calculated with respect to the primary vertex (PV). From all reconstructed proton-proton collision points, the PV is chosen as the one with the smallest
is calculated with respect to the primary vertex (PV). From all reconstructed proton-proton collision points, the PV is chosen as the one with the smallest  pointing angle, as in Refs. [42,43,44]. The pointing angle is the angle formed by the
pointing angle, as in Refs. [42,43,44]. The pointing angle is the angle formed by the  candidate momentum and the vector from the PV to the reconstructed
candidate momentum and the vector from the PV to the reconstructed  candidate vertex. Furthermore, if in this procedure any of the tracks used in the
candidate vertex. Furthermore, if in this procedure any of the tracks used in the  candidate reconstruction is included in the fit of the chosen PV, the track is removed, and the PV is refitted.
candidate reconstruction is included in the fit of the chosen PV, the track is removed, and the PV is refitted.
For the  candidates, two additional, oppositely charged, high-purity [45] tracks, assumed to be pions and having
candidates, two additional, oppositely charged, high-purity [45] tracks, assumed to be pions and having  , are included in the
, are included in the  meson vertex fit, while the rest of the selection criteria are the same.
meson vertex fit, while the rest of the selection criteria are the same.
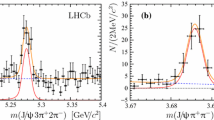
Measured invariant mass distributions of  (upper) and
(upper) and  (lower) candidates. The overlaid results from the fit are described in the text
(lower) candidates. The overlaid results from the fit are described in the text
4 Observation of the \(\text {B}^{0}_{\mathrm{s}} \rightarrow \uppsi (\text {2S})\text {K}^{0}_{\mathrm{S}}\) decay
The measured  invariant mass distribution is presented in Fig. 1 (
invariant mass distribution is presented in Fig. 1 ( ). The \(\text {B}^{0}\) signal (left peak) is described with a double Gaussian function with common mean, whose parameters are free to vary in an unbinned maximum-likelihood fit. It is found in simulation that the
). The \(\text {B}^{0}\) signal (left peak) is described with a double Gaussian function with common mean, whose parameters are free to vary in an unbinned maximum-likelihood fit. It is found in simulation that the  signal (right peak) has the same shape as the
signal (right peak) has the same shape as the  signal, but it is about 10% wider, because of the larger energy release in the decay. Therefore, the \(\text {B}^{0}_{\mathrm{s}}\) signal is modelled with a double Gaussian function of the same shape as the \(\text {B}^{0}\) signal, with the resolution parameters scaled by the ratio of the widths found in the simulation. The background is modelled with an exponential function. The good quality of the fit is verified by calculating the \(\chi ^2\) between the binned distribution and the fit function, resulting in \(\chi ^2=83\) for 91 degrees of freedom.
signal, but it is about 10% wider, because of the larger energy release in the decay. Therefore, the \(\text {B}^{0}_{\mathrm{s}}\) signal is modelled with a double Gaussian function of the same shape as the \(\text {B}^{0}\) signal, with the resolution parameters scaled by the ratio of the widths found in the simulation. The background is modelled with an exponential function. The good quality of the fit is verified by calculating the \(\chi ^2\) between the binned distribution and the fit function, resulting in \(\chi ^2=83\) for 91 degrees of freedom.
The ratio of signal yields  is extracted from the fit. Its uncertainty is calculated by taking into account the correlation between the uncertainties in \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) yields, which are found to be \(113 \pm 23\) and \(16660 \pm 140\), respectively, where the uncertainties are statistical only.
is extracted from the fit. Its uncertainty is calculated by taking into account the correlation between the uncertainties in \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) yields, which are found to be \(113 \pm 23\) and \(16660 \pm 140\), respectively, where the uncertainties are statistical only.
The statistical significance of the  signal is evaluated with the likelihood ratio technique, comparing the background-only and signal-plus-background hypotheses, with the standard asymptotic formula [46], assuming that the conditions to apply Wilks’ theorem [47] are satisfied. For a significance estimation, the mass difference between the \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) signals is fixed to the known value of \(83.78\,\mathrm{MeV}\) [13]. The obtained significance is 5.2 standard deviations and varies in the range 5.1–5.4 standard deviations when accounting for the systematic uncertainties due to the choice of the fit model, discussed in Sect. 7.
signal is evaluated with the likelihood ratio technique, comparing the background-only and signal-plus-background hypotheses, with the standard asymptotic formula [46], assuming that the conditions to apply Wilks’ theorem [47] are satisfied. For a significance estimation, the mass difference between the \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) signals is fixed to the known value of \(83.78\,\mathrm{MeV}\) [13]. The obtained significance is 5.2 standard deviations and varies in the range 5.1–5.4 standard deviations when accounting for the systematic uncertainties due to the choice of the fit model, discussed in Sect. 7.
5 Observation of the \(\text {B}^{0} \rightarrow \uppsi (\text {2S})\text {K}^{0}_{\mathrm{S}}\uppi ^{+}\uppi ^{-}\) decay
As shown in Fig. 1 ( ), the measured
), the measured  mass distribution presents a clear
mass distribution presents a clear  signal peak on top of a relatively small background. The \(\text {B}^{0}\) signal is modelled with a double Gaussian function with common mean with all parameters free to vary, and the combinatorial background is described by an exponential function.
signal peak on top of a relatively small background. The \(\text {B}^{0}\) signal is modelled with a double Gaussian function with common mean with all parameters free to vary, and the combinatorial background is described by an exponential function.
Studies of simulated events show that the  decay contributes to the reconstructed
decay contributes to the reconstructed  mass distribution when the charged kaon is reconstructed as a pion. This relevant background contribution is accounted for in the fit to data by including a dedicated component with a freely varying normalization and a fixed shape that is obtained from simulation (Fig. 1,
mass distribution when the charged kaon is reconstructed as a pion. This relevant background contribution is accounted for in the fit to data by including a dedicated component with a freely varying normalization and a fixed shape that is obtained from simulation (Fig. 1,  ).
).
The signal yield  is found to be \(3498 \pm 87\), where the uncertainty is statistical only. The \(\chi ^2\) between the binned distribution and the fit function is 75 for 92 degrees of freedom, demonstrating the good quality of the fit. The significance of the
is found to be \(3498 \pm 87\), where the uncertainty is statistical only. The \(\chi ^2\) between the binned distribution and the fit function is 75 for 92 degrees of freedom, demonstrating the good quality of the fit. The significance of the  signal, evaluated as described in Sect. 4, exceeds 30 standard deviations.
signal, evaluated as described in Sect. 4, exceeds 30 standard deviations.
The intermediate invariant mass distributions, corresponding to the four-body  decay, are produced using the
decay, are produced using the  [48] technique to subtract the non-\(\text {B}^{0}\) background, using the
[48] technique to subtract the non-\(\text {B}^{0}\) background, using the  distribution fit described above. The correlations between the intermediate invariant masses and
distribution fit described above. The correlations between the intermediate invariant masses and  have been checked to be below 10%. Figures 2 and 3 show the 2- and 3-body invariant mass distributions. Overlaid are the predictions of the 4-body phase space simulations, which provide poor description of the data since the simulations do not account for the intermediate resonance structure. The simulation after application of the reweighting procedure described in Sect. 7 is also shown. The mass distributions of
have been checked to be below 10%. Figures 2 and 3 show the 2- and 3-body invariant mass distributions. Overlaid are the predictions of the 4-body phase space simulations, which provide poor description of the data since the simulations do not account for the intermediate resonance structure. The simulation after application of the reweighting procedure described in Sect. 7 is also shown. The mass distributions of  and one or two light mesons (
and one or two light mesons ( ,
,  ,
,  ,
,  ) do not present any significant narrow peak that could indicate a contribution from an exotic charmonium state. The small excess at about 4.3
) do not present any significant narrow peak that could indicate a contribution from an exotic charmonium state. The small excess at about 4.3 in the
in the  distribution (Fig. 2, bottom left) is not significant, and there is no similar excess in the
distribution (Fig. 2, bottom left) is not significant, and there is no similar excess in the  distribution (Fig. 2, middle left). Moreover, exotic states previously found in this mass range are known to have large natural widths [12, 13]. Signs of the
distribution (Fig. 2, middle left). Moreover, exotic states previously found in this mass range are known to have large natural widths [12, 13]. Signs of the  (Fig. 2, middle and bottom right),
(Fig. 2, middle and bottom right),  (Fig. 2, top left), and
(Fig. 2, top left), and  (Fig. 3, top right) resonances are seen in the mass distributions of
(Fig. 3, top right) resonances are seen in the mass distributions of  ,
,  , and
, and  , respectively.
, respectively.
Distributions of 2-body intermediate invariant masses from the  decay. The data distributions (black dots) are background subtracted. Overlaid are the predictions of phase space simulations (red triangles), as well as the predictions after applying the reweighting procedure described in Sect. 7 (grey squares)
decay. The data distributions (black dots) are background subtracted. Overlaid are the predictions of phase space simulations (red triangles), as well as the predictions after applying the reweighting procedure described in Sect. 7 (grey squares)
Distributions of 3-body intermediate invariant masses from the  decay. Data distributions (black dots) are background subtracted. Overlaid are the predictions of phase space simulations (red triangles), as well as the predictions after applying the reweighting procedure described in Sect. 7 (grey squares)
decay. Data distributions (black dots) are background subtracted. Overlaid are the predictions of phase space simulations (red triangles), as well as the predictions after applying the reweighting procedure described in Sect. 7 (grey squares)
6 Efficiencies
The total reconstruction efficiency for each decay channel is evaluated using samples of simulated events. It is calculated as the number of reconstructed events divided by the number of generated events, and includes the detector acceptance, trigger, and candidate reconstruction efficiencies. Only the ratios of such efficiencies are needed to measure the ratios \(R_{\mathrm{s}}\) and  , thus reducing the systematic uncertainties associated with muon and track reconstruction.
, thus reducing the systematic uncertainties associated with muon and track reconstruction.
The obtained efficiency ratios are found to be

where the uncertainties are statistical only and are related to the size of the simulated event samples. The first ratio is close to unity, as expected, while the second ratio is significantly greater than unity because of the presence of two additional tracks in the denominator. The lifetimes of heavy and light \(\text {B}^{0}_{\mathrm{s}}\) meson eigenstates differ by about \(0.2\,{\mathrm{ps}}\) [13], which can have an impact on the efficiency  . It was verified that the corresponding variations of \(\text {B}^{0}_{\mathrm{s}}\) lifetime result in negligible changes in the efficiency.
. It was verified that the corresponding variations of \(\text {B}^{0}_{\mathrm{s}}\) lifetime result in negligible changes in the efficiency.
The validation of Monte Carlo samples is performed by comparing distributions of variables used in the event selection between simulation and background-subtracted data. No significant deviation is found, and thus no systematic uncertainties in the efficiency ratio are assigned related to data-simulation discrepancies in those variables.
7 Systematic uncertainties
Many systematic uncertainties, related to the efficiency of the trigger as well as the reconstruction and identification of the muons, cancel out in the measured ratios \(R_{\mathrm{s}}\) and  . Since the
. Since the  and
and  decays have the same number of tracks in the final state, uncertainties related to the track reconstruction are of the same size and correlated, and therefore cancel out when propagated to the measured ratio \(R_{\mathrm{s}}\). For the ratio
decays have the same number of tracks in the final state, uncertainties related to the track reconstruction are of the same size and correlated, and therefore cancel out when propagated to the measured ratio \(R_{\mathrm{s}}\). For the ratio  , we consider an additional uncertainty of 4.2% from the uncertainty in the tracking efficiency of two additional pions [49].
, we consider an additional uncertainty of 4.2% from the uncertainty in the tracking efficiency of two additional pions [49].
The systematic uncertainty related to the choice of the fit model is evaluated by testing different models. The largest deviation in the measured ratio from its baseline value is taken as a systematic uncertainty, separately for the variations of the signal and background models. Several alternative signal models were considered. One is a double Gaussian function for \(\text {B}^{0}\) and \(\text {B}^{0}_{\mathrm{s}}\) signals with the resolution shape fixed to the expectations taken from simulation with only the resolution scaling parameter being free in the fit. Another signal model is a Student’s t-distribution [50] with the value of the n parameter fixed to the one measured in simulation. Alternative background models include polynomials of the second and third degrees, an exponential multiplied by a polynomial, and a power function multiplied by an exponential, where in all cases the background shape parameters are free to vary in the fits.
The uncertainty related to the finite size of the simulation samples (used to measure the efficiencies in Sect. 6) is also considered as a systematic uncertainty.
The uncertainty associated with the shape of the  contribution to the
contribution to the  invariant mass distribution is estimated by varying the shape parameters within their uncertainties. The largest deviation of
invariant mass distribution is estimated by varying the shape parameters within their uncertainties. The largest deviation of  from the baseline value is 0.5% which is taken as a systematic uncertainty.
from the baseline value is 0.5% which is taken as a systematic uncertainty.
As discussed in Sect. 5, the simulation for the  decay does not take into account the intermediate resonance structure, leading to a significant disagreement between data and simulation in the 2- and 3-body mass distributions. This results in a potential bias in the efficiency reported in Sect. 6. To estimate the corresponding systematic uncertainty, the simulated sample is reweighted to be consistent with the data, and the difference between the baseline efficiency and the efficiency obtained on the weighted sample is taken as a systematic uncertainty. Due to the limited number of events, it is impossible to assign weights taking the ratio of data to simulation in bins of multi-dimensional phase space of the considered 4-body decay. An iterative procedure has been developed that operates with one-dimensional weights corresponding to each 2- and 3-body invariant mass, gradually making the mass distributions on weighted simulation sample closer and closer to data, until a satisfactory agreement in all intermediate invariant mass distributions is achieved. The distributions of invariant masses obtained with the weighted simulation sample are presented in Figs. 2 and 3. The efficiency obtained on the weighted simulation sample deviates from the baseline value by 5%, which is taken as a systematic uncertainty due to the intermediate resonance structure. This efficiency correction procedure with iterative reweighting is verified using a dedicated simulation sample instead of data, in which the contributions from
decay does not take into account the intermediate resonance structure, leading to a significant disagreement between data and simulation in the 2- and 3-body mass distributions. This results in a potential bias in the efficiency reported in Sect. 6. To estimate the corresponding systematic uncertainty, the simulated sample is reweighted to be consistent with the data, and the difference between the baseline efficiency and the efficiency obtained on the weighted sample is taken as a systematic uncertainty. Due to the limited number of events, it is impossible to assign weights taking the ratio of data to simulation in bins of multi-dimensional phase space of the considered 4-body decay. An iterative procedure has been developed that operates with one-dimensional weights corresponding to each 2- and 3-body invariant mass, gradually making the mass distributions on weighted simulation sample closer and closer to data, until a satisfactory agreement in all intermediate invariant mass distributions is achieved. The distributions of invariant masses obtained with the weighted simulation sample are presented in Figs. 2 and 3. The efficiency obtained on the weighted simulation sample deviates from the baseline value by 5%, which is taken as a systematic uncertainty due to the intermediate resonance structure. This efficiency correction procedure with iterative reweighting is verified using a dedicated simulation sample instead of data, in which the contributions from  and
and  resonances are included with arbitrary magnitudes.
resonances are included with arbitrary magnitudes.
All uncertainties described above, excluding the one related to \(f_{\mathrm{s}}/f_{\mathrm{d}}\) for the ratio \(R_{\mathrm{s}}\), are summarized in Table 1 together with a total systematic uncertainty, calculated as a sum in quadrature of the individual sources.
A measurement of the ratio of the \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) fragmentation fractions, \(f_{\mathrm{s}}/f_{\mathrm{d}}\), in proton-proton collisions at the LHC has been recently reported by the LHCb Collaboration [51]:  , where
, where  in GeV is the transverse momentum of a
in GeV is the transverse momentum of a  meson produced in \(13\,\mathrm{TeV}\) proton-proton collisions. The ratio was found to be independent of the rapidity of the
meson produced in \(13\,\mathrm{TeV}\) proton-proton collisions. The ratio was found to be independent of the rapidity of the  meson, but with a significant dependence on the transverse momentum of the
meson, but with a significant dependence on the transverse momentum of the  candidate. The
candidate. The  distribution used in this analysis is shown in Fig. 4, where the background is subtracted using
distribution used in this analysis is shown in Fig. 4, where the background is subtracted using  . Using the LHCb result and the average
. Using the LHCb result and the average  in our events of \(31.2\,\mathrm{GeV}\), the \(f_{\mathrm{s}}/f_{\mathrm{d}}\) value for the kinematic range of this analysis is obtained to be \(f_{\mathrm{s}}/f_{\mathrm{d}} = 0.208 \pm 0.007\). The LHCb \(f_{\mathrm{s}}/f_{\mathrm{d}}\) measurement is mostly dependent on the events with
in our events of \(31.2\,\mathrm{GeV}\), the \(f_{\mathrm{s}}/f_{\mathrm{d}}\) value for the kinematic range of this analysis is obtained to be \(f_{\mathrm{s}}/f_{\mathrm{d}} = 0.208 \pm 0.007\). The LHCb \(f_{\mathrm{s}}/f_{\mathrm{d}}\) measurement is mostly dependent on the events with  , while the majority of the events in this analysis have
, while the majority of the events in this analysis have  . Therefore, we assign an additional systematic uncertainty on \(f_{\mathrm{s}}/f_{\mathrm{d}}\) as the difference between 0.208 and the value obtained under the assumption that \(f_{\mathrm{s}}/f_{\mathrm{d}}\) becomes constant (0.2278) in the region
. Therefore, we assign an additional systematic uncertainty on \(f_{\mathrm{s}}/f_{\mathrm{d}}\) as the difference between 0.208 and the value obtained under the assumption that \(f_{\mathrm{s}}/f_{\mathrm{d}}\) becomes constant (0.2278) in the region  . This additional uncertainty is estimated to be 0.020, and the total uncertainty on \(f_{\mathrm{s}}/f_{\mathrm{d}}\) is obtained by summing it in quadrature with the uncertainty of 0.007 obtained above. The resulting fragmentation fraction ratio used in the \(R_{\mathrm{s}}\) measurement is \({f_{\mathrm{s}}/f_{\mathrm{d}}=0.208\pm 0.021}\), with a relative uncertainty of 10%.
. This additional uncertainty is estimated to be 0.020, and the total uncertainty on \(f_{\mathrm{s}}/f_{\mathrm{d}}\) is obtained by summing it in quadrature with the uncertainty of 0.007 obtained above. The resulting fragmentation fraction ratio used in the \(R_{\mathrm{s}}\) measurement is \({f_{\mathrm{s}}/f_{\mathrm{d}}=0.208\pm 0.021}\), with a relative uncertainty of 10%.
8 Measured branching fractions
The branching fraction ratio of the  decay relative to the
decay relative to the  one is measured using Eq. (1) to be
one is measured using Eq. (1) to be

where the last uncertainty is related to the used value \({f_{\mathrm{s}}/f_{\mathrm{d}}=0.208\pm 0.021}\). Since the knowledge of \(f_{\mathrm{s}}/f_{\mathrm{d}}\) at large  can be updated with future measurements, allowing to improve the \(R_{\mathrm{s}}\) evaluation, we also provide the measurement of the product
can be updated with future measurements, allowing to improve the \(R_{\mathrm{s}}\) evaluation, we also provide the measurement of the product

In addition, the transverse momentum distribution of the measured  candidates is presented in Fig. 4 and in the HEPData record for this analysis [30].
candidates is presented in Fig. 4 and in the HEPData record for this analysis [30].
The branching fraction ratio of the  decay with respect to the
decay with respect to the  one is measured to be
one is measured to be

This ratio is very close to the similar ratio measured with  instead of
instead of  [52].
[52].
Using the world average value  [13], the branching fractions of the two newly observed decays are evaluated:
[13], the branching fractions of the two newly observed decays are evaluated:

where the last uncertainties are from the uncertainty in  .
.
9 Summary
The  and
and  decays are observed using proton-proton collision data collected by the CMS experiment at \(13\,\mathrm{TeV}\) with an integrated luminosity of 103
decays are observed using proton-proton collision data collected by the CMS experiment at \(13\,\mathrm{TeV}\) with an integrated luminosity of 103 . Their branching fractions are measured with respect to the
. Their branching fractions are measured with respect to the  decay to be
decay to be  , and
, and  , where the last uncertainty in the first ratio corresponds to the uncertainty in the ratio of production cross sections of \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) mesons. The 2- and 3-body invariant mass distributions of the
, where the last uncertainty in the first ratio corresponds to the uncertainty in the ratio of production cross sections of \(\text {B}^{0}_{\mathrm{s}}\) and \(\text {B}^{0}\) mesons. The 2- and 3-body invariant mass distributions of the  decay products do not show significant exotic narrow structures in addition to the known light meson resonances. Further studies with more data will be needed to investigate more precisely the internal dynamics of the
decay products do not show significant exotic narrow structures in addition to the known light meson resonances. Further studies with more data will be needed to investigate more precisely the internal dynamics of the  decay, and to perform CP asymmetry measurements in the two observed decays in the future.
decay, and to perform CP asymmetry measurements in the two observed decays in the future.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Release and preservation of data used by the CMS Collaboration as the basis for publications is guided by the CMS policy as stated in “CMS data preservation, re-use and open access policy” (https://cms-docdb.cern.ch/cgibin/PublicDocDB/RetrieveFile?docid=6032 &filename=CMSDataPolicyV1.2.pdf &version=2).”]
References
Belle Collaboration, Observation of a narrow charmoniumlike state in exclusive \(\text{B}^\pm \rightarrow \text{ K}^\pm {\pi }^+{\pi }^{-}{\rm J}/{\psi }\) decays. Phys. Rev. Lett. 91, 262001 (2003). https://doi.org/10.1103/PhysRevLett.91.262001. arXiv:hep-ex/0309032
CDF Collaboration, Evidence for a narrow near-threshold structure in the \(\text{ J }/{\psi }\phi \) mass spectrum in \(\text{ B}^{+}\rightarrow \text{ J }/{\psi }\phi \text{ K}^+\) decays. Phys. Rev. Lett. 102, 242002 (2009). https://doi.org/10.1103/PhysRevLett.102.242002. arXiv:0903.2229
CDF Collaboration, Observation of the \(Y(4140)\) structure in the \(\text{ J }/{\psi }\phi \) mass spectrum in \(\text{ B}^{\pm }\rightarrow \text{ J }/{\psi }\phi \text{ K}^{\pm }\) decays. Mod. Phys. Lett. A 32, 1750139 (2017). https://doi.org/10.1142/S0217732317501395. arXiv:1101.6058
CMS Collaboration, Observation of a peaking structure in the \(\text{ J }/{\psi }\phi \) mass spectrum from \(\text{ B}^{\pm }\rightarrow \text{ J }/{\psi }\phi \text{ K}^{\pm }\) decays. Phys. Lett. B 734, 261 (2014). https://doi.org/10.1016/j.physletb.2014.05.055. arXiv:1309.6920
LHCb Collaboration, Amplitude analysis of \(\text{ B}^{+}\rightarrow \text{ J }/{\psi }\phi \text{ K}^{+}\) decays. Phys. Rev. D 95, 012002 (2017). https://doi.org/10.1103/PhysRevD.95.012002. arXiv:1606.07898
BaBar Collaboration, Observation of a broad structure in the \({\pi }^{+} {\pi }^{-} \text{ J }/{\psi }\) mass spectrum around 4.26 GeV/c\(^2\). Phys. Rev. Lett 95, 142001 (2005). https://doi.org/10.1103/PhysRevLett.95.142001. arXiv:hep-ex/0506081
BESIII Collaboration, Precise measurement of the \(e^+e^-\rightarrow {\pi }^{+} {\pi }^{-} \text{ J }/{\psi }\) cross section at center-of-mass energies from 3.77 to 4.60 GeV. Phys. Rev. Lett 118, 092001 (2017). https://doi.org/10.1103/PhysRevLett.118.092001. arXiv:1611.01317
Belle Collaboration, Observation of a resonancelike structure in the \({\pi }^{\pm } {\psi }^\prime \) mass distribution in exclusive \(\text{ B } \rightarrow \text{ K }{\pi }^{\pm } {\psi }^\prime \) decays. Phys. Rev. Lett. 100, 142001 (2008). https://doi.org/10.1103/PhysRevLett.100.142001. arXiv:0708.1790
Belle Collaboration, Dalitz analysis of \(\text{ B } \rightarrow \text{ K }{\pi }^{+} {\psi }^\prime \) decays and the \({\rm Z}(4430)^+\). Phys. Rev. D 80, 031104 (2009). https://doi.org/10.1103/PhysRevD.80.031104. arXiv:0905.2869
Belle Collaboration, Experimental constraints on the spin and parity of the \({\rm Z}(4430)^+\). Phys. Rev. D 88, 074026 (2013). https://doi.org/10.1103/PhysRevD.88.074026. arXiv:1306.4894
LHCb Collaboration, Observation of the resonant character of the \({\rm Z}(4430)^-\) state. Phys. Rev. Lett 112, 222002 (2014). https://doi.org/10.1103/PhysRevLett.112.222002. arXiv:1404.1903
A. Hosaka et al., Exotic hadrons with heavy flavors: X, Y, Z, and related states. Prog. Theor. Exp. Phys 2016, 062C01 (2016). https://doi.org/10.1093/ptep/ptw045. arXiv:1603.09229
Particle Data Group, P.A. Zyla et al., Review of particle physics. Prog. Theor. Exp. Phys. 2020, 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
N. Cabibbo, Unitary symmetry and leptonic decays. Phys. Rev. Lett. 10, 531 (1963). https://doi.org/10.1103/PhysRevLett.10.531
Belle Collaboration, Observation of large CP violation in the neutral B meson system. Phys. Rev. Lett. 87, 091802 (2001). https://doi.org/10.1103/PhysRevLett.87.091802. arXiv:hep-ex/0107061
BaBar Collaboration, Observation of CP violation in the \(\text{ B}^{0}\) meson system. Phys. Rev. Lett. 87, 091801 (2001). https://doi.org/10.1103/PhysRevLett.87.091801. arXiv:hep-ex/0107013
BaBar Collaboration, Evidence for CP violation in \(\text{ B}^{0} \rightarrow \text{ J }/{\psi } {\pi }^{0}\) decays. Phys. Rev. Lett. 101, 021801 (2008). https://doi.org/10.1103/PhysRevLett.101.021801. arXiv:0804.0896
BaBar Collaboration, Measurement of time-dependent CP asymmetry in \(\text{ B}^{0}\rightarrow \text{ c }{\bar{c}}{\rm K}^{(*)0}\) decays. Phys. Rev. D 79, 072009 (2009). https://doi.org/10.1103/PhysRevD.79.072009. arXiv:0902.1708
Belle Collaboration, Precise measurement of the CP violation parameter \(\sin 2\phi _1\) in \(\text{ B}^{0}\rightarrow (\text{ c }{\bar{c}}){\rm K}^{0}\) decays. Phys. Rev. Lett. 108, 171802 (2012). https://doi.org/10.1103/PhysRevLett.108.171802. arXiv:1201.4643
LHCb Collaboration, Measurement of the CP-violating phase \(\beta \) in \(\text{ B}^{0}\rightarrow \text{ J }/{\psi } {\pi }^{+}{\pi }^{-}\) decays and limits on penguin effects. Phys. Lett. B 742, 38 (2015). https://doi.org/10.1016/j.physletb.2015.01.008. arXiv:1411.1634
LHCb Collaboration, Measurement of CP violation in \(\text{ B}^{0}\rightarrow \text{ J }/{\psi } \text{ K}^{0}_{{\rm S}}\) decays. Phys. Rev. Lett 115, 031601 (2015). https://doi.org/10.1103/PhysRevLett.115.031601. arXiv:1503.07089
LHCb Collaboration, Measurement of the time-dependent CP asymmetries in \(\text{ B}^{0}_{{\rm s}}\rightarrow \text{ J }/{\psi } \text{ K}^{0}_{{\rm S}}\). JHEP 06, 131 (2015). https://doi.org/10.1007/JHEP06(2015)131. arXiv:1503.07055
LHCb Collaboration, Measurement of \(CP\) violation in \(\text{ B}^{0}\rightarrow \text{ J }/{\psi } \text{ K}^{0}_{{\rm S}}\) and \(\text{ B}^{0}\rightarrow {\psi } \text{(2S)K }^{0}_{{\rm S}}\) decays. JHEP 11, 170 (2017). https://doi.org/10.1007/JHEP11(2017)170. arXiv:1709.03944
Belle Collaboration, Measurement of the branching fraction and time-dependent CP asymmetry for \(\text{ B}^{0}\rightarrow \text{ J }/{\psi } {\pi }^{0}\) decays. Phys. Rev. D 98, 112008 (2018). https://doi.org/10.1103/PhysRevD.98.112008. arXiv:1810.01356
LHCb Collaboration, Updated measurement of time-dependent \(CP\)-violating observables in \(\text{ B}^{0}_{{\rm s}}\rightarrow \text{ J }/{\psi } \text{ K}^{+}\text{ K}^{-}\) decays. Eur. Phys. J. C 79, 706 (2019). https://doi.org/10.1140/epjc/s10052-019-7159-8. arXiv:1906.08356 [Erratum: https://doi.org/10.1140/epjc/s10052-020-7875-0]
CMS Collaboration, Measurement of the CP-violating phase \(\phi _{\rm s}\) in the \(\text{ B}^{0}_{{\rm s}}\rightarrow \text{ J }/{\psi }\phi (1020)\rightarrow \mu ^{+}\mu ^{-}\text{ K}^+\text{ K}^-\) channel in proton–proton collisions at \(\sqrt{s} =\) 13 TeV. Phys. Lett. B 816, 136188 (2021). https://doi.org/10.1016/j.physletb.2021.136188. arXiv:2007.02434
ATLAS Collaboration, Measurement of the CP-violating phase \(\phi _s\) in \(\text{ B}^{0}_{{\rm S}} \rightarrow \text{ J }/{\psi }\phi \) decays in ATLAS at 13 TeV. Eur. Phys. J. C 81, 342 (2021). https://doi.org/10.1140/epjc/s10052-021-09011-0. arXiv:2001.07115
CMS Collaboration, CMS luminosity measurement for the 2017 data-taking period at \(\sqrt{s} = 13\) TeV, CMS Physics Analysis Summary CMS-PAS-LUM-17-004 (2018)
CMS Collaboration, CMS luminosity measurement for the 2018 data-taking period at \(\sqrt{s}=13\) TeV, CMS Physics Analysis Summary CMS-PAS-LUM-18-002 (2019)
HEPData record for this analysis (2021). https://doi.org/10.17182/hepdata.114370
CMS Collaboration, The CMS experiment at the CERN LHC. JINST 3, S08004 (2008). https://doi.org/10.1088/1748-0221/3/08/S08004
CMS Collaboration, The CMS trigger system. JINST 12, P01020 (2017). https://doi.org/10.1088/1748-0221/12/01/P01020. arXiv:1609.02366
CMS Collaboration, Performance of the CMS Level-1 trigger in proton-proton collisions at \(\sqrt{s}=13\) TeV. JINST 15, P10017 (2020). https://doi.org/10.1088/1748-0221/15/10/P10017. arXiv:2006.10165
T. Sjöstrand et al., An introduction to PYTHIA 82. Comput. Phys. Commun. 191, 159 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012
CMS Collaboration, Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements. Eur. Phys. J. C 80 (2020). https://doi.org/10.1140/epjc/s10052-019-7499-4. arXiv:1903.12179
D.J. Lange, The EvtGen particle decay simulation package. Nucl. Instrum. Meth. A 462, 152 (2001). https://doi.org/10.1016/S0168-9002(01)00089-4
E. Barberio, B. van Eijk, Z. Wa̧s, PHOTOS—a universal Monte Carlo for QED radiative corrections in decays. Comput. Phys. Commun. 66, 115 (1991). https://doi.org/10.1016/0010-4655(91)90012-A
E. Barberio, Z. Wa̧s, PHOTOS—a universal Monte Carlo for QED radiative corrections: version 2.0. Comput. Phys. Commun 79, 291 (1994). https://doi.org/10.1016/0010-4655(94)90074-4
GEANT4 Collaboration, GEANT4—a simulation toolkit. Nucl. Instrum. Meth. A 506, 250 (2003). https://doi.org/10.1016/S0168-9002(03)01368-8
CMS Collaboration, Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at \(\sqrt{s}= 13\) TeV. JINST 13, P06015 (2018). https://doi.org/10.1088/1748-0221/13/06/P06015. arXiv:1804.04528
CMS Collaboration, CMS tracking performance results from early LHC operation. Eur. Phys. J. C 70, 1165 (2010). https://doi.org/10.1140/epjc/s10052-010-1491-3. arXiv:1007.1988
CMS Collaboration, Search for the X(5568) state decaying into \(\text{ B}^{0}_{{\rm S}}{\pi }^{\pm }\) in proton-proton collisions at \(\sqrt{s} = \) 8 TeV. Phys. Rev. Lett 120, 202005 (2018). https://doi.org/10.1103/PhysRevLett.120.202005. arXiv:1712.06144
CMS Collaboration, Study of the \(\text{ B}^{+}\rightarrow \text{ J }/{\psi }{\bar{\Lambda }}{\rm p}\) decay in proton-proton collisions at \( \sqrt{s} \) = 8 TeV. JHEP 12, 100 (2019). https://doi.org/10.1007/JHEP12(2019)100. arXiv:1907.05461
CMS Collaboration, Observation of the \(\Lambda ^{0}_{{\rm b}} \rightarrow \text{ J }/{\psi } \Lambda \phi \) decay in proton-proton collisions at \(\sqrt{s}=\) 13 TeV. Phys. Lett. B 802, 135203 (2020). https://doi.org/10.1016/j.physletb.2020.135203. arXiv:1911.03789
CMS Collaboration, Description and performance of track and primary-vertex reconstruction with the CMS tracker. JINST 9, P10009 (2014). https://doi.org/10.1088/1748-0221/9/10/P10009. arXiv:1405.6569
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011). https://doi.org/10.1140/epjc/s10052-011-1554-0. arXiv:1007.1727 [Erratum: https://doi.org/10.1140/epjc/s10052-013-2501-z]
S.S. Wilks, The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann. Math. Stat. 9, 60 (1938). https://doi.org/10.1214/aoms/1177732360
M. Pivk, F.R. Le Diberder, \({}_{s}{\cal{P}}\)lot: a statistical tool to unfold data distributions. Nucl. Instrum. Meth. A 555, 356 (2005). https://doi.org/10.1016/j.nima.2005.08.106. arXiv:physics/0402083
CMS Collaboration, Tracking POG results for pion efficiency with the \(\text{ D}^{*}\) meson using data from 2016 and 2017, CMS Detector Performance Note CMS-DP-2018-050 (2018)
S. Jackman, Bayesian analysis for the social sciences. Wiley, New Jersey (2009). https://doi.org/10.1002/9780470686621
LHCb Collaboration, Precise measurement of the \(f_{s}/f_{d}\) ratio of fragmentation fractions and of \(\text{ B}^{0}_{{\rm s}}\) decay branching fractions. Phys. Rev. D 104, 032005 (2021). https://doi.org/10.1103/PhysRevD.104.032005. arXiv:2103.06810
LHCb Collaboration, Observation of the \(\text{ B}^{0}_{{\rm S}} \rightarrow \text{ J }/{\psi } \text{ K}^{0}_{{\rm s} }\text{ K}^{\pm } {\pi }^{\mp }\) decay. JHEP 07, 140 (2014). https://doi.org/10.1007/JHEP07(2014)140. arXiv:1405.3219
Acknowledgements
We congratulate our colleagues in the CERN accelerator departments for the excellent performance of the LHC and thank the technical and administrative staffs at CERN and at other CMS institutes for their contributions to the success of the CMS effort. In addition, we gratefully acknowledge the computing centres and personnel of the Worldwide LHC Computing Grid and other centres for delivering so effectively the computing infrastructure essential to our analyses. Finally, we acknowledge the enduring support for the construction and operation of the LHC, the CMS detector, and the supporting computing infrastructure provided by the following funding agencies: BMBWF and FWF (Austria); FNRS and FWO (Belgium); CNPq, CAPES, FAPERJ, FAPERGS, and FAPESP (Brazil); MES and BNSF (Bulgaria); CERN; CAS, MoST, and NSFC (China); MINCIENCIAS (Colombia); MSES and CSF (Croatia); RIF (Cyprus); SENESCYT (Ecuador); MoER, ERC PUT and ERDF (Estonia); Academy of Finland, MEC, and HIP (Finland); CEA and CNRS/IN2P3 (France); BMBF, DFG, and HGF (Germany); GSRI (Greece); NKFIA (Hungary); DAE and DST (India); IPM (Iran); SFI (Ireland); INFN (Italy); MSIP and NRF (Republic of Korea); MES (Latvia); LAS (Lithuania); MOE and UM (Malaysia); BUAP, CINVESTAV, CONACYT, LNS, SEP, and UASLP-FAI (Mexico); MOS (Montenegro); MBIE (New Zealand); PAEC (Pakistan); MSHE and NSC (Poland); FCT (Portugal); JINR (Dubna); MON, RosAtom, RAS, RFBR, and NRC KI (Russia); MESTD (Serbia); MCIN/AEI and PCTI (Spain); MOSTR (Sri Lanka); Swiss Funding Agencies (Switzerland); MST (Taipei); ThEPCenter, IPST, STAR, and NSTDA (Thailand); TUBITAK and TAEK (Turkey); NASU (Ukraine); STFC (United Kingdom); DOE and NSF (USA). Rachada-pisek Individuals have received support from the Marie-Curie programme and the European Research Council and Horizon 2020 Grant, contract Nos. 675440, 724704, 752730, 758316, 765710, 824093, 884104, and COST Action CA16108 (European Union); the Leventis Foundation; the Alfred P. Sloan Foundation; the Alexander von Humboldt Foundation; the Belgian Federal Science Policy Office; the Fonds pour la Formation à la Recherche dans l’Industrie et dans l’Agriculture (FRIA-Belgium); the Agentschap voor Innovatie door Wetenschap en Technologie (IWT-Belgium); the F.R.S.-FNRS and FWO (Belgium) under the “Excellence of Science – EOS” – be.h project n. 30820817; the Beijing Municipal Science & Technology Commission, No. Z191100007219010; the Ministry of Education, Youth and Sports (MEYS) of the Czech Republic; the Deutsche Forschungsgemeinschaft (DFG), under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306, and under project number 400140256-GRK2497; the Lendület (“Momentum”) Programme and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, the New National Excellence Program ÚNKP, the NKFIA research grants 123842, 123959, 124845, 124850, 125105, 128713, 128786, and 129058 (Hungary); the Council of Science and Industrial Research, India; the Latvian Council of Science; the Ministry of Science and Higher Education and the National Science Center, contracts Opus 2014/15/B/ST2/03998 and 2015/19/B/ST2/02861 (Poland); the Fundação para a Ciência e a Tecnologia, grant CEECIND/01334/2018 (Portugal); the National Priorities Research Program by Qatar National Research Fund; the Ministry of Science and Higher Education, projects no. 0723-2020-0041 and no. FSWW-2020-0008, and the Russian Foundation for Basic Research, project No.19-42-703014 (Russia); MCIN/AEI/10.13039/501100011033, ERDF “a way of making Europe”, and the Programa Estatal de Fomento de la Investigación Científica y Técnica de Excelencia María de Maeztu, grant MDM-2017-0765 and Programa Severo Ochoa del Principado de Asturias (Spain); the Stavros Niarchos Foundation (Greece); the Rachadapisek Sompot Fund for Postdoctoral Fellowship, Chulalongkorn University and the Chulalongkorn Academic into Its 2nd Century Project Advancement Project (Thailand); the Kavli Foundation; the Nvidia Corporation; the SuperMicro Corporation; the Welch Foundation, contract C-1845; and the Weston Havens Foundation (USA).
Author information
Authors and Affiliations
Yerevan Physics Institute, Yerevan, Armenia
A. Tumasyan
Institut für Hochenergiephysik, Vienna, Austria
W. Adam, J. W. Andrejkovic, T. Bergauer, S. Chatterjee, K. Damanakis, M. Dragicevic, A. Escalante Del Valle, R. Frühwirth, M. Jeitler, N. Krammer, L. Lechner, D. Liko, I. Mikulec, P. Paulitsch, F. M. Pitters, J. Schieck, R. Schöfbeck, D. Schwarz, S. Templ, W. Waltenberger & C. -E. Wulz
Institute for Nuclear Problems, Minsk, Belarus
V. Chekhovsky, A. Litomin & V. Makarenko
Universiteit Antwerpen, Antwerpen, Belgium
M. R. Darwish, E. A. De Wolf, T. Janssen, T. Kello, A. Lelek, H. Rejeb Sfar, P. Van Mechelen, S. Van Putte & N. Van Remortel
Vrije Universiteit Brussel, Brussels, Belgium
E. S. Bols, J. D’Hondt, A. De Moor, M. Delcourt, H. El Faham, S. Lowette, S. Moortgat, A. Morton, D. Müller, A. R. Sahasransu, S. Tavernier, W. Van Doninck & D. Vannerom
Université Libre de Bruxelles, Brussels, Belgium
D. Beghin, B. Bilin, B. Clerbaux, G. De Lentdecker, L. Favart, A. K. Kalsi, K. Lee, M. Mahdavikhorrami, I. Makarenko, L. Moureaux, S. Paredes, L. Pétré, A. Popov, N. Postiau, E. Starling, L. Thomas, M. Vanden Bemden, C. Vander Velde & P. Vanlaer
Ghent University, Ghent, Belgium
T. Cornelis, D. Dobur, J. Knolle, L. Lambrecht, G. Mestdach, M. Niedziela, C. Rendón, C. Roskas, A. Samalan, K. Skovpen, M. Tytgat, B. Vermassen & L. Wezenbeek
Université Catholique de Louvain, Louvain-la-Neuve, Belgium
A. Benecke, A. Bethani, G. Bruno, F. Bury, C. Caputo, P. David, C. Delaere, I. S. Donertas, A. Giammanco, K. Jaffel, Sa. Jain, V. Lemaitre, K. Mondal, J. Prisciandaro, A. Taliercio, M. Teklishyn, T. T. Tran, P. Vischia & S. Wertz
Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
G. A. Alves, C. Hensel, A. Moraes & P. Rebello Teles
Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
W. L. Aldá Júnior, M. Alves Gallo Pereira, M. Barroso Ferreira Filho, H. Brandao Malbouisson, W. Carvalho, J. Chinellato, E. M. Da Costa, G. G. Da Silveira, D. De Jesus Damiao, V. Dos Santos Sousa, S. Fonseca De Souza, C. Mora Herrera, K. Mota Amarilo, L. Mundim, H. Nogima, A. Santoro, S. M. Silva Do Amaral, A. Sznajder, M. Thiel, F. Torres Da Silva De Araujo & A. Vilela Pereira
Universidade Estadual Paulista (a), Universidade Federal do ABC (b), São Paulo, Brazil
C. A. Bernardes, L. Calligaris, T. R. Fernandez Perez Tomei, E. M. Gregores, D. S. Lemos, P. G. Mercadante, S. F. Novaes & Sandra S. Padula
Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
A. Aleksandrov, G. Antchev, R. Hadjiiska, P. Iaydjiev, M. Misheva, M. Rodozov, M. Shopova & G. Sultanov
University of Sofia, Sofia, Bulgaria
A. Dimitrov, T. Ivanov, L. Litov, B. Pavlov, P. Petkov & A. Petrov
Beihang University, Beijing, China
T. Cheng, T. Javaid, M. Mittal & L. Yuan
Department of Physics, Tsinghua University, Beijing, China
M. Ahmad, G. Bauer, C. Dozen, Z. Hu, J. Martins, Y. Wang & K. Yi
Institute of High Energy Physics, Beijing, China
E. Chapon, G. M. Chen, H. S. Chen, M. Chen, F. Iemmi, A. Kapoor, D. Leggat, H. Liao, Z. -A. Liu, V. Milosevic, F. Monti, R. Sharma, J. Tao, J. Thomas-Wilsker, J. Wang, H. Zhang & J. Zhao
State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
A. Agapitos, Y. An, Y. Ban, C. Chen, A. Levin, Q. Li, X. Lyu, Y. Mao, S. J. Qian, D. Wang, J. Xiao & H. Yang
Sun Yat-Sen University, Guangzhou, China
M. Lu & Z. You
Institute of Modern Physics and Key Laboratory of Nuclear Physics and Ion-beam Application (MOE), Fudan University, Shanghai, China
X. Gao, H. Okawa & Y. Zhang
Zhejiang University, Hangzhou, China, Zhejiang, China
Z. Lin & M. Xiao
Universidad de Los Andes, Bogota, Colombia
C. Avila, A. Cabrera, C. Florez & J. Fraga
Universidad de Antioquia, Medellin, Colombia
J. Mejia Guisao, F. Ramirez & J. D. Ruiz Alvarez
University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
D. Giljanovic, N. Godinovic, D. Lelas & I. Puljak
University of Split, Faculty of Science, Split, Croatia
Z. Antunovic, M. Kovac & T. Sculac
Institute Rudjer Boskovic, Zagreb, Croatia
V. Brigljevic, D. Ferencek, D. Majumder, M. Roguljic, A. Starodumov & T. Susa
University of Cyprus, Nicosia, Cyprus
A. Attikis, K. Christoforou, G. Kole, M. Kolosova, S. Konstantinou, J. Mousa, C. Nicolaou, F. Ptochos, P. A. Razis, H. Rykaczewski & H. Saka
Charles University, Prague, Czech Republic
M. Finger, M. Finger Jr. & A. Kveton
Escuela Politecnica Nacional, Quito, Ecuador
E. Ayala
Universidad San Francisco de Quito, Quito, Ecuador
E. Carrera Jarrin
Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
A. A. Abdelalim & E. Salama
Center for High Energy Physics (CHEP-FU), Fayoum University, El-Fayoum, Egypt
M. A. Mahmoud & Y. Mohammed
National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
S. Bhowmik, R. K. Dewanjee, K. Ehataht, M. Kadastik, S. Nandan, C. Nielsen, J. Pata, M. Raidal, L. Tani & C. Veelken
Department of Physics, University of Helsinki, Helsinki, Finland
P. Eerola, H. Kirschenmann, K. Osterberg & M. Voutilainen
Helsinki Institute of Physics, Helsinki, Finland
S. Bharthuar, E. Brücken, F. Garcia, J. Havukainen, M. S. Kim, R. Kinnunen, T. Lampén, K. Lassila-Perini, S. Lehti, T. Lindén, M. Lotti, L. Martikainen, M. Myllymäki, J. Ott, M. m. Rantanen, H. Siikonen, E. Tuominen & J. Tuominiemi
Lappeenranta University of Technology, Lappeenranta, Finland
P. Luukka, H. Petrow & T. Tuuva
IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
C. Amendola, M. Besancon, F. Couderc, M. Dejardin, D. Denegri, J. L. Faure, F. Ferri, S. Ganjour, P. Gras, G. Hamel de Monchenault, P. Jarry, B. Lenzi, J. Malcles, J. Rander, A. Rosowsky, M. Ö. Sahin, A. Savoy-Navarro, M. Titov & G. B. Yu
Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
S. Ahuja, F. Beaudette, M. Bonanomi, A. Buchot Perraguin, P. Busson, A. Cappati, C. Charlot, O. Davignon, B. Diab, G. Falmagne, S. Ghosh, R. Granier de Cassagnac, A. Hakimi, I. Kucher, J. Motta, M. Nguyen, C. Ochando, P. Paganini, J. Rembser, R. Salerno, U. Sarkar, J. B. Sauvan, Y. Sirois, A. Tarabini, A. Zabi & A. Zghiche
Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
J. -L. Agram, J. Andrea, D. Apparu, D. Bloch, G. Bourgatte, J -M. Brom, E. C. Chabert, C. Collard, D. Darej, J. -C. Fontaine, U. Goerlach, C. Grimault, A. -C. Le Bihan, E. Nibigira & P. Van Hove
Institut de Physique des 2 Infinis de Lyon (IP2I), Villeurbanne, France
E. Asilar, S. Beauceron, C. Bernet, G. Boudoul, C. Camen, A. Carle, N. Chanon, D. Contardo, P. Depasse, H. El Mamouni, J. Fay, S. Gascon, M. Gouzevitch, B. Ille, I. B. Laktineh, H. Lattaud, A. Lesauvage, M. Lethuillier, L. Mirabito, S. Perries, K. Shchablo, V. Sordini, L. Torterotot, G. Touquet, M. Vander Donckt & S. Viret
Georgian Technical University, Tbilisi, Georgia
I. Lomidze, T. Toriashvili & Z. Tsamalaidze
RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
V. Botta, L. Feld, K. Klein, M. Lipinski, D. Meuser, A. Pauls, N. Röwert, J. Schulz & M. Teroerde
RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
A. Dodonova, D. Eliseev, M. Erdmann, P. Fackeldey, B. Fischer, T. Hebbeker, K. Hoepfner, F. Ivone, L. Mastrolorenzo, M. Merschmeyer, A. Meyer, G. Mocellin, S. Mondal, S. Mukherjee, D. Noll, A. Novak, A. Pozdnyakov, Y. Rath, H. Reithler, A. Schmidt, S. C. Schuler, A. Sharma, L. Vigilante, S. Wiedenbeck & S. Zaleski
RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
C. Dziwok, G. Flügge, W. Haj Ahmad, O. Hlushchenko, T. Kress, A. Nowack, O. Pooth, D. Roy, A. Stahl, T. Ziemons & A. Zotz
Deutsches Elektronen-Synchrotron, Hamburg, Germany
H. Aarup Petersen, M. Aldaya Martin, P. Asmuss, S. Baxter, M. Bayatmakou, O. Behnke, A. Bermúdez Martínez, S. Bhattacharya, A. A. Bin Anuar, F. Blekman, K. Borras, D. Brunner, A. Campbell, A. Cardini, C. Cheng, F. Colombina, S. Consuegra Rodríguez, G. Correia Silva, M. De Silva, L. Didukh, G. Eckerlin, D. Eckstein, L. I. Estevez Banos, O. Filatov, E. Gallo, A. Geiser, A. Giraldi, A. Grohsjean, M. Guthoff, A. Jafari, N. Z. Jomhari, H. Jung, A. Kasem, M. Kasemann, H. Kaveh, C. Kleinwort, R. Kogler, D. Krücker, W. Lange, K. Lipka, W. Lohmann, R. Mankel, I. -A. Melzer-Pellmann, M. Mendizabal Morentin, J. Metwally, A. B. Meyer, M. Meyer, J. Mnich, A. Mussgiller, A. Nürnberg, Y. Otarid, D. Pérez Adán, D. Pitzl, A. Raspereza, B. Ribeiro Lopes, J. Rübenach, A. Saggio, A. Saibel, M. Savitskyi, M. Scham, V. Scheurer, S. Schnake, P. Schütze, C. Schwanenberger, M. Shchedrolosiev, R. E. Sosa Ricardo, D. Stafford, N. Tonon, M. Van De Klundert, F. Vazzoler, R. Walsh, D. Walter, Q. Wang, Y. Wen, K. Wichmann, L. Wiens, C. Wissing & S. Wuchterl
University of Hamburg, Hamburg, Germany
R. Aggleton, S. Albrecht, S. Bein, L. Benato, P. Connor, K. De Leo, M. Eich, K. El Morabit, F. Feindt, A. Fröhlich, C. Garbers, E. Garutti, P. Gunnellini, M. Hajheidari, J. Haller, A. Hinzmann, G. Kasieczka, R. Klanner, T. Kramer, V. Kutzner, J. Lange, T. Lange, A. Lobanov, A. Malara, C. Matthies, A. Mehta, A. Nigamova, K. J. Pena Rodriguez, M. Rieger, O. Rieger, P. Schleper, M. Schröder, J. Schwandt, J. Sonneveld, H. Stadie, G. Steinbrück, A. Tews & I. Zoi
Karlsruher Institut fuer Technologie, Karlsruhe, Germany
J. Bechtel, S. Brommer, M. Burkart, E. Butz, R. Caspart, T. Chwalek, W. De Boer, A. Dierlamm, A. Droll, N. Faltermann, M. Giffels, J. O. Gosewisch, A. Gottmann, F. Hartmann, C. Heidecker, U. Husemann, P. Keicher, R. Koppenhöfer, S. Maier, S. Mitra, Th. Müller, M. Neukum, G. Quast, K. Rabbertz, J. Rauser, D. Savoiu, M. Schnepf, D. Seith, I. Shvetsov, H. J. Simonis, R. Ulrich, J. Van Der Linden, R. F. Von Cube, M. Wassmer, M. Weber, S. Wieland, R. Wolf, S. Wozniewski & S. Wunsch
Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
G. Anagnostou, G. Daskalakis, A. Kyriakis, D. Loukas & A. Stakia
National and Kapodistrian University of Athens, Athens, Greece
M. Diamantopoulou, D. Karasavvas, P. Kontaxakis, C. K. Koraka, A. Manousakis-Katsikakis, A. Panagiotou, I. Papavergou, N. Saoulidou, K. Theofilatos, E. Tziaferi, K. Vellidis & E. Vourliotis
National Technical University of Athens, Athens, Greece
G. Bakas, K. Kousouris, I. Papakrivopoulos, G. Tsipolitis & A. Zacharopoulou
University of Ioánnina, Ioánnina, Greece
K. Adamidis, I. Bestintzanos, I. Evangelou, C. Foudas, P. Gianneios, P. Katsoulis, P. Kokkas, N. Manthos, I. Papadopoulos & J. Strologas
MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
M. Csanad, K. Farkas, M. M. A. Gadallah, S. Lökös, P. Major, K. Mandal, G. Pasztor, A. J. Rádl, O. Surányi & G. I. Veres
Wigner Research Centre for Physics, Budapest, Hungary
M. Bartók, G. Bencze, C. Hajdu, D. Horvath, F. Sikler & V. Veszpremi
Institute of Nuclear Research ATOMKI, Debrecen, Hungary
S. Czellar, D. Fasanella, F. Fienga, J. Karancsi, J. Molnar, Z. Szillasi & D. Teyssier
Institute of Physics, University of Debrecen, Debrecen, Hungary
P. Raics, Z. L. Trocsanyi & B. Ujvari
Karoly Robert Campus, MATE Institute of Technology, Gyongyos, Hungary
T. Csorgo, F. Nemes & T. Novak
National Institute of Science Education and Research, HBNI, Bhubaneswar, India
S. Bahinipati, C. Kar, P. Mal, T. Mishra, V. K. Muraleedharan Nair Bindhu, A. Nayak, P. Saha, N. Sur, S. K. Swain & D. Vats
Panjab University, Chandigarh, India
S. Bansal, S. B. Beri, V. Bhatnagar, G. Chaudhary, S. Chauhan, N. Dhingra, R. Gupta, A. Kaur, H. Kaur, M. Kaur, P. Kumari, M. Meena, K. Sandeep, J. B. Singh & A. K. Virdi
University of Delhi, Delhi, India
A. Ahmed, A. Bhardwaj, B. C. Choudhary, M. Gola, S. Keshri, A. Kumar, M. Naimuddin, P. Priyanka, K. Ranjan, S. Saumya & A. Shah
Saha Institute of Nuclear Physics, HBNI, Kolkata, India
M. Bharti, R. Bhattacharya, S. Bhattacharya, D. Bhowmik, S. Dutta, S. Dutta, B. Gomber, M. Maity, P. Palit, P. K. Rout, G. Saha, B. Sahu, S. Sarkar & M. Sharan
Indian Institute of Technology Madras, Madras, India
P. K. Behera, S. C. Behera, P. Kalbhor, J. R. Komaragiri, D. Kumar, A. Muhammad, L. Panwar, R. Pradhan, P. R. Pujahari, A. Sharma, A. K. Sikdar & P. C. Tiwari
Bhabha Atomic Research Centre, Mumbai, India
K. Naskar
Tata Institute of Fundamental Research-A, Mumbai, India
T. Aziz, S. Dugad & M. Kumar
Tata Institute of Fundamental Research-B, Mumbai, India
S. Banerjee, R. Chudasama, M. Guchait, S. Karmakar, S. Kumar, G. Majumder, K. Mazumdar & S. Mukherjee
Indian Institute of Science Education and Research (IISER), Pune, India
A. Alpana, S. Dube, B. Kansal, A. Laha, S. Pandey, A. Rastogi & S. Sharma
Isfahan University of Technology, Isfahan, Iran
H. Bakhshiansohi, E. Khazaie & M. Zeinali
Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
S. Chenarani, S. M. Etesami, M. Khakzad & M. Mohammadi Najafabadi
University College Dublin, Dublin, Ireland
M. Grunewald
INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
M. Abbrescia, R. Aly, C. Aruta, A. Colaleo, D. Creanza, N. De Filippis, M. De Palma, A. Di Florio, A. Di Pilato, W. Elmetenawee, F. Errico, L. Fiore, G. Iaselli, M. Ince, S. Lezki, G. Maggi, M. Maggi, I. Margjeka, V. Mastrapasqua, S. My, S. Nuzzo, A. Pellecchia, A. Pompili, G. Pugliese, D. Ramos, A. Ranieri, G. Selvaggi, L. Silvestris, F. M. Simone, Ü. Sözbilir, R. Venditti & P. Verwilligen
INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
G. Abbiendi, C. Battilana, D. Bonacorsi, L. Borgonovi, L. Brigliadori, R. Campanini, P. Capiluppi, A. Castro, F. R. Cavallo, C. Ciocca, M. Cuffiani, G. M. Dallavalle, T. Diotalevi, F. Fabbri, A. Fanfani, P. Giacomelli, L. Giommi, C. Grandi, L. Guiducci, S. Lo Meo, L. Lunerti, S. Marcellini, G. Masetti, F. L. Navarria, A. Perrotta, F. Primavera, A. M. Rossi, T. Rovelli & G. P. Siroli
INFN Sezione di Catania, Università di Catania, Catania, Italy
S. Albergo, S. Costa, A. Di Mattia, R. Potenza, A. Tricomi & C. Tuve
INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
G. Barbagli, A. Cassese, R. Ceccarelli, V. Ciulli, C. Civinini, R. D’Alessandro, E. Focardi, G. Latino, P. Lenzi, M. Lizzo, M. Meschini, S. Paoletti, R. Seidita, G. Sguazzoni & L. Viliani
INFN Laboratori Nazionali di Frascati, Frascati, Italy
L. Benussi, S. Bianco & D. Piccolo
INFN Sezione di Genova, Università di Genova, Genoa, Italy
M. Bozzo, F. Ferro, R. Mulargia, E. Robutti & S. Tosi
INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
A. Benaglia, G. Boldrini, F. Brivio, F. Cetorelli, F. De Guio, M. E. Dinardo, P. Dini, S. Gennai, A. Ghezzi, P. Govoni, L. Guzzi, M. T. Lucchini, M. Malberti, S. Malvezzi, A. Massironi, D. Menasce, L. Moroni, M. Paganoni, D. Pedrini, B. S. Pinolini, S. Ragazzi, N. Redaelli, T. Tabarelli de Fatis, D. Valsecchi & D. Zuolo
INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Napoli, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
S. Buontempo, F. Carnevali, N. Cavallo, A. De Iorio, F. Fabozzi, A. O. M. Iorio, L. Lista, S. Meola, P. Paolucci, B. Rossi & C. Sciacca
INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
P. Azzi, N. Bacchetta, D. Bisello, P. Bortignon, A. Bragagnolo, R. Carlin, P. Checchia, T. Dorigo, U. Dosselli, F. Gasparini, U. Gasparini, G. Grosso, L. Layer, E. Lusiani, M. Margoni, F. Marini, A. T. Meneguzzo, J. Pazzini, P. Ronchese, R. Rossin, F. Simonetto, G. Strong, M. Tosi, H. Yarar, M. Zanetti, P. Zotto, A. Zucchetta & G. Zumerle
INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
C. Aimè, A. Braghieri, S. Calzaferri, D. Fiorina, P. Montagna, S. P. Ratti, V. Re, C. Riccardi, P. Salvini, I. Vai & P. Vitulo
INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
P. Asenov, G. M. Bilei, D. Ciangottini, L. Fanò, M. Magherini, G. Mantovani, V. Mariani, M. Menichelli, F. Moscatelli, A. Piccinelli, M. Presilla, A. Rossi, A. Santocchia, D. Spiga & T. Tedeschi
INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy, Università di Siena, Siena, Italy
P. Azzurri, G. Bagliesi, V. Bertacchi, L. Bianchini, T. Boccali, E. Bossini, R. Castaldi, M. A. Ciocci, V. D’Amante, R. Dell’Orso, M. R. Di Domenico, S. Donato, A. Giassi, F. Ligabue, E. Manca, G. Mandorli, D. Matos Figueiredo, A. Messineo, M. Musich, F. Palla, S. Parolia, G. Ramirez-Sanchez, A. Rizzi, G. Rolandi, S. Roy Chowdhury, A. Scribano, N. Shafiei, P. Spagnolo, R. Tenchini, G. Tonelli, N. Turini, A. Venturi & P. G. Verdini
INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
P. Barria, M. Campana, F. Cavallari, D. Del Re, E. Di Marco, M. Diemoz, E. Longo, P. Meridiani, G. Organtini, F. Pandolfi, R. Paramatti, C. Quaranta, S. Rahatlou, C. Rovelli, F. Santanastasio, L. Soffi & R. Tramontano
INFN Sezione di Torino, Università di Torino, Turin, Italy, Università del Piemonte Orientale, Novara, Italy
N. Amapane, R. Arcidiacono, S. Argiro, M. Arneodo, N. Bartosik, R. Bellan, A. Bellora, J. Berenguer Antequera, C. Biino, N. Cartiglia, M. Costa, R. Covarelli, N. Demaria, M. Grippo, B. Kiani, F. Legger, C. Mariotti, S. Maselli, A. Mecca, E. Migliore, E. Monteil, M. Monteno, M. M. Obertino, G. Ortona, L. Pacher, N. Pastrone, M. Pelliccioni, M. Ruspa, K. Shchelina, F. Siviero, V. Sola, A. Solano, D. Soldi, A. Staiano, M. Tornago, D. Trocino, G. Umoret & A. Vagnerini
INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
S. Belforte, V. Candelise, M. Casarsa, F. Cossutti, A. Da Rold, G. Della Ricca & G. Sorrentino
Kyungpook National University, Daegu, Korea
S. Dogra, C. Huh, B. Kim, D. H. Kim, G. N. Kim, J. Kim, J. Lee, S. W. Lee, C. S. Moon, Y. D. Oh, S. I. Pak, S. Sekmen & Y. C. Yang
Chonnam National University, Institute for Universe and Elementary Particles, Kwangju, Korea
H. Kim & D. H. Moon
Hanyang University, Seoul, Korea
B. Francois, T. J. Kim & J. Park
Korea University, Seoul, Korea
S. Cho, S. Choi, B. Hong, K. Lee, K. S. Lee, J. Lim, J. Park, S. K. Park & J. Yoo
Department of Physics, Kyung Hee University, Seoul, Republic of Korea
J. Goh & A. Gurtu
Sejong University, Seoul, Korea
H. S. Kim & Y. Kim
Seoul National University, Seoul, Korea
J. Almond, J. H. Bhyun, J. Choi, S. Jeon, J. Kim, J. S. Kim, S. Ko, H. Kwon, H. Lee, S. Lee, B. H. Oh, M. Oh, S. B. Oh, H. Seo, U. K. Yang & I. Yoon
University of Seoul, Seoul, Korea
W. Jang, D. Y. Kang, Y. Kang, S. Kim, B. Ko, J. S. H. Lee, Y. Lee, J. A. Merlin, I. C. Park, Y. Roh, M. S. Ryu, D. Song, I. J. Watson & S. Yang
Department of Physics, Yonsei University, Seoul, Korea
S. Ha & H. D. Yoo
Sungkyunkwan University, Suwon, Korea
M. Choi, H. Lee, Y. Lee & I. Yu
College of Engineering and Technology, American University of the Middle East (AUM), Egaila, Kuwait, Dasman, Kuwait
T. Beyrouthy & Y. Maghrbi
Riga Technical University, Riga, Latvia
K. Dreimanis & V. Veckalns
Vilnius University, Vilnius, Lithuania
M. Ambrozas, A. Carvalho Antunes De Oliveira, A. Juodagalvis, A. Rinkevicius & G. Tamulaitis
National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
N. Bin Norjoharuddeen & Z. Zolkapli
Universidad de Sonora (UNISON), Hermosillo, Mexico
J. F. Benitez, A. Castaneda Hernandez, H. A. Encinas Acosta, L. G. Gallegos Maríñez, M. León Coello, J. A. Murillo Quijada, A. Sehrawat & L. Valencia Palomo
Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
G. Ayala, H. Castilla-Valdez, E. De La Cruz-Burelo, I. Heredia-De La Cruz, R. Lopez-Fernandez, C. A. Mondragon Herrera, D. A. Perez Navarro, R. Reyes-Almanza & A. Sánchez Hernández
Universidad Iberoamericana, Mexico City, Mexico
S. Carrillo Moreno, C. Oropeza Barrera & F. Vazquez Valencia
Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
I. Pedraza, H. A. Salazar Ibarguen & C. Uribe Estrada
University of Montenegro, Podgorica, Montenegro
J. Mijuskovic & N. Raicevic
University of Auckland, Auckland, New Zealand
D. Krofcheck
University of Canterbury, Christchurch, New Zealand
P. H. Butler
National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
A. Ahmad, M. I. Asghar, A. Awais, M. I. M. Awan, M. Gul, H. R. Hoorani, W. A. Khan, M. A. Shah, M. Shoaib & M. Waqas
AGH University of Science and Technology Faculty of Computer Science, Electronics and Telecommunications, Krakow, Poland
V. Avati, L. Grzanka & M. Malawski
National Centre for Nuclear Research, Swierk, Poland
H. Bialkowska, M. Bluj, B. Boimska, M. Górski, M. Kazana, M. Szleper & P. Zalewski
Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
K. Bunkowski, K. Doroba, A. Kalinowski, M. Konecki & J. Krolikowski
Laboratório de Instrumentaç ao e Física Experimental de Partículas, Lisbon, Portugal
M. Araujo, P. Bargassa, D. Bastos, A. Boletti, P. Faccioli, M. Gallinaro, J. Hollar, N. Leonardo, T. Niknejad, M. Pisano, J. Seixas, O. Toldaiev & J. Varela
Joint Institute for Nuclear Research, Dubna, Russia
S. Afanasiev, D. Budkouski, I. Golutvin, I. Gorbunov, V. Karjavine, V. Korenkov, A. Lanev, A. Malakhov, V. Matveev, V. Palichik, V. Perelygin, M. Savina, V. Shalaev, S. Shmatov, S. Shulha, V. Smirnov, O. Teryaev, N. Voytishin, B. S. Yuldashev, A. Zarubin & I. Zhizhin
Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
G. Gavrilov, V. Golovtcov, Y. Ivanov, V. Kim, E. Kuznetsova, V. Murzin, V. Oreshkin, I. Smirnov, D. Sosnov, V. Sulimov, L. Uvarov, S. Volkov & A. Vorobyev
Institute for Nuclear Research, Moscow, Russia
Yu. Andreev, A. Dermenev, S. Gninenko, N. Golubev, A. Karneyeu, D. Kirpichnikov, M. Kirsanov, N. Krasnikov, A. Pashenkov, G. Pivovarov & A. Toropin
Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
V. Epshteyn, V. Gavrilov, N. Lychkovskaya, A. Nikitenko, V. Popov, A. Stepennov, M. Toms, E. Vlasov & A. Zhokin
Moscow Institute of Physics and Technology, Moscow, Russia
T. Aushev
National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
O. Bychkova, R. Chistov, M. Danilov, A. Oskin, P. Parygin, S. Polikarpov & A. Tulupov
P.N. Lebedev Physical Institute, Moscow, Russia
V. Andreev, M. Azarkin, I. Dremin, M. Kirakosyan & A. Terkulov
Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
A. Belyaev, E. Boos, M. Dubinin, L. Dudko, A. Ershov, A. Gribushin, V. Klyukhin, O. Kodolova, I. Lokhtin, S. Obraztsov, S. Petrushanko, V. Savrin & A. Snigirev
Novosibirsk State University (NSU), Novosibirsk, Russia
V. Blinov, T. Dimova, L. Kardapoltsev, A. Kozyrev, I. Ovtin, O. Radchenko & Y. Skovpen
Institute for High Energy Physics of National Research Centre ‘Kurchatov Institute’, Protvino, Russia
I. Azhgirey, I. Bayshev, D. Elumakhov, V. Kachanov, D. Konstantinov, P. Mandrik, V. Petrov, R. Ryutin, S. Slabospitskii, A. Sobol, S. Troshin, N. Tyurin, A. Uzunian & A. Volkov
National Research Tomsk Polytechnic University, Tomsk, Russia
A. Babaev & V. Okhotnikov
Tomsk State University, Tomsk, Russia
V. Borshch, V. Ivanchenko & E. Tcherniaev
University of Belgrade: Faculty of Physics and VINCA Institute of Nuclear Sciences, Belgrade, Serbia
P. Adzic, M. Dordevic, P. Milenovic & J. Milosevic
Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
M. Aguilar-Benitez, J. Alcaraz Maestre, A. Álvarez Fernández, I. Bachiller, M. Barrio Luna, Cristina F. Bedoya, C. A. Carrillo Montoya, M. Cepeda, M. Cerrada, N. Colino, B. De La Cruz, A. Delgado Peris, J. P. Fernández Ramos, J. Flix, M. C. Fouz, O. Gonzalez Lopez, S. Goy Lopez, J. M. Hernandez, M. I. Josa, J. León Holgado, D. Moran, Á. Navarro Tobar, C. Perez Dengra, A. Pérez-Calero Yzquierdo, J. Puerta Pelayo, I. Redondo, L. Romero, S. Sánchez Navas, L. Urda Gómez & C. Willmott
Universidad Autónoma de Madrid, Madrid, Spain
J. F. de Trocóniz
Universidad de Oviedo, Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Oviedo, Spain
B. Alvarez Gonzalez, J. Cuevas, C. Erice, J. Fernandez Menendez, S. Folgueras, I. Gonzalez Caballero, J. R. González Fernández, E. Palencia Cortezon, C. Ramón Álvarez, V. Rodríguez Bouza, A. Soto Rodríguez, A. Trapote, N. Trevisani & C. Vico Villalba
Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
J. A. Brochero Cifuentes, I. J. Cabrillo, A. Calderon, J. Duarte Campderros, M. Fernandez, C. Fernandez Madrazo, P. J. Fernández Manteca, A. García Alonso, G. Gomez, C. Martinez Rivero, P. Martinez Ruiz del Arbol, F. Matorras, P. Matorras Cuevas, J. Piedra Gomez, C. Prieels, A. Ruiz-Jimeno, L. Scodellaro, I. Vila & J. M. Vizan Garcia
University of Colombo, Colombo, Sri Lanka
M. K. Jayananda, B. Kailasapathy, D. U. J. Sonnadara & D. D. C. Wickramarathna
Department of Physics, University of Ruhuna, Matara, Sri Lanka
W. G. D. Dharmaratna, K. Liyanage, N. Perera & N. Wickramage
CERN, European Organization for Nuclear Research, Geneva, Switzerland
T. K. Aarrestad, D. Abbaneo, J. Alimena, E. Auffray, G. Auzinger, J. Baechler, P. Baillon, D. Barney, J. Bendavid, M. Bianco, A. Bocci, C. Caillol, T. Camporesi, M. Capeans Garrido, G. Cerminara, N. Chernyavskaya, S. S. Chhibra, S. Choudhury, M. Cipriani, L. Cristella, D. d’Enterria, A. Dabrowski, A. David, A. De Roeck, M. M. Defranchis, M. Deile, M. Dobson, M. Dünser, N. Dupont, A. Elliott-Peisert, F. Fallavollita, A. Florent, L. Forthomme, G. Franzoni, W. Funk, S. Ghosh, S. Giani, D. Gigi, K. Gill, F. Glege, L. Gouskos, E. Govorkova, M. Haranko, J. Hegeman, V. Innocente, T. James, P. Janot, J. Kaspar, J. Kieseler, M. Komm, N. Kratochwil, C. Lange, S. Laurila, P. Lecoq, A. Lintuluoto, K. Long, C. Lourenço, B. Maier, L. Malgeri, S. Mallios, M. Mannelli, A. C. Marini, F. Meijers, S. Mersi, E. Meschi, F. Moortgat, M. Mulders, S. Orfanelli, L. Orsini, F. Pantaleo, E. Perez, M. Peruzzi, A. Petrilli, G. Petrucciani, A. Pfeiffer, M. Pierini, D. Piparo, M. Pitt, H. Qu, T. Quast, D. Rabady, A. Racz, G. Reales Gutiérrez, M. Rovere, H. Sakulin, J. Salfeld-Nebgen, S. Scarfi, C. Schwick, M. Selvaggi, A. Sharma, P. Silva, W. Snoeys, P. Sphicas, S. Summers, K. Tatar, V. R. Tavolaro, D. Treille, P. Tropea, A. Tsirou, J. Wanczyk, K. A. Wozniak & W. D. Zeuner
Paul Scherrer Institut, Villigen, Switzerland
L. Caminada, A. Ebrahimi, W. Erdmann, R. Horisberger, Q. Ingram, H. C. Kaestli, D. Kotlinski, U. Langenegger, M. Missiroli, L. Noehte & T. Rohe
ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
K. Androsov, M. Backhaus, P. Berger, A. Calandri, A. De Cosa, G. Dissertori, M. Dittmar, M. Donegà, C. Dorfer, F. Eble, K. Gedia, F. Glessgen, T. A. Gómez Espinosa, C. Grab, D. Hits, W. Lustermann, A. -M. Lyon, R. A. Manzoni, L. Marchese, C. Martin Perez, M. T. Meinhard, F. Nessi-Tedaldi, J. Niedziela, F. Pauss, V. Perovic, S. Pigazzini, M. G. Ratti, M. Reichmann, C. Reissel, T. Reitenspiess, B. Ristic, D. Ruini, D. A. Sanz Becerra, V. Stampf, J. Steggemann & R. Wallny
Universität Zürich, Zurich, Switzerland
C. Amsler, P. Bärtschi, C. Botta, D. Brzhechko, M. F. Canelli, K. Cormier, A. De Wit, R. Del Burgo, J. K. Heikkilä, M. Huwiler, W. Jin, A. Jofrehei, B. Kilminster, S. Leontsinis, S. P. Liechti, A. Macchiolo, P. Meiring, V. M. Mikuni, U. Molinatti, I. Neutelings, A. Reimers, P. Robmann, S. Sanchez Cruz, K. Schweiger, M. Senger & Y. Takahashi
National Central University, Chung-Li, Taiwan
C. Adloff, C. M. Kuo, W. Lin, A. Roy, T. Sarkar & S. S. Yu
National Taiwan University (NTU), Taipei, Taiwan
L. Ceard, Y. Chao, K. F. Chen, P. H. Chen, P. s. Chen, H. Cheng, W. -S. Hou, Y. y. Li, R. -S. Lu, E. Paganis, A. Psallidas, A. Steen, H. y. Wu, E. Yazgan & P. r. Yu
Department of Physics, Faculty of Science, Chulalongkorn University, Bangkok, Thailand
B. Asavapibhop, C. Asawatangtrakuldee & N. Srimanobhas
Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
F. Boran, S. Damarseckin, Z. S. Demiroglu, F. Dolek, I. Dumanoglu, E. Eskut, Y. Guler, E. Gurpinar Guler, C. Isik, O. Kara, A. Kayis Topaksu, U. Kiminsu, G. Onengut, K. Ozdemir, A. Polatoz, A. E. Simsek, B. Tali, U. G. Tok, S. Turkcapar & I. S. Zorbakir
Physics Department, Middle East Technical University, Ankara, Turkey
G. Karapinar, K. Ocalan & M. Yalvac
Bogazici University, Istanbul, Turkey
B. Akgun, I. O. Atakisi, E. Gulmez, M. Kaya, O. Kaya, Ö. Özçelik, S. Tekten & E. A. Yetkin
Istanbul Technical University, Istanbul, Turkey
A. Cakir, K. Cankocak, Y. Komurcu & S. Sen
Istanbul University, Istanbul, Turkey
S. Cerci, I. Hos, B. Isildak, B. Kaynak, S. Ozkorucuklu, H. Sert, C. Simsek, D. Sunar Cerci & C. Zorbilmez
Institute for Scintillation Materials of National Academy of Science of Ukraine, Kharkov, Ukraine
B. Grynyov
National Scientific Center, Kharkov Institute of Physics and Technology, Kharkov, Ukraine
L. Levchuk
University of Bristol, Bristol, UK
D. Anthony, E. Bhal, S. Bologna, J. J. Brooke, A. Bundock, E. Clement, D. Cussans, H. Flacher, M. Glowacki, J. Goldstein, G. P. Heath, H. F. Heath, L. Kreczko, B. Krikler, S. Paramesvaran, S. Seif El Nasr-Storey, V. J. Smith, N. Stylianou, K. Walkingshaw Pass & R. White
Rutherford Appleton Laboratory, Didcot, UK
K. W. Bell, A. Belyaev, C. Brew, R. M. Brown, D. J. A. Cockerill, C. Cooke, K. V. Ellis, K. Harder, S. Harper, M. -L. Holmberg, J. Linacre, K. Manolopoulos, D. M. Newbold, E. Olaiya, D. Petyt, T. Reis, T. Schuh, C. H. Shepherd-Themistocleous, I. R. Tomalin & T. Williams
Imperial College, London, UK
R. Bainbridge, P. Bloch, S. Bonomally, J. Borg, S. Breeze, O. Buchmuller, V. Cepaitis, G. S. Chahal, D. Colling, P. Dauncey, G. Davies, M. Della Negra, S. Fayer, G. Fedi, G. Hall, M. H. Hassanshahi, G. Iles, J. Langford, L. Lyons, A. -M. Magnan, S. Malik, A. Martelli, D. G. Monk, J. Nash, M. Pesaresi, B. C. Radburn-Smith, D. M. Raymond, A. Richards, A. Rose, E. Scott, C. Seez, A. Shtipliyski, A. Tapper, K. Uchida, T. Virdee, M. Vojinovic, N. Wardle, S. N. Webb & D. Winterbottom
Brunel University, Uxbridge, UK
K. Coldham, J. E. Cole, A. Khan, P. Kyberd, I. D. Reid, L. Teodorescu & S. Zahid
Baylor University, Waco, TX, USA
S. Abdullin, A. Brinkerhoff, B. Caraway, J. Dittmann, K. Hatakeyama, A. R. Kanuganti, B. McMaster, M. Saunders, S. Sawant, C. Sutantawibul & J. Wilson
Catholic University of America, Washington, DC, USA
R. Bartek, A. Dominguez, R. Uniyal & A. M. Vargas Hernandez
The University of Alabama, Tuscaloosa, AL, USA
A. Buccilli, S. I. Cooper, D. Di Croce, S. V. Gleyzer, C. Henderson, C. U. Perez, P. Rumerio & C. West
Boston University, Boston, MA, USA
A. Akpinar, A. Albert, D. Arcaro, C. Cosby, Z. Demiragli, E. Fontanesi, D. Gastler, S. May, J. Rohlf, K. Salyer, D. Sperka, D. Spitzbart, I. Suarez, A. Tsatsos, S. Yuan & D. Zou
Brown University, Providence, RI, USA
G. Benelli, B. Burkle, X. Coubez, D. Cutts, M. Hadley, U. Heintz, J. M. Hogan, T. Kwon, G. Landsberg, K. T. Lau, D. Li, M. Lukasik, J. Luo, M. Narain, N. Pervan, S. Sagir, F. Simpson, E. Usai, W. Y. Wong, X. Yan, D. Yu & W. Zhang
University of California, Davis, Davis, CA, USA
J. Bonilla, C. Brainerd, R. Breedon, M. Calderon De La Barca Sanchez, M. Chertok, J. Conway, P. T. Cox, R. Erbacher, G. Haza, F. Jensen, O. Kukral, R. Lander, M. Mulhearn, D. Pellett, B. Regnery, D. Taylor, Y. Yao & F. Zhang
University of California, Los Angeles, CA, USA
M. Bachtis, R. Cousins, A. Datta, D. Hamilton, J. Hauser, M. Ignatenko, M. A. Iqbal, T. Lam, W. A. Nash, S. Regnard, D. Saltzberg, B. Stone & V. Valuev
University of California, Riverside, Riverside, CA, USA
Y. Chen, R. Clare, J. W. Gary, M. Gordon, G. Hanson, G. Karapostoli, O. R. Long, N. Manganelli, W. Si, S. Wimpenny & Y. Zhang
University of California, San Diego, La Jolla, CA, USA
J. G. Branson, P. Chang, S. Cittolin, S. Cooperstein, D. Diaz, J. Duarte, R. Gerosa, L. Giannini, J. Guiang, R. Kansal, V. Krutelyov, R. Lee, J. Letts, M. Masciovecchio, F. Mokhtar, M. Pieri, B. V. Sathia Narayanan, V. Sharma, M. Tadel, F. Würthwein, Y. Xiang & A. Yagil
Department of Physics, University of California, Santa Barbara, Santa Barbara, CA, USA
N. Amin, C. Campagnari, M. Citron, G. Collura, A. Dorsett, V. Dutta, J. Incandela, M. Kilpatrick, J. Kim, B. Marsh, H. Mei, M. Oshiro, M. Quinnan, J. Richman, U. Sarica, F. Setti, J. Sheplock, P. Siddireddy, D. Stuart & S. Wang
California Institute of Technology, Pasadena, CA, USA
A. Bornheim, O. Cerri, I. Dutta, J. M. Lawhorn, N. Lu, J. Mao, H. B. Newman, T. Q. Nguyen, M. Spiropulu, J. R. Vlimant, C. Wang, S. Xie, Z. Zhang & R. Y. Zhu
Carnegie Mellon University, Pittsburgh, PA, USA
J. Alison, S. An, M. B. Andrews, P. Bryant, T. Ferguson, A. Harilal, C. Liu, T. Mudholkar, M. Paulini, A. Sanchez & W. Terrill
University of Colorado Boulder, Boulder, CO, USA
J. P. Cumalat, W. T. Ford, A. Hassani, G. Karathanasis, E. MacDonald, R. Patel, A. Perloff, C. Savard, N. Schonbeck, K. Stenson, K. A. Ulmer, S. R. Wagner & N. Zipper
Cornell University, Ithaca, NY, USA
J. Alexander, S. Bright-Thonney, X. Chen, Y. Cheng, D. J. Cranshaw, S. Hogan, J. Monroy, J. R. Patterson, D. Quach, J. Reichert, M. Reid, A. Ryd, W. Sun, J. Thom, P. Wittich & R. Zou
Fermi National Accelerator Laboratory, Batavia, IL, USA
M. Albrow, M. Alyari, G. Apollinari, A. Apresyan, A. Apyan, L. A. T. Bauerdick, D. Berry, J. Berryhill, P. C. Bhat, K. Burkett, J. N. Butler, A. Canepa, G. B. Cerati, H. W. K. Cheung, F. Chlebana, K. F. Di Petrillo, J. Dickinson, V. D. Elvira, Y. Feng, J. Freeman, Z. Gecse, L. Gray, D. Green, S. Grünendahl, O. Gutsche, R. M. Harris, R. Heller, T. C. Herwig, J. Hirschauer, B. Jayatilaka, S. Jindariani, M. Johnson, U. Joshi, T. Klijnsma, B. Klima, K. H. M. Kwok, S. Lammel, D. Lincoln, R. Lipton, T. Liu, C. Madrid, K. Maeshima, C. Mantilla, D. Mason, P. McBride, P. Merkel, S. Mrenna, S. Nahn, J. Ngadiuba, V. Papadimitriou, N. Pastika, K. Pedro, C. Pena, F. Ravera, A. Reinsvold Hall, L. Ristori, E. Sexton-Kennedy, N. Smith, A. Soha, L. Spiegel, S. Stoynev, J. Strait, L. Taylor, S. Tkaczyk, N. V. Tran, L. Uplegger, E. W. Vaandering & H. A. Weber
University of Florida, Gainesville, FL, USA
P. Avery, D. Bourilkov, L. Cadamuro, V. Cherepanov, R. D. Field, D. Guerrero, M. Kim, E. Koenig, J. Konigsberg, A. Korytov, K. H. Lo, K. Matchev, N. Menendez, G. Mitselmakher, A. Muthirakalayil Madhu, N. Rawal, D. Rosenzweig, S. Rosenzweig, K. Shi, J. Wang, Z. Wu, E. Yigitbasi & X. Zuo
Florida State University, Tallahassee, FL, USA
T. Adams, A. Askew, R. Habibullah, V. Hagopian, K. F. Johnson, R. Khurana, T. Kolberg, G. Martinez, H. Prosper, C. Schiber, O. Viazlo, R. Yohay & J. Zhang
Florida Institute of Technology, Melbourne, FL, USA
M. M. Baarmand, S. Butalla, T. Elkafrawy, M. Hohlmann, R. Kumar Verma, D. Noonan, M. Rahmani & F. Yumiceva
University of Illinois at Chicago (UIC), Chicago, IL, USA
M. R. Adams, H. Becerril Gonzalez, R. Cavanaugh, S. Dittmer, O. Evdokimov, C. E. Gerber, D. J. Hofman, A. H. Merrit, C. Mills, G. Oh, T. Roy, S. Rudrabhatla, M. B. Tonjes, N. Varelas, J. Viinikainen, X. Wang & Z. Ye
The University of Iowa, Iowa City, IA, USA
M. Alhusseini, K. Dilsiz, L. Emediato, R. P. Gandrajula, O. K. Köseyan, J. -P. Merlo, A. Mestvirishvili, J. Nachtman, H. Ogul, Y. Onel, A. Penzo, C. Snyder & E. Tiras
Johns Hopkins University, Baltimore, MD, USA
O. Amram, B. Blumenfeld, L. Corcodilos, J. Davis, A. V. Gritsan, S. Kyriacou, P. Maksimovic, J. Roskes, M. Swartz & T.Á. Vámi
The University of Kansas, Lawrence, KS, USA
A. Abreu, J. Anguiano, C. Baldenegro Barrera, P. Baringer, A. Bean, Z. Flowers, T. Isidori, S. Khalil, J. King, G. Krintiras, A. Kropivnitskaya, M. Lazarovits, C. Le Mahieu, C. Lindsey, J. Marquez, N. Minafra, M. Murray, M. Nickel, C. Rogan, C. Royon, R. Salvatico, S. Sanders, E. Schmitz, C. Smith, Q. Wang, Z. Warner, J. Williams & G. Wilson
Kansas State University, Manhattan, KS, USA
S. Duric, A. Ivanov, K. Kaadze, D. Kim, Y. Maravin, T. Mitchell, A. Modak & K. Nam
Lawrence Livermore National Laboratory, Livermore, CA, USA
F. Rebassoo & D. Wright
University of Maryland, College Park, MD, USA
E. Adams, A. Baden, O. Baron, A. Belloni, S. C. Eno, N. J. Hadley, S. Jabeen, R. G. Kellogg, T. Koeth, Y. Lai, S. Lascio, A. C. Mignerey, S. Nabili, C. Palmer, M. Seidel, A. Skuja, L. Wang & K. Wong
Massachusetts Institute of Technology, Cambridge, MA, USA
D. Abercrombie, G. Andreassi, R. Bi, W. Busza, I. A. Cali, Y. Chen, M. D’Alfonso, J. Eysermans, C. Freer, G. Gomez Ceballos, M. Goncharov, P. Harris, M. Hu, M. Klute, D. Kovalskyi, J. Krupa, Y. -J. Lee, C. Mironov, C. Paus, D. Rankin, C. Roland, G. Roland, Z. Shi, G. S. F. Stephans, J. Wang, Z. Wang & B. Wyslouch
University of Minnesota, Minneapolis, MN, USA
R. M. Chatterjee, A. Evans, J. Hiltbrand, Sh. Jain, B. M. Joshi, M. Krohn, Y. Kubota, J. Mans, M. Revering, R. Rusack, R. Saradhy, N. Schroeder, N. Strobbe & M. A. Wadud
University of Nebraska-Lincoln, Lincoln, NE, USA
K. Bloom, M. Bryson, S. Chauhan, D. R. Claes, C. Fangmeier, L. Finco, F. Golf, C. Joo, I. Kravchenko, I. Reed, J. E. Siado, G. R. Snow, W. Tabb, A. Wightman, F. Yan & A. G. Zecchinelli
State University of New York at Buffalo, Buffalo, NY, USA
G. Agarwal, H. Bandyopadhyay, L. Hay, I. Iashvili, A. Kharchilava, C. McLean, D. Nguyen, J. Pekkanen, S. Rappoccio & A. Williams
Northeastern University, Boston, MA, USA
G. Alverson, E. Barberis, Y. Haddad, Y. Han, A. Hortiangtham, A. Krishna, J. Li, J. Lidrych, G. Madigan, B. Marzocchi, D. M. Morse, V. Nguyen, T. Orimoto, A. Parker, L. Skinnari, A. Tishelman-Charny, T. Wamorkar, B. Wang, A. Wisecarver & D. Wood
Northwestern University, Evanston, IL, USA
S. Bhattacharya, J. Bueghly, Z. Chen, A. Gilbert, T. Gunter, K. A. Hahn, Y. Liu, N. Odell, M. H. Schmitt & M. Velasco
University of Notre Dame, Notre Dame, IN, USA
R. Band, R. Bucci, M. Cremonesi, A. Das, N. Dev, R. Goldouzian, M. Hildreth, K. Hurtado Anampa, C. Jessop, K. Lannon, J. Lawrence, N. Loukas, D. Lutton, J. Mariano, N. Marinelli, I. Mcalister, T. McCauley, C. Mcgrady, K. Mohrman, C. Moore, Y. Musienko, R. Ruchti, A. Townsend, M. Wayne, M. Zarucki & L. Zygala
The Ohio State University, Columbus, OH, USA
B. Bylsma, L. S. Durkin, B. Francis, C. Hill, M. Nunez Ornelas, K. Wei, B. L. Winer & B. R. Yates
Princeton University, Princeton, NJ, USA
F. M. Addesa, B. Bonham, P. Das, G. Dezoort, P. Elmer, A. Frankenthal, B. Greenberg, N. Haubrich, S. Higginbotham, A. Kalogeropoulos, G. Kopp, S. Kwan, D. Lange, D. Marlow, K. Mei, I. Ojalvo, J. Olsen, D. Stickland & C. Tully
University of Puerto Rico, Mayaguez, PR, USA
S. Malik & S. Norberg
Purdue University, West Lafayette, IN, USA
A. S. Bakshi, V. E. Barnes, R. Chawla, S. Das, L. Gutay, M. Jones, A. W. Jung, D. Kondratyev, A. M. Koshy, M. Liu, G. Negro, N. Neumeister, G. Paspalaki, S. Piperov, A. Purohit, J. F. Schulte, M. Stojanovic, J. Thieman, F. Wang, R. Xiao & W. Xie
Purdue University Northwest, Hammond, IN, USA
J. Dolen & N. Parashar
Rice University, Houston, TX, USA
D. Acosta, A. Baty, T. Carnahan, M. Decaro, S. Dildick, K. M. Ecklund, S. Freed, P. Gardner, F. J. M. Geurts, A. Kumar, W. Li, B. P. Padley, R. Redjimi, J. Rotter, W. Shi, A. G. Stahl Leiton, S. Yang, L. Zhang & Y. Zhang
University of Rochester, Rochester, NY, USA
A. Bodek, P. de Barbaro, R. Demina, J. L. Dulemba, C. Fallon, T. Ferbel, M. Galanti, A. Garcia-Bellido, O. Hindrichs, A. Khukhunaishvili, E. Ranken, R. Taus & G. P. Van Onsem
The Rockefeller University, New York, NY, USA
K. Goulianos
Rutgers, The State University of New Jersey, Piscataway, NJ, USA
B. Chiarito, J. P. Chou, A. Gandrakota, Y. Gershtein, E. Halkiadakis, A. Hart, M. Heindl, O. Karacheban, I. Laflotte, A. Lath, R. Montalvo, K. Nash, M. Osherson, S. Salur, S. Schnetzer, S. Somalwar, R. Stone, S. A. Thayil, S. Thomas & H. Wang
University of Tennessee, Knoxville, TN, USA
H. Acharya, A. G. Delannoy, S. Fiorendi & S. Spanier
Texas A &M University, College Station, TX, USA
O. Bouhali, M. Dalchenko, A. Delgado, R. Eusebi, J. Gilmore, T. Huang, T. Kamon, H. Kim, S. Luo, S. Malhotra, R. Mueller, D. Overton, D. Rathjens & A. Safonov
Texas Tech University, Lubbock, TX, USA
N. Akchurin, J. Damgov, V. Hegde, K. Lamichhane, S. W. Lee, T. Mengke, S. Muthumuni, T. Peltola, I. Volobouev, Z. Wang & A. Whitbeck
Vanderbilt University, Nashville, TN, USA
E. Appelt, S. Greene, A. Gurrola, W. Johns, A. Melo, K. Padeken, F. Romeo, P. Sheldon, S. Tuo & J. Velkovska
University of Virginia, Charlottesville, VA, USA
M. W. Arenton, B. Cardwell, B. Cox, G. Cummings, J. Hakala, R. Hirosky, M. Joyce, A. Ledovskoy, A. Li, C. Neu, C. E. Perez Lara, B. Tannenwald & S. White
Wayne State University, Detroit, MI, USA
N. Poudyal
University of Wisconsin-Madison, Madison, WI, USA
S. Banerjee, K. Black, T. Bose, S. Dasu, I. De Bruyn, P. Everaerts, C. Galloni, H. He, M. Herndon, A. Herve, U. Hussain, A. Lanaro, A. Loeliger, R. Loveless, J. Madhusudanan Sreekala, A. Mallampalli, A. Mohammadi, D. Pinna, A. Savin, V. Shang, V. Sharma, W. H. Smith, D. Teague, S. Trembath-Reichert & W. Vetens
TU Wien, Vienna, Austria
R. Frühwirth, M. Jeitler, J. Schieck & C. -E. Wulz
Institute of Basic and Applied Sciences, Faculty of Engineering, Arab Academy for Science, Technology and Maritime Transport, Alexandria, Egypt
M. R. Darwish
Université Libre de Bruxelles, Brussels, Belgium
T. Kello & X. Gao
Universidade Estadual de Campinas, Campinas, Brazil
J. Chinellato
Federal University of Rio Grande do Sul, Porto Alegre, Brazil
G. G. Da Silveira & C. A. Bernardes
The University of the State of Amazonas, Manaus, Brazil
F. Torres Da Silva De Araujo
University of Chinese Academy of Sciences, Beijing, China
T. Javaid, G. M. Chen, H. S. Chen & Z. -A. Liu
Department of Physics, Tsinghua University, Beijing, China
C. Dozen
UFMS, Nova Andradina, Brazil
J. Martins
Department of Physics, Nanjing Normal University, Nanjing, China
K. Yi
The University of Iowa, Iowa City, IA, USA
K. Yi
Institute for Theoretical and Experimental Physics named by A.I. Alikhanov of NRC ‘Kurchatov Institute’, Moscow, Russia
A. Starodumov
Joint Institute for Nuclear Research, Dubna, Russia
M. Finger, M. Finger Jr. & Z. Tsamalaidze
Helwan University, Cairo, Egypt
A. A. Abdelalim
Zewail City of Science and Technology, Zewail, Egypt
A. A. Abdelalim
British University in Egypt, Cairo, Egypt
E. Salama
Ain Shams University, Cairo, Egypt
E. Salama & T. Elkafrawy
Purdue University, West Lafayette, IN, USA
A. Savoy-Navarro & M. Stojanovic
Université de Haute Alsace, Mulhouse, France
J. -L. Agram & J. -C. Fontaine
Tbilisi State University, Tbilisi, Georgia
T. Toriashvili
Erzincan Binali Yildirim University, Erzincan, Turkey
W. Haj Ahmad
CERN, European Organization for Nuclear Research, Geneva, Switzerland
A. Stahl, F. Hartmann, D. Valsecchi, S. Meola, P. Paolucci & T. Virdee
RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
K. Borras, A. Kasem & X. Coubez
University of Hamburg, Hamburg, Germany
E. Gallo & C. Schwanenberger
Isfahan University of Technology, Isfahan, Iran
A. Jafari
Brandenburg University of Technology, Cottbus, Germany
W. Lohmann & O. Karacheban
Forschungszentrum Jülich, Juelich, Germany
M. Scham
Physics Department, Faculty of Science, Assiut University, Assiut, Egypt
M. M. A. Gadallah
Karoly Robert Campus, MATE Institute of Technology, Gyongyos, Hungary
S. Lökös
Institute of Physics, University of Debrecen, Debrecen, Hungary
M. Bartók & J. Karancsi
Institute of Nuclear Research ATOMKI, Debrecen, Hungary
D. Horvath
Universitatea Babes-Bolyai-Facultatea de Fizica, Cluj-Napoca, Romania
D. Horvath
MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
Z. L. Trocsanyi
Faculty of Informatics, University of Debrecen, Debrecen, Hungary
B. Ujvari
Wigner Research Centre for Physics, Budapest, Hungary
T. Csorgo & F. Nemes
IIT Bhubaneswar, Bhubaneswar, India
S. Bahinipati
Institute of Physics, Bhubaneswar, India
V. K. Muraleedharan Nair Bindhu, A. Nayak & D. Vats
Punjab Agricultural University, Ludhiana, India
N. Dhingra
UPES-University of Petroleum and Energy Studies, Dehradun, India
J. B. Singh
Shoolini University, Solan, India
M. Bharti
University of Hyderabad, Hyderabad, India
B. Gomber
University of Visva-Bharati, Santiniketan, India
M. Maity & T. Sarkar
Indian Institute of Science (IISc), Bangalore, India
J. R. Komaragiri, D. Kumar, L. Panwar & P. C. Tiwari
Indian Institute of Technology (IIT), Mumbai, India
K. Naskar
Deutsches Elektronen-Synchrotron, Hamburg, Germany
H. Bakhshiansohi
Department of Physics, Isfahan University of Technology, Isfahan, Iran
H. Bakhshiansohi & E. Khazaie
Sharif University of Technology, Tehran, Iran
M. Zeinali
Department of Physics, University of Science and Technology of Mazandaran, Behshahr, Iran
S. Chenarani
INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
R. Aly
Italian National Agency for New Technologies, Energy and Sustainable Economic Development, Bologna, Italy
S. Lo Meo
Centro Siciliano di Fisica Nucleare e di Struttura Della Materia, Catania, Italy
S. Albergo, S. Costa & A. Tricomi
Scuola Superiore Meridionale, Università di Napoli Federico II, Naples, Italy
L. Lista
Università di Napoli ‘Federico II’, Naples, Italy
L. Layer
Consiglio Nazionale delle Ricerche-Istituto Officina dei Materiali, Perugia, Italy
P. Asenov & F. Moscatelli
Riga Technical University, Riga, Latvia
V. Veckalns
Consejo Nacional de Ciencia y Tecnología, Mexico City, Mexico
I. Heredia-De La Cruz
IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
J. Mijuskovic
Institute for Nuclear Research, Moscow, Russia
V. Matveev & Y. Musienko
National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
V. Matveev
Institute of Nuclear Physics of the Uzbekistan Academy of Sciences, Tashkent, Uzbekistan
B. S. Yuldashev
St. Petersburg Polytechnic University, St. Petersburg, Russia
V. Kim
University of Florida, Gainesville, Florida, USA
E. Kuznetsova
Imperial College, London, UK
A. Nikitenko
P.N. Lebedev Physical Institute, Moscow, Russia
R. Chistov, M. Danilov & S. Polikarpov
California Institute of Technology, Pasadena, CA, USA
M. Dubinin & C. Pena
Budker Institute of Nuclear Physics, Novosibirsk, Russia
V. Blinov, T. Dimova, L. Kardapoltsev, A. Kozyrev, I. Ovtin, O. Radchenko & Y. Skovpen
Faculty of Physics, University of Belgrade, Belgrade, Serbia
P. Adzic
Trincomalee Campus, Eastern University, Nilaveli, Sri Lanka
B. Kailasapathy
INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
F. Fallavollita
National and Kapodistrian University of Athens, Athens, Greece
P. Sphicas
Ecole Polytechnique Fédérale Lausanne, Lausanne, Switzerland
J. Wanczyk, K. Androsov & J. Steggemann
Universität Zürich, Zurich, Switzerland
L. Caminada, M. Missiroli & L. Noehte
Stefan Meyer Institute for Subatomic Physics, Vienna, Austria
C. Amsler
Laboratoire d’Annecy-le-Vieux de Physique des Particules, IN2P3-CNRS, Annecy-le-Vieux, France
C. Adloff
Şırnak University, Sirnak, Turkey
S. Damarseckin
Near East University, Research Center of Experimental Health Science, Nicosia, Turkey
I. Dumanoglu & K. Cankocak
Konya Technical University, Konya, Turkey
Y. Guler & E. Gurpinar Guler
Piri Reis University, Istanbul, Turkey
K. Ozdemir
Adiyaman University, Adiyaman, Turkey
B. Tali, S. Cerci & D. Sunar Cerci
Necmettin Erbakan University, Konya, Turkey
K. Ocalan
Bozok Universitetesi Rektörlügü, Yozgat, Turkey
M. Yalvac
Marmara University, Istanbul, Turkey
M. Kaya
Milli Savunma University, Istanbul, Turkey
O. Kaya
Kafkas University, Kars, Turkey
S. Tekten
Istanbul Bilgi University, Istanbul, Turkey
E. A. Yetkin
Hacettepe University, Ankara, Turkey
S. Sen
Istanbul University-Cerrahpasa, Faculty of Engineering, Istanbul, Turkey
I. Hos
Ozyegin University, Istanbul, Turkey
B. Isildak
Vrije Universiteit Brussel, Brussels, Belgium
N. Stylianou
School of Physics and Astronomy, University of Southampton, Southampton, UK
A. Belyaev
Rutherford Appleton Laboratory, Didcot, UK
M. -L. Holmberg
IPPP Durham University, Durham, UK
G. S. Chahal
Monash University, Faculty of Science, Clayton, Australia
J. Nash
Università di Torino, Turin, Italy
P. Rumerio
Bethel University, St. Paul, MN, USA
J. M. Hogan
Karamanoğlu Mehmetbey University, Karaman, Turkey
S. Sagir
United States Naval Academy, Annapolis, MD, USA
A. Reinsvold Hall
Bingol University, Bingol, Turkey
K. Dilsiz
Georgian Technical University, Tbilisi, Georgia
A. Mestvirishvili
Sinop University, Sinop, Turkey
H. Ogul
Erciyes University, Kayseri, Turkey
E. Tiras
Institute of Modern Physics and Key Laboratory of Nuclear Physics and Ion-beam Application (MOE), Fudan University, Shanghai, China
L. Zhang
Texas A &M University at Qatar, Doha, Qatar
O. Bouhali
Kyungpook National University, Daegu, Korea
T. Kamon
- A. Tumasyan
You can also search for this author in PubMed Google Scholar
- W. Adam
You can also search for this author in PubMed Google Scholar
- J. W. Andrejkovic
You can also search for this author in PubMed Google Scholar
- T. Bergauer
You can also search for this author in PubMed Google Scholar
- S. Chatterjee
You can also search for this author in PubMed Google Scholar
- K. Damanakis
You can also search for this author in PubMed Google Scholar
- M. Dragicevic
You can also search for this author in PubMed Google Scholar
- A. Escalante Del Valle
You can also search for this author in PubMed Google Scholar
- R. Frühwirth
You can also search for this author in PubMed Google Scholar
- M. Jeitler
You can also search for this author in PubMed Google Scholar
- N. Krammer
You can also search for this author in PubMed Google Scholar
- L. Lechner
You can also search for this author in PubMed Google Scholar
- D. Liko
You can also search for this author in PubMed Google Scholar
- I. Mikulec
You can also search for this author in PubMed Google Scholar
- P. Paulitsch
You can also search for this author in PubMed Google Scholar
- F. M. Pitters
You can also search for this author in PubMed Google Scholar
- J. Schieck
You can also search for this author in PubMed Google Scholar
- R. Schöfbeck
You can also search for this author in PubMed Google Scholar
- D. Schwarz
You can also search for this author in PubMed Google Scholar
- S. Templ
You can also search for this author in PubMed Google Scholar
- W. Waltenberger
You can also search for this author in PubMed Google Scholar
- C. -E. Wulz
You can also search for this author in PubMed Google Scholar
- V. Chekhovsky
You can also search for this author in PubMed Google Scholar
- A. Litomin
You can also search for this author in PubMed Google Scholar
- V. Makarenko
You can also search for this author in PubMed Google Scholar
- M. R. Darwish
You can also search for this author in PubMed Google Scholar
- E. A. De Wolf
You can also search for this author in PubMed Google Scholar
- T. Janssen
You can also search for this author in PubMed Google Scholar
- T. Kello
You can also search for this author in PubMed Google Scholar
- A. Lelek
You can also search for this author in PubMed Google Scholar
- H. Rejeb Sfar
You can also search for this author in PubMed Google Scholar
- P. Van Mechelen
You can also search for this author in PubMed Google Scholar
- S. Van Putte
You can also search for this author in PubMed Google Scholar
- N. Van Remortel
You can also search for this author in PubMed Google Scholar
- E. S. Bols
You can also search for this author in PubMed Google Scholar
- J. D’Hondt
You can also search for this author in PubMed Google Scholar
- A. De Moor
You can also search for this author in PubMed Google Scholar
- M. Delcourt
You can also search for this author in PubMed Google Scholar
- H. El Faham
You can also search for this author in PubMed Google Scholar
- S. Lowette
You can also search for this author in PubMed Google Scholar
- S. Moortgat
You can also search for this author in PubMed Google Scholar
- A. Morton
You can also search for this author in PubMed Google Scholar
- D. Müller
You can also search for this author in PubMed Google Scholar
- A. R. Sahasransu
You can also search for this author in PubMed Google Scholar
- S. Tavernier
You can also search for this author in PubMed Google Scholar
- W. Van Doninck
You can also search for this author in PubMed Google Scholar
- D. Vannerom
You can also search for this author in PubMed Google Scholar
- D. Beghin
You can also search for this author in PubMed Google Scholar
- B. Bilin
You can also search for this author in PubMed Google Scholar
- B. Clerbaux
You can also search for this author in PubMed Google Scholar
- G. De Lentdecker
You can also search for this author in PubMed Google Scholar
- L. Favart
You can also search for this author in PubMed Google Scholar
- A. K. Kalsi
You can also search for this author in PubMed Google Scholar
- K. Lee
You can also search for this author in PubMed Google Scholar
- M. Mahdavikhorrami
You can also search for this author in PubMed Google Scholar
- I. Makarenko
You can also search for this author in PubMed Google Scholar
- L. Moureaux
You can also search for this author in PubMed Google Scholar
- S. Paredes
You can also search for this author in PubMed Google Scholar
- L. Pétré
You can also search for this author in PubMed Google Scholar
- A. Popov
You can also search for this author in PubMed Google Scholar
- N. Postiau
You can also search for this author in PubMed Google Scholar
- E. Starling
You can also search for this author in PubMed Google Scholar
- L. Thomas
You can also search for this author in PubMed Google Scholar
- M. Vanden Bemden
You can also search for this author in PubMed Google Scholar
- C. Vander Velde
You can also search for this author in PubMed Google Scholar
- P. Vanlaer
You can also search for this author in PubMed Google Scholar
- T. Cornelis
You can also search for this author in PubMed Google Scholar
- D. Dobur
You can also search for this author in PubMed Google Scholar
- J. Knolle
You can also search for this author in PubMed Google Scholar
- L. Lambrecht
You can also search for this author in PubMed Google Scholar
- G. Mestdach
You can also search for this author in PubMed Google Scholar
- M. Niedziela
You can also search for this author in PubMed Google Scholar
- C. Rendón
You can also search for this author in PubMed Google Scholar
- C. Roskas
You can also search for this author in PubMed Google Scholar
- A. Samalan
You can also search for this author in PubMed Google Scholar
- K. Skovpen
You can also search for this author in PubMed Google Scholar
- M. Tytgat
You can also search for this author in PubMed Google Scholar
- B. Vermassen
You can also search for this author in PubMed Google Scholar
- L. Wezenbeek
You can also search for this author in PubMed Google Scholar
- A. Benecke
You can also search for this author in PubMed Google Scholar
- A. Bethani
You can also search for this author in PubMed Google Scholar
- G. Bruno
You can also search for this author in PubMed Google Scholar
- F. Bury
You can also search for this author in PubMed Google Scholar
- C. Caputo
You can also search for this author in PubMed Google Scholar
- P. David
You can also search for this author in PubMed Google Scholar
- C. Delaere
You can also search for this author in PubMed Google Scholar
- I. S. Donertas
You can also search for this author in PubMed Google Scholar
- A. Giammanco
You can also search for this author in PubMed Google Scholar
- K. Jaffel
You can also search for this author in PubMed Google Scholar
- Sa. Jain
You can also search for this author in PubMed Google Scholar
- V. Lemaitre
You can also search for this author in PubMed Google Scholar
- K. Mondal
You can also search for this author in PubMed Google Scholar
- J. Prisciandaro
You can also search for this author in PubMed Google Scholar
- A. Taliercio
You can also search for this author in PubMed Google Scholar
- M. Teklishyn
You can also search for this author in PubMed Google Scholar
- T. T. Tran
You can also search for this author in PubMed Google Scholar
- P. Vischia
You can also search for this author in PubMed Google Scholar
- S. Wertz
You can also search for this author in PubMed Google Scholar
- G. A. Alves
You can also search for this author in PubMed Google Scholar
- C. Hensel
You can also search for this author in PubMed Google Scholar
- A. Moraes
You can also search for this author in PubMed Google Scholar
- P. Rebello Teles
You can also search for this author in PubMed Google Scholar
- W. L. Aldá Júnior
You can also search for this author in PubMed Google Scholar
- M. Alves Gallo Pereira
You can also search for this author in PubMed Google Scholar
- M. Barroso Ferreira Filho
You can also search for this author in PubMed Google Scholar
- H. Brandao Malbouisson
You can also search for this author in PubMed Google Scholar
- W. Carvalho
You can also search for this author in PubMed Google Scholar
- J. Chinellato
You can also search for this author in PubMed Google Scholar
- E. M. Da Costa
You can also search for this author in PubMed Google Scholar
- G. G. Da Silveira
You can also search for this author in PubMed Google Scholar
- D. De Jesus Damiao
You can also search for this author in PubMed Google Scholar
- V. Dos Santos Sousa
You can also search for this author in PubMed Google Scholar
- S. Fonseca De Souza
You can also search for this author in PubMed Google Scholar
- C. Mora Herrera
You can also search for this author in PubMed Google Scholar
- K. Mota Amarilo
You can also search for this author in PubMed Google Scholar
- L. Mundim
You can also search for this author in PubMed Google Scholar
- H. Nogima
You can also search for this author in PubMed Google Scholar
- A. Santoro
You can also search for this author in PubMed Google Scholar
- S. M. Silva Do Amaral
You can also search for this author in PubMed Google Scholar
- A. Sznajder
You can also search for this author in PubMed Google Scholar
- M. Thiel
You can also search for this author in PubMed Google Scholar
- F. Torres Da Silva De Araujo
You can also search for this author in PubMed Google Scholar
- A. Vilela Pereira
You can also search for this author in PubMed Google Scholar
- C. A. Bernardes
You can also search for this author in PubMed Google Scholar
- L. Calligaris
You can also search for this author in PubMed Google Scholar
- T. R. Fernandez Perez Tomei
You can also search for this author in PubMed Google Scholar
- E. M. Gregores
You can also search for this author in PubMed Google Scholar
- D. S. Lemos
You can also search for this author in PubMed Google Scholar
- P. G. Mercadante
You can also search for this author in PubMed Google Scholar
- S. F. Novaes
You can also search for this author in PubMed Google Scholar
- Sandra S. Padula
You can also search for this author in PubMed Google Scholar
- A. Aleksandrov
You can also search for this author in PubMed Google Scholar
- G. Antchev
You can also search for this author in PubMed Google Scholar
- R. Hadjiiska
You can also search for this author in PubMed Google Scholar
- P. Iaydjiev
You can also search for this author in PubMed Google Scholar
- M. Misheva
You can also search for this author in PubMed Google Scholar
- M. Rodozov
You can also search for this author in PubMed Google Scholar
- M. Shopova
You can also search for this author in PubMed Google Scholar
- G. Sultanov
You can also search for this author in PubMed Google Scholar
- A. Dimitrov
You can also search for this author in PubMed Google Scholar
- T. Ivanov
You can also search for this author in PubMed Google Scholar
- L. Litov
You can also search for this author in PubMed Google Scholar
- B. Pavlov
You can also search for this author in PubMed Google Scholar
- P. Petkov
You can also search for this author in PubMed Google Scholar
- A. Petrov
You can also search for this author in PubMed Google Scholar
- T. Cheng
You can also search for this author in PubMed Google Scholar
- T. Javaid
You can also search for this author in PubMed Google Scholar
- M. Mittal
You can also search for this author in PubMed Google Scholar
- L. Yuan
You can also search for this author in PubMed Google Scholar
- M. Ahmad
You can also search for this author in PubMed Google Scholar
- G. Bauer
You can also search for this author in PubMed Google Scholar
- C. Dozen
You can also search for this author in PubMed Google Scholar
- Z. Hu
You can also search for this author in PubMed Google Scholar
- J. Martins
You can also search for this author in PubMed Google Scholar
- Y. Wang
You can also search for this author in PubMed Google Scholar
- K. Yi
You can also search for this author in PubMed Google Scholar
- E. Chapon
You can also search for this author in PubMed Google Scholar
- G. M. Chen
You can also search for this author in PubMed Google Scholar
- H. S. Chen
You can also search for this author in PubMed Google Scholar
- M. Chen
You can also search for this author in PubMed Google Scholar
- F. Iemmi
You can also search for this author in PubMed Google Scholar
- A. Kapoor
You can also search for this author in PubMed Google Scholar
- D. Leggat
You can also search for this author in PubMed Google Scholar
- H. Liao
You can also search for this author in PubMed Google Scholar
- Z. -A. Liu
You can also search for this author in PubMed Google Scholar
- V. Milosevic
You can also search for this author in PubMed Google Scholar
- F. Monti
You can also search for this author in PubMed Google Scholar
- R. Sharma
You can also search for this author in PubMed Google Scholar
- J. Tao
You can also search for this author in PubMed Google Scholar
- J. Thomas-Wilsker
You can also search for this author in PubMed Google Scholar
- J. Wang
You can also search for this author in PubMed Google Scholar
- H. Zhang
You can also search for this author in PubMed Google Scholar
- J. Zhao
You can also search for this author in PubMed Google Scholar
- A. Agapitos
You can also search for this author in PubMed Google Scholar
- Y. An
You can also search for this author in PubMed Google Scholar
- Y. Ban
You can also search for this author in PubMed Google Scholar
- C. Chen
You can also search for this author in PubMed Google Scholar
- A. Levin
You can also search for this author in PubMed Google Scholar
- Q. Li
You can also search for this author in PubMed Google Scholar
- X. Lyu
You can also search for this author in PubMed Google Scholar
- Y. Mao
You can also search for this author in PubMed Google Scholar
- S. J. Qian
You can also search for this author in PubMed Google Scholar
- D. Wang
You can also search for this author in PubMed Google Scholar
- J. Xiao
You can also search for this author in PubMed Google Scholar
- H. Yang
You can also search for this author in PubMed Google Scholar
- M. Lu
You can also search for this author in PubMed Google Scholar
- Z. You
You can also search for this author in PubMed Google Scholar
- X. Gao
You can also search for this author in PubMed Google Scholar
- H. Okawa
You can also search for this author in PubMed Google Scholar
- Y. Zhang
You can also search for this author in PubMed Google Scholar
- Z. Lin
You can also search for this author in PubMed Google Scholar
- M. Xiao
You can also search for this author in PubMed Google Scholar
- C. Avila
You can also search for this author in PubMed Google Scholar
- A. Cabrera
You can also search for this author in PubMed Google Scholar
- C. Florez
You can also search for this author in PubMed Google Scholar
- J. Fraga
You can also search for this author in PubMed Google Scholar
- J. Mejia Guisao
You can also search for this author in PubMed Google Scholar
- F. Ramirez
You can also search for this author in PubMed Google Scholar
- J. D. Ruiz Alvarez
You can also search for this author in PubMed Google Scholar
- D. Giljanovic
You can also search for this author in PubMed Google Scholar
- N. Godinovic
You can also search for this author in PubMed Google Scholar
- D. Lelas
You can also search for this author in PubMed Google Scholar
- I. Puljak
You can also search for this author in PubMed Google Scholar
- Z. Antunovic
You can also search for this author in PubMed Google Scholar
- M. Kovac
You can also search for this author in PubMed Google Scholar
- T. Sculac
You can also search for this author in PubMed Google Scholar
- V. Brigljevic
You can also search for this author in PubMed Google Scholar
- D. Ferencek
You can also search for this author in PubMed Google Scholar
- D. Majumder
You can also search for this author in PubMed Google Scholar
- M. Roguljic
You can also search for this author in PubMed Google Scholar
- A. Starodumov
You can also search for this author in PubMed Google Scholar
- T. Susa
You can also search for this author in PubMed Google Scholar
- A. Attikis
You can also search for this author in PubMed Google Scholar
- K. Christoforou
You can also search for this author in PubMed Google Scholar
- G. Kole
You can also search for this author in PubMed Google Scholar
- M. Kolosova
You can also search for this author in PubMed Google Scholar
- S. Konstantinou
You can also search for this author in PubMed Google Scholar
- J. Mousa
You can also search for this author in PubMed Google Scholar
- C. Nicolaou
You can also search for this author in PubMed Google Scholar
- F. Ptochos
You can also search for this author in PubMed Google Scholar
- P. A. Razis
You can also search for this author in PubMed Google Scholar
- H. Rykaczewski
You can also search for this author in PubMed Google Scholar
- H. Saka
You can also search for this author in PubMed Google Scholar
- M. Finger
You can also search for this author in PubMed Google Scholar
- M. Finger Jr.
You can also search for this author in PubMed Google Scholar
- A. Kveton
You can also search for this author in PubMed Google Scholar
- E. Ayala
You can also search for this author in PubMed Google Scholar
- E. Carrera Jarrin
You can also search for this author in PubMed Google Scholar
- A. A. Abdelalim
You can also search for this author in PubMed Google Scholar
- E. Salama
You can also search for this author in PubMed Google Scholar
- M. A. Mahmoud
You can also search for this author in PubMed Google Scholar
- Y. Mohammed
You can also search for this author in PubMed Google Scholar
- S. Bhowmik
You can also search for this author in PubMed Google Scholar
- R. K. Dewanjee
You can also search for this author in PubMed Google Scholar
- K. Ehataht
You can also search for this author in PubMed Google Scholar
- M. Kadastik
You can also search for this author in PubMed Google Scholar
- S. Nandan
You can also search for this author in PubMed Google Scholar
- C. Nielsen
You can also search for this author in PubMed Google Scholar
- J. Pata
You can also search for this author in PubMed Google Scholar
- M. Raidal
You can also search for this author in PubMed Google Scholar
- L. Tani
You can also search for this author in PubMed Google Scholar
- C. Veelken
You can also search for this author in PubMed Google Scholar
- P. Eerola
You can also search for this author in PubMed Google Scholar
- H. Kirschenmann
You can also search for this author in PubMed Google Scholar
- K. Osterberg
You can also search for this author in PubMed Google Scholar
- M. Voutilainen
You can also search for this author in PubMed Google Scholar
- S. Bharthuar
You can also search for this author in PubMed Google Scholar
- E. Brücken
You can also search for this author in PubMed Google Scholar
- F. Garcia
You can also search for this author in PubMed Google Scholar
- J. Havukainen
You can also search for this author in PubMed Google Scholar
- M. S. Kim
You can also search for this author in PubMed Google Scholar
- R. Kinnunen
You can also search for this author in PubMed Google Scholar
- T. Lampén
You can also search for this author in PubMed Google Scholar
- K. Lassila-Perini
You can also search for this author in PubMed Google Scholar
- S. Lehti
You can also search for this author in PubMed Google Scholar
- T. Lindén
You can also search for this author in PubMed Google Scholar
- M. Lotti
You can also search for this author in PubMed Google Scholar
- L. Martikainen
You can also search for this author in PubMed Google Scholar
- M. Myllymäki
You can also search for this author in PubMed Google Scholar
- J. Ott
You can also search for this author in PubMed Google Scholar
- M. m. Rantanen
You can also search for this author in PubMed Google Scholar
- H. Siikonen
You can also search for this author in PubMed Google Scholar
- E. Tuominen
You can also search for this author in PubMed Google Scholar
- J. Tuominiemi
You can also search for this author in PubMed Google Scholar
- P. Luukka
You can also search for this author in PubMed Google Scholar
- H. Petrow
You can also search for this author in PubMed Google Scholar
- T. Tuuva
You can also search for this author in PubMed Google Scholar
- C. Amendola
You can also search for this author in PubMed Google Scholar
- M. Besancon
You can also search for this author in PubMed Google Scholar
- F. Couderc
You can also search for this author in PubMed Google Scholar
- M. Dejardin
You can also search for this author in PubMed Google Scholar
- D. Denegri
You can also search for this author in PubMed Google Scholar
- J. L. Faure
You can also search for this author in PubMed Google Scholar
- F. Ferri
You can also search for this author in PubMed Google Scholar
- S. Ganjour
You can also search for this author in PubMed Google Scholar
- P. Gras
You can also search for this author in PubMed Google Scholar
- G. Hamel de Monchenault
You can also search for this author in PubMed Google Scholar
- P. Jarry
You can also search for this author in PubMed Google Scholar
- B. Lenzi
You can also search for this author in PubMed Google Scholar
- J. Malcles
You can also search for this author in PubMed Google Scholar
- J. Rander
You can also search for this author in PubMed Google Scholar
- A. Rosowsky
You can also search for this author in PubMed Google Scholar
- M. Ö. Sahin
You can also search for this author in PubMed Google Scholar
- A. Savoy-Navarro
You can also search for this author in PubMed Google Scholar
- M. Titov
You can also search for this author in PubMed Google Scholar
- G. B. Yu
You can also search for this author in PubMed Google Scholar
- S. Ahuja
You can also search for this author in PubMed Google Scholar
- F. Beaudette
You can also search for this author in PubMed Google Scholar
- M. Bonanomi
You can also search for this author in PubMed Google Scholar
- A. Buchot Perraguin
You can also search for this author in PubMed Google Scholar
- P. Busson
You can also search for this author in PubMed Google Scholar
- A. Cappati
You can also search for this author in PubMed Google Scholar
- C. Charlot
You can also search for this author in PubMed Google Scholar
- O. Davignon
You can also search for this author in PubMed Google Scholar
- B. Diab
You can also search for this author in PubMed Google Scholar
- G. Falmagne
You can also search for this author in PubMed Google Scholar
- S. Ghosh
You can also search for this author in PubMed Google Scholar
- R. Granier de Cassagnac
You can also search for this author in PubMed Google Scholar
- A. Hakimi
You can also search for this author in PubMed Google Scholar
- I. Kucher
You can also search for this author in PubMed Google Scholar
- J. Motta
You can also search for this author in PubMed Google Scholar
- M. Nguyen
You can also search for this author in PubMed Google Scholar
- C. Ochando
You can also search for this author in PubMed Google Scholar
- P. Paganini
You can also search for this author in PubMed Google Scholar
- J. Rembser
You can also search for this author in PubMed Google Scholar
- R. Salerno
You can also search for this author in PubMed Google Scholar
- U. Sarkar
You can also search for this author in PubMed Google Scholar
- J. B. Sauvan
You can also search for this author in PubMed Google Scholar
- Y. Sirois
You can also search for this author in PubMed Google Scholar
- A. Tarabini
You can also search for this author in PubMed Google Scholar
- A. Zabi
You can also search for this author in PubMed Google Scholar
- A. Zghiche
You can also search for this author in PubMed Google Scholar
- J. -L. Agram
You can also search for this author in PubMed Google Scholar
- J. Andrea
You can also search for this author in PubMed Google Scholar
- D. Apparu
You can also search for this author in PubMed Google Scholar
- D. Bloch
You can also search for this author in PubMed Google Scholar
- G. Bourgatte
You can also search for this author in PubMed Google Scholar
- J -M. Brom
You can also search for this author in PubMed Google Scholar
- E. C. Chabert
You can also search for this author in PubMed Google Scholar
- C. Collard
You can also search for this author in PubMed Google Scholar
- D. Darej
You can also search for this author in PubMed Google Scholar
- J. -C. Fontaine
You can also search for this author in PubMed Google Scholar
- U. Goerlach
You can also search for this author in PubMed Google Scholar
- C. Grimault
You can also search for this author in PubMed Google Scholar
- A. -C. Le Bihan
You can also search for this author in PubMed Google Scholar
- E. Nibigira
You can also search for this author in PubMed Google Scholar
- P. Van Hove
You can also search for this author in PubMed Google Scholar
- E. Asilar
You can also search for this author in PubMed Google Scholar
- S. Beauceron
You can also search for this author in PubMed Google Scholar
- C. Bernet
You can also search for this author in PubMed Google Scholar
- G. Boudoul
You can also search for this author in PubMed Google Scholar
- C. Camen
You can also search for this author in PubMed Google Scholar
- A. Carle
You can also search for this author in PubMed Google Scholar
- N. Chanon
You can also search for this author in PubMed Google Scholar
- D. Contardo
You can also search for this author in PubMed Google Scholar
- P. Depasse
You can also search for this author in PubMed Google Scholar
- H. El Mamouni
You can also search for this author in PubMed Google Scholar
- J. Fay
You can also search for this author in PubMed Google Scholar
- S. Gascon
You can also search for this author in PubMed Google Scholar
- M. Gouzevitch
You can also search for this author in PubMed Google Scholar
- B. Ille
You can also search for this author in PubMed Google Scholar
- I. B. Laktineh
You can also search for this author in PubMed Google Scholar
- H. Lattaud
You can also search for this author in PubMed Google Scholar
- A. Lesauvage
You can also search for this author in PubMed Google Scholar
- M. Lethuillier
You can also search for this author in PubMed Google Scholar
- L. Mirabito
You can also search for this author in PubMed Google Scholar
- S. Perries
You can also search for this author in PubMed Google Scholar
- K. Shchablo
You can also search for this author in PubMed Google Scholar
- V. Sordini
You can also search for this author in PubMed Google Scholar
- L. Torterotot
You can also search for this author in PubMed Google Scholar
- G. Touquet
You can also search for this author in PubMed Google Scholar
- M. Vander Donckt
You can also search for this author in PubMed Google Scholar
- S. Viret
You can also search for this author in PubMed Google Scholar
- I. Lomidze
You can also search for this author in PubMed Google Scholar
- T. Toriashvili
You can also search for this author in PubMed Google Scholar
- Z. Tsamalaidze
You can also search for this author in PubMed Google Scholar
- V. Botta
You can also search for this author in PubMed Google Scholar
- L. Feld
You can also search for this author in PubMed Google Scholar
- K. Klein
You can also search for this author in PubMed Google Scholar
- M. Lipinski
You can also search for this author in PubMed Google Scholar
- D. Meuser
You can also search for this author in PubMed Google Scholar
- A. Pauls
You can also search for this author in PubMed Google Scholar
- N. Röwert
You can also search for this author in PubMed Google Scholar
- J. Schulz
You can also search for this author in PubMed Google Scholar
- M. Teroerde
You can also search for this author in PubMed Google Scholar
- A. Dodonova
You can also search for this author in PubMed Google Scholar
- D. Eliseev
You can also search for this author in PubMed Google Scholar
- M. Erdmann
You can also search for this author in PubMed Google Scholar
- P. Fackeldey
You can also search for this author in PubMed Google Scholar
- B. Fischer
You can also search for this author in PubMed Google Scholar
- T. Hebbeker
You can also search for this author in PubMed Google Scholar
- K. Hoepfner
You can also search for this author in PubMed Google Scholar
- F. Ivone
You can also search for this author in PubMed Google Scholar
- L. Mastrolorenzo
You can also search for this author in PubMed Google Scholar
- M. Merschmeyer
You can also search for this author in PubMed Google Scholar
- A. Meyer
You can also search for this author in PubMed Google Scholar
- G. Mocellin
You can also search for this author in PubMed Google Scholar
- S. Mondal
You can also search for this author in PubMed Google Scholar
- S. Mukherjee
You can also search for this author in PubMed Google Scholar
- D. Noll
You can also search for this author in PubMed Google Scholar
- A. Novak
You can also search for this author in PubMed Google Scholar
- A. Pozdnyakov
You can also search for this author in PubMed Google Scholar
- Y. Rath
You can also search for this author in PubMed Google Scholar
- H. Reithler
You can also search for this author in PubMed Google Scholar
- A. Schmidt
You can also search for this author in PubMed Google Scholar
- S. C. Schuler
You can also search for this author in PubMed Google Scholar
- A. Sharma
You can also search for this author in PubMed Google Scholar
- L. Vigilante
You can also search for this author in PubMed Google Scholar
- S. Wiedenbeck
You can also search for this author in PubMed Google Scholar
- S. Zaleski
You can also search for this author in PubMed Google Scholar
- C. Dziwok
You can also search for this author in PubMed Google Scholar
- G. Flügge
You can also search for this author in PubMed Google Scholar
- W. Haj Ahmad
You can also search for this author in PubMed Google Scholar
- O. Hlushchenko
You can also search for this author in PubMed Google Scholar
- T. Kress
You can also search for this author in PubMed Google Scholar
- A. Nowack
You can also search for this author in PubMed Google Scholar
- O. Pooth
You can also search for this author in PubMed Google Scholar
- D. Roy
You can also search for this author in PubMed Google Scholar
- A. Stahl
You can also search for this author in PubMed Google Scholar
- T. Ziemons
You can also search for this author in PubMed Google Scholar
- A. Zotz
You can also search for this author in PubMed Google Scholar
- H. Aarup Petersen
You can also search for this author in PubMed Google Scholar
- M. Aldaya Martin
You can also search for this author in PubMed Google Scholar
- P. Asmuss
You can also search for this author in PubMed Google Scholar
- S. Baxter
You can also search for this author in PubMed Google Scholar
- M. Bayatmakou
You can also search for this author in PubMed Google Scholar
- O. Behnke
You can also search for this author in PubMed Google Scholar
- A. Bermúdez Martínez
You can also search for this author in PubMed Google Scholar
- S. Bhattacharya
You can also search for this author in PubMed Google Scholar
- A. A. Bin Anuar
You can also search for this author in PubMed Google Scholar
- F. Blekman
You can also search for this author in PubMed Google Scholar
- K. Borras
You can also search for this author in PubMed Google Scholar
- D. Brunner
You can also search for this author in PubMed Google Scholar
- A. Campbell
You can also search for this author in PubMed Google Scholar
- A. Cardini
You can also search for this author in PubMed Google Scholar
- C. Cheng
You can also search for this author in PubMed Google Scholar
- F. Colombina
You can also search for this author in PubMed Google Scholar
- S. Consuegra Rodríguez
You can also search for this author in PubMed Google Scholar
- G. Correia Silva
You can also search for this author in PubMed Google Scholar
- M. De Silva
You can also search for this author in PubMed Google Scholar
- L. Didukh
You can also search for this author in PubMed Google Scholar
- G. Eckerlin
You can also search for this author in PubMed Google Scholar
- D. Eckstein
You can also search for this author in PubMed Google Scholar
- L. I. Estevez Banos
You can also search for this author in PubMed Google Scholar
- O. Filatov
You can also search for this author in PubMed Google Scholar
- E. Gallo
You can also search for this author in PubMed Google Scholar
- A. Geiser
You can also search for this author in PubMed Google Scholar
- A. Giraldi
You can also search for this author in PubMed Google Scholar
- A. Grohsjean
You can also search for this author in PubMed Google Scholar
- M. Guthoff
You can also search for this author in PubMed Google Scholar
- A. Jafari
You can also search for this author in PubMed Google Scholar
- N. Z. Jomhari
You can also search for this author in PubMed Google Scholar
- H. Jung
You can also search for this author in PubMed Google Scholar
- A. Kasem
You can also search for this author in PubMed Google Scholar
- M. Kasemann
You can also search for this author in PubMed Google Scholar
- H. Kaveh
You can also search for this author in PubMed Google Scholar
- C. Kleinwort
You can also search for this author in PubMed Google Scholar
- R. Kogler
You can also search for this author in PubMed Google Scholar
- D. Krücker
You can also search for this author in PubMed Google Scholar
- W. Lange
You can also search for this author in PubMed Google Scholar
- K. Lipka
You can also search for this author in PubMed Google Scholar
- W. Lohmann
You can also search for this author in PubMed Google Scholar
- R. Mankel
You can also search for this author in PubMed Google Scholar
- I. -A. Melzer-Pellmann
You can also search for this author in PubMed Google Scholar
- M. Mendizabal Morentin
You can also search for this author in PubMed Google Scholar
- J. Metwally
You can also search for this author in PubMed Google Scholar
- A. B. Meyer
You can also search for this author in PubMed Google Scholar
- M. Meyer
You can also search for this author in PubMed Google Scholar
- J. Mnich
You can also search for this author in PubMed Google Scholar
- A. Mussgiller
You can also search for this author in PubMed Google Scholar
- A. Nürnberg
You can also search for this author in PubMed Google Scholar
- Y. Otarid
You can also search for this author in PubMed Google Scholar
- D. Pérez Adán
You can also search for this author in PubMed Google Scholar
- D. Pitzl
You can also search for this author in PubMed Google Scholar
- A. Raspereza
You can also search for this author in PubMed Google Scholar
- B. Ribeiro Lopes
You can also search for this author in PubMed Google Scholar
- J. Rübenach
You can also search for this author in PubMed Google Scholar
- A. Saggio
You can also search for this author in PubMed Google Scholar
- A. Saibel
You can also search for this author in PubMed Google Scholar
- M. Savitskyi
You can also search for this author in PubMed Google Scholar
- M. Scham
You can also search for this author in PubMed Google Scholar
- V. Scheurer
You can also search for this author in PubMed Google Scholar
- S. Schnake
You can also search for this author in PubMed Google Scholar
- P. Schütze
You can also search for this author in PubMed Google Scholar
- C. Schwanenberger
You can also search for this author in PubMed Google Scholar
- M. Shchedrolosiev
You can also search for this author in PubMed Google Scholar
- R. E. Sosa Ricardo
You can also search for this author in PubMed Google Scholar
- D. Stafford
You can also search for this author in PubMed Google Scholar
- N. Tonon
You can also search for this author in PubMed Google Scholar
- M. Van De Klundert
You can also search for this author in PubMed Google Scholar
- F. Vazzoler
You can also search for this author in PubMed Google Scholar
- R. Walsh
You can also search for this author in PubMed Google Scholar
- D. Walter
You can also search for this author in PubMed Google Scholar
- Q. Wang
You can also search for this author in PubMed Google Scholar
- Y. Wen
You can also search for this author in PubMed Google Scholar
- K. Wichmann
You can also search for this author in PubMed Google Scholar
- L. Wiens
You can also search for this author in PubMed Google Scholar
- C. Wissing
You can also search for this author in PubMed Google Scholar
- S. Wuchterl
You can also search for this author in PubMed Google Scholar
- R. Aggleton
You can also search for this author in PubMed Google Scholar
- S. Albrecht
You can also search for this author in PubMed Google Scholar
- S. Bein
You can also search for this author in PubMed Google Scholar
- L. Benato
You can also search for this author in PubMed Google Scholar
- P. Connor
You can also search for this author in PubMed Google Scholar
- K. De Leo
You can also search for this author in PubMed Google Scholar
- M. Eich
You can also search for this author in PubMed Google Scholar
- K. El Morabit
You can also search for this author in PubMed Google Scholar
- F. Feindt
You can also search for this author in PubMed Google Scholar
- A. Fröhlich
You can also search for this author in PubMed Google Scholar
- C. Garbers
You can also search for this author in PubMed Google Scholar
- E. Garutti
You can also search for this author in PubMed Google Scholar
- P. Gunnellini
You can also search for this author in PubMed Google Scholar
- M. Hajheidari
You can also search for this author in PubMed Google Scholar
- J. Haller
You can also search for this author in PubMed Google Scholar
- A. Hinzmann
You can also search for this author in PubMed Google Scholar
- G. Kasieczka
You can also search for this author in PubMed Google Scholar
- R. Klanner
You can also search for this author in PubMed Google Scholar
- T. Kramer
You can also search for this author in PubMed Google Scholar
- V. Kutzner
You can also search for this author in PubMed Google Scholar
- J. Lange
You can also search for this author in PubMed Google Scholar
- T. Lange
You can also search for this author in PubMed Google Scholar
- A. Lobanov
You can also search for this author in PubMed Google Scholar
- A. Malara
You can also search for this author in PubMed Google Scholar
- C. Matthies
You can also search for this author in PubMed Google Scholar
- A. Mehta
You can also search for this author in PubMed Google Scholar
- A. Nigamova
You can also search for this author in PubMed Google Scholar
- K. J. Pena Rodriguez
You can also search for this author in PubMed Google Scholar
- M. Rieger
You can also search for this author in PubMed Google Scholar
- O. Rieger
You can also search for this author in PubMed Google Scholar
- P. Schleper
You can also search for this author in PubMed Google Scholar
- M. Schröder
You can also search for this author in PubMed Google Scholar
- J. Schwandt
You can also search for this author in PubMed Google Scholar
- J. Sonneveld
You can also search for this author in PubMed Google Scholar
- H. Stadie
You can also search for this author in PubMed Google Scholar
- G. Steinbrück
You can also search for this author in PubMed Google Scholar
- A. Tews
You can also search for this author in PubMed Google Scholar
- I. Zoi
You can also search for this author in PubMed Google Scholar
- J. Bechtel
You can also search for this author in PubMed Google Scholar
- S. Brommer
You can also search for this author in PubMed Google Scholar
- M. Burkart
You can also search for this author in PubMed Google Scholar
- E. Butz
You can also search for this author in PubMed Google Scholar
- R. Caspart
You can also search for this author in PubMed Google Scholar
- T. Chwalek
You can also search for this author in PubMed Google Scholar
- W. De Boer
You can also search for this author in PubMed Google Scholar
- A. Dierlamm
You can also search for this author in PubMed Google Scholar
- A. Droll
You can also search for this author in PubMed Google Scholar
- N. Faltermann
You can also search for this author in PubMed Google Scholar
- M. Giffels
You can also search for this author in PubMed Google Scholar
- J. O. Gosewisch
You can also search for this author in PubMed Google Scholar
- A. Gottmann
You can also search for this author in PubMed Google Scholar
- F. Hartmann
You can also search for this author in PubMed Google Scholar
- C. Heidecker
You can also search for this author in PubMed Google Scholar
- U. Husemann
You can also search for this author in PubMed Google Scholar
- P. Keicher
You can also search for this author in PubMed Google Scholar
- R. Koppenhöfer
You can also search for this author in PubMed Google Scholar
- S. Maier
You can also search for this author in PubMed Google Scholar
- S. Mitra
You can also search for this author in PubMed Google Scholar
- Th. Müller
You can also search for this author in PubMed Google Scholar
- M. Neukum
You can also search for this author in PubMed Google Scholar
- G. Quast
You can also search for this author in PubMed Google Scholar
- K. Rabbertz
You can also search for this author in PubMed Google Scholar
- J. Rauser
You can also search for this author in PubMed Google Scholar
- D. Savoiu
You can also search for this author in PubMed Google Scholar
- M. Schnepf
You can also search for this author in PubMed Google Scholar
- D. Seith
You can also search for this author in PubMed Google Scholar
- I. Shvetsov
You can also search for this author in PubMed Google Scholar
- H. J. Simonis
You can also search for this author in PubMed Google Scholar
- R. Ulrich
You can also search for this author in PubMed Google Scholar
- J. Van Der Linden
You can also search for this author in PubMed Google Scholar
- R. F. Von Cube
You can also search for this author in PubMed Google Scholar
- M. Wassmer
You can also search for this author in PubMed Google Scholar
- M. Weber
You can also search for this author in PubMed Google Scholar
- S. Wieland
You can also search for this author in PubMed Google Scholar
- R. Wolf
You can also search for this author in PubMed Google Scholar
- S. Wozniewski
You can also search for this author in PubMed Google Scholar
- S. Wunsch
You can also search for this author in PubMed Google Scholar
- G. Anagnostou
You can also search for this author in PubMed Google Scholar
- G. Daskalakis
You can also search for this author in PubMed Google Scholar
- A. Kyriakis
You can also search for this author in PubMed Google Scholar
- D. Loukas
You can also search for this author in PubMed Google Scholar
- A. Stakia
You can also search for this author in PubMed Google Scholar
- M. Diamantopoulou
You can also search for this author in PubMed Google Scholar
- D. Karasavvas
You can also search for this author in PubMed Google Scholar
- P. Kontaxakis
You can also search for this author in PubMed Google Scholar
- C. K. Koraka
You can also search for this author in PubMed Google Scholar
- A. Manousakis-Katsikakis
You can also search for this author in PubMed Google Scholar
- A. Panagiotou
You can also search for this author in PubMed Google Scholar
- I. Papavergou
You can also search for this author in PubMed Google Scholar
- N. Saoulidou
You can also search for this author in PubMed Google Scholar
- K. Theofilatos
You can also search for this author in PubMed Google Scholar
- E. Tziaferi
You can also search for this author in PubMed Google Scholar
- K. Vellidis
You can also search for this author in PubMed Google Scholar
- E. Vourliotis
You can also search for this author in PubMed Google Scholar
- G. Bakas
You can also search for this author in PubMed Google Scholar
- K. Kousouris
You can also search for this author in PubMed Google Scholar
- I. Papakrivopoulos
You can also search for this author in PubMed Google Scholar
- G. Tsipolitis
You can also search for this author in PubMed Google Scholar
- A. Zacharopoulou
You can also search for this author in PubMed Google Scholar
- K. Adamidis
You can also search for this author in PubMed Google Scholar
- I. Bestintzanos
You can also search for this author in PubMed Google Scholar
- I. Evangelou
You can also search for this author in PubMed Google Scholar
- C. Foudas
You can also search for this author in PubMed Google Scholar
- P. Gianneios
You can also search for this author in PubMed Google Scholar
- P. Katsoulis
You can also search for this author in PubMed Google Scholar
- P. Kokkas
You can also search for this author in PubMed Google Scholar
- N. Manthos
You can also search for this author in PubMed Google Scholar
- I. Papadopoulos
You can also search for this author in PubMed Google Scholar
- J. Strologas
You can also search for this author in PubMed Google Scholar
- M. Csanad
You can also search for this author in PubMed Google Scholar
- K. Farkas
You can also search for this author in PubMed Google Scholar
- M. M. A. Gadallah
You can also search for this author in PubMed Google Scholar
- S. Lökös
You can also search for this author in PubMed Google Scholar
- P. Major
You can also search for this author in PubMed Google Scholar
- K. Mandal
You can also search for this author in PubMed Google Scholar
- G. Pasztor
You can also search for this author in PubMed Google Scholar
- A. J. Rádl
You can also search for this author in PubMed Google Scholar
- O. Surányi
You can also search for this author in PubMed Google Scholar
- G. I. Veres
You can also search for this author in PubMed Google Scholar
- M. Bartók
You can also search for this author in PubMed Google Scholar
- G. Bencze
You can also search for this author in PubMed Google Scholar
- C. Hajdu
You can also search for this author in PubMed Google Scholar
- D. Horvath
You can also search for this author in PubMed Google Scholar
- F. Sikler
You can also search for this author in PubMed Google Scholar
- V. Veszpremi
You can also search for this author in PubMed Google Scholar
- S. Czellar
You can also search for this author in PubMed Google Scholar
- D. Fasanella
You can also search for this author in PubMed Google Scholar
- F. Fienga
You can also search for this author in PubMed Google Scholar
- J. Karancsi
You can also search for this author in PubMed Google Scholar
- J. Molnar
You can also search for this author in PubMed Google Scholar
- Z. Szillasi
You can also search for this author in PubMed Google Scholar
- D. Teyssier
You can also search for this author in PubMed Google Scholar
- P. Raics
You can also search for this author in PubMed Google Scholar
- Z. L. Trocsanyi
You can also search for this author in PubMed Google Scholar
- B. Ujvari
You can also search for this author in PubMed Google Scholar
- T. Csorgo
You can also search for this author in PubMed Google Scholar
- F. Nemes
You can also search for this author in PubMed Google Scholar
- T. Novak
You can also search for this author in PubMed Google Scholar
- S. Bahinipati
You can also search for this author in PubMed Google Scholar
- C. Kar
You can also search for this author in PubMed Google Scholar
- P. Mal
You can also search for this author in PubMed Google Scholar
- T. Mishra
You can also search for this author in PubMed Google Scholar
- V. K. Muraleedharan Nair Bindhu
You can also search for this author in PubMed Google Scholar
- A. Nayak
You can also search for this author in PubMed Google Scholar
- P. Saha
You can also search for this author in PubMed Google Scholar
- N. Sur
You can also search for this author in PubMed Google Scholar
- S. K. Swain
You can also search for this author in PubMed Google Scholar
- D. Vats
You can also search for this author in PubMed Google Scholar
- S. Bansal
You can also search for this author in PubMed Google Scholar
- S. B. Beri
You can also search for this author in PubMed Google Scholar
- V. Bhatnagar
You can also search for this author in PubMed Google Scholar
- G. Chaudhary
You can also search for this author in PubMed Google Scholar
- S. Chauhan
You can also search for this author in PubMed Google Scholar
- N. Dhingra
You can also search for this author in PubMed Google Scholar
- R. Gupta
You can also search for this author in PubMed Google Scholar
- A. Kaur
You can also search for this author in PubMed Google Scholar
- H. Kaur
You can also search for this author in PubMed Google Scholar
- M. Kaur
You can also search for this author in PubMed Google Scholar
- P. Kumari
You can also search for this author in PubMed Google Scholar
- M. Meena
You can also search for this author in PubMed Google Scholar
- K. Sandeep
You can also search for this author in PubMed Google Scholar
- J. B. Singh
You can also search for this author in PubMed Google Scholar
- A. K. Virdi
You can also search for this author in PubMed Google Scholar
- A. Ahmed
You can also search for this author in PubMed Google Scholar
- A. Bhardwaj
You can also search for this author in PubMed Google Scholar
- B. C. Choudhary
You can also search for this author in PubMed Google Scholar
- M. Gola
You can also search for this author in PubMed Google Scholar
- S. Keshri
You can also search for this author in PubMed Google Scholar
- A. Kumar
You can also search for this author in PubMed Google Scholar
- M. Naimuddin
You can also search for this author in PubMed Google Scholar
- P. Priyanka
You can also search for this author in PubMed Google Scholar
- K. Ranjan
You can also search for this author in PubMed Google Scholar
- S. Saumya
You can also search for this author in PubMed Google Scholar
- A. Shah
You can also search for this author in PubMed Google Scholar
- M. Bharti
You can also search for this author in PubMed Google Scholar
- R. Bhattacharya
You can also search for this author in PubMed Google Scholar
- S. Bhattacharya
You can also search for this author in PubMed Google Scholar
- D. Bhowmik
You can also search for this author in PubMed Google Scholar
- S. Dutta
You can also search for this author in PubMed Google Scholar
- S. Dutta
You can also search for this author in PubMed Google Scholar
- B. Gomber
You can also search for this author in PubMed Google Scholar
- M. Maity
You can also search for this author in PubMed Google Scholar
- P. Palit
You can also search for this author in PubMed Google Scholar
- P. K. Rout
You can also search for this author in PubMed Google Scholar
- G. Saha
You can also search for this author in PubMed Google Scholar
- B. Sahu
You can also search for this author in PubMed Google Scholar
- S. Sarkar
You can also search for this author in PubMed Google Scholar
- M. Sharan
You can also search for this author in PubMed Google Scholar
- P. K. Behera
You can also search for this author in PubMed Google Scholar
- S. C. Behera
You can also search for this author in PubMed Google Scholar
- P. Kalbhor
You can also search for this author in PubMed Google Scholar
- J. R. Komaragiri
You can also search for this author in PubMed Google Scholar
- D. Kumar
You can also search for this author in PubMed Google Scholar
- A. Muhammad
You can also search for this author in PubMed Google Scholar
- L. Panwar
You can also search for this author in PubMed Google Scholar
- R. Pradhan
You can also search for this author in PubMed Google Scholar
- P. R. Pujahari
You can also search for this author in PubMed Google Scholar
- A. Sharma
You can also search for this author in PubMed Google Scholar
- A. K. Sikdar
You can also search for this author in PubMed Google Scholar
- P. C. Tiwari
You can also search for this author in PubMed Google Scholar
- K. Naskar
You can also search for this author in PubMed Google Scholar
- T. Aziz
You can also search for this author in PubMed Google Scholar
- S. Dugad
You can also search for this author in PubMed Google Scholar
- M. Kumar
You can also search for this author in PubMed Google Scholar
- S. Banerjee
You can also search for this author in PubMed Google Scholar
- R. Chudasama
You can also search for this author in PubMed Google Scholar
- M. Guchait
You can also search for this author in PubMed Google Scholar
- S. Karmakar
You can also search for this author in PubMed Google Scholar
- S. Kumar
You can also search for this author in PubMed Google Scholar
- G. Majumder
You can also search for this author in PubMed Google Scholar
- K. Mazumdar
You can also search for this author in PubMed Google Scholar
- S. Mukherjee
You can also search for this author in PubMed Google Scholar
- A. Alpana
You can also search for this author in PubMed Google Scholar
- S. Dube
You can also search for this author in PubMed Google Scholar
- B. Kansal
You can also search for this author in PubMed Google Scholar
- A. Laha
You can also search for this author in PubMed Google Scholar
- S. Pandey
You can also search for this author in PubMed Google Scholar
- A. Rastogi
You can also search for this author in PubMed Google Scholar
- S. Sharma
You can also search for this author in PubMed Google Scholar
- H. Bakhshiansohi
You can also search for this author in PubMed Google Scholar
- E. Khazaie
You can also search for this author in PubMed Google Scholar
- M. Zeinali
You can also search for this author in PubMed Google Scholar
- S. Chenarani
You can also search for this author in PubMed Google Scholar
- S. M. Etesami
You can also search for this author in PubMed Google Scholar
- M. Khakzad
You can also search for this author in PubMed Google Scholar
- M. Mohammadi Najafabadi
You can also search for this author in PubMed Google Scholar
- M. Grunewald
You can also search for this author in PubMed Google Scholar
- M. Abbrescia
You can also search for this author in PubMed Google Scholar
- R. Aly
You can also search for this author in PubMed Google Scholar
- C. Aruta
You can also search for this author in PubMed Google Scholar
- A. Colaleo
You can also search for this author in PubMed Google Scholar
- D. Creanza
You can also search for this author in PubMed Google Scholar
- N. De Filippis
You can also search for this author in PubMed Google Scholar
- M. De Palma
You can also search for this author in PubMed Google Scholar
- A. Di Florio
You can also search for this author in PubMed Google Scholar
- A. Di Pilato
You can also search for this author in PubMed Google Scholar
- W. Elmetenawee
You can also search for this author in PubMed Google Scholar
- F. Errico
You can also search for this author in PubMed Google Scholar
- L. Fiore
You can also search for this author in PubMed Google Scholar
- G. Iaselli
You can also search for this author in PubMed Google Scholar
- M. Ince
You can also search for this author in PubMed Google Scholar
- S. Lezki
You can also search for this author in PubMed Google Scholar
- G. Maggi
You can also search for this author in PubMed Google Scholar
- M. Maggi
You can also search for this author in PubMed Google Scholar
- I. Margjeka
You can also search for this author in PubMed Google Scholar
- V. Mastrapasqua
You can also search for this author in PubMed Google Scholar
- S. My
You can also search for this author in PubMed Google Scholar
- S. Nuzzo
You can also search for this author in PubMed Google Scholar
- A. Pellecchia
You can also search for this author in PubMed Google Scholar
- A. Pompili
You can also search for this author in PubMed Google Scholar
- G. Pugliese
You can also search for this author in PubMed Google Scholar
- D. Ramos
You can also search for this author in PubMed Google Scholar
- A. Ranieri
You can also search for this author in PubMed Google Scholar
- G. Selvaggi
You can also search for this author in PubMed Google Scholar
- L. Silvestris
You can also search for this author in PubMed Google Scholar
- F. M. Simone
You can also search for this author in PubMed Google Scholar
- Ü. Sözbilir
You can also search for this author in PubMed Google Scholar
- R. Venditti
You can also search for this author in PubMed Google Scholar
- P. Verwilligen
You can also search for this author in PubMed Google Scholar
- G. Abbiendi
You can also search for this author in PubMed Google Scholar
- C. Battilana
You can also search for this author in PubMed Google Scholar
- D. Bonacorsi
You can also search for this author in PubMed Google Scholar
- L. Borgonovi
You can also search for this author in PubMed Google Scholar
- L. Brigliadori
You can also search for this author in PubMed Google Scholar
- R. Campanini
You can also search for this author in PubMed Google Scholar
- P. Capiluppi
You can also search for this author in PubMed Google Scholar
- A. Castro
You can also search for this author in PubMed Google Scholar
- F. R. Cavallo
You can also search for this author in PubMed Google Scholar
- C. Ciocca
You can also search for this author in PubMed Google Scholar
- M. Cuffiani
You can also search for this author in PubMed Google Scholar
- G. M. Dallavalle
You can also search for this author in PubMed Google Scholar
- T. Diotalevi
You can also search for this author in PubMed Google Scholar
- F. Fabbri
You can also search for this author in PubMed Google Scholar
- A. Fanfani
You can also search for this author in PubMed Google Scholar
- P. Giacomelli
You can also search for this author in PubMed Google Scholar
- L. Giommi
You can also search for this author in PubMed Google Scholar
- C. Grandi
You can also search for this author in PubMed Google Scholar
- L. Guiducci
You can also search for this author in PubMed Google Scholar
- S. Lo Meo
You can also search for this author in PubMed Google Scholar
- L. Lunerti
You can also search for this author in PubMed Google Scholar
- S. Marcellini
You can also search for this author in PubMed Google Scholar
- G. Masetti
You can also search for this author in PubMed Google Scholar
- F. L. Navarria
You can also search for this author in PubMed Google Scholar
- A. Perrotta
You can also search for this author in PubMed Google Scholar
- F. Primavera
You can also search for this author in PubMed Google Scholar
- A. M. Rossi
You can also search for this author in PubMed Google Scholar
- T. Rovelli
You can also search for this author in PubMed Google Scholar
- G. P. Siroli
You can also search for this author in PubMed Google Scholar
- S. Albergo
You can also search for this author in PubMed Google Scholar
- S. Costa
You can also search for this author in PubMed Google Scholar
- A. Di Mattia
You can also search for this author in PubMed Google Scholar
- R. Potenza
You can also search for this author in PubMed Google Scholar
- A. Tricomi
You can also search for this author in PubMed Google Scholar
- C. Tuve
You can also search for this author in PubMed Google Scholar
- G. Barbagli
You can also search for this author in PubMed Google Scholar
- A. Cassese
You can also search for this author in PubMed Google Scholar
- R. Ceccarelli
You can also search for this author in PubMed Google Scholar
- V. Ciulli
You can also search for this author in PubMed Google Scholar
- C. Civinini
You can also search for this author in PubMed Google Scholar
- R. D’Alessandro
You can also search for this author in PubMed Google Scholar
- E. Focardi
You can also search for this author in PubMed Google Scholar
- G. Latino
You can also search for this author in PubMed Google Scholar
- P. Lenzi
You can also search for this author in PubMed Google Scholar
- M. Lizzo
You can also search for this author in PubMed Google Scholar
- M. Meschini
You can also search for this author in PubMed Google Scholar
- S. Paoletti
You can also search for this author in PubMed Google Scholar
- R. Seidita
You can also search for this author in PubMed Google Scholar
- G. Sguazzoni
You can also search for this author in PubMed Google Scholar
- L. Viliani
You can also search for this author in PubMed Google Scholar
- L. Benussi
You can also search for this author in PubMed Google Scholar
- S. Bianco
You can also search for this author in PubMed Google Scholar
- D. Piccolo
You can also search for this author in PubMed Google Scholar
- M. Bozzo
You can also search for this author in PubMed Google Scholar
- F. Ferro
You can also search for this author in PubMed Google Scholar
- R. Mulargia
You can also search for this author in PubMed Google Scholar
- E. Robutti
You can also search for this author in PubMed Google Scholar
- S. Tosi
You can also search for this author in PubMed Google Scholar
- A. Benaglia
You can also search for this author in PubMed Google Scholar
- G. Boldrini
You can also search for this author in PubMed Google Scholar
- F. Brivio
You can also search for this author in PubMed Google Scholar
- F. Cetorelli
You can also search for this author in PubMed Google Scholar
- F. De Guio
You can also search for this author in PubMed Google Scholar
- M. E. Dinardo
You can also search for this author in PubMed Google Scholar
- P. Dini
You can also search for this author in PubMed Google Scholar
- S. Gennai
You can also search for this author in PubMed Google Scholar
- A. Ghezzi
You can also search for this author in PubMed Google Scholar
- P. Govoni
You can also search for this author in PubMed Google Scholar
- L. Guzzi
You can also search for this author in PubMed Google Scholar
- M. T. Lucchini
You can also search for this author in PubMed Google Scholar
- M. Malberti
You can also search for this author in PubMed Google Scholar
- S. Malvezzi
You can also search for this author in PubMed Google Scholar
- A. Massironi
You can also search for this author in PubMed Google Scholar
- D. Menasce
You can also search for this author in PubMed Google Scholar
- L. Moroni
You can also search for this author in PubMed Google Scholar
- M. Paganoni
You can also search for this author in PubMed Google Scholar
- D. Pedrini
You can also search for this author in PubMed Google Scholar
- B. S. Pinolini
You can also search for this author in PubMed Google Scholar
- S. Ragazzi
You can also search for this author in PubMed Google Scholar
- N. Redaelli
You can also search for this author in PubMed Google Scholar
- T. Tabarelli de Fatis
You can also search for this author in PubMed Google Scholar
- D. Valsecchi
You can also search for this author in PubMed Google Scholar
- D. Zuolo
You can also search for this author in PubMed Google Scholar
- S. Buontempo
You can also search for this author in PubMed Google Scholar
- F. Carnevali
You can also search for this author in PubMed Google Scholar
- N. Cavallo
You can also search for this author in PubMed Google Scholar
- A. De Iorio
You can also search for this author in PubMed Google Scholar
- F. Fabozzi
You can also search for this author in PubMed Google Scholar
- A. O. M. Iorio
You can also search for this author in PubMed Google Scholar
- L. Lista
You can also search for this author in PubMed Google Scholar
- S. Meola
You can also search for this author in PubMed Google Scholar
- P. Paolucci
You can also search for this author in PubMed Google Scholar
- B. Rossi
You can also search for this author in PubMed Google Scholar
- C. Sciacca
You can also search for this author in PubMed Google Scholar
- P. Azzi
You can also search for this author in PubMed Google Scholar
- N. Bacchetta
You can also search for this author in PubMed Google Scholar
- D. Bisello
You can also search for this author in PubMed Google Scholar
- P. Bortignon
You can also search for this author in PubMed Google Scholar
- A. Bragagnolo
You can also search for this author in PubMed Google Scholar
- R. Carlin
You can also search for this author in PubMed Google Scholar
- P. Checchia
You can also search for this author in PubMed Google Scholar
- T. Dorigo
You can also search for this author in PubMed Google Scholar
- U. Dosselli
You can also search for this author in PubMed Google Scholar
- F. Gasparini
You can also search for this author in PubMed Google Scholar
- U. Gasparini
You can also search for this author in PubMed Google Scholar
- G. Grosso
You can also search for this author in PubMed Google Scholar
- L. Layer
You can also search for this author in PubMed Google Scholar
- E. Lusiani
You can also search for this author in PubMed Google Scholar
- M. Margoni
You can also search for this author in PubMed Google Scholar
- F. Marini
You can also search for this author in PubMed Google Scholar
- A. T. Meneguzzo
You can also search for this author in PubMed Google Scholar
- J. Pazzini
You can also search for this author in PubMed Google Scholar
- P. Ronchese
You can also search for this author in PubMed Google Scholar
- R. Rossin
You can also search for this author in PubMed Google Scholar
- F. Simonetto
You can also search for this author in PubMed Google Scholar
- G. Strong
You can also search for this author in PubMed Google Scholar
- M. Tosi
You can also search for this author in PubMed Google Scholar
- H. Yarar
You can also search for this author in PubMed Google Scholar
- M. Zanetti
You can also search for this author in PubMed Google Scholar
- P. Zotto
You can also search for this author in PubMed Google Scholar
- A. Zucchetta
You can also search for this author in PubMed Google Scholar
- G. Zumerle
You can also search for this author in PubMed Google Scholar
- C. Aimè
You can also search for this author in PubMed Google Scholar
- A. Braghieri
You can also search for this author in PubMed Google Scholar
- S. Calzaferri
You can also search for this author in PubMed Google Scholar
- D. Fiorina
You can also search for this author in PubMed Google Scholar
- P. Montagna
You can also search for this author in PubMed Google Scholar
- S. P. Ratti
You can also search for this author in PubMed Google Scholar
- V. Re
You can also search for this author in PubMed Google Scholar
- C. Riccardi
You can also search for this author in PubMed Google Scholar
- P. Salvini
You can also search for this author in PubMed Google Scholar
- I. Vai
You can also search for this author in PubMed Google Scholar
- P. Vitulo
You can also search for this author in PubMed Google Scholar
- P. Asenov
You can also search for this author in PubMed Google Scholar
- G. M. Bilei
You can also search for this author in PubMed Google Scholar
- D. Ciangottini
You can also search for this author in PubMed Google Scholar
- L. Fanò
You can also search for this author in PubMed Google Scholar
- M. Magherini
You can also search for this author in PubMed Google Scholar
- G. Mantovani
You can also search for this author in PubMed Google Scholar
- V. Mariani
You can also search for this author in PubMed Google Scholar
- M. Menichelli
You can also search for this author in PubMed Google Scholar
- F. Moscatelli
You can also search for this author in PubMed Google Scholar
- A. Piccinelli
You can also search for this author in PubMed Google Scholar
- M. Presilla
You can also search for this author in PubMed Google Scholar
- A. Rossi
You can also search for this author in PubMed Google Scholar
- A. Santocchia
You can also search for this author in PubMed Google Scholar
- D. Spiga
You can also search for this author in PubMed Google Scholar
- T. Tedeschi
You can also search for this author in PubMed Google Scholar
- P. Azzurri
You can also search for this author in PubMed Google Scholar
- G. Bagliesi
You can also search for this author in PubMed Google Scholar
- V. Bertacchi
You can also search for this author in PubMed Google Scholar
- L. Bianchini
You can also search for this author in PubMed Google Scholar
- T. Boccali
You can also search for this author in PubMed Google Scholar
- E. Bossini
You can also search for this author in PubMed Google Scholar
- R. Castaldi
You can also search for this author in PubMed Google Scholar
- M. A. Ciocci
You can also search for this author in PubMed Google Scholar
- V. D’Amante
You can also search for this author in PubMed Google Scholar
- R. Dell’Orso
You can also search for this author in PubMed Google Scholar
- M. R. Di Domenico
You can also search for this author in PubMed Google Scholar
- S. Donato
You can also search for this author in PubMed Google Scholar
- A. Giassi
You can also search for this author in PubMed Google Scholar
- F. Ligabue
You can also search for this author in PubMed Google Scholar
- E. Manca
You can also search for this author in PubMed Google Scholar
- G. Mandorli
You can also search for this author in PubMed Google Scholar
- D. Matos Figueiredo
You can also search for this author in PubMed Google Scholar
- A. Messineo
You can also search for this author in PubMed Google Scholar
- M. Musich
You can also search for this author in PubMed Google Scholar
- F. Palla
You can also search for this author in PubMed Google Scholar
- S. Parolia
You can also search for this author in PubMed Google Scholar
- G. Ramirez-Sanchez
You can also search for this author in PubMed Google Scholar
- A. Rizzi
You can also search for this author in PubMed Google Scholar
- G. Rolandi
You can also search for this author in PubMed Google Scholar
- S. Roy Chowdhury
You can also search for this author in PubMed Google Scholar
- A. Scribano
You can also search for this author in PubMed Google Scholar
- N. Shafiei
You can also search for this author in PubMed Google Scholar
- P. Spagnolo
You can also search for this author in PubMed Google Scholar
- R. Tenchini
You can also search for this author in PubMed Google Scholar
- G. Tonelli
You can also search for this author in PubMed Google Scholar
- N. Turini
You can also search for this author in PubMed Google Scholar
- A. Venturi
You can also search for this author in PubMed Google Scholar
- P. G. Verdini
You can also search for this author in PubMed Google Scholar
- P. Barria
You can also search for this author in PubMed Google Scholar
- M. Campana
You can also search for this author in PubMed Google Scholar
- F. Cavallari
You can also search for this author in PubMed Google Scholar
- D. Del Re
You can also search for this author in PubMed Google Scholar
- E. Di Marco
You can also search for this author in PubMed Google Scholar
- M. Diemoz
You can also search for this author in PubMed Google Scholar
- E. Longo
You can also search for this author in PubMed Google Scholar
- P. Meridiani
You can also search for this author in PubMed Google Scholar
- G. Organtini
You can also search for this author in PubMed Google Scholar
- F. Pandolfi
You can also search for this author in PubMed Google Scholar
- R. Paramatti
You can also search for this author in PubMed Google Scholar
- C. Quaranta
You can also search for this author in PubMed Google Scholar
- S. Rahatlou
You can also search for this author in PubMed Google Scholar
- C. Rovelli
You can also search for this author in PubMed Google Scholar
- F. Santanastasio
You can also search for this author in PubMed Google Scholar
- L. Soffi
You can also search for this author in PubMed Google Scholar
- R. Tramontano
You can also search for this author in PubMed Google Scholar
- N. Amapane
You can also search for this author in PubMed Google Scholar
- R. Arcidiacono
You can also search for this author in PubMed Google Scholar
- S. Argiro
You can also search for this author in PubMed Google Scholar
- M. Arneodo
You can also search for this author in PubMed Google Scholar
- N. Bartosik
You can also search for this author in PubMed Google Scholar
- R. Bellan
You can also search for this author in PubMed Google Scholar
- A. Bellora
You can also search for this author in PubMed Google Scholar
- J. Berenguer Antequera
You can also search for this author in PubMed Google Scholar
- C. Biino
You can also search for this author in PubMed Google Scholar
- N. Cartiglia
You can also search for this author in PubMed Google Scholar
- M. Costa
You can also search for this author in PubMed Google Scholar
- R. Covarelli
You can also search for this author in PubMed Google Scholar
- N. Demaria
You can also search for this author in PubMed Google Scholar
- M. Grippo
You can also search for this author in PubMed Google Scholar
- B. Kiani
You can also search for this author in PubMed Google Scholar
- F. Legger
You can also search for this author in PubMed Google Scholar
- C. Mariotti
You can also search for this author in PubMed Google Scholar
- S. Maselli
You can also search for this author in PubMed Google Scholar
- A. Mecca
You can also search for this author in PubMed Google Scholar
- E. Migliore
You can also search for this author in PubMed Google Scholar
- E. Monteil
You can also search for this author in PubMed Google Scholar
- M. Monteno
You can also search for this author in PubMed Google Scholar
- M. M. Obertino
You can also search for this author in PubMed Google Scholar
- G. Ortona
You can also search for this author in PubMed Google Scholar
- L. Pacher
You can also search for this author in PubMed Google Scholar
- N. Pastrone
You can also search for this author in PubMed Google Scholar
- M. Pelliccioni
You can also search for this author in PubMed Google Scholar
- M. Ruspa
You can also search for this author in PubMed Google Scholar
- K. Shchelina
You can also search for this author in PubMed Google Scholar
- F. Siviero
You can also search for this author in PubMed Google Scholar
- V. Sola
You can also search for this author in PubMed Google Scholar
- A. Solano
You can also search for this author in PubMed Google Scholar
- D. Soldi
You can also search for this author in PubMed Google Scholar
- A. Staiano
You can also search for this author in PubMed Google Scholar
- M. Tornago
You can also search for this author in PubMed Google Scholar
- D. Trocino
You can also search for this author in PubMed Google Scholar
- G. Umoret
You can also search for this author in PubMed Google Scholar
- A. Vagnerini
You can also search for this author in PubMed Google Scholar
- S. Belforte
You can also search for this author in PubMed Google Scholar
- V. Candelise
You can also search for this author in PubMed Google Scholar
- M. Casarsa
You can also search for this author in PubMed Google Scholar
- F. Cossutti
You can also search for this author in PubMed Google Scholar
- A. Da Rold
You can also search for this author in PubMed Google Scholar
- G. Della Ricca
You can also search for this author in PubMed Google Scholar
- G. Sorrentino
You can also search for this author in PubMed Google Scholar
- S. Dogra
You can also search for this author in PubMed Google Scholar
- C. Huh
You can also search for this author in PubMed Google Scholar
- B. Kim
You can also search for this author in PubMed Google Scholar
- D. H. Kim
You can also search for this author in PubMed Google Scholar
- G. N. Kim
You can also search for this author in PubMed Google Scholar
- J. Kim
You can also search for this author in PubMed Google Scholar
- J. Lee
You can also search for this author in PubMed Google Scholar
- S. W. Lee
You can also search for this author in PubMed Google Scholar
- C. S. Moon
You can also search for this author in PubMed Google Scholar
- Y. D. Oh
You can also search for this author in PubMed Google Scholar
- S. I. Pak
You can also search for this author in PubMed Google Scholar
- S. Sekmen
You can also search for this author in PubMed Google Scholar
- Y. C. Yang
You can also search for this author in PubMed Google Scholar
- H. Kim
You can also search for this author in PubMed Google Scholar
- D. H. Moon
You can also search for this author in PubMed Google Scholar
- B. Francois
You can also search for this author in PubMed Google Scholar
- T. J. Kim
You can also search for this author in PubMed Google Scholar
- J. Park
You can also search for this author in PubMed Google Scholar
- S. Cho
You can also search for this author in PubMed Google Scholar
- S. Choi
You can also search for this author in PubMed Google Scholar
- B. Hong
You can also search for this author in PubMed Google Scholar
- K. Lee
You can also search for this author in PubMed Google Scholar
- K. S. Lee
You can also search for this author in PubMed Google Scholar
- J. Lim
You can also search for this author in PubMed Google Scholar
- J. Park
You can also search for this author in PubMed Google Scholar
- S. K. Park
You can also search for this author in PubMed Google Scholar
- J. Yoo
You can also search for this author in PubMed Google Scholar
- J. Goh
You can also search for this author in PubMed Google Scholar
- A. Gurtu
You can also search for this author in PubMed Google Scholar
- H. S. Kim
You can also search for this author in PubMed Google Scholar
- Y. Kim
You can also search for this author in PubMed Google Scholar
- J. Almond
You can also search for this author in PubMed Google Scholar
- J. H. Bhyun
You can also search for this author in PubMed Google Scholar
- J. Choi
You can also search for this author in PubMed Google Scholar
- S. Jeon
You can also search for this author in PubMed Google Scholar
- J. Kim
You can also search for this author in PubMed Google Scholar
- J. S. Kim
You can also search for this author in PubMed Google Scholar
- S. Ko
You can also search for this author in PubMed Google Scholar
- H. Kwon
You can also search for this author in PubMed Google Scholar
- H. Lee
You can also search for this author in PubMed Google Scholar
- S. Lee
You can also search for this author in PubMed Google Scholar
- B. H. Oh
You can also search for this author in PubMed Google Scholar
- M. Oh
You can also search for this author in PubMed Google Scholar
- S. B. Oh
You can also search for this author in PubMed Google Scholar
- H. Seo
You can also search for this author in PubMed Google Scholar
- U. K. Yang
You can also search for this author in PubMed Google Scholar
- I. Yoon
You can also search for this author in PubMed Google Scholar
- W. Jang
You can also search for this author in PubMed Google Scholar
- D. Y. Kang
You can also search for this author in PubMed Google Scholar
- Y. Kang
You can also search for this author in PubMed Google Scholar
- S. Kim
You can also search for this author in PubMed Google Scholar
- B. Ko
You can also search for this author in PubMed Google Scholar
- J. S. H. Lee
You can also search for this author in PubMed Google Scholar
- Y. Lee
You can also search for this author in PubMed Google Scholar
- J. A. Merlin
You can also search for this author in PubMed Google Scholar
- I. C. Park
You can also search for this author in PubMed Google Scholar
- Y. Roh
You can also search for this author in PubMed Google Scholar
- M. S. Ryu
You can also search for this author in PubMed Google Scholar
- D. Song
You can also search for this author in PubMed Google Scholar
- I. J. Watson
You can also search for this author in PubMed Google Scholar
- S. Yang
You can also search for this author in PubMed Google Scholar
- S. Ha
You can also search for this author in PubMed Google Scholar
- H. D. Yoo
You can also search for this author in PubMed Google Scholar
- M. Choi
You can also search for this author in PubMed Google Scholar
- H. Lee
You can also search for this author in PubMed Google Scholar
- Y. Lee
You can also search for this author in PubMed Google Scholar
- I. Yu
You can also search for this author in PubMed Google Scholar
- T. Beyrouthy
You can also search for this author in PubMed Google Scholar
- Y. Maghrbi
You can also search for this author in PubMed Google Scholar
- K. Dreimanis
You can also search for this author in PubMed Google Scholar
- V. Veckalns
You can also search for this author in PubMed Google Scholar
- M. Ambrozas
You can also search for this author in PubMed Google Scholar
- A. Carvalho Antunes De Oliveira
You can also search for this author in PubMed Google Scholar
- A. Juodagalvis
You can also search for this author in PubMed Google Scholar
- A. Rinkevicius
You can also search for this author in PubMed Google Scholar
- G. Tamulaitis
You can also search for this author in PubMed Google Scholar
- N. Bin Norjoharuddeen
You can also search for this author in PubMed Google Scholar
- Z. Zolkapli
You can also search for this author in PubMed Google Scholar
- J. F. Benitez
You can also search for this author in PubMed Google Scholar
- A. Castaneda Hernandez
You can also search for this author in PubMed Google Scholar
- H. A. Encinas Acosta
You can also search for this author in PubMed Google Scholar
- L. G. Gallegos Maríñez
You can also search for this author in PubMed Google Scholar
- M. León Coello
You can also search for this author in PubMed Google Scholar
- J. A. Murillo Quijada
You can also search for this author in PubMed Google Scholar
- A. Sehrawat
You can also search for this author in PubMed Google Scholar
- L. Valencia Palomo
You can also search for this author in PubMed Google Scholar
- G. Ayala
You can also search for this author in PubMed Google Scholar
- H. Castilla-Valdez
You can also search for this author in PubMed Google Scholar
- E. De La Cruz-Burelo
You can also search for this author in PubMed Google Scholar
- I. Heredia-De La Cruz
You can also search for this author in PubMed Google Scholar
- R. Lopez-Fernandez
You can also search for this author in PubMed Google Scholar
- C. A. Mondragon Herrera
You can also search for this author in PubMed Google Scholar
- D. A. Perez Navarro
You can also search for this author in PubMed Google Scholar
- R. Reyes-Almanza
You can also search for this author in PubMed Google Scholar
- A. Sánchez Hernández
You can also search for this author in PubMed Google Scholar
- S. Carrillo Moreno
You can also search for this author in PubMed Google Scholar
- C. Oropeza Barrera
You can also search for this author in PubMed Google Scholar
- F. Vazquez Valencia
You can also search for this author in PubMed Google Scholar
- I. Pedraza
You can also search for this author in PubMed Google Scholar
- H. A. Salazar Ibarguen
You can also search for this author in PubMed Google Scholar
- C. Uribe Estrada
You can also search for this author in PubMed Google Scholar
- J. Mijuskovic
You can also search for this author in PubMed Google Scholar
- N. Raicevic
You can also search for this author in PubMed Google Scholar
- D. Krofcheck
You can also search for this author in PubMed Google Scholar
- P. H. Butler
You can also search for this author in PubMed Google Scholar
- A. Ahmad
You can also search for this author in PubMed Google Scholar
- M. I. Asghar
You can also search for this author in PubMed Google Scholar
- A. Awais
You can also search for this author in PubMed Google Scholar
- M. I. M. Awan
You can also search for this author in PubMed Google Scholar
- M. Gul
You can also search for this author in PubMed Google Scholar
- H. R. Hoorani
You can also search for this author in PubMed Google Scholar
- W. A. Khan
You can also search for this author in PubMed Google Scholar
- M. A. Shah
You can also search for this author in PubMed Google Scholar
- M. Shoaib
You can also search for this author in PubMed Google Scholar
- M. Waqas
You can also search for this author in PubMed Google Scholar
- V. Avati
You can also search for this author in PubMed Google Scholar
- L. Grzanka
You can also search for this author in PubMed Google Scholar
- M. Malawski
You can also search for this author in PubMed Google Scholar
- H. Bialkowska
You can also search for this author in PubMed Google Scholar
- M. Bluj
You can also search for this author in PubMed Google Scholar
- B. Boimska
You can also search for this author in PubMed Google Scholar
- M. Górski
You can also search for this author in PubMed Google Scholar
- M. Kazana
You can also search for this author in PubMed Google Scholar
- M. Szleper
You can also search for this author in PubMed Google Scholar
- P. Zalewski
You can also search for this author in PubMed Google Scholar
- K. Bunkowski
You can also search for this author in PubMed Google Scholar
- K. Doroba
You can also search for this author in PubMed Google Scholar
- A. Kalinowski
You can also search for this author in PubMed Google Scholar
- M. Konecki
You can also search for this author in PubMed Google Scholar
- J. Krolikowski
You can also search for this author in PubMed Google Scholar
- M. Araujo
You can also search for this author in PubMed Google Scholar
- P. Bargassa
You can also search for this author in PubMed Google Scholar
- D. Bastos
You can also search for this author in PubMed Google Scholar
- A. Boletti
You can also search for this author in PubMed Google Scholar
- P. Faccioli
You can also search for this author in PubMed Google Scholar
- M. Gallinaro
You can also search for this author in PubMed Google Scholar
- J. Hollar
You can also search for this author in PubMed Google Scholar
- N. Leonardo
You can also search for this author in PubMed Google Scholar
- T. Niknejad
You can also search for this author in PubMed Google Scholar
- M. Pisano
You can also search for this author in PubMed Google Scholar
- J. Seixas
You can also search for this author in PubMed Google Scholar
- O. Toldaiev
You can also search for this author in PubMed Google Scholar
- J. Varela
You can also search for this author in PubMed Google Scholar
- S. Afanasiev
You can also search for this author in PubMed Google Scholar
- D. Budkouski
You can also search for this author in PubMed Google Scholar
- I. Golutvin
You can also search for this author in PubMed Google Scholar
- I. Gorbunov
You can also search for this author in PubMed Google Scholar
- V. Karjavine
You can also search for this author in PubMed Google Scholar
- V. Korenkov
You can also search for this author in PubMed Google Scholar
- A. Lanev
You can also search for this author in PubMed Google Scholar
- A. Malakhov
You can also search for this author in PubMed Google Scholar
- V. Matveev
You can also search for this author in PubMed Google Scholar
- V. Palichik
You can also search for this author in PubMed Google Scholar
- V. Perelygin
You can also search for this author in PubMed Google Scholar
- M. Savina
You can also search for this author in PubMed Google Scholar
- V. Shalaev
You can also search for this author in PubMed Google Scholar
- S. Shmatov
You can also search for this author in PubMed Google Scholar
- S. Shulha
You can also search for this author in PubMed Google Scholar
- V. Smirnov
You can also search for this author in PubMed Google Scholar
- O. Teryaev
You can also search for this author in PubMed Google Scholar
- N. Voytishin
You can also search for this author in PubMed Google Scholar
- B. S. Yuldashev
You can also search for this author in PubMed Google Scholar
- A. Zarubin
You can also search for this author in PubMed Google Scholar
- I. Zhizhin
You can also search for this author in PubMed Google Scholar
- G. Gavrilov
You can also search for this author in PubMed Google Scholar
- V. Golovtcov
You can also search for this author in PubMed Google Scholar
- Y. Ivanov
You can also search for this author in PubMed Google Scholar
- V. Kim
You can also search for this author in PubMed Google Scholar
- E. Kuznetsova
You can also search for this author in PubMed Google Scholar
- V. Murzin
You can also search for this author in PubMed Google Scholar
- V. Oreshkin
You can also search for this author in PubMed Google Scholar
- I. Smirnov
You can also search for this author in PubMed Google Scholar
- D. Sosnov
You can also search for this author in PubMed Google Scholar
- V. Sulimov
You can also search for this author in PubMed Google Scholar
- L. Uvarov
You can also search for this author in PubMed Google Scholar
- S. Volkov
You can also search for this author in PubMed Google Scholar
- A. Vorobyev
You can also search for this author in PubMed Google Scholar
- Yu. Andreev
You can also search for this author in PubMed Google Scholar
- A. Dermenev
You can also search for this author in PubMed Google Scholar
- S. Gninenko
You can also search for this author in PubMed Google Scholar
- N. Golubev
You can also search for this author in PubMed Google Scholar
- A. Karneyeu
You can also search for this author in PubMed Google Scholar
- D. Kirpichnikov
You can also search for this author in PubMed Google Scholar
- M. Kirsanov
You can also search for this author in PubMed Google Scholar
- N. Krasnikov
You can also search for this author in PubMed Google Scholar
- A. Pashenkov
You can also search for this author in PubMed Google Scholar
- G. Pivovarov
You can also search for this author in PubMed Google Scholar
- A. Toropin
You can also search for this author in PubMed Google Scholar
- V. Epshteyn
You can also search for this author in PubMed Google Scholar
- V. Gavrilov
You can also search for this author in PubMed Google Scholar
- N. Lychkovskaya
You can also search for this author in PubMed Google Scholar
- A. Nikitenko
You can also search for this author in PubMed Google Scholar
- V. Popov
You can also search for this author in PubMed Google Scholar
- A. Stepennov
You can also search for this author in PubMed Google Scholar
- M. Toms
You can also search for this author in PubMed Google Scholar
- E. Vlasov
You can also search for this author in PubMed Google Scholar
- A. Zhokin
You can also search for this author in PubMed Google Scholar
- T. Aushev
You can also search for this author in PubMed Google Scholar
- O. Bychkova
You can also search for this author in PubMed Google Scholar
- R. Chistov
You can also search for this author in PubMed Google Scholar
- M. Danilov
You can also search for this author in PubMed Google Scholar
- A. Oskin
You can also search for this author in PubMed Google Scholar
- P. Parygin
You can also search for this author in PubMed Google Scholar
- S. Polikarpov
You can also search for this author in PubMed Google Scholar
- A. Tulupov
You can also search for this author in PubMed Google Scholar
- V. Andreev
You can also search for this author in PubMed Google Scholar
- M. Azarkin
You can also search for this author in PubMed Google Scholar
- I. Dremin
You can also search for this author in PubMed Google Scholar
- M. Kirakosyan
You can also search for this author in PubMed Google Scholar
- A. Terkulov
You can also search for this author in PubMed Google Scholar
- A. Belyaev
You can also search for this author in PubMed Google Scholar
- E. Boos
You can also search for this author in PubMed Google Scholar
- M. Dubinin
You can also search for this author in PubMed Google Scholar
- L. Dudko
You can also search for this author in PubMed Google Scholar
- A. Ershov
You can also search for this author in PubMed Google Scholar
- A. Gribushin
You can also search for this author in PubMed Google Scholar
- V. Klyukhin
You can also search for this author in PubMed Google Scholar
- O. Kodolova
You can also search for this author in PubMed Google Scholar
- I. Lokhtin
You can also search for this author in PubMed Google Scholar
- S. Obraztsov
You can also search for this author in PubMed Google Scholar
- S. Petrushanko
You can also search for this author in PubMed Google Scholar
- V. Savrin
You can also search for this author in PubMed Google Scholar
- A. Snigirev
You can also search for this author in PubMed Google Scholar
- V. Blinov
You can also search for this author in PubMed Google Scholar
- T. Dimova
You can also search for this author in PubMed Google Scholar
- L. Kardapoltsev
You can also search for this author in PubMed Google Scholar
- A. Kozyrev
You can also search for this author in PubMed Google Scholar
- I. Ovtin
You can also search for this author in PubMed Google Scholar
- O. Radchenko
You can also search for this author in PubMed Google Scholar
- Y. Skovpen
You can also search for this author in PubMed Google Scholar
- I. Azhgirey
You can also search for this author in PubMed Google Scholar
- I. Bayshev
You can also search for this author in PubMed Google Scholar
- D. Elumakhov
You can also search for this author in PubMed Google Scholar
- V. Kachanov
You can also search for this author in PubMed Google Scholar
- D. Konstantinov
You can also search for this author in PubMed Google Scholar
- P. Mandrik
You can also search for this author in PubMed Google Scholar
- V. Petrov
You can also search for this author in PubMed Google Scholar
- R. Ryutin
You can also search for this author in PubMed Google Scholar
- S. Slabospitskii
You can also search for this author in PubMed Google Scholar
- A. Sobol
You can also search for this author in PubMed Google Scholar
- S. Troshin
You can also search for this author in PubMed Google Scholar
- N. Tyurin
You can also search for this author in PubMed Google Scholar
- A. Uzunian
You can also search for this author in PubMed Google Scholar
- A. Volkov
You can also search for this author in PubMed Google Scholar
- A. Babaev
You can also search for this author in PubMed Google Scholar
- V. Okhotnikov
You can also search for this author in PubMed Google Scholar
- V. Borshch
You can also search for this author in PubMed Google Scholar
- V. Ivanchenko
You can also search for this author in PubMed Google Scholar
- E. Tcherniaev
You can also search for this author in PubMed Google Scholar
- P. Adzic
You can also search for this author in PubMed Google Scholar
- M. Dordevic
You can also search for this author in PubMed Google Scholar
- P. Milenovic
You can also search for this author in PubMed Google Scholar
- J. Milosevic
You can also search for this author in PubMed Google Scholar
- M. Aguilar-Benitez
You can also search for this author in PubMed Google Scholar
- J. Alcaraz Maestre
You can also search for this author in PubMed Google Scholar
- A. Álvarez Fernández
You can also search for this author in PubMed Google Scholar
- I. Bachiller
You can also search for this author in PubMed Google Scholar
- M. Barrio Luna
You can also search for this author in PubMed Google Scholar
- Cristina F. Bedoya
You can also search for this author in PubMed Google Scholar
- C. A. Carrillo Montoya
You can also search for this author in PubMed Google Scholar
- M. Cepeda
You can also search for this author in PubMed Google Scholar
- M. Cerrada
You can also search for this author in PubMed Google Scholar
- N. Colino
You can also search for this author in PubMed Google Scholar
- B. De La Cruz
You can also search for this author in PubMed Google Scholar
- A. Delgado Peris
You can also search for this author in PubMed Google Scholar
- J. P. Fernández Ramos
You can also search for this author in PubMed Google Scholar
- J. Flix
You can also search for this author in PubMed Google Scholar
- M. C. Fouz
You can also search for this author in PubMed Google Scholar
- O. Gonzalez Lopez
You can also search for this author in PubMed Google Scholar
- S. Goy Lopez
You can also search for this author in PubMed Google Scholar
- J. M. Hernandez
You can also search for this author in PubMed Google Scholar
- M. I. Josa
You can also search for this author in PubMed Google Scholar
- J. León Holgado
You can also search for this author in PubMed Google Scholar
- D. Moran
You can also search for this author in PubMed Google Scholar
- Á. Navarro Tobar
You can also search for this author in PubMed Google Scholar
- C. Perez Dengra
You can also search for this author in PubMed Google Scholar
- A. Pérez-Calero Yzquierdo
You can also search for this author in PubMed Google Scholar
- J. Puerta Pelayo
You can also search for this author in PubMed Google Scholar
- I. Redondo
You can also search for this author in PubMed Google Scholar
- L. Romero
You can also search for this author in PubMed Google Scholar
- S. Sánchez Navas
You can also search for this author in PubMed Google Scholar
- L. Urda Gómez
You can also search for this author in PubMed Google Scholar
- C. Willmott
You can also search for this author in PubMed Google Scholar
- J. F. de Trocóniz
You can also search for this author in PubMed Google Scholar
- B. Alvarez Gonzalez
You can also search for this author in PubMed Google Scholar
- J. Cuevas
You can also search for this author in PubMed Google Scholar
- C. Erice
You can also search for this author in PubMed Google Scholar
- J. Fernandez Menendez
You can also search for this author in PubMed Google Scholar
- S. Folgueras
You can also search for this author in PubMed Google Scholar
- I. Gonzalez Caballero
You can also search for this author in PubMed Google Scholar
- J. R. González Fernández
You can also search for this author in PubMed Google Scholar
- E. Palencia Cortezon
You can also search for this author in PubMed Google Scholar
- C. Ramón Álvarez
You can also search for this author in PubMed Google Scholar
- V. Rodríguez Bouza
You can also search for this author in PubMed Google Scholar
- A. Soto Rodríguez
You can also search for this author in PubMed Google Scholar
- A. Trapote
You can also search for this author in PubMed Google Scholar
- N. Trevisani
You can also search for this author in PubMed Google Scholar
- C. Vico Villalba
You can also search for this author in PubMed Google Scholar
- J. A. Brochero Cifuentes
You can also search for this author in PubMed Google Scholar
- I. J. Cabrillo
You can also search for this author in PubMed Google Scholar
- A. Calderon
You can also search for this author in PubMed Google Scholar
- J. Duarte Campderros
You can also search for this author in PubMed Google Scholar
- M. Fernandez
You can also search for this author in PubMed Google Scholar
- C. Fernandez Madrazo
You can also search for this author in PubMed Google Scholar
- P. J. Fernández Manteca
You can also search for this author in PubMed Google Scholar
- A. García Alonso
You can also search for this author in PubMed Google Scholar
- G. Gomez
You can also search for this author in PubMed Google Scholar
- C. Martinez Rivero
You can also search for this author in PubMed Google Scholar
- P. Martinez Ruiz del Arbol
You can also search for this author in PubMed Google Scholar
- F. Matorras
You can also search for this author in PubMed Google Scholar
- P. Matorras Cuevas
You can also search for this author in PubMed Google Scholar
- J. Piedra Gomez
You can also search for this author in PubMed Google Scholar
- C. Prieels
You can also search for this author in PubMed Google Scholar
- A. Ruiz-Jimeno
You can also search for this author in PubMed Google Scholar
- L. Scodellaro
You can also search for this author in PubMed Google Scholar
- I. Vila
You can also search for this author in PubMed Google Scholar
- J. M. Vizan Garcia
You can also search for this author in PubMed Google Scholar
- M. K. Jayananda
You can also search for this author in PubMed Google Scholar
- B. Kailasapathy
You can also search for this author in PubMed Google Scholar
- D. U. J. Sonnadara
You can also search for this author in PubMed Google Scholar
- D. D. C. Wickramarathna
You can also search for this author in PubMed Google Scholar
- W. G. D. Dharmaratna
You can also search for this author in PubMed Google Scholar
- K. Liyanage
You can also search for this author in PubMed Google Scholar
- N. Perera
You can also search for this author in PubMed Google Scholar
- N. Wickramage
You can also search for this author in PubMed Google Scholar
- T. K. Aarrestad
You can also search for this author in PubMed Google Scholar
- D. Abbaneo
You can also search for this author in PubMed Google Scholar
- J. Alimena
You can also search for this author in PubMed Google Scholar
- E. Auffray
You can also search for this author in PubMed Google Scholar
- G. Auzinger
You can also search for this author in PubMed Google Scholar
- J. Baechler
You can also search for this author in PubMed Google Scholar
- P. Baillon
You can also search for this author in PubMed Google Scholar
- D. Barney
You can also search for this author in PubMed Google Scholar
- J. Bendavid
You can also search for this author in PubMed Google Scholar
- M. Bianco
You can also search for this author in PubMed Google Scholar
- A. Bocci
You can also search for this author in PubMed Google Scholar
- C. Caillol
You can also search for this author in PubMed Google Scholar
- T. Camporesi
You can also search for this author in PubMed Google Scholar
- M. Capeans Garrido
You can also search for this author in PubMed Google Scholar
- G. Cerminara
You can also search for this author in PubMed Google Scholar
- N. Chernyavskaya
You can also search for this author in PubMed Google Scholar
- S. S. Chhibra
You can also search for this author in PubMed Google Scholar
- S. Choudhury
You can also search for this author in PubMed Google Scholar
- M. Cipriani
You can also search for this author in PubMed Google Scholar
- L. Cristella
You can also search for this author in PubMed Google Scholar
- D. d’Enterria
You can also search for this author in PubMed Google Scholar
- A. Dabrowski
You can also search for this author in PubMed Google Scholar
- A. David
You can also search for this author in PubMed Google Scholar
- A. De Roeck
You can also search for this author in PubMed Google Scholar
- M. M. Defranchis
You can also search for this author in PubMed Google Scholar
- M. Deile
You can also search for this author in PubMed Google Scholar
- M. Dobson
You can also search for this author in PubMed Google Scholar
- M. Dünser
You can also search for this author in PubMed Google Scholar
- N. Dupont
You can also search for this author in PubMed Google Scholar
- A. Elliott-Peisert
You can also search for this author in PubMed Google Scholar
- F. Fallavollita
You can also search for this author in PubMed Google Scholar
- A. Florent
You can also search for this author in PubMed Google Scholar
- L. Forthomme
You can also search for this author in PubMed Google Scholar
- G. Franzoni
You can also search for this author in PubMed Google Scholar
- W. Funk
You can also search for this author in PubMed Google Scholar
- S. Ghosh
You can also search for this author in PubMed Google Scholar
- S. Giani
You can also search for this author in PubMed Google Scholar
- D. Gigi
You can also search for this author in PubMed Google Scholar
- K. Gill
You can also search for this author in PubMed Google Scholar
- F. Glege
You can also search for this author in PubMed Google Scholar
- L. Gouskos
You can also search for this author in PubMed Google Scholar
- E. Govorkova
You can also search for this author in PubMed Google Scholar
- M. Haranko
You can also search for this author in PubMed Google Scholar
- J. Hegeman
You can also search for this author in PubMed Google Scholar
- V. Innocente
You can also search for this author in PubMed Google Scholar
- T. James
You can also search for this author in PubMed Google Scholar
- P. Janot
You can also search for this author in PubMed Google Scholar
- J. Kaspar
You can also search for this author in PubMed Google Scholar
- J. Kieseler
You can also search for this author in PubMed Google Scholar
- M. Komm
You can also search for this author in PubMed Google Scholar
- N. Kratochwil
You can also search for this author in PubMed Google Scholar
- C. Lange
You can also search for this author in PubMed Google Scholar
- S. Laurila
You can also search for this author in PubMed Google Scholar
- P. Lecoq
You can also search for this author in PubMed Google Scholar
- A. Lintuluoto
You can also search for this author in PubMed Google Scholar
- K. Long
You can also search for this author in PubMed Google Scholar
- C. Lourenço
You can also search for this author in PubMed Google Scholar
- B. Maier
You can also search for this author in PubMed Google Scholar
- L. Malgeri
You can also search for this author in PubMed Google Scholar
- S. Mallios
You can also search for this author in PubMed Google Scholar
- M. Mannelli
You can also search for this author in PubMed Google Scholar
- A. C. Marini
You can also search for this author in PubMed Google Scholar
- F. Meijers
You can also search for this author in PubMed Google Scholar
- S. Mersi
You can also search for this author in PubMed Google Scholar
- E. Meschi
You can also search for this author in PubMed Google Scholar
- F. Moortgat
You can also search for this author in PubMed Google Scholar
- M. Mulders
You can also search for this author in PubMed Google Scholar
- S. Orfanelli
You can also search for this author in PubMed Google Scholar
- L. Orsini
You can also search for this author in PubMed Google Scholar
- F. Pantaleo
You can also search for this author in PubMed Google Scholar
- E. Perez
You can also search for this author in PubMed Google Scholar
- M. Peruzzi
You can also search for this author in PubMed Google Scholar
- A. Petrilli
You can also search for this author in PubMed Google Scholar
- G. Petrucciani
You can also search for this author in PubMed Google Scholar
- A. Pfeiffer
You can also search for this author in PubMed Google Scholar
- M. Pierini
You can also search for this author in PubMed Google Scholar
- D. Piparo
You can also search for this author in PubMed Google Scholar
- M. Pitt
You can also search for this author in PubMed Google Scholar
- H. Qu
You can also search for this author in PubMed Google Scholar
- T. Quast
You can also search for this author in PubMed Google Scholar
- D. Rabady
You can also search for this author in PubMed Google Scholar
- A. Racz
You can also search for this author in PubMed Google Scholar
- G. Reales Gutiérrez
You can also search for this author in PubMed Google Scholar
- M. Rovere
You can also search for this author in PubMed Google Scholar
- H. Sakulin
You can also search for this author in PubMed Google Scholar
- J. Salfeld-Nebgen
You can also search for this author in PubMed Google Scholar
- S. Scarfi
You can also search for this author in PubMed Google Scholar
- C. Schwick
You can also search for this author in PubMed Google Scholar
- M. Selvaggi
You can also search for this author in PubMed Google Scholar
- A. Sharma
You can also search for this author in PubMed Google Scholar
- P. Silva
You can also search for this author in PubMed Google Scholar
- W. Snoeys
You can also search for this author in PubMed Google Scholar
- P. Sphicas
You can also search for this author in PubMed Google Scholar
- S. Summers
You can also search for this author in PubMed Google Scholar
- K. Tatar
You can also search for this author in PubMed Google Scholar
- V. R. Tavolaro
You can also search for this author in PubMed Google Scholar
- D. Treille
You can also search for this author in PubMed Google Scholar
- P. Tropea
You can also search for this author in PubMed Google Scholar
- A. Tsirou
You can also search for this author in PubMed Google Scholar
- J. Wanczyk
You can also search for this author in PubMed Google Scholar
- K. A. Wozniak
You can also search for this author in PubMed Google Scholar
- W. D. Zeuner
You can also search for this author in PubMed Google Scholar
- L. Caminada
You can also search for this author in PubMed Google Scholar
- A. Ebrahimi
You can also search for this author in PubMed Google Scholar
- W. Erdmann
You can also search for this author in PubMed Google Scholar
- R. Horisberger
You can also search for this author in PubMed Google Scholar
- Q. Ingram
You can also search for this author in PubMed Google Scholar
- H. C. Kaestli
You can also search for this author in PubMed Google Scholar
- D. Kotlinski
You can also search for this author in PubMed Google Scholar
- U. Langenegger
You can also search for this author in PubMed Google Scholar
- M. Missiroli
You can also search for this author in PubMed Google Scholar
- L. Noehte
You can also search for this author in PubMed Google Scholar
- T. Rohe
You can also search for this author in PubMed Google Scholar
- K. Androsov
You can also search for this author in PubMed Google Scholar
- M. Backhaus
You can also search for this author in PubMed Google Scholar
- P. Berger
You can also search for this author in PubMed Google Scholar
- A. Calandri
You can also search for this author in PubMed Google Scholar
- A. De Cosa
You can also search for this author in PubMed Google Scholar
- G. Dissertori
You can also search for this author in PubMed Google Scholar
- M. Dittmar
You can also search for this author in PubMed Google Scholar
- M. Donegà
You can also search for this author in PubMed Google Scholar
- C. Dorfer
You can also search for this author in PubMed Google Scholar
- F. Eble
You can also search for this author in PubMed Google Scholar
- K. Gedia
You can also search for this author in PubMed Google Scholar
- F. Glessgen
You can also search for this author in PubMed Google Scholar
- T. A. Gómez Espinosa
You can also search for this author in PubMed Google Scholar
- C. Grab
You can also search for this author in PubMed Google Scholar
- D. Hits
You can also search for this author in PubMed Google Scholar
- W. Lustermann
You can also search for this author in PubMed Google Scholar
- A. -M. Lyon
You can also search for this author in PubMed Google Scholar
- R. A. Manzoni
You can also search for this author in PubMed Google Scholar
- L. Marchese
You can also search for this author in PubMed Google Scholar
- C. Martin Perez
You can also search for this author in PubMed Google Scholar
- M. T. Meinhard
You can also search for this author in PubMed Google Scholar
- F. Nessi-Tedaldi
You can also search for this author in PubMed Google Scholar
- J. Niedziela
You can also search for this author in PubMed Google Scholar
- F. Pauss
You can also search for this author in PubMed Google Scholar
- V. Perovic
You can also search for this author in PubMed Google Scholar
- S. Pigazzini
You can also search for this author in PubMed Google Scholar
- M. G. Ratti
You can also search for this author in PubMed Google Scholar
- M. Reichmann
You can also search for this author in PubMed Google Scholar
- C. Reissel
You can also search for this author in PubMed Google Scholar
- T. Reitenspiess
You can also search for this author in PubMed Google Scholar
- B. Ristic
You can also search for this author in PubMed Google Scholar
- D. Ruini
You can also search for this author in PubMed Google Scholar
- D. A. Sanz Becerra
You can also search for this author in PubMed Google Scholar
- V. Stampf
You can also search for this author in PubMed Google Scholar
- J. Steggemann
You can also search for this author in PubMed Google Scholar
- R. Wallny
You can also search for this author in PubMed Google Scholar
- C. Amsler
You can also search for this author in PubMed Google Scholar
- P. Bärtschi
You can also search for this author in PubMed Google Scholar
- C. Botta
You can also search for this author in PubMed Google Scholar
- D. Brzhechko
You can also search for this author in PubMed Google Scholar
- M. F. Canelli
You can also search for this author in PubMed Google Scholar
- K. Cormier
You can also search for this author in PubMed Google Scholar
- A. De Wit
You can also search for this author in PubMed Google Scholar
- R. Del Burgo
You can also search for this author in PubMed Google Scholar
- J. K. Heikkilä
You can also search for this author in PubMed Google Scholar
- M. Huwiler
You can also search for this author in PubMed Google Scholar
- W. Jin
You can also search for this author in PubMed Google Scholar
- A. Jofrehei
You can also search for this author in PubMed Google Scholar
- B. Kilminster
You can also search for this author in PubMed Google Scholar
- S. Leontsinis
You can also search for this author in PubMed Google Scholar
- S. P. Liechti
You can also search for this author in PubMed Google Scholar
- A. Macchiolo
You can also search for this author in PubMed Google Scholar
- P. Meiring
You can also search for this author in PubMed Google Scholar
- V. M. Mikuni
You can also search for this author in PubMed Google Scholar
- U. Molinatti
You can also search for this author in PubMed Google Scholar
- I. Neutelings
You can also search for this author in PubMed Google Scholar
- A. Reimers
You can also search for this author in PubMed Google Scholar
- P. Robmann
You can also search for this author in PubMed Google Scholar
- S. Sanchez Cruz
You can also search for this author in PubMed Google Scholar
- K. Schweiger
You can also search for this author in PubMed Google Scholar
- M. Senger
You can also search for this author in PubMed Google Scholar
- Y. Takahashi
You can also search for this author in PubMed Google Scholar
- C. Adloff
You can also search for this author in PubMed Google Scholar
- C. M. Kuo
You can also search for this author in PubMed Google Scholar
- W. Lin
You can also search for this author in PubMed Google Scholar
- A. Roy
You can also search for this author in PubMed Google Scholar
- T. Sarkar
You can also search for this author in PubMed Google Scholar
- S. S. Yu
You can also search for this author in PubMed Google Scholar
- L. Ceard
You can also search for this author in PubMed Google Scholar
- Y. Chao
You can also search for this author in PubMed Google Scholar
- K. F. Chen
You can also search for this author in PubMed Google Scholar
- P. H. Chen
You can also search for this author in PubMed Google Scholar
- P. s. Chen
You can also search for this author in PubMed Google Scholar
- H. Cheng
You can also search for this author in PubMed Google Scholar
- W. -S. Hou
You can also search for this author in PubMed Google Scholar
- Y. y. Li
You can also search for this author in PubMed Google Scholar
- R. -S. Lu
You can also search for this author in PubMed Google Scholar
- E. Paganis
You can also search for this author in PubMed Google Scholar
- A. Psallidas
You can also search for this author in PubMed Google Scholar
- A. Steen
You can also search for this author in PubMed Google Scholar
- H. y. Wu
You can also search for this author in PubMed Google Scholar
- E. Yazgan
You can also search for this author in PubMed Google Scholar
- P. r. Yu
You can also search for this author in PubMed Google Scholar
- B. Asavapibhop
You can also search for this author in PubMed Google Scholar
- C. Asawatangtrakuldee
You can also search for this author in PubMed Google Scholar
- N. Srimanobhas
You can also search for this author in PubMed Google Scholar
- F. Boran
You can also search for this author in PubMed Google Scholar
- S. Damarseckin
You can also search for this author in PubMed Google Scholar
- Z. S. Demiroglu
You can also search for this author in PubMed Google Scholar
- F. Dolek
You can also search for this author in PubMed Google Scholar
- I. Dumanoglu
You can also search for this author in PubMed Google Scholar
- E. Eskut
You can also search for this author in PubMed Google Scholar
- Y. Guler
You can also search for this author in PubMed Google Scholar
- E. Gurpinar Guler
You can also search for this author in PubMed Google Scholar
- C. Isik
You can also search for this author in PubMed Google Scholar
- O. Kara
You can also search for this author in PubMed Google Scholar
- A. Kayis Topaksu
You can also search for this author in PubMed Google Scholar
- U. Kiminsu
You can also search for this author in PubMed Google Scholar
- G. Onengut
You can also search for this author in PubMed Google Scholar
- K. Ozdemir
You can also search for this author in PubMed Google Scholar
- A. Polatoz
You can also search for this author in PubMed Google Scholar
- A. E. Simsek
You can also search for this author in PubMed Google Scholar
- B. Tali
You can also search for this author in PubMed Google Scholar
- U. G. Tok
You can also search for this author in PubMed Google Scholar
- S. Turkcapar
You can also search for this author in PubMed Google Scholar
- I. S. Zorbakir
You can also search for this author in PubMed Google Scholar
- G. Karapinar
You can also search for this author in PubMed Google Scholar
- K. Ocalan
You can also search for this author in PubMed Google Scholar
- M. Yalvac
You can also search for this author in PubMed Google Scholar
- B. Akgun
You can also search for this author in PubMed Google Scholar
- I. O. Atakisi
You can also search for this author in PubMed Google Scholar
- E. Gulmez
You can also search for this author in PubMed Google Scholar
- M. Kaya
You can also search for this author in PubMed Google Scholar
- O. Kaya
You can also search for this author in PubMed Google Scholar
- Ö. Özçelik
You can also search for this author in PubMed Google Scholar
- S. Tekten
You can also search for this author in PubMed Google Scholar
- E. A. Yetkin
You can also search for this author in PubMed Google Scholar
- A. Cakir
You can also search for this author in PubMed Google Scholar
- K. Cankocak
You can also search for this author in PubMed Google Scholar
- Y. Komurcu
You can also search for this author in PubMed Google Scholar
- S. Sen
You can also search for this author in PubMed Google Scholar
- S. Cerci
You can also search for this author in PubMed Google Scholar
- I. Hos
You can also search for this author in PubMed Google Scholar
- B. Isildak
You can also search for this author in PubMed Google Scholar
- B. Kaynak
You can also search for this author in PubMed Google Scholar
- S. Ozkorucuklu
You can also search for this author in PubMed Google Scholar
- H. Sert
You can also search for this author in PubMed Google Scholar
- C. Simsek
You can also search for this author in PubMed Google Scholar
- D. Sunar Cerci
You can also search for this author in PubMed Google Scholar
- C. Zorbilmez
You can also search for this author in PubMed Google Scholar
- B. Grynyov
You can also search for this author in PubMed Google Scholar
- L. Levchuk
You can also search for this author in PubMed Google Scholar
- D. Anthony
You can also search for this author in PubMed Google Scholar
- E. Bhal
You can also search for this author in PubMed Google Scholar
- S. Bologna
You can also search for this author in PubMed Google Scholar
- J. J. Brooke
You can also search for this author in PubMed Google Scholar
- A. Bundock
You can also search for this author in PubMed Google Scholar
- E. Clement
You can also search for this author in PubMed Google Scholar
- D. Cussans
You can also search for this author in PubMed Google Scholar
- H. Flacher
You can also search for this author in PubMed Google Scholar
- M. Glowacki
You can also search for this author in PubMed Google Scholar
- J. Goldstein
You can also search for this author in PubMed Google Scholar
- G. P. Heath
You can also search for this author in PubMed Google Scholar
- H. F. Heath
You can also search for this author in PubMed Google Scholar
- L. Kreczko
You can also search for this author in PubMed Google Scholar
- B. Krikler
You can also search for this author in PubMed Google Scholar
- S. Paramesvaran
You can also search for this author in PubMed Google Scholar
- S. Seif El Nasr-Storey
You can also search for this author in PubMed Google Scholar
- V. J. Smith
You can also search for this author in PubMed Google Scholar
- N. Stylianou
You can also search for this author in PubMed Google Scholar
- K. Walkingshaw Pass
You can also search for this author in PubMed Google Scholar
- R. White
You can also search for this author in PubMed Google Scholar
- K. W. Bell
You can also search for this author in PubMed Google Scholar
- A. Belyaev
You can also search for this author in PubMed Google Scholar
- C. Brew
You can also search for this author in PubMed Google Scholar
- R. M. Brown
You can also search for this author in PubMed Google Scholar
- D. J. A. Cockerill
You can also search for this author in PubMed Google Scholar
- C. Cooke
You can also search for this author in PubMed Google Scholar
- K. V. Ellis
You can also search for this author in PubMed Google Scholar
- K. Harder
You can also search for this author in PubMed Google Scholar
- S. Harper
You can also search for this author in PubMed Google Scholar
- M. -L. Holmberg
You can also search for this author in PubMed Google Scholar
- J. Linacre
You can also search for this author in PubMed Google Scholar
- K. Manolopoulos
You can also search for this author in PubMed Google Scholar
- D. M. Newbold
You can also search for this author in PubMed Google Scholar
- E. Olaiya
You can also search for this author in PubMed Google Scholar
- D. Petyt
You can also search for this author in PubMed Google Scholar
- T. Reis
You can also search for this author in PubMed Google Scholar
- T. Schuh
You can also search for this author in PubMed Google Scholar
- C. H. Shepherd-Themistocleous
You can also search for this author in PubMed Google Scholar
- I. R. Tomalin
You can also search for this author in PubMed Google Scholar
- T. Williams
You can also search for this author in PubMed Google Scholar
- R. Bainbridge
You can also search for this author in PubMed Google Scholar
- P. Bloch
You can also search for this author in PubMed Google Scholar
- S. Bonomally
You can also search for this author in PubMed Google Scholar
- J. Borg
You can also search for this author in PubMed Google Scholar
- S. Breeze
You can also search for this author in PubMed Google Scholar
- O. Buchmuller
You can also search for this author in PubMed Google Scholar
- V. Cepaitis
You can also search for this author in PubMed Google Scholar
- G. S. Chahal
You can also search for this author in PubMed Google Scholar
- D. Colling
You can also search for this author in PubMed Google Scholar
- P. Dauncey
You can also search for this author in PubMed Google Scholar
- G. Davies
You can also search for this author in PubMed Google Scholar
- M. Della Negra
You can also search for this author in PubMed Google Scholar
- S. Fayer
You can also search for this author in PubMed Google Scholar
- G. Fedi
You can also search for this author in PubMed Google Scholar
- G. Hall
You can also search for this author in PubMed Google Scholar
- M. H. Hassanshahi
You can also search for this author in PubMed Google Scholar
- G. Iles
You can also search for this author in PubMed Google Scholar
- J. Langford
You can also search for this author in PubMed Google Scholar
- L. Lyons
You can also search for this author in PubMed Google Scholar
- A. -M. Magnan
You can also search for this author in PubMed Google Scholar
- S. Malik
You can also search for this author in PubMed Google Scholar
- A. Martelli
You can also search for this author in PubMed Google Scholar
- D. G. Monk
You can also search for this author in PubMed Google Scholar
- J. Nash
You can also search for this author in PubMed Google Scholar
- M. Pesaresi
You can also search for this author in PubMed Google Scholar
- B. C. Radburn-Smith
You can also search for this author in PubMed Google Scholar
- D. M. Raymond
You can also search for this author in PubMed Google Scholar
- A. Richards
You can also search for this author in PubMed Google Scholar
- A. Rose
You can also search for this author in PubMed Google Scholar
- E. Scott
You can also search for this author in PubMed Google Scholar
- C. Seez
You can also search for this author in PubMed Google Scholar
- A. Shtipliyski
You can also search for this author in PubMed Google Scholar
- A. Tapper
You can also search for this author in PubMed Google Scholar
- K. Uchida
You can also search for this author in PubMed Google Scholar
- T. Virdee
You can also search for this author in PubMed Google Scholar
- M. Vojinovic
You can also search for this author in PubMed Google Scholar
- N. Wardle
You can also search for this author in PubMed Google Scholar
- S. N. Webb
You can also search for this author in PubMed Google Scholar
- D. Winterbottom
You can also search for this author in PubMed Google Scholar
- K. Coldham
You can also search for this author in PubMed Google Scholar
- J. E. Cole
You can also search for this author in PubMed Google Scholar
- A. Khan
You can also search for this author in PubMed Google Scholar
- P. Kyberd
You can also search for this author in PubMed Google Scholar
- I. D. Reid
You can also search for this author in PubMed Google Scholar
- L. Teodorescu
You can also search for this author in PubMed Google Scholar
- S. Zahid
You can also search for this author in PubMed Google Scholar
- S. Abdullin
You can also search for this author in PubMed Google Scholar
- A. Brinkerhoff
You can also search for this author in PubMed Google Scholar
- B. Caraway
You can also search for this author in PubMed Google Scholar
- J. Dittmann
You can also search for this author in PubMed Google Scholar
- K. Hatakeyama
You can also search for this author in PubMed Google Scholar
- A. R. Kanuganti
You can also search for this author in PubMed Google Scholar
- B. McMaster
You can also search for this author in PubMed Google Scholar
- M. Saunders
You can also search for this author in PubMed Google Scholar
- S. Sawant
You can also search for this author in PubMed Google Scholar
- C. Sutantawibul
You can also search for this author in PubMed Google Scholar
- J. Wilson
You can also search for this author in PubMed Google Scholar
- R. Bartek
You can also search for this author in PubMed Google Scholar
- A. Dominguez
You can also search for this author in PubMed Google Scholar
- R. Uniyal
You can also search for this author in PubMed Google Scholar
- A. M. Vargas Hernandez
You can also search for this author in PubMed Google Scholar
- A. Buccilli
You can also search for this author in PubMed Google Scholar
- S. I. Cooper
You can also search for this author in PubMed Google Scholar
- D. Di Croce
You can also search for this author in PubMed Google Scholar
- S. V. Gleyzer
You can also search for this author in PubMed Google Scholar
- C. Henderson
You can also search for this author in PubMed Google Scholar
- C. U. Perez
You can also search for this author in PubMed Google Scholar
- P. Rumerio
You can also search for this author in PubMed Google Scholar
- C. West
You can also search for this author in PubMed Google Scholar
- A. Akpinar
You can also search for this author in PubMed Google Scholar
- A. Albert
You can also search for this author in PubMed Google Scholar
- D. Arcaro
You can also search for this author in PubMed Google Scholar
- C. Cosby
You can also search for this author in PubMed Google Scholar
- Z. Demiragli
You can also search for this author in PubMed Google Scholar
- E. Fontanesi
You can also search for this author in PubMed Google Scholar
- D. Gastler
You can also search for this author in PubMed Google Scholar
- S. May
You can also search for this author in PubMed Google Scholar
- J. Rohlf
You can also search for this author in PubMed Google Scholar
- K. Salyer
You can also search for this author in PubMed Google Scholar
- D. Sperka
You can also search for this author in PubMed Google Scholar
- D. Spitzbart
You can also search for this author in PubMed Google Scholar
- I. Suarez
You can also search for this author in PubMed Google Scholar
- A. Tsatsos
You can also search for this author in PubMed Google Scholar
- S. Yuan
You can also search for this author in PubMed Google Scholar
- D. Zou
You can also search for this author in PubMed Google Scholar
- G. Benelli
You can also search for this author in PubMed Google Scholar
- B. Burkle
You can also search for this author in PubMed Google Scholar
- X. Coubez
You can also search for this author in PubMed Google Scholar
- D. Cutts
You can also search for this author in PubMed Google Scholar
- M. Hadley
You can also search for this author in PubMed Google Scholar
- U. Heintz
You can also search for this author in PubMed Google Scholar
- J. M. Hogan
You can also search for this author in PubMed Google Scholar
- T. Kwon
You can also search for this author in PubMed Google Scholar
- G. Landsberg
You can also search for this author in PubMed Google Scholar
- K. T. Lau
You can also search for this author in PubMed Google Scholar
- D. Li
You can also search for this author in PubMed Google Scholar
- M. Lukasik
You can also search for this author in PubMed Google Scholar
- J. Luo
You can also search for this author in PubMed Google Scholar
- M. Narain
You can also search for this author in PubMed Google Scholar
- N. Pervan
You can also search for this author in PubMed Google Scholar
- S. Sagir
You can also search for this author in PubMed Google Scholar
- F. Simpson
You can also search for this author in PubMed Google Scholar
- E. Usai
You can also search for this author in PubMed Google Scholar
- W. Y. Wong
You can also search for this author in PubMed Google Scholar
- X. Yan
You can also search for this author in PubMed Google Scholar
- D. Yu
You can also search for this author in PubMed Google Scholar
- W. Zhang
You can also search for this author in PubMed Google Scholar
- J. Bonilla
You can also search for this author in PubMed Google Scholar
- C. Brainerd
You can also search for this author in PubMed Google Scholar
- R. Breedon
You can also search for this author in PubMed Google Scholar
- M. Calderon De La Barca Sanchez
You can also search for this author in PubMed Google Scholar
- M. Chertok
You can also search for this author in PubMed Google Scholar
- J. Conway
You can also search for this author in PubMed Google Scholar
- P. T. Cox
You can also search for this author in PubMed Google Scholar
- R. Erbacher
You can also search for this author in PubMed Google Scholar
- G. Haza
You can also search for this author in PubMed Google Scholar
- F. Jensen
You can also search for this author in PubMed Google Scholar
- O. Kukral
You can also search for this author in PubMed Google Scholar
- R. Lander
You can also search for this author in PubMed Google Scholar
- M. Mulhearn
You can also search for this author in PubMed Google Scholar
- D. Pellett
You can also search for this author in PubMed Google Scholar
- B. Regnery
You can also search for this author in PubMed Google Scholar
- D. Taylor
You can also search for this author in PubMed Google Scholar
- Y. Yao
You can also search for this author in PubMed Google Scholar
- F. Zhang
You can also search for this author in PubMed Google Scholar
- M. Bachtis
You can also search for this author in PubMed Google Scholar
- R. Cousins
You can also search for this author in PubMed Google Scholar
- A. Datta
You can also search for this author in PubMed Google Scholar
- D. Hamilton
You can also search for this author in PubMed Google Scholar
- J. Hauser
You can also search for this author in PubMed Google Scholar
- M. Ignatenko
You can also search for this author in PubMed Google Scholar
- M. A. Iqbal
You can also search for this author in PubMed Google Scholar
- T. Lam
You can also search for this author in PubMed Google Scholar
- W. A. Nash
You can also search for this author in PubMed Google Scholar
- S. Regnard
You can also search for this author in PubMed Google Scholar
- D. Saltzberg
You can also search for this author in PubMed Google Scholar
- B. Stone
You can also search for this author in PubMed Google Scholar
- V. Valuev
You can also search for this author in PubMed Google Scholar
- Y. Chen
You can also search for this author in PubMed Google Scholar
- R. Clare
You can also search for this author in PubMed Google Scholar
- J. W. Gary
You can also search for this author in PubMed Google Scholar
- M. Gordon
You can also search for this author in PubMed Google Scholar
- G. Hanson
You can also search for this author in PubMed Google Scholar
- G. Karapostoli
You can also search for this author in PubMed Google Scholar
- O. R. Long
You can also search for this author in PubMed Google Scholar
- N. Manganelli
You can also search for this author in PubMed Google Scholar
- W. Si
You can also search for this author in PubMed Google Scholar
- S. Wimpenny
You can also search for this author in PubMed Google Scholar
- Y. Zhang
You can also search for this author in PubMed Google Scholar
- J. G. Branson
You can also search for this author in PubMed Google Scholar
- P. Chang
You can also search for this author in PubMed Google Scholar
- S. Cittolin
You can also search for this author in PubMed Google Scholar
- S. Cooperstein
You can also search for this author in PubMed Google Scholar
- D. Diaz
You can also search for this author in PubMed Google Scholar
- J. Duarte
You can also search for this author in PubMed Google Scholar
- R. Gerosa
You can also search for this author in PubMed Google Scholar
- L. Giannini
You can also search for this author in PubMed Google Scholar
- J. Guiang
You can also search for this author in PubMed Google Scholar
- R. Kansal
You can also search for this author in PubMed Google Scholar
- V. Krutelyov
You can also search for this author in PubMed Google Scholar
- R. Lee
You can also search for this author in PubMed Google Scholar
- J. Letts
You can also search for this author in PubMed Google Scholar
- M. Masciovecchio
You can also search for this author in PubMed Google Scholar
- F. Mokhtar
You can also search for this author in PubMed Google Scholar
- M. Pieri
You can also search for this author in PubMed Google Scholar
- B. V. Sathia Narayanan
You can also search for this author in PubMed Google Scholar
- V. Sharma
You can also search for this author in PubMed Google Scholar
- M. Tadel
You can also search for this author in PubMed Google Scholar
- F. Würthwein
You can also search for this author in PubMed Google Scholar
- Y. Xiang
You can also search for this author in PubMed Google Scholar
- A. Yagil
You can also search for this author in PubMed Google Scholar
- N. Amin
You can also search for this author in PubMed Google Scholar
- C. Campagnari
You can also search for this author in PubMed Google Scholar
- M. Citron
You can also search for this author in PubMed Google Scholar
- G. Collura
You can also search for this author in PubMed Google Scholar
- A. Dorsett
You can also search for this author in PubMed Google Scholar
- V. Dutta
You can also search for this author in PubMed Google Scholar
- J. Incandela
You can also search for this author in PubMed Google Scholar
- M. Kilpatrick
You can also search for this author in PubMed Google Scholar
- J. Kim
You can also search for this author in PubMed Google Scholar
- B. Marsh
You can also search for this author in PubMed Google Scholar
- H. Mei
You can also search for this author in PubMed Google Scholar
- M. Oshiro
You can also search for this author in PubMed Google Scholar
- M. Quinnan
You can also search for this author in PubMed Google Scholar
- J. Richman
You can also search for this author in PubMed Google Scholar
- U. Sarica
You can also search for this author in PubMed Google Scholar
- F. Setti
You can also search for this author in PubMed Google Scholar
- J. Sheplock
You can also search for this author in PubMed Google Scholar
- P. Siddireddy
You can also search for this author in PubMed Google Scholar
- D. Stuart
You can also search for this author in PubMed Google Scholar
- S. Wang
You can also search for this author in PubMed Google Scholar
- A. Bornheim
You can also search for this author in PubMed Google Scholar
- O. Cerri
You can also search for this author in PubMed Google Scholar
- I. Dutta
You can also search for this author in PubMed Google Scholar
- J. M. Lawhorn
You can also search for this author in PubMed Google Scholar
- N. Lu
You can also search for this author in PubMed Google Scholar
- J. Mao
You can also search for this author in PubMed Google Scholar
- H. B. Newman
You can also search for this author in PubMed Google Scholar
- T. Q. Nguyen
You can also search for this author in PubMed Google Scholar
- M. Spiropulu
You can also search for this author in PubMed Google Scholar
- J. R. Vlimant
You can also search for this author in PubMed Google Scholar
- C. Wang
You can also search for this author in PubMed Google Scholar
- S. Xie
You can also search for this author in PubMed Google Scholar
- Z. Zhang
You can also search for this author in PubMed Google Scholar
- R. Y. Zhu
You can also search for this author in PubMed Google Scholar
- J. Alison
You can also search for this author in PubMed Google Scholar
- S. An
You can also search for this author in PubMed Google Scholar
- M. B. Andrews
You can also search for this author in PubMed Google Scholar
- P. Bryant
You can also search for this author in PubMed Google Scholar
- T. Ferguson
You can also search for this author in PubMed Google Scholar
- A. Harilal
You can also search for this author in PubMed Google Scholar
- C. Liu
You can also search for this author in PubMed Google Scholar
- T. Mudholkar
You can also search for this author in PubMed Google Scholar
- M. Paulini
You can also search for this author in PubMed Google Scholar
- A. Sanchez
You can also search for this author in PubMed Google Scholar
- W. Terrill
You can also search for this author in PubMed Google Scholar
- J. P. Cumalat
You can also search for this author in PubMed Google Scholar
- W. T. Ford
You can also search for this author in PubMed Google Scholar
- A. Hassani
You can also search for this author in PubMed Google Scholar
- G. Karathanasis
You can also search for this author in PubMed Google Scholar
- E. MacDonald
You can also search for this author in PubMed Google Scholar
- R. Patel
You can also search for this author in PubMed Google Scholar
- A. Perloff
You can also search for this author in PubMed Google Scholar
- C. Savard
You can also search for this author in PubMed Google Scholar
- N. Schonbeck
You can also search for this author in PubMed Google Scholar
- K. Stenson
You can also search for this author in PubMed Google Scholar
- K. A. Ulmer
You can also search for this author in PubMed Google Scholar
- S. R. Wagner
You can also search for this author in PubMed Google Scholar
- N. Zipper
You can also search for this author in PubMed Google Scholar
- J. Alexander
You can also search for this author in PubMed Google Scholar
- S. Bright-Thonney
You can also search for this author in PubMed Google Scholar
- X. Chen
You can also search for this author in PubMed Google Scholar
- Y. Cheng
You can also search for this author in PubMed Google Scholar
- D. J. Cranshaw
You can also search for this author in PubMed Google Scholar
- S. Hogan
You can also search for this author in PubMed Google Scholar
- J. Monroy
You can also search for this author in PubMed Google Scholar
- J. R. Patterson
You can also search for this author in PubMed Google Scholar
- D. Quach
You can also search for this author in PubMed Google Scholar
- J. Reichert
You can also search for this author in PubMed Google Scholar
- M. Reid
You can also search for this author in PubMed Google Scholar
- A. Ryd
You can also search for this author in PubMed Google Scholar
- W. Sun
You can also search for this author in PubMed Google Scholar
- J. Thom
You can also search for this author in PubMed Google Scholar
- P. Wittich
You can also search for this author in PubMed Google Scholar
- R. Zou
You can also search for this author in PubMed Google Scholar
- M. Albrow
You can also search for this author in PubMed Google Scholar
- M. Alyari
You can also search for this author in PubMed Google Scholar
- G. Apollinari
You can also search for this author in PubMed Google Scholar
- A. Apresyan
You can also search for this author in PubMed Google Scholar
- A. Apyan
You can also search for this author in PubMed Google Scholar
- L. A. T. Bauerdick
You can also search for this author in PubMed Google Scholar
- D. Berry
You can also search for this author in PubMed Google Scholar
- J. Berryhill
You can also search for this author in PubMed Google Scholar
- P. C. Bhat
You can also search for this author in PubMed Google Scholar
- K. Burkett
You can also search for this author in PubMed Google Scholar
- J. N. Butler
You can also search for this author in PubMed Google Scholar
- A. Canepa
You can also search for this author in PubMed Google Scholar
- G. B. Cerati
You can also search for this author in PubMed Google Scholar
- H. W. K. Cheung
You can also search for this author in PubMed Google Scholar
- F. Chlebana
You can also search for this author in PubMed Google Scholar
- K. F. Di Petrillo
You can also search for this author in PubMed Google Scholar
- J. Dickinson
You can also search for this author in PubMed Google Scholar
- V. D. Elvira
You can also search for this author in PubMed Google Scholar
- Y. Feng
You can also search for this author in PubMed Google Scholar
- J. Freeman
You can also search for this author in PubMed Google Scholar
- Z. Gecse
You can also search for this author in PubMed Google Scholar
- L. Gray
You can also search for this author in PubMed Google Scholar
- D. Green
You can also search for this author in PubMed Google Scholar
- S. Grünendahl
You can also search for this author in PubMed Google Scholar
- O. Gutsche
You can also search for this author in PubMed Google Scholar
- R. M. Harris
You can also search for this author in PubMed Google Scholar
- R. Heller
You can also search for this author in PubMed Google Scholar
- T. C. Herwig
You can also search for this author in PubMed Google Scholar
- J. Hirschauer
You can also search for this author in PubMed Google Scholar
- B. Jayatilaka
You can also search for this author in PubMed Google Scholar
- S. Jindariani
You can also search for this author in PubMed Google Scholar
- M. Johnson
You can also search for this author in PubMed Google Scholar
- U. Joshi
You can also search for this author in PubMed Google Scholar
- T. Klijnsma
You can also search for this author in PubMed Google Scholar
- B. Klima
You can also search for this author in PubMed Google Scholar
- K. H. M. Kwok
You can also search for this author in PubMed Google Scholar
- S. Lammel
You can also search for this author in PubMed Google Scholar
- D. Lincoln
You can also search for this author in PubMed Google Scholar
- R. Lipton
You can also search for this author in PubMed Google Scholar
- T. Liu
You can also search for this author in PubMed Google Scholar
- C. Madrid
You can also search for this author in PubMed Google Scholar
- K. Maeshima
You can also search for this author in PubMed Google Scholar
- C. Mantilla
You can also search for this author in PubMed Google Scholar
- D. Mason
You can also search for this author in PubMed Google Scholar
- P. McBride
You can also search for this author in PubMed Google Scholar
- P. Merkel
You can also search for this author in PubMed Google Scholar
- S. Mrenna
You can also search for this author in PubMed Google Scholar
- S. Nahn
You can also search for this author in PubMed Google Scholar
- J. Ngadiuba
You can also search for this author in PubMed Google Scholar
- V. Papadimitriou
You can also search for this author in PubMed Google Scholar
- N. Pastika
You can also search for this author in PubMed Google Scholar
- K. Pedro
You can also search for this author in PubMed Google Scholar
- C. Pena
You can also search for this author in PubMed Google Scholar
- F. Ravera
You can also search for this author in PubMed Google Scholar
- A. Reinsvold Hall
You can also search for this author in PubMed Google Scholar
- L. Ristori
You can also search for this author in PubMed Google Scholar
- E. Sexton-Kennedy
You can also search for this author in PubMed Google Scholar
- N. Smith
You can also search for this author in PubMed Google Scholar
- A. Soha
You can also search for this author in PubMed Google Scholar
- L. Spiegel
You can also search for this author in PubMed Google Scholar
- S. Stoynev
You can also search for this author in PubMed Google Scholar
- J. Strait
You can also search for this author in PubMed Google Scholar
- L. Taylor
You can also search for this author in PubMed Google Scholar
- S. Tkaczyk
You can also search for this author in PubMed Google Scholar
- N. V. Tran
You can also search for this author in PubMed Google Scholar
- L. Uplegger
You can also search for this author in PubMed Google Scholar
- E. W. Vaandering
You can also search for this author in PubMed Google Scholar
- H. A. Weber
You can also search for this author in PubMed Google Scholar
- P. Avery
You can also search for this author in PubMed Google Scholar
- D. Bourilkov
You can also search for this author in PubMed Google Scholar
- L. Cadamuro
You can also search for this author in PubMed Google Scholar
- V. Cherepanov
You can also search for this author in PubMed Google Scholar
- R. D. Field
You can also search for this author in PubMed Google Scholar
- D. Guerrero
You can also search for this author in PubMed Google Scholar
- M. Kim
You can also search for this author in PubMed Google Scholar
- E. Koenig
You can also search for this author in PubMed Google Scholar
- J. Konigsberg
You can also search for this author in PubMed Google Scholar
- A. Korytov
You can also search for this author in PubMed Google Scholar
- K. H. Lo
You can also search for this author in PubMed Google Scholar
- K. Matchev
You can also search for this author in PubMed Google Scholar
- N. Menendez
You can also search for this author in PubMed Google Scholar
- G. Mitselmakher
You can also search for this author in PubMed Google Scholar
- A. Muthirakalayil Madhu
You can also search for this author in PubMed Google Scholar
- N. Rawal
You can also search for this author in PubMed Google Scholar
- D. Rosenzweig
You can also search for this author in PubMed Google Scholar
- S. Rosenzweig
You can also search for this author in PubMed Google Scholar
- K. Shi
You can also search for this author in PubMed Google Scholar
- J. Wang
You can also search for this author in PubMed Google Scholar
- Z. Wu
You can also search for this author in PubMed Google Scholar
- E. Yigitbasi
You can also search for this author in PubMed Google Scholar
- X. Zuo
You can also search for this author in PubMed Google Scholar
- T. Adams
You can also search for this author in PubMed Google Scholar
- A. Askew
You can also search for this author in PubMed Google Scholar
- R. Habibullah
You can also search for this author in PubMed Google Scholar
- V. Hagopian
You can also search for this author in PubMed Google Scholar
- K. F. Johnson
You can also search for this author in PubMed Google Scholar
- R. Khurana
You can also search for this author in PubMed Google Scholar
- T. Kolberg
You can also search for this author in PubMed Google Scholar
- G. Martinez
You can also search for this author in PubMed Google Scholar
- H. Prosper
You can also search for this author in PubMed Google Scholar
- C. Schiber
You can also search for this author in PubMed Google Scholar
- O. Viazlo
You can also search for this author in PubMed Google Scholar
- R. Yohay
You can also search for this author in PubMed Google Scholar
- J. Zhang
You can also search for this author in PubMed Google Scholar
- M. M. Baarmand
You can also search for this author in PubMed Google Scholar
- S. Butalla
You can also search for this author in PubMed Google Scholar
- T. Elkafrawy
You can also search for this author in PubMed Google Scholar
- M. Hohlmann
You can also search for this author in PubMed Google Scholar
- R. Kumar Verma
You can also search for this author in PubMed Google Scholar
- D. Noonan
You can also search for this author in PubMed Google Scholar
- M. Rahmani
You can also search for this author in PubMed Google Scholar
- F. Yumiceva
You can also search for this author in PubMed Google Scholar
- M. R. Adams
You can also search for this author in PubMed Google Scholar
- H. Becerril Gonzalez
You can also search for this author in PubMed Google Scholar
- R. Cavanaugh
You can also search for this author in PubMed Google Scholar
- S. Dittmer
You can also search for this author in PubMed Google Scholar
- O. Evdokimov
You can also search for this author in PubMed Google Scholar
- C. E. Gerber
You can also search for this author in PubMed Google Scholar
- D. J. Hofman
You can also search for this author in PubMed Google Scholar
- A. H. Merrit
You can also search for this author in PubMed Google Scholar
- C. Mills
You can also search for this author in PubMed Google Scholar
- G. Oh
You can also search for this author in PubMed Google Scholar
- T. Roy
You can also search for this author in PubMed Google Scholar
- S. Rudrabhatla
You can also search for this author in PubMed Google Scholar
- M. B. Tonjes
You can also search for this author in PubMed Google Scholar
- N. Varelas
You can also search for this author in PubMed Google Scholar
- J. Viinikainen
You can also search for this author in PubMed Google Scholar
- X. Wang
You can also search for this author in PubMed Google Scholar
- Z. Ye
You can also search for this author in PubMed Google Scholar
- M. Alhusseini
You can also search for this author in PubMed Google Scholar
- K. Dilsiz
You can also search for this author in PubMed Google Scholar
- L. Emediato
You can also search for this author in PubMed Google Scholar
- R. P. Gandrajula
You can also search for this author in PubMed Google Scholar
- O. K. Köseyan
You can also search for this author in PubMed Google Scholar
- J. -P. Merlo
You can also search for this author in PubMed Google Scholar
- A. Mestvirishvili
You can also search for this author in PubMed Google Scholar
- J. Nachtman
You can also search for this author in PubMed Google Scholar
- H. Ogul
You can also search for this author in PubMed Google Scholar
- Y. Onel
You can also search for this author in PubMed Google Scholar
- A. Penzo
You can also search for this author in PubMed Google Scholar
- C. Snyder
You can also search for this author in PubMed Google Scholar
- E. Tiras
You can also search for this author in PubMed Google Scholar
- O. Amram
You can also search for this author in PubMed Google Scholar
- B. Blumenfeld
You can also search for this author in PubMed Google Scholar
- L. Corcodilos
You can also search for this author in PubMed Google Scholar
- J. Davis
You can also search for this author in PubMed Google Scholar
- A. V. Gritsan
You can also search for this author in PubMed Google Scholar
- S. Kyriacou
You can also search for this author in PubMed Google Scholar
- P. Maksimovic
You can also search for this author in PubMed Google Scholar
- J. Roskes
You can also search for this author in PubMed Google Scholar
- M. Swartz
You can also search for this author in PubMed Google Scholar
- T.Á. Vámi
You can also search for this author in PubMed Google Scholar
- A. Abreu
You can also search for this author in PubMed Google Scholar
- J. Anguiano
You can also search for this author in PubMed Google Scholar
- C. Baldenegro Barrera
You can also search for this author in PubMed Google Scholar
- P. Baringer
You can also search for this author in PubMed Google Scholar
- A. Bean
You can also search for this author in PubMed Google Scholar
- Z. Flowers
You can also search for this author in PubMed Google Scholar
- T. Isidori
You can also search for this author in PubMed Google Scholar
- S. Khalil
You can also search for this author in PubMed Google Scholar
- J. King
You can also search for this author in PubMed Google Scholar
- G. Krintiras
You can also search for this author in PubMed Google Scholar
- A. Kropivnitskaya
You can also search for this author in PubMed Google Scholar
- M. Lazarovits
You can also search for this author in PubMed Google Scholar
- C. Le Mahieu
You can also search for this author in PubMed Google Scholar
- C. Lindsey
You can also search for this author in PubMed Google Scholar
- J. Marquez
You can also search for this author in PubMed Google Scholar
- N. Minafra
You can also search for this author in PubMed Google Scholar
- M. Murray
You can also search for this author in PubMed Google Scholar
- M. Nickel
You can also search for this author in PubMed Google Scholar
- C. Rogan
You can also search for this author in PubMed Google Scholar
- C. Royon
You can also search for this author in PubMed Google Scholar
- R. Salvatico
You can also search for this author in PubMed Google Scholar
- S. Sanders
You can also search for this author in PubMed Google Scholar
- E. Schmitz
You can also search for this author in PubMed Google Scholar
- C. Smith
You can also search for this author in PubMed Google Scholar
- Q. Wang
You can also search for this author in PubMed Google Scholar
- Z. Warner
You can also search for this author in PubMed Google Scholar
- J. Williams
You can also search for this author in PubMed Google Scholar
- G. Wilson
You can also search for this author in PubMed Google Scholar
- S. Duric
You can also search for this author in PubMed Google Scholar
- A. Ivanov
You can also search for this author in PubMed Google Scholar
- K. Kaadze
You can also search for this author in PubMed Google Scholar
- D. Kim
You can also search for this author in PubMed Google Scholar
- Y. Maravin
You can also search for this author in PubMed Google Scholar
- T. Mitchell
You can also search for this author in PubMed Google Scholar
- A. Modak
You can also search for this author in PubMed Google Scholar
- K. Nam
You can also search for this author in PubMed Google Scholar
- F. Rebassoo
You can also search for this author in PubMed Google Scholar
- D. Wright
You can also search for this author in PubMed Google Scholar
- E. Adams
You can also search for this author in PubMed Google Scholar
- A. Baden
You can also search for this author in PubMed Google Scholar
- O. Baron
You can also search for this author in PubMed Google Scholar
- A. Belloni
You can also search for this author in PubMed Google Scholar
- S. C. Eno
You can also search for this author in PubMed Google Scholar
- N. J. Hadley
You can also search for this author in PubMed Google Scholar
- S. Jabeen
You can also search for this author in PubMed Google Scholar
- R. G. Kellogg
You can also search for this author in PubMed Google Scholar
- T. Koeth
You can also search for this author in PubMed Google Scholar
- Y. Lai
You can also search for this author in PubMed Google Scholar
- S. Lascio
You can also search for this author in PubMed Google Scholar
- A. C. Mignerey
You can also search for this author in PubMed Google Scholar
- S. Nabili
You can also search for this author in PubMed Google Scholar
- C. Palmer
You can also search for this author in PubMed Google Scholar
- M. Seidel
You can also search for this author in PubMed Google Scholar
- A. Skuja
You can also search for this author in PubMed Google Scholar
- L. Wang
You can also search for this author in PubMed Google Scholar
- K. Wong
You can also search for this author in PubMed Google Scholar
- D. Abercrombie
You can also search for this author in PubMed Google Scholar
- G. Andreassi
You can also search for this author in PubMed Google Scholar
- R. Bi
You can also search for this author in PubMed Google Scholar
- W. Busza
You can also search for this author in PubMed Google Scholar
- I. A. Cali
You can also search for this author in PubMed Google Scholar
- Y. Chen
You can also search for this author in PubMed Google Scholar
- M. D’Alfonso
You can also search for this author in PubMed Google Scholar
- J. Eysermans
You can also search for this author in PubMed Google Scholar
- C. Freer
You can also search for this author in PubMed Google Scholar
- G. Gomez Ceballos
You can also search for this author in PubMed Google Scholar
- M. Goncharov
You can also search for this author in PubMed Google Scholar
- P. Harris
You can also search for this author in PubMed Google Scholar
- M. Hu
You can also search for this author in PubMed Google Scholar
- M. Klute
You can also search for this author in PubMed Google Scholar
- D. Kovalskyi
You can also search for this author in PubMed Google Scholar
- J. Krupa
You can also search for this author in PubMed Google Scholar
- Y. -J. Lee
You can also search for this author in PubMed Google Scholar
- C. Mironov
You can also search for this author in PubMed Google Scholar
- C. Paus
You can also search for this author in PubMed Google Scholar
- D. Rankin
You can also search for this author in PubMed Google Scholar
- C. Roland
You can also search for this author in PubMed Google Scholar
- G. Roland
You can also search for this author in PubMed Google Scholar
- Z. Shi
You can also search for this author in PubMed Google Scholar
- G. S. F. Stephans
You can also search for this author in PubMed Google Scholar
- J. Wang
You can also search for this author in PubMed Google Scholar
- Z. Wang
You can also search for this author in PubMed Google Scholar
- B. Wyslouch
You can also search for this author in PubMed Google Scholar
- R. M. Chatterjee
You can also search for this author in PubMed Google Scholar
- A. Evans
You can also search for this author in PubMed Google Scholar
- J. Hiltbrand
You can also search for this author in PubMed Google Scholar
- Sh. Jain
You can also search for this author in PubMed Google Scholar
- B. M. Joshi
You can also search for this author in PubMed Google Scholar
- M. Krohn
You can also search for this author in PubMed Google Scholar
- Y. Kubota
You can also search for this author in PubMed Google Scholar
- J. Mans
You can also search for this author in PubMed Google Scholar
- M. Revering
You can also search for this author in PubMed Google Scholar
- R. Rusack
You can also search for this author in PubMed Google Scholar
- R. Saradhy
You can also search for this author in PubMed Google Scholar
- N. Schroeder
You can also search for this author in PubMed Google Scholar
- N. Strobbe
You can also search for this author in PubMed Google Scholar
- M. A. Wadud
You can also search for this author in PubMed Google Scholar
- K. Bloom
You can also search for this author in PubMed Google Scholar
- M. Bryson
You can also search for this author in PubMed Google Scholar
- S. Chauhan
You can also search for this author in PubMed Google Scholar
- D. R. Claes
You can also search for this author in PubMed Google Scholar
- C. Fangmeier
You can also search for this author in PubMed Google Scholar
- L. Finco
You can also search for this author in PubMed Google Scholar
- F. Golf
You can also search for this author in PubMed Google Scholar
- C. Joo
You can also search for this author in PubMed Google Scholar
- I. Kravchenko
You can also search for this author in PubMed Google Scholar
- I. Reed
You can also search for this author in PubMed Google Scholar
- J. E. Siado
You can also search for this author in PubMed Google Scholar
- G. R. Snow
You can also search for this author in PubMed Google Scholar
- W. Tabb
You can also search for this author in PubMed Google Scholar
- A. Wightman
You can also search for this author in PubMed Google Scholar
- F. Yan
You can also search for this author in PubMed Google Scholar
- A. G. Zecchinelli
You can also search for this author in PubMed Google Scholar
- G. Agarwal
You can also search for this author in PubMed Google Scholar
- H. Bandyopadhyay
You can also search for this author in PubMed Google Scholar
- L. Hay
You can also search for this author in PubMed Google Scholar
- I. Iashvili
You can also search for this author in PubMed Google Scholar
- A. Kharchilava
You can also search for this author in PubMed Google Scholar
- C. McLean
You can also search for this author in PubMed Google Scholar
- D. Nguyen
You can also search for this author in PubMed Google Scholar
- J. Pekkanen
You can also search for this author in PubMed Google Scholar
- S. Rappoccio
You can also search for this author in PubMed Google Scholar
- A. Williams
You can also search for this author in PubMed Google Scholar
- G. Alverson
You can also search for this author in PubMed Google Scholar
- E. Barberis
You can also search for this author in PubMed Google Scholar
- Y. Haddad
You can also search for this author in PubMed Google Scholar
- Y. Han
You can also search for this author in PubMed Google Scholar
- A. Hortiangtham
You can also search for this author in PubMed Google Scholar
- A. Krishna
You can also search for this author in PubMed Google Scholar
- J. Li
You can also search for this author in PubMed Google Scholar
- J. Lidrych
You can also search for this author in PubMed Google Scholar
- G. Madigan
You can also search for this author in PubMed Google Scholar
- B. Marzocchi
You can also search for this author in PubMed Google Scholar
- D. M. Morse
You can also search for this author in PubMed Google Scholar
- V. Nguyen
You can also search for this author in PubMed Google Scholar
- T. Orimoto
You can also search for this author in PubMed Google Scholar
- A. Parker
You can also search for this author in PubMed Google Scholar
- L. Skinnari
You can also search for this author in PubMed Google Scholar
- A. Tishelman-Charny
You can also search for this author in PubMed Google Scholar
- T. Wamorkar
You can also search for this author in PubMed Google Scholar
- B. Wang
You can also search for this author in PubMed Google Scholar
- A. Wisecarver
You can also search for this author in PubMed Google Scholar
- D. Wood
You can also search for this author in PubMed Google Scholar
- S. Bhattacharya
You can also search for this author in PubMed Google Scholar
- J. Bueghly
You can also search for this author in PubMed Google Scholar
- Z. Chen
You can also search for this author in PubMed Google Scholar
- A. Gilbert
You can also search for this author in PubMed Google Scholar
- T. Gunter
You can also search for this author in PubMed Google Scholar
- K. A. Hahn
You can also search for this author in PubMed Google Scholar
- Y. Liu
You can also search for this author in PubMed Google Scholar
- N. Odell
You can also search for this author in PubMed Google Scholar
- M. H. Schmitt
You can also search for this author in PubMed Google Scholar
- M. Velasco
You can also search for this author in PubMed Google Scholar
- R. Band
You can also search for this author in PubMed Google Scholar
- R. Bucci
You can also search for this author in PubMed Google Scholar
- M. Cremonesi
You can also search for this author in PubMed Google Scholar
- A. Das
You can also search for this author in PubMed Google Scholar
- N. Dev
You can also search for this author in PubMed Google Scholar
- R. Goldouzian
You can also search for this author in PubMed Google Scholar
- M. Hildreth
You can also search for this author in PubMed Google Scholar
- K. Hurtado Anampa
You can also search for this author in PubMed Google Scholar
- C. Jessop
You can also search for this author in PubMed Google Scholar
- K. Lannon
You can also search for this author in PubMed Google Scholar
- J. Lawrence
You can also search for this author in PubMed Google Scholar
- N. Loukas
You can also search for this author in PubMed Google Scholar
- D. Lutton
You can also search for this author in PubMed Google Scholar
- J. Mariano
You can also search for this author in PubMed Google Scholar
- N. Marinelli
You can also search for this author in PubMed Google Scholar
- I. Mcalister
You can also search for this author in PubMed Google Scholar
- T. McCauley
You can also search for this author in PubMed Google Scholar
- C. Mcgrady
You can also search for this author in PubMed Google Scholar
- K. Mohrman
You can also search for this author in PubMed Google Scholar
- C. Moore
You can also search for this author in PubMed Google Scholar
- Y. Musienko
You can also search for this author in PubMed Google Scholar
- R. Ruchti
You can also search for this author in PubMed Google Scholar
- A. Townsend
You can also search for this author in PubMed Google Scholar
- M. Wayne
You can also search for this author in PubMed Google Scholar
- M. Zarucki
You can also search for this author in PubMed Google Scholar
- L. Zygala
You can also search for this author in PubMed Google Scholar
- B. Bylsma
You can also search for this author in PubMed Google Scholar
- L. S. Durkin
You can also search for this author in PubMed Google Scholar
- B. Francis
You can also search for this author in PubMed Google Scholar
- C. Hill
You can also search for this author in PubMed Google Scholar
- M. Nunez Ornelas
You can also search for this author in PubMed Google Scholar
- K. Wei
You can also search for this author in PubMed Google Scholar
- B. L. Winer
You can also search for this author in PubMed Google Scholar
- B. R. Yates
You can also search for this author in PubMed Google Scholar
- F. M. Addesa
You can also search for this author in PubMed Google Scholar
- B. Bonham
You can also search for this author in PubMed Google Scholar
- P. Das
You can also search for this author in PubMed Google Scholar
- G. Dezoort
You can also search for this author in PubMed Google Scholar
- P. Elmer
You can also search for this author in PubMed Google Scholar
- A. Frankenthal
You can also search for this author in PubMed Google Scholar
- B. Greenberg
You can also search for this author in PubMed Google Scholar
- N. Haubrich
You can also search for this author in PubMed Google Scholar
- S. Higginbotham
You can also search for this author in PubMed Google Scholar
- A. Kalogeropoulos
You can also search for this author in PubMed Google Scholar
- G. Kopp
You can also search for this author in PubMed Google Scholar
- S. Kwan
You can also search for this author in PubMed Google Scholar
- D. Lange
You can also search for this author in PubMed Google Scholar
- D. Marlow
You can also search for this author in PubMed Google Scholar
- K. Mei
You can also search for this author in PubMed Google Scholar
- I. Ojalvo
You can also search for this author in PubMed Google Scholar
- J. Olsen
You can also search for this author in PubMed Google Scholar
- D. Stickland
You can also search for this author in PubMed Google Scholar
- C. Tully
You can also search for this author in PubMed Google Scholar
- S. Malik
You can also search for this author in PubMed Google Scholar
- S. Norberg
You can also search for this author in PubMed Google Scholar
- A. S. Bakshi
You can also search for this author in PubMed Google Scholar
- V. E. Barnes
You can also search for this author in PubMed Google Scholar
- R. Chawla
You can also search for this author in PubMed Google Scholar
- S. Das
You can also search for this author in PubMed Google Scholar
- L. Gutay
You can also search for this author in PubMed Google Scholar
- M. Jones
You can also search for this author in PubMed Google Scholar
- A. W. Jung
You can also search for this author in PubMed Google Scholar
- D. Kondratyev
You can also search for this author in PubMed Google Scholar
- A. M. Koshy
You can also search for this author in PubMed Google Scholar
- M. Liu
You can also search for this author in PubMed Google Scholar
- G. Negro
You can also search for this author in PubMed Google Scholar
- N. Neumeister
You can also search for this author in PubMed Google Scholar
- G. Paspalaki
You can also search for this author in PubMed Google Scholar
- S. Piperov
You can also search for this author in PubMed Google Scholar
- A. Purohit
You can also search for this author in PubMed Google Scholar
- J. F. Schulte
You can also search for this author in PubMed Google Scholar
- M. Stojanovic
You can also search for this author in PubMed Google Scholar
- J. Thieman
You can also search for this author in PubMed Google Scholar
- F. Wang
You can also search for this author in PubMed Google Scholar
- R. Xiao
You can also search for this author in PubMed Google Scholar
- W. Xie
You can also search for this author in PubMed Google Scholar
- J. Dolen
You can also search for this author in PubMed Google Scholar
- N. Parashar
You can also search for this author in PubMed Google Scholar
- D. Acosta
You can also search for this author in PubMed Google Scholar
- A. Baty
You can also search for this author in PubMed Google Scholar
- T. Carnahan
You can also search for this author in PubMed Google Scholar
- M. Decaro
You can also search for this author in PubMed Google Scholar
- S. Dildick
You can also search for this author in PubMed Google Scholar
- K. M. Ecklund
You can also search for this author in PubMed Google Scholar
- S. Freed
You can also search for this author in PubMed Google Scholar
- P. Gardner
You can also search for this author in PubMed Google Scholar
- F. J. M. Geurts
You can also search for this author in PubMed Google Scholar
- A. Kumar
You can also search for this author in PubMed Google Scholar
- W. Li
You can also search for this author in PubMed Google Scholar
- B. P. Padley
You can also search for this author in PubMed Google Scholar
- R. Redjimi
You can also search for this author in PubMed Google Scholar
- J. Rotter
You can also search for this author in PubMed Google Scholar
- W. Shi
You can also search for this author in PubMed Google Scholar
- A. G. Stahl Leiton
You can also search for this author in PubMed Google Scholar
- S. Yang
You can also search for this author in PubMed Google Scholar
- L. Zhang
You can also search for this author in PubMed Google Scholar
- Y. Zhang
You can also search for this author in PubMed Google Scholar
- A. Bodek
You can also search for this author in PubMed Google Scholar
- P. de Barbaro
You can also search for this author in PubMed Google Scholar
- R. Demina
You can also search for this author in PubMed Google Scholar
- J. L. Dulemba
You can also search for this author in PubMed Google Scholar
- C. Fallon
You can also search for this author in PubMed Google Scholar
- T. Ferbel
You can also search for this author in PubMed Google Scholar
- M. Galanti
You can also search for this author in PubMed Google Scholar
- A. Garcia-Bellido
You can also search for this author in PubMed Google Scholar
- O. Hindrichs
You can also search for this author in PubMed Google Scholar
- A. Khukhunaishvili
You can also search for this author in PubMed Google Scholar
- E. Ranken
You can also search for this author in PubMed Google Scholar
- R. Taus
You can also search for this author in PubMed Google Scholar
- G. P. Van Onsem
You can also search for this author in PubMed Google Scholar
- K. Goulianos
You can also search for this author in PubMed Google Scholar
- B. Chiarito
You can also search for this author in PubMed Google Scholar
- J. P. Chou
You can also search for this author in PubMed Google Scholar
- A. Gandrakota
You can also search for this author in PubMed Google Scholar
- Y. Gershtein
You can also search for this author in PubMed Google Scholar
- E. Halkiadakis
You can also search for this author in PubMed Google Scholar
- A. Hart
You can also search for this author in PubMed Google Scholar
- M. Heindl
You can also search for this author in PubMed Google Scholar
- O. Karacheban
You can also search for this author in PubMed Google Scholar
- I. Laflotte
You can also search for this author in PubMed Google Scholar
- A. Lath
You can also search for this author in PubMed Google Scholar
- R. Montalvo
You can also search for this author in PubMed Google Scholar
- K. Nash
You can also search for this author in PubMed Google Scholar
- M. Osherson
You can also search for this author in PubMed Google Scholar
- S. Salur
You can also search for this author in PubMed Google Scholar
- S. Schnetzer
You can also search for this author in PubMed Google Scholar
- S. Somalwar
You can also search for this author in PubMed Google Scholar
- R. Stone
You can also search for this author in PubMed Google Scholar
- S. A. Thayil
You can also search for this author in PubMed Google Scholar
- S. Thomas
You can also search for this author in PubMed Google Scholar
- H. Wang
You can also search for this author in PubMed Google Scholar
- H. Acharya
You can also search for this author in PubMed Google Scholar
- A. G. Delannoy
You can also search for this author in PubMed Google Scholar
- S. Fiorendi
You can also search for this author in PubMed Google Scholar
- S. Spanier
You can also search for this author in PubMed Google Scholar
- O. Bouhali
You can also search for this author in PubMed Google Scholar
- M. Dalchenko
You can also search for this author in PubMed Google Scholar
- A. Delgado
You can also search for this author in PubMed Google Scholar
- R. Eusebi
You can also search for this author in PubMed Google Scholar
- J. Gilmore
You can also search for this author in PubMed Google Scholar
- T. Huang
You can also search for this author in PubMed Google Scholar
- T. Kamon
You can also search for this author in PubMed Google Scholar
- H. Kim
You can also search for this author in PubMed Google Scholar
- S. Luo
You can also search for this author in PubMed Google Scholar
- S. Malhotra
You can also search for this author in PubMed Google Scholar
- R. Mueller
You can also search for this author in PubMed Google Scholar
- D. Overton
You can also search for this author in PubMed Google Scholar
- D. Rathjens
You can also search for this author in PubMed Google Scholar
- A. Safonov
You can also search for this author in PubMed Google Scholar
- N. Akchurin
You can also search for this author in PubMed Google Scholar
- J. Damgov
You can also search for this author in PubMed Google Scholar
- V. Hegde
You can also search for this author in PubMed Google Scholar
- K. Lamichhane
You can also search for this author in PubMed Google Scholar
- S. W. Lee
You can also search for this author in PubMed Google Scholar
- T. Mengke
You can also search for this author in PubMed Google Scholar
- S. Muthumuni
You can also search for this author in PubMed Google Scholar
- T. Peltola
You can also search for this author in PubMed Google Scholar
- I. Volobouev
You can also search for this author in PubMed Google Scholar
- Z. Wang
You can also search for this author in PubMed Google Scholar
- A. Whitbeck
You can also search for this author in PubMed Google Scholar
- E. Appelt
You can also search for this author in PubMed Google Scholar
- S. Greene
You can also search for this author in PubMed Google Scholar
- A. Gurrola
You can also search for this author in PubMed Google Scholar
- W. Johns
You can also search for this author in PubMed Google Scholar
- A. Melo
You can also search for this author in PubMed Google Scholar
- K. Padeken
You can also search for this author in PubMed Google Scholar
- F. Romeo
You can also search for this author in PubMed Google Scholar
- P. Sheldon
You can also search for this author in PubMed Google Scholar
- S. Tuo
You can also search for this author in PubMed Google Scholar
- J. Velkovska
You can also search for this author in PubMed Google Scholar
- M. W. Arenton
You can also search for this author in PubMed Google Scholar
- B. Cardwell
You can also search for this author in PubMed Google Scholar
- B. Cox
You can also search for this author in PubMed Google Scholar
- G. Cummings
You can also search for this author in PubMed Google Scholar
- J. Hakala
You can also search for this author in PubMed Google Scholar
- R. Hirosky
You can also search for this author in PubMed Google Scholar
- M. Joyce
You can also search for this author in PubMed Google Scholar
- A. Ledovskoy
You can also search for this author in PubMed Google Scholar
- A. Li
You can also search for this author in PubMed Google Scholar
- C. Neu
You can also search for this author in PubMed Google Scholar
- C. E. Perez Lara
You can also search for this author in PubMed Google Scholar
- B. Tannenwald
You can also search for this author in PubMed Google Scholar
- S. White
You can also search for this author in PubMed Google Scholar
- N. Poudyal
You can also search for this author in PubMed Google Scholar
- S. Banerjee
You can also search for this author in PubMed Google Scholar
- K. Black
You can also search for this author in PubMed Google Scholar
- T. Bose
You can also search for this author in PubMed Google Scholar
- S. Dasu
You can also search for this author in PubMed Google Scholar
- I. De Bruyn
You can also search for this author in PubMed Google Scholar
- P. Everaerts
You can also search for this author in PubMed Google Scholar
- C. Galloni
You can also search for this author in PubMed Google Scholar
- H. He
You can also search for this author in PubMed Google Scholar
- M. Herndon
You can also search for this author in PubMed Google Scholar
- A. Herve
You can also search for this author in PubMed Google Scholar
- U. Hussain
You can also search for this author in PubMed Google Scholar
- A. Lanaro
You can also search for this author in PubMed Google Scholar
- A. Loeliger
You can also search for this author in PubMed Google Scholar
- R. Loveless
You can also search for this author in PubMed Google Scholar
- J. Madhusudanan Sreekala
You can also search for this author in PubMed Google Scholar
- A. Mallampalli
You can also search for this author in PubMed Google Scholar
- A. Mohammadi
You can also search for this author in PubMed Google Scholar
- D. Pinna
You can also search for this author in PubMed Google Scholar
- A. Savin
You can also search for this author in PubMed Google Scholar
- V. Shang
You can also search for this author in PubMed Google Scholar
- V. Sharma
You can also search for this author in PubMed Google Scholar
- W. H. Smith
You can also search for this author in PubMed Google Scholar
- D. Teague
You can also search for this author in PubMed Google Scholar
- S. Trembath-Reichert
You can also search for this author in PubMed Google Scholar
- W. Vetens
You can also search for this author in PubMed Google Scholar
Consortia
CMS Collaboration
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Tumasyan, A., Adam, W., Andrejkovic, J.W. et al. Observation of B\(^0\) \(\rightarrow \) \(\uppsi \)(2S)K\(^0_\mathrm {S}\uppi ^+\uppi ^-\) and B\(^0_\mathrm {s}\) \(\rightarrow \) \(\uppsi \)(2S)K\(^0_\mathrm {S}\) decays. Eur. Phys. J. C 82, 499 (2022). https://doi.org/10.1140/epjc/s10052-022-10315-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10315-y
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative


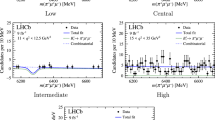





 distribution in data for the
distribution in data for the  signal. The last bin includes the overflow
signal. The last bin includes the overflow