Complexity growth in Gubser–Rocha models with momentum relaxation

Abstract

The Einstein–Maxwell–Axion–Dilaton (EMAD) theories, based on the Gubser–Rocha (GR) model, are very interesting in holographic calculations of strongly correlated systems in condensed matter physics. Due to the presence of spatially dependent massless axionic scalar fields, the momentum is relaxed, and we have no translational invariance at finite charge density. It would be of interest to study some aspects of quantum information theory for such systems in the context of AdS/CFT where EMAD theory is a holographic dual theory. For instance, in this paper we investigate the complexity and its time dependence for charged AdS black holes of EMAD theories in diverse dimensions via the complexity equals action (CA) conjecture. We will show that the growth rate of the holographic complexity violates Lloyd’s bound at finite times. However, as shown at late times, it depends on the strength of the momentum relaxation and saturates the bound for these black holes.

1 Introduction

Strongly correlated systems in condensed matter physics include some interesting phenomena which are not easy to analyze theoretically; however, in the context of holography [1, 2], there are some practical ways to map them to the dual weakly interacting systems [3,4,5,6,7]. For instance, linear T-resistivity in strange metals has a remarkable degree of universality which is not observed in general Fermi liquids with quadratic temperature dependence for resistivity [8,9,10,11], or the divergent conductivity of systems with momentum relaxation due to a broken translational symmetry which occurs in more realistic condensed matter materials [12,13,14,15,16,17]. In this way, the GR models [18] and the Einstein–Maxwell–Axion–Dilaton (EMAD) theories [19, 20], based on the GR model, are among the most interesting theories and provide nice areas for the study of electric and magnetic transport phenomena in a strongly coupled system. The EMAD models can also be a dilatonic generalization of EMA theories proposed in [21].

Apart from this holographic approach for solving strongly coupled field theories in condensed matter physics, the AdS/CFT correspondence [22,23,24,25,26] has been far more deep and revealing than merely providing a classical geometrical computational tool for strongly coupled field theory phenomena. Thinking about how field theory codes various phenomena on the gravity side has led to the recognition of various concepts from quantum information. These include information geometry [27], Von-Neumann [28] and Renyi entropy [29], mutual information [30], tensor networks [31, 32], computational complexity [33], fidelity or relative entropy [34], and quantum error-correcting codes [35], to name only a few. Among them, entanglement entropy has been the most fundamental for study, as it measures the correlation between two subsystems [36,37,38]. However, entanglement entropy may not be enough to probe the degrees of freedom in the interior of the black hole, since the volume of the black hole continues to grow even if the spacetime reach thermal equilibrium [39]. This motivates the introduction of holographic complexity in quantum information theory [33, 40]. As a measure, quantum complexity describes how many simple elementary gates (unitary operators) are needed to obtain a particular state from some chosen reference state [41,42,43]. (For more definitions in quantum field theories see, e.g., [44,45,46,47])

In the context of AdS/CFT correspondence, two holographic prescriptions have been suggested to compute the complexity; the “complexity = volume” (CV) conjecture [33, 40] and the “complexity = action” (CA) conjecture [48, 49]. In the CV conjecture, the complexity of a state is proportional to the volume of the Einstein–Rosen bridge which connects two boundaries of an eternal black hole, i.e., ${\mathcal {C}}_{V}= {\mathcal {V}}/G\,\ell$ where G is the Newton’s constant and $\ell$ is an arbitrary length scale, while in the CA picture it is proportional to the bulk action evaluated in a certain spacetime region known as the Wheeler–De Witt (WDW) patch, i.e., ${\mathcal {C}}_A = I_{WDW}/\pi \hbar$. By construction, the CA proposal is devoid of the ambiguity associated with arbitrary length scale $\ell$ that appears in the CV picture. There are two conceptual features here: (i) A gravity system for which the holographic complexity has been studied extensively is the eternal two-sided AdS black hole [50] which is dual to a thermofield double state in dual boundary field theory,

$$\begin{aligned} |\psi _{TFD}\rangle =\frac{1}{\sqrt{Z}}\sum _j e^{-{E_j}/({2T})} e^{-i E_{j}(t_{L}+t_{R})}|E_j\rangle _L |E_j\rangle _R\,,\end{aligned}$$

(1.1)

where L and R refer to the left and right entangled regions of the two-sided black hole, respectively. The entanglement is due to the Einstein–Rosen bridge that connects the left and right boundary CFTs. (ii) For AdS black holes of mass M in the CA conjecture, the late time behavior of the change rate of complexity reaches a constant value

$$\begin{aligned} \dot{{\mathcal {C}}}_A\le {2M}, \end{aligned}$$

(1.2)

where in the rest of the paper we assume that $\pi \hbar = 1$. This is often referred to as Lloyd’s bound [51], which in the case of charged and rotating black holes is generalized respectively to [49, 52]

$$\begin{aligned}&\dot{{\mathcal {C}}}_A\le 2\big [(M-\mu Q)-(M-\mu Q)_{gs}\big ],\nonumber \\&\dot{{\mathcal {C}}}_A\le 2\big [(M-\Omega J )-(M-\Omega J )_{gs}\big ]. \end{aligned}$$

(1.3)

Here,“gs” denotes the ground state of the black hole. The hope that the holographic complexity might provide useful information about the spacetime structure behind the horizon has led to intense investigation of the CA and CV proposals in various gravity theories, probing their structure and properties [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77].

In the light of the above discussion, it would be of interest to study the complexity for charged AdS black holes in EMAD theories which may be examined in holographic models of quantum information theory and quantum computation. Another motivation is to investigate whether the contribution of different fields in EMAD theory may affect Lloyd’s bound for the corresponding black holes here, or whether in general there is a violation for this bound. In particular, we will compute the holographic complexity and its time evolution for charged single-horizon solutions of four-, five-, and $(d+1)$-dimensional EMAD theories using the CA conjecture. We study both the early and late time limit for the growth rate of complexity. This may not only allow us to further constrain the validity of these holographic conjectures, but also provide other examples in the growing list of literature where Lloyd’s bound can be explicitly violated.

It was shown in [48] that for small Reissner–Nordstrom AdS black holes¹ of mass M and charge q in EM theory, Lloyd’s bound at late time is given by $\dot{{{\mathcal {C}}}}_A = 2 M - \mu q$, while for charged AdS black holes in a simple class of Einstein–Maxwell–Dilaton (EMD) theories, one has $\dot{{{\mathcal {C}}}}_A=2 M -\mu q - C$, where C is a constant term [78]. On the other hand, we showed in [79] that for neutral black branes in EMA theory, the momentum relaxation term does not explicitly change the late time limit $\dot{{\mathcal {C}}}_A=2M$. Actually, this fact is another main motivation for us to investigate in this paper whether the momentum relaxation term would correct Lloyd’s bound in EMAD theories.

The outline of the paper is as follows: In Sect. 2, we review the holographic complexity in the CA picture. We evaluate the action on a WDW patch that has null boundary surfaces in addition to time/space-like boundaries. In this sense, we should consider some extra actions to remove the ambiguities for null surfaces [80]. In Sect. 3, we calculate the complexity growth of charged AdS black holes for EMAD holographic models in diverse dimensions. We also provide a numerical study on $\dot{{\mathcal {C}}}_A$ to find how Lloyd’s bound is violated. In Sect. 4, we summarize our results and present a discussion about computed bounds in different theories.

2 Holographic complexity via CA conjecture

Our main interest in this paper is to investigate the time dependence of holographic complexity; however, there are two distinct methods for calculating the complexity growth rate in the CA picture. The first, by Brown et al. [48, 49], involves the calculation of $\dot{{\mathcal {C}}}_A$ at late times, while in the proposal by Lehner et al. [80], the complexity is evaluated as well as its time evolution. In general, they are not equivalent but give identical very late time results [81]. The main difference between the two methods is that in the former, there is no way to violate Lloyd’s bound, while as we have shown, the bound is violated from above in the latter. Therefore, we use the second approach to study the holographic complexity and its time evolution for charged AdS solutions of EMAD theories. The essential ingredient in the CA conjecture is evaluating the action on a WDW patch [48, 49]. However, we follow the method in Ref. [54], where the action on the WDW patch not only includes the bulk and the Gibbons–Hawking–York (GHY) boundary terms [82, 83], but also embraces boundary segments of joint terms due to the intersection of time-like, space-like, and null boundaries [84]. This will be the general strategy that will be followed in the next section.

The bulk actions for holographic EMAD models are denoted by $I_{{\text {bulk}}}$ and are essentially different in different dimensions. However, the contributions of the GHY surface terms are the same for all of them, as follows

$$\begin{aligned} I_{{\text {surf}}}=\frac{1}{8\pi G}\int _{{\mathcal {B}}} d^{d} x \sqrt{h} K-\frac{1}{8\pi G}\int _{\mathcal {B'}} d\lambda \, d^{d-1}\theta \sqrt{\gamma }\,\kappa , \end{aligned}$$

(2.1)

where K is the extrinsic curvature of the time-like or space-like boundaries (${\mathcal {B}}$), and $\kappa$ is the extrinsic curvature of the null segments (${\mathcal {B}}'$). Here, $h_{\mu \nu }$ and $\gamma _{\mu \nu }$ are the induced metrics on ${\mathcal {B}}$ and ${\mathcal {B}}'$, respectively, so that $K_{\mu \nu }=-h_{\mu }^{\rho } h_{\nu }^{\sigma } \nabla _{(\rho }n_{\sigma )}$ and $\kappa =-N_{\mu } k^{\nu } \nabla _{\nu } k^{\mu }$, where $n_{\mu }$ and $k_{\mu }$ are outward-pointing unit normal vectors on them. $\lambda$ parameterizes the null generator of the null boundary such that for affine parametrization, $\kappa = 0$ [80].

The joint actions are given by

$$\begin{aligned} I_{jnt}=\frac{1}{8\pi G}\int _{\Sigma } d^{d-1}x \sqrt{\sigma }\,\eta + \frac{1}{8\pi G}\int _{\Sigma '} d^{d-1}x \sqrt{\sigma }\,a, \end{aligned}$$

(2.2)

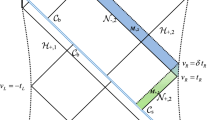
where $\eta$ corresponds to the intersection of time-like or space-like boundaries, while a is related to intersecting of null surfaces. As shown in Fig. 1, the WDW patch has intersections of null surfaces with the time-like or space-like boundaries at $r={\epsilon }$ and $r=r_{\text {max}}$, but since they have no time dependence [60], it is not necessary to consider them here. Thus, only the contribution of null meeting point $r_{m}$ remains for joint action.

There is also a counterterm action for the null surfaces as

$$\begin{aligned} I_{ct}=\frac{1}{8\pi G} \int _{\mathcal {B'}} d\lambda \,d^{d-1}\theta \sqrt{\gamma }\, \Theta \log {(\ell _{c}\Theta )}\,, \end{aligned}$$

(2.3)

which is introduced to ensure reparametrization invariance on the null boundaries and does not change the variational principle. Indeed, the parameter expansion $\Theta$ is the relative rate of change of the cross-sectional area of a bundle of null generators which is denoted by

$$\begin{aligned} \Theta =\partial _{\lambda } \log {\sqrt{\gamma }}, \end{aligned}$$

(2.4)

and $\ell _{c}$ is an arbitrary length scale (for further discussion see, e.g., [80]). Therefore, we should investigate the following total action on the WDW patch

$$\begin{aligned} {I}_{WDW}=I_{{\text {bulk}}}+I_{{\text {surf}}}+I_{jnt}+I_{ct}\,. \end{aligned}$$

(2.5)

In Fig. 1 we have plotted the Penrose diagram of a two-sided AdS black hole with single horizon $r_h$. The gray shaded region is the WDW patch bounded by the light sheets sent from the two asymptotic symmetric time slices $t_L$ and $t_R$ such that $t_L=t_R\equiv t/2$. The WDW patch includes two equivalent sectors where the future and past null boundaries of the right sector are given respectively by

$$\begin{aligned} {t_L}=r_{}^{*} (r)-{r}_{\infty }^{*}\,,\qquad -{t_R}=r_{}^{*} (r)-{r}_{\infty }^{*}\,. \end{aligned}$$

(2.6)

In general, $r^{*}$ is a tortoise coordinate defined as $dr^{*} (r)={d r}/{f ( r)}$ upon which the new coordinates $v=t+r^{*} (r)$ and $u=t-r^{*} (r)$ are defined, and $\lim _{r \rightarrow \infty } r_{}^{*} (r) = {r}_{\infty }^{*}$. Also, $r_m$ is the meeting point of null boundaries before reaching the past singularity at critical time $t_c=2({r}_{\infty }^{*}-r_{}^{*} (0))$.

Fig. 1

Penrose diagram of the WDW patch for AdS black holes. $r_0$ is the physical singularity, and $r={\varepsilon }$ and $r=r_{\text {max}}$ are the IR and UV cut off surfaces, respectively

3 Holographic complexity for EMAD theories

In this section we consider the holographic complexity and its time evolution for three families of holographic EMD theory based on the GR model in the presence of a momentum relaxation term constructed from axionic scalar fields. The general bulk action of EMAD theories in arbitrary dimensions is given by [19]

$$\begin{aligned} I&= {1 \over 16\pi G_{d+1}} {\int _{}^{}} d^{d+1}x \sqrt{-g}\Bigg [ R - \frac{1}{2}(\partial _\mu \phi )^2 + V(\phi )\nonumber \\&\quad - \frac{1}{4} Z(\phi ) F_{\mu \nu }^2 -\frac{1}{2} \sum _{I=1}^{d-1}(\partial _\mu \psi _{I})^2 \Bigg ], \end{aligned}$$

(3.1)

where $G_{d+1}$, $\phi (r)$, and $F_{\mu \nu }\!=\!\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }$ are the ${d+1}$-dimensional Newton’s constant, dilaton field, and field strength of the U(1) gauge field $A_{\mu }$, respectively. Also, $V(\phi )$ is a dilatonic scalar potential, and $Z(\phi )$ is a coupling function between the Maxwell and dilaton fields. The axionic scalar fields enter the bulk action only through the kinetic term $\partial _{\mu }\psi _{I}$, and the sources are linear in the boundary, i.e., $\psi ^{(0)}_{I} \propto \beta _{I i} x^i$ [21], where $\beta$ represents the strength of the momentum relaxation for which

$$\begin{aligned}&\beta ^2\equiv \frac{1}{2}\sum _{i=1}^{d-1} \vec {\beta }_{i}\cdot \vec {\beta }_{i}, \qquad \vec {\beta }_{i}\cdot \vec {\beta }_{j}=\sum _{I=1}^{d-1}{\beta }_{Ii}\, {\beta }_{I j} =\beta ^2 \delta _{i j} \nonumber \\&\qquad \forall \, i, j=1,2,\ldots ,d-1. \end{aligned}$$

(3.2)

The field equations of the action (3.1) are given by

$$\begin{aligned}&R_{\mu \nu }-\frac{V(\phi )}{d-1}g_{\mu \nu }-\frac{1}{2} \partial _{\mu } \phi \,\partial _{\nu } \phi -\frac{1}{2} Z(\phi ) {F_{\mu }}^{\rho }F_{\nu \rho }\nonumber \\&\quad -\frac{1}{4(d-1)} g_{\mu \nu } Z(\phi ) F^2-\frac{1}{2} \sum _{I=1}^{d-1} {\partial _{\mu } \psi _I \,\partial _{\nu } \psi _I}=0,\nonumber \\&\quad \nabla _{\mu }\left( Z(\phi ) F^{\mu \nu }\right) =0,\nonumber \\&\quad \Box \psi _I=0,\qquad I=1,\ldots ,d-1,\nonumber \\&\quad \Box \phi +\frac{d V(\phi )}{d\phi }-\frac{1}{4} \frac{d Z(\phi )}{d\phi } F^2=0. \end{aligned}$$

(3.3)

In general, the analytical charged solutions of these equations are described by the following ansatz as

$$\begin{aligned} ds^2 = e^{2A(r)} \left( -h(r) \, dt^2 + d\vec {x}^2\right) + \frac{e^{2B(r)}}{h(r)} dr^2, \end{aligned}$$

(3.4)

where $d\vec {x}^2$ is the line element of $(d-1)$-dimensional spatial flat space.² In this regard, we evaluate the total action (2.5) on the WDW patch shown in Fig. 1 for each theory. We also determine Lloyd’s bound on the rate of complexity at late times.

Since we are going to analyze the holographic complexity of charged black holes in asymptotically AdS space, it is expected that we should consider the causal structure of the Reissner–Nordstrom AdS black hole given in figure 14 of [60], in which the WDW patch has two intersecting points corresponding to either future or past null boundaries, where at the late time they coincide with the inner and outer horizons, respectively. But, as will be shown for charged black holes in this paper, the inner Cauchy horizon is replaced by a curvature singularity at $r=0$; therefore, the causal structure is described by the one for the AdS-Schwarzschild black hole as depicted in Fig. 1.

3.1 $AdS_4$ black holes

In four dimensions, the EMAD theory is constructed from two parts: an EMD theory obtained from dimensional reduction of $AdS_4\times S^{7}$ in M- theory to triple intersection of M5-branes that have the three-equal-charge black hole [86], and a kinetic term from two massless axionic scalar fields $\psi _{I}$ with $I=1,2$ [19]. This theory is described by the following bulk action

$$\begin{aligned} {I}_{{\text {bulk}}}&= \!{1 \over 16\pi G_4}\int d^4x \sqrt{-g}\Bigg [ R - {1 \over 4} e^{\phi } F_{\mu \nu }^2 - {3 \over 2} (\partial _\mu \phi )^2 \nonumber \\&\quad + {6 \over L^2} \cosh \phi -\tfrac{1}{2} \sum _{I=1}^2 {(\partial _\mu \psi _I)}^2 \Bigg ] \nonumber \\&= {1 \over 16\pi G_4}\int d^4x \sqrt{-g} {\mathcal {L}}_1, \, \end{aligned}$$

(3.5)

where ${\mathcal {L}}_1$ is the Lagrangian density introduced for later convenience. For $\phi (r) = 0$, the model reduces to the action in Ref. [21, 87] for which we have extensively considered its holographic complexity in Ref. [79]. Holographic calculations of this model have been studied in Refs. [88,89,90,91]. Substituting the ansatz (3.4) in the equations of motion, we obtain

$$\begin{aligned} A(r)= & {} -B(r)=\log \frac{r}{L}+\frac{3}{4}\log \left( 1 + \frac{Q}{r}\right) ,\nonumber \\ \phi (r)= & {} \frac{1}{2}\log \left( 1 + \frac{Q}{r}\right) ,\nonumber \\ h(r)= & {} 1- \frac{L^4 \beta ^2}{2 (Q + r)^2} - \frac{(Q + r_h)^3 }{(Q + r)^3}\bigl (1 - \frac{L^4 \beta ^2}{2 (Q + r_h)^2}\bigr ),\nonumber \\ \psi _I= & {} \beta _{I i} x^i,\nonumber \\ A_\mu dx^\mu= & {} A_{t}(r) dt,A_{t}(r)\nonumber \\= & {} \frac{r- r_h}{Q + r}\sqrt{\frac{3Q (Q + r_h)}{L^2} \bigl (1 - \frac{L^4 \beta ^2}{2 (Q + r_h)^2}\bigr )}, \end{aligned}$$

(3.6)

where Q represents a charge parameter, and L is a length scale that henceforth we set as $L=1$. We can recast the solution (3.4) in the form of a general AdS black hole as

$$\begin{aligned} ds^2 =-f(r)\, dt^2 +{U(r)} d\vec {x}^2 + \frac{1}{f(r)} dr^2, \end{aligned}$$

(3.7)

in which

$$\begin{aligned} f(r)&= \frac{r^{1/2} (r- r_h ) \left( 3 Q^2 + r_h^2 + r_h r + r^2 + 3 Q (r_h + r)\right) }{(Q + r)^{3/2}}\nonumber \\&\quad -\frac{ r^{1/2} (r-r_h )\beta ^2 }{2 (Q + r)^{3/2}}, \nonumber \\ U(r)&=r^{1/2} (Q + r)^{3/2}. \end{aligned}$$

(3.8)

This expression of f(r) explicitly shows that the solution has two singularities at $r=r_h$ and $r=0$ where the first corresponds to the event horizon, and the latter is the spacetime singularity. Substituting the functions (3.8) and parameters (3.6) into the Lagrangian (3.5), we have

$$\begin{aligned}&\sqrt{-g} {{\mathcal {L}}}_1 = - \frac{3 \bigl (Q^4 + 4 r^4 + Q^3 (-3 r_h + 10 r) - 3 Q^2 (r_h^2 - 6 r^2) - Q (r_h^3 - 14 r^3)\bigr )}{2 (Q + r)^2} - \frac{3 Q (Q + r_h) \beta ^2}{4 (Q + r)^2}. \end{aligned}$$

(3.9)

As alluded to in the introduction, it is customary to write the late time behavior of $\dot{{\mathcal {C}}}_A$ in terms of the physical parameters of black holes; thus, we should calculate them for each solution. The mass of the black hole is given by

$$\begin{aligned} M={ V_2 \over 16\pi G_4} 2\omega ,\qquad \omega =(Q + r_h)^3\left( 1-\frac{\beta ^2}{2(Q + r_h)^{2}}\right) , \end{aligned}$$

(3.10)

where $\omega$ is a mass parameter, and $V_2$ is the dimensionless volume of two-dimensional spatial geometry $\vec {x}$. In the zero dissipation $\beta \rightarrow 0$, the mass parameter reduces to $\omega =Q^3$ for extremal limit $r_h=0$ in Ref. [18]. Also, in the limit $Q\rightarrow 0$, one achieves the mass of a neutral black hole given by Eq. (2.36) in Ref. [79]. The chemical potential and black hole charge are obtained from $A_t$ in (3.6) as

$$\begin{aligned} \mu= & {} \sqrt{3Q (Q + r_h) \left( 1 - \frac{ \beta ^2}{2 (Q + r_h)^2}\right) },\nonumber \\ q= & {} \frac{V_2}{16\pi G_4}\sqrt{3Q (Q + r_h)^3 \left( 1 - \frac{ \beta ^2}{2 (Q + r_h)^2}\right) }, \end{aligned}$$

(3.11)

where the chemical potential can be read off from the asymptotic value of the electric potential $A_{t}(r\rightarrow \infty )$, and q is computed from Gauss’s law. The temperature and entropy of the black hole are obtained from

$$\begin{aligned} T= & {} \frac{f(r)'}{4\pi }\Big |_{r=r_h}=\frac{r_h^{1/2} \bigl (6 (Q + r_h)^2 - \beta ^2\bigr )}{8 \pi (Q + r_h)^{3/2}},\nonumber \\ S= & {} \frac{A_h}{4G_4}\Big |_{r=r_h}=\frac{V_2}{4 G_4} r_h^{1/2} (Q + r_h)^{3/2}, \end{aligned}$$

(3.12)

where prime is the derivative with respect to r, and $A_h=V_2 U(r_h)$ is the area of the event horizon, such that

$$\begin{aligned} T S=\frac{V_2}{8 \pi G_4} \frac{r_h}{4} \left( 6 (Q + r_h)^2 - \beta ^2\right) . \end{aligned}$$

(3.13)

3.1.1 The growth rate of complexity

We will now proceed to compute the time evolution of the holographic complexity via the CA proposal. Due to the left–right symmetry of the WDW patch for a planar AdS black hole in Fig. 1, we only work on the right side for times $t>t_c$ and then multiply the final result by a factor of 2 for the symmetric left side. The contribution of the bulk action (3.5) is given by

$$\begin{aligned} I_{{\text {bulk}}}&= 2\,\, \left( I_{{\text {bulk}}}^{\,{\!}{1}}+I_{{\text {bulk}}}^{\,{\!}{2}}+I_{{\text {bulk}}}^{\,{\!}{3}}\right) \nonumber \\&=\frac{V_2}{8\pi G_4}\left[ \int _{\epsilon }^{r_h}\left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) +2\int _{r_h}^{r_{\text {max}}}\right. \nonumber \\&\quad \times \left. \left( {r}_{\infty }^{*}-r_{}^{*} (r)\right) +\int _{r_m}^{r_h}\left( -\frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \right] \,\nonumber \\&\quad \times \sqrt{-g}\, {\mathcal {L}}_1\, dr,\nonumber \\&=I_{{\text {bulk}}}^{0}+\frac{V_2}{8\pi G_4} \int _{\epsilon }^{r_m}\left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \, \sqrt{-g}\, {\mathcal {L}}_1\, dr, \end{aligned}$$

(3.14)

where $I_{{\text {bulk}}}^{0}$ is the time-independent part; therefore, we have

$$\begin{aligned} \frac{d I_{{\text {bulk}}}}{dt }&= \frac{V_2}{16\pi G_4 } \Bigg [-3 Q^2 r - \frac{9}{2} Q r^2 - 2 r^3 - \frac{3Q (Q+r_h)^3}{2 (Q + r)}\nonumber \\&\quad + \frac{3 Q (Q+r_h)\beta ^2}{4 (Q + r)}\Bigg ]_{\epsilon }^{r_{m}}. \end{aligned}$$

(3.15)

According to Fig. 1, the boundary action includes two distinguished parts: a time-like surface at the IR cutoff and a space-like surface at the UV cutoff point. The extrinsic curvature for the ansatz (3.7) is as follows

$$\begin{aligned} K=\frac{1}{2}\left( \frac{\partial _r f(r)}{\sqrt{f(r)}}+2 \sqrt{f(r)}\partial _r{\ln \left( U(r)\right) }\right) , \end{aligned}$$

(3.16)

where the normal vectors corresponding to these surfaces are given by

$$\begin{aligned} r&={\epsilon }:\quad \mathbf{t}=t_{\mu }\nonumber \\ dx^{\mu }&=-\frac{dr}{\sqrt{-f(\epsilon )}},\nonumber \\ r&=r_{\text {max}}:\quad \mathbf{s}=s_{\mu }\nonumber \\ dx^{\mu }&=\frac{dr}{\sqrt{f(r_{\text {max}})}}. \end{aligned}$$

(3.17)

Again, by supposing a factor of 2 for the left sector of patch, we have

$$\begin{aligned} I_{{\text {surf}}}&=2\,(I_{{\text {surf}}}^{r=\epsilon }+I_{{\text {surf}}}^{r=r_{\text {max}}})\nonumber \\&=I_{{\text {surf}}}^0+\frac{V_2}{4\pi G_4}\sqrt{h} K\nonumber \\&\quad \times \left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \Big |_{r=\epsilon }. \end{aligned}$$

(3.18)

Here, $I_{{\text {surf}}}^0$ includes the contribution of the UV cutoff surfaces which is independent of time; thus the time evolution of the GHY surface term is

$$\begin{aligned} \frac{d I_{\text {surf}}}{dt}&=\frac{V_2}{8\pi G_4} \Big [-\frac{3 \bigl (Q^3 (3 r_h - 5 r) + 3 Q^2 (r_h^2 + 2 r_h r - 5 r^2) + Q (r_h^3 + 6 r_h^2 r - 13 r^3) + 2 r (r_h^3 - 2 r^3)\bigr )}{4 (Q + r)} \nonumber \\&\quad -\frac{ (8 r^2+5 Q r- 6 r_h r-3 Q r_h )\beta ^2}{8 (Q + r)}\Big ]_{r=\epsilon }. \end{aligned}$$

(3.19)

It has been shown in Ref. [60] that the null joint contributions at the UV cutoff surfaces have no time dependence, so we need only to consider the joint at $r_{m}$. Assume that $k_1$ and $k_2$, the null vectors associated with two past null boundaries intersecting at $r_{m}$, are defined by

$$\begin{aligned} k_1&=\xi \left( -dt+\frac{dr}{f(r)}\right) , \nonumber \\ k_2&=\xi \left( dt+\frac{dr}{f(r)}\right) , \end{aligned}$$

(3.20)

where $\xi$ is a normalization constant for null vectors. Following [80], the joint term $a\!=\!\ln |-\frac{ k_1\cdot k_2}{2}|$ in the action (2.2) can be evaluated as

$$\begin{aligned} I_{jnt}=\frac{V_2}{8\pi G_4} \Bigg [- \log \bigl (\frac{f(r)}{\xi ^2}\bigr ) U(r)\Bigg ]_{r=r_m}. \end{aligned}$$

(3.21)

Due to the implicit time dependence of $r_m$ with equation $\frac{t}{2}-{r}_{\infty }^{*}+r_{}^{*} (r_m)=0$, or

$$\begin{aligned} \frac{dr_m}{dt}=-\frac{f(r_m)}{2}, \end{aligned}$$

(3.22)

and ${dI_{jnt}}/{dt}=-\frac{f(r_{m})}{2} \,{dI_{jnt}}/{dr_m}$, the time evolution of this contribution is

$$\begin{aligned} \frac{dI_{jnt}}{dt}&=\frac{V_2}{16\pi G_4} \Bigg [U(r) \partial _{r} { f(r)} \nonumber \\&\quad + f(r)\partial _{r} { U(r)} \log \left( \frac{f(r)}{\xi ^2}\right) \Bigg ] _{r=r_m}, \end{aligned}$$

(3.23)

and after substituting from (3.8) we obtain

$$\begin{aligned}&\frac{dI_{jnt}}{dt}=\frac{V_2}{32\pi G_4}\Bigg [\frac{Q^3(Q+7r)+Q{r}^2(15Q+13{r})+4{r}^4-(Q-2{r}) (Q+r_h)^3}{(Q + {r})} - \frac{\left( 2 r r_h +Q (3 r - r_h)\right) \beta ^2}{2(Q + r)} \nonumber \\&+\log \bigl (\frac{f({r})}{\xi ^2}\bigr ) (Q + 4 {r}) ({r} - r_h) \left( \frac{3 Q^2 + {r}^2 + {r} r_h + r_h^2 + 3 Q ({r} + r_h)}{ (Q + {r})}-\frac{\beta ^2}{2 (Q + {r})}\right) \Bigg ] _{r=r_m}. \end{aligned}$$

(3.24)

In the late time limit where ${r_m}$ reaches the horizon at $r_h$, we have

$$\begin{aligned} \frac{dI_{jnt}}{dt}{\Bigg |}_{t>>t_c}= \frac{V_2}{8\pi G_4} \Bigg [\frac{3}{2} r_h (Q + r_h)^2 - \frac{1}{4} r_h \beta ^2\Bigg ]= T S,\nonumber \\ \end{aligned}$$

(3.25)

which, as is expected, at the extremal limit becomes zero. The counterterm action (2.3) for parametrization of the past and future null boundaries is

$$\begin{aligned} I_{ct}&=2\,(I_{ct}^{\text {future}}+I_{ct}^{\text {past}})\nonumber \\&=\frac{V_2}{4\pi G_4}\left( \int _{{\epsilon }}^{r_{\text {max}}}+\int _{r_m}^{r_{\text {max}}}\right) \nonumber \\&\quad \times \partial _{r} { U(r)} \log \left( \frac{\ell _{c}\xi \partial _{r} U(r)}{U(r)}\right) dr, \end{aligned}$$

(3.26)

where we have used the affine parameter $\lambda =r/\xi$, where $\xi$ is a constant, so the total action with the counterterm does not depend on the parametrization of the null surfaces [54], and the expansion (2.4) takes the form

$$\begin{aligned} \Theta =\frac{\xi \partial _{r} U(r)}{U(r)}. \end{aligned}$$

(3.27)

Then, from (3.22), the time evolution of the counterterm action becomes

$$\begin{aligned}&\frac{dI_{ct}}{dt} =\frac{V_2}{8\pi G_4}\Bigg [ \frac{ (r- r_h) (Q + 4 r)\bigl (6 Q^2 + 2 r_h^2 - \beta ^2 + 2 r_h r + 2 r^2 + 6 Q (r_h + r)\bigr )}{8 (Q + r)} \log {\frac{l_c \xi (Q + 4 r)}{2 r (Q + r)}}\Bigg ]_{r={r_m}}. \end{aligned}$$

(3.28)

Although the growth rates of the joint and counterterm actions depend on the parametrization constant $\xi$ for null surfaces, it is found that the rate of complexity from the total action (2.5) is independent of it. In other words, the contribution of the joint action for $\xi$ is eliminated by the one for the counterterm action.

3.1.2 Late time behavior

To understand how $\dot{{{\mathcal {C}}}}_A$ violates Lloyd’s bound, we first investigate its late time behavior. Using the quantities in (3.10) and (3.11), we obtain

$$\begin{aligned} \dot{{{\mathcal {C}}}}_A\Big |_{LT}&= \frac{d I_{WDW}}{dt }{\Bigg |}_{t>> t_c}\nonumber \\&= \frac{V_2}{8\pi G_4} \left[ \frac{9}{2} Q r_h^2 + 2 r_h^3 + r_h (3 Q^2 - \beta ^2)\right] \nonumber \\&=2M- \mu q- \frac{V_2}{16\pi G_4} \left[ Q^3-\frac{1}{2} Q \beta ^2\right] . \end{aligned}$$

(3.29)

It is obvious that in the extremal limit ($r_h=0$), the late time behavior vanishes. Also, the result shows that it is not only dilaton theory that contributes to the changes in the late time limit of charged black holes in (1.3), see e.g. Ref. [78], but the presence of momentum dissipation also makes a difference. The ratios $\dot{{{\mathcal {C}}}}_A/\big (\dot{{{\mathcal {C}}}}_A\big )_{LT}$ are plotted for different values of Q and $\beta$ in Fig. 2, where “LT” stands for the late time behavior given in Eq. (3.29). As is obvious, $\dot{{{\mathcal {C}}}}_A$ violates Lloyd’s bound for this kind of black hole from above.

Fig. 2

The growth rate of complexity relative to its late time limit for different values of charge and momentum relaxation

3.2 $AdS_5$ black holes

The extension of the GR model [18] in five dimensions to EMAD theories with momentum relaxation was proposed in Ref. [19]. The EMD part comes from 10D-type IIB string theory with geometry $AdS_5\times S^5$ as the near horizon limit of D3-branes [92]. With a similar trend, the translational invariance is broken by adding a kinetic term of axionic scalar fields $\psi _I$’s. The holographic charge transport and linear resistivity for charged $AdS_5$ black holes in this model were reviewed in Refs. [19, 90]. The bulk action of 5D EMAD theory is

$$\begin{aligned} I_{{\text {bulk}}}&= {1 \over 16\pi G_5}\int d^5x \sqrt{-g} \left[ R - {1 \over 4} e^{4\phi } F_{\mu \nu }^2 - 12 (\partial _\mu \phi )^2\right. \nonumber \\&\quad \left. + {1 \over L^2} (8e^{2\phi } + 4e^{-4\phi }) -\frac{1}{2} \sum _{I=1}^3 {(\partial _\mu \psi _I)}^2 \right] \nonumber \\&={1 \over 16\pi G_5}\int d^5 x \sqrt{-g} {\mathcal {L}}_2, \, \end{aligned}$$

(3.30)

where the field content of this model is analogous to the 4D case discussed in Sect. 3.1. The analytical charged solution in this theory is given by the general ansatz (3.4) but with three-dimensional spatial space $d\mathbf {x}^2$, such that

$$\begin{aligned} A(r)= & {} \log {r \over L} + {1 \over 3} \log \left( 1 + {Q \over r^2} \right) , \nonumber \\ B(r)= & {} -\log {r \over L} - {2 \over 3} \log \left( 1 + {Q \over r^2} \right) , \nonumber \\ \psi _I= & {} \beta \delta _{I i} x^i, \nonumber \\ h(r)= & {} 1- \frac{ \beta ^2}{4 (Q + r^2)} - \frac{(Q + r_h^2)^2 }{(Q + r^2)^2} \bigl (1 - \frac{ \beta ^2}{4 (Q + r_h^2)}\bigr ),\nonumber \\ \phi (r)= & {} {1 \over 6} \log \left( 1 + {Q\over r^2} \right) ,\nonumber \\ A_t(r)= & {} \sqrt{2 Q \bigl (1 - \frac{ \beta ^2}{4 (Q + r_h^2)}\bigr )} (1- \frac{ (Q + r_h^2)}{(Q + r^2)}). \end{aligned}$$

(3.31)

Again, we set $L=1$ without loss of generality. This is an asymptotically AdS black hole which can be rewritten with a warped factor w(r) as

$$\begin{aligned} ds^2 =e^{w(r)} \left( -f(r)\, dt^2 +{U(r)} d\mathbf {x}^2 + \frac{1}{f(r)} \,{d}r^2 \right) , \end{aligned}$$

(3.32)

where

$$\begin{aligned} w(r)= & {} - {1 \over 3} \log \left( 1 + {Q \over r^2} \right) ,\\ f(r)= & {} \frac{(r^2-r_h^2) (2 Q+ r_h^2 + r^2)}{Q + r^2}-\frac{ (r^2-r_h^2 )\beta ^2}{4 (Q + r^2)},\\ {U(r)}= & {} (Q + r^2). \end{aligned}$$

The mass of the black hole is given by

$$\begin{aligned} M={ V_3 \over 16\pi G_5}\, 3\omega ,\qquad \omega = (Q + r_h^2)^2\left( 1-\frac{\beta ^2}{4(Q + r_h^2)}\right) , \end{aligned}$$

(3.33)

where $V_3$ is the volume of the three-dimensional flat space. In the limit $\beta =0$, it gives the mass parameter in Ref. [18], while in the limit $Q=0$, it yields the mass of neutral black branes we obtained in [79] for $d=4$. The chemical potential and charge of the black hole are computed from the gauge potential in (3.31) as

$$\begin{aligned} \mu= & {} \sqrt{2 Q \bigl (1 - \frac{ \beta ^2}{4 (Q + r_h^2)}\bigr )},\nonumber \\ q= & {} { V_3 \over 8\pi G_5} (Q + r_h^2) \sqrt{2 Q \bigl (1 - \frac{ \beta ^2}{4 (Q + r_h^2)}\bigr )}. \end{aligned}$$

(3.34)

On the other hand, the temperature and entropy of the black hole are

$$\begin{aligned} T=\frac{1}{8 \pi } r_h (8 - \frac{ \beta ^2}{Q + r_h^2}),\qquad S=\frac{V_3}{4 G_5} r_h (Q + r_h^2) \end{aligned}$$

(3.35)

so that one has

$$\begin{aligned} T S=\frac{V_3}{8 \pi G_5} \frac{ r_h^2}{4} \bigl (8 (Q + r_h^2) - \beta ^2\bigr ). \end{aligned}$$

(3.36)

3.2.1 The growth rate of complexity

Following the prescription in Sect. 2, we obtain the growth rate of holographic complexity for charged $AdS_5$ black holes of 5D EMAD theory in the CA picture. The WDW patch in this case is also described by Fig. 1, and we need to compute the total action (2.5) on it. In this regard, the contribution of the bulk action on three different regions $\,{\!}{1}$, $\,{\!}{2}$, and $\,{\!}{3}$ for times $t>t_c$ is given by

$$\begin{aligned} I_{{\text {bulk}}}= & {} 2\,\, \left( I_{{\text {bulk}}}^{\,{\!}{1}}+I_{{\text {bulk}}}^{\,{\!}{2}}+I_{{\text {bulk}}}^{\,{\!}{3}}\right) \nonumber \\= & {} \frac{V_3}{8\pi G_5}\left[ \int _{\epsilon }^{r_h}\left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \right. \nonumber \\&\left. +2\int _{r_h}^{r_{\text {max}}}\left( {r}_{\infty }^{*}-r_{}^{*} (r)\right) \right. \nonumber \\&\left. +\int _{r_m}^{r_h}\left( -\frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \right] \, \sqrt{-g}\, {\mathcal {L}}_2\, dr,\nonumber \\= & {} I_{{\text {bulk}}}^{0}+\frac{V_3}{8\pi G_5} \int _{\epsilon }^{r_m}\left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \, \sqrt{-g}\, {\mathcal {L}}_2\, dr,\nonumber \\ \end{aligned}$$

(3.37)

where $I_{{\text {bulk}}}^{0}$ is the independence of the time and ${\mathcal {L}}_2$ is the Lagrangian density of (3.30), so that based on (3.31) gives us

$$\begin{aligned} \sqrt{-g}{{\mathcal {L}}}_{2}&= - \frac{8 r \bigl (Q^3 + Q^2 (7 r^2-2 r_h^2 ) + Q (8 r^4-r_h^4 )+ 3 r^6 \bigr )}{3 (Q + r^2)^{2}}\nonumber \\&\quad - \frac{2 r Q (Q + r_h^2) \beta ^2}{3(Q + r^2)^{2}}. \end{aligned}$$

(3.38)

Thus, the time derivative of (3.37) yields

$$\begin{aligned} \frac{d I_{{\text {bulk}}}}{dt }&= \frac{V_3}{8\pi G_5} \left[ - \tfrac{4}{3} Q r^2 - r^4 - \frac{2 Q (Q + r_h^2)^2}{3 (Q + r^2)} \right. \nonumber \\&\quad \left. + \frac{Q (Q + r_h^2) \beta ^2}{6 (Q + r^2)}\right] _{\epsilon }^{r_{m}}. \end{aligned}$$

(3.39)

Note that the time evolution of this result comes from the differential equation of $r_m$ for the past null junction given in (3.22).

In order to find the extrinsic curvature for geometry (3.32), we define the normal vector $n_{\mu }=(0,n_r,0,0,0)$, where $n_r=\sqrt{\frac{f(r)}{W(r)}}$, and for simplicity we choose $W(r)=e^{w(r)}$. Thus, from the definition in Sect. 2, we can achieve the following expression

$$\begin{aligned} K= \frac{4 f(r) \,U(r)\, W(r)' + W(r) \bigl (3 f(r)\, U(r)' + f(r)' \,U(r)\bigr )}{2 f(r)^{1/2}\,U(r)\,W(r)^{3/2}}, \end{aligned}$$

(3.40)

where the prime is the derivative with respect to r. For times $t > t_c$, the boundary action (2.1) becomes

$$\begin{aligned} I_{{\text {surf}}}=I_{{\text {surf}}}^0+\frac{V_3}{4\pi G_5}\sqrt{h} K\,\left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \Big |_{r=\epsilon }. \end{aligned}$$

(3.41)

Therefore, its time derivative gives

$$\begin{aligned} \frac{d I_{\text {surf}}}{dt}= \frac{V_3}{8\pi G_5 } \sqrt{h} { K {\Bigg |}_{r=\epsilon }}, \end{aligned}$$

(3.42)

in which

$$\begin{aligned}&\sqrt{h}K\nonumber \\&\quad =- \frac{2 \bigl (Q^2 (7 r^2-4 r_h^2 ) + 2 Q (7 r^4-r_h^4 - 3 r_h^2 r^2) + 3 r^2 (2 r^4-r_h^4)\bigr )}{3 (Q + r^2)}\nonumber \\&\qquad -\frac{ \bigl (6 r_h^2 r^2 - 9 r^4 + Q (4 r_h^2 - 7 r^2)\bigr ) \beta ^2}{12 (Q + r^2)}. \end{aligned}$$

(3.43)

For the null joint contribution of intersecting the two past null boundaries at $r = r_m$ with outward-directed null vectors defined in (3.20), we have

$$\begin{aligned} I_{jnt}=-\frac{V_3}{8\pi G_5 } \,\left[ U(r)^{3/2} \,W(r)^{3/2} \log \Bigl (\frac{\bigl |W(r) f(r)\bigr |}{\xi ^2}\Bigr )\right] _{r=r_m}, \end{aligned}$$

(3.44)

where the implicit time dependence of this term is through the Eq. (3.22). For the background functions in (3.32), the joint term can then be evaluated as

$$\begin{aligned} \frac{dI_{jnt}}{dt}&= \frac{V_3}{ 8\pi G_5 } \Bigg [\frac{ (Q + 3 r^2) (r^2 - r_h ^2) (2 Q + r^2 + r_h^2)}{3 r^{1/3} (Q + r^2)^{4/3}}\nonumber \\&\quad \times \log \Bigl (\frac{\bigl |W(r) f(r)\bigr |}{\xi ^2}\Bigr ) \nonumber \\&\quad +\frac{8 Q^2 r^2 + 7 Q r^4 + 3 r^6 - (Q - 3 r^2)(2 Q+r_h^2) r_h^2}{3 r^{1/3} (Q + r^2)^{4/3}}\nonumber \\&\quad -\left( \frac{(Q + 3 r^2) (r^2 - r_h ^2)}{12 r^{1/3} (Q + r^2)^{4/3}} \times \log \Bigl (\frac{\bigl |W(r) f(r)\bigr |}{\xi ^2}\Bigr )\right. \nonumber \\&\quad \left. + \frac{Q(r^2 - r_h ^2)+3 r^2(Q +r_h^2)}{12 r^{1/3} (Q + r^2)^{4/3}}\right) \beta ^2 \Bigg ]_{r=r_m}, \end{aligned}$$

(3.45)

in which

$$\begin{aligned}&\log \left( \frac{\bigl |W(r) f(r)\bigr |}{\xi ^2}\right) \nonumber \\&\quad =\log \left( \frac{r^{2/3} (r^2- r_h^2 ) (2 Q + r^2 + r_h^2 - {\beta ^2} /4)}{\xi ^2 (Q + r^2)^{4/3}}\right) . \end{aligned}$$

(3.46)

In the late time limit, one can find that the growth rate of the joint action is proportional to the product of the temperature and entropy

$$\begin{aligned} \frac{dI_{jnt}}{dt}{\Bigg |}_{t>>t_c} = \frac{V_3}{ 8\pi G_5 } \Bigg [2 r_h^2 (Q^2 + r_h^2) - \tfrac{1}{4} r_h^2 \beta ^2\Bigg ]= T\,S, \end{aligned}$$

(3.47)

which at the extremal limit vanishes.

The boundary counterterm (2.3) requires an evaluation of the expansion scalar (2.4) in the null boundaries of the WDW patch; thus, with the parametrization $\lambda =r/\xi$, we obtain

$$\begin{aligned} \Theta = \frac{3 \xi }{2} \left( \frac{U(r)'}{U(r)} + \frac{W(r)'}{W(r)}\right) . \end{aligned}$$

(3.48)

Similar to the action (3.26), the evaluation for $\epsilon$ vanishes and the UV regulator surface at $r_{\text {max}}$ only contributes a fixed constant; therefore, the time dependence comes only from the term evaluated at the meeting point $r_m$. Now, by virtue of dynamical Eq. (3.22), we can determine time evolution of the counterterm action as

$$\begin{aligned} \frac{dI_{ct}}{dt}&=\frac{V_3}{16\pi G_5} \Bigg [\frac{( r^2- r_h^2 ) (Q + 3 r^2) (2 Q + r_h^2 + r^2-\beta ^2 /4 )}{(Q + r^2)}\nonumber \\&\quad \times \log \left( \frac{l_c \xi (Q + 3r^2)}{ r(Q + r^2)}\right) \Bigg ]_{r=r_m}. \end{aligned}$$

(3.49)

3.2.2 Late time behavior

The rate of the complexity at very late times for the total action (2.5) is given by

$$\begin{aligned} \frac{d I_{WDW}}{dt }{\Bigg |}_{t>>t_c}= \frac{V_3}{8\pi G_5 } \Bigg [4 Q r_h^2 + 3 r_h^4 - \tfrac{3}{4} r_h^2 \beta ^2\Bigg ], \end{aligned}$$

(3.50)

where by using the quantities in Eqs. (3.33) and (3.34) we can rewrite it as

$$\begin{aligned} \dot{{{\mathcal {C}}}}_A\Big |_{LT}=\frac{d I_{WDW}}{dt }{\Bigg |}_{t>>t_c}=2M - \mu q- \frac{V_3}{16\pi G_5 }\left[ 2Q^2-\frac{1}{2} Q \beta ^2\right] . \end{aligned}$$

(3.51)

As is obvious, the momentum relaxation and dilatonic field terms have explicit contributions in Lloyd’s bound due to the charge parameter Q. The ratios $\dot{{{\mathcal {C}}}}_A/\big (\dot{{{\mathcal {C}}}}_A\big )_{LT}$ are plotted for different values of Q and $\beta$ in Fig. 3. As seen in the figure, $\dot{{{\mathcal {C}}}}_A$ violates Lloyd’s bound for this kind of black hole from above.

Fig. 3

The growth rate of complexity relative to its late time limit for different values of the charge and momentum relaxation

3.3 Warped $AdS_{d+1}$ black holes

Since the 4D and 5D EMAD theories used for studies have analytical solutions, it would be of interest to investigate a generalized theory in arbitrary dimensions. This model was proposed in Ref. [19], and still allows analytical charged solutions. The holographic characteristics of strange metals for this model were studied in Refs. [19, 90].

Let us consider a general $(d+1)$-dimensional EMAD theory given by the action (3.1) with the following Lagrangian density

$$\begin{aligned} {\mathcal {L}}_3 = R - \frac{1}{2}(\partial _\mu \phi )^2 + V(\phi ) - \frac{1}{4} Z(\phi ) F_{\mu \nu }^2 -\frac{1}{2} \sum _{i=1}^{d-1}{(\partial _\mu \psi _I)}^2, \end{aligned}$$

(3.52)

where the functions $Z(\phi )$ and $V(\phi )$ are assumed to have the following specific forms [19]

$$\begin{aligned} Z(\phi )&=e^{-(d-2) \delta \phi },\nonumber \\ V(\phi )&=V_1 e^{\frac{ (d-2 ) (d-1) \delta ^2-2 }{2 (d-1) \delta }\phi } + V_2 e^{-\frac{2 }{(d-1) \delta }\phi }\nonumber \\&\quad + V_3 e^{(d-2) \delta \phi }. \end{aligned}$$

(3.53)

Here, $V_1$, $V_2$, and $V_3$ are three constant parameters given by

$$\begin{aligned} V_1= & {} \frac{8 (d-2 ) (d-1)^3 \delta ^2}{\bigl ( (d-1) (d-2)\delta ^2+2\bigr )^2},\nonumber \\ V_2= & {} \frac{(d-2)^2 (d-1)^2 \bigl ( d(d-1) \delta ^2-2\bigr ) \delta ^2}{\bigl ( (d-1)(d-2) \delta ^2+2\bigr )^2},\nonumber \\ V_3= & {} \frac{4d (d-1) - 2 (d-1)^2(d-2)^2 \delta ^2}{\bigl ( (d-1)(d-2) \delta ^2+2\bigr )^2}, \end{aligned}$$

(3.54)

where $\delta$ is a free parameter. It should be noted that for $d=3$, by choosing $\delta =\sqrt{\frac{1}{3}}$ and redefinition of $\phi \rightarrow -\sqrt{3}\phi$, the bulk action (3.52) is reduced to 4D EMAD theory given in (3.5), while for $d=4$, $\delta =\sqrt{\frac{1}{6}}$, and redefinition of $\phi \rightarrow -\sqrt{24}\phi$, it yields the 5D theory described by (3.30).

Equations (3.3) admit an analytical charged black hole solution defined by the ansatz (3.4) with the following quantities

$$\begin{aligned} A&=\frac{1}{2} \log \nonumber \\&\quad \Bigl (r^{2 - \frac{4}{ (d-1)(d-2) \delta ^2+2}} (Q + r^{d-2})^{\frac{4}{(d-2) \left( (d-1)(d-2) \delta ^2+2\right) }}\Bigr ),\nonumber \\ \psi _I&=\beta \delta _{I i} x^i,\nonumber \\ B&=\frac{1}{2} \log \bigl (r^{\frac{4 (d-2)}{ (d-1)(d-2) \delta ^2+2}-2} (Q + r^{d-2})^{-\frac{4}{ (d-1)(d-2) \delta ^2+2}}\bigr ),\nonumber \\ \phi (r)&=- \frac{2 ( d-1) \delta }{ (d-1)(d-2) \delta ^2+2} \log \left( 1 + \frac{Q }{r^{d-2}}\right) , \nonumber \\ h(r)&= \left( 1 - \frac{\beta ^2}{2 ( d-2) (Q + r^{ d-2})^{\frac{2}{ d-2}}}\right) - \frac{ (Q + r_h^{ d-2})^{\frac{d}{ d-2}} }{ (Q + r^{ d-2})^{\frac{d}{ d-2}}} \nonumber \\&\quad \times \left( 1 - \frac{\beta ^2}{2 ( d-2) (Q + r_h^{ d-2})^{\frac{2}{ d-2}}}\right) ,\nonumber \\ A_t(r)&=\sqrt{\frac{d Q}{d-2}} (Q + r_h^{ d-2})^{-\frac{ d-4}{2 ( d-2)}}\nonumber \\&\quad \times \sqrt{1 - \frac{ \beta ^2}{2 ( d-2) (Q + r_h^{ d-2})^{\frac{2}{ d-2}}}} \nonumber \\&\quad \times (1 - \frac{Q + r_h^{d-2}}{Q + r^{ d-2}}). \end{aligned}$$

(3.55)

Here, $r_h$ is the location of the event horizon, and we have set $L=1$. In analogy to the previous sections, we can recast this geometry as an asymptotically $AdS_{d+1}$ black hole

$$\begin{aligned} ds^2 =e^{w(r)} \left( -f(r)\, dt^2 +{U(r)}\, d \Sigma _{d-1}^2 + \frac{1}{f(r)} \,\, \mathrm {d}r^2\right) , \end{aligned}$$

(3.56)

where $W(r)=e^{w(r)}$, and the corresponding functions are obtained as

$$\begin{aligned} f(r)&=g(r)^{-\frac{2 (d-1)}{( d-2) \bigl ( (d-1)(d-2) \delta ^2+2\bigr )}} {\mathcal {F}}(r),\nonumber \\ U(r)&=g(r)^{\frac{d-1}{2( d-2) \bigl ( (d-1)(d-2) \delta ^2+2\bigr )}},\nonumber \\ W(r)&=g(r)^{-\frac{2 (d-3)}{( d-2) \bigl ( (d-1)(d-2) \delta ^2+2\bigr )}},\quad g(r)=1 + \frac{Q }{r^{d-2}}, \nonumber \\ {\mathcal {F}}(r)&= r^2 \Bigg (- \frac{r_h^d}{r^d} g(r_h)^{\frac{4 ( d-1)}{( d-2) \bigl ( (d-1)(d-2) \delta ^2+2\bigr )}}\nonumber \\&\quad + g(r)^{\frac{4 ( d-1)}{( d-2) \bigl ( (d-1)(d-2) \delta ^2+2\bigr )}}\Bigg )\nonumber \\&\quad - \frac{\beta ^2}{2 (d-2)} (1 -\frac{ r_h^{d-2}}{r^{d-2}}) . \end{aligned}$$

(3.57)

In this paper, we will consider the case with $\delta =\sqrt{\frac{2}{d(d-1)}}$, which corresponds to the GR model in higher dimensions, and the IR geometry is conformal to $AdS_2 \times R^{d-1}$ [19]. It is observed that $\delta =0$ corresponds to a Reissner–Nordstrom AdS black hole, but in general one can consider an arbitrary value of $\delta \in \left[ 0,\sqrt{\frac{2}{d(d-1)}}\right]$. Further discussion for $\delta =\frac{1}{\sqrt{3}}$ can be found in Ref. [90]. For this reason, the mass of the black hole is given by

$$\begin{aligned} M= & {} {V_{d-1} \over 16\pi G_{d+1}} (d-1) \, \omega ,\nonumber \\ \omega= & {} (Q + r_h^{d-2})^{ \frac{d}{d-2}} \left( 1-\frac{ \beta ^2}{2(d-2) (Q + r_h^{d-2})^{ \frac{2}{d-2}}}\right) ,\nonumber \\ \end{aligned}$$

(3.58)

where $V_{d-1}$ is the volume of a ($d-1$)-dimensional flat space with the line element $d \Sigma _{d-1}^2$. The chemical potential and charge of the black hole can be found from $A_{t}(r)$ in (3.55) as

$$\begin{aligned} q&= {V_{d-1} \over 16\pi G_{d+1}} \nonumber \\&\quad \times \sqrt{d (d-2) Q (Q + r_h^{ d-2})^{\frac{ d}{( d-2)}} \left( 1 - \frac{ \beta ^2}{2 ( d-2) (Q + r_h^{ d-2})^{\frac{2}{ d-2}}}\right) }\,,\nonumber \\ \mu&= \sqrt{\frac{d Q}{d-2}\,(Q + r_h^{ d-2})^{-\frac{ d-4}{( d-2)}}\left( 1 - \frac{ \beta ^2}{2 ( d-2) (Q + r_h^{ d-2})^{\frac{2}{ d-2}}}\right) }\,. \end{aligned}$$

(3.59)

The temperature and entropy of the black hole at the event horizon are given by

$$\begin{aligned} T= & {} \frac{r_h^{ d/2 -1}}{4 \pi }\biggl ( d (Q + r_h^{ d-2})^{-\frac{d-4}{2( d-2)}} - \frac{1}{2} (Q + r_h^{ d-2})^{-\frac{d}{2 (d-2)}} \beta ^2 \biggr ),\nonumber \\ S= & {} \frac{V_{d-1}}{4 G_{d+1} } r_h^{ d/2 -1} (Q + r_h^{ d-2})^{\frac{d}{2 ( d-2)}}, \end{aligned}$$

(3.60)

such that

$$\begin{aligned} T S =\frac{V_{d-1}}{16\pi G_{d+1} } \bigg [ d r_h^{ d-2} (Q + r_h^{d-2})^{\frac{2}{ d-2}} - \tfrac{1}{2} r_h^{ d-2} \beta ^2\bigg ]. \end{aligned}$$

(3.61)

3.3.1 The growth rate of complexity

The time evolution of holographic complexity for AdS black holes of generalized EMAD theory on the WDW patch shown in Fig. 1 is determined by the rate of action (2.5) via the CA proposal. Therefore, for the bulk action (3.1) on the right sector of the WDW patch denoted by regions $\,{\!}{1}$, $\,{\!}{2}$, and $\,{\!}{3}$, we have

$$\begin{aligned} I_{{\text {bulk}}}(t>t_c)= & {} 2 \left( I_{{\text {bulk}}}^{\,{\!}{1}}+I_{{\text {bulk}}}^{\,{\!}{2}}+I_{{\text {bulk}}}^{\,{\!}{3}}\right) \nonumber \\= & {} I_{{\text {bulk}}}^{0}+\frac{V_{d-1}}{8\pi G_{d+1}} \int _{\epsilon }^{r_m}\left( \frac{t}{2}+{r}_{\infty }^{*}-r_{}^{*} (r)\right) \,\nonumber \\&\times \sqrt{-g}\, {\mathcal {L}}_3\, dr, \end{aligned}$$

(3.62)

where, similar to the previous subsections, $I_{{\text {bulk}}}^{0}$ is independent of the time, and ${\mathcal {L}}_3$ is the Lagrangian density in Eq. (3.52) evaluated on the background (3.55). Thus, the growth rate of the bulk contribution becomes

$$\begin{aligned} \frac{d I_{\text {bulk}}}{dt }&= \frac{V_{d-1}}{8\pi G_{d+1} }\nonumber \\&\quad \times \left[ -\frac{\bigl (\frac{( d-2) Q}{2 ( d-1)} + r^{ d-2}\bigr ) }{(Q + r^{ d-2})^{-\frac{2}{ d-2}}}\right. + \frac{d Q (Q + r_h^{ d-2})^{\frac{d}{ d-2}}}{2(d-1) (Q + r^{ d-2})} \nonumber \\&\quad \left. + \frac{d Q (Q + r_h^{ d-2}) \beta ^2}{4 ( d-1) (d-2) (Q + r^{ d-2})}\right] _{\epsilon }^{r_{m}}. \end{aligned}$$

(3.63)

The extrinsic curvature for the boundary GHY surface term calculated for the normal vector with $n_r=\sqrt{\frac{f(r)}{W(r)}}$ is obtained from (3.56) as

$$\begin{aligned} \sqrt{h}K&=\frac{1}{2}\,U(r)^{\frac{( d-1)}{2} }W(r)^{\frac{( d-1)}{2}} f(r)' \nonumber \\&\quad + \frac{1}{2}\,f(r)\, U(r)^{\frac{( d-1)}{2}}\nonumber \\&\quad \times W(r)^{\frac{(d-3)}{2}} \left( ( d-1) W(r) U(r)' + d\, U(r) W(r)'\right) ,\nonumber \\ \end{aligned}$$

(3.64)

which from (3.55) yields

$$\begin{aligned} \sqrt{h}K= & {} -\,d (Q + r^{ d-2})^{\frac{d}{ d-2}} + \frac{d^2 Q}{2 ( d-1) (Q + r^{ d-2})^{-\frac{2}{ d-2}}} \nonumber \\&+ \frac{d \bigl (\frac{( d-2) Q}{ d-1} + r^{ d-2}\bigr ) (Q + r_h^{ d-2})^{\frac{d}{ d-2}}}{2 (Q + r^{ d-2})}\nonumber \\&+\frac{Q \bigl ((2d-1) r^{ d-2} - d r_h^{ d-2}\bigr ) \beta ^2}{4 ( d-1) (Q + r^{ d-2})} \nonumber \\&+ \frac{r^{ d-2} \bigl (2 ( d-1) r^{ d-2} - d r_h^{ d-2}\bigr ) \beta ^2}{4 ( d-2) (Q + r^{ d-2})}. \end{aligned}$$

(3.65)

As noted in Eq. (3.18), the boundary contribution coming from the time-like surface at the UV cutoff regulator $r=r_{\text {max}}$ yields a fixed constant, i.e., they do not contribute to the time derivative of the action, and with affinely parametrized null normals ($\kappa =0$), the null surface term vanishes. Thus, we only need to consider the boundary surface at the future singularity which is given by

$$\begin{aligned} \frac{dI_{\text {surf}}}{dt}= \frac{V_{d-1}}{ 8\pi G_{d+1}} \sqrt{h} K {\Bigg |}_{r=\epsilon }. \end{aligned}$$

(3.66)

The final result for the joint action at the meeting point $r = r_m$, shown in Fig. 1, is given by

$$\begin{aligned} I_{jnt}= -\frac{V_{d-1}}{ 8\pi G_{d+1}} \left[ U(r)^{\frac{d-1}{2}} W(r)^{\frac{d-1}{2}}\log \bigl (\frac{f(r) W(r)}{\xi ^2}\bigr ) \right] _{r=r_m}, \end{aligned}$$

(3.67)

where $\xi$ is the normalization constant appearing in the null normals (3.20), i.e., $k\cdot \partial _t \big |_{r\rightarrow \infty }=\pm \xi$. According to the time dependence of $r_m$ through Eq. (3.22), the evolution of this action has the following form

$$\begin{aligned} \frac{dI_{jnt}}{dt}&=\frac{V_{d-1}}{ 8\pi G_{d+1} } \Bigg [\frac{ (Q+r^ {d-2} )^{\frac{2}{d-2}} \bigl ((d-2) Q + 2 (d-1) r^{d-2}\bigr ) \bigl (2 + (d-1) \log (\frac{{\mathcal {F}}(r)}{\xi ^2}) \bigr )}{4 (d-1) } \nonumber \\&\quad -\frac{(d-2) \bigl (Q - (d-1) r^{d-2}\bigr ) (Q+r_h^{d-2})^{\frac{d}{d-2}}}{2 (d-1 ) (Q+r^{d-2})}\nonumber \\&\quad +\frac{\bigl ((1 + \frac{Q }{r^{d-2}}) - d (1 + \frac{Q }{r_h^{d-2}}) \bigr ) (r\,r_h)^{d-2} \beta ^2}{4 (d-1) (Q+r^{d-2})} \nonumber \\&\quad - \frac{\bigl ((d-2) Q + 2 (d-1) r^{d-2}\bigr ) (Q+r_h^{d-2})^{\frac{d}{d-2}}\log (\frac{{\mathcal {F}}(r)}{\xi ^2})}{4(Q+r^{d-2}) }\nonumber \\&\quad - \frac{\bigl ((d-2 ) Q + 2 (d-1) r^{d-2}\bigr ) ( r^{d-2} - r_h^{d-2}) \beta ^2 \log (\frac{{\mathcal {F}}(r)}{\xi ^2})}{8 (d-2) (Q+r^{d-2})}\Bigg ]_{r=r_m}, \end{aligned}$$

(3.68)

in which

$$\begin{aligned}&{\mathcal {F}}(r) \nonumber \\&\quad =r^{\frac{d-2}{d-1}} (Q+ r^{d-2})^{-\frac{d}{d-1}}\left( ( Q+ r^{d-2})^{\frac{d}{d-2}} \right. \nonumber \\&\qquad \left. - (Q{+} r_h^{d-2})^{\frac{d}{d-2}}{-} \frac{ \beta ^2}{2(d-2)} \Bigl (r^{d-2}{-}r_h^{d-2}\Bigr )\right) . \end{aligned}$$

(3.69)

As shown before, in the late time limit, $r_m$ coincides with the event horizon $r_h$; then from Eq. (3.61), the joint term (3.68) leads to

$$\begin{aligned} \frac{dI_{jnt}}{dt}{\Bigg |}_{t>>t_c}&=\frac{V_{d-1}}{16\pi G_{d+1}} \bigg [ d r_h^{ d-2} (Q + r_h^{d-2})^{\frac{2}{ d-2}} - \frac{1}{2} r_h^{ d-2} \beta ^2\bigg ]\nonumber \\&=TS. \end{aligned}$$

(3.70)

By fixing the parametrization of null generators as $\lambda =r/\xi$, the boundary counterterm action for the null boundaries is defined by the following expansion parameter

$$\begin{aligned} \Theta= & {} \frac{(d-1) \xi }{2} \left( \frac{U(r)'}{U(r)} + \frac{W(r)'}{W(r)}\right) \nonumber \\= & {} \frac{( d-2) Q + 2 (d-1) r^{d-2}}{2 r (Q + r^{ d-2})} \xi , \end{aligned}$$

(3.71)

such that the time evolution of the counterterm action becomes

$$\begin{aligned} \frac{dI_{ct}}{dt}= & {} \frac{V_{d-1}}{16\pi G_{d+1}}\Bigg [\frac{( d-2) Q + 2 (d-1) r^{d-2}}{(Q + r^{ d-2})}\nonumber \\&\times \biggl ( \frac{ \bigl ( (Q + r^{ d-2})^{\frac{d}{ d-2}}- (Q + r_h^{ d-2})^{\frac{d}{ d-2}}\bigr )}{2}\nonumber \\&\times \frac{( r^{ d-2}- r_h^{ d-2} )}{4 ( d-2)} \beta ^2 \biggr ) \nonumber \\&\times \log \biggl ( \frac{( d-2) Q + 2 (d-1) r^{d-2}}{2 r (Q + r^{ d-2})} l_c \xi \biggr ) \Bigg ]_{r=r_m}.\nonumber \\ \end{aligned}$$

(3.72)

3.3.2 Late time behavior

Now we are ready to calculate the rate of holographic complexity at large times for the total action $I_{WDW}$ by summing over the above results according to Eq. (2.5) as

$$\begin{aligned} \dot{{{\mathcal {C}}}}_A\Big |_{LT}= & {} \frac{d I_{WDW}}{dt }{\Bigg |}_{t>>t_c}\nonumber \\= & {} \frac{V_{d-1}}{ 16\pi G_{d+1} } \Bigg [-(d-2 ) Q^{\frac{d}{d-2}} + (Q + r_h^{ d-2})^{\frac{2}{ d-2}} \nonumber \\&\times \left( ( d-2) Q {+} 2 ( d{-}1) r_h^{ d{-}2}\right) {-} \frac{( d-1) r_h^{ d-2} \beta ^2}{( d-2)}\Bigg ].\nonumber \\ \end{aligned}$$

(3.73)

Substituting from (3.58) and (3.59) in Eq. (3.73) we obtain

$$\begin{aligned} \dot{{{\mathcal {C}}}}_A\Big |_{LT}=2 M - \mu q - \frac{V_{d-1}}{ 16\pi G_{d+1} } \Bigg [ ( d-2) Q^{\frac{d}{ d-2}} - \frac{1}{2} Q \beta ^2\Bigg ]. \end{aligned}$$

(3.74)

In the absence of a momentum relaxation term, this result reduces to the following Lloyd’s bound for the $(d+1)$-dimensional charged AdS black holes in the generalized GR model

$$\begin{aligned} \dot{{{\mathcal {C}}}}_A\Big |_{LT}=2M_0-\mu _0 q_0-D,\qquad D=\frac{V_{d-1}}{ 16\pi G_{d+1} }( d-2) Q^{\frac{d}{d-2}}, \end{aligned}$$

(3.75)

where the quantities $M_0$, $\mu _0$, and $q_0$ are given by the relations (3.58) and (3.59) when $\beta =0$. It should be also noted that both Eqs. (3.74) and (3.75) vanish in the extremal limit $r_h=0$.

Table 1 Late time limit of $\dot{{{\mathcal {C}}}}_A$ for single-horizon black holes (BHs) in different theories

4 Conclusions and outlook

One of the main implications in the context of AdS/CFT duality, which relates the physics of the black holes in the gravity side to the information theory in dual field theory, is the notion of quantum complexity. In other words, holographic methods are powerful tools to study the properties of strongly correlated systems by mapping them to the dual weakly interacting systems. In this regard, the GR models are of great importance. In this paper, we investigated the holographic complexity for charged AdS black holes in these models when the translational invariance is broken in diverse dimensions. Following the prescription in [54], with the inclusion of joint and counterterm actions for null boundaries [80], we studied the growth rate of complexity on the WDW patch shown in Fig. 1 for a modification of the GR model to holographic theory containing axion fields which yields the momentum relaxation (EMAD theories).

We have shown that though the time evolution of the joint and counterterm for null surfaces depend separately on the normalization condition $\xi$, which is needed to remove the reparametrization ambiguity of null boundaries, the sum of the two terms in $\dot{{{\mathcal {C}}}}_A=dI_{WDW}/dt$ is independent of $\xi$. We examined the standard calculations for the three most commonly used models, i.e., four-, five-, and $(d+1)$-dimensional EMAD theories with single-horizon charged AdS black holes. According to the curves in Figs. 2 and 3, the growth rate of holographic complexity is finite for early times in each case, although it violates Lloyd’s bound. However, at late times, it saturates the corresponding bound which is not 2M. In particular, the results for the GR model and EMAD theories in arbitrary dimensions are given by Eqs. (3.75) and (3.74), respectively.

To enable a comparison of our results with other literature, we have summarized the late time behavior of $\dot{{{\mathcal {C}}}}_A$ for neutral and charged AdS black holes in different theories in Table 1. It is shown that for neutral black holes of mass M, Lloyd’s bound is equal to 2M even by adding the momentum relaxation term or higher-order curvature corrections. For charged solutions with a single horizon, we have the contribution of a chemical potential term as well. When there are nonlinear expressions of dilatonic or gauge fields, we have an extra term in the bound due to these corrections.³ Finally, we have shown that in the presence of a momentum relaxation term in EMAD theory, we have a correction of Q and $\beta$, which are given in the last two rows in Table 1.

It would also be of interest to study the holographic complexity for other generalizations of the holographic axion models in [21, 87] by considering a special gauge-axion higher derivative term [97, 98] of the form

$$\begin{aligned} S&=\frac{1}{16\pi G_4}\int d^4 x \sqrt{-g}\nonumber \\&\quad \times \left[ R-2\Lambda -V(X)-\frac{1}{4}\left( 1+{\mathcal {K}}Tr[X]\right) F_{\mu \nu }F^{\mu \nu }\right] , \end{aligned}$$

(4.1)

where $X^{I}=\beta \delta _{i}^{I}x^{i}$ are the axionic scalar fields or other holographic axion models in [99, 100].