1 Introduction

Charged dust spheres have been thoroughly studied within the context of Einstein’s general relativity, over the last century as the simplest matter composed models of stars or the universe as a whole. Dust consists of a pressure-free fluid of non-interacting particles. The collapse to a point singularity of such distributions is countered by repulsive Coulombic forces on account of the presence of the electromagnetic field. The effects of the magnetic field may be negated as gauge freedom allows for the suppression of the magnetic field so that only the electric part of the Maxwell field is actively involved in the dynamics. Attempts at modelling the electron as a charged dust were not successful on account of unrealistic charge–to–mass, charge–to–radius and mass–to–radius ratios that contradict the actually measured values [1]. A further motivation to investigate charged celestial phenomena is in the work of Cherubini et al. [2] where it is claimed that the creation of positron-electron pairs in the dyadosphere of charged black holes could serve as a mechanism to drive gamma-ray bursts [3]. Detailed studies of electromagnetic black holes were conducted by Ruffini et al. [4,5,6,7,8].

In this work we study charged dust stars in higher dimensions and with higher curvature effects induced by the Gauss–Bonnet invariants. It is reasonable to ask why such objects would be of interest since common experience suggests that only the four dimensional spacetime manifold is physically accessible. Although this is true, the existence of extra dimensions has not been ruled out by any experimental evidence and such speculations have proliferated for several decades. The Large Hadron Collider project searched for evidence of higher dimensions but could not detect any large extra dimensions, however, the existence of microscopic compactified topologically curled extra dimensions has not been eliminated. Motivations for higher dimensional study are usually made on the grounds that higher curvature gravity is a string inspired theory [9]. Dimensions of order 10 and 11 are commonplace in quantum field theory in the context of superstring theory and its generalization \(M-\)theory. In addition, there is also the pursuit of a grand unified theory which harmonizes quantum field theory and gravitational theory. If such a theory exists then it follows that gravity should also embody higher dimensions.

Higher dimensional theories are by no means novel. The seminal work of Kaluza [10] and Klein [11] studied such in the context of 5 dimensional electromagnetic field theory and ascribed four dimensions to the electromagnetic field, 10 to the usual spacetime dimensions and an extra dimension to a scalar field called a scalaron. More recently brane-world cosmologies requiring higher dimensions received considerable attention although their importance has since waned [12].

Alternate, extended or modified theories of gravity have aroused considerable interest recently in view of the inadequacy of the general theory of relativity to explain anomalous behavior of gravitational phenomena such as the late time accelerated expansion of the universe without resorting to postulating the existence of exotic matter fields such as dark energy and dark matter with negative pressures driving the cosmic accelerated expansion. In particular, Einstein–Gauss–Bonnet (EGB) theory has been intensively studied over the last few decades. EGB belongs to the class of Lovelock polynomials [13, 14] which serve as the most general tensorial higher curvature gravity theories that generalize general relativity and that produce second order equations of motion. Ostrogradsky ghosts are avoided, the Bianchi identities are satisfied and energy conservation laws hold. Importantly the EGB Lagrangian appears in the low energy effective action of heterotic string theory and the coupling constant is identified with the string tension [15]. The EGB action is constructed from quadratic forms of the Riemann tensor, Ricci tensor and the Ricci scalar. Even if there is some skepticism against the influence of higher dimensions in an area such as stellar modelling, investigations into such objects potentially analyze the self consistency of such theories. A theory may explain the cosmic accelerated expansion at late times, but the question of whether the same theory admits physically viable models of stars and galaxies must also be confronted. It is in this spirit we undertake to examine higher dimensional stars in the context of extra curvature.

The Lovelock construction and its special cases EGB and pure Lovelock gravity are natural extensions of general relativity to higher dimensions. Recall that in Lovelock theory the critical spacetime dimensions d are \(d = 2N + 1\) and \(d = 2N + 2\) where N is the order of the Lovelock polynomial [16]. EGB theory is the quadratic case of the Lovelock polynomial and incorporates the Einstein contribution (\(N = 1\)) as well as the \(N = 2\) term. In dimensions less than 5 the Lovelock polynomial is the same as that of general relativity. Note that pure Lovelock gravity entails a single term of the Lovelock polynomial as the generator of the Lagrangian as opposed to the sum of the terms. Important properties of pure Lovelock gravity such as its impact on black holes were considered in [17, 18] while the dynamical structure of pure Lovelock gravity was examined in [19]. A most intriguing result is reported in [20] where it is shown that for \(d = 3N + 1\) there exists higher dimensional manifolds that mimic the four dimensional standard case. In other words it is impossible to tell if one is in a four dimensional spacetime or 7 dimensional one as both exterior fields have a 1/r fall-off. In pure Lovelock geometry the coupling constants have no importance and consequently one drawback is that higher curvature effects may not be switched off as can be achieved in full Lovelock theory by setting the coupling constants to vanish. Nevertheless the \(N = 1\) case corresponds to four dimensions, the standard Einstein theory and all its successes are regained. Using a Chern-Simons gauge Chamseddine showed that both odd and even pure Lovelock Lagrangians are dynamical [21,22,23,24,25,26,27]. Of late, an odd dimensional universe model was considered in [28] and shown to be dynamical and not kinematic as some have previously claimed [29]. The even dimensional case was treated in [30] and closed compact astrophysical models are admitted since a bounded hypersphere exists.

Exact solutions for five dimensional neutral static perfect fluid metrics were only recently discovered [31,32,33,34] in view of the complexity of the master field equation. The six dimensional EGB theory is more complicated than the five dimensional counterpart, however, physically reasonable stellar models have been found in this framework as well [35, 36]. Promoting the fluid to the charged regime makes the problem considerably simpler and a physically reasonable model was presented in [37]. In the case of charged stars there are two free variables to be prescribed upfront for a complete model. Additionally, as is well known in the Einstein case, it is also true in the charged EGB case that all of the dynamical and electric quantities may be expressed in terms of the metric potentials which implies that any metric, barring a few classes, will generate a complete charged fluid model. Naturally, it would be far-fetched to expect that a random choice of metric will result in a model that obeys elementary conditions for physical admissability. For example, it is hardly conceivable that an equation of state between the pressure and density would exist. It was shown in [37] that the EGB terms assisted the model to conform to what is physically reasonable whereas the absence of the EGB term yielded defective models. The complexity level of the system of nonlinear partial differential equations increases if some restriction is imposed at the outset. This is the case for charged dust or a prescribed equation of state. While there still remains one more choice to be made, the problem is nevertheless nontrivial. In the case of charged dust the pressure vanishes and the master equation consists of the two metric potentials. One must be prescribed and the other found by integration; thereafter the energy density, electric field intensity and proper charge density may be determined. We analyze this problem along these lines. The associated problem in the standard Einstein theory was discussed by Hansraj et al. [38] where it was shown that all static charged dust distributions in spherical symmetry possess a necessary curvature singularity at the stellar centre and an algorithm to detect all charged dust solutions was proposed. In the work at hand, such an algorithm was not forthcoming. Note that the exterior field of a static spherically symmetric distribution of charged matter in EGB theory is given by the Wiltshire [39] metric. Ordinarily we take the junction condition to be the same as in Einstein theory namely the vanishing of the pressure at a boundary hypersurface. The actual boundary conditions have been considered by Davis [40] however are not yet in a form that is easily applicable. In the current problem of charged dust, we follow the custom as in the standard theory that the vanishing of the energy density is required to determine the boundary if it exists.

This paper is structured as follows. We derive the master equation for charged dust spheres in 5 and 6 dimensions which are the only two dimensions of importance. Then we prove that the spatial metric potentials are constrained within the Boulware-Deser potential as upper and lower bounds for a physically realistic model where the energy density, electric field intensity and proper charge density are all positive. We proceed to find general classes of exact solutions for charged dust fluids incorporating higher curvature terms. Some special cases are examined to find closed form solutions in terms of elementary functions. We conclude with a discussion.

2 Einstein–Gauss–Bonnet Gravity

The action

$$\begin{aligned} S=\frac{1}{2\kappa } \int R \sqrt{-g} d^4 x, \end{aligned}$$
(1)

is the standard Einstein–Hilbert action of general relativity. Here \(g = \det (g_{ab}) \) is the determinant of the metric tensor \(g_{ab}\), R is the Ricci scalar and \(\kappa = 8\pi Gc^{-4}\) where G is the Newton’s gravitational constant and c is the speed of light in vacuum. The Lovelock tensor in d dimensions may be written as

$$\begin{aligned} {\mathcal {G}}_{ab} = \sum ^{[(d-1)/2]}_{n=0} \alpha _n {\mathcal {G}}_{ab}^n, \end{aligned}$$
(2)

so that the Lovelock [13, 14] Lagrangian has the form

$$\begin{aligned} {\mathcal {L}} = \sum ^{n}_{n=0} \alpha _n {\mathcal {R}}^n \end{aligned}$$
(3)

where \( {\mathcal {R}}^n {=} \frac{1}{2^n} \delta ^{c_1 d_1...c_n d_n}_{a_1 b_1... a_n b_n} \Pi ^n_{r=1} R^{a_r b_r}_{c_r d_r} \) and \(R^{a b}_{c d}\) is the Riemann or curvature tensor. Also \( \delta ^{c_1 d_1...c_n d_n}_{a_1 b_1... a_n b_n} {=} \frac{1}{n!} \delta ^{c_1}_{\big [a_1} \delta ^{d_1}_{b_1}... \delta ^{c_n}_{a_n} \delta ^{d_n}_{b_n \big ]}\) is the required Kronecker delta. The quantity [v] refers to the greatest integer value satisfying \([v] \le v\). Note that \({\mathcal {G}}_{ab}\) is obtained by suitable contractions on a tensor product of n copies of the Riemann tensor that trivially vanish whenever \(n > [(d-1)/2]\). In the event that \(d = 3, 4\), \({\mathcal {G}}_{ab}^n\) vanishes for all \(n > 1\). The Lovelock terms become a total derivative or a topological invariant for \( d = 3, 4\) and hence do not contribute to the dynamics. Moreover, each term \({\mathcal {R}}^n\) in \({\mathcal {L}}\) represents the dimensional extension of the Euler density in 2n dimensions and contribute to the field equations only if \(n < d/2\). For this reason, the critical spacetime dimensions of Lovelock gravity are \(d = 2n + 1\) and \(d = 2n + 2\). In the case of EGB gravity \( n = 2\) so the critical dimensions are \(d = 5, 6\). For \(n = 3\), the salient dimensions are 7, 8 and so on. A detailed treatment of this aspect may be found in [41,42,43]. The Lovelock action (3) may be expanded as

$$\begin{aligned} {\mathcal {L}}= & {} \sqrt{-g}\left( \alpha _0 + \alpha _1R + \alpha _2 \left( R^2 + R_{a b c d} R^{a b c d} - 4R_{c d} R^{c d} \right) \right. \\&\left. +\alpha _3 {\mathcal {O}}(R^3)\right) \end{aligned}$$

in general. Up to second order of the Lovelock polynomial we define the Gauss–Bonnet (GB) term as

$$\begin{aligned} {\mathcal {R}}^2 = R^2 + R_{a b c d} R^{a b c d} - 4R_{c d} R^{c d} \end{aligned}$$

often denoted as \(L_{GB}\). This term arises in the low energy effective action of heterotic string theory [15]. As a result the Einstein–Gauss–Bonnet field equations are given by

$$\begin{aligned} G^{a}_{b} + \alpha H^{a}_{b} = T^{a}_{b} \end{aligned}$$
(4)

where

$$\begin{aligned} H_{ab}= & {} 2\left( R R_{ab} - 2R_{ac}R^c_b - 2R^{cd}R_{acbd} + R^{cde}_{a} R_{bcde} \right) \\&- \frac{1}{2} g_{ab} {\mathcal {R}}^2. \end{aligned}$$

and we have followed the custom of using geometrized units such that \(\kappa = 1\). The Gauss–Bonnet action is written as

$$\begin{aligned} S = \int \sqrt{-g} \left[ \frac{1}{2} \left( R - 2\Lambda + \alpha L_{GB}\right) \right] d^n x + S_{ \text{ matter }} \end{aligned}$$
(5)

where \(\alpha \) is the GB coupling constant. The constant \(\alpha \) is linked with the string tension in string theory [15]. The remarkable feature of the GB action lies in the fact that despite the Lagrangian being quadratic in the Ricci tensor, Ricci scalar and the Riemann tensor, the equations of motion turn out to be second order quasilinear. The GB term has no effect for \(n \le 4\) as it is topological or becomes a total derivative but is generally non-zero for \(n > 4\). We now consider the 5 and 6 dimensional cases in turn. These are the critical spacetime dimensions when the order of the Lovelock polynomial is 2.

3 General field equations

The general static d-dimensional spherically symmetric metric is taken to be

$$\begin{aligned} ds^2 = -e^{\nu } dt^2 + e^{\lambda } dr^2 + r^2 d\Omega ^2_{d-2} \end{aligned}$$
(6)

where \(d\Omega ^2_{d-2}\) is the metric on a unit \((d-2)\)-sphere and where \(\nu = \nu (r)\) and \(\lambda = \lambda (r)\) are the metric potentials. The energy–momentum tensor for the comoving fluid velocity vector \(u^a=e^{-\nu /2} \delta ^{a}_{0}\) has the form \( T^a_{b}= \text{ diag } \left( -\rho ,\, p,\, p,\, p,\, p, \,\,\ldots \,\right) \) for a neutral perfect fluid.

The Lovelock–Maxwell system of field equations is given by

$$\begin{aligned} G_{ab} + \alpha H_{ab}= & {} T_{ab} + E_{ab} \end{aligned}$$
(7)
$$\begin{aligned} F_{ab;c} + F_{bc;a} + F_{ca;b}= & {} 0 \end{aligned}$$
(8)
$$\begin{aligned} F^{ab}{}{}_{;b}= & {} J^a \end{aligned}$$
(9)

where \({ E_{ab}}\) is the electric field intensity tensor, \({F_{ab}}\) is the Faraday tensor and J is the d-current density. The electrostatic field tensor is defined by

$$\begin{aligned} E_{ab} = F_{ac}F_b{}^{c} - \frac{1}{4}g_{ab}F_{cd}F^{cd} \end{aligned}$$
(10)

where \({ F_{ab}}\) is skew–symmetric. The d-current density for a non-conducting fluid is given by \( J^a=\sigma u^a \) where \(\sigma \) is the proper charge density. The electromagnetic field tensor \({F_{ab}}\) is defined in terms of the d-potential A by

$$\begin{aligned} F_{ab} = A_{b;a} - A_{a;b}. \end{aligned}$$
(11)

Gauge freedom permits the choice of the d-potential with a single non-vanishing component in the form \( A_a = (\phi (r),0,0,\,\ldots \,) \nonumber \) so that the magnetic field is eliminated and only the electric field is dynamic. The sole surviving component of the Faraday tensor \(F_{ab}\) is given by \( F_{01} = -\phi '(r) \) with the help of (11). The corresponding contravariant component may be expressed in the form \( F^{01} = e^{-2(\nu +\lambda )}\phi '(r) = e^{-(\nu +\lambda )}E(r) \) where we have set

$$\begin{aligned} E(r) = e^{-(\nu +\lambda )}\phi '(r) \end{aligned}$$
(12)

to be the electric field intensity in harmony with Herrera and Ponce de Leon [44]. The electromagnetic field energy tensor components (10) evaluate to \( E^a_{b}=\text{ diag } \Big ( -\frac{1}{2}E^2,\, -\frac{1}{2}E^2,\, \frac{1}{2}E^2,\, \frac{1}{2}E^2, \frac{1}{2} E^2, \,\,\ldots \, \Big ).\) Equation (9) generates the condition

$$\begin{aligned} e^{-\lambda }\left( r^2 E\right) '=r^2 \sigma \end{aligned}$$
(13)

which will enable the computation of the proper charge density \(\sigma \). The conservation laws \(\left( T^{ab} + E^{ab}\right) _{}{}_{;b} = 0 \) reduce to the equation

$$\begin{aligned} p' + (\rho + p)\nu ' = \frac{E}{r^2}\left( r^2 E\right) ' \end{aligned}$$
(14)

sometimes called the equation of hydrodynamical equilibrium or the continuity equation. Note that the repulsion due to electric charges are assumed to be distinct from the classical pressure p. The contribution of the Coulombic repulsion is expressed through the Faraday tensor (11). From Eq. (14) it may be inferred that the absence of both isotropic particle pressure p and the electrostatic field intensity E is not physically viable. In such a case, either \(\rho = 0\) corresponding to the vacuum which is already known or \(\nu = \) a constant suggesting geodesic motion. Of course any one of E or p could vanish. In the former case a variety of perfect fluid distributions may be sought [31,32,33] while in the latter case charged dust distributions may be investigated as is being undertaken in this study.

The Einstein–Gauss–Bonnet–Maxwell (EGBM) Eqs. (7)–(9) when expanded read as

$$\begin{aligned} \rho + \frac{E^2}{2}= & {} \frac{(d-2)e^{-\lambda }\left\{ \left[ r^3\lambda ' +r^2(d-3)\left( e^{\lambda }-1\right) \right] - {\bar{\alpha }} \left( e^{-\lambda }-1\right) \left( 2r\lambda ' - (d-5)(1-e^{\lambda } )\right) \right\} }{2r^4} \nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned} p_r -\frac{E^2}{2}= & {} \frac{(d-2)e^{-\lambda }\left\{ \left[ r^2(d-3)(e^{\lambda }-1)-r^3\nu '\right] + {\bar{\alpha }} \left( e^{-\lambda } - 1\right) \left( 2r\nu ' - (d- 5)(e^{\lambda } -1)\right) \right\} }{2r^4} \end{aligned}$$
(16)
$$\begin{aligned} p_{\theta } + \frac{E^2}{2}= & {} -\frac{e^{-\lambda }}{4r^2} \left[ r^2(2\nu '' +\nu '^2 -\nu '\lambda ') + 2(d-3)r(\nu '-\lambda ') +2(d-3)(d-4)(1-e^{\lambda })\right] \nonumber \\&+ \frac{{\bar{\alpha }} e^{-\lambda } \left[ \left( 1-e^{-\lambda }\right) \left\{ r^2(2\nu '' +\nu '^2 -\nu '\lambda ') + (d-5)(2r(\nu ' -\lambda ') + (d-6)(1-e^{\lambda })) \right\} \right] }{2r^{4}} \nonumber \\&+\frac{{\bar{\alpha }} e^{-2\lambda }\nu ' \lambda '}{r^2} \end{aligned}$$
(17)

where we have set \({\bar{\alpha }} =(d-3)(d-4)\alpha \) following Dadhich [45]. The change of coordinates \(x=Cr^2\), \(e^{-\lambda }= Z(x)\) and \(e^{\nu } = y^2(x)\) used often historically is motivated by the fact that the nonlinear isotropy of pressure equation becomes a second order linear differential equation in one of the variables. Under this change of variables Eqs. (15) to (17) transform to the system The most general EGBM field equations is given by

$$\begin{aligned} \frac{\rho }{C} +\frac{E^2}{2C}= & {} \frac{(d-2)\left[ -2x{\dot{Z}}+(d-3)(1-Z)\right] }{2x}\nonumber \\&+ \frac{(d-2){{{\bar{\alpha }}}}(1-Z)C\left[ -4x{\dot{Z}} +(d-5)(1-Z)\right] }{2x^2} \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} \frac{p_r}{C} - \frac{E^2}{2C}= & {} \frac{(d-2)\left[ -4xZ{\dot{y}} +(d-3)(1-Z)y \right] }{2xy} \nonumber \\&+ \frac{(d-2){{{\bar{\alpha }}}} (1-Z)C\left[ 8xZ{\dot{y}} -(d-5)(1-Z)y\right] }{2x^2 y} \nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned} \frac{p_{\theta }}{C} + \frac{E^2}{2C}= & {} -\frac{1}{2xy}\left[ 8x^2 Z\ddot{y} + \left( 4(d-2)xZ+4x^2{\dot{Z}}\right) {\dot{y}}\right. \nonumber \\&\left. + \left( 2(d-3)x{\dot{Z}} +(d-3)(d-4)(Z-1)\right) y\right] \nonumber \\&+ \frac{{{{\bar{\alpha }}}}C}{2x^2 y} \left[ 16x^2 Z(1-Z)\ddot{y}\right. \nonumber \\&\left. +\left( 8(d-4) xZ (1-Z) +8x^2{\dot{Z}}(1-3Z)\right) {\dot{y}} \right. \nonumber \\&\left. +(1-Z)\left( 4(d-5)x{\dot{Z}} -\beta (1-Z)\right) y \right] \end{aligned}$$
(20)

where we have introduced the simplification \(\beta = 2 {\bar{\alpha }} C\). The equation of pressure isotropy \(p_r = p_{\theta }\) takes the form

$$\begin{aligned} 0= & {} 4x^2 Z\left[ x+2{{{\bar{\alpha }}}} C(1-Z)\right] \ddot{y}\nonumber \\&+2x\left[ x^2 {\dot{Z}} -2{{{\bar{\alpha }}}}C\left( 2Z(1-Z) -(1-3Z)x{\dot{Z}}\right) \right] {\dot{y}} \nonumber \\&+ ({\dot{Z}}x -Z+1)((d-3)x+ 2{{\bar{\alpha }}}C (d-5) (1-Z))y \nonumber \\ \end{aligned}$$
(21)

in the case that the electrostatic field is turned off. This is done to obtain the corresponding vacuum metric which will feature prominently in the discussion on the physical acceptability of solutions. For the exterior we put \(Z = y^2\) in (21) which gives the differential equation

$$\begin{aligned}&\left( 2 x y {\dot{y}}-y^2+1\right) \left( (d-3) x-\beta (d-5) \left( y^2-1\right) \right) \nonumber \\&\quad +4 x^2 y \left( \beta -\beta y^2+x\right) \ddot{y} \nonumber \\&\quad +4 x {\dot{y}} \left( -3 \beta x y^2 {\dot{y}}+x (\beta +x) {\dot{y}}+\beta y^3-\beta y \right) = 0 \end{aligned}$$
(22)

with general solution

$$\begin{aligned} y = \sqrt{Z} = 1 + \frac{x}{\beta }\left( 1 \pm \sqrt{1 - 2\beta c_2 - \frac{8\beta c_1}{(d-1)x^{\frac{d-1}{2}}}} \right) \end{aligned}$$
(23)

where we identify the quantity \(\frac{8\beta c_1}{(d-1)}\) with the gravitational mass of the hypersphere. The result (23) is the same as the Boulware–Deser solution when \(c_2 = 0\). Note that the second integration constant \(c_2\) arises because the isotropy equation is second order. The same result may be achieved by setting the energy density (18) to a constant \(\rho _0\) to obtain the generalized interior Schwarzschild metric potential

$$\begin{aligned} Z = 1 + \frac{x}{\beta }\left( 1 \pm \sqrt{1 + \frac{4\beta \rho _0}{(d-2)(d-1)} + \frac{\beta ^2 c_3}{x^{\frac{d-1}{2}}}} \right) \end{aligned}$$
(24)

and as a bonus we obtain the exterior

$$\begin{aligned} Z = 1 + \frac{x}{\beta }\left( 1 \pm \sqrt{1 + \frac{\beta c_3}{x^{\frac{d-1}{2}}}} \right) \end{aligned}$$
(25)

by setting \(\rho _0 = 0\) since there is no matter in the exterior. The solutions (23) and (25) may be reconciled if the constants are related by \(c_1 = -\frac{\beta c_3 (d-1)}{8}\). Note that in order for the exterior metric to be asymptotically flat, which is physically reasonable, only the negative branch of Z may be considered while the positive branch must be discarded. Clearly \(\alpha = 0 = \beta \) is not tenable in (25) however, if (25) is expanded as a series in powers of \(\beta \) then the limiting case \(\beta \) approaching 0 gives the exterior Schwarzschild metric in d dimensions.

As mentioned earlier, the critical dimensions in EGB theory are 5 and 6 in fact \(2N + 1\) and \(2N + 2\) for the general N-th order Lovelock polynomial. Therefore we proceed now to consider the 5 and 6 dimensional cases in turn.

4 The five dimensional case

The field Eqs. (15)–(17) assume the form

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{3}{xy}\left[ 2Z{\dot{y}} - {\dot{Z}}y\right] \left[ \beta (1-Z) +x\right] \end{aligned}$$
(26)
$$\begin{aligned} \frac{E^2}{C}= & {} \frac{6 (1-Z)}{x} - \frac{12 Z {\dot{y}}}{y} - \frac{12\beta ( 1-Z) Z {\dot{y}}}{x y} \end{aligned}$$
(27)
$$\begin{aligned} 0= & {} 2 x Z \left( \beta (1-Z) + x \right) \ddot{y} \nonumber \\&+ \left( x^2 {\dot{Z}} + 12xZ + \beta \left[ 10Z(1-Z) +x{\dot{Z}}(1-3Z) \right] \right) {\dot{y}} \nonumber \\&+ \left( x {\dot{Z}} -5(1-Z) \right) y \end{aligned}$$
(28)
$$\begin{aligned} \frac{\sigma ^2}{C}= & {} \frac{4Z}{x}\left( x{\dot{E}} + E \right) ^2 \end{aligned}$$
(29)

when \(p = 0\) for dust. In the above system of Eqs. (26), (27) and (29) may be taken as definitions for the density \(\rho \), electric field intensity E and the proper charge density \(\sigma \) respectively. Observe that each of these three equations contains at least three of the unknowns thus eliminating them as viable options to commence with since there remains only one choice to be made. We are forced to accept Eq. (28) as the master field equation and one of the metric potentials must be specified a priori. We may rewrite Eq. (28) in terms of \({\dot{Z}}\) and Z as

$$\begin{aligned}&\left( x^2{\dot{y}} + xy + \beta x{\dot{y}}\right) {\dot{Z}} - 3 \beta x{\dot{y}}Z{\dot{Z}} -2\beta \left( x\ddot{y} +10{\dot{y}}\right) Z^2 \nonumber \\&\quad +\left( 2\beta x\ddot{y}+2x^2\ddot{y}+12x{\dot{y}}+10\beta {\dot{y}}+5y\right) Z -5y = 0 \nonumber \\ \end{aligned}$$
(30)

however, the Eq. (30) is nonlinear in Z. It may still be possible to utilize this form to locate exact solutions. But before proceeding to find exact solutions it is important to determine whether solutions satisfying the most elementary physical demands exist. Clearly it is required that the energy density and electric field intensity both be positive. These conditions will place restrictions on acceptable exact solutions. Note that that the causality requirement that the sound speed does not exceed the light speed within the star may not be examined meaningfully since the usual constraint on the sound speed squared \(0 \le \frac{dp}{d\rho } < 1\) is trivially satisfied. Ordinarily a hypersurface of vanishing pressure is expected to indicate a boundary of a star, however, since the pressure vanishes everywhere it is customary to consider the hypersurface where the energy density vanishes as the onset of the vacuum exterior.

Fig. 1
figure 1

Plots of feasible spatial potential regions for \(C_1 = 0\)

Full size image
Fig. 2
figure 2

Plots of feasible spatial potential regions for \(C_1 = 2\)

Full size image
Fig. 3
figure 3

Plots of feasible spatial potential regions for \(C_1 = - 2\)

Full size image

5 Existence of physically reasonable charged 5D dust fluids

In order for models to represent realistic distributions of charged dust, it is necessary that the density and the quantity \(E^2\) remain positive everywhere. Note that the positivity of \(\sigma ^2\) is guaranteed so it does not feature in this discussion. We take \(\alpha > 0\) as it is related to the string tension although a negative value is not necessarily ruled out.

  • Let us firstly assume that \(x + \beta (1-Z) > 0\) that is \(Z < 1 + \frac{x}{\beta }\) in (26). Then positivity of energy density demands that

    $$\begin{aligned} \frac{{\dot{y}}}{y} \ge \frac{{\dot{Z}}}{2Z} \end{aligned}$$
    (31)

    from (26). Additionally ensuring that \(E^2 \ge 0\) requires that

    $$\begin{aligned} \frac{{\dot{y}}}{y} \le \frac{1-Z}{2Z\left( x+\beta (1-Z)\right) } \end{aligned}$$
    (32)

    Now (31) and (32 ) together generate the relationship

    $$\begin{aligned} \left( x+\beta (1-Z)\right) {\dot{Z}} + Z - 1 \le 0. \end{aligned}$$
    (33)

    For equality (33) is an Abel equation of the first kind and belongs to a class that can be solved explicitly in the form

    $$\begin{aligned} Z=\frac{\beta + x \pm \sqrt{\beta ^2 + x^2 + 2\beta C_1}}{\beta } \end{aligned}$$
    (34)

    where \(C_1\) is a constant of integration. Essentially (34) solves an algebraic quadratic equation so we may infer that for a positive density and \(E^2\) the functions Z should satisfy

    $$\begin{aligned}&1+\frac{x}{\beta }\left( 1-\sqrt{1 + \frac{\beta ^2 + 2\beta C_1}{x^2}} \right) \le Z \le 1\nonumber \\&\quad +\frac{x}{\beta }\left( 1+ \sqrt{1 + \frac{\beta ^2 + 2\beta C_1}{x^2}} \right) \end{aligned}$$
    (35)

    Observe that the constraining functions in (35) are exactly the same as the negative and positive branches of the Boulware–Deser (34) metric potential applicable to uncharged fluids in 5 dimensions. Recall that we are considering the case \(Z < 1 + \frac{x}{\beta }\) so we conclude that physically reasonable charged dust spatial metric potentials lie in the interval

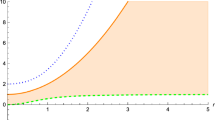
    $$\begin{aligned} 1+\frac{x}{\beta }\left( 1 - \sqrt{1 + \frac{\beta ^2 + 2\beta C_1}{x^2}} \right)< Z < 1+\frac{x}{\beta } \end{aligned}$$
    (36)

    for this case. Note also that \(Z=1 +\frac{x}{\beta }\) is the well-known Schwarzschild interior metric potential. To justify the inequality (36) we may denote \(\Delta = 1+\frac{\beta ^2 + 2\beta C_1}{x^2}\) and then it is easy to observe that \(1+\frac{x}{\beta } > 1+\frac{x}{\beta }\left( 1-\sqrt{\Delta }\right) \) and \(1+\frac{x}{\beta } < 1+\frac{x}{\beta }\left( 1+\sqrt{\Delta }\right) \) for all \(\beta > 0\) and \(\Delta >0\). At the extremes both the energy density as well as the electric field vanish resulting in a vacuum with no electromagnetic field, hence the Boulware–Deser spacetime and not the Wiltshire metric emerges. This is an interesting behavior for charged dust fluids. In summary, we find that for metric potential functions that lie below \(Z=1+\frac{x}{\beta }\), the left branch of the Boulware–Deser metric is a lower bound and the Schwarzschild interior is the upper bound.

    Effectively we have shown that only metric potentials lying between the Boulware-Deser branches may yield models of charged dust with a positive density and square of electric field intensity. We emphasize that this is only a necessary condition and not a sufficient one. Moreover, even if such a suitable function is selected, there is no guarantee that the y function satisfying the differential Eq. (28) will in fact be suitable to generate a well behaved model.

  • Next suppose \(Z > 1+\frac{x}{\beta }\).

    This time, the inequality in (31) is reversed. Also

    $$\begin{aligned} \frac{{\dot{y}}}{y} \ge \frac{1-Z}{2Z(x+\beta (1-Z))} \end{aligned}$$
    (37)

    since \(x+\beta (1-Z)\) is now negative. Now we have that

    $$\begin{aligned} \frac{{\dot{Z}}}{2Z} \le \frac{1-Z}{2Z(x+\beta (1-Z))}\end{aligned}$$

    as before and consequently

    $$\begin{aligned} 1+\frac{x}{\beta }\left( 1-\sqrt{\Delta } \right) \le Z \le 1+\frac{x}{\beta }\left( 1+ \sqrt{\Delta } \right) . \end{aligned}$$
    (38)

    But \(Z>1+\frac{x}{\beta }\) forces the constraint

    $$\begin{aligned} 1+\frac{x}{\beta } \le Z \le 1+\frac{x}{\beta }\left( 1+\sqrt{\Delta }\right) \end{aligned}$$
    (39)

revealing that for metric functions lying above \(Z = 1+\frac{x}{\beta }\) the right arm of the Boulware-Deser metric serves as an upper bound while the Schwarzschild interior metric is the lower bound.

We illustrate these constraint functions graphically to check the veracity of our deductions. Figures 1, 2 and 3 depict three different typical values for \(C_1\) namely 2, \(-2\), and 0 respectively. In each plot the thick line represents the plus branch of the Boulware–Deser metric and the dashed curve represents the minus branch of the Boulware–Deser metric. The thin lines represents the Schwarzschild metric potential \(Z=1 +\frac{x}{\beta }=1+\frac{r^2}{\beta }\). To characterize the generic behavior of the functions we have plotted curves for \(\beta \) = 1, 2 and 3 on the same system of axes. Favorable spatial potentials must accordingly lie between the thick lines and their dashed counterpart. What this analysis shows is that physically reasonable charged dust solutions in EGBM theory are not ruled out.

6 Some exact EGBM 5D charged dust solutions

Locating exact interior metrics by solving (28) is a complicated mathematical problem. We now present some solutions expressible in closed form. We also comment on some well known ansatze which have been considered in the context of ordinary Einstein gravity.

6.1 Constant spatial potential

Amongst the simplest prescriptions for the spatial potential is the case \(Z= k\) for some constant k. When constructing models of compact stars, it is known that the prescription of a constant spatial potential results in isothermal behavior in the pure Gauss–Bonnet theory and its generalization pure Lovelock theory [46]. Equation (28) assumes the form

$$\begin{aligned} x(x-\beta (k-1))\ddot{y} + (6x-5\beta (k-1)){\dot{y}} +\frac{5(k-1)}{2k} y=0 \nonumber \\ \end{aligned}$$
(40)

which may be recognized as a hypergeometric differential equation. The solution of Eq. (40) may be expressed in the form

$$\begin{aligned} y= & {} c_1z^{\frac{3\sqrt{3k+2}}{2\sqrt{k}}-\frac{5}{2}}\nonumber \\&\times \,\,{_2F_1}\left( -\frac{3}{2} -\frac{3\sqrt{3k+2}}{2\sqrt{k}}, \frac{5}{2}-\frac{3\sqrt{3k+2}}{2\sqrt{k}}, 1-\frac{\sqrt{5(3k+2)}}{\sqrt{k}},\frac{1}{z}\right) \nonumber \\&c_2z^{\frac{-3\sqrt{3k+2}}{2\sqrt{k}}-\frac{5}{2}} \nonumber \\&\times \,\,{_2F_1}\left( -\frac{3}{2} +\frac{3\sqrt{3k+2}}{2\sqrt{k}}, \frac{5}{2} +\frac{3\sqrt{3k+2}}{2\sqrt{k}}, 1 + \frac{\sqrt{5(3k+2)}}{\sqrt{k}},\frac{1}{z}\right) \nonumber \\ \end{aligned}$$
(41)

where \(c_1\) and \(c_2\) are constants of integration and \({_2F_1}\) is the well known hypergeometric function. Hypergeometric functions possess some special cases that are realizable as elementary functions however it was not possible to detect any such solutions except for the case \(k = 1\). The solution in this case is

$$\begin{aligned} y= -\frac{A}{5x^5} + B \end{aligned}$$
(42)

where A and B are constants of integration. The density, electric field intensity and proper charge density are given by

$$\begin{aligned} \rho= & {} -\frac{30 A}{A r^2-5 B r^{12}} \end{aligned}$$
(43)
$$\begin{aligned} E^2= & {} \frac{60 A}{A r^2-5 B r^{12}} \end{aligned}$$
(44)
$$\begin{aligned} \sigma ^2= & {} \frac{120 A \left( A+20 B r^{10}\right) ^2}{r^4 \left( A- 5 B r^{10}\right) ^3} \end{aligned}$$
(45)

A major defect of this model is that the relationship \(E^2 = -2\rho \) arises which is unacceptable as a negative energy density is implied. Moreover note that the energy density may not vanish for a suitable radius suggesting the absence of any bounding hypersurface. Accordingly this case does not deserve any further attention.

6.2 Einstein universe ansatz

Einstein assumed a constant temporal potential y in order to solve his system of equations in the standard theory. The consequence is an unphysical cosmological model with constant energy density and pressure in the uncharged case. Setting \(y = \) a constant in (28) generates the potential

$$\begin{aligned} Z= 1 + Kx^{-5} \end{aligned}$$
(46)

where K is an integration constant. Inserting (46) into (26) gives the density as

$$\begin{aligned} \rho = \frac{-15\beta K^2}{x^{12}} + \frac{15K}{x^6} \end{aligned}$$
(47)

and the electric field intensity as

$$\begin{aligned} E^2 = \frac{-6K}{x^6} \end{aligned}$$
(48)

which immediately suggests that \(K < 0\). But this now forces \(\rho < 0\) from (47) since \(\beta \) is positive. This contradiction demonstrates that no realistic configuration of charged dust can exist with the Einstein universe prescription of a constant temporal potential in the EGB framework. Observe that the special case of the standard charged five dimensional Einstein universe may be considered by putting \(\beta = 0\) above. In this case \(\rho = \frac{15K}{x^6}\) and \(E^2 = \frac{-6K}{x^6}\). Again it is clear that no K value exists such that both density and \(E^2\) are positive. Hence a charged dust Einstein universe in the standard theory also fails to be a realistic proposition.

6.3 The Schwarzschild ansatz \(Z=1+x\)

Consider the metric potential \(Z = 1 + x\) which yields the Schwarzschild metric in Lovelock theory (Dadhich [46]). The general solution to Eq. (28) with \(p = 0\) is given in terms of hypergeometric functions as

$$\begin{aligned} y= & {} A \, \, {_2F_1}\left( \frac{11\sqrt{\beta -1} -\sqrt{121\beta -73}}{\sqrt{\beta -1}}, \right. \nonumber \\&\left. \frac{11\sqrt{\beta -1} +\sqrt{121\beta -73}}{\sqrt{\beta -1}},\left[ \frac{1}{2}\right] ,1+x\right) \nonumber \\&+B v \, \, {_2F_1} \left( \frac{13\sqrt{\beta -1} + \sqrt{121\beta -73}}{\sqrt{\beta -1}}, \right. \nonumber \\&\left. \frac{13\sqrt{\beta -1} - \sqrt{121\beta -73}}{\sqrt{\beta -1}},\left[ \frac{3}{2} \right] ,1+x \right) \end{aligned}$$
(49)

where A and B are constants of integration and the symbol \({_2F_1}\) has its usual meaning. In addition we have put \(v=\sqrt{1+x}\).

It is desirable to isolate values of \(\beta \) that admit closed form solutions in order for us to generate a complete model. Some nontrivial values for \(\beta \) exists for which the hypergeometric function reduces to elementary functions:

  • \(\beta = \frac{1}{2}\) The numerical value \(\beta = \frac{1}{2}\) reduces the solution (49) to closed form

    $$\begin{aligned} y= \frac{5A (7 x+8) + 14 B \left( x^3-4 x^2+24 x+64\right) v}{35 x^5} \end{aligned}$$
    (50)

    where A and B are integration constants.

  • \(\beta = \frac{1}{3}\)

    $$\begin{aligned} y = \frac{A \sqrt{x+1}}{x^5}+\frac{2 B \left( 5 x^4-8 x^3+16 x^2-64 x-128\right) }{35 x^5} \nonumber \\ \end{aligned}$$
    (51)

The presence of a persistent singularity at the stellar centre in these models is not of concern. Given that Coulombic repulsion is present it is not expected that the stellar centre is reachable. In this case, the models may be considered to be an atmosphere of charged dust surrounding some other matter configuration with a regular centre. We note that for each of the solutions mentioned above, the undesirable behaviour of a negative density or electric field intensity is present. Hence we do not display the complete models. In summary it may be noted that no physically viable charged dust model has been found in the 5 dimensional EGB case.

6.4 Specifying the temporal potential

An alternative approach in seeking exact solutions for charged dust in 5 dimensional EGB theory is to utilise Eq. (30) and to propose a suitable function y which is the temporal potential. The prescription \(y = \frac{1}{x^4}\) has the advantage of generating the exact solution pair

$$\begin{aligned} Z = \frac{4 \beta +3 x \pm \sqrt{16 \beta ^2-24 \beta K+144 \beta x+9 x^2}}{12 \beta } \end{aligned}$$
(52)

where K is an integration constant. At this point both branches of solutions are potentially useful, however through empirical testing with the help of plots the negative branch generated more pleasing physically appropriate behavior. The energy density, electric field intensity and proper charge density are given respectively, by

$$\begin{aligned}&\frac{\rho }{C} = \frac{\left( 8 \beta +v+9 x\right) \left( -9 x \left( 3 v-136 \beta \right) -32 \beta \left( -4 \beta +v+6 k\right) +81 x^2\right) }{48 \beta x^2 v} \end{aligned}$$
(53)
$$\begin{aligned}&\frac{E^2}{C} = \frac{27 x^2-9 x \left( 16 \beta +v\right) +8 \beta \left( 4 \beta -v+6 k\right) }{6 \beta x^2} \end{aligned}$$
(54)
$$\begin{aligned}&\frac{\sigma ^2}{C} = \frac{9 \left( 4 \beta -v+3 x\right) \left( x \left( 112 \beta -3 v\right) +4 \beta \left( 10 \beta +2 v-3 k\right) +9 x^2\right) ^2}{2 \beta ^2 x v^2 \left( -9 x \left( 16 \beta +v\right) +8 \beta \left( 4 \beta -v+6 k\right) +27 x^2\right) } \end{aligned}$$
(55)

where we have put \(v = \sqrt{8 \beta (2 \beta -3 k)+9 x^2+144 \beta x}\) to shorten the expressions. Since the quantities above are complicated and not conducive to an analytic treatment, we construct graphical plots for the EGB case with \(\beta = \frac{1}{2}\) and using the constant value \(K = -100\) which was determined through fine-tuning until physically reasonable profiles emerged and \(C = 1\).

Analyzing the plots in Fig.  4. it may be noted that the presence of higher curvature EGB terms reduce the radius of the charged dust sphere for the same density values. Alternatively we may say that the EGB spheres have a lower energy density for the same radial values. This differential appears to decrease as the radius increases. In other words the EGB and GR spheres become indistinguishable for very large radii. The same conclusions are valid for the electrostatic field intensity E. With regards to the proper charge density \(\sigma \) the plots indicate that they are roughly the same throughout the distribution with only minor variations.

7 The six dimensional case

In six dimensions more higher curvature terms are active and can influence the dynamics. Hence it is expected that the undesirable features found in the 5D case may be absent here. Setting \(p = 0\) and \(d = 6\) in (18)–(20) the system

$$\begin{aligned}&\frac{4\left( x+\beta (1-Z)\right) \left( 2Z{\dot{y}}-{\dot{Z}}y\right) }{x y} = \frac{\rho }{C} \end{aligned}$$
(56)
$$\begin{aligned}&\frac{-8x\left( x + \beta (1 - Z) \right) Z {\dot{y}} + (1-Z) (6x + \beta (1 - Z)) y}{x^{2} y} = \frac{E^2}{2C} \end{aligned}$$
(57)
$$\begin{aligned}&4x^2Z\left( x + 3\beta (1-Z)\right) \ddot{y} + 2x\left( x^2{\dot{Z}} +8xZ + 3\beta \left( 6Z(1-Z) \right. \right. \nonumber \\&\quad \left. \left. + {\dot{Z}}x(1-3Z)\right) \right) {\dot{y}} \nonumber \\&\quad +3\left( (\beta (1-Z) + x)({\dot{Z}}x +Z-1) -2x(1-Z)\right) y =0 \end{aligned}$$
(58)
$$\begin{aligned}&\frac{4Z}{x}\left( x{\dot{E}}+E\right) ^2 = \frac{\sigma ^2}{C^2} \end{aligned}$$
(59)

governing the dynamics of six dimensional charged dust emerges. In order to obtain the exterior metric for static 6D charged stars in EGB, we set \(Z = y^2\). This generates the potentials

$$\begin{aligned} y^2 = Z = 1 + \frac{x}{3\beta }\left( 1 + \sqrt{1+ \frac{8\beta C_1}{x^3} - \frac{3\beta C_2}{x^{\frac{5}{2}}}} \right) \end{aligned}$$
(60)

which is equivalent to the Wiltshire solution [39] in 6D. Note that in comparison with Wiltshire we assign the interpretation \(8\beta C_1\) as the charge contribution and \(3\beta C_2\) as the active gravitational mass of the hypersphere. Observe that expanding (60) in powers of \(\beta \) and taking \(\beta \rightarrow 0\) gives the 6 dimensional Reissner–Nordstrom solution. As was done with the 5D case we first investigate what metric potentials are admissible for physically realistic charged dust models.

Fig. 4
figure 4

Energy density \(\rho \), electrostatic field intensity E and proper charge density \(\sigma \) versus radius x for the 5D EGB case (\(\beta = \frac{1}{2}\)) and the 5D GR case (\(\beta = 0\))

Full size image

7.1 Existence of physically reasonable solutions

Bounds on the potential function Z may be established in the same way as for the 5 dimensional case and so we omit the detailed calculations. It turns out that for the case \(Z < 1 + \frac{x}{\beta }\) the applicable constraint is

$$\begin{aligned} 1 +\frac{x}{\beta }\left( 1-\sqrt{1+ \frac{\beta ^2 C_1}{x^{5/2}}} \right) \le Z \le 1+\frac{x}{\beta } \end{aligned}$$
(61)

where the rightmost term is the negative branch of the Boulware–Deser [9] potential for 6 dimensional spacetime. In the case \(Z > 1 + \frac{x}{\beta }\) we obtain the condition

$$\begin{aligned} 1+\frac{x}{\beta } \le Z \le 1 +\frac{x}{\beta }\left( 1+\sqrt{1+ \frac{\beta ^2 C_1}{x^{5/2}}} \right) \end{aligned}$$
(62)

constraining Z. Again it is noted that the positive and negative branches of the Boulware–Deser [9] metric act as upper and lower bounds for all acceptable spatial metric potentials. We do not display typical plots of feasible regions since the profiles follow the same structure as that for the five dimensional case.

8 Some exact charged dust hyperspheres in 6D

8.1 Constant spatial potential (\(Z = K\))

The simplest physically interesting choice of Z is \(Z = K\) a constant. The solution in this case may be expressed as hypergeometric functions of x in terms of parameters \(\beta \) and K. We were unable to determine suitable parameters that yielded closed form solutions.

The solution in terms of hypergeometric functions is given by

$$\begin{aligned} y= & {} _2F_1 \left( \frac{1}{2} + v - {\bar{v}}, \frac{1}{2} - v - {\bar{v}}, 1-{\bar{v}},\frac{x}{3\beta (K-1)} \right) A x^{-1-{\bar{v}}} \nonumber \\&+ _2F_1 \left( \frac{1}{2} + v + {\bar{v}}, \frac{1}{2} - v + {\bar{v}}, 1+{\bar{v}},\frac{x}{3\beta (K-1)} \right) B x^{-1+ {\bar{v}}} \nonumber \\ \end{aligned}$$
(63)

where we have relabeled \(v = \frac{3}{2\sqrt{K}}\) and \({\bar{v}} = \sqrt{\frac{3K + 1}{K}}\) and A and B are constants of integration. For the special case \(Z = 1\), the solution takes on the simple form

$$\begin{aligned} y= B -\frac{A}{3 x^3} \end{aligned}$$
(64)

however it turns out that this solution is not physically viable for the same reasons the 5D case failed. The density and electric field cannot both be positive.

8.2 Einstein ansatz in 6D

In contrast with the 5D case, the 6D situation offers richer physical behavior. Setting \(y = \) a constant in (58) generates the potential

$$\begin{aligned} Z = 1 + \frac{x}{\beta } \left( 1+\sqrt{\frac{\beta ^2 H}{x^4}+1}\right) \end{aligned}$$
(65)

where H is an integration constant. Curiously the interior solution (65) is equivalent to the 9 dimensional uncharged Boulware–Deser vacuum solution (25). Correspondingly the density, electric field intensity and charge density have the forms

$$\begin{aligned} \rho= & {} \frac{4 \left( 3 \sqrt{\frac{\beta ^2 H}{r^8}+1}+2\right) \left( r^8 \left( \sqrt{\frac{\beta ^2 H}{r^8}+1}+1\right) - \beta ^2 H\right) }{\beta r^{10} \sqrt{\frac{\beta ^2 H}{r^8}+1}} \nonumber \\ \end{aligned}$$
(66)
$$\begin{aligned} E^2= & {} \frac{3 \beta H}{r^8} \end{aligned}$$
(67)
$$\begin{aligned} \sigma ^2= & {} \frac{24 H}{r^{10}} \left( r^2 \left( \sqrt{\frac{\beta ^2 H}{r^8}+1}+1\right) +\beta \right) \end{aligned}$$
(68)

respectively in the canonical variable r. Note that in 6D the constant temporal potential does not yield a defective model as in the Einstein universe of the standard theory and the 5D Gauss–Bonnet gravity. The density vanishes for at least one real valued positive radius \(r = \frac{\root 4 \of {b} \root 8 \of {H}}{\root 8 \of {3}}\) which may be taken as identifying a hypersurface acting as the boundary of the charged distribution. So a 6D charged dust model with constant temporal potential yields a bounded compact hypersphere.

8.3 The Schwarzschild ansatz \(Z=1+x\)

Next we proceed to set \(Z=1+x\) which corresponds to the Schwarzschild ansatz. The field Eq. (58) reduces to the form

$$\begin{aligned} 2x(1+x)\ddot{y} + (9x+8){\dot{y}} + \frac{3\beta }{3\beta - 1} y = 0. \end{aligned}$$
(69)

The general solution is expressible in terms of hypergeometric functions in the form

$$\begin{aligned} y= & {} {_2F_1} \left( \frac{7\sqrt{3\beta -1}+\sqrt{123\beta -1}}{4\sqrt{3\beta -1}},\right. \nonumber \\&\left. \frac{7\sqrt{3\beta -1}-\sqrt{123\beta -1}}{4\sqrt{3\beta -1}}, \left[ \frac{1}{2}\right] ,1+x \right) A \nonumber \\&+ \sqrt{1+x} \,\, {_2F_1} \left( \frac{9\sqrt{3\beta -1}+\sqrt{123\beta -1}}{4\sqrt{3\beta -1}}, \right. \nonumber \\&\left. \frac{9\sqrt{3\beta -1}-\sqrt{123\beta -1}}{4\sqrt{3\beta -1}}, \left[ \frac{3}{2}\right] ,1+x \right) B \end{aligned}$$
(70)

where A and B are integration constants.As previously, we endeavor to locate exact solutions for suitable values of the parameters.

  • The special case \(\beta = \frac{1}{2}\) that is \(\alpha C = \frac{1}{8}\)

    In this case the gravitational potential has the form

    $$\begin{aligned}&y=\frac{3 B\left( x^3 \tanh ^{-1}v\left( 945x +840 \right) -v\left( 945x^3 -210 x^2+56 x-16 \right) \right) }{128 x^3}+A \left( x+\frac{8}{9}\right) \end{aligned}$$
    (71)

    It is easy to calculate the density, electric field intensity and charge density however following rigorous testing of the model with a large number of choices for the constants, no physically viable model emerged. Accordingly we omit displaying the expressions for the electrodynamical quantities.

  • The case \(\beta = \frac{14}{41}\)

    Through the process of empirical testing, a further special case generates an exact solution namely \(\beta = \frac{14}{41}\). The temporal potential evaluates to

    $$\begin{aligned} y&= \frac{c_1}{19458855} \left( 19458855 x^8+87814320 x^7\right. \nonumber \\&\left. +166135200 x^6+170881920 x^5+103564800 x^4\right. \nonumber \\&\left. \left. +37416960 x^3+7741440 x^2+819200 x+32768\right) \sqrt{x+1}\right) \nonumber \\&+\frac{498945 c_2}{146028888064 x^3}\left( -6511697713295775 x^{11}\right. \nonumber \\&\left. -31556688918279525 x^{10} \right. \nonumber \\&\left. -64522515840212430 x^9-72293575848282360 x^8\right. \nonumber \\&\left. -48213595767308400 x^7 \right. \nonumber \\&\left. -19432718772754560 x^6-4576886077121280 x^5\right. \nonumber \\&\left. -570854724940800 x^4 \right. \nonumber \\&\left. -29320501155840 x^3-157398958080 x^2\right. \nonumber \\&\left. +334639305 \left( 19458855 x^8+87814320 x^7 \right. \right. \nonumber \\&\left. \left. +166135200 x^6+170881920 x^5+103564800 x^4 \right. \right. \nonumber \\&\left. \left. +37416960 x^3+7741440 x^2 \right. \right. \nonumber \\&\left. \left. +819200 x+32768\right) \sqrt{x+1} x^3 \tanh ^{-1}\left( \sqrt{x+1}\right) \right. \nonumber \\&\left. +2998075392 x-57933824 \right) \end{aligned}$$
    (72)

    The solution is rather cumbersome and not suitable for detailed analysis. It does display the familiar defect of a singularity at the center of the distribution \(x = 0\). Note that it has been shown elsewhere [38] that a singularity is an essential feature of spherically symmetric charged dust in the standard Einstein theory. Higher curvature effects do not appear to remove these singularities at least in the metric functions. Notwithstanding singularities, thorough testing of the above two exact solutions using a variety of parameter space choices did not yield a model with reasonable physical behaviour. This does not mean that such does not exist in general since we have shown rigorously that such models exist.

8.4 Specifying the temporal potential

In order to detect exact solutions, Eq. (58) may be rearranged as a nonlinear first order differential equation in Z(x) of the Ricatti type. In this form, specifying the potential y(x) may lead to an exact solution. Speculating with the form \(y = x^n\), for n some rational number, a few cases arise with prospects for an exact solution. It emerges that the choice \(y = x^{-\frac{3}{2}}\) for the 6D EGB case generates the potential

$$\begin{aligned} Z = \frac{1}{4} \left( 1 \pm \frac{x}{\beta } \sqrt{x^{\frac{3}{2}} (8x + 9\beta ) + 16\beta x C_3} \right) \end{aligned}$$
(73)

where \(C_3\) is an integration constant. Relaxing to the GR case (\(\beta = 0\)) we see that \(y = x^n\) leads to the general solution \(Z = \frac{9}{(3+2n)^2} + x^{-(3+2n)} C_4\) where \(C_4\) is a constant of integration. Sadly the choice \(n = -\frac{3}{2}\) which worked in the 6D EGB case is ruled out in its Einstein GR counterpart case. Accordingly a graphical comparison between the EGB and the GR is not feasible.

9 Conclusion

We have obtained the equations of motion for charged dust in 5 and 6 dimensional EGB. An important result emanating from our calculations is that physically viable models of charged dust may only be constructed subject to the spatial metric potential having the branches of the Boulware–Deser metric of uncharged EGB gravity as bounds. In both 5 and 6 dimensions it was possible to find some exact solutions however it was not possible to check their physical reasonableness due to the very complicated forms of the resulting expressions. A 5 dimensional charged dust model with physically pleasing profiles was developed and compared to its general relativity counterpart. It was found that the higher curvature terms tended to reduce the density and electrostatic field intensity of the sphere for the same value of the radius in the general relativity case. The proper charge density experienced only marginal changes and the EGB and GR cases were fairly indistinguishable in the scale employed. Interestingly in the case of the 6 dimensional hypersphere with the Einstein ansatz of a constant temporal potential a closed compact astrophysical object was possible. In all cases a singularity at the stellar centre was unavoidable and points to this being a generic feature of charged dust models. For this reason, the exact solutions found in this work may be taken to represent atmospheres of charged dust surrounding other spherical distributions with regular central behavior.