1 Introduction

The black hole is one of the important predictions in general relativity, and people have been trying to find this mysterious object in the universe. With the intense efforts over the last years, the Event Horizon Telescope (EHT) has recently acquired an ultra-high angular resolution image of accretion flows around a supermassive black hole in M87 [1,2,3,4,5,6]. According to the first image of M87, there is a bright ring around the interior of the dark. The bright ring, as an important observation feature of the black hole, which is called photon ring. And, the dark area in the center is called the shadow of black hole. For a distant observer, the shadow appears as a two-dimensional dark zone, and it resulted from the gravitational light deflection by the black hole [7,8,9,10,11]. The outer edge of the shadow in a black hole image located at the photon ring, that is, the photon ring is the light ray that escapes from the orbit of bound photons around a black hole to a distant observer. Hence, the photon ring is also defined as the apparent boundary or critical curve [12, 13]. In the case of the Schwarzschild black hole, the orbit of bound photons is \(r=3M\) and the critical curve has a value \(b=3\sqrt{3}M\), where M is the mass of the black hole and b is defined as the impact parameter. Therefore, the interior of the critical curve is also used to represent the shadow of a black hole.

The accretion matter surrounding the black hole has a nonnegligible influence on the shadow of the black hole, and it plays an indispensable role in the observation of the shadow of the black hole. Based on the research [14], the geometrically and optically thick accretion disk was found to affect the shadow of the black hole. And, the shadow of a black hole around by the thin accretion disks has been studied carefully in Ref. [13], it was pointed out that there are not only photon rings , but also lensing rings outside the black hole shadow. In addition, the change of the emission region will affect the width and brightness of the lensing rings. Besides the size of the observed shadow is very much dependent on the emission model, the details of accretion have little effect on the dark central area. On the other hand, the black hole also has shadow that is spherically symmetric when the accretion matter is spherically symmetric [15]. Soon after, the related research about the shadows cast by the four-dimensional Gauss-Bonnet black hole with spherical accretions, and the observed specific intensity of the shadow images for the black hole in the quintessence dark energy model has also been studied [16, 17].

The study of black hole shadow provides a feasible method for detecting the characteristics of black holes, and more and more interesting studies have been obtained in general relativity, as well as modified theories of gravity [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Indeed, the accretion flow is generally not spherically symmetric in the universe, but the simplified spherical model is helpful to explore the basic properties of accretion in the usual general-relativistic magnetohydrodynamics models [5]. On the other hand, the torsion is a widespread existence in gravitational theory, especially the theory of quantum gravity [44,45,46,47,48,49,50,51,52,53,54]. In [55], Blagojevic et al. studied the entropy of black hole from the boundary conformal structure in three-dimensional gravity with torsion. Then, Chakraborty et al. proved that the existence of spacetime torsion does not affect the entropy-area relationship of the system [56]. Recently, the orbits of particles, the entropy and the thermodynamics of the black hole with torsion have been studied in the context of the Poincaré gauge theory of gravity [57,58,59]. Among them, the effects of torsion appear as a single parameter in the line element. The black hole solution in [57,58,59] is similar with the Reissner–Nordström solution, but the charge is produced by the gravitational field in vacuum, which is differs from the standard electric charge in the Reissner–Nordström metric. By the above arguments, studying the shadow of black holes with torsion would be a matter of interest. In this paper, we explore the shadow and observed intensities of black hole with different values of torsion charge. When the black hole is wrapped by different accretion models, we study the effect of torsion charge on the photon ring, lensing ring and shadow of the black hole. Moreover, we further compare the observation characteristics of black hole shadow under different torsion charges with the observation results of Schwarzschild spacetime, so as it can be used to distinguish black holes in the context of the Poincaré gauge theory of gravity from the Schwarzschild black hole. And in addition, it is also a part of this work to constraint the torsion charge parameters from the shadow of the black given. hole.

The organization of the paper is as follows: In Sect. 2, we introduce the orbits of photon and effective potential for the black hole with torsion charge in the context of the Poincaré gauge theory of gravity; in Sect. 3, we show the images of the black hole which is surrounding by the thin disk accretion; in Sect. 4, we investigate the shadows and photon spheres with the spherical accretion, and find that the observed specific intensity in these two different accretion models (static and infalling spherical accretion) is obviously different; in Sect. 5, a brief review and discussion of the main results are given.

2 The orbits of photon and effective potential for the black hole with torsion

In this section, our aim is to investigate the light deflection caused by the four-dimensional static black hole in the context of the Poincaré gauge theory of gravity (PGT), we want to explore the motion of light ray near a black hole. Considering that the most general Lagrangian function is a quadratic function established by the irreducible decomposition of curvature and torsion, the Lagrangian form we adopt in Poincaré gauge theory is [58]

$$\begin{aligned} L_{g}= & {} -\frac{A_0}{2}R+\frac{B}{24}R^2 \nonumber \\&+\frac{A_1}{8}\Big (T_{\nu \sigma \mu }T^{\nu \sigma \mu }+2T_{\nu \sigma \mu }T^{\mu \sigma \nu }-4T_\mu T^\mu \Big ). \end{aligned}$$
(1)

Here, \(A_0\), \(A_{1}\) and B are coupling constants and R is the Ricci scalar. In this case, one can obtain the static vacuum solution for a spacetime with non-vanishing torsion, which takes the form

$$\begin{aligned} ds^2=-N (r) d t^2+\frac{1}{N (r)} d r^2 +r^2 d \Omega ^2, \end{aligned}$$
(2)

and

$$\begin{aligned} N (r)=1-\frac{2 M}{r}+\frac{\mathcal {S}}{r^2}, \end{aligned}$$
(3)

where \(d \Omega ^2=d\theta ^2+\sin ^2 \theta d\varphi ^2\) is the line element on a unit sphere, which describe the spacetime of a four-dimensional spherically symmetric black hole in PGT gravity. In addition, M is related to the mass of the black hole. And, the parameter \(\mathcal {S}\) is related to the spin of matter, which is produced by the gravitational field in vacuum called torsion charge. In this solution, the torsion charge parameter \(\mathcal {S}\) can be assumed as a positive or negative value. Note that the root of the metric function is the horizon of the black hole, which is located at

$$\begin{aligned} r_\pm =M\pm \sqrt{M^2-\mathcal {S}}. \end{aligned}$$
(4)

Here, \(r_+\) is the larger root which corresponds to the event horizon (Killing horizon) of the black hole. It should be pointed out that the above equation following condition \(M^2\ge \mathcal {S}\). If \(0<\mathcal {S}\le 1\), the metric (3) coincides with the one of Reissner–Nordström spacetime, and one can find that \(r_+(PGT)<r(GR)\). The negative values for \(\mathcal {S}\) are not allowed in the context of General Relativity. Due to the negative value for \(\mathcal {S}\) are permitted in this spacetime, we can get \(r_+(PGT)>r(GR)\), that is, the black hole region is enlarged in this case. In particular, the Schwarzschild radius is equal in Poincaré gauge theory and general relativity \(r_+(PGT)=r(GR)\) in the limiting case of \(\mathcal {S}=0\).

Table 1 The numerical result of photon sphere radius \(r_p\), critical impact parameter \(b_{p}\) and event horizon \(r_e\) under the different values of \(\mathcal {S}\), in which \(M = 1\)
Full size table

Since the wavelength of the actual light source is smaller than the size of the black hole, we can discuss the problem of black hole shadow in the scope of geometrical optics. The key problem in this work is to find the behavior of the light ray in the region near the black hole. Following the geodesic motion and with the help of the Euler-Lagrange equation, the motion equations can be express as

$$\begin{aligned} \frac{d}{d \lambda }\left( \frac{\partial \mathcal {I}}{\partial {\dot{x}}^{\mu }}\right) =\frac{\partial \mathcal {I}}{\partial x^{\mu }}. \end{aligned}$$
(5)

In which \(\lambda \) is the affine parameter and \({\dot{x}}^{\mu }\) is the four-velocity of the light ray. The Lagrangian \(\mathcal {I}\) can be specifically written as

$$\begin{aligned}&\mathcal {I}=\frac{1}{2}g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }\nonumber \\&\quad =\frac{1}{2}\left( -N(r){\dot{t}}^2+\frac{{\dot{r}}^2}{N(r)}+r^2\left( \dot{\theta }^2+\sin ^2\theta {\dot{\varphi }}^2\right) \right) , \end{aligned}$$
(6)

This is a spherically symmetric space-time, and the metric coefficients in Eq. (2) do not depend explicitly on the time t and azimuthal angle \(\varphi \). Hence, there are two conserved quantities, i.e.,energy E and angular momentum L. In this work, we pay close attention to the motion of photons on the equatorial plane, which means \(\theta =\frac{\pi }{2}\), and \({\dot{\theta }}=0\) [9]. From the Euler-Lagrangian equations, we can obtain

$$\begin{aligned} E={\dot{t}} N(r),\quad {\dot{\varphi }}=\pm \frac{1}{r^2}. \end{aligned}$$
(7)

Substitute Eq. (7) into Eq. (6), which is

$$\begin{aligned}&{\dot{t}}=\frac{1}{b_c N(r)},\nonumber \\&\quad {\dot{r}}^2=E^2-\frac{L^2}{r^2}N(r). \end{aligned}$$
(8)

There, we take the affine parameter \(\lambda \rightarrow \frac{\lambda }{|L|}\) [16, 17]. It is worth mentioning that the impact parameter \(b_c=\frac{L}{E}\), which represents the ratio of angular momentum to energy. Therefore, we can get anther form of Eq. (8), that is

$$\begin{aligned} {\dot{r}}^2+V_{{eff}}=\frac{1}{b_c^2}, \end{aligned}$$
(9)

and

$$\begin{aligned} V_{{eff}}=\frac{1}{r^2} N(r). \end{aligned}$$
(10)

where \(V_{{eff}}\) is an effective potential. Moreover, the effective potential \(V_{{eff}}\) in the position of the photon ring should satisfy the following conditions

$$\begin{aligned} V_{{eff}}=\frac{1}{b_c^2}, \quad V_{{eff}}'=0. \end{aligned}$$
(11)

In the four-dimensional symmetric spactime, the radius \(r_p\) and critical impact parameter \(b_p\) of photon sphere follow

$$\begin{aligned} r_p{}^2=b_p^2 N(r),\quad 2 b_p^2 N(r)^2=r_p^3N'(r). \end{aligned}$$
(12)

Through the above equation, we can obtain the position of the photon sphere radius \(r_p\) and the critical impact parameter \(b_p\). We take different values of the torsion charge \(\mathcal {S}\), and list the relevant numerical results which are shown in the Table 1.

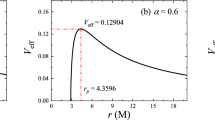
From Table 1, one can see that both the radius of photon sphere \(r_p\) and critical impact parameter \(b_p\) show a decreased trend with the increase of \(\mathcal {S}\), as well as the radius of event horizon \(r_e\). Compared with Schwarzschild spacetime, the presence of negative parameter \(\mathcal {S}\) enhances the size of the event horizon and photon sphere, that is, the boundary of black hole shadow is expanded. The effective potential is a very important physical quantity in judging the motion behavior of photons near black holes. Taking \(\mathcal {S}=-0.99\) as an example, we plot the graph of effective potential \(V_{eff}\), which are shown in Fig. 1a. Moreover, Fig. 1b shows the black hole effective potential when \(\mathcal {S}\) takes different values in Poincaré gauge theory (including Schwarzschild black hole solution).

Fig. 1
figure 1

The profiles of the effective potential \(V_{eff}\) and impact parameter \(b_c\) , in which \(M=1\). a The change trend of effective potential when \(\mathcal {S}=-0.99\). b The effective potential for different values \(\mathcal {S}\)

Full size image

In Fig. 1a, the results show that there is no effective potential \(V_{eff}\) in the region within the event horizon of black hole \((r<r_e)\). The effective potential increases from the horizon and reaches its maximum at the photon sphere, and then decreased. In the special position \(b_c=b_p\), the light ray is in a critical state of being captured and escaping, and it will rotate around the black hole infinitely many times due to the angular velocity is not zero, this case corresponds to the Region 2 (red lines) in Fig. 1a. Hence, the position of the photon sphere radius corresponds to the Region 2. For the case of \(b_c>b_p\), the light will encounter the potential barrier and then the path of light will have a turning point at \({\dot{r}}^2=0\). Therefore, the photons do not fall into the black hole, which corresponds to Region 1 in Fig. 1a. For the case of \(b_c<b_p\), the photons fall directly into the black hole and cannot be observed by observers, which corresponds to Region 3 in Fig. 1a. In Fig. 1b, it found that the increase of the torsion charge \(\mathcal {S}\) will lead to an increase in the peak value of the effective potential, and the positive torsion charge \(\mathcal {S}\) has a higher effective potential peak. Therefore, a larger torsion charge leads to a weaker peak effective potential at a smaller radius.

In order to describe the trajectory of light, we can get the concrete expression of photon motion equation with the help of Eqs. (7) and (8), which is

$$\begin{aligned} \frac{{dr}}{d \varphi }=\pm r^2\sqrt{\frac{1}{{b_c}^2}-\frac{1}{r^2}\left[ 1-\frac{2 M}{r}+\frac{\mathcal {S}}{r^2}\right] }. \end{aligned}$$
(13)

After introduce a new parameter \(u=1/r\), the Eq. (13) can be rewritten as

$$\begin{aligned} \mathcal {R}(u,b)\equiv \frac{d u}{d \varphi }=\sqrt{\frac{1}{b_c{}^2}-u^2\left[ 1-2M u+ \mathcal {S} u^2\right] }. \end{aligned}$$
(14)
Fig. 2
figure 2

The trajectory of the light ray for the different value of torsion charge \(\mathcal {S}\) in the polar coordinates \((r, \varphi )\), in which \(M=1\). The black hole is shown as a black disk, and the green lines, red lines and black lines correspond to \(b > b_p\), \(b = b_p\) and \(b < b_p\), respectively

Full size image

The geometry behavior of geodesics depends on Eq. (14). Therefore, we can plot the trajectory of the light ray for different values of torsion charges, which is shown in Fig. 2. In the case of \(b_c>b_p\) (green lines in Fig. 2), one can find that the trajectory of the light ray deflected. The light ray move toward the black hole from infinity approaching one closest point, and move away from the black hole back to infinity. In the case of \(b_c<b_p\), the light ray fall into the black hole, which is corresponds to black lines in Fig. 2. In particular, for the case of \(b_c=b_p\), the light ray revolves around the black hole, neither falling into nor escaping from the black hole, which is the position of the photon sphere (red lines in Fig. 2). From Fig. 2, the radius of the black disk is smaller, but the deflection degree of light ray is more higher when the parameter \(\mathcal {S}\) is increase. That is, the light density that can be obtained by a distant observers will increase, and the brightness of the shadow observation image is different in the spacetime (2).

3 The shadows of black hole surrounding by the thin disk accretion

In this section, we study the shadow and appearance of black hole to a distant observer \((r\rightarrow \infty )\), in which the accretion emission from different locations near the black hole. In the background of the optically and geometrically thin disk accretion around the black hole, we turn our attention to investigate the black hole shadow, photon rings and lensing rings of the black hole, due to these are important features of the black hole.

3.1 Light bending: diret, lensed and photon ring

As mentioned in Ref. [13], they reanalyzed the orbit of the photon and redefined the photon ring and lensing ring. As a result, the fundamental difference between the lensing rings and photon rings is the number of times a light ray intersects the disk plane outside the event horizon. In order to distinguish the photon rings from the lensing rings in spacetime (2), one can define the total number of light orbits near the black hole is \(n=\frac{\varphi }{2\pi }\) according to Ref. [13]. If the number of orbits \( n < 3/4\), the trajectories of light ray will intersect the equatorial plane only once, corresponding to the direct emissions. If the number of orbits \( 3/4< n < 5/4\), the light ray crossing the equatorial plane at least twice, corresponding to the lensing rings. If the number of orbits \( n > 5/4\), the trajectories of light ray will intersect the equatorial plane at least 3 times, that is, the photon ring. Here, we take \(S=-0.99\), \(S=0.1\) and \(S=0.80\) as examples, and show the results of these ray classification

$$\begin{aligned} \mathcal {S}=-0.99 {\left\{ \begin{array}{ll} \text {Direct emission}: n<3/4,~~~ b_c< 5.777 ~~ \text {and} ~~ b_c> 6.8315 \\ \text {Lensing ring}: 3/4<n<5/4,~~~ 5.777<b_c< 5.927 ~~ \text {and} ~~ 5.95647<b_c<6.8315 \\ \text {Photon ring}: n>5/4,~~~ 5.927< b_c < 5.95647 \end{array}\right. } \end{aligned}$$
(15)
$$\begin{aligned} \mathcal {S}=0.1 {\left\{ \begin{array}{ll} \text {Direct emission}: n<3/4,~~~ b_c< 4.92189 ~~ \text {and} ~~ b_c> 6.0919 \\ \text {Lensing ring}: 3/4<n<5/4,~~~ 4.92189<b_c< 5.09889 ~~ \text {and} ~~ 5.14106<b_c<6.0919 \\ \text {Photon ring}: n>5/4,~~~ 5.09889< b_c < 5.14106 \end{array}\right. } \end{aligned}$$
(16)
$$\begin{aligned} \mathcal {S}=0.80 {\left\{ \begin{array}{ll} \text {Direct emission}: n<3/4,~~~ b_c< 4.05252 ~~ \text {and} ~~ b_c>5.49194 \\ \text {Lensing ring}: 3/4<n<5/4,~~~ 4.05252<b_c<4.31136 ~~ \text {and} ~~ 4.39299<b_c< 5.49194 \\ \text {Photon ring}: n>5/4,~~~ 4.31136< b_c < 4.39299 \end{array}\right. } \end{aligned}$$
(17)

To show the differences of these classifications more intuitively, we will show them in Fig. 3. The colors correspond to \(n < 3/4\) (red lines), \(3/4< n < 5/4\) (blue lines)and \(n > 5/4\) (green lines), defined as the direct, lensed, and photon ring trajectories, respectively. From Fig. 3, one can find that the region and range of lensing ring, photon ring and direct emission will change when the value of \(\mathcal {S}\) is different. With the increase of the value of \(\mathcal {S}\), the range occupied by the lensing ring and the photon ring becomes larger, but the value of the corresponding impact parameter decreases. These differences are particularly evident between \(\mathcal {S} =-0.99\) and \(\mathcal {S} = 0.8\). It reflects that the radius of the photon ring and event horizon of the black hole will decrease with the increase of the value of \(\mathcal {S}\). The corresponding photon trajectories near the black hole are shown in Fig. 4, which is the polar coordinates (\(b_c, \varphi \)). When the torsion charge \(\mathcal {S}\) takes a negative value, the area occupied by the blue line and the green line is smaller than that \(\mathcal {S}\) takes a positive value. In other words, with the increase of torsion charge, the thickness of lens ring and photon ring gradually becomes thicker.

Fig. 3
figure 3

The variation trend of orbit number \(n= \frac{\varphi }{2\pi }\) with the impact parameter \(b_c\) for the different value \(\mathcal {S}\), in which \(M = 1\)

Full size image
Fig. 4
figure 4

The corresponding photon trajectory near the black hole, where M = 1. The spacings in impact parameter are 1/5, 1/100, 1/1000, for the direct (red), lensing (blue), and photon ring (green) bands, respectively. Here, the dashed red line is the photon ring and the black solid disk represents the outer boundary of event horizon

Full size image

3.2 Observational appearance of thin disk emission

As well as known, the emission is always accumulated in a certain finite region near the black hole such as the accretion disk. In this work, we take the disk to lie in the equatorial plane of the black hole. Meanwhile, the static observer is assumed to locate at the north pole, and the lights emitted from the accretion disk is considered isotropic in the rest frame of the static observer. The emitted specific intensity and frequency can be expressed as \(I^{{em}}(r)\) and \( v_e \) in the static frame. Therefore, an observer in infinity can receive the specific intensity should be \(I^{{obs}} (r)\) and redshifted frequency \( v_o =\sqrt{N(r)} v_e \). Considering \(I^{{em}}/ v _e{}^3\) is conserved along a light ray [13, 17], we have the observed specific intensity

$$\begin{aligned} I^{{obs}} (r)=N(r)^{3/2}I^{{em}}(r). \end{aligned}$$
(18)

So the total specific intensity is obtained by integral over all frequencies, that is

$$\begin{aligned} I(r)&=\int I^{{obs}}(r)d v_o \nonumber \\&=\int N(r)^2I^{{em}}(r)d v _e=N(r)^2I^{{em}}(r), \end{aligned}$$
(19)

where \(I^{{em}}=\int I^{{em}}(r)d v_e \) has denoted the total emitted intensity from the accretion disk. When the light ray is traced backward from the observer through the disk, it will pick up the brightness from the disk emission. As discussed earlier, in the case of \(3/4<n<5/4\), the light ray will bend around the black hole, intersecting with the disk for the second time on the backside (the blue line in Fig. 3 represents). Further, the light ray will intersect with the disk for the third time on the front side again for \(n>5/4\)(the green line in Fig. 3 represents). As a result, the light ray gets extra brightness from the thin disk when it passages through the disk. The observed intensity is a sum of the intensities from each intersection, namely

$$\begin{aligned} I(r)=\sum _n N(r)^2I^{{em}}|_{r=r_n(b)}. \end{aligned}$$
(20)

Here, \(r_n(b)\) can be defined as a transfer function, it is the radial position of the \(n^{th}\) intersection with the emission disk plane outside the event horizon. As an ideal model, we do not consider the absorption and reflection of light by accretion disks, due to it will reduce the observation intensity. What needs to be emphasized is that the demagnified scale is determined by the slope of the transfer function, and \(dr/d\varphi \) called the demagnification factor. When the value of \(\mathcal {S}\) is changed, the relation between impact parameter \(b_c\) and the transfer function is shown in Fig. 5.

Fig. 5
figure 5

The first three transfer functions for black hole with the different values of torsion charge \(\mathcal {S}\), in which \(M=1\). The black, orange, and red line represent the direct emission, lensed ring emission, and photon ring emission, respectively

Full size image

In Fig. 5, which are represent the radial coordinate of the first \(n=1\) (black line), second \(n=2\) (orange line), and third \(n=3\) (red line) intersections with the emission disk. The first transfer function corresponds to the direct image of the disk, which is essentially the redshifted source profile. The second transfer function gives a highly demagnified image of the backside of the disk, referred to as the lensing ring. And the third transfer function will give an extremely demagnified image of the front side of the disk due to the slope is about infinite, referred to as the photon ring. Moreover, we find that when \(\mathcal {S}\) takes a large value, the slope of the second transfer function will not reach a large value in the initial interval, that is, the image of the lensing ring will not be highly demagnetized at the initial position.

Armed with the previous preparations, we further study consider concrete emission profile intensity on the basis of Eq. (20). Considering that the innermost stable circular orbit represents the boundary between test particles orbiting the black hole and test particles falling into black hole. Firstly, we assume that the emission is sharply peaked at \(r_{isco}\), and the emission follow the decay function of the power of second order. That is

$$\begin{aligned} I_1^{{em}}(r) ={\left\{ \begin{array}{ll}\left( \frac{1}{r-(r_{isco}-1)}\right) ^2, &{} r>r_{{isco}} \\ 0, &{}r \le r_{{isco}} \end{array}\right. } \end{aligned}$$
(21)

Then, we consider the emission is a decay function of the power of third order, and the sharply peaked at the photon sphere but decays fast to zero, such as

$$\begin{aligned} I_2^{em}(r) ={\left\{ \begin{array}{ll}\left( \frac{1}{r-(r_{ph}-1)}\right) ^3, &{} r> r_{p} \\ 0, &{}r \le r_{p} \end{array}\right. } \end{aligned}$$
(22)

Finally, the emission starts from the outer edge of the event horizon \(r_e\) and belongs to the form of moderate decay, which is

$$\begin{aligned} I_3^{em}(r) ={\left\{ \begin{array}{ll} \frac{\frac{\pi }{2}-\tan ^{-1}(r-(r_{isco}-1))}{\frac{\pi }{2}-\tan ^{-1}(r_{ph})} , &{} r>r_e \\ 0, &{}r \le r_e \end{array}\right. } \end{aligned}$$
(23)

We can plot the observed intensities \(I^{obs}(r)\) of these emission profiles, which are shown in Fig. 6 for \(\mathcal {S}=-0.99\). And, the relevant results are also shown when \(\mathcal {S}=0.80\) in Fig. 7. In Figs. 6 and 7, the left column is the profiles of various emissions \(I^{em}(r)\), the middle is the relationship between observed intensities \(I^{obs}(r)\) and impact parameter \(b_c\), and the right column shows the two-dimensional density plots of the observed emission \(I^{obs}(r)\), respectively. It is worth mentioning that the emitted and observed intensities \(I^{em}(r)\) and \(I^{obs}(r)\) are normalized to the maximum value of the emitted intensity outside the horizon.

Fig. 6
figure 6

Observational appearances of a geometrically and optically thin disk with different profiles near black hole, where the torsion charge \(\mathcal {S}=-0.99\). The panels in the first, second, and third row are for the scenarios of the emitted functions \(I_1^{{em}}(r)\), \(I_2^{{em}}(r)\), and \(I_3^{{em}}(r)\), respectively

Full size image
Fig. 7
figure 7

Observational appearances of a geometrically and optically thin disk with different profiles near black hole, where the torsion charge \(\mathcal {S}=0.8\). The panels in the first, second, and third row are for the scenarios of the emitted functions \(I_1^{{em}}(r)\), \(I_2^{{em}}(r)\), and \(I_3^{{em}}(r)\), respectively

Full size image

In the first emission model \( I_1^{{em}}(r)\), one can see that the emission peaks at \(r\simeq 7.30 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 4.54 M\) for \(\mathcal {S}=0.80\)), and the observed direct emission peaks \( I_1^{{obs}}(r)\) at \(r\simeq 8.30 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 5.40 M\) for \(\mathcal {S}=0.8\)). The observed peak position is larger than the emission peak position, which is caused by the gravitational lensing effect. The lensing ring and photon ring are separated, and both are in a very narrow range. Specifically, the observed lensing ring emission is presented at \(6.20M\sim 6.73M\) for \(\mathcal {S}=-0.99\) (\(4.66 M\sim 5.39 M\) for \(\mathcal {S}=0.80\)). And, the observation intensity provided by the lensing ring is very small, accounting about \(1.32\%\) for \(\mathcal {S}=-0.99\) (\(1.85\%\) for \(\mathcal {S}=0.80\)) of the total observation flux. In addition, the photon ring emission occur at \(r\simeq 5.94 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 4.37 M\) for \(\mathcal {S}=0.80\)). The contribution of photon ring to the total observed flux is only \(0.063\%\) for \(\mathcal {S}=-0.99\) ( \(0.098\%\) for \(\mathcal {S}=0.80\)), which is not take into account. Comparing Figs. 6 and 7, one can find that there is almost no observed peak of the photon ring when \(\mathcal {S}= -0.99\). Therefore, the contribution of photon ring to the total observed flux can be ignored when \(\mathcal {S}\) is negative, and the photon ring is almost invisible in the two-dimensional observation appearance in the third column of Fig. 6. Hence, the observed intensity is mainly determined by direct emission, and the observed flux provided by lensing ring is a small part, the photon ring contributes a negligible part.

In the second emission model \( I_2^{{em}}(r)\), the emission peak extends to the position near the outside of the event horizon \(r\simeq 3.56 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 2.30 M\) for \(\mathcal {S}=0.80\)). And meanwhile, the observed direct emission peaks \( I_2^{{obs}}(r)\) at \(r\simeq 4.55 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 4.36 M\) for \(\mathcal {S}=0.8\)). Interestingly, the photon ring and lensing ring are combined in a very narrow range, and we can not distinguish them. Moreover, the negative \(\mathcal {S}\) makes the position of the direct observation peak closer to the emission peak than when \(\mathcal {S}\) is positive (or the Schwarzschild spacetime). In this process, the observed lensing ring and photon ring at the range \( 5.90 M \sim 6.22 M\) for \(\mathcal {S}=-0.99\) (\( 4.31 M \sim 4.84 M\) for \(\mathcal {S}=0.8\)), and the contribution of the lensing ring and photon ring emission to the total observed intensity is \(0.83\%\) for \(\mathcal {S}=-0.99\) (\(1.39\%\) for \(\mathcal {S}=0.8\)). In the second emission model, the results show that the contribution of the lensing ring to the observation intensity weakened. Therefore, the observation luminosity mainly depends on direct emission, and the observation intensity provided by photon ring and lens ring is a very small part.

In the third emission model \( I_3^{{em}}(r)\), the emission peak extends to the position near the outside of the photon ring \(r\simeq 2.42 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 1.45 M\) for \(\mathcal {S}=0.80\)). Then, the observed direct emission peaks \( I_3^{{obs}}(r)\) at \(r\simeq 6.10 M\) for \(\mathcal {S}=-0.99\) (\(r\simeq 4.36 M\) for \(\mathcal {S}=0.8\)). Similar to the second emission model, the photon ring is wrapped in the lensing ring region, and the observed lensing ring and photon ring at the range of \( 5.80 M \sim 6.85 M\) for \(\mathcal {S}=-0.99\) (\( 4.40 M \sim 5.51 M\) for \(\mathcal {S}=0.8\)). In addition, the observed intensity of photon ring and lensing ring accounts for \(2.69\%\) for \(\mathcal {S}=-0.99\) ( \(2.85\%\) for \(\mathcal {S}=0.8\)). In this emission mode, that the proportion of lens ring and photon ring to the total observed flux is significantly enhanced compared with the first two models, and the contribution of photon ring and lensing ring to the observed intensity can not be ignored. That is, a bright light band will appear at the position of the lensing ring outside the black hole shadow, and the size of the light band becomes wider as the value of \(\mathcal {S}\) increases.

By comparing the results of Figs. 6 and 7, the results show that different emission models will lead to different observation appearance, and the contribution of photon ring and lens ring to the total observation flux will also change. It is worth mentioning that in the first emission model, due to the emergence of negative torsion charge \(\mathcal {S}\), the photon ring cannot be observed in the two-dimensional observation image, while an extremely weak ring will appear in the interior of the black disk when \(\mathcal {S}\) is positive. However, the negative enhances the total observation intensity, that is, the observation intensity will weaken with the increase of \(\mathcal {S}\). Hence, the change of the torsion charge parameter \(\mathcal {S}\) will not only change the optical observation intensity of black hole shadow, but also affect the proportion of photon ring and lens ring to the total observation intensity.

Fig. 8
figure 8

The two-dimensional shadow image from Fig. 6 before blurring (top row), and the two-dimensional image after blurring (bottom row)with a Gaussian filter with standard derivation equal to 1/12 the field of view (simulating the nominal resolution of the Event Horizon Telescope)

Full size image

In anticipation, it is believed that the observed emission will peak near the photon ring, which is a robust feature of the emission model. After analyzing the model of a black hole surrounded by a thin disk, one can find that this is not the case. Especially, the results show that photon ring cannot be observed directly in the two-dimensional observation map when the torsion charge parameter \(\mathcal {S}\) is negative, and the lensing ring is also not optimistic about the observation results. In the case of \(\mathcal {S}=0.80\), there is an weaker ring inside the black disk, i.e., the photon ring, which is imperceptible when \(\mathcal {S}=-0.99\). Since the area occupied by the photon ring is too narrow and does not make a significant contribution to the observed flux, the photon ring may not be relevant to the EHT observation. According to the geometry of the emission region and its emission model, the lensing ring contributes to the the EHT observation, although the main contribution is still provided by direct emission. Therefore, we blurred the images obtained in Fig. 6 to roughly correspond to the EHT resolution, and show the comparison results in Fig. 8 (The simple blurring does not correspond to the EHT image reconstructions). Evidently, the sharp features of the lens ring in the simulated observation results are washed out after fuzzy processing, and the existence of photon ring can not be observed directly. In the leftmost column in Fig. 8, we can see that the observed peak appears in the area outside the lensing ring. In the middle column, the observed peak is inside the range of lensing ring. In the rightmost column, the position of the observation peak in the blurred image is within the range of the lens ring. In this spacetime, the observation intensity and shadow area after blurring are stronger than those in Schwarzschild spacetime [13] due to the effect of negative \(\mathcal {S}\) value, and the light band appearing in the rightmost column has a larger intensity and size than Schwarzschild spacetime. Hence, the effectiveness of EHT mass measurement depends on the detailed physical assumptions of the simulated image used to fit the observation results.

4 Shadows and photon spheres with spherical accretions

In this section, we intend to investigate another accretion model, which is the spherical optical accretion. Specifically, we consider spherical accretion on a gravitating object, which is assumed to be optically thin. In addition, two different processes are mainly considered, that is, the static spherical accretion and infalling spherical accretion.

4.1 The static spherical accretion

We will investigate the shadow image and photon spheres of the black hole with torsion charge, and the spherical accretion matter is stationary. As mentioned in Refs. [60, 61], the specific intensity observed by the observer \(\mathrm (erg s^{-1} cm^{-2} str^{-1} Hz^{-1})\) can be shown as

$$\begin{aligned} \mathcal {I}_{{\nu _{obs}}}=\int _{\gamma }g^3 j( \nu _e) dl_{{prop}}, \end{aligned}$$
(24)

where

$$\begin{aligned} g=\frac{\nu _o}{\nu _e}. \end{aligned}$$
(25)

In which, g is the redshift factor, \(\nu _e\) is the photon frequency and \(\nu _o\) is observed photon frequency. In the rest frame of the emitter, \(j( \nu _e)\) is the emissivity per unit volume, and \(dl_{{prop}}\) is the infinitesimal proper length. In a four-dimensional static spherically symmetric spacetime, the redshift factor can be obtained as \(g=N(r)^{1/2}\). By considering a simple model that the radiation of light is monochromatic with a fixed frequency as \(\nu _f\), we can get

$$\begin{aligned} j\left( \nu _e\right) \propto \frac{\delta \left( \nu _e-\nu _f\right) }{r^2}, \end{aligned}$$
(26)

and

$$\begin{aligned} {dl}_{{prop}}=\sqrt{\frac{1}{N(r)}{dr}^2+r^2{d \varphi }^2}. \end{aligned}$$
(27)

Here, \(\delta \) is the delta function, and Eq. (26) take the radial profile as \(1/r^2\). Hence, Eq. (27) can be rewrite as

$$\begin{aligned} {dl}_{{prop}}=\sqrt{\frac{1}{N(r)}+r^2\left( \frac{{d\varphi }}{{dr}}\right) ^2}{dr}. \end{aligned}$$
(28)

On the basis of Eqs. (13), (24) and (28), the specific intensity observed by a static observer at infinity is

$$\begin{aligned} I_{{obs}}=\int _{\gamma }\frac{N(r)^{3/2}}{r^2}\sqrt{\frac{1}{N(r)}+r^2\left( \frac{{d\varphi }}{{dr}}\right) ^2}{dr}. \end{aligned}$$
(29)

From Eq. (29), one can find that the observation intensity depends largely on the torsion charge \(\mathcal {S}\) and is also limited by the impact parameter \(b_c\). It is worth mentioning that the intensity is circularly symmetric, with the impact parameter \(b_c\) of the radius, and satisfy the relationship \({b_c}^2=x^2+y^2\). In order to intuitively demonstrate the change of intensity \(I_{{obs}}\) with parameters \(\mathcal {S}\) and \(b_c\), we show the variation relationship between observation intensity \(I_{{obs}}\) and impact parameter \(b_c\) when \(\mathcal {S}\) takes different values, which are shown in Fig. 9.

Fig. 9
figure 9

Profiles of the specific intensity \(I_{obs}\) seen by a distant observer for a static spherical accretion. The red line, green line and blue line represent respectively the torsion charge \(\mathcal {S}=-0.99\), \(\mathcal {S}=0.1\) and \(\mathcal {S}=0.80\)

Full size image

From Fig. 9, the position of the critical impact parameter \(b_p\) is always the place with the strongest luminosity, regardless of the positive or negative of the torsion charge \(\mathcal {S}\). When the value of \(b_c\) is large enough \(b_c\gg b_p\), the refracted light tends to disappear, resulting in the disappearance of the observed intensity. As expected, the luminosity of the region outside the photon sphere gradually decreases with the increase of impact parameter \(b_c\). Figure 10 shows the two-dimensional shadow, and the dark area surrounded by the bright ring in the middle is the shadow area. Comparing Figs. 9 and 10, the result show that both the size of the observed shadow and intensity of luminosity are affected by the parameter \(\mathcal {S}\). That is, the radius of the photon sphere decreases with the larger value of S, but the observed intensity increases. In the case of \(\mathcal {S}=0.80\), the peak value of observable intensity is obviously higher than that of \(\mathcal {S}=-0.99\). Therefore, the negative torsional charge \(\mathcal {S}\) expands the shadow area, but it also weakens the observation light intensity. In the spacetime of (2), the parameter \(\mathcal {S}\) plays an important role in observation, and its change will directly affect the observation intensity that can be obtained by distant observers, as well as the shadow size. Interestingly, the inner region of the shadow is not entirely dark in Fig. 10, and the region near the inner edge of the black hole shadow has obvious observed luminosity. Actually, it is caused by a small part of the radiation of the accretion flow inside the photon ring can escape to infinity.

Fig. 10
figure 10

The optical appearance of black hole shadows and photon rings cast by the static spherical accretion in (x, y) plane, where the torsion charge \(\mathcal {S}\) takes different value

Full size image

4.2 The infalling spherical accretion

In this section, we consider a more realistic situation that the optically thin accretion to move in towards the black hole. The optically thin accretion is considered to be infalling matters, which is a real accretion flow because the most accretion matters are in the universe should not be static. For simplicity, we also take the radiation power and emission coefficient, as measured in the rest frame of the infalling accretion. Hence, Eq. (29) still can be used to study the shadow while radial infalling spherical accretion. It is worth mentioning that the velocity of the infalling accretion will affect the redshift factor of accretion, the redshift factor of infalling accretion can be expressed as

$$\begin{aligned} g=\frac{k _{\alpha }u_{{obs}}^{\alpha }}{k _{\beta }u_e^{\beta }}. \end{aligned}$$
(30)

Here, \(k ^{\mu }={\dot{x}}_{\mu }\) is the four-velocity of the photon, \(u_e^{\mu }\) is the four-velocity of the accreting matter, and \(u_{{obs}}^{\mu }=(1,0,0,0)\) is the four-velocity of the distant observer. When the accretion matter is in radial free fall into the black hole of the spacetime (2), the four-velocity of the infalling spherical accretion is

$$\begin{aligned} u^t_{\mathrm{e}} = \frac{1}{N(r)},~~~ u^r_{\mathrm{e}} = - \sqrt{ 1 - N(r) } ,~~~ u^\theta _{\mathrm{e}} = u^\phi _{\mathrm{e}} = 0. \end{aligned}$$
(31)

For the photons, the four-velocity was found in Eq. (7) and Eq. (8). In addition, \(k_t=1/b_c\) is a constant, and from \( k_{\gamma }k^{\gamma }=0\) we can get \(k_{\gamma }\). Hence, we have

$$\begin{aligned} \frac{k_{\gamma }}{k_t}=\pm \frac{ 1}{N(r)}\sqrt{N(r)\left( \frac{1}{N(r)}-\frac{b_c^2}{r^2}\right) }, \end{aligned}$$
(32)

where the sign \(+(-)\) is when the photon approaches (goes) away from the black hole. The redshift factor in Eq. (30) is therefore given by

$$\begin{aligned} g=\frac{1}{u_e^t+k_{\gamma }/k_eu_e^r}, \end{aligned}$$
(33)

and the proper length can be written as

$$\begin{aligned} {dl}_{{prop}}=k_{\gamma }u_e^{\gamma }d \lambda =\frac{k_t}{g\left| k_r\right| }{dr}. \end{aligned}$$
(34)

In which, \(\lambda \) is the affine parameter along the photon path \(\gamma \), and \(\lambda \) has to be evaluated along the path of the photon. Integrating the intensity over all the observed frequencies, we obtain the observed flux, that is

$$\begin{aligned} I_{{obs}}\propto \int _{\gamma }\frac{g^3k_t}{r^2 \left| k_r\right| } dr. \end{aligned}$$
(35)

With the help of above equation, the total photon intensity and two-dimensional shadow of the black hole with an infalling accretion can be investigate. Figure 11 shows the total photon intensity of black hole under the different values of \(\mathcal {S}\). One can find that with the increase of impact parameter \(b_c\), the intensity also increases, but it decreases sharply after reaching the peak at \(b_c=b_{p}\). In the adjacent area of \(b_{p}\), the change rate of intensity of the infalling accretion is greater than that of static accretion. In addition, the observed intensity of infalling accretion is obviously smaller than that of the static model when the relevant state parameters are the same. That result is the most striking feature for both the static and infalling accretion models. Therefore, the observed luminosity of shadow under with different parameters \(\mathcal {S}\) is compared when the black hole is surrounded by those two accretion models, which is shown in Table 2. (The observed intensities are normalized to the maximum value of the emitted intensity outside the horizon). As can be seen from Table 2, the observed luminosity in the case of static spherical accretion is two orders of magnitude brighter or even higher than that in the case of infalling accretion.

Fig. 11
figure 11

Image of the corresponding intensities using the infalling accretion seen by a distant observer. The red line, green line and blue line represent respectively the torsion charge \(\mathcal {S}=-0.99\), \(\mathcal {S}=0.1\) and \(\mathcal {S}=0.80\)

Full size image
Table 2 The observed intensity of the black hole shadow with static and infalling spherical accretion under different values of torsion charge parameters \(\mathcal {S}\)
Full size table

The corresponding two-dimensional image of the intensity is plotted in Fig. 12. The result show that the range and peak value of observed intensity are more weaker compare with the static accretion. Therefore, the central region of the intensity for the infalling accretion is darker, which can be explained by the Doppler effect. In Fig. 12, the parameter \(\mathcal {S}\) still affects the size of the observed shadow, even the observed intensity. The intensity increases with the value of \(\mathcal {S}\) increases, and its growth rate is much greater than that of static accretion case. Note that the radius of the shadow and the position of the photon sphere are consistent under the different accretion (the static and infalling spherical accretion), which means that the spherical accretion will affect the intensity of the shadow but does not affect the radius of the shadow.

Fig. 12
figure 12

The optical appearance of black hole shadows and photon rings cast by the infalling spherical accretion in (x, y) plane, where the torsion charge \(\mathcal {S}\) takes different value

Full size image

5 Conclusions and discussions

The black hole cannot be directly observed, but we can observe it indirectly with the help of luminescent materials outside the black holes. Therefore, the observational characteristics of the black hole are closely related to the luminescence condition around black holes. In the context of Poincaré gauge theory of gravity (PGT), our interest in this paper is to study the shadows of the black hole which is surrounded by the different accretion models. We pay close attention to the influence of torsion charge \(\mathcal {S}\) on the black hole shadow in this spacetime, as well as the characteristics of the observable shadow image, which can be used as a method to distinguish between PGT gravity black hole and Schwarzschild black hole.

The shadow radius is determined by the critical impact parameter \(b_p\), which is limited by the torsion charge \(\mathcal {S}\). Naturally, one can get the different radius of photon ring and shadow while the parameter \(\mathcal {S}\) changed. The results indicate that the radius and critical impact parameter \(b_p\) of the photon ring decrease with the increase of \(\mathcal {S}\), and the negative torsion charge \(\mathcal {S}\) amplifies the region of black hole shadow compared with Schwarzschild spacetime. Through the study of observed specific intensity of the thin disk accretion, the result show that the observed intensities are dominated by the direct emission, while the lensing ring providing only a small contribution to the total flux and the photon ring made a negligible contribution. Although the observer can obtain higher observation intensity in the case of negative torsion charge, the contribution of photon ring and lensing ring to the total observation flux is reduced. Therefore, the light band around the black hole shadow will be brighter but narrower than the Schwarzschild spacetime, which might be regarded as a characteristic for us to distinguish black holes in PGT gravity from the Schwarzschild black hole.

In particular, we also investigated the shadows and photon sphere in two different cases of spherical accretions, namely the static and infalling spherically symmetric accretions. An important observable signature is that the inner area of infalling accretion case is obviously darker than that of static accretion case, and the difference between the observed intensities of the two models is two orders of magnitude or even higher. In the different spherical accretion models, the outer edge of the shadows is always located at the radius of photon sphere, which means that the shadow has an identical size in these two accretion models as long as the parameters \(\mathcal {S}\) are not changed. In other words, the shadow is independent of the behavior of the accretion matters, which is uniquely determined by the spacetime metric. Because the larger torsion charge leads to a stronger peak effective potential at a smaller black hole radius, which leads to the increase of the deflectable light density, as well as the observation intensity. This means the observed specific intensities and the shadow images of the black hole are different for various parameters \(\mathcal {S}\).

In addition, based on the shadow of M87 detected by the Event Horizon Telescope, we noted that the diameter of the shadow in units of mass M for M87 is \(d_{M87} \equiv D \cdot \delta / M \approx 11 \pm 1.5 \) with D and \(\delta \) are the angular size of the shadow and the distance to M87. This means the ranges of the diameter are \(9.5 \thicksim 12.5\) and \(8 \thicksim 14\) for 1\(\delta \) and 2\(\delta \) uncertainties. In view of this, the torsion charge of black hole would be naturally limited by using the diameter of shadow. For 1\(\delta \) uncertainty, it turns out that the torsion charge should be approximately fixed to the range \(-1.501M \thicksim 0.4601M\). And for 2\(\delta \) uncertainty, we find that this range expanded approximately to the region \(-2.915M \thicksim 1M\).

In this paper, since we consider the background of static spherical symmetry, the results of the optical appearance of black hole shadows wrapped by different accretion models simulated on the equatorial disk are general. For the spherical accretion model, the simulation results on the equatorial disk can reflect the overall observational properties of the black hole shadow. However, it is important to further explore images of the black hole observed at various observation points [62]. Hence, it will be an interesting topic to explore the optical observation appearance of black hole shadows from different angles in Poincaré gravity gauge theory. In our next work, we will study the shadow of the black hole from different observation angles, so that we can more fully understand the geometric structure and physical properties of the black hole.