Charmless $B_s\rightarrow V S$ decays in PQCD approach

Abstract

In this work, we investigate the $B_s\rightarrow V S$ decays in the perturbative QCD approach, where V and S denote the vector meson and scalar meson respectively. Based on the two-quark structure, considering two different scenarios for describing the scalar mesons, we calculate the branching fractions and the direct CP asymmetries of all $B_s\rightarrow VS$ decays. Most branching fractions are predicted to be at $10^{-7}$ to $10^{-5}$, which could be measured in the LHCb and Belle-II experiments, especially for these color-allowed decays $B_s\rightarrow \kappa (800)(K_0^*(1430))K^*$ and $B_s\rightarrow K_0^{*-}(1430)\rho ^+$. It is found that the branching fractions of $B_s\rightarrow K_0^{*0}(1430){\bar{K}}^{*0}$ and $B_s\rightarrow K_0^{*+}(1430){\bar{K}}^{*-}$ are very sensitive to the scenarios, which can be used to determine whether $K_0^{*0}(1430)$ belongs to the ground state or the first excited state, if the data were available. We also note that some decays have large direct CP asymmetries, some of which are also sensitive to the scenarios, such as the $B_s \rightarrow a_0^+(1450)K^{*-}$ and the $B_s\rightarrow f_0(1500) K^{*0}$ decays. Since the experimental measurements of $B_s\rightarrow VS$ decays are on the way, combined with the available data in the future, we expect the theoretical predictions will shed light on the structure of the scalar mesons.

1 Introduction

In contrast to the vector and tensor mesons, the identification of the scalar mesons is still controversial, though the quark model has achieved great successes for several decades. Scalar resonances are difficult to resolve because of their large decay widths which cause a strong overlap between resonances and background, and also because several decay channels open up [1,2,3]. Furthermore, one expects non-$q{{\bar{q}}}$ scalar objects, like glueballs and multiquark states in the mass range below 1800 MeV. In the theoretical studies, two different scenarios [4] have been often adopted to describe the scalar mesons, depending on the studies of the mass spectrum and the strong as well as eletromagnetic decays of the scalar mesons. In the so-called scenario I (S-I), all the scalar mesons are viewed as the traditional two-quark $q{\bar{q}}$ state, and the mesons with mass below 1 GeV, such as $a_0(980)$, $\kappa (800)$, and $f_0(500)/f_0(980)$, are the lowest lying two-quark bound states, while the mesons heavier than 1 GeV, such as $K_0^*(1430)$, $a_0(1450)$ and $f_0(1370)/f_0(1500)$, are the corresponding first excited states. In the scenario II (S-II), only those heavier mesons are interpreted as the two-quark ground states, while the light scalar mesons are the four-quark bound states or meson-meson bound states, etc. The S-II corresponds to the case that light scalar mesons are four-quark bound states, while all scalar mesons are made of two quarks in S-I. Although S-II is much preferred [4,5,6,7,8,9], the final conclusion has not been confirmed yet.

Since the first B meson decay mode $B\rightarrow f_0(980)K$ has been observed by Belle in 2002 through the three-body decay $K^{\pm }\pi ^{\mp }\pi ^{\pm }$ [10], which was subsequently confirmed by BaBar [11], there has been some significant progresses in the study of hadronic B decays involving scalar mesons, both experimentally and theoretically. On the experimental side, there are large amounts of measurements of B decays to scalar mesons reported by Belle [12,13,14,15], BaBar [16,17,18,19,20,21,22,23] and LHCb [24], which are summarized in Ref. [3]. On the theoretical side, two-body B meson decays to scalar mesons have been explored widely in different approaches, such as the QCD factorization (QCDF) [4,5,6, 25,26,27] and the perturbative QCD approach (PQCD) [28,29,30,31,32,33,34,35,36]. Combinations of the well measured experimental data with the precise theoretical predictions provide us another way to determine the nature of the scalar mesons.

It is well known to us that one cannot calculate the decay rate of two-body B decay from the first principle due to the complexity of QCD. In the past decades, beyond the naive factorization approach [37,38,39], three major QCD-inspired approaches had been proposed to deal with the charmless non-leptonic B decays, based on the effective theories, namely, QCDF [40, 41], PQCD [42,43,44], and soft-collinear effective theory (SCET) [45,46,47]. The difference between them is only on the treatment of dynamical degrees of freedom at different mass scales, namely the power counting. There are various energy scales involved in the hadronic B decays, and the factorization theorem allows us to calculate them separately. First, the physics from the electroweak scale down to b quark mass scale is described by the renormalization group running of the Wilson coefficients of effective four-quark operators. Secondly, the hard part with scale from b quark mass scale to the factorization scale $\sqrt{\Lambda m_B}$ are calculated in PQCD [48]. When doing the integration of the momentum fraction x of the light quark, end point singularity will appear in the collinear factorization (QCDF and SCET) which breaks down the factorization theorem. In PQCD, the inner transverse momentum $k_T$ of the light quarks in meson is kept, which could kill the endpoint singularity. There exist also double logarithms from the overlap of collinear and soft divergence, and the resummation of these double logarithms leads to a Sudakov form factor, which suppresses the long distance contributions and improves the applicability of PQCD. The physics below the factorization scale is non-perturbative in nature, which is described by the hadronic wave functions of mesons. They are not perturbatively calculable, but universal for all the decay processes. Since all logarithm corrections have been summed by renormalization group equations, the factorization formula does not depend on the renormalization scale. In the literatures, $B_{u,d} \rightarrow SP, SV$ and $B_{s} \rightarrow SP$ decays have been studied extensively based on PQCD, where P, V and S stand for pseudoscalar, vector and scalar mesons, respectively. For the sake of completeness, we shall study $B_s\rightarrow SV$ decays in PQCD approach in this work.

The layout of the present paper is as follows. In the next section we briefly introduce the framework of PQCD approach and wave functions of both the initial meson (B meson) and the final mesons (V and S). In Sect. 3, the calculation of the decay amplitude is performed in PQCD approach, and the explicit expressions are presented in this section. The numerical results and detailed discussions appear in Sect. 4. Finally, in the last section we summarize this work briefly.

2 Formalism and wave function

It is convenient to study the B meson decays in the B meson rest framework, where two daughters of the B meson fly back to back with high energy. In this case, the inner massive b quark carries almost all of the energy of the B meson and the massless spectator quark (s quark) is soft in the initial state. In the final state, the three light quarks produced from the b quark weak decay are energetic and move fast. In order to form a final meson, a hard gluon is needed to kick the soft spectator quark to make it change from soft-like to collinear-like. The hard part of the interaction becomes six-quark operator rather than four-quark. The soft dynamics here is included in the meson wave functions.

As aforementioned, there are three typical scales in B meson weak decay. The first one is the W boson mass $m_W$. The physics higher it is weak interaction and can be calculated perturbatively getting the Wilson coefficients $C(m_W)$ at the scale $m_W$. Using the renormalization group, we can run the Wilson coefficients from the $m_W$ scale to the “b” quark mass $m_b$ scale. The physics lying between the $m_b$ and the factorizable scale t, namely “hard kernel H” in PQCD approach, which is governed by exchanging a hard gluon, can be perturbatively calculated in PQCD approach. Finally, the physics below the scale t is soft and nonperturbative, which can be described by the universal hadronic wave functions of the initial and final states. According to the factorization mentioned above, the decay amplitude in PQCD approach can be written as the convolution of the Wilson coefficients $C(\mu )$, the hard kernel $H(x_i,b_i,t)$, and the initial and final hadronic wave functions [49, 50]:

$$\begin{aligned} A= & {} \int _0^1dx_1dx_Vdx_S\int _0^{\infty }b_1db_1b_Vdb_Vb_Sdb_S\,Tr[C(t)\nonumber \\&\otimes H(x_i,b_i,t)\otimes \Phi _B(x_1,b_1)\otimes \Phi _V(x_V,b_V)\otimes \Phi _S(x_S,b_S)\nonumber \\&\otimes S_t(x_i) \otimes \exp \left[ -s(P,b) -2 \int _{1/b}^t \frac{ d {\bar{\mu }}}{{\bar{\mu }}} \gamma _q (\alpha _s ({\bar{\mu }})) \right] , \end{aligned}$$

(1)

where the $x_i(i=1,V,S)$ is the momentum fraction of the light quark in the initial and final states. The $b_i$ is the conjugate variable of the transverse momentum $k_{iT}$ of the quark in mesons. C(t) are the corresponding Wilson coefficients of four quark operators, $\Phi (x)$ are the universal meson wave functions and the variable t denotes the largest energy scale of hard kernel $H(x_i,b_i,t)$, which is the typical energy scale in PQCD approach and the Wilson coefficients are evolved to this scale. The exponential of s(P, b) function is the so-called Sudakov form factor resulting from the resummation of double logarithms occurred in the QCD loop corrections, which can suppress the contribution from the non-perturbative region. Since logarithm corrections have been summed by renormalization group equations, the above factorization formula does not depend on the renormalization scale $\mu$ explicitly. The corrections also cause the double logarithms $\ln ^2 x_i$, which can also be resummed to the jet function $S_t(x_i)$ [42, 51].

The effective Hamiltonian relevant for $B_s\rightarrow VS$ has the form [52]

$$\begin{aligned} {\mathscr {H}}_{eff}= & {} \frac{G_F}{\sqrt{2}}\Bigg \{V_{ub}^*V_{uq}(C_1(\mu )O_1(\mu ) +C_{2}(\mu )O_2(\mu ))\nonumber \\&-V_{tb}^*V_{tq}\sum _{i=3}^{10}C_i(\mu )O_i(\mu )\Bigg \}+\mathrm{h.c.}, \end{aligned}$$

(2)

where the $V_{u(t)b}$ and $V_{u(t)q}$ are the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, with $q=d,s$ quark. The $O_{1-10}(\mu )$ are the local four-quark operators corresponding to the $B_s\rightarrow VS$ decays, which can be divided into the following three categories,

• current-current (tree) operators:

  $$\begin{aligned} O_1= & {} ({\bar{b}}_{\alpha }u_{\beta })_{V-A}({\bar{u}}_{\beta }q_{\alpha })_{V-A},\;\;\nonumber \\ O_2= & {} ({\bar{b}}_{\alpha }u_{\alpha })_{V-A}({\bar{u}}_{\beta }q_{\beta })_{V-A}, \end{aligned}$$

  (3)

• QCD penguin operators:

  $$\begin{aligned} O_3= & {} ({\bar{b}}_{\alpha }q_{\alpha })_{V-A}\sum _{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\beta })_{V-A},\;\nonumber \\ O_4= & {} ({\bar{b}}_{\alpha }q_{\beta })_{V-A}\sum _{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\alpha })_{V-A},\nonumber \\ O_5= & {} ({\bar{b}}_{\alpha }q_{\alpha })_{V-A}\sum _{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\beta })_{V+A},\;\nonumber \\ O_6= & {} ({\bar{b}}_{\alpha }q_{\beta })_{V-A}\sum _{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\alpha })_{V+A}, \end{aligned}$$

  (4)

• electro-weak penguin operators:

  $$\begin{aligned} O_7= & {} \frac{3}{2}({\bar{b}}_{\alpha }q_{\alpha })_{V-A}\sum _{q^{\prime }}e_{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\beta })_{V+A},\;\nonumber \\ O_8= & {} \frac{3}{2}({\bar{b}}_{\alpha }q_{\beta })_{V-A}\sum _{q^{\prime }}e_{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\alpha })_{V+A},\nonumber \\ O_9= & {} \frac{3}{2}({\bar{b}}_{\alpha }q_{\alpha })_{V-A}\sum _{q^{\prime }}e_{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\beta })_{V-A},\;\nonumber \\ O_{10}= & {} \frac{3}{2}({\bar{b}}_{\alpha }q_{\beta })_{V-A}\sum _{q^{\prime }}e_{q^{\prime }}({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\alpha })_{V-A}, \end{aligned}$$

  (5)

where the subscripts $\alpha$ and $\beta$ are the color indices. The $q^{\prime }$ are the active quarks at the scale $m_b$, namely $q^{\prime }=u,d,s$ quarks in this work. The symbol $({\bar{b}}_{\alpha }q_{\alpha })_{V-A}$ is the left handed current with the explicit expression ${\bar{b}}_{\alpha }\gamma _{\mu }(1-\gamma _5)q_{\alpha }$. The right handed current $({\bar{q}}^{\prime }_{\beta }q^{\prime }_{\beta })_{V+A}$ has the expression ${\bar{q}}^{\prime }_{\beta }\gamma _{\mu }(1+\gamma _5)q^{\prime }_{\beta }$.

In PQCD, the wave functions are the most important input parameters. For the initial $B_s$ meson, its wave function has been widely studied [44, 53], and the expression can be given as

(6)

where the numerically suppressed term has been neglected. The $\phi _B(x_1,b_1)$ is the light-cone distribution amplitudes (LCDA) with the explicit expression as

$$\begin{aligned} \phi _{B_s}(x,b){=}N_{B}x^{2}(1{-}x)^{2}\exp \left[ -\frac{1}{2} \left( \frac{xm_{B_s}}{\omega }\right) ^{2} {-}\frac{\omega ^{2}b^{2}}{2}\right] \;,\nonumber \\ \end{aligned}$$

(7)

where the $N_B$ is the normalization constant, which can be determined by the normalization condition

$$\begin{aligned} \int _0^1 dx \phi _{B_s}(x,b=0)=\frac{f_{B_s}}{2\sqrt{6}}, \end{aligned}$$

(8)

with the decay constant $f_{B_s}=(0.23\pm 0.02)\mathrm{GeV}$ [44, 53,54,55]. The corresponding shape parameter $\omega$ in the LCDA of the $B_s$ meson is usually taken the value $(0.5\pm 0.05)\mathrm{GeV}$. A model-independent determination of the B meson DA from an Euclidean lattice was attempted very recently [56]. We also note that only the B meson LCDA associated with the leading Lorentz structure in Eq. (7) is considered, while other power-suppressed pieces are negligible within the accuracy of the current work [57, 58].

In the two-quark picture of S-I and S-II, the two kinds of decay constants of scalar meson S are defined by:

$$\begin{aligned} \langle S(p)|{{\bar{q}}}_2\gamma _\mu q_1|0\rangle =f_Sp_\mu , \,\,\,\,\,\,\,\,\,\,\, \langle S(p)|{{\bar{q}}}_2 q_1|0\rangle =m_S\bar{f_S}. \end{aligned}$$

(9)

The $f_S$ and ${\bar{f}}_S$ are the vector and scalar decay constants respectively, which can be related with each other through the equation of motion

$$\begin{aligned} {{\bar{f}}}_S= & {} \mu _Sf_S, \qquad \quad \mathrm{with}~~ \mu _S=\frac{m_S}{m_2(\mu )-m_1(\mu )}, \end{aligned}$$

(10)

$m_{1(2)}$ being the running current quark mass. It is obvious that the vector decay constant is highly suppressed by the tiny mass difference between the two running current quarks. Therefore, in contrast to the scalar one, the vector decay constant of the scalar meson, namely $f_S$, will vanish in the SU(3) limit.

As for the light scalar meson wave function, the twist-2 and twist-3 LCDAs for different components could be combined into a single matrix element [4,5,6]

(11)

with the twist-2 LCDA $\phi _S(x)$ and twist-3 LCDA $\phi _S^{s(t)}(x)$. The $n=(1,0,\mathbf{0 }_T)$ and $v=(0,1,\mathbf{0 }_T)$ are the light-like unit vector. Similar to the $B_s$ meson, the LCDAs of the scalar meson also obey the normalization conditions

$$\begin{aligned} \int _0^1 dx \phi _S(x)=f_S,\;\;\;\int _0^1 dx \phi _S^{s(t)}(x)={\bar{f}}_S. \end{aligned}$$

(12)

The twist-2 LCDA can be expanded as the Gegenbauer polynomials

$$\begin{aligned} \phi _S(x,\mu )= & {} \frac{3}{2\sqrt{6}}x(1-x)[f_S(\mu )\nonumber \\&+{\bar{f}}_S\sum _{m=1}^{\infty }B_m(\mu )C_m^{3/2}(2x-1)], \end{aligned}$$

(13)

where $C_m^{3/2}(2x-1)$ are the Gegenbauer polynomials, and $B_m(\mu )$ are the corresponding Gegenbauer momenta. For the two twist-3 LCDAs, the asymptotic forms are adopted

$$\begin{aligned} \phi _S^s(x)=\frac{{\bar{f}}_S}{2\sqrt{6}},\;\;\;\phi _S^t(x)=\frac{{\bar{f}}_S}{2\sqrt{6}}(1-2x). \end{aligned}$$

(14)

The explicit values of the parameters ${\bar{f}}_S$ and $B_m$are collected in Table 1.

Table 1 Decay constants ${{\bar{f}}}_S$ (in unit of MeV) and Gegenbauer moments at scale $\mu =1\mathrm{GeV}$ in S-I and S-II [4,5,6]

The light vector meson has the longitudinal polarization vector $\epsilon _L$ and the transverse polarization one $\epsilon _T$, whose definition can refer to Refs. [59, 60]. Because another final state is a scalar meson, the transverse polarization component of the vector meson does not contribute to the decay amplitudes, required by the angular momentum conservation. The longitudinal wave function of the vector meson is given as [61]

(15)

The $\phi _V(x)$ and $\phi _V^{t,s}(x)$ are the twist-2 and twist-3 LCDAs respectively, whose expressions are given as

$$\begin{aligned} \phi _V(x)= & {} \frac{3f_V}{\sqrt{6}}x(1-x)\left[ 1+a_{1V}^{\parallel }C_1^{3/2}(t)+a_{2V}^{\parallel }C_2^{3/2}(t)\right] ,\nonumber \\ \phi _V^t(x)= & {} \frac{3f_V^T}{2\sqrt{6}}t^2,\;\;\phi _V^s(x)=-\frac{3f_V^T}{2\sqrt{6}}t, \end{aligned}$$

(16)

with $t=2x-1$. The $f_V^{(T)}$ are the decay constants of the vector meson with the following values [61, 62]:

$$\begin{aligned} f_{\rho }^{\parallel }= & {} (216\pm 3)\mathrm{MeV},\;\; f_{\omega }^{\parallel }=(187\pm 5)\mathrm{MeV},\;\;\nonumber \\ f_{K^*}^{\parallel }= & {} (220\pm 5)\mathrm{MeV},\;\; f_{\phi }^{\parallel } = (215\pm 5)\mathrm{MeV},\nonumber \\ f_{\rho }^{\perp }= & {} (165\pm 9)\mathrm{MeV},\;\; f_{\omega }^{\perp }=(151\pm 9)\mathrm{MeV},\;\;\nonumber \\ f_{K^*}^{\perp }= & {} (185\pm 10)\mathrm{MeV},\;\; f_{\phi }^{\perp }=(186\pm 9)\mathrm{MeV}. \end{aligned}$$

(17)

As for the Gegenbauer moments $a_{1,2}^{\parallel }$, they have been calculated within the QCD sum rules [63, 64], which values at $\mu =1$ GeV are given as

$$\begin{aligned} a_1^{\parallel }(K^*)= & {} 0.03\pm 0.02, a_2^{\parallel }(\rho )=0.15\pm 0.07,\;\;\nonumber \\ a_2^{\parallel }(K^*)= & {} 0.11\pm 0.09, a_2^{\parallel }(\phi )=0.18\pm 0.08. \end{aligned}$$

(18)

It is noted that for these vector mesons with definite G parity, ie. $\rho (\omega )$ and $\phi$, $a_1^{\parallel }=0$.

In the calculations, the other parameters we used are also given as [3]

$$\begin{aligned} \Lambda _{{\overline{MS}}}^{f=4}= & {} 0.25\pm 0.05 \,\mathrm{{GeV}}, m_{B_s}=5.366 \,\mathrm{{GeV}},\;\nonumber \\ f_{B_s}= & {} (0.236\pm 0.03) \,\mathrm{{GeV}},\;\tau _{B_S}=1.527 ps,\nonumber \\ |V_{ud}|= & {} 0.97401\pm 0.00011, |V_{us}|=0.22650\pm 0.00048,\;\nonumber \\ |V_{ub}|= & {} 0.00361^{+0.00011}_{-0.00009}, |V_{td}|=0.00854^{+0.00023}_{-0.00016},\;\nonumber \\ |V_{ts}|= & {} 0.03978^{+0.00082}_{-0.00060}, |V_{tb}|=0.999172^{+0.000024}_{-0.000035},\nonumber \\ \alpha= & {} (84.9^{+5.1}_{-4.5})^{\circ }, \gamma =(72.1^{+4.1}_{-4.5})^{\circ }. \end{aligned}$$

(19)

3 Perturbative calculations

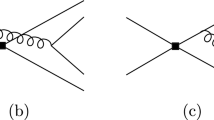
In PQCD, there are eight diagrams corresponding to the $B_s\rightarrow VS$ decays at leading order, which are shown in Fig. 1. The four diagrams in first line are the emission type diagrams, where the first two diagrams can be factorized into the product of the decay constant and the transition form factor, while the last two are called hard-scattering emission diagrams. The diagrams in the second line are annihilation type diagrams. Similarly, the first two are the factorizable diagrams, while the last two ones are nonfactorizable.

Using the weak hamiltonian and the wave functions determined above, we start to perform the perturbative calculations and present the explicit expressions of decay amplitudes corresponding to the each diagram in Fig. 1. For the sake of simplicity, we define some symbols to describe the decay amplitudes with the different currents. The LL denotes $(V-A)(V-A)$ current, and the LR(SP) represents the $(V-A)(V+A)$ ($(S-P)(S+P)$) current.

Fig. 1

Leading order Feynman diagrams contributing to the $B_s\,\rightarrow VS$ decays in PQCD approach

The first two factorizable emission diagrams (a) and (b) in Fig.1, each decay amplitude can be separated into the decay constant of emitted meson ($M_2$) and the $B\rightarrow M_3$ transition form factor. The decay amplitudes with respect to the LL, LR and SP currents are

$$\begin{aligned} {F}_{S}^{LL,LR}= & {} 8\pi C_F f_S m_B^4 \int _{0}^1dx_1dx_V\nonumber \\&\times \int _0^{\infty }b_1db_1b_Vdb_V\phi _B(x_1,b_1)\nonumber \\&\times \bigg \{\Big [\phi _V(x_V)(1+x_V)-r_V(2x_V-1)(\phi _V^s(x_V)\nonumber \\&+\phi _V^t(x_V))\Big ]E_{ef}(t_a)h_{ef}(x_1,x_V(1-r_S^2),b_1,b_V)\nonumber \\&+2r_V\phi _V^s(x_V)E_{ef}(t_b)h_{ef}\nonumber \\&\times (x_V,x_1(1-r_S^2),b_V,b_1)\bigg \}, \end{aligned}$$

(20)

$$\begin{aligned} {F}_{S}^{SP}= & {} -16 \pi C_F {\bar{f}}_S m_B^4\int _0^1dx_1dx_V\nonumber \\&\times \int _0^{\infty }b_1db_1b_Vdb_V\phi _B(x_1,b_1)r_S\nonumber \\&\times \bigg \{\Big [\phi _V(x_V)+r_V\left[ \phi _V^s(x_V)(x_V+2)\right. \nonumber \\&\left. -x_V\phi _V^t(x_V)\right] \Big ]E_{ef}(t_a)h_{ef}(x_1,x_V(1-r_S^2),b_1,b_V)\nonumber \\&+2r_V\phi _V^s(x_V)E_{ef}(t_b)h_{ef}\nonumber \\&\times (x_V,x_1(1-r_S^2),b_V,b_1)\bigg \}, \end{aligned}$$

(21)

where $r_{S(V)}=m_{S(V)}/{m_{B_s}}$ and the color factor $C_F=4/3$. The explicit expressions of the functions $E_{ef}(t_{a,b})$, $h_{ef}$ and the hard scales $t_{a,b}$ have been given in the Ref. [53]. The subscript “S” denotes that the scalar meson is emitted. When the vector meson is emitted, the corresponding contributions is also given as

$$\begin{aligned} {F}_V^{LL,LR}= & {} 8\pi C_F f_Vm_B^4\int _0^1dx_1dx_S\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\nonumber \\&\times \bigg \{\Big [\phi _S(x_S)(x_S+1)+r_S(1-2x_S)[\phi _S^s(x_S)\nonumber \\&+\phi _S^t(x_S)]\Big ]E_{ef}(t_a)h_{ef}(x_1,x_V(1-r_S^2),b_1,b_V)\nonumber \\&+2r_S\phi _S^s(x_S)E_{ef}(t_b)h_{ef}\nonumber \\&\times (x_V,x_1(1-r_S^2),b_V,b_1)\bigg \}. \end{aligned}$$

(22)

We note that the $(S-P)(S+P)$ type operators can not contribute to the amplitude with a vector emitted, because the vector meson cannot be produced through this kind of operators.

For these two hard-scattering diagrams ((c) and (d)), the decay amplitudes contain all three wave functions. The expressions corresponding to three currents are given as below

$$\begin{aligned} {M}_S^{LL}= & {} -16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int _0^1dx_1dx_Sdx_V\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\phi _S(x_S)\nonumber \\&\times \bigg \{\Big [(x_S-1)\phi _V(x_V)+r_Vx_V(\phi _V^s(x_V)-\phi _V^t(x_V))\Big ]\nonumber \\&\times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_S)\nonumber \\&+\Big [(x_S+x_V)\phi _V(x_V)-r_Vx_V(\phi _V^s(x_V)+\phi _V^t(x_V))\Big ]\nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_S)\bigg \}, \end{aligned}$$

(23)

$$\begin{aligned} {M}_S^{LR}= & {} 16\sqrt{\frac{2}{3}}\pi C_Fr_Sm_B^4\int _0^1dx_1dx_Vdx_S\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\nonumber \\&\times \bigg \{\bigg [r_V\Big [\phi _S^s(x_S)(\phi _V^s(x_V)(x_S-x_V-1)\nonumber \\&-\phi _V^t(x_V)(x_S+x_V-1))\nonumber \\&+\phi _S^t(x_S)(\phi _V^s(x_V)(x_S+x_V-1)\nonumber \\&+\phi _V^t(x_V)(1+x_V-x_S))\Big ]\nonumber \\&+\phi _V(x_V)(x_S-1)(\phi _S^s(x_S)+\phi _S^t(x_S))\bigg ]\nonumber \\&\times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_S)\nonumber \\&+\bigg [r_V\Big [\phi _S^s(x_S)(\phi _V^s(x_V)(x_S+x_V)\nonumber \\&+\phi _V^t(x_V)(x_V-x_S))+\phi _S^t(x_S)(\phi _V^s(x_V)(x_V-x_S)\nonumber \\&+\phi _V^t(x_V)(x_S+x_V))\Big ]\nonumber \\&+x_S\phi _V(x_V)(\phi _S^s(x_S)-\phi _S^t(x_S))\bigg ]\nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_S)\bigg \}, \end{aligned}$$

(24)

$$\begin{aligned} {M}_S^{SP}= & {} -16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int _0^1dx_1dx_Vdx_S\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\phi _S(x_S)\nonumber \\&\times \bigg \{\Big [\phi _V(x_V)(x_S-x_V-1)+r_Vx_V(\phi _V^s(x_V)+\phi _V^t(x_V))\Big ] \nonumber \\&\times E_{enf}(t_c)h_{enf}(\alpha ,\beta _1,b_1,b_S)\nonumber \\&+\Big [x_S\phi _V(x_V)+r_Vx_V(\phi _Vt(x_V)-\phi _V^s(x_V))\Big ]\nonumber \\&\times E_{enf}(t_d)h_{enf}(\alpha ,\beta _2,b_1,b_S)\bigg \}, \end{aligned}$$

(25)

where the functions $E_{enf}$, $h_{enf}$ and the inner functions can be found in Ref. [53]. For the diagrams with a vector meson emitted, the decay amplitudes can be obtained by doing the following substitutes in the three decay amplitudes above

$$\begin{aligned} \phi _{V}^{(s,t)}(x_V)\leftrightarrow \phi _S^{(s,t)}(x_S),\;x_S\leftrightarrow x_V,\,r_V\leftrightarrow r_S. \end{aligned}$$

(26)

When the emitted meson is a vector meson, the two hard-scattering diagrams (c) and (d) will cancel with each other, because the wave function of vector meson are symmetric under the exchange $x\rightarrow (1-x)$. However, when the scalar meson is emitted, the amplitudes will not be cancelled anymore, but enhanced by each other, because the LCDAs of the scalar meson are antisymmetric. So, the hard-scattering diagrams with a vector emitted are usually suppressed, and the diagrams emitting a scalar meson will provide sizable contributions or even dominate the decay amplitude, especially in those color-suppressed type decays.

For the annihilation diagrams (e) and (f), the factorizable amplitudes with a scalar meson as the $M_2$ meson flying along the n direction are

$$\begin{aligned} {A}_{S}^{LL,LR}= & {} 8\pi C_F f_{B_s} m_B^4\int _0^1dx_Vdx_S\nonumber \\&\times \int _0^{\infty }b_Vdb_Vb_Sdb_S \bigg \{\Big [\phi _S(x_S)\phi _V(x_V)(x_V-1)\nonumber \\&+2r_Sr_V\phi _S^s(x_S)(\phi _V^t(x_V)x_V-\phi _V^s(x_V)(x_V-2))\Big ]\nonumber \\&\times E_{af}(t_e)h_{af}(\alpha _1,\beta ,b_S,b_V)\nonumber \\&+\Big [x_S\phi _V(x_V)\phi _S(x_S)-2r_Vr_S\phi _V^s(x_V)(\phi _S^s(x_S)(x_S+1)\nonumber \\&+\phi _S^t(x_S)(x_S-1))\Big ]E_{af}(t_f)h_{af}(\alpha _2,\beta ,b_V,b_S)\bigg \}, \end{aligned}$$

(27)

$$\begin{aligned} {A}_S^{SP}= & {} -16\pi C_F f_{B_s} m_B^4 \int _0^1dx_Vdx_S\nonumber \\&\times \int _0^{\infty }b_Vdb_Vb_Sdb_S \bigg \{\Big [2r_S\phi _V(x_V)\phi _S^s(x_S)\nonumber \\&+\phi _S(x_S)r_V(x_V-1)(\phi _V^s(x_V)+\phi _V^t(x_V))\Big ]\nonumber \\&\times E_{af}(t_e)h_{af}(\alpha _1,\beta ,b_S,b_V)\nonumber \\&-\Big [\phi _V(x_V)r_Sx_S(\phi _S^t(x_S)-\phi _S^s(x_S))\nonumber \\&+2r_V\phi _S(x_S)\phi _V^s(x_V)\Big ]\nonumber \\&\times E_{af}(t_f)h_{af}(\alpha _2,\beta ,b_V,b_S)\bigg \}. \end{aligned}$$

(28)

Similarly, the contributions ${A}_V^{LL,LR,SP}$ from the diagrams with a vector flying along n direction can be got easily from the substitutes in Eq. (26). The corresponding scales and hard functions are also be referred to in Ref. [53].

Finally, the rest two diagrams are non-factorizable annihilation diagrams, whose amplitudes with different operators are listed as follows

$$\begin{aligned} {W}_S^{LL}= & {} -16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int _0^1dx_1dx_Vdx_S\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\nonumber \\&\times \bigg \{\bigg [x_S\phi _S(x_S)\phi _V(x_V)\nonumber \\&-r_Sr_V\Big [\phi _S^s(x_S)(\phi _V^s(x_V)(x_S-x_V+3)\nonumber \\&+\phi _V^t(x_V)(1-x_S-x_V))\nonumber \\&+\phi _S^t(x_S)(\phi _V^s(x_V)(x_S+x_V-1)\nonumber \\&+\phi _V^t(x_V)(1-x_S+x_V))\Big ]\bigg ] \nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_S)\nonumber \\&+\bigg [r_Vr_S\Big [\phi _S^s(x_S)(\phi _V^s(x_V)(x_S-x_V+1)\nonumber \\&+\phi _V^t(x_V)(x_S+x_V-1))\nonumber \\&+\phi _S^t(x_S)(\phi _V^s(x_V)(1-x_S-x_V)\nonumber \\&-\phi _V^t(x_V)(x_S-x_V+1))\Big ]\nonumber \\&+\phi _V(x_V)\phi _S(x_S)(x_V-1)\bigg ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_S)\bigg \}, \end{aligned}$$

(29)

$$\begin{aligned} {W}_S^{LR}= & {} 16\sqrt{\frac{2}{3}}\pi C_F m_B^4 \int _0^1dx_1dx_Sdx_V\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\nonumber \\&\times \bigg \{\Big [r_S\phi _V(x_V)(\phi _S^s(x_S)+\phi _S^t(x_S))(x_S-2)\nonumber \\&-r_V\phi _S(x_S)(\phi _V^s(x_V)-\phi _V^t(x_V))(x_V+1)\Big ]\nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_S)\nonumber \\&+\Big [r_V\phi _S(x_S)(\phi _V^s(x_V)-\phi _V^t(x_V))(x_V-1)\nonumber \\&-r_S\phi _V(x_V)x_S(\phi _S^s(x_S)+\phi _S^t(x_S))\Big ] \nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_S)\bigg \}, \end{aligned}$$

(30)

$$\begin{aligned} {W}_S^{SP}= & {} 16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int _0^1dx_1dx_Sdx_V\nonumber \\&\times \int _0^{\infty }b_1db_1b_Sdb_S\phi _B(x_1,b_1)\nonumber \\&\times \bigg \{\bigg [\phi _V(x_V)\phi _S(x_S)(x_V-1)\nonumber \\&+r_Sr_V\Big [\phi _S^s(x_S)[\phi _V^s(x_V)(x_S-x_V+3)\nonumber \\&+\phi _V^t(x_V)(x_S+x_V-1)]\nonumber \\&+\phi _S^t(x_S)[\phi _V^t(x_V-x_S+1)\nonumber \\&-\phi _V^s(x_V)(x_S+x_V-1)]\Big ]\bigg ]\nonumber \\&\times E_{anf}(t_g)h_{anf}(\alpha ,\beta _1,b_1,b_S)\nonumber \\&+\bigg [x_S\phi _S(x_S)\phi _V(x_V)\nonumber \\&-r_Sr_V\Big [\phi _S^s(x_S)[\phi _V^s(x_V)(x_S-x_V+1)\nonumber \\&+\phi _V^t(x_V)(1-x_S-x_V)]\nonumber \\&+\phi _S^t(x_S)[\phi _V^s(x_V)(x_S+x_V-1)\nonumber \\&-\phi _V^t(x_V)(1+x_S-x_V)]\Big ]\bigg ]\nonumber \\&\times E_{anf}(t_h)h_{anf}(\alpha ,\beta _2,b_1,b_S)\bigg \}. \end{aligned}$$

(31)

Using the same substitutions as Eq. (26), we get the amplitudes corresponding to the diagrams with a vector meson along the n direction in final states. It is worth noting that the annihilation type diagrams can be perturbatively calculated in PQCD approach, and are the main sources of the strong phase, which are required by the direct CP asymmetry.

4 Numerical results and discussions

With the above analytic decay amplitudes, we can calculate the branching fractions and direct CP asymmetries of all $B_s\rightarrow VS$ decays. Although the conventional four-quark picture [1] for the lighter scalar meson can be used to interpret the mass degeneracy of $f_0(980)$ and $a_0(980)$, the case that the widths of $\kappa (800)$ and $\sigma (600)$ is broader than those of $a_0(980)$ and $f_0(980)$, and the large couplings of $f_0(980)$ and $a_0(980)$ decays to $K{\bar{K}}$, it is very difficult for us to predict the $B_s$ decays in the four-quark assumption due to the unknown wave functions and the decay constants beyond the conventional quark model. In Table 2, we list the branching fractions and direct CP asymmetries of the $B_s\rightarrow VS$ decays involving the scalar mesons with mass below $1~ \mathrm{GeV}$ based on two-quark assumption. In Tables 3 and 4, the branching fractions and direct CP asymmetries of the $B_s\rightarrow VS$ decays involving the heavy scalar mesons around 1.5 GeV are presented under S-I and S-II, respectively, though S-II is preferred [6]. We note that there are not any available experimental data till now, and we thus hope that our theoretical investigations will provide some useful suggestions for experimentalists. If some decays could be measured in future, the comparison between experimental data and theoretical predictions could shed light on the inner structures of the scalar mesons.

We acknowledge that there are a few of the uncertainties in the theoretical calculations, such as ones from the input parameters and from higher order radiative and power corrections. In this work, we have considered three kinds of uncertainties. The first uncertainties are caused by the input nonperturbative parameters, namely the decay constants ($f_{B_S}$, $f_V^{(T)}$, $f_S$ and ${\bar{f}}_S$) of the mesons in initial and final states, the shape parameter $\omega$ in $B_s$ meson wave function and the Gegenbauer moments in the distribution amplitudes of the final mesons. One can find that this kind of errors are almost the largest one among the three kinds, therefore much precise parameters from nonperturbative approaches are called in future. Because the CP asymmetries are fractions, the uncertainties in the numerators and denominators can be cancelled by each other, leading that the CP asymmetries are not sensitive to these nonperturbative parameters. The second uncertainties reflect the effects of the radiative corrections and the power corrections, which are characterized by changing the QCD scale $\Lambda _{QCD}=0.25\pm 0.05$ GeV and varying the hard scale t from 0.8t to 1.2t. It is found that the direct CP asymmetries are sensitive to these corrections, and that’s because the corrections affect the hard kernels and change the strong phases remarkably. The third kind of uncertainties are from the CKM matrix elements shown in Eq. (19).

Supposing that the light scalar mesons are the two-quark lying states, we find from Table 2 that the branching fractions of the pure annihilation decays $B_s\rightarrow a_0(980)\rho$ are at the order of ${{{\mathscr {O}}}}(10^{-7})$, due to the power suppression. Because ${\bar{u}}u$ and ${\bar{d}}d$ have opposite signs in $a_0(980)$ and $\rho ^0$, while they have same signs in $\omega$, the cancellations between contributions of ${{\bar{u}}} u$ and ${{\bar{d}}} d$ in decay $B_s\rightarrow a_0(980)\omega$ lead its branching fraction of decay being as small as $10^{-9}$ far smaller than that of $B_s\rightarrow a_0(980)\rho ^0$. For the decay $B_s\rightarrow a_0(980)\phi$, although the spectator strange quark can enter the $\phi$ meson, the factorizable emission diagrams have null contributions, because the scalar meson $a_0(980)$ cannot be produced through $(V\pm A)$ currents. Furthermore, the nonfactorizable emission diagrams are color-suppressed or electroweak penguin suppressed. As a result, the branching fraction of $B_s\rightarrow a_0(980)\phi$ is also at the order of $\mathcal{O}(10^{-7})$.

Table 2 The CP averaged branching fractions and the direct CP asymmetries of the $B_s\rightarrow a_0(980)[\kappa (800)]V$ decays in S-I

Table 3 The CP averaged branching fractions (in $10^{-6}$) of the $B_s\rightarrow S V$ decays involving the heavier scalar mesons in S-I and S-II

Table 4 The direct CP asymmetries (${\mathscr {A}}_{CP}^{dir}$) (in $\%$) of the $B_s\rightarrow V S$ decays involving the heavier scalar mesons in S-I and S-II

For those decays involving $\kappa (800)$ or $K^*(892)$, it is found that the branching fractions of $B_s\rightarrow K^{*0}(892){\bar{\kappa }}^0(800)$ and $B_s\rightarrow K^{*+}(892)\kappa ^-(800)$ decays with an emitted vector are smaller than those of $B_s\rightarrow \kappa ^0(800){\bar{K}}^{*0}(892)$ and $B_s\rightarrow \kappa ^+(800)K^{*-}(892)$ decays with an emitted $\kappa (800)$. In fact, these four decays are controlled by transitions ${{\bar{b}}}\rightarrow {{\bar{s}}} {{\bar{q}}} q$ ($q=u, d$), which is penguin dominant process. The tree operators are suppressed by the CKM matrix elements $V_{us}V_{ub}^*$, in comparison with $V_{ts}V_{tb}^*$ corresponding to the penguin operators. In the $B_s\rightarrow K^{*0}(892){\bar{\kappa }}^0(800)$ and $B_s\rightarrow K^{*+}(892)\kappa ^-(800)$ decays, the interferences between the emission type penguin contributions and the chiral enhanced annihilation contributions are constructive, while the interferences are destructive in two latter decays $B_s\rightarrow \kappa ^0(800){\bar{K}}^{*0}$ and $B_s\rightarrow \kappa ^+(800)K^{*-}$.

For the decays $B_s\rightarrow \rho ^+\kappa ^-(800)$ and $B_s\rightarrow a_0^+(980)K^{*-}$ decays that are dominated by the tree diagrams, the spectator strange quarks enter into the $\kappa ^-(800)$ and $K^{*-}$, respectively. The branching fraction of $B_s\rightarrow \rho ^+\kappa ^-(800)$ is much larger than that of $B_s\rightarrow a_0^+(980)K^{*-}$, due to the very tiny vector decay constant of $a_0^+(980)$. We also note that the branching fraction of $B_s \rightarrow {\bar{\kappa }}^0(800)\rho ^0[\omega ]$ is much smaller than that of decay $B_s\rightarrow a_0(980){\bar{K}}^{*0}$. Because both decays are color-suppressed processes, the emission diagrams with the $\rho ^0[\omega ]$ emission are suppressed by the small Wilson coefficients $C_1+C_2/3$. Furthermore, for $B_s\rightarrow {\bar{\kappa }}^0(800)\rho ^0[\omega ]$ decay, the contributions from nonfactorizable emission diagrams (c) and (d) are cancelled by each other, while in decay $B_s\rightarrow a_0^+(980)K^{*-}$ the two diagrams strengthen with each other and are enhanced by the large Wilson coefficient $C_2$. These two reasons lead to this large difference. At last, the pure penguin type $B_s\rightarrow {\bar{\kappa }}^0(800)\phi (1020)$ decay has a very small branching fraction, because it is suppressed by the small CKM elements $V_{td}V^*_{tb}$.

In Table 2, the direct CP asymmetries of concerned decay modes are also presented. One finds that there are three large CP asymmetries in $B_s\rightarrow a_0^+(980)K^{*-}$, $B_s\rightarrow {\bar{\kappa }}^0\rho ^0$ and $B_s\rightarrow {\bar{\kappa }}^0 \omega$. For the $B_s\rightarrow a_0^+(980)K^{*-}$ decays, the contributions from tree operators in emission diagrams are suppressed by the tiny vector constant of $a_0^+(980)$, which leads to that the penguin contributions are comparable with the tree contributions. Thus, the large CP asymmetry in this decay is sizable, because the direct CP asymmetry is proportional to the interference between the tree and penguin contributions. Similarly, the tree contributions of $B_s\rightarrow {\bar{\kappa }}^0\rho ^0[\omega ]$ are suppressed by the small Wilson coefficients $C_1+C_2/3$, and the large CP asymmetries in these two decays are understandable. However, for the decay $B_s\rightarrow a_0(980){\bar{K}}^{*0}$, the nonfactorizable emission diagrams with the scalar meson $a_0(980)$ emission are enhanced by the large Wilson coefficient $C_2$, so the contributions from tree operators dominate the decay amplitude. So, the CP asymmetry of $B_s\rightarrow a_0(980){\bar{K}}^{*0}$ is smaller than the corresponding decay $B_s\rightarrow {\bar{\kappa }}^0\rho ^0$. In short, the fact that the large emission diagrams with a scalar meson emitted are suppressed by the tiny vector decay constant of scalar meson or forbidden required by the charge conjugation invariance or conservation of vector current leads to the large direct CP asymmetries. The similar phenomena also appear in the corresponding $B_{u,d}\rightarrow VS$ decays. For instance, the direct CP asymmetries of $B^{-(0)}\rightarrow f_0(980)\rho ^{-(0)}$ decays in Ref. [6] are almost $70\%$. In addition, for the penguin operator dominated decays, such as $B_s\rightarrow \kappa ^+K^{*-}$ and $B_s \rightarrow {\bar{\kappa }}^0(800)\phi$, the CP asymmetries are about zero, as we expected. In the experimental side, some decays with both large branching fractions and large direct CP asymmetries, such as the $B_s\rightarrow a_0^{+}(980)[a_0^{+}(1450)]K^{*-}$ decays, are suggested to be measured in the experiments.

For $f_0(980)$ and $\sigma$, the experimental data of $D_s^+\rightarrow f_0(980)\pi$, $\phi \rightarrow f_0(980)\gamma$ and the observed relation $\Gamma (J/\psi \rightarrow f_0(980)\omega )\simeq \frac{1}{2}\Gamma (J/\psi \rightarrow f_0(980)\phi )$ imply that the $f_0(980)$ and $\sigma$ have a similar mixing as the $\eta$-$\eta ^{\prime }$, so under two-quark assumption we define

$$\begin{aligned} \left( \begin{array}{c} \sigma \\ f_0(980) \end{array} \right) = \left( \begin{array}{cc} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \end{array} \right) \left( \begin{array}{c} |{{\bar{n}}} n\rangle \\ |{{\bar{s}}} s\rangle \end{array} \right) , \end{aligned}$$

(32)

with ${\bar{n}}n=({\bar{u}}u+{\bar{d}}d)/\sqrt{2}$. The mixing angle $\theta$ has not been well determined by current experimental measurements, though there are various constraints from different measurements. In Refs. [66,67,68], the authors summarized the current experiments data, such as the branching fractions of $J/\psi \rightarrow f_0\omega$, $J/\psi \rightarrow f_0\phi$ [69] and the couplings of $f_0\rightarrow \pi \pi / K K$ [70,71,72,73], and constrained the mixing angle $\theta$ to be in the ranges of $[25^\circ ,40^\circ ]$ and $[140^\circ , 165^{\circ }]$. A LHCb measurement of the upper limit on the branching fraction product ${B}({B}^0\rightarrow J/\psi f_0(980))\times {B}(f_0(980)\rightarrow \pi ^+\pi ^-)$ constrains the mixing angle $\mid \theta \mid <30^{\circ }$ [74]. In Ref. [6], $B^-\rightarrow f_0(980)K^-/f_0(980)K^{*-}$ can be accommodated with $\theta$ in the vicinity of $20^{\circ }$, and the mixing angle is adopted as $17^{\circ }$. In short, we can not obtain a universal mixing angle $\theta$ to accommodate to all the current experimental measurements, and we therefore set the mixing angle $\theta$ to be a free parameter in current work.

For the isosinglet scalar mesons $f_0(1370)$, $f_0(1500)$ and $f_0(1710)$, many schemes had been proposed to describe the mixing, and we adopt the typical one obtained in [75, 76]

$$\begin{aligned} \begin{pmatrix} f_0(1370) \\ f_0(1500) \\ f_0(1710) \\ \end{pmatrix} =\begin{pmatrix} 0.78 &{} 0.51 &{} -0.36 \\ -0.54 &{} 0.84 &{} 0.03 \\ 0.32 &{} 0.18 &{} 0.93 \\ \end{pmatrix} \begin{pmatrix} |{{\bar{n}}} n\rangle \\ |{{\bar{s}}} s\rangle \\ |G\rangle \\ \end{pmatrix}, \end{aligned}$$

(33)

$|G\rangle$ denoting the pure scalar glueball state. It is evident that $f_0(1710)$ is composed primarily of the scalar glueball, $f_0(1500)$ is close to an SU(3) octet, and $f_0(1370)$ consists of an approximated SU(3) singlet with some glueball component ($\sim 10\%$). Unlike $f_0(1370)$, the glueball content of $f_0(1500)$ is very tiny because an SU(3) octet does not mix with the scalar glueball. However, the wave function of glueball is unavailable, and the corresponding contribution cannot be calculated now. In this case, for decays with $f_0(1370)$ and $f_0(1500)$, the contributions of glueball have been ignored because of small fractions. For decays with $f_0(1710)$, we shall not discuss them in this work.

Fig. 2

The branching fractions of the $B_s\rightarrow f_0(980)[\sigma ]V$ decays versus the $f_0(980)-\sigma$ mixing angle $\theta$

Fig. 3

The direct CP asymmetries of the $B_s\rightarrow f_0(980)[\sigma ]V$ decays versus the $f_0(980)-\sigma$ mixing angle $\theta$

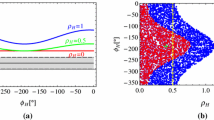
In Figs. 2 and  3, we plot the branching fractions and the direct CP asymmetries of the $B_s\rightarrow f_0(980)[\sigma ]V$ decays versus the $f_0(980)-\sigma$ mixing angle $\theta$ defined in Eq. (4), respectively. When the experimental data are available, these curves could be used to determine the mixing angle $\theta$. For example, if an obvious direct CP asymmetry of $B_s\rightarrow f_0(980)\phi$ decay were measured, the $\theta$ would be an obtuse angle. In fact, for the decay $B_s\rightarrow f_0(980)\phi$, when the mixing angle is about $145^{\circ }$, the total penguin contribution is highly suppressed by the cancellation between the two type of penguin contributions from ${\bar{s}}s$ component and ${\bar{n}}n$ component, respectively, thus it is comparable to the small tree contribution from the ${\bar{n}}n$ component. The remarkable interference between those two contributions leads to a large CP asymmetry. Similarly, a large CP asymmetry in $B_s\rightarrow \sigma \phi$ denotes that the mixing angle $\theta$ is an acute angle. The reason is very similar to that of $B_s\rightarrow f_0(980)\phi$ decay.

In Refs. [32, 77], we have studied the two-body $B\rightarrow K^{*}_{0,2}(1430)f_0(980)/\sigma$ decays and the three-body $B_{(s)}\rightarrow \phi \pi \pi$ decays with the $f_0(980)$ as the resonance in detail. Based on PQCD predictions and the measurements from the BaBar [78] and LHCb [79], if $\theta \sim 145^{\circ }$, the theoretical predictions of the branching ratios are in good agreement with experimental measurements, which indicates that an obtuse angle is preferred. Here, since there are no any available data, we also adopt the $\theta =145^{\circ }$ and list the predictions as

$$\begin{aligned} {B}(B_s\rightarrow \sigma {\bar{K}}^{*0})= & {} (2.0^{+0.8+0.3+0.1}_{-0.7-0.4-0.0})\times 10^{-6},\nonumber \\ {B}(B_s\rightarrow \sigma \rho ^0)= & {} (8.8^{+3.9+1.6+0.4}_{-3.6-1.6-0.3})\times 10^{-8},\nonumber \\ {B}(B_s\rightarrow \sigma \omega )= & {} (2.8^{+2.4+1.3+0.4}_{-0.7-0.3-0.3})\times 10^{-8},\nonumber \\ {B}(B_s\rightarrow \sigma \phi )= & {} (13.3^{+5.7+3.6+0.3}_{-4.4-3.3-0.4})\times 10^{-6},\nonumber \\ {B}(B_s\rightarrow f_0(980){\bar{K}}^{*0})= & {} (1.8^{+0.6+0.3+0.1}_{-0.6-0.3-0.1})\times 10^{-6},\nonumber \\ {B}(B_s\rightarrow f_0(980)\rho ^0)= & {} (2.3^{+1.1+0.3+0.1}_{-0.8-0.2-0.1})\times 10^{-7},\nonumber \\ {B}(B_s\rightarrow f_0(980)\omega )= & {} (9.7^{+5.0+1.5+0.0}_{-4.2-1.4-0.3})\times 10^{-7},\nonumber \\ {B}(B_s\rightarrow f_0(980)\phi )= & {} (4.8^{+3.4+2.4+0.2}_{-2.2-1.5-0.0})\times 10^{-7}. \end{aligned}$$

(34)

Table 5 The CP asymmetry parameters of ${{{\bar{B}}}}^0_{s}\rightarrow {\bar{K}}_0^*(1430) {K}^{(*)}+ c.c.$ decays

Although recent study in Ref. [6] indicated that the S-II is favored for describing the heavier scalar mesons, we still calculated the branching fractions and the direct CP asymmetries of the $B_s\rightarrow VS$ decays involving a heavier scalar meson with the mass around 1.5 GeV under both scenarios, and the numerical results are summarized in the Tables 3 and 4, respectively. From the tables, it is found that the branching fractions of decays with heavy scalar are a little larger than those with light one. Because under two-quark assumption, the light scalar mesons and the corresponding heavy ones have same quark components, the situation of the decays with heavier scalar mesons are similar to the decays with light ones. For the sake of simplicity, we will not discuss them any more. As the heavier scalar mesons can be described in two possible scenarios, we would like to check which scenario is preferable based on our predictions. One can find from Table 3 that the branching fractions of $B_s \rightarrow K_0^{*}(1430)K^{*}$ under S-II are much larger than those under S-I. For example, the branching fraction of charged channel $B_s \rightarrow K_0^{*+}(1430)K^{*-}$ under S-II is about $3.8\times 10^{-5}$, which is larger than the result based on S-I by almost one order of magnitude. These decays were also studied in [80, 81]. Therefore, the future measurements of these four decays in LHCb or Belle-II will help us to differentiate two scenarios. Besides the branching fractions, we also find that the direct CP asymmetries of some decays under the different scenarios vary greatly, for example, the large CP asymmetries of $B_s\rightarrow a_0^+(1450)K^{*-}$ and $B_s\rightarrow f_0(1500)K^{*0}$ decays have different sign under the two scenarios. If the large amount of experimental data continues to accumulate, the comparison between our predictions and future measurements could also help us to study the nature of scalar particles. For comparison, we also present the recent results of $B_s\rightarrow {K}_0^*(1430)V$ decays in QCDF [65] in Tables 3 and 4. It is found that most of our results are larger than those of QCDF, except $B_s \rightarrow K_0^{*+}(1430)K^{*-}$ and $B_s \rightarrow K_0^{*0}(1430){\bar{K}}^{*0}$ under S-I. In PQCD, we also note that the form factor of $F_0^{B_s\rightarrow K^*_0(1430)}(0)=-0.32 (0.56)$ in S-I (S-II) [82], the absolute values of which are much larger than those adopted in [65]. In this respect, more reliable form factors of $B_s\rightarrow K^*_0(1430)$ or wave functions of $K_0^*(1430)$ are needed. The strong phases come from charm loop and power corrections in QCDF, while in PQCD they origin from the non-factorizable hard scatting diagrams and annihilation diagrams. Therefore, the direct CP asymmetries are very large. In fact, this is one of the main differences between QCDF and PQCD.

Specially, $B_{s}$ can decay into ${\bar{K}}_0^*(1430){K}^{*}$ and its CP conjugate state ${K}_0^*(1430){\bar{K}}^{*}$ simultaneously. Recently, the sum of branching fractions of ${B}^0_{d}\rightarrow {\bar{K}}_0^*(1430) {K}+ c.c.$ was measured in LHCb experiment [83], instead of the individual rates. Accordingly, we calculate the sums of the branching fractions of decays $B(B_{s}\rightarrow {\bar{K}}_0^*(1430){K}^{*}+ c.c.)$, and the results are given as

$$\begin{aligned}&B(B_{s}\rightarrow {K}_0^{*-}(1430){K}^{*+}+ c.c.) \nonumber \\&\quad = \left\{ \begin{array}{l c} (18.6^{+4.0+3.8+0.6}_{-4.3-3.4-0.6})\times 10^{-6}&{} \text {S-I}; \\ (63.8^{+22.4+14.2+1.2}_{-17.5-9.8-1.2})\times 10^{-6} &{} \text {S-II}; \end{array}\right. \end{aligned}$$

(35)

$$\begin{aligned}&B(B_{s}\rightarrow {K}_0^{*0}(1430){\bar{K}}^{*0}+ c.c.) \nonumber \\&\quad = \left\{ \begin{array}{l c} (20.8^{+10.4+5.6+0.6}_{-7.6-3.8-0.6})\times 10^{-6}&{} \text {S-I}; \\ (69.6^{+23.6+6.0+1.4}_{-15.1-5.2-1.9})\times 10^{-6} &{} \text {S-II}. \end{array}\right. \end{aligned}$$

(36)

In addition, the CP violations of $B_{s}\rightarrow {\bar{K}}_0^*(1430) {K}^{(*)}+ c.c.$ decays are much more complicated because ${\bar{K}}_0^*(1430) {K}^{(*)}+ c.c.$ are not CP eigenstates. We take $B_{s}\rightarrow {K}_0^{*-}(1430){K}^{*+}+ c.c.$ as an example and define

$$\begin{aligned} A_f= & {} \langle K_0^{*+}(1430)K^{*-}|B_s^0\rangle ,\nonumber \\ A_{{{\bar{f}}}}= & {} \langle K_0^{*-}(1430)K^{*+}| B_s^0\rangle ; \nonumber \\ {{\bar{A}}}_f= & {} \langle K_0^{*+}(1430)K^{*-}|{{\bar{B}}}_s^0\rangle ,\nonumber \\ {{\bar{A}}}_{{{\bar{f}}}}= & {} \langle K_0^{*-}(1430)K^{*+}|{{\bar{B}}}_s^0\rangle ; \end{aligned}$$

(37)

The time-dependent decay rates of $B^0_s$ and ${{\bar{B}}}^0_s$ to a flavor-specific final state, $f= K_0^{*+}(1430)K^{*-}$, are given by [84]

$$\begin{aligned} \frac{d\Gamma _{B^0_s\rightarrow f}(t)}{dt}= & {} \frac{1}{2}|A_f|^2 (1+|\lambda _f|^2) e^{-\Gamma _s t} \left[ \cosh \left( \frac{\Delta \Gamma _s t}{2}\right) \right. \nonumber \\&+ D_f \sinh \left( \frac{\Delta \Gamma _s t}{2}\right) +C_f \cos \left( \Delta m_s t\right) \nonumber \\&\left. - S_f \sin \left( \Delta m_s t\right) \right] , \end{aligned}$$

(38)

$$\begin{aligned} \frac{d\Gamma _{{\bar{B}}^0_s\rightarrow f}(t)}{dt}= & {} \frac{1}{2}|A_f|^2 \left| \frac{p}{q}\right| ^2 (1+|\lambda _f|^2) e^{-\Gamma _s t} \left[ \cosh \left( \frac{\Delta \Gamma _s t}{2}\right) \right. \nonumber \\&+ D_f \sinh \left( \frac{\Delta \Gamma _s t}{2}\right) - C_f \cos \left( \Delta m_s t\right) \nonumber \\&\left. + S_f \sin \left( \Delta m_s t\right) \right] , \end{aligned}$$

(39)

with

$$\begin{aligned} \lambda _{f} = \frac{q}{p}\frac{{\bar{A}}_{f}}{A_{f}},\,\,\,\,\,\,{\bar{\lambda }}_{{\bar{f}}} = \frac{p}{q}\frac{{A}_{{{\bar{f}}}}}{{\bar{A}}_{{\bar{f}}}}. \end{aligned}$$

(40)

p and q relate the $B^0_s$ meson mass eigenstates, $B_{H,L}$, to the flavor eigenstates, $B^0_s$ and ${\bar{B}}^0_s$ via:

$$\begin{aligned} |B_L\rangle= & {} p|B^0_s\rangle +q|{\bar{B}}^0_s\rangle ,\nonumber \\ |B_H\rangle= & {} p|B^0_s\rangle -q|{\bar{B}}^0_s\rangle , \end{aligned}$$

(41)

with $|p|^2+|q|^2=1$. Similar equations can be written for the CP-conjugate decays, replacing $A_f$ by ${\bar{A}}_{{\bar{f}}}$, $\lambda _f$ by ${\bar{\lambda }}_{{\bar{f}}}$, $|p/q|^2$ by $|q/p|^2$, $C_f$ by $C_{{{\bar{f}}}}$, $S_f$ by $S_{{{\bar{f}}}}$, and $D_f$ by $D_{{{\bar{f}}}}$. The CP asymmetry observables $C_f$, $S_f$, $D_f$, $C_{{\bar{f}}}$, $S_{{\bar{f}}}$ and $D_{{\bar{f}}}$ are then given by [84]

$$\begin{aligned} C_f= & {} \frac{ 1 - |\lambda _{f}|^{2} }{ 1 + |\lambda _{f}|^{2}} \,,\quad S_f = \frac{ 2 (\lambda _f) }{ 1 + |\lambda _{f}|^{2}} \nonumber \\ D_f= & {} \frac{ 2 \mathrm{Re}(\lambda _f) }{ 1 + |\lambda _{f}|^{2} } ,\quad C_{{\bar{f}}} = \frac{ 1 - |{\bar{\lambda }}_{{\bar{f}}}|^{2} }{ 1 + |{\bar{\lambda }}_{{\bar{f}}}|^{2}} \,,\quad \nonumber \\ S_{{\bar{f}}}= & {} \frac{ 2 \mathrm{Im}({\bar{\lambda }}_{{\bar{f}}}) }{ 1 +|{\bar{\lambda }}_{{\bar{f}}}|^{2} }\,,\quad D_{{\bar{f}}} = \frac{ 2 \mathrm{Re}({\bar{\lambda }}_{{\bar{f}}}) }{ 1 + |{\bar{\lambda }}_{{\bar{f}}}|^{2} } \,. \end{aligned}$$

(42)

Our results for these observables are first given in Table 5. For the decays ${{\bar{B}}}_s^0 \rightarrow {{\bar{K}}}_0^{*0} {K}^{*0}+c.c.$, we find $C_f=C_{{{\bar{f}}}}$, because only penguin operators are involved. The time-dependence CP asymmetries of these decays have also been studied in [65]. As aforementioned, the origins of the strong phases are different in QCDF and PQCD, and we hope the future measurements could discriminate two different approaches.

5 Summary

In this work we studied $B_s \rightarrow VS$ decays within the framework of PQCD approach, where S denotes a scalar meson. Under two scenarios for describing the nature of the scalar meson, we calculated the branching fractions and the direct CP asymmetries of these decay modes. It is shown that the branching fractions of some decays are at the order of $10^{-6}$, which can be measured in the running experiments such as the LHCb and the Belle-II. We also note that some decays have large direct CP asymmetries, such as the $B_s\rightarrow a_0^+K^{*-}$ decays, because the contributions with a scalar meson emission are suppressed or vanish. For the decays involving heavier scalar meson, the decays $B_s \rightarrow K_0^{*}(1430)K^{*}$ could be used to distinguish which scenario is preferable for describing the scalar mesons.