1 Introduction

In 2019, the LHCb Collaboration first reported the doubly charmed baryon \(\Xi _{cc}^{++}\) with the determined mass \(M_{\Xi _{cc}^{++}}=3.621\) GeV [1, 2] and lifetime \(\tau _{\Xi ^{++}_{cc}}=0.256\,{\hbox {ps}}\)  [3]. This is the first time to confirm a baryon consists of two charm quarks and a u quark. This discovery has caused great attention in hadron physics, and led to a new round of researches on the heavy baryons, which may hint that more and more baryons with two even three heavy quarks would be detected in the near future [4]. However, there are still no significant signals for the isospin partner of \(\Xi _{cc}^{++}\)  [5] and the \(\Xi _{bc}\)  [6]. \(\Xi ^{++}_{cc}\) contains two charm quarks which constraint the (cc)-diquark could only be flavor symmetric, while in the other case, the two different heavy-flavor quarks in the baryons could be both in the flavor symmetric and antisymmetric. In this work, we would focus on the latter ones, the baryons with flavor constituents (bcq) with q denoting a light quark u, d, or s.

Different from a meson, a baryon consists of three quarks and has the \(\frac{1}{2}\)-integer spin and hence obeys the Fermi-Dirac statistics principle. The Pauli principle states that the wave function of a baryon should be antisymmetric under the interchange of any two quarks inside. The baryon wave functions includes four parts, spatial, spin, color, and flavor, and it is the whole \(\psi (\mathrm {baryon})=\psi (\mathrm {space})\psi (\mathrm {spin})\psi (\mathrm {color})\psi (\mathrm {flavor})\) works that should be anti-symmetric under the interchange of any two quarks. Notice this principle also works for a diquark system inside the baryon, and here we regard all these four parts as the identical quark’s different properties. Since the naturally occurring particle is always a color singlet, any two quarks inside a baryon are in the color anti-triplet in order to form a colorless particle. Hence the color part is always anti-symmetric and the others together are symmetric. In the orbital ground state, there is no angular dependence and thus the spatial part is symmetric. For a doubly heavy diquark system consisting of two quarks of the same flavor, such as the case in \(\Xi _{cc}\) or \(\Xi _{bb}\), there is no other choices, it is flavor symmetric and hence symmetric in spin, which means it could only be in \(1^+\) state. We have discussed this case in a previous work [7]. However, for a doubly heavy diquark system consisting of two different quarks, namely the (bc) case, its flavor could be both symmetric or anti-symmetric, namely, it could be in both \(1^+\) and \(0^+\) state. The former one has also been incorporated in Ref. [7], and in this work first we would focus on the latter one, the doubly heavy baryons with \(0^+\) (bc)-diquark cores; then we deal with the real physical baryons states by considering the mixing effects between the \(1^+\) and \(0^+\) (bc)-diquark cores.

The \(0^+\) (bc)-diquark core combined with a third light quark can form the \(J^P=\frac{1}{2}^+\) baryon state in S-wave. We would first construct the Salpeter wave functions, and then give the mass spectra and numerical wave functions by solving the corresponding three-dimensional (Bethe–)Salpeter equations under instantaneous approximation. For the \(\frac{1}{2}^+\) (bcq) baryon states, it can be formed by both the \(0^+\) and \(1^+\) (bc)-diquark cores, and hence usually the doublets \(\Xi _{bc}(\Omega _{bc})\) and \(\Xi _{bc}'(\Omega '_{bc})\) are the mixing states of these two. These mixing effects would be considered by the coupled BSE. The masses of the \(\Xi ^{(\prime )}_{bc}\) and \(\Omega ^{(\prime )}_{bc}\) are predicted to lie in \(6.8{-}7.1\,{\hbox {GeV}}\) and \(6.9{-}7.1\,{\hbox {GeV}}\) respectively [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Notice that in Refs. [21,22,23,24] the \(\frac{1}{2}^+\) (bcq) baryon doublets are labeled by the definite spin of the (cq)-diquark, while in Refs. [9, 10, 12,13,14,15,16,17,18, 20] the baryons are labeled by the (bc)-diquark spin. The naming conventions used in this work are: unprimed symbols \(\Xi _{bc}\) and \(\Omega _{bc}\) to denote the baryon states with the dominate \(1^+\) (bc)-diquark, while the primed symbols \(\Xi '_{bc}\) and \(\Omega '_{bc}\) to label the ones with the dominate \(0^+\) (bc)-diquark.

In this work, we will deal with the doubly heavy baryons with (bcq) flavors within the framework of the instantaneous Bethe–Salpeter equation, which has already been successfully used to cope with the doubly heavy baryons with \(1^+\) diquark cores [7], the recently observed pentaquark \(P_c\) and fully heavy tetraquark \( T_{QQ{\bar{Q}}{\bar{Q}}}\) states [25, 26], and also generally applied to the meson mass spectra [27,28,29], the hadronic transitions and decays [30,31,32,33,34,35,36]. The theoretical calculations from BS methods have achieved satisfactory consistences with the experimental measurements, which give us more confidence and thereby inspire us to apply the same methods in baryon bound problems. Our basic scheme is to reduce the three-body baryon bound problem into two two-body bound problems. Namely, the two heavy quarks first form a compact diquark core in color anti-triplet, and then the diquark combined with a third quark forms the colorless baryon. In Refs. [37,38,39,40] the Bethe–Salpeter methods have already been used to study the properties of the diquark, although different interaction kernels are adopted. By supposing a quark exchange between diquark and the third quark, Refs. [41,42,43] built the effective instantaneous BS equation for a baryon; while in Refs. [44,45,46,47,48,49,50,51] a different scheme to deal with the baryon is adopted based on the diquark–quark picture in the heavy quark limit.

This paper is organized as follow. In Sect. 2 the \(0^+\) diquark mass spectra and wave function are obtained by solving the corresponding diquark BSE, and then the relevant form factors describing the diquark–gluon interaction are calculated. In Sect. 3 we derive the BSE of a \(\frac{1}{2}^+\) baryon as the bound state of a \(0^+\) diquark and a third quark. In Sect. 4 the BSE and the corresponding wave function of the general \(\frac{1}{2}^+\) (bcq) baryons is given including the mixing effects between the \(1^+\) and \(0^+\) (bc)-diquark transition. In Sect. 5 the mass spectra, numerical wave functions, and the mixing effects are presented for the (bcq) baryons with \(J^P=\frac{1}{2}^+\). Finally, we give a brief summary in Sect. 6.

2 Bethe–Salpeter equation of the \(0^+\) diquarks and the relevant form factors

In order to have a self-contained discussion, we first review the BS methods for a diquark and the interaction kernel used; then the \(0^+\) (bc)-diquark Salpeter wave function is solved to calculate the relevant form factors.

2.1 Bethe–Salpeter equation and wave function of the \(0^+\) diquark core

In the momentum space, the diquark Bethe–Salpeter equation can be expressed as [7]

$$\begin{aligned} \Gamma _c(P_\mathrm {D},s)=\int \frac{\mathrm {d}4 u}{(2\pi )^4} iK_c(s-u) \left[ S(u_1)\Gamma _c(P_\mathrm {D},u)S(-u_2) \right] , \nonumber \\ \end{aligned}$$
(2.1)

where \(\Gamma _c\) is related to the diquark vertex \(\Gamma _\mathrm {D}\) by \(\Gamma _\mathrm {D}=\Gamma _c C\), and \(C\equiv i\gamma ^0\gamma ^2\) denotes the charge conjugate operator; the interaction kernel \(K_c(s-u)=\frac{1}{2}K_\mathrm {M}(s-u)\), where \(K_\mathrm {M}\) denotes the interaction kernel in a meson and will be introduced more detailed later; \(P_\mathrm {D}\) is the total momentum of the diquark; \(S(s_{1})\) and \(S(-s_2)\) are the Dirac propagators, and \(s_{1(2)}\) is the corresponding momentum. The internal momentum s and u are defined as

$$\begin{aligned} s=\lambda _2s_1-\lambda _1s_2,\quad u=\lambda _2 u_1-\lambda _1 u_2, \end{aligned}$$

where \(\lambda _i \equiv \frac{m_i}{m_1+m_2}~(i=1,2),\) and \(m_i\) denotes the constituent quark mass. From the BS vertex, the BS wave function can be naturally defined as

$$\begin{aligned} \psi _c(P_\mathrm {D},s)=S(s_1)\Gamma _c(P_\mathrm {D},s)S(-s_2). \end{aligned}$$
(2.2)

Notice the original diquark Bethe–Salpeter wave function is related to the above \(\psi _c\) by \(\psi _\mathrm {D}=\psi _c C\). By solving the Eq. (2.1) we can obtain the diquark vertex \(\Gamma _\mathrm {D}\) or the diquark BS wave function \(\psi _\mathrm {D}\).

Throughout this work we would study under the instantaneous approximation (IA), which states the interaction potential we used are static and does not depend on the time component of the exchanged momentum, namely, \(K_c(s-u)\sim K_c(s_{\!\perp }-u_{\!\perp })\). Under this approximation, the integration over the time component of s can be further absorbed into the wave function. Namely, we can define the three-dimensional Salpeter wave function as

$$\begin{aligned} \varphi _c(P_\mathrm {D},s_{\!\perp }) \equiv i\int \frac{\mathrm {d}s_{0}}{2\pi }\psi _c(P_\mathrm {D},s), \end{aligned}$$
(2.3)

where \(s_{0}\equiv \frac{s\cdot P_\mathrm {D}}{M_\mathrm {D}}\) and \(M_\mathrm {D}\) is the constituent mass of the diquark; \(s_{\!\perp } \equiv s-s_{0} \frac{s\cdot P_\mathrm {D}}{M_\mathrm {D}}\). By performing the contour integral over \(s_{0}\) on both sides of Eq. (2.2), we obtain the three-dimensional (Bethe–)Salpeter equation [7],

$$\begin{aligned} M_\mathrm {D} \varphi _c(P_\mathrm {D},s_{\!\perp })= & {} (\omega _1+\omega _2) H(s_{1\perp })\varphi _c(s_{\!\perp })\nonumber \\&+\frac{1}{2} \left[ H(s_{1\perp }) W(s_{\!\perp }) - W(s_{\!\perp }) H(s_{2\perp })\right] ,\nonumber \\ \end{aligned}$$
(2.4)

where the kinetic energy of the constituent quark is defined as \(\omega _i\equiv ({m_i^2-s_{i\perp }^2})^{\frac{1}{2}}\) with \(s_{i\perp }=s_i- \frac{s\cdot P_\mathrm {D} P_\mathrm {D}}{M^2_\mathrm {D}}\). The dimensionless operator \({H}(s_{i\perp })\) is the usual Dirac Hamiltonian divided by \(\omega _i\), namely,

(2.5)

Also we define \(W(s_{\!\perp }) \equiv \gamma ^0\Gamma _c(P_\mathrm {D},s_{\!\perp })\gamma _0\) to denote the potential energy part of the inner constituents. Notice if the Lorentz structure in the kernel \(K(s_{\!\perp }-u_{\!\perp })\) is the type \(\gamma ^0\otimes \gamma _0\), \(W(s_{\!\perp })\) would be a scalar integration, which is just the case we deal with in this work. The three-dimensional vertex is expressed as

$$\begin{aligned} \Gamma _c( s_{\!\perp }) =\int \frac{\mathrm {d}^3 u_{\!\perp }}{(2\pi )^3} K_c(s_{\!\perp }-u_{\!\perp }) \varphi _c( u_{\!\perp }). \end{aligned}$$
(2.6)

Namely, the integration over \(u_0\equiv \frac{u \cdot P_\mathrm {D}}{M_\mathrm {D}}\) has been absorbed into the definition of the Salpeter wave function \(\varphi _c(u_{\!\perp })\), and now we only need to deal with the problem of the three-dimensional integration.

Also the Salpeter wave function \(\varphi _c(P_\mathrm {D},s_{\!\perp })\) fulfills the following constraint condition,

$$\begin{aligned} {\hat{H}}(s_{1\perp }) \varphi _c(s_{\!\perp }) + \varphi _c(s_{\!\perp }){\hat{H}}(s_{2\perp }) =0. \end{aligned}$$
(2.7)

The normalization condition of the Salpeter wave function reads

$$\begin{aligned} \int \frac{\mathrm d^3 s_{\!\perp }}{(2\pi )^3} \, \mathrm {tr}~ \varphi _c^{\dagger }(s_{\!\perp }) {\hat{H}}(s_{1\perp })\varphi _c(s_{\!\perp })=2M_\mathrm {D}. \end{aligned}$$
(2.8)

Note that the results above are also available for a meson system.

Since a diquark consists of two quarks rather than the quark–antiquark pair in a meson, the diquark parity is then just opposite with the corresponding meson. Considering the Lorentz structure, total angular momentum and parity, the three-dimensional BS wave function of a diquark with \(J^P=0^+\) can be constructed as

(2.9)

where the abbreviation \(s_n\equiv {s_{\!\perp }}/{|\vec s\,|}\) is used; the undetermined radial wave functions \(f_i~(i=1,\ldots ,4)\) can be further reduced to two by the constraint condition in Eq. (2.7), which gives the following two constraint conditions,

$$\begin{aligned} f_3= -\frac{|\vec s\,|(\omega _1-\omega _2)}{m_1\omega _2+ m_2\omega _1}f_1,\quad f_4= -\frac{|\vec s\,|(\omega _1+\omega _2)}{ m_1\omega _2+m_2\omega _1}f_2.\nonumber \\ \end{aligned}$$
(2.10)

Notice that the wave function of a meson with \(J^{P}=0^{-}\) shares the same form with Eq. (2.9).

Inserting Eq. (2.9) into the Eq. (2.7), and then taking different traces, we can obtain two coupled eigenvalue equations, which can be solved numerically. The detailed procedures on solving the BSE of two-fermion systems have been presented in many previous works  [7, 34, 52, 53] and we will not copy the procedures here again. The normalization of above wave function can now be simply expressed as,

$$\begin{aligned} \int \frac{\mathrm {d}^3\vec s}{(2\pi )^3} \frac{8\omega _1\omega _2}{M_\mathrm {D}(m_1\omega _2+m_2\omega _1)}f_1(|\vec s\,|)f_2\left( |\vec s\,|\right) =1. \end{aligned}$$
(2.11)

From this equation we know that the Salpeter wave function \(f_i\) has the dimension of \({\hbox {GeV}}^{-1}\).

2.2 Interaction kernel

Since the interaction kernels in a baryon and a diquark system are directly related to that in a meson, we will specify the interaction potential in a meson bound system first. As mentioned above, throughout this paper, we work under the instantaneous approximation. Then the interaction kernel of a meson based on the one-gluon exchange, reads in the momentum space,

$$\begin{aligned} iK_\mathrm {M}(\vec t\,)=iV (\vec t\,)\gamma ^\alpha \otimes \gamma _\alpha , \end{aligned}$$
(2.12)

where t denotes the momentum transfer in the interaction; and the potential \(V(\vec t\,)\) in the Coulomb gauge behaves as  [52, 54,55,56]

$$\begin{aligned}&V(\vec t\,)= -\frac{4}{3} \frac{4\pi \alpha _s(\vec t\,)}{\vec t\,^2+a_1^2}\nonumber \\&+\left[ (2\pi )^3 \delta ^3(\vec t\,)\left( \frac{\lambda }{a_2}+V_0 \right) - \frac{8\pi \lambda }{(\vec t\,^2+a_2^2)^2} \right] , \end{aligned}$$
(2.13)

where \(\frac{4}{3}\) is the color factor; \(a_{1(2)}\) is introduced to avoid the divergence in small momentum transfer zone; the kernel describing the confinement effects is introduced phenomenologically, which is characterized by the string constant \(\lambda \) and the factor \(a_2\). Based on the famous Cornell potential  [57, 58], which behaves as the one-gluon exchange Coulomb-type potential at short distance and a linear growth confinement one at long distance, the potential used here is modified as the aforementioned one to incorporate the color screening effects [59, 60] in the linear confinement potential. \(V_0\) is a free constant fixed by fitting the meson data. The strong coupling constant \(\alpha _s\) has the following form,

$$\begin{aligned} \alpha _s(\vec t\,)=\frac{12\pi }{(33-2N_f)}\frac{1}{\ln \left( a+ {\vec t\,^2}/{\Lambda ^2_{\mathrm {QCD}}}\right) }, \end{aligned}$$

where \(\Lambda _\mathrm {QCD}\) is the scale of the strong interaction, \(N_f\), the active flavor, and \(a=e\) is a regulator constant.

For later convenience, we split V into two parts as

$$\begin{aligned} V(\vec t\,)=(2\pi )^3\delta ^3 (\vec t\,) V_1+V_2 (\vec t\,), \end{aligned}$$
(2.14)

where

$$\begin{aligned} V_1 \equiv \frac{\lambda }{a_2}+V_0 ,\quad V_2(\vec t\,)\equiv - \frac{8\pi \lambda }{(\vec t\,^2+a_2^2)^2} -\frac{4}{3} \frac{4\pi \alpha _s(\vec t\,)}{\vec t\,^2+a_1^2}. \end{aligned}$$

Namely, all the dependence on \(\vec t\) is collected into \(V_{2}(\vec t\,)\), while \(V_{1}\) is just a constant.

The quark–antiquark pair in the meson is in the color singlet, while the quark–quark pair inside the baryon is in the color anti-triplet. The corresponding color factors then are then \(\frac{4}{3}\) and \(-\frac{2}{3}\) respectively. The interaction kernel of the diquark inside a baryon can then be expressed as,

$$\begin{aligned} K_\mathrm {D}(\vec t\,)=-\frac{1}{2} V(\vec t\,)\gamma ^\alpha \otimes (\gamma _\alpha )^\mathrm {T}. \end{aligned}$$
(2.15)

This ‘half rule’ used here has been widely adopted in previous works involved the quark–quark bound problems [10, 22, 61]. It is exact in the one-gluon exchange limit and has been validated by the measurement of the \(\Xi _{cc}^{++}\) mass. Its successful extension beyond weak coupling implies that the heavy quark potential factorizes into a color dependent and a space-dependent part, with the latter being the same for quark–quark and quark–antiquark pairs. The relative factor of \(\frac{1}{2}\) then results from the color algebra, just as in the weak-coupling limit  [62]. Also in this work, we focus on the baryons with at least doubly heavy quarks, and then we will only consider the time component \((\alpha =0)\) of the interaction kernel, since the space components are suppressed by a factor \(\frac{v}{c}\) when there is heavy quark involved in the interaction. This is also consistent with the analysis in Ref. [63].

The numerical values of the model parameters used in this work are just the same with that we applied in previous calculations [7, 28, 31,32,33,34,35,36], and determined by fitting to the corresponding mesons namely,

$$\begin{aligned}&a =e=2.7183,\quad \lambda =0.21~{\hbox {GeV}}^2, \\&\quad \Lambda _\text {QCD} =0.27~{\hbox {GeV}},\quad a_1 =a_2=0.06~{\hbox {GeV}}, \end{aligned}$$

and the constitute quark masses used are

$$\begin{aligned}&m_u =0.305~{\hbox {GeV}},\quad m_d =0.311~{\hbox {GeV}},\quad m_s =0.5~{\hbox {GeV}}, \\&\quad m_c =1.62~{\hbox {GeV}},\quad m_b=4.96~{\hbox {GeV}}. \end{aligned}$$

The free parameter \(V_0\) is fixed by fitting the meson mass \(m_{B_c}\) to the experimental value. In this work, we found \(V_0=-0.21~{\hbox {GeV}}\) for the \(0^+\) (bc)-diquark. Finally, the corresponding (bc)-diquark mass are \(M_{(bc)}(1S)=6.563\,{\hbox {GeV}}\) and \(M_{(bc)}(2S)=6.892\,{\hbox {GeV}}\) for the ground and the first radially excited states respectively, and the corresponding radial wave functions are showed in Fig. 1.

Fig. 1
figure 1

Radial wave functions for the \(0^+\) (bc)-diquark in a the ground state and b the first radial excited state

Full size image
Fig. 2
figure 2

Scattering vertex between the diquark and a gluon

Full size image

The \(0^+\) diquark wave function at zero point is helpful in many applications, which is defined as

(2.16)

where \(\psi _\mathrm {P}\) and \(\psi _\mathrm {A}\) are calculated from the Salpeter radial wave functions,

$$\begin{aligned} \psi _\mathrm {P} = \int \frac{\mathrm d^3 \vec s}{(2\pi )^3} f_1,\quad \psi _\mathrm {A} = \int \frac{\mathrm d^3 \vec s}{(2\pi )^3} f_2. \end{aligned}$$
(2.17)

The obtained numerical results are \(\psi _\mathrm {P}=0.311 \) and \(\psi _\mathrm {A}=0.274\,{\hbox {GeV}}^2\) for the ground state; \(\psi _\mathrm {P}=0.273\) and \(\psi _\mathrm {A}=0.230\,{\hbox {GeV}}^2\) for the first excited state.

2.3 The diquark form factors and wave function at zero point

The Feynman diagrams of the doubly heavy diquark coupling to a gluon are showed in Fig. 2. The variables involved are defined as: \(M_\mathrm {1}\) denotes the diquark effective mass; \(p~(p^{\prime }{})\), the diquark momenta before (after) coupling to the gluon. The internal momenta \(s'\) in the final state is defined as \(s^{\prime }=\lambda ^{\prime }_2s^{\prime }_1-\lambda ^{\prime }_1s^{\prime }_2\), where \(\lambda '_i \equiv \frac{m'_i}{m_1'+m_2'}=\lambda _i\) since \(m_i^{\prime }=m_i\). Also in Fig. 3a \(s'_1=s_1\), then s and \(s'\) are related by \(s'=\lambda _1(p-p')+s\).

Considering the Lorentz conditions and the vector current conservation, the form factor \({\mathcal {A}}^{\mu }\) of the \(0^+\rightarrow 0^+\) diquark coupling a gluon can generally be expressed as,

$$\begin{aligned} {\mathcal {A}}^{\mu }=C_{00} (p+p')^\mu , \end{aligned}$$
(2.18)

where \(C_{00}\) here are explicitly dependent on \(\Delta p^2\) with \(\Delta p\equiv p-p'\) denoting the momentum transfer. On the other hand, according to the Feynman diagram Fig. 2, the form factor \({\mathcal {A}}^\mu \) can be directly expressed by the transition amplitude,

$$\begin{aligned} {\mathcal {A}}^{\mu }=\frac{1}{2}\left( {\mathcal {A}}_1+{\mathcal {A}}_2 \right) , \end{aligned}$$
(2.19)

where the factor \(\frac{1}{2}\) comes from the normalization convention; the amplitude \({\mathcal {A}}_{1(2)}\) corresponds to the process when the gluon interacts with the b(c)-quark. \({\mathcal {A}}_1\) is explicitly described by the BS vertex as,

$$\begin{aligned} {\mathcal {A}}_1= & {} -\int \frac{\mathrm {d}^4 s}{(2\pi )^4} \mathrm {tr}~\bar{\Gamma }_c(p',s') S(s_1)\Gamma _c(p,s) S(-s_2) \gamma ^\mu S(-s'_2)\nonumber \\= & {} C^{(1)}_{00}(p+p')^\mu . \end{aligned}$$
(2.20)

By performing the contour integration over \(s^0\), \({\mathcal {A}}_1\) can be further expressed by the three-dimensional integral of the Salpeter wave functions \(\varphi _c\). Also it is easy to obtain \({\mathcal {A}}_2\) by interchange \(m_1\) and \(m_2\), namely,

$$\begin{aligned} {\mathcal {A}}_2=C^{(2)}_{00}(p+p')^\mu ={\mathcal {A}}_1(m_1\rightleftharpoons m_2), \end{aligned}$$

and then we obtain the form factor as \(C_{00}=\frac{1}{2}\left[ C^{(1)}_{00}+C^{(2)}_{00}\right] \).

Fig. 3
figure 3

The obtained form factors \(C_{11}\), \(C_{00}\), and \(C_{10}\) of the diquark in a the ground state, and b the first excited state

Full size image

Inserting the \(0^+\) Salpeter wave function, namely, Eq. (2.9), into above equation, by calculating the trace and the integration, we get the numerical values of the diquark form factors, which are graphically shown in Fig. 3.

The form factor describing \(1^+\) to \(0^+\) (or vice versa) diquark transition is directly related to the mixing effects between the \(\frac{1}{2}^+\) baryon doublet \(\Xi _{bc}\) and \(\Xi '_{bc}\), or \(\Omega _{bc}\) and \(\Omega '_{bc}\). Note this transition could only happen through the P-wave gluon exchange. By a similar analysis, the form factor for \({1^+}\) to \({0^+}\) diquark transition can be expressed as,

$$\begin{aligned} {\mathcal {A}}^{\alpha \mu }=\frac{1}{2}\left( {\mathcal {A}}^{\alpha \mu }_1+ {\mathcal {A}}^{\alpha \mu }_2 \right) =i \frac{2E_{\!F}}{M_{(0)} M_{(1)} } C_{10} \epsilon ^{\alpha \mu pp'}, \end{aligned}$$
(2.21)

where \(\epsilon ^{\alpha \mu pp'}=\epsilon ^{\alpha \mu \nu \beta }p_\nu p'_\beta \) and \(\epsilon ^{\alpha \mu \nu \beta }\) is the Levi-Civita antisymmetric tensor; the extra Lorentz index \(\alpha \) comes from the vector wave function of the initial \(1^+\) diquark; \(M_{(0)}\) and \(M_{(1)}\) are the \(0^+\) and \(1^+\) diquark masses respectively; the factor \( E_F \) here helps keep the dimensions of the \(C_{ij}\) consistent and \(E_{F}=({M^2_F+\vec p\,'^2})^{\frac{1}{2}}\) with \(M_F\) denoting the constituent mass of the diquark after transition, which is \(M_{(0)}\) in the \(1^+\rightarrow 0^+\) transition and is \(M_{(1)}\) in the \(0^+\rightarrow 1^+\) transition. Notice flavor-symmetric \(\psi (\mathrm {flavor})\) of the diquark becomes antisymmetric after the transition. The Feynman amplitude \({\mathcal {A}}^{\alpha \mu }_1\) is explicitly expressed by the BS vertex as,

$$\begin{aligned} {\mathcal {A}}^{\alpha \mu }_1= & {} -\int \frac{\mathrm {d}^4 s}{(2\pi )^4} \mathrm {tr}~\bar{\Gamma }_c(p',s') S(s_1)\Gamma ^{\alpha }_c(p,s) S(-s_2)\nonumber \\&\times \gamma ^\mu S(-s'_2)=i\frac{2E_F}{M_{(0)} M_{(1)}} C^{(1)}_{10} \epsilon ^{\alpha \mu pp'}, \end{aligned}$$
(2.22)

where the \(1^+\) Salpeter wave function had been given in our previous work [7]. And again we have \({\mathcal {A}}^{\alpha \mu }_2 = {\mathcal {A}}^{\alpha \mu }_1(m_1\rightleftharpoons m_2)\). Then the form factor \(C_{10}=\frac{1}{2}[C^{(1)}_{10}+C_{10}^{(2)}]\) can be obtained numerically by a similar procedure as above, and the obtained numerical result is also displayed in Fig. 3. The form factor \({\mathcal {A}}^{\alpha \mu }\) for the \(0^+\) to \(1^+\) (bc)-diquark transition is just the same with that in the \(1^+\rightarrow 0^+\) case.

3 \(\frac{1}{2}^+\) baryons consisting of the \(0^+\) doubly heavy diquark core and a light quark

Fig. 4
figure 4

Bethe–Salpeter equation of the baryon based on the diquark–quark picture. P denotes the baryon momentum, \(p_1(k_1)\), the diquark momentum, and \(p_2(k_2)\), the third quark momentum ; The Romans (blue) denote the Dirac indices

Full size image

In this section, we first give the Bethe–Salpeter equation of the doubly heavy baryon as the bound state of the \(0^+\) heavy diquark core and the remaining light quark; then in the instantaneous approximation, we derive the corresponding three-dimensional Salpeter equation; finally, the baryon Salpeter wave functions are constructed and solved to obtain the \(J^P=\frac{1}{2}^+\) (bcq) baryons.

3.1 BSE of baryons with \(0^+\) heavy diquark cores

The baryon BSE based on the diquark–quark picture is showed schematically in Fig. 4, which is expressed by the matrix notation as,

$$\begin{aligned} \Gamma (P,q,\xi )= & {} \int \frac{\mathrm {d}^4 k}{(2\pi )^4} (-i)K(p_1,k_1;p_2,k_2)\nonumber \\&\times \left[ S(k_2)\Gamma (P,k,\xi ) D(k_1)\right] , \end{aligned}$$
(3.1)

where \((-i)K(p_1,k_1;p_2,k_2)\) represents the effective quark-diquark interaction kernel, which depends on the diquark and the third quark’s momenta \(p_1,~k_1\) and \(p_2,~k_2\) respectively; \(\Gamma (P,q,\xi )\), the baryon vertex; P, the baryon momentum, \(P^2=M^2\) with M denoting the baryon mass; r, the baryon polarization state; \(S(k_2)\), the Dirac propagator of quark with momentum \(k_2\); \(D(k_1)\) is the scalar propagator; the baryon wave function can be defined as usual

$$\begin{aligned} B(P,q,\xi )=S(p_2) \Gamma (P,q,\xi ) D(p_1) . \end{aligned}$$
(3.2)

The symbols P and \(\xi \) in the BS vertex \(\Gamma (P,q,\xi )\) and wave function \(B(P,q,\xi )\) would be temporarily omitted unless it is necessary to write them explicitly. The two internal momenta q and k in the baryon BSE are defined as usual,

$$\begin{aligned} q=\alpha _2 p_1 - \alpha _1 p_2,\quad k=\alpha _2 k_1 - \alpha _1 k_2, \end{aligned}$$

where \(\alpha _i\equiv \frac{m_i}{m_1+m_2}\); \(m_1\) denotes the diquark effective mass, and \(m_2\), the third quark constituent mass. With the momentum conservation, by simple analysis, there are only 4 independent variables here, which can be chosen as, the baryon total momentum P, quark-diquark internal momentum k and q, and the internal momentum of the diquark s. Then other variables can be expressed by these four variables. We point out that the Bethe–Salpeter equation given here can also be applied to deal with the pentaquark states formed by a (pseudo)scalar meson and a baryon [25].

The effective interaction kernel \((-i)K(p_1,k_1;p_2,k_2)\) can be considered as the diquark–quark scattering, which is expressed by the BS vertex as,

$$\begin{aligned}&(-i)K_{ii'}(p_1,k_1;p_2,k_2) \nonumber \\&\quad = iV (k-q) \gamma ^\mu _{ii'} \frac{1}{2}\int \frac{\mathrm {d}^4 s}{(2\pi )^4} \mathrm {tr}~ \bar{\Gamma }_\mathrm {c}(p_1,s') S(s_1)\nonumber \\&\qquad \times \Gamma _\mathrm {c}(k_1,s) S(-s_2) \gamma _\mu S(-s'_2)+(m_1\rightleftharpoons m_2). \end{aligned}$$
(3.3)

Notice that the integration part in Eq. (3.3) above is just the \(0^+\) diquark form factor which we have obtained in previous section, only the on-shell \(p,~p'\) replaced by the off-shell momenta \(k_1\) and \(p_1\) respectively. Here the on-shell form factors are generalized as an effective description on the coupling of the diquark to a gluon; besides, we do not consider the self-energy correction of the doubly heavy (bc)-diquark. Then the interaction kernel \((-iK)\) can now be written as a simple expression,

$$\begin{aligned} (-i)K(p_1,k_1;p_2,k_2)=- iV (k-q){\mathcal {A}}_{\mu } \gamma ^\mu , \end{aligned}$$
(3.4)

where \({\mathcal {A}}_{\mu }=C_{00} (p_1+k_1)_\mu \) is the obtained \(0^+\) (bc)-diquark form factor. Notice that now the interaction potential between the diquark and the light quark is smeared by the diquark form factor \(C_{00}\). As mentioned above, we only concentrate on the dominate time component of this vector interaction.

Now we move to obtain the three-dimensional Salpeter equation (SE) of the baryons. First, we define the baryon Salpeter wave function as usual \(\varphi (q_\perp ) \equiv -i\int \frac{\mathrm d q_P}{2\pi } B(q)\), where \(q_P={\hat{P}}\cdot q\), and \(q_\perp =q-q_P {\hat{P}}\) with \({\hat{P}}\equiv \frac{P}{M}\). On the other hand, under the instantaneous approximation, the interaction potential \(V (k-q)\sim V (k_\perp - q_\perp )\), which is equivalent to \(q^0=k^0\), and thus we have \(\varrho \equiv (k_1+p_1)^0=2(\alpha _1M+q_P)\). Notice the factor \(\varrho \) plays an important role in the derivation of the three-dimensional SE. Now the BS vertex in Eq. (3.1) can be expressed as \(\Gamma (q)=\varrho \gamma ^0 \Theta (q_\perp )\), where \(\Theta \) is a three-dimensional integral over \(k_\perp \), namely,

$$\begin{aligned} \Theta (q_\perp ) \equiv \int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \varkappa (k_\perp -q_\perp ) \varphi (k_\perp ), \end{aligned}$$
(3.5)

where the instantaneous kernel \(\varkappa (x) \equiv C_{00} V(x)\). Notice now both \(\varkappa \) and \(\Theta \) does not explicitly depend on the \(q_P\) nor M.

Performing a contour integral over \(q_P\) on both sides of Eq. (3.2), we obtain the following three-dimensional (Bethe–)Salpeter equation (see Appendix A.1),

$$\begin{aligned} M\varphi =(w_1+w_2) H_2( p_{2\perp })\varphi + {H_2}(p_{2\perp }) \Theta , \end{aligned}$$
(3.6)

where \(w_i=(M_i^2+\vec p_i^{\,2})^{\frac{1}{2}}\) with \(M_1\) and \(M_2\) denoting the masses of diquark and the third quark respectively; \(H_2(p_{2\perp })=\frac{1}{w_2}(p_{2\perp }^{\alpha } \gamma _\alpha +M_2)\gamma _0\); the bound state mass M behaves as the eigenvalue of above baryon Salpeter equation. The meaning of this equation is quite obvious. The baryon mass has two contributions, the kinetic energy part and the potential energy part. The normalization of the baryon wave function behaves as,

$$\begin{aligned} \int \frac{\mathrm {d}^3 q_\perp }{(2\pi )^3} \frac{1}{M}\bar{\varphi }(P,q_\perp ,\xi ') O \varphi (P,q_\perp ,\xi )=\delta _{\xi \xi '}, \end{aligned}$$
(3.7)

where the operator O is defined as \( O \equiv \gamma ^0\left( \alpha _1 M H_2 + w_q \right) \) with \( w_q \equiv \alpha _2w_1-\alpha _1w_2\), and the more detailed derivations can be found in Appendix A.2.

3.2 Baryon Salpeter wave functions with \(J^P=\frac{1}{2}^+\)

In the ground state, namely, the angular momentum \(L=0\), the \(0^+\) (bc)-diquark and a light quark u, d, or s can form the \(J^P=\frac{1}{2}^+\) baryon states \(\Xi '^+_{bc}\), \(\Xi '^0_{bc}\), or \(\Omega '_{bc}\), which can be described by the following Salpeter wave function,

(3.8)

where the new abbreviation \(y\equiv \frac{q_\perp }{|\vec q\,|}\) is used; the radial wave functions \(h_i(|\vec q\,|)~(i=1,2)\) are just explicitly dependent on \(|\vec q\,|\); \(u(P,\xi )\) is the Dirac spinor with polarization state indicated by \(\xi \). It is clear to see that \(h_1\) and \(h_2\) parts represent the S and P-wave components, respectively.

Inserting the \(\frac{1}{2}^+\) Salpeter wave function into the Eq. (3.7), summing over the polarization states \(\xi \), then we obtain the following specific normalization condition,

$$\begin{aligned}&\int \frac{\mathrm {d}^3 q_\perp }{(2\pi )^3} 2\left[ w_q(h_1^2+h_2^2)\nonumber \right. \\&\quad \left. +\alpha _1M\frac{1}{w_2}(M_2h_1^2-2qh_1h_2-M_2h_2^2) \right] =1. \end{aligned}$$
(3.9)

Then inserting this wave function into the obtained Salpeter Eq. (3.6),

$$\begin{aligned}&MAu(P,\xi )=(w_1+w_2) H_2( p_{2\perp })A u(P,\xi ) + {H}_2(p_{2\perp })\nonumber \\&\quad \times \int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \varkappa (k_\perp -q_\perp ) A(k_\perp )u(P,\xi ). \end{aligned}$$
(3.10)

Multiplied by \({\bar{u}}(P,\xi )\) and then summing over the polarization states, we can eliminate the spinor in above equation. Next by taking different traces, we obtain 2 coupled eigenvalue equations on the baryon mass M,

$$\begin{aligned} Mh_1(\vec q\,)= & {} +E_1 h_1(\vec q\,)-E_2 h_2(\vec q\,)\nonumber \\&+\frac{1}{w_2} \int \frac{\mathrm d^3 \vec k}{(2\pi )^3} \mathcal {V}_2(\vec q-\vec k) \left[ m_2 h_1(\vec k) -q\cos \theta h_2(\vec k)\right] ,\nonumber \\ Mh_2(\vec q\,)= & {} -E_2 h_1(\vec q\,)-E_1h_2(\vec q\,) \nonumber \\&-\frac{1}{w_2}\int \frac{\mathrm d^3 \vec k}{(2\pi )^3} \mathcal {V}_2 (\vec q-\vec k) \left[ q h_1(\vec k) +m_2\cos \theta h_2(\vec k)\right] ,\nonumber \\ \end{aligned}$$
(3.11)

where \(E_1=\frac{M_2}{w_2}(w_1+w_2+\mathcal {V}_1)\), \(E_2=\frac{q}{M_2}E_1\); \(\mathcal {V}_i\equiv C_{00} V_{i}\); \(\theta \) denotes the angle between \(\vec k\) and \(\vec q\). Solving these eigen equations numerically, we can obtain the mass spectra and the corresponding wave functions.

4 Bethe–Salpeter equation of the (bcq) baryons incorporating the mixing effects

Generally, the (bc)-diquark core in \(\Xi _{bc}\) or \(\Omega _{bc}\) is in the mixing state of \(0^+\) and \(1^+\). To obtain the real physical baryon states, the inner transition between the axialvector and the scalar (bc)-diquark states should be incorporated in solving the BSE. This inner transitions then connect the flavor symmetric (bcq) baryon states with the flavor antisymmetric ones.

4.1 Bethe–Salpeter equation considering the mixing effects

Fig. 5
figure 5

Bethe–Salpeter equations of the baryons with different flavors consist of two coupled equations in the diquark picture. The Greeks (red) are used for the Lorentz indices; the Romans (blue), the Dirac indices. \(P,~p_1(k_1),~p_2(k_2)\) denote the momenta of the baryon, constituent diquark, and the light quark respectively; \(K_{mn}\,(m=1,0)\) denotes the effective interaction kernel between the diquark and the third quark in a baryon

Full size image

The Bethe–Salpeter equations of the doubly heavy baryons with different flavors are schematically depicted in Fig. 5. Notice in Fig. 5a there is an extra Feynman diagram compared with that of the baryons with pure \(1^+\) (bc)-diquark, namely the “\(K_{01}\)” part; and in Fig. 5b there is the extra “\(K_{10}\)” Feynman diagram compared with that of the baryons consisting of the pure \(0^+\) (bc)-diquark core. The corresponding BSEs are expressed as the four-dimensional integral of the inner relative momentum k,

$$\begin{aligned} \Gamma ^\alpha (q)&=\int \frac{\mathrm d^4 k}{(2\pi )^4} (-i)K_{11}^{\alpha \beta }[S(k_2) \Gamma ^\gamma (k) D_{\beta \gamma }(k_1)]\nonumber \\&\quad + (-i)K_{01}^{\alpha }[S(k_2) \Gamma (k) D(k_1)], \end{aligned}$$
(4.1)
$$\begin{aligned} \Gamma (q)&=\int \frac{\mathrm d^4 k}{(2\pi )^4} (-i)K^{\beta }_{10}[S(k_2) \Gamma ^\gamma (k) D_{\beta \gamma }(k_1)]\nonumber \\&\quad + (-i)K_{00} [S(k_2) \Gamma (k) D(k_1)]. \end{aligned}$$
(4.2)

Before moving on, we specify the symbols used in above equations. \(\Gamma ^{(\alpha )}(q)\), denotes the baryon vertex dominated by the \(1^+\,(0^+)\) diquark, and the two baryon vertexes are now coupled together for the existence of the kernels \(K_{10}\) and \(K_{01}\). Also notice there are four different interaction kernels, where \(K_{11}^{\alpha \beta }(P,k,q)\) denotes the one responsible for the \(1^+ \rightarrow 1^+\) heavy diquark transition, and then \(K^\alpha _{01}\), \(K^\beta _{10}\), and \(K_{00}\) are implied. As usual, M represents the mass of the baryon and we have \(P^2=M^2\). The constituent mass of the diquark is now represented by \(M_{1(i)} \) with \(i=0\) for the \(0^+\) and \(i=1\) for the \(1^+\) diquark. The inner relative momenta q and k are now defined as

$$\begin{aligned} q=\alpha _{2(i)}p_1-\alpha _{1(i)}p_2,\quad k=\alpha _{2(i)}k_1-\alpha _{1(i)} k_2, \end{aligned}$$

with \(\alpha _{1(i)}\equiv \frac{M_{1(i)}}{M_{1(i)}+M_2}\) and \(\alpha _{2(i)}=1-\alpha _{1(i)}\). is the Dirac propagator of the third quark as usual, while the effective propagator of the \(1^+\) diquark reads [7],

$$\begin{aligned}&D^{\alpha \beta }(p_1) =D(p_1)d^{\alpha \beta }(p_{1\perp }),\\&d^{\alpha \beta }(p_{1\perp })= -g^{\alpha \beta }+\frac{p_{1\perp }^\alpha p_{1\perp }^\beta }{M_{1(1)}^2}, \end{aligned}$$

where \(D(p_1)=i\frac{1}{p_1^2-M_{1(1)}^2+i\epsilon }\) is the usual scalar propagator.

We define two Bethe–Salpeter wave functions as usual,

$$\begin{aligned} B_\alpha (P,q,\xi )&\equiv S(p_2) \Gamma ^\beta (P,q,\xi ) D_{\alpha \beta }(p_1) , \end{aligned}$$
(4.3)
$$\begin{aligned} B(P,q,\xi )&\equiv S(p_2) \Gamma (P,q,\xi ) D(p_1). \end{aligned}$$
(4.4)

Here the \(B_\alpha (P,q,\xi )\) and \(B(P,q,\xi )\) represent the wave functions of the baryons formed by the axialvector and scalar diquarks, respectively. The total momentum P and the polarization state \(\xi \) in the BS wave function \(B_{(\alpha )}(P,q,\xi )\) and vertex \(\Gamma ^{(\beta )}(P,q,\xi )\) would be omitted unless it is necessary to specify them. The \(\frac{1}{2}^+\) baryons with different flavors can be generally expressed as \(\begin{pmatrix} B^\alpha \\ B \end{pmatrix}\), with \(\begin{pmatrix} B^\alpha \\ 0 \end{pmatrix}\) and \(\begin{pmatrix} 0 \\ B \end{pmatrix}\) describing the baryons with flavor-symmetric and antisymmetric (bc)-diquark inside respectively. Note now the mixing effects are naturally reflected in the wave functions. Using the wave functions, the coupled BSEs in Eq. (4.1) and Eq. (4.2) can also be rewritten in the matrix form

$$\begin{aligned}&S^{-1}(p_2) \begin{bmatrix} (D^{\alpha \beta })^{-1}(p_1) &{}0 \\ 0 &{}D^{-1}(p_1) \end{bmatrix} \begin{pmatrix} B_\beta [q] \\ B[q] \end{pmatrix}\nonumber \\&\quad = \int \frac{\mathrm {d}^4k}{(2\pi )^4} (-i)\begin{bmatrix} K_{11}^{\alpha \beta } &{} K_{01}^{\alpha }\\ K_{10}^{\beta } &{} K_{00} \end{bmatrix} \begin{pmatrix} B_\beta [k] \\ B[k] \end{pmatrix}, \end{aligned}$$
(4.5)

where \(S^{-1}(p_2)\) and \([D^{(\alpha \beta )}]^{-1}(p_1)\) are the inverses of the corresponding propagators. The normalization condition is generally expressed as,

$$\begin{aligned}&\int \frac{\mathrm {d}^4 q}{(2\pi )^4}\frac{\mathrm {d}^4 k}{(2\pi )^4} \begin{pmatrix}\bar{B}_\alpha [q,\xi ']&{\bar{B}}[q,\xi ']\end{pmatrix}\nonumber \\&\quad \times \frac{\partial }{\partial P^0} \left[ \mathrm {I}^{\alpha \beta }(P,k,q) \right] \begin{pmatrix}{B}_\beta [k, \xi ] \\ B[k,\xi ]\end{pmatrix} = i2M \delta _{\xi \xi '}, \end{aligned}$$
(4.6)

where \(\mathrm {I}^{\alpha \beta }\) reads

$$\begin{aligned}&\mathrm {I}^{\alpha \beta }(P,k,q)=(2\pi )^4 \delta ^4(k-q) S^{-1}(p_2)\nonumber \\&\quad \times \begin{bmatrix} [D^{\alpha \beta }(p_1)]^{-1} &{}0 \\ 0 &{}D^{-1}(p_1) \end{bmatrix} + i\begin{bmatrix} K_{11}^{\alpha \beta } &{} K_{01}^{\alpha }\\ K_{10}^{\beta } &{} K_{00} \end{bmatrix}. \end{aligned}$$
(4.7)

4.2 Salpeter equations under the instantaneous approximation

Using the obtained form factors, the four interaction kernels can now be expressed as,

$$\begin{aligned} \left\{ \begin{aligned} K^{\alpha \beta }_{11} (P,k,q)&= g^{\alpha \beta }(p_1+k_{1})^\nu [ C_{11} V(k-q)]\gamma _\nu ,\\ K^\alpha _{01}(P,k,q)&= i \frac{2w_{1(1)}}{M_{1(1)}M_{1(0)}} \epsilon ^{\alpha \nu k_1 p_1} [ C_{01} V(k-q)]\gamma _\nu ,\\ {K}_{00}(P,k,q)&= (p_1+k_{1})^\nu [ C_{00}V(k-q)]\gamma _\nu ,\\ K^\alpha _{10}(P,k,q)&= i \frac{2w_{1(0)}}{M_{1(1)} M_{1(0)}} \epsilon ^{\alpha \nu k_1 p_1} [ C_{10}V(k-q)]\gamma _\nu , \end{aligned} \right. \nonumber \\ \end{aligned}$$
(4.8)

where \((p_1+k_1)=\varrho {\hat{P}}+(k+q)_\perp \) is dependent on both M and \(q_P\), and we used the abbreviation \(\varrho =2(\alpha _1M+q_{P})\); the diquarks’ kinetic energy parts \(w_{1(i)}=(M_{1(i)}^2 - p_{1\perp }^2)^{\frac{1}{2}}\) are different for the difference of the diquark mass \(M_{1(1)}\) and \(M_{1(0)}\). As usual, we deal with the BSEs under the instantaneous approximation, namely, \(V(k-q)\sim V(k_\perp -q_\perp )\), and also we only consider the time component parts of the Lorentz structure in the kernels. Then we further define four instantaneous interaction kernels,

$$\begin{aligned} \left\{ \begin{aligned} \varkappa _{11}^{\alpha \beta } (k_\perp ,q_\perp )&\equiv \left[ C_{11}V(k_\perp -q_\perp )\right] g^{\alpha \beta } ,\\ \varkappa _{01}^{\alpha }(k_\perp ,q_\perp )&\equiv [C_{01}V(k_\perp -q_\perp )] i \frac{ \epsilon ^{\alpha 0 k_{\!\perp } q_{\perp }} }{M_{1(0)}M_{1(1)}} ,\\ \varkappa _{00}(k_\perp ,q_\perp )&\equiv [C_{00} V(k_\perp -q_\perp ) ] , \\ \varkappa _{10}^{\alpha }(k_\perp ,q_\perp )&\equiv [C_{10}V(k_\perp -q_\perp )] i \frac{\epsilon ^{\alpha 0 k_{\!\perp } q_{\perp }} }{M_{1(0)}M_{1(1)}}, \end{aligned} \right. \end{aligned}$$
(4.9)

where the potential reads \(V(k_\perp -q_\perp )=(2\pi )^3 \delta ^3(k_\perp -q_\perp ) V_1+V_2(k_\perp -q_\perp )\); notice that the \(V_1\) part in the potential does not contribute to the \(\varkappa _{01}^\alpha \) and the \(\varkappa _{10}^\alpha \) since the Dirac delta function. The four instantaneous interaction kernels \(\varkappa (k_\perp ,q_\perp )\) here do not depend on the time component of k or q, and the Lorentz structure factor \(\gamma _0\) is also split out for later convenience. Now the BS vertexes can be expressed as

$$\begin{aligned} \Gamma ^\alpha (q)&= \gamma _0\left[ \varrho \Theta ^\alpha _{11}(q_\perp ) + 2w_{1(1)} \Theta _{01}^\alpha (q_\perp ) \right] , \end{aligned}$$
(4.10)
$$\begin{aligned} \Gamma (q)&= \gamma _0 \left[ \varrho \Theta _{00}(q_\perp ) + 2w_{1(0)} \Theta _{01}(q_\perp ) \right] , \end{aligned}$$
(4.11)

where the 4 three-dimensional vertexes \(\Theta _{11}^\alpha \), \(\Theta _{01}^\alpha \), \(\Theta _{00}\) and \(\Theta _{10}\) are only explicitly dependent on \(q_\perp \) and defined as,

$$\begin{aligned} \left\{ \begin{aligned} \Theta _{11}^\alpha (q_\perp )&=\int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \varkappa _{11}^{\alpha \beta }(k_\perp -q_\perp ) \varphi _\beta (k_\perp ),\\ \Theta ^\alpha _{01}(q_\perp )&=\int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \varkappa ^\alpha _{01}(k_\perp ,q_\perp ) \varphi (k_\perp ),\\ \Theta _{00}(q_\perp )&=\int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \varkappa _{00}(k_\perp -q_\perp ) \varphi (k_\perp ),\\ \Theta _{10}(q_\perp )&=\int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \varkappa ^\alpha _{10}(k_\perp ,q_\perp ) \varphi _\alpha (k_\perp ). \end{aligned} \right. \end{aligned}$$
(4.12)

Performing the contour integral over \(q_P\) on both sides of Eqs. (4.3) and (4.4), we can obtain the three-dimensional Salpeter equations (SE),

$$\begin{aligned} \varphi _\alpha (q_\perp )&=d_{\alpha \beta } \left[ \frac{\Lambda ^+ \gamma _0 }{M-w_{1(1)}-w_2} \left( \Theta ^\beta _{11}+ \Theta ^\beta _{01} \right) \nonumber \right. \\&\quad - \left. \frac{\Lambda ^- \gamma _0}{M+w_{1(1)}+w_2} \left( \Theta ^\beta _{11} - \Theta ^\beta _{01} \right) \right] , \end{aligned}$$
(4.13)
$$\begin{aligned} \varphi (q_\perp )&=\frac{\Lambda ^+ \gamma _0}{M-w_{1(0)}-w_2} \left( \Theta _{00}+ \Theta _{10} \right) \nonumber \\&\quad - \frac{\Lambda ^- \gamma _0}{M+w_{1(0)}+w_2} \left( \Theta _{00} - \Theta _{10} \right) , \end{aligned}$$
(4.14)

where the projector operators are defined as \(\Lambda ^\pm (p_{2\perp })\gamma _0=\frac{1}{2}\left( 1 \pm {H_2} \right) \), and the abbreviation is the usual Dirac Hamiltonian divided by \(w_2\). Define the positive and negative energy wave functions as \(\varphi ^{\pm }_{(\alpha )}(q_\perp )=\Lambda ^\pm \gamma ^0 \varphi _{(\alpha )}\), and \(\varphi _{(\alpha )}=\varphi _{(\alpha )}^++\varphi _{(\alpha )}^-\). Notice in the weak binding condition \(M\sim (w_{1(i)}+w_2)\), \(\varphi ^+\gg \varphi ^-\), and the positive energy wave function \(\varphi ^+(q_\perp )\) usually dominates in the Salpeter wave function \(\varphi _{(\alpha )}\). The SEs can be further rewritten as the following simple Shrödinger type

$$\begin{aligned} \begin{aligned} M \varphi _\alpha&= \left( w_{1(1)}+w_2 \right) H_2\varphi _\alpha + \left( H_2 \Theta _{11}^\beta + \Theta _{01}^\beta \right) d_{\alpha \beta } , \\ M \varphi&= \left( w_{1(0)}+w_2 \right) H_2\varphi + \left( H_2 \Theta _{00} + \Theta _{10}\right) . \end{aligned} \end{aligned}$$
(4.15)

The obtained coupled SEs can also be written as the matrix form,

$$\begin{aligned}&M\begin{pmatrix}\varphi _\alpha \\ \varphi \end{pmatrix}=\left[ \begin{pmatrix}w_{1(1)} &{} \\ &{} w_{1(0)} \end{pmatrix} +w_2 \right] H_2 \begin{pmatrix}\varphi _\alpha \\ \varphi \end{pmatrix} \nonumber \\&\quad +\int \frac{\mathrm d^3 k_\perp }{(2\pi )^3} \begin{pmatrix} d_{\alpha \beta } H_2 \varkappa _{11}^{\beta \gamma } &{} d_{\alpha \beta } \varkappa _{01}^{\beta } \\ \varkappa _{10}^\gamma &{} H_2 \varkappa _{00} \end{pmatrix} \begin{pmatrix}\varphi _\gamma \\ \varphi \end{pmatrix}, \end{aligned}$$
(4.16)

which is the fundamental equation of this work.

The obtained three-dimensional BSE, namely, Eq. (4.16), indicates that the mass contributions of the \(J^P=\frac{1}{2}^+\) baryons originate from two parts, the kinetic energy and the potential energy; in the later one, the mixing effects are included naturally in the Salpeter equation. Also notice Eq. (4.16) is in fact the eigenvalue equation of the wave function \(\begin{pmatrix}\varphi _\alpha \\ \varphi \end{pmatrix}\) with the baryon mass M as the eigenvalue.

The normalization of the Salpeter wave functions are similar as before. Since we only consider the time component of the interaction kernel, \(K^\alpha _{01}(P,k,q)\simeq K_{01}^{\alpha }(k_\perp ,q_\perp )\) has no dependence on \(P^0\) and \(q_P\), and the anti-diagonal parts of the normalization kernel \(\mathrm {I}^{\alpha \beta }(P,k,q)\) in Eq. (4.7) vanish after the partial differential over \(P^0\). The inverse of the vector propagator reads,

$$\begin{aligned} D^{-1}_{\alpha \beta }(p_1)=\vartheta _{\alpha \beta }D^{-1}(p_1), \end{aligned}$$

where \(\vartheta ^{\alpha \beta }\equiv - (g^{\alpha \beta }+{p^\alpha _{1\perp } p^\beta _{1\perp }}/{w_{1(1)}^2} )\) and fulfills \(\vartheta ^{\alpha \beta }d_{\beta \gamma }=\delta ^{\alpha }_{\gamma }\); and now there is no \(P^0\) dependence in the numerator of \(D^{-1}_{\alpha \beta }(p_1)\). Inserting the inverses of the propagators, we further obtain the normalization condition for the general Salpeter wave function,

$$\begin{aligned} \int \frac{\mathrm {d}^3 q_\perp }{(2\pi )^3} \frac{1}{M} \begin{pmatrix}\bar{\varphi }_\alpha [\xi ']&\bar{\varphi }[\xi '] \end{pmatrix} \begin{bmatrix} \vartheta ^{\alpha \beta } O_{1} &{} 0 \\ 0 &{}O_{0} \end{bmatrix} \begin{pmatrix} \varphi _\beta [\xi ] \\ \varphi [\xi ] \end{pmatrix} =\delta _{\xi \xi '},\nonumber \\ \end{aligned}$$
(4.17)

with the operator \(O_{i}\equiv \gamma ^0\left[ \alpha _{1(i)} M H_2+ w_{q(i)} \right] \), and \(w_{q(i)} \equiv \alpha _{2(i)} w_{1(i)}-\alpha _{1(i)} w_2\), where \(i=1(0) \) denotes the \(1^+(0^+)\) heavy diquark.

4.3 Salpeter wave functions for the baryons with different flavors

The \(J^P=\frac{1}{2}^+\) Salpeter wave function formed by the \(1^+\) diquark and a \(\frac{1}{2}^+\) light quark has been given in the previous work [7],

$$\begin{aligned} \varphi _{\alpha }(P,q_\perp ,\xi ) = A_\alpha (q_\perp )\gamma ^5 u(P,r) , \end{aligned}$$
(4.18)

with

where the radial wave function \(g_i(|\vec q\,|)~(i=1,\ldots ,4)\) just depends on \(|\vec q\,|\) explicitly. It is clear to see that \(g_1\) corresponds to the S-wave component, \(g_{2(3)}\) the P-wave components, and \(g_4\) contributes to both the S and D partial waves (see Ref. [7] for a detailed expression in terms of the spherical harmonics \(Y_l^m\)).

Fig. 6
figure 6

Mass spectra (in GeV) of the low-lying \(J^P=\frac{1}{2}^+\) (bcq) baryons. The solid (dotted) line denotes the baryons with the inside (bc)-diquarks in the flavor-symmetric (anti-symmetric)

Full size image
Table 1 Mass spectra (in GeV) of the low lying \(J^P=\frac{1}{2}^+\) (bcq) baryons. The baryon states are labeled by the notations \(N\!L(n^{2S+1}L_J)\), where \(N\!L\) describe the radial and orbital quantum numbers between the (bc)-diquarks and the light quark, while \((n^{2S+1}L_J)\) are used to describe the corresponding states of the inside (bc)-diquarks. Type I represents the results obtained from the pure \(1^+\) and \(0^+\) (bc)-diquarks, while type II contains the mixing effects between the \(1^+\) and \(0^+\) (bc)-diquarks insider the baryons obtained by solving Eq. (4.16)
Full size table

Combined with the \(\frac{1}{2}^+\) Salpeter wave function formed by the \(0^+\) diquark and a \(\frac{1}{2}^+\) quark, namely,

(4.19)

we construct the Salpeter wave function for the \(J^P=\frac{1}{2}^+\) baryons with different flavors as

$$\begin{aligned} \begin{pmatrix} \varphi _\alpha (P,q_\perp ,\xi ) \\ \varphi (P,q_\perp ,\xi ) \end{pmatrix} = \begin{pmatrix} A_\alpha (q_\perp ) \\ A(q_\perp ) \end{pmatrix} u(P,\xi ). \end{aligned}$$
(4.20)

By inserting the wave functions into Eq. (4.17) and summing over the spin states, we obtain the following normalization condition,

(4.21)

From this normalization, we can define two integrals \(\mathrm {I}_{(1)}\) and \(\mathrm {I}_{(0)}\) to represent the percentages of the two components in the baryon Salpeter wave function,

(4.22)

where we have \(\mathrm {I}_{1}+\mathrm {I}_{0}=1\); it can be seen obviously that \(\mathrm {I}_{1}\,(\mathrm {I}_{0})\) denotes the weight of a baryon with its (bc)-diquark core in \(1^+\,(0^+)\) state, or equivalently speaking, in the flavor-symmetric (antisymmetric) state. Namely, the methods developed here also allow us to investigate the mixing effects of in the \(\frac{1}{2}^+\) (bcq) baryons, and the numerical results will presented in the following section.

5 Mass spectra and wave functions of the (bcq) baryons

For the \(J^P=\frac{1}{2}^+\) (bcu) and (bcs) baryons with pure \(0^+\) (cb)-diquarks, the parameters \(V_0\) used are \(-0.360\) and \(-0.336\) GeV respectively, which are determined by the spin-weighted average methods [7] by fitting to the corresponding meson spectra.

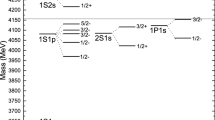
The obtained mass spectra for the \(\frac{1}{2}^+\) (bcq) baryons are listed in Table 1 and also shown in Fig. 6, with both the 1S and 2S (bc)-diquark cores. Type I are the results from the pure \(1^+\) and \(0^+\) (bc)-diquarks, while type II are obtained by solving Eq. (4.16) which has incorporated the mixing effects between the \(1^+\) and \(0^+\) (bc)-diquarks insider the baryons. Here, to reflect the dominant characteristic, we still label baryon states by the nonrelativistic notations \(N\!L(n^{2S+1}L_J)\) with the first two quantum numbers \(N\!L\) describing the baryons formed by the diquarks and third light quark, while \(n^{2S+1}L_J\) describing the states of diquarks; for example, \(1S(2^{3}S_1)\) denotes the radial quantum number of the (bc)-diquark core is \(n=2\) with its orbital angular momentum being in S-wave, and the radial quantum number of the baryon is \(N=1\) with the orbital angular momentum of the diquark–quark being in S-wave. Our results show that the masses of the \(2S(1^3S_1)\), \(1D(1^3S_1)\) \(\Xi _{bc}\) and the \(2S(1^1S_0)\) \(\Xi '_{bc}\) are very close, and theses three states locate in the mass range \(7.440\sim 7.470\,{\hbox {GeV}}\).

Fig. 7
figure 7

BS radial wave functions of the \(J^P=\frac{1}{2}^+\) (bcu) baryons for the first five energy levels with the S-wave (bc)-diquark cores

Full size image
Table 2 Comparisons of the mass predictions for the \(\frac{1}{2}^+\) (bcq) baryons (in GeV). The unprimed \(\Xi _{bc}\) and \(\Omega _{bc}\) denote the baryons with \(1^+\) (bc)-diquark cores, and the primed ones correspond to those with \(0^+\) (bc)-diquark cores
Full size table
Table 3 Comparisons of the mass splittings \((M_{\Xi _{bc}'}-M_{\Xi _{bc}})\) and \((M_{\Omega _{bc}'}-M_{\Omega _{bc}})\) in MeV. The unprimed \(\Xi _{bc}\) and \(\Omega _{bc}\) denote the \(\frac{1}{2}^+\) (bcq) baryons with \(1^+\) (bc)-diquark cores, and the primed ones correspond to those with \(0^+\) (bc)-diquark cores
Full size table

Figure 7 graphically shows the BS wave functions of the \(\frac{1}{2}^+\) (bcu) baryons in the first five energy levels when the (bc)-diquarks are in the S-wave states. Note that \(g_{1-4}\) and \(g_{5-6}\) correspond to the baryons formed by the \(1^+\) and \(0^+\) (bc)-diquark cores, respectively. Firstly note that in the relativistic wave functions, \(\frac{1}{2}^+\) (bcq) baryons contain all the S-, P-, and D-wave components. By analyzing the node structures and wave forms, we can find that, though \(\Xi _{bc}\) and \(\Xi '_{bc}\) are dominated by the states with \(1^+\) and \(0^+\) (bc)-diquark cores respectively, there still exist the mixing effects from each other. By calculating the \(\mathrm I_1\) and \(\mathrm I_0\) in Eq. (4.22), we obtain that \(\mathrm {I}_1(\Xi _{bc})\) for the \(1S(1^3S_1)\) and \(2S(1^3S_1)\) states are both about \(98.8\%\), namely, the mixing components from the baryon states with \(0^+\) diquark are \(\sim \!1.2\%\). However, for \(\Xi _{bc}\) in the \(1D(1^3S_1)\) state, the mixing effects from the \(\Xi '_{bc}[2S(1^1S_0)]\) can reach \(\sim \!9.2\%\) and hence cannot be ignored, which can also be seen from Fig. 7e directly. For \(\Omega _{bc}^{(\prime )}\), the obtained mixing effect are less than \(1\%\) in all the low lying states. The numerical results indicate the mixing effects are quite small between the flavor-symmetric and -antisymmetric (bc)-diquarks in \(\Xi ^{(\prime )}_{bc}\) and \(\Omega ^{(\prime )}_{bc}\) in the ground and the first radially excited states. The small mixing also states that it is a good choice to take (bc) as the diquark with definite spin in the ground states of \(\Xi ^{(\prime )}_{bc}\) and \(\Omega ^{(\prime )}_{bc}\) systems. Besides the mixing effects from the \(\Xi _{bc}'[2S(1^1S_0)]\) state, Fig. 7e also shows that both the 2S (dark green solid) and 1D (light green dotted) partial waves have great contributions to the \(1D(1^3S_1)\) state and the 2S-1D mixing effects should not be omitted either in analysis.

Table 2 shows a comparison of our predictions for the ground state baryons with others’. Our results are generally consistent with others’. The mass of \(\Omega _{bc}\) is about 100 MeV greater than the corresponding \(\Xi _{bc}\), which is consistent with the relevant meson spectra, \(M_{D^{(*)}_s}-M_{D^{(*)0}}=104\,(105)\,{\hbox {MeV}}\), and \(M_{B^{(*)}_s}-M_{B^{(*)}}=88\,(90)\,{\hbox {MeV}}\). The mass splitting between \(\Xi _{bc}'(\Omega _{bc}')\) and \(\Xi _{bc}(\Omega _{bc})\) is another interesting point and the corresponding comparisons are listed in Table 3, in which the average values for \((M_{\Xi _{bc}'}-M_{\Xi _{bc}})\) and \((M_{\Omega _{bc}'}-M_{\Omega _{bc}})\) are about 19 and 20 MeV respectively. Notice that the lattice results in Ref. [20] show the different signs with others’; also in Refs. [21,22,23,24] the \(\frac{1}{2}^+\) (bcq) baryon doublet is labeled by the definite spin of the (cq)-diquark which is different from the definite spin of the (bc)-diquark used here. By using the Clebsch–Gordan coefficients, the baryon under different diquark basis can be expressed as

$$\begin{aligned} \begin{bmatrix} |(bc)_0q\rangle \\ |(bc)_1q\rangle \end{bmatrix}= & {} \begin{bmatrix} -\frac{1}{2}&{} -\frac{\sqrt{3}}{2} \\ +\frac{\sqrt{3}}{2} &{} -\frac{1}{2}\end{bmatrix} \begin{bmatrix} |b(cq)_0\rangle \\ |b(cq)_1\rangle \end{bmatrix}\nonumber \\= & {} \begin{bmatrix} -\frac{1}{2}&{} +\frac{\sqrt{3}}{2} \\ -\frac{\sqrt{3}}{2} &{} -\frac{1}{2}\end{bmatrix} \begin{bmatrix} |(qb)_0c\rangle \\ |(qb)_1c\rangle \end{bmatrix}, \end{aligned}$$
(5.1)

where \(|(bc)_0q\rangle \) denotes the baryon state when the b- and c-quark inside the baryon form the spin-0 diquark, and then others are implied. Above relations can be considered a rotation within different diquark basis and the rotation angles are respectively \(120^\circ \) and \(-120^\circ \).

6 Summary

In this work, based on the diquark picture and the instantaneous approximation, we have built the theoretical framework to deal with the doubly heavy baryons with (bcq) flavors, especially the mixing effects between the \(1^+\) and \(0^+\) (bc)-diquark cores inside the baryons are considered in the Bethe–Salpeter kernel and wave functions. We constructed the Salpeter wave functions for the \(J^P=\frac{1}{2}^+\) doubly heavy baryons. The mass spectra \(M[{\Xi ^{(')}_{bc}}]=6.930\,(6.942)\,{\hbox {GeV}}\) and \(M[\Omega ^{(')}_{bc}]=7.032\,(7.045)\,{\hbox {GeV}}\) are obtained by solving the corresponding BSE. Our predictions are generally consistent with other researches. By using the obtained BS wave functions, we calculated the mixing effects in \(\Xi _{bc}-\Xi '_{bc}\) and \(\Omega _{bc}-\Omega '_{bc}\), and the numerical results show that there only exist quite small (\(\sim \!1\%\)) mixing effects between the \(\frac{1}{2}^+\) (bcq) baryons in ground states; while the mixing effects can reach \(\sim \!10\%\) in the 1D \(\Xi _{bc}\) and \(\Xi _{bc}'\). The obtained BS wave function would make it possible to do the precise calculations on the lifetimes, production and decays of the corresponding \(\Xi ^{(\prime )}_{bc}\) and \(\Omega ^{(\prime )}_{bc}\).