1 Introduction

It is known that if a mass term is added in the Lagrangian of a massless U(1) gauge field, the Lagrangian will be not gauge invariant. In order to preserve the gauge invariance of a massive vector field, early in 1938, in Stüeckelberg theory [1], a real Stüeckelberg scalar field, which has the same mass with the vector field, was introduced. Then in 1960s Higgs mechanism [2, 3] was incorporated into particle physics to explain the mass for gauge bosons. There is also an extra scalar field (Higgs field) coupled with the U(1) gauge field.

In brane world theory [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], higher dimensional U(1) gauge field acts as a series of Kaluza–Klein (KK) modes on the brane. Due to the extra dimensions the vector KK modes can be massive. Thus it is natural to ask whether the Lagrangian of these massive vector KK modes is gauge invariant. It was found that for a free bulk U(1) gauge field, with a gauge free KK decomposition, some scalar KK modes coupling with the vector ones appear [31,32,33,34]. Because of these scalar KK modes the massive vector ones were identified to be gauge invariant. For example, in a brane, for which the warp factor is \(e^{2A(z)}\) with z denoting the extra dimension [31], the gauge free KK decomposition was chosen as:

$$\begin{aligned} X_{\upmu }= & {} \sum _n{{\hat{X}}_{\upmu }^{( n )}( x^\upmu ) \uprho _{1}^{( n )}( z ) e^{b_1A( z )}} \end{aligned}$$
(1)
$$\begin{aligned} X_{z}= & {} \sum _n{\upphi ^{( n )}( x^\upmu ) \uprho _{2}^{( n )}( z ) e^{b_2A( z )}} \end{aligned}$$
(2)

where \(A(z), ~\uprho _1^{( n )}( z ),~\uprho _2^{( n )}( z )\) are supposed to be functions of extra dimension, \({\hat{X}}_{\upmu }^{( n )}( x^\upmu ),~\upphi ^{( n )}(x^\upmu )\) represent the vector and scalar KK modes respectively, and \(b_1,~b_2\) are constants. By substituting this KK decomposition into the bulk action and the equations of motion ( EOM ) for the bulk field and setting \(b_1,~b_2\) some proper values, the effective action was proved to be gauge invariant. But if a gauge was fixed to make \(X_z=0\) before the KK decomposition, there was no scalar KK mode [35,36,37,38,39,40,41,42,43,44,45,46,47,48].

On the other hand, it is expected that the vector KK modes for the U(1) gauge field can be localized on the brane. However, in a brane with codimension one it is difficult to localize these KK modes. It needs some kinds of localization mechanism [31, 32, 38, 40,41,42, 45, 47, 48]. For example, in Ref. [45] a coupling between a bulk U(1) gauge field and a dilaton was taken into account, which resulted that the massless vector KK mode can be localized on the brane. While in a Bloch brane model, a coupling between a bulk U(1) gauge field and one of the background scalar fields was considered in Ref. [46], where some vector resonances were found. In Refs. [47], the authors added a dynamic mass term for the bulk U(1) gauge field to localize the massless vector KK mode. But in these works a gauge was also fixed for the bulk U(1) gauge field, which led to the miss of the scalar KK modes.

In the present work, we will use the general KK decomposition (1) to investigate the gauge invariance and localization of the vector KK modes for a the bulk U(1) gauge field under above three kinds of localization mechanism [45,46,47]. Under localization mechanism the bulk action for a bulk U(1) gauge field is different with that for a free case. Therefore, the effective action may be different. We wonder whether the effective action can be formalized to a gauge invariant one. Moreover, to make the gauge invariance be finally preserved on the brane, whether the massive vector KK modes and their accompanying scalar ones can be localized at the same time.

The paper is organized as follows. First we will briefly review how to get a gauge invariant effective action for a free bulk U(1) gauge field with the gauge free KK decomposition (1) in Sect. 2. Then in Sect. 3, under three kinds of localization mechanism, we will study the gauge invariance and the localization for the KK modes in details. Finally, a brief discussion and conclusion will be given in Sect. 4.

2 Gauge invariant KK modes of a free bulk U(1) gauge field

In Refs. [31,32,33,34] with the general KK decomposition (1) the gauge invariance of massive vector KK modes for a free bulk U(1) gauge field in branes with codimension one or more was discussed. Here we give a brief review on a brane with codimension one. The line-element of the spacetime is assumed as

$$\begin{aligned} ds^2=e^{2A(z)}( {\hat{g}}_{\upmu \upnu }dx^{\upmu }dx^{\upnu }+dz^2), \end{aligned}$$
(3)

where the warp factor \(e^{2A(z)}\) is a function of extra dimension only, and \({\hat{g}}_{\upmu \upnu }\) is the induced metric of the brane.

For a free bulk U(1) gauge field, its action is \(S=-\frac{1}{4}\int d^5 x\sqrt{-g}\;Y^{MN}Y_{MN}\) with \(Y_{MN}=\partial _M X_N-\partial _N X_M\) the field strength. Substitute the gauge free KK decomposition (1) into the bulk action with \(b_1=b_2=-1\), we work out the effective action:

$$\begin{aligned} S_{1}= & {} -\frac{1}{4} \sum _{n,n'}\int d^{4} x\sqrt{-{\hat{g}}} \Bigg [I_1^{(nn')}{\hat{Y}}_{\upmu \upnu } {\hat{Y}}^{\upmu \upnu }\nonumber \\&+I_3^{(nn')}{\hat{X}}_\upmu ^{(n)}{\hat{X}}^{(n')\upmu }+I_2^{(nn')}\partial _{\upmu }\upphi ^{(n)}\partial ^{\upmu }\upphi ^{(n')}\nonumber \\&-I_4^{(nn')}\big (\partial _{\upmu }\upphi ^{(n)}{\hat{X}}^{(n')\upmu }+{\hat{X}}_\upmu ^{(n)}\partial ^{\upmu }\upphi ^{(n')}\big )\Bigg ], \end{aligned}$$
(4)

where we define \(I_1^{(nn')}\equiv \int d z\; \uprho _{1}^{(n)} \uprho _{1}^{(n')}, I_2^{(nn')}\equiv \frac{1}{2} \int d z \;\uprho _{2}^{(n)} \uprho _{2}^{(n')}, I_3^{(nn')}\equiv \frac{1}{2} \int d z\;\text {e}^{A} \partial _z\big (\uprho _{1}^{(n)} \text {e}^{-\frac{1}{2} A}\big ) \partial _z\big (\uprho _{1}^{(n')} \text {e}^{-\frac{1}{2} A}\big ),\) and \( I_4^{(nn')}\equiv \frac{1}{2} \int d z\;\text {e}^{-\frac{1}{2}A}\uprho _{2}^{(n)}\partial _z\big (\uprho _{1}^{(n')}\text {e}^{-\frac{1}{2} A}\big ) \). This effective action is similar with that in the Stueckelberg mechanism, although the scalar KK modes are all massless here. Motived by the Stueckelberg mechanism, it is wondered that if the last three terms in the effective action can be written as the form \(\big (\partial _{\upmu }\upphi ^{(n)}-m^{(n)}{\hat{X}}^{(n)}_\upmu \big )^2\), the effective action will be just gauge invariant. To this end, we consider the EOM of the KK modes.

From this effective action (4), the EOM for the KK modes are derived:

$$\begin{aligned}&I_1^{(nn')} \frac{1}{\sqrt{-{\hat{g}}}} \partial _{\upnu }\left( \sqrt{-{\hat{g}}} {\hat{Y}}^{\upnu \upmu }\right) +I_4^{(nn')} \partial ^{\upmu }\upphi ^{(n)} -I_3^{(nn')}{\hat{X}}^{(n)\upmu }=0,\nonumber \\ \end{aligned}$$
(5a)
$$\begin{aligned}&I_2^{(nn')} \partial _{\upmu }\big (\sqrt{-{\hat{g}}} \partial ^{\upmu }\upphi ^{(n)}\big ) -I_4^{(nn')}\partial _{\upmu }(\sqrt{-{\hat{g}}} {\hat{X}}^{(n)\upmu })=0. \end{aligned}$$
(5b)

Then substitute the KK decomposition into the EOM for the bulk field \(\partial _R(\sqrt{-g} Y^{RN})=0\), the EOM take the following form:

$$\begin{aligned}&\frac{1}{\sqrt{-{\hat{g}}}} \partial _{\upnu }\left( \sqrt{-{\hat{g}}} {\hat{Y}}^{\upnu \upmu }\right) -\uplambda _1~ \partial ^{\upmu }\upphi ^{(n)} + \uplambda _2~{\hat{X}}^{(n)\upmu }=0, \end{aligned}$$
(6a)
$$\begin{aligned}&\partial _{\upmu }\big (\sqrt{-{\hat{g}}} \partial ^{\upmu }\upphi ^{(n)}\big ) -\uplambda _3~\partial _{\upmu }(\sqrt{-{\hat{g}}} {\hat{X}}^{(n)\upmu })=0 \end{aligned}$$
(6b)

with \(\uplambda _1=\text {e}^{-\frac{1}{2}A} \partial _{z}\big (\text {e}^{\frac{1}{2}A} \uprho _{2}^{(n)}\big )/(2\uprho _{1}^{(n)})\), \(\uplambda _2=\text {e}^{-\frac{1}{2}A}\partial _{z}\big (\text {e}^{A}\partial _z(\uprho _{1}^{(n)}\text {e}^{-\frac{1}{2}A})\big )/(2\uprho _{1}^{(n)})\), \(\uplambda _3=\text {e}^{\frac{1}{2}A}\partial _z\big (\text {e}^{-\frac{1}{2}A}\uprho _{1}^{(n)} \big )/\uprho _{2}^{(n)}\). It is certain that the Eqs. (5) and (6) are consistent. In light of this, some important results could be got:

  • First it can be seen that \(I_1^{(nn')}=\updelta _{nn'}\) (which is called the the orthonormality condition) and \(\uplambda _2=-I_3^{(nn)}\). As \(I_3^{(nn)}\) has a mass dimension, we mark \(I_3^{(nn)}=\frac{1}{2}m^{(n)2}\), and find that the vector KK modes satisfy a Schrödinger-like equation:

    $$\begin{aligned} \big (-\partial _{z,z}+V_{\text {vec}}(z)\big )\uprho _1^{(n)}=m^{(n)2}\;\uprho _1^{(n)}, \end{aligned}$$
    (7)

    with the effective potential \( V_{\text {vec}}(z)=\frac{1}{4}\left( \partial _{z} A\right) ^{2}+\frac{1}{2} \partial _{z,z}A\).

  • Then with above Schrödinger-like Eq. (7) and \(I_2^{(nn)}=2, I_4^{(nn)}=-\uplambda _1, I_4^{(nn)}=\uplambda _2\), we have \(I_4^{(nn)}=m^{(n)}\). The relationships between \(\uprho _{1}^{(n)}\) and \(\uprho _{2}^{(n)}\) are simplified as:

    $$\begin{aligned} \text {e}^{-\frac{1}{2}A} \partial _{z}\big (\text {e}^{\frac{1}{2}A} \uprho _{2}^{(n)}\big )= & {} 2m^{(n)}\uprho _1 ^{(n)}, \end{aligned}$$
    (8)
    $$\begin{aligned} \text {e}^{\frac{1}{2}A}\partial _z\big (\uprho _{1}^{(n)} \text {e}^{-\frac{1}{2}A}\big )= & {} -\frac{1}{2}m^{(n)}\uprho _2^{(n)}. \end{aligned}$$
    (9)

  • Further substitute the relationships (8) and (9) into the definitions \(I_1^{(nn)}\sim I_4^{(nn)}\), we get \(I_2^{(nn)}=2, I_3^{(nn)}=\frac{1}{2}m^{(n)2}, I_4^{(nn)}=m^{(n)}\), so that the effective action is finally written as:

    $$\begin{aligned} S_1= & {} -\frac{1}{4}\sum _{n} \int d^4x\sqrt{-{\hat{g}}}\nonumber \\&\times \bigg [ {\hat{Y}}_{\upmu \upnu }^{( n )}{\hat{Y}}^{(n)\upmu \upnu } +2 ( \partial _{\upmu }\upphi ^{( n )}\!-\!\frac{1}{2}m^{(n)}{\hat{X}}_{\upmu }^{( n )} )^2 \bigg ].\qquad \end{aligned}$$
    (10)

    It is clear that under a gauge transformation \({\hat{X}}_{\upmu }^{( n )} \rightarrow {\hat{X}}_{\upmu }^{( n )}+\partial _{\upmu }\upgamma ^{( n )}\), \(\upphi ^{( n )} \rightarrow \upphi ^{( n )}+\frac{1}{2}m^{(n)}\upgamma ^{( n )}\), where \(\upgamma ^{( n )}\) is a scalar field on the brane, this effective action is gauge invariant.

  • For the scalar KK modes, with the relationships (8) and (9), a Schrödinger-like equation also can be derived:

    $$\begin{aligned} \big (-\partial _{z,z}+V_{\text {sca}}(z)\big )\uprho _2^{(n)}=m^{(n)2}\;\uprho _2^{(n)}, \end{aligned}$$
    (11)

    with the effective potential \( V_{\text {sca}}(z)=\frac{1}{4}\left( \partial _{z} A\right) ^{2}-\frac{1}{2} \partial _{z,z}A\).

With above ideas, in the literatures [33, 34] there were detailed talk about whether the number of the extra dimension impacts on the gauge invariance of the effective action in form. But there was no discussion about whether the massive vector KK modes and their accompanying scalar ones can be localized on the brane.

In fact, in a brane with one extra dimensions, in order to localize the vector KK modes, some kinds of localization mechanism must be considered. In Refs. [45,46,47] three kinds of localization mechanism were discussed. But as a gauge was always chosen for the bulk U(1) gauge field, there was no scalar KK mode. However, when the gauge free KK decomposition (1) is performed, some scalar KK modes will appear accompanying with the vector ones. Addition with the localization mechanism, it is achievable to discuss the gauge invariance and localization of the KK modes simultaneously.

To this end, we will carry out the research by two steps:

  • Firstly, under the similar assumption of two orthonormality conditions as \(I_1^{(nn')}=\updelta _{nn'}, I_2^{(nn')}=2\updelta _{nn'}\), we will investigate whether the effective action under different localization mechanism can be formalized as the gauge invariant form (10).

  • Secondly, with the brane solution we will seek for the localized massive vector KK modes and their accompanying scalar ones, i.e., the KK modes satisfying the orthonormality conditions.

We will prove that the gauge invariance of the effective action is not only ensured by the bulk gauge invariance of the field but also by the localization of the massive vector KK modes and their accompanying scalar ones, which are affected by the geometry of the background.

3 KK modes of bulk U(1) gauge field under different localization mechanism

In order to get the effective action and Schrödinger-like equations for the vector and scalar KK modes, the same approach reviewed above will be used. We will always first give the effective action derived from substituting the KK decomposition (1) into the bulk action. Then through comparing the EOM for the KK modes derived from two ways, a Schrödinger-like equation for the vector KK modes can be found, and the relationships between the vector and scalar KK modes also can be obtained, with which the effective action could be deeply simplified and a Schrödinger-like equation for scalar KK modes will be had. At last the gauge invariance and localization of the KK modes are studied in detail.

3.1 Localized gauge invariant KK modes of bulk U(1) gauge field coupled with a dilaton field

In Ref. [45], a brane model generated by a dilaton \(\uppi (z)\) and a scalar field \(\upphi (z)\) in a five dimensional spacetime was set up. Here we consider one of the solution:

$$\begin{aligned} A(z)= & {} -\frac{v^2}{9}\bigg (\ln \cosh ^2(az) +\frac{1}{2}\tanh ^2(az)\bigg ), \end{aligned}$$
(12)
$$\begin{aligned} \upphi (z)= & {} v\tanh (az), \quad \uppi (z)=\sqrt{3} \;A(z), \end{aligned}$$
(13)

where v, a are both constants. In this brane model, in order to localize the vector KK modes, the coupling between the bulk U(1) gauge field and the dilaton field \(\uppi (z)\) was brought in:

$$\begin{aligned} S_1=-\frac{1}{4}\int {d^5x\sqrt{-g}\;e^{\uptau \uppi }Y_{MN}Y^{MN}}, \end{aligned}$$
(14)

where \(\uptau \) is the coupling constant.

If substitute the KK decomposition (1) (\(b_1=b_2=-\frac{\sqrt{3}\uptau +1}{2}\)) into the bulk action (14), we can get the same effective action as (4) with the same \(I_1^{(nn')}\) and \(I_2^{(nn')}\) but different \(I_3^{(nn')}\) and \(I_4^{(nn')}\):

$$\begin{aligned} I_3^{(nn')}\equiv & {} \frac{1}{2}\int d z\;\text {e}^{(\sqrt{3}\uptau +1 )A} \partial _z\bigg (\uprho _{1}^{(n)} \text {e}^{-\frac{\sqrt{3}\uptau +1}{2} A}\bigg )\nonumber \\&\times \partial _z\bigg (\uprho _{1}^{(n')} \text {e}^{-\frac{\sqrt{3}\uptau +1}{2} A}\bigg ), \end{aligned}$$
(15)
$$\begin{aligned} I_4^{(nn')}\equiv & {} \int d z\;\text {e}^{-\frac{\sqrt{3}\uptau +1}{2}A}\uprho _{2}^{(n)}\nonumber \\&\times \partial _z\bigg (\uprho _{1}^{(n')}\text {e}^{-\frac{\sqrt{3}\uptau +1}{2} A}\bigg ). \end{aligned}$$
(16)

And substitute the KK decomposition into the bulk EOM (\(\partial _R(\sqrt{-g} e^{\uptau \uppi }Y^{RN})=0\)), the obtained equations are also the same in form with (6) but different \(\uplambda _1\sim \uplambda _3\):

$$\begin{aligned} \uplambda _1= & {} \frac{\text {e}^{-\frac{1+\sqrt{3}\uptau }{2}A} \partial _{z}\bigg (\text {e}^{\frac{\sqrt{3}\uptau +1}{2}A} \uprho _{2}^{(n)}\bigg )}{2\uprho _{1}^{(n)}}, \end{aligned}$$
(17)
$$\begin{aligned} \uplambda _2= & {} \frac{\text {e}^{-\frac{\sqrt{3}\uptau +1}{2}A}\partial _{z}\bigg (\text {e}^{(1+\sqrt{3}\uptau )A}\partial _z(\uprho _{1}^{(n)}\text {e}^{-\frac{\sqrt{3}\uptau +1}{2}A})\bigg )}{2\uprho _{1}^{(n)}}, \end{aligned}$$
(18)
$$\begin{aligned} \uplambda _3= & {} \frac{\text {e}^{\frac{\sqrt{3}\uptau +1}{2}A}\partial _z\bigg (\text {e}^{-\frac{1+\sqrt{3}\uptau }{2}A}\uprho _{1}^{(n)} \bigg )}{\uprho _{2}^{(n)}}. \end{aligned}$$
(19)

Through the same procedure with the free case, some similar results are got:

  • For the vector KK modes, they are constrained by a Schrödinger-like equation:

    $$\begin{aligned} \left( -\partial _{z,z}+V_{\text {eff1}}\right) \uprho _1^{(n)}= & {} m^{(n)2}\;\uprho _1^{(n)}, \end{aligned}$$
    (20)

    with the effective potential \(V_{\text {eff1}}\)

    $$\begin{aligned} V_{\text {eff1}}= & {} \frac{(1+\sqrt{3 } \uptau )^{2}}{4}\left( \partial _{z} A\right) ^{2}+\frac{1+\sqrt{3 } \uptau }{2} \partial _{z,z} A. \end{aligned}$$
    (21)

  • The relationships between \(\uprho _{1}^{(n)}\) and \(\uprho _{2}^{(n)}\) now become:

    $$\begin{aligned} \text {e}^{-\frac{1+\sqrt{3}\uptau }{2}A} \partial _{z}\bigg (\text {e}^{\frac{\sqrt{3}\uptau +1}{2}A} \uprho _{2}^{(n)}\bigg )= & {} -2m^{(n)}\uprho _1 ^{(n)}, \end{aligned}$$
    (22)
    $$\begin{aligned} \text {e}^{\frac{\sqrt{3}\uptau +1}{2}A}\partial _z\bigg (\uprho _{1}^{(n)} \text {e}^{-\frac{1+\sqrt{3}\uptau }{2}A}\bigg )= & {} \frac{1}{2}m^{(n)}\uprho _2^{(n)}. \end{aligned}$$
    (23)

  • For the scalar KK modes, they are all massless. With the relationships (22) and (23), a Schrödinger-like equation also can be got:

    $$\begin{aligned} \left( -\partial _{z,z}+V_{\text {eff2}}\right) \uprho _2^{(n)}= & {} m^{(n)2}\;\uprho _2^{(n)}, \end{aligned}$$
    (24)

    with

    $$\begin{aligned} V_{\text {eff2}}= & {} \frac{(1+\sqrt{3 } \uptau )^{2}}{4}\left( \partial _{z} A\right) ^{2}-\frac{1+\sqrt{3 } \uptau }{2} \partial _{z,z} A. \end{aligned}$$
    (25)

Because of the relationships (22) and (23), under the two orthonormality conditions \(I_1^{(nn')}=\updelta _{nn'}, I_2^{(nn')}=2\updelta _{nn'}\), we find \(I_4^{(nn)}=m^{(n)}\). So that for this case the effective action is also the same to (10), which is gauge invariant. The difference is that the masses of the vector KK modes \(m^{(n)}\) are determined by the effective potentials (21) and (25). Despite this, we need to study whether the massive vector KK modes and their accompanying scalar ones can be both localized on the brane:

  • For the vector and scalar zero mode, we have \(\uprho _1^{(0)}\propto \text {e}^{\frac{\sqrt{3}\uptau +1}{2}A}\) and \(\uprho _2^{(0)}\propto \text {e}^{-\frac{\sqrt{3}\uptau +1}{2}A}\). And we can check whether they satisfy the orthonormality conditions:

    $$\begin{aligned} \int dz \;\uprho _1^{(0)2}\propto & {} \int dz \;\text {e}^{(\sqrt{3}\uptau +1)A}, \end{aligned}$$
    (26)
    $$\begin{aligned} \int dz \;\uprho _2^{(0)2}\propto & {} \int dz \;\text {e}^{-(\sqrt{3}\uptau +1)A}. \end{aligned}$$
    (27)

    With the solution of the brane world (12), we see that when \(\uptau > -\sqrt{1/3}\), the vector zero mode can be localized on the brane, but the zero scalar one can not. For \(\uptau < -\sqrt{1/3}\), the result is reversed. If \(\uptau = -\sqrt{1/3}\), both the vector and scalar zero mode can not be localized on the brane. It is not possible for the zero vector and scalar mode are localized at the same time.

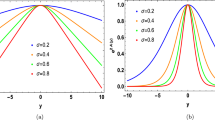
  • We see that the mass parameter \(m^{(n)}\) in the Schrödinger-like Eqs. (20) and (24) only represents the mass of the vector KK modes. The scalar ones are all massless, which are implied in the effective action (10). It is different with the massive Stueckelberg fields. Therefore, if we seek for the localized massive vector KK modes and their accompanying scalars, the mass spectra solved from the two Schrodinger-like equations must be the same. We analyse the behaviour of these two effective potentials as (21) and (25) with the warp factor (12) as \(V_{\text {eff1}}(0)=-V_{\text {eff2}}(0),~V_{\text {eff1}}(\infty )=V_{\text {eff2}}(\infty )=\text {constant}\). The values of the two effective potentials are opposite at \(z=0\), but the same at infinity. We plot the shapes of them in Fig. 1, which are PT-like ones. There must be bound massive vector KK modes. Consider the solution of the warp fact (12), we calculate the mass spectrum for the vector KK modes from (20) and (24) with \(v=1,a=1,\uptau =30\) respectively. The same mass spectrum is found: \(m^{(1)}=15.59, m^{(2)}=26.89, m^{(3)}=33.41\). This shows that for a massive bound vector KK mode there is a bound massless scalar one coupling with it. We plot the wave function for \(\uprho _{1}^{(n)}\) and \(\uprho _{2}^{(n)}\) in Fig. 2.

Fig. 1
figure 1

The effective potentials \(V_{\text {eff1}}\) and \(V_{\text {eff2}}\) with \(v=1,a=1,\uptau =30\)

Full size image
Fig. 2
figure 2

The wave functions \(\uprho _{1}^{(n)}\) and \(\uprho _{2}^{(n)}\) for bound vector and scalar KK modes with \(v=1,a=1,\uptau =30\)

Full size image

3.2 Resonant KK modes of bulk U(1) gauge field coupled with a background scalar field

In Ref. [46], another coupling between a bulk U(1) gauge field and a background scalar field \(\upchi \) was studied in some Bloch brane models:

$$\begin{aligned} S_1=-\frac{1}{4}\int {d^5x\sqrt{-g}\;\upchi Y_{MN}Y^{MN}}, \end{aligned}$$
(28)

where \(\upchi \) is to generate the Bloch branes. In this subsection, we consider a degenerated Bloch brane solution:

$$\begin{aligned} \upchi (y)= & {} \frac{2 v}{\sqrt{\sqrt{1-16 c_0} \cosh (4 b v y)+1}}, \end{aligned}$$
(29)
$$\begin{aligned} A(y)= & {} \frac{2\left( 8 c_0+\sqrt{1-16 c_0}+1\right) v^2}{9 \left( \sqrt{1-16 c_0}+1\right) ^2}\nonumber \\&-\frac{2 v^2 \left( \sqrt{1-16 c_0} \cosh (4 b v y)+8 c_0+1\right) }{9 \left( \sqrt{1-16 c_0} \cosh (4 b v y)+1\right) ^2} \nonumber \\&+ \frac{4v^2\log \bigg (\frac{\sqrt{1-16 c_0}+1}{\sqrt{1-16 c_0} \cosh (4 b v y)+1}\bigg )}{9}, \end{aligned}$$
(30)

where b, v are constants, \(c_0<1/16\), and the line element \(ds^{2}=\text {e}^{2A(y)}\upeta _{\upmu \upnu }dx^{\upmu }dx^{\upnu }+dy^{2}\) is used. (But when we talk about the KK modes of the U(1) vector field, we still use the line element (3) for convenience. The two coordinate systems can be transformed as \(dy=\text {e}^{A}dz\).)

Here we set \(b_1=b_2=-\frac{1}{2}\) and consider the gauge free KK decomposition (1) into the bulk action, then the effective action is formalized as (4) with

$$\begin{aligned} I_1^{(nn')}\equiv & {} \int d z\;{\upchi (z)}\; \uprho _{1}^{(n)} \uprho _{1}^{(n')}, \end{aligned}$$
(31)
$$\begin{aligned} I_2^{(nn')}\equiv & {} \frac{1}{2} \int d z \;{\upchi (z)}\;\uprho _{2}^{(n)} \uprho _{2}^{(n')}, \end{aligned}$$
(32)
$$\begin{aligned} I_3^{(nn')}\equiv & {} \frac{1}{2} \int d z\;{\upchi (z)}\;\text {e}^{A} \partial _z\big (\uprho _{1}^{(n)} \text {e}^{-\frac{1}{2} A}\big )\big (\uprho _{1}^{(n')} \text {e}^{-\frac{1}{2} A}\big ), \end{aligned}$$
(33)
$$\begin{aligned} I_4^{(nn')}\equiv & {} \frac{1}{2}\int d z\;\;{\upchi (z)}\;\text {e}^{\frac{1}{2}A}\uprho _{2}^{(n)}\partial _z\big (\uprho _{1}^{(n')}\text {e}^{-\frac{1}{2} A}\big ). \end{aligned}$$
(34)

Substitute the KK decomposition into the bulk EOM (\(\partial _R(\sqrt{-g} \;\upchi \;Y^{RN})=0\)), the EOM also take the same form as (6) with different constants \(\uplambda _1\sim \uplambda _3\):

$$\begin{aligned} \uplambda _1= & {} \frac{\text {e}^{-\frac{1}{2}A}\partial _{z}\left( \text {e}^{\frac{1}{2}A}\;\uprho _{2}^{(n)} \;\upchi \right) }{2\uprho _{1}^{(n)}\upchi },\nonumber \\ \uplambda _2= & {} \frac{\text {e}^{-\frac{1}{2}A}\partial _{z}\left( \text {e}^{A}\;\partial _z\big (\uprho _{1}^{(n)} \text {e}^{-\frac{1}{2} A}\big )\;\upchi \right) }{2\uprho _{1}^{(n)}\upchi },\nonumber \\ \uplambda _3= & {} \frac{\text {e}^{\frac{1}{2}A} \;\upchi \;\partial _z\big (\uprho _{1}^{(n)}\text {e}^{-\frac{1}{2} A}\big )}{\uprho _{2}^{(n)}\;\upchi }. \end{aligned}$$
(35)

For simplicity, we introduce \({\tilde{\uprho }}_{1}^{(n)} =\uprho _{1}^{(n)} \sqrt{\upchi },~{\tilde{\uprho }}_{2}^{(n)} =\uprho _{2}^{(n)} \sqrt{\upchi }\). Then the Schrödinger-like equations and the relationships of the KK modes can be got:

  • For the vector KK modes, there is a Schrödinger-like equation:

    $$\begin{aligned} \left( -\partial _{z,z}+V_{\text {eff3}}\right) {\tilde{\uprho }}_1^{(n)}= & {} m^{(n)2}\;{\tilde{\uprho }}_1^{(n)}, \end{aligned}$$
    (36)

    where the effective potential is

    $$\begin{aligned} V_{\text {eff}3}= & {} \frac{1}{2}A(z)'' +\frac{1}{4}A(z)'^2 \nonumber \\&+\frac{A'(z) \upchi '(z)}{2 \upchi (z)}+\frac{\upchi ''(z)}{2 \upchi (z)}-\frac{\upchi ^{'2}(z)}{4 \upchi ^{2}(z)}. \end{aligned}$$
    (37)

  • The relationships between \({\tilde{\uprho }}_1^{(n)}\) and \({\tilde{\uprho }}_2^{(n)}\) are

    $$\begin{aligned} \text {e}^{-\frac{1}{2}A}\partial _{z}\left( \text {e}^{\frac{1}{2}A}\;{\tilde{\uprho }}_{2}^{(n)} \;\upchi ^{\frac{1}{2}}\right)= & {} -2{\tilde{\uprho }}_{1}^{(n)}\upchi ^{\frac{1}{2}} \;m^{(n)}, \end{aligned}$$
    (38)
    $$\begin{aligned} \text {e}^{\frac{1}{2}A} \;\partial _z\big (\text {e}^{-\frac{1}{2} A}{\tilde{\uprho }}_{1}^{(n)}\;\upchi ^{-\frac{1}{2}}\big )= & {} \frac{1}{2}{\tilde{\uprho }}_{2}^{(n)}\;\upchi ^{-\frac{1}{2}}\;m^{(n)}. \end{aligned}$$
    (39)

  • For the scalar KK modes, there is also a Schrödinger-like equation

    $$\begin{aligned} \left( -\partial _{z,z}+V_{\text {eff4}}\right) {\tilde{\uprho }}_2^{(n)}= & {} m^{(n)2}\;{\tilde{\uprho }}_2^{(n)}, \end{aligned}$$
    (40)

    with the effective potential

    $$\begin{aligned} V_{\text {eff}4}= & {} \frac{1}{4}A(z)'^2-\frac{1}{2}A(z)''\nonumber \\&+\frac{A'(z) \upchi '(z)}{2 \upchi (z)}-\frac{\upchi ''(z)}{2 \upchi (z)}+\frac{3\upchi ^{'2}(z)}{4 \upchi ^{2}(z)}. \end{aligned}$$
    (41)

With above information we can check the gauge invariance of the effective action and the localization of the KK modes:

  • With the relationships (38) and (39), the effective action can finally be simplified as the gauge invariant one (10). The different is that the vector and scalar KK modes are now constrained by the effective potentials (37) and (41).

  • For the degenerated Bloch brane solution (29) and (30), the zero vector KK mode \(\uprho _1^{(0)}\propto \text {e}^{\frac{1}{2}A}\upchi ^{\frac{1}{2}}\) can be localized on the brane, but the zero scalar one \(\uprho _2^{(0)}\propto \text {e}^{-\frac{1}{2}A}\upchi ^{-\frac{1}{2}}\) can not. This means that for the localized zero vector, there is not a localized scalar one accompanying with it.

  • For the massive vector KK modes, the effective potentials (37) and (41) are both volcano-type, which are shown in Fig. 3 with \(b=1,v=1, c_0=1/16-10^{-20}\) for the brane solution (29) and (30). There maybe some resonances. The resonances are the modes that have finite lifetime on the brane. In order to find the resonances, a parameter P(m) is usually defined as

    $$\begin{aligned} P(m)=\frac{\int _{-z_{b}}^{z_{b}} {\tilde{\uprho }}_1^{(n)2}(z) d z}{\int _{-z_{c}}^{z_{c}} {\tilde{\uprho }}_1^{(n)2}(z) d z} \end{aligned}$$
    (42)

    where \(z_c > z_b\) and \(2z_b\) is of about the thickness of the brane. From the Schrödinger-like Eq. (36) we see that different mass of the vector KK modes \(m^{(n)}\) corresponds to different \({\tilde{\uprho }}^{(n)}_1\), so that P(m) is the function of the mass. If P(m) has a peak, this implies that this KK mode is quasi-localized on the brane, which has a finite lifetime on the brane. And the lifetime of the resonant KK modes can be defined as \(\uptau '=(\updelta m)^{-1}\) with \(\updelta m\) the width in mass at half maximum of each peak. We can calculate the mass spectra of the vector resonances from Schrödinger-like Eqs. (36) and (40) respectively in the degenerated Bloch brane with \(b=1\), \(v=1\), \(c_0=1/16-10^{-20}\), which are list in Table 1. It is surprised that the masses of the resonant vector KK modes are different solved from the two Schrödinger-like Eqs. (36) and (40). This is because the effective potentials (37) and (41) are so different. This tells us that for a vector resonant KK mode there is not a resonant scalar one accompanying with it, which is different with that for the bound KK modes.

Fig. 3
figure 3

The effective potentials \(V_{\text {eff}3}\) and \(V_{\text {eff}4}\) in a degenerated Bloch brane

Full size image
Table 1 The mass \(m^{(n)}\), lifetime \(\uptau '\) for resonances in a degenerated Bloch brane
Full size table

For above two cases, through the KK decomposition (1) without any gauge fixed for the bulk U(1) gauge field, although the gauge invariant effective action are both formalized as (10), only for the first case, the massive bound vector KK modes are localized on the brane accompanying with bound scalar ones, i.e., the gauge invariance is preserved. In the following case, a mass term of the bulk field is introduced in order to localize the vector KK modes. The mass term breaks the gauge invariance of the bulk U(1) gauge field, but is it possible that through the KK decomposition and KK reduction the gauge invariance can be rebuilt?

3.3 KK modes for bulk U(1) gauge field with a mass term

In Ref. [47], a mass term was added for a bulk U(1) gauge field, its action was:

$$\begin{aligned} S_1 = -\frac{1}{4}\int d^5x\sqrt{-g}\left( Y_{MN}Y^{MN}+2{\mathcal {M}}^2X_MX^M \right) , \end{aligned}$$
(43)

where \({\mathcal {M}}^2\) is set to be proportional to the scalar curvature R as \({\mathcal {M}}^2=-\frac{1}{16}R\). With a gauge fixed KK decomposition (\(X_z=0\)), the zero vector KK mode was found to be localized on the brane [47]. Here we consider the gauge free KK decomposition (1), with which there will be scalar modes.

Substitute the KK decomposition (1) (with \(b_1=b_2=-1/2\)) into the bulk action (43), we can get the effective action:

$$\begin{aligned} S_1= & {} -\frac{1}{4}\sum _m{\sum _{n}{\int {d^4x\sqrt{-{\hat{g}}} \bigg [ I_{1}^{( nn' )}{\hat{Y}}_{\upmu \upnu }^{( n)}{\hat{Y}}^{\upmu \upnu ( n' )}}}} \nonumber \\&+I_{2}^{( nn' )}\partial _{\upmu }\upphi ^{( n )}\partial ^{\upmu }\upphi ^{( n' )} +I_{3}^{( nn )}{\hat{X}}_{\upmu }^{( n )}{\hat{X}}^{( n' )\upmu } \nonumber \\&-I_{4}^{( nn' )}({\hat{X}}_{\upmu }^{( n )}\partial ^{\upmu }\upphi ^{( n' )}+ \partial _{\upmu }\upphi ^{( n)}{\hat{X}}^{\upmu ( n' )})\nonumber \\&+I_{5}^{( nn' )}{\hat{X}}_{\upmu }^{( n )}{\hat{X}}^{( n' )\upmu } +I_{6}^{( nn' )}\upphi ^{( n )}\upphi ^{( n' )} \bigg ], \end{aligned}$$
(44)

where \(I_{1}^{( nn' )}\), \(I_{2}^{( nn' )}\), \(I_{3}^{( nn' )}\), \(I_{4}^{( mn )}\) are exactly the same with that for a free bulk U(1) gauge field, but

$$\begin{aligned} I_{5}^{( nn' )}= & {} \int {{\mathcal {M}}^2e^{2A}\uprho _{1}^{( n )}\uprho _{1}^{( n' )}dz}, \nonumber \\ I_{6}^{( nn' )}= & {} \int {{\mathcal {M}}^2e^{2A}\uprho _{2}^{( n )}\uprho _{2}^{( n' )}dz}. \end{aligned}$$
(45)

We can see that the mass term \({\mathcal {M}}^2X_MX^M\) in the bulk action generates a mass term for the vector KK modes \(I_{5}^{( nn' )}{\hat{X}}_{\upmu }^{( n )}{\hat{X}}^{( n' )\upmu }\) and for the scalar ones \(I_{6}^{( nn' )}\upphi ^{( n )}\upphi ^{( n' )}\) on the brane respectively. However, there is no term denoting the coupling between the vector and massive scalar ones, such as \((\partial _\upmu {\hat{X}}^\upmu + \upphi ^{(n)})^2 \) similar to the Stueckelberg mechanism. Therefore, we guess that it is very difficult to produce the gauge invariance of the massive vector KK modes on the brane. To prove this, we also need the help of the EOM.

When the KK decomposition is substituted into the bulk EOM \(\partial _{M}\left( \sqrt{-g} \;Y^{MN}\right) -\sqrt{-g} {\mathcal {M}}^2 X^{N}=0\), the EOM can be written as:

$$\begin{aligned}&\frac{1}{\sqrt{-{\hat{g}}}} \partial _{\upnu }\left( \sqrt{-{\hat{g}}} {\hat{Y}}^{\upnu \upmu }\right) -\uplambda _1 \partial ^{\upmu }\upphi ^{(n)} + \uplambda _2~{\hat{X}}^{(n)\upmu }=0, \end{aligned}$$
(46a)
$$\begin{aligned}&\partial _{\upmu }\big (\sqrt{-{\hat{g}}} \partial ^{\upmu }\upphi ^{(n)}\big ) -\uplambda _3 \partial _{\upmu }(\sqrt{-{\hat{g}}} {\hat{X}}^{(n)\upmu })- \uplambda _4\;\upphi ^{(n)}=0.\nonumber \\ \end{aligned}$$
(46b)

with the same \(\uplambda _1\) and \(\uplambda _3\) for a free bulk U(1) gauge field, but different \(\uplambda _2, \uplambda _4\):

$$\begin{aligned} \uplambda _2= & {} \left[ \frac{\text {e}^{-\frac{1}{2}A}\partial _{z}\left( \text {e}^{A}\;\partial _z\big (\uprho _{1}^{(n)} \text {e}^{-\frac{1}{2} A}\big )\right) }{2\uprho _{1}^{(n)}} -\text {e}^{2A}{\mathcal {M}}^2\right] ,\nonumber \\ \uplambda _4= & {} \text {e}^{2A}{\mathcal {M}}^2. \end{aligned}$$
(47)

And another group of EOM can be got from the effective action (44):

$$\begin{aligned}&I_1^{(nn')} \frac{1}{\sqrt{-{\hat{g}}}} \partial _{\upnu }\left( \sqrt{-{\hat{g}}} {\hat{Y}}^{\upnu \upmu }\right) +I_4^{(nn')} \partial ^{\upmu }\upphi ^{(n)}\nonumber \\&\quad -(I_3^{(nn')}+I_5^{(nn')}){\hat{X}}^{(n)\upmu }=0, \end{aligned}$$
(48a)
$$\begin{aligned}&I_2^{(nn')} \partial _{\upmu }\bigg (\sqrt{-{\hat{g}}} \partial ^{\upmu }\upphi ^{(n)}\bigg ) -I_4^{(nn')}\partial _{\upmu }\bigg (\sqrt{-{\hat{g}}} {\hat{X}}^{(n)\upmu }\bigg )\nonumber \\&\quad -I_6^{(nn')}\;\upphi ^{(n)}=0. \end{aligned}$$
(48b)

Compare the EOM (46) and (48) the most remarkable result we discover is that

$$\begin{aligned} \uplambda _4=\text {e}^{2 A}\;{\mathcal {M}}^2=I_6^{(nn)}=\text {constant}. \end{aligned}$$
(49)

As \(I_6^{(nn)}\) denotes the mass of the scalar KK modes, which should be a constant, the above equation results in that \({\mathcal {M}}^2=0\). When \({\mathcal {M}}^2=0\), the case becomes the one we talked about in Sect. 2, i.e., for a free bulk U(1) gauge field.

This suggests that in a brane with one extra dimension, if we would like to get gauge invariant massive vector KK modes, the bulk action should not be the form as (44). The term \({\mathcal {M}}^2 X_M X^M \) not only destroys the gauge invariance of the bulk action but also of the effective action on the brane.

4 Discussions and conclusions

In this work we investigated the gauge invariance and the localization of the massive vector KK modes on the brane with one extra dimension. Firstly, we found that the bulk gauge invariance is very important to the origin of the brane gauge invariance. For example,

  • For the bulk action of a U(1) vector field, if it contains the term \(Y^{MN}Y_{MN}\) \((Y^{\upmu \upnu }Y_{\upmu \upnu }+Y^{\upmu y}Y_{\upmu y})\), which is gauge invariant, through a gauge free KK decomposition the term \(Y^{\upmu y}Y_{\upmu y}\) can be decomposed into the terms \(C_1\;\partial _\upmu \upphi ^{(n)}\partial ^\upmu \upphi ^{(n)} \), \(C_2\;{\hat{X}}_{\upmu }^{(n)}{\hat{X}}^{\upmu (n)}\) and \(C_3\;\partial _\upmu \upphi ^{(n)}{\hat{X}}^{\upmu (n)} \) on the brane, which display the kink momentum of the scalar KK modes, the self-interaction of the vector KK modes and the coupling between the massive vector KK modes and the massless scalar ones. \(C_1 \sim C_3\) are different coupling constants. If these three terms can be rewritten as \(\big (\partial _{\upmu }\upphi ^{(n)}-m^{(n)}{\hat{X}}^{(n)}_\upmu \big )^2\) with \(m^{(n)}\) the mass of the vector KK mode, it will be just gauge invariant in form.

  • If there is a term such as \({\mathcal {M}}^2X_MX^M \) in the bulk action, which in fact destroys the gauge invariance of it, it will contribute some masses for the vector KK modes, and lead to the massive scalar KK modes. However, it does not create the term denoting the coupling between the vector KK modes and the massive scalar ones, such as \((\partial _\upmu {\hat{X}}^\upmu + \upphi ^{(n)})^2 \) similar to the Stueckelberg mechanism, therefore, there is no way to produce the gauge invariance of the effective action.

For our first two examples, for a gauge invariant bulk action \(CY^{MN}Y_{MN}\) with C denoting different localization mechanism, the effective action can be both formalized as a gauge invariant one. This is because with the assumption \(C_1=\updelta _{nn'}\), it was found that there is a relationship between \(C_2\) and \(C_3\), with which these terms can be rewritten as the gauge invariant form. However, it is not sure whether the relationship between \(C_2\) and \(C_3\) always can be got in more general situation, which should be given a deep research. For the third example, as the mass term added in the bulk action, a gauge invariant effective action on the brane can not be got.

Meanwhile, the localization mechanism and the brane solution determine whether the massive vector KK modes and their accompanying scalar ones can be both localized on the brane. This is to say they also impact on the gauge invariance of the effective action. In this work, only for the first example, the massive vector KK modes and their accompanying scalar ones are found to be localized on the brane at the same time.