1 Introduction

The charmed mesons are the ground states of the c, \({\bar{q}}\) (which q can be the light quarks of u, d and s). They are abundantly produced in high-energy colliders. The \(D^{\pm }\) and \(D^{0}\) pseudoscalar (P) mesons are binding systems of \(c{\bar{d}}\) and \(c{\bar{u}}\) with spin 0, respectively, and the \(D^{*\pm }\) and \(D^{*}\) are their corresponding vector (V) states with spin 1. Carrying a heavy flavor with a light quark, they make the unique heavy mesons in the standard model. Thus, the study of them has attracted particular attention of experimenters and theoreticians, particularly, ever since observation of the first charm quark in 1976 and subsequent detection of the D mesons [1].

Experimentally, charmed mesons production has been widely measured in pp collisions at \(\sqrt{s} = 7TeV\) in the hadronization of charm and bottom quarks in jets [2] and in bottom hadron decays [3] by the ATLAS collaboration, the ALICE collaboration [4, 5] and the LHCb collaboration [6]. Also, the CDF collaboration [7] at the Tevatron collider has measured the open-charm production in proton–antiproton (\(p{\bar{p}}\)) collisions at \(\sqrt{s}=1.96 TeV\). Furthermore, the D mesons production has been measured in ep interactions at the HERA collider by the ZEUS [8] and H1 [9] collaborations, and in \(e^{-}e^{+}\) annihilation, at the \(Z^{0}\) resonance by different collaborations [10,11,12,13,14,15,16,17,18].

Almost all these data have been compared with different theoretical predictions, including the fixed-order next-to-leading-logarithm (FONLL) approach in Refs. [19, 20], the general-mass variable-flavor-number scheme (GM-VFNS) [21, 22] calculations, and the NLO quantum chromodynamic (NLO QCD) calculations matched with an MC@NLO simulation [23]. The cross section of D mesons based on the \(k_{t}\) factorization approach has been published in the LO and NLO accuracies at LHC energy and compared to experimental results [24].

In the high-\(p_{T}\) region, the main mechanism for producing a hadron is parton fragmentation. The theoretical predictions of the heavy hadron production cross section, in this region, are based on the factorization approach [19, 20]. In this way, the cross section of hadron production is computed as a convolution of three terms: the partonic hard scattering cross section (\({\hat{\sigma }}\)), the parton distribution functions (PDFs) of the incoming protons, and the FF, \(D^{LO}(z)\), that give the probability for the splitting of a parton with high transverse momentum into the desired hadron plus other partons. In fact, the factorization theorem allows us to separate the short-distance, high-energy parton production, and the long-distance fragmentation process. Thus, it provides necessary tools to derive a cross section of hadron production in a systematic manner. The short-distance part is computed through a perturbative calculation [25], and the PDFs and the FFs can be parameterized based on experimental data. The PDFs of the proton are prevalently parameterized by different predictions such as MSTW [26] and MMHT [27].

The typical formula of a differential cross section for producing a hadron h in the collision of hadrons of A and B can be factorized at LO in \(\alpha _{s}\) as:

$$\begin{aligned} \mathrm{d}\sigma ^{LO}= & {} \frac{1}{2x_{A}x_{B}s}\sum _{a_{A}a_{B}}\frac{(4\pi \alpha _{s})^2}{w(a_{A})w(a_{B})}f_{a_{A}/A}(x_{A},\mu ) \nonumber \\&\times f_{a_{B/B}}(x_{B},\mu ) D^{LO}(z,\mu )\psi ^{(4)}(\vec {a},\vec {p})\mathrm{d}x_{A}\mathrm{d}x_{B}\mathrm{d}z\mathrm{d}\Gamma _{2},\nonumber \\ \end{aligned}$$
(1)

where the \(\psi ^{(4)}\) functions have been calculated by Ellis and Sexton in Ref. [28], and A and B are the incoming hadrons.

In Eq. (1), \(\vec {p}=\lbrace p_{A},p_{B},p_{1},p_{2}\rbrace \) and \(\vec {a}=\lbrace a_{A},a_{B},a_{1},a_{2}\rbrace \) denote the four vectors and flavor indices of partons, respectively, \(s=(p_{A}+p_{B})^{2}\) and w(a) are the number of spins and colors for particle a, \(x_{A}\) and \(x_{B}\) are momentum fractions, z is the energy fraction of the produced hadron, and \(f_{a_{A}/A}(x_{A},\mu )\) and \(f_{a_{B}/B}(x_{B},\mu )\) are the PDFs.

Different theoretical models have been proposed for the mechanism of heavy-light meson production via a fragmentation process at LO and NLO accuracies. Each model contains different parameters which can be effective in the theoretical results of the FF. The LO FF of a heavy quark to light-heavy meson was first calculated by Peterson et al. [29]. The function obtained in Peterson’s model is proportional to \(\Delta E^{-2}\), where \(\Delta E\) is the difference between the final state energy and initial heavy quark energy. Collins and Spillers [30] evaluated the FF at a typical value of \(\left\langle k_{T}^{2}\right\rangle \). In their model, the probability of the transition is related to the hadronic structure function. In Bratten’s model, the PQCD fragmentation function was calculated from the general gauge-invariant definition by integrating over the invariant mass s of the fragmenting quark. The FF of Suzuki’s model [31] is calculated in Feynman gauge by neglecting Fermi motion, integrating over the transverse momentum of final parton and averaging over the spin of the initial heavy quark states and sum over the spin of the final states. In Ref. [32], the FF is calculated at LO accuracy for producing a free on-shell \(Q{\bar{Q}}\) state \(D_{Q\rightarrow h}\) according initial conditions of Suzuki’s model by considering different spin states of the initial quark.

The experimental observations indicate that the heavy quark fragmentation into the D mesons is not well modeled in theoretical calculations. In order to achieve a better theoretical estimation of the charmed mesons production cross section, here we consider the FF at the NLO accuracy in the factorization approach as well as \({\hat{\sigma }}\) and the PDFs at NLO accuracy.

The FFs of a heavy quark into a light-heavy meson [33] and heavy quarkonia [34] have been computed at NLO accuracy by adopting the assumptions of Suzuki’s model at LO accuracy [31]. The NLO corrections have been applied on the right side of the fragmentation process \(c(p_{2})\rightarrow c{\bar{q}}(k)+q(k_{3})\) in which q can be light quarks (u, d, s). In this process, \(p_{2}=(\sqrt{s_{1}},0,\sqrt{s_{1}},p_{2T})\) is the four momentum of the fragmenting parton, \(k=z(\sqrt{s_{1}},0,\sqrt{s_{1}},0)\) is the four momentum of the final meson and \(k_{3}=((1-z-x)\sqrt{s_{1}},0,(1-z-x)\sqrt{s_{1}},k_{3T})\) is the four momentum of the outcoming quark. In the real corrections, a gluon with the four momentum \({\bar{k}}=(x\sqrt{s_{1}},0,x\sqrt{s_{1}},0)\) is added on the right side of this process so that it carries momentum fraction x of the initial parton’s momentum, and this fraction is zero in the rest of the NLO corrections. The conservation of four energy–momentum yields to the relation \(p_{2}={\bar{k}}+k_{3}+k\), so in the rest frame of the \(Q{\bar{q}}\) binding state (the same as Ref. [31]), the minimum squared energy of the fragmenting quark is obtained as \(s_{1}=\frac{m_{q}^{2}+M^{2}+k_{3T}^{2}}{z(2-z)} \), where \(m_{q}\) and \(m_{Q}\) are the mass of the light quark and the heavy quark, respectively, and \(M=m_{q}+m_{Q}\).

The FF is obtained for this process at the NLO accuracy as:

$$\begin{aligned} D^{NLO}(z)= & {} \int \vert {\mathcal {M}}_{Soft}\vert ^{2}\mathrm{d}\Gamma _{3}^{Soft}+\int \vert {\mathcal {M}}^{Hard}\vert ^{2}\mathrm{d}\Gamma _{3}^{Hard} \nonumber \\&+\int \vert {\mathcal {M}}^{Virtual}\vert ^{2}\mathrm{d}\Gamma _{2}, \end{aligned}$$
(2)

where \(\vert {\mathcal {M}}\vert ^{2}\) is the squared amplitude, and \(\mathrm{d}\Gamma _{3}\) and \(\mathrm{d}\Gamma _{2}\) are the three-body and two-body phase spaces of the final states in the real and virtual corrections. The phase-space slicing technique with two cutoffs [35], collinear and soft cutoff \(\delta _{c}\) and \(\delta _{s}\), respectively, has been applied for calculating the phase-space integral and the cancellation of soft and collinear singularities. The dimensional regularization is adopted to regularize the infrared (IR) and ultraviolet (UV) divergences, and it is done in \(d=4-2\varepsilon \) dimensional space-time. The final-state hard collinear and soft singularities appearing in the FF are canceled with the addition of the LO diagrams to the renormalized one-loop real and virtual diagrams. More details of the NLO calculations by using dimensional regularization technique and two slicing method have been completely explained in Refs. [33,34,35,36].

After cancellation of all the divergences, the total FF for this process at the NLO accuracy is obtained as follows:

(3)

where \(D^{LO}\) can be referred to the FF at LO for vector, V, and pseudoscalar, P, states [33, 34]. Suzuki’s FFs for pseudoscalar and vector state are respectively \(D_{P}^{LO}\) and \(D_{V}^{LO}=2D_{T}+D_{L}\) as:

$$\begin{aligned} D_{P}^{LO}(z)= & {} \frac{N^{\prime }(4\pi \alpha _{s})^{2}}{zH(z)}\bigg (\bigg [\frac{2+a}{1+a}-\frac{1+a}{az}-\frac{a(1+2a)}{(1-z)(1+a)} \nonumber \\&-\frac{rz}{(1+a)(1-z)}\bigg ]^{2}+\frac{rz^{2}}{(1-z)^{2}}\bigg ), \end{aligned}$$
(4)
$$\begin{aligned} D_{L}(z)= & {} \frac{N^{\prime }(4\pi \alpha _{s})^{2}}{zH(z)}\bigg (\bigg [\frac{a+1}{z}-\frac{z(a+r)}{(1-z)(a+1)}\bigg ]^{2} \nonumber \\&+\frac{z^{2}r(1-a)}{(1-z)^{2}(1+a)^{2}}\bigg ), \end{aligned}$$
(5)
$$\begin{aligned} D_{T}(z)= & {} \frac{N^{\prime }(4\pi \alpha _{s})^{2}}{zH(z)}\bigg (\bigg [1-\frac{a}{1-z}\bigg ]^{2}+r\bigg [1+\frac{1}{(1-z)^{2}}\bigg ]\bigg ).\nonumber \\ \end{aligned}$$
(6)

In the above equations, \(N^{\prime }\) is a normalization constant, \(a=\frac{m_{q}}{m_{Q}}\), \(r=\frac{\langle k_{3T}^{2}\rangle }{m_{Q}^{2}}\) and \(\beta =\sqrt{1-(4am_{Q}^{2})/s_{2}}\) where \(s_{2}=m_{q}^2+M^{2}\) is the mass invariant for producing \(q+Q{\bar{q}}\) according to the kinematic of Ref. [33], and \(\mu _{0} = m_{Q} +2m_{q}\) is the initial scale of factorization. F(z), H(z) and \(t_{12}=-2k_{1}\cdot p_{2}\) are the functions of z as:

$$\begin{aligned} F(z)= & {} \frac{1}{2}-\frac{z\left( a^{2}+z-1)\right) +rz}{(a+1)^{2}(z-1)}, \end{aligned}$$
(7)
$$\begin{aligned} H(z)= & {} \bigg [1-\frac{(1+a)^{2}}{z}-\frac{a^{2}+r}{1-z}\bigg ], \end{aligned}$$
(8)
$$\begin{aligned} t_{12}= & {} 2m_{Q}^{2}\bigg [1-\frac{1+a}{z}+\frac{(1+r)z}{a+1}\bigg ]. \end{aligned}$$
(9)

All terms of order and the soft and collinear cutoffs ,\(\delta _{s}\) and \(\delta _{c}\), are neglectable. The final function \(D^{NLO}(z,\mu _{0})\) depends on z and a factorization scale \(\mu _{0}\). Since the FF generally contains terms like \(\ln (\mu ^{2} /m_{Q}^{2})\), in order to correctly take into account the possible large logarithmic terms, it should be evolved from \(\mu _{0}\) to a higher and arbitrary scale \(\mu _{f}\) by using the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution equations [37, 38].

Here, we would like to derive the cross section at NLO accuracy for pseudoscalar and vector D mesons production in the 1S wave state at a center of mass energy \(\sqrt{s}= 7 TeV\) via the fragmentation process of a heavy c quark. By doing this, we indicate the importance of the NLO corrections of FF in the production cross section of these light-heavy mesons.

In the remainder of the present paper, in Sect. 2, we briefly present the calculation of the production cross section using the factorization approach and two slicing method. In Sect. 3, the numerical evaluation of the cross section is performed for vector and pseudoscalar states of D mesons produced via the fragmentation process of the c quark at NLO accuracy. In this section, our numerical results are presented and compared with experimental data and theoretical predictions in the low- and high-transverse-momentum \(p_{T}\) region.

2 Inclusive production cross section at NLO

The calculations of the production cross section of hadrons are typically performed with a combination of analytical and numerical integration techniques. In the course of the NLO calculations, UV singularities appear in loop integrals where the momenta go to infinity. They are removed through the renormalization tools. Soft or IR divergences often arise in the calculations owing to the existence of a massless field, such as a gluon in QCD theory. They appear in both loop and phase-space integrals and are found in the low-energy region where the integration momenta go to zero. The calculation of these singularities should be made in such a way that no information of observable physics quantities is lost in terms. There are several techniques for handling the cancellations of divergences in the higher-order corrections, such as MC techniques. In this technique, the phase-space slicing method can be served to perform NLL calculations. In this method, two cutoff parameters are used to separate the phase-space regions of the soft and collinear singularities from the non-singular regions. This method would be useful for the transition from partonic to hadronic states and also study of a wide variety of high-energy processes. On this basis, we use this method as tools for calculation of the production cross section of D mesons at pp collision. For the case of LO, the differential cross section is calculated through Eq. (1). This equation involves lowest order two-to-two subprocesses, \(d{\hat{\sigma }}_{2\rightarrow 2}\), which have two-body final states. In addition, the FF obtained at the LO is served to calculate the \(\mathrm{d}\sigma ^{LO}\). For the calculation of the NLO case through factorization theorems, we should consider the following procedure: as a first step, \(d{\hat{\sigma }}\) should be calculated at the NLO that is independent of the species of the produced hadron so it can be applied in the pQCD factorization formula to product a heavy quark (Q) or heavy antiquark (\({\bar{Q}}\)). These calculations involve higher-order two-to-three subprocesses, \(d{\hat{\sigma }}_{2\rightarrow 3}\), which lead to both two- and three-body final states. The calculation of the squared matrix elements of subprocesses \(d{\hat{\sigma }}_{2\rightarrow 2}\) and \(d{\hat{\sigma }}_{2\rightarrow 3}\) is performed based on the VEGAS algorithms described in Refs. [39, 40]. The dominant parton processes leading to the production of a heavy quark–antiquark pair in final states are:

$$\begin{aligned}&q+{\bar{q}}\rightarrow Q+{\bar{Q}},\ \ g+g\rightarrow Q+{\bar{Q}},\ \\&g+g\rightarrow Q+{\bar{Q}}+g,\ \ q+g\rightarrow Q+{\bar{Q}}+q. \end{aligned}$$

The subprocess cross section for n body processes at NLO accuracy is written as:

$$\begin{aligned} d{\hat{\sigma }}_{2\rightarrow n}=d{\hat{\sigma }}^{LO}_{2\rightarrow n}+d{\hat{\sigma }}^{NLO}_{2\rightarrow n}, \end{aligned}$$
(10)

where \(\mathrm{d}\sigma ^{NLO}_{2\rightarrow n}\) contains virtual and real corrections:

$$\begin{aligned} d{\hat{\sigma }}^{NLO}_{2\rightarrow n}=d{\hat{\sigma }}^{Vir}_{2\rightarrow n}+d{\hat{\sigma }}^{Real}_{2\rightarrow n}, \end{aligned}$$
(11)

and \(d{\hat{\sigma }}_{Real}\) involves the soft and collinear corrections of cross section as:

$$\begin{aligned} d{\hat{\sigma }}^{Real}=d{\hat{\sigma }}^{soft}+d{\hat{\sigma }}^{coll}. \end{aligned}$$
(12)

Here, \(d{\hat{\sigma }}_{Real}\) and \(d{\hat{\sigma }}_{Vir}\) can be precisely found by adapting two- and three-body differential cross sections of Refs. [35, 36].

The second step is to apply the NLO FF calculated in Ref. [33] to the total differential cross section. Thus, at NLO accuracy, the general structure of calculation of the total differential cross section is written as:

$$\begin{aligned} \mathrm{d}\sigma =\mathrm{d}\sigma ^{LO}+\mathrm{d}\sigma ^{NLO}_{A+B\rightarrow i+h}+\mathrm{d}\sigma ^{NLO}_{{A+B\rightarrow i+j+h}}, \end{aligned}$$
(13)

where \(\mathrm{d}\sigma ^{LO}\) is the LO cross section, \(\mathrm{d}\sigma ^{NLO}_{A+B\rightarrow i+h}\) and \(\mathrm{d}\sigma ^{NLO}_{A+B\rightarrow i+j+h}\) denote the NLO cross sections of two- and three-body cases, respectively. Our strategy in calculation of the NLO cross section is regularization of the poles appearing in the amplitude by employing the two cutoff phase-space slicing method.

In the two-body process, i and j are the outcoming partons where the j parton fragments into h hadron. The differential cross section for the two-body process is factorized to the FF as follows:

$$\begin{aligned} \mathrm{d}\sigma _{A+B\rightarrow i+h}=d{\hat{\sigma }}_{A+B\rightarrow i+j}D_{j\rightarrow h}(z)\mathrm{d}z, \end{aligned}$$
(14)

where the contribution of NLO corrections is written as:

$$\begin{aligned}&\mathrm{d}\sigma ^{NLO}_{A+B\rightarrow i+h}=\mathrm{d}\sigma ^{HO}+\mathrm{d}\sigma ^{CT}=\left[ G^{HO}+G^{CT}\right] \nonumber \\&\quad \times D_{j\rightarrow h}(z)\mathrm{d}z \mathrm{d}\Gamma _{2}, \end{aligned}$$
(15)

where \(G^{HO}\) and \(G^{CT}\) are the higher-order part and factorization counterterm part, respectively, which are a function of \(\psi ^{4}\) and \(\psi ^{6}\), and their structures are found in Ref. [36]. To remove singularities appearing in \(\mathrm{d}\sigma ^{NLO}_{A+B\rightarrow i+h}\), we introduce the mass factorization scale for fragmentation function as:

$$\begin{aligned} D_{j\rightarrow h}(z,\mu _{f})= & {} D(z)_{j\rightarrow h}\nonumber \\&+\left( -\frac{1}{\epsilon }\right) \left[ \frac{\alpha _{s}}{2\pi }\frac{\Gamma (1-\epsilon )}{\Gamma (1-2\epsilon )}\left( \frac{4\pi \mu _{r}^{2}}{\mu _{f}^{2}}\right) ^{\epsilon }\right] \nonumber \\&\times \int _{z}^{1}D_{j^{\prime }\rightarrow h}(z/y)P^{+}_{j\prime {j}}(y)\frac{\mathrm{d}y}{y}, \end{aligned}$$
(16)

where \(\mu _{f}\) is the final-state factorization scale, and \(P^{+}_{j\prime {j}}\)’s are the regulated splitting functions which can be found in Ref. [37]. By replacing Eq. (16) with D(z) in Eq. (14), two body processes are obtained as follows:

(17)

The two-to-three contribution to the inclusive cross section for producing a hadron h via fragmentation process can be written as:

$$\begin{aligned}&\mathrm{d}\sigma ^{NLO}_{A+B\rightarrow i+j+h}\nonumber \\&\quad =\frac{1}{2x_{A}x_{B}s}\sum _{a_{A}a_{B}}\frac{(4\pi \alpha _{s})^3}{w(a_{A})w(a_{B})}{\mathcal {F}}f_{a_{A}/A}(x_{A}) f_{a_{B/B}}(x_{B})\nonumber \\&\qquad \times \Psi (\vec {a},\vec {p})D^{NLO}(z)\mathrm{d}x_{A}\mathrm{d}x_{B}\mathrm{d}z\mathrm{d}\Gamma _{3}, \end{aligned}$$
(18)

where

$$\begin{aligned} {\mathcal {F}}=\left( \frac{4\pi \mu _{r}^{2}}{2p_{A}\cdot p_{B}}\right) ^{\varepsilon }\frac{\Gamma (1-\varepsilon )}{\Gamma (1-2\varepsilon )}. \end{aligned}$$
(19)

The expressions for the three-body squared matrix elements may be found in Ref. [28]. The above equation can be split into three terms as

$$\begin{aligned} \mathrm{d}\sigma _{A+B\rightarrow i+j+h}=\mathrm{d}\sigma ^{soft}+\mathrm{d}\sigma ^{coll}+\mathrm{d}\sigma ^{finite}, \end{aligned}$$
(20)

in which the three-body phase space,(\(p_{A}+p_{B}\rightarrow p_{i}+p_{j}+p_{k}\)), is divided into three parts, soft, collinear and non-collinear, with two parameters \(\delta _{c}\) and \(\delta _{s}\). The phase-space integration of the non-collinear region, which is free of singularities, is performed numerically, while in the soft and collinear regions, the phase-space integrations are done analytically in \(D = 4 -2\epsilon \) dimensions.

The soft terms are as follows:

$$\begin{aligned} \mathrm{d}\sigma ^{soft}_{A+B\rightarrow i+h+k}=\frac{1}{2\phi }\int \vert {\mathcal {M}}_{3}^{soft}\vert ^{2}D_{j\rightarrow h}(z)\mathrm{d}\Gamma _{3}\vert _{soft}\mathrm{d}z,\nonumber \\ \end{aligned}$$
(21)

where \(\phi \) is the usual flux factor which depends on the incident particle masses \(m_{A}\), \(m_{B}\) and the partonic center of momentum energy squared, s. Here, the k parton is considered as the third particle. It should be noted that the condition \(p_{3}\) being soft is defined by \(\delta _{s}>\frac{2p^{0}_{3}}{\sqrt{s}}\) where \(s=(p_{A}+p_{B})^{2}\) and \(p_{3}^{0}\) is the energy of the soft parton. The square of soft amplitude is obtained as follows:

$$\begin{aligned}&\vert {\mathcal {M}}_{3}^{soft}\vert ^{2}\simeq \left( 4\pi \alpha _{s}\right) \mu _{f}^{2\epsilon }\sum _{n,m=A,B,i,j}\frac{p_{n}\cdot p_{m}}{(p_{n}\cdot p_{3})(p_{m}\cdot p_{3})}\psi _{nm}^{0},\nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned}&\mathrm{d}\Gamma _{3}\vert _{soft}=\frac{\mathrm{d}p_{3}^{3-2\epsilon }}{2p^{0}_{3} (2\pi )^{3-2\epsilon }}\mathrm{d}\Gamma _{2}, \end{aligned}$$
(23)

where \(\mathrm{d}\Gamma _{2}\) is the two-body phase-space differential of i and j partons, and \(p_{3}\) is the gloun’s four momentum in the \(p_{A}+p_{B}\) rest frame as:

$$\begin{aligned} p_{3}=p_{3}^{0}\left( 1,\sin \theta _{1}\sin \theta _{3},\sin \theta _{1}\cos \theta _{3},\cos \theta _{1}\right) , \end{aligned}$$

and

$$\begin{aligned} dp_{3}^{3-2\epsilon }=dp_{3}^{0}\left( P_{3}^{0}\right) ^{2-2\epsilon }\sin ^{1-2\epsilon }\theta _{1}\mathrm{d}\theta _{1}\sin ^{-2\epsilon }\theta _{2}\mathrm{d}\theta _{2}\Omega _{-2\epsilon },\nonumber \\ \end{aligned}$$
(24)

where

$$\begin{aligned} \Omega _{-2\epsilon }=\frac{2\pi ^{(1-2\epsilon )/2}}{\Gamma \left( \frac{1-2\epsilon }{2}\right) }=\frac{2\pi ^{(3-2\epsilon )/2}\Gamma \left( 1-\epsilon \right) }{\sqrt{\pi }2^{2\epsilon }\Gamma \left( 1-2\epsilon \right) }. \end{aligned}$$
(25)

Thus, we have:

$$\begin{aligned}&\mathrm{d}\Gamma _{3}\vert _{soft}=\left[ \left( \frac{4\pi }{2p_{A}\cdot p_{B}}\right) ^{\epsilon }\frac{\Gamma (1-\epsilon )}{\Gamma (1-2\epsilon )}\frac{1}{2(2\pi )^{2}}\right] \mathrm{d}\Gamma _{2}\mathrm{d}S,\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned}&\mathrm{d}S=\frac{1}{\pi }\left( \frac{4\pi }{2p_{A}\cdot p_{B}}\right) ^{-\epsilon }\int _{0}^{\delta _{s}\sqrt{s}/2}dP_{3}^{0}\left( P_{3}^{0}\right) ^{1-2\epsilon }\sin ^{1-2\epsilon }\theta _{1} \nonumber \\&\qquad \quad \times \mathrm{d}\theta _{1}\sin ^{-2\epsilon }\theta _{2}\mathrm{d}\theta _{2}. \end{aligned}$$
(27)

So the soft contribution is written as:

$$\begin{aligned} \mathrm{d}\sigma ^{soft}=\frac{\alpha _{s}}{2\pi }{\mathcal {F}}\sum _{n,m=A,B,i,j}\mathrm{d}\sigma _{n,m}^{0}\int \frac{p_{n}\cdot p_{m}}{p_{n}\cdot p_{3}p_{3}\cdot p_{m}}\mathrm{d}S,\nonumber \\ \end{aligned}$$
(28)

where \(\mathrm{d}\sigma _{n,m}^{0}\) is as follows:

$$\begin{aligned} \mathrm{d}\sigma _{n,m}^{0}=\frac{1}{2\phi }\sum \psi _{nm}^{0}\mathrm{d}\Gamma _{2}, \end{aligned}$$
(29)

where \(\psi _{nm}^{0}\) is the square the color-connected Born amplitude, and \(\phi \) is the usual flux factor which depends on the partonic energy squared s and the incident particle masses \(m_{A}\) and \(m_{B}\). Integration over their soft region is defined by \(p_{3}^{0}<\delta _{s}\sqrt{2p_{A}\cdot p_{B}}/2\). Therefore, the contribution of the soft cross section is as follows:

$$\begin{aligned}&\mathrm{d}\sigma ^{soft}_{A+B\rightarrow i+h+k}\nonumber \\&\quad =\frac{1}{2x_{A}x_{B}s}\sum _{a_{A}a_{B}}\frac{(4\pi \alpha _{s})^2}{w(a_{A})w(a_{B})}{\mathcal {F}}\frac{\alpha _{s}}{2\pi }f_{a_{A}/A}(x_{A}) f_{a_{B/B}}(x_{B}) \nonumber \\&\qquad \times \Psi (\vec {a},\vec {p})D^{NLO}_{j\rightarrow h}(z)\left( \frac{A_{2}^{s}}{\epsilon ^{2}}+\frac{A_{1}^{s}}{\epsilon }+A_{0}^{s}\right) \mathrm{d}x_{A}\mathrm{d}x_{B}\mathrm{d}z\mathrm{d}\Gamma _{2},\nonumber \\ \end{aligned}$$
(30)

where \(A^{s}_{i}\)’s (with \(i=0,1,2\)) are in accordance with Eqs. (101–103) in Ref. [35].

The collinear singularities associated with the non- fragmenting parton in the final state correspond to gluon or quark emission. For the collinear region, the integral limit is \(k_{3}^{0}>\delta _{s}\sqrt{2p_{A}\cdot p_{B}}/2\). The collinear contribution of the differential cross section at NLO is written as follows:

$$\begin{aligned} \mathrm{d}\sigma ^{coll}_{A+B\rightarrow i+h+k}\simeq & {} \frac{1}{2\phi }\int \vert {\mathcal {M}}_{3}^{coll}\vert ^{2}_{p_{j}\Vert p_{k}} D_{j\rightarrow h}(z)\mathrm{d}\Gamma _{3}\vert _{p_{j}\Vert p_{k}}\mathrm{d}z,\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned} \mathrm{d}\Gamma _{3}\vert _{p_{j}\Vert p_{k}}= & {} \frac{\mathrm{d}^{3-2\epsilon }p_{k}}{2(2\pi )^{3-2\epsilon }}\frac{p^{0}_{jk}}{p_{j}^{0}p_{j}^{0}}\mathrm{d}\Gamma _{2}=\frac{(4\pi )^{\epsilon }}{16\pi ^{2}}\frac{\Gamma (1-\epsilon )}{\Gamma (1-2\epsilon )} \nonumber \\&\times \left[ s_{jk}y(1-y)\right] ^{-\epsilon }\mathrm{d}y\mathrm{d}s_{jk}\mathrm{d}\Gamma _{2}, \end{aligned}$$
(32)

where

$$\begin{aligned}&\vert {\mathcal {M}}_{3}^{coll}(A+B\rightarrow i+j+k)\vert ^{2}_{p_{j}\Vert p_{k}}\nonumber \\&\quad \simeq \frac{2}{s_{jk}}\vert {\mathcal {M}}_{2}(A+B\rightarrow i+j^{\prime })\vert ^{2} \nonumber \\&\qquad \times (4\pi \alpha _{s}) P_{jj^{\prime }}(y,\epsilon )\mu ^{2\epsilon }_{r}, \end{aligned}$$
(33)

where \(s_{jk}\simeq 2p_{j}\cdot p_{k}\) and \(P_{ij}\) are unregulated splitting functions related to usual Altarelli–Parisi splitting kernels, which are as follows

$$\begin{aligned} P_{ij}(y,\epsilon )=P_{ij}(y)+\epsilon P^{\prime }_{ij}(y). \end{aligned}$$
(34)

Here, the \(j^{\prime }\) parton splits into a j and k collinear pair. Now, by inserting Eqs. (32,33) into Eq. (31) and integrating over \(\mathrm{d}s_{jk}\), we have:

$$\begin{aligned}&\mathrm{d}\sigma ^{coll}_{A+B\rightarrow i+h+k}\nonumber \\&\quad \simeq \mathrm{d}\sigma _{A+B\rightarrow i+j^{\prime }}\frac{\alpha _{s}}{2\phi }{\mathcal {F}}\left( -\frac{1}{\epsilon }\right) \delta _{c}^{-\epsilon }\int y^{-\epsilon }(1-y)^{-\epsilon } \nonumber \\&\qquad \times P_{jj^{\prime }}(y,\epsilon )D_{j\rightarrow h}(x)\delta (xy-z)\mathrm{d}y\mathrm{d}x\mathrm{d}z. \end{aligned}$$
(35)

The limits of integration on y for the splitting functions \(P_{qq}\) and \(P_{gg}\) are \(\delta _{s}\le y\le 1-\delta _{s}\), and for the splitting functions \(P_{gq}\) and \(P_{qg}\), are \(0\le y\le 1-\delta _{s}\). It should be noted that a method for evaluating the angular integral of the soft and collinear differential cross section has been mentioned in Ref. [35].

The structure of the finite three-body differential cross section \(\mathrm{d}\sigma ^{finite}\) is presented as:

(36)

where \(\mathrm{d}\rho \) involves the momenta differential in four space-time dimensions and some kinematic factors. After subtracting the soft and collinear terms from the first term, the singularities are canceled, and the finite contribution is defined as:

(37)

where \(\mu _{f}\) is the factorization scale, and \({\tilde{f}}\) and \({\tilde{D}}\) functions are modified PDFs and FFs which are given as follows:

$$\begin{aligned}&{\tilde{f}}_{i\rightarrow h}(z,\mu _{f}^{2})= \sum _{j}\int _{z}^{1-\delta _{s}\delta _{ij}} f_{j\rightarrow h}(z/y,\mu _{f}^{2}){\tilde{P}}_{ij}\frac{\mathrm{d}y}{y}, \end{aligned}$$
(38)
$$\begin{aligned}&{\tilde{P}}_{ij}=P_{ij}(y)\ln \left[ \frac{y(1-y)\delta _{c}s}{\mu _{f}^{2}}\right] -P_{ij}^{\prime }(y). \end{aligned}$$
(39)

To obtain \({\tilde{D}}\), f should be replaced by D in the above equation. The integration on phase space contains the logarithms in the soft cutoff \(\delta _{s}\) and single poles in \(d=4-2\varepsilon \). The final-state differential cross section is dependent on the soft and collinear cutoffs through the boundaries imposed on their phase space (\(\delta _{c} \ll \delta _{s}\)). In the approximation where the cutoffs are small, terms of order \(\delta _{s}\) can be neglected. The mass singularities are factorized into the FF, and the remaining collinear singularities are factorized and absorbed into the PDFs \(f_{a_{i}}(x_{i})\) [41, 42], so the final result is finite in a \(d=4\) dimension. The sum of the soft, collinear and ultraviolet renormalized terms is finite, and the final result for physics observables are independent of the cutoffs. In the course of calculations, the average over initial quark spin and the sum over final spin states were performed. In order to make the theoretical predictions for differential and total cross section, the Mathematica FeynCalc package [43, 44] was used to carry out the color and Dirac traces, and the Apart package [45] and the FIRE package [46] were used to do partial fractions, and the master integrals were calculated using the LoopTools package [47]. There are Fortran codes corresponding to [28, 48] which calculate the one-loop scalar integrals and the matrix elements of amplitude. Here, we attempt to make more reliable predictions for the cross section production of D mesons by using the NLO corrections on the FF and compare them with the presently available results.

3 The numerical results and conclusion

In this paper, we have computed the production cross section \(\sigma \), and the differential cross section \(\mathrm{d}\sigma /dp_{T}\), as a function of \(p_{T}\), of charmed mesons (\(D^{0}\), \(D^{\pm }\), \(D_{s}^{pm}\) and vector mesons \(D^{*}\) and \(D^{*\pm }\)) via the fragmentation process at NLO accuracy in a pQCD approach. The NLO FF calculations of \(c\rightarrow c{\bar{q}}+q\), which q can be u, d and s, have been completely done in our previews work in Refs. [33, 34]. Actually, our present results are complementary of previous work. In the course of calculations, we adopted the two-loop formula of the running strong coupling constant \(\alpha _{s}\) as follows:

$$\begin{aligned} \alpha _{s}(\mu ^{2})=\frac{4\pi }{\beta _{0}\ln \left( \frac{\mu ^{2}}{\Lambda ^{2}}\right) }\left( 1-\frac{\beta _{1}\ln \left( \ln \left( \frac{\mu ^{2}}{\Lambda ^{2}}\right) \right) }{\beta _{0}^{2}\ln \left( \frac{\mu ^{2}}{\Lambda ^{2}}\right) }\right) , \end{aligned}$$
(40)

where \(\beta _{0}=11-2/3n_{f}\) and \(\beta _{1}=\left( 102-38/3n_{f}\right) \) are the one- and two-loop coefficients of the \(\beta \) function in QCD, respectively. We obtain \(\Lambda ^{n_{f}=3}=0.387\) GeV and \(\Lambda ^{n_{f}=4}=0.337\) GeV according to \(\alpha _{s}(m_{Z})=0.118\) (with \(m_{Z}=91.187 \) GeV) [49]. In calculations of the production cross section of the hadron at NLO accuracy, the factorization scale \(\mu _{f}\) should be larger than \(\mu _{0}\), so it is defined from the order of \(p_{T}\) as \(\mu _{f}= \sqrt{m^{2}_{Q} +p^{2}_{T,Q}}\). We set the renormalization scale, \(\mu _{r}\), to be \(\mu _{r}=2m_{q}\), which is the minimum value of the invariant mass of the virtual gluon.

In numerical calculations of the cross section, the Vegas program was used for integrating over the phase space [40], and the PDFs were adopted from the MSTW predictions at LO and NLO accuracies [26]. Here, the numerical results of cross sections are presented and compared with the ALICE and ATLAS data at energy scale \(\sqrt{s}=7 TeV\). The ATLAS experimental data have been reported in the range of transverse momentums in a low-\(p_{T}\) region (\(3.5<p_{T}<20\) GeV) and high-\(p_{T}\) region (\(20<p_{T}<100\) GeV) [50], and the ALICE experimental data have been presented in a region of \(2<p_{T}<20\) GeV. It must be stated that the range of pseudorapidity for the ATLAS data is \(\vert \eta \vert <2.1\), and the range of rapidity for the ALICE data is \(\vert y\vert <0.5\).

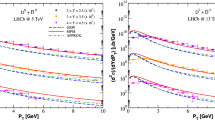
By using the mentioned parameters, the cross sections of D mesons production were obtained numerically at LO and NLO accuracies. In Fig. 1, the differential cross section distributions of the \(D^{\pm }_{s}\) mesons in c quark fragmentation are presented at LO and NLO accuracies.

Fig. 1
figure 1

The differential cross sections of mesons \(D^{\pm }_{s}\) as a function of \(p_{T}\) compared to ALICE data

Full size image

The differential cross sections for \(D^{0}\) and \(D^{*}\) mesons are shown in Fig. 2. The D mesons production threshold cannot be lower than approximately 2 GeV. Thus, in low \(p_{T}\) from 0 to 2 GeV, the \(\mathrm{d}\sigma /\mathrm{d}p_{T}\) threshold increases and reaches a maximum at \(p_{T} =2 \) GeV and then decreases towards \(p_{T} =100 \) GeV [50]. The sharp fall-off of the differential cross section distribution is expected in the framework of our study. This distribution for vector meson \(D^{*}\) is slightly larger than the one for pseudoscalar meson \(D^{0}\) at both LO and NLO accuracies, which may be due to their mass and spin alignment.

Fig. 2
figure 2

The differential cross sections of \(D_{0}\) and \(D^{*}\) mesons as a function of \(p_{T}\) in \(\vert y\vert <0.5\)

Full size image
Fig. 3
figure 3

The differential cross sections of \(D^{*\pm }\) (up) and \(D^{\pm }\) (down) mesons as a function of \(p_{T}\) compared to ATLAS data (symbols)

Full size image

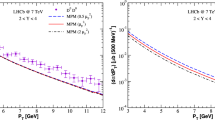
In Fig. 3, our results for \(D^{*\pm }\) and \(D^{\pm }\) are compared with ATLAS data at \(3.5<p_{T}<100\) GeV and \(\vert \eta \vert <2.1\). As it is seen, by increasing the \(p_{T}\) distribution, the cross section at the NLO accuracy gets closer to the data than the calculations in LO. Actually, the compatibility of NLO calculations with the data is seen especially in \(2<p_{T}<8\) GeV for \(D^{*\pm }\) and \(D^{\pm }\) mesons. The transverse momentum distribution of the \(D^{0}\) meson is shown in Fig. 4 at \(2<p_{T}<20\) GeV and rapidity \(\vert y\vert =0.5\) and compared with ALICE data and the KMR model [51] for Peterson parameterization with \(\epsilon _{c}=0.02\). According to this figure, a comparison shows cross sections at the NLO accuracy have good agreement with ALICE data [4], and it also corresponds to the upper limit of KMR uncertainties. In the bottom panel of Figs. 3 and 4, the ratios of experimental data to our results at both LO and NLO are displayed as a function of \(p_{T}\). The ratio of our results at NLO to ALICE data for \(D^{0}\) and \(D_{s}^{\pm }\) mesons gets near to 1 approximately at \(2<p_{T}<8\) GeV. These ratios indicate that our results are in good agreement with the experimental data in the low-\(p_{T}\) region. For mesons \(D^{\pm }\) and \(D^{*\pm }\), the downward trend of this ratio is also observed in the range of 8–40 GeV. As can be seen in Figs. 1, 2, 3 and 4, by applying the NLO corrections into the calculations, the differential cross section increases for the all states.

Fig. 4
figure 4

The differential cross section of \(D^{0}\) compared with ALICE data and the KMR model at \(2<p_{T}<20\) GeV

Full size image
Table 1 The production cross sections of \(D^{0}\) and \(D^{*}\) mesons with \(\vert \eta \vert <2.1\) at \(3.5< p_{T} <20\) GeV. The uncertainties in our results are just due to the quark’s mass
Full size table
Table 2 The low-\(p_{T}\), \(3.5<p_{T} < 20 \) GeV, and high-\(p_{T}\), \(20<p_{T} < 100 \) GeV, cross sections of \(D^{*\pm }\), \(D^{\pm }\) and \(D^{\pm }_{s}\) production with \(\vert \eta \vert <2.1\). Our results are presented at LO and NLO accuracies
Full size table

In Table 1, we present our calculations of \(D^{0}\) and \(D^{*}\) mesons cross sections at both LO and NLO accuracies at \(\vert \eta \vert <2.1\) and at transverse momentums between \(3.5< p_{T} < 20\) GeV and \(20< p_{T} <100\) GeV. In Table 2, the cross section values of \(D_{s}^{\pm }\), \(D^{\pm }\) and \(D^{*\pm }\) are presented in the low-\(p_{T}\) region (\(3.5< p_{T} < 20\) GeV) and high-\(p_{T}\) region (\(20< p_{T} <100\) GeV). In this table, our calculations at LO and NLO accuracies are compared with experimental data from ATLAS and also with theoretical results from FNOLL [19, 20, 52] and MC@NLO [23, 53] predictions. Therefore, it can be concluded that our results are comparable to these data and predictions within their uncertainties. The uncertainties in our results are just due to the mass of quarks.

At a specific collision energy, the mass of the light and heavy quarks has a significant effect on not only the fragmentation probabilities, but also the value of \(\mu \) and the PDFs and subsequently the production cross section. Here, the effective mass of the heavy quark (c) and the light quarks (u, d, s) and their uncertainties are considered as follows:

$$\begin{aligned}&m_{c}=1.5\pm 0.1,\ \ m_{u}=0.3\pm 0.01, \\&m_{d}=0.32\pm 0.01,\ \ m_{s}=0.48\pm 0.02. \end{aligned}$$

It should be pointed out that the effective mass of a heavy quark is set to nonzero in the partonic cross sections, the light quarks are considered massless in the proton, and the nonzero values of the effective mass of light quarks only enter through the initial conditions of the FFs. Our numerical results in Tables 1 and 2 show that the NLO QCD corrections increase the lowest-order cross section by about \(50\%\) in a factorization approach. Based on the obtained values in Tables 1 and 2, the ratio of neutral to charged D mesons production at both the LO and NLO accuracies can be calculated as:

$$\begin{aligned} R_{u/d}=\frac{\sigma (D^{0})+\sigma (D^{*})}{\sigma (D^{\pm })+\sigma (D^{*\pm })}\simeq 1.11\pm 0.1. \end{aligned}$$
(41)

This result agrees with the measured \(R_{u/d}\) value in \(e^{-}p\) interactions and the \(e^{-}e^{+}\) collider which are approximately unity. It is consistent with isospin invariance, which implies that u and d quarks are produced equally in charm fragmentation [8].

At a certain energy, the production probability inversely depends on quark mass, so a decrease in quark mass will increase the production probability, and vice versa. Since the s-quark is heavier than u- and d-quarks, the \(D_{s}^{\pm }\) mesons cross section becomes smaller than the other D mesons. According to our results in Table 2, at high \(p_{T}\), the strangeness-suppression factor of 0.24 is obtained, which agrees with measured data [50].

$$\begin{aligned} \gamma _{s/d}=\frac{\sigma (D^{\pm }_{s})}{\sigma (D^{\pm })+\sigma (D^{*\pm })Br(D^{*\pm }\rightarrow D^{0}\pi ^{+})}, \end{aligned}$$
(42)

where \(Br(D^{*\pm }\rightarrow D^{0}\pi ^{+}) = 0.677 \pm 0.005\) [54] is the branching fraction of the \(D^{*\pm }\rightarrow D^{0}\pi ^{+}\) decay.

In summary, we have derived the NLO cross section for a fragmentation process of a c quark to charmed mesons (\(D^{\pm }_{s}\), \(D^{0}\), \(D^{*}\), \(D^{*\pm }\) and \(D^{\pm }\)) using a factorization approach. In this paper, the phase-space integrals of two- and three-body subprocess cross sections have been calculated at NLO accuracy by applying the two-cutoff phase-space slicing method. After applying the NLO subprocess cross section and the NLO FF, we have presented the results of a hadronic production cross section in pp collision at high and low transverse momenta. Our results indicate a good overall agreement with the data, and their discrepancy may be explained as an indication of uncalculated QCD effects. It should be emphasized again that we have considered only uncertainties due to the quark mass. It should be noted that we have not followed the widespread habit of estimating theory uncertainties by varying factorization and renormalization scales by factors of 2 up and down. Of course, there is also the option to extend the calculations and present numerical results for these additional sources of uncertainties.