1 Introduction

Black holes, created by gravitational collapse of sufficiently massive stars, are fascinating objects in the universe. Starting from fairly mundane initial conditions, the fluctuations of vacuum near the event horizon cause black holes to evaporate and the evaporation process is inconsistent with the quantum mechanical principle that a pure state always evolves to another pure state [1]. Recently, more and more attentions have been not only paid on the understanding of the black hole information loss paradox [2,3,4,5], but also on the behavior of quantum correlations in relativistic setting [6,7,8,9,10,11,12,13,14,15,16,17,18]. The latter gives birth to the relativistic quantum information, which is devoted to study the preparation and precession of quantum information in the framework of general relativity. For this reason, the studies on relativistic quantum information is believed to be helpful for making deeper understanding in the entropy and information loss problems of black holes [19,20,21].

String theory is a promising candidate for a consistent theory of quantum mechanics and theory of gravitation. According to string theory, the scalar field would correspond to a dilaton, with an exponential coupling to an invariant. Choosing the invariant to be the Lagrangian of the electromagnetic field, one can obtain a solution of static dilatonic black hole, i.e., the Garfinkle–Horowitz–Strominger (GHS) dilaton black hole [22, 23]. One of the most important prediction of string theory differs from the general relativity is that the presence of dilaton can change the properties of the black hole geometries [24,25,26,27]. Therefore, it is needless to say that the studies on characteristics of dilaton black holes would be of utmost interest both for theory of gravity and quantum mechanics.

On the other hand, quantum correlations can be categorized into three hierarchies: Entanglement, quantum steering and Bell nonlocality, among which entanglement is the weakest and Bell nonlocality is the strongest [28]. The quantum steering, first proposed by Schrödinger [29, 30] in response to the well-known EPR paradox [31], describes the ability of one observer to nonlocally affect the other observer’s state through local measurements. The operational framework of quantum steering was formulated in the innovative work of Wiseman et al. [32], where the resource definition of steerability is given in terms of the impossibility to describe the conditional states at one party by the local hidden state model. One distinct feature of quantum steering which differs from other quantum correlations is asymmetry, which has been demonstrated in theory [33,34,35,36] and experiment [37,38,39]. Recently, we studied the behaviors of quantum entanglement for scalar modes [40] and quantum discord for Dirac modes [41] in the background of a GHS dilaton black hole and found that quantum correlations are sensitive indicators of spacetime parameters.

In this paper, we investigate the Gaussian quantum steering and its symmetrical property under the influence of a GHS dilaton black hole. We consider the distribution of quantum steerability among three-body systems: subsystem A observed by Alice who stays at the asymptotically flat region, subsystem B observed by Bob who hovers near the GHS dilaton black hole, subsystem \({\bar{B}}\) observed by a virtual anti-Bob restricted by the event horizon of the black hole. We obtain a phase-space description for the dynamics of Gaussian quantum state under the influence of the GHS dilaton gravity. By calculating quantum steering \({{\mathcal {G}}}^{\ A \rightarrow B}\) and \({{\mathcal {G}}}^{\ B \rightarrow A}\), we can quantitatively determine the degree of steerability of the subsystem B (A) from the measurements of A (B). It is found that when the dilaton charge is close to mass of the black hole, the steerability between Alice and Bob is obviously affected by the dilaton parameter. Throughout the paper, the units G = c = \(\hbar \) = \(\kappa _B\) = 1 are used.

The structure of the paper is as follows. In Sect. 2 we discuss the scalar field dynamics and second quantization near the GHS dilaton black hole. In Sect. 3 we review the definition and measurement of bipartite Gaussian quantum steerability. In Sect. 4 we study the distribution and asymmetry of Gaussian quantum steerability in GHS dilaton black holes. In the final section we make a brief summary.

2 Vacuum structure of coupled massive scalar field

The metric for a GHS black hole can be written as [22, 23]

$$\begin{aligned} ds^2= & {} -\left( \frac{r-2M}{r-2D}\right) dt^2 \nonumber \\&\quad +\left( \frac{r-2M}{r-2D}\right) ^ {-1}dr^2+r\left( r-2D\right) d\Omega ^2, \end{aligned}$$
(1)

where M is the mass of the black hole and D is the dilaton charge. The dynamics of a massive scalar field obeys the Klein-Gordon equation

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }(\sqrt{-g}g^{\mu \nu }\partial _{\nu })\psi -\mu \psi =0, \end{aligned}$$
(2)

where \(\mu \) is the mass of the scalar field.

Solving the Klein-Gordon near the event horizon \(r=r_{+}\) of the GHS black hole, one obtains the outgoing modes inside and outside the event horizon

$$\begin{aligned} \phi _{out,\omega lm}(r<r_{+})=e^{i\omega u}Y_{lm}(\theta ,\varphi ), \end{aligned}$$
(3)
$$\begin{aligned} \phi _{out,\omega lm}(r>r_{+})=e^{-i\omega u}Y_{lm}(\theta ,\varphi ), \end{aligned}$$
(4)

where \(v=t+r^*\) and \(u=t-r^*\), and \(r^*\) is the tortoise coordinate in the GHS spacetime.

Employing the Schwarzschild modes given in Eqs. (3) and (4), the scalar field \(\Phi \) near the event horizon can be expanded as

$$\begin{aligned} \Phi= & {} \sum _{lm}\int d\omega [b_{in,\omega lm}\psi _{in,\omega lm}(r<r_{+})\nonumber \\&+b^{\dag }_{in,\omega lm}\psi ^{*}_{in,\omega lm}(r<r_{+})\nonumber \\&\nonumber +b_{out,\omega lm}\psi _{out,\omega lm}(r>r_{+})\nonumber \\&+b^{\dag }_{out,\omega lm}\psi ^{*}_{out,\omega lm}(r>r_{+})], \end{aligned}$$
(5)

where \(b_{in,\omega lm}\) and \(b^{\dag }_{in,\omega lm}\) are the annihilation and creation operators acting on the states of the interior region of the dilaton black hole. \(b_{out,\omega lm}\) and \(b^{\dag }_{out,\omega lm}\) are the operators acting on the vacuum of the exterior region, respectively. The Schwarzschild vacuum state for the scalar field can be defined as

$$\begin{aligned} b_{in,\omega lm}|0\rangle _{in}=b_{out,\omega lm}|0\rangle _{out}=0. \end{aligned}$$
(6)

On the other hand, by defining the light-like Kruskal coordinates U and V [40],

$$\begin{aligned}&U=-4(M-D)e^{-u/(4M-4D)},\quad \nonumber \\&V=4(M-D)e^{v/(4M-4D)},\quad \mathrm{if\quad r>r_{+}};\nonumber \\&U=4(M-D)e^{-u/(4M-4D)},\quad \nonumber \\&V=4(M-D)e^{v/(4M-4D)}, \quad \mathrm{if\quad r<r_{+}}, \end{aligned}$$
(7)

we can rewrite the Schwarzschild modes to

$$\begin{aligned}&\phi _{out,\omega lm}(r<r_{+})=e^{-4(M-D)i\omega \ln [-U/(4M-4D)]}Y_{lm}(\theta ,\varphi ), \end{aligned}$$
(8)
$$\begin{aligned}&\phi _{out,\omega lm}(r>r_{+})=e^{4(M-D)i\omega \ln [U/(4M-4D)]}Y_{lm}(\theta ,\varphi ). \end{aligned}$$
(9)

Making an analytic continuation for Eqs. (8) and (9), a complete basis for positive frequency modes are obtained according to the suggestion of Damour–Ruffini [42]

$$\begin{aligned} \phi _{I,\omega lm}= & {} e^{2\pi \omega (M-D)}\phi _{out,\omega lm}(r>r_+)\nonumber \\&+e^{-2\pi \omega (M-D)}\phi ^*_{out,\omega lm}(r<r_+), \end{aligned}$$
(10)
$$\begin{aligned} \phi _{II,\omega lm}= & {} e^{-2\pi \omega (M-D)}\phi ^*_{out,\omega lm}(r>r_+)\nonumber \\&+e^{2\pi \omega (M-D)}\phi _{out,\omega lm}(r<r_+). \end{aligned}$$
(11)

By second-quantizing the scalar field \(\Phi \) in terms of and in the GHS spacetime, one can define the Kruskal vacuum \(\left| 0\right\rangle _K\)

$$\begin{aligned} a_{K,\omega lm}\left| 0\right\rangle _K=0, \end{aligned}$$
(12)

where \(a_{K,\omega lm}\) is the annihilation operator acting on the Kruskal modes. Then we calculate the Bogoliubov transformations between the field operators which act on the Schwarzschild vacuum and Kruskal vacuum, respectively. After normalizing the state vector, it is found that the Kruskal vacuum can be expressed as a maximally entangled two-mode squeezed state [40]

$$\begin{aligned} \left| 0\right\rangle _K= & {} \sqrt{1-e^{-8\pi \omega (M-D)}}\sum _{n=0}^\infty e^{-4n\pi \omega (M-D)}\nonumber \\&\times \left| n\right\rangle _{in}\otimes \left| n\right\rangle _{out}, \end{aligned}$$
(13)

where \(\left| n\right\rangle _{in}\) and \(\left| n\right\rangle _{out}\) are excited-states for Schwarzschild modes inside and outside the event horizon.

3 Measurement of quantum steerability for continuous variables

In this section we briefly introduce the measurement of Gaussian quantum steering. We consider a pair of local observables \(R_A\) on subsystem A and \(R_B\) on subsystem B in a bipartite state \(\rho _{AB}\). As proposed in [32, 43], a Gaussian state \(\rho _{AB}\) is \(A\rightarrow B\) steerable iff the following condition is violated by Alice’s Gaussian measurements

$$\begin{aligned} {\sigma _{AB}} + i\,({0_A} \oplus {\Omega _B}) \ge 0, \end{aligned}$$
(14)

where \(\Omega _i = \bigoplus _1^{2} {{\ 0\ \ 1}\atopwithdelims (){-1\ 0}}\), and \(\sigma _{AB} = \left( {\begin{array}{*{20}{c}} A &{} C \\ {{C^\mathsf{T}}} &{} B \\ \end{array}} \right) _i\) is the covariance matrix of a bipartite system, which describes a physical quantum state iff it satisfies the bona fide uncertainty principle relation \( {\sigma _{AB}} + i\,({\Omega _{AB}} ) \ge 0\). The condition given in Eq. (14) equals to two simultaneous conditions: (i) \(A > 0\), and (ii) \({M^B_{\sigma }} + i{\Omega _B} \ge 0\), where \(M^B_{\sigma } = B - {C^\mathsf{T}}{A^{ - 1}}C\) is the Schur complement of A in the CM \(\sigma _{AB}\). Note that the first condition is always satisfied because the matrix \(\sigma _A\) is a physical covariance matrix. Therefore, \(\sigma _{AB}\) is \(A \rightarrow B\) steerable iff the symmetric covariance matrix \(M^B_{\sigma }\) is not bona fide [32].

The symmetric matrix \(M^B_{\sigma }\) can be diagonalized by a symplectic transformation \(S_B\) such that \(S_B M^B_{\sigma } S_B^\mathsf{T}=\text {diag}\{{\bar{\nu }}^B_1,{\bar{\nu }}^B_1,\ldots ,{\bar{\nu }}^B_m,{\bar{\nu }}^B_m\}\) [44], where \(\{{\bar{\nu }}^B_{j}\}\) are the symplectic eigenvalues of \(M^B_{\sigma }\). Then the \(A \rightarrow B\) quantum steering can be calculated in terms of the symplectic eigenvalues [43]

$$\begin{aligned} {{\mathcal {G}}}^{A \rightarrow B}(\sigma _{AB}):= \max \left\{ 0,\, -\sum \limits _{j:{{{\bar{\nu }}}_j^B}<1} \ln ({{\bar{\nu }}}_j^B) \right\} . \end{aligned}$$
(15)

If the steered party Bob has only one mode, the \(A\rightarrow B\) Gaussian steerability can be expressed as

$$\begin{aligned} \begin{aligned} {{\mathcal {G}}}^{A \rightarrow B}(\sigma _{AB})=\max \big \{0,\, {\varvec{S}}(A)-{\varvec{S}}(\sigma _{AB}) \big \}, \end{aligned} \end{aligned}$$
(16)

where \({\varvec{S}}(\sigma )=\frac{1}{2}\ln \left( {det}\sigma \right) \) is Rényi-2 entropy [45].

4 Distribution of Gaussian quantum steerability in GHS dilaton black hole

4.1 Reduction of quantum steerability between the initially correlated modes

In this subsection we seek for a phase-space description for the Gaussian quantum state and study the dynamics of quantum steering under the influence of the GHS dilaton black hole. We assume that the observer Alice stays at the asymptotically flat region, while Bob observing subsystem B hovers near the GHS dilaton black hole. The initial state shared between them is a two-mode squeezed Gaussian state, which is given by the covariance matrix

$$\begin{aligned}&\sigma ^\mathrm{(G)}_{AB}(s)\nonumber \\&\quad = \left( \begin{array}{cccc} \cosh (2s)&{}\quad 0&{}\quad \sinh (2s)&{}\quad 0\\ 0&{}\quad \cosh (2s)&{}\quad 0&{}\quad -\sinh (2s)\\ \sinh (2s)&{}\quad 0&{}\quad \cosh (2s)&{}\quad 0\\ 0&{}\quad -\sinh (2s)&{}\quad 0&{}\quad \cosh (2s) \end{array}\right) ,\nonumber \\ \end{aligned}$$
(17)

where s is the squeezing of the initial state. It has been shown in Eq. (13) that the Kruskal vacuum is a maximally entangled two-mode squeezed state in terms of Schwarzschild modes inside and outside regions. After some calculations, we find that the two mode squeezed transformation can be expressed by a symplectic operator in the phase-space, which is

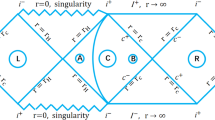
$$\begin{aligned} S_{B,{\bar{B}}}(D) = \left( \!\!\begin{array}{cccc} \frac{1}{\sqrt{1-e^{-8\pi \omega (M-D)}}}&{} 0&{} \frac{e^{-4\pi \omega (M-D)}}{\sqrt{1-e^{-8\pi \omega (M-D)}}}&{} 0\\ 0&{} \frac{1}{\sqrt{1-e^{-8\pi \omega (M-D)}}}&{}0&{} -\frac{e^{-4\pi \omega (M-D)}}{\sqrt{1-e^{-8\pi \omega (M-D)}}}\\ \frac{e^{-4\pi \omega (M-D)}}{\sqrt{1-e^{-8\pi \omega (M-D)}}} &{} 0&{} \frac{1}{\sqrt{1-e^{-8\pi \omega (M-D)}}}&{} 0\\ 0&{} -\frac{e^{-4\pi \omega (M-D)}}{\sqrt{1-e^{-8\pi \omega (M-D)}}}&{} 0&{} \frac{1}{\sqrt{1-e^{-8\pi \omega (M-D)}}} \end{array}\!\!\right) . \end{aligned}$$
(18)

After the action of the two mode squeezed transformation, the entire system involves three subsystems: subsystem A described by the Kruskal observer Alice, subsystem B described by the Schwarzschild observer Bob, and the subsystem \({\bar{B}}\) described by the virtual observer anti-Bob inside the event horizon. Then we can obtain the covariance matrix \(\sigma _{AB{\bar{B}}}\) of the tripartite quantum system [7],

$$\begin{aligned} \nonumber \sigma _{AB {\bar{B}}}(s,D)= & {} \big [I_A \oplus S_{B,{\bar{B}}}(D)\big ] \big [\sigma ^\mathrm{(G)}_{AB}(s) \oplus I_{{\bar{B}}}\big ]\\&\times \big [I_A \oplus S_{B,{\bar{B}}}(D)\big ]\,, \end{aligned}$$
(19)

where \(S_{B,{\bar{B}}}(D)\) is the phase-space representation of the two-mode squeezing operation given in Eq. (18).

Because the exterior region of the black hole is causally disconnected to the inner region over the event horizon, Alice and Bob cannot approach the mode \({\bar{B}}\) in the inner region. Then, one obtains the covariance matrix \(\sigma _{AB}(s,D)\) for Alice and Bob by tracing across the mode \({\bar{B}}\)

$$\begin{aligned} \sigma _{AB}= \left( {\begin{array}{*{20}{c}} \mathcal {A}_{AB} &{}\quad \mathcal {C}_{AB} \\ {{\mathcal {C}_{AB}^\mathsf{T}}} &{}\quad \mathcal {B}_{AB} \\ \end{array}} \right) , \end{aligned}$$
(20)

where

$$\begin{aligned} \mathcal {A}_{AB}= & {} \cosh (2s)I_2, \\ \mathcal {C}_{AB}= & {} \left[ \frac{\sinh (2s)}{\sqrt{1-e^{-8\pi \omega (M-D)}}}\right] Z_2, \end{aligned}$$

with \(Z_2 =\left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad -1 \\ \end{array} \right) \), and

$$\begin{aligned} \mathcal {B}_{AB}=\left[ \frac{e^{-8\pi \omega (M-D)}+\cosh (2s)}{1-e^{-8\pi \omega (M-D)}}\right] I_2. \end{aligned}$$

Employing Eq. (16), the analytic expression of the \(A \rightarrow B\) Gaussian steering is found to be

$$\begin{aligned} {{\mathcal {G}}}^{A \rightarrow B}(\sigma _{AB})=\max \left\{ 0,\, \ln {\frac{\cosh (2s)\left( 1-e^{-8(M-D)\pi \omega }\right) }{1+e^{-8(M-D)\pi \omega }\cosh (2s) }}\right\} . \end{aligned}$$
(21)

From Eq. (21), we can see that the \(A \rightarrow B\) Gaussian steerability depends not only the squeezing parameter s, but also the mass and dilaton charge of the black hole.

To check if the quantum steerability is symmetric in the GHS black hole, we define the Gaussian steering asymmetry

$$\begin{aligned} {{\mathcal {G}}}^{\Delta }_{AB}=\left| {{\mathcal {G}}}^{B \rightarrow A}-{{\mathcal {G}}}^{A \rightarrow B} \right| , \end{aligned}$$
(22)

where the \({{\mathcal {G}}}^{B \rightarrow A}\) for the state Eq. (20) is found to be

$$\begin{aligned} {{\mathcal {G}}}^{B \rightarrow A}(\sigma _{AB})=\max \big \{0,\, \ln {\frac{\cosh (2s)+e^{-8(M-D)\pi \omega }}{1+e^{-8(M-D)\pi \omega }\cosh (2s) }}\big \}. \end{aligned}$$
(23)
Fig. 1
figure 1

The Gaussian quantum steerability \({{\mathcal {G}}}^{A \rightarrow B}\)(left) and \({{\mathcal {G}}}^{B \rightarrow A}\)(right) are functions of the dilaton parameter D of the GHS dilaton black hole and the frequency \(\omega \) of the field. The initial squeezing parameter and mass parameter are fixed as \(s=1\) and \(M=1\)

Full size image

In Fig. 1, we plot the steerability \({{\mathcal {G}}}^{A \rightarrow B}\) and \({{\mathcal {G}}}^{B \rightarrow A}\) as a function of the dilaton charge D and the frequency \(\omega \) under the fixed conditions of the squeezing parameter \(s=1\) and the black hole mass \(M=1\). It is found that as the dilaton charge D increases, both the \(A\rightarrow B\) and \(B\rightarrow A\) steering decrease rapidly. This means that the gravity induced by the dilaton field will destroy the steerability between the initially modes. It is interesting to note that the \(A\rightarrow B\) steering suffers from a “sudden death” (the white line), while the \(B\rightarrow A\) steering smoothly reduce to zero as the dilaton charge D approaches the mass M of the black hole. We know that quantum steering is one kind of necessary quantum resource for quantum information processing tasks by employing one-side trusted devices. For example, Branciard et al. used it for one-sided device-independent quantum key distribution [40]. The existence of quantum steering would assure the performance of one-way quantum information tasks. Therefore, the “sudden death” and “sudden birth” of quantum steering indicates a sudden change revulsion quantum channel near the event horizon of the GHS dilaton black hole. This is quite different from the behavior of quantum entanglement in the same spacetime because the latter decays to zero only in the limit of \(D\rightarrow M\) [16], which corresponds to an extreme black hole. Here we find that under the influence of dilaton charge, the quantum steering between Alice and Bob will “sudden death”, which is in contrast with entanglement results. That is to say, quantum steering is less robust than entanglement under the influence of spacetime effects and it is always asymmetric near the event horizon of a GHS dilaton black hole.

Fig. 2
figure 2

The Gaussian steerability asymmetry between A and B as a function of the dilaton parameter D and the frequency \(\omega \) in the GHS dilaton spacetime. The initial squeezing parameter and mass parameter are fixed as \(s=1\) and \(M=1\), respectively

Full size image

To check the degree of steerability asymmetry in the GHS dilaton black hole, the Gaussian steerability asymmetry defined Eq. (22) is calculated. In Fig. 2 we plot the Gaussian steerability asymmetry between Alice and Bob as a function of the dilaton parameter D and frequency \(\omega \). At the beginning, the steerability asymmetry is zero, which verifies the fact \({{\mathcal {G}}}^{A \rightarrow B}={{\mathcal {G}}}^{B \rightarrow A}\) at this moment. We find that the steerability asymmetry between Alice and Bob increases with the increase of D, which means that the gravity induced by dilaton field generates steerability asymmetry. When D increases to a critical point s = arccosh\((\frac{1}{1-2e^{-8\pi \omega (M-D)}})\), the steerability asymmetry begins to decrease. Obviously, when D approaches this certain critical point, the asymmetry of Alice and Bob’s steerability reaches its maximum value, which is also the condition for the “sudden death” of \(A\rightarrow B\) steerability in Fig. 1a. In other words, when the state is unsteerable in the direction of \(A\rightarrow B\), the steerability asymmetry takes the maximum value. This situation indicates that the system has experiences a transition from two-way steerable to one-way steerable.

4.2 Generating quantum steerability between the initially uncorrelated modes

In this subsection, we study the dynamics of quantum steering between mode B and mode \({\bar{B}}\). The covariance matrix between the observer Bob outside the GHS dilaton black hole, and the observer anti-Bob inside the event horizon, is obtained by tracing over the mode A

$$\begin{aligned} \sigma _{B{\bar{B}}}(s,r) = \left( {\begin{array}{*{20}{c}} \mathcal {A}_{B{\bar{B}}} &{}\quad \mathcal {C}_{B{\bar{B}}} \\ {{\mathcal {C}_{B{\bar{B}}}^\mathsf{T}}} &{}\quad \mathcal {B}_{B{\bar{B}}} \\ \end{array}} \right) , \end{aligned}$$
(24)

where

$$\begin{aligned} \mathcal {A}_{B{\bar{B}}}= & {} \left[ \frac{e^{-8\pi \omega (M-D)}+\cosh (2s)}{1-e^{-8\pi \omega (M-D)}}\right] I_2, \\ \mathcal {C}_{B{\bar{B}}}= & {} \left[ \frac{2e^{-4\pi \omega (M-D)}\cosh ^2(s)}{1-e^{-8\pi \omega (M-D)}}\right] Z_2, \end{aligned}$$

and

$$\begin{aligned} \mathcal {B}_{B{\bar{B}}}=\left[ \frac{1+e^{-8\pi \omega (M-D)}\cosh (2s)}{1-e^{-8\pi \omega (M-D)}}\right] I_2. \end{aligned}$$

Using the Eq. (24), we can calculate the expressions for the \(B \rightarrow {\bar{B}}\) and \({\bar{B}} \rightarrow B\) steering, which are found to be

$$\begin{aligned} {{\mathcal {G}}}^{B \rightarrow {\bar{B}}} = \max \left\{ 0,\, \ln {\frac{1+sech(2s)e^{-8(M-D)\pi \omega }}{1 -e^{-8(M-D)\pi \omega } }}\right\} , \end{aligned}$$
(25)

and

$$\begin{aligned} {{\mathcal {G}}}^{{\bar{B}} \rightarrow B} = \max \left\{ 0,\, \ln {\frac{sech(2s)+e^{-8(M-D)\pi \omega }}{1 -e^{-8(M-D)\pi \omega } }}\right\} , \end{aligned}$$
(26)

respectively.

Fig. 3
figure 3

The Gaussian quantum steerability \({{\mathcal {G}}}^{B \rightarrow {\bar{B}}}\)and \({{\mathcal {G}}}^{{\bar{B}} \rightarrow B}\) as a function of the dilaton parameter D of the GHS dilaton black hole. The initial squeezing parameter, mass parameter and frequency \(\omega \) are fixed as \(s=1\), \(M=1\) and \(\omega =0.5\) respectively

Full size image

In Fig. 3 we plot the Gaussian quantum steerability between Bob and anti-Bob as a function of the dilaton parameter D. It is shown that there is no quantum steering between Bob and anti-Bob at the beginning, at which time \({{\mathcal {G}}}^{B \rightarrow {\bar{B}}}={{\mathcal {G}}}^{{\bar{B}} \rightarrow B}=0\). As the increase of the dilaton parameter D, the quantum steerability is generated between Bob and anti-Bob, which means that the gravity induced by dilaton field generates steering-type quantum correlations between the causally disconnected regions. In other words, Bob and anti-Bob can steer each other’s state by local measurements even though they are separated by the event horizon. Again, it is worthy to find that the \({{\mathcal {G}}}^{B \rightarrow {\bar{B}}}\) steering smoothly increase with increasing dilaton charge, while the \({{\mathcal {G}}}^{{\bar{B}} \rightarrow B}\) appears a “sudden birth” behavior under the influence of dilaton gravity.

It is worth to note that the maximizing condition for the \(\sigma _{B {\bar{B}}}\) steering asymmetry is s = arccosh\((\frac{1}{1-2e^{-8\pi \omega (M-D)}})\), too. This condition is in fact the one when the \(A \rightarrow B\) steering appears “sudden death” in Fig. 1a. In other words, the steering asymmetry is maximal when the steering appears “sudden death”. Therefore the appearance of “sudden death” of steering indicates the transition between one-way steerable and both-way steerable for the two-mode Gaussian state under the influence of dilaton charge. Again, the maximal steering asymmetry for the state \(\sigma _{B {\bar{B}}}\) is obtained when the \({\bar{B}} \rightarrow B\) steering appears “sudden birth” in Fig. 3. Then we arrive at the conclusion that the steering asymmetry is maximal when the steering appears “sudden death” and “sudden birth”.

Fig. 4
figure 4

The Gaussian steerability asymmetry between B and \({\bar{B}}\) as a function of the dilaton parameter D. The initial squeezing parameter, mass parameter and frequency \(\omega \) are fixed as \(s=1\), \(M=1\) and \(\omega =0.5\) respectively

Full size image

In Fig. 4, we plot the Gaussian steerability asymmetry between B and \({\bar{B}}\) as a function of the dilaton parameter D in the GHS black hole. It is found that the steerability asymmetry between B and \({\bar{B}}\) is also generated by the gravity of dilaton charge. Although the steering between Alice and Bob is a monotonic decreasing function of D while the steering between B and \({\bar{B}}\) is a monotonic increasing function of D, their asymmetry appears the same asymmetric behavior. Interestingly, the maximum steering asymmetry between Bob and anti-Bob is exactly the same as the steering asymmetry between Alice and Bob. In addition, both of the steering asymmetries disappear in the limit of \(D=M\). In this case, the steerabilities between Bob and anti-Bob take the maximum, while the steerability between Alice and Bob disappears completely. This means that the quantum correlations have been entirely distributed to the regions across the event horizon. That is, even if the two regions are causally disconnected, Bob and anti-Bob can steer each other, which proves that the quantum steering is a nonlocal quantum correlation.

5 Conclusions

In this work, we study the distribution and asymmetry of Gaussian quantum steering in the background of a GHS dilaton black hole. We give a phase space description for the evolution of quantum states in the GHS spacetime. It is shown that the steering between Alice and Bob is a monotonic decreasing function of the dilaton charge while the steering between Bob and anti-Bob monotonically increased. In addition, the steering between Alice and Bob suffers from a “sudden death” before the dilaton charge approaches the mass of the black hole. This means that the gravity induced by dilaton field can destroy the steering of the initial state but it generates steering-type quantum correlations between the causally disconnected regions at the same time. It is found that the steering from anti-Bob to Bob experiences as “sudden birth” with the increases of dilaton field, which is quite different from the behaviors of entanglement in the same spacetime background [40]. It is nontrivial to find that the steering is always asymmetric and the maximum steering asymmetry is obtained at the same critical point s = arccosh\((\frac{1}{1-2e^{-8\pi \omega (M-D)}})\) both for the \(A \rightarrow B\) and \({\bar{B}} \rightarrow B\) steering. In addition, the peaks of steering asymmetry are attained when the \(A \rightarrow B\) steering suffers a “sudden death” or the \({\bar{B}} \rightarrow B\) steering experiences a “sudden birth”. That is to say, the attainment of maximal steering asymmetry indicates a critical point between the two-way and one-way steerable in the GHS spacetime.