Nonlinear corrections on the parametrization methods

Abstract

We present nonlinear corrections (NLCs) to the distribution functions at low values of x and $Q^{2}$ using the parametrization $F_{2}(x,Q^{2})$ and $F_{L}(x,Q^{2})$. We use a direct method to extract nonlinear corrections to the ratio of structure functions and the reduced cross section in the next-to-next-to-leading order (NNLO) approximation with respect to the parametrization method (PM). Comparisons between the nonlinear results with the bounds in the color dipole model (CDM) and HERA data indicate the consistency of the nonlinear behavior of the gluon distribution function at low x and low $Q^{2}$. The nonlinear longitudinal structure functions are comparable with the H1 Collaboration data in a wide range of $Q^{2}$ values. Consequently, the nonlinear corrections at NNLO approximation to the reduced cross sections at low and moderate $Q^{2}$ values show good agreement with the HERA combined data. These results at low x and low $Q^{2}$ can be applied to the LHeC region for analyses of ultra-high-energy processes.

1 Introduction

Based on the parton model and perturbative quantum chromodynamics (pQCD), the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution equations [1,2,3,4] successfully and quantitatively interpret the $Q^{2}$ dependence of parton distribution functions (PDFs). The small-x behavior due to DGLAP equations is driven by input distributions at a starting scale $Q=Q_{0}$. In recent years, several different parametrizations of the PDF from a global fit to the available data have been introduced [5,6,7,8]. PDF groups, such as Refs.[5,6,7], analyze HERA data [9] in their global analysis. Recently, in Ref. [8], the authors presented PDFs using a wide variety of high-precision Large Hadron Collider (LHC) data in addition to the combined HERA I + II deep inelastic scattering data set. LHC covered a data sample of over $140~ \mathrm {fb}^{-1}$ at the $13~ \mathrm {TeV}$ run for both ATLAS and CMS collaborations. The CT global analyses [8] explored a broad range of parametric forms for the parton distribution functions at the starting scale, $Q=Q_{0}$. In CT18, the initial non-perturbative parametrizations are written in the following formal form

$$\begin{aligned} f_{i}(x,Q_{0})=\alpha _{0}x^{\alpha _{1}-1}(1-x)^{\alpha _{2}}P_{i}(y,\alpha _{3},\alpha _{4},\ldots ), \end{aligned}$$

where the coefficients $\alpha _{1}$ and $\alpha _{2}$ control the asymptotic behavior of $f_{i}(x,Q_{0})$ in the limits $x{\rightarrow }0$ and 1, and $P_{i}$ is a sum of Bernstein polynomials dependent on $y=f(x)$ which is very flexible across the whole interval $0<x<1$.

At an extremely small value of the Bjorken variable x, the pQCD evolution provides a rather singular behavior of the PDFs which strongly violates the Froissart boundary [10]. With respect to HERA data, some new parametrizations of the proton structure function have been proposed by authors in Refs. [11, 12] in a wide range of $Q^{2}$ values which are in a full accordance with the Froissart predictions. These parametrizations are relevant in investigations of ultra-high-energy processes, such as scattering of cosmic neutrinos off hadrons. The importance of ultra-high energies is in exploring extreme regions of the $(Q^{2}, x)$ phase space, where non-accelerator data exist [13, 14]. Studies about energy boosting not only confirm HERA investigations but also provide crucial benchmarks for further investigations of the high-energy limit of QCD at the Large Hadron Electron Collider (LHeC) [15] The kinematic extension of the LHeC will allow us to examine the nonlinear dynamics at low x [16,17,18]. The nonlinear region is approached when the reaction is mediated by multi-gluon exchange. Indeed, the gluon–gluon recombination processes cause the growth of the gluon density to slow down at smaller values of x and $Q^{2}$ (but still $Q^{2}{\gg }\Lambda ^{2}_{QCD}$) [19,20,21,22]. In this region, gluon recombination terms, which lead to nonlinear corrections to the evolution equations, can become significant. Gluon recombination in deep inelastic and diffractive scattering were reported some time ago in Refs. [22, 23], respectively. The gluon density cannot grow forever because hadronic cross sections comply with the unitary bound known as the Froissart bound [10]. Indeed, the unitarity (or Froissart bound states) does not grow faster than $\sigma <\pi d^{2}\ln ^{2}(s/s_{0})$ where d is some typical hadronic scale, and s is the Mandelstam variable denoting the square of the total invariant energy of the process. The gluon recombination effects tame the growth of the gluon density towards low x. These effects induce nonlinear power corrections to the DGLAP equations. Some studies of the nonlinear behavior of PDFs have been given in Refs. [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] in recent years.

Low-x physics at the LHeC and Future Circular Collider hadron-electron (FCC-he) is an area for discovery of nonlinear effects. This extends the kinematic reach, of maximum $Q^{2}{\simeq }1~\mathrm {TeV}^{2}$ and $x{\propto }Q^{2}/s{\simeq }~10^{-5\cdots -6}$ for LHeC and $10^{-7}$ for the FCC-he , where parton interaction must to become nonlinear. The extended kinematic range of the LHeC provides unique avenues to explore the possible onset of nonlinear QCD dynamics at small x [15,16,17,18]. In Ref. [44], PDF4LHC15 includes HERA data down to $x{\simeq }~10^{-4}$ which is successfully described via the DGLAP framework.

The nonlinear evolution in high-density QCD is considered in a shock wave color field of the target in Ref. [45]. The authors have considered deeply inelastic scattering at very high energies in the saturation regime and have developed a formalism which allows successive evaluation of the nonlinearities in the generalized evolution equation for the dipole densities. In Ref. [46], the authors have discussed the results of the analytical and numerical analysis of the nonlinear Balitsky–Kovchegov equation. One of the important outcomes studied in Ref. [46] is the existence of the saturation scale $Q_{s}(x)$ which is a characteristic scale at which the parton recombination effects become important. The solution to the nonlinear equation has the property of geometric scaling in the regime where $k<Q_{s}(x )$, whereas in the case when $k>Q_{s}(x)$, the solution enters the linear regime, where k is the gluon transverse momenta. The phenomenological implications of the parton distribution function sets with small-x resummation for the longitudinal structure function $F_{L}$ at HERA have been investigated in Refs. [47, 48]. Also, a resolution of incorporating the $\ln (1/x)$-resummation terms into the HERA PDF fits has been investigated using the xFitter program. Authors in Ref. [49] have tried to investigate solutions of the nonlinear evolution equation in the non-perturbative part of the low-x region.

The nonlinear terms have been calculated by Gribov–Levin– Ryskin (GLR) and Mueller–Qiu (MQ) in [50, 51]. GLR originally showed how to qualitatively modify the DGLAP gluon evolution equation in order to incorporate effects of gluon recombination Then, MQ derived the singlet evolution equation for the conversion of gluon to quarks. The modified evolution equations, due to the fusion of two gluon ladders, are denoted as the GLR-MQ equations

$$\begin{aligned} \frac{\partial {xg(x,Q^{2})}}{\partial {\ln }Q^{2}}= & {} \frac{\partial {xg(x,Q^{2})}}{\partial {\ln }Q^{2}}|_\mathrm{DGLAP}\nonumber \\&-\frac{81}{16}\frac{\alpha _{s}(Q^{2})}{{\mathcal {R}}^{2}Q^{2}}\int _{\chi }^{1}\frac{\mathrm{d}z}{z}\left[ \frac{x}{z}g\left( \frac{x}{z},Q^{2}\right) \right] ^{2}, \end{aligned}$$

(1)

and

$$\begin{aligned} \frac{\partial {F_{2}(x,Q^{2})}}{\partial {\ln }Q^{2}}= & {} \frac{\partial {F_{2}(x,Q^{2})}}{\partial {\ln }Q^{2}}|_\mathrm{DGLAP}\nonumber \\&-\frac{5}{18}\frac{27\alpha _{s}(Q^{2})}{160{\mathcal {R}}^{2}Q^{2}}[xg(x,Q^{2})]^{2}, \end{aligned}$$

(2)

where $g(x,Q^{2})$ is the gluon density, and $xg(x,Q^{2})=G(x,Q^{2})$ is the gluon density momentum. Here, $\chi =\frac{x}{x_{0}}$, and $x_{0}$ is the boundary condition that the gluon distribution (i.e., $G(x,Q^{2})$) joints smoothly onto the linear region. The correlation length ${\mathcal {R}}$ determines the size of the nonlinear terms. This value depends on how the gluon ladders are coupled to the nucleon or on how the gluons are distributed within the nucleon. The ${\mathcal {R}}$ is approximately equal to $\simeq 5~\mathrm {GeV}^{-1}$ if the gluons are populated across the proton, and it is equal to $\simeq 2~\mathrm {GeV}^{-1}$ if the gluons have a hotspot-like structure. Here, the higher-dimensional gluon distribution(i.e., higher twist) is assumed to be zero. In the small-x region, the saturation scale $Q_{s}^{2}(x)$ ($Q_{s}^{2}=Q_{0}^{2}(x/x_{0})^{-\lambda }$ where $Q_{0}$ and $x_{0}$ are free parameters) indicates the saturation limit where the DGLAP and GLR-MQ terms in the nonlinear equation become equal and is usually defined as [13, 14, 52]

$$\begin{aligned}&\frac{\partial {xg(x,Q^{2})}}{\partial {\ln }Q^{2}}|_{Q^{2}=Q^{2}_{s}(x)}=0\quad \mathrm {and}\\&\frac{\partial {xS(x,Q^{2})}}{\partial {\ln }Q^{2}}|_{Q^{2}=Q^{2}_{s}(x)}=0, \end{aligned}$$

where $xS(x,Q^{2})$ is the sea quark distribution. At $Q^{2}>Q^{2}_{s}(x)$, the linear DGLAP part in the region of applicability of the DGLAP+GLRMQ is dominant, and at $Q^{2}<Q^{2}_{s}(x)$, the GLRMQ terms dominant as all nonlinear terms become important, or equivalently,

$$\begin{aligned} \frac{\text {nonlinear \,terms}}{\mathrm {linear\,terms}}|_{Q^{2}=Q^{2}_{s}(x)}=1. \end{aligned}$$

This balances the linear and nonlinear splitting effects at $Q^{2}=Q^{2}_{s}(x)$.

This paper is organized as follows. In the next section, the theoretical formalism is presented, including the nonlinear evolution and the parametrization models. In Sect. 3, we present a detailed numerical analysis and our main results. We then confront these results with the CDM bounds and the HERA data at low values of $Q^{2}$. In the last section, we summarize our main conclusions and remarks.

2 Theoretical formalism

The structure function $F_{2}$ is expressed through the quark and gluon densities as

$$\begin{aligned} F_{2}(x,Q^{2})= & {} B_{2,s}(x,Q^{2}){\otimes }F_{2}^{s}(x,Q^{2})\nonumber \\&+<e^{2}>B_{2,g}(x,Q^{2}){\otimes }xg(x,Q^{2}), \end{aligned}$$

(3)

where $B_{2,a}(a=s,g)$ are the common Wilson coefficient functions, and the symbol ${\otimes }$ denotes a convolution according to the usual prescription, $f(x){\otimes }g(x)=\int _{x}^{1}\frac{\mathrm{d}y}{y}f(y)g(\frac{x}{y})$. Here, using the fact that the non-singlet contribution can be ignored safely at low values of x, the DGLAP evolution equations can be written as

$$\begin{aligned} \frac{{\partial }F_{2}^{s}(x,Q^{2})}{{\partial }{\ln }Q^{2}}= & {} -\frac{a_{s}(Q^{2})}{2}\left[ \left( P_{ss}^{(0)}(x) +a_{s}(Q^{2}){\widetilde{P}}_{ss}^{(1)}(x)+\cdots \right) \right. \nonumber \\&\left. {\otimes }F_{2}^{s}(x,Q^{2}) +<e^{2}>\left( P_{sg}^{(0)}(x)\right. \right. \nonumber \\&\left. \left. +a_{s}(Q^{2}){\widetilde{P}}_{sg}^{(1)}(x) +\cdots \right) {\otimes }xg(x,Q^{2})\right] ,\nonumber \\ \frac{{\partial }xg(x,Q^{2})}{{\partial }{\ln }Q^{2}}= & {} -\frac{a_{s}(Q^{2})}{2}\left[ <e^{2}>^{-1}\left( P_{gs}^{(0)}(x) +a_{s}(Q^{2})\right. \right. \nonumber \\&\left. \left. {\times } {\widetilde{P}}_{gs}^{(1)}(x) +\cdots \right) {\otimes }F_{2}^{s}(x,Q^{2})\right. \nonumber \\&\left. +\left( P_{gg}^{(0)}(x) +a_{s}(Q^{2}){\widetilde{P}}_{gg}^{(1)}(x)+\cdots \right) \right. \nonumber \\&\left. {\otimes }xg(x,Q^{2})\right] , \end{aligned}$$

(4)

where

$$\begin{aligned} {\widetilde{P}}_{ab}^{(n)}(x)={P}_{ab}^{(n)}(x)+[B_{2,s}+B_{2,g}+\cdots ]\otimes {P}_{ab}^{(0)}(x)+\cdots . \end{aligned}$$

The quantities of ${\widetilde{P}}_{ab}^{}$ are expressed via the known splitting and Wilson coefficient functions in Refs. [53,54,55,56], and $P_{ab}$ is the splitting functions in [57, 58]. The running coupling in the high-loop corrections of the above equation is expressed entirely thorough the variable $a_{s}(Q^{2})$ where $a_{s}(Q^{2})=\frac{\alpha _{s}(Q^{2})}{4\pi }$. Also, $<e^{k}>$ is the average of the charge $e^{k}$ for the active quark flavors, $<e^{k}>=n_{f}^{-1}\sum _{i=1}^{n_{f}}e_{i}^{k}$.

In perturbative QCD, the longitudinal structure function in terms of the coefficient functions at small x is given by [59]

$$\begin{aligned} F_{L}(x,Q^{2})= & {} C_{L,q}(\alpha _{s},x){\otimes }F_{2}^{s}(x,Q^{2})\nonumber \\&+<e^{2}>C_{L,g}(\alpha _{s},x){\otimes }xg(x,Q^{2}), \end{aligned}$$

(5)

where the coefficient functions can be written as [60]

$$\begin{aligned} C_{L,a}(\alpha _{s},x)=\sum _{n=1}a_{s}(Q^{2})^{n}c_{L,a}^{n}(x), \end{aligned}$$

(6)

and n is the order in the running coupling.

The proton structure function is parametrized in Refs. [11, 12] with a global fit function to the ZEUS data and to combined HERA data, respectively, for $F_{ 2}(x,Q^{2})$ in a wide range of $Q^{2}$ at $x< 0.1$ as

$$\begin{aligned} F_{ 2} (x,Q^{2})= & {} (1- x)\left[ \frac{F_{P}}{1 -x_{P}} + A(Q^{2})\ln \left( \frac{x_{P}}{ x}\frac{1 - x}{ 1 - x_{P}}\right) \right. \nonumber \\&\left. +B(Q^{2}) \ln ^{2}\left( \frac{x_{P}}{ x}\frac{1 - x}{ 1 - x_{P}}\right) \right] . \end{aligned}$$

(7)

Here, $x_{P}$ is an approximate fixed point observed in the data where curves of $F^{p}_{2}(x,Q^{2})$ for different $Q^{2}$ cross. Also,

$$\begin{aligned} A(Q^{2}) = a_{0} + a_{1} {\ln }Q^{2} + a_{2} {\ln }^{2} Q^{2}, \end{aligned}$$

and

$$\begin{aligned} B(Q^{2}) = b_{0} + b_{1} {\ln }Q^{2} + b_{2} {\ln }^{2} Q^{2}. \end{aligned}$$

The fitted parameters are tabulated in Table 1. In terms of the measured structure function $F_{2}(x,Q^{2})$ (i.e., Eq. (7)), the gluon distribution function is determined due to the Laplace transform method in Ref. [11]. In the case of four massless quarks, the gluon distribution function is obtained with a quadratic expression in both $\ln {Q^{2}}$ and $\ln {(1/x)}$ for $0<x ~{\le }~ 0.06$ as

$$\begin{aligned} G(x,Q^{2})= & {} \frac{3}{5}\left[ -2.94-0.359~{\ln }Q^{2}-0.101~{\ln }^{2}Q^{2}\right. \nonumber \\&\left. +\left( 0.594-0.0792~{\ln }Q^{2}-0.000578~{\ln }^{2}Q^{2}\right) \right. \nonumber \\&\left. {\times }\ln (1/x)+(0.168+0.138~{\ln }Q^{2}\right. \nonumber \\&\left. +0.0169~{\ln }^{2}Q^{2})\ln ^{2}(1/x)\right] . \end{aligned}$$

(8)

Table 1 The effective parameters at low x for $0.11~\mathrm {GeV}^{2}<Q^{2}<1200~\mathrm {GeV}^{2}$ are defined by the following values

In Refs. [61,62,63], the behavior of the longitudinal structure function due to the Mellin transform and Regge theory have been considered respectively. The authors in Refs. [61, 62] obtained analytical relations for the longitudinal structure function at LO and NLO approximations in terms of the effective parameters of the parametrization of the proton structure function. With respect to the Mellin transform method, the LO and NLO longitudinal structure functions are obtained at low x by the following forms

$$\begin{aligned} F_{L}^{\mathrm {LO}}(x,Q^{2})= & {} (1- x)^{n}\sum _{m=0}^{2}C_{m}(Q^{2})L^{m}, \end{aligned}$$

(9)

where $L^{,}$s are the logarithmic terms, and

$$\begin{aligned} F_{L}^{\mathrm {NLO}}(x,Q^{2})= & {} \frac{1}{\left[ 1+\frac{1}{3}a_{s}(Q^{2})L_{C} ({\widehat{\delta }}^{(1)}_{sg}-{\widehat{R}}^{(1)}_{L,g})\right] }\nonumber \\&\times \left\{ \left[ 1-a_{s}(Q^{2}) ({\overline{\delta }}^{(1)}_{sg}-{\overline{R}}^{(1)}_{L,g})\right] F_{L}^{\mathrm {LO}}(x,Q^{2})\right. \nonumber \\&\left. -a^{2}_{s}(Q^{2})\left[ \frac{1}{3}{\widehat{B}}^{(1)}_{L,s}L_{A}+{\overline{B}}^{(1)}_{L,s}\right] F_{2}(x,Q^{2}) \right\} .\nonumber \\ \end{aligned}$$

(10)

The coefficient functions at LO and NLO approximations are summarized in Appendix A, and the effective parameters are defined in Table 2. Therefore, the parametrization of $\sigma _{r}(x,Q^{2})$ in terms of the Froissart-bounded parametrizations of $F_{2}(x,Q^{2})$ and $F_{L}(x,Q^{2})$ at LO and NLO approximations read as

$$\begin{aligned} \sigma _{r}^{(n)}(x,Q^{2})= & {} D(Q^{2})(1-x)^{\nu }\sum _{m=0}^{2}A_{m}(Q^{2})L^{m}\nonumber \\&-f(y)F_{L}^{(n)}(x,Q^{2}) \end{aligned}$$

(11)

where $f(y)={y^2}/{Y_{+}}$, $Y_{+}=1+(1-y)^2$ and $y=Q^{2}/{sx}$. The first- and second-order results (i.e., $n=1$ and 2) show the LO ($n=1$) and NLO ($n=2$) longitudinal coefficient functions. Recently, the nonlinear modification of the evolution of the gluon density at small x is considered in the leading order of perturbation theory in Ref. [64]. In Ref. [25], the important role of absorptive effects and power corrections in low-x DGLAP evolution are considered. These effects flat the behavior of the low-x gluon density which arises from the freezing of $\alpha _{s}$ at low $Q^{2}$ values. In the following, the extraction of the nonlinear corrections provides means for determining distribution functions and reduced cross sections at low x and low $Q^{2}$ values with respect to the phenomenological assumptions. In the following, these nonlinear modifications will be applied to the distribution functions at high-order corrections.

Table 2 The effective parameters used in Appendix A with respect to Eqs. (9) and (10) in Refs. [61, 62]

3 Results and discussions

The effects of nonlinear gluon corrections are obtained by solving the GLR-MQ equation (i.e., Eq. (1)) in standard form

$$\begin{aligned} \frac{\partial {G(x,Q^{2})}}{\partial {\ln }Q^{2}}= & {} \frac{\partial {G(x,Q^{2})}}{\partial {\ln }Q^{2}}|_\mathrm{DGLAP}\nonumber \\&-\frac{81}{16}\frac{\alpha _{s}(Q^{2})}{{\mathcal {R}}^{2}Q^{2}}\int _{\chi }^{1}\frac{\mathrm{d}z}{z}G^{2}\left( \frac{x}{z},Q^{2}\right) . \end{aligned}$$

(12)

By solving the above equation (i.e., Eq. (12)), the nonlinear corrections to the gluon distribution function (i.e., $G^{\mathrm {NLC}}(x,Q^{2})$ ) are obtained by the following form as

$$\begin{aligned}&G^{\mathrm {NLC}}(x,Q^{2})=G^{\mathrm {NLC}}(x,Q_{0}^{2})+\left[ G(x,Q^{2})-G(x,Q_{0}^{2})\right] \nonumber \\&\quad -\int _{Q_{0}^{2}}^{Q^{2}}\frac{81}{16}\frac{\alpha _{s}(Q^{2})}{{\mathcal {R}}^{2}Q^{2}}\int _{\chi }^{1}\frac{\mathrm{d}z}{z}G^{2}\left( \frac{x}{z},Q^{2}\right) d{\ln }Q^{2}\nonumber \\ \end{aligned}$$

(13)

where $G(x,Q^{2})$ and $G(x,Q_{0}^{2})$ are the unshadowed gluon distributions and obtained from the solutions to standard DGLAP equations determined through a fit to HERA data (according to Eq. (8)). We note that at $x{\ge }x_{0}(=10^{-2})$, the nonlinear corrections are negligible. At the initial scale $Q_{0}^{2}$, the low-x behavior of the nonlinear gluon distribution is assumed to be [52]

$$\begin{aligned} G^{\mathrm {NLC}}(x,Q_{0}^{2})= & {} G(x,Q_{0}^{2})\left\{ 1+\frac{27\pi {\alpha _{s}(Q_{0}^{2})}}{16{\mathcal {R}}^{2}Q_{0}^{2}}\theta (x_{0}-x)\right. \nonumber \\&\left. {\times }\left[ G(x,Q_{0}^{2})-G(x_{0},Q_{0}^{2})\right] \right\} ^{-1}. \end{aligned}$$

(14)

Indeed, authors in Ref. [52] impose shadowing corrections by modifying gluon density for $x<x_{0}$, where the leading shadowing approximation $g_\mathrm{sat}$ is the value of the gluon which would saturate the unitarity limit as $xg_\mathrm{sat}(x,Q^{2})=\frac{16{\mathcal {R}}^{2}Q^{2}}{27{\pi }\alpha _{s}(Q^{2})}$. The nonlinear correction to the longitudinal structure function is defined as

$$\begin{aligned} F^\mathrm{NLC}_{L}(x,Q^{2})&=C_{L,q}(\alpha _{s},x){\otimes }F_{2}^{s}(x,Q^{2})\nonumber \\&\quad +<e^{2}>C_{L,g}(\alpha _{s},x){\otimes }G^\mathrm{NLC}(x,Q^{2}). \end{aligned}$$

(15)

Therefore, the nonlinear correction to the reduced cross section is defined by

$$\begin{aligned} \sigma ^\mathrm{NLC}_{r}(x,Q^{2})= & {} F_{2}(x,Q^{2})-f(y)F^\mathrm{NLC}_{L}(x,Q^{2}). \end{aligned}$$

(16)

The analysis is performed in the ranges of $10^{-5}{\le }x{\le }10^{-2}$ and $1{\le }Q^{2}{\le }1000~\mathrm {GeV}^{2}$. The computed results of the nonlinear distribution functions are compared with the parametrization methods [11, 61, 62] and the experimental data [65,66,67].

Fig. 1

The linear and nonlinear gluon distribution function at $R=2~\mathrm {GeV}^{-1}$ for $Q^{2}=10, 30, 50$ and $100~\mathrm {GeV^{2}}$ with respect to the parametrization model [11] and GLR-MQ equation [50, 51], respectively

Fig. 2

The nonlinear gluon distribution function at $R=2~\mathrm {GeV}^{-1}$ and $n_{f}=4$ at $Q^{2}=1.9~\mathrm {GeV^{2}}$ compared with the power corrections arises from the freezing of the running coupling with $\mu _{0}^{2}=0$ and $1~\mathrm {GeV^{2}}$ [25]

In Fig. 1, the computed results of the nonlinear gluon distribution function are compared with the linear parametrization model [11]. This behavior is considered at $x<10^{-2}$ for $Q^{2}=10, 30, 50$ and $100~\mathrm {GeV^{2}}$ in the hotspot point where the value of this parameter is defined to be $R=2~\mathrm {GeV^{-1}}$ in this paper. In Fig. 2, we show the nonlinear results at an input $Q^{2}=1.9~\mathrm {GeV^{2}}$ in comparison with the absorptive corrections at low x and the power corrections at low $Q^{2}$ values in Ref. [25]. As can be observed in Fig. 2, the behavior of the gluon distribution is flat due to the freezing of $\alpha _{s}$ in comparison with the nonlinear behavior due to the parametrization model. The confinement effect is expected to modify the running of the QCD coupling $\alpha _{s}(Q^{2})$ to $\alpha _{s}(Q^{2}+\mu _{0}^{2})$ where $\mu _{0}$ is the factorization scale. The results are compared with $\mu _{0}^{2}=0$, corresponding to no effects of confinement, and with those obtained for $\mu _{0}^{2}=1~\mathrm {GeV}^{2}$ in Ref. [25].

Fig. 3

Results of the ratio $G(x,Q^{2})/F_{2}(x,Q^{2})$ at $Q^{2}=5, 100$ and $1000~\mathrm {GeV^{2}}$ vs. x obtained from a the linear and b the nonlinear parametrization model

In Fig. 3, we make a critical study of the ratio $G/F_{2}$ proposed in recent years [68,69,70,71,72] at linear and nonlinear corrections, which is frequently used to extract the gluon distribution from the proton structure function. The ratio $G/F_{2}$ is obtained at $Q^{2}=5, 100$ and $1000~\mathrm {GeV^{2}}$ at low values of x with respect to the nonlinear behavior of the gluon distribution function due to the parametrization model. As can be observed in Fig. 3, this ratio in a wide range of x and $Q^{2}$ values is dependent not only on $Q^{2}$ but also on x at linear and nonlinear corrections. A purely $Q^{2}$ or x independence of the ratio was found in Refs. [69,70,71,72] to be not global in general as compared with our results with respect to the parametrization model.

Fig. 4

The derivative $(\partial {F_{2}}/\partial {\ln }Q^{2})_{x}$ plotted as a function of $Q^{2}$ for fixed x compared with the H1 Collaboration data [65] as accompanied with total errors. The linear and nonlinear behaviors are obtained from the parametrization model

H1 Collaboration [65] shows that measurement of the derivative $(\partial {F_{2}}/\partial {\ln }Q^{2})_{x}$ has long been recognized as a powerful constraint of the gluon density and running coupling. For each bin of x, H1 Collaboration [65] shows that these derivatives are described by the function $b(x)+2c(x){\ln }Q^{2}$, while in the parametrization model, it described in terms of ${\ln }Q^{2}$ and ${\ln }x$ [11]. In Fig. 4, the linear and nonlinear behavior of the quantity $(\partial {F_{2}}/\partial {\ln }Q^{2})_{x}$ is considered and compared with the H1 Collaboration data [65] as accompanied with total errors. The nonlinear correction to the derivative $(\partial {F_{2}}/\partial {\ln }Q^{2})_{x}$ is performed due to the nonlinear gluon interaction effects in Eq. (2). The nonlinear behavior of the quantity is comparable with the H1 Collaboration data in comparison with the linear behavior at low x. The nonlinear effects can be tested at a superior statistical accuracy attainable at the LHeC and FCC-he.

Fig. 5

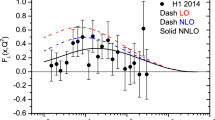
The nonlinear longitudinal structure function $F_{L}$ at NLO and NNLO approximations averaged over x at different $Q^{2}$. The average value of x for each $Q^{2}$ is given above each data point. The nonlinear results at NLO (solid) and NNLO (dashed) compared to the H1 Collaboration data [67] as accompanied with total errors, the parametrization model [61, 62] (dashed-dot) and CT18 [8] (dot) at the NNLO approximation at a fixed value of the invariant mass $W=230~ \mathrm {GeV}$

Fig. 6

Results of the ratio $F_{L}/F_{2}$ obtained from the nonlinear corrections at NNLO approximation at fixed $Q^{2}$ values. The ratio compared with the color dipole picture bounds (i.e., $F_{L}/F_{2}=1/3$ and 3/11), H1 Collaboration data [67] as accompanied with total errors, and the parametrization model [11, 61, 62]

In the following, we present the nonlinear results that have been obtained for the longitudinal structure function $F_{L}(x, Q^{2})$, the ratio $F_{L}(x, Q^{2})/F_{2}(x, Q^{2})$ and the reduced cross section $\sigma _{r}(x, Q^{2})$ from data mediated by the parametrization of $F_{2}(x, Q^{2})$. The results for the longitudinal structure function are presented in Fig. 5 and compared with the H1 data [67] as accompanied with total errors where the average x for each $Q^{2}$ is provided on the upper scale of the figure. We use the nonlinear longitudinal structure function at NLO and NNLO approximations where effects of the nonlinear corrections to the gluon distribution are taken into account. Nonlinear results at NLO and NNLO approximations are compared to the parametrization of $F_{L}$ at NLO approximation [61, 62] and also CT18 [8] at NNLO approximation (CT18 results have been obtained at a fixed value of the invariant mass W as $W=230~ \mathrm {GeV}$). In Fig. 6, the nonlinear correction to the ratio $F_{L}/F_{2}$ at NNLO approximation is calculated and presented. In this figure, the ratio of the structure functions are compared with the H1 Collaboration data [67]. The error bars of the ratio $F_{L}/F_{2}$ are determined by $\Delta ({\frac{F_{L}}{F_{2}}})=\frac{F_{L}}{F_{2}}\sqrt{ ({\frac{{\Delta }F_{L}}{F_{L}}})^{2}+({\frac{{\Delta }F_{2}}{F_{2}}})^2}$, where ${\Delta }F_{L}$ and ${\Delta }F_{2}$ are collected from the H1 experimental data in Ref. [67]. The nonlinear results obtained of the ratio $F_{L}/F_{2}$ are comparable to the results of the color dipole model bounds [73] and experimental data [67]. These comparisons are very good at low and high $Q^{2}$ values, even compared to the parametrization model [11, 61, 62]. The good agreement between the nonlinear correction at NNLO analysis and the experimental data indicates that these results have a bound asymptotic behavior and that they are compatible with the color dipole model bounds. As can be observed in Fig. 6, the ratio has little dependence on the x evolution.

Fig. 7

The NNLO predictions for the reduced DIS cross section at $Q^{2}=8.5$ and $18~\mathrm {GeV^{2}}$ available. The H1 data for some representative fixed values of $Q^{2}$ are taken from [66] as accompanied with total errors. The nonlinear corrections of the reduced cross section at NNLO approximation compared with the parametrization model

In Fig. 7, we present the nonlinear corrections to the reduced cross section at NNLO approximation at $Q^{2}=8.5$ and $18~\mathrm {GeV^{2}}$. As can be seen in this figure, one can conclude that the nonlinear corrections to the results essentially improve the good agreement with data in comparison with the parametrization model at low $Q^{2}$. HERA combined data [66] are taken with center of mass energy $\sqrt{s}=318~\mathrm {GeV}$ as accompanied with total errors. These low-x predictions are fully compatible with the H1 data presented in [66]. The nonlinear corrections are depicted and compared with the linear parametrization models in this figure. Consequently, the nonlinear corrections make it possible to perform the high-order corrections to the ultra-high-energy processes.

4 Summary

In conclusion, we have studied the effects of adding the nonlinear corrections to the distribution functions for transition from the linear to nonlinear regions. We use the parametrization of $F_{2}(x,Q^{2})$ and $F_{L}(x,Q^{2})$ as baselines. The nonlinear corrections to the distribution functions, to the derivative of the proton structure function, to the ratio of structure functions, and to the reduced cross sections at NNLO approximation are considered. Comparing these quantities with the parametrization and the color dipole models indicates that the nonlinear corrections are enriched by the behavior of distribution functions at low $Q^{2}$. The transition of the ratio $F_{L}/F_{2}$ from the linear to the nonlinear behavior is considered and shows that it is in good agreement with the color dipole model bounds not only at high $Q^{2}$ but also at low $Q^{2}$ values. Comparison of the reduced cross sections with respect to the nonlinear corrections with HERA data at low and moderate $Q^{2}$ values shows that this transition has been performed with good accuracy in comparison with the HERA combined data. It has been found that at low and moderated $Q^{2}$, NNLO results correspond to the experimental data and parametrization methods. The nonlinear method can be used in low x and low $Q^{2}$ at the LHeC project.

Appendix A

The coefficient functions read as

$$\begin{aligned} C_{2}= & {} {\widehat{A}}_{2}+\frac{8}{3}a_{s}(Q^{2})DA_{2}\nonumber \\ C_{1}= & {} {\widehat{A}}_{1}+\frac{1}{2}{\widehat{A}}_{2}\nonumber \\&+\frac{8}{3}a_{s}(Q^{2})D\left[ A_{1}+\left( 4\zeta _{2}-\frac{7}{2}\right) A_{2}\right] \nonumber \\ C_{0}= & {} {\widehat{A}}_{0}+\frac{1}{4}{\widehat{A}}_{2}\nonumber \\&-\frac{7}{8}{\widehat{A}}_{2}+\frac{8}{3}a_{s}(Q^{2})D\left[ A_{0} +\left( 2\zeta _{2}-\frac{7}{4}\right) A_{1}\nonumber \right. \\&\left. +\left( \zeta _{2}-4\zeta _{3}-\frac{17}{8}\right) A_{2}\right] , \end{aligned}$$

(17)

$$\begin{aligned} {\widehat{A}}_{2}= & {} {\widetilde{A}}_{2}\nonumber \\ {\widehat{A}}_{1}= & {} {\widetilde{A}}_{1}+2DA_{2}\frac{\mu ^{2}}{\mu ^{2}+Q^{2}}\nonumber \\ {\widehat{A}}_{0}= & {} {\widetilde{A}}_{0}+DA_{1}\frac{\mu ^{2}}{\mu ^{2}+Q^{2}}\nonumber \\ {\widetilde{A}}_{i}= & {} {\widetilde{D}}A_{i}+D{\overline{A}}_{i}\frac{Q^{2}}{Q^{2}+\mu ^{2}}\nonumber \\ {\widetilde{D}}= & {} \frac{M^{2}Q^{2}[(2-\lambda )Q^{2}+\lambda M^{2}]}{[Q^{2}+M^{2}]^{3}}\nonumber \\ {\overline{A}}_{m}= & {} a_{m1}+2a_{m2}L_{2},\quad a_{02}=0. \end{aligned}$$

(18)

and

$$\begin{aligned} {\widehat{B}}^{(1)}_{L,s}= & {} 8C_{F}\left[ \frac{25}{9}n_{f}-\frac{449}{72}C_{F}+(2C_{F}-C_{A})\nonumber \right. \\&\times \left. \left( \zeta _{3}+2\zeta _{2}-\frac{59}{72}\right) \right] \nonumber \\ {\overline{B}}^{(1)}_{L,s}= & {} \frac{20}{3}C_{F}(3C_{A}-2n_{f})\nonumber \\ {\widehat{\delta }}^{(1)}_{sg}= & {} \frac{26}{3}C_{A}\nonumber \\ {\overline{\delta }}^{(1)}_{sg}= & {} 3C_{F}-\frac{347}{18}C_{A}\nonumber \\ {\widehat{R}}^{(1)}_{L,g}= & {} -\frac{4}{3}C_{A}\nonumber \\ {\overline{R}}^{(1)}_{L,g}= & {} -5C_{F}-\frac{4}{9}C_{A}\nonumber \\ L_{A}= & {} L+\frac{A_{1}}{2A_{2}}\nonumber \\ L_{C}= & {} L+\frac{C_{1}}{2C_{2}}\nonumber \\ L= & {} \ln (1/x)+L_{1}\nonumber \\ L_{1}= & {} {\ln }\frac{Q^{2}}{Q^{2}+\mu ^{2}}\nonumber \\ L_{2}= & {} {\ln }\frac{Q^{2}+\mu ^{2}}{\mu ^{2}}\nonumber \\ A_{i}(Q^{2})= & {} \sum _{k=0}^{2}a_{ik}L_{2}^{k},\quad (i=1,2)\nonumber \\ A_{0}= & {} a_{00}+a_{01}L_{2}\nonumber \\ D= & {} \frac{Q^{2}(Q^{2}+\lambda M^{2})}{(Q^{2}+M^{2})^2}. \end{aligned}$$

(19)