1 Introduction

A new approach to General Relativity has been proposed by Chamseddine and Mukhanov in 2003, called mimetic gravity. The important property of their approach is that the conformal symmetry is respected as an internal degree of freedom [1]. Chamseddine and Mukhanov in their interesting proposal, have written the physical metric in terms of an auxiliary metric and a scalar field. In fact, the metric is given by

$$\begin{aligned} g_{\mu \nu }= -{\tilde{g}}^{\varrho \sigma }\,\phi _{,\varrho }\,\phi _{,\sigma } \,{\tilde{g}}_{\mu \nu }\,, \end{aligned}$$
(1)

where the free non-dynamical scalar field \(\phi \) encodes the conformal mode of the gravity. Also, the definition (1) shows that if we perform a Weyl transformation on the auxiliary metric (\({\tilde{g}}_{\mu \nu }\)), the physical metric (\(g_{\mu \nu }\)) remains invariant. Using the Eq. (1) gives the following constraint on the scalar field [1]

$$\begin{aligned} g^{\mu \nu }\phi _{,\mu }\phi _{,\nu }=-1\,. \end{aligned}$$
(2)

In the action of the mimetic gravity introduced in Ref. [1], there is a contribution of the matter fields coupled to \(g_{\mu \nu }\) that leads to an extra term in the Einstein’s field equations. In the sense that the dependence of this extra term to the scale factor is \(a^{-3}\), it is considered as a source of dark matter. The mimetic gravity scenario has been explored in another mathematical approach, by adding the Lagrange multipliers in the action of the theory [2, 3]. In Ref. [4], some ghost-free models of the mimetic gravity have been discussed. The authors of Ref. [5] have considered a potential for the mimetic field in a Lagrange multiplier approach, leading to some interesting results. In fact, they have shown that if we take the appropriate potential terms, it is possible to consider the mimetic field as inflaton, quintessence, or phantom fields. The mimetic gravity has attracted a lot of attention and the authors have extended it to the braneworld scenario [6], non-minimal coupling model [7, 8], f(G) gravity [9], Horndeski gravity [10, 11], f(R) theories [12,13,14], unimodular f(R) gravity [15] and Galileon gravity [16]. In studying the perturbations in mimetic gravity models, it is necessary to have the ghost and gradient instabilities-free models. In Ref. [17] it is shown that the direct coupling between the curvature of the space-time and the higher derivatives of the mimetic field can help to overcome such instabilities in some ranges of the parameters space. See the papers in Refs. [18,19,20,21,22,23,24,25,26,27,28,29,30] for more works on the (in)stability issue.

On the other hand, to solve some problems of the standard model of cosmology, the inflation paradigm has been introduced, where a single canonical scalar field (inflaton) with a flat potential has been considered. The flat potential causes the slow-roll of the inflaton and enough exponential expansion of the early universe. In this simple model, the dominant modes of the primordial perturbations are predicted to be scale-invariant, adiabatic and Gaussian [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. However, there is a lot of attention to the extended inflation models predicting the non-Gaussian distributed perturbations [46,47,48,49,50,51,52,53,54,55].

One interesting inflation model is the DBI (Dirac–Born–Infeld) inflation [56,57,58,59,60,61]. In the string based DBI model, where the radial position of a D3 brane characterizes the scalar field [56, 58], it is possible to have large non-Gaussianity that many authors are interested to [58,59,60,61,62,63,64,65,66,67]. Another string-based scalar field is the tachyon field [68, 69] which is an interesting scalar field in the inflation models [61, 70,71,72]. We have included the DBI and tachyon field in the mimetic models in our previous works. In Ref.  [73], we have assumed that the scalar field of the DBI model is a mimetic scalar field. By considering the Lagrange multiplier approach and assuming the power-law inflation, we have studied the inflation and perturbations in this model and shown that this model in some ranges of the model’s parameter space is free of the ghost and gradient instabilities. We have also shown that, in those ranges of the model’s parameter space, the values of the perturbations parameters are observationally viable. In fact, with the Mimetic DBI (MDBI) model, there is no need to consider such complicated higher-order terms in the action of mimetic gravity. In Ref.  [74], we have considered the tachyon field in the mimetic gravity setup and within the Lagrange multiplier approach. We have adopted both power-law and intermediate scale factors and studied the inflation in the tachyon mimetic model. We have shown that, in both cases, the mimetic model is free of instabilities in some ranges of the model’s parameters. Also, those ranges of the parameters that lead to instabilities free tachyon mimetic model, give observationally viable perturbation parameters.

In the continuation of the previous works, in this paper, we study other aspects of the MDBI model. Now, we consider the MDBI model with an intermediate scale factor [75,76,77] that gives another type of potential. In this regard, we show that the intermediate MDBI model also is an instabilities-free mimetic model that is consistent with observational data. Therefore, with this new work on the MDBI model, we prove that to have an instabilities-free mimetic model there is no need to restrict ourselves to one type of potential (or scale factor). The MDBI model is a simple mimetic model that gives a viable cosmological model with both power-law and intermediate scale factor (corresponding to two types of potential). This makes the MDBI model more favorable. Also, in this paper, we study the non-Gaussian features of the primordial perturbations that is one of the important issues in the inflationary models. The prediction of the intermediate MDBI model for the sound speed of the perturbations and also the amplitude of the perturbations in equilateral configuration is the issue that hasn’t been studied in the MDBI model previously.

This paper is organized as follows: in Sect. 2, we review the MDBI model in the Lagrange multiplier approach. In this section, we present the perturbation parameters (the scalar spectral index, the tensor spectral index, and the tensor-to-scalar ratio) that are functions of the Lagrange multiplier. The amplitude of the non-Gaussianity in the equilateral configuration is also presented in this section, which is related to the Lagrange multiplier via the sound speed of the model. In Sect. 3, we introduce the intermediate MDBI model where the scale factor is given by \(a=a_{0}\exp (bt^{\beta })\). By this scale factor, we find the Hubble parameter in terms of the intermediate parameters \(\beta \) and b. Then, by obtaining the potential and the Lagrange multiplier in terms of the Hubble parameter, we find the slow-roll parameters in the intermediate MDBI model. Also in this section, we study the model numerically and show that the intermediate MDBI model in some ranges of its parameter space is free of the ghost and gradient instabilities. In Sect. 4, by performing numerical analysis, we compare the results with Planck2018 observational data. In this regard, we show that the intermediate MDBI model for some values of \(\beta \) and b, which lead to the instabilities-free model, gives observationally viable values of the perturbation parameters. We also present some predictions of the model on the non-Gaussian feature of the primordial perturbations. In Sect. 5, we present a summary of our work.

2 Mimetic DBI model

The action of the DBI mimetic gravity, in the presence of the Lagrange multiplier and a potential term, is given by

$$\begin{aligned} S= & {} \int d^{4}x\sqrt{-g}\Bigg [\frac{R}{2\kappa ^{2}}-{{\mathcal {F}}}^{-1}(\phi )\sqrt{1+{\alpha }{{\mathcal {F}}}(\phi )\partial _{\nu }\phi \,\partial ^{\nu }\phi }\nonumber \\&+\lambda (g^{\mu \nu }\partial _{\mu }\phi \,\partial _{\nu }\phi +1)-V(\phi ) \Bigg ], \end{aligned}$$
(3)

where R is the Ricci scalar, \(V(\phi )\) presents the potential of the scalar field, \({{\mathcal {F}}}^{-1}(\phi )\) is the inverse brane tension (note that, the D3-brane passes a compact manifold which geometry of its throat is related to the \({{\mathcal {F}}}^{-1}(\phi )\)). Also, \(\kappa \) is the gravitational constant, defined as \(\kappa ^{2}=\frac{8\pi G}{c^{4}}\). The parameter \(\alpha \) is a coupling parameter which is corresponding to the string theory parameter. Although we adopt a DBI-like Lagrangian in our work, the scalar field \(\phi \) is not a DBI field. It is a mimetic field obeying the constraint (2). This means that its dimension is \([T]=[M]^{-1}\), demonstrating the dimension of time (note that we work in natural units where the speed of light is \(c=1\) and also \(\hbar =1\)). Since the action should be dimensionless, to have dimensional consistency, there should be a coupling parameter \(\alpha \) with dimension \([M]^4=[T]^{-4}\) in the Lagrangian term, as shown in Eq. (3). This parameter is corresponding to the string theory parameter presented in [56]. Also, \(\lambda \) is a Lagrange multiplier by which we enter the mimetic constraint (2) in the action.

If we vary action (3) with respect to the metric, we find the following Einstein’s field equations (\(G_{\mu \nu }=\kappa ^{2}T_{\mu \nu }\))

$$\begin{aligned} G_{\mu \nu }= & {} \kappa ^{2}\Bigg [-g_{\mu \nu }{{\mathcal {F}}}^{-1}\sqrt{1+{\alpha }{{\mathcal {F}}}\,g^{\mu \nu }\,\partial _{\mu }\phi \,\partial _{\nu }\phi }-g_{\mu \nu }V\nonumber \\&+g_{\mu \nu }\,\lambda \Big (g^{\mu \nu }\,\partial _{\mu }\phi \,\partial _{\nu }\phi +1\Big )-2\lambda \,\partial _{\mu }\phi \,\partial _{\nu }\phi \nonumber \\&+{\alpha }\partial _{\mu }\phi \,\partial _{\nu }\phi \Big (1+{{\mathcal {F}}}\,g^{\mu \nu }\,\partial _{\mu }\phi \,\partial _{\nu }\phi \Big )^{-\frac{1}{2}}\Bigg ]\,. \end{aligned}$$
(4)

By using the flat FRW metric as the background,

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)\delta _{ij}dx^{i}dx^{j}\,, \end{aligned}$$
(5)

the field equations (4) give the following Friedmann equations in this model

$$\begin{aligned}&3H^{2}=\kappa ^{2}\Bigg [\frac{{{\mathcal {F}}}^{-1}}{\sqrt{1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2}}}+V-\lambda \Big (1+{\dot{\phi }}^{2}\Big )\Bigg ]\,, \end{aligned}$$
(6)
$$\begin{aligned}&2{\dot{H}}+3H^{2}=\kappa ^{2}\Bigg [{{\mathcal {F}}}^{-1}\,\sqrt{1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2}}+V+\lambda \Big ({\dot{\phi }}^{2}-1\Big )\Bigg ]\,.\nonumber \\ \end{aligned}$$
(7)

The equation of motion of the mimetic field \(\phi \) in the MDBI model is obtained by varying the action (3) with respect to \(\phi \)

$$\begin{aligned}&\frac{{\alpha }\ddot{\phi }}{(1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2})^{\frac{3}{2}}}+\frac{3H{\alpha }{\dot{\phi }}}{(1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2})^{\frac{1}{2}}} -2\lambda \Big (\ddot{\phi }+3H{\dot{\phi }}\Big )\nonumber \\&\quad +V' -\lambda '(1-{\dot{\phi }}^{2})=-\frac{{{\mathcal {F}}}'}{{{\mathcal {F}}}^{2}} \Bigg [\frac{3{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2}-2}{2(1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2})^{\frac{1}{2}}}\Bigg ]\,. \end{aligned}$$
(8)

Also, by varying action (3) with respect to \(\lambda \) we reach the constraint (2).

In this paper, we are going to consider the MDBI setup as an inflation model. The slow-roll parameters in the inflation model are given by the following definitions

$$\begin{aligned} \epsilon \equiv -\frac{{\dot{H}}}{H^{2}}\,,\quad \eta \equiv \frac{1}{H}\frac{d \ln \epsilon }{dt}\,,\quad s\equiv \frac{1}{H}\frac{d \ln c_{s}}{dt}\,, \end{aligned}$$
(9)

where \(c_{s}\) is the sound speed of the perturbations, defined as \(c_{s}^{2}=\frac{P_{,X}}{\rho _{,X}}\) (the subscript “, X” shows derivative with respect to \(X=-\frac{1}{2}\partial _{\nu }\phi \,\partial ^{\nu }\phi \)). In our model, the square of sound speed is given by

$$\begin{aligned} c_{s}^{2}=\frac{{\alpha }\left( 1-{\alpha }{{\mathcal {F}}} {\dot{\phi }}^{2}\right) ^{-\frac{1}{2}}-2\lambda }{{\alpha }\left( 1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2}\right) ^{-\frac{3}{2}}-2\lambda }\,, \end{aligned}$$
(10)

which should satisfy the constraint \(0<c_{s}^{2}\le c^2\) (note that c is the local speed of light). In the case of \(c\equiv 1\), the constraint becomes as \(0<c_{s}^{2}\le 1\) [78, 79].

To seek the observational viability of the MDBI model, it is important to compare the values of the perturbation parameters with Planck2018 data [80, 81]. The Planck collaboration has considered that in the case of the statistical isotropy, the two-point correlations of the CMB anisotropies are described by the angular power spectra [82,83,84,85,86]. In fact, the following expressions for the contributions from the scalar and tensor perturbations in the CMB angular power spectra have been used [87]

$$\begin{aligned} C_{l}^{ab,s}= & {} \int _{0}^{\infty } \frac{dk}{k} \Delta _{l,a}^{s} (k) \, \Delta _{l,b}^{s} (k)\, {{\mathcal {A}}}_{s} (k)\,, \end{aligned}$$
(11)
$$\begin{aligned} C_{l}^{ab,T}= & {} \int _{0}^{\infty } \frac{dk}{k} \Delta _{l,a}^{T} (k) \, \Delta _{l,b}^{T} (k)\, {{\mathcal {A}}}_{T} (k)\,, \end{aligned}$$
(12)

where \(a,b=T,E,B\). Also, l is the multipole moment number, \(\Delta _{l,A}^{s}\) and \(\Delta _{l,A}^{T}\) are the transfer functions,Footnote 1 and \({{\mathcal {A}}}_{j}(k)\) (\(j=d,T\)) is the primordial power spectrum, identified by the physics of the primordial universe [87]. In one procedure to compare the inflationary parameters with data, the Planck collaboration has expanded the scalar and tensor power spectra in a model-independent form as [81, 87]

$$\begin{aligned}&{{\mathcal {A}}}_{s} (k)=A_{s}\left( \frac{k}{k_{*}}\right) ^{n_{s}-1+\frac{1}{2}\frac{dn_{s}}{d\ln k}\ln \big (\frac{k}{k_{*}}\big )+\frac{1}{6}\frac{d^{2}n_{s}}{d\ln k^{2}}\ln \big (\frac{k}{k_{*}}\big )^{2}+\cdots }\,, \end{aligned}$$
(13)
$$\begin{aligned}&{{\mathcal {A}}}_{T} (k)=A_{T}\left( \frac{k}{k_{*}}\right) ^{n_{T}+\frac{1}{2}\frac{dn_{T}}{d\ln k}\ln \big (\frac{k}{k_{*}}\big )+\cdots }\,, \end{aligned}$$
(14)

where, \(A_{j}\) is introduced as the amplitude of the scalar (for \(j=s\)) or tensor (for \(j=T\)) perturbations. Also, \(\frac{dn_{j}}{d\ln k}\) is the the running of the scalar (for \(j=s\)) or tensor (for \(j=T\)) spectral index and \(\frac{d^{2}n_{s}}{d\ln k^{2}}\) is the running of the running of the scalar spectral index. The ratio between the tensor and scalar amplitudes

$$\begin{aligned} r=\frac{{{\mathcal {A}}}_{T}(k_{*})}{{{\mathcal {A}}}_{s}(k_{*})}\,, \end{aligned}$$
(15)

is an important perturbation parameter, named tensor-to-scalar ratio.

To perform numerical analysis and compare the results with Planck2018 data, we should obtain the perturbation parameters in the MDBI model. The scale dependence of the scalar spectral index, at the time of sound horizon exit of the physical scales (\(c_{s}k=aH\)), is identified by

$$\begin{aligned} n_{s}-1=\frac{d \ln {{\mathcal {A}}}_{s}}{d\ln k}\Bigg |_{c_{s}k=aH}\,. \end{aligned}$$
(16)

Calculating the perturbation parameters at pivot scale \(k=k_{*}\) causes that the running term doesn’t appear in the definition (16). For the MDBI model, the amplitude of the scalar spectral index is given by [73]

$$\begin{aligned} {{\mathcal {A}}}_{s}=\frac{H^{2}}{8\pi ^{2}{{\mathcal {W}}}_{s}c_{s}^{3}}\,, \end{aligned}$$
(17)

where

$$\begin{aligned} {{\mathcal {W}}}_{s}=\frac{\left( {{\mathcal {F}}}\,{\alpha }\,{\dot{\phi }}^{2}\lambda \,\sqrt{1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2}}-\lambda \,\sqrt{1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2}}+{\alpha } \right) {\dot{\phi }}^{2}}{2{H}^{2} \left( 1-{\alpha }{{\mathcal {F}}}{\dot{\phi }}^{2} \right) ^{3/2}}\,. \end{aligned}$$
(18)

Positive values of \({{\mathcal {W}}}_{s}\) makes the model free of the ghost instability. Now, we find the scalar spectral index as follows

$$\begin{aligned} n_{s}=1-6\epsilon +2\eta -s\,, \end{aligned}$$
(19)

which is expressed in terms of the slow-roll parameters.

Equation (14) gives the following tensor spectral index

$$\begin{aligned} n_{T}=\frac{d \ln {{\mathcal {A}}}_{T}}{d\ln k}\Bigg |_{k=aH}\,. \end{aligned}$$
(20)

The parameter \({{\mathcal {A}}}_{T}\), the amplitude of the tensor perturbations, is given by

$$\begin{aligned} {{\mathcal {A}}}_{T}=\frac{2\kappa ^{2}H^{2}}{\pi ^{2}}\,, \end{aligned}$$
(21)

leading to

$$\begin{aligned} n_{T}=-2\epsilon \,. \end{aligned}$$
(22)

We can find the tensor-to-scalar ratio from Eqs.  (15) and (22) as follows

$$\begin{aligned} r=16\,c_{s}\,\epsilon \,, \end{aligned}$$
(23)

or

$$\begin{aligned} r=-8\,c_{s}\,n_{T}\,. \end{aligned}$$
(24)

Equation (24) is an important equation, named the consistency relation, which in the simple single filed inflation with a canonical scalar field simplifies to \(r=16\epsilon \).

To get more information about the viability of an inflation model, it is useful to study the non-Gaussian feature of the primordial perturbations. Although the two-point correlation characterizes the Gaussian perturbations, to get the additional statistical information related to the non-Gaussian distribution, we should consider three and higher-order correlations. In the interaction picture, the 3-point correlation for the spatial curvature perturbation \(\Psi \) is given by [46, 50, 90]

$$\begin{aligned} \langle {\Psi }(\mathbf{k }_{1})\,{\Psi }(\mathbf{k }_{2})\,{\Psi }(\mathbf{k }_{3})\rangle= & {} (2\pi )^{3}\delta ^{3}(\mathbf{k }_{1}+\mathbf{k }_{2}\nonumber \\&+\mathbf{k }_{3}){{\mathcal {B}}}_{\Psi }(\mathbf{k }_{1},\mathbf{k }_{2},\mathbf{k }_{3})\,, \end{aligned}$$
(25)

where

$$\begin{aligned} {{\mathcal {B}}}_{\Psi }(\mathbf{k }_{1},\mathbf{k }_{2},\mathbf{k }_{3})=\frac{(2\pi )^{4}{{\mathcal {A}}}_{s}}{\prod _{i=1}^{3} k_{i}^{3}}\, {{\mathcal {G}}}_{\Psi }(\mathbf{k }_{1},\mathbf{k }_{2},\mathbf{k }_{3})\,, \end{aligned}$$
(26)

and \({{\mathcal {A}}}_{s}\) is given by (17). The parameter \({{\mathcal {G}}}_{\Psi }\) in Eq. (26) is defined as

$$\begin{aligned} {{\mathcal {G}}}_{\Psi }=\frac{3}{4}\Bigg (1-\frac{1}{c_{s}^{2}}\Bigg ){{\mathcal {S}}}_{1}+\frac{1}{4}\Bigg (1-\frac{1}{c_{s}^{2}}\Bigg ){{\mathcal {S}}}_{2} +\frac{3}{2}\Bigg (\frac{1}{c_{s}^{2}}-1\Bigg ){{\mathcal {S}}}_{3}\,,\nonumber \\ \end{aligned}$$
(27)

where the shapes of the non-Gaussianity are given by

$$\begin{aligned} {{\mathcal {S}}}_{1}= & {} \frac{2}{K}\sum _{i>j}k_{i}^{2}\,k_{j}^{2}-\frac{1}{K^{2}}\sum _{i\ne j}k_{i}^{2}\,k_{j}^{3}\,, \end{aligned}$$
(28)
$$\begin{aligned} {{\mathcal {S}}}_{2}= & {} \frac{1}{2}\sum _{i}k_{i}^{3}+\frac{2}{K}\sum _{i>j}k_{i}^{2}\,k_{j}^{2}-\frac{1}{K^{2}}\sum _{i\ne j}k_{i}^{2}\,k_{j}^{3}\,, \end{aligned}$$
(29)
$$\begin{aligned} {{\mathcal {S}}}_{3}= & {} \frac{\left( k_{1}\,k_{2}\,k_{3}\right) ^{2}}{K^{3}}\,, \end{aligned}$$
(30)

and

$$\begin{aligned} K=k_{1}+k_{2}+k_{3}\,. \end{aligned}$$
(31)

Equation (26) shows that the three-point correlator depends on the three momenta \(k_{1}\) , \(k_{2}\) and \(k_{3}\). Note that these momenta should satisfy the translation and rotational invariance. By defining the following dimensionless parameter, called “nonlinearity parameter”,

$$\begin{aligned} f=\frac{10}{3}\frac{{{\mathcal {G}}}_{\Psi }}{\sum _{i=1}^{3}k_{i}^{3}}\,, \end{aligned}$$
(32)

we can measure the amplitude of the non-Gaussianity. The nonlinearity parameter depends on the shape of the non-Gaussianity. Different values of the momenta lead to different shapes and there is a maximal signal for each shape in a special configuration of the three momenta.

However, as has been demonstrated in Refs. [57, 91,92,93], for the k-inflation and higher-order derivative models, the maximal peak of the signal occurs at the equilateral configuration, where \(k_{1}=k_{2}=k_{3}\). In this regard, here also, we obtain the parameter \({{\mathcal {G}}}_{\Psi }\) in this configuration and at the leading-order as [57,58,59]

$$\begin{aligned} {{\mathcal {G}}}_{\Psi }^{equil}=\frac{17}{72}k^3\left( 1-\frac{1}{c_{s}^{2}}\right) \,, \end{aligned}$$
(33)

leading to the following nonlinearity parameter

$$\begin{aligned} f^{equil}=\frac{85}{324}\left( 1-\frac{1}{c_{s}^{2}}\right) \,. \end{aligned}$$
(34)

This equation is very important to explore the non-Gaussian feature of the primordial perturbations in an inflation model and compare with observational data.

In the following, we study the intermediate inflation in the MDBI model and perform some numerical analysis on this model.

3 Intermediate MDBI model

One of the interesting scenarios in inflation models is intermediate inflation. In the intermediate inflation, the scale factor evolves faster than the power-law inflation (\(a=t^{p}\)) but slower than the standard de Sitter inflation (\(a=\exp (Ht)\)) [75,76,77]. In fact, in the intermediate inflation the evolution of the scale factor is given by

$$\begin{aligned} a=a_{0}\,\exp \left( b\,t^{\beta }\right) \,, \end{aligned}$$
(35)

where b is a constant and \(0<\beta <1\). This scale factor leads to the following Hubble parameter

$$\begin{aligned} H(N)=N \left( {\frac{N}{b}} \right) ^{-{\frac{1}{\beta }}}\beta \,. \end{aligned}$$
(36)

To obtain the main perturbation parameters in the intermediate inflation, we should follow [94, 95] and find the potential in terms of the Hubble parameter and its derivatives. From now on, we assume \({{\mathcal {F}}}^{-1}(\phi )=V(\phi )\).

Note that, in Ref. [58], it has been demonstrated that for \(AdS_5\) throat, the warp factor \({{\mathcal {F}}}^{-1}(\phi )\) is equal to \(\frac{\varsigma }{\phi ^{4}}\). Also, in the case with \(AdS_5 \times X\) geometry, the potential of a DBI field is quartic. Another interesting case is clarified in Refs. [96, 97]. In those papers, the authors have shown that with \({{\mathcal {F}}}\sim e^{m\phi }\) and \(V\sim e^{-m\phi }\) (with m to be a constant), we can get the Lagrangian of the DBI model. Following Refs. [96, 97], we consider \({{\mathcal {F}}}^{-1}(\phi )=V(\phi )\) in our calculations. In fact, it is always possible to have viable DBI inflation with these choices of functions. However, in this paper, we construct the potential (and therefore, \({{\mathcal {F}}}\)) for intermediate inflation from background equations. In this way, there is no need to choose an arbitrary function for V and \({{\mathcal {F}}}\).

Now, we introduce a new scalar field \(\varphi \). This field is identified by the number of e-folds N and parameterizes the scalar field \(\phi \) as \(\phi =\phi (\varphi )\). From these points and by using Eq. (7), we obtain the potential in the intermediate inflation as follows

$$\begin{aligned} V=\frac{\Big [2H H' +3H^{2} \Big ]^{2}}{{\kappa }^{2} \Big [-{\kappa }^{2}\,{\alpha }+4H H'+6H^{2} \Big ] }\,. \end{aligned}$$
(37)

Note that, in the above and forthcoming equations, a prime refers to the derivative of the parameter with respect to N, and also we have \(H=H(N)\). From Eqs. (6) and (37) we get

$$\begin{aligned} \lambda= & {} \frac{9\,{H}^{4}{{\mathcal {X}}}-3\,{H}^{2}{{\mathcal {X}}}\alpha {\kappa }^{2}-9\,{H}^{4}- 12\,{H}^{3}H'}{-2{{\mathcal {M}}}{{\mathcal {X}}}{\kappa } ^{2}} \nonumber \\&+\frac{-4\,H^{2}H'^{2}{{\mathcal {X}}}-4\,H^{2}H'^{2}}{-2{{\mathcal {M}}}{{\mathcal {X}}}{\kappa } ^{2}}, \end{aligned}$$
(38)

where

$$\begin{aligned} {{\mathcal {M}}}= & {} 6{H}^{2}+4H\,H'-{\alpha }\,{\kappa }^ {2}\,,\quad \nonumber \\ {{\mathcal {X}}}= & {} \sqrt{1-{\frac{{\alpha }{\kappa }^{2}\,{{\mathcal {M}}} }{ \big ( 3{H}^{2}+2\,H\,H' \big ) ^{2}}}}\,. \end{aligned}$$
(39)

The slow-roll parameters in terms of the Hubble parameter and its derivatives are given by the following expressions

$$\begin{aligned}&\epsilon =\frac{3}{2}-\frac{3}{2}\,\frac{1}{{\kappa }^{2}} \left( {\frac{{{\mathcal {X}}}\,{{{\mathcal {N}}}}^{2}}{{{\mathcal {M}}}}}+{ \frac{ {{\mathcal {N}}} ^{2}}{{{\mathcal {M}}}}} \right) \Bigg ( {\frac{{{{\mathcal {N}}}}^{2}}{{\kappa }^{2}{{\mathcal {M}}}{{\mathcal {X}}}} }+{\frac{{{{\mathcal {N}}}}^{2}}{{\kappa }^{2}{{\mathcal {M}}}}}\nonumber \\&\quad +{\frac{9\, H ^{4}{{\mathcal {X}}}-3\, H ^{2} {{\mathcal {X}}}\,{\kappa }^{2}\alpha -9\, H ^{4}- 12 H ^{3}H' -4\, H ^{2} H'^{2}{{\mathcal {X}}}-4\, H ^{2} H'^{2}}{{\kappa }^{2}{{\mathcal {M}}}{{\mathcal {X}}}}} \Bigg ) ^{-1}\nonumber \\ \end{aligned}$$
(40)

where \(H\equiv H(N)\) and \({{\mathcal {N}}}=2HH'+3H^2\)

$$\begin{aligned} \eta =-3\,{\frac{{{\mathcal {N}}} \Big [ {{\mathcal {N}}} \left( \frac{1}{2}\, \left( {{\mathcal {X}}} +1 \right) ^{2} {{\mathcal {N}}} ^{2}+{{\mathcal {K}}} \left( {{\mathcal {X}}} +\frac{1}{2} \right) \right) {{\mathcal {X}}}' + \left( {{\mathcal {X}}} +1 \right) \left( {{\mathcal {K}}} {{\mathcal {N}}}' -\frac{1}{2}\,{{\mathcal {N}}} {{\mathcal {K}}}' \right) {{\mathcal {X}}} \Big ] }{\epsilon \,H\, \Big [ \left( {{\mathcal {X}}} +1 \right) {{\mathcal {N}}} ^{2}+{{\mathcal {K}}} \Big ] ^{2}}} \nonumber \\,, \end{aligned}$$
(41)

with

$$\begin{aligned} {{\mathcal {K}}}= & {} 9 H ^{4}{{\mathcal {X}}} -3\, H ^{2}{{\mathcal {X}}} {\kappa } ^{2}\alpha -9\, H ^{4}-12\, H ^{3}H'\nonumber \\&-4\, H ^{2} H'^{2}{{\mathcal {X}}} -4\, H ^{2} H'^{2} \,, \end{aligned}$$
(42)
$$\begin{aligned} s= & {} \frac{1}{4}\frac{ \left[ \bigg ( -\frac{\lambda }{2} \left( \alpha +2V \right) V' +V \lambda ' \left( \alpha -V \right) \bigg ) \sqrt{V-\alpha }+\frac{V^{\frac{3}{2}}}{2} V' \alpha \right] {\alpha }^{2}}{\sqrt{V } \left( \lambda \sqrt{V-\alpha }-\frac{\alpha }{2}\sqrt{V } \right) \left( \alpha -V \right) \left( \lambda \left( \alpha -V \right) \sqrt{V-\alpha }+\frac{\alpha }{2} V^{\frac{3}{2}} \right) } \nonumber \\,. \end{aligned}$$
(43)

In the intermediate inflation, the slow-roll parameter \(\epsilon \) takes the following form

$$\begin{aligned} \epsilon= & {} \frac{1}{12}\frac{1}{{N}^{2}\beta } \Bigg [ \Bigg ( 2\,\alpha \,{b}^{-2\,{ \beta }^{-1}} \left( \beta -1 \right) {N}^{{\frac{2+2\,\beta }{\beta }}}\nonumber \\&- 12\, \bigg ( -\frac{1}{4}{b}^{-2\,{\beta }^{-1}}{N}^{{\frac{3\,\beta +2}{\beta }}}\alpha + \left( -\frac{2}{3}+ \left( N+\frac{2}{3} \right) \beta \right) \nonumber \\&\times \left( \beta -1 \right) {N}^{3} \bigg ) \beta \Bigg ) {\mathrm{e}^{{\frac{-2\, \ln \left( N \right) +2\,\ln \left( b \right) }{\beta }}}}-3\,{N}^{3} \alpha \,\beta \Bigg ] \nonumber \\&\times \Bigg [ \left( -\frac{2}{3}+ \left( N+\frac{2}{3} \right) \beta \right) \beta \,{b}^{2}{\mathrm{e}^{2\,{\frac{ \left( \beta -1 \right) \left( \ln \left( N \right) -\ln \left( b \right) \right) }{\beta } }}}-\frac{1}{6}\,N\alpha \Bigg ] ^{-1} \nonumber \\,. \end{aligned}$$
(44)
Fig. 1
figure 1

Ranges of the model’s parameters that lead to the gradient instability-free intermediate MDBI inflation (left panel) and the ghost instability-free intermediate MDBI model (right panel). These figures have been plotted for \(N=60\)

Full size image
Fig. 2
figure 2

The evolution of \(c_{s}^{2}\) and \({{\mathcal {W}}}_{s}\) of the intermediate MDBI model versus the e-folds number during inflation, with \(b=10\) and \(0.340<\beta <0.400\). The arrow shows the direction in which the parameter \(\beta \) increases

Full size image
Fig. 3
figure 3

The evolution of the potential in the intermediate MDBI model versus the scalar filed \(\phi \), with \(b=10\) and \(0.340<\beta <0.400\). The arrow shows the direction in which the parameter \(\beta \) increases

Full size image

The slow-roll parameters \(\eta \) and s are very long and complicated, so we avoid writing these parameters here. By using the above equations, we can express the perturbation parameters in terms of the model’s parameters. In Ref. [73], we have shown that the MDBI model with power-law scale factor is free of ghost and gradient instabilities. Now, in this paper, we show numerically that the intermediate MDBI model also, in some ranges of the model’s parameter space, is free of the instabilities. In this regard, by using Eqs. (37) and (38) and by assuming \({{\mathcal {F}}}=V^{-1}\), we can obtain the sound speed (Eq. (10)) in the intermediate MDBI model. Any range of the parameter space in which we have \(c_{s}^{2}>0\), leads to the gradient instability-free intermediate MDBI model. Note that, another constraint on the sound speed is \(c_{s}\le c\), where c is the value of the local speed of light. This constraint is required from causality. If we consider the scale factor (35) and perform some numerical analysis, we find that the range of the parameter space lead to \(0<c_{s}^{2}\le 1\) (with \(c\equiv 1\)). The result is shown in Fig. 1. Note that, in this figure and forthcoming figures we have adopted \(\kappa =1\) and \(\alpha =1\). The pink region in the left panel of Fig. 1 shows the ranges of the parameters \(\beta \) and b leading to the gradient instability-free intermediate MDBI model. Now, we study \({{\mathcal {W}}}_{s}\) to see if the intermediate MDBI model is free of ghost instability. To this end, we use Eqs. (18), (37), (38) and (39). By performing the numerical analysis, we find the result shown in the right panel of Fig. 1. In summary, the intermediate MDBI model in some ranges of its parameter space is free of gradient and ghost instabilities, which is a good result.

To ensure there are no instabilities during the whole inflationary evolution, we plot parameters \(c_{s}^{2}\) and \({{\mathcal {W}}}_{s}\) versus the e-folds number N, for some sample values of the model’s parameter. The results are shown in Fig. 2. This figure has been plotted with \(b=10\) and \(0.340<\beta <0.400\) (we see in the next section that, these adopted values of b and \(\beta \) are observationally viable). As this figure shows, both conditions \(0<c_{s}^{2}\le 1\) and \({{\mathcal {W}}}_{s}>0\) are satisfied during inflation.

Now, we study the behavior of the potential (37) versus the scalar field. To this end, we consider \(N=\int Hdt=\int Hd\phi \) (where we have used the constraint (1)) and from Eqs. (36) and (37) we obtain

$$\begin{aligned} V(\phi )= \frac{1}{6}\,{\frac{{\phi }^{3\,\beta -2}{\beta }^{2}{b}^{2} \left( 3\,\beta \,b\,{ \phi }^{\beta }+2\,\beta -2 \right) ^{2}}{{\kappa }^{2} \left( \frac{2}{3}\,\beta \,b \left( \beta -1 \right) {\phi }^{2\,\beta }+{\phi }^{3\,\beta }{\beta }^ {2}{b}^{2}-\frac{\alpha }{6}\,{\kappa }^{2}{\phi }^{\beta +2} \right) }}\nonumber \\,. \end{aligned}$$
(45)

By using this equation, we can perform a numerical study on the evolution of the potential versus the scalar field. The result is shown in Fig. 3. At the initial times, where inflation happens, the potential is large, and also the friction term \(3H{\dot{\phi }}\).

Fig. 4
figure 4

The evolution of the slow-roll parameter \(\epsilon \) of the intermediate MDBI model versus the e-folds number during inflation, with \(b=10\) and \(0.340<\beta <0.400\). The arrow shows the direction in which the parameter \(\beta \) increases

Full size image
Fig. 5
figure 5

The upper panels show the ranges of the model’s parameter space that lead to the observationally viable values of the scalar spectral index (the left one) and tensor-to-scalar ratio (the right one), obtained from Planck2018 TT, TE, EE + lowE + lensing + BAO + BK14 data. The lower panel shows the range of the model’s parameter space that leads to the observationally viable values of the tensor spectral index, obtained from Planck2018 TT, TE, EE + lowE + lensing + BK14 + BAO + LIGO and Virgo2016 data. These figures have been plotted for \(N=60\)

Full size image
Fig. 6
figure 6

Tensor-to-scalar ratio versus the scalar spectral index for the intermediate MDBI model. To plot this figure, we have adopted \(0<\beta <1\) and \(N=60\)

Full size image

It is worth checking if inflation ends in this setup. The inflation ends when one of the slow-roll parameters reaches unity. In this regard, we study the first slow-roll parameter \(\epsilon \) versus the e-folds number N. The result is shown in Fig. 4. As the figure shows, in this model inflation ends after about 60 e-folds (which is also corresponding to the minimum of the potential) and the graceful exit of inflation towards the matter-dominated era can be achieved. Note that, since the scale factor in the intermediate inflation evolves faster than the one in the power-law inflation and slower than the one in the exponential inflation, the same situation happens for the slow-roll parameter \(\epsilon \). In this model also, it is possible to have the seeds for the observed dark matter. In fact, by considering the conservation of the energy-momentum tensor (as \(\nabla ^{\mu }\,T_{\mu \nu }=0\)), we obtain

$$\begin{aligned}&\frac{1}{\sqrt{-g}}\partial _{\mu }\left[ \sqrt{-g}\left( -\frac{\partial ^{\mu }\phi }{\sqrt{1+{\alpha }{{\mathcal {F}}}\partial ^{\mu }\phi \,\partial _{\mu }\phi }}+2\lambda g^{\mu \nu }\partial _{\nu }\phi \right) \right] \nonumber \\&\quad =-V'+\frac{{{\mathcal {F}}}'}{{{\mathcal {F}}}^{2}}\left[ \frac{2+3{\alpha }{{\mathcal {F}}}g^{\mu \nu }\partial _{\mu }\phi \, \partial _{\nu }\phi }{2\sqrt{1+{\alpha }{{\mathcal {F}}}g^{\mu \nu }\partial _{\mu }\phi \, \partial _{\nu }\phi }}\right] \,. \end{aligned}$$
(46)

By considering the constraint (2) and \(H^{2}=\frac{\kappa ^{2}}{3}\rho \), from Eqs. (6) and (46) we have

$$\begin{aligned}&\frac{1}{\sqrt{-g}}\partial _{\mu }\left[ \sqrt{-g}\left( \rho -V-{{\mathcal {F}}}^{-1}\sqrt{1-{\alpha }{{\mathcal {F}}}}\right) \right] \nonumber \\&\quad = -V'+\frac{{{\mathcal {F}}}'}{{{\mathcal {F}}}^{2}}\left[ \frac{2-3{\alpha }{{\mathcal {F}}}}{2\sqrt{1-{\alpha }{{\mathcal {F}}}}}\right] \,. \end{aligned}$$
(47)

After the end of the inflation, at the moment we reach the minimum of the potential, we have \(V={{\mathcal {F}}}^{-1}=constant\). At that point, the slope of the potential is zero and so is the right-hand side of the Eq. (46). In this case, we have

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left[ \sqrt{-g}\left( \rho -V-{{\mathcal {F}}}^{-1}\sqrt{1-{\alpha }{{\mathcal {F}}}}\right) \right] = 0\,, \end{aligned}$$
(48)

and therefore

$$\begin{aligned} \rho = \frac{{{\mathcal {C}}}}{a^{3}}+V+{{\mathcal {F}}}^{-1}\sqrt{1-\alpha {{\mathcal {F}}}}\,, \end{aligned}$$
(49)

where \({{\mathcal {C}}}\) is a constant with dimension \([M]^{4}\). In this way, the seeds of the dark matter are obtained and the term \(\frac{{{\mathcal {C}}}}{a^{3}}\) determines the amount of dark matter in the intermediate MDBI model. Note that, although in the inflation era (where the right-hand side of the Eq. (47) is not zero) it is possible to have a term like \(\frac{{{\mathcal {C}}}}{a^{3}}\), this term is diluted away quickly. However, after the end of inflation, this term has an important role. Also, by considering the gravitational particle production at the end of inflation, it is possible to get the observed radiation and baryons in the universe [98]. Although the potential is a function of time and increases again, the gravitational created particles dominate the potential term near the minimum. Then, by increasing the time, the potential term (and also, \({{\mathcal {F}}}^{-1}\sqrt{1-{{\mathcal {F}}}}\) term) dominates the particles and probably becomes the dark energy component leading to the late-time acceleration of the universe.

In the next section, we study the observational viability of this model with the Planck2018 data.

4 Comparing with the Planck2018 observational data

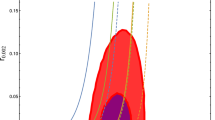
When an inflation model is constructed, it is important to check if its results are consistent with observational data. The observational data give some constraints on the perturbation parameters such as the scalar spectral index, the tensor spectral index, and the tensor-to-scalar ratio. Also, the observational data sets constraints on the amplitudes of the non-Gaussianity in the equilateral configuration. Therefore, by studying these parameters in an inflation model and comparing the results with observational data, we can explore the viability of the model. The constraint on the scalar spectral index, from Planck2018 TT, TE, EE + lowE + lensing + BAO + BK14 data, based on \(\Lambda \)CDM\(+r+\frac{dn_{s}}{d\ln k}\) model, is \(n_{s}=0.9658\pm 0.0038\). This dataset gives the constraint on the tensor-to-scalar ratio as \(r<0.072\). Also, Planck2018 TT, TE, EE + lowE + lensing + BK14 + BAO + LIGO and Virgo2016 constraint on the tensor spectral index is as \(-0.62<n_{T}<0.53\). By using these data, we can obtain some constraints on the intermediate parameters \(\beta \) and b. By substituting Eqs. (40), (41) and (43) for the intermediate inflation in the Eqs. (19), (22), (23), we obtain the tensor-to-scalar ratio, the scalar spectral index and the tensor spectral index in terms of the parameters \(\beta \) and b. Then, we perform numerical analysis on these parameters and compare the results with observational data. Our numerical analysis shows that, for \(0<b\le 10\), depending on the values of b, the scalar spectral index in the intermediate MDBI model is consistent with observational data if \(0.345< \beta < 0.387\). This is shown in the left-upper panel of Fig. 5. The tensor-to-scalar ratio in this model is consistent with observational data if, depending on the values of b, \(0.341< \beta < 1\). This is shown in the right-upper panel of Fig. 5. Also, we have found that the range \(0.044< \beta < 1\) leads to the observationally viable values of the tensor spectral index in the intermediate MDBI model. This is shown in the lower panel of Fig. 5. We have also studied the tensor-to-scalar ratio versus the scalar spectral index in the background of Planck2018 TT, TE, EE+lowE+lensing +BAO +BK14 data at \(68\%\) CL and \(95\%\) CL. The results are shown in Fig. 6. From this figure, we have obtained some constraints on the parameter \(\beta \) that are summarized in Table 1. The tensor-to-scalar ratio versus the tensor spectral index in the background of Planck2018 TT, TE, EE+lowE+lensing +BAO +BK14 data (Fig. 7) is another studied case that gives some more constraints presented in Table 1.

Table 1 The ranges of the parameter \(\beta \) in which the tensor-to-scalar ratio, the scalar spectral index, and the tensor spectral index of the intermediate MDBI model are consistent with different data sets
Full size table
Fig. 7
figure 7

Tensor-to-scalar ratio versus the tensor spectral index for the intermediate MDBI model. To plot this figure, we have adopted \(0<\beta <1\) and \(N=60\)

Full size image

Another important property in studying an inflation model is the non-Gaussian feature of the primordial perturbations. As we mentioned earlier, the amplitude of the non-Gaussianity is related to the sound speed of the perturbations and in this way, it is related to the model’s parameter space. In this regard, studying the non-Gaussian features of the perturbations in the inflation models helps us get more information about the models. We study the amplitude of the non-Gaussianity in equilateral configurations. By considering the constraints on the model’s parameters obtained from the observational viability of the scalar and tensor spectral index and the tensor-to-scalar ratio from Planck2018, we analyze the non-Gaussianity in the intermediate MDBI inflation numerically. Here, we consider the non-Gaussianity parameter \(f^{equil}\), which is related to the sound speed by Eq. (34). By using Eqs. (10), (37) and (38) and also assuming \({{\mathcal {F}}}^{-1}=V\), we relate the square of the sound speed of the primordial perturbations to the model’s parameters. The square of the sound speed is also related to the tensor-to-scalar ratio via Eq. (23). In this regard, the constraints on r set some constraints on \(c_{s}^{2}\) that is shown in Fig. 8.

Fig. 8
figure 8

The square of the sound speed versus the tensor-to-scalar ratio for the intermediate MDBI model. To plot this figure, we have adopted \(0.340<\beta <0.4\), \(0<b<10\) and \(N=60\)

Full size image
Fig. 9
figure 9

The left panel shows the ranges of the intermediate MDBI model’s parameters leading to the observationally viable values of the equilateral non-Gaussianity. The right panels show the prediction of the intermediate MDBI model for equilateral non-Gaussianity. These figures have been plotted for \(N=60\)

Full size image

The planck2018 combined temperature and polarization analysis gives the constraint on the sound speed of the DBI model as \(c_{s}^{DBI}\ge 0.086\), at \(95\%\) CL. Also, this data gives the constraint on the sound speed of the general \(P(X,\phi )\) model (where, \(X=-\frac{1}{2}\partial _{\nu }\phi \,\partial ^{\nu }\phi \)) as \(c_{s}\ge 0.021\), at \(95\%\) CL. According to our numerical analysis, shown in Fig. 8, the values of the sound speed in our intermediate MDBI model are consistent with both constraints.

By having the constraints on the model’s parameters \(\beta \), b and therefore \(c_{s}^{2}\), we can predict the non-Gaussian feature of the primordial perturbations in the intermediate MDBI model from Eq. (34). The Planck2018 data gives the constraint on the equilateral configuration of the non-Gaussianity as \(f^{equil}=-26\pm 47\). By using this constraint, we can find the range of the parameter space leading to the observationally viable values of the equilateral non-Gaussianity in the intermediate MDBI model. The result is shown in the left panel of Fig. 9. Also, the right panels of Fig. 9 show the prediction of the model for the equilateral amplitude of the non-Gaussianity, where we have used the observationally viable ranges of the parameters b and \(\beta \) which are obtained from the comparing of the tensor-to-scalar ratio and scalar spectral index with Planck2018 TT, TE, EE + lowE + lensing + BAO + BK14 data at \(95\%\) CL. Note that, we have used the same ranges of the parameters to plot Figs. 6 and 7. However, plot 6 is \(r-n_s\) behavior and plot 7 is \(r-n_T\) behavior. From the slope of the \(r-n_s\) plot, we see that it is possible to have larger values of r, but these larger values are corresponding to smaller values of \(n_s\), which are not observationally viable. Therefore, we haven’t shown those parts of the plot which are not consistent with observational data. However, the situation is different for \(r-n_T\). As Fig. 7 shows, if we consider the larger values of r, the parameter \(n_T\) is still consistent with observational data.

Table 2 The prediction of the model for the equilateral amplitude of the non-Gaussianity, obtained from the observationally viable values of the parameter \(\beta \) at \(68\%\) CL and \(95\%\) CL
Full size table

Up to here, we have numerically studied the perturbation parameters \(n_{s}\), \(n_{T}\) and r and also the non-Gaussianity parameter \(f_{NL}^{equil}\), to find some constraints on the model’s parameters. According to the obtained results, for every parameter, there are some ranges in the parameter space which make the model observationally viable. However, we are interested in the case where all parameters are consistent with Planck2018 data in the same range. By this, we mean that it is interesting to find a range for the parameters \(\beta \) and b where we have an instabilities-free and observationally viable intermediate MDB model. Our data analysis to obtain such ranges shows that by \(0<b\le 10\) and \(0.345<\beta <0.387\), it is possible to have an instabilities-free intermediate MDBI model that gives the observationally viable perturbations. Also, with these ranges, the values of the equilateral amplitude of the non-Gaussianity are consistent with observational data.

5 A short discussion on the difference between the power-law MDBI and intermediate MDBI models

In Ref. [73], we have studied the power-law DBI and power-law MDBI models, where \(a=a_{0}t^{n}\), with details. We have obtained the main inflation and perturbation parameters in both models and performed a numerical analysis on those parameters. According to our analysis in Ref. [73], the result of the numerical analysis on the perturbation parameters of the power-law DBI model is not consistent with Planck2018 observational data. Then, we have considered the power-law MDBI model. We have shown that the power-law MDBI model is an instabilities-free model. We have also shown that the scalar spectral index and the tensor-to-scalar ratio in the power-law MDBI model are consistent with Planck2018 TT, TE, EE + lowE +lensing data at \(95\%\) CL. However, these perturbation parameters in the power-law MDBI model are not consistent with Planck2018 TT, TE, EE + lowE + lensing + BK14 + BAO data, where the combination of the BICEP2/Keck Array 2014 and Planck2018 data is considered. Note that, in the case of constant sound speed, it is possible to get observational consistency, however, our attention is on the varying sound speed case. In this paper, We have shown that if we consider an intermediate MDBI model, the perturbation parameters \(n_{s}\) and r are consistent with Planck2018 TT, TE, EE + lowE + lensing + BK14 + BAO data at both \(68\%\) CL and \(95\%\) CL. This is an interesting advantage of the intermediate MDBI model over the power-law MDBI model.

We have also explored the non-Gaussian feature of the primordial perturbation in the power-law DBI and power-law MDBI models, in Ref. [73]. In that paper, it has been shown that the amplitude of the primordial non-Gaussianity in the power-law DBI model is too large to be consistent with Planck2018 observational data. Also, we have shown that the prediction of the power-law MDBI model for the amplitude of the equilateral non-Gaussianity is very small (of the order of \(10^{-4}\)). However, as we have seen in the current paper, the equilateral non-Gaussianity in the intermediate MBI model is in the range \(-16.7<f^{equil}<-12.5\). This is a result that is consistent with planck2018 data.

It seems that, by considering both perturbation and non-Gaussianity parameters, the intermediate MDBI model is consistent with Planck2018 data and therefore is more favorable.

6 Summary and conclusion

Recently, it has been shown that to have a ghost and gradient instabilities-free mimetic gravity model, one can consider a DBI-like term in the action of the mimetic gravity and adopt a power-law scale factor. In this paper, we have considered a MDBI model with intermediate scale factor as \(a=a_{0}\exp (bt^{\beta })\). In this regard, we have studied the intermediate inflation in the MDBI model. We have shown that, with the intermediate MDBI model, it is possible to have a mimetic gravity model that is free of ghost and gradient instabilities in some ranges of the intermediate parameters b and \(\beta \). This means that, in those ranges of the parameters, we have \(0<c_{s}^{2}\le 1\) and \({{\mathcal {W}}}_{s}>0\). To seek the observational viability of the models, we have studied the perturbation and non-Gaussianity parameters of this model and compare the results with observational data. From Planck2018 TT, TE, EE + lowE + lensing + BAO + BK14 data, we have the value of the scalar spectral index as \(n_{s}=0.9658\pm 0.0038\). This implies that, for \(0<b\le 10\), the constraint on the \(\beta \) is as \(0.345< \beta <0.387\). Planck2018 TT, TE, EE+lowE+lensing + BAO + BK14 constraint on the tensor-to-scalar ratio is \(r<0.072\), leading to \(0.341< \beta < 1\) for \(0<b\le 10\). From Planck2018 TT, TE, EE + lowE + lensing + BK14 + BAO + LIGO and Virgo2016 data, the constraint on the tensor spectral index is \(-0.62<n_{T}<0.53\). In this regard, we find that for \(0<b\le 10\), the range \(0.044< \beta < 1\) leads to the observationally viable values of the tensor spectral index in the intermediate MDBI model. We have also studied \(r-n_{s}\) and \(r-n_{T}\) behaviors of the intermediate MDBI model in comparison to the observational data at \(68\%\) CL and \(95\%\) CL and found some constraints summarized in the tables.

Another important aspect of the inflation models is the non-Gaussian feature of the primordial perturbations. In this paper, we have studied the non-Gaussianity in the equilateral configuration. We have considered the \(k_{1}=k_{2}=k_{3}\) limit, where the equilateral configuration has a peak. By studying this configuration of the non-Gaussianity and considering the observationally viable ranges of the parameters b and \(\beta \), we have predicted the amplitudes of the non-Gaussianity in our intermediate MDBI model.

As a summary, we have shown that our proposed intermediate MDBI model with \(0<b\le 10\) and \(0.345<\beta <0.387\), is instabilities-free and gives the observationally viable perturbation and non-Gaussianity parameters.