Physical constraints derived from FCNC in the 3-3-1-1 model

Abstract

We investigate several phenomena related to FCNCs in the $\text {3-3-1-1}$ model. The sources of FCNCs at the tree-level from both the gauge and Higgs sectors are clarified. Experiments on the oscillation of mesons most stringently constrain the tree-level FCNCs. The lower bound on the new physics scale is imposed more tightly than in the previous, $\text {M}_{\text {new}}>12$ TeV. Under this bound, the tree-level FCNCs make a negligible contribution to the $\text {Br}(B_s \rightarrow \mu ^+ \mu ^-)$, $\text {Br}(B \rightarrow K^{*} \mu ^+ \mu ^-)$ and $\text {Br}(B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-})$. The branching ratio of radiative decay $b \rightarrow s \gamma$ is enhanced by the ratio $\frac{v}{u}$ via diagrams with the charged Higgs mediation. In contrast, the charged currents of new gauge bosons significantly contribute to the decay process $\mu \rightarrow e \gamma$.

1 Introduction

The analysis of phenomena related to flavor-changing neutral currents (FCNCs) plays an important role in constraining the parameters of the Standard Model (SM) and testing physics beyond the standard model (BSM). In recent years, the most extensively studied processes related to FCNCs in B-physics, particularly the exclusive $b \rightarrow s$ transition. The first place to look for new physics (NP) in $b \rightarrow s$ transitions is $B_q-{\bar{B}}_q$ mixing with $q=d,s$. The mass splitting $\Delta M_d$ has been measured with high precision [1], whereas the measurement of $\Delta M_s$ [2, 3] is complicated because of the rapid oscillation of ${B}_s$ meson. The measurement results of Br$(B_s \rightarrow \mu ^+ \mu ^-)$ [4,5,6,7], Br$(b \rightarrow s \gamma )$ [8,9,10,11], are almost in agreement with the SM predictions. However, some small tensions related to the above processes have been persisted and confirmed by independent measurements. These tensions can be understood due to uncertainties of the form factors, CKM elements, or by the presence of NP. Moreover, the ratios of branching fractions $R_{K}, R_{K^*}$, and several observables of the $B \rightarrow K(K^*) l^+l^-$ ($l=\mu ,e$) decays have been determined [12,13,14,15,16,17,18,19,20,21,22,23,24]. All the results of these measurements have confirmed the deviation from the predictions of the SM. Unlike the angular observables, the various ratios of branching fractions can not be explained via underestimating hadron effects. This result has inspired physicists to investigate these decay processes and see whether some NP models can better explain the experimental data.

Recently, Dong and his collaborators have pointed out the simple extension of the SM in which the gauge symmetry has been extended to the $SU(3)_C \times SU(3)_L \times U(1)_X \times U(1)_N$ group, referred to as the $\text {3-3-1-1}$ model. This model contains both mathematical and phenomenological aspects of the 3-3-1 model [25,26,27,28,29,30]. Therefore, the $\text {3-3-1-1}$ model has all the good features of the $\text {3-3-1}$ models [31,32,33,34]. The difference between the $\text {3-3-1-1}$ model and previous $\text {3-3-1}$ versions is the nature of $B-L$ symmetry . In the 3-3-1-1 model, the $B-L$ symmetry is known as a non-commutative gauge symmetry. Therefore, there exists a unification between the electroweak and $B-L$ interactions [35], which is similar to the Glashow-Weinberg-Salam theory. In addition, the model also provides a natural, comprehensive scenario to account for neutrino masses, dark matter, inflation, and leptogenesis [35].

Another feature of the 3-3-1-1 model is that flavor-violating interactions appear in both the quark and lepton sectors. The quark families transform differently under $SU(3)_L$. So, they lead to tree-level flavor-changing neutral currents (FCNCs) that couple to the new neutral gauge bosons, $Z_2, Z_N$, and the new neutral Higgs bosons. The role of FCNCs coupled to $Z_2, Z_N$ in the oscillation of mesons has been studied in [32, 36]. The authors only focused on the NP short-distance tree-level contribution caused by new neutral gauge bosons to the mass difference of mesons in those studies. The authors used only the NP contributions to compare with the experimental values. Thus, they have pointed out the lower bound on the NP scale in the TeVs. However, considering all NP and SM contributions to the meson oscillations, the lower bound may be more constrained than the previously known ones [32, 36].

In this paper, we study all tree-level FCNCs associated with both Higgs and gauge bosons. The contributions coming from the FCNCs combined with these of SM are subject to strong constraints from meson mixing parameters. Phenomenological aspects related to FCNCs at tree-level, namely $B_s \rightarrow \mu ^{+} \mu ^{-}$, $B \rightarrow K^{*} \mu ^+ \mu ^-$ and $B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$ decays are expensive goals. Additionally, the 3-3-1-1 model predicts the existence of new charged particles, such as new non-Hermitian gauge bosons $Y_{\mu }^{\pm }$, the charged Higgs bosons $H_{4,5}^{\pm }$. They couple to both SM quarks, leptons to new heavy quarks, leptons, respectively. These interactions are the source for yielding the charged lepton flavor violation (LFV) processes $l_i \rightarrow l_j \gamma$ and $b \rightarrow s \gamma$ decay.

We organize our paper as follows. In Sect. 2, we briefly overview the $\text {3-3-1-1}$ model. In Sect. 3, we describe the tree-level FCNCs and study their effects on the mass difference of mesons. We predict the NP contributions to the rare decays of $B_s \rightarrow \mu ^{+} \mu ^{-}$, $B \rightarrow K^{*} \mu ^+ \mu ^-$ and $B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$ processes based on the constrained parameter space. Section 4 studies the one-loop calculation of the relevant Feynman diagrams, which relate to the $b\rightarrow s\gamma$ and $\mu \rightarrow e \gamma$. The consequences of the parameters on the branching ratio of these decays are implied from the experimental data studied. Our conclusions are given in Sect. 5.

2 A summary of the 3-3-1-1 model

2.1 Symmetry and particle content

The gauge symmetry of the model is $SU(3)_C \times SU(3)_L\times U(1)_X \times U(1)_N$, where $SU(3)_C$ is the color group, $SU(3)_L$ is an extension of the $SU(2)_L$ weak-isospin, and $U(1)_X$, $U(1)_N$ define the electric charge Q and $B-L$ operators [36] as follows

$$\begin{aligned} Q=T_3+\beta T_8+ X, \quad B-L=\beta ^\prime T_8+N, \end{aligned}$$

(1)

where $\beta , \beta ^\prime$ are coefficients, and both are free from anomalies. The parameters $\beta ,\beta ^{\prime }$ determine the Q and $B-L$ charges of new particles. In this work, we consider the model with $\beta =-\frac{1}{\sqrt{3}}$. This is the simple 3-3-1-1 model for dark matter [31]. The leptons and quarks, free of all gauge anomalies, transform as

$$\begin{aligned} \psi _{aL}= & {} (\nu _{aL}, e_{aL}, (N_{aR})^c)^T \sim (1,3, -1/3,-2/3), \nonumber \\ \nu _{aR}\sim & {} (1,1,0,-1), \quad e_{aR} \sim (1,1, -1,-1), \nonumber \\ Q_{\alpha L}= & {} (d_{\alpha L},-u_{\alpha L}, D_{\alpha L})^T \sim (3,3^*,0,0), \nonumber \\ Q_{3L}= & {} (u_{3L},d_{3L},U_L)^T\sim (3,3,1/3,2/3), \nonumber \\ u_{aR}\sim & {} (3,1,2/3,1/3),\quad d_{aR}\sim (3,1,-1/3,1/3), \nonumber \\ U_R\sim & {} (3,1,2/3,4/3),\quad D_{aR}\sim (3,1,-1/3,-2/3), \end{aligned}$$

(2)

where $a=1,2,3$, $\alpha =1,2$ are the generation indexes. The scalar sector, which is necessary for realistic symmetry breaking and mass generation, consists of the following Higgs fields [31]

$$\begin{aligned} \eta ^T= & {} (\eta ^0_1, \eta _2^-,\eta _3^0)^T \sim (1,3,-1/3,1/3),\nonumber \\ \rho ^T= & {} (\rho _1^+,\rho _2^0,\rho _3^+)^T \sim (1,3,2/3,1/3), \nonumber \\ \chi ^T= & {} (\chi _1^0, \chi _2^-, \chi _3^0)^T \sim (1,3,-1/3,-2/3),\nonumber \\ \phi\sim & {} (1,1,0,2). \end{aligned}$$

(3)

The electrically-neutral scalars can develop vacuum expectation values (VEVs)

$$\begin{aligned}<\eta _{1}^0>= & {} \frac{u}{\sqrt{2}}, \quad<\rho _2^0>=\frac{v}{\sqrt{2}}, \nonumber \\<\chi _3^0>= & {} \frac{w}{\sqrt{2}}, \quad <\phi >=\frac{\Lambda }{\sqrt{2}}, \end{aligned}$$

(4)

and break the symmetry of model via the following scheme

$$\begin{aligned} \begin{array}{l} SU(3)_C\otimes SU(3)_L\otimes U(1)_{X} \otimes U(1)_N\\ \downarrow \Lambda \\ SU(3)_C\otimes SU(3)_L \otimes U(1)_X \otimes P\\ \downarrow w \\ SU(3)_C\otimes SU(2)_L \otimes U(1)_{B-L}\otimes P\\ \downarrow u,v \\ SU(3)_C \otimes U(1)_{Q}\otimes P, \\ \end{array} \end{aligned}$$

where P is understood as the matter parity (W-parity) and takes the form: $P=(-1)^{3(B-L)+2s}$. All SM particles have W-parity of $+1$ (called even W-particle) while new fermions have W-parity of $-1$ (called odd W-particle). With W-parity preserved, the lightest odd W-particle can not decay. If the lightest particle has a neutral charge, it may account for dark matter (see [31]). The VEVs, u, v, break the electroweak symmetry and generate the mass for SM particles with the consistent condition: $u^2+v^2=246^2 \ \text {GeV}^2$. The VEVs, $w,\Lambda ,$ break $SU(3)_L, U(1)_N$ groups and generate the mass for new particles. For consistency, we assume $w,\Lambda \gg u,v$.

2.2 Scalar sector

Let us rewrite the scalar potential [32, 33] that consists of three terms, $V= V(\phi )+ V(\eta , \rho , \chi ) +V_{\text {mix}}$, where

$$\begin{aligned} V(\phi )= & {} \mu _\phi ^2 \phi ^\dag \phi +\lambda (\phi ^\dag \phi )^2, \nonumber \\ V(\eta , \chi , \rho )= & {} \mu _1^2 \rho ^\dag \rho +\mu _2^2 \chi ^\dag \chi + \mu ^2_3 \eta ^\dag \eta \nonumber \\&+\lambda _1(\rho ^\dag \rho )^2+\lambda _2(\chi ^\dag \chi )^2+ \lambda _3 (\eta ^\dag \eta )^2, \nonumber \\ V_{\text {mix}}= & {} \lambda _4 (\rho ^\dag \rho )(\chi ^\dag \chi )+\lambda _5(\rho ^\dag \rho )(\eta ^\dag \eta )\nonumber \\&+\lambda _6 (\chi ^\dag \chi )(\eta ^\dag \eta ) +\lambda _7(\rho ^\dag \chi )(\chi ^\dag \rho )\nonumber \\&+\lambda _8 (\rho ^\dag \eta )(\eta ^\dag \rho )+ \lambda _9(\chi ^\dag \eta )(\eta ^\dag \chi )\nonumber \\&+\lambda _{10}(\phi ^\dag \phi )(\rho ^\dag \rho )+\lambda _{11}(\phi ^\dag \phi )(\chi ^\dag \chi )\nonumber \\&+(f \epsilon ^{mnp}\eta _m\rho _n \chi _p +H.c.). \end{aligned}$$

(5)

Due to the W-parity conservation, only neutral scalar fields carrying W-parity of $+1$ can develop VEV. After symmetry breaking, there is no mixing between the even and odd W-fields (see in [33]). For the even W-particle spectrum, the model has predicted

• Four neutral physical particles with CP-even, one identified as the SM-like Higgs boson H and the three remaining particles, $H_i, i=1,2,3$, are new heavy fields, having the following form

  $$\begin{aligned} H= & {} \frac{u\mathfrak {R}(\eta _1^0)+v \mathfrak {R}(\rho _2^0) }{\sqrt{u^2+v^2}}, \nonumber \\ H_1= & {} \frac{-v\mathfrak {R}(\eta _1^0)+u \mathfrak {R}(\rho _2^0) }{\sqrt{u^2+v^2}}, \nonumber \\ H_2= & {} \cos \varphi \mathfrak {R}(\chi _3) +\sin \varphi \mathfrak {R}(\phi ), \nonumber \\ H_3= & {} -\sin \varphi \mathfrak {R}(\chi _3)+\cos \varphi \mathfrak {R}(\phi ), \end{aligned}$$

  (6)

  where $\tan (2\varphi )= -\frac{\lambda _{11}w \Lambda }{\lambda \Lambda ^2 -\lambda _2 w^2}$.

• One neutral CP-odd particle

  $$\begin{aligned} {\mathcal {A}}\simeq \frac{v \mathfrak {I}(\eta _1)+u \mathfrak {I}(\rho _2)}{\sqrt{u^2+v^2}}. \end{aligned}$$

  (7)

• Two charged fields that are given as follows

  $$\begin{aligned} H_4^\pm&= \frac{v \chi _2^\pm +\omega \rho _3^\pm }{\sqrt{v^2+\omega ^2}}, \quad H_5^\pm =\frac{v\eta _2^\pm +u \rho _1^\pm }{\sqrt{u^2+v^2}}. \end{aligned}$$

  (8)

For the odd W-particle spectrum, there exists a complex scalar particle

$$\begin{aligned} H^{'0}= \frac{1}{\sqrt{u^2+w^2}}\left( u \chi _1^{0*}+w \eta ^0_3 \right) .\end{aligned}$$

(9)

For convenience, we list a few mass expressions for the physical fields that we will use for the calculations below

$$\begin{aligned} m_{H_1}^2= & {} -\frac{fw}{\sqrt{2}}\left( \frac{v}{u}+\frac{u}{v}\right) , \nonumber \\ m_{{\mathcal {A}}}^2= & {} -\frac{f}{\sqrt{2}}\left( \frac{uw}{v}+\frac{vw}{u}+\frac{uv}{w}\right) ,\nonumber \\ m^2_{H_4}= & {} \left( \frac{\lambda _7}{2}-\frac{fu}{\sqrt{2}vw} \right) \left( v^2+w^2 \right) , \nonumber \\ m^2_{H_5}= & {} \left( \frac{\lambda _8}{2}-\frac{fw}{\sqrt{2}uv}\right) \left( u^2+v^2 \right) . \end{aligned}$$

(10)

2.3 Fermion masses

The Yukawa interactions in the quark sector are written in [31] as follows

$$\begin{aligned} {\mathcal {L}}^{\text {quark}}_{\text {Yukawa}}= & {} h^U{\bar{Q}}_{3L}\chi U_R + h^D_{\alpha \beta }{\bar{Q}}_{\alpha L} \chi ^* D_{\beta R}+ h^u_a {\bar{Q}}_{3L}\eta u_{aR} \nonumber \\&+h^d_a{\bar{Q}}_{3L}\rho d_{aR} + h^d_{\alpha a} {\bar{Q}}_{\alpha L}\eta ^* d_{aR} \nonumber \\&+h^u_{\alpha a } {\bar{Q}}_{\alpha L}\rho ^* u_{aR} +H.c.. \end{aligned}$$

(11)

After symmetry breaking, the up-quarks and down-quarks receive mass. Their mixing mass matrices have the following form

$$\begin{aligned} m_{\alpha a}^u= & {} \frac{1}{\sqrt{2}}h_{\alpha a}^u v, \quad m_{3a}^u =-\frac{1}{\sqrt{2}}h_a^u u, \nonumber \\ m_{\alpha a}^d= & {} -\frac{1}{\sqrt{2}}h_{\alpha a}^d u, \quad m_{3a}^d =-\frac{1}{\sqrt{2}}h_a^d v. \end{aligned}$$

(12)

In the general case, these matrices are not flavor-diagonal. They can be diagonalized by the unitary matrices $V_{u_{L,R}}, V_{d_{L,R}}$ as

$$\begin{aligned} V_{u_L}^\dag m^u V_{u_R}= & {} {\mathcal {M}}_u =\text {Diag}(m_{u_1}, m_{u_2},m_{u_3}), \nonumber \\ V_{d_L}^\dag m^d V_{d_R}= & {} {\mathcal {M}}_d =\text {Diag}(m_{d_1}, m_{d_2},m_{d_3}). \end{aligned}$$

(13)

It means that the mass eigenstates relate to the flavor states by

$$\begin{aligned} u^\prime _{L,R}= & {} (u_{1L,R}^\prime , u_{2L,R}^\prime , u_{3L,R}^\prime )^T\nonumber \\= & {} V^{\dagger }_{u_{L,R}}(u_{1L,R},u_{2L,R},u_{3L,R})^T,\nonumber \\ d^\prime _{L,R}= & {} (d_{1L,R}^\prime , d_{2L,R}^\prime , d_{3L,R}^\prime )^T\nonumber \\= & {} V^{\dagger }_{d_{L,R}}(d_{1L,R},d_{2L,R},d_{3L,R})^T. \end{aligned}$$

(14)

The CKM matrix is defined as $V_{\text {CKM}}=V_{u_{L}}^\dag V_{d_L}$.

The Yukawa interactions for leptons are written by

$$\begin{aligned} {\mathcal {L}}_{\mathrm {Yukawa}}^{\text {lepton}}= & {} h^e_{ab}{\bar{\psi }}_{aL}\rho e_{bR}\nonumber \\&+h^\nu _{ab}{\bar{\psi }}_{aL}\eta \nu _{bR}+h'^\nu _{ab}{\bar{\nu }}^c_{aR}\nu _{bR}\phi +H.c.. \end{aligned}$$

(15)

The charged leptons have a Dirac mass $[M_\text {l}]_{ab}=-\frac{h_{ab}^e v}{\sqrt{2}}$. The flavor states $e_a$ are related to the physical states $e_a^\prime$ by using two unitary matrices $U^l_{L,R}$ as

$$\begin{aligned} e_{aL}=(U^l_L)_{ab}e^\prime _{bL}, \quad e_{aR}=(U^l_R)_{ab}e^\prime _{bR}. \end{aligned}$$

(16)

The neutrinos have both Dirac and Majorana mass terms. In the flavor states, $n_L=(\nu _L, \nu _R^c)^T$, the neutrino mass terms can be written as follows

$$\begin{aligned} {\mathcal {L}}^\nu _{\text {mass}}= & {} -\frac{1}{2} {\bar{n}}_L \left( \begin{array}{cc} 0 &{} M^D_\nu \\ (M_\nu ^{D})^T &{} M_R^\nu \end{array} \right) n_L+H.c.\nonumber \\= & {} -\frac{1}{2} {\bar{n}}_L M^\nu n_L +H.c., \end{aligned}$$

(17)

where $[M^D_\nu ]_{ab}= -\frac{h_{ab}^\nu }{\sqrt{2}}u$, $[M_{\nu }^R]_{ab}=-\sqrt{2}h^{\prime \nu }_{ab} \Lambda$. The mass eigenstates $n_L^\prime$ are related to the neutrino flavor states as $n_L^\prime = U^{\nu \dag } n_L$, where $U^\nu$ is a $6 \times 6$ matrix and written in terms of

$$\begin{aligned} U^\nu =\left( \begin{array}{cc} U^\nu _L &{} V^\nu \\ (V^{\nu })^ T &{} U_R^\nu \end{array} \right) . \end{aligned}$$

(18)

The new neutral fermions $N_{a}$ are a Majorana field, and they obtain their mass via effective interactions [32, 33]. We suppose that the flavor states $N_a$ relate to the mass eigenstates $N_a^\prime$ by using the unitary matrices $U^N_{L,R}$ as

$$\begin{aligned} N_{aL}=(U_L^N)_{ab}N^\prime _{bL}, \quad N_{aR}=(U^N_R)_{ab}N^\prime _{bR}. \end{aligned}$$

(19)

2.4 Gauge bosons

Let us review the characteristics of the gauge sector. In addition to the SM gauge bosons, the 3-3-1-1 model also predicts six new gauge bosons: $X^{0,0*}, Y^\pm , Z_2, Z_N$. The gauge bosons are even W-parity except for the X, Y gauge bosons that carry odd W-parity. The masses of new gauge bosons have been given in [32, 33] as

$$\begin{aligned} m_{Z_2}^2\simeq & {} \frac{g^2}{18}\left\{ (3+t_X^2)w^2+4t_N^2(w^2+9\Lambda ^2) \right. \nonumber \\&-\left. \sqrt{[(3\!+\!t_X^2)w^2\!-\!4t_N^2(w^2\!+\!9\Lambda ^2)]^2\!+\!16(3+t_X^2)t_N^2w^4}\right\} ,\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} m_{Z_N}^2\simeq & {} \frac{g^2}{18}\left\{ (3+t_X^2)w^2+4t_N^2(w^2+9\Lambda ^2) \right. \nonumber \\&+\left. \sqrt{[(3\!+t_X^2)w^2\!-\!4t_N^2(w^2\!+\!9\Lambda ^2)]^2\!+\!16(3+t_X^2)t_N^2w^4}\right\} , \nonumber \\ m_W^2= & {} \frac{g^2}{4}(u^2+v^2), \quad m^2_X =\frac{g^2}{4}\left( u^2+w^2 \right) , \nonumber \\ m^2_Y= & {} \frac{g^2}{4}\left( v^2+w^2\right) . \end{aligned}$$

(21)

3 Rare processes mediated by new gauge bosons and new scalars at the tree-level

3.1 Meson mixing at tree level

In previous works [32, 36], the authors have considered the FCNCs that couple to the new neutral gauge bosons $Z_2$ and $Z_N$ at tree-level. Due to the different arrangements between generations of quarks, the SM quarks couple to two Higgs triplets. Therefore, there exist FCNCs coupled to the new neutral Higgs bosons at tree-level. These interactions derive from the Yukawa Lagrangian (11). After rotating to the physical basis via using Eqs. (12), (13), (14), we obtain the following

$$\begin{aligned} {\mathcal {L}}_{\text {NC}}^{\text {Higgs}}= & {} -\frac{g}{2m_W}\left( {\bar{d}}^{\prime }_L{\mathcal {M}}_d d_R^\prime + {\bar{u}}^{\prime }_L {\mathcal {M}}_u u_R^\prime \right) H\nonumber \\&+\frac{g}{2 m_W}\left( t_\beta {\bar{d}}^{\prime }_L{\mathcal {M}}_d d_R^\prime -\frac{1}{t_\beta }{\bar{u}}^{\prime }_L {\mathcal {M}}_u u_R^\prime \right) H_1 \nonumber \\&+\frac{ig}{2 m_W}\left( t_\beta {\bar{d}}^{\prime }_L{\mathcal {M}}_d d_R^\prime +\frac{1}{t_\beta }{\bar{u}}^{\prime }_L {\mathcal {M}}_u u_R^\prime \right) {\mathcal {A}}\nonumber \\&+\frac{g}{2m_W}\left( {\bar{d}}^{\prime }_L\Gamma ^d d^\prime _R+{\bar{u}}^{\prime }_L\Gamma ^u u^\prime _R\right) H_1\nonumber \\&+\frac{ig}{2m_W}\left( {\bar{d}}^{\prime }_L\Gamma ^d d^\prime _R-{\bar{u}}^{\prime }_L\Gamma ^u u^\prime _R\right) {\mathcal {A}}+ H.c., \end{aligned}$$

(22)

where $t_\beta = \tan \beta =\frac{v}{u}$, and $\Gamma ^u, \Gamma ^d$ are defined as:

$$\begin{aligned} \Gamma ^u_{ ij}= & {} \frac{2}{s_{2\beta }}(V_{u_L}^\dag )_{i 3} (V_{u_L})_{3k} m_{u_k}(V_{u_R}^\dag )_{ka}(V_{u_R})_{a j},\nonumber \\ \Gamma ^d_{ij}= & {} -\frac{2}{s_{2\beta }}(V_{d_L}^\dag )_{i 3}(V_{d_L})_{3k}m_{d_k}(V_{d_R}^\dag )_{ka}(V_{d_R})_{a j}. \end{aligned}$$

(23)

The first three terms of Eq. (22) are proportional to the quark mass matrices, and thus they are flavor-conserving interactions. The remaining terms are the FCNCs coupled to the new neutral Higgs bosons, including CP-even $H_1$ and CP-odd ${\mathcal {A}}$.

The Lagrangian of tree-level FCNCs mediated by $Z_2, Z_N$, which has been studied in [32], has the following form

$$\begin{aligned} {\mathcal {L}}_{\text {FCNC}}^{\text {gauge}}= & {} -\sum _{q^\prime =u^\prime ,d^\prime }\Theta _{ij}^q \left\{ {\bar{q}}^{\prime }_{iL}\gamma ^\mu q^{\prime }_{jL}(g_2 Z_{2 \mu }+g_N Z_{N \mu }) \right\} , \end{aligned}$$

(24)

where

$$\begin{aligned} \Theta _{ij}^q= & {} \frac{1}{\sqrt{3}}(V_{q_L}^*)_{3i}(V_{q_L})_{3j},\nonumber \\ g_2= & {} g\left( \cos \xi \frac{1}{\sqrt{1-t_w^2/3}}+\sin \xi \frac{2t_N}{\sqrt{3}} \right) , \nonumber \\ g_N= & {} g\left( -\sin \xi \frac{1}{\sqrt{1-t_w^2/3}}+\cos \xi \frac{2t_N}{\sqrt{3}} \right) . \end{aligned}$$

(25)

$\xi$ is a mixing angle that is determined by $\tan 2\xi =\frac{4 \sqrt{3+t_X^2}t_N w^2}{(3+t_X^2)w^2-4t_N^2(w^2+9\Lambda ^2)}$, $t_N=\frac{g_N}{g}$, and $t_X=\frac{g_X}{g}=\frac{\sqrt{3}s_W}{\sqrt{3-4s_W^2}}$ with $s_W=\sin \theta _W$.

We now investigate the impact of FCNCs associated with both new gauge and scalar bosons on the oscillation of mesons. From FCNCs given in Eqs. (22)–(24), we obtain the effective Lagrangian that affects the meson mixing as

$$\begin{aligned} {\mathcal {L}}_{\text {effective}}= & {} \frac{g^2}{4m_W^2}\left\{ (\Gamma ^q_{ij})^2 \left( \frac{1}{m_{H_1}^2}- \frac{1}{m_{{\mathcal {A}}}^2} \right) \left( {\bar{q}}^{\prime }_{iL} q^\prime _{jR} \right) ^2\right. \nonumber \\&\left. +(\Gamma _{ji}^{q *})^2 \left( \frac{1}{m_{H_1}^2}-\frac{1}{m_{{\mathcal {A}}}^2}\right) \left( {\bar{q}}^{\prime }_{iR} q^\prime _{jL} \right) ^2\right\} \nonumber \\&+ \frac{g^2}{4m_W^2}\left\{ \Gamma _{ji}^{q*}\Gamma _{ij}^{q} \left( \frac{1}{m_{H_1}^2}+\frac{1}{m_{{\mathcal {A}}}^2} \right) \right. \nonumber \\&\left. ({\bar{q}}^{\prime }_{iL}q^\prime _{jR})({\bar{q}}^{\prime }_{iR} q^\prime _{jL})+\Gamma _{ji}^{q *}\Gamma _{ij}^q\right. \nonumber \\&\left. \left( \frac{1}{m_{H_1}^2}+\frac{1}{m_{{\mathcal {A}}}^2} \right) ({\bar{q}}^{\prime }_{iR} q^\prime _{jL})({\bar{q}}^{\prime }_{iL} q^\prime _{jR})\right\} \nonumber \\&-\Theta _{ij}^2\left( \frac{g_2^2}{m_{Z_2}^2}+\frac{g_N^2}{m_{Z_N}^2} \right) ({\bar{q}}^{\prime }_{iL} \gamma ^\mu q^\prime _{jL})^2 , \end{aligned}$$

(26)

with q denoting either u or d quark. This Lagrangian gives contributions to the mass difference of the meson systems as given

$$\begin{aligned}&(\Delta m_K)_{\text {NP}} =\mathfrak {R}\left\{ \frac{2}{3}\Theta _{12}^2 \left( \frac{g_2^2}{m_{Z_2}^2}+\frac{g_N^2}{m_{Z_N}^2} \right) \right. \nonumber \\&\qquad \left. +\frac{5g^2}{48 m_W^2}\left( (\Gamma _{12}^{d})^2+(\Gamma _{21}^{d*})^2\right) \left( \frac{1}{m_{H_1}^2}-\frac{1}{m_{{\mathcal {A}}}^2} \right) \right. \nonumber \\&\qquad \times \left. \left( \frac{m_K}{m_s+m_d} \right) ^2 \right\} m_K f_K^2\nonumber \\&\qquad -\mathfrak {R}\left\{ \frac{g^2\Gamma _{21}^{d*}\Gamma _{12}^d}{4m_W^2}\left( \frac{1}{m_{H_1}^2}+\frac{1}{m_{{\mathcal {A}}}^2} \right) \left( \frac{1}{6}+\frac{m_K^2}{(m_s+m_d)^2} \right) \right\} m_K f_K^2, \nonumber \\&\quad (\Delta m_{B_d})_{\text {NP}} =\mathfrak {R}\left\{ \frac{2}{3}\Theta _{13}^2 \left( \frac{g_2^2}{m_{Z_2}^2}+\frac{g_N^2}{m_{Z_N}^2} \right) \right. \nonumber \\&\left. \qquad +\frac{5g^2}{48 m_W^2}\left( (\Gamma _{13}^{d})^2+(\Gamma _{31}^{d*})^2 \right) \right. \nonumber \\&\left. \qquad \times \left( \frac{1}{m_{H_1}^2} -\frac{1}{m_{{\mathcal {A}}}^2}\right) \left( \frac{m_{B_d}}{m_b+m_d} \right) ^2 \right\} m_{B_d} f_{B_d}^2\nonumber \\&\qquad -\mathfrak {R}\left\{ \frac{g^2\Gamma _{31}^{d*}\Gamma _{13}^d}{4m_W^2}\left( \frac{1}{m_{H_1}^2}+\frac{1}{m_{{\mathcal {A}}}^2} \right) \left( \frac{1}{6}+\frac{m_{B_d}^2}{(m_b+m_d)^2} \right) \right\} m_{B_d} f_{B_d}^2,\nonumber \\&(\Delta m_{B_s})_{\text {NP}} =\mathfrak {R}\left\{ \frac{2}{3}\Theta _{23}^2 \left( \frac{g_2^2}{m_{Z_2}^2}+\frac{g_N^2}{m_{Z_N}^2} \right) \right. \nonumber \\&\left. \qquad +\frac{5g^2}{48 m_W^2}\left( (\Gamma _{32}^{d*})^2 +(\Gamma _{23}^{d})^2\right) \right. \nonumber \\&\left. \qquad \times \left( \frac{1}{m_{H_1}^2}-\frac{1}{m_{{\mathcal {A}}}^2} \right) \left( \frac{m_{B_s}}{m_s+m_b} \right) ^2 \right\} m_{B_s} f_{B_s}^2\nonumber \\&\qquad -\mathfrak {R}\left\{ \frac{g^2\Gamma _{32}^{d*}\Gamma _{23}^d}{4m_W^2}\left( \frac{1}{m_{H_1}^2}+\frac{1}{m_{{\mathcal {A}}}^2} \right) \left( \frac{1}{6}+\frac{m_{B_s}^2}{(m_s+m_b)^2} \right) \right\} m_{B_s} f_{B_s}^2. \nonumber \!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(27)

We would like to remind the reader that the theoretical predictions of the meson mass differences account for both SM and all tree-level contributions. It hints that meson mass differences can be separated as

$$\begin{aligned} \Delta m_{K,B_d,B_s}= & {} (\Delta m_{K,B_d,B_s})_{\text {SM}}+(\Delta m_{K,B_d,B_s})_{\text {NP}}, \end{aligned}$$

(28)

where the SM contributions to the meson mass differences are given by [37, 38]

$$\begin{aligned} (\Delta m_K)_{\mathrm {SM}}= & {} 0.467\times 10^{-2}/ps,\nonumber \\ (\Delta m_{B_d})_{\mathrm {SM}}= & {} (0.575^{+0.093}_{-0.090})/ps,\nonumber \\ (\Delta m_{B_s})_{\mathrm {SM}}= & {} (18.6^{+2.4}_{-2.3})/ps. \end{aligned}$$

(29)

The theoretical predictions, given in Eq. (28), are compared with the experimental values as given in [39, 40]

$$\begin{aligned} (\Delta m_K)_{\mathrm {exp}}= & {} 0.5293(9)\times 10^{-2}/ps,\nonumber \\ (\Delta m_{B_d})_{\mathrm {exp}}= & {} 0.5065(19)/ps,\nonumber \\ (\Delta m_{B_s})_{\mathrm {exp}}= & {} 17.749(20)/ps. \end{aligned}$$

(30)

However, due to the long-distance effect in $\Delta m_K$, the uncertainties in this system are considerable. Therefore, we require the theory to produce the data for the kaon mass difference within 30%, namely

$$\begin{aligned}&-0.3<\frac{(\Delta m_{K})_{\text {NP}}}{(\Delta m_{K})_{\text {exp}}}< 0.3 . \end{aligned}$$

(31)

The SM predictions for B-meson mass difference are more accurate than those of kaon, and we have the following constraints by combining quadrature of the relative errors in the SM predictions and measurements [41]

$$\begin{aligned} 0.6<\frac{(\Delta m_{B_d})_{\mathrm {exp}}}{(\Delta m_{B_d})_{\mathrm {SM}}}<1.17, \quad 0.71<\frac{(\Delta m_{B_s})_{\mathrm {exp}}}{(\Delta m_{B_s})_{\mathrm {SM}}}<1.2,\nonumber \\ \end{aligned}$$

(32)

or equivalently

$$\begin{aligned} -0.4<\frac{(\Delta m_{B_d})_{\text {NP}}}{(\Delta m_{B_d})_{\mathrm {SM}}}<0.17, \quad -0.29<\frac{(\Delta m_{B_s})_{\text {NP}}}{(\Delta m_{B_s})_{\mathrm {SM}}}<0.2 . \nonumber \!\!\!\!\!\!\!\\ \end{aligned}$$

(33)

Let us do a numerical study from a set of all the input parameters that are taken by [40, 42,43,44,45]

$$\begin{aligned} m_d= & {} 4.88(20) , \quad m_s= 93.44(68), \nonumber \\ m_b= & {} 4198(12), \quad m_t =172.4(7)\times 10^3,\nonumber \\ f_K= & {} 155.7(3), \quad m_K=497.611(13),\nonumber \\ f_{B_d}= & {} 190(1.3),\quad m_{B_d}=5279.65(12),\nonumber \\ f_{B_s}= & {} 230(1.3),\quad m_{B_s}=5366.88(14),\nonumber \\ |(V_{\mathrm {CKM}})_{33}(V_{\mathrm {CKM}})_{31}^{*}|= & {} 0.0087(2), \nonumber \\ |(V_{\mathrm {CKM}})_{33}(V_{\mathrm {CKM}})_{32}^{*}/(V_{\mathrm {CKM}})_{23}|= & {} 0.982(1), \nonumber \\ |(V_{\mathrm {CKM}})_{23}|= & {} 0.04200(64). \end{aligned}$$

(34)

All mass parameters are in MeV. Besides, we assume $t_N=1,g=\sqrt{4\pi \alpha }/s_W$, where $\alpha =1/128$ and $s_W^2=0.231$. The mixing matrix for right-handed quarks, $V_{u R}$, is a unitary matrix, whereas $V_{d R}$ is parameterized by three mixing angles, $\theta _{12}^R,\theta _{13}^R$ and $\theta _{23}^R$, as

$$\begin{aligned} \text {V}_{dR}\!=\! & {} \left( \! \begin{array}{ccc} c^R_{12}c^R_{23}-s^R_{12}s^R_{13}s^R_{23} &{}-s^R_{12}c^R_{13} &{}-c^R_{12}s^R_{23}-s^R_{12}s^R_{13}c^R_{23}\\ s^R_{12}c^R_{23}+c^R_{12}s^R_{13}s^R_{23} &{}c^R_{12}c^R_{13} &{} -s^R_{12}s^R_{23}+c^R_{12}s^R_{13}c^R_{23}\\ c^R_{13}s^R_{23} &{}-s^R_{13}&{}c^R_{13}c^R_{23}\\ \nonumber \end{array}\! \right) ,\!\!\!\!\!\!\!\\ \end{aligned}$$

(35)

where $s^R_{ig}=\sin \theta ^R_{ij}$, $c^R_{if}=\cos \theta ^R_{ij}$. For instance, we can choose $\theta _{12}^R=\pi /6,\theta _{13}^R=\pi /4$ and $\theta _{23}^R=\pi /3$. The NP scales require the following constraints $w \sim \Lambda \sim -f \gg u,v$, due to the condition of diagonalization for the mixing mass matrices in [32].

Fig. 1

Constraints for w and u from the meson mass differences $\Delta m_{K}$,$\Delta m_{B_s}$ and $\Delta m_{B_d}$. The available region for $\Delta m_K$ is the whole frame, whereas the orange and green regions are for $\Delta m_{B_s}$ and $\Delta m_{B_d}$

We first study the role of FCNCs coupled to the scalar fields, $H_1, {\mathcal {A}}$, in meson mixing parameters. To see its effect, we change the f-parameter, which only affects the masses of the $H_1, {\mathcal {A}}$ (see in Eq. (10)). Specifically, in Fig. 1, we draw contours of the mass differences $\Delta m_K$, $\Delta m_{B_s}$, and $\Delta m_{B_d}$, as functions of the NP scale w and u for three different choices of f-parameter as $f=-1000$ GeV, $f=-5000$ GeV and $f=-10{,}000$ GeV. There are almost no differences between the three figures. That is, the mixing parameters are affected slightly by FCNCs coupled to the scalar fields.

Next, we consider the contributions of FCNCs coupled to new gauge bosons to the meson mixing parameters. To estimate how important they are, we compare their contributions with those of the new scalar bosons. The ratio of these two contributions is presented in Fig. 2. The results show that the significant contribution comes from the FCNCs of new gauge bosons. It once again clarifies the small effect of the new scalar fields on the meson mixing systems.

Finally, we investigate the constraints on the VEVs from $\Delta m_{K, B_s, B_d}$. In Fig. 1, the allowed region of parameters that satisfies the constraints given in Eqs. (31), (33) is the green one. The electroweak symmetry breaking energy scale, u, is not constrained by conditions imposed on the meson mass mixing parameters. However, these conditions affect the NP scale w. From Fig. 1, we obtain a lower bound on the NP scale, $w>$ 12 TeV. This lower bound is more stringent and is remarkably larger than that obtained previously [32]. This difference is because, in the previous study, the authors compared the NP contributions with experimental values and ignored the SM contributions to the theoretical predictions. Moreover, Eq. (131) in [32], the authors used $(\Delta m_{B_s})_{\text {NP}} < \frac{1}{(100 \ \text {TeV})^2} m_{B_s}f_{B_s}^2 \simeq 41.2871 /ps$, the upper limit for $(\Delta m_{B_s})_{\text {NP}}$ is even greater than that of the experimental value given in Eq. (30). This is not reasonable because the theoretical prediction must consist of both SM and NP contributions. We must also consider the uncertainties of both SM and experimental predictions. Thus, the NP contributions have to be constrained by the conditions given in Eqs. (31, 33).

Fig. 2

The figures present the dependence of ratios $\Delta m_{K,B_s,B_d}^{H_1,A}/\Delta m_{K,B_s,B_d}^{Z_2,Z_N}$ on the NP scale w

3.2 $B_s \rightarrow \mu ^+ \mu ^-$, $B \rightarrow K^* \mu ^+ \mu ^- \ \text {and} \ B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$

Rare decays of B meson, in particular of the decay induced by the quark level transition, $B_s \rightarrow \mu ^+ \mu ^-$, $B\rightarrow K^* \mu ^+ \mu ^-$ and $B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$, are sensitive to physics beyond the SM. The NP effects can be quantified via the language of the effective theory. The effective Hamiltonian related to the above decays is determined by the quark FCNCs given in (22), (24) and the lepton flavor-conserving neutral currents (LFCNCs). The LFCNCs coupled to the neutral scalars, $H_1, {\mathcal {A}}$, obtained from Eq. (15) as follows

$$\begin{aligned} -\frac{g}{2 m_{W}}\frac{u}{v} {\bar{l}}^{\prime }_{aL} M^{lD}_{ab} l^\prime _{bR} (H_1+i{\mathcal {A}})+H.c., \end{aligned}$$

(36)

where $M^{lD} =\text {Diag}(m_e, m_\mu ,m_\tau )$. It is worth noting that there is no neutral Higgs mediated FCNC in the lepton sector. The interactions of $Z_2$ and $Z_N$ with two charged leptons have been written in [31] read

$$\begin{aligned}&-\frac{g}{2c_W} {\bar{f}}\gamma ^\mu \left( g_V^{Z_2}(f)-g_A^{Z_2}(f) \gamma _5\right) f Z_{2 \mu }\nonumber \\&\quad -\frac{g}{2c_W}{\bar{f}}\gamma ^\mu \left( g_V^{Z_N}(f) -g_{A}^{Z_N}(f) \gamma _5 \right) f Z_{N \mu } , \end{aligned}$$

(37)

where the form of coefficients $g_V^{Z_2,Z_N}, g_A^{Z_2,Z_N}$ are found in [31].

Combining the quark FCNCs and the LFCNCs, we obtain the effective Hamiltonian for $B_s \rightarrow \mu ^+ \mu ^-$, $B \rightarrow K^* \mu ^+ \mu ^-$ and $B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$ processes as follows

$$\begin{aligned} {\mathcal {H}}_{\text {eff}}= & {} -\frac{4G_F}{\sqrt{2}}V_{tb}V^*_{ts}\sum _{i=9,10,S,P}\left( C_i(\mu ){\mathcal {O}}_i(\mu )\right. \nonumber \\&\left. +\,C^\prime _i(\mu ){\mathcal {O}}^\prime _i(\mu )\right) , \end{aligned}$$

(38)

where the operators are defined by

$$\begin{aligned} {\mathcal {O}}_9= & {} \frac{e^2}{(4\pi )^2}({\bar{s}}\gamma _\mu P_L b)({\bar{l}}\gamma ^\mu l), \nonumber \\ {\mathcal {O}}_{10}= & {} \frac{e^2}{(4\pi )^2}({\bar{s}} \gamma _\mu P_L b)({\bar{l}} \gamma ^\mu \gamma ^5 l), \end{aligned}$$

(39)

$$\begin{aligned} {\mathcal {O}}_S= & {} \frac{e^2}{(4 \pi )^2}({\bar{s}}P_R b)({\bar{l}}l), \nonumber \\ {\mathcal {O}}_P= & {} \frac{e^2}{(4 \pi )^2}\left( {\bar{s}}P_R b \right) \left( {\bar{l}}\gamma _5 l\right) . \end{aligned}$$

(40)

The operators ${\mathcal {O}}^\prime _{\text {9,10,S,P}}$ are obtained from ${\mathcal {O}}_{\text {9,10,S,P}}$ by replacing $P_L\leftrightarrow P_R$. Their Wilson coefficients consist of the SM leading and tree-level NP contributions. For $C_{9,10}$ we split into the SM and NP contributions as: $C_{9,10}=C_{9,10}^{\text {SM}}+C_{9,10}^{\text {NP}}$, where the central points of $C_{9,10}^{\text {SM}}$ are given in [46], $C_{10}^{\text {SM}}=-4.198, C_{9}^{\text {SM}}=4.344$, and the $C_{9,10,\text {S,P}}^{\text {NP}}$ are written by

$$\begin{aligned} C_9^{\text {NP}}\!=\! & {} -\Theta _{23}\frac{m_W^2}{c_W V_{tb}V_{ts}^*}\frac{(4\pi )^2}{e^2}\left( \frac{g_2}{g}\frac{g_V^{Z_2}(f)}{m_{Z_2}^2}\!+\!\frac{g_N}{g}\frac{g_V^{Z_N}(f)}{m_{Z_N}^2}\right) , \nonumber \\ C_{10}^{\text {NP}}= & {} \Theta _{23}\frac{m_W^2}{c_W V_{tb}V_{ts}^*}\frac{(4\pi )^2}{e^2}\left( \frac{g_2}{g}\frac{g_A^{Z_2}(f)}{m_{Z_2}^2}+\frac{g_N}{g}\frac{g_A^{Z_N}(f)}{m_{Z_N}^2}\right) .\nonumber \!\!\!\!\!\!\!\\ \end{aligned}$$

(41)

Noting that $C_{\text {S,P}}^{\text {SM}}=C_{\text {S,P}}^{\prime \text {SM}}=0$. Therefore, the $C_{\text {S,P}},C^{'}_{\text {S,P}}$ are obtained by NP contributions as follows

$$\begin{aligned} C_S^{\text {NP}}= & {} \frac{8 \pi ^2 }{e^2}\frac{1}{V_{tb}V_{ts}^*}\frac{\Gamma ^d_{23}\Gamma ^l_{\alpha \alpha }}{m_{H_1}^2}, \nonumber \\ C_S^{\prime \text {NP}}= & {} \frac{8 \pi ^2}{e^2}\frac{1}{V_{tb}V_{ts}^*}\frac{\left( \Gamma ^d_{32}\right) ^*\Gamma ^l_{\alpha \alpha }}{m_{H_1}^2},\nonumber \\ C_P^{\text {NP}}= & {} -\frac{8 \pi ^2}{e^2}\frac{1}{V_{tb}V_{ts}^*}\frac{\Gamma ^d_{23}\Delta ^l_{\alpha \alpha }}{m_{A}^2}, \nonumber \\ C_P^{\prime \text {NP}}= & {} \frac{8 \pi ^2}{e^2}\frac{1}{V_{tb}V_{ts}^*}\frac{\left( \Gamma ^d_{32}\right) ^*\Delta ^l_{\alpha \alpha }}{m_{A}^2}, \end{aligned}$$

(42)

where $\Gamma ^l_{\alpha \alpha }=\Delta ^l_{\alpha a}=\frac{u}{v}m_{l_\alpha }$.

From the effective Hamiltonian given in (38), we obtain the branching ratio of the $B_s \rightarrow l_{\alpha }^+ l_{\alpha }^-$ decay

$$\begin{aligned}&\text {Br}(B_s \rightarrow l_\alpha ^+ l_\alpha ^-)_{\text {theory}} = \frac{\tau _{B_s}}{64 \pi ^3}\alpha ^2 G_F^2 f_{B_s}^2\nonumber \\&\quad \times |V_{tb}V^*_{ts}|^2 m_{B_s} \sqrt{1-\frac{4m_{l_\alpha }^2}{m_{B_s}^2}} \nonumber \\&\quad \times \left\{ \left( 1-\frac{4m_{l_\alpha }^2}{m_{B_s}^2}\right) \left| \frac{m_{B_s}^2}{m_b+m_s} \left( C_S-C_S^\prime \right) \right| ^2\right. \nonumber \\&\left. \quad +\left| 2m_{l_\alpha }\left( C_{10}-C_{10}^\prime \right) +\frac{m_{B_s}^2}{m_b+m_s}\left( C_P-C_P^\prime \right) \right| ^2\right\} , \end{aligned}$$

(43)

where $\tau _{B_s}$ is the total lifetime of the $B_s$ meson. If including the effect of oscillations in the $B_s-{\bar{B}}_s$ system, the theoretical and experimental results are related by [47]

$$\begin{aligned} \text {Br}(B_s\rightarrow l_\alpha ^+ l_\alpha ^-)_{\text {exp}} \simeq \frac{1}{1-y_s}\text {Br}(B_s\rightarrow l_\alpha ^+ l_\alpha ^-)_{\text {theory}}, \end{aligned}$$

(44)

where $y_s =\frac{\Delta \Gamma _{B_s}}{2\Gamma _{B_s}}= 0.0645(3)$ [39]. For $B_s \rightarrow e^+e^-$, the SM prediction [48] is

$$\begin{aligned} \text {Br}(B_s \rightarrow e^+ e^-)_{\text {SM}}= (8.54 \pm 0.55) \times 10^{-14}, \end{aligned}$$

(45)

and the experimental bound has been given in [49] as

$$\begin{aligned} \text {Br}(B_{s}\rightarrow e^+ e^-)_{\text {exp}} < 2.8 \times 10^{-7}. \end{aligned}$$

(46)

The SM contribution to the branching ratio of $B_s \rightarrow e^+ e^-$ is strongly suppressed to the current experimental upper bound. It may be an excellent place to look for NP. Completely contrary to $B_{s}\rightarrow e^+ e^-$, the very recent measurement of the branching ratio $(B_s\rightarrow \mu ^{+}\mu ^{-})$ is given by [7]

$$\begin{aligned} \text {Br}(B_s\rightarrow \mu ^+ \mu ^-)_{\text {exp}}=(3.09^{+0.46\ +0.15}_{-0.43 \ -0.11 } ) \times 10^{-9}. \end{aligned}$$

(47)

This experimental upper bound closes to the central value of the SM prediction (including the effect of $B_s-{\bar{B}}_s$ oscillations) that has been studied in [50]

$$\begin{aligned} \text {Br}\left( B_s \rightarrow \mu ^+ \mu ^- \right) _{\text {SM}}=\left( 3.66 \pm 0.14 \right) \times 10^{-9}.\end{aligned}$$

(48)

It shows that experimental results are in slight tension with the SM prediction of Br$(B_s \rightarrow \mu ^+ \mu ^-)$. NP effects in $B_s \rightarrow \mu ^+ \mu ^-$ lead to new stringent constraints on NP scale. Let us concentrate on the numerical study of $B_s \rightarrow \mu ^+ \mu ^-$.

Fig. 3

The left panel draws the $\text {Br}(B_s \rightarrow \mu ^{+} \mu ^{-})$: red curve presents the prediction values of the 3-3-1-1 model, gray line represents the central values of the SM prediction. The blue and green lines represent the experimental upper and lower bounds. The right panel predicts the NP contributions to the Wilson coefficients. Here both panels are plotted by fixing: $\Lambda =1000w,f=-w,u=200 \ \text {GeV}$. Other parameters are selected as done in the Sect. 3

In Fig. 3, the red curve in the left panel demonstrates the $\text {Br}(B_s \rightarrow \mu ^{+} \mu ^{-})$ in the $\text {3-3-1-1}$ model as a function of the new symmetry breaking scale. The predicted results are only consistent with the current experimental bounds if the VEV, w, is larger than $\text {5 TeV}$. This bound is not as strict as the constraints obtained from studying the meson oscillations in Sect. 3.1. So, the best fit region pulls for both $({\bar{B}}_s-B_s)$ mixing and $\text {Br}(B_s \rightarrow \mu ^+ \mu ^-)$ experimental bounds is $w> 12$ TeV. In the right panel of Fig. 3, we draw the NP contributions to each Wilson coefficient. Compared to the $C_{9,10}^{\text {NP}}$, the $C_{\text {S,P}}$ are further suppressed by a factor of $10^{-4} \div 10^{-5}$. So, the main contribution of the NP to the $\text {Br}(B_s \rightarrow \mu ^{+} \mu ^{-})$ comes from the $C_{10}^{\text {NP}}$. In the limit $w > \text {12 TeV}$, the $C_{10}^{\text {NP}}$ is positive. It causes the $\text {Br}(B_s \rightarrow \mu ^{+} \mu ^{-})$ reduced about $5\%$ , which brings the theoretical prediction and experimental values get closer together.

If the $C_{10}^{\text {NP}}$ affects the decay process $B_s \rightarrow \mu ^+ \mu ^-$, the $C_{9}^{\text {NP}}$ plays a crucial role in $B \rightarrow K^* \mu ^+ \mu ^-$ decay. The current experimental measurements of the $b \rightarrow s \mu ^+ \mu ^-$ have attracted and led to many model-independent global analyses [51,52,53,54,55,56,57,58] assuming the presence of NP. The anomalies of the $B \rightarrow K^* \mu ^+ \mu ^-$ decay were explained if there exists a large negative contribution to the Wilson coefficient $C_{9}^{\text {NP}}$. The best-fit point for the $C_9^{\text {NP}}$ varies around $-1.1$. The green line in the right panel of Fig. 3 predicts the $C_9^{\text {NP}}$ in the $\text {3-3-1-1}$ model. In the limit, $w> 12 \ \text {TeV}$, we obtain its maximal prediction value $C_9^{\text {NP}} \simeq -0.01$. So, the NP coming from the $\text {3-3-1-1}$ model can not explain the anomalies of $B \rightarrow K^* \mu ^+ \mu ^-$ process.

The measurements of the branching fraction of the decay $B^+\rightarrow K^+ \mu ^+ \mu ^-$ [23, 24] have turned out to be slightly on the low side compared to SM expectations. Both the $C_9, C_{10}$ contribute to the $\text {Br}\left( B^+\rightarrow K^+ \mu ^+ \mu ^-\right)$. As predicted by the 3-3-1-1 model, the NP contribution to these parameters is minimal (see Fig. 3) because the NP scale satisfies the constraint $w >12 \ \text {TeV}$. Both the $C_{9}^{\text {NP}}$ and $C_{10}^{\text {NP}}$ are too low and far from the values of global analysis, see in [51,52,53,54]. Thus, we believe that the NP effects in $B^+ \rightarrow K^+ \mu ^+ \mu ^-$ remain small in the 3-3-1-1 model.

4 Radiative processes

4.1 $b \rightarrow s \gamma$ decay

The branching fraction and the photon energy spectrum of the radiative penguin $b \rightarrow \text {s} \gamma$ process have been firstly reported by CLEO experiment, Br$(b \rightarrow s \gamma )=(3.21\pm 0.43 \pm 0.27^{+0.18}_{-0.10}) \times 10^{-4}$ [8]. Recently, HFLAV group has obtained the average result by combining the measurements from CLEO, BaBar and Belle, Br$(b \rightarrow s \gamma )=(3.32\pm 0.15) \times 10^{-4}$ [39] for a photon-energy cut-off $E_{\gamma }>1.6$ GeV. This result is in good agreement with the SM prediction up to Next-to-Next-to-Leading Order (NNLO) Br$(b \rightarrow s \gamma )=(3.36 \pm 0.23) \times 10^{-4}$ [59, 60], with the same energy cut-off $E_{\gamma }$. It suggests that the NP contributions to this process, if any, have to be small. Thus, studying the $b\rightarrow s \gamma$ decay can give a strong constraint on the NP scale. The radiative process $b \rightarrow s \gamma$ is most conveniently described in the framework of an effective theory that arises after decoupling of new particles. Excluding the charged currents associated with the $W_{\mu }^\pm$ gauge boson, the $\text {3-3-1-1}$ model contains new charged currents, which couple to the new charged gauge bosons $Y_\mu ^\pm$, two charged Higgs bosons $H_4^\pm , H_5^\pm$, and the $\text {FCNCs}$ coupled to the $Z_{2,N}$ as given in Eq. (24). All of the above currents generate the $b \rightarrow s \gamma$ process.

Let us write down the charged scalar currents related to $b \rightarrow s \gamma$. The $H_4^\pm$ only couples to the exotic quarks, so it does not create the flavor-changing charged currents (FCCCs) for SM quarks. While $H_5^{\pm }$ couples to the SM quarks and creates the scalar FCCCs. The relevant Lagrangian is

$$\begin{aligned} {\mathcal {L}}_{\text {Yukawa}}^{H_5^\pm }=\frac{g}{\sqrt{2}m_W}\left\{ {\bar{d}}^{\prime }_L{\mathcal {X}} {\mathcal {M}}_uu^\prime _R+{\bar{d}}^{\prime }_R{\mathcal {M}}_d {\mathcal {Y}} u^\prime _L\right\} H_5^{-} +H.c., \nonumber \!\!\!\!\!\!\!\\ \end{aligned}$$

(49)

where ${\mathcal {Y}}=t_\beta V_{\text {CKM}}^{\dagger } -\frac{2}{s_{2\beta }}{\mathcal {T}}$ and ${\mathcal {X}}=\frac{1}{t_\beta } V_{\text {CKM}}^{\dagger } -\frac{2}{s_ {2\beta }}{\mathcal {T}}$. The ${\mathcal {T}}$ is defined as ${\mathcal {T}}_{ij}=(V_{d_L}^\dag )_{i3}(V_{u_L})_{3j}$, $s_{2\beta }=\sin 2\beta , t_{2\beta }=\tan 2\beta$. The charged currents associated with the $W^\pm , Y^\pm$, are described by the $\text {V-A}$ currents as follows

$$\begin{aligned} {\mathcal {L}}_{W,Y}^{\text {quark}}= & {} \frac{g}{2\sqrt{2}}{\bar{u}}^{\prime }\gamma ^\mu (1-\gamma _5)W^+_\mu V_{\text {CKM}}d^\prime +H.c. \nonumber \\&+ \frac{g}{2\sqrt{2}}\left\{ {\bar{d}}^{\prime }_j (V_{d_L}^*)_{j3}\gamma ^\mu (1-\gamma _5)Y^-_\mu U \right. \nonumber \\&\left. +{\bar{D}}_{\alpha }\gamma ^\mu (1-\gamma _5)Y^-_\mu (V_{u_L})_{\alpha j}u^\prime _{j}\right\} +H.c. . \end{aligned}$$

(50)

The effective Hamiltonian for the decay $b \rightarrow s \gamma$ is

$$\begin{aligned} {\mathcal {H}}_{\text {eff}}^{b \rightarrow s \gamma }= & {} -\frac{4G_F}{\sqrt{2}}V_{tb}V_{ts}^{*}[C_7(\mu _b){\mathcal {O}}_7\nonumber \\&+C_8(\mu _b){\mathcal {O}}_8 + C_7'(\mu _b){\mathcal {O}}'_7+C_8'(\mu _b){\mathcal {O}}'_8], \end{aligned}$$

(51)

with $\mu _b={\mathcal {O}}(m_b)$. The electromagnetic and chromomagnetic dipole operators ${\mathcal {O}}_7,{\mathcal {O}}_8$ are defined as

$$\begin{aligned} {\mathcal {O}}_7= & {} \frac{e}{(4\pi )^2} m_b({\bar{s}}_{\alpha }\sigma _{\mu \nu }P_R b_{\alpha })F^{\mu \nu }, \nonumber \\ {\mathcal {O}}_8= & {} \frac{g_s}{(4\pi )^2} m_b({\bar{s}}_{\alpha }\sigma _{\mu \nu }T^a_{\alpha \beta }P_R b_{\beta })G^{a \mu \nu }, \end{aligned}$$

(52)

and the primed operators ${\mathcal {O}}_{7,8}'$ are obtained by replacing $P_L \leftrightarrow P_R$. The Wilson coefficients $C_{7,8}(\mu _b)$ split as the sum of the SM and 3-3-1-1 contributions

$$\begin{aligned} C_{7,8}(\mu _b)=C_{7,8}^{\text {SM}}(\mu _b)+C_{7,8}^{\text {NP}}(\mu _b). \end{aligned}$$

(53)

Note that the Wilson coefficients $C_{7,8}'$ will be ignored in our calculation since they are suppressed by the ratio $m_s/m_b$. The SM Wilson coefficients $C_{7,8}^{\text {SM}}$ at the scale $\mu \sim m_W$ are first given by [61]

$$\begin{aligned} C^{\text {SM}(0)}_7(m_W)= & {} \frac{m_t^2}{m_W^2}f_{\gamma }\left( \frac{m_t^2}{m_W^2}\right) , \nonumber \\ C_{8}^{\text {SM}(0)}(m_W )= & {} \frac{m_t^2}{m_W^2}f_g \left( \frac{m_t^2}{m_W^2}\right) , \end{aligned}$$

(54)

where the index 0 indicates that the Wilson coefficients are calculated without QCD correction.

The NP contributes to $C_{7,8}^{\text {NP}}$ at the quantum level via the higher order charged current interactions in Eqs. (49), (50) and the FCNCs given in Eq. (24). They can be split into each contribution as follows

$$\begin{aligned} C_{7,8}^{\text {NP}(0)}=C_{7,8}^{H_5(0)}(m_{H_5})+C_{7,8}^{Y(0)}(m_Y)+C_{7,8}^{Z_{2,N}(0)}(m_{Z_{2,N}}), \end{aligned}$$

(55)

where

$$\begin{aligned} C_{7}^{H_5(0)}(m_{H_5})= & {} \frac{m_t^2}{m_{H_5}^2}\left[ \frac{1}{3} t_{\beta }^2 f_{\gamma }\left( \frac{m_t^2}{m_{H_5}^2}\right) +f^{\prime }_{\gamma } \left( \frac{m_t^2}{m_{H_5}^2}\right) \right] , \nonumber \\ C_{8}^{H_5(0)}(m_{H_5} )= & {} \frac{m_t^2}{m_{H_5}^2}\left[ \frac{1}{3}t_{\beta }^2 f_{g}\left( \frac{m_t^2}{m_{H_5}^2}\right) +f^{\prime }_{g} \left( \frac{m_t^2}{m_{H_5}^2}\right) \right] , \nonumber \\ C_{7}^{Y(0)}(m_Y)= & {} \frac{m_W^2}{m_Y^2}\frac{m_U^2}{m_Y^2}f_{\gamma }\left( \frac{m_U^2}{m_Y^2}\right) , \nonumber \\ C_{8}^{Y(0)}(m_Y )= & {} \frac{m_W^2}{m_Y^2} \frac{m_U^2}{m_Y^2}f_g \left( \frac{m_U^2}{m_Y^2}\right) , \end{aligned}$$

(56)

with all functions $f_{\gamma ,g}$ and $f'_{\gamma ,g}$ are defined as shown below

$$\begin{aligned} f_{\gamma }(x)= & {} \frac{(7-5x-8x^2)}{24(x-1)^3}+\frac{x(3x-2)}{4(x-1)^4} \ln {x}, \nonumber \\ f^{\prime }_{\gamma }(x)= & {} \frac{(3-5x)}{12(x-1)^2}+\frac{(3x-2)}{6(x-1)^3}\ln {x}, \nonumber \\ f_{g}(x)= & {} \frac{2+5x-x^2}{8(x-1)^3}-\frac{3x}{4(x-1)^4}\ln {x}, \nonumber \\ f^{\prime }_{g}(x)= & {} \frac{3-x}{4(x-1)^2}-\frac{1}{2(x-1)^3}\ln {x}. \end{aligned}$$

(57)

The $C_{7}^{Z_{2,N}(0)}(m_{Z_{2,N}})$ are obtained by the FCNCs coupled to the $Z_{2,N}$ and have a form as given in [63]

$$\begin{aligned} C_{7}^{Z_{2,N}(0)}(m_{Z_{2,N}})= & {} -\frac{2}{9g^2}\frac{m_W^2}{m_{Z_{2,N}}^2} \sum _{f=d,s,b}\frac{g^{fs*}_{L}g^{fb}_{L}}{V_{ts}^{*}V_{tb}}\nonumber \\&+\frac{2}{3g^2}\frac{m_W^2}{m_{Z_{2,N}}^2}\sum _{f=d,s,b}\frac{m_f}{m_b}\frac{g^{fs*}_{L}g^{fb}_{R}}{V_{ts}^{*}V_{tb}}, \nonumber \\ C_{8}^{Z_{2,N}(0)}(m_{Z_{2,N}} )= & {} -3C_7^{Z_{2,N}}(m_{Z_{2,N}}) \end{aligned}$$

(58)

with $g^{ff}_{L,R}=[g_V^{Z_{2,N}}(f)\pm g_A^{Z_{2,N}}(f)]/2$ are the flavor-conversing couplings given in [31] while $g^{fs,fb}$ are the flavor-violating couplings defined in Eq. (24).

Noting that QCD corrections to $b \rightarrow s \gamma$ are important and have to be included to complete the analysis. The Ref. [62] predicted $C_{7,8}^{\text {SM}}$ up to NNLO, $C_7^{\text {SM}}(\mu _b)=-0.3523$ for $\mu _b=2.5$ GeV. The recent calculations of the NP contributions to the $C_{7, 8}^{\text {NP}}$ have been considered at the Leading Order (LO) [63, 64]. In the following work, we study the effect of QCD corrections on the $C_{7,8}^{\text {NP}}$ at the LO. In the $\text {3-3-1-1}$ model, there are four heavy scales: $m_Y$, $m_{Z_{2,N}}$ and $m_{H_5}$ . The difference between these scales can be ignored because the effects of QCD running are less important at high energies. Hence, we assume all calculations are at the same scale. For instance, we choose $\mu \sim m_Y$. The QCD corrections for $C^{Z_{2,N}}_{7}$ are given by

$$\begin{aligned} C_{7}^{Z_{2,N}}(\mu _b)=\kappa _7C_7^{Z_{2,N}}(m_Y)+\kappa _8 C_8^{Z_{2,N}}(m_Y)+\Delta _{Z_{Z_{2,N}}}(\mu _b),\nonumber \!\!\!\!\!\!\\ \end{aligned}$$

(59)

where $\kappa _{7,8}$ are NP magic numbers $\kappa _7=0.39,\kappa _8=0.130$ at $\mu \sim 10$ TeV [64]. $\Delta _{Z_{2,N}}(\mu _b)$ are the contributions coming from the mixing of new neutral current-current operators, generated by the exchange of $Z_{2,N}$ with the dipole operators ${\mathcal {O}}_{7,8}$

$$\begin{aligned} \Delta _{Z_{Z_{2,N}}}(\mu _b)= & {} \sum _{\begin{array}{c} A=L,R,\\ f=u,c,t,d,s,b \end{array}}\kappa ^f_{LA}\Delta _{LA}C_2^f(w)\nonumber \\&+\sum _{A=L,R}{\hat{\kappa }}^d_{LA}\Delta _{LA}{\hat{C}}^d_2(w),\nonumber \\ \Delta _{LA}C_2^f(m_Y)= & {} -\frac{2}{g^2}\frac{g_L^{sb*}g_A^{ff}}{V_{ts}^{*}V_{tb}}, \nonumber \\ \Delta _{LA}{\hat{C}}_2^d(m_Y)= & {} -\frac{2}{g^2}\frac{g_L^{sd*}g_A^{bd}}{V_{ts}^{*}V_{tb}} \end{aligned}$$

(60)

For $w=10$ TeV, we have $m_Y\simeq 3.2$ TeV, and obtain $C_{7}^{Z_{2,N}}(\mu _b)\simeq {\mathcal {O}}(10^{-5})$, which is strongly suppressed by the SM prediction, $C_7^{\text {SM}}(\mu _b)=-0.3523$. Therefore, in the next calculation, $C_{7}^{Z_{2,N}}$ can be ignored. If including the LO of QCD corrections, the $C_{7}^{Y}$ and $C_7^{H_5}$ have the form as [63, 64]

$$\begin{aligned} C_{7}^{Y}(\mu _b)= & {} \kappa _7C_7^{Y}(m_Y)+\kappa _8 C_8^{Y}(m_Y), \nonumber \\ C_{7}^{H_5}(\mu _b)= & {} \kappa _7C_7^{H_5}(m_Y)+\kappa _8 C_8^{H_5}(m_Y). \end{aligned}$$

(61)

The branching ratio Br$(b \rightarrow s \gamma )$ is given as

$$\begin{aligned} \text {Br}(b \rightarrow s \gamma )= & {} \frac{6\alpha }{\pi C}\frac{|V_{ts}^{*}V_{tb}|^2}{|V_{cb}|^2}(|C_7(\mu _b)|^2\nonumber \\&+N(E_{\gamma }))\text {Br}(b\rightarrow c e{\bar{\nu }}_e) , \end{aligned}$$

(62)

where $N(E_{\gamma })=3.6(6)\times 10^{-3}$ is a non-perturbative contribution, $C=|V_{ub}/V_{cb}|^2\Gamma (b\rightarrow ce{\bar{\nu }}_e)/\Gamma (b\rightarrow ue{\bar{\nu }}_e)=0.580(16)$ [62] and branching ratio for semi-leptonic decay Br$(b\rightarrow ce{\bar{\nu }}_e)=0.1086(35)$ [40]. Other parameters are input as in Sect. 3.1.

The Br$(b \rightarrow s \gamma )$ behaves as a function of the new particle masses, such as $m_{Y}, m_{H_5}, m_{U}$. These masses are understood as free parameters. In the limit, $u,v \ll -f\frac{u^2+v^2}{uv} \sim w \sim \Lambda$, they can be rewritten as

$$\begin{aligned} m_Y^2 \simeq \frac{g^2w^2}{4}, \quad m_{H_5}^2 \simeq \frac{w^2}{\sqrt{2}}, \quad m_{U} = -\frac{h^Uw}{\sqrt{2}}, \end{aligned}$$

(63)

where, $g=\sqrt{4\pi \alpha / s_W^2} \simeq 0.63$, $h^U$ is unknown parameter. So, $m_U$ is arbitrary at the TeV energy scale, which can be higher or smaller than two other masses, $m_{H_5}, m_Y$. Without loss of generality, we investigate the mass hierarchy of new particles according to three scenarios: $m_{H_5}> m_{Y} > m_U$, $m_{H_5}> m_{U} > m_Y$, and $m_{U}> m_{H_5} >m_Y$.

Fig. 4

The dependence of the Br$(b \rightarrow s \gamma )$ on the NP scale w in the limit, $u,v \ll -f\frac{u^2+v^2}{uv} \sim w \sim \Lambda$. The solid black lines indicate the current experimental constraint Br$(b\rightarrow s\gamma )=(3.32\pm 0.15)\times 10^{-4}$ [39]

In Fig. 4, we show the dependence of Br$(b \rightarrow s \gamma )$ on the NP scale w in the limit $u,v \ll -f\frac{u^2+v^2}{uv} \sim w \sim \Lambda$. Each panel corresponds to the scenarios of mass hierarchy and three different choices of $t_\beta$. We see that the branching ratio strongly depends on the values of $t_\beta$ where the term containing $t_\beta$ comes from $C_7^{H_5}$. So we conclude that $C_7^{H_5}$ plays an important role in the radiative decay process $b \rightarrow s \gamma$. This is true for all three scenarios of the mass hierarchy. Besides, Fig. 4 indicates that the mass hierarchy does not affect Br$(b \rightarrow s \gamma )$ much. This result is understood as the main contribution coming from $C_7^{H_5}$, and it is stronger than other contributions by the coefficient $t_\beta ^2$. In the large $t_\beta$ limit, the Br$(b \rightarrow s \gamma ) \simeq |C_7^{H_5}|^2 \simeq \frac{t_\beta ^2}{w^2}$. The lower bound on the NP scale depends on the value of the $t_\beta$, specifically, $w \ge 1 \ \text {TeV}$ for $t_\beta =1$; $w \ge 4.1 \ \text {TeV}$ for $t_\beta =10$; $w \ge 7.7 \ \text {TeV}$ for $t_\beta =20$. These limits are weaker than the ones mentioned above.

To close this section, we consider the influence of NP on the $\text {Br}(b\rightarrow s \gamma )$ in the limit $u,v \ll -f \sim w \sim \Lambda$. In Fig. 5, we see that the dependence of branching ratio on $t_\beta$ is not as strong as predicted in Fig. 4. This difference can be explained by the dependence of $m_{H_5}$ on $t_{\beta }$, $m_{H_5}= 0.85 w\sqrt{\left( t_{\beta }+{1}/{t_\beta }\right) }$. Therefore, Br$(b \rightarrow s \gamma ) \simeq |C_7^{H_5}|^2 \simeq t_{\beta }^2\frac{1}{m_{H_5}^2}\simeq t_{\beta }\frac{1}{w^2}$, whereas Br$(b \rightarrow s \gamma ) \simeq t_{\beta }^2\frac{1}{w^2}$ for the previous case. This leads to the lower limit of the NP also changing for each choice of $t_\beta$. In the limit given in Sect. 3.1, $w > 12 \ \text {TeV}$, the affect of $t_{\beta }$ to Br$(b\rightarrow s\gamma )$ becomes trivial and the predicted branching ratio approaches the central value of the experimental bounds.

Fig. 5

The dependence of the branching ratio Br$(b \rightarrow s \gamma )$ on the NP scale w in the limit $u,v \ll -f \sim w \sim \Lambda$. The solid black lines indicate the current experimental constraint Br$(b\rightarrow s\gamma )=(3.32\pm 0.15)\times 10^{-4}$ [39]

4.2 Charged lepton flavor violation

The charged lepton flavor violation (CLFV) processes are strongly suppressed in the SM with right-handed neutrinos, Br$(l_i \rightarrow l_j \gamma ) \simeq 10^{-55}$. Meanwhile, the current experimental bounds limits are given as [40]

$$\begin{aligned} \text {Br}(\mu ^- \rightarrow e^- \gamma )< & {} 4.2 \times 10^{-13}, \nonumber \\ \text {Br}(\tau ^- \rightarrow e^- \gamma )< & {} 3.3 \times 10^{-8}, \nonumber \\ \text {Br}(\tau ^- \rightarrow \mu ^- \gamma )< & {} 4.4 \times 10^{-8}. \end{aligned}$$

(64)

It implies that the CLFV processes open a large window for studying the NP signals beyond the SM. Note that in the SM with right-handed neutrinos, the decay processes, $l_i \rightarrow l_j \gamma$, come from the one-loop level with $W^\pm$ mediated in the loop. The $\text {Br}(l_i \rightarrow l_j \gamma )$ is suppressed due to the mixing matrix elements of the neutrinos. The 3-3-1-1 model anticipates the existence of additional charged currents associated with the new charged particles, $Y^\pm , H^\pm _{4,5}$. Consequently, the new one-loop diagrams in the model may contribute significantly to the $\text {Br} \left( l_i \rightarrow l_j \gamma \right)$. This branching ratio may reach the upper experimental bound given in Eq. (64). In order to study the CLFV processes, we first write down the relevant Lagrangian based on the physical states as follows

$$\begin{aligned}&{\mathcal {L}}^{\text {lepton}}_{\mathrm {Scalar}}\supset \frac{h_{ab}^e u}{\sqrt{u^2+v^2}}\left( {\bar{\nu }}^{\prime }_{kL}(U^{\nu *}_L)_{ka}+\overline{(\nu ^{\prime }_{kR})^c} V^{\nu *}_{ka} \right) \\&\quad \times (U^l_{R})_{bj}e_{jR}^\prime H_5^+ +\frac{h_{ab}^e \omega }{\sqrt{v^2+\omega ^2}}\overline{(N^\prime _{kR})^c}(U_R^{N })_{ka}\nonumber \\&\quad \times (U^l_{ R})_{bj}e_{jR}^\prime H_4^+\\&\quad +\frac{h_{ab}^\nu v}{\sqrt{u^2+v^2}}{\bar{e}}^{\prime }_{jL}(U_{L}^{l*})_{ja}\left( (V^{\nu T})_{bk}(\nu _{kL}^\prime )^c\right. \nonumber \\&\quad \left. +(U^{\nu }_R)_{bk}\nu _{kR}^\prime \right) H_5^- \\&\quad +\frac{h_{ab}^\nu \omega }{\sqrt{u^2+\omega ^2}}\overline{(N^\prime _{jR})^c}(U_R^{N *})_{ja}\nonumber \\&\quad \times \left( (V^{\nu T})_{bk}(\nu _{kL}^\prime )^c+(U^{\nu }_R)_{bk}\nu _{kR}^\prime \right) H_o^\prime + H.c. \end{aligned}$$

The charged currents associated with the new gauge bosons are written in the physical states as follows

$$\begin{aligned} {\mathcal {L}}_{W,Y}^{\text {lepton}}= & {} -\frac{g}{\sqrt{2}} \left\{ \overline{\nu }_{aL}\gamma ^\mu e_{aL}W_\mu ^+ +\overline{e}_{aL}\gamma ^\mu (N_{aR})^cY_\mu ^- \right\} +H.c. \nonumber \\= & {} -\frac{g}{\sqrt{2}}\left\{ \left( {\bar{\nu }}^{\prime }_{kL}(U^{\nu *}_L)_{ka}\!+\! \overline{(\nu _{kR}^\prime )^c}V^{\nu *}_{ka} \right) \gamma ^\mu (U^l_{ L})_{aj}e_{jL}^\prime W^+_\mu \right. \nonumber \\&\left. + {\bar{e}}^{\prime }_{kL} (U^{l*}_L)_{ka}\gamma ^\mu (U_{R}^{N*})_{aj}(N^\prime _{jR})^c Y^-_\mu \right\} +H.c.. \end{aligned}$$

(65)

Next, we write the effective Lagrangian relevant for the $\mu \rightarrow e \gamma$ processes in the traditional form

$$\begin{aligned} {\mathcal {L}}_{\text {eff}}^{\mu \rightarrow e\gamma }= & {} -4\frac{e G_F}{\sqrt{2}}m_\mu \left( A_R {\bar{e}} \sigma _{\mu \nu }P_R \mu \right. \nonumber \\&\left. +A_L {\bar{e}} \sigma _{\mu \nu }P_L \mu \right) F^{\mu \nu }+H.c., \end{aligned}$$

(66)

where the factors $A_L, A_R$ are obtained by calculating all the one-loop diagrams. We use the ’t Hooft–Feynman gauge and keep the external lepton masses for calculations. The obtained results are inspired by [66]. The factors $A_{L, R}$ are divided into individual contributions, as shown below

$$\begin{aligned} A_{L,R}= & {} A_{L,R}^W+A_{L,R}^Y+A_{L,R}^{H_5}+A_{L,R}^{H_4}, \end{aligned}$$

(67)

where

$$\begin{aligned} A_R^W= & {} -\frac{eg^2}{32\pi ^2 m_W^2} \sum _{j=1}^{3} (U^{\nu *}_L)_{\mu j} (U^{\nu }_L)_{ e j}f\left( \frac{m_{\nu _j}^2}{m_W^2}\right) , \nonumber \\ A_L^W= & {} -\frac{eg^2 m_e}{32\pi ^2 m_W^2 m_{\mu }} \sum _{j=1}^{3} (U^{\nu *}_L)_{\mu j} (U^{\nu }_L)_{ e j} f\left( \frac{m_{\nu _j}^2}{m_W^2}\right) , \nonumber \\ A_R^Y= & {} -\frac{eg^2}{32\pi ^2 m_Y^2} \sum _{j=1}^{3} (U^{N *}_R)_{\mu j} (U^{N }_R)_{e j} f\left( \frac{m_{N_j}^2}{m_Y^2}\right) , \nonumber \\ A_L^Y= & {} -\frac{eg^2 m_e}{32\pi ^2 m_Y^2 m_{\mu }} \sum _{j=1}^{3} (U^{N *}_R)_{\mu j} (U^{N}_R)_{ e j} f\left( \frac{m_{N_j}^2}{m_Y^2}\right) , \nonumber \\ A_L^{H_5}= & {} -\frac{eg^2 m_e m_{\mu }}{32\pi ^2 m_W^2 m_{H_5}^2t_{\beta }^2} \sum _{j=1}^{3} (U^{\nu *}_L)_{\mu j} (U^{\nu }_L)_{ e j} g\left( \frac{m_{\nu _j}^2}{m_{H_5}^2}\right) \nonumber \\&- \frac{eg^2 m_e v^2}{64\pi ^2 m_W^2 m_{H_5}^2 m_{\mu }} \sum _{j,k=1}^{3} (h^{\nu *})_{\mu j}(h^{\nu })_{e j} (U^{\nu }_R)_{jk}\nonumber \\&\times (U^{\nu *}_R)_{j k}g\left( \frac{M_{\nu _{j}}^2}{m_{H_5}^2}\right) \nonumber \\&- \frac{eg^2 v^2m_e}{64\pi ^2 m_W^2 m_{H_5}^2 m_{\mu }} \sum _{j,k=1}^{3} (h^{\nu *})_{\mu j}(h^{\nu })_{e j}\nonumber \\&\times (V^{\nu T})_{jk} (V^{\nu T*})_{j k}g\left( \frac{M_{\nu _{j}}^2}{m_{H_5}^2}\right) , \nonumber \\ A_R^{H_5}= & {} -\frac{eg^2 m_e^2}{32\pi ^2 m_W^2 m_{H_5}^2 t_{\beta }^2} \sum _{j=1}^{3} (U^{\nu *}_L)_{\mu j} (U^{\nu }_L)_{ e j} g\left( \frac{m_{\nu _j}^2}{m_{H_5}^2}\right) \nonumber \\&- \frac{eg^2 v^2}{64\pi ^2 m_W^2 m_{H_5}^2 } \sum _{j,k=1}^{3} (h^{\nu *})_{\mu j}(h^{ \nu })_{e j} (U^{\nu }_R)_{jk}\nonumber \\&\times (U^{\nu *}_R)_{j k} g\left( \frac{M_{\nu _{j}}^2}{m_{H_5}^2}\right) \nonumber \\&- \frac{eg^2 v^2}{64\pi ^2 m_W^2 m_{H_5}^2 } \sum _{j,k=1}^{3} (h^{\nu *})_{\mu j}(h^{\nu })_{e j}(V^{\nu T})_{jk} \nonumber \\&\times (V^{\nu T*})_{j k}g\left( \frac{M_{\nu _{j}}^2}{m_{H_5}^2}\right) , \nonumber \\ A_L^{H_4}= & {} -\frac{eg^2 m_e m_{\mu }}{32\pi ^2 m_Y^2 m_{H_4}^2t_{\beta \prime }^2} \sum _{j=1}^{3} (U^{N *}_R)_{\mu j} (U^{N }_R)_{e j} g\left( \frac{m_{N_j}^2}{m_{H_4}^2}\right) , \nonumber \\ A_R^{H_4}= & {} -\frac{eg^2 m_e^2}{32\pi ^2 m_Y^2 m_{H_4}^2 t_{\beta \prime }^2} \sum _{j=1}^{3} (U^{N*}_R)_{\mu j} (U^{N }_R)_{e j} g\left( \frac{m_{N_j}^2}{m_{H_4}^2}\right) ,\nonumber \\ \end{aligned}$$

(68)

The functions f(x) and g(x) are defined by

$$\begin{aligned} f(x)= & {} \frac{10-43x+78x^2-48x^3+4x^4+18x^3\log {x}}{12 (x-1)^4},\nonumber \\ g(x)= & {} \frac{1-6x+3x^2+2x^3-6x^2\log {x}}{12(x-1)^4}. \end{aligned}$$

(69)

The notations $m_{\nu _j}, M_{\nu _{j}}, m_e, m_{\mu }$ are understood as the masses of light, heavy neutrinos, electron, and muon, respectively.

From the effective Lagrangian (66), we finally got the branching ratio $\text {Br}(\mu \rightarrow e \gamma )$ as follows

$$\begin{aligned} \text {Br}(\mu \rightarrow e \gamma )= & {} \frac{12\pi ^2}{G_F^2}(|A_L|^2+|A_R|^2)\text {Br}(\mu \rightarrow e \tilde{\nu _{e}} \nu _{\mu }),\nonumber \\ \end{aligned}$$

(70)

where $G_F=\frac{g^2}{4\sqrt{2}m_W^2}$ is the Fermi coupling constant, $\text {Br}(\mu \rightarrow e \tilde{\nu _{e}} \nu _{\mu }) =100 \%$ as given in [40].

Before considering numerical calculations of the branching ratio $\text {Br}(\mu \rightarrow e \gamma )$, let us make some assumptions. We assume that a diagonal matrix presents the Yukawa couplings $h^e_{ab}$ in the flavor basis. Thus, the matrix $U^{\nu }_L$ is identified as the PMNS matrix $U_{\text {PMNS}}$, which has been measured experimentally. Both the mixing matrices $U^\nu _R, V^{\nu }$ as well as $U_{L,R}^N$ are new and not constrained by experiments. To simplify, we suppose that the Yukawa couplings of the right-handed neutrinos $h^{ \prime \nu }$ are presented by a diagonal matrix. This indicates that the Majorana neutrino mass matrix has the form as $M_R^{\nu }=\text {Diag}(M_{\nu _1}, M_{\nu _2},M_{\nu _3})$ and thus the right-handed neutrino mixing mass matrix $U^\nu _R$ is a unit matrix. The mixing matrix $V^{\nu }$ is also assumed to be diagonal. Finally, for the mixing matrix of the new leptons $U_{R}^N$, we can use three arbitrary angles $\theta ^N_{ij}, (i,j=1,2,3)$ and a Dirac CP phase $\delta ^N$ to parameterize.

With the above option, the Yukawa couplings $h^e, h^{\prime \nu }$ can be translated into the charged lepton and sterile neutrino masses as follows

$$\begin{aligned} h^e= & {} -\frac{\sqrt{2}}{v} \text {Diag}\left( m_{e}, m_{\mu }, m_{\tau } \right) , \nonumber \\ h^{\prime \nu }= & {} -\frac{1}{\sqrt{2}\Lambda } \text {Diag}\left( M_{\nu _1}, M_{\nu _2}, M_{\nu _3} \right) . \end{aligned}$$

(71)

The Yukawa couplings $h^\nu$, which determine the neutrino Dirac mass, are rewritten by using Casas-Ibarra parametrization as given in [65]

$$\begin{aligned} h^{\nu }\!=\!\frac{\sqrt{2}}{u}\!\left( \! \begin{array}{ccc} \sqrt{M_{\nu _1}} &{}0 &{}0\\ 0 &{} \sqrt{M_{ \nu _2}} &{} 0 \\ 0&{} 0&{} \sqrt{M_{\nu _3}} \\ \end{array} \right) R \!\left( \! \begin{array}{ccc} \sqrt{m_{\nu _1}} &{}0 &{} 0\\ 0 &{} \sqrt{m_{\nu _2}} &{} 0 \\ 0&{} 0&{} \sqrt{m_{\nu _3}} \\ \end{array} \right) U^{\nu \dagger }_L,\nonumber \!\!\!\!\!\!\!\\ \end{aligned}$$

(72)

where R is an orthogonal matrix which is presented via arbitrary angles as the following

$$\begin{aligned} R= & {} \left( \begin{array}{ccc} {\hat{c}}_2{\hat{c}}_3 &{}-{\hat{c}}_1 {\hat{s}}_3-{\hat{s}}_1{\hat{s}}_2{\hat{c}}_3 &{}{\hat{s}}_1{\hat{s}}_3-{\hat{c}}_1{\hat{s}}_2{\hat{c}}_3\\ {\hat{c}}_2{\hat{s}}_3 &{}{\hat{c}}_1 {\hat{c}}_3-{\hat{s}}_1{\hat{s}}_2{\hat{s}}_3 &{}-{\hat{s}}_1{\hat{c}}_3-{\hat{c}}_1{\hat{s}}_2{\hat{s}}_3 \\ {\hat{s}}_2 &{}{\hat{s}}_1 {\hat{c}}_2 &{}{\hat{s}}_1{\hat{c}}_2\\ \end{array} \right) \end{aligned}$$

(73)

with ${\hat{s}}_i=\sin {\hat{\theta }}_{i}$, ${\hat{c}}_i=\cos {\hat{\theta }}_{i}, i=1,2,3$ and ${\hat{\theta }}_{ij}\in [0,\pi /2]$.

For the magnitudes of relevant masses and the VEVs, we also work on the limits $u,v \ll w\sim \Lambda$, $u^2+v^2=246^2 \ \text {GeV}^2$. To be consistent with the unitary bound [67], we need the constraint: $m_N < 16m_{Y}$. The masses of new charged Higgs $H_{4,5}^{\pm }$ and new gauge boson $Y^{\pm }$ are approximately taken as similar in the Sect. 4.1. In keeping with constraints from dark matter studies in [32], the new fermion mass is at the TeV scale. The mixing angle $t_{\beta ^{\prime }}$ can be expressed via the energy scales u, w such as $t_{\beta ^{\prime }}=\sqrt{246^2-u^2}/w$. Other known parameters are taken from [40] as given

$$\begin{aligned} m_W= & {} 80.385\ \text {GeV}, \quad m_e=0.5109989461 \ \text {MeV}, \nonumber \\ m_{\mu }= & {} 105.6583745 \ \text {MeV} , \nonumber \\ \sin ^2(\theta _{12})= & {} 0.307, \quad \sin ^2(\theta _{23})=0.51, \nonumber \\ \sin ^2(\theta _{13})= & {} 0.021,\quad \alpha =\frac{1}{137}, \nonumber \\ \Delta m_{12}^2= & {} 7.53 \times 10^{-5} \ \text {eV}^2, \quad \Delta m_{23}^2=2.45 \times 10^{-3} \ \text {eV}^2,\nonumber \!\!\!\!\!\!\!\\ \end{aligned}$$

(74)

where $\theta _{ij}$ are the mixing angles of the neutrino mixing matrix.

In addition, the branching ratio $\text {Br}(\mu \rightarrow e \gamma )$ also depends on the unknown parameters, such as six mixing angles (${\hat{\theta }}_{ij}$, $\theta _{ij}^N$), one CP phase $\delta ^N$, the masses of new particles $m_N, M_{\nu _i}$. In the following, we are going to present the results of numerical calculations for the case where unknown parameters are chosen as

$$\begin{aligned} \theta ^N_{12}= & {} \pi /6, \quad \theta ^N_{13}=\pi /3, \nonumber \\ \theta ^N_{23}= & {} \pi /4, \quad \delta ^N=0, \nonumber \\ {\hat{\theta }}_{1}= & {} \pi /3, \quad {\hat{\theta }}_{2}=\pi /4, \nonumber \\ {\hat{\theta }}_{3}= & {} \pi /6, \nonumber \\ m_{\nu _1}= & {} 0.01 \ \text {eV} , \quad M_{\nu _1}=10^9 \ \text {GeV}, \nonumber \\ M_{\nu _2}= & {} M_{\nu _3}=10^3 M_{\nu _1}, \nonumber \\ m_{N_1}= & {} 2000 \ \text {GeV}, \quad m_{N_2}=2200 \ \text {GeV}, \nonumber \\ m_{N_3}= & {} 2400 \ \text {GeV}. \end{aligned}$$

(75)

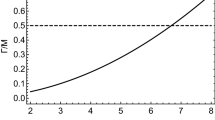
The Fig. 6 estimates the value of each contribution into the Br$(\mu \rightarrow e \gamma )$. The dominant contribution comes from the new gauge bosons $Y^\pm$. The NP scale is strongly constrained by the experiments [40], $\text {Br}(\mu \rightarrow e \gamma )_{\text {exp}} < 4.2 \times 10^{-13}$. To be consistent with this bound, the NP scale satisfies $w > 7.3$ TeV, which is similar to the bound derived from studying the $b \rightarrow s \gamma$ decay.

Fig. 6

The figure presents the dependence of the branching ratio $\text {Br}(\mu \rightarrow e \gamma )$ on the NP scale w for each contribution. The solid black line indicates the upper from the experiment [40]. Here $u=10$ GeV

The Fig. 7 demonstrates $\text {Br}(\mu \rightarrow e \gamma )_{\text {total}}$ as a function of NP scale w with three different values of the electroweak scale, u, $u=5$ GeV, $u=10$ GeV and $u=20$ GeV. There is no separation between the graphs corresponding to different choices of u. As a result, the $\text {Br}(\mu \rightarrow e \gamma )_{\text {total}}$ depends very weakly on the u. It is important to keep in mind that the factors $A_{L,R}^{H_4,H_5}$ are greatly influenced by the electroweak scales u and v. Therefore, this result shows that the charged currents associated with the charged Higgs particles have negligible influence on the $\mu \rightarrow e \gamma$ decay and may be ignored. Strong constraints are imposed on the charged current associated with new gauge bosons.

Fig. 7

The figure presents the comparison of the dependence of the total branching ratio Br$(\mu \rightarrow e \gamma )_{\text {total}}$ on the NP scale w with $u=5$ GeV, $u=10$ GeV and $u=20$ GeV, respectively. The solid black line indicates the upper bound from the experiment [40]

5 Conclusions

In the 3-3-1-1 model, the tree-level FCNCs appear due to the non-universal assignment of quark families. Experiments on meson oscillations strongly constrain these interactions. We computed the mass difference for $K^0 - {\bar{K}}^0, B_d^0- {\bar{B}}^0_d, B_s^0- {\bar{B}}^0_s$ based on the tree-level FCNCs and noticed that the main contributions to the meson oscillations come from the new neutral gauge bosons mediation. The NP scale is strongly constrained by the experimental bounds on mixing mass parameters. We have obtained the lower bound on the new gauge boson mass $\text {M}_{\text {new}}>12$ TeV, which is more stringent than the constraint previously given in [32]. This change is because previous studies omitted the contributions of new Higgs, especially those of the SM. Our result is consistent with that of [68]. We also studied the tree-level FCNCs affecting the branching ratio of $B_s \rightarrow \mu ^+ \mu ^-$, $B\rightarrow K^* \mu ^+ \mu ^-$ and $B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$. In the parameter region consistent with the experimental constraints on the meson mass difference, the tree-level FCNCs give small contributions to these branching ratios, which is consistent with the measurement $B_s \rightarrow \mu ^+ \mu ^-$ [4,5,6,7] but can not explain the $B \rightarrow K^* \mu ^+ \mu ^-$ and $B^{+}\rightarrow K^{+}\mu ^{+}\mu ^{-}$ anomalies [16,17,18,19,20,21,22,23,24].

For the radiative decay processes, we concentrated on the flavor-changing $b \rightarrow s\gamma$ decay. The large contribution arises from the Wilson coefficient $C_7^{H_5}$ yielded from one-loop diagrams with the new charged Higgs boson mediation. In spite of the enhanced contributions due to the factor $t_{\beta }=v/u$, the predicted branching ratio $\text {Br}(b \rightarrow s\gamma )$ is consistent with the measurement [39], if $\text {M}_{\text {new}}$ is chosen as above mentioned. In contrast to the $b \rightarrow s\gamma$ decay, the branching ratio of the lepton flavor-violating $\mu \rightarrow e \gamma$ decay obtains a large contribution from one-loop diagrams with new gauge bosons exchange. Due to the large mixing of new neutral leptons, the branching ratio $\text {Br}( \mu \rightarrow e \gamma )$ can reach the experimental upper bound.