Detecting long-lived multi-charged particles in neutrino mass models with MoEDAL

Abstract

A certain class of neutrino mass models predicts long-lived particles whose electric charge is four or three times larger than that of protons. Such particles, if they are light enough, may be produced at the LHC and detected. We investigate the possibility of observing those long-lived multi-charged particles with the MoEDAL detector, which is sensitive to long-lived particles with low velocities ($\beta$) and a large electric charge (Z) with $\Theta \equiv \beta /Z \lesssim 0.15$. We demonstrate that multi-charged scalar particles with a large Z give three-fold advantage for MoEDAL; reduction of $\Theta$ due to strong interactions with the detector, and enhancement of the photon-fusion process, which not only increases the production cross-section but also lowers the average production velocity, reducing $\Theta$ further. To demonstrate the performance of MoEDAL on multi-charged long-lived particles, two concrete neutrino mass models are studied. In the first model, the new physics sector is non-coloured and contains long-lived particles with electric charges 2, 3 and 4. A model-independent study finds MoEDAL can expect more than 1 signal event at the HL-LHC ($L = 300$ $\hbox {fb}^{-1}$) if these particles are lighter than 600, 1100 and 1430 GeV, respectively. These compare with the current ATLAS limits 650, 780 and 920 GeV for $L = 36$ $\hbox {fb}^{-1}$. The second model has a coloured new physics sector, which possesses long-lived particles with electric charges 4/3, 7/3 and 10/3. The corresponding MoEDAL’s mass reaches at the HL-LHC are 1400, 1650 and 1800 GeV, respectively, which compare with the current CMS limits 1450, 1480 and 1510 GeV for $L = 36$ $\hbox {fb}^{-1}$. In a model-specific study we explore the parameter space of neutrino mass generation models and identify the regions that can be probed with MoEDAL at the end of Run-3 and the High-Luminosity LHC.

1 Introduction

Finding new particles or at least setting limits on their existence is one of the main objectives of the experiments at the Large Hadron Collider (LHC). for Run 1 and 2, the focus was mainly on searches in the missing energy channel, motivated by models involving Dark Matter candidates, such as supersymmetry. Recently, a lot of effort has been put into the analyses for more unorthodox signatures, which include, for example, multi-jet [1, 2] (-lepton [3]), mono-jet [4, 5], displaced vertices [6, 7] and disappearing track [8, 9] signatures.

Signatures of long-lived particles are one of such exotic signatures that attracted attention recently.¹ The search strategy varies depending on the lifetime of the particle. For intermediate lifetimes, ${{{\mathcal {O}}}}(1)\,\mathrm{cm} \lesssim c \tau \lesssim {{{\mathcal {O}}}}(10)\,\mathrm{cm}$, searches for displaced vertices and disappearing tracks are effective. If the particles are electrically charged and have very long lifetimes, $c \tau \gtrsim \mathcal{O}(1)\,\mathrm{m}$, ATLAS and CMS detectors may register them as a slow-moving particle in their muon systems or a particle with an anomalously high ionising power in their electromagnetic calorimeters. Searches of this kind are often called heavy stable charged particle (HSCP) searches.

It has been pointed out recently that the MoEDAL (Monopole and Exotics Detector at the LHC) detector may also be capable of searching for charged meta-stable particles ($c \tau \gtrsim {{{\mathcal {O}}}}(1)$ m) and give independent (and sometimes complementary) constraints on them from ATLAS and CMS [11, 12]. MoEDAL is largely a passive detector that has been designed primarily to look for magnetic monopoles [13,14,15,16]. It is located around the interaction point in the VErtex LOcator (VELO) cavern of the LHCb experiment. The principal component² of the MoEDAL detector is a large array (circa 120 $m^2$) of nuclear track detectors (NTDs) made of multiple CR39 and Makrofol plastic sheets stacked together. Magnetic monopoles are expected to have a large magnetic charge required by the Dirac quantization condition, $Q_m = 2 \pi n/Q_e$ ($n \in \mathrm Z$), and therefore be highly ionising. Such particles, if they travel through an NTD panel, would leave a microscopic damage along their trajectories, which can be revealed by dismantling NTD panels and putting plastic sheets in an etching solution. The signature of highly ionising particle is the presence of double cone shaped etch-pits, with sizes in the range 20 to 50 $\mu m$, collinear in all sheets of plastic within a single NTD module. Combining information from multiple etch-pits allows to reconstruct particle trajectories and infer their electric charge with resolution better than 0.05e, with e being elementary charge. During Run-2, NTD panels were exposed for a year, after which they were disassembled and transported to an external laboratory, where the plastic sheets were etched and scanned using optical microscopes. For the Run-3 data taking period, an automated system controlled by artificial intelligence is being prepared to accelerate analyses.

Not only magnetic monopoles but any electrically charged particles with high ionisation power can leave a similar signature in an NTD. The condition for electrically charged particles to be detected by MoEDAL is given by $\Theta \equiv \beta /Z < 0.15$, where $\beta$ is the velocity of the particle and $Z \equiv Q/|e|$ is the electric charge measured in the proton charge units. It imposes an effective cut-off on fast-moving particles, allowing to highly suppress SM background. In order to further suppress the background to a negligible level, NTD panels are located at distances $\sim 2$ m from the interaction point. Therefore, those anomalously heavy ionising particles must also be long-lived at least with $c \tau \gtrsim {{{\mathcal {O}}}}(1)$ m to reach the NTD panels. Detection of singly charged particles at MoEDAL has recently been studied [12]. The study focused on supersymmetric status and considered a gluino cascade decay chain involving two long-lived (LL) particles, ${{\tilde{\chi }}}_1^0$ and $\tilde{\tau }^{\pm }$;  $pp \rightarrow {{\tilde{g}}} {{\tilde{g}}}$, ${{\tilde{g}}} \rightarrow jj [\tilde{\chi }^0_1]_{\mathrm{LL}}$, $[{{\tilde{\chi }}}^0_1]_{\mathrm{LL}} \rightarrow \tau ^{\pm } [{{\tilde{\tau }}}^{\mp }]_{\mathrm{LL}}$. It has been demonstrated that MoEDAL can probe regions of the parameter space which have not been excluded by the HSCP searches currently performed by ATLAS and CMS. In Ref. [11] the study has been extended to a more comprehensive list of supersymmetric particles, as well as for doubly charged scalars and fermions. In this paper we augment these studies by investigating MoEDAL’s performance for multiply charged long-lived particles with $Z \gtrsim 2$. We also demonstrate the importance of the previously neglected photon-fusion production channel for scalar particles and update the earlier results obtained in Ref. [11].

Searches for long-lived multi-charged particles are interesting, since such particles often appear in phenomenological models. For example, an electroweak triplet scalar field with hypercharge $Y=1$ is introduced in the type-II seesaw model for neutrino masses. Another example is a doubly charged Higgsino, which can be found in supersymmetric left-right symmetric models.

The smallness of the observed neutrino masses has motivated a variety of models proposed in the literature. In particular, radiative neutrino mass models have a long tradition [17,18,19,20], since they provide automatically a suppression for neutrino masses, for a review see [21]. Systematic classifications for different radiative models have been published for 1-loop [22], 2-loop [23] and even 3-loop [24] models. For our current paper, we will consider a special class of 1-loop models, first discussed in [25]. 1-loop neutrino mass models often add a discrete symmetry to the SM gauge group. The purpose of this is twofold. First, it allows to remove unwanted tree-level contributions and, second, such models contain a candidate for the Dark Matter in the universe. The proto-type model for this class is the scotogenic model [26]. The models presented in [25] are orthogonal to this ansatz in the sense that they are automatically the leading contribution to the neutrino mass, without the addition of a new ad-hoc symmetry. The resulting models cannot contain SM singlet fermions³, instead they contain multiply charged particles, both fermionic fields and scalars. Due to the small neutrino mass and the high electric charge these new fields are typically very long-lived particles. In this paper we consider two concrete models of this class and derive MoEDAL’s sensitivities to the long-lived particles predicted in them. We provide model-independent MoEDAL detection reach for types of particles anticipated in the selected class of models, and we also interpret our numerical results in the concrete examples to identify viable parameter regions that can be explored by MoEDAL at the LHC Run-3 and the High Luminosity LHC (HL-LHC), under the condition that the given parameter set can fit the observed data for the neutrino masses.

The rest of the paper is organised as follows. In Sect. 2 we briefly review the two radiative neutrino mass models studied in this paper and discuss the lifetimes of multi-charged particles in the models. We then describe our analysis method for the estimation of the expected signal events at MoEDAL in Sect. 3. In Sect. 4 (5) we present our numerical results for the first (second) neutrino mass models. The first half of each of these two sections focuses on the model-independent sensitivities for the multi-charged long-lived particles with $Z \ge 2$ treating their lifetimes as a free parameter. We then show, in the second half of the sections, the model-dependent results for Model-1 and Model-2, and identify the parameter regions that can fit the neutrino mass data and also will be explored by MoEDAL at the LHC Run-3 and HL-LHC. We conclude our study in Sect. 6.

2 Neutrino mass models and multi-charged long-lived particles

In this section we briefly review two variants of radiative neutrino mass models with similar features. These models have been introduced and discussed for the first time in Ref. [25]. In this class of models, the Standard Model (SM) is extended with two scalar fields, $S_1$ and $S_3$, which are singlet and triplet representations of $SU(2)_L$, respectively, and three pairs of vector-like fermions $(F_i, {{\bar{F}}}_i)$ $(i = 1,2,3)$ in $SU(2)_L$ in doublet representations. In the first model (Model-1), all beyond the Standard Model (BSM) fields are colour singlets, while the new fields are in colour (anti-)triplet representations in the second model (Model-2).

Table 1 The BSM fields and their quantum numbers in Model-1. The index i ($=1,2,3$) distinguishes the three copies of $(F, {{\bar{F}}})$ fields. Since lepton number is broken in the model, the lepton number assignment in this table should be understood as being valid in the limit $\lambda _5 \rightarrow 0$, see text

The quantum numbers of the BSM fields in Model-1 are summarised in Table 1. With these charge assignments the BSM Lagrangian is given by

$$\begin{aligned} {{{\mathcal {L}}}}_{\mathrm{BSM}}= & {} {{{\mathcal {L}}}}_{\mathrm{kin}} - \left[ (h_{ee})_{ij} e^c_i e^c_j S_1^\dagger + (h_F)_{ij} L_i F_j S_1^\dagger \right. \nonumber \\&+\left. (h_{{{\bar{F}}}})_{ij} L_i {{\bar{F}}}_j S_3 \,+\, \mathrm{h.c.} \right] \nonumber \\&- \left[ \lambda _5 H H S_1 S_3^\dagger \,+\, \mathrm{h.c.} \right] \nonumber \\&+ \lambda _2 |H|^2 |S_1|^2 + \lambda _{3a} |H|^2 |S_3|^2 \nonumber \\&+ \lambda _{3b} |H S_3|^2 + \lambda _4 |S_1|^4 \nonumber \\&+ \lambda _{6a} |S_3^\dagger S_3|^2 + \lambda _{6b} |S_3 S_3|^2 + \lambda _7 |S_1|^2 |S_3|^2. \end{aligned}$$

(2.1)

Here the mass terms of the BSM fields ($m_{S_1}^2 |S_1|^2 + m_{S_3}^2 |S_3|^2 + m_{F_i} {{\bar{F}}}_i F_i$) are included in $\mathcal{L}_{\mathrm{kin}}$. It should be stressed that the $\lambda _5$ term breaks the lepton number symmetry and is therefore indispensable for neutrino mass generation. In the limit of $\lambda _5\rightarrow 0$ all BSM fields have definite lepton numbers, as quoted in Table 1. Note that, in each operator the BSM fields appear even times, except for the $h_{ee}$ term. This means one can introduce a BSM parity by assigning an odd (even) charge to the BSM (SM) fields. When the BSM parity is exact, i.e. $(h_{ee})_{ij} = 0$, the lightest BSM particle cannot decay. The $(h_{ee})_{ij}$ coupling therefore controls the decay lifetime of the lightest BSM particle. We must stress that the limit $(h_{ee})_{ij} = 0$ is not allowed phenomenologically, since it would lead to a charged stable relic excluded by cosmology.

Since a non-vanishing $\lambda _5$ breaks lepton number it may be taken to be small and the theory can remain technically natural in the sense of t’Hooft. Similarly, if either $(h_F)_{ij}$ or $(h_{{{\bar{F}}}})_{ij}$ were absent, lepton number would be conserved and if both are absent simultaneously the BSM fermion number symmetry, $F_i \rightarrow e^{i \theta } F_i$, ${{\bar{F}}}_i \rightarrow e^{-i \theta } {{\bar{F}}}_i$, becomes exact. Therefore a configuration in which both $(h_F)_{ij}$ and $(h_{{{\bar{F}}}})_{ij}$ are small is radiatively stable, i.e. technically natural.

Fig. 1

The one-loop diagram generating the neutrino masses

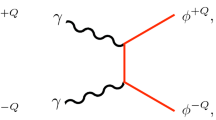
In this class of models a dimension-5 operator for neutrino masses, roughly of order

$$\begin{aligned} \frac{\lambda _5 N_c}{32 \pi ^2 \Lambda ^2} \left[ h_{{{\bar{F}}}}^T m_F h_F + h_F^T m_F h_{{{\bar{F}}}} \right] _{ij} \cdot L_i H L_j H, \end{aligned}$$

(2.2)

is radiatively generated by integrating out the BSM fields through the diagram in Fig. 1, where $N_c$ is the number of colours of the particles in the loop and $\Lambda$ is the mass scale of the BSM particles, with $\Lambda \sim \max ( m_{F_i}, m_{S_1}, m_{S_3})$. Assuming all heavy masses are approximately equal to each other and $h_F$ and $h_{{{\bar{F}}}}$ are diagonal, the neutrino masses are roughly given by

$$\begin{aligned} m_\nu ~\sim ~ 0.05 \cdot N_c \cdot \left( \frac{\lambda _5}{10^{-6}} \right) \left( \frac{h_F h_{\bar{F}}}{10^{-4}} \right) \left( \frac{1\,\mathrm{TeV}}{\Lambda } \right) \,\mathrm{eV}. \end{aligned}$$

(2.3)

Note that in the numerical parts of this work, we do not use Eq. (2.3). Instead, we fit neutrino masses and angles, taking the full 1-loop calculation as presented in [25], based on the general formulas given in [27].

The BSM fields have large $SU(2)_L$ and $U(1)_Y$ charges, which results in the presence of multiply charged particles in the mass eigenstates. In particular, the $S_3$ field includes doubly, triply and quadruply charged particles, denoted by $S^{+2}, S^{+3}$ and $S^{+4}$, respectively. The $S^{+2}$ mixes with the $S_1$ field. The mass matrix for doubly charged scalars is given by

$$\begin{aligned} \begin{pmatrix} m_{S_1}^2 - \frac{1}{2} \lambda _2 v^2 &{}\quad \frac{1}{2} \lambda _5 v^2 \\ \frac{1}{2} \lambda _5 v^2 &{}\quad m_{S_3}^2 - \frac{1}{2} \lambda _{3a} v^2 \\ \end{pmatrix} \end{aligned}$$

(2.4)

Those multi-charged particles may be long-lived, if

$$\begin{aligned} m_{S_3} \ll m_{S_1}, m_F, \end{aligned}$$

(2.5)

Throughout this paper we assume this mass hierarchy. To simplify the parameter space searches, we will also assume that $\lambda _i v^2 \ll m^2_{S_3}$, for $i=2,(3a),(3b),5$, i.e. except for $\lambda _5$ the exact values of the quartic couplings do not matter numerically. This assumption results in the members of the multiplet $S_3$ being nearly degenerate in mass. With the assumption $m_{S_3} \ll m_{S_1}$, the lighter and heavier mass eigenstates of doubly charged particles are $S^{+2} \simeq S_3$ and $S_1^{+2} \simeq S_1$, respectively. The mass eigenvalues can be approximated as

$$\begin{aligned} m^2_{S_1^{+2}}= & {} m_{S_1}^2 - \frac{1}{2} \lambda _2 v^2, \end{aligned}$$

(2.6)

$$\begin{aligned} m^2_{S^{+2}}= & {} m_{S_3}^2 - \frac{1}{2} \lambda _{3a} v^2. \end{aligned}$$

(2.7)

The mass degeneracy between $S^{+3}$ and $S^{+4}$ is also lifted due to the electroweak symmetry breaking. The physical masses are given by

$$\begin{aligned} m^2_{S^{+3}}= & {} m_{S_3}^2 - \frac{1}{2} ( \lambda _{3a} + \frac{1}{2} \lambda _{3b} ) v^2, \end{aligned}$$

(2.8)

$$\begin{aligned} m^2_{S^{+4}}= & {} m_{S_3}^2 - \frac{1}{2} \left( \lambda _{3a} + \lambda _{3b} \right) v^2, \end{aligned}$$

(2.9)

Fig. 2

Diagrams for possible decays for $S^{+4}$, $S^{+3}$ and $S^{+2}$. The same particle decays into both $L=-4$ (left) and $L=-2$ (right) final states, thus its lepton number is not fixed, once either $\lambda _5$ or $h_F\times h_{{{\bar{F}}}}$ is non-zero. For simplicity, we assign the lepton number violation to $\lambda _5$ in the following. Observing both decay modes would be an experimental demonstration of lepton number violation

With the mass assumption Eq. (2.5), $S^{+4},S^{+3}$ and $S^{+2}$ are lighter than other BSM particles. These particles carry lepton number $L=-4$ (in the unphysical limit $\lambda _5=0$) and decay directly into the Standard Model particles.⁴ Due to the large electric charge, the multiplicity of the decay final states tends to be large, incurring strong phase-space suppression factors.

The main decay modes for $S^{+4}$ are 4-body modes; $S^{+4} \rightarrow 4 \ell ^+$ and $S^{+4} \rightarrow W^+ W^+ \ell \ell$, as shown in Fig. 2. The approximate formulae for the partial decay rates, valid for $v^2 \ll m_{S_3} \ll m_{S_1}, m_F$, are given roughly by [25]

$$\begin{aligned} \Gamma (S^{+4} \rightarrow \ell _\alpha ^+ \ell _\beta ^+ \ell _\gamma ^+ \ell _\delta ^+)\sim & {} \frac{|(h_{ee})_{\alpha \beta }|^2}{192 \cdot (4 \pi )^5} \cdot \left| \left\langle \frac{h^{\gamma \delta }_{F {{\bar{F}}}}}{m_F} \right\rangle \right| ^2 \cdot \frac{m^7_{S_3}}{m^4_{S_1}}, \end{aligned}$$

(2.10)

$$\begin{aligned} \Gamma (S^{+4} \rightarrow W^+ W^+ \ell _\alpha ^+ \ell _\beta ^+ )\sim & {} \frac{|g_2^2 (h_{ee})_{\alpha \beta }|^2}{48 \cdot (4 \pi )^5} \cdot \left( \frac{\lambda _5 v^2}{m^2_{S_1}} \right) ^2 \cdot \frac{m^5_{S_3}}{m^4_{W}},\nonumber \\ \end{aligned}$$

(2.11)

where

$$\begin{aligned} \left| \left\langle \frac{h^{\gamma \delta }_{F \bar{F}}}{m_F} \right\rangle \right| ~\equiv ~ \left| \sum _k \frac{h_F^{\gamma k} h_{{{\bar{F}}}}^{\delta k} + h_F^{\delta k} h_{\bar{F}}^{\gamma k} }{m_{F_k}} \right| \end{aligned}$$

(2.12)

is an effective reduced coupling introduced in [25]. It is worth noting that the decay mode $\Gamma (S^{+4} \rightarrow 4 \ell ^+)$ is proportional to $h_F h_{{{\bar{F}}}}$, while the decay $\Gamma (S^{+4} \rightarrow W^+ W^+ \ell ^+ \ell ^+)$ is proportional to $\lambda _5$. Neutrino masses require that the product of these parameters is small, see Eq. (2.3). We stress again, that we do not use approximate Eqs. (2.10)-(2.11) in our numerical work. Instead, the widths are calculated numerically at each parameter point using MadGraph 5 [28,29,30]. A simultaneous observation of both final states would be an experimental proof of lepton number violation.

The two competing main decay modes of $S^{+3}$ are $S^{+3} \rightarrow \ell ^+ \ell ^+ \ell ^+ \nu$ and $S^{+3} \rightarrow W^+ \ell ^+ \ell ^+$. As for $S^{+4}$, the former is L-conserving and the latter L-violating. The partial decay rates are approximately given by

$$\begin{aligned} \Gamma (S^{+3} \rightarrow \ell _\alpha ^+ \ell _\beta ^+ \ell _\gamma ^+ \nu _\delta ^+)\sim & {} \frac{|(h_{ee})_{\alpha \beta }|^2}{192 \cdot (4 \pi )^5} \cdot \left| \left\langle \frac{h^{\gamma \delta }_{F {{\bar{F}}}}}{m_F} \right\rangle \right| ^2 \cdot \frac{m^7_{S_3}}{m^4_{S_1}}, \end{aligned}$$

(2.13)

$$\begin{aligned} \Gamma (S^{+3} \rightarrow W^+ \ell _\alpha ^+ \ell _\beta ^+ )\sim & {} \frac{|g_2 (h_{ee})_{\alpha \beta }|^2}{16 \cdot (4 \pi )^3} \cdot \left( \frac{\lambda _5 v^2}{m^2_{S_1}} \right) ^2 \cdot \frac{m^3_{S_3}}{ m^2_{W}}. \nonumber \\ \end{aligned}$$

(2.14)

Notice that the approximate formula for the decay rate Eq. (2.13) is identical to Eq. (2.10) for the $S^{+4}$ decay. This is because these two decays are related by $SU(2)_L$ symmetry.

Finally, the partial decay rates for the two main decay modes of $S^{+2}$, $S^{+2} \rightarrow \nu \nu \ell ^+ \ell ^+$ and $S^{+2} \rightarrow \ell ^+ \ell ^+$ are given by

$$\begin{aligned} \Gamma (S^{+2} \rightarrow \ell _\alpha ^+ \ell _\beta ^+ \nu _\gamma ^+ \nu _\delta ^+)\sim & {} \frac{|(h_{ee})_{\alpha \beta }|^2}{192 \cdot (4 \pi )^5} \cdot \left| \left\langle \frac{h^{\gamma \delta }_{F {{\bar{F}}}}}{m_F} \right\rangle \right| ^2 \cdot \frac{m^7_{S_3}}{m^4_{S_1}}, \end{aligned}$$

(2.15)

$$\begin{aligned} \Gamma (S^{+2} \rightarrow \ell _\alpha ^+ \ell _\beta ^+ )\sim & {} \frac{|(h_{ee})_{\alpha \beta }|^2}{4 \pi } \cdot \left( \frac{\lambda _5 v^2}{m^2_{S_1}} \right) ^2 \cdot m_{S_3}. \nonumber \\ \end{aligned}$$

(2.16)

The approximate formula for 4-body decay mode is again the same as Eqs. (2.10) and (2.13) due to the $SU(2)_L$ symmetry. This 4-body decay is subdominant unless $\lambda _5$ is extremely small.

The second variant of this type of radiative neutrino mass models (Model-2), that we will study in the numerical parts later on, can be obtained simply from Model-1 by giving colour (anti-)triplet charges to the BSM fields in Model-1, with some related changes in hyper-charge assignments. We distinguish the fields and particles in Model-2 with tilde from those in Model-1. Namely, we write Model-2 fields as ${{\tilde{S}}}_{1}, {{\tilde{S}}}_{3}, {{\tilde{F}}}_i, \tilde{{{\bar{F}}}}_i$. In order to break the BSM parity and let the lightest BSM particle decay, the $h_{ee}$ operator in Model-1 should be replaced by

$$\begin{aligned} (h_{ee})_{ij} e^c_i e^c_j S_1^\dagger ~\rightarrow ~ (h_{ed})_{ij} d^c_i e^c_j {{\tilde{S}}}_1^\dagger . \end{aligned}$$

(2.17)

This implies that the difference of hypercharges between ${{\tilde{S}}}_1$ and $S_1$ must be $-2/3$. In order to keep all the other operators in Eq. (2.1), the hyper-charge of the other BSM fields must be modified also by this amount. Also, assuming the operators in Eq. (2.17) do not break the lepton number (we assume it is broken by the non-vanishing $\lambda _5$ coupling), we must assign $L = -1$ for ${{\tilde{S}}}_1$, and the lepton number assignment for all other fields must be modified accordingly. In summary, the BSM fields of Model-2 can be obtained by the following replacements from Model-1:

$$\begin{aligned} \begin{array}{rcl} \mathbf{Model}\text {-}{} \mathbf{1} &{} ~ &{} \mathbf{Model}\text {-}{} \mathbf{2} \\ S_1 (\mathbf{1}, \mathbf{1}, 2)_{-2} &{} \rightarrow &{} {{\tilde{S}}}_1 (\bar{\mathbf{3}}, \mathbf{1}, 4/3)_{-1} \\ S_3 (\mathbf{1}, \mathbf{3}, 3)_{-4} &{} \rightarrow &{} {{\tilde{S}}}_3 (\bar{\mathbf{3}}, \mathbf{3}, 7/3)_{-3} \\ F (\mathbf{1}, \mathbf{2}, 5/2)_{-3} &{} \rightarrow &{} {{\tilde{F}}} (\mathbf{3}, \mathbf{2}, 11/6)_{-2} \\ {{\bar{F}}} (\mathbf{1}, \mathbf{2}, -5/2)_{3} &{} \rightarrow &{} \tilde{{{\bar{F}}}} (\bar{\mathbf{3}}, \mathbf{2}, -11/6)_{2}, \end{array} \end{aligned}$$

(2.18)

where the three numbers in the brackets represent the representations of $SU(3)_c \times SU(2)_L \times U(1)_Y$ and the subscripts denote our assignment of the lepton number.

With this charge assignment, the Lagrangian of Model-2 is the same as that for Model-1 in Eq. (2.1) with the replacement in Eqs. (2.17) and (2.18). The mechanism and formula for neutrino mass generation, Eqs. (2.2) and (2.3), are unchanged (with $N_c = 3$). Due to the shift of hypercharge, the electric charge of Model-2 fields are also shifted from those of Model-1 by $-2/3$. For example, the SU(2) triplet field, $\tilde{S}_3$, includes the three states with electric charges $Z = 4/3$, 7/3 and 10/3, denoted by ${{\tilde{S}}}^{+4/3}$, ${{\tilde{S}}}^{+7/3}$ and ${{\tilde{S}}}^{+10/3}$, respectively. The ${{\tilde{S}}}^{+4/3}$ mixes with the singlet field ${{\tilde{S}}}_1$ and give two physical states, as in Model-1 for $S^{+2}$ and $S_1$. The formula for the physical masses, Eqs. (2.7), (2.8) and (2.9), are unchanged with the obvious replacement; $S^{+2} \rightarrow {{\tilde{S}}}^{+4/3}$, $S^{+3} \rightarrow {{\tilde{S}}}^{+7/3}$ and $S^{+4} \rightarrow {{\tilde{S}}}^{+10/3}$. The formulae for the partial decay rates of ${{\tilde{S}}}^{+10/3}$, $\tilde{S}^{+7/3}$, ${{\tilde{S}}}^{+4/3}$ are unchanged from Eq. (2.10) to Eq. (2.16) with the replacement $\ell ^+_\alpha \rightarrow \bar{d}_\alpha$ in the final state and $(h_{ee})_{\alpha \beta } \rightarrow (h_{ed})_{\alpha \beta }$.

3 The estimation of signal events

In our numerical analysis we first implement the model described in the previous section in SARAH [31, 32]. The output is plugged into SPheno [33, 34] to calculate the mass spectra, mixing matrices and scalar two-body and fermionic three-body decays. Finally, these information are fed into MadGraph 5 [28,29,30], which is used for event generation as well as numerical evaluation for the decay rates and the production cross-sections. For the cross section calculation we use the LUXqed17$\_$plus$\_$PDF4LHC15$\_$nnlo$\_$100. This PDF, based on Manohar et al. [35, 36], combines QCD partons from PDF4LHC15 [37] with an improved calculation of the photon density in the proton.

In order to estimate the expected number of signal events in the MoEDAL detector, we closely follow the procedure described in detail in [11, 13]. First, Monte Carlo events for the pair production of exotic particles at the 13 TeV LHC are generated using MadGraph 5. Having the velocity vectors of charged particles in hands, we check whether or not there is a MoEDAL’s NTD panel in the direction of a charged particle. We implement this by a function $\omega (\mathbf{p}_i)$ of the particle i’s momentum vector $\mathbf{p}_i$. Namely, $\omega (\mathbf{p}_i) = 1$ if there is an NTD panel in the direction of $\mathbf{p}_i$ and 0 otherwise. Here we assume MoEDAL’s Run-3 configuration where all NTD panels are facing to the interaction point at right angle. In this case, given that a charged particle hits an NTD panel, the detection efficiency can be modeled by the step function

$$\begin{aligned} \Theta \left( 0.15 \cdot Z_i - \beta _i \right) , \end{aligned}$$

(3.1)

where $Z_i$ and $\beta _i$ are the electric charge and the magnitude of the velocity of the particle i ($i = 1,2$), respectively, and $\Theta (x) = 1$ for $x \ge { 0}$ and 0 otherwise. Finally, the probability that a charged particle with lifetime $\tau _i$ survives until it reaches an NTD panel is given by

$$\begin{aligned} P_{\mathrm{surv}}(\mathbf{p}_i) ~=~ \exp \left( - \frac{L_\mathrm{NTD}(\mathbf{p}_i) }{ \beta _i \gamma _i c \tau _i } \right) , \end{aligned}$$

(3.2)

where $L_{\mathrm{NTD}}(\mathbf{p}_i)$ is the distance from the interaction point to the NTD panel in the direction of the momentum vector $\mathbf{p}_i$ of the charged particle i. In summary, the number of expected signal events with the integrated luminosity ${{{\mathcal {L}}}}$ is given by

$$\begin{aligned} N_{\mathrm{sig}} ~=~ \sigma \cdot {{{\mathcal {L}}}} \cdot \epsilon , \end{aligned}$$

(3.3)

with

$$\begin{aligned} \epsilon ~=~ \left\langle \, \sum _{i=1,2} \omega (\mathbf{p}_i) \cdot P_{\mathrm{surv}}( \mathbf{p}_i ) \cdot \Theta \left( 0.15 \cdot Z_i - \beta _i \right) \right\rangle _{\mathrm{MC}}, \end{aligned}$$

(3.4)

where $\sigma$ is the production cross-section of the exotic particles and $\langle \cdots \rangle _{\mathrm{MC}}$ represents the Monte Carlo average.

4 Numerical analysis for colour singlet models

As described in the previous section, exotic particles in Model-1 are colour singlets. Among them the scalar SU(2)-triplet, $S_3$, may be long-lived when the other exotic states (a scalar SU(2)-singlet, $S_1$, and vector-like SU(2)-triplet fermions, F and ${{\bar{F}}}$) are heavier than $S_3$ and the model parameters are fitted to explain the neutrino masses. In this section, we first investigate the collider properties of the three mass eigenstates of $S_3$ and derive the model independent exclusion reach in the first subsection. We then interpret the results for Model-1 and identify the parameter region that can be probed by MoEDAL at the Run-3 of LHC.

4.1 Results for colour-singlet multi-charged particles

The $S_3$ and its conjugate state have three almost mass degenerate eigenstates denoted by $S^{4 \pm }$, $S^{3 \pm }$ and $S^{2 \pm }$ with electric charges $\pm 4$, $\pm 3$ and $\pm 2$, respectively. All these particles can be long-lived and potentially contribute to the signal at MoEDAL depending on the model parameters. There are three types of production mechanisms; (i) Drell–Yan pair production process exchanging a Z or $\gamma$ (ii) photon fusion pair production process (iii) associated productions, $S^{4\pm } S^{3\mp }$ and $S^{3\pm } S^{2\mp }$, via a $W^\pm$ exchange.

Fig. 3

The leading-order cross-sections of various production modes in Model-1 and -2. The dashed curves correspond to the cross-sections without the photon fusion process. The orange curve represents cross-sections for associated productions, $pp \rightarrow S^{\pm 3} S^{\mp 2}$ or $S^{\pm 4} S^{\mp 3}$ (their cross-sections are the same), mediated by a s-channel W-boson. The cyan curve shows the QCD cross-sections of the single pair production mode in Model-2, i.e. $pp \rightarrow {{\tilde{S}}}^{+4/3} {{\tilde{S}}}^{-4/3}$, $\tilde{S}^{+7/3} {{\tilde{S}}}^{-7/3}$ and ${{\tilde{S}}}^{+10/3} {{\tilde{S}}}^{-10/3}$

We show in Fig. 3 the pair production cross-sections for $S^{\pm 4}$ (blue), $S^{\pm 3}$ (green) and $S^{\pm 2}$ (red) by the solid curves, which include both contributions from the Drell–Yan (s-channel $Z/\gamma$) and photon fusion processes. To see the impact of the photon fusion process, we also show the cross-sections without the photon fusion by the dashed curves. We see that the photon fusion contribution is very important for scalar particles with higher electric charge multiplicity, $|Q| = Z e$. For example, at the mass around 300 GeV, the photon fusion contribution enhances the cross-section by $\sim 30$ % for $S^{\pm 2}$, while for $S^{\pm 4}$ it makes up more than 50 % of the total. This is because the contribution of the s-channel photon exchange diagram is proportional to $|Q|^2$, while the cross-section of the photon fusion process is proportional to $|Q|^4$. Another reason why the photon fusion is important is as follows. The Drell–Yan s-channel process exchanging a spin-1 gauge boson generally suffers from a p-wave suppression in the scalar particle production, since the s-wave production mode is forbidden by the angular momentum conservation. This also explains another feature we see in the plot that the photon fusion becomes relatively more enhanced in the higher mass region, because at higher masses having large velocities costs more energy and the cross-section gets suppressed by the parton distribution function. The associated production, $pp \rightarrow S^{\pm 4} S^{\mp 3}$ (or $S^{\pm 3} S^{\mp 2}$, since these modes have the same leading-order cross-section), mediated by the s-channel W-boson, is also shown by the orange curve.

The size of this cross-section is as large as the $S^{\mp 3}$ pair production cross-section and give non-negligible effects when studying the implications for the concrete model in the next subsection. Finally we show the cross-section for the pair productions of coloured particles in Model-2 by the cyan curve, which we will discuss in detail in the next section.

Fig. 4

Velocity distributions of the produced multi-charged particles in various production modes in Model-1 and -2. The masses are set to be 500 GeV for all particles. The dashed curves correspond to the velocity distributions without the contribution from the photon fusion process. The orange curve include the contributions from two associated production modes, $pp \rightarrow S^{+3} S^{-2}$ and $S^{+4} S^{-3}$, mediated by a s-channel W-boson. The cyan curve shows the velocity distribution by the QCD production in Model-2, i.e. $pp \rightarrow {{\tilde{S}}}^{+4/3} \tilde{S}^{-4/3}$, ${{\tilde{S}}}^{+7/3} {{\tilde{S}}}^{-7/3}$ and ${{\tilde{S}}}^{+10/3} {{\tilde{S}}}^{-10/3}$

In Fig. 4 we show the velocity distributions for charged scalar production, where the masses are taken to be 500 GeV for all particles. The same colour scheme is used as in Fig. 3. As in the previous plot, the solid histograms are for the production with the photon fusion process and the dashed histograms represent to the production without it.

As can be seen, the particle velocities are lower in general when the photon fusion is included. This is because the s-wave mode is forbidden in the Drell–Yan processes and the produced particles are required to have non-zero velocities. This also explains why the particles with larger |Q| have lower velocities on average because the photon fusion is relatively more enhanced for larger |Q| compared to the Drell–Yan process.

As explained earlier, the MoEDAL detector is sensitive to particles that have a large electric charge and small velocities with $\beta < 0.15 \cdot Z$. The vertical dashed lines in Fig. 4 show the threshold velocities for the particles with $Z (= |Q/e|) = 2$, 3 and 4. As can be seen, the detection sensitivity is significantly larger for a particle with larger Z because (a) the threshold velocity increases and (b) the average production velocity decreases.

Fig. 5

Model-independent detection reach at MoEDAL in the (m, $c \tau$) parameter plane for individual particles of Model-1. The solid dashed and dotted contours correspond to $N_{\mathrm{sig}} = 1$, 2 and 3, respectively. In the left (right) panel the integrated luminosity of 30 (300) $\hbox {fb}^{-1}$ is assumed

Figure 5 shows the region in the (m vs $c \tau$) parameter plane in which the expected number of events detected by MoEDAL, $N_{\mathrm{sig}}$, exceeds 1 (solid), 2 (dashed) and 3(dotted) with the integrated luminosity of 30 $\hbox {fb}^{-1}$ (left) and 300 $\hbox {fb}^{-1}$ (right). These luminosities are expected to be delivered at the end of Run-3 and High-Luminosity LHC run, respectively. In this part of the study we only consider the particle-antiparticle pair production of a single species, e.g. $pp \rightarrow S^{+4} S^{-4}$. In this case the expected number of signal events depends only on the mass and lifetime of the particle, which we treat as free parameters. The results are therefore model-independent.

The top panels in Fig. 5 show the expected sensitivities (green regions) for the doubly charged scalar particle $S^{\pm 2}$. Since the expected background at MoEDAL with assumed luminosities is much less than 1, $N_{\mathrm{sig}} = 3$ approximately corresponds to the 95 % CL exclusion when observing no signal event. As can be seen, the mass reach for $N_{\mathrm{sig}} = 1$ (3) with $c \tau \gtrsim 100$ m amounts to $m_{S^{\pm 2}} \simeq 290$ (190) GeV in Run-3 (30 $\hbox {fb}^{-1}$) This can be compared to the corresponding mass reach $m_{S^{\pm 2}} \simeq 160$ GeV for $N_{\mathrm{sig}} = 1$ obtained in the previous study [11] where the photon fusion process was not taken into account. For HL-LHC with 300 $\hbox {fb}^{-1}$, the mass reach is extended to $m_{S^{\pm 2}} \simeq 600$ (400) for $N_{\mathrm{sig}} = 1$ (3).

The panels in the second (blue) and third (red) rows of Fig. 5 show the expected sensitivities for triply ($S^{\pm 3}$) and quadruply ($S^{\pm 4}$) charged scalar particles, respectively. As can be seen, the mass reaches for $c \tau \gtrsim 100$ m are significantly extended compared to that of $S^{\pm 2}$. In the long lifetime limit, MoEDAL with the Run-3 luminosity can probe $S^{\pm 3}$ up to $m_{S^{\pm 3}} \simeq 610$ (430) GeV, while for $S^{\pm 4}$ the reach is further extended up to $m_{S^{\pm 4}} \simeq 960$ (700) GeV with $N_{\mathrm{sig}} = 1$ (3). At the HL-LHC, the mass reach for $S^{\pm 3}$ is improved to be 1100 (850) GeV, whilst the mass reach for $S^{\pm 4}$ is found to be 1430 (1200) GeV with $N_\mathrm{sig} = 1$ (3)

Our first neutrino mass model (Model-1) has a triply charged vector-like fermion pair $F^{\pm 3}$. Although those fermions are not expected to be long-lived, we show the model-independent MoEDAL sensitivity for $F^{\pm 3}$ for completeness.⁵ Since Dirac fermions have twice more degrees of freedom than complex scalars and their Drell–Yan process is not p-wave suppressed, their production cross-section is significantly larger than the scalar particles with the same charge. This leads to greater sensitivity than the scalar case. With the integrated luminosity of 30 $\hbox {fb}^{-1}$, we see that MoEDAL can probe $F^{\pm 3}$ up to $m_{F^{\pm 3}} \simeq 1030$ (800) GeV for $N_\mathrm{sig}=1$ (3). For 300 $\hbox {fb}^{-1}$ we see the mass reach improves up to 1550 (1300) GeV for $N_{\mathrm{sig}}=1$ (3).

One can notice in Fig. 5 that for very high values of decay length $c\tau \ge 100$ m the detection reach for MoEDAL practically does not change. This is a consequence of the experimental setup and applies to all types of particles. In order to be detected at MoEDAL, a particle needs to deposit energy in all layers of the NTD panel, which means it cannot decay before reaching the detector, nor within it. When particle’s decay length becomes large, the probability of reaching MoEDAL detector asymptotically approaches unity, and particle can be thought of being quasi-stable. Further increase in $c\tau$ provides little benefit for detection reach, which is now determined mostly by the production cross-section, luminosity and particles’ velocity distribution, as can be seen from Eqs. (3.3) and (3.4).

Table 2 Summary for the model-independent mass reaches (in GeV) of the multi-charged particles in Model-1 by MoEDAL (2nd and 3rd columns). The first column shows the current mass bounds from the ATLAS analysis [38] with 36 $\hbox {fb}^{-1}$. The numbers in the double-brackets correspond to our naive estimate of the mass bounds (see the text). The second column represents the projected mass reach in Run-3 (300 $\hbox {fb}^{-1}$) obtained in [39]. The numbers outside (inside) the brackets in the third and fourth columns represent MoEDAL’s mass reaches with $N_{\mathrm{sig}} \ge 3$ (1) assuming $L = 30$ (Run-3) and 300 (HL-LHC) $\hbox {fb}^{-1}$, respectively

In Table 2 we summarise the model-independent mass reaches (in GeV) for the multi-charged particles in Model-1 obtained in this subsection and compare these results with the current bounds and future projections from the heavy stable charged particle (HSCP) searches by ATLAS and CMS (if available). The current mass bounds are taken (estimated) from the ATLAS analysis [38] with the 36 $\hbox {fb}^{-1}$ data. In the ATLAS analysis [38], the result was interpreted only for fermionic particles. We estimated the bounds on the scalar particles, $S^{\pm 2}$, $S^{\pm 3}$ and $S^{\pm 4}$, by naively imposing the cross-section bounds for fermionic particles on the cross-sections of our scalar particles in Model-1, assuming that the ATLAS’ signal efficiency is not very sensitive to the spins. Numbers in double-brackets in the first column are obtained in this way and should be taken with a grain of salt. To our knowledge the Run-3 projection is available only for fermionic particles [39]. In [39], the projected mass reach for $F^{\pm 3}$ for Run-3 LHC was estimated at 1500 GeV. The numbers outside (inside) the brackets in the third and fourth columns represent MoEDAL’s mass reaches with $N_{\mathrm{sig}} \ge 3$ (1), assuming $L = 30$ (Run-3) and 300 (HL-LHC) $\hbox {fb}^{-1}$, respectively.

As can be seen in Table 2 we do not have very good hope to observe Model-1 particles at MoEDAL in Run-3 LHC, since the majority of the region in which MoEDAL is sensitive has already been excluded (except for a small ($\sim 40$ GeV) range for $S^{\pm 4}$). The situation is brighter at HL-LHC. There, MoEDAL can explore $S^{\pm 3}$, $S^{\pm 4}$ and $F^{\pm 3}$ in the regions that are allowed by the current constraints from the HSCP searches.

4.2 Interpretation of the results for Model-1

In this subsection, we investigate the MoEDAL sensitivity for the neutrino mass model with the non-coloured BSM sector described in the previous section. In the model-independent study presented in the previous subsection, we treated the lifetimes of various particles as free and independent parameters. On the other hand, in this subsection the lifetimes are calculated as functions of model parameters which fit the experimental data about the neutrino masses and mixing angles.

The Lagrangian of Model-1 is given in Eq. (2.1). Among many dimensionless parameters, phenomenologically important ones are $(h_{ee})_{ij}$, $\lambda _5$ and the product $h_F h_{{{\bar{F}}}}$. In the following analysis, we assume only the 1-1 component of $(h_{ee})_{ij}$ is non-zero for simplicity, but the extension to other cases are trivial and will be discussed later. The $h_{ee}$ ($=(h_{ee})_{11}$) and $\lambda _5$ couplings control the L-violating decays; $S^{+4} \rightarrow W^+ W^+ \ell ^+ \ell ^+$, $S^{+3} \rightarrow W^+ \ell ^+ \ell ^+$ and $S^{+2} \rightarrow \ell ^+ \ell ^+$, while the decay rate for the L-conserving ones; $S^{+4} \rightarrow 4 \ell ^+$, $S^{+3} \rightarrow \nu \ell ^+ \ell ^+ \ell ^+$ and $S^{+2} \rightarrow \nu \nu \ell ^+ \ell ^+$, are determined by $h_{ee}$ and $h_F h_{{{\bar{F}}}}$ (see Fig. 2). The L-violating decays depend on the mass parameters $m_{S_3}$ and $m_{S_1}$, while L-conserving ones depend also on $m_{F_i}$ ($i=1,2,3$). The above decay modes are the dominant ones and the multi-charged particles can be long-lived when $m_{S_3} < m_{S_1}, m_{F_i}$. We therefore assume this mass hierarchy and fix $m_{F_1} = 3$ TeV throughout this section for simplicity.

The dimensionless couplings and mass parameters relevant to the decays are also important for determination of the neutrino masses. The approximate formula for the neutrino masses is given in Eq. (2.3). In the following numerical analysis, we perform a parameter fit for the neutrino data and choose $h_F$ and $h_{{{\bar{F}}}}$ for the given $\lambda _5$ and mass parameters of the model, which will be used in the calculation of the lifetimes and the expected signal events in the MoEDAL detector.

Fig. 6

Lifetimes of multi-charged particles, $S^{\pm 4}$ (blue solid) $S^{\pm 3}$ (green dashed) and $S^{\pm 2}$ (red dotted), in Model-1 as functions of $\lambda _5$, where $h_F$ and $h_{{{\bar{F}}}}$ are fitted to the neutrino data. The $m_{S_1}$ is taken to be 3 and 10 TeV in the left and right plots, respectively. The other parameters are fixed as $h_{ee} = 0.1$, $m_{S_3} = 750$ GeV and $m_{F_i} = 3$ TeV ($i = 1,2,3$)

In Fig. 6 we show the lifetimes of $S^{\pm 4}$ (blue solid), $S^{\pm 3}$ (green dashed) and $S^{\pm 2}$ (red dotted) as a function of $\lambda _5$, where $h_F$ and $h_{{{\bar{F}}}}$ are chosen to fit the neutrino masses and mixing angles. We take $m_{S_1} = 3$ TeV in the left panel and 10 TeV in the right. The other masses are fixed as $m_{S_3} = 750$ GeV and $m_{F_i} = 3$ TeV. The lifetimes are calculated taking $(h_{ee})_{11} = 0.1$ for simplicity, while the lifetimes for other values of $(h_{ee})_{ij}$ can be obtained by simple rescaling since the lifetimes are proportional to $(\sum _{ij} |(h_{ee})_{ij}|^2)^{-1}$. In both plots, the black horizontal lines indicates $c \tau = 1$ m, which is the typical lifetime required for detection at the MoEDAL.

On can see from the plots that in the region with $\lambda _5 \gtrsim 10^{-4}$, the lifetimes increase as $\lambda _5$ decreases. This is because in this region the L-violating diagrams, which is proportional to $\lambda _5$ at the amplitude level, are dominant. On the other hand, in the region with $\lambda _5 \lesssim 10^{-6}$, the response is opposite and the lifetimes decrease as $\lambda _5$ decreases. This is due to the fact that in this region the dominant decays are the L-conserving modes, proportional to $h_F$ and $h_{{{\bar{F}}}}$, while the product $h_F h_{{{\bar{F}}}}$ is inversely related to $\lambda _5$ through the neutrino mass fit. In the region where the L-conserving processes are dominant, the lifetimes of $S^{\pm 4}$, $S^{\pm 3}$ and $S^{\pm 2}$ coincide. This is anticipated since these decays are related by $SU(2)_L$ and share the same formulae of decay rates neglecting small effects of electroweak symmetry breaking, as discussed in Sect. 2. The lifetimes of multi-charged particles are peaked at particular values of $\lambda _5$, at which the sizes of L-conserving and L-violating decays become comparable. This happens around $\lambda _5 \sim 10^{-5}$, $3\times 10^{-6}$ and $10^{-6}$ for $m_{S^{\pm 4}}$, $m_{S^{\pm 3}}$ and $m_{S^{\pm 2}}$, respectively, with a slight dependence of $m_{S_1}$ as can be seen from the two plots in Fig. 6.

Fig. 7

MoEDAL’s detection sensitivity for Model-1 in the ($m_{S_3}$, $\lambda _5$) plane. In the regions inside the solid, dashed and dotted contours, MoEDAL expects to observe more than 1, 2 and 3 events, respectively. The region with $N_{\mathrm{sig}} \ge 3$ will be excluded at 95% CL if MoEDAL does not observe any signal event. The left and right panels correspond to $L = 30$ and 300 $\hbox {fb}^{-1}$, respectively. We take $m_{F_i} = 3$ TeV ($i = 1,2,3$) for all plots and $m_{S_1} = 3$ (10) TeV in the top (bottom) panels. The $h_{F}$ and $h_{{{\bar{F}}}}$ are fitted to the neutrino data. In the grey region one of these couplings tend to be non-perturbative; $\mathrm{max}_{ij} \left( |(h_{F})_{ij}|, |(h_{{{\bar{F}}}})_{ij}| \right) \ge 2$

In Fig. 7 we show the MoEDAL sensitivity for Model-1 in the ($m_{S_3}$, $\lambda _5$) parameter plane. The two plots on the left assume an integrated luminosity of 30 $\hbox {fb}^{-1}$ (Run-3), while in the right plots 300 $\hbox {fb}^{-1}$ (HL-LHC) is assumed. Here we take all production modes into account including associated productions $pp \rightarrow S^{\pm 4} S^{\mp 3}$ and $S^{\pm 3} S^{\mp 2}$. We set $m_{F_i} = 3$ TeV for all plots, while $m_{S_1}$ is taken to be 3 (10) TeV for the top (bottom) plots. In the region shaded with grey, around $\lambda _5 \sim 10^{-9}$, $\mathrm{max}_{ij} \left( |(h_{F})_{ij}|, |(h_{{{\bar{F}}}})_{ij}| \right) \ge 2$, so the model tends to be non-perturbative.

As we see in the top right plot with $m_{S_1} = 3$ TeV and $L = 30$ $\hbox {fb}^{-1}$, MoEDAL can probe the model up to $m_{S_3} = 1000$ (800) GeV with $N_{\mathrm{sig}} = 1$ (3) for $\lambda _5 \sim 10^{-5}$, at which the lifetime of $S^{\pm 4}$ is maximized. The reach of $m_{S_3}$ is degraded to $\sim 600$ GeV for both $N_{\mathrm{sig}} = 1$ and 3 if $\lambda _5$ is taken around $10^{-3}$ or $10^{-7}$. For a larger luminosity $L = 300$ $\hbox {fb}^{-1}$, the sensitivity is improved up to $\sim 1450$ (1250) GeV for $N_{\mathrm{sig}} = 1$ (3) at $\lambda _5 \sim 10^{-5}$. For different values of $\lambda _5$ the sensitivities are degraded. For example, MoEDAL can probe the model only up to $m_{S_3} \sim 750$ GeV if $\lambda _5 \sim 10^{-3}$ or $10^{-7}$. Moving to the bottom plots with $m_{S_1} = 10$ TeV, we see that the contours of $N_{\mathrm{sig}} = 1$ and 3 become more flat and the highest mass reaches become more stable for a variation of $\lambda _5$. This is because the decay rates get extra suppression due to large $m_{S_1}$, and $c \tau$ comes down to the $\sim 10$ m range only for $\lambda _5 \lesssim 10^{-7}$ or $\gtrsim 10^{-3}$ as can be seen in the right plot of Fig. 6. In the range $10^{-6} \gtrsim \lambda _5 \gtrsim 10^{-4}$, MoEDAL can probe the model up to $m_{S_3} \sim 1000$ (800) GeV for $N_{\mathrm{sig}} = 1$ (3) with $L=30$ $\hbox {fb}^{-1}$ (Run-3). For the larger luminosity $L=300$ $\hbox {fb}^{-1}$ (HL-LHC), the reach is extended to 1500 (1250) GeV for $N_{\mathrm{sig}} = 1$ (3). In all plots the maximum reaches for $m_{S_3}$ roughly correspond to the maximum reaches for $m_{S^{\pm 4}}$ in the previous subsection.

Fig. 8

$N_{\mathrm{sig}} = 1$ contours for different values of $h_{ee}$ in Model-1. We take $m_{S_1} = 3$ and 10 TeV in the left and right plots, respectively. We assume $L = 30$ $\hbox {fb}^{-1}$ and $m_{F_i} = 3$ TeV ($i = 1,2,3$)

We have so far fixed $h_{ee}$ to be 0.1. In Fig. 8 we show the impact of $h_{ee}$ on the detectability of the model at MoEDAL. In the plots, different curves represent $N_{\mathrm{sig}} = 1$ contours with different values of $h_{ee}$. As previously, we fix $m_{F_i} = 3$ TeV and take $m_{S_1} = 3$ and 10 TeV in the left and right plots, respectively. Both L-conserving and L-violating decays are proportional to $h_{ee}$ at the amplitude level and the lifetimes of multi-charged particles in the $S_3$ triplet are inversely proportional to $|h_{ee}|^2$. In the left plot with $m_{F_i} = 3$ TeV, we see that the maximal reach of $m_{S_3}$ becomes less sensitive to $\lambda _5$ for smaller $h_{ee}$, since the decay rates are suppressed for smaller $h_{ee}$. In the right plot with $m_{S_1} = 10$ TeV this tendency is even stronger since the decay rates have extra suppression due to the larger value of $m_{F_i}$.

5 Numerical analysis for coloured models

5.1 Results for colour-triplet multi-charged particles

In this section we study the second model (Model-2) of neutrino mass generation, which we have described in Sect. 2. The model is obtained from Model-1 by changing the $SU(3)_c$ representation of particles from singlet to (anti-)triplet ($S \rightarrow {{\tilde{S}}}$ and $F \rightarrow {{\tilde{F}}}$) as is shown in Eq. (2.18). Another modification is the BSM parity breaking term in the Lagrangian; $(h_{ee})_{ij} e^c_i e^c_j S_1^\dagger \rightarrow (h_{ed})_{ij} d^c_i e^c_j S_1^\dagger$. This is necessary for gauge invariance and making the lightest BSM particle unstable. With these modifications, the Lagrangian of Model-2 is the same as that of Model-1 and the relevant decays are:

$$\begin{aligned} \begin{array}{lcll} &{} &{} L~\mathrm{conserving}, &{} L~\mathrm{violating} \\ {{\tilde{S}}}^{+10/3} &{} \rightarrow &{} \ell ^+ \ell ^+ \ell ^+ {{\bar{d}}}, &{} W^+ W^+ \ell ^+ {{\bar{d}}} \\ {{\tilde{S}}}^{+7/3} &{} \rightarrow &{} \nu \ell ^+ \ell ^+ {{\bar{d}}}, &{} W^+ \ell ^+ {{\bar{d}}} \\ {{\tilde{S}}}^{+4/3} &{} \rightarrow &{} \nu \nu \ell ^+ {{\bar{d}}}, &{} \ell ^+ {{\bar{d}}} \end{array} \end{aligned}$$

(5.1)

We call the first decay modes in Eq. (5.1) (with neutrinos or without Ws) L-conserving and the second decay modes L-violating, assigning $L=3$ for ${{\tilde{S}}}_3$. With the replacement $\ell _\alpha ^+ \rightarrow {{\bar{d}}}_\alpha$ and $(h_{ee})_{\alpha \beta } \rightarrow (h_{ed})_{\alpha \beta }$, the decay rate formulae for those decays are unchanged from those of the corresponding decays in Model-1, which are found in Sect. 2.

There is one possible complication for decays of Model-2 particles. If, for example, ${{\tilde{S}}}^{10/3}$ forms a hadron together with a d-quark, by moving the ${{\bar{d}}}$ in the final state into the initial state hadron, one can consider a 3-body decay $({{\tilde{S}}}^{+10/3} d)_{\mathrm{had}} \rightarrow \ell ^+ \ell ^+ \ell ^+$. However, a dimensional analysis tells us that the hadronic 3-body decay is subdominant. For example for $m_{{{\tilde{S}}}_3} = 600$ GeV we estimate

$$\begin{aligned} \frac{\Gamma [({{\tilde{S}}}^{+10/3} d)_{\mathrm{had}} \rightarrow \ell ^+ \ell ^+ \ell ^+]}{\Gamma [{{\tilde{S}}}^{+10/3} \rightarrow \ell ^+ \ell ^+ \ell ^+ {{\bar{d}}}]} ~\sim ~ \frac{P_3 f_{\pi }^2}{P_4 m^2_{{{\tilde{S}}}_3}} ~\sim ~ 10^{-5}, \end{aligned}$$

(5.2)

where $f_{\pi }$ is the pion decay constant and $P_n \equiv [4 \cdot (4 \pi )^{2n-3} \cdot (n-1)! \cdot (n-2)!]^{-1}$ is the n-body phase-space factor. We therefore do not consider this type of decays in our analysis.

In Model-2, the long-lived multi-charged particles that may be detected at MoEDAL are the states originated in the $SU(2)_L$ triplet field ${{\tilde{S}}}_3$, denoted by ${{\tilde{S}}}^{+4/3}$, ${{\tilde{S}}}^{+7/3}$ and ${{\tilde{S}}}^{+10/3}$. These states correspond to $S^{+2}$, $S^{+3}$ and $S^{+4}$ in Model-1 but there are two main differences. One is that their electric charge is smaller by 2/3 compared to the corresponding particles in Model-1. Another difference is that the multi-charged particles in Model-2 are colour (anti-)triplet states.

Due to the colour charge the particle-anti-particle pair productions, $pp \rightarrow {{\tilde{S}}}^{+10/3} {{\tilde{S}}}^{-10/3}$, ${{\tilde{S}}}^{+7/3} \tilde{S}^{-7/3}$ and ${{\tilde{S}}}^{+4/3} {{\tilde{S}}}^{-4/3}$, via QCD interaction with the gg and $q {{\bar{q}}}$ initial states are the dominant production mechanism for the long-lived particles in Model-2. The contributions from the EW interaction are negligible and the above three pair production modes have approximately the same cross-section, which is shown in Fig. 3 by the cyan curve. As can be seen in Fig. 3, the cross-section is almost two orders of magnitude larger than that of $pp \rightarrow S^{+4} S^{-4}$ in Model-1 at $m_{S_3} \sim 400$ GeV. The coloured particle production is relatively more enhanced compared to the non-coloured particle production at the lower mass region, because the parton distribution function of gluons gets very large for smaller values of the parton energy fraction, x.

Fig. 9

The model-independent detection reach at MoEDAL in the (m, $c \tau$) parameter plane for individual particles of Model-2. The red, green and blue contours correspond to the results obtained with the hadronisation parameter $k = 0.3$, 0.5 and 0.7, respectively, and solid dashed and dotted contours represent $N_{\mathrm{sig}} = 1$, 2 and 3, respectively. In the left (right) panel the integrated luminosity of 30 (300) $\hbox {fb}^{-1}$ is assumed

Table 3 Summary for the model-independent mass reaches (in GeV) of the multi-charged particles in Model-2 by MoEDAL (2nd and 3rd columns). In the first column, the numbers in the double-brackets show the estimated mass bounds obtained in [39] by rescaling the 8 TeV CMS result [40] to the 13 TeV LHC with $L = 36$ $\hbox {fb}^{-1}$. The second column represents the projected mass reach for Run-3 (300 $\hbox {fb}^{-1}$) obtained in [39]. The numbers outside (inside) the brackets in the third and fourth columns represent MoEDAL’s mass reaches with $N_{\mathrm{sig}} \ge 3$ (1) assuming $L = 30$ (Run-3) and 300 (HL-LHC) $\hbox {fb}^{-1}$, respectively

Fig. 10

Lifetimes of multi-charged particles, ${{\tilde{S}}}^{\pm 10/3}$ (blue solid) ${{\tilde{S}}}^{\pm 7/3}$ (green dashed) and ${{\tilde{S}}}^{\pm 4/3}$ (red dotted), in Model-2 as functions of $\lambda _5$, where $h_F$ and $h_{{{\bar{F}}}}$ are fitted to the neutrino data. The $m_{{{\tilde{S}}}_1}$ is taken to be 3 and 10 TeV in the left and right plots, respectively. The other parameters are fixed as $h_{ed} = 0.1$, $m_{{{\tilde{S}}}_3} = 750$ GeV and $m_{{{\tilde{F}}}_i} = 3$ TeV ($i = 1,2,3$)

The velocity distribution of the produced coloured particles is shown in Fig. 4 by the cyan curve. As can be seen, the velocity of coloured particles are the smallest on average compared to the non-coloured ones. This is because unlike the Drell–Yan production of EW particles, the production rate from the gg initial state does not suffer from the p-wave suppression. Moreover, as mentioned above, the parton distribution function of gluons is strongly enhanced for smaller energy fraction, x, preferring near-threshold productions with low velocities.

Once the multi-charged long-lived particles are produced they hadronise into colour singlet states before decaying. After hadronising, charges of the long-lived particles are shifted by the constituent quarks. A precise simulation for predicting the hadronic final states is complicated and beyond the scope of this study. Instead, we use the following crude model of hadronisation in order to see the effect of the charge shift due to hadronisation. In our hadronisation model, ${{\tilde{S}}} = ({{\tilde{S}}}^{+10/3}, \, \tilde{S}^{+7/3}, \, {{\tilde{S}}}^{+4/3})$ is hadronised into a mesonic state with the probability k and into a baryonic state with the probability $1-k$. We consider the following two mesonic states and assume that those states appear with the same probability:

$$\begin{aligned}&\text{ Spin-1/2 } \text{ mesons: } \text{ probability } \text{ k } \nonumber \\&{{\tilde{S}}} + u_{L/R} ~~~~ (+ 2/3) \nonumber \\&{{\tilde{S}}} + d_{L/R} ~~~~ (- 1/3), \end{aligned}$$

(5.3)

where the numbers in the brackets represent the charge shift. For baryonic states, we consider four spin-0 states and two spin-1 states, assuming the democratic probabilities for appearance:

$$\begin{aligned}&\text{ Spin-0 } \text{ baryons: } \text{ probability }\ \frac{2}{3}(1-k) \nonumber \\&{{\tilde{S}}} + {{\bar{u}}}_L {{\bar{u}}}_R ~~~~ (- 4/3) \nonumber \\&{{\tilde{S}}} + {{\bar{d}}}_L {{\bar{d}}}_R ~~~~ (+ 2/3) \nonumber \\&{{\tilde{S}}} + {{\bar{u}}}_L {{\bar{d}}}_R ~~~~ (- 1/3) \nonumber \\&{{\tilde{S}}} + {{\bar{d}}}_L {{\bar{u}}}_R ~~~~ (- 1/3) \nonumber \\&\text{ Spin-1 } \text{ baryons: } \text{ probability }\ \frac{1}{3}(1-k) \nonumber \\&{{\tilde{S}}} + {{\bar{u}}}_L {{\bar{d}}}_L ~~~~ (- 1/3) \nonumber \\&{{\tilde{S}}} + {{\bar{u}}}_R {{\bar{d}}}_R ~~~~ (- 1/3), \end{aligned}$$

(5.4)

Finally, we vary the parameter k from 0.3 to 0.7 to roughly understand the size of the uncertainty from the hadronisation effect. We emphasis again that we use this naive hadronisation model only for the purpose of a ballpark estimate of the MoEDAL’s detectability of the model. More precise treatment of hadronisation may be necessary to fully understand the MoEDAL’s performance.

Fig. 11

MoEDAL’s detection sensitivity for Model-2 in the ($m_{S_3}$, $\lambda _5$) plane. The red, green and blue contours correspond to the results obtained with the hadronisation parameter $k = 0.3$, 0.5 and 0.7, respectively. In the regions inside the solid, dashed and dotted contours, MoEDAL expects to observe more than 1, 2 and 3 events, respectively. The region with $N_{\mathrm{sig}} \ge 3$ will be excluded at 95% CL if MoEDAL does not observe any signal event. The left and right panels correspond to $L = 30$ and 300 $\hbox {fb}^{-1}$, respectively. We take $m_{{{\tilde{F}}}_i} = 3$ TeV ($i = 1,2,3$) for all plots and $m_{{{\tilde{S}}}_1} = 3$ (10) TeV in the top (bottom) panels. The $h_{F}$ and $h_{{{\bar{F}}}}$ are fitted to the neutrino data. In the grey region one of these couplings tend to be non-perturbative; $\mathrm{max}_{ij} \left( |(h_{F})_{ij}|, |(h_{\bar{F}})_{ij}| \right) \ge 2$

Fig. 12

$N_{\mathrm{sig}} = 1$ contours for different values of $h_{ed}$ in Model-2. The hadronisation parameter k is fixed to 0.5. We take $m_{S_1} = 3$ and 10 TeV in the left and right plots, respectively. We assume $L = 30$ $\hbox {fb}^{-1}$ and $m_{F_i} = 3$ TeV ($i = 1,2,3$)

We show in Fig. 9 the expected sensitivities for MoEDAL to detect multi-charged long-lived particles in Model-2. The results are regarded as model-independent and presented in the (m, $c \tau$) plane. The plots on the left (right) column correspond to $L = 30$ (300) $\hbox {fb}^{-1}$, which is achievable in Run-3 LHC (HL-LHC). Here we show the sensitivities calculated with the hadronisation parameter $k = 0.3$, 0.5 and 0.7 with red, green and blue contours, respectively. One can immediately see that the effect of the hadronisation parameters on the detection reach is not strong. From $k = 0.3$ to 0.7, the mass reach changes about 50 GeV for ${{\tilde{S}}}^{\pm 4/3}$. For $\tilde{S}^{\pm 10/3}$, the effect is even smaller; the impact on the mass reach is about 30 GeV for varying k from 0.3 to 0.7. This is because a change of the signal acceptance in varying the velocity threshold, $\beta _{\mathrm{th}} = 0.15 \cdot Z$, is milder for larger Z, as can be seen in Fig. 4. We also see that larger k provides a higher mass reach in the plots. On the other hand, the solid, dashed and dotted curves correspond to $N_{\mathrm{sig}} = 1$, 2 and 3. The top two plots show the detection reach for ${{\tilde{S}}}^{\pm 4/3}$. We see that for $N_{\mathrm{sig}} = 1$ (3) MoEDAL can probe ${{\tilde{S}}}^{\pm 4/3}$ up to $\sim$1050 (880) GeV with $L=30$ $\hbox {fb}^{-1}$. At HL-LHC with $L = 300$ $\hbox {fb}^{-1}$ the mass reach improves up to $\sim 1400$ (1250) with $N_{\mathrm{sig}} = 1$ (3). The plots in the second line show MoEDAL’s sensitivity for ${{\tilde{S}}}^{\pm 7/3}$. One can see that the mass reach with $N_{\mathrm{sig}}= 1$ (3) is $\sim$1250 (1080) GeV with $L = 30$ $\hbox {fb}^{-1}$ (Run-3) and 1650 (150) GeV with $L = 300$ $\hbox {fb}^{-1}$ (HL-LHC). The detection reaches for ${{\tilde{S}}}^{\pm 10/3}$ are shown in the bottom two plots. With 30 $\hbox {fb}^{-1}$ (Run-3) the reach is $\sim 1400$ (1200) GeV for $N_{\mathrm{sig}} = 1$ (3) and with 300 $\hbox {fb}^{-1}$ (HL-LHC) this is improved up to $\sim 1800$ (1600) GeV.

In Table 3 we summarise the results obtained in this subsection and compare them with the current bounds and future projections from HSCP searches (if available). The mass reaches are shown in the GeV unit. In the first column, the numbers in the double-brackets represent the estimated mass bounds obtained in [39] by rescaling the 8 TeV CMS result [40] to the 13 TeV LHC with $L = 36$ $\hbox {fb}^{-1}$. The second column represents the projected mass reach for Run-3 (300 $\hbox {fb}^{-1}$) obtained in [39]. The numbers outside (inside) the brackets in the third and fourth columns represent MoEDAL’s mass reaches with $N_{\mathrm{sig}} \ge 3$ (1) assuming $L = 30$ (Run-3) and 300 (HL-LHC) $\hbox {fb}^{-1}$, respectively. We see in Table 3 that the estimated current bounds from the HSCP searches are rather strong and the regions where MoEDAL has sensitivity for Run-3 are already excluded. However, MoEDAL can explore ${{\tilde{S}}}^{\pm 7/3}$ and ${{\tilde{S}}}^{\pm 10/3}$ in some mass regions that are not excluded at the HL-LHC with $L = 300$ $\hbox {fb}^{-1}$.

5.2 Interpretation of the results for Model-2

We discuss in this section MoEDAL’s sensitivity to Model-2 combining all production modes studied in the previous subsection. Our goal is to identify the parameter regions to be explored by MoEDAL at LHC Run-3 (30 $\hbox {fb}^{-1}$) and HL-LHC (300 $\hbox {fb}^{-1}$) within the subspace of model parameters in which the experimental values of neutrino mass and mixing angles are fitted.

We start by showing the lifetimes of multi-charged long-lived particles in Model-2 as functions of $\lambda _5$ in Fig. 10, where $h_F$ and $h_{{{\bar{F}}}}$ are fitted to the neutrino data. We fix $m_{{{\tilde{S}}}_3} = 750$ GeV, $m_{\tilde{F}_i} = 3$ TeV and $h_{ed} = 0.1$ and take $m_{{{\tilde{S}}}_1} = 3$ and 10 TeV in the left and right plots, respectively. As can be seen, the results are very similar to those for Model-1 shown in Fig. 6, which should be understood since the decay rate formulae are the same between Model-1 and -2 and the neutrino mass formula is also the same except for the colour factor, $N_c$. We see, however, that the lifetimes for Model-2 particles are slightly (about a factor of two times) longer than the corresponding particles in Model-1. As mentioned in the previous section for Fig. 6, in the large $\lambda _5$ region ($\lambda _5 \gg 10^{-5}$) the L-violating decay modes, whose decay rate is proportional to $|\lambda _5|^2$, dominate over the L-conserving modes. On the contrary, in the small $\lambda _5$ region ($\lambda _5 \ll 10^{-6}$) the L-conserving modes are dominant since their decay rates are proportional to $h_F h_{{{\bar{F}}}}$, which is inversely related to $\lambda _5$ through the neutrino masses. The black horizontal lines in Fig. 10 represent $c \tau = 1$ m, which is the typical lifetime for the MoEDAL detector. We see that we expect the multi-charged particles to have long enough lifetime for MoEDAL when $10^{-7} \lesssim \lambda _5 \lesssim 10^{-3}$ for $m_{S_3} = 3$ TeV and $5 \cdot 10^{-8} \lesssim \lambda _5 \lesssim 10^{-2}$ for $m_{S_3} = 10$ TeV.

In Fig. 11 we show MoEDAL’s sensitivity to Model-2 in the ($m_{{{\tilde{S}}}_3}$, $\lambda _5$) plane. The plots on the left (right) correspond to $L = 30$ (300) $\hbox {fb}^{-1}$ and we take $m_{\tilde{S}_1} = 3$ (10) TeV in the top (bottom) plots. We fix $m_{\tilde{F}_i} = 3$ TeV and $h_{ed} = 0.1$ for all plots. As in Fig. 9, we vary the parameter k in our hadronisation model as $k=0.3$ (red), 0.5 (green) and 0.7 (blue) to see the impact of the uncertainty of the hadronisation effect. We present the contours corresponding to $N_{\mathrm{sig}} = 1$, 2 and 3 with the solid, dashed and dotted curves, respectively. In the grey region at the bottom of the plots, we have $\mathrm{max}_{ij} \left( |(h_{F})_{ij}|, |(h_{{{\bar{F}}}})_{ij}| \right) \ge 2$ and the result may not be trusted due to a large coupling. We first note that varying the hadronisation parameter k from 0.3 to 0.7, the mass reach changes only $\sim$30 GeV. We therefore think the conclusion of our analysis is rather robust despite our crude hadronisation model. The highest reach for $m_{{{\tilde{S}}}_3}$ roughly agrees with the model-independent mass reach of $m_{{{\tilde{S}}}^{\pm 10/3}}$ studied in the previous section, though the reach for the $m_{{{\tilde{S}}}_3}$ parameter is slightly higher due to the effect of other particles.

On the top two plots with $m_{{{\tilde{S}}}_1} = 3$ TeV, we see that the highest reach for $m_{{{\tilde{S}}}_3}$ with $N_{\mathrm{sig}} = 1$ is $\sim$1400 (1800) GeV for $L = 30$ (300) $\hbox {fb}^{-1}$ with $\lambda _5 \sim 10^{-5}$, at which the lifetime of ${{\tilde{S}}}^{\pm 4}$ is maximized. Around $\lambda _5 \sim 10^{-3}$ or $10^{-7}$, MoEDAL can expect to observe more than 1 signal event only up to $m_{{{\tilde{S}}}_3} \sim 800$ (1000) GeV for $L = 30$ (300) $\hbox {fb}^{-1}$. Moving to the bottom plots with $m_{{{\tilde{S}}}_1} = 10$ TeV, we see that the range of $\lambda _5$ that gives the highest reach for $m_{{{\tilde{S}}}_3}$ becomes wider compared to the top plots with $m_{{{\tilde{S}}}_1} = 3$ TeV and the reach of $m_{{{\tilde{S}}}_3}$ becomes slightly higher. This is because the lifetimes of the multi-charged particles in the ${{\tilde{S}}}_3$ multiplet get prolonged due to larger $m_{{{\tilde{S}}}_1}$ compared to the case with $m_{{{\tilde{S}}}_1} = 3$ TeV. The highest reach for $m_{\tilde{S}_3}$ is obtained around $\lambda _5 \sim 10^{-5}$ and it is $\sim 1500$ (1900) GeV with $L = 30$ (300) $\hbox {fb}^{-1}$ with $N_{\mathrm{sig}} = 1$. The reach is degraded for different values of $\lambda _5$ as can be seen in Fig. 11.

Before closing this section we show the response of MoEDAL’s detection capability to variations of the coupling $h_{ed}$ for Model-2 in the ($m_{{{\tilde{S}}}_3}$, $\lambda _5$) plane in Fig. 12. Here we fix $L = 30$ $\hbox {fb}^{-1}$, $k = 0.5$ and $m_{{{\tilde{F}}}_i} = 3$ TeV and take $m_{{{\tilde{S}}}_1} = 3$ and 10 TeV in the left and right plots, respectively. As can be seen, the region in which MoEDAL has a sensitivity is wider for smaller $h_{ed}$ since the lifetimes of multi-charged particles are longer. Comparing these plots with the corresponding plots in Fig. 8 for Model-1, we see that MoEDAL’s is more sensitive to the $h_{ed}$ coupling than the $h_{ee}$ coupling in the Model-1 case. This is because the electric charges, Z, of the Model-2 particles are smaller than those of the Model-1 particles and the signal efficiency is more sensitive to the lifetimes in Model-2.

6 Conclusions

In this paper we investigated the possibility of observing long-lived particles whose electric charges are larger than 1 with the MoEDAL detector for Run-3 and High-Luminosity phase of the LHC. In particular, we took two concrete models of radiative neutrino mass generation and studied MoEDAL’s performance for the long-lived multi-charged particles found in those models. In the first model (Model-1), the BSM sector is non-coloured and has three long-lived particles ($S^{\pm 2}$, $S^{\pm 3}$, $S^{\pm 4}$) with electric charges $Z = 2$, 3 and 4. In the second model (Model-2), the BSM sector is coloured and the long-lived particles (${{\tilde{S}}}^{\pm 4/3}$, ${{\tilde{S}}}^{\pm 7/3}$, ${{\tilde{S}}}^{\pm 10/3}$) have fractional charges $Z = 4/3$, 7/3 and 10/3. In both models, the lifetimes of the multi-charged particles are controlled by the $\lambda _5$, $h_F$, $h_{{{\bar{F}}}}$ couplings as well as the BSM parity breaking coupling $h_{ee}$ ($h_{ed}$) for Model-1(2). In addition $\lambda _5$ and the product $h_F h_{{{\bar{F}}}}$ are related through the constraints from the neutrino masses and mixing angles.

We demonstrated that multi-charged scalar particles with a large Z present several advantages for MoEDAL. First, the ionisation power increases with larger Z and it relaxes the upper limit on the production velocity required to be detected by MoEDAL. Secondly, it raises the cross-sections due to the large enhancement of the photon fusion process. In particular, the Drell–Yan process is p-wave suppressed for scalar particles, meaning that the cross-section vanishes when the production velocity goes to zero. The photon fusion process is free from the p-wave suppression and it allows to access lower production velocities, which helps improve significantly MoEDAL’s detection efficiency.

Our study was comprised of the model-independent and model-specific parts and in the former we studied MoEDAL’s detection capabilities for individual particles treating their masses and lifetimes as free parameters. The results of this part of study are summarised in Fig. 5 and Table 2 for Model-1 and in Fig. 9 and Table 3 for Model-2. By taking the optimistic criteria $N_{\mathrm{sig}} \ge 1$, MoEDAL can explore the Model-1 particles up to 290, 610 and 960 GeV for $S^{\pm 2}$, $S^{\pm 3}$ and $S^{\pm 4}$ in Run-3 ($L = 30$ $\hbox {fb}^{-1}$) and 600, 1100 and 1430 GeV at HL-LHC ($L = 300$ $\hbox {fb}^{-1}$). These numbers can be compared to the current constraints 650, 780 and 920 GeV from the HSCP searches. Although a large part of the region that is accessible to MoEDAL in Run-3 is already excluded, MoEDAL can explore some phenomenologically viable regions at HL-LHC. For Model-2, MoEDAL can explore the region with $N_{\mathrm{sig}} \ge 1$ up to 1050, 1250 and 1400 GeV for ${{\tilde{S}}}^{\pm 4/3}$, ${{\tilde{S}}}^{\pm 7/3}$ and $\tilde{S}^{\pm 10/3}$ for Run-3 ($L = 30$ $\hbox {fb}^{-1}$). At the high-luminosity phase, these mass reaches are improved up to 1400, 1600 and 1800 GeV. Comparing these with the estimated current bounds, 1450, 1480 and 1510 GeV for ${{\tilde{S}}}^{\pm 4/3}$, ${{\tilde{S}}}^{\pm 7/3}$ and ${{\tilde{S}}}^{\pm 10/3}$, we concluded that although we do not have much hope to see the exotic particles of Model-2 in Run-3, MoEDAL can explore some part of the allowed parameter regions at the HL-LHC.

In the model-specific part of the study, we explored the subset of the parameter space in which the neutrino data are fitted and identify the regions to which MoEDAL is sensitive. We find that MoEDAL’s sensitivity is maximised around $\lambda _5 \sim 10^{-5}$, at which the lifetime of $S^{\pm 4}$ in Model-1 (and ${{\tilde{S}}}^{\pm 10/3}$ in Model-2) is the longest. The maximum reach of the $m_{S_3}$ ($m_{{{\tilde{S}}}_3}$) parameter was found to be roughly the same as the corresponding mass reach of $S^{\pm 4}$ ($S^{\pm 10/3}$).

Finally, we comment that in this study the NTD response was modelled by only considering the particle velocity and charge. In reality, the efficiency may also depend on the incidence angle of the particle trajectory with respect to the NTD panel plane. Although this effect is not expected to be significant, it may be included in future studies in order to accurately assess the performance of the long-lived particle searches at MoEDAL.