1 Introduction

As an interesting quantum phenomenon, neutrino oscillations (NOs) had been put forward over half a century [1, 2], which exists that the leptonic flavor (including electron, muon, and tau) can be transformed subsequently into the different flavors. Attributing to the linear superposition of nondegenerate mass eigenstates of the neutrino flavor states, the oscillation takes place in reality. In recent years, many studies and experiments have revealed the interesting details about oscillation parameters [3,4,5,6,7]. In order to verify the quantumness of neutrino oscillations, Leggett–Garg inequality (LGI) had been taken into account [8,9,10,11,12,13], which is deemed as one of good candidates for testing whether neutrinos oscillations exist the quantumness or not. Indeed, it indicates that what observed in neutrino oscillation experiments violates the classical limits offered by LGI [14].

On the other hand, owing to the weak interactions of neutrinos, the decoherence effect during NOs is relatively weak compared with those in other particle systems that are widely utilized in the course of quantum-information processing. To date, there have been some promising works contributing to exploring the quantumness of neutrino oscillations [15,16,17,18,19,20,21,22], those quantumness investigations including three-flavor and two-flavor neutrino oscillations. In general, the NOs are under the three flavors frame, while the model of NOs can be reduced to effective two-flavor neutrino oscillations in some experimentally relevant cases [18]. Notably, two-flavor NOs are just applicable in some special cases, so exploring the relevant quantum properties of three flavors NOs is more comprehensive and representative. Technically, three flavors neutrino oscillations can be seen as a three-mode system, namely three-qubit system [23, 24], like a generalized class of W-state in quantum optics. In the experimental aspect, there are ensembles of reactor and accelerator neutrinos from the various neutrino sources, including Daya Bay [3], KamLAND [4], MINOS [5], MINOS+ [6] and T2K [7]. As a matter of fact, MINOS+ is an updated version based on MINOS, the Main Injector Neutrino Oscillation Search (MINOS) experiment has been going on for seven years, from 2005 to 2012, and it can make accurate measurements of neutrino oscillation parameters over distance of 735 km by using the Neutrinos at the Main Injector (NuMI) neutrino beam and two detectors. Since 2013, the NuMI beam and the electronics in same detectors were upgraded, MINOS+ experiment thus is viewed as the escalated version of MINOS experiment. MINOS experiment used low-energy beam at an energy of 3GeV, while MINOS+ experiment medium-energy beam spectrum peaks at 7GeV. Besides, a new measurement of electron antineutrino disappearance by using the fully-constructed Daya Bay Reactor Neutrino Experiment was reported [3], and the distance that can make precise measurement of neutrino oscillation parameters are 0.5 and 1.6 km with the energy from 1 to 8 MeV.

Schrödinger [25] proposed the concept of entanglement many decades ago, which is the amazing characteristic in quantum mechanics, resulting in various interesting applications in quantum information processing. If we assumed that a pure state is entangled, this state must be unfactorizable, for example, this singlet state, \(\frac{1}{{\sqrt{2} }}(\left| { \uparrow \downarrow } \right\rangle + \left| { \downarrow \uparrow } \right\rangle )\), of two spin-\(\frac{1}{2}\) particles is unfactorizable, so we can say that state is entangled.

In 1927, Heisenberg [26] proposed the celebrated uncertainty principle, which is deemed as one of the important features distinguishing quantum world from classical counterpart. Later, Kennard [27] and Robertson [28] constructed a standard deviation inequation, \(\Delta \hat{R}\mathrm{{ }}\Delta \hat{S} \ge | {\langle \psi |[ {\hat{R},\hat{S}} ]| \psi \rangle } |/2\), to show the uncertainty principle, where \(\Delta \hat{R} = \sqrt{\langle {{\hat{R}^2}} \rangle - {{\langle \hat{R} \rangle }^2}}\) and \({\langle \hat{R} \rangle }\) means the expectations value of operator \(\hat{R}\). The lower bound of the relation is not an optimal prediction result, because it is dependent on the systemic state \(\rho \), which will result in a trivial lower bound (zero) if the system is prepared in one of the eigenstates of \(\hat{R}\) or \(\hat{S}\). Note that, Deutsch [29] in 1983 took entropy measure into account for depicting the uncertainty principle, leading to the well-known entropic uncertainty relation (EUR), compared with the standard deviation, the lower bound of EUR is state-independent so that the EUR can predict the measured uncertainty better. After that, many efforts have been made to improve the form of EUR [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. Among these investigations, tripartite uncertainty relations are of fundamental importance to reveal the quantumness of practical multipartite systems. Motivated by this, we here observe the uncertainty relations in the process of neutrino oscillations, which was originally proposed by Renes and Boileau [32].

Entanglement and EUR are very useful in quantum information processing. Specifically, entanglement, as one of the quantum resources, plays an important role in achieving various quantum tasks, such as teleportation [47], quantum computation [48], and so on. While EUR can be widely applied to security analysis of quantum communication [49], quantum teleportation [50], quantum steering [51], quantum randomness [52], and wave-particle duality [53] (also see the review [54]). Recently, Blasone et al. focused on exploring the uncertainty relation, and interestingly derived the flavor-energy uncertainty relation (TEUR) of NOs in the context of quantum field theory [55]. In this article, we treat the three neutrinos state as three-qubit system to explore their intrinsic quantum properties, and compare the corresponding theoretical predictions of the entropic uncertainty [32] and the entanglement [56,57,58] with those in experimental results from Daya Bay [3] and MINOS+ [6], respectively. This will benefit to quantification of the uncertainty and entanglement during realistic NOs, and represents a step towards the goal of practical quantum information processing via neutrino systems.

The article is organized as follows. In Sect. 2, we recall the model of three flavors neutrino, and the methods of exploring entanglement (entanglement of formation, negativity and concurrence) and uncertainty relations. In Sects. 3 and 4, we investigate the entanglement and uncertainty of electron neutrino oscillations at Daya Bay collaboration and muon neutrino oscillations at MINOS+ collaboration, respectively. In final, the summary and discussions are given.

2 The three-flavor neutrino model

The three flavors of neutrinos \(\left| {{\upsilon _e}} \right\rangle \), \(\left| {{\upsilon _\mu }} \right\rangle \) and \(\left| {{\upsilon _\tau }} \right\rangle \) are a linear superposition of three mass eigenstates \(\left| {{\upsilon _1}} \right\rangle \), \(\left| {{\upsilon _2}} \right\rangle \) and \(\left| {{\upsilon _3}} \right\rangle \), which are given by

$$\begin{aligned} \left| {{\upsilon _\alpha }} \right\rangle = \sum _k^{} {{\hat{U}_{\alpha k}}\left| {{\upsilon _k}} \right\rangle }, \end{aligned}$$
(1)

where \(\alpha = e,\mu ,\tau \) and \(k = 1,2,3\). \({\hat{U}_{\alpha k}}\) are the elements of a 3\(\times \)3 Pontecorvo–Maki–Nakagawa–Sakita (PMNS) mixing matrix [2] which is parameterized by three mixing angles ( \({\theta _{12}}\), \({\theta _{13}}\), \({\theta _{23}}\)) and a charge conjugation and parity (CP), the matrix can be expressed as

$$\begin{aligned} \hat{U}=\left( \!\!{\begin{array}{*{20}{c}} {{c_{12}}{c_{13}}}&{}{{s_{12}}{c_{13}}}&{}{{s_{13}}{e^{ - i{\delta _{CP}}}}}\\ { - {s_{12}}{c_{23}} - {c_{12}}{s_{13}}{s_{23}}{e^{i{\delta _{CP}}}}}&{}{{c_{12}}{c_{23}} - {s_{12}}{s_{13}}{s_{23}}{e^{i{\delta _{CP}}}}}&{}{{c_{13}}{s_{23}}}\\ {{s_{12}}{s_{23}} - {c_{12}}{s_{13}}{c_{23}}{e^{i{\delta _{CP}}}}}&{}{ - {c_{12}}{s_{23}} - {s_{12}}{s_{13}}{c_{23}}{e^{i{\delta _{CP}}}}}&{}{{c_{13}}{c_{23}}} \end{array}}\!\right) , \end{aligned}$$
(2)

where \({c_{ij}} = \cos {\theta _{ij}}\) and \({s_{ij}} = \sin {\theta _{ij}}\). Since the CP violating phase has not been observed yet, here we will neglect it in the following discussion. We assume that the massive neutrino states \(\left| {{\upsilon _k}} \right\rangle \) are eigenstates of the Hamiltonian with energy eigenvalues \({E_k}\), and the time evolution of the mass eigenstates \(\left| {{\upsilon _k}} \right\rangle \) can be depicted as

$$\begin{aligned} \left| {{\upsilon _k}(t)} \right\rangle = {e^{ - \frac{i}{h}{E_k}t}}\left| {{\upsilon _k}(0)} \right\rangle , \end{aligned}$$
(3)

where \(\left| {{\upsilon _k}(0)} \right\rangle \) means the mass eigenstates at \(t = 0\). As a result, one can obtain the evolution of the flavor neutrino states as

$$\begin{aligned} \left| {{\upsilon _\alpha }(t)} \right\rangle&= {a_{\alpha e}}(t)\left| {{\upsilon _e}} \right\rangle + {a_{\alpha \mu }}(t)\left| {{\upsilon _\mu }} \right\rangle + {a_{\alpha \tau }}(t)\left| {{\upsilon _\tau }} \right\rangle , \end{aligned}$$
(4)
$$\begin{aligned} {a_{\alpha \beta }}&= \sum _k^{} {{\hat{U}_{\alpha k}}{e^{ - \frac{i}{h}{E_k}t}}\hat{U}_{\beta k}^ * }. \end{aligned}$$
(5)

The probability of detecting flavor neutrino \(\beta \) from the initial \(\alpha \) flavor neutrino is [59]

$$\begin{aligned} {P_{\alpha \rightarrow \beta }}= & {} {\delta _{\alpha \beta }}\! -\! 4\sum \limits _{k> j}^{} {{\mathrm{Re}} ({\hat{U}}_{\alpha k}^ * \hat{U}_{\beta k}^{}\hat{U}_{\alpha j}^{}\hat{U}_{\beta j}^ * )\sin ^2\left( \Delta m_{kj}^2\frac{{L{c^3}}}{{4\hbar E}}\right) }\nonumber \\&+ 2\sum \limits _{k > j}^{} {\mathrm{Im}(\hat{U}_{\alpha k}^ * \hat{U}_{\beta k}^{}\hat{U}_{\alpha j}^{}\hat{U}_{\beta j}^ * )\sin \left( \Delta m_{kj}^2\frac{{L{c^3}}}{{2\hbar E}}\right) } , \end{aligned}$$
(6)

where E is the energy of the neutrino with different values for diverse neutrino experiments, \(\Delta m_{kj}^2 = m_k^2 - m_j^2\), and L is the distance that the neutrino particle traveled between source and detector with \(L = ct\) (c means the speed of the light). By the calculation, one can work out the probabilities in states \(\left| {{\upsilon _\alpha }} \right\rangle \) and \(\left| {{\upsilon _\beta }} \right\rangle \) as the survival probability \({P_{{\upsilon _\alpha } \rightarrow {\upsilon _\alpha }}} = {\left| {{a_{\alpha \alpha }}(t)} \right| ^2}\) and the oscillation probability \({P_{{\upsilon _\alpha } \rightarrow {\upsilon _\beta }}} = {\left| {{a_{\alpha \beta }}(t)} \right| ^2}\), and \({P_{{\upsilon _\alpha } \rightarrow {\upsilon _\alpha }}} + {P_{{\upsilon _\alpha } \rightarrow {\upsilon _\beta }}} = {\left| {{a_{\alpha \alpha }}(t)} \right| ^2}+{\left| {{a_{\alpha \beta }}(t)} \right| ^2}=1\) is held. The allowed ranges of neutrino mixing parameters [59] are obtained by a global fit, we will use the best fit values of parameters in the following calculation as

$$\begin{aligned}&\Delta m_{21}^2 = 7.50 \times {10^{ - 5}} \, \mathrm{e{V^2}},\nonumber \\&\Delta m_{31}^2 = 2.457 \times {10^{ - 3}} \, \mathrm{e{V^2}},\nonumber \\&\Delta m_{32}^2 = 2.382 \times {10^{ - 3}} \, \mathrm{e{V^2}},\nonumber \\&{\theta _{12}} = {33.48^ \circ },\quad {\theta _{23}} = {42.3^ \circ },\quad {\theta _{13}} = {8.50^ \circ }. \end{aligned}$$
(7)

The neutrino modes in the occupation number basis from Ref. [15] can be mapped into

$$\begin{aligned} \left| {{\upsilon _e}} \right\rangle \equiv {\left| 1 \right\rangle _e} \otimes {\left| 0 \right\rangle _\mu } \otimes {\left| 0 \right\rangle _\tau } \equiv \left| {100} \right\rangle ,\nonumber \\ \left| {{\upsilon _\mu }} \right\rangle \equiv {\left| 0 \right\rangle _e} \otimes {\left| 1 \right\rangle _\mu } \otimes {\left| 0 \right\rangle _\tau } \equiv \left| {010} \right\rangle ,\nonumber \\ \left| {{\upsilon _\tau }} \right\rangle \equiv {\left| 0 \right\rangle _e} \otimes {\left| 0 \right\rangle _\mu } \otimes {\left| 1 \right\rangle _\tau } \equiv \left| {001} \right\rangle . \end{aligned}$$
(8)

And the time evolution of a flavor eigenstate \(\alpha = e,\mu ,\tau \) in the occupation number basis can be written as

$$\begin{aligned} \left| {\psi _\alpha {{(t)} }} \right\rangle = {a_{\alpha e}}(t)\left| {100} \right\rangle + {a_{\alpha \mu }}(t)\left| {010} \right\rangle + {a_{\alpha \tau }}(t)\left| {001} \right\rangle . \end{aligned}$$
(9)

To probe the properties of quantumness in the three-flavor neutrino oscillation system, we can resort to entanglement of formation (EOF), which is one of the methods of entanglement measurement, it has been defined by Ref. [56]. Considered that a density matrix \(\rho \) with a pair of quantum systems A and B, decompose this density matrix \(\rho \) into all ensembles of pure-state \(\left| {{\psi _i}} \right\rangle \) and corresponding probabilities \({p_i}\),

$$\begin{aligned} \rho = \sum \limits _i {{p_i}\left| {{\psi _i}} \right\rangle \left\langle {{\psi _i}} \right| } . \end{aligned}$$
(10)

For every pure state in this ensemble, the entanglement of formation is defined as the entropy of the subsystem A or B:

$$\begin{aligned} \mathrm{EOF}(|\psi {_i}\rangle ) = - \mathrm{Tr}({\rho _A}\log _2 {\rho _A}) = - \mathrm{Tr}({\rho _B}\log _2 {\rho _B}), \end{aligned}$$
(11)

where \(\rho _{A(B)}\) represents the partial trace of \(\rho \) to obtain the reduced density matrix of A(B). Therefore, the entanglement of formation of the mixed state is defined as the average entanglement of the decomposed pure state, and it is minimized in all decompositions of \(\rho \):

$$\begin{aligned} \mathrm{EOF}(\rho ) = \min \sum \limits _i {{p_i}\mathrm{EOF}({|\psi _i}\rangle )}. \end{aligned}$$
(12)

Then, one can make an extension to the case of an arbitrary tripartite pure state \({\rho _{ABC }}(t)\), where the entanglement quantified by EOF can be typically simplified into [60]

$$\begin{aligned} \mathrm{EOF}({\rho _{ABC}}(t)) = \frac{1}{2}\left[ {S({\rho _A}) + S({\rho _B}) + S({\rho _C})} \right] , \end{aligned}$$
(13)

where the von Neumann entropy \(S(\rho _A ) = - \mathrm{Tr}(\rho _A \log \rho _A )\) with the reduced density matrices \({\rho _A} = \mathrm{Tr}{_{B C }}({\rho _{AB C }}(t))\), and same with \(\rho _B \), \(\rho _C \).

In addition, there is another methodology to quantify the entanglement of system, says negativity (\({{\mathcal {N}}}\)), which is defined by [58]

$$\begin{aligned} {{\mathcal {N}}} = {\left( {{{{\mathcal {N}}} _{A - B C }}{{{\mathcal {N}}} _{B - C A}}{{{\mathcal {N}}} _{C - A B }}} \right) ^{\frac{1}{3}}}, \end{aligned}$$
(14)

where \({{{\mathcal {N}}} _{A - B C }} = - \sum _i^{} {\lambda _i^A} \), \({{{\mathcal {N}}} _{B - C A}} = - \sum _j^{} {\lambda _j^B } \) and \({{{\mathcal {N}}} _{C - AB }} = - \sum _k^{} {\lambda _k^C } \), with \(\lambda _\varepsilon ^\alpha \) (\(\alpha = A,B ,C \) and \(\varepsilon =i,j,k\)) are the negative eigenvalues [61] of the partial transpose \(\rho _{AB C }^{{T_\alpha }}(t)\) with respect to the matrix \({\rho _{AB C }}(t)\).

Additionally, concurrence is considered as a good candidate for quantifying the entanglement of system. Wooters proposed the explicit mathematical expression of the entanglement with respect to a two-qubit system [57]. Recently, Guo and Gour had revealed that concurrence is available to measure the entanglement of three-qubit states [62], which form can be given by

$$\begin{aligned} {\mathcal {C}}(\rho _{ABC}) = {\left[ {3 - \mathrm{Tr}{{({\rho _A})}^2} - \mathrm{Tr}{{({\rho _B})}^2} - \mathrm{Tr}{{({\rho _C})}^2}} \right] ^{\frac{1}{2}}}. \end{aligned}$$
(15)

On the other hand, the uncertainty principle is deemed as an important feature of the quantum world, which typically differs from the counterpart in classical one. Renes and Boileau put forward the tripartite entropy-based uncertainty relation [32]

$$\begin{aligned} S(\hat{R}|B ) + S(\hat{S} |C ) \ge {q_{MU}}, \end{aligned}$$
(16)

where \(S(\hat{R}|B)\) and \(S(\hat{S}|C)\) are denoted as the conditional von Neumann entropies, \(S( \hat{R} |B) = S({\rho _{\hat{R}B}}) - S({\rho _B})\), \({q_{MU}} = -\log _2 c(\hat{R},\hat{S})\), and \(c = {\max _{i,j}}\{ {{{| {\langle {\Phi _{_i}^{\hat{R}}| {\psi _{_j}^{\hat{S}}} } \rangle } |}^2}} \}\) means the maximal overlap between the observables \(\hat{R}\) and \(\hat{S}\) with \(| {\Phi _i^{\hat{R}}} \rangle \) and \(| {\psi _{_j}^{\hat{S}}} \rangle \) denoting the corresponding eigenstates. We can explain this by a guessing game: Alice, Bob and Charlie are three players in this game. Firstly we prepare a tripartite state \({\rho _{ABC }}\), and then distribute the three particles A, B and C to Alice, Bob and Charlie respectively. Alice choose a measurement (\(\hat{R}\) or \(\hat{S}\)) randomly on particle A and obtain the outcome. After measurement, Alice tells Bob and Charlie about her measurement choice, in the end, if both Bob and Charlie predict the measurement outcome of Alice, we can say that Bob and Charlie have won this game. That is so-called monogamy game. Because of the monogamy of entanglement, Eq. (16) shows uncertainty through this guessing game, if Bob makes a precise guess in the case that Alice measured \(\hat{R}\) on A, as a result, Charlie cannot produce a good guess in the case that Alice measured \(\hat{S}\) on A, and vice versa.

To explore EUR in the neutrino oscillations, we can derive the following inequalities

$$\begin{aligned}&S(\left. {\mathbb {X}} \right| B) + S(\left. {\mathbb {Z}} \right| C) \ge {q_{MU}}, \nonumber \\&S(\left. \mathbb {Y }\right| B) + S(\left. {\mathbb {X}} \right| C) \ge {q_{MU}}, \nonumber \\&S(\left. {\mathbb {Z}}\right| B) + S(\left. {\mathbb {Y}} \right| {C}) \ge {q_{MU}}, \end{aligned}$$
(17)

with regard to three arbitrary non-commuting operators \({\mathbb {X}}\), \({\mathbb {Y}}\) and \({\mathbb {Z}}\). By adding the above three inequalities, one can attain the total entropic uncertainty relation

$$\begin{aligned}&S(\left. {\mathbb {X}} \right| B) + S(\left. {\mathbb {Z}} \right| C) + S(\left. {\mathbb {Y}} \right| B) \nonumber \\&\quad +S(\left. {\mathbb {X}} \right| C) + S(\left. {\mathbb {Z}} \right| B) + S(\left. {\mathbb {Y}} \right| C) \ge 3{q_{MU}}. \end{aligned}$$
(18)

Herein, the total uncertainty of incompatible measurements is termed as \({\mathcal {U}}=S({\mathbb {X}} |B) + S({\mathbb {Y}} |B) +S({\mathbb {Z}} |B) +S( {\mathbb {X}} |C) + S({\mathbb {Y}} |C)+S({\mathbb {Z}} |C)\).

Fig. 1
figure 1

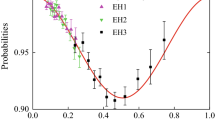
The survival probability \({\nu _e} \rightarrow {\nu _e}\) as a function of the distance traveled per energy L/E with initial electron flavor state. The theoretical predictions (red line) and the experimental data from Daya Bay collaboration [3] in three underground experimental halls (EH1: blue, circle; EH2: green, square; EH3: black, rhombus) have been shown

Full size image

3 EOF, negativity, concurrence and measurement uncertainty in electron neutrino oscillations

If the electron neutrino is prepared at the initial time \(t=0\), the evolutionary state of the initial electron neutrino can be expressed as

$$\begin{aligned} \left| {\psi _e {{(t)}}} \right\rangle = {a_{ee}}(t)\left| {100} \right\rangle + {a_{e\mu }}(t)\left| {010} \right\rangle + {a_{e\tau }}(t)\left| {001} \right\rangle , \end{aligned}$$
(19)

and the corresponding density matrix is \(\rho _{ABC}^e(t) = |{\psi _e {{(t)}}}\rangle \langle {\psi _e {{(t)}}}|\), which matrix form can be written as

$$\begin{aligned} \rho _{ABC}^e(t) = \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{\rho _{22}^e}}&{}{{\rho _{23}^e}}&{}0&{}{{\rho _{25}^e}}&{}0&{}0&{}0\\ 0&{}{{\rho _{32}^e}}&{}{{\rho _{33}^e}}&{}0&{}{{\rho _{35}^e}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{\rho _{52}^e}}&{}{{\rho _{53}^e}}&{}0&{}{{\rho _{55}^e}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right) \end{aligned}$$
(20)

with the elements

$$\begin{aligned} {\rho _{22}^e}\!&=\! {\left| {{a_{e\tau }}(t)} \right| ^2};{\rho _{23}^e}\! =\! {a_{e\tau }}(t)a_{_{e\mu }}^ * (t);{\rho _{25}^e}\! = \!{a_{e\tau }}(t)a_{_{ee}}^ * (t); \nonumber \\ {\rho _{32}^e}\!&=\! {a_{e\mu }}(t)a_{_{e\tau }}^ * (t);{\rho _{33}^e}\! =\! {\left| {{a_{e\mu }}(t)} \right| ^2};{\rho _{35}^e}\! =\! {a_{e\mu }}(t)a_{_{ee}}^ * (t); \nonumber \\ {\rho _{52}^e}\!&=\! {a_{ee}}(t)a_{_{e\tau }}^ * (t);{\rho _{53}^e}\! =\! {a_{ee}}(t)a_{_{e\mu }}^ * (t);{\rho _{55}^e}\! =\! {\left| {{a_{ee}}(t)} \right| ^2}. \end{aligned}$$
(21)

And the corresponding probabilities that we find the electron neutrinos in the electron flavor state \(\left| {{\upsilon _e}} \right\rangle \), the muon flavor state \(\left| {{\upsilon _\mu }} \right\rangle \) , and the tau flavor state \(\left| {{\upsilon _\tau }} \right\rangle \) are \({P_{ee}} = {\left| {{a_{ee}}(t)} \right| ^2}\), \({P_{e\mu }} = {\left| {{a_{e\mu }}(t)} \right| ^2}\) and \({P_{e\tau }} = {\left| {{a_{e\tau }}(t)} \right| ^2}\), respectively. Both the experimental results and corresponding theoretical predictions of survival probabilities \({\nu _e} \rightarrow {\nu _e}\) are plotted with the respect to the ratio L/E with the dimension km/MeV in Fig. 1, where EH1, EH2 and EH3 are the data addressed from Daya Bay collaboration for three different experimental halls [3]. It is obvious that Fig. 1 shows a concave curve. Explicitly, one can observe that the survival probability \({P_{ee}}\) first decreases and subsequently increases, and comes to the minimum at around \(L/E=0.5\) km/MeV. Notably, the survival probability \({P_{ee}}\) is always greater than 0.9, even if it reaches the minimum.

Fig. 2
figure 2

Negativity (\({{\mathcal {N}}}\)) and entanglement of formation (EOF) and concurrence (\({\mathcal {C}}\)) as a function of the distance traveled per energy L/E with an initial electron flavor state. a The pink line denotes the theoretical EOF expressed by Eq. (22); b The wine line denotes the theoretical concurrence in Eq. (24). c The violet line denotes the theoretical negativity in Eq. (23); d Comparison of three entanglement measures (violet line: Negativity; pink line: Entanglement of Formation; wine line: Concurrence) for initial electron flavor state. And the experiment data are from Daya Bay collaboration [3] in three underground experimental halls (EH1: blue, circle; EH2: green, square; EH3: black, rhombus)

Full size image

To observe the entanglement of system in the current consideration, one can compute the systemic EOF as

$$\begin{aligned} \mathrm{EOF}^e =&- \frac{1}{2} [{P_{ee}} \log _2{P_{ee}} + {P_{e\mu }} \log _2{P_{e\mu }}+ {P_{e\tau }} \log _2{P_{e\tau }} \nonumber \\&+ ({P_{e\mu }} + {P_{e\tau }}) \log _2({P_{e\mu }} + {P_{e\tau }}) \nonumber \\&+ ({P_{ee}} + {P_{e\tau }}) \log _2({P_{ee}} + {P_{e\tau }}) \nonumber \\&+ ({P_{e\mu }} + {P_{ee}}) \log _2({P_{e\mu }} + {P_{ee}})] \end{aligned}$$
(22)

by resorting to Eq. (13), which consists of the survival probability \(P_{ee}\) and the oscillation probabilities \(P_{e\mu }\) and \(P_{e\tau }\) in the course of the electron neutrino oscillations.

Additionally, with regard to the negativity, we need to make partial transpose for \(\rho _{ABC}^e(t) \) at first, and obtain \(\rho _{ABC }^{{T_A }}(t)\), \(\rho _{ABC }^{{T_B }}(t)\) and \(\rho _{ABC }^{{T_C }}(t)\), respectively. As a result, the negativity can be exactly worked out

$$\begin{aligned} {{\mathcal {N}}}^e \!= \!{(\sqrt{{P_{ee}}} \mathrm{{ }}\sqrt{{P_{e\mu }}\! +\! {P_{e\tau }}} \mathrm{{ }}\sqrt{{P_{ee}}} \mathrm{{ }}\sqrt{{P_{e\mu }}} \mathrm{{ }}\sqrt{{P_{ee}} \!+\! {P_{e\mu }}} \mathrm{{ }}\sqrt{{P_{e\tau }}} )^{\frac{1}{3}}} \end{aligned}$$
(23)

from Eq. (14).

According to Eq. (15), the expression of concurrence in electron neutrino oscillations can be written as

$$\begin{aligned} {\mathcal {C}}^e\!= \! \sqrt{3\! -\! 3(P_{ee}^2\! +\! P_{e\mu }^2\! +\! P_{e\tau }^2)\! -\! 2{P_{e\mu }}{P_{e\tau }}\! -\! 2{P_{ee}}({P_{e\mu }} \!+\! {P_{e\tau }})}. \end{aligned}$$
(24)

In order to probe the entropic uncertainty relation in the current scenario, we resort to three Pauli operators \(\varvec{\sigma }=\{\hat{\sigma }_x,\hat{\sigma }_y,\hat{\sigma }_z\}\) as the measurement’s incompatibility of qubit A, and obtain the post-measurement states as

$$\begin{aligned}&\rho _{{\hat{\sigma } _i}B}^e(t)\! =\! \sum \limits _{k = 1}^2 {[(\left| {{i_k}} \right\rangle \langle {i_k}|\! \otimes \! \mathbb {I})\rho _{AB}^e(t)(\left| {{i_k}} \right\rangle \langle {i_k}|\! \otimes \! \mathbb {I} )]} , \nonumber \\&\rho _{{\hat{\sigma } _i}C}^e(t)\! =\! \sum \limits _{k = 1}^2 {[(\left| {{i_k}} \right\rangle \langle {i_k}|\! \otimes \! \mathbb {I})\rho _{AC}^e(t)(\left| {{i_k}} \right\rangle \langle {i_k}|\! \otimes \! \mathbb {I})]}, \end{aligned}$$
(25)

where \(\left| {{i_k}} \right\rangle \) (\(i = x,y,z,\) and \(k = 1,2\)) are the eigenvectors of the Pauli measurement \({\hat{\sigma } _i}\), and \(\mathbb {I}\) denotes the identity matrix. In terms of Eq. (18), the total entropic uncertainty \({\mathcal {U}}\) can be analytically expressed as

$$\begin{aligned} {\mathcal {U}}= & {} 4[H_\mathrm{bin}(\lambda _1)-1]+ {P_{e\mu }}\log _2{P_{e\mu }} +{P_{e\tau }}\log _2{P_{e\tau }}\nonumber \\&-2{P_{ee}}\log _2{P_{ee}}+3[({P_{ee}} + {P_{e\mu }})\log _2({P_{ee}}\! + {P_{e\mu }}) \nonumber \\&+ ({P_{e\tau }} + {P_{ee}})\log _2({P_{e\tau }} + {P_{ee}})] \end{aligned}$$
(26)

in the electron neutrino oscillations, where a binary entropy \(H_\mathrm{bin}(\lambda _1)=-\lambda _1 \log _2\lambda _1-(1-\lambda _1)\log _2(1-\lambda _1)\) with \(\lambda _{1}=\frac{1}{2} (1-\sqrt{{{({P_{e e}} + {P_{e \mu }})}^2}+ 2({P_{e e}}-{P_{e \mu }} ){P_{e \tau }} + P_{e \tau }^2})\).

In Fig. 2, we have shown the variation of EOF, negativity (\({{\mathcal {N}}}\)) and concurrence (\({\mathcal {C}}\)) with the increasing L/E from both experimental and theoretical aspects. Herein, the experimental data is from Daya Bay collaboration [3], but actually, we can only get the survival probability \({P_{ee}}\) from experiment. In order to quantify the total entropic uncertainty, EOF, negativity and concurrence, we combine the ratio \(\xi _1 = {P_{e\tau }}/{P_{e\mu }}\) in theoretical prediction and \({P_{ee}} + {P_{e\mu }} + {P_{e\tau }} = 1\), and consequently the oscillation probabilities \(P_{e\mu }\) and \(P_{e\tau }\) can be obtained. According to Eqs. (22)–(24), EOF, \({\mathcal {C}}\) and \({{\mathcal {N}}}\) have been numerically plotted in Fig. 2. Following the figure, one can directly see that the evolution of the entanglements are non-monotonic along with the increasing distance traveled per energy L/E, and entanglement shows a trend of increase first and then decrease. In order to better understand the hierarchical relation among the mentioned three different entanglement measures (EOF, \({\mathcal {N}}\) and \({\mathcal {C}}\)), we plotted the entanglement as a function of the distance traveled per energy L/E with an initial electron flavor state in Fig. 2d. It shows that the concurrence is able to capture more quantum resource compared with the others, and the negativity is less than concurrence and EOF. Moreover, we also estimate the goodness of fit between the experimental data and our theoretical predictions by means of calculating \(\chi ^2/\)NDF. Explicitly, the \(\chi ^2/\)NDF of concurrence and EOF are equal to 5.353/30 and 23.218/30 respectively, which correspond to the p-value of 1 and 0.80618. With these in consideration, we claim that the experiment results well confirm to our theoretical predictions within the error bars, and concurrence and EOF shall be more reliable tools to quantify the entanglement than negativity while accomplishing the prospective quantum telecommunications in the electron NOs.

In Fig. 3, we have shown the variation of the total entropic uncertainty (\({\mathcal {U}}\)) with the increasing L/E from both experimental and theoretical aspects. Obviously, it shows that the total entropic uncertainty \({\mathcal {U}}\) is always greater than its lower bound, which manifests that the EUR in Eq. (18) is hold all the time. The uncertainty presents a trend of decrease first and then increase. Besides, it is worth noting that the uncertainty and entanglement (EOF and \({\mathcal {C}}\)) exhibit the characteristic of anti-correlation, we find that the measured uncertainty would reach the minimum value when the entanglement maximizes at around \(L/E=0.5\)km/MeV, as illustrated in Figs. 2 and 3. From the perspective of theory, this is because that the essence of quantum entanglement is a type of nonclassical correlation, and in principle the stronger quantum correlation would induce the smaller uncertainty of measurement, that is, the larger entanglement, the smaller uncertainty, and vice versa. Our numerical results also verify this very well. Additionally, the \(\chi ^2/\)NDF of the total entropic uncertainty \({\mathcal {U}}\) is 23.636/30, corresponding to the p-value of 0.78823, which supports that our theoretical results are compatible with the experimental one.

Fig. 3
figure 3

The total entropic uncertainty (\({\mathcal {U}}\)) as a function of the distance traveled per energy L/E with an initial electron flavor state. The olive line represents the theoretical value of the total entropic uncertainty in Eq. (26); the red line corresponds to the lower bound of the total EUR, the right-hand side of Eq. (18), the experiment data are from Daya Bay collaboration [3] in three underground experimental halls (EH1: blue, circle; EH2: green, square; EH3: black, rhombus)

Full size image
Fig. 4
figure 4

The survival probability \({\nu _\mu } \rightarrow {\nu _\mu }\) as a function of the distance traveled per energy L/E with an initial muon flavor state. The line denotes the theoretical predictions, and the black squares represent the experiment data from MINOS+ collaboration [6]

Full size image

4 EOF, negativity, concurrence and measurement uncertainty in muon neutrino oscillations

If we prepare a muon neutrino at the initial time \(t=0\), the evolutionary muon neutrino state can be written as

$$\begin{aligned} \left| {\psi _\mu {{(t)} }} \right\rangle \! =\! {a_{\mu e}}(t)\left| {100} \right\rangle \! +\! {a_{\mu \mu }}(t)\left| {010} \right\rangle \! +\! {a_{\mu \tau }}(t)\left| {001} \right\rangle , \end{aligned}$$
(27)

in the occupation number basis, and the corresponding density matrix is \(\rho _{ABC}^\mu (t) = \left| {\psi _\mu {{(t)}}} \right\rangle \left\langle {\psi _\mu {{(t)}}} \right| \), which can be described as

$$\begin{aligned} \rho _{ABC}^\mu (t) = \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{\rho _{22}^\mu }}&{}{{\rho _{23}^\mu }}&{}0&{}{{\rho _{25}^\mu }}&{}0&{}0&{}0\\ 0&{}{{\rho _{32}^\mu }}&{}{{\rho _{33}^\mu }}&{}0&{}{{\rho _{35}^\mu }}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{\rho _{52}^\mu }}&{}{{\rho _{53}^\mu }}&{}0&{}{{\rho _{55}^\mu }}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right) \end{aligned}$$
(28)

with

$$\begin{aligned} {\rho _{22}^\mu }\!&=\! {\left| {{a_{\mu \tau }}(t)} \right| ^2};{\rho _{23}^\mu }\! =\! {a_{\mu \tau }}(t)a_{{\mu \mu }}^ * (t);{\rho _{25}^\mu }\! =\! {a_{\mu \tau }}(t)a_{{\mu e}}^ * (t); \nonumber \\ {\rho _{32}^\mu }\!&=\! {a_{\mu \mu }}(t)a_{{\mu \tau }}^ * (t);{\rho _{33}^\mu }\! =\! {\left| {{a_{\mu \mu }}(t)} \right| ^2};{\rho _{35}^\mu }\! =\! {a_{\mu \mu }}(t)a_{{\mu e}}^ * (t); \nonumber \\ {\rho _{52}^\mu }\!&=\! {a_{\mu e}}(t)a_{_{\mu \tau }}^ * (t);{\rho _{53}^\mu }\! =\! {a_{\mu e}}(t)a_{{\mu \mu }}^ * (t);{\rho _{55}^\mu }\! =\! {\left| {{a_{\mu e}}(t)} \right| ^2}. \end{aligned}$$
(29)

We denote the survival probability \({P_{\mu \mu }} = {\left| {{a_{\mu \mu }}} \right| ^2}\), and the oscillation probabilities \({P_{\mu e}} = {\left| {{a_{\mu e}}} \right| ^2}\) and \({P_{\mu \tau }} = {\left| {{a_{\mu \tau }}} \right| ^2}\) in the current architecture. By adopting the experimental data from MINOS+ collaboration [6], we draw the survival probability \({\nu _\mu } \rightarrow {\nu _\mu }\) with respect to the ratio L/E with the dimension km/GeV in Fig. 4. From the figure, it shows that the survival probability dramatically vibrates and is non-monotonic with the growing L/E.

Fig. 5
figure 5

Entanglement of formation (EOF), concurrence (\({\mathcal {C}}\)) and negativity (\({\mathcal {N}}\)), as a function of L/E with an initial muon flavor state. a The red line denotes the theoretical EOF in Eq. (30); b The purple line denotes the theoretical concurrence in Eq. (32); c The blue line denotes our theoretical prediction for negativity in Eq. (31); d Comparison of three entanglement measures (blue line: Negativity (\({\mathcal {N}}\)); red line: Entanglement of Formation (EOF); purple line: Concurrence (\({\mathcal {C}}\))) for initial muon flavor state. And the black squares stand for the experiment data from MINOS+ collaboration [6]

Full size image

To explore the quantumness of the system in the muon neutrino oscillation, one can calculate the EOF and negativity of the system as

$$\begin{aligned} \mathrm{EOF}^\mu \! =&-\! \frac{1}{2} [{P_{\mu e}} \log _2{P_{\mu e}} \!+\! {P_{\mu \mu }} \log _2{P_{\mu \mu }} \!+\! {P_{\mu \tau }} \log _2{P_{\mu \tau }} \nonumber \\&+ ({P_{\mu \mu }} + {P_{\mu \tau }}) \log _2({P_{\mu \mu }} + {P_{\mu \tau }}) \nonumber \\&+ ({P_{\mu e}} + {P_{\mu \tau }}) \log _2({P_{\mu e}} + {P_{\mu \tau }}) \nonumber \\&+ ({P_{\mu \mu }} + {P_{\mu e}}) \log _2({P_{\mu \mu }} + {P_{\mu e}})] \end{aligned}$$
(30)

and

$$\begin{aligned} {{{\mathcal {N}}}^\mu } \!=\! {\left( \sqrt{{P_{\mu e}}} \mathrm{{ }}\sqrt{{P_{\mu \mu }} \!+\! {P_{\mu \tau }}} \mathrm{{ }}\sqrt{{P_{\mu e}}} \mathrm{{ }}\sqrt{{P_{\mu \mu }}} \mathrm{{ }}\sqrt{{P_{\mu e}} \!+\! {P_{\mu \mu }}} \mathrm{{ }}\sqrt{{P_{\mu \tau }}} \right) ^{\frac{1}{3}}}, \end{aligned}$$
(31)

respectively.

Moreover, according to Eq. (15), the expression of concurrence in muon neutrino oscillations can be written as

$$\begin{aligned} {{\mathcal {C}}^\mu }\!= \! \sqrt{3\! -\! 3(P_{\mu e}^2\! +\! P_{\mu \mu }^2\! +\! P_{\mu \tau }^2)\! -\! 2{P_{\mu \mu }}{P_{\mu \tau }}\! -\! 2{P_{\mu e}}({P_{\mu \mu }} \!+\! {P_{\mu \tau }})}. \end{aligned}$$
(32)

After performing Pauli measurements on qubit B in the states of \(\rho _{_{AB}}^\mu (t) \) and \(\rho _{_{BC}}^\mu (t) \), the post-measurement states were given by

$$\begin{aligned} \rho _{A{\sigma _i}}^\mu (t) = \sum \limits _{i = 1}^2 {[(\mathbb {I} \otimes \left| {{i_k}} \right\rangle \langle {i_k}|)\rho _{AB}^\mu (t)(\mathbb {I} \otimes \left| {{i_k}} \right\rangle \langle {i_k}|)]} , \nonumber \\ \rho _{{\sigma _i}C}^\mu (t) = \sum \limits _{i = 1}^2 {[(\left| {{i_k}} \right\rangle \langle {i_k}| \otimes \mathbb {I})\rho _{BC}^\mu (t)(\left| {{i_k}} \right\rangle \langle {i_k}| \otimes \mathbb {I})]}. \end{aligned}$$
(33)

Thereafter, we can quantify the total entropic uncertainty \({\mathcal {U}}\) as follows

$$\begin{aligned} {\mathcal {U}}= & {} S\left( {\hat{\sigma }_x\left| A \right. } \right) + S\left( {\hat{\sigma }_y\left| A \right. } \right) + S\left( {\hat{\sigma }_z\left| A \right. } \right) \nonumber \\&+S\left( {\hat{\sigma }_x\left| C \right. } \right) + S\left( {\hat{\sigma }_y\left| C \right. } \right) + S\left( {\hat{\sigma }_z\left| C \right. } \right) , \end{aligned}$$
(34)

which analytical expression can be written as

$$\begin{aligned} {\mathcal {U}}= \,&4[H_\mathrm{bin}(\lambda _2)-1] -2{P_{\mu \mu }}\log _2{P_{\mu \mu }} + {P_{\mu e}}\log _2{P_{\mu e}} \nonumber \\&+ {P_{\mu \tau }}\log _2{P_{\mu \tau }}+3[({P_{\mu e}} + {P_{\mu \mu }})\log _2({P_{\mu e}}+ {P_{\mu \mu }})\nonumber \\&+ ({P_{\mu \tau }} +{P_{\mu \mu }})\log _2({P_{\mu \tau }} + {P_{\mu \mu }})], \end{aligned}$$
(35)

with \(\lambda _{2}=\frac{1}{2}(1-\sqrt{{{({P_{\mu e}}{+}{P_{\mu \mu }})}^2} {+}2({P_{\mu \mu }} {-}{P_{\mu e}}){P_{\mu \tau }}+ P_{\mu \tau }^2})\).

Figure 5 has drawn the dynamics of the entanglement of system (EOF, negativity and concurrence) as a function of the ratio L/E with an initial muon flavor state, and as a comparison, we plotted the three theoretical entanglements in Fig. 5d. In the figure, the experimental results are based on the data from MINOS+ collaboration [6]. Same as the Daya Bay collaboration [3], MINOS+ collaboration only offers the survival probability \({P_{\mu \mu }}\) rather than the oscillation probability, so here we use the ratio \(\xi _2 = {P_{\mu \tau }}/{P_{\mu e}}\) in terms of theoretical prediction, and \({P_{\mu \mu }} + {P_{\mu e }} + {P_{\mu \tau }} = 1\) to acquire the oscillation probabilities \({P_{\mu e}}\) and \({P_{\mu \tau }}\). Then the entanglement of system (EOF, negativity and concurrence) and the total entropic uncertainty \({\mathcal {U}}\) can be worked out, as described in Figs. 5 and 6. Explicitly, one can observe that as the ratio L/E increases, the entanglement grows first, then decreases to a certain value, and fluctuates constantly, as shown in Fig. 5a–c. From Fig. 5d, it is apparent that the amount of concurrence and EOF is greater than that of negativity. It implies that more quantum resource measured by concurrence and EOF can be applied to realistic quantum information processing. With this in mind, we say that concurrence and EOF are more effective than negativity when quantifying the applicable quantum resource in muon NOs, which in essence conforms to the statement made before.

Fig. 6
figure 6

The total entropic uncertainty (\({\mathcal {U}}\)) as a function of L/E with an initial muon flavor state. The green line represents the theoretical total entropic uncertainty in Eq. (35); The red line represents the bound of EUR in Eq. (18), the black squares stand for the experiment data from MINOS+ collaboration [6]

Full size image

Figure 6 has drawn the dynamics of the total entropic uncertainty \({\mathcal {U}}\) as a function of the ratio L/E. It is easy to see that the uncertainty for both experimental results and our theoretical predictions is more than the bound all the time, as shown in Fig. 6, suggesting that the inequality of the total entropic uncertainty relation in Eq. (18) has been verified. Specifically, the uncertainty decreases firstly and then inflates, afterwards keeps fluctuating with the growing L/E. In addition, it is worth noting that \({\mathcal {U}}\) reaches its maximum, when EOF and \({{\mathcal {N}}}\) remain the minimum at around \(L/E=500\)km/GeV. Furthermore, it is straightforward to see that the uncertainty is inversely correlated with the entanglement of system (EOF and concurrence) in the current consideration by comparing Figs. 5 and 6, which is essentially in agreement with the statement made before.

5 Conclusion

To conclude, we have observed the nonclassical features in neutrino oscillations through quantum entanglement and the measured uncertainty in the framework of initial electron and muon neutrinos. For an initial electron flavor NOs, we have demonstrated that concurrence is more suitable for entanglement estimation than EOF or negativity. Contrarily, as to an initial muon flavor NOs, concurrence and EOF are more suitable for quantifying entanglement than negativity. Furthermore, as two particular characteristics of the quantum world, the entropy-based uncertainty and the entanglement of system intrinsically exhibit an anti-correlation relation in neutrino oscillations, implying that the stronger entanglement will lead to the smaller uncertainty, and vice versa. Our consequence is also a good verification of this point. The decrease in uncertainty and the increase in entanglement allow neutrino systems to provide more quantum resources. Thereby, to manifest highly genuine quantum features will be beneficial to achieve the small uncertainty of the incompatible measurements in the neutrinos.

By virtue of the genuine quantumness during NOs, there have been some promising works [63, 64] to investigate the telecommunications by using neutrinos. In addition, Stancil et al. [65] demonstrated the feasibility of furnishing a low-rate communication link by utilizing the NuMI beam line and the MINERvA detector at Fermilab. With these in mind, all of those efforts should pave an avenue to apply neutrinos to the prospective distant communication. Therefore, we believe that our explorations offer an insight into the intrinsic quantumness of NOs, and are of fundamental importance to the practical information processing and communication by neutrinos.