1 Introduction

Collisions between heavy ions accelerated at ultra-relativistic energies provide the necessary conditions to form a deconfined state of matter, the Quark Gluon Plasma [1]. In this phase, the fundamental constituents of quantum chromodynamics (QCD), the quarks and gluons, are not anymore confined inside their usual hadronic bags. The transition to a QGP from normal hadronic matter is expected to take place at a temperature of about 155 MeV, and an energy density of about 0.5 GeV/fm\(^3\), according to lattice QCD calculations [2,3,4]. These conditions can be reached in collisions between Pb ions at the Large Hadron Collider (LHC) [5,6,7].

Heavy ion collisions also provide the possibility to study novel QCD phenomena that are otherwise not accessible experimentally. One characteristic example is related to local parity (P) as well as charge conjugation and parity (CP) symmetry violation in strong interactions. The possibility to observe parity violation in the strong interaction using relativistic heavy-ion collisions has been discussed in [8,9,10] and was further reviewed in [11,12,13,14,15,16,17,18,19]. In QCD, this symmetry violation originates from the interaction between the chiral fermions of the theory and topologically non-trivial gluonic fields that induce net-chirality. In the presence of a strong magnetic field, such as the one created in peripheral heavy ion collisions with a magnitude of around \(10^{15}\) T [20,21,22], these interactions lead to an asymmetry between left and right-handed quarks. The generated net-chirality, in turns, leads to an excess of positively and negatively charged particles moving in opposite directions relative to the system’s symmetry plane. This introduces an electromagnetic current and the creation of an electric dipole moment of QCD matter. The experimental search for these effects has intensified recently, following the realisation that the subsequent creation of charged hadrons results in an experimentally accessible magnitude of charge separation along the direction of this magnetic field, and perpendicular to the symmetry plane. This phenomenon is called the Chiral Magnetic Effect (CME) [23] and its existence was recently reported in semi-metals like zirconium pentatelluride (\(ZrTe_5\)) [24].

Early enough it was realised that a way to probe these effects is to rely on measuring two-particle azimuthal correlations relative to the reaction plane (\(\Psi _{\mathrm {RP}}\)) [25], the plane defined by the impact parameter and the beam axis. Since then, intensive experimental efforts have been made to identify unambiguously signals of the CME. The first measurements using this approach were reported by the STAR Collaboration in Au–Au collisions at \(\sqrt{s_{\mathrm {NN}}} = 0.2\) TeV [26, 27] and were consistent with initial expectations for a charge separation relative to the reaction plane due to the CME. Soon after, the first results from the LHC in Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 2.76\) TeV were reported and showed a quantitatively similar effect [28]. This agreement between the results is up until this moment hard to comprehend considering the differences in the centre-of-mass energy and consequently in the multiplicity density [29]. In addition, the magnetic field and the way it evolves is, in principle, different between the two energies [20,21,22]. Overall, this agreement hinted at the dominant role of background effects in both measurements [30]. These background effects were, in parallel, identified as coming from local charge conservation coupled to the anisotropic expansion of the system in non-central collisions [31, 32]. The field turned its focus to finding a way to constrain and quantify the background and the CME contribution to such measurements.

In Ref. [33], the ALICE Collaboration presented the first ever upper limit of 26–33\(\%\) at \(95\%\) confidence level for the CME contribution, using an Event Shape Engineering (ESE) technique [34]. At the same time, the CMS Collaboration reported an upper limit of 7% at \(95\%\) confidence level using a similar procedure, albeit without a quantification of the possible dependence of these results on the elliptic flow value [35]. In parallel, new measurements of the STAR Collaboration in Au–Au collisions at a centre-of-mass energy \(\sqrt{s_{\mathrm {NN}}} = 200\) GeV [36,37,38] could not exclude a small contribution of the CME signal to these measurements. Finally, results obtained from the analysis of data collected from the beam energy scan at \(\sqrt{s_{\mathrm {NN}}} =\,\)7.7, 11.5, 19.6, 27, 39 and 62.4 GeV [38] were still qualitatively consistent with expectations from parity violating effects in heavy ion collisions. To study background effects the CMS [39] and the STAR [40] collaborations studied charge dependent correlations in both p–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV and in p–Au and d–Au collisions at \(\sqrt{s_{\mathrm {NN}}} = 0.2\) TeV, respectively. Both results illustrate that these correlations are similar to those measured in heavy-ion collisions. The authors concluded that these findings could have important implications for the interpretation of the heavy-ion data since it is expected that the results in these “small” systems are dominated by background effects. However these latter studies are lacking a quantitative estimate of the reaction plane independent background [26, 27] and therefore could not be used to extract a definite conclusion. Finally, the ALICE Collaboration recently reported their updated upper limits of 15–18\(\%\) at 95\(\%\) confidence level for the centrality interval 0–40\(\%\) by studying charge dependent correlations relative to the third order symmetry plane [41]. Overall, the extraction of the CME signal has been exceptionally challenging.

In this article we follow a different approach by performing a systematic study of the correlators used in CME searches for Pb–Pb and Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV (for Pb ions) [28, 41] and at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV (for Xe ions) [42] with the Anomalous-Viscous Fluid Dynamics (AVFD) framework [43,44,45]. This is a state-of-the-art model that describes the initial state of the collision using a Glauber prescription, and accounts for the development of the early stage electromagnetic fields as well as for the propagation of anomalous fermion currents. The expanding medium is treated after 0.6 fm/c via a 2+1 dimensional viscous hydrodynamics (VISH2+1) code with value of shear and bulk viscosities over entropy density of \(\eta /s\) = 0.08 and \(\zeta /s = 0\).Beyond a decoupling energy density of \(\epsilon = 0.18\) fm\(/c^3\) the system is described by a hadron cascade model (UrQMD) [46]. The analysis is performed in the same kinematic ranges as the experimental measurements for primary charged particles that have a pseudorapidity of \(|\eta | < 0.8\) and transverse momentum of \(0.2< p_{\mathrm {T}} < 5\) GeV/c. The goal of this study is to extract the relevant values that govern the CME signal and the background in the AVFD model that will allow for a quantitative description of the centrality dependence of the charged dependent correlations measured in various colliding systems and energies at the LHC.

The article is organised as follows: Sect. 2 presents the main observables, followed by a discussion on how the model is calibrated in Sect. 3. The main results are presented in Sect. 4. The article concludes with a summary.

2 Experimental observables

A way to probe the parity violating effects is by introducing P-odd coefficients \(a_{n,\alpha }\) in the Fourier series frequently used in studies of azimuthal anisotropy [47]. This leads to the expression

$$\begin{aligned} \frac{dN}{d\varphi } \approx 1 + 2\sum _{n} \Big [v_n \cos [n(\varphi - \Psi _n)] + a_n \sin [n(\varphi - \Psi _n)]\Big ] \nonumber \!\!\!\!\!\!\!\\ \end{aligned}$$
(1)

where N is the number of particles, \(\varphi \) is the azimuthal angle of the particle and \(v_n\) are the corresponding flow coefficients (\(v_1\): directed flow, \(v_2\): elliptic flow, \(v_3\): triangular flow etc.). The n-th order symmetry plane of the system, \(\Psi _n\), is introduced to take into account that the overlap region of the colliding nuclei exhibits an irregular shape [48,49,50,51,52]. This originates from the initial density profile of nucleons participating in the collision, which is not isotropic and differs from one event to the other. In case of a smooth distribution of matter produced in the overlap zone, the angle \(\Psi _{n}\) coincides with that of the reaction plane, \(\Psi _{\mathrm{RP}}\). In Eq. 1, \(a_1\) is the leading order P-odd term that reflects the magnitude, while higher harmonics (i.e. \(a_2\) and above) represent the specific shape of the CME signal.

In Ref. [25], Voloshin proposed that the leading order P-odd coefficient can be probed through the study of charge-dependent two-particle correlations relative to the reaction plane \(\Psi _{\mathrm{RP}}\). In particular, the expression discussed is of the form \(\langle \cos (\varphi _{\alpha } + \varphi _{\beta } - 2\Psi _{\mathrm{RP}}) \rangle \), where \(\alpha \) and \(\beta \) denote particles with the same or opposite charge. This expression can probe correlations between the leading P-odd terms for different charge combinations \(\langle a_{1,\alpha } a_{1,\beta } \rangle \). This can be seen if one expands the correlator using Eq. 1 according to

$$\begin{aligned}&\langle \cos (\varphi _{\alpha } + \varphi _{\beta } - 2\Psi _{\mathrm{RP}}) \rangle \nonumber \\&\quad =\langle \cos \big [(\varphi _{\alpha } - \Psi _{\mathrm{RP}}) + (\varphi _{\beta } - \Psi _{\mathrm{RP}})\big ] \rangle \nonumber \\&\quad = \langle \cos (\Delta \varphi _{\alpha } + \Delta \varphi _{\beta }) \rangle \nonumber \\&\quad =\langle \cos \Delta \varphi _{\alpha } \cos \Delta \varphi _{\beta } \rangle - \langle \sin \Delta \varphi _{\alpha } \sin \Delta \varphi _{\beta } \rangle \nonumber \\&\quad =\langle v_{1,\alpha }v_{1,\beta } \rangle + {\mathrm {B}}_{{\mathrm {in}}} - \langle a_{1,\alpha } a_{1,\beta }\rangle - {\mathrm {B}}_{\mathrm{out}}, \end{aligned}$$
(2)

where \({\mathrm {B}}_{\mathrm{in}}\) and \({\mathrm {B}}_{\mathrm{out}}\) represent the parity-conserving correlations projected onto the in- and out-of-plane directions [25]. The terms \(\langle \cos \Delta \varphi _{\alpha } \cos \Delta \varphi _{\beta }\rangle \) and \(\langle \sin \Delta \varphi _{\alpha }\sin \Delta \varphi _{\beta }\rangle \) in Eq. 2 quantify the correlations with respect to the in- and out-of-plane directions, respectively. The term \(\langle v_{1,\alpha }v_{1,\beta } \rangle \), i.e. the product of the first order Fourier harmonics or directed flow, is expected to have negligible charge dependence in the mid-rapidity region [53]. In addition, for a symmetric collision system the average directed flow at mid-rapidity is zero.

A generalised form of Eq. 2, describing also higher harmonics, is given by the mixed-harmonics correlations and reads

$$\begin{aligned} \gamma _{{\mathrm {m}},{\mathrm {n}}} = \langle \cos ({\mathrm {m}}\varphi _{\alpha } + {\mathrm {n}}\varphi _{\beta } - ({\mathrm {m}} + {\mathrm {n}})\Psi _{|{\mathrm {m}}+{\mathrm {n}}|})\rangle , \end{aligned}$$
(3)

where \({\mathrm {m}}\) and \({\mathrm {n}}\) are integers. Setting \({\mathrm {m}} = 1\) and \({\mathrm {n}} = 1\) (i.e. \(\gamma _{1,1}\)) leads to Eq. 2.

In order to independently evaluate the contributions from correlations in- and out-of-plane, one can also measure a two-particle correlator of the form

$$\begin{aligned}&\langle \cos (\varphi _{\alpha } - \varphi _{\beta }) \rangle \nonumber \\&\quad =\langle \cos \big [(\varphi _{\alpha } - \Psi _{\mathrm{RP}}) - (\varphi _{\beta } - \Psi _{\mathrm{RP}})\big ] \rangle \nonumber \\&\quad = \langle \cos (\Delta \varphi _{\alpha } - \Delta \varphi _{\beta }) \rangle \nonumber \\&\quad =\langle \cos \Delta \varphi _{\alpha } \cos \Delta \varphi _{\beta } \rangle + \langle \sin \Delta \varphi _{\alpha } \sin \Delta \varphi _{\beta } \rangle \nonumber \\&\quad =\langle v_{1,\alpha }v_{1,\beta } \rangle + {\mathrm {B}}_{\mathrm{in}} + \langle a_{1,\alpha } a_{1,\beta }\rangle + {\mathrm {B}}_{\mathrm{out}}, \end{aligned}$$
(4)

This provides access to the two-particle correlations without any dependence on the symmetry plane angle which can be generalised according to

$$\begin{aligned} \delta _{\mathrm {m}} = \langle \cos [{\mathrm {m}}(\varphi _{\alpha } - \varphi _{\beta })] \rangle . \end{aligned}$$
(5)

This correlator, owing to its construction, is affected if not dominated by background contributions. Charge-dependent results for \(\delta _1\), together with the relevant measurements of \(\gamma _{1,1}\) were first reported in Ref. [28] and made it possible to separately quantify the magnitude of correlations in- and out-of-plane.

3 Model calibration and parametrisation

The goal of this study is to extract the values that control the CME signal and the background in the AVFD model that will allow for a quantitative simultaneous description of the centrality dependence of the charged dependent correlations, i.e. \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) measured in Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV [28, 41] and in Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV [42]. Here, \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) denote the difference of \(\delta _1\) and \(\gamma _{1,1}\) between opposite- and same-sign pairs. Within the AVFD framework, the CME signal is controlled by the axial current density \(n_5/{\mathrm {s}}\) which dictates the imbalance between right- and left-handed fermions induced in the initial stage of each event. The parameter that governs the background is represented by the percentage of local charge conservation (LCC) within an event. This number can be considered as the amount of positive and negative charged partners emitted from the same fluid element relative to the total multiplicity of the event. The model samples the momenta of these balancing charges independently in the local rest frame of the fluid element (see Ref. [54] for more details.

The first step in the whole procedure was to calibrate the model without the inclusion of any CME or LCC effects, in what will be referred to in the rest of the text as “baseline”. This involved tuning the input parameters to describe the centrality dependence of bulk measurements, such as the charged particle multiplicity density \(dN/d\eta \) [55,56,57] and \(v_2\) [58,59,60] in Pb–Pb and Xe–Xe collisions at various LHC energies. Overall the model was able to describe the experimental measurements within 15%. Finally, we also checked that the slopes of the transverse momentum (\(p_T\)) spectra of pions, kaons and protons, in the baseline sample of AVFD have a similar centrality dependence as the one reported by ALICE in Refs. [61,62,63].

Fig. 1
figure 1

The dependence of the average value of the magnetic field perpendicular to the reaction plane (\(\mathbf{B} _y\)) on centrality for Pb–Pb and Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) and \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV, respectively

Full size image

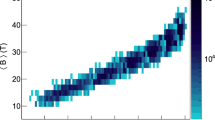
One of the key ingredients in the development of the CME in the final state, is the early stage electromagnetic field. The AVFD model performs an event-by-event simulation of the electromagnetic field value projected along the symmetry plane, accounting for the decorrelation between the field direction and the true reaction plane due to fluctuations [43]. The initial strength of this field mainly depends on the atomic number of the nuclei that collide and the center-of-mass energy of the collision. Figure 1 presents the centrality dependence of the magnitude of \(\mathbf{B} \), as simulated by AVFD at \(t_0 = 0\), for Pb–Pb and Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) and \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV, respectively. The values for both systems reach and for some centralities even exceed \(10^{16}\) T. In addition, the magnitude of \(\mathbf{B} \) for a given centrality interval in collisions between Pb-ions is larger than the corresponding value in Xe–Xe collisions by a factor which reflects the ratio of the atomic numbers of the two nuclei.

Fig. 2
figure 2

The time evolution of the average value of the magnetic field perpendicular to the reaction plane \((\mathbf{B} )\) for the 40–50% centrality interval in Pb–Pb and Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) and \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV, respectively

Full size image

The magnitude of the field evolves as a function of time in the model according to

$$\begin{aligned} B(\tau ,x)=\frac{B_0}{1+\tau ^2/\tau _B^2}, \end{aligned}$$
(6)

where \(\tau _B\) is the magnetic field lifetime which is set, in this work, conservatively to 0.2 fm/c, for both collision systems. Figure 2 presents the time evolution of the magnitude of \(\mathbf{B} \) for an indicative centrality interval i.e. 40-50% for both Pb–Pb (solid line) and Xe–Xe collisions (dashed line).

The next step in the calibration of the model required extracting the dependence of the correlators \(\Delta \gamma _{1,1}\) based on Eq. 2 and \(\Delta \delta _1\) (see Eq. 4) on both the axial current density \(n_5/{\mathrm {s}}\) and the percentage of LCC. For this, new AVFD samples were produced for all centralities of both systems and energies, for which the amount of CME induced signal was incremented i.e., using \(n_5/{\mathrm {s}}\) = 0.05, 0.07 and 0.1, while at the same time keeping the percentage of LCC fixed at zero. In addition, to gauge the dependence of both correlators on the background, similar number of events as before were produced where, this time, \(n_5/{\mathrm {s}}\) was fixed at zero but the percentage of LCC was incremented every time. In particular, the values selected for the Pb-system were 33 and 50%.Footnote 1

Fig. 3
figure 3

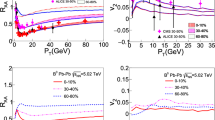
The centrality dependence of \(\Delta \delta _1\) (upper panel) and \(\Delta \gamma _{1,1}\) (lower panel), the charge dependent difference of \(\delta _1\) and \(\gamma _{1,1}\) between opposite- and same-sign pairs, in Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV. The results from the analysis of the baseline sample are represented by the green markers. The various bands show the AVFD expectations for \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) for various values of \(n_5/{{\mathrm {s}}}\) (red bands) and percentage of LCC (blue bands)

Full size image
Fig. 4
figure 4

The centrality dependence of \(\Delta \delta _1\) (upper panel) and \(\Delta \gamma _{1,1}\) (lower panel), the charge dependent difference of \(\delta _1\) and \(\gamma _{1,1}\) between opposite- and same-sign pairs, in Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV. The results from the analysis of the baseline sample are represented by the green markers. The various bands show the AVFD expectations for \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) for various values of \(n_5/{{\mathrm {s}}}\) (red bands) and percentage of LCC (blue bands)

Full size image

Figure 3 presents the centrality dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\), in the upper and lower panels, respectively. The plots show results obtained from the analysis of events of Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV. The green markers are extracted from the analysis of the baseline sample and, in both cases, exhibit non-zero values for the majority of the centrality intervals. These non-zero values are due to the existence of hadronic resonances in the model whose decay products are affected by both radial and elliptic flow. In addition, the same plots present how the magnitude of these correlators develop for various values of the axial current density \(n_5/{{\mathrm {s}}}\) which are represented by the red bands. It can be seen that with increasing values of \(n_5/{\mathrm {s}}\) the two correlators exhibit opposite trends: while \(\Delta \delta _1\) decreases, the values of \(\Delta \gamma _{1,1}\) increase. This opposite behaviour originates from the different sign the CME contributes to \(\delta _1\) (Eq. 4) and \(\gamma _{1,1}\) (Eq. 2) and, consequently, to \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\). Finally, when fixing the value of \(n_5/{\mathrm {s}}\) to zero and progressively increasing the percentage of LCC in the sample (black curves in Fig. 3), the values of both \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) increase. However, the latter correlator exhibits a smaller sensitivity than \(\Delta \delta _1\) to the background owning to the fact that it is constructed as the difference in the magnitude of background effects in- and out-of-plane (see Eq. 2).

Similarly, Fig. 4 presents the centrality dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\), this time in Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV. Also here the results for the baseline AVFD sample are represented with the green markers, while the red and black bands correspond to samples with progressively increasing values of \(n_5/{\mathrm {s}}\) and percentage of LCC, respectively. The same qualitative observations are also found in this system: the baseline sample exhibits non-zero values for both \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\), these two correlators have opposite trends with increasing \(n_5/{\mathrm {s}}\) and \(\Delta \delta _1\) exhibits bigger sensitivity on the LCC percentage than \(\Delta \gamma _{1,1}\).

Fig. 5
figure 5

The centrality dependence of \(\Delta \delta _1\) grouped in two scenarios: zero \(n_5/{\mathrm {s}}\) but various choices of LCC (upper panel) and non-zero \(n_5/{\mathrm {s}}\) but LCC fixed to zero (lower panel). The various bands show the AVFD expectations for \(\Delta \delta _1\) for Pb–Pb collisions and Xe–Xe collisions, with blue and green bands, respectively. The results of the baseline sample are represented by the filled and open markers

Full size image
Fig. 6
figure 6

The centrality dependence of \(\Delta \gamma _{1,1}\) grouped in two scenarios: zero \(n_5/{\mathrm {s}}\) but various choices of LCC (upper panel) and non-zero \(n_5/{\mathrm {s}}\) but LCC fixed to zero (lower panel). The various bands show the AVFD expectations for \(\Delta \delta _1\) for Pb–Pb collisions and Xe–Xe collisions, with blue and green bands, respectively. The results of the baseline sample are represented by the filled and open markers

Full size image

To directly compare the values of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) between these two collision systems, the results are organised based on the input parameters used: zero \(n_5/{\mathrm {s}}\) but various choices of LCC and non-zero \(n_5/{\mathrm {s}}\) but LCC fixed to zero. Figures 5 and 6, summarize the centrality dependence of the results for \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\).

In the first case, the baseline and LCC being 15 and 50% for Pb–Pb collisions at \(\sqrt{s_{NN}}=5.02\) TeV and for Xe–Xe collisions at \(\sqrt{s_{NN}}=5.44\) TeV are chosen. The upper panel of Fig. 5 illustrates that for a fixed LCC percentage, the values of \(\Delta \delta _1\) are higher for the Xe–Xe than for the Pb–Pb samples. For a fixed centrality, while the effect of radial flow between these two systems is similar [63], the charged particle multiplicity in Pb–Pb is 60–70% higher than the corresponding value in Xe–Xe collisions [56, 57]. This could lead to a faster dilution of the correlations induced by the LCC mechanism in the larger system, reflected in this difference of \(\Delta \delta _1\). At the same time, the upper panel of Fig. 6 shows that the values of \(\Delta \gamma _{1,1}\) for the two systems do not exhibit any significant difference. This is in line with the expectation that the sensitivity of \(\Delta \gamma _{1,1}\) to the background is significantly reduced with respect to \(\Delta \delta _1\).

In the second case of non-zero axial current density, the samples containing \(n_5/{\mathrm {s}}=0.05, 0.07\) and 0.10 are chosen. The lower panel of Fig. 5 shows that \(\Delta \delta _1\) is similar between the two systems since it is primarily affected by background contributions. This correlator needs higher values of \(n_5/{\mathrm {s}}\) (e.g. \(n_5/{\mathrm {s}} = 0.1\) in the plot) to start observing some differences. Finally, the lower panel of Fig. 6 illustrates that the magnitude of \(\Delta \gamma _{1,1}\) is higher in the Xe–Xe than in the Pb–Pb samples. Although the value of the magnetic field is higher for the larger Pb-system, as shown in Fig. 1, the significantly larger multiplicity that this system has, leads to a larger dilution effect reflected in the ordering of the corresponding curves in the plot.

Fig. 7
figure 7

The dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) in the upper and lower panels, respectively, on the percentage of local charge conservation in the analysed samples of Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV for the 40–50% centrality interval

Full size image
Fig. 8
figure 8

The dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) in the upper and lower panels, respectively, on the axial current density \(n_5/{\mathrm {s}}\) in the analysed samples of Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV for the 40–50% centrality interval

Full size image

The previous results for each colliding system and energy can be grouped in a different way that allows to parametrise the dependence of each of the correlators on the LCC percentage and on \(n_5/{\mathrm {s}}\). Figures 7 and 8 present how \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) develop as a function of the LCC percentage and \(n_5/{\mathrm {s}}\), respectively. Results for the 40–50% centrality interval of Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV are indicatively chosen to illustrate the procedure. An identical protocol was used for all centrality intervals of both colliding systems. One can see that both \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) exhibit a linear dependence on the percentage of LCC, with the latter being less sensitive and thus having a smaller slope. Finally, these two correlators exhibit a quadratic dependence on \(n_5/{\mathrm {s}}\) with opposite trend, originating from the dependence of \(\delta _1\) and \(\gamma _{1,1}\) on \(\langle a_{1,\alpha } a_{1,\beta }\rangle \) and \(-\langle a_{1,\alpha } a_{1,\beta }\rangle \) in Eqs. 4 and 2, respectively. This \(a_1\) coefficient, in turns, has been shown in Ref. [43, 44] to be proportional to the value of \(n_5/{\mathrm {s}}\).

Following this procedure for all centrality intervals of Pb–Pb and Xe–Xe collisions, one is able to parametrise the dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) according to:

$$\begin{aligned} \Delta \delta _1= & {} c_2 \cdot (n_5/{\mathrm {s}})^2 + c_1 \cdot (n_5/{\mathrm {s}}) + b_1 \cdot ({\mathrm {LCC}}) + b_0, \end{aligned}$$
(7)
$$\begin{aligned} \Delta \gamma _{1,1}= & {} e_2 \cdot (n_5/{\mathrm {s}})^2 + e_1 \cdot (n_5/{\mathrm {s}}) + d_1 \cdot ({\mathrm {LCC}}) + d_0, \end{aligned}$$
(8)

where \(e_2\), \(e_1\), \(d_1\), \(d_0\), \(c_2\), \(c_1\), \(b_1\) and \(b_0\) are real numbers constrained from the simultaneous fit of the corresponding dependencies of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) for each centrality interval of every collision system and energy. The parametrisation of Eqs. 7 and 8 assumes that the two components that control the CME signal and the background are not correlated. This is a reasonable assumption considering that the two underlying physical mechanism are independent and take place at different times in the evolution of a heavy ion collision.

4 Results

Having the dependence of both \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) on \(n_5/{\mathrm {s}}\) and LCC parametrised from Eqs. 7 and 8, one can deduce the values of these two parameters that govern the CME signal and the background for each centrality, colliding system and energy that allows, at the same time, for a quantitative description of the measured centrality dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) at LHC energies.

Fig. 9
figure 9

The centrality dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) in the upper and lower panels, respectively. The data points represent the experimental measurements in Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV [41]. The green band shows the results obtained from the tuned AVFD sample (see text for details)

Full size image

Figure 9 presents the results of such procedure for Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV. The data points, extracted from Ref. [41] for both correlators are described fairly well by the tuned model. A similarly satisfactory description is also achieved for the results of Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV [42].

Fig. 10
figure 10

The centrality dependence of the LCC percentage (upper panel) and the axial current density \(n_5/{\mathrm {s}}\) that allows to describe simultaneously the experimental measurements of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) [28, 41, 42] in all collision systems and energy studied in this article

Full size image

Figure 10 presents the final result of the whole procedure. The plots show the centrality dependence of the pairs of LCC percentage (upper panel) and \(n_5/{\mathrm {s}}\) (lower panel) that are needed to describe with AVFD the experimental measurements of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\). The different markers represent results for different collision systems and energies. It can be seen that all systems can be described by large values of LCC that range from 40\(\%\) for peripheral up to around 60\(\%\) for more central Pb–Pb collisions. There is no significant difference observed in these values among the two sets of results.

Furthermore, the lower panel of Fig. 10 illustrates that there is no significant centrality dependence of \(n_5/{\mathrm {s}}\). However, there is a dependence on the colliding system. More particularly, the experimental results from the analysis of Xe–Xe collisions lead to values of \(n_5/{\mathrm {s}}\) which are compatible with zero within the uncertainties for all centrality intervals. A fit with a constant function results into values of \(0.011 \pm 0.005\). This naturally results into a CME fraction which is compatible with zero. At the same time, the results for Pb–Pb collisions can be described by non-zero values of axial current densities, again for the entire centrality region studied. The corresponding fit leads to a value of \(0.034 \pm 0.003\) i.e., significantly above the background-only scenario. The resulting CME fraction gives an upper level of around 20%, compatible with the values reported at the LHC.

5 Summary

In this article we presented a systematic study of charge dependent azimuthal correlations which are commonly used experimentally to probe the Chiral Magnetic Effect using the Anomalous-Viscous Fluid Dynamics framework [43, 44]. After tuning the model to reproduce, within 15%, basic experimental measurements such as the centrality dependence of the charged particle multiplicity density and the elliptic flow we were able to parametrise the dependence of both \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) on the LCC percentage, the main contribution to the background, and the axial current density \(n_5/{\mathrm {s}}\) which dictates the amount of CME signal. The resulting parametrisation is subject to uncertainties stemming from e.g. the better tuning of the baseline, the lifetime of the magnetic field which was conservatively chosen to be 0.2 fm/c etc.

This procedure was followed for Pb–Pb collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.02\) TeV, as well as for Xe–Xe collisions at \(\sqrt{s_{\mathrm {NN}}} = 5.44\) TeV. This parametrisation allowed for the estimation of the values of both the LCC percentage and \(n_5/{\mathrm {s}}\) needed to describe quantitatively and at the same time the centrality dependence of \(\Delta \delta _1\) and \(\Delta \gamma _{1,1}\) measured experimentally [28, 41, 42]. The measurements in Xe–Xe are consistent with a background only scenario, with values of \(n_5/{\mathrm {s}}\) compatible with zero. On the other hand, the results of Pb–Pb collisions require \(n_5/{\mathrm {s}}\) with significantly non-zero values.