1 Introduction

Observations of the distant SNIa indicate that the current Universe has undergone an accelerated expansion phase [1,2,3]. This phenomenon has been confirmed by other observations and experiments, such as the cosmic microwave background (CMB) [4,5,6], large-scale structure (LSS) and baryon acoustic oscillation (BAO) [7,8,9,10,11,12], high-redshift galaxies [13], high-redshift galaxy clusters [14, 15] and weak gravitational lensing [16,17,18]. The accelerated expansion stage can be achieved by a large-scale modification of the standard theory of gravity, or by introducing a strange cosmic fluid with negative pressure called dark energy (DE) [1,2,3]. The Einstein’s cosmological constant \(\varLambda \) with constant equation of state (EoS) parameter equal to \(-1\), is the first and simplest DE candidate. Taking into account the cosmological constant \(\varLambda \) and cold dark matter (CDM), one can give a standard cosmological model, the so-called \(\varLambda \)CDM model, which is compatible with observational data. However, this model has two basic problems: fine-tuning and cosmic coincidence [19,20,21,22,23].

In order to solve these problems, different DE models with time-varying EoS parameters have been proposed in the literature. One of the models is the holographic dark energy (HDE) model (see Sect. 2) which was first proposed by [24] based on the holographic principle. The HDE model has been extensively studied from the perspective of theory and observation [25,26,27,28,29,30,31,32,33]. We refer the reader to recent review of the HDE model [34] in which various observational and theoretical aspects of the model have been investigated.

On the other hand, we can study the expansion of the Universe without assuming a specific cosmological model. These methods are so-called model-independent methods. One of these methods is the Gaussian process method which is defined on the basis of the distribution over functions. The covariance function defined in this method connects two different data points. Since the data and its derivatives follow a Gaussian function, the covariance function can predict data values in other redshifts [35]. Another model-independent method is the smoothing method, which can smooth the luminosity distance relative to the redshift. In smoothing method, the best fit values of the cosmological parameters can be determined by parameterizing the cosmological quantities [36]. Finally, another model-independent method to study the history of the expansion of the Universe that we used in this work is the cosmography method (see Sect. 3). As a well-known method in cosmology, cosmography method has been widely used in the literature [37,38,39,40,41,42,43,44,45,46,47]. This method was first proposed by [37] and [38] to distinguish between various dark energy models. Capozzilo and Salzano [39] used cosmography method to study the dynamics of galaxy clusters in f(R) theory of gravity. They showed that cosmography method can be used to distinguish GR from alternative theories. Capozzilo and his colleagues also used cosmography method to study the expansion history of the Universe and showed that the results may be different from the standard model of cosmology [40]. Their results show that despite the deceleration parameter error, the jerk parameter has \(2\sigma \) tension, and it also shows that the snap parameter has a tail for large negative values that match the value of \(\varLambda \)CDM.

Recently, the authors of [44] used the cosmography technique and also the observational data related to the distance modulus (also called Hubble diagram) of SNIa, quasars and GRB to show a big tension between the cosmography parameters of \(\varLambda \)CDM model and those obtained from model-independent cosmography method. In addition, using the Hubble diagram of SNIa, quasars and GRB, the standard \(\varLambda \)CDM model and some important dynamical DE models such as CPL and Pade parametrization, have been studied in the context of cosmography method [46]. It has been shown that the \(\varLambda \)CDM model has serious problems with these observations, but CPL and Pade parameterizations may have better consistency at least at the \(2\sigma \) level.

In this article, we use different combinations of Hubble diagrams from SNIa, quasars, and GRB to study the HDE model in the context of cosmography method, and compare the results with the results of standard \(\varLambda \)CDM cosmology. We use the minimization of the error function \(\chi ^2\) in the context of the Markov Chain Monte Carlo (MCMC) algorithm to calculate the best fit values of the cosmographic parameters in the HDE and \(\varLambda \)CDM models. We emphasize that in order to calculate the best fit values of the cosmographic parameters, we first use the Hubble diagram of SNIa, quasars, and GRB to constrain the cosmological parameters of the model. By comparing the constrained values of the cosmographic parameters of the HDE and \(\varLambda \)CDM models with the values obtained from the model-independent cosmography method, we can check these models and their consistency with the Hubble diagram observations. In the next step, we reconstruct the Hubble parameter in the context of cosmography method and compare it with the observed Hubble data, H(z). In order to make this comparison, we calculate the error function \(\chi ^2\) based on the H(z) data, and evaluate the consistency of HDE, \(\varLambda \)CDM, and model-independent cosmography method with these observations.

The layout of this paper is as follows. We introduce the HDE model in Sect. 2 and cosmography method in Sect. 3. In Sect. 4, we put observational constrains on the cosmographic parameters using different combinations of the Hubble diagram data. In Sect. 5, we reconstruct the Hubble parameter of the models and compare it with observed H(z) data points. In Sect. 6, we conclude this work.

2 The HDE model

The holographic principle is one of the most important principles of quantum gravity. Based on this principle, all the information contained in the volume of space can be represented as a hologram, corresponding to the theory located on the boundary of the space [48, 49]. In fact, according to the holographic principle, the number of degrees of freedom of a finite-size system should be finite and bounded by the corresponding area of its boundary [50]. In this regard, the total energy of a physical system with a size of L should not exceed the mass of a black hole of the same size, i.e., \(L^3\rho _\varLambda \le LM_P^2\), where \(\rho _\varLambda \) is the quantum zero-point energy density caused by the UV cutoff \(\varLambda \) and \(M_P\) is the Planck mass (\(M_P^2 = 1/8\pi G\)). In the context of cosmology, in order to explain the accelerated expansion of the universe, Li [24] proposed a dark energy model based on the holographic principle, the so-called holographic dark energy (HDE) model. In this model, the vacuum energy of the holographic principle is considered as DE. The density of DE in HDE model is given by the following relation [24]:

$$\begin{aligned} \rho _{DE} = \frac{3c^2}{8\pi G L^2}, \end{aligned}$$
(1)

where c is the model parameter of the HDE which is positive and constant. It should be noted that the HDE model is defined in terms of an IR cut-off L in Eq. (1). The IR cut-off L can be defined based on the Hubble horizon, particle horizon or event horizon as follows:

  • Hubble horizon: The first and simplest choice for IR cut-off is the Hubble length, i.e., \(L= H^{-1}\). In this choice, the density of DE will be closer to the value expected from observations and will be proportional to the square of the Hubble parameter, i.e., \(\rho _{DE} \propto H^2\). Although this choice can solve the fine-tuning problem, we will get a wrong equation of state for the HDE model, so the current accelerated expansion cannot be achieved [51,52,53,54].

  • Particle horizon: The next option for IR cutoff is the particle horizon. This option cannot explain the accelerated expansion of the universe [24].

  • Event horizon: This option was first proposed by [24] for the IR cutoff. The length scale L is defined by the event horizon, which is given by:

    $$\begin{aligned} L = R_{h} = a\int _{t}^{\infty }\frac{dt}{a(t)}=a\int _{a}^{\infty }\frac{da}{Ha(t)^2}, \end{aligned}$$
    (2)

where a is the scale factor, t is the cosmic time and H is the Hubble parameter. In this case we can write the energy density of DE as:

$$\begin{aligned} \rho _{DE} = \frac{3c^2}{8\pi GR_{h}^{2}}. \end{aligned}$$
(3)

By selecting the event horizon as the IR cutoff, the HDE model can explain the late-time acceleration consistent with the observation [55,56,57]. We note that in this case, coincidence and fine-tuning issues will be resolved [24].

Now, let’s start with a Freidmann–Robertson–Walker (FRW) Universe in a flat geometry filled with pressureless matter and HDE. Notice that we will use the third option (event horizon) as the IR cutoff from now on. In this case, the dynamics of the Universe is given by:

$$\begin{aligned} H^2=\frac{8\pi G}{3}(\rho _{m}+\rho _{DE}), \end{aligned}$$
(4)

where \(\rho _{m}\) is the energy density of the pressureless matter, \(\rho _{DE}\) is the energy density of DE, and H is the Hubble parameter. We mention that the contribution of radiation on the total energy budget of the Universe at low redshifts is negligible.

In the non-interacting models, the different components of the Universe evolve separately. Hence, the evolution of the energy density of the pressureless matter and DE are described by the following continuity equations:

$$\begin{aligned}&{\dot{\rho }}_{m}+3H\rho _m=0, \end{aligned}$$
(5)
$$\begin{aligned}&{\dot{\rho }}_{DE}+3H(1+w_{DE})\rho _{DE}=0, \end{aligned}$$
(6)

where over-dot is the derivative with respect to cosmic time, and \(w_{DE}\) is the equation of state (EoS) parameter of DE.

Taking the time derivative of Eq. (3), using Eq. (6) and \(\dot{R_h}=1+HR\), we can obtain the EoS parameter of DE in HDE model as [29, 58]:

$$\begin{aligned} w_{DE}=-\frac{1}{3}\left( 1+\frac{2\sqrt{\varOmega _{DE}}}{c}\right) , \end{aligned}$$
(7)

where \(\varOmega _{DE}\) is the dimensionless density parameter of the DE component. Using Eq. (3) and the critical energy density \(\rho _{c}=\frac{3H^2}{8\pi G}\), we can obtain the energy density of DE in HDE model as follow:

$$\begin{aligned} \varOmega _{DE}=\frac{\rho _{DE}}{\rho _{c}}=\frac{c^2}{(HR_h)^2}. \end{aligned}$$
(8)

The evolution of energy density of DE can be obtained by taking a derivative of Eq. (8) with respect to scale factor. Then using the relation between redshift and scale factor \(a=\frac{1}{1+z}\), we have

$$\begin{aligned} \frac{d\varOmega _{DE}}{dz}=-\frac{1}{1+z}\varOmega _{DE}(1-\varOmega _{DE})(1+\frac{2\sqrt{\varOmega _{DE}}}{c}). \end{aligned}$$
(9)

Also, using the Eq. (4) and Eqs. (5–6), the dimensionless Hubble parameter \(E(z)=\frac{H(z)}{H_0}\) can be written as:

$$\begin{aligned} E^2(z)=\frac{\varOmega _{m0}(1+z)^3}{1-\varOmega _{DE}}, \end{aligned}$$
(10)

where \(\varOmega _{m0}\) is the present value of the dimensionless matter density. Also, the evolution of \(\varOmega _{DE}\) is given by Eq. (9). Note that we study the HDE model at the late time where the energy density of radiation is negligible. The model parameter c of the HDE model is a key parameter that determines the historical evolution of the expansion of the Universe in the context of the HDE model. A detailed study of the HDE model and the use of cosmological data (both high redshift CMB and low redshift data) to constrain the model parameter c can be found in [58]. According to the value of the model parameter c, the EoS parameter of the HDE model can be greater or less than \(w_{\varLambda } = -1\), where \(w_{\varLambda }\) is the EoS parameter of cosmological constant. By fixing the energy density parameter of current DE to \(\varOmega _{DE,0} = 0.7\), we see that for \(c<0.83\) (\(c>0.83\)) the current EoS parameter is less than (greater than) the fiducial value \(w_{\varLambda } = -1\). In addition to the model parameter c, the density parameter of matter \(\varOmega _{m0}\) is another parameter on which the dynamics of the expanding Universe depends. Note that we assume a flat FRW Universe, so \(\varOmega _{DE,0} = 1- \varOmega _{m0}\). Hence, the main cosmological parameters of the HDE model are reduced to \(\varOmega _{m0}\) and c.

3 The cosmography approach

Cosmography is a model-independent way of expressing the dynamics of the universe, without presupposing a particular cosmological model. In this way, cosmological quantities are expanded as a Taylor series around current time, where the coefficients of the Taylor expansion can be constrained by observational data. The cosmographic parameters in the context of the FRW Universe are defined as the time derivatives of the cosmic scale factor as follows [59]:

$$\begin{aligned} H(t)= & {} \frac{a^{(1)}}{a},\nonumber \\ q(t)= & {} -\frac{a^{(2)}}{aH^2}, \nonumber \\ j(t)= & {} \frac{a^{(3)}}{aH^3}, \nonumber \\ s(t)= & {} \frac{a^{(4)}}{aH^4}, \nonumber \\ l(t)= & {} \frac{a^{(5)}}{aH^5}, \end{aligned}$$
(11)

where \(a^{(n)}\) is the nth time derivative of the scale factor. The cosmographic parameters do not depend on the form of the DE fluid, since they are not functions of the EoS parameter of DE. These parameters are introduced as Hubble parameter (H), deceleration parameter (q), jerk parameter (j), snap parameter (s) and lerk parameter (l). The cosmographic parameters, when calculated at the present time, are the effective observables to reconstruct the history of the expanding Universe at low redshifts. In this context, one can reconstruct the scale factor a(t) in terms of the cosmographic series at the present time as follows:

$$\begin{aligned} a(t)\simeq & {} 1+ H_0 (t-t_0) - \frac{q_0}{2} H_0^2 (t-t_0)^2 \nonumber \\&+\frac{j_0}{6} H_0^3 (t-t_0)^3 + \frac{s_0}{24} H_0^4 (t-t_0)^4 + \frac{l_0}{120} H_0^5 (t-t_0)^5.\nonumber \\ \end{aligned}$$
(12)

Note that behind each cosmographic parameter is a physical point. The Hubble parameter H indicates the expansion or contraction of the Universe. \(H>0\) stands for \({\dot{a}}>0\) and indicates the expansion of the Universe, and conversely \(H<0\) indicates the contraction of the Universe. In an expanding Universe (\(H>0\)), the sign of q indicates the accelerated or decelerated phase of the expansion. A positive q means that gravity dominates over the other species, indicating a slowed expansion, while a negative q shows that repulsive effects overcome gravity, indicating an accelerated expansion. The change in the parameter q, which indicates the transition epoch from slowed to accelerated expansion, is determined by jerk parameter j. A positive j indicates that there is a transition time in which the expansion phase of the Universe is changed. According to this transition, the parameter q tends to zero and then changes the sign. The cosmographic coefficients s and l become important at higher redshifts. The variation of s is basically due to the sign of the lerk parameter l and indicates how the shape of the Hubble expansion becomes smooth at higher redshifts. It is useful to obtain the various time derivatives of the Hubble parameter H as functions of the cosmographic parameters. Using the relations of Eq. (11), we can obtain

$$\begin{aligned} H^{(1)}= & {} -H^2(1+q),\nonumber \\ H^{(2)}= & {} H^3(3q+j+2),\nonumber \\ H^{(3)}= & {} H^4(-3q^2-12q-4j+s-6), \nonumber \\ H^{(4)}= & {} H^5(30q^2+60q+10qj+20j-5s+l+24),\nonumber \\ \end{aligned}$$
(13)

where \(H^{(n)}\) is the nth time derivative of the Hubble parameter H. Using Taylor Series, we can now reconstruct the Hubble expansion of the Universe at low redshifts. In this context, the Taylor Series of the Hubble parameter up to the fourth order in redshift z around the present time (\(z = 0\)) can be written as

$$\begin{aligned} H(z) \simeq H_0+\frac{dH}{dz}(z=0) z + \frac{d^2H}{dz^2} (z=0) \dfrac{z^2}{2} \nonumber \\ + \frac{d^3H}{dz^3} (z=0) \dfrac{z^3}{6} + \frac{d^4H}{dz^4} (z=0) \dfrac{z^4}{24}. \end{aligned}$$
(14)

Taylor series (14) is valid for small redshifts (\(z<1\)) and does not converge at higher redshifts. Thus, since much of the observational data is at higher redshifts than \(z=1\), the above Taylor series cannot be used to reconstruct the Hubble expansion at \(z>1\). In order to solve the above convergence problem, one can define a new redshift variable, the \(\zeta -redshift\) [40, 46, 60] as follows:

$$\begin{aligned} z\rightarrow \zeta =\frac{z}{1+z}. \end{aligned}$$
(15)

This definition improves the convergence problem without changing the the Hubble expansion scenario of the Universe. Moreover, other parameterizations such as \(\zeta =arctan(z)\) and various Pade approximations based on rational functions have been proposed [45]. It has been shown that the Pade approximation is a good parametrization to reconstruct the Hubble parameter at very high redshifts where we encounter the CMB data. On the other hand, the parametrization \(z/(1+z)\), which is a simple approximation compared to Pade polynomials is well fitted to observations at low and middle redshifts [45]. In this work, we use the \(\zeta =z/(1+z)\) parametrization and so we can write the Taylor expansion of the Hubble parameter around the present time (\(\zeta =0\)) as follows:

$$\begin{aligned} H(\zeta )\simeq & {} H_0+\frac{dH}{d\zeta }(\zeta =0) \zeta + \frac{d^2H}{d\zeta ^2}(\zeta =0) \dfrac{\zeta ^2}{2}\nonumber \\&+ \frac{d^3H}{d\zeta ^3}(\zeta =0) \dfrac{\zeta ^3}{6} + \frac{d^4H}{d\zeta ^4}(\zeta =0) \dfrac{\zeta ^4}{24}. \end{aligned}$$
(16)

Now we convert the time derivatives in Eq. (13) to the derivatives with respect to \(\zeta \), put the results in Eq. (16) and use Eq. (11) in order to find the reconstructed dimensionless Hubble parameter \(E=H/H_0\) as follows [46]:

$$\begin{aligned} E(\zeta )=\dfrac{H(\zeta )}{H(\zeta =0)}=1+C_1 \zeta + \dfrac{C_2 \zeta ^2}{2}+\dfrac{C_3 \zeta ^3}{6}+\dfrac{C_4 \zeta ^4}{24},\nonumber \\ \end{aligned}$$
(17)

where the various coefficients \(C_i\) are obtained in terms of cosmographic parameters as:

$$\begin{aligned} C_1= & {} 1+q_0, \nonumber \\ C_2= & {} 2-q^2_0+2q_0+j_0, \nonumber \\ C_3= & {} 6+3q^3_0-3q^2_0+6q_0-4q_0j_0+3j_0-s_0, \nonumber \\ C_4= & {} -15q^4_0+12q^3_0+25q^2_0j_0+7q_0s_0-4j^2_0\nonumber \\&-16q_0j_0-12q^2_0+l_0-4s_0+12j_0+24q_0+24,\nonumber \\ \end{aligned}$$
(18)

in which \( q_0 \), \( j_0 \), \( s_0 \) and \( l_0 \) are the current values of the cosmographic parameters.

We now calculate the cosmographic parameters in the HDE cosmology. As we saw in Sect. 2, the free parameters in the HDE model are \(\varOmega _{m0}\) and c. With some simple calculations, we can derive the cosmographic parameters in the HDE model in terms of the free parameters of the model. For this purpose, by deriving the Freidmann equation in (4) in time and using the continuity relations in Eqs. (5 and 6), we can obtain the following equations in HDE cosmology:

$$\begin{aligned} \frac{{\dot{H}}}{H^2}= & {} -\frac{3}{2}\left( 1+w_{DE}\varOmega _{DE}\right) , \end{aligned}$$
(19)
$$\begin{aligned} \frac{{\ddot{H}}}{H^3}= & {} \frac{9}{2}\left[ \left( 1-\varOmega _{DE}\right) \left( 1-\varOmega _{DE}^{3/2}\frac{w_{DE}}{3c}\right) +\left( 1+w_{DE}\right) ^2\varOmega _{DE}\right] ,\nonumber \\ \end{aligned}$$
(20)

where the overdots represent the derivative according to cosmic time. Substituting Eqs. (19 and 20) into Eq. (13), we can calculate the cosmography parameters in HDE cosmology as follows:

$$\begin{aligned} q= & {} \frac{1}{2}(1+3w_{DE}\varOmega _{DE}), \end{aligned}$$
(21)
$$\begin{aligned} j= & {} \frac{9}{2}[(1-\varOmega _{DE})\left( 1-\varOmega _{DE}^{3/2}\frac{w_{DE}}{3c}\right) \nonumber \\&+ (1+w_{DE})^2\varOmega _{DE}]-3q-2. \end{aligned}$$
(22)

Note that the higher derivatives of the Hubble parameter in the HDE model to obtain s and l are so complicated that they lead to very costly relations. Therefore, we ignore the input of these relations. Moreover, from the observational point of view, we cannot make reasonable constraints on the parameters \(s_0\) and \(l_0\) (see [44, 46]). From a mathematical point of view, we know that associated terms of the higher derivatives of the Hubble parameter in the Taylor expansion have a smaller contribution than the first terms of the expansion. Now we want to test Eqs. (21 and 22) in limiting cases. For the Einstein de-Sitter (EdS) Universe (\(\varOmega _m = 1.0\)), Eqs. (21 and 22) yield the reference values \(q=0.5\) and \(j=1\), as expected. Setting also \(\varOmega _{DE,0} = 0.7\) and \(w_{DE} = -1\), we obtain \(q_0=-0.55\) which is the deceleration parameter of the concordance \(\varLambda \)CDM model at the present time.

4 Observational constraints on cosmographic parameters

In this section, we put observational constraints on the cosmographic parameters, using the data from the Hubble diagram of SNIa, quasars and GRB. We use the Pantheon catalog for SNIa and refer the reader to the full discussion and complete details of the observational data related to quasars and GRB in [44, 46]. In order to constraint the cosmographic parameters in a model-independent way, we let the cosmographic parameters (\(q_0\), \(j_0\), \(s_0\) and \(l_0\)) be free parameters in the MCMC algorithm. We then calculate the error function \(\chi ^2\) for each set of random values of the cosmographic parameters in the parameter space of \(q_0\), \(j_0\), \(s_0\) and \(l_0\). Here the error function is

$$\begin{aligned} \chi ^2=\sum _{i}\frac{[\mu _{t}(z_{i})-\mu _{obs}(z_{i})]^2}{\sigma ^{2}_{i}}, \end{aligned}$$
(23)

where \(\mu _{t}(z_{i})\) is the theoretical prediction of the distance modulus (the difference between apparent magnitude m and absolute magnitude M) at a given redshift \(z_i\) and \(\mu _{obs}(z_{i})\) is the observed value at \(z_i\). The theoretical distance modulus is

$$\begin{aligned} \mu _{t}(z)=5 \log _{10}[(1+z)\int _{0}^{z}\frac{dz}{E(z)}]+\mu _{0}, \end{aligned}$$
(24)

where \(\mu _{0}=42.384-5 \log _{10}(h)\) is the current value of the distance modulus and \(h=H_0/100\). Note that to calculate \(\mu _{t}\) in model-independent cosmography method, we substitute Eq. (17) into Eq. (24) and use Eq. (18). Since the absolute magnitude M and the Hubble parameter h are degenerate in the calculation of the distance modulus, we can marginalize over these nuisance parameters by taking the expansion of \(\chi ^2\) around \(\mu _{0}\) as

$$\begin{aligned} \chi ^2=A+2B\mu _{0}+C\mu _{0}^2, \end{aligned}$$
(25)

where

$$\begin{aligned}&A=\sum _{i}\frac{[\mu _{t}(z_{i};\mu _{0}=0)-\mu _{obs}(z_{i})]^2}{\sigma ^{2}_{i}}\nonumber \\&B=\sum _{i}\frac{\mu _{t}(z_{i};\mu _{0}=0)-\mu _{obs}(z_{i})}{\sigma ^{2}_{i}}\nonumber \\&C=\sum _{i}\frac{1}{\sigma ^{2}_{i}}\;. \end{aligned}$$
(26)

If we equate the differentiation of Eq. (25) with respect to \(\mu _{0}\) with zero, we find \(\mu _{0} = -B/C\). Then we substitute \(\mu _{0}\) into Eq. (25) and obtain

$$\begin{aligned} {\tilde{\chi }}^{2}= A -\frac{B^2}{C}. \end{aligned}$$
(27)

Note that in Eq. (27) we omit the influence of nuisance parameters M and h. In order to find the best-fit values of the cosmographic parameters in a model-independent cosmography method, we minimize \({\tilde{\chi }}^{2}\) in the context of the MCMC algorithm using the different combinations of the Hubble diagram data. The various combinations of the Hubble diagram data from SNIa (Pantheon), quasars and GRB are as follows: (i) sample I (Pantheon), (ii) sample II (Pantheon + GRB), (iii) sample III (Pantheon + quasars) and (iv) sample IV (Pantheon + GRB + quasars). For each sample, we minimize the total error function, \({\tilde{\chi }}_{tot}^{2}\), defined as follows:

$$\begin{aligned} {sample\; I:}~~&{\tilde{\chi }}^2_{tot}={\tilde{\chi }}^2_{Pantheon},\nonumber \\ {sample\; II:}~~&{\tilde{\chi }}^2_{tot}={\tilde{\chi }}^2_{Pantheon}+{\tilde{\chi }}^2_{GRB},\nonumber \\ {sample\; III:}~~&{\tilde{\chi }}^2_{tot}={\tilde{\chi }}^2_{Pantheon}+{\tilde{\chi }}^2_{Quasar},\nonumber \\ {sample\; IV:}~~&{\tilde{\chi }}^2_{tot}={\tilde{\chi }}^2_{Pantheon}+{\tilde{\chi }}^2_{Quasar}+{\tilde{\chi }}^2_{GRB}.\nonumber \\ \end{aligned}$$
(28)
Table 1 The best-fit values of the cosmological parameters \(\varOmega _{m0}\), c and \(w_{DE,0}\) within the \(1-\sigma \), \(2-\sigma \) and \(3- \sigma \) uncertainties using the Hubble diagram data from Pantheon, quasars and GRB
Full size table
Fig. 1
figure 1

The \(1-\sigma \), \(2-\sigma \) and \(3-\sigma \) confidence regions of the cosmological parameters \(\varOmega _{m0}\) and c in the HDE model using the various combinations of the Hubble diagram data from Pantheon, quasars and GRB

Full size image
Table 2 Left part: the best-fit values of the cosmographic parameters \(q_0\) and \(j_0\) in the HDE model calculated within the \(1-\sigma \), \(2-\sigma \) and \(3-\sigma \) errors obtained from the Hubble diagram of Pantheon, quasars and GRB. Right part: same as left part, but for the concordance \(\varLambda \)CDM model
Full size table
Fig. 2
figure 2

The \(1-\sigma \), \(2-\sigma \) and \(3-\sigma \) confidence regions for the deceleration parameter \(q_0\) and the jerk parameter \(j_0\) obtained from the cosmography method. Also, the best-fit values of \(q_0\) and \(j_0\) with \(1-\sigma \) error have been shown for the HDE and \(\varLambda \)CDM cosmologies. The upper-left (upper-right) panel shows the results for Pantheon (Pantheon + GRB) sample. The bottom-left (lower-right) panel shows the results for Pantheon + Quasars (Pantheon + Quasars + GRB) sample

Full size image

Results for the model-independent cosmography method, which include the best-fit values of the cosmographic parameters within the \(1 - \sigma \) uncertainty were presented in Table (2) of our previous work [46]. In order to find the best fit values of the cosmographic parameters in the HDE cosmology, we should first find the best-fit values of the free parameters of the model using the various data samples discussed above. We mention that the free parameters of the HDE model are the model parameter c and the matter density parameter \(\varOmega _{m0}\). Moreover, we add another column in our MCMC chain by using Eq. (7) to obtain the best fit-value of the current EoS parameter of DE, \(w_{DE,0}\), in the HDE model. Note that in this step we use Eqs. (9 and 10) to calculate the Hubble parameter and then Eq. (24) to calculate the distance modulus. Numerical results of our analysis within \(1 - \sigma \) (\(68 \%\) confidence level), \(2 - \sigma \) (\(95 \%\) confidence level) and \(3 - \sigma \) (\(98 \%\) confidence level) are shown in Table 1. First, we see that in the case of the Pantheon sample, the current energy density of matter is about 0.3, which implies that \(30\%\) of the energy budget of the low-redshift flat Universe is occupied by presserless matter and the rest is in the form of DE in the HDE cosmology. The best-fit value of the HDE model parameter is \(0.74^{+0.11}_{-0.20}\), which is smaller than the critical value 0.83, implying that the current EoS parameter of the HDE model can vary in the phantom regime. One can observe that in the case of the Pantheon sample, the best-fit value of \(w_{DE,0}\) varies in the phantom regime, but its upper bound can exceed the constant line \(w_{\varLambda }=-1\) even in \(1 - \sigma \) error. Second, in the case of the Pantheon + GRB sample, our results show a slight increase of the current matter density and a decrease in the value of the model parameter c compared to previous case. In this case, we see that the best-fit value of c is smaller than the critical value 0.83 with an uncertainty of \(1 - \sigma \), which means that \(w_{DE,0}\) varies in the phantom regime with a confidence level of \(68\%\). This behavior is consistent with our MCMC output for \(w_{DE,0}\) in the last column of Table 1, where we obtain the same result for \(1 - \sigma \) error. Hence, adding the GRB data to Pantheon, we conclude that the current EoS parameter of the HDE model can be distinguished from the value of the cosmological constant \(w_{\varLambda }=-1\) at least in the \(1 - \sigma \) range. Third, in the case of the Pantheon + quasars sample, the current matter density is roughly \(16\%\) larger than our result in the Pantheon sample. The model parameter c is smaller than the critical value 0.83 in a large range of \(3 - \sigma \). We obtain that the constrained parameter \(w_{DE,0}\) differs from \(w_{\varLambda }=-1\) in the \(3 - \sigma \) confidence interval. Finally, we obtain the same results in the case of Pantheon+GRB+ quasars as in the case of Pantheon+quasars case. In Fig. 1, we show the best-fit values of the cosmological parameters \(\varOmega _{m0}\) and c within \(3 - \sigma \) uncertainty. We see that in the case of Pantheon + quasars + GRB sample, we can constraint the cosmological parameters more tightly than in the case of Pantheon sample.

Using the results of our MCMC analysis for the parameters c, \(\varOmega _{m0}\) and \(w_{DE,0}\) and also Eqs. (21, 22), we can now place constraints on the cosmographic parameters \(q_0\) and \(j_0\) in the HDE cosmology. The results are shown in the left panel of Table 2. Note that we also perform our analysis for the concordance \(\varLambda \)CDM cosmology and present the results in the right panel of Table 2. In the following, we explain our numerical results for each sample used in this work.

Pantheon sample In this case, we obtain \(q_{0}=-0.678\pm 0.097\), \(j_{0}=1.95^{+0.65}_{-0.87}\) for the HDE model and \(q_{0}=-0.572\pm 0.019\) for the standard \(\varLambda \)CDM cosmology (see also Table 2). Note that in the \(\varLambda \)CDM model the jerk parameter is equal to the constant value \(+1.00\). The best-fit and also \(1-\), \(2-\) and \(3 - \sigma \) confidence intervals of \(q_0\) and \(j_0\) in the model-independent cosmography method are shown by contour plots in Fig. 2. In the case of the Pantheon sample (top-left), we observe that both the HDE and \(\varLambda \)CDM models lie in the confidence regions of the \(q_0 - j_0\) plane. We can thus conclude that both models are consistent with the data of Pantheon sample in the context of the cosmography method.

Pantheon+GRB sample In this case, we get \(q_{0}=-0.708^{+0.10}_{-0.091}\) for HDE and \(q_{0}=-0.572\pm 0.019\) for the \(\varLambda \)CDM model (see also Table 2). We see that the parameter \(q_0\) in the HDE model is consistent with the result of the model-independent cosmography method in the \(68\%\) confidence region and has a tension of \(1.34\sigma \) with the \(\varLambda \)CDM model. Moreover, we obtain the constrained value of \(j_0\) in the HDE model as \(j_0=2.20^{+0.67}_{-0.92}\) which lies in the confidence regions of the cosmography method and has a \(1.3\sigma \) tension with the constant value \(j_0 =1.00\) in the \(\varLambda \)CDM cosmology. Looking at the upper-right panel of Fig. 1, we observe that the concordance \(\varLambda \)CDM model has a big tension with the confidence regions of the cosmographic parameters obtained from the cosmography method, while the HDE model is fully consistent.

Pantheon + Quasar In this case (see the third row of Table 2), we observe that \(q_0\) (\(j_0\)) of the HDE model differs from the \(\varLambda \)CDM model value by up to \(2.5\sigma \) (\(2.2\sigma \)). Also, the deceleration parameter \(q_0\) and the jerk parameter \(j_0\) in the HDE model agree with the results of the model-independent cosmography (Fig. 1, lower left panel). Note that the best-fit point of the HDE model in the \(q_0-j_0\) plane is outside the confidence regions of the cosmography method. However, we should emphasize that by assuming the error bars of \(q_0\) and \(j_0\) for the HDE model, we can see the consistency of the model with the cosmography method. This is not the case for the concordance \(\varLambda \)CDM model where it deviates completely from the confidence regions of the cosmography method in the \(q_0 - j_0\) plane even if we assume the error bars.

Pantheon + Quasar + GRB Finally, we combine all the data from the Hubble diagram, including those from the Pantheon, GRB and quasars. In this case, the best-fit values of deceleration and jerk parameters of the HDE model within the uncertainty of \(1 - \sigma \) are \(q_0=-0.799^{+0.089}_{-0.075}\) and \(j_0=3.09^{+0.61}_{-0.89}\). Also, the best-fit value of \(q_0\) for the \(\varLambda \)CDM model is \(-0.559^{+0.019}_{-0.019}\) (see also Table 2). Our results show \(2.63\sigma \) and \(2.35\sigma \) tensions between the HDE and the \(\varLambda \)CDM models, respectively for parameters \(q_0\) and \(j_0\). Same as our results in Pantheon+Quasar case, we observe that the best-fit value of the HDE model in the \(q_0-j_0\) plane is outside the confidence bounds but when we accept the error bars, we obtain agreement of the HDE model with the cosmography method (see lower-right panel in Fig. 2). On the other hand, we observe that the \(\varLambda \)CDM model deviates completely from the confidence regions in the \(q_0 - j_0\) plane, implying that this model has a big tension with the combined Hubble diagram from Pantheon, GRB and quasars. From the above analysis, it can be concluded that the best-fit values of the cosmographic parameters obtained from the Pantheon sample (\(q_{0}=-0.678\pm 0.097\), \(j_{0}=1.95^{+0.65}_{-0.87}\)) are the minimum values resulted from various Hubble diagram data. The difference between these values and the values of the best-fit cosmographic parameters of the \(\varLambda \)CDM model is at least in the \(1\sigma \) error. We can assume \(q_{0}=-0.678\pm 0.097\) & \(j_{0}=1.95^{+0.65}_{-0.87}\) as the viable condition that the lower values of them cannot be achieved in the HDE model using the Hubble diagram observations.

We now compare our numerical results with the results of previous studies for the HDE models. In [61], the authors studied the HDE model from the viewpoint of cosmography method. They used the Hubble diagram of SNIa in the Union 2 compilation from [62] and obtained \(q_0=-0.589^{+0.084}_{-0.084}\), \(j_0=1.359^{+0.518}_{-0.518}\) and \(s_0=0.091^{0.468}_{-0.468}\), in a model-independent cosmography method. Using the high redshift CMB data and SNIa observations, they put constraints on the matter density parameter in the HDE model and then obtained the best-fit values of the cosmography parameters in the HDE cosmology. Their results for the HDE model are consistent with the results of the model-independent cosmography and are also consistent with the results for the standard \(\varLambda \)CDM Universe. In the same study, the authors of [63] placed constraints on the cosmographic parameters of the HDE model using the Hubble diagram of supernovae from the Union 2.1 catalog [64], BAO experiments [65] and H(z) data. They obtained \(q_0=-0.582^{+0.059}_{-0.059}\) and \(j_0=0.96^{+0.17}_{-0.16}\), which cover the standard model results with \(1\sigma \) error (see also [66]). We note that our results in this current analysis are completely different from these studies. Compared to these studies, we obtained higher values of the cosmographic parameters for the HDE and model-independent cosmography scenarios, while the results for the standard \(\varLambda \)CDM model did not change significantly (see Table 2). This difference is mainly due to the use of Hubble diagrams of SNIa, quasars and GRB at higher redshifts in our analysis. We conclude that the high redshifts Hubble diagram data can rule out the standard \(\varLambda \)CDM model, while the HDE model still agrees with these data. In [45], Capozzielo, et. al., applied two different y parameterizations and Pade polynomials in the cosmography method , using both the low-redshift (H(z) and SNIa) and high-redhsift (CMB shift parameter) data. In their analysis, the cosmography method based on the Pade polynomials can be consistent with the standard \(\varLambda \)CDM model for both \(H(z)+SNIa\) and \(H(z)+SNIa+CMB\)-shift parameter samples. They showed that the parametrization \(y=z/(1+z)\) (the parametrization used in our work) cannot well fitted to high redhsift CMB data as equal as the Pade parametrization. Furthermore, their results of cosmography method based on the \(y=z/(1+z)\) parametrization at low-redshift is in agreement with our results for the Pantheon sample in the present work.

5 Hubble parameter reconstruction

Fig. 3
figure 3

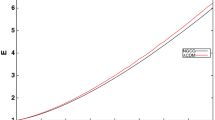
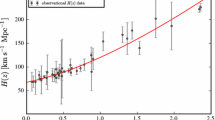
The reconstructed Hubble parameter H(z) based on the best-fit values of the cosmographic parameters \(q_0\) and \(j_0\) for the model-independent approach, HDE and \(\varLambda \)CDM scenarios. The red band shows the \(3-\sigma \) confidence region of the reconstructed Hubble parameter in the model-independent method. The upper left (upper right) panel shows results obtained using the Pantheon (Pantheon + GRB) sample. The bottom left (bottom right) panel shows results obtained using the Pantheon + quasars (Pantheon + GRB + quasars) sample

Full size image

In this section, we reconstruct the Hubble parameter as a function of redshift using the cosmographic parameters obtained in our analysis. For this purpose, we use Eqs. (17 and 18) and the best-fit values of the cosmographic parameters in the HDE and \(\varLambda \)CDM models presented in Table 2. We also set the Hubble constant as \(H_0=70\) \(kms^{-1}/Mpc\) based on the recent observations of standard sirens [76]. This value is consistent with the predicted Hubble constant form both Planck experiments [77] at high redshifts and measurements at low redshifts [78] within \(68\%\) confidence level. Figure 3 shows the reconstructed Hubble parameter H(z) for various samples listed in Table 2. The upper-left (upper-right) panel shows the reconstructed H(z) based on the best-fit values of the cosmographic parameters obtained from the Pantheon (Pantheon + GRB) sample. The lower-left and lower-right panels show our results obtained from Pantheon + Quasars and Pantheon + Quasars + GRB samples, respectively. In all panels, the red band is the \(3-\sigma \) confidence level of the reconstructed H(z) in the model-independent cosmography method computed using the upper and lower bounds on the best-fit of the cosmographic parameters from [46]. The observational data shown here are 36 different H(z) data points collected in Table 3 with their references. Note that among the many observational data in cosmology, the H(z) data is the only data set that directly measures the cosmic expansion of the Universe. Thus, by comparing with the H(z) data, we are able to examine the reconstructed Hubble parameter of the HDE and \(\varLambda \)CDM models in our analysis. We see that at redshifts higher than \(z\sim 1\), the reconstructed Hubble parameter in the \(\varLambda \)CDM model deviates from the confidence band of cosmography method. This property is valid for all cases of the combined Hubble diagram samples. However, the deviation is smallest in the case of Pantheon+GRB (top-right panel). On the other hand, we observe that the reconstructed H(z) in the HDE model is well within the confidence band. Quantitatively, using the H(z) data, we can compute the error function \(\chi ^2\) for each model as follows:

$$\begin{aligned} \chi _{H}^2 = \sum _{i} \frac{[H_{obs}(z_i) - H_{rec}(z_i)]^2}{\sigma _i^2}, \end{aligned}$$
(29)

where \(H_{obs}(z_i)\) is the observational data point at redshift \(z_i\) and \(H_{rec}(z_i)\) is the reconstructed Hubble parameter at \(z_i\). The numerical results are presented in Table 4. We observe that in all samples the model-independent cosmography method has the smallest value of \(\chi _{H}^2\) and the standard \(\varLambda \)CDM model has the largest value. Comparing with the H(z) data in the redshift range \(0.07< z < 2.36\), we see that the model-independent cosmography method is the best case to reconstruct the Hubble parameter in good agreement with the observations. On the other hand, the standard \(\varLambda \)CDM model is the worst model. The HDE model is the middle model compared to the other two scenarios. It is interesting to note that the high value of \(\chi _{H}^2\) in the \(\varLambda \)CDM model is related to the large difference between \(H_{rec}\) of the model and the observational data point \(H_{obs} = 226^{+8.0}_{-8.0}\) at redshift \(z_i = 2.36\) (pink data in Fig. 3). Since the error bar of this observed data is very small compared, it can increase the value of \(\chi _{H}^2\) specifically for a model with a larger deviation from this data point at \(z_i = 2.36\). Note that the smaller value of error bar causes the higher value of \(\chi _{H}^2\) in Eq. (5). This observed data point was calculated by measuring the large-scale cross-correlation of quasars with the Lyman \(\alpha \) forest absorption, using over 164,000 quasars from Data Release 11 of the SDSS-III Baryon Oscillation Spectroscopic Survey [75]. While observational data for H(z) are mainly obtained using the differential age method on luminous red galaxies in clusters (see for example [67]). We now remove this data point from our analysis and recompute \(\chi _{H}^2\) for each scenario. The results are presented in Table 5. We see that for all samples, the high value of \(\chi _{H}^2\) in the \(\varLambda \)CDM model reported in the previous case are now reduced to very low values. Quantitatively, we observe that in all combined samples of Hubble diagrams from Pantheon, quasars and GRB, the \(\chi _{H}^2\) decreases by about \(68\%\) in the\(\varLambda \)CDM model. This decrement for the HDE model is approximately \(34\%\), \(16\%\), \(14\%\), and \(16\%\) for Pantheon, Pantheon+GRB, Pantheon+Quasars and Pantheon+GRB+Quasars, respectively. We conclude that in the absence of the data point \(H_{obs} = 226^{+8.0}_{-8.0}\) at redshift \(z_i = 2.36\), our results are modified to obtain better agreement of both the HDE and \(\varLambda \)CDM models with the H(z) observations. This result is more pronounced for the standard \(\varLambda \)CDM cosmology. Note that the reconstructed Hubble parameter is still the best case in the model-independent cosmography. Finally, let us compare the model-independent cosmography method, HDE and \(\varLambda \)CDM scenarios at redshifts \(z<1\). To make this comparison, we recalculate \(\chi _{H}^2\) using 28 distinct observed data points of H(z) data at redshifts \(z<1\) from Table 3. Figure 4 shows the reconstructed Hubble parameter for different combinations of Hubble diagram data and also observational data points of H(z) at \(z<1\). We see that the model-independent cosmography method, the HDE and the \(\varLambda \)CDM scenarios are well fitted to the observations. The numerical results of our analysis are given in Table 6. Interestingly, we see that the best model with the minimum of \(\chi _{H}^2\) is the \(\varLambda \)CDM model, which is even better than the model-independent cosmography method. This result holds for all combinations of Hubble diagrams from Pantheon, quasars and GRB samples. On the other hand, the HDE model has the largest \(\chi _{H}^2\) value, indicating that this model is the worst compared to the other two scenarios. This result is also valid for all Hubble diagram samples.

This behavior of the standard \(\varLambda \)CDM and the HDE models at redshifts \(z<1\) and \(z>1\) is related to our prediction of the luminosity distance calculated in these models. Since the energy density of DE in the \(\varLambda \)CDM model is constant, we observe that the luminosity distance calculated at the higher redshift is different from the observed value, while the difference is not significant at lower redshift. On the contrary, due to the dynamical behavior of DE in the HDE model, the difference between the observed luminosity distance and the calculated value decreases as the redshift increases from \(z<1\) to \(z>1\).

Table 3 The H(z) data and their references used in our analysis
Full size table
Table 4 The \(\chi _{H}^2\) values for model-independent cosmography approach, HDE and \(\varLambda \)CDM scenarios resulted from all H(z) observational data points in Table 3
Full size table
Table 5 The \(\chi _{H}^2\) values for model-independent cosmography approach, HDE and \(\varLambda \)CDM scenarios resulted from observational H(z) data points in Table 3 except the last one numbered 36
Full size table
Fig. 4
figure 4

Same as Fig. 3, but for \(z<1\)

Full size image
Table 6 The \(\chi _{H}^2\) values for model-independent cosmography approach, HDE and \(\varLambda \)CDM scenarios resulted from 28 observational data points at \(z<1\) in Table 3 numbered by 1–28
Full size table

6 Conclusions

The cosmography method is a useful key to study the DE models in the expanding Universe. In this method, we apply a Taylor expansion to the Hubble parameter via cosmic redshift. Then, we define the cosmographic parameters, namely deceleration, jerk, snap and lerk parameters, which are related to the derivative of the Hubble parameter at the present time. Using the cosmological observations to constraints the cosmographic parameters can help us reconstruct the Hubble parameter and depict the expansion history of the Universe at low redshifts. Measuring the discrepancy between the cosmographic parameters obtained in the DE model and the parameters obtained from the model-independent cosmography method can be regarded as the tension between the DE model and observations. In this work, we used the Hubble diagram of SNIa, quasars and GRB as independent observations over a wide range of redshifts to constraints the cosmographic parameters of the HDE cosmology in the context of the MCMC algorithm. We also computed the constrained values of the cosmographic parameters for the standard \(\varLambda \)CDM Universe and compared our results for both the HDE and the standard models with the results of the model-independent cosmography method. We have shown that both the HDE and the \(\varLambda \)CDM models are consistent with the Hubble diagram of SNIa observations. We extended our sample by adding the Hubble diagram of quasars and GRB and observed a big tension between the standard \(\varLambda \)CDM and the model-independent cosmography method. In the case of the HDE model, we have explicitly shown that there is no tension between the cosmographic parameters of the model and those from the model-independent method. This result is valid for various combinations of the Hubble diagrams from SNIa, quasars and GRB. In the next step by using the constrained values of the cosmographic parameters obtained in our analysis, we reconstructed the Hubble parameter as a function of redshift and compared the result with the observed H(z) data. We showed that the model-independent cosmography method (\(\varLambda \)CDM model) has the largest consistency (smallest consistency) and the HDE model has the medium consistency with H(z) observations over a redshift range \(0.07< z < 2.36\). We obtained better consistency of the HDE and \(\varLambda \)CDM cosmologies with H(z) data, by removing the data point \(226^{+8.0}_{-8.0}\) at \(z_i=2.36\). However, the model-independent cosmography method is still the best scenario. Finally, we investigated the HDE and the concordance \(\varLambda \)CDM models, using the H(z) data at redshifts \(z<1\). We showed that the H(z) observations at \(z<1\) favor the \(\varLambda \)CDM model rather than the HDE model. At these redshifts, we concluded that the \(\varLambda \)CDM model has the greatest compatibility with the H(z) observations, even better than the model-independent cosmography method.