1 Introduction

To solve the gauge hierarchy problem, the top quark partners with vectorlike couplings to the weak sector are predicted in many new physics (NP) scenarios beyond the Standard Model (SM), such as little Higgs models [1], extra dimensions [2], twin Higgs models [3], and composite Higgs models (CHMs) [4]. In these models, the contribution to the Higgs boson from the top quark loop could be canceled by the new vectorlike top partners (for a review, see [5]), and strategies for discovering the new top partners have been developed at both the Tevatron [6] and the LHC [7, 8]. In this work, we use the model-independent framework presented in Ref. [8] which only include the vectorlike top quark T with charge 2/3. At a center of mass energy of 13 TeV in Run 2, both the ATLAS and CMS Collaborations have presented searches for pair production of vectorlike top partners, and set limits in the range \(1.3-1.42\) TeV depending on their branching ratios [9,10,11,12,13,14,15,16,17,18]. Furthermore, the combination performed by ATLAS collaboration excluded the top partner masses up to 1.31 TeV [19].

So far, collider searches for a vectorlike top partner have mostly carried out under the assumption that it decays into Standard Model particles, namely, \(T\rightarrow bW\), \(T\rightarrow tZ\) and \(T\rightarrow th\). A huge cache of literature has built up regarding the phenomenology of the top partners [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. However, it is possible for vector-like top partner to decay exotically [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. The production of vectorlike top partners can be in pairs via the strong interaction, or singly in association with the SM bottom quarks via the electroweak (EW) interaction. Compared with the pair production process, single top partner production process is induced by electro-weak coupling, as shown in Fig. 1, which has a larger phase space and can be enhanced by the collinear effect from the light quark emitting a W-boson in high energy region [65]. On the other hand, the EW couplings of the T quarks to the SM third-generation quarks are highly model dependent, which determine the rates of the single T quark production modes. As a result, searches for singly produced top partners can be used to probe these EW couplings, which would serve a as a complementary channel to for future collider once the top partner is discovered and its mass determined.

Fig. 1
figure 1

The Feynman diagrams for the process \(pp \rightarrow T\bar{b}j\)

Full size image

In comparison with the existing searches for various decay modes, the \(h \rightarrow \gamma \gamma \) channel has a small cross section but has the great advantage that most QCD backgrounds are gone, such as done in Refs. [66,67,68,69,70,71]. The rough estimation by Backovic et al [44] has shown that it is challenging to observe the T quark with the diphoton decay channel at the 14 TeV LHC due to the small production cross section. In recent years, the proposed higher center-of-mass energy colliders have been discussed worldwide [72, 74, 76], such as High Energy LHC (HE-LHC) with 27 TeV c.m. energy [75] and Future Circular Collider in hadron-hadron mode (FCC-hh) with 100 TeV c.m. energy [76]. The authors of Ref. [77] have estimated the reach for discovering (or excluding) vectorlike quarks and determining their properties via the pair production process at the next generation of prototype hadron colliders, with a centre of mass energy of 33 and 100 TeV. In this work, we investigate the single top partner production process \(pp \rightarrow T\bar{b}j\) via the decay channel \(T\rightarrow t(\rightarrow b \ell \nu _{\ell })h( \rightarrow \gamma \gamma )\) in a simplified framework at the HE-LHC and FCC-hh.

This paper is arranged as follows. In Sect. 2, we briefly describe the simplified model and calculate the single top partner production cross section at the HE-LHC and FCC-hh. In Sect. 3, we discuss the observability of the top partner through the single production process \(pp \rightarrow T(\rightarrow th)\bar{b}j\) with the \(h\rightarrow \gamma \gamma \) decay channel. This section also includes the estimations for the signal and background, the simulations and the detector effects for HE-LHC and FCC-hh. Finally, we conclude and summarize our main results and findings in Sect. 4.

2 Top partner in the simplified model

2.1 Brief review of the simplified model

The simplified model consists of a vectorlike top partner T with the same electric charge and color as the SM top quark. In addition to their quark-like QCD and EM couplings via the usual covariant derivative recipe, the top partners can couple to SM quarks q and weak bosons \(V \in \{W, Z, H\}\), via new TqV vertices. Following the notation of Ref. [8], the relevant Lagrangian of the vectorlike top partner can be expressed as

$$\begin{aligned} \mathcal {L}= & {} \kappa _T\left\{ \sqrt{\frac{\zeta _i\xi ^{T}_{W}}{\Gamma ^0_{W}}} \frac{g}{\sqrt{2}} [\bar{T}_{L/R} W^+_\mu \gamma ^\mu d^{\,i}_{L/R}]\right. \nonumber \\&+ \sqrt{\frac{\zeta _i\xi ^{T}_{Z}}{\Gamma ^0_{Z}}} \frac{g}{2c_W} [\bar{T}_{L/R} Z_\mu \gamma ^\mu u^i_{L/R}] \nonumber \\&\left. - \sqrt{\frac{\zeta _i\xi ^{T}_{H}}{\Gamma ^0_{H}}} \frac{M_T}{v} [\bar{T}_{R/L} H u^i_{L/R}] \right\} + \text {h.c.} , \end{aligned}$$
(1)

where \(M_T\) is the mass of vectorlike top partners, \(c_W\) is the usual cosine of the weak mixing angle, \(v\simeq 246\) GeV and \(\Gamma ^0_V\) are functions of \(m_V/M_T\). \(\xi ^V\) parameters controlling the relative strengths of the V couplings to top partners, and \(\zeta _i\) parameters governing the mix of SM quark generations i in each coupling. \(\xi \) and \(\zeta \) are defined as \(\sum _{V} \xi ^{V} = 1\) and \(\sum _{i} \zeta _i = 1\), meaning \(\zeta _i\xi ^{V} = \text {BR}(T \rightarrow Vq_i)\) (for a detailed review, see [8]).

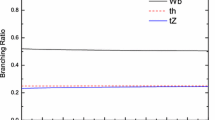
In this work, we consider the case that the top partners only coupling with the third-generation quarks and heavy bosons, and the branching ratio of T couple to the bosons are taken as \(Wb:Zb:Ht=2:1:1\). Thus there are only two free parameters: the top quark partner mass \(m_T\) and the coupling strength \(\kappa _{T}\) for a given top partner mass. Minimal extensions of the SM with one unique vectorlike quark representation where the vectorlike quark has large couplings are excluded by other constraints (such as EW precision tests or corrections to SM couplings) [8, 78]. However, the bounds may be weakened in more involved models: new physics, in the form of mixings either in the quark or bosonic sectors due to additional representations of vectorlike quarks or new gauge bosons or scalar fields, must contribute to generate the relations between couplings. As a model-independent analysis, we take the the coupling parameter \(\kappa _{T}\le ~0.3\).

2.2 The cross sections of single T

For the simulations of the HE-LHC and FCC-hh collider phenomenology, the model file of the singlet T quark [79] is implemented via the FeynRules package [80]. The cross sections are calculated at leading order (LO) using MadGraph5-aMC@NLO [81] with NNPDF23L01 PDFs [82], considering the renormalisation and factorisation scales to be \(\mu _R=\mu _F=m_T/2\). The numerical values of the input parameters are taken as follows [83]:

$$\begin{aligned} m_h&=125.1\mathrm{~GeV}, \quad m_t=172.9\mathrm{~GeV}, \quad m_W=80.379\mathrm{~GeV},\nonumber \\ m_Z&=91.1876\mathrm{~GeV}, \quad \alpha _{s}(m_Z)=0.1185,\nonumber \\ G_F&=1.166370\times 10^{-5}\ \mathrm{GeV}^{-2}. \end{aligned}$$
(2)
Fig. 2
figure 2

a The dependence of the cross sections for the process \(pp\rightarrow T\bar{b}j+\bar{T}bj\) on the T quark mass \(m_T\) at 14 TeV LHC, HE-LHC and FCC-hh with \(\kappa _{T}=0.1\); b the cross sections of top partners single production and pair production versus its mass at the FCC-hh

Full size image

In Fig. 2a, we show the dependence of the cross sections for the process \(pp\rightarrow T\bar{b}j+\bar{T}bj\) on the T quark mass \(m_T\) at the 14 TeV LHC, HE-LHC and FCC-hh for \(\kappa _{T}=0.1\). Compared the results at the 14 TeV LHC, one can see that the discovery potential for top partners would be increased largely with the higher collision energy at the HE-LHC and FCC-hh. In Fig. 2b we present the cross sections of single T production and pair production versus its mass at the FCC-hh. As the top partner mass grows, the cross section of single production decreases slower than that of pair production due to a larger phase space. Thus single T production can become the dominant production mechanism at the future high-energy pp colliders for high top partner masses. Obviously, the cross section of single \(T-\)quark production is proportional to the square of the WTb coupling strength \(\kappa _{T}\) for a given top partner mass.

3 Collider simulation and analysis

3.1 The signal-to-background analysis

The signals is mainly produced through the process

$$\begin{aligned} pp\rightarrow T\bar{b}(\rightarrow th)j \rightarrow t(\rightarrow bW\rightarrow b\ell ^{+} \nu _{\ell })h(\rightarrow \gamma \gamma ) \bar{b}j.\nonumber \\ \end{aligned}$$
(3)

where \(\ell = e, \mu \). Note that the analysis has included the charge-conjugate process. Because for equal values of the TZt and TWb couplings, the cross-section for Zt fusion is about one order of magnitude smaller than for Wb fusion [23] and thus can be neglected for this T-singlet search.

The final state for the signal is characterised by two photons, one lepton, one high-momentum b-jet and missing transverse energy from the undetected neutrino. Besides, the outgoing light quark in the process depicted in Fig. 1 often produces a jet in the forward region of the detector. We do not consider the second b-jet from the gluon splitting since this b-jet is typically of low energy and often falls outside the detector acceptance [18]. If several b-tagged jets are found, the jet with the highest transverse momentum is used. The main background processes include: the resonant backgrounds \(t\bar{t}h\) and thj in which the Higgs boson decays to diphotons, and the non-resonant backgrounds \(t\bar{t}\gamma \gamma \), \(tj\gamma \gamma \) and \(\gamma \gamma W^{\pm }jj\).

Note that the reducible backgrounds such as \(tjj\gamma \), \(t\bar{t}\gamma \) and \(t\bar{t}\gamma j\) can also be the sources of backgrounds with fake photons due to misidentified jets or electrons. By using the jet faking photon rate given in Ref. [84], we found that the cross section of \(tjj\gamma \) process with faked photon was found to be at least one order of magnitude smaller than the cross section of process without faked photon after applying the suitable cuts. Recently, the ATLAS collaboration searched for \(h\rightarrow \gamma \gamma \) channel signatures [85] and found that the overall \(\gamma j\) background is about a quarter of the pure diphoton background. These jet faking photon effects are not properly modeled in our MC simulations. Therefore, for simplicity, we add a faking photon background that is 1.25 times \(tj\gamma \gamma \) after selection cuts to the overall background.

The signal and background samples are generated at LO by using the Monte Carlo event generator MadGraph5-aMC@NLO [81], interfaced to Pythia 8.20 [86] for the parton showering. All produced jets are forced to be clustered using the FASTJET 3.2 [87] assuming the anti-\(k_{t}\) algorithm with a cone radius of \(R=0.4\) [88]. All event samples are fed into the Delphes 3.4.2 [89] with the default HE-LHC and FCC-hh detector card. For photon identification, the maximum of isolation efficiency is 95% with transverse momentum \(P_T> 10\) GeV and \(|\eta |<2.5\) at both the HE-LHC and the FCC-hh, and decreases to 80% for \(2.5<|\eta |<4\) at HE-LHC and for \(4<|\eta |<6\) at FCC-hh. Finally, event analysis is performed by using MadAnalysis5 [90].

Here it should be mentioned that we calculate the cross sections at LO for single T production for some benchmark masses with the couplings set to 0.1. The NLO predictions for single vectorlike quark production is studied in Ref. [91] and the results show that the NLO-to-LO cross section ratio being about 1 for heavy top partner masses. We use the narrow-width T partner assumptionFootnote 1 which is valid for \(\kappa _{T}\le 0.3\) [10]. For the SM background process \(pp\rightarrow t\bar{t}h\), we rescale the LO cross sections to the corresponding higher order QCD results with the K-factor, i.e., \(K=1.3\) [95,96,97]. For the sake of simplicity, others SM background processes, we have rescaled their cross sections by a K-factor of 1.5. This approximation does not have a significant impact on our derived sensitivities. We point out that in general variations of the above branching ratio is possible due to the presence of top partners in the fermionic loop that appears in \(h\rightarrow \gamma \gamma \). However, as a model-independent analysis, we assume that the presence of vector-like top partners in \(h\rightarrow \gamma \gamma \) loop would not change the SM branching ratio value of 0.23%.

In order to identify objects, we chose the basic cuts at parton level for the signals and SM backgrounds as follows:

$$\begin{aligned} \begin{aligned}&\mathrm {HE-LHC:} p_{T}^{\ell /\gamma }>~25~\text {GeV},&\quad p_{T}^{j/b}>~30~\text {GeV},\\&\quad |\eta _{\ell /\gamma /b}|<~2.5, |\eta _{j}|<~5,\\&\quad \mathrm {FCC-hh:} p_{T}^{\ell /\gamma }>~25~\text {GeV},&\quad p_{T}^{j/b}>~30~\text {GeV},\\&\quad |\eta _{\ell /\gamma /b}|<~3, |\eta _{j}|<~6,\\ \end{aligned} \end{aligned}$$
(4)

where \(\Delta R=\sqrt{\Delta \Phi ^{2}+\Delta \eta ^{2}}\) is the separation in the rapidity-azimuth plane, \(p_{T}^{\gamma ,\ell , b, j}\) are the transverse momentum of photons, leptons, b-jets and jets.

Fig. 3
figure 3

Normalised distributions for the signals and SM backgrounds at LO for the HE-LHC at 27 TeV

Full size image

In Fig. 3, we plot some differential distributions for signals and SM backgrounds at the HE-LHC, such as the transverse momentum distributions of the two photons (\(p_{T}^{\gamma _{1}}, p_{T}^{\gamma _{2}}\)), the separations \(\Delta R_{\gamma \gamma }\), the invariant mass distributions of the two photons, \(M_{\gamma _{1}\gamma _{2}}\), and the transverse mass distribution for the top quark and the top partners ( system). Here the transverse masses of the top quark and the top partner are respectively defined as [98]

(5)
(6)

where \(\mathbf {p}_{T,\ell }\), \(\mathbf {p}_{T,b}\) and \(\mathbf {p}_{T,\gamma }\) are the transverse momenta of the charged leptons, b quarks and photons, respectively, and is the missing transverse momentum determined by the negative sum of visible momenta in the transverse direction.

One can see that the two photons in the signal and the resonant backgrounds have the harder \(p_{T}\) spectrum than those in the non-resonant backgrounds. Because the Higgs boson is highly boosted for the heavy top partner, \(\Delta R_{\gamma _{1},\gamma _{2}}\) tends to be small in signal events. While \(\Delta R_{\gamma _{1},\gamma _{2}}\) in non-resonant background process would be quite random because they mainly come from charged particle radiation. Here we need to emphasize that the cone size used in photon isolation is \(\Delta R = 0.4\), and thus the signal event with two final state photons being too close to each other will be discarded. The Higgs boson in resonant background process is generally not too boosted, and thus the two photons from the decay of the Higgs boson tend to go back to back. Furthermore, the signal and the resonant backgrounds have the diphoton invariant-mass peak at the mass of Higgs boson. Besides, the cut on the transverse mass of the top candidate is needed since the lepton and b-jet are assumed to originate from the leptonic decaying top quark. Furthermore, the transverse mass distribution has an end point around the top partner mass in the signal, which can be used to further remove the SM background.

According to the above analysis, we can impose the following set of cuts.

  • Cut 1  There are only one isolated lepton, at least two jets and one of which must be b-tagged. If several b-tagged jets are found, the jet with the highest \(p_T\) is used. Besides, the light untagged jet is required to have \(2.5< \mid \eta _{j}\mid < 6\), which is referred to as forward jet.

  • Cut 2  Exactly two photons and the leading (sub-leading) photons with \(p_{T}>200~(60) \mathrm{~GeV}\), the distance between two photons lies in \(\Delta R_{\gamma _{1},\gamma _{2}}< 1.0\).

  • Cut 3  The invariant mass of the diphoton pair to be in the range \(m_h\pm 5\) GeV.

  • Cut 4  The transverse mass of the top quark is required as \(100 ~\mathrm{GeV}< M_T^{b\ell } < 200 \mathrm{GeV}\).

  • Cut 5  The transverse mass of the top partner is required as \(M_T^{\gamma _{1}\gamma _{2}b\ell } > 1000 \mathrm{GeV}\).

Table 1 The cut flow of the cross sections (in \(\times 10^{-3}\) fb) for the signals and SM backgrounds at the HE-LHC with \(\kappa _{T}=0.1\)
Full size table
Table 2 The cut flow of the cross sections (in \(\times 10^{-3}\) fb) for the signals and SM backgrounds at the FCC-hh with \(\kappa _{T}=0.1\)
Full size table
Fig. 4
figure 4

The exclusion limit (at \(95\%\) CL) (left) and discovery prospects (at \(5\sigma \)) (right) contour plots for the signal in \(\kappa _{T}-m_{T}\) planes at HE-LHC with integral luminosity 15 ab\(^{-1}\) and at the FCC-hh with integral luminosity 30 ab\(^{-1}\)

Full size image
Fig. 5
figure 5

The 95% CL excluded and \(5\sigma \) observed cross section times BR rates for the single-T signal as a function of the vectorlike top partner mass \(m_T\) at the HE-LHC (left) and FCC-hh (right). Here we consider the systematic uncertainty as \(\delta =10\%\)

Full size image

In Tables 1 and 2, we show the cut flow of the signal and background cross sections after each selection for \(\kappa _{T}=0.1\) and three benchmark top partner masses. One can see that the backgrounds are suppressed very efficiently after imposing all listed cuts at the HE-LHC and FCC-hh.

3.2 Sensitivity at the HE-LHC and FCC-hh

Following Ref. [99], we use the following expression to estimate the expected discovery and exclusion significance, \(Z_\text {disc}\) and \(Z_\text {excl}\):

$$\begin{aligned} \begin{aligned} Z_\text {disc}&= \sqrt{2\left[ (s+b)\ln \left( \frac{(s+b)(1+\delta ^2 b)}{b+\delta ^2 b(s+b)}\right) - \frac{1}{\delta ^2 }\ln \left( 1+\delta ^2\frac{s}{1+\delta ^2 b}\right) \right] } \\ Z_\text {excl}&=\sqrt{2\left[ s-b\ln \left( \frac{b+s+x}{2b}\right) - \frac{1}{\delta ^2 }\ln \left( \frac{b-s+x}{2b}\right) \right] - \left( b+s-x\right) \left( 1+\frac{1}{\delta ^2 b}\right) }, \end{aligned} \end{aligned}$$
(7)

with

$$\begin{aligned} \begin{aligned} x=\sqrt{(s+b)^2- 4 \delta ^2 s b^2/(1+\delta ^2 b)}. \end{aligned} \end{aligned}$$
(8)

Here, s and b stand for the numbers of signal and SM background events after cuts where the integrated luminosity are take as 15 ab\(^{-1}\) at HE-LHC and 30 ab\(^{-1}\) at FCC-hh, respectively. \(\delta \) is the percentage systematic error on the SM background estimate. In this work we choose two cases: no systematics (\(\delta =0\)) and a systematic uncertainty of \(\delta =10\%\) for both the HE-LHC and FCC-hh.

In Fig. 4, the exclusion limit at \(95\%\) CL and \(5\sigma \) discovery prospects lines are drawn as a function of the top partner mass and coupling strength \(\kappa _{T}\). From this figure we can see that the numerical results at the FCC-hh are more sensitive to the value of systematic error than those at the HE-LHC, this is because the larger SM background events at the FCC-hh. For \(\delta =0\) and \(\kappa _{T}=0.3\), top partner can be probed at \(5\sigma \) level with mass about 1.5 TeV at the HE-LHC and up to 2.1 TeV at the FCC-hh thorough the single production followed the \(T\rightarrow th\) decay channel, while the 95% exclusion limits for top partner mass can be reached at about 1.7 TeV at HE-LHC and 2.6 TeV at the FCC-hh. And to estimate the impact of systematic uncertainty, for \(\delta =10\%\) and \(\kappa _{T}=0.3\), we find that top partner mass can be reached at about 1.75 TeV at the FCC-hh, while the exclusion limit for top partner mass to be about 2.3 TeV at the FCC-hh.

Because our results are obtained from fixed branching ratio of \(T\rightarrow th\) in a simplified model, e.g., \(BR(T\rightarrow th)\simeq 0.25\%\), while the latter for different decay channels can be altered in other models, in Fig. 5, we plot the projected sensitivity in terms of the production cross section times branching ratio [\(\sigma _T\times \mathrm{BR}(T\rightarrow th)\)] as a function of the vectorlike top partner mass. We find that, at the HE-LHC with the integrated luminosity 15 ab\(^{-1}\), single-T production and decay rates such that \(\sigma _T\times \mathrm{BR}(T\rightarrow th)\sim 52{-}142\) fb could be discovered for \(m_T\in [1.3, 2.0]\) TeV, while the cross sections \(\sim 20{-}55\) fb will be excluded. At the FCC-hh with the integrated luminosity 30 ab\(^{-1}\), \(\sigma _T\times \mathrm{BR}(T\rightarrow th)\sim 0.3{-}1.8\) pb could be discovered for \(m_T\in [1.3, 2.5]\) TeV, while the cross sections \(\sim 0.1{-}0.6\) pb will be excluded.

It should be mentioned that our analyses have not included pileup effects. In a fully realistic analysis it is important to include the effects from pileup and the effects of applying the appropriate pileup removal technique [100,101,102,103], which is beyond the scope of this paper.

4 Conclusion

The vectorlike top partners play a central role in many NP models which attempt to address the hierarchy problem. In this paper, we have studied the prospects of observing single top partner production at future HE-LHC and FCC-hh via the \(T\rightarrow th\) decay channel, followed by a leptonic top decay and \(h\rightarrow \gamma \gamma \). We performed a model-independent analysis of this process within a simplified model which only includes two free parameters, the top partner mass \(m_T\) and the EW coupling constant \(\kappa _{T}\). The discovery prospects at \(5\sigma \) and exclusion limits at \(95\%\) CL in the parameter plane of the two variables \(m_T\) and \(\kappa _{T}\) were obtained at HE-LHC with integral luminosity 15 ab\(^{-1}\) and at the FCC-hh with integral luminosity 30 ab\(^{-1}\), respectively. For \(\delta =0\) and \(\kappa _{T}=0.3\), top partner can be probed at \(5\sigma \) level with mass 1.5 TeV at the HE-LHC and up to 2.1 TeV at the FCC-hh thorough the single production followed the \(T\rightarrow th\) decay channel, while the 95% exclusion limits for top partner mass can be reached at about 1.7 TeV at HE-LHC and 2.6 TeV at the FCC-hh. For \(\delta =10\%\) and \(\kappa _{T}=0.3\), top partner mass can be reached at about 1.75 TeV at the FCC-hh, while the exclusion limit for top partner mass to be about 2.3 TeV at the FCC-hh.

For some NP models where the top quark partners have couplings to the third generation of SM quarks, we presented the projected sensitivity in terms of the single production cross section times branching ratio for the \(T\rightarrow th\) channel. The numerical results show that, at the HE-LHC with the integrated luminosity 15 ab\(^{-1}\), \(\sigma _T\times \mathrm{BR}(T\rightarrow th)\sim 52{-}142\) fb could be discovered for \(m_T\in [1.3, 2.0]\) TeV, while the cross sections \(\sim 20{-}55\) fb will be excluded. If we take the integrated luminosity of the FCC-hh as 30 ab\(^{-1}\), \(\sigma _T\times \mathrm{BR}(T\rightarrow th)\sim 0.3-1.8\) pb could be discovered for \(m_T\in [1.3, 2.5]\) TeV, while the cross sections \(\sim 0.1{-}0.6\) pb will be excluded.