Leaks of CP violation in the real two-Higgs-doublet model

Abstract

We discuss the $Z_2$ symmetric two-Higgs-doublet model with a real soft-breaking term (real 2HDM). We explain in detail why it is not tenable to assume CP conservation in the scalar sector to keep the dimension two term real, while CP is violated by the dimension four Yukawa couplings. We propose the calculation of the infinite tadpole of the (would-be) pseudoscalar neutral scalar. We construct a simple toy model with the same flaws, where the unrenormalizable infinity is easier to calculate. We then consider the same tadpole in the real 2HDM. We spearhead this effort focusing on diagrams involving solely bare quantities. This involves hundreds of Feynman three-loop diagrams that could feed the CP violation from the quark into the scalar sector, and is only possible with state of the art automatic computation tools. Remarkably, some intermediate results agree when using three independent derivations, including the peculiar cancellation of the leading pole divergence due to a subtle interplay between masses and the Jarlskog invariant, which we calculate analytically. The calculation is not complete however, since the full two-loop renormalization of the real 2HDM is not yet available in the literature. Still, we argue convincingly that there is an irremovable infinity.

1 Introduction

The exact implementation of the symmetry breaking sector of the gauge theory describing fundamental particles is one of the most interesting open problems. In particular, the recent discovery at LHC of a $125\, \text {GeV}$ fundamental scalar ($h_{125}$) [1, 2] begs the question of how many fundamental scalars there are in Nature. The Standard Model (SM) contains one single scalar doublet, but there is no fundamental requirement for this choice.

Indeed, there have been countless studies on models with two or more Higgs doublets; for reviews see [3,4,5] and references therein. The most studied model includes two Higgs doublets (2HDM) with a $Z_2$ symmetry, softly broken by a real parameter, with the additional requirement that the vacuum expectation values (vev) are taken as real. As such, the scalar sector by itself is CP conserving. The $Z_2$ symmetry is carried over to the fermions in such a way that only one scalar couples to all fermions of a given charge. The crucial point is that the experimentally observed CP violation [6] is accounted for by complex Yukawa couplings. This is sometimes referred to as the “real 2HDM”, because the soft $Z_2$ breaking parameter is taken as real. Remarkably, this most prevalent model can suffer from theoretical inconsistencies regarding renormalization, a fact that is mostly ignored.¹ This is the problem we address in detail here.

The paper is organized as follows. In Sect. 2, we discuss the inconsistency of requiring CP conservation in the potential of the real 2HDM, while allowing for CP violation elsewhere. We argue that, at sufficient high order in perturbation theory, there could be divergences in CP-violating one-point and two-point functions that one can not remove by the counterterms provided by the theory. We show in Sect. 3 that this is precisely what happens in a toy model suffering from the same inconsistency as the real 2HDM. Then, in Sect. 4, we present the result for the leading pole of the three-loop one-point function of the alleged CP-odd physical field of the real 2HDM. We describe in Sect. 5 the details of the different steps involved in the three-loop calculation. In Sect. 6, we summarize our conclusions.

2 Shortcomings of the real 2HDM

Let us consider a $SU(2)_L \otimes U(1)_Y$ gauge theory with two Higgs-doublets $\varPhi _a$, with the same hypercharge 1/2, and with real vacuum expectation values (vevs)

$$\begin{aligned} \langle \varPhi _a \rangle = \left( \begin{array}{c} 0\\ v_a/\sqrt{2} \end{array} \right) ,\quad (a=1,2), \end{aligned}$$

(1)

with $v = \sqrt{v_1^2 + v_2^2} = 246~\text {GeV}$. Our definition for the charge is $Q=T_3 + Y$, and we introduce the angle $\beta$ through

$$\begin{aligned} \tan {\beta }= v_2/v_1. \end{aligned}$$

(2)

The most general 2HDM scalar potential may be written as

$$\begin{aligned} V_H= & {} m_{11}^2 \varPhi _1^\dagger \varPhi _1 + m_{22}^2 \varPhi _2^\dagger \varPhi _2 - \left[ m_{12}^2 \varPhi _1^\dagger \varPhi _2 + {\mathrm {H.c.}} \right] \nonumber \\&+\, \tfrac{1}{2} \uplambda _1 (\varPhi _1^\dagger \varPhi _1)^2 + \tfrac{1}{2} \uplambda _2 (\varPhi _2^\dagger \varPhi _2)^2 + \uplambda _3 (\varPhi _1^\dagger \varPhi _1) (\varPhi _2^\dagger \varPhi _2) \nonumber \\&+\, \uplambda _4 (\varPhi _1^\dagger \varPhi _2) (\varPhi _2^\dagger \varPhi _1) + \left[ \tfrac{1}{2} \uplambda _5 (\varPhi _1^\dagger \varPhi _2)^2 + {\mathrm {H.c.}} \right] \nonumber \\&+ \left[ \uplambda _6 (\varPhi _1^\dagger \varPhi _1) (\varPhi _1^\dagger \varPhi _2) + \uplambda _7 (\varPhi _2^\dagger \varPhi _2) (\varPhi _1^\dagger \varPhi _2) + {\mathrm {H.c.}} \right] , \end{aligned}$$

(3)

where “H.c.” stands for Hermitian conjugation. The coefficients $m_{11}^2$, $m_{22}^2$, and $\uplambda _1,\ldots ,\uplambda _4$ are real while $m_{12}^2$, $\uplambda _5$, $\uplambda _6$ and $\uplambda _7$ may be complex.

When extending this model to the fermion sector, one finds flavour changing neutral scalar interactions, which are very strongly constrained by experiments on neutral meson systems. This problem can be solved by imposing a $Z_2$ symmetry: $\varPhi _1 \rightarrow \varPhi _1$; $\varPhi _2 \rightarrow - \varPhi _2$ [8, 9]. If the symmetry is exact, then the quadratic term $m_{12}^2 = 0$, and the quartic terms $\uplambda _6 = \uplambda _7=0$. (The quartic term $\uplambda _5$ can then be made real by a simple rephasing of $\varPhi _2$.) This has the consequence that the model has no decoupling limit. That is, one cannot make arbitrarily large the masses of the new particles resultant from the presence of the second scalar doublet, thus approaching smoothly the SM limit. Such a decoupling is a desirable feature, especially since the couplings probed by current LHC data are consistent with the SM predictions, within errors of order 20% [10]. Decoupling is recovered by reintroducing $m_{12}^2 \ne 0$ [11], which, because it breaks softly the $Z_2$ symmetry, does not affect the renormalizability of the theory.

Most articles addressing this model then make the choice that $m_{12}^2$ and $\uplambda _5$ are both real and the vevs are real, arguing that CP conservation in the scalar sector has been imposed (choice 1). Then one would proceed to discuss the various implementations of the $Z_2$ symmetry in the fermion sector, and perform a variety of fits to experiment. Among these, one must fit the well measured CP violation with origin in the Cabibbo–Kobayashi–Maskawa (CKM) matrix [12, 13], accommodated by the complex Yukawa couplings (choice 2). The problem is that choice 1 and choice 2 are incompatible.

Indeed, either one applies the CP symmetry to the whole Lagrangian, in which case the Yukawa couplings are real and one cannot account for the observed CP violation; or, else, one does not apply CP symmetry anywhere, allowing the Yukawa couplings to be complex, but then allowing also for a complex $m_{12}^2$.² Said otherwise, requiring complex CKM and excluding the parameter $\text {Im}\left( m_{12}^2\right)$ leads to a non-renormalizable theory. At sufficiently high loop level, the CP violation in the quark sector will leak into the scalar sector, through a divergent contribution that cannot be absorbed by a $\text {Im}\left( m_{12}^2\right)$ counterterm, which was absent from the theory from the start.

So why do all articles fitting the real 2HDM “model” to experiment ignore this problem? Because the divergent contribution can only be shown to happen in at least three loops. However, precisely because they are divergent, the problem cannot be ignored if one wishes to use a theoretically sound model.

Given the fact that the problem seems to occur due to (the lack of) $\text {Im}\left( m_{12}^2\right)$, one could be tempted to assume that such a dimension two operator could not affect renormalizability. And indeed, it cannot affect renormalizability due to its soft-breaking of the $Z_2$ symmetry. But the problem with CP symmetry being invoked is not that it is broken by $m_{12}^2$ (real or complex); rather, it is (hard) broken by the dimension four Yukawa couplings.

It is true that one can look at the real 2HDM as a limiting case of the $Z_2$ 2HDM, softly broken by a complex $m_{12}^2$. This model is known as the complex 2HDM (C2HDM) and has been studied in detail; see, for example [14,15,16,17,18,19,20,21,22,23]. In that case, one can choose any tree-level values for the parameters, and, in particular, set $\text {Im}\left( m_{12}^2 \right) = 0$ at tree level. In that context, setting $\text {Im}\left( m_{12}^2 \right) = 0$ at tree level, does not constitute a problem, since the theory does have its counterterm and is renormalizable. Is this the same as the real 2HDM? No: setting $\text {Im}\left( m_{12}^2 \right) = 0$ in the C2HDM means that we are studying a very specific corner of tree-level parameter space of a more general model. The real 2HDM, where there is no $\text {Im}\left( m_{12}^2 \right)$ nor its counterterm, is not a consistent model.

There is a more physical way to state the non renormalization problem. In any 2HDM there are three neutral scalars ($h_1$, $h_2$, and $h_3$), and a pair of charged scalars $H^\pm$. Typically, it is assumed that the lightest neutral scalar ($h_1$) coincides with the 125GeV particle found at LHC.³ In the real 2HDM, the (proclaimed) lack of CP violation in the scalar sector, leads to the separation of the three neutral scalars into one single CP odd scalar (A) and two CP even (usually denoted by h for the lightest and H for the heaviest). If the CKM CP violation indeed seeps into the scalar sector, then there should be divergent contributions to the h-A and H-A two-point functions. There will also be divergent contributions to the A tadpole. Since such terms are absent from the real scalar sector at tree level, there are no counterterms to absorb those infinities, and the theory is formally inconsistent.

2.1 The scalar sector

We start from the scalar sector of the real 2HDM

$$\begin{aligned} V_r&=\, m_{11}^2 \varPhi _1^\dagger \varPhi _1 + m_{22}^2 \varPhi _2^\dagger \varPhi _2 - m_{12}^2 \left[ \varPhi _1^\dagger \varPhi _2 + \varPhi _2^\dagger \varPhi _1 \right] \nonumber \\&+\, \tfrac{1}{2} \uplambda _1 (\varPhi _1^\dagger \varPhi _1)^2 + \tfrac{1}{2} \uplambda _2 (\varPhi _2^\dagger \varPhi _2)^2 + \uplambda _3 (\varPhi _1^\dagger \varPhi _1) (\varPhi _2^\dagger \varPhi _2) \nonumber \\&+\, \uplambda _4 (\varPhi _1^\dagger \varPhi _2) (\varPhi _2^\dagger \varPhi _1) + \tfrac{1}{2} \uplambda _5 \left[ (\varPhi _1^\dagger \varPhi _2)^2 + (\varPhi _2^\dagger \varPhi _1)^2 \right] , \nonumber \\ \end{aligned}$$

(4)

with all parameters real, and we parametrize the fields in the original basis as

$$\begin{aligned} \varPhi _1= & {} \left( \begin{array}{c} c_\beta G^+ - s_\beta H^+\\ * \tfrac{1}{\sqrt{2}} \left[ v c_\beta + (c_\alpha H - s_\alpha h) + i (c_\beta G^0 - s_\beta A) \right] \end{array} \right) , \nonumber \\ \varPhi _2= & {} \left( \begin{array}{c} s_\beta G^+ + c_\beta H^+\\ \tfrac{1}{\sqrt{2}} \left[ v s_\beta + (s_\alpha H + c_\alpha h) + i (s_\beta G^0 + c_\beta A) \right] \end{array} \right) . \end{aligned}$$

(5)

Throughout $c_\theta =\cos {\theta }$ and $s_\theta =\sin {\theta }$, for whatever angle $\theta$ appears as a sub-index. Comparing (1) and (5), we recognize the choice $v_1 = v c_\beta$ and $v_2= v s_\beta$. With that choice, $G^+$ and $G^0$ will be massless and $H^+$ is the physical charged scalar of mass $m_{H^\pm }^2$.⁴ These facts are confirmed by substituting (5) in (4). Performing the expansion, one sees that there is no linear term in A (and, thus, no possibility to absorb any infinities that might appear in A tadpoles at loop level), nor are there any quadratic hA or HA terms (and, similarly, no possibility to absorb any infinities that might appear in the corresponding two-point functions at loop level).

The expansion does contain linear (tadpole) terms for H ($t_H$) and h ($t_h$). Equating these tadpoles to zero, one obtains the same conditions that one would obtain by finding the stationarity conditions $\partial V_r/\partial v_1=0$ and $\partial V_r/\partial v_2=0$ directly from (4). Those two equations can be solved for $m_{11}^2$ and $m_{22}^2$, which are then substituted back into the expression for the potential. After this substitution using the vacuum conditions, there are no quadratic $G^0G^0$ and $G^+ G^-$ terms. There are also no mixed $G^0 A$ or $G^\pm H^\mp$ terms, meaning that as expected $G^0$ and $G^+$ are Goldstone bosons, while A and $H^+$ are already mass eigenstates. One finds quadratic terms of the type HH, hh, and hH. The angle $\alpha$ is chosen to kill the latter, meaning that h and H are the physical fields. Using $v=246~\text {GeV}$ and $m_h=125~\text {GeV}$, the scalar sector of the real 2HDM is parametrized by six further parameters: the mixing angles $\alpha$ and $\beta$; the masses $m_H$, $m_A$, $m_{H^\pm }$; and the soft-breaking parameter $m_{12}^2= \text {Re}\left( m_{12}^2\right)$.

2.2 CP violation from the CKM matrix

In the SM and in the real 2HDM, CP violation arises from the complex Yukawa couplings. When the quark fields are rotated into their mass basis, all CP violation phases are contained in the CKM matrix [12, 13]. But, each quark field can still be rephased at will, thus moving the CP violating phase around the various entries of the CKM matrix. The only rephasing invariant quantity is [29,30,31]

$$\begin{aligned} I^{\alpha i}_{\beta j} = \text {Im}\left( V_{\alpha i} V_{\beta j} V_{\alpha j}^*V_{\beta i}^*\right) , \end{aligned}$$

(6)

where $\alpha \ne \beta$ and $i \ne j$. We use the notation of [32], where Greek letters $\alpha , \beta , \gamma , \dots$ refer to up-type quarks $u_\alpha = u, c, t$, while Roman letters $i, j, k, \dots$ refer to down-type quarks $d_i = d, s, b$. There are nine distinct four quark combinations with different flavours: (ds), (db), and (sb) for the down-type quarks times the three for up-type quarks: (uc), (ut), and (ct). Using the unitarity of the CKM matrix, the following symmetries hold

$$\begin{aligned} I^{\alpha i}_{\beta j} = I^{\beta j}_{\alpha i} = - I^{\alpha j}_{\beta i} = - I^{\beta i}_{\alpha j}, \end{aligned}$$

(7)

showing that indeed there is only one independent CP violating quantity. The antisymmetry with respect to interchange of same quark-type indices is easiest to see in the form

$$\begin{aligned} I^{\alpha i}_{\beta j} = J\, \sum _{\gamma , k} \epsilon _{\alpha \beta \gamma }\, \epsilon _{i j k}, \end{aligned}$$

(8)

where J is the Jarlskog invariant [29,30,31], defined for example as $J=I^{ud}_{cs}$. Notice that $I^{ud}_{cs} \ne 0$ even though only quarks from the first two families are involved. This does not contradict the fact that there would be no CP violating phase in the SM if there existed only two families of quarks. The fact that the CKM matrix is $3 \times 3$ unitary (and, thus, has one irremovable complex phase) is built into Eq. (8). Nevertheless, in CP violating processes with no external quarks (and, thus, a quark loop), the appearance of four CKM (V) factors can only occur in diagrams at the three loop level and above.

As emphasized by Pospelov and Khriplovich [33] and by Booth [34] in the context of the electric dipole moments (edm) of the W and the electron, the antisymmetry of $I^{\alpha i}_{\beta j}$ is very powerful. Any CP violating amplitude from a fermion box diagram will appear as the product $I^{\alpha i}_{\beta j}$ with some amplitude

$$\begin{aligned} {\mathcal {A}}(m_{u_\alpha },m_{u_\beta },m_{d_i},m_{d_j}). \end{aligned}$$

(9)

When all contributions are summed over ($\alpha$, $\beta$, i, and j), all terms in ${\mathcal {A}}(m_{u_\alpha },m_{u_\beta },m_{d_i},m_{d_j})$ symmetric under $\alpha \leftrightarrow \beta$, or $i \leftrightarrow j$ will not contribute. A much more involved analysis along these lines was used in [33, 34] to show that the SM electroweak contributions to the electric dipole moments of the W and the electron vanish to two-loop and three-loop approximation, respectively.

3 A theoretically unsound toy model

To better illustrate our claim, we consider here a toy model that suffers from the same inconsistency as the real 2HDM. In both models, CP conservation is enforced in a particular sector of an otherwise CP violating theory. As a consequence, CP violating radiative effects end up contaminating the alleged CP conserving sector, thus leading to divergences that cannot be absorbed by the counterterms. The major feature of our toy model is that such divergences show up immediately at one-loop order. Therefore, it constitutes a simple materialization of the same theoretical pathology that we claim to be present at three-loop or above in the real 2HDM.

The present model is inspired in a model by Pilaftsis [35], which, however, does not suffer from the flaw we wish to point out. Consider two Abelian gauge symmetries $U(1)_Q$ and $U(1)_B$, with gauge bosons $A_{\mu }$ and $B_{\mu }$, respectively. Suppose also four complex scalars, $\varPhi _1$, $\varPhi _2$, $\chi _L$ and $\chi _R$, with charges

$$\begin{aligned}&Q(\varPhi _1) = 0, \, Q(\varPhi _2) = 0, \, Q(\chi _L) = 1, \, Q(\chi _R) = 1, \end{aligned}$$

(10)

$$\begin{aligned}&B(\varPhi _1) = 1, \, B(\varPhi _2) = 1, \, B(\chi _L) = -\dfrac{1}{5}, \, B(\chi _R) = \dfrac{4}{5},\nonumber \\ \end{aligned}$$

(11)

where Q and B represent the conserved charges of $U(1)_Q$ and $U(1)_B$, respectively. A discrete symmetry D is imposed on the fields, under which:

$$\begin{aligned} \varPhi _1 {\mathop {\rightarrow }\limits ^{D}} - \varPhi _1, \ \ \varPhi _2 {\mathop {\rightarrow }\limits ^{D}} \varPhi _2, \ \ \chi _L {\mathop {\rightarrow }\limits ^{D}} - \chi _L, \ \ \chi _R {\mathop {\rightarrow }\limits ^{D}} \chi _R. \end{aligned}$$

(12)

However, D is allowed to be softly broken. The complete renormalizable Lagrangian can then be written in four terms,

$$\begin{aligned} {\mathcal {L}} = {\mathcal {L}}_{kin} + {\mathcal {L}}_{\varPhi } + {\mathcal {L}}_{\chi } + {\mathcal {L}}_{\varPhi \chi }, \end{aligned}$$

(13)

where ${\mathcal {L}}_{kin}$ represents the kinetic terms⁵ and

$$\begin{aligned} - {\mathcal {L}}_{\varPhi }= & {} \mu _1^2 \varPhi _1^* \varPhi _1 + \mu _2^2 \varPhi _2^* \varPhi _2 + \mu ^2 \varPhi _1^* \varPhi _2 + (\mu ^2)^* \, \varPhi _2^* \varPhi _1 \nonumber \\&+ \uplambda _1 {\left( \varPhi _1^{*} \varPhi _1 \right) }^2 + \uplambda _2 {\left( \varPhi _2^{*} \varPhi _2 \right) }^2 + \uplambda _{34} \, \varPhi _1^{*} \varPhi _1 \varPhi _2^{*} \varPhi _2 \nonumber \\&+ \uplambda _5 { \left( \varPhi _1^{*} \varPhi _2 \right) }^2 + \uplambda _5^* {\left( \varPhi _2^{*} \varPhi _1 \right) }^2, \end{aligned}$$

(14a)

$$\begin{aligned} - {\mathcal {L}}_{\chi }= & {} m_L^2 \, \chi _L \chi _L^* + m_R^2 \, \chi _R \chi _R^* + \rho _1 (\chi _L^* \chi _L)^2 \nonumber \\&+ \rho _2 (\chi _R^* \chi _R)^2 + \rho _{34} \, \chi _L^* \chi _L \chi _R^* \chi _R, \end{aligned}$$

(14b)

$$\begin{aligned} - {\mathcal {L}}_{\varPhi \chi }= & {} f_1 \, \varPhi _1 \chi _L \chi _R^* + f_1^* \, \varPhi _1^* \chi _L^* \chi _R + f_2 \, \varPhi _2 \chi _L \chi _R^* \nonumber \\&+ f_2^* \, \varPhi _2^* \chi _L^* \chi _R + g_1 \, \varPhi _1^{*} \varPhi _1 \chi _L^* \chi _L + g_2 \, \varPhi _2^{*} \varPhi _2\chi _L^* \chi _L \nonumber \\&+ \, g_3 \, \varPhi _1^{*} \varPhi _1 \chi _R^* \chi _R + \, g_4 \, \varPhi _2^{*} \varPhi _2 \chi _R^* \chi _R. \end{aligned}$$

(14c)

The parameters $\mu ^2$, $\uplambda _5$, $f_1$ and $f_2$ are in general complex, while the remaining ones are real by construction. The terms involving $\mu ^2$ and $f_2$ break the symmetry D softly. It is easy to show that the conditions for CP conservation are:

$$\begin{aligned} \text {Im} \left[ \mu ^2 \, f_1 \, f_2^* \right]= & {} 0, \end{aligned}$$

(15a)

$$\begin{aligned} \text {Im} \Big [ \uplambda _5 \, f_1^2 \,(f_2^*)^2 \Big ]= & {} 0, \end{aligned}$$

(15b)

$$\begin{aligned} \text {Im} \Big [ \uplambda _5^* \, (\mu ^2)^2 \Big ]= & {} 0. \end{aligned}$$

(15c)

Mimicking the usual real 2HDM treatment, we take $\langle \varPhi _1 \rangle$ and $\langle \varPhi _2 \rangle$ real and parametrize

$$\begin{aligned} \varPhi _1= & {} \tfrac{1}{\sqrt{2}} \left( v_1 + H_1 + i A_1 \right) , \end{aligned}$$

(16a)

$$\begin{aligned} \varPhi _2= & {} \tfrac{1}{\sqrt{2}} \left( v_2 + H_2 + i A_2 \right) , \end{aligned}$$

(16b)

where $v_1$, $v_2$ are real and non-negative, and $H_1$, $H_2$, $A_1$, and $A_2$ are real fields. The vevs $v_1$ and $v_2$ break spontaneously the gauge symmetry $U(1)_B$. Recall that $\mu ^2$, $\uplambda _5$, $f_1$, $f_2$ are in general complex.

But suppose we force CP to be conserved in ${\mathcal {L}}_{\varPhi }$ by the ad-hoc imposition that $\mu ^2$ and $\uplambda _5$ are real. This we will do in the following. It will lead to irremovable divergences at one-loop, as we now show.

We start by determining the minimization (or tadpole) equations. These are:⁶

$$\begin{aligned} 0= & {} t_{H_1} := \dfrac{\partial {\mathcal {L}}_{\varPhi }}{\partial H_1}\bigg |_{< >=0} \nonumber \\= & {} -v_1 \left( \mu _1^2 + \dfrac{v_2}{v_1} \mu ^2 + v_1^2 \uplambda _1 + \dfrac{1}{2} v_2^2 \uplambda _{34} + v_2^2 \, \uplambda _5\right) , \end{aligned}$$

(17a)

$$\begin{aligned} 0= & {} t_{H_2} := \dfrac{\partial {\mathcal {L}}_{\varPhi }}{\partial H_2}\bigg |_{< >=0} \nonumber \\= & {} -v_2 \left( \mu _2^2 + \dfrac{v_1}{v_2} \mu ^2 + v_2^2 \uplambda _2 + \dfrac{1}{2} v_1^2 \uplambda _{34} + \, v_1^2 \, \uplambda _5\right) , \end{aligned}$$

(17b)

where $t_{H_1}, t_{H_2}$ represent the tree-level tadpoles for $H_1$, $H_2$, respectively, and $< >=0$ means that the expectation values of all fields on the right hand side of Eqs. (16) are set to zero. Recall that we are taking $\mu ^2$ and $\uplambda _5$ as real parameters. For that reason, the mass matrices for $H_1$ and $H_2$, on the one hand, and $A_1$ and $A_2$, on the other, can be separately diagonalized. We thus define the angles $\theta$ and $\beta$ such that:

$$\begin{aligned} \left( \begin{array}{c} H_{1} \\ H_{2} \end{array}\right)= & {} \left( \begin{array}{cc} c_{\theta } &{} -s_{\theta } \\ s_{\theta } &{} c_{\theta } \end{array}\right) \left( \begin{array}{l} h \\ H \end{array}\right) , \end{aligned}$$

(18a)

$$\begin{aligned} \left( \begin{array}{c} A_{1} \\ A_{2} \end{array}\right)= & {} \left( \begin{array}{cc} c_{\beta } &{} -s_{\beta } \\ s_{\beta } &{} c_{\beta } \end{array}\right) \left( \begin{array}{c} G^0 \\ A \end{array}\right) , \end{aligned}$$

(18b)

where h and H are the CP even states, and A and $G^0$ are the CP odd states, where $G^0$ is the massless would-be Goldstone boson.⁷ We continue using the short notation $s_x \equiv \sin (x)$, $c_x \equiv \cos (x)$, for a generic angle x. As for the ${\mathcal {L}}_{\chi }$ sector, the mass matrix is given by

$$\begin{aligned} -{\mathcal {L}}^{\chi }_{\text {mass}}= \left( \begin{array}{cc} \chi _L^*&\chi _R^* \end{array}\right) \left( \begin{array}{cc} a &{} b^* \\ b &{} c \end{array}\right) \left( \begin{array}{c} \chi _L \\ \chi _R \end{array}\right) , \end{aligned}$$

(19)

with

$$\begin{aligned} a= & {} \frac{1}{2} g_1 v_1^2+\frac{1}{2} g_2 v_2^2+m_L^2, \end{aligned}$$

(20a)

$$\begin{aligned} b= & {} \dfrac{f_1 v_1+ f_2 v_2}{\sqrt{2}}, \end{aligned}$$

(20b)

$$\begin{aligned} c= & {} \frac{1}{2} g_3 v_1^2+\frac{1}{2} g_4 v_2^2+m_R^2, \end{aligned}$$

(20c)

where a and c are real, while b is in principle complex. However, we can rephase $\chi _R$ through $\chi _R \rightarrow e^{i \, \text {arg}(b)} \chi _R$ so that it absorbs the phase of b. In the new basis, then, b is real, which implies that the mass matrix in Eq. (19) is symmetric.⁸ We thus need an orthogonal matrix with a new angle $\phi$ to diagonalize the states:

$$\begin{aligned} \left( \begin{array}{c} \chi _L \\ \chi _R \end{array}\right) = \left( \begin{array}{cc} c_{\phi } &{} -s_{\phi } \\ s_{\phi } &{} c_{\phi } \end{array}\right) \left( \begin{array}{c} \chi _1 \\ \chi _2 \end{array}\right) , \end{aligned}$$

(21)

where $\chi _1$ and $\chi _2$ are the (complex) diagonalized states with (real) masses $M_1$ and $M_2$.

When considering the theory up to one-loop level, one should renormalize it in order to obtain finite S-matrix elements. This is done through the usual procedure: taking an independent set of parameters, identifying them with bare quantities (represented in the following with the index 0) and relating them to their renormalized equivalents through a counterterm. Tadpoles can be taken care of through the tadpole scheme identified by PRTS in [36]. It then follows from the set of Eqs. (17) that:

$$\begin{aligned} \delta t_{H_1}:= & {} -v_1 \bigg ( \mu _{1,0}^2 \!+\! \dfrac{v_2}{v_1} \mu _0 ^2 \!+\! v_1^2 \uplambda _{1,0} + \dfrac{1}{2} v_2^2 \uplambda _{34,0} \!+\! v_2^2 \, \uplambda _{5,0}\bigg ), \nonumber \\ \end{aligned}$$

(22a)

$$\begin{aligned} \delta t_{H_2}:= & {} -v_2 \bigg ( \mu _{2,0}^2 \!+\! \dfrac{v_1}{v_2} \mu _0 ^2 \!+\! v_2^2 \uplambda _{2,0} + \dfrac{1}{2} v_1^2 \uplambda _{34,0} \!+\! v_1^2 \, \uplambda _{5,0}\bigg ),\nonumber \\ \end{aligned}$$

(22b)

where the tadpole counterterms $\delta t_{H_1}$ and $\delta t_{H_2}$ are such that $\delta t_{H_1} = -T_{H_1}$ and $\delta t_{H_2} = -T_{H_2}$, with $T_{H_1}$ and $T_{H_2}$ being the one-loop tadpole for $H_1$ and $H_2$, respectively. The set of (22) fixes the values for $v_1$ and $v_2$ at one-loop level. Note that, since we imposed CP conservation in ${\mathcal {L}}_{\varPhi }$, there are no tadpole counterterms for the CP odd fields. Specifically, in the mass basis,

$$\begin{aligned} \delta t_{A} = 0. \end{aligned}$$

(23)

But it is easy to see that this is inconsistent. Indeed, there is a one-loop tadpole for A, whose diagrams are represented in Fig. 1. The sum of diagrams is divergent. In fact,

Fig. 1

Feynman diagrams contributing to the one-loop tadpole of the CP odd state

$$\begin{aligned} \left( T_{A}\right) \Big |_{\text {div}} = - \dfrac{1}{\varepsilon } \dfrac{{c_{\phi }} \, {s_{\phi }} \, \left( M_1^2 - M_2^2 \right) \, \text {Im}[f_2]}{8 \, \sqrt{2} \, \pi ^2 \, c_{\beta }}, \end{aligned}$$

(24)

in $d=4-2\varepsilon$ dimensions, where $T_{A}$ represents the one-loop tadpole for A and $\big |_{\text {div}}$ means that we consider only divergent parts.

The origin of the problem lies in the fact that we imposed $\mu ^2$ and $\uplambda _5$ to be real. To clarify this point, let us provisionally take these parameters to be complex, as they originally were. By rewriting Eq. (14a) in terms of bare quantities, and separating the real and imaginary parts of $\mu _0^2$ and $\uplambda _{5,0}$, the terms proportional to these parameters are:

$$\begin{aligned} \begin{aligned}&- {\mathcal {L}}_{\varPhi _0} \ni \mu _0^2 \, \varPhi _{1,0}^* \varPhi _{2,0} + (\mu _0^2)^* \, \varPhi _{2,0}^* \varPhi _{1,0} \\&\quad + \uplambda _{5,0} \, \left( \varPhi _{1,0}^* \varPhi _{2,0}\right) ^2 + \uplambda _{5,0}^* \, \left( \varPhi _{2,0}^* \varPhi _{1,0}\right) ^2 \\&= \text {Re} [\mu _0^2] (\varPhi _{1,0}^* \varPhi _{2,0} + \varPhi _{2,0}^* \varPhi _{1,0}) \\&\quad + \text {Re} [\uplambda _{5,0}] \Big \{\left( \varPhi _{1,0}^* \varPhi _{2,0}\right) ^2 + \left( \varPhi _{2,0}^* \varPhi _{1,0}\right) ^2\Big \} \\&\quad + i \, \text {Im} [\mu _0^2] \left( \varPhi _{1,0}^* \varPhi _{2,0} - \varPhi _{2,0}^* \varPhi _{1,0}\right) \\&\quad + i \, \text {Im} [\uplambda _{5,0}] \Big \{\left( \varPhi _{1,0}^* \varPhi _{2,0}\right) ^2 - \left( \varPhi _{2,0}^* \varPhi _{1,0}\right) ^2\Big \}. \end{aligned} \end{aligned}$$

(25)

As a consequence, when we set $\text {Im} [\mu _0^2] = \text {Im} [\uplambda _{5,0}] = 0$, we are not including in the model the terms of the two last lines of Eq. (25). Naturally, since such terms are not in the model, there is no counterterm for the parameters involved therein. That is, there is neither $\text {Im} [\delta \mu ^2]$ nor $\text {Im} [\delta \uplambda _5]$.⁹ Now, it is a matter of course that this would not be a problem if the fact that we did not include the terms in the last two lines of Eq. (25) would follow from a symmetry that forbade them. In other words, should there be a symmetry in the theory that proscribed those terms, they could logically not be included; and since the symmetry would prevent any Green’s functions generated by such terms from showing up, there would never be divergences involved therein, so that the absence of counterterms for them would never be a problem. So, for example, if CP was a symmetry of the theory, it would preclude those terms, in which case the absence of $\text {Im} [\delta \mu ^2]$ and $\text {Im} [\delta \uplambda _5]$ would not be inconsistent.

However, CP is not a symmetry of theory: even if we try to impose it in the ${\mathcal {L}}_{\varPhi }$ sector, it still is violated in the ${\mathcal {L}}_{\varPhi \chi }$ sector through the phases of $f_1$ and $f_2$, as Eqs. (15a) and (15b) show. So, there is no CP symmetry forbidding the terms in the last two lines of Eq. (25). As a consequence, even if we exclude them, CP violating radiative effects can nonetheless contribute to the Green’s functions involved therein. Such Green’s functions will in general be divergent; but since the last two lines of Eq. (25) were not included in the theory, there will in general not be enough counterterms to absorb them.

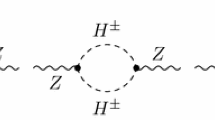
We have already seen one example of Green’s function that indeed cannot be renormalized: the one-loop 1-point function $T_{A}$. Other examples are the one-loop CP violating 2-point functions $\Sigma ^{G^0 h}$, $\Sigma ^{G^0 H}$, $\Sigma ^{A h}$ and $\Sigma ^{A H}$ for the scalar-pseudoscalar mixing of $G^0 \, h$, $G^0 \, H$, $A\, h$ and $A\, H$, respectively. Their Feynman diagrams are represented in Fig. 2.

Fig. 2

Feynman diagrams contributing to the one-loop CP violating 2-point functions

Just like in the case of $T_{A}$, there simply is no counterterm for these functions, which nonetheless are divergent. Their divergent parts are:

$$\begin{aligned}&\Sigma ^{G^0 h}(k^2)\Big |_{\text {div}} = \Sigma ^{AH}(k^2)\Big |_{\text {div}} \nonumber \\&\quad = - \dfrac{1}{\varepsilon } \, \sin (\beta - \theta ) \, \frac{\text {Im}\left[ f_2\right] \left( f_1 + f_2 \tan \beta \right) }{16 \pi ^2}, \end{aligned}$$

(26a)

$$\begin{aligned}&\Sigma ^{Ah}(k^2)\Big |_{\text {div}} = - \Sigma ^{G^0 H}(k^2)\Big |_{\text {div}} \nonumber \\&\quad = - \dfrac{1}{\varepsilon } \, \cos (\beta - \theta ) \, \frac{\text {Im}\left[ f_2\right] \left( f_1 + f_2 \tan \beta \right) }{16 \pi ^2}. \end{aligned}$$

(26b)

In conclusion, the fact that we imposed $\mu ^2$ and $\uplambda _5$ to be real leads to several divergences that cannot be removed by counterterms.

There are two ways to heal this model: either CP is imposed as a whole, or it is not imposed at all. In the first case, all the three relations in Eqs. (15) should be verified, which implies that there is a basis where $\mu ^2$, $\uplambda _5$, $f_1$ and $f_2$ are all real. In this scenario, therefore, CP violating Green’s functions are precluded, which implies, in particular, that no divergent CP violating Green’s functions will appear in any order. This is consistent with what we obtained in Eqs. (24) and (26), which vanish in the limit of real $f_1$ and $f_2$. In the second case, $\mu ^2$, $\uplambda _5$, $f_1$ and $f_2$ are in general complex parameters, which implies that their counterterms are also in general complex. Since CP is violated, there are no scalar states with well-defined CP, and Green’s functions will in general be CP violating. The model is renormalizable as long as all the terms compatible with the symmetries are included. Finally, note that, in such a CP violating scenario, there may be regions of the parameter space in which $\uplambda _5$ and $\mu ^2$ are real, and $f_1$ and $f_2$ complex. But this is a completely different situation from that where one builds a theory taking ab initio $\uplambda _5$ and $\mu ^2$ real, while $f_1$ and $f_2$ in general complex. In fact, while the former situation corresponds to a particular solution of a consistent, renormalizable theory, the latter suffers from the inconsistencies we have shown.

4 Three-loop tadpole for A in the real 2HDM

Our goal is to check whether the complex phases of the fermion mixing matrices introduce CP violating effects into the otherwise CP conserving scalar sector of the real 2HDM via radiative corrections. For this purpose, we focus on the effects of quark-mixing. The quantity that signifies quark-induced CP violation in a convention independent way is the Jarlskog invariant J in Eq. (8). So, we are looking for radiative corrections to the 2HDM which contain this quantity. As the simplest check, we have looked for diagrams proportional to J, contributing to the A tadpole. As argued above, this can only happen in amplitudes with at least four vertices, each containing a factor of $V_{u_\alpha d_j}$ and additionally, a vertex to couple to A (none of the A-couplings have CKM-factors). Therefore, the first possible appearance of J in A-tadpoles is at three loops. This is indeed what we find at the amplitude-level.

Fig. 3

Example of pair of Feynman diagrams where J factorizes (for fixed $\alpha ,\beta ,i,j$). They differ only by the direction of fermion flow (or equivalently by the exchange of the two down-type quarks, $d_i \leftrightarrow d_j$)

An example of a pair of diagrams yielding the Jarlskog invariant is shown in Fig. 3. If contributions of this kind were divergent, then one would lack the respective counterterm needed to absorb these divergences within the real 2HDM. Therefore, we checked for the existence of a leading $1/\varepsilon ^3$-pole in said contributions, which would be a strong indication for the necessity of a genuine three-loop A-tadpole counterterm. For this purpose, we generated all three-loop A-tadpole amplitudes $T_A$ with the only condition being that a fixed set of quarks $\{u_\alpha , u_\beta , d_i, d_j\}$ must be contained. Other contributions are CP conserving operators and, thus, irrelevant to our discussion.

Our calculation was carried out in three independent ways (two numeric; one analytical), fully explained in Sect. 5. The result is¹⁰

(27)

where there is no sum over repeated indices, and

$$\begin{aligned} M^{\alpha i}_{\beta j} =&(m_{u_\alpha }^2 - m_{u_\beta }^2) (m_{d_i}^2 - m_{d_j}^2) \nonumber \\&\times (m_{u_\alpha }^2 - m_{d_i}^2 + m_{u_\beta }^2 - m_{d_j}^2). \end{aligned}$$

(28)

The fact that such different calculational techniques yielded the same result is truly significant.

Remarkably, when summing over all different sets of up- and down-type quark contributions, the leading pole vanishes exactly. Indeed, it is easy to show that summing the combination $M^{\alpha i}_{\beta j} I^{\alpha i}_{\beta j}$ over all the nine distinct sets of four different quarks (two up-type and two down-type), the result vanishes. Notice that both $M^{\alpha i}_{\beta j}$ and $I^{\alpha i}_{\beta j}$ are antisymmetric under $\alpha \leftrightarrow \beta$ (or $i \leftrightarrow j$). Thus, the vanishing of Eq. (27) is not due to the simple symmetry reasons mentioned in connection with Eq. (9). It is the specific form of the mass term $M^{\alpha i}_{\beta j}$ in Eq. (28) which makes this possible. We cannot see how one would have guessed from the start this rather peculiar mass combination. We resonate with Khriplovich and Pospelov’s remark in the context of edm that: “We cannot get rid of the feeling that this simple result (...) should have a simple transparent explanation. Unfortunately, we have not been able to find it.”

But the physical consequence is quite clear:

$$\begin{aligned} \sum _{\alpha< \beta } \sum _{i<j} \left( T_{A}\right) ^{\alpha i}_{\beta j} = {\mathcal {O}}(\varepsilon ^{-2}). \end{aligned}$$

(29)

It remains uncertain whether this cancellation has a physical origin or it is to be interpreted as accidental. There is the possibility that the next order $1/\varepsilon ^2$-poles would be non-vanishing. Otherwise, a genuine CP violating tadpole counterterm for A would only become relevant at the four-loop level.

5 Details of the calculation

In this section, we discuss our derivation of (27). First note that a complete calculation of the renormalized three-loop tadpole for A would require the full renormalization of the model at both one-loop and two-loop order. Although unlikely, one cannot exclude the possibility that combinations of the one- and two-loop counterterms of a CP-conserving scalar sector conspire to cancel the divergences of a CP-violating three-loop tadpole. Secondly, one caveat in our calculation is the treatment of amplitudes with an uneven number of $\gamma$-matrices together with $\gamma _5$. We chose to work in naive dimensional regularisation with the expectation that the leading $\varepsilon$-poles do not depend on the choice of a $\gamma _5$-scheme. This claim is supported by the findings in [37] at the one-loop level.

As mentioned before, at least three generations of quarks are necessary to generate a CP-violating tadpole. Therefore, we focus on a particular set of diagrams. Let us then define $S^{\{dcbt\}}$ as the set of all the three-loop tadpole diagrams for A containing the quarks d, c, b, t. We started by generating the amplitudes for $S^{\{dcbt\}}$ in an $R_\xi$-gauge. We did this through two independent softwares: FeynMaster [38] (which makes use of FeynRules [39] and QGRAF [40]) and FeynArts [41].¹¹ At three loops, there are 360 amplitudes containing the quarks d, c, b and t. However, 120 among them involve two closed loops of fermions, which means that they can never factorize the Jarlskog invariant J; and since a) the tadpole for A violates CP and b) all the CP-violation in the real 2HDM must be proportional to J (with J being the only rephasing-invariant quantity signifying CP-violation), those diagrams must sum up to zero. We checked this explicitly using FeynCalc [42,43,44].

We then focused on the remaining 240 diagrams. After simplifying the Lorentz and Dirac algebra of the 240 diagrams with FeynCalc, another 32 diagrams, such as the ones with two internal W-boson loops, vanish immediately (in naive dimensional regularisation) due to the chirality of the interactions involved. This eventually left us with 208 diagrams which can be categorized as follows:

• 1. The first group of diagrams can be generated from connecting A to any fermion line in Fig. 4 and the corresponding ones with reversed fermion flow giving 16 diagrams. The same goes for all possible vector boson and scalar insertions, namely

  $$\begin{aligned} \{HW,WH,HG,GH,HH,GW,WG,GG\}. \end{aligned}$$

  Diagrams where we connect A to a line with an attached W-loop vanish though, leaving us with $8\times 16 - 4 \times 4 = 112$ diagrams.

• 2. An example of the second group is shown in Fig. 5. From this diagram and the one with reversed fermion flow, we get 8 diagrams by cyclic permutations of the fermions. The A can be connected to either $\{WH,HW,GH,HG\}$ and we can have either a W-, H-, or G-loop in the diagram. This gives $3 \times 4 \times 8 = 96$ diagrams.

Fig. 4

Attaching A to the fermion lines of these diagrams and the ones with reversed fermion flow generates the first category of relevant diagrams

Fig. 5

The second set of relevant diagrams is generated from permutations of the fermions in this diagram and by replacing the W-insertions with a Goldstone boson

We proceeded to numerically evaluate the most divergent part of the 208 diagrams using FIESTA [45] in Feynman gauge, i.e. at $\xi _W=1$. In order to generate input integrals, the FeynCalc function ApartFF was essential for decomposing the diagrams via partial fractioning. This decomposition yielded scalar integrals for which we could easily get an accurate result from FIESTA. One integral type needed additional attention though, namely the one with a scalar product in the numerator and five different propagator factors (see Appendix A for a discussion). This type of integral yielded large error estimates in FIESTA, such that the results could no be trusted. In order to obtain an exact result for those, we used integration-by-parts identities with FIRE [46] to decompose this integral type into a set of scalar integrals. The intermediate steps required to link FeynCalc, FIRE and FIESTA were performed by two independent sets of private codes.

For the numerical input values of the scalar sector, one should choose a point in parameter space which does not violate any theoretical or experimental constraints. The theoretical bounds include boundedness from below, perturbative unitarity [47,48,49] as well as electroweak precision measurements using the oblique parameters S, T and U [4]. The experimental constraints include the exclusion bounds from Higgs searches at LHC that were verified using HiggsBounds [50, 51] and the signal strengths for the SM-like Higgs boson were forced to be within 2$\sigma$ of the fits given in [10, 52]. Among the points that pass all constraints, we pick the following one:

$$\begin{aligned} \begin{aligned} \alpha&= -0.83797 \\ \beta&= 0.73908 \\ m_{H^{\pm }}&= 581.18~\text {GeV}, \\ m_H&= 592.81~\text {GeV}, \\ m_{A}&= 597.44~\text {GeV}, \\ m_{12}^2&= 19.458~\text {TeV}. \end{aligned} \end{aligned}$$

(30)

Using these together with (B.1), the result for the most divergent part of $S^{\{dcbt\}}$ is:

$$\begin{aligned} \left( i T_{A}\right) ^{cd}_{tb} = 2392.6~(\text {GeV})^3 \times \dfrac{1}{\varepsilon ^3} J + {\mathcal {O}}(\varepsilon ^{-2}). \end{aligned}$$

(31)

We tried to ascertain whether sets of diagrams with different combinations of quarks could possibly cancel with each other by checking the result for another set of quarks. For example, consider the set of diagrams $S^{\{dcst\}}$, defined as identical to $S^{\{dcbt\}}$ except that the b quark is replaced by an s quark. Using the same point in parameter space (Eq. 30), the result for the most divergent part of $S^{\{dcst\}}$ is

$$\begin{aligned} \left( i T_{A}\right) ^{cd}_{ts} = - 0.91341 \, \, (\text {GeV})^3 \times \dfrac{1}{\varepsilon ^3} \, J + {\mathcal {O}}(\varepsilon ^{-2}). \end{aligned}$$

(32)

Clearly, the numbers differ, which might lead one to believe that summing over the results for all quarks combinations would likely yield a non-zero result.

Only later, our attention was drawn to TVID [53, 54], a software package for the numerical evaluation of arbitrary three-loop vacuum integrals – see also [55]. The authors discuss a set of three master integrals into which any three-loop tadpole diagram can be decomposed. Using the same amplitude decomposition as for our numerical evaluation, we were then able to map to this set of master-integrals and use the analytic pole expressions of TVID (or equivalently of Ref. [56]) to acquire the result for the $1/\varepsilon ^3$-pole shown in (27).¹² After confirming that the analytic results coincided with our previous numerical findings, we were able to sum over all possible quark combinations using (27) to find the surprising result of the poles cancelling, as shown in (29).

6 Conclusions

We argued that the real 2HDM can suffer from theoretical inconsistencies, as the simultaneous enforcement of CP conservation in the potential and allowance of CP violation in another sector may lead to divergences that cannot be removed by the counterterms. Because such divergences cannot show up at two-loop level and below, the unsoundness of the model has been by and large ignored in the literature. But the problem cannot be dismissed. In order to highlight its potential theoretical unsoundness we introduced a simple toy model, characterized by the same inconsistency as the real 2HDM. There, and as we showed, the irremovable divergences (that are expected at least at three-loops in the real 2HDM) show up immediately at one-loop level. This simple example ought to make the point: the real 2HDM could suffer from the same kind of pathology. We addressed this claim by calculating the leading pole of the three-loop one-point function of the A field in the real 2HDM. We showed that, surprisingly, the pole vanishes exactly after summing all contributions. This does not mean that the model is sound after all, but only that its unsoundness is likely to be found either at lower order in $1/\varepsilon$ or upon two-loop renormalization, or possibly at four-loop order. A complete discussion would require the full one- and two-loop renormalization as well as a discussion of the $\gamma _5$-scheme beyond naive dimensional regularisation though.

We hope that our work spurs further interest in this subject and that a full calculation will become possible in the future.

Appendices

Appendix A: Integral decomposition

As mentioned in Sect. 5, one integral type in our amplitude decomposition needed special attention. The one in question is

$$\begin{aligned}&U_5^{(1,2)} (m_1,m_2,m_3,m_4,m_5) \nonumber \\&= i \frac{e^{3\gamma _E \varepsilon }}{\pi ^{3d/2}}\int \! \! \mathrm {d}^d q_1 \, \mathrm {d}^d q_2 \, \mathrm {d}^d q_3 \frac{q_1 \cdot q_2}{(q_1^2 - m_1^2) (q_2^2 - m_2^2) (q_3^2 - m_3^2)} \nonumber \\&\qquad \times \frac{1}{ \big ((q_1-q_3)^2-m_4^2\big ) \big ((q_2- q_3)^2 - m_5^2\big ) }. \end{aligned}$$

(A.1)

Evaluating integrals of this kind with FIESTA yields small yet non-zero error estimates already for the leading pole which is why the numerical results could not be trusted. Therefore, we made use of the integration by parts routines of FIRE to decompose $U_5^{(1,2)}$ into a set of scalar integrals, which in turn yield vanishing error estimates for the leading poles when evaluated with FIESTA. Using analytic expressions for the leading poles of the resulting integral decomposition also made it possible to recombine everything into a joint expression for the leading pole of $U_5^{(1,2)}$, viz.

$$\begin{aligned} U_5^{(1,2)}&(m_1,m_2,m_3,m_4,m_5) \nonumber \\ =&\frac{1}{24 \varepsilon ^3} \Big [ (m_1^2 + m_2^2)^2 + (m_2^2 + m_5^2)^2 + (m_3^2 + m_4^2)^2 \nonumber \\&\quad \quad + (m_3^2 + m_5^2)^2 -4(m_2^2-m_3^2)^2 +m_2^4 + m_3^4 \Big ] \nonumber \\&\qquad + {\mathcal {O}}(\varepsilon ^{-2}). \end{aligned}$$

(A.2)

Appendix B: Numerical input values

$$\begin{aligned} \begin{aligned} m_W&= 80.358~\text {GeV}, \\ m_u&= 2.2 \times 10^{-3}~\text {GeV}, \\ m_d&= 4.8 \times 10^{-3}~\text {GeV}, \\ m_c&= 1.4464~\text {GeV}, \\ m_s&= 0.093~\text {GeV}, \\ m_t&= 172.5~\text {GeV}, \\ m_b&= 4.8564~\text {GeV}, \\ e&= 0.30812, \\ \sin \theta _w&= 0.47206. \end{aligned} \end{aligned}$$

(B.1)