Expectation management

Abstract

We consider the application of a Fleischer–Jegerlehner-like treatment of tadpoles to the calculation of neutral scalar masses (including the Higgs) in general theories beyond the Standard Model. This is especially useful when the theory contains new scalars associated with a small expectation value, but comes with its own disadvantages. We show that these can be overcome by combining with effective field theory matching. We provide the formalism in this modified approach for matching the quartic coupling of the Higgs via pole masses at one loop, and apply it to both a toy model and to the $\mu$NMSSM as prototypes where the standard treatment can break down.

1 Introduction

The mass of the SM-like Higgs boson, discovered by ATLAS and CMS [1,2,3], is now an electroweak precision observable, thanks to its outstandingly accurate determination at the LHC [4,5,6], and it plays an important role in constraining the allowed parameter space of Beyond-the-Standard-Model (BSM) theories. On the one hand, the Higgs mass is a prediction in supersymmetric theories (see Ref. [7] and references therein for a recent review) and interestingly it depends most heavily on the electroweak couplings and scale – quantities that are already known from other observations – while it is only at loop level that a dependence on the scale of supersymmetric particles appears. This property has spurred significant developments in precision scalar-mass calculations, advanced in recent years by the KUTS initiative [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54] as described in the report [7]. On the other hand, in non-supersymmetric theories, the Higgs mass is not a prediction by itself, but it can be used to extract the Higgs quartic coupling and, in turn, investigate the stability of the electroweak vacuum. In this context, a precise calculation is essential to produce reliable results on vacuum stability (see Refs. [55,56,57,58,59] for works in the SM) and to correctly appreciate the potential impact of new particles [60,61,62,63,64,65].

We refer the interested reader to Ref. [7] and references therein for an in-depth review of Higgs-mass computations, and we only recall here the main steps involved (applicable for any BSM theory). The standard calculational technique begins with the extraction of SM-like parameters – namely the electroweak and strong gauge couplings, the quark and lepton Yukawa couplings, and the Higgs vacuum expectation value (vev) – from observables. Adding then the BSM parameters to these, the Higgs (and other particle) masses can be calculated, along with any other desired predictions. The relevant observables for the electroweak sector are typically, as in calculations in the SM, either $M_Z, M_W, \alpha (0)$ or $M_Z, G_F, \alpha (0)$ where $M_{Z,W}$ are the Z and W boson masses, $\alpha (0)$ is the fine-structure constant extracted in the Thompson limit, and $G_F$ is the Fermi constant. This latter quantity is extracted from muon three-body decays, whereas the others are related essentially to self-energies. In general, this extraction of the SM-like couplings and the Higgs vev can be performed at one-loop for any theory, but the two-loop relationships are only known for the SM and a small subset of other models in certain limits.

At the tree level, the expectation value v of the Higgs boson is related to the other parameters in the theory by the requirement that the theory be at the minimum of the potential. To be concrete, consider the Higgs potential of the SM, $V = \mu ^2\,| H|^2 + \lambda \,| H|^4$; then the minimisation condition gives

$$\begin{aligned} 0&= \mu ^2 + \lambda \, v^2\, . \end{aligned}$$

(1.1)

Since we do not have an observable for $\mu ^2$ we typically use this equation to eliminate it, giving the Higgs mass to be

$$\begin{aligned} m_h^2&= \mu ^2 + 3\, \lambda \, v^2 = 2\, \lambda \, v^2\,. \end{aligned}$$

(1.2)

However, once we go beyond tree level, there are several possible choices. The approach typically taken in BSM theories, and in the SM in Ref. [66], is to insist that the expectation value v is a fixed “observable”, and instead keep solving for $\mu ^2$ order-by-order in perturbation theory. In this way,

$$\begin{aligned} \mu ^2&= - \lambda \, v^2 - \frac{1}{v}\, \frac{\partial \Delta V}{\partial h}\bigg |_{h=0} \equiv - \lambda \, v^2 - \frac{1}{v}\, t_h\,, \end{aligned}$$

(1.3)

where $\Delta V$ are the loop corrections to the effective potential, and then the Higgs pole mass $M_h$ reads

$$\begin{aligned} M_h^2&= 2\,\lambda \, v^2 - \frac{1}{v}\, t_h + \Pi _{hh}{\left( M_h^2\right) } \equiv 2\, \lambda \, v^2 + \Delta M_h^2\,, \end{aligned}$$

(1.4)

where $\Pi _{hh}{\left( M_h^2\right) }$ is the Higgs self-energy evaluated on-shell. One of the chief advantages of this approach is that tadpole diagrams do not appear in any processes, since they vanish by construction.

On the other hand, while this is in principle a straightforward procedure to follow, it is complicated by the fact that the self-energies and effective potential implicitly depend on $\mu ^2$. In Landau gauge, or the gaugeless limit, this leads to the “Goldstone Boson Catastrophe” at two loops [67,68,69,70] – its solution appears by consistently solving the above equation order by order [27, 33]. Indeed, one way to formalise this is as a finite (or possibly IR-divergent) counterterm for $\mu ^2$:

$$\begin{aligned} \mathcal {L}&\supset - \left( \mu ^2 + \delta \mu ^2 + \lambda \, v^2\right) v\, h - \frac{1}{2} \left( \mu ^2 + \delta \mu ^2 + 3\,\lambda \, v^2\right) h^2 + \cdots \,, \end{aligned}$$

(1.5)

where $\delta \mu ^2 = - \frac{1}{v}\,t_h.$ Another drawback is that it manifestly breaks gauge invariance, since the loop corrections above depend on the gauge; and it also means that the expectation value v is not an $\overline{MS}$ parameter, so the renormalisation-group equations for the expectation value are no longer just given by those of $\mu ^2$ and $\lambda$, but have extra contributions [71, 72].

However, there is a further drawback to the above procedure which we wish to highlight in this paper. When considering a BSM theory with additional scalars that may have an expectation value, it is typical to take the same approach as for the scalar field in the SM and fix their expectation values, solving the additional tadpole equations for other dimensionful parameters – for example, their mass-squared parameters, or sometimes a cubic scalar coupling. To take the example of a real singlet S with mass-squared Lagrangian parameter $m_S^2$ – not to be confused with the pole mass, which we denote $M_S$ – and expectation value $v_S$, this means that analagously to Eq. (1.3),

$$\begin{aligned} m_S^2&= \left( m_S^2\right) ^{\mathrm{tree}} - \frac{1}{v_S}\, \frac{\partial \Delta V}{\partial S} . \end{aligned}$$

(1.6)

If the loop corrections are not large, and $v_S$ is not small, this is completely acceptable – so for models such as the NMSSM there is generally no problem. However, if we consider a different theory or regions of the parameter space where $v_S$ is small, for example if $m_S \gg v$ and $v_S \propto v^2$ (as may be found in examples of EFT matching [41]) then we can easily find the case that $\delta m_S^2 > \left( m_S^2\right) ^\mathrm{tree}$. This makes the calculation unreliable.

The archetypal example of this problem is the case where the neutral scalar obtaining an expectation value actually comes from an SU(2) triplet ${\mathbf {T}}$ with expectation value $v_T$ and mass-squared $m_T^2$ – for example in Dirac-gaugino models [73,74,75,76]. In that case, $v_T \propto v^2/m_T^2$ multiplied by other dimensionful parameters of the theory. Moreover, we require that $v_T \lesssim 4$ GeV from electroweak-precision constraints, generally requiring $m_T > rsim 1$ TeV. So then

$$\begin{aligned} \delta m_T^2&\sim \frac{1}{4\ \mathrm{GeV}} \times \frac{1}{16\pi ^2} \times {\mathcal {O}}{\left( \mathrm{TeV}^3 \right) } \sim 2.5 \times {\mathcal {O}}{\left( \mathrm{TeV}^2 \right) }\,, \end{aligned}$$

(1.7)

i.e. we see that there is a severe problem whenever $v_T/m_T$ is of the order of a loop factor.

Moreover, for such cases where $v_S$ is small, this procedure works in the opposite way to that which we would desire. In BSM theories the scalar expectation values beyond v are not top-down inputs or tied closely to some observables, whereas we may typically want to define the masses and couplings as fixed by some high-energy boundary conditions (for example constrained or minimal SUGRA conditions where soft masses have a common origin). In this case we would like to solve the tadpole equations for $v_S$; even if this would typically lead to coupled cubic equations, nowadays it is almost trivial to solve them numerically, or start from an approximation.

In this paper we will instead examine an alternative procedure, proposed by Fleischer and Jegerlehner in examining Higgs decays in the SM [77], which has the potential to solve both of these issues. Instead of taking the expectation values as fixed, we take them to be the tree-level solutions of the tadpole equations. This means that we do not work at the “true” minimum of the potential and must include tadpole diagrams in all processes. While this implies the addition of some new Feynman diagrams in the Higgs mass calculation, it is not technically more complicated than including finite counterterm insertions for $\mu ^2$. This approach has the additional advantages that, since the Lagrangian is specified in terms of $\overline{\mathrm{MS}}$ parameters only, the result is manifestly gauge independent, and the expectation values are just the solutions to the tree-level tadpole equations. For these reasons, it has been used and advocated in the SM, in particular at two loops in Refs. [57, 78,79,80,81,82]; and applied to certain extensions of the Two Higgs Doublet Model (THDM) when considering decays [83,84,85,86]. We also note that this approach is closely related to the various on-shell renormalisations used in  e.g. Refs. [87,88,89,90] in the THDM and the Minimal Supersymmetric Standard Model (MSSM).

In the example of the SM at the one-loop order, this would mean

$$\begin{aligned} M_h^2&= 2\, \lambda \, v^2 - \frac{6\,\lambda \, v}{m_h^2}\, t_h^{(1)} + \Pi _{hh}^{(1)}{\left( m_h^2\right) }\,, \end{aligned}$$

(1.8)

where the superscripts in brackets indicate the loop order, and we put the momentum in the self-energy at the tree-level Higgs mass in order to respect the order of perturbation theory. In other words, the tadpole contribution is suppressed by the mass-squared of the Higgs, although – since $m_h^2 = 2\, \lambda \, v^2$ – here we find that they have a very similar form to the previous approach. On the other hand, in the case of a heavy singlet or triplet the contributions to the singlet self-energy would be similarly suppressed by $m_S^2$, and we can have $m_S$ much greater than the triplet coupling – so the corrections to the singlet mass would be well under control.

On the other hand, in the BSM context this approach was proposed by Ref. [91] for the following very different reason: by no-longer forcing the electroweak expectation value to have its observed value, we allow new physics to disturb the electroweak hierarchy. In the above approach, the contribution $- \frac{6\,\lambda \,v}{m_h^2}\, t_h^{(1)} = - \frac{3}{v}\,t_h^{(1)}$ is effectively the contribution from a shift in v. We can view the calculation as equivalent to counterterms for the expectation value $\delta ^{(1)} v$, where

$$\begin{aligned} \mathcal {L}&\supset \!-\! \left( \mu ^2 \!+\! \lambda \, v^2\right) v\, h \!-\! \left( \mu ^2 \!+\! 3\, \lambda \, v^2\right) \delta ^{(1)} v\, h \!-\! \cdots \end{aligned}$$

(1.9)

so that now

$$\begin{aligned} \delta ^{(1)} v&= - \frac{1}{m_h^2}\, t_h^{(1)}\,. \end{aligned}$$

(1.10)

In this case, if there is heavy new physics at a scale $\Lambda \gg m_h$, then we shift the Higgs expectation value up to that new scale suppressed only by a loop factor. Indeed in Ref. [91] the proposal was to use

$$\begin{aligned} \frac{\delta m_h^2}{m_h^2}&\equiv \frac{1}{m_h^2} \left[ -\frac{3}{v}\, t_h^{(1)} + \Pi _{hh}^{(1)}{\left( m_h^2\right) }\right] \end{aligned}$$

(1.11)

as as a measure of fine-tuning of the theory.

Another perspective on the difference between the two approaches is given by viewing the SM as an EFT. In this case, in the EFT the SM receives corrections to both $\mu ^2$ and $\lambda$ at the matching scale from integrating out heavy states which can be done with $v=0$. As discussed in Ref. [27], when expanding in v, in order to respect gauge invariance we must have:

$$\begin{aligned} \Delta V&= \Delta V_{0} + \frac{1}{2} \left. \Delta V_{hh}\right| _{v=0}\,v^{2} + {\mathcal {O}}{\left( v^{4}\right) } + \cdots ,\, \nonumber \\ \Pi _{hh}{\left( m_{h}^{2}\right) }&= \left. \Delta V_{hh}\right| _{v=0} + {\mathcal {O}}{\left( v^{2}\right) } \end{aligned}$$

(1.12)

and therefore $t_{h} = v\left. \Delta V_{hh}\right| _{v=0} + \cdots$ This shows that the EFT-matching correction to $\mu ^{2}$, which is $\left. \Delta V_{hh}\right| _{v=0}$, and the origin of the hierarchy problem, correspond to $t_{h}/v$ to lowest order in v. Hence in the “standard” approach of Eq. (1.4) this cancels out and leaves only corrections proportional to $v^{2}$ – whereas in the modified approach it remains and gives a large shift to the Higgs mass.

However, the reappearance of the hierarchy is a problem for the light Higgs mass, whereas the problem we wished to solve actually appeared in new, heavy states! If we wish to explore theories which may remain natural while having heavy states, such as those in Ref. [91], then the modified tadpole approach should work best. There must consequently be some trade-off between losing control of the light Higgs and losing control of the heavier states (and losing gauge invariance too). In Sect. 2 we will set up the necessary general formalism and explore this in detail for a toy model.

However, there are two potential solutions to allow us to have the best of both worlds:

• 1. Retain counterterms for $\mu ^{2}$ as in Eq. (1.5) for the SM Higgs, but only for them. This is somewhat tricky to automate, since we must make a special case of the electroweak sector, and we also lose gauge invariance.

• 2. For cases where the tuning of the hierarchy becomes large, use EFT pole matching [26] with the modified treatment of tadpoles. This way, the heavy states remain entirely under control, we keep the heavy masses and couplings as top-down inputs (that remain genuinely $\overline{\mathrm{MS}}$ or $\overline{\mathrm{DR}}'$), and we have gauge invariance built-in.

In Sect. 4 we will adopt the second approach for the example of the general NMSSM (and apply it specifically to the variant known as the $\mu$NMSSM [63]). We establish the necessary formalism for the matching and give a detailed examination, via implementing the computation in a modified SPheno [92, 93] code generated from SARAH [13, 16, 33, 94,95,96,97,98].

2 Treatment of tadpoles for theories with heavy scalars

For a general renormalisable field theory, once we have solved the vacuum minimisation conditions and diagonalised the mass matrices, we can write the potential in terms of real scalar fields $\{ \phi _{i} \}$ as

$$\begin{aligned} V&= \text {const} + \frac{1}{2}\,m_{i}^{2}\,\phi _{i}^{2} + \frac{1}{6}\,a_{ijk}\,\phi _{i}\,\phi _{j}\,\phi _{k} + \frac{1}{24}\,\lambda _{ijkl}\,\phi _{i}\,\phi _{j}\,\phi _{k}\,\phi _{l}\, . \end{aligned}$$

(2.1)

If we take the standard approach and fix the expectation values, adjusting the mass parameters order by order in perturbation theory, then as described in Ref. [27] we can write the pole masses as

$$\begin{aligned} \left( M_{i}^{2}\right) ^{(1)}&= m_{i}^{2} + \Delta _{ii} + \Pi _{ii}^{(1)}{\left( m_{i}^{2}\right) } \equiv m_{i}^{2} + \Delta M_{i}^{2}\, . \end{aligned}$$

(2.2)

To define the shifts $\Delta _{ii}$ in a general way, we must start from some basis of fields $\big \{\phi _{i}^{0}\big \}$ split into expectation values and fluctuations so that $\phi _{i}^{0} \equiv v_{i} + {\hat{\phi }}_{i}^{0}$ and then diagonalise the fields via ${\hat{\phi }}_{i}^{0} = R_{ij}\,\phi _{i}$. In the simplest case where we solve the tadpole equations for some mass-squared parameters in the original basis and where we ignore pseudoscalars, we can then write

$$\begin{aligned} \Delta _{ii} = - \sum _{k} R_{ki}^{2}\, \frac{1}{v_{k}} \left. \frac{\partial \Delta V}{\partial {\hat{\phi }}_{k}^{0}}\right| _{{\hat{\phi }}_{k}^{0}=0} = - \sum _{k,l} R_{ki}^{2}\, R_{lk}\, \frac{1}{v_{k}}\, t_{l}^{(1)}\,. \end{aligned}$$

(2.3)

The generalisation to solving for other variables (such as cubic scalar couplings) and to include pseudoscalar mass shifts is given in Ref. [33].

On the other hand, taking the modified approach and including the tadpole diagrams, the pole masses up to one loop are simply

$$\begin{aligned} \left( M_{i}^2\right) ^{(1)}&= {\hat{m}}_{i}^2 - \frac{1}{{\hat{m}}_{j}^{2}}\, a_{iij}\,t_{j}^{(1)} + \Pi _{ii}^{(1)}{\left( {\hat{m}}_{i}^{2}\right) } \equiv {\hat{m}}_{i}^{2} + {\hat{\Pi }}_{ii}^{(1)}{\left( {\hat{m}}_{i}^{2}\right) }\,, \end{aligned}$$

(2.4)

where we have defined ${\hat{m}}_{i}^{2}$ to be the tree-level mass when we are using the modified scheme (we will later drop the distinction between $m_{i}$ and ${\hat{m}}_{i}$, see below) and ${\hat{\Pi }}_{ij}\big (p^{2}\big )$ for later use to be the self-energies including the tadpoles. The expressions for the tadpoles and self-energies at one loop can be found e.g. in Refs. [27, 99]; this calculation is therefore more straightforward to automate, being purely diagrammatic in nature. An explicitly gauge-invariant expression for this (i.e. one where there are no gauge-fixing parameters present) will be given in future work.

At this point the reader may object that, no matter what technique we use to calculate masses, the result for a given theory should be the same up to higher-loop corrections. Unfortunately this is made obscure by the difficulties in general in defining the parameters of our theory. To compare the two calculations for the same parameter point, in the standard approach we are invited to treat the expectation values as fundamental, so if we start from a theory defined in this way, we must:

• 1. Calculate loop-level masses in the standard approach for a given choice of expectation values (with the associated problems when those expectation values are small).

• 2. Extract the Lagrangian parameters from the loop-corrected tadpole equations.

• 3. Solve the tree-level vacuum stability equations with these new parameters, obtaining the expectation values for use in the alternative approach.

• 4. Compute the new tree-level spectrum using these expectation values

• 5. Compute the loop-corrected masses in the alternative approach.

Let us denote the tree-level masses and expectation values in the alternative approach as ${\hat{m}}_{i}$ and ${\hat{v}}_{i}$, and for simplicity assume that we solve the tadpole equations for some mass-squared parameters (rather than cubic couplings, say). Then, by passing back to the basis in which the fields are not diagonalised, where the Lagrangian mass parameters are $m_{0,ij}^{2} = {\hat{m}}_{0,ij}^{2} + \delta m_{0,ij}^2$ and the Lagrangian couplings are $a_{0,ijk},$ $\lambda _{0,ijkl}$, we can carry out the above steps and solve perturbatively for the expectation values ${\hat{v}}_{i}$ in the modified scheme:

$$\begin{aligned} 0&= \big (m_{0,ij}^2 + \delta m_{0,ij}^2\big )\, v_{j} + \frac{1}{2}\, a_{0,ijk}\, v_{j}\, v_{k} + \frac{1}{6}\, \lambda _{0,ijkl}\, v_{j}\, v_{k}\, v_{l} + t_{0,i}\nonumber \\&= \big (m_{0,ij}^2 + \delta m_{0,ij}^2\big )\, {\hat{v}}_j + \frac{1}{2}\, a_{0,ijk}\, {\hat{v}}_j\, {\hat{v}}_k + \frac{1}{6}\, \lambda _{0,ijkl}\, {\hat{v}}_j\, {\hat{v}}_k\, {\hat{v}}_l\,. \end{aligned}$$

(2.5)

We have written $t_{0,i}$ for the one-loop tadpole to emphasise that it is in the undiagonalised basis; to go to the mass-diagonal basis we need to rotate by the matrix $R_{ij}$ as above. Writing ${\hat{v}}_i =v_i + \delta v_i$ we obtain

$$\begin{aligned} 0&= - t_{0,i} + {\mathcal {M}}_{0, ij}^2\, \delta v_j, \end{aligned}$$

(2.6)

where ${\mathcal {M}}_{0,ij}^2$ is the tree-level mass matrix of scalars in the standard scheme. This can be trivially solved by rotating to the mass-diagonal basis. We then write the tree-level mass matrix in the alternative scheme as

$$\begin{aligned} \hat{{\mathcal {M}}}_{0, ij}^2&= {\mathcal {M}}_{0,ij}^2 + \delta m_{0,ij}^2 + a_{0,ijk}\, \delta v_k + \lambda _{0,ijkl}\, v_k\, \delta v_l\,. \end{aligned}$$

(2.7)

Using the same matrix $R_{ij}$ we can rotate this to obtain¹

$$\begin{aligned} {\hat{m}}_{i}^2 = \big (R^T\, \hat{{\mathcal {M}}}_{0}^2\, R\big )_{ii}&= m_i^2 + \Delta _{ii} + a_{iik}\, \frac{t_k^{(1)}}{m_k^2} + {\mathcal {O}}(\text {2-loop}). \end{aligned}$$

(2.8)

Inserting this into (2.4) gives (2.2).

Of course, this comes with the associated problems of defining the theory in the standard approach: if we have a small expectation value, then (as we shall illustrate below) the loop corrections in $\Delta _{ii}$ can be very large, so the mass of the heavy scalar may differ greatly from the tree-level one. Making a conversion in this way just ensures that we see the same problem in the alternative treatment. Instead, for such points we should start with a theory defined in the alternative manner.

Then, to compare the same point for the standard calculation one should:

• 1. Calculate loop-level masses in the alternative approach for a given choice of masses and couplings.

• 2. Iteratively solve the loop-level vacuum stability equations to obtain the loop-corrected expectation values $v_i$ for use in the standard scheme.

• 3. Use these expectation values to compute the tree-level spectrum for use in the standard scheme (if we are using the approach with “consistent tadpoles”)²

• 4. Compute the loop-corrected masses in the standard approach.

In this way, we should obtain the same result (up to higher-order differences) for our desired point as in the alternative scheme. However, the key complicating factor is step 2: it assumes that we can efficiently and accurately find the true minimum of the potential. This can only be done by iteration of the tadpole equations; this involves recomputing the masses and couplings of the theory at each step and is therefore often numerically expensive (especially at higher loop orders). On the other hand, if we do this perturbatively, then we are effectively using the alternative scheme!

2.1 Disclaimer

While the above discussion is reassuring for the consistency of our calculations, in the following we will not (for the most part) compare masses at the same parameter point, for the obvious reason that the results would be almost the same. Instead, what we want to illustrate is the difficulty in even defining our theory: in the standard approach, since we are required to choose a vacuum-expectation value for the heavy singlet fields (which are not physical parameters), the phenomenologist will often use a guess or a tree-level-approximate solution for this, rather than iteratively solve the tadpole equations (which, in any case, would lead to a different input value depending on the chosen loop order). We shall take this naive approach below, and compare (in most cases) theories with the same tree-level spectrum by taking the expecation values to be the same in both the standard and modified schemes. Of course, according to the discussion above, these are not the same parameter points: we are instead illustrating the differences in methods of defining the theory, and will show how the alternative scheme gives a much more stable and efficient definition (at least in cases where the hierarchy problem for the light Higgs does not become severe).

2.2 A toy model

Let us now apply the above general expressions to the simplest toy model that can illustrate the differences of prescriptions for dealing with radiative corrections to tadpoles. This consists of the abelian Goldstone model coupled to a real singlet S, and has scalar potential

$$\begin{aligned} V&= \mu ^2\,| H|^2 + \frac{1}{4}\,\lambda \,| H|^4 + \frac{1}{2}\,m_S^2\,S^2 + a_{SH}\,S\,| H|^2\nonumber \\&\quad + \lambda _{SH}\,S^2\,| H |^2 + a_S\,S^3 + \lambda _S\,S^4 \end{aligned}$$

(2.9)

with the fields

$$\begin{aligned} H&\equiv \frac{1}{\sqrt{2}}\left( v + h + i\,G\right) , \quad S \equiv v_S + {\hat{S}}\,, \end{aligned}$$

(2.10)

v and $v_S$ denoting the Higgs and singlet vacuum expectation values (vevs), respectively. The minimisation conditions at the tree level yield the equations

$$\begin{aligned} -\mu ^2&= \frac{1}{4}\,\lambda \,v^2 + a_{SH}\,v_S + \lambda _{SH}\,v_S^2\, \end{aligned}$$

(2.11a)

$$\begin{aligned} \left( m_S^2 + \lambda _{SH}\, v^2\right) v_S&= -\frac{1}{2}\,a_{SH}\,v^2 - 3\,a_S\,v_S^2 - 4\,\lambda _S\,v_S^3 \end{aligned}$$

(2.11b)

that lead to the tree-level (squared) mass matrix for the scalars (which do not mix with the massless pseudoscalar):

$$\begin{aligned} {\mathcal {M}}^2_\text {tree}&= \begin{pmatrix} \frac{1}{2}\,\lambda \,v^2 &{}\quad a_{SH}\,v + 2\,\lambda _{SH}\,v\,v_S \\ a_{SH}\,v + 2\,\lambda _{SH}\,v\,v_S &{}\quad m_S^2 + \lambda _{SH}\,v^2 + 6\, a_S\,v_S + 12\,\lambda _S\,v_S^2 \end{pmatrix}. \end{aligned}$$

(2.12)

Fig. 1

left: one-loop tadpole diagrams; middle: one-loop self-energy diagrams appearing in standard and modified calculation; right: additional self-energy diagrams in the modified approach

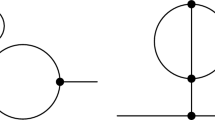
The one-particle irreducible one-loop contributions to the one- and two-point functions (see Fig. 1) of this toy model are given by

$$\begin{aligned} t_i^{(1)}&= -\,\frac{\kappa }{2}\,a_{ijj}\,A{\left( m_j^2\right) }\, \end{aligned}$$

(2.13a)

$$\begin{aligned} \Pi _{ij}^{(1)}{\left( p^2\right) }&= \kappa \left[ \frac{1}{2}\,\lambda _{ijkk}\,A{\left( m_k^2\right) } - \frac{1}{2}\,a_{ikl}\,a_{jkl}\,B{\left( p^2,m_k^2,m_l^2\right) } \right] \nonumber \\ \end{aligned}$$

(2.13b)

with A and B denoting the scalar one-point and two-point one-loop integrals in the conventions of e.g. Refs. [27, 99], $\kappa \equiv (16\pi ^2)^{-1}$ and $p^2$ denoting the external momentum. In the approach of keeping the vevs fixed, we find for the one-loop pole masses:

$$\begin{aligned} \left( M_i^2\right) ^{(1)}&= m_i^2 - R_{i1}^2\,\frac{1}{v}\,t_h^{(1)} - R_{i2}^2\,\frac{1}{v_S}\,t_S^{(1)} + \Pi _{ii}{\left( m_i^2\right) }\,, \end{aligned}$$

(2.14)

where $t_h^{(1)} = \partial \Delta V\big /\partial h\big |_{h,{\hat{S}}=0}$ , $t_S^{(1)}= \partial \Delta V\big /\partial S\big |_{h,{\hat{S}}=0}$ . Thus the tadpole corrections suffer from the division by the vev; in particular, the mass predictions can become numerically unstable in scenarios with a small singlet vev. Let us see this in practice for our example when $m_S^2$ is large; in this case

$$\begin{aligned} v_S \sim - \frac{a_{SH}\,v^2}{2\,m_S^2}, \qquad R \sim \begin{pmatrix} 1 &{} - \frac{a_{SH}\,v}{m_S^2} \\ \frac{a_{SH}\,v}{m_S^2} &{} 1 \end{pmatrix}. \end{aligned}$$

(2.15)

If we take v small and just look at the singlet mass in the limit $p^2 \rightarrow 0$ for simplicity,³ we have

$$\begin{aligned} \Delta M_S^2 \approx \Pi _{SS}(0) - \frac{1}{v_S}\, t_S \supset - \frac{3\,a_S\, m_S^2\, \kappa }{v_S} \left( \,\overline{\text {log}}\, m_S^2 - 1\right) + \cdots \end{aligned}$$

(2.16)

where $\overline{\text {log}} m_S^2 \equiv \log m_S^2/Q^2$ for renormalisation scale Q. When the system is really decoupled and $v=0$, then $v_S \sim m_S^2\big /(6a_S)$ and this expression remains well-controlled, but when $0 < v \ll m_S$ – which is the case we are interested in – we instead have

$$\begin{aligned} \Delta M_S^2&\propto \frac{6\, a_S\, m_S^4 }{16\,\pi ^2\, a_{SH}\,v^2}\ \overline{\text {log}}\, m_S^2 \end{aligned}$$

(2.17)

which can be very large compared to $m_S^2$.

Fig. 2

$M_h$ (left) and $M_S$ (right) as a function of $a_{SH}$. $m_S^\mathrm{tree}=Q=2000\,\mathrm{GeV}$, $a_S=100~\mathrm{GeV}$, $\lambda =0.52$, $\lambda _{SH}=0$, $\lambda _S=1/24$. The tree-level values are shown with the green curves, while the red and blue curves correspond to the one-loop results using respectively the standard (Eq. (2.2)) and modified (Eq. (2.4)) treatments of tadpoles

Fig. 3

$M_h$ (left) and $M_S$ (right) as a function of $m_S^\mathrm{tree}$. $Q=m_S^\mathrm{tree}$, $a_{SH}=150~\mathrm{GeV}$, $a_S=100~\mathrm{GeV}$, $\lambda =0.52$, $\lambda _{SH}=0$, $\lambda _S=1/24$. The colours for the different curves are the same as in Fig. 2

Fig. 4

$M_h$ (left) and $M_S$ (right) as a function of $a_{SH}$. $m_S^\mathrm{tree}=1000~\mathrm{GeV}$, $Q=5000~\mathrm{GeV}$, $a_S=0~\mathrm{GeV}$, $\lambda =0.52$, $\lambda _{SH}=0$, $\lambda _S=1/24$. The colours for the different curves are the same as in Fig. 2

Fig. 5

$M_h$ (left) and $M_S$ (right) as a function of $a_{SH}$. $m_S^\mathrm{tree}=Q=500\,\mathrm{GeV}$, $a_S=0~\mathrm{GeV}$, $\lambda _{SH}=0$, $\lambda =0.52$, $\lambda _S=1/24$. The colours for the different curves are the same as in Fig. 2

If we take the modified approach to tadpoles, then the relevant generic expression for the self-energy is

(2.18)

and for our example

$$\begin{aligned} {\hat{\Pi }}_{SS}^{(1)}{\left( m_S^2\right) }&\approx \Pi _{SS}(0) - \frac{a_{SH}^2\, \kappa }{2\,m_h^2}\,A{\left( m_S^2\right) } - \frac{3\,a_S^2\, \kappa }{m_S^2}\, A{\left( m_S^2\right) } + \cdots \nonumber \\&\sim - \frac{\kappa }{2} \left( \frac{a_{SH}^2 }{m_h^2} - 24\,\lambda _S\right) m_S^2\ \overline{\text {log}}\, m_S^2\,. \end{aligned}$$

(2.19)

Provided that $a_{SH} \lesssim m_h$ this is well under control, in contrast to the previous “standard” approach.

2.3 Numerical examples

In this section we shall illustrate the different behaviours of the two approaches to tadpoles in the toy model defined in Eq. (2.9) through numerical examples. For this purpose, we present results for the one-loop pole masses $M_h$ and $M_S$ computed diagrammatically both in the standard approach – following Eq. (2.2) – and in the modified approach of equation (2.4). We shall consider points defined to have the same tree-level spectrum, but whose loop-corrected masses differ according to the scheme used. As described in the disclaimer above, these are not therefore the same points in parameter space: this illustrates the difficulty in defining the model.

For all the following figures, we set $\lambda =0.52$, to reproduce a light “Higgs” (noting that there are no gauge fields) near 125 GeV, and we also fix $\lambda _{SH}=0$ and $\lambda _S=1/24$. In each case, we shall fix the $\overline{\mathrm{MS}}$ parameter $m_S$ and solve the tree-level tadpole equations numerically to obtain $v_S$ and fix $v = 246 \mathrm{GeV}$. Then the calculation in the modified scheme gives the correct value for the scalar masses. For comparison, in each of the Figs. 2, 3, 4 and 5 we use these same values as inputs for the conventional scheme, where we treat the derived value for $v_S$ as the “all orders” expectation value; this means that, in the standard scheme, $(m_S^2)^\mathrm{mod.} = (m_S^2)^\mathrm{tree}$, the tree-level value, and is not actually the $\overline{\mathrm{MS}}$ mass-squared parameter any more. Hence, as mentioned above, these represent different parameter points now; only the tree-level spectra are the same. To avoid ambiguity, we shall therefore use $(m_S^2)^\mathrm{tree}$ since it is the input value for both schemes. In this way we see that two ways of defining the theory at tree-level can give, at times, drastically different results. In Sect. 2.3 we provide as a consistency check a comparison of the approaches with a conversion of the parameters.

In Fig. 2, we show first $M_h$ (left side) and $M_S$ (right side) as a function of the trilinear coupling $a_{SH}$, at tree level (green curves) and at one loop in the standard (red curves) and modified (blue curves) schemes for the tadpoles. We choose here a scenario with a large Lagrangian mass term $m_S^\mathrm{tree} =2000~\mathrm{GeV}$ and a non-zero trilinear self-coupling $a_S=100~\mathrm{GeV}$ for the singlet (and we also fix the renormalisation scale to be $Q=2000~\mathrm{GeV}$). Consequently, we find ourselves exactly in the dangerous region $0<v\ll m_S$, c.f. Eq. (2.17), and as expected from our theoretical discussion, we find that the standard treatment of the tadpoles breaks down. On the one hand, for $M_h$ one can observe that the radiative corrections are larger in the standard approach and lead to larger variations of the loop-corrected mass than in the modified tadpole scheme. On the other hand, more strikingly, the results for $M_S$ in the standard approach are manifestly spurious. Indeed, while the loop corrections in the modified scheme remain very small (the green tree-level and blue one-loop curves are almost superimposed), in the standard scheme the corrections are huge: for large $a_{SH} > rsim v$ – meaning not too small values of the singlet vev $v_S$ – they already amount to several hundred GeV, and if one decreases $a_{SH}$ (thereby increasing $\Delta M_S^2$, c.f. Eq. (2.17)) the singlet pole mass becomes tachyonic below $a_{SH}=v$.

Next, in Fig. 3, we fix the trilinear coupling $a_{SH}=150~\mathrm{GeV}$ and now consider $M_h$ (left) and $M_S$ (right) as a function of the Lagrangian mass term $m_S^\mathrm{tree}$. We also set $Q=m_S^\text {tree}$ and $a_S=100~\mathrm{GeV}$. Once again, with our choice of a non-zero singlet trilinear self-coupling $a_S$ and relatively small $a_{SH}$ – hence also a small singlet vev – we expect the standard approach to exhibit instabilities. For $M_h$ (left side of Fig. 3) both approaches behave relatively well and no instability seems to occur, although the radiative corrections are significantly larger in the standard scheme. However, for $M_S$ the calculation in the standard approach (red curve) once again breaks down when $m_S^\mathrm{tree}$ is increased – equivalently for small $v_S$ – while the loop corrections to $M_S$ in the modified approach (blue curve) remain minute.

In Fig. 4, we illustrate the behaviour of Eq. (2.19). We plot once more $M_h$ (left) and $M_S$ (right) as a function of the trilinear coupling $a_{SH}$, but now for a scenario where $a_S=0$ (in order to avoid large corrections $\Delta M_S^2$ in the standard scheme), and with $m_S^\mathrm{tree} =1000~\mathrm{GeV}$ and $Q=5000~\mathrm{GeV}$ so as to increase the size of the logarithms $\overline{\text {log}} \, (m_S^2)^\mathrm{tree}$ . For small values of $a_{SH}$, both schemes (red and blue curves) produce very similar results, however, as $a_{SH}$ becomes larger the radiative corrections to $M_h$ as well as $M_S$ increase significantly in the modified tadpole scheme, leading to less reliable predictions (especially for $a_{SH} > rsim 300$–$400~\mathrm{GeV}$).

Finally, we present in Fig. 5 an example of scenario in which both ways to treat the tadpole contributions give reliable results. We take a small singlet mass parameter $m_S=500~\mathrm{GeV}$, set $a_S=0$ and maintain $a_{SH}<200~\mathrm{GeV}$. We observe here that the radiative corrections to $M_h$ and $M_S$ remain well behaved in both approaches.

2.4 Comparisons at the same point

Here, for clarity (and as a consistency check) we shall follow the (first) prescription in Sect. 2 and compare the two schemes for computing the one-loop masses in our toy model at the same parameter point. We consider the same input parameters as in Fig. 3, except that now we scan over the true $\overline{\mathrm{MS}}$ mass $m_S$ in both schemes. The calculation in the modified scheme is therefore identical to those in Fig. 3, but we then solve the tadpole equations for $\mu ^2$ and $m_S^2$ at the one-loop order to find the values of $v, v_S$; while the value for v changes little, the equation for $v_S$ becomes

$$\begin{aligned} 0&= \left( m_S^2 + \lambda _{SH}\, v^2\right) v_S + \frac{1}{2}\,a_{SH}\,v^2 + 3\,a_S\,v_S^2 + 4\,\lambda _S\,v_S^3 + t_S \big (m_S^2\big )\,. \end{aligned}$$

(2.20)

We then use this new value for $v_S$ to compute the tree and loop-level spectra in the standard scheme. In Fig. 6 we employ consistent tadpoles, so that we obtain a value for $(m_S^2)^\mathrm{tree}$ which satisfies Eq. (2.11b) and use this to compute the tree-level spectrum, and as input for the loop computation with the appropriate perturbative shifts to the loop mass; neglecting mixing between the light and heavy scalars we have

$$\begin{aligned} (M_S^2)^\mathrm{tree}&\simeq -\frac{a_{SH}\, v^2}{2\, v_S} + v_S \left( 3\, a_S + 8\, v_S\, \lambda _S\right) , \end{aligned}$$

(2.21a)

$$\begin{aligned} M_S^2&\simeq (M_S^2)^\mathrm{tree} {-} \frac{1}{v_S}\, t_S\big ((m_S^2)^\mathrm{tree}\big ) {+} \Pi _{SS}\big ((M_S^2)^\mathrm{tree};(m_S^2)^\mathrm{tree}\big )\, . \end{aligned}$$

(2.21b)

We have written $(m_S^2)^\mathrm{tree}$ in the arguments of the tadpoles and self-energies to show the explicit dependence in the loop functions. In the left and right-hand plots of Fig. 6 we therefore see that the shift between $m_S^2$ and $(m_S^2)^\mathrm{tree}$ becomes very large, and this leads to a breakdown of the (primitive) iterative algorithm that we use to solve for $v_S$, hence the standard scheme curves end near $m_S = 1250$ GeV, while the modified scheme has no such issue and the difference between loop-corrected and tree-level masses is negligible. This gives a different perspective on the general problem of calculating masses in such models. On the other hand, we see that, while the tree-level masses can differ significantly (even for the light “Higgs”) the loop masses agree to a high precision, as they should.

Fig. 6

$M_h$ (left) and $M_S$ (right) as a function of the true $\overline{\mathrm{MS}}$ parameter $m_S$ in both the standard and modified schemes, where the standard scheme is performed according to the “consistent tadpole” prescription. Other parameters as in Fig. 3

Fig. 7

$M_h$ (left) and $M_S$ (right) as a function of the true $\overline{\mathrm{MS}}$ parameter $m_S$ in both the standard and modified schemes, where the standard scheme does not involve “consistent tadpoles” but the true $\overline{\mathrm{MS}}$ mass $m_S$ is used everywhere. Other parameters as in Fig. 3

For a final comparison, we give in Fig. 7 the same computation but where, instead of “consistent tadpoles” we use the true $\overline{\mathrm{MS}}$ mass $m_S^2$ obtained from Eq. (2.20) in all of the loop functions so that

$$\begin{aligned} (M_S^2)^\mathrm{tree}&\simeq -\frac{a_{SH} v^2}{2\, v_S} + v_S \left( 3\, a_S + 8\, v_S\, \lambda _S\right) - \frac{1}{v_S}\, t_S \big ( m_S^2\big )\, \end{aligned}$$

(2.22a)

$$\begin{aligned} M_S^2&\simeq (M_S^2)^\mathrm{tree} + \Pi _{SS} \big ( (M_S^2)^\mathrm{tree};m_S^2\big )\, . \end{aligned}$$

(2.22b)

Aside from a shuffling of the tadpole term between the “tree-level” mass in the standard scheme, which now ensures that all of the curves on the right-hand side of Fig. 7 lie on top of each other (modulo the same proviso that the algorithm for finding $v_S$ breaks down) the differences between these two versions of the standard scheme then only exist at two loops. From Fig. 7 it would seem that avoiding the consistent tadpoles would be preferable in these cases, but of course then the above equations mix tree-level and loop-level quantities, so we have problems with EFT matching at one loop (because subleading logarithms do not cancel) and infra-red issues at two loops.

3 Pole mass matching with tadpole insertions

When matching two theories via pole masses, care must be taken that subleading logarithms are correctly subtracted. The best way to do this is to expand the expressions on both sides of the matching relation in terms of the same parameters; the most efficient way to do this is to use those of the high-energy theory (HET) even though this adds a layer of complication because it is the SM parameters that we know from the bottom-up observations. To this end we require the shifts in the vacuum expectation value as well as gauge, Yukawa and of course quartic couplings.

The most straightforward way to match the vacuum-expectation value of the Higgs is via matching the Z mass, which gives (see e.g. Refs. [26, 29, 41]):

$$\begin{aligned} v_{\mathrm {SM}}^2&= v_{\mathrm {HET}}^2 + \frac{4}{g_Y^2 + g_2^2} \left[ {\hat{\Pi }}_{ZZ}^{\mathrm {HET}}(0) - {\hat{\Pi }}_{ZZ}^{\mathrm {SM}}(0) \right] + {\mathcal {O}}{\left( v^4\right) } \,. \end{aligned}$$

(3.1)

If we match the one-loop Higgs mass in the SM to the HET, where the light Higgs mass at tree level is $m_0$, then we have

$$\begin{aligned}&2\,\lambda _{\mathrm {SM}}\, v^2_{\mathrm {SM}} + {\hat{\Pi }}_{hh}^{\mathrm {SM}}{\left( 2\,\lambda _{\mathrm {SM}}\, v^2_{\mathrm {SM}}\right) } = m_0^2 + {\hat{\Pi }}_{hh}^{\mathrm {HET}}{\left( m_0^2\right) } \end{aligned}$$

(3.2a)

$$\begin{aligned}&\lambda _{\mathrm {SM}} = \frac{1}{2\, v_{\mathrm {HET}}^2} \bigg \{ m_0^2 + {\hat{\Pi }}_{hh}^{\mathrm {HET}}{\left( m_0^2\right) } - {\hat{\Pi }}_{hh}^{\mathrm {SM}}{\left( m_0^2\right) } \nonumber \\&\qquad \qquad \qquad - \frac{4\,m_0^2 }{v_{\mathrm {HET}}^2\left( g_Y^2 + g_2^2\right) } \Big [{\hat{\Pi }}_{ZZ}^{\mathrm {HET}}(0) - {\hat{\Pi }}_{ZZ}^{\mathrm {SM}}(0)\Big ]\bigg \}. \end{aligned}$$

(3.2b)

It should be noted that – in order to preserve gauge invariance, and cancel large logarithms exactly without introducing spurious subleading ones – the matching of the quartic coupling should be performed according to this equation, as opposed to performing some iteration, matching eigenvalues of the mass matrices, or separately matching the expectation values and Higgs mass (as performed in some codes) [32, 51]. With the prescription of including tadpole diagrams, this leads to

$$\begin{aligned} {\hat{\Pi }}_{hh}&\equiv \Pi _{hh} - a^{hhk}\, \frac{1}{m_k^2}\, t_k\,, \quad {\hat{\Pi }}_{ZZ} \equiv \Pi _{ZZ} - g^{ZZk}\, \frac{1}{m_k^2}\, t_k\, . \end{aligned}$$

(3.3)

In the SM with ${\mathcal {L}} \supset - \lambda _{\mathrm {SM}}\,| H|^4$ we have

$$\begin{aligned} {\hat{\Pi }}_{hh}^{\mathrm {SM}}&\equiv \Pi _{hh}^{\mathrm {SM}} - \frac{6\, \lambda \, v}{m_h^2}\, t_h^{\mathrm {SM}} = \Pi _{hh}^{\mathrm {SM}} - \frac{3}{v}\, t_h^{\mathrm {SM}},\nonumber \\ {\hat{\Pi }}_{ZZ}^{\mathrm {SM}}&\equiv \Pi _{ZZ}^{\mathrm {SM}} - \frac{2\, M_Z^2}{v\, m_h^2}\, t_k^{\mathrm {SM}}\, \end{aligned}$$

(3.4)

and so

$$\begin{aligned} {\hat{\Pi }}_{hh}^{\mathrm {SM}} - \frac{m_h^2}{M_Z^2}\, {\hat{\Pi }}_{ZZ}^{\mathrm {SM}}&= \Pi _{hh}^{\mathrm {SM}} - \frac{m_h^2}{M_Z^2}\, \Pi _{ZZ}^{\mathrm {SM}} - \frac{3}{v}\, t_h^{\mathrm {SM}} + \frac{2}{v}\, t_h^{\mathrm {SM}}\nonumber \\&= \Delta M^2_{\mathrm {SM}} - \frac{m_h^2}{M_Z^2}\, \Pi _{ZZ}^{\mathrm {SM}}\,, \end{aligned}$$

(3.5)

where the $\Delta M^2_{\mathrm {SM}}$ is now just the standard set of vacuum conditions as in Eqs. (1.4) or (2.2). So what we have shown is that the modified treament of tadpoles cancels out exactly in the matching of the light Higgs, for the SM part. Of course, the shift in the matching condition should only depend on the Lagrangian parameters, which are not affected by the treatment of tadpoles, so the same is true for the matching in the HET part up to terms of higher order in v.

We have already implicitly shown how the change in scheme affects the matching of the gauge bosons; now for fermions we have

$$\begin{aligned} \Gamma _{F_i F_j}(p)&= i \left( /\!\!\!\!{p}- m_{F}\right) \delta _{ij}+ i \left[ /\!\!\!\!{p} \left( P_{L}\,{\hat{\Sigma }}_{ij}^{L}{\left( p^{2}\right) } + P_R\,{\hat{\Sigma }}_{ij}^{R}{\left( p^{2}\right) }\right) \right. \nonumber \\&\quad \left. + P_L\,{\hat{\Sigma }}_{ij}^{SL}{\left( p^{2}\right) } + P_R\,{\hat{\Sigma }}_{ij}^{SR}{\left( p^{2}\right) }\right] . \end{aligned}$$

(3.6)

For fermions at one loop we can write the mass-matrix corrections as

$$\begin{aligned} \delta m_F&= - \Sigma ^{SL} - \frac{1}{2} \left( \Sigma ^R\, m + m\, \Sigma ^L\right) . \end{aligned}$$

(3.7)

This means that our tadpole shift just affects

$$\begin{aligned} \delta \Sigma ^{SL}&= \delta \Sigma ^{SR} = \frac{1}{m_k^2}\, y^{ijk}\, \frac{\partial V}{\partial \phi _k}\,, \end{aligned}$$

(3.8)

where $y^{ijk}$ are the Yukawa couplings, that can be written in terms of Weyl spinors $\{\psi _i\}$ as

$$\begin{aligned} {\mathcal {L}} \supset - \frac{1}{2}\, y^{ijk}\, \psi _i\, \psi _j\, \phi _k\,. \end{aligned}$$

(3.9)

To match the Yukawa couplings via the pole masses of the quarks, the matching of the electroweak expectation value must also be included; working in the basis with diagonalised Yukawa couplings, we can match the diagonal elements as (using $Y^F \equiv y^{FFh}$ for h the SM Higgs and a general fermion F)

$$\begin{aligned} M_F&= v\, Y^F - \Sigma ^{SL} - \frac{1}{2} \left( \Sigma ^R\, m + m\, \Sigma ^L\right) , \end{aligned}$$

(3.10a)

$$\begin{aligned} Y^F_{\mathrm {SM}}&= Y^{F}_{\mathrm {HET}} \nonumber \\&\quad + \frac{1}{v_{\mathrm {HET}}} \left[ (\delta m_F)^{\mathrm {HET}} - (\delta m_F)^{\mathrm {SM}} - \frac{1}{m_k^2}\, y^{FFk}_{\mathrm {HET}}\, t_k + \frac{1}{m_h^2}\, Y^{F}_{\mathrm {SM}}\, t_h^{\mathrm {SM}} \right] \nonumber \\&\quad - \frac{Y^F_{\mathrm {HET}}}{2\, M_Z^2} \left[ {\hat{\Pi }}_{ZZ}^{\mathrm {HET}}(0) - {\hat{\Pi }}_{ZZ}^{\mathrm {SM}}(0)\right] \nonumber \\&= Y^{F}_{\mathrm {HET}} + \frac{1}{v_{\mathrm {HET}}} \left[ (\delta m_F)^{\mathrm {HET}} - (\delta m_F)^{\mathrm {SM}} - \frac{1}{m_k^2}\, y^{FFk}_{\mathrm {HET}}\, t_k \right] \nonumber \\&\quad - \frac{Y^F_{\mathrm {HET}}}{2\, M_Z^2} \left[ {\hat{\Pi }}_{ZZ}^{\mathrm {HET}} (0) - \Pi _{ZZ}^{\mathrm {SM}} (0) \right] , \end{aligned}$$

(3.10b)

where we once again see that the shift in the tadpole scheme cancels out exactly in the SM part. This procedure is particularly important since the shift to the expectation value arising in Eq. (3.1) is very large, as discussed in the introduction. In this case, since the corrections to $\mu ^2$ – and therefore also to $v^2$ – are very large, it becomes impractical in an implementation to actually use the “correct” value of $v^2$ in the high-energy theory. Indeed, this can even become impossible, if $\delta \mu ^2$ is such that $\mu ^2$ would become positive in the SM! Instead, provided we take v much less than the matching scale, we can just treat it as perturbation parameter to extract the SM values. In our numerical calculation in the next section we do exactly this: we just use the SM value of v in both high- and low-energy theories, but use the correct shifts of the expectation values in the matching of the parameters. This is very similar to a standard EFT calculation, which assumes e.g. in split supersymmetry that the heavy Higgs masses are tuned according to the mixing angle given as an input, and takes $v=0$ explicitly, since we are not interested in corrections to Lagrangian parameters of order $v^2\big /M^2$ where M is the matching scale.

4 Application in the $\mu$NMSSM

In the introduction, we explained that the modified treatment of tadpoles can be useful for stability under perturbation theory of heavy scalar masses when they are associated with a small expectation value. In Sect. 2 we showed how it worked in practice in a toy model. In Sect. 3 we described how, for theories where the new scalars are substantially above the electroweak scale, it can be practically applied via EFT matching of the pole masses. Here, we shall apply this technique to a real test case, the $\mu$NMSSM.

4.1 NMSSM, $\mu$NMSSM and GNMSSM

The superpotential of the most general form of the NMSSM – the GNMSSM – is [101, 102]

$$\begin{aligned} W_{\mathrm {GNMSSM}}&= Y_u\, Q \cdot H_u\, U - Y_d\, Q \cdot H_d\, D - Y_e\, L \cdot H_d\, E \\&\quad + \frac{1}{3}\, \kappa \, S^3 + ( \mu + \lambda \, S) H_u\cdot H_d + \xi \, S + \frac{1}{2}\, \mu _S\, S^2 \end{aligned}$$

and the supersymmetry-breaking terms in the Higgs sector are

$$\begin{aligned} V_\mathrm{soft}&\supset m_S^2\, | S|^2 + m_{H_u}^2\, | H_u|^2 + m_{H_d}^2 | H_d|^2 \nonumber \\&\quad + \bigg ( B_\mu \, H_u \cdot H_d + T_\lambda \, S\, H_u \cdot H_d + \frac{1}{3}\, T_\kappa \, S^3 \nonumber \\&\quad + \frac{1}{2}\, B_S\, S^2 + \xi _S\, S + \text {h.c.} \bigg )\,. \end{aligned}$$

(4.1)

Once the singlet develops an expectation value, we can write effective terms

$$\begin{aligned} \mu _{\mathrm{eff}}&\equiv \mu + \frac{1}{\sqrt{2}}\, \lambda \, v_S\,, \nonumber \\ B_{\mathrm{eff}}&\equiv B_\mu + \frac{1}{\sqrt{2}}\, T_\lambda \, v_S + \lambda \left( \xi + \frac{1}{\sqrt{2}}\, \mu _S\, v_S + \frac{1}{2}\, \kappa \, v_S^2\right) \end{aligned}$$

(4.2)

and the tadpole equations become

$$\begin{aligned} 0&= - B_{\mathrm{eff}} \cot \beta + m_{H_u}^2 + \mu _{\mathrm{eff}}^2 - \frac{M_Z^2}{2}\, c_{2\beta } + \frac{1}{2}\, \lambda \, c_\beta ^2\, \end{aligned}$$

(4.3a)

$$\begin{aligned} 0&= - B_{\mathrm{eff}} \tan \beta + m_{H_d}^2 + \mu _{\mathrm{eff}}^2 + \frac{M_Z^2}{2}\, c_{2\beta } + \frac{1}{2}\, \lambda \, s_\beta ^2\, \end{aligned}$$

(4.3b)

$$\begin{aligned} 0&= v_S \left( B_S + m_{S}^2 + \mu _S^2 + 2\, \kappa \, \xi \right) \nonumber \\&\quad + \frac{1}{\sqrt{2}}\, v_S^2 \left( T_\kappa + 3\,\kappa \, \mu _S\right) + \kappa ^2\, v_S^3 \nonumber \\&\quad + \sqrt{2}\,\mu _S\,\xi + \sqrt{2}\,\xi _S \nonumber \\&\quad + \frac{1}{2\,\sqrt{2}}\,v^2 \Big ( 2\,\lambda \, \mu _{\mathrm{eff}} - \left( T_\lambda + 2\, \kappa \, \lambda \, v_S + \mu _S\, \lambda \right) s_{2\beta } \Big )\,. \end{aligned}$$

(4.3c)

The first two lines are essentially modified versions of the MSSM tadpole equations with an extra term from the $\lambda$ coupling. The third line, however, is the crucial one for our discussion. In a general non-supersymmetric theory, we can redefine singlet fields to remove their tadpole terms. However, in the GNMSSM, which has tadpole parameters $\xi$ in the superpotential and $\xi _S$ in the soft-breaking terms, we can only remove one of these, or the combination $\sqrt{2}\, \mu _S\, \xi + \sqrt{2}\, \xi _S$.

Clearly in the GNMSSM, it is most logical to choose a linear combination of the singlet tadpole terms $\xi$ and $\xi _S$ (or just one) as the variable to be eliminated by the tadpole equations. However, this is not possible in the NMSSM or $\mu$NMSSM, since these terms vanish by the assumption of (at least partial) ${\mathbb {Z}}_3$ symmetry. Then aside from $(m_{H_u}^2,m_{H_d}^2)$ or $(\mu ,B_\mu )$, the dimensionful parameter that we can now choose for elimination via the singlet tadpole equation is one of $\big \{m_S^2,\mu _{\mathrm{eff}},T_\lambda ,T_\kappa \big \}$.

We are interested in the case that the singlet is rather heavier than the SM-like Higgs, so that $v^2\big /m_S^2 \ll {1}$. This is clearly at best problematic in the NMSSM, since $\mu _\mathrm{eff}, B_\mathrm{eff} \propto v_S$ so if we imagine $v_S \sim$ GeV we will have very light higgsinos, pseudoscalar/charged Higgs and difficulties solving the tadpole equations. Hence we turn to the $\mu$NMSSM, where we neglect all terms that break the ${\mathbb {Z}}_3$ symmetry except for $\mu$ and $B_\mu$, and find

$$\begin{aligned} v_S&\simeq - v^2 \left( \frac{ 2\,\lambda \, \mu - T_\lambda \, s_{2\beta }}{2\,\sqrt{2}\, m_S^2 }\right) , \end{aligned}$$

(4.4)

where the true value can be found numerically.

The logical choice for this case is to solve for $T_\lambda$. In this case we have

$$\begin{aligned} \Delta T_\lambda&= - \frac{2\,\sqrt{2}}{v^2\,s_{2\beta }}\, \frac{\partial \Delta V}{\partial v_S}\,, \end{aligned}$$

(4.5)

and the terms in the mass matrix become

$$\begin{aligned} {\mathcal {M}}^2_{h_u^0 h_u^0}&\supset -\frac{v_S\, t_S^{(1)}}{v^2\, s_\beta \, c_\beta } + \cdots \propto \frac{t_S^{(1)}}{m_S^2}\,, \nonumber \\ {\mathcal {M}}^2_{h_u^0 s_R}&= - \frac{m_S^2\, v_S + t_S^{(1)}}{v\, s_\beta } + \cdots \,. \end{aligned}$$

(4.6)

Note that this is in the “flavour basis” before we diagonalise the fields at tree level, so the contributions to the light Higgs and heavy singlet masses are $\propto t_S^{(1)}\big /m_S^2$ .

On the other hand, this choice leads to a (potentially very) large quantum correction to $T_\lambda$. Suppose we want to investigate gauge-mediation scenarios where trilinears are small (nearly vanishing), or are otherwise specified by the top-down inputs – this would be completely inappropriate. Furthermore, we have to not only take into account shifts in the masses but also the couplings – this is moderately cumbersome to implement at one loop, but much more so if we want to compute the two-loop corrections. Indeed, it is not included in the algorithm to generate “consistent vacuum equations” of Refs. [27, 70], which assumes that the parameters that we solve the tadpole equations for only affect scalar masses.

To solve both of these issues the simplest choice is to solve for $m_S^2$, and this leads to exactly the same problem as in the toy model, that the corrections to the singlet mass scale as $t_S^{(1)}\big /v_S$ leading to numerical instabilities for tiny $v_S$. Hence this model is an excellent prototype for comparing the different approaches to solving the tadpole equations.

4.2 Numerical comparison of tadpole schemes

In the $\mu$NMSSM and GNMSSM, we not only have a Higgs sector, but also squarks, sleptons, a gluino and electroweakinos. In particular the colourful states have a large impact on the mass of the light Higgs, and, when they are heavy enough to be safe from current collider searches, they cause the “little hierarchy problem” to manifest itself. If we try to apply our modified tadpole scheme directly to these models, then we find all of the problems associated with this little hierarchy in our Higgs-mass calculation. Therefore it is only sensible to use EFT matching for the light Higgs mass. In this section we shall endeavour to show that with such an approach we can solve the technical difficulties with computing the masses of both light and heavy Higgs bosons.

We shall present here numerical investigations of several scenarios of the $\mu$NMSSM and GNMSSM illustrating the differences between the two approaches to the treatment of tadpoles, both using EFT matching. For this, we compare results obtained using the original version of SPheno code obtained directly from SARAH (for the model SMSSM), as well as with a version of the Fortran output extensively modified according to the prescriptions described in Sect. 3.⁴

Fig. 8

$M_{h_1}$ (left) and $M_{h_2}$ and $M_{h_3}$ (right) as a function of $v_S$ in a scenario of the $\mu$NMSSM. The other inputs are taken as follows: $\lambda =\kappa =0.1$, $T_\lambda =200\text { GeV}$, $T_\kappa =-10\text { GeV}$, $\mu =100\text { GeV}$, $B_\mu =6\cdot 10^5\text { GeV}^2$. Tree-level values are shown with green curves, while the red and blue curves correspond to the pole masses computed at one loop, respectively with the standard and modified approaches to the tadpoles. The colour coding of the lines remains the same for all figures in this Section 

In these calculations we must refer the reader again to our disclaimer, that we shall compare parameter points that generate the same tree-level spectrum in the two schemes, but that differ from each other at higher order; because this provides the clearest illustration of the problems faced (namely how to even define the parameter point). In contrast to the toy model, we will give no examples with a complete conversion of parameters, i.e. a comparison of both calculations at the same point, since the actual procedure of converting between the schemes is too onerous for technical reasons. In the SARAH/SPheno code, while a numerical solution of the tadpole equations (required for providing $\overline{\mathrm{MS}}$ input to the standard scheme) is in principle possible, it is labourious and not implemented for loop computations where the variable to solve for is the vacuum expectation value.⁵ Therefore, again we take the tree-level value of $v_S$ as input for the modified scheme, and treat it as the “all-orders” expectation value in the standard scheme (with consistent tadpoles) thus ensuring the same tree-level spectrum, but potentially vastly different results at one loop due to the large corrections to $m_S^2$ in the standard scheme. Again we stress that this is typical of the ambiguity in defining a parameter point that the phenomenologist is invited to suffer, thanks to the expedient in the standard scheme of hiding loop corrections in the definition of the expectation values.

In Sect. 4.2.1 we give an example of the above reasoning in the $\mu$NMSSM. For illustration in Sect. 4.2.2 we also give examples in the GNMSSM where we solve the tadpoles for the same variables ($m_{H_u}^2$, $m_{H_d}^2$, $m_S^2$) which allows us to compare several different scenarios.

4.2.1 $\mu$NMSSM

In Fig. 8, we present the behaviour of the three CP-even mass eigenvalues – i.e. the lightest Higgs mass $M_{h_1}$ (left side) and the masses of the additional CP-even states $M_{h_2}$ and $M_{h_3}$ (right side) – as a function of the singlet vev $v_S$ in a $\mu$NMSSM scenario, where the underlying parameters are given in the caption. The tree-level values are shown in green, while the one-loop results using the standard and the modified treatments of tadpoles are in red and blue respectively. We consider here a low range of values for $v_S$, so that, following our discussion in the previous section, we expect the standard approach to perform poorly for the singlet-like mass eigenstate. This is indeed what we observe if we turn to the right-side plot: for lower $v_S$ ($\lesssim 0.1$–$1\text { GeV}$) the singlet-like scalar is the heaviest eigenstate $h_3$, while after level crossing it is $h_2$ for larger $v_S$. For the entire range of $v_S$ the mass corrections in the standard approach are huge, and they grow as large as 50 TeV for $v_S=0.001\text { GeV}$ – i.e. 250% of the tree-level result! On the other hand, if we look instead at the lightest Higgs boson $h_1$, we find that the radiative corrections are somewhat larger with the modified treatment of the tadpole diagrams, and increase significantly with $v_S$ in this scenario – due to the contributions from the tadpole diagram with a relatively large value of $T_\lambda =200\text { GeV}$ and a relatively small tree-level mass of the singlet-like state.

4.2.2 GNMSSM

While the $\mu$NMSSM provides an excellent prototype for the case of a heavy singlet with a small expectation value, where we cannot hide the loop corrections in a tadpole term, since it is a subset of the GNMSSM we can find more varied scenarios exhibiting the same behaviour. Of course, this is with the proviso that (with less justification in general) we restrict ourselves to solving the tadpole equations for $m_S^2$.

We have devised three types of scenarios:

• Scenario 1: large singlet vev and intermediate $\lambda$;

• Scenario 2: small singlet vev and small $\lambda$;

• Scenario 3: small singlet vev but large $\lambda$.

Table 1 summarises the values taken for the BSM input parameters relevant for SPheno – note that we have adjusted the soft terms $m_0$ (scalar mass) and $A_0$ (scalar trilinear coupling) in order to obtain a mass for the lightest Higgs boson within the interval $[123~\mathrm{GeV},127~\mathrm{GeV}]$. We should also emphasise that the numbers in Table 1 are given to SPheno as high-scale inputs (as this only requires a limited set of values). We then convert these into low-scale input parameters using the standard version of the $\mu$NMSSM SPheno code, and the plots presented in the following are obtained by varying one of the low-scale inputs. In light of the analytic expressions in the previous section, we can expect the two approaches to the tadpoles to give relatively similar results in scenario 1, where the singlet vev is large. However, in scenarios 2 and 3, the singlet vev is taken to be small, so that the differences between the two schemes should be more pronounced. Scenario 3 furthermore allows us to investigate the effect of increasing the coupling $\lambda$.

Table 1 Definitions of the input parameters in the considered $\mu$NMSSM scenarios. Some of the BSM parameters are not modified, and remain the same for the three scenario. Namely, we take: $\tan \beta =10$, $m_{12}=2~\mathrm{TeV}$, $A_0=3~\mathrm{TeV}$, $B_0=0$, $m_A=500~\mathrm{GeV}$, $T_\kappa =-0.5~\mathrm{GeV}$. The renormalisation scale is kept at $Q=3~\text {TeV}$ for all computations. Finally, the numbers marked with a “$\dagger$” are varied for some of the parameter scans

Fig. 9

$M_{h_1}$ (left) and $M_{h_2}$ and $M_{h_3}$ (right) as a function of $\lambda$, in scenario 1. The other inputs are taken as in Table 1. Tree-level values are shown with green curves, while the red and blue curves correspond to the pole masses computed at one loop, respectively with the standard and modified approaches to the tadpoles

Fig. 10

$M_{h_1}$ (left) and $M_{h_2}$ and $M_{h_3}$ (right) as a function of the soft trilinear coupling $T_\lambda$, in scenario 2. The values of the other BSM parameters are taken as in Table 1

Fig. 11

$M_{h_1}$ (left) and $M_{h_2}$ and $M_{h_3}$ (right) as a function of $v_S$, in scenario 2. Input values for the other BSM parameters are given in Table 1

We show first in Fig. 9 the behaviour of the lightest Higgs mass $M_{h_1}$ (left side) and of the additional CP-even Higgs-boson masses $M_{h_2}$ and $M_{h_3}$ (right side) as a function of the superpotential coupling $\lambda$. Among the two BSM states $h_2$ and $h_3$, the former is singlet-like while the latter is doublet-like, in this figure. As can be seen in the right-hand side plot of Fig. 9, the heavy Higgs bosons receive only minute mass corrections in either of the approaches for tadpoles. For the lightest scalar mass $M_{h_1}$, the results in the two schemes are also in excellent agreement. However, we have cut off the plot before $\lambda =0.19$ because beyond this value perturbativity is lost: in the standard approach the singlet-like pseudoscalar Higgs becomes tachyonic at one loop (from a tree-level mass of 750 GeV!). If we continued the plot into this regime we would see the predictions diverging, with the standard approach predicting ever decreasing masses and the modified approach increasing ones for larger $\lambda$ (compare 104 GeV and 138 GeV respectively for $\lambda =0.3$).

Next, we turn to scenario 2, i.e. we consider a small $\lambda =0.01$ and small singlet vev $v_S=1~\mathrm{GeV}$. Figure 10 shows the behaviour of the CP-even masses as a function of the soft trilinear coupling $T_\lambda$, at tree level and one loop (the colouring of the curves is the same as previously explained). We should emphasise that we have made sure to fulfill constraints from vacuum stability (and the absence of a charge-breaking minimum) on $T_\lambda$ – see Ref. [63] – and the tree-level mass of the charged Higgs boson remains positive for the entire range of $T_\lambda$ investigated here. While for $M_{h_1}$ (left side) and $M_{h_2}$ (lower curves of the right-side plot) it seems essentially impossible to distinguish the two approaches to the tadpole treatment, the radiative corrections to $M_{h_3}$ – the mass of the singlet-like scalar – are clearly much larger with the standard method, and the result of the modified scheme is certainly more reliable. As a concrete comparison, we have for the intermediate value $T_\lambda =2~\text {TeV}$ a one-loop correction to $M_{h_3}$ of 2752 GeV (i.e. 24% of the tree-level result) in the standard approach, but only of –4.5 GeV in the modified scheme.

We can confirm that the large difference between the two treatments of the tadpoles arises from the small value of the singlet vev $v_S$. Indeed, in Fig. 11, we present the same three CP-even scalar masses for $v_S$ varying between 0.5 and 100 GeV. One can observe that the results using both approaches for all three masses are in good agreement for large values of the singlet vev. A short comment should be made for $M_{h_1}$: indeed, as $v_S$ increases the results from the two schemes seem to grow apart, and it is somewhat difficult to determine which one should be trusted more in this case. We note that the radiative corrections to $M_{h_1}$ keep increasing with $v_S$ in the standard approach while their size remains relatively stable in the modified scheme. On the other hand, if we consider the situation for $v_S > rsim 0.5~\mathrm{GeV}$, the breakdown of the standard approach for small singlet vevs becomes obvious. Indeed, considering the different results for the mass $M_{h_3}$ of the CP-even singlet-like scalar at $v_S=0.5~\mathrm{GeV}$, the one-loop corrections in the standard scheme amount to 6.5 TeV – in other words, 40% of the tree-level result – compared to only –3.3 GeV (–0.02% of the tree-level mass) in the modified scheme.

Fig. 12

$M_{h_1}$ (left) and $M_{h_2}$ and $M_{h_3}$ (right) as a function of $T_\lambda$, in scenario 3. The other BSM inputs are taken as in Table 1

Fig. 13

$M_{h_1}$ (left) and $M_{h_2}$ and $M_{h_3}$ (right) as a function of $v_S$, in scenario 3. The values of the other relevant inputs are given in Table 1

Lastly, we consider the type of scenario 3, i.e. what happens if we keep a small singlet vev $v_S=1~\mathrm{GeV}$ but increase the coupling $\lambda$ to 0.15. In Fig. 12, we present the CP-even scalar masses as a function of $T_\lambda$ – having once again made sure to maintain vacuum stability [63]. Considering first the masses of the two doublet-like scalars $h_1$ and $h_2$, we observe an excellent agreement of the results from the two tadpole schemes for low to intermediate values of $T_\lambda$ – for $0\le T_\lambda \lesssim 4~\text {TeV}$. However, as $T_\lambda$ becomes larger, the corrections to $M_{h_1}$ and $M_{h_2}$ in the modified approach start growing out of control. This appears similar to the loss of accuracy of the modified scheme that we encountered in the toy model of Sect. 2 when increasing the trilinear coupling $a_{SH}$, which plays the same role as $T_\lambda$ – see Eq. (2.19) and Fig. 4. Turning however to the singlet-like mass $M_{h_3}$ we find (as in Fig. 10 for scenario 2) that the radiative corrections are huge with the standard treatment of tadpoles, but remain well-behaved with the modified one. Interestingly, having increased the value of $\lambda$ has not made the breakdown of the standard calculation for the singlet-like mass more severe than in scenario 2. Nevertheless, the one-loop result $M_{h_3}$ using the modified tadpole scheme is undoubtedly more reliable here.

Finally, we present in Fig. 13 the behaviour of the CP-even scalar masses as a function of the singlet vev $v_S$ – restricting our attention to the low range $0.5~\mathrm{GeV}\le v_S\le 5~\mathrm{GeV}$. As can be read from Table 1, we have chosen for this figure a large value of the soft trilinear coupling $T_\lambda =7.5~\text {TeV}$, which corresponds to the right parts of the plots in Fig. 12. Therefore, it is not surprising that we observe some discrepancy between the results of the two tadpole schemes for all three masses, as discussed above. More interestingly, we can compare the size of the loop corrections to $M_{h_3}$ in the two approaches, as we vary $v_S$. On the one hand, in the standard approach, the one-loop corrections increase from 2.3 TeV (19% of the tree-level result) for $v_S=2.5~\mathrm{GeV}$ to as much as 9 TeV (40% of the tree-level mass) for $v_S=0.75~\mathrm{GeV}$, for instance. On the other hand, in the modified scheme, the effects remain minute and vary from –46 GeV for $v_S=2.5~\mathrm{GeV}$ to –3.6 GeV for $v_S=0.75~\mathrm{GeV}$ (this amounts to –0.38% and –0.02% of the results at tree level, respectively).

5 Conclusions

We have shown the advantages and limitations of taking a different prescription for the solution of tadpole equations. In contrast to previous applications of this technique, in the SM or as a measure of fine-tuning, we have shown that it can be very useful when new scalars having a small expectation value are present in the theory, and in the case that they are much heavier than the electroweak scale, it is best employed via the matching of pole masses in an EFT approach. While this technique offers the advantages of perturbative stability for the heavy scalar masses, easy generalisability (the corrections are simply computed diagramatically rather than via taking derivatives of the tadpole equations) and gauge invariance, it can also lead to numerical instabilities in extracting the light Higgs mass, and the loss of the ability to match the electroweak expectation value.

In future work, other than a general numerical implementation in SARAH, it would be interesting to explore a hybrid approach (along the lines of option 1 described at the end of the introduction), where only the electroweak expectation value is fixed by appropriate counterterms. On the other hand, we intend to consider the corrections at two loops in this approach, and we shall also provide general expressions for the one-loop self-energies which are explicitly gauge independent.