1 Introduction

Gravitational wave (GW) astronomy has begun since the detection of GWs from mergers of black holes or neutron stars by the LIGO and Virgo collaborations [1,2,3,4,5,6]. Besides these GWs from mergers, the GWs can also be generated from perturbations of the theory of inflation. However, the current constraint of the tensor-to-scalar ratio on CMB scales is \(r<0.064\) at \(95\%\) confidence level [7] by the Planck 2018 data in combination with BICEP2/Keck Array, which is too small to be detected in the near future.

Although at first order in perturbation theory the scalar and tensor perturbations are decoupled, however, at second order they are coupled, so the second-order GWs can be induced from scalar perturbations when it reenters the Hubble radius in the radiation-dominated (RD) era [8, 9]. In most of the inflationary models, the induced second-order GW is generically negligible compared to the first-order GWs. However, if the power spectrum of scalar perturbations is enhanced at small scales, the second-order GWs can be sizable or even larger than the first-order one [10,11,12,13,14,15,16,17,18,19,20,21,22].

One way to realize the enhancement of the power spectrum at small scales in single-field inflation is using an inflection point [23,24,25,26,27]. The inflection point is a point such that both the first- and the second-order derivatives of the potential vanish. Near the inflection point the Hubble slow-roll parameter \(|\eta _H|>3\), so the slow-roll approximation fails and the ultra-slow-roll trajectory supersedes, which gives rise to a large peak in the scalar power spectrum at small scales, and induces GWs with a peak in the energy spectrum. Such an inflection point can be generated in critical Higgs inflation with the running of a large non-minimal coupling [28,29,30], or generated in the framework of supergravity [31, 32] or string theory [33,34,35,36] etc.

The previous models with a single inflection point lead to only one peak in the scalar power spectrum, with a width of about 20 e-folding numbers. As is well known the e-folding number during inflation is about 50–60, so it seems possible to generate two peaks in the power spectrum using inflection points. Thus in this paper, we shall investigate the possibility to induce a GW spectrum with double peaks by a scalar power spectrum which has two peaks at small scales. We show that such a kind of power spectrum can be generated from the potential with three inflection points, which is realized in a model with polynomial potential or in a Higgs-like \(\phi ^4\) potential with the running of a quartic coupling by radiative corrections. By fine-tuning the parameters of the models, we show that the double peak GW signal can be detected by SKA, LISA and other detectors in the near future. Recently, the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) reported the hint of the stochastic GW signal in its 12.5-year observation of the pulsar timing array (PTA), which can be fitted by a power law \(\Omega _{{\mathrm{GW}}}\propto f^{5-\gamma }\) with the exponent \(5-\gamma \in (-1.5, 0.5)\) at \(1\sigma \) confidence level [37,38,39,40,41]. We found that one of the peaks of the power spectrum at \(k\sim 10^{6}~{\mathrm {Mpc}}^{-1}\) in our models can explain the NANOGrav signal.

Moreover, the enhancement of scalar perturbations at small scales leads to the production of primordial black holes (PBHs) via gravitational collapse in the radiation-dominated era [42,43,44,45,46,47]. Although various observations have constrained the fraction of dark matter (DM) in the form of PBHs, there still exist open windows where PBHs possibly present a significant fraction of, or even all, the DM in our Universe [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]. So we also estimate the generation of PBHs, and get the mass distribution and abundance of PBHs, which can account for a dominant component of dark matter.

The paper is organized as follows. In the next section, we briefly review the mechanism of the GWs induced by first-order scalar perturbations. In Sect. 3, we set up two inflationary models with three inflection points which can induce GWs with a double peak spectrum. The numerical results of the inflaton dynamics, the energy spectrum of the induced GWs, and the mass distribution and abundance of PBHs in the two models are presented in Sect. 4. The last section is devoted to a summary.

2 Gravitational waves induced by scalar perturbations

In this section, we shall briefly review the computation of induced GWs; for more details see Refs. [70,71,72,73,74,75]. In the conformal Newtonian gauge, the perturbed metric is written as

$$\begin{aligned} {{\mathrm {d}}} s^{2}=-a^{2}(1+2 \Psi ) {{\mathrm {d}}} \eta ^{2}+a^{2}\left[ (1-2 \Psi ) \delta _{i j}+\frac{1}{2} h_{i j}\right] {{\mathrm {d}}} x^{i} {{\mathrm {d}}} x^{j}, \end{aligned}$$
(1)

where \(\Psi \) is the scalar perturbations, and the Fourier components of tensor perturbations \(h_{ij}\) are defined as usual by

$$\begin{aligned} h _ { i j } (\eta , {\mathbf {x}}) = \int \frac{ {\mathrm{d}}^3 {\mathbf {k}} }{ ( 2 \pi ) ^ { 3 / 2 } } e ^ { i {\mathbf {k}} \cdot {\mathbf {x}} } \left[ h_{\mathbf {k}}^ { + } ( \eta ) {\mathrm {e}}_{ij}^+ ( {\mathbf {k}} ) + h_{\mathbf {k}}^\times ( \eta ) {\mathrm {e}}_{ij}^\times ({\mathbf {k}}) \right] , \end{aligned}$$
(2)

where the two polarization tensors are

$$\begin{aligned}&{e_{i j}^{(+)}({\mathbf {k}})=\frac{1}{\sqrt{2}}\left[ e_{i}({\mathbf {k}}) e_{j}({\mathbf {k}})-{\overline{e}}_{i}({\mathbf {k}}) {\overline{e}}_{j}({\mathbf {k}})\right] }, \nonumber \\&{e_{i j}^{( \times )}({\mathbf {k}})=\frac{1}{\sqrt{2}}\left[ e_{i}({\mathbf {k}}) {\overline{e}}_{j}({\mathbf {k}})+{\overline{e}}_{i}({\mathbf {k}}) e_{j}({\mathbf {k}})\right] }, \end{aligned}$$
(3)

with the basis vectors \(e_{i}({\mathbf {k}})\) and \({\overline{e}}_{i}({\mathbf {k}})\) orthogonal to each other and to \({\mathbf {k}}\). In the following, we shall omit the polarization index for simplicity.

In the Fourier space, the equation of motion of tensor modes can be derived from the Einstein equation as

$$\begin{aligned} h_{{\mathbf {k}}}^{\prime \prime }(\eta )+2 {\mathcal {H}} h_{{\mathbf {k}}}^{\prime }(\eta )+k^{2} h_{{\mathbf {k}}}(\eta )=S_{{\mathbf {k}}}(\eta ), \end{aligned}$$
(4)

where \(S_{{\mathbf {k}}}(\eta )\) is the Fourier transformation of the source term,

$$\begin{aligned}&S_{{\mathbf {k}}}(\eta )=4 \int \frac{{\mathrm{d}}^{3} p}{(2 \pi )^{3 / 2}} {\mathrm {e}}_{i j}({\mathbf {k}}) p_i p_j \Bigg (2 \Psi _{{\mathbf {p}}} \Psi _{\mathbf {k-p}}\nonumber \\&\quad +\frac{4}{3(1+w) {\mathcal {H}}^{2}} \left( \Psi ^{\prime }_{{\mathbf {p}}}+{\mathcal {H}} \Psi _{{\mathbf {p}}}\right) \left( \Psi ^{\prime }_{\mathbf {k-p}}+{\mathcal {H}} \Psi _{\mathbf {k-p}}\right) \Bigg ). \end{aligned}$$
(5)

The scalar perturbations \(\Psi _{{\mathbf {k}}}\) can be split into the primordial value \(\psi _{{\mathbf {k}}}\) and the transfer function \(\Psi (k\eta )\),

$$\begin{aligned} \Psi _{{\mathbf {k}}} \equiv \Psi (k \eta ) \psi _{{\mathbf {k}}}. \end{aligned}$$
(6)

If the peak mode enters the horizon in the RD era, the equation of state is \(\omega =1/3\), and then the transfer function becomes

$$\begin{aligned} \Psi (x)=\frac{9}{x^{2}}\left( \frac{\sin (x / \sqrt{3})}{x / \sqrt{3}}-\cos (x / \sqrt{3})\right) . \end{aligned}$$
(7)

For the modes well inside the horizon, the density parameter of the GWs within the logarithmic interval of the wave numbers can be expressed in terms of the power spectrum of GWs,

$$\begin{aligned} \Omega _{{\mathrm {GW}}}(\eta , k)\equiv \dfrac{1}{\rho _{c}}\dfrac{{\mathrm{d}}\rho _{{\mathrm {GW}}}}{{\mathrm{d}}\ln k} = \frac{1}{24}\left( \frac{k}{{\mathcal {H}}}\right) ^{2} \overline{{{\mathcal {P}}}_{h}(\eta , k)}, \end{aligned}$$
(8)

with \(\rho _c\) is the critical energy density of the Universe, the overline denotes the oscillation average and the two polarization modes are summed. The power spectrum \({{\mathcal {P}}}_{h}(\eta , k)\) is defined as

$$\begin{aligned} \left\langle h_{{\mathbf {k}}}(\eta ) h_{{\mathbf {p}}}(\eta )\right\rangle = \frac{2 \pi ^{2}}{k^{3}} \delta ^{3}({\mathbf {k}}+{\mathbf {p}}) {{\mathcal {P}}}_{h}(\eta , k). \end{aligned}$$
(9)

Using the Green function method, the solution to the equation for \(h_{{\mathbf {k}}}\) is

$$\begin{aligned} h_{{\mathbf {k}}}(\eta )=\frac{1}{a(\eta )}\int ^{\eta } {{\mathrm {d}}} {\overline{\eta }} G_{{\mathbf {k}}}(\eta , {\overline{\eta }}) a({\overline{\eta }}) S_{{\mathbf {k}}}({\overline{\eta }}), \end{aligned}$$
(10)

where the Green function \(G_{{\mathbf {k}}}(\eta , {\overline{\eta }})\) satisfies

$$\begin{aligned} G_{{\mathbf {k}}}^{\prime \prime }(\eta , {\overline{\eta }})+\left( k^{2}-\frac{a^{\prime \prime }(\eta )}{a(\eta )}\right) G_{{\mathbf {k}}}(\eta , {\overline{\eta }})=\delta (\eta -{\overline{\eta }}), \end{aligned}$$
(11)

with the primes denoting derivatives with respect to \(\eta \). In the RD era,

$$\begin{aligned} \begin{aligned} G_{{\mathbf {k}}}(\eta , {\overline{\eta }})=\frac{1}{k}\sin (k \eta -k {\overline{\eta }}). \end{aligned} \end{aligned}$$
(12)

Assuming \(\psi _{{\mathbf {k}}}\) is Gaussian, the four-point correlation function of \(\psi _{{\mathbf {k}}}\) can be transformed into the two-point correlation function. Then we obtain the power spectrum by introducing three dimensionless variables \(u \equiv |{\mathbf {k}}-{\mathbf {p}}| / k\), \(v \equiv |{\mathbf {p}}| / k\) and \(x \equiv k \eta \) [13]. We have

$$\begin{aligned} {{\mathcal {P}}}_{h}(\eta , k)= & {} 4 \int _{0}^{\infty } {\mathrm{d}} v \int _{|1-v|}^{1+v} {\mathrm{d}} u\left( \frac{4 v^{2}-\left( 1+v^{2}-u^{2}\right) ^{2}}{4 u v}\right) ^{2}\nonumber \\&\times {\mathcal {I}}^{2}(x, u, v) {{\mathcal {P}}}_{{\mathcal {R}}}(k u) {{\mathcal {P}}}_{{\mathcal {R}}}(k v). \end{aligned}$$
(13)

Considering the late-time limit \(x \rightarrow \infty \), the term \({\mathcal {I}}(x, u, v)\) in the RD era can be calculated as

$$\begin{aligned} \begin{aligned}&{\mathcal {I}}_{RD}(x \rightarrow \infty , u, v)\\&\quad =\frac{3\left( u^{2}+v^{2}-3\right) }{4 u^{3} v^{3} x}\Bigg \{\sin x\Bigg [-4 u v\\&\qquad +(u^{2}+v^{2}-3) \log \left| \frac{3-(u+v)^{2}}{3-(u-v)^{2}}\right| \Bigg ] \\&\qquad -\pi (u^{2}+v^{2}-3) \Theta (v+u-\sqrt{3}) \cos x\Bigg \}.\end{aligned} \end{aligned}$$
(14)

After taking the oscillation average, one can obtain

$$\begin{aligned}&\overline{{\mathcal {I}}_{RD}^{2}(x \rightarrow \infty , u, v)} = \dfrac{1}{2}\left( \frac{3}{4 u^{3} v^{3} x}\right) ^{2}\left( u^{2}+v^{2}-3\right) ^{2} \nonumber \\&\quad \times \Big \{ \Big [-4 u v+\left( u^{2}+v^{2}-3\right) \ln \left| \frac{3-(u+v)^{2}}{3-(u-v)^{2}}\right| \Big ]^{2} \nonumber \\&\quad +\left[ \pi \left( u^{2}+v^{2}-3\right) \Theta (u+v-\sqrt{3})\right] ^{2} \Big \}. \end{aligned}$$
(15)

Together with Eqs. (8) and (13), and using \({\mathcal {H}}=1/\eta \) in the radiation-dominated era, we finally get the energy spectrum of GWs,

$$\begin{aligned}&\Omega _{{\mathrm {GW}}}(\eta ,k) \nonumber \\&\quad = \dfrac{1}{12}\int _{0}^{\infty } {\mathrm{d}}v \int _{|1-v|}^{1+v} {\mathrm{d}}u \left( \frac{4 v^{2}{-}\left( 1+v^{2}-u^{2}\right) ^{2}}{4 u v}\right) ^{2} {{\mathcal {P}}}_{{\mathcal {R}}}(k u) {{\mathcal {P}}}_{{\mathcal {R}}}(k v) \nonumber \\&\quad \times \left( \frac{3}{4 u^{3} v^{3} }\right) ^{2}(u^{2}+v^{2}-3)^{2} \nonumber \\&\quad \times \Big \{\Big [-4 u v+(u^{2}+v^{2}-3) \ln \left| \frac{3-(u+v)^{2}}{3-(u-v)^{2}}\right| \Big ]^{2}\nonumber \\&\quad +\left[ \pi (u^{2}+v^{2}-3) \Theta (u+v-\sqrt{3})\right] ^{2} \Big \}. \end{aligned}$$
(16)

3 The models

3.1 Model I: A polynomial potential with inflection points

Motivated by an effective field theory with a cutoff scale \(\Lambda \), a polynomial potential can be generally given by [76,77,78,79,80,81]

$$\begin{aligned} V_{\mathrm {eff}}(\phi )=\sum _{n=0} \frac{b_{n}}{n !}\left( \frac{\phi }{\Lambda }\right) ^{n}. \end{aligned}$$
(17)

We ignore the constant term and the first-order term to make the potential and its first-order derivative vanish at the origin. In order to build a model with three inflection points, where both the first- and the second-order derivatives of V vanish, we must have six free parameters, thus we truncate the effective potential to the eighth order. Then the potential can be parameterized as

$$\begin{aligned} V_{\mathrm {eff}}(\phi )= & {} V_{0}\left[ \frac{c_{2}}{2 !}\left( \frac{\phi }{\Lambda }\right) ^{2}+\frac{c_{3}}{3 !}\left( \frac{\phi }{\Lambda }\right) ^{3}+\frac{c_{4}}{4 !}\left( \frac{\phi }{\Lambda }\right) ^{4}+\frac{c_{5}}{5 !}\left( \frac{\phi }{\Lambda }\right) ^{5}\right. \nonumber \\&\left. +\frac{c_{6}}{6 !}\left( \frac{\phi }{\Lambda }\right) ^{6}+\frac{c_{7}}{7 !}\left( \frac{\phi }{\Lambda }\right) ^{7}+\frac{1}{8 !}\left( \frac{\phi }{\Lambda }\right) ^{8}\right] , \end{aligned}$$
(18)

where \(V_0\) is an overall factor, which can be constrained by the amplitude of scalar perturbations \(A_s\), and \(c_{2-7}\) are six free parameters.

Although in some choices of parameter space such a potential allows for the existence of inflection points, it is non-renormalizable. So here we introduce an appropriate factor and then the potential becomes

$$\begin{aligned} V(\phi )=\frac{V_{\mathrm {eff}}(\phi )}{\left( 1+\xi \phi ^{2}\right) ^{2}}. \end{aligned}$$
(19)

Such a factor usually arises from the scalar field non-minimal coupling to gravity [76, 81]. In some choices of parameter space, the potential \(V(\phi )\) can generate three inflection points which give an approximate scale-invariant spectrum at CMB scales, and at the same time generate two large peaks in the power spectrum at small scales to induce double peaks GW spectrum.

For convenience of discussion, we assume that the potential has three inflection points at \(\phi _i (i=1,2,3)\), respectively, where \(V'(\phi _i)=0\) and \(V''(\phi _i)=0\). More generally, in order to study the slight deviations from a perfect inflection point, we introduce three more free parameters \(\alpha _i\) and set \(V'(\phi _i)=\alpha _i\) and \(V''(\phi _i)=0\). Then the parameters \(c_{2\sim 7}\) in Eq. (18) can be expressed as functions of \(\phi _i\) and \(\alpha _i\). By fine-tuning the parameters, one can get a potential with three inflection points, which both consists with the CMB constraints, and induces a second-order GW spectrum with double peaks.

For instance, we take the following parameter set:

$$\begin{aligned}&V_0=6.96\times 10^{-11},\quad \Lambda =0.5,\quad \xi = 0.4, \nonumber \\&\phi _1=0.49,\quad \alpha _1= -8.485824\times 10^{-6},\nonumber \\&\phi _2=1.09,\quad \alpha _2= -2.104572\times 10^{-5},\nonumber \\&\phi _3=2,\quad \alpha _3=7.2\times 10^{-7}, \end{aligned}$$
(20)

and the corresponding potential is shown in Fig. 1.

Fig. 1
figure 1

Scalar potential \(V(\phi )\) of Model I for the parameter set (20)

Full size image

We can see that there are three inflection points. The inflation starts near the first inflection point at high scales and leads to a nearly scale-invariant spectrum, then slowly rolls down the smooth plateau-like regions with a nearly constant Hubble friction. Whenever the inflaton meets a cliff, it speeds up quickly, until it reaches the next inflection point plateau, where the Hubble friction rapidly slows it down again. Such a point leads to a phase of ultra-slow-roll lasting about 20 e-folding numbers, which generates a large peak in the power spectrum. Similarly, near the last inflection point, the inflaton becomes ultra-slow-roll again and generates the second peak of the power spectrum.

3.2 Model II: A Higgs-like potential with the running of quartic coupling

In this subsection, we shall consider a Higgs-like potential. During inflation the field value is large, so only the quartic part of the potential matters. Although the \(\phi ^4\) model is ruled out by the CMB observations, if one consider the interactions between the inflaton and other fields, required for reheating, the situation will be changed [82]. The radiative corrections can be accounted for through the running of the quartic coupling; then the potential is approximated by

$$\begin{aligned}&V(\phi )=\frac{\lambda (\phi )}{4!}\phi ^4, \end{aligned}$$
(21)

with \(\lambda (\phi )\) is an effective field-dependent coupling, it can be parameterized as [26, 82]

$$\begin{aligned} \lambda= & {} \lambda _0\Bigg [1+b_1\ln \Bigg (\frac{\phi ^2}{\phi _0^2}\Bigg )+b_2\ln \Bigg (\frac{\phi ^2}{\phi _0^2}\Bigg )^2+b_3\ln \Bigg (\frac{\phi ^2}{\phi _0^2}\Bigg )^3 \nonumber \\&+b_4\ln \Bigg (\frac{\phi ^2}{\phi _0^2}\Bigg )^4+b_5\ln \Bigg (\frac{\phi ^2}{\phi _0^2}\Bigg )^5+b_6\ln \Bigg (\frac{\phi ^2}{\phi _0^2}\Bigg )^6\Bigg ], \end{aligned}$$
(22)

where the overall factor \(\lambda _0\) can be constrained by the amplitude of scalar perturbations \(A_s\), and the logarithms come from two-loop and higher-order terms in the Coleman–Weinberg expansion [83]. In order to make the potential have three inflection points, we truncate it to sixth order here.

Similar to Model I, we assume that the potential has three inflection points at \(\phi _1, \phi _2\) and \(\phi _3\), respectively, and set \(V'(\phi _i)=\beta _i\) and \(V''(\phi _i)=0\) to study the slight deviations from a perfect inflection point. Then the six parameters \(b_{1\sim 6}\) in Eq. (22) can be expressed as functions of \(\phi _i\) and \(\beta _i\). For some parameter sets, the potential \(V(\phi )\) can also generate three inflection points which lead to predictions in good agreement with the current CMB measurements and induce a GW energy spectrum with double peaks. For instance, we take the following parameter set:

$$\begin{aligned}&\lambda _0=0.8983\times 10^{-13},\quad \phi _0= 1.7, \nonumber \\&\phi _1=0.473,\quad \beta _1=-0.0501578,\nonumber \\&\phi _2=1.1,\quad \beta _2= -0.2150073,\nonumber \\&\phi _3=2,\quad \beta _3=0.00355, \end{aligned}$$
(23)

and the corresponding potential is shown in Fig. 2.

Fig. 2
figure 2

Scalar potential \(V(\phi )\) of Model II for the parameter set (23)

Full size image
Fig. 3
figure 3

Hubble slow-roll parameters \(\epsilon _H\) and \(\eta _H\) as functions of the e-folding number \(N_e\) in Model I for parameter set (20) (left panel), Model II for parameter set (23) (right panel). The dashed lines indicate the values 1 and 3

Full size image

4 Numerical results

In this section, we shall numerically calculate the power spectrum of scalar perturbations and the energy spectrum of the induced GWs in Model I for parameter set (20) and in Model II for parameter set (23), respectively; then we compare the results of \(\Omega _{{\mathrm {GW}},0}\) to the expected sensitivity curves of several planned GW detectors. We also calculate the abundance of PBHs produced in the two models using the Press–Schechter approach [84] of gravitational collapse.

4.1 Inflaton dynamics

It has been pointed out in several references that near the inflection point the potential becomes extremely flat, thus the slow-roll approximation fails and is superseded by the ultra-slow-roll trajectory [85,86,87,88]. So one must use the Hubble slow-roll parameters instead the traditional one [89,90,91], which is defined as

$$\begin{aligned}&\epsilon _H=-\frac{{\dot{H}}}{H^2},\nonumber \\&\eta _H=-\frac{{\ddot{H}}}{2H{\dot{H}}}=\epsilon _H-\frac{1}{2}\frac{{\mathrm{d}}\ln \epsilon _H}{{\mathrm{d}}N_e}, \end{aligned}$$
(24)

with dots representing derivatives with respect to cosmic time, and \(N_e\) denoting the e-folding number. In Fig. 3, we plot the Hubble slow-roll parameters \(\epsilon _H\) and \(\eta _H\) as functions of \(N_e\) for the two models, respectively.

We can see that near the inflection points the Hubble slow-roll parameter \(|\eta _H|>3\), so the inflation becomes ultra-slow-roll, which leads to large valleys on the curve of \(\epsilon _H\) lasting 15–20 e-folding numbers, and this will give rise to double peaks in the scalar power spectrum.

The scalar spectral index as well as the tensor-to-scalar ratio can be expressed using \(\epsilon _H\) and \(\eta _H\) as

$$\begin{aligned}&n_s=1-4\epsilon _H+2\eta _H,\nonumber \\&r=16\epsilon _H. \end{aligned}$$
(25)

For the two models, the numerical results of \(n_s\) and r are present in Table 1. The amplitude of the primordial curvature perturbations \(A_s\) and the e-folding numbers during inflation \(N_e\) are also listed there.

Table 1 The numerical results for the two models
Full size table

The results are in agreement with the current CMB constraints \(n_s=0.9649\pm 0.0042\), \(r<0.064\) and \(\ln (10^{10}A_s)=3.044\pm 0.014\) from Planck 2018 [6].

Since the slow-roll approximation fails near the inflection point, the calculation of the scalar perturbations using the approximate expression \({{\mathcal {P}}}_{{\mathcal {R}}}\simeq \frac{1}{8\pi ^2M_P^2}\frac{H^2}{\epsilon _H}\) will underestimate the power spectrum [26, 31]. Thus it is necessary to solve the Mukhanov–Sasaki (MS) equation of the mode function numerically, and then the power spectrum can be calculated by

$$\begin{aligned} {{\mathcal {P}}}_{{\mathcal {R}}}=\frac{k^3}{2\pi ^2}\left| \frac{u_k}{z}\right| ^2_{k\ll {\mathcal {H}}}. \end{aligned}$$
(26)

The numerical results of scalar power spectrum for the two models are shown in Fig. 4. The blue line is the numerical result of the MS equation and the orange line is the approximate result.

Fig. 4
figure 4

Primordial power spectrum of scalar perturbations predicted by Model I for parameter set (20) (left panel), and by Model II for parameter set (23) (right panel). Also we show the upper bound from \(\mu \)-distortion for a delta function power spectrum (black line) and for the steepest growth \(k^4\) power spectrum (brown line) [92]

Full size image

We can see that, for both models, the scalar power spectrum matches the Planck observations at CMB scales, and it has two large peaks at small scales with a height of about seven orders of magnitude higher than the spectrum at CMB scales, Such peaks will lead to the production of non-negligible second-order GWs with a double peak energy spectrum.

It is interesting to note that in Ref. [92], the authors pointed out that in canonical single-field inflation, the steepest growth index of the power spectrum before the peak is \(k^4\), and we find that in our models the growth index is \(k^{2.8}\) and \(~k^{2.3}\) in Model I and \(k^{2.9},k^{2.2}\) for the peaks in Model II (the red dashed line of Fig. 4), which are all slower than \(k^4\). The constraints to the primordial power spectrum from \(\mu \)-distortion are also shown in Fig. 4.

4.2 Energy spectrum of the induced GWs

Using the scalar power spectrum obtained in the previous subsection, and we consider the GW energy spectrum at the present time \(\Omega _{{\mathrm {GW}}, 0}\) to be related to the one produced in the RD era as [72]

$$\begin{aligned} \Omega _{{\mathrm {GW}}, 0}=0.83 \left( \frac{g_{*,0}}{g_{*,p}}\right) ^{-1 / 3} \Omega _{r, 0} \Omega _{{\mathrm {GW}}}, \end{aligned}$$
(27)

with \(\Omega _{r, 0}\simeq 9.1\times 10^{-5}\) the current density fraction of radiation, \(g_{*,0}\) and \(g_{*,p}\) the effective degrees of freedom for energy density at the present time and at the time when the peak mode crosses the horizon, respectively. We numerically calculate the energy spectrum of the induced GWs for the two models and show them as functions of the present value of the frequency f in Fig. 5, with

$$\begin{aligned} f \approx 0.03~{\mathrm {Hz}} \frac{k}{2\times 10^7~{\mathrm {pc}}^{-1}}. \end{aligned}$$
(28)

The sensitivity curves of several planned GW detectors are also shown [30, 93,94,95,96,97].

Fig. 5
figure 5

Energy spectrum of the induced GWs at the present time predicted by Model I for parameter set (20) (left panel), and by Model II for parameter set (23) (right panel). The curves in the upper part are the expected sensitivity curves of the Square Kilometer Array (SKA), European Pulsar Timing Array (EPTA), Astrodynamical Space Test of Relativity using Optical-GW detector (ASTROD-GW), Taiji, Laser Interferometer Space Antenna (LISA), TianQin, Advanced Laser Interferometer Antenna (ALIA), Big Bang Observer (BBO), Deci-hertz Interferometer GW Observatory (DECIGO), Einstein Telescope (ET), Advanced LIGO (aLIGO), respectively. These sensitivity curves are taken from Refs. [30, 93,94,95,96,97] The green region shows the \(2 \sigma \) confidence level of the NANOGrav results with the tilt of \(5-\gamma =-1\) (left panel) and \(5-\gamma =-1.5\) (right panel) [37]

Full size image

We can see that the energy spectrum of the induced GWs has double peaks. The peak at low frequency, about \(10^{-9}\)–\(10^{-8}Hz\), lies above the expected sensitivity curves of SKA and EPTA for both models, and the peak at high frequency, about 0.01–1Hz, is within the frequency range of LISA [93], ALIA, Taiji [94] and TianQin [96], and the energy spectrum curves lie above the expected sensitivity curves. So such a kind of GWs can be detected in near future.

Table 2 The numerical results of PBHs production for the two models
Full size table
Fig. 6
figure 6

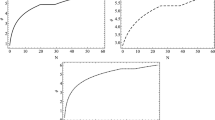
The abundance of PBHs produced in Model I for parameter set (20) (left panel), and in Model II for parameter set (23) (right panel). The curves in the upper part are the observational constraints on the PBH abundance, which are taken from Ref. [80]

Full size image

Recently, the NANOGrav collaboration has published an analysis of 12.5-year of PTA, which can be explained by the stochastic GWs [37,38,39,40,41]. The potential GW signal can be fitted by a power-law spectrum around \(f_{{\mathrm{yr}}}\simeq 3.1\times 10^{-8}\) Hz,

$$\begin{aligned} \Omega _{{\mathrm{GW}}}(f)=\frac{2\pi ^2f_{{\mathrm{yr}}}^2}{3H_0^2}A^2_{{\mathrm{GWB}}}\left( \frac{f}{f_{{\mathrm{yr}}}}\right) ^{5-\gamma }, \end{aligned}$$
(29)

where \(H_0\equiv 100 h\) km/s/Mpc and the exponent \(5-\gamma \in (-1.5,0.5)\) at \(1\sigma \) confidence level. In Fig. 5 we also show the observed GWs for \(5-\gamma =-1\) (left panel) and \(5-\gamma =-1.5\) (right panel) with \(2 \sigma \) uncertainty on \(A_{{\mathrm{GWB}}}\). We can see that the peak of induced GW spectrum at frequencies around nanohertz can also explain the NANOGrav signals.

In addition, since the energy spectrum has two peaks, if one of the peaks at nHz is detected by observers, the other peak at 0.01 Hz should be detected by other detectors, like LISA, in the future. Thus it is different from the models with only one peak, which can only be detected in one frequency range. So the double peak models can be distinguished from other single peak models [16,17,18,19, 98,99,100].

4.3 Production of primordial black holes

When the large amplitude of primordial fluctuations re-enters the Hubble horizon after inflation, it will undergo gravitational collapse and form PBHs if the fluctuation is significantly large. The mass of the resulting PBHs is assumed to be proportional to the horizon mass at re-entry time,

$$\begin{aligned} M=\gamma M_H=\gamma \frac{4}{3}\pi \rho H^{-3}, \end{aligned}$$
(30)

which can be approximated by [101]

$$\begin{aligned} M\simeq 10^{18} \text {g} \left( \frac{\gamma }{0.2}\right) \left( \frac{g_*}{106.75}\right) ^{-1/6} \left( \frac{k}{7\times 10^{13}~\text {Mpc}^{-1}}\right) ^{-2}, \end{aligned}$$
(31)

where \(\gamma \sim 0.2\) depends on the details of the gravitational collapse [102], and \(g_*\sim 106.75\) is for the effective degrees of freedom for energy density.

In the context of the Press–Schechter model of gravitational collapse, assuming that the probability distribution of density perturbations is Gaussian with width \(\sigma (M)\), the mass fraction in PBHs of mass M is given by

$$\begin{aligned} \beta (M)\equiv \frac{\rho _{{\mathrm{PBH}}}(M)}{\rho _{{\mathrm{tot}}}}= & {} \frac{1}{\sqrt{2 \pi \sigma ^2(M)}}\int ^{\infty }_{\delta _c}d\delta \text {exp}\left( \frac{-\delta ^2}{2 \sigma ^2(M)}\right) \nonumber \\= & {} \frac{1}{2}\text {erfc}\left( \frac{\delta _c}{\sqrt{2\sigma ^2(M)}}\right) , \end{aligned}$$
(32)

where \(\delta _c\simeq 0.45\) is the threshold for collapse [103, 104]. The variance of the comoving density perturbations \(\sigma ^2(M)\) is assumed to be coarse-grained at a scale \(R=1/k\), during the radiation-dominated era, which is given by

$$\begin{aligned} \sigma ^2(M(k))=\frac{16}{81}\int \frac{{\mathrm{d}}q}{q}(qR)^4P_{R}(q)W(qR)^2, \end{aligned}$$
(33)

with the smoothing window function W(x) taken to be a Gaussian, \(W(x)=\text {exp}(-x^2/2)\). Then integrating over all masses M one can get the present abundance of PBHs,

$$\begin{aligned} \Omega _{{\mathrm{PBH}}}=\int \frac{{\mathrm{d}}M}{M}\Omega _{{\mathrm{PBH}}}(M), \end{aligned}$$
(34)

with

$$\begin{aligned}&\frac{\Omega _{{\mathrm{PBH}}}(M)}{\Omega _{{\mathrm{DM}}}}{=}\left( \frac{\beta (M)}{1.6\times 10^{-16}}\right) \left( \frac{\gamma }{0.2}\right) ^{3/2} \left( \frac{g_*}{106.75}\right) ^{-1/4} \left( \frac{M}{10^{18} \text {g}}\right) ^{-1/2},\nonumber \\ \end{aligned}$$
(35)

where \(\Omega _{{\mathrm{DM}}}\simeq 0.26\) is the total dark matter abundance [105].

The numerical results show that the two peak models can give rise to two PBHs populations with different masses. The results of the PBHs mass and abundance are presented in Table 2.

We can see that only one type of PBHs with mass around \(10^{-16}{-}10^{-15}M_{\odot }\) can be a significant fraction of dark matter, and the abundance of the other mass is too small. The abundance of PBHs for the two models and the observational constraints from Ref. [80] are shown in Fig. 6

5 Summary

In this paper, we investigate the possibility to induce double peaks of the GW spectrum from single-field inflationary models with inflection points. We found that such a double peak spectrum can be realized by the polynomial potential from effective field theory with a cut-off scale (Model I) or realized by the Higgs-like \(\phi ^4\) potential with the running of a quartic coupling from radiative corrections (Model II). In order to generate an inflationary potential with three inflection points, and make the predictions fall in the observational windows, fine-tuning of several parameters and the initial condition on the scalar field is necessary. We find that, for some choices of parameter sets, the inflection point at large scales makes the prediction of the scalar spectral index and the tensor-to-scalar ratio consistent with the current CMB constraints, and the other two inflection points generate two large peaks in the power spectrum at small scales to induce GWs with a double peak spectrum. We calculated the energy spectrum of GWs numerically and have shown that the peak at low frequency \(10^{-9}{-}10^{-8}~\text {Hz}\) lies above the expected sensitivity curves of SKA and EPTA, which can explain the NANOGrav signal. The peak at high frequency \(0.01{-}1~\text {Hz}\) lies above the expected sensitivity curves of LISA, ALIA, Taiji, TianQin, etc., so it can be detected in the near future. In addition, since the double peak energy spectrum can be detected by observers in different frequency ranges, it can be distinguished from other, single peak, models. Moreover, we also calculated the abundance of PBHs produced in the two models using the Press–Schechter approach [84] of gravitational collapse, and we found that the PBHs with the mass around \(10^{-16}{-}10^{-15}M_{\odot }\) can account for a significant fraction of dark matter.