Averaging generalized scalar field cosmologies I: locally rotationally symmetric Bianchi III and open Friedmann–Lemaître–Robertson–Walker models

Abstract

Scalar field cosmologies with a generalized harmonic potential and a matter fluid with a barotropic Equation of State (EoS) with barotropic index $\gamma$ for locally rotationally symmetric (LRS) Bianchi III metric and open Friedmann–Lemaître–Robertson–Walker (FLRW) metric are investigated. Methods from the theory of averaging of nonlinear dynamical systems are used to prove that time-dependent systems and their corresponding time-averaged versions have the same late-time dynamics. Therefore, simple time-averaged systems determine the future asymptotic behavior. Depending on values of barotropic index $\gamma$ late-time attractors of physical interests for LRS Bianchi III metric are Bianchi III flat spacetime, matter dominated FLRW universe (mimicking de Sitter, quintessence or zero acceleration solutions) and matter-curvature scaling solution. For open FLRW metric late-time attractors are a matter dominated FLRW universe and Milne solution. With this approach, oscillations entering nonlinear system through Klein–Gordon (KG) equation can be controlled and smoothed out as the Hubble factor H – acting as a time-dependent perturbation parameter – tends monotonically to zero. Numerical simulations are presented as evidence of such behaviour.

1 Introduction

Scalar fields have played important roles in the physical description of the universe in inflationary scenario [1, 2] as well as an explanation of late time acceleration of the universe. Examples of the latter are a quintessence scalar field [3,4,5,6] (generalizing the cosmological constant), a phantom scalar field (which, however, suffers ghosts instabilities [7]), a quintom scalar field model [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], a chiral cosmology [25,26,27,28], or multi-scalar field models (which describe various epochs of the cosmological history [29,30,31]). Scalar field theories like scalar tensor theories, and many others have been exhaustively studied for example in [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109] by means of qualitative techniques of dynamical systems from [110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126]. Some works related to Einstein–Klein–Gordon, Maxwell, Yang–Mills, Einstein–Vlasov systems, etc., are also studied in [127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145]. Perturbation methods and averaging methods were used in [127, 128] with interest in early and late-time dynamics. Slow-fast methods were used, for example, in theories based on a generalized uncertainty principle (GUP), say in [146, 147]. The amplitude-angle transformation was used in [148, 149] to study scalar field’s oscillations driven by generalized harmonic potentials. In reference [150] interacting scalar field cosmologies with generalized harmonic potentials for flat and negatively curved FLRW metrics, and for Bianchi I metrics were studied. Asymptotic and averaging methods were used to obtain stability conditions for several solutions of interest as $H \rightarrow 0$, where H is the Hubble parameter. These results suggest that the asymptotic behavior of time-averaged model is independent of coupling function and geometry. Averaging theory was used in reference [151] to study periodic orbits of Hamiltonian systems describing a universe filled with a scalar field; and in reference [152] to study future asymptotics of LRS Bianchi type III cosmologies with a massive scalar field. In reference [153] a theorem about large-time behaviour of solutions of Spatially Homogeneous (SH) cosmology with oscillatory behaviour (when H is non negative and monotonic decreasing to zero) was presented. In references [149, 154] scalar field cosmologies with arbitrary potential and with arbitrary coupling to matter were studied. In particular, generalized harmonic potentials and exponential couplings to matter in the sense of [101,102,103,104] were examined. This paper is a sequel of [149, 154], where asymptotic methods and averaging theory [155,156,157,158,159,160,161] were used to obtain relevant information about solution’s space of scalar field cosmologies with generalized harmonic potential: (i) in vacuum, (ii) in presence of matter. As in [152], we construct averaged versions of original systems where oscillations of solutions are smoothed out. Then, the analysis is reduced to study late-time dynamics of a simpler averaged system where oscillations entering the full system through KG equation can be controlled.

This research program – named “Averaging Generalized Scalar Field Cosmologies”– has three steps according to three cases of study: (I) Bianchi III and open FLRW model, (II) Bianchi I and flat FLRW model and (III) Kantowski–Sachs (KS) and closed FLRW. This paper is devoted to case I, and cases II and III will be studied in two companion papers [164, 165]. The main aspect in the present work is the interaction of KG fields and field equations. The paper is organized as follows. In Sect. 2 we discuss the class of generalized harmonic potentials in which we are interested. In Sect. 3 we introduce the models. In Sect.  4 we apply averaging methods to analyze periodic solutions of a scalar field with self-interacting potentials within the class of generalized harmonic potentials [148]. In particular, in Sect. 4.3 LRS Bianchi III metric is studied. In Sect. 4.4 is investigated FLRW metrics with negative curvature. In Sect. 5 we study averaged systems. Bianchi III metric is studied in Sects. 5.1, and 5.2 is devoted to FLRW metric with negative curvature (open FLRW). Finally, in Sect. 6 our main results are discussed. In  Appendix A is proved our main Theorem. In  Appendix B center manifold calculations for nonhyperbolic equilibrium points are presented. In  Appendix C numerical evidences supporting the results of Sect. 4 are presented.

2 Generalized harmonic potential

Chaotic inflation is a model of cosmic inflation which takes the potential term V of a hypothetical inflaton field $\phi$ as $V(\phi )= \frac{m_\phi ^2 \phi ^2}{2}$, the so-called harmonic potential ($\phi ^2$-interaction) [201,202,203,204]. Whereas other inflationary models assume a monotonic decreasing potential with $\phi$; assuming in an ad hoc way that inflaton field has a large amplitude “at Big Bang”, then slowly “roll down” the potential. The idea of [201] is that instead of inflaton rolls down and sits on its potential minimum at equilibrium, quantum fluctuations stochastically (“chaotically”) drive it out of its minimum back and forward. Wherever this happens cosmic inflation sets in and blows up the region of ambient spacetime in which inflaton happened to fluctuate out of its equilibrium. Relevant experimental results disfavoring $\phi ^2$-interaction are due to [205, 206]. These results state that chaotic inflation generically predicts large values of tensor-to-scalar ratio r. In contrast to recent measurements which show low upper bounds on r. Notwithstanding, we investigate variations of $\phi ^2$-potential and we do not refer to tensor-to-scalar ratio issue for the potential (4).

The action integral of interest is

$$\begin{aligned}&\int d{ }^4 x \sqrt{|g|}\left[ \frac{1}{2} R -\frac{1}{2} g^{\mu \nu }\nabla _\mu \phi \nabla _\nu \phi -V(\phi )+ {\mathscr {L}}_{m}\right] . \end{aligned}$$

(1)

It is expressed in a system of units in which $8\pi G=c=\hslash =1$ where ${\mathscr {L}}_{m}$ is the Lagrangian density of matter, R is the curvature scalar, $\phi$ is the scalar field, $\nabla _\alpha$ is the covariant derivative and the scalar field potential $V(\phi )$ of interest in this research is given by

$$\begin{aligned} V(\phi )= \mu ^3 \left[ b f \left( 1-\cos \left( \frac{\phi }{f}\right) \right) +\frac{\phi ^2}{\mu }\right] , \quad b> 0. \end{aligned}$$

(2)

It is related but not equal to monodromy potential of [162] used in the context of loop-quantum gravity, which is a particular case of general monodromy potential [163]. In references [148,149,150] were proved that potential of [162, 163] for $p=2$, say $V(\phi )= \mu ^3 \left[ \frac{\phi ^2}{\mu } + b f \cos \left( \frac{\phi }{f}\right) \right]$, $b\ne 0$ is not good to describe the late-time FLRW universe driven by a scalar field because it has two symmetric local negative minimums which are related to Anti-de-Sitter solutions.

Fig. 1

Generalized harmonic potentials. Comparison with $\phi$-squared potentials

Therefore, in [148, 149] we have studied the potential

$$\begin{aligned} V(\phi )= \frac{\phi ^2}{2}+ f\left[ 1- \cos \left( \frac{\phi }{f}\right) \right] \end{aligned}$$

(3)

obtained by setting $\mu =\frac{\sqrt{2}}{2}$ and $b \mu =2$ in Eq. (2). The potential (3) provides non-negative local minimums which can be related to a late-time accelerated universe. In Sect. 2.4 of [149] a scalar field cosmology with potential (3) non–minimally coupled to matter with coupling function $\chi =\chi _0 e^{\frac{\lambda \phi }{4-3\gamma }}$ was studied, where $\lambda$ is a constant and the barotropic index satisfies $0\le \gamma \le 2, \quad \gamma \ne \frac{4}{3}$ for FLRW metrics with $k=-1, 0$ and Bianchi I metric. The late time attractors are associated to equilibrium points with $\phi =\phi ^*$ whenever $\phi ^*$ is a local non zero minimum of $V(\phi )$. For FLRW metrics, global minimum is unstable to curvature perturbations for $\gamma >\frac{2}{3}$. Therefore, the result in [107] is confirmed, that for $\gamma >\frac{2}{3}$ the curvature has a dominant effect on late evolution of the universe and it will eventually dominate both perfect fluid and scalar field energy densities. For Bianchi I model, the global minimum with $V(0)=0$ is unstable to shear perturbations.

Additionally, potentials like $V(\phi )=\varLambda ^4 \left[ 1- \cos \left( \frac{\phi }{f}\right) \right]$ are of interest in context of axion models [207]. In [208] axionic dark matter model with a modified periodic potential for pseudoscalar field $V(\phi , \varPhi _*)= \frac{m_A^2 {\varPhi _*}^2}{2 \pi ^2}\left[ 1- \cos \left( \frac{2 \pi \phi }{\varPhi _*}\right) \right]$ in the framework of axionic extension of Einstein-aether theory was studied. This periodic potential has minima at $\phi =n \varPhi _*, n \in {\mathbb {Z}}$, whereas maxima when $n \rightarrow m + \frac{1}{2}$ are found. Near the minimum when $\phi =n \varPhi _* + \psi$ and $|\psi |$ is small, $V \rightarrow \frac{m_A^2 \psi ^2}{2}$ where $m_A$ the axion rests mass.

The previous statements justify the study of potential (2), which can be expressed as

$$\begin{aligned} V(\phi )=\mu ^2 \phi ^2 + f^2 \left( \omega ^2-2 \mu ^2\right) \left( 1-\cos \left( \frac{\phi }{f}\right) \right) , \end{aligned}$$

(4)

by introducing an angular frequency $\omega \in {\mathbb {R}}$ through conditions $b \mu ^3+2 f \mu ^2-f \omega ^2=0$ and $\omega ^2-2 \mu ^2>0$. Their applicability will be revealed in Sect. 4.

The generalized harmonic potentials (3) and (4) belong to the class of potentials studied by [127]. Potential (4) has the following generic features:

• 1. V is a real-valued smooth function $V\in C^{\infty } ({\mathbb {R}})$ with $\lim _{\phi \rightarrow \pm \infty } V(\phi )=+\infty$.

• 2. V is an even function $V(\phi )=V(-\phi )$.

• 3. $V(\phi )$ has always a local minimum at $\phi =0$; $V(0)=0, V'(0)=0, V''(0)= \omega ^2> 0$.

• 4. There is a finite number of values $\phi _c \ne 0$ satisfying $2 \mu ^2 \phi _c +f \left( \omega ^2-2 \mu ^2\right) \sin \left( \frac{\phi _c }{f}\right) =0$, which are extreme points of $V(\phi )$. They are local maximums or local minimums depending on whether $V''(\phi _c):= 2 \mu ^2+\left( \omega ^2- 2 \mu ^2\right) \cos \left( \frac{\phi _c }{f}\right) <0$ or $V''(\phi _c)>0$. For $\left| \phi _c\right| >\frac{f(\omega ^2-2 \mu ^2)}{2 \mu ^2}= \phi _*$ this set is empty.

• 5. There exist $V_{\max }= \max _{\phi \in [-\phi _*,\phi _*]} V(\phi )$ and $V_{\min }= \min _{\phi \in [-\phi _*,\phi _*]} V(\phi )=0$. The function V has no upper bound but it has a lower bound equal to zero.

The asymptotic features of potential (4) are the following. Near global minimum $\phi =0$, we have $V(\phi ) \sim \frac{\omega ^2 \phi ^2}{2}+{\mathscr {O}}\left( \phi ^3\right) , \quad \text {as} \; \phi \rightarrow 0$. That is, $\omega ^2$ can be related to the mass of the scalar field near its global minimum. As $\phi \rightarrow \pm \infty$ cosine- correction is bounded, then, $V(\phi ) \sim \mu ^2 \phi ^2+{\mathscr {O}}\left( 1\right) \quad \text {as} \; \phi \rightarrow \pm \infty$. This makes it suitable to describe oscillatory behavior in cosmology.

Setting $\mu =\frac{\sqrt{2}}{2}$, $\omega =\sqrt{2}$, we have

$$\begin{aligned} V(\phi )= \frac{\phi ^2}{2} + f^2 \left[ 1-\cos \left( \frac{\phi }{f}\right) \right] . \end{aligned}$$

(5)

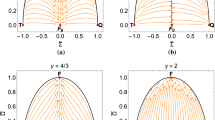
Setting $\mu =\frac{\sqrt{2}}{2}, \; \omega = \sqrt{\frac{f-1}{f}}$, the potential of [148,149,150] (3) is recovered. Although (3) can be derived as a particular case of our study, cases of interest with $f\ll 1$ leads to complex frequency $\omega = \sqrt{|\frac{f-1}{f}|} i$, in contradiction to $\omega \in {\mathbb {R}}$. Therefore, potential (4) will not contain potential studied in [148,149,150], unless we set $f>1$ and $\omega = \sqrt{\frac{f-1}{f}}$. In Fig. 1 potentials (5) and (3) are depicted.

3 Spatially homogeneous scalar field cosmologies

In general relativity (GR) the SH but anisotropic spacetimes are known as either Bianchi or KS metrics. In Bianchi models, the spacetime manifold is foliated along the time axis with three dimensional homogeneous hypersurfaces. Bianchi spacetimes contain many important cosmological models that have been used to study anisotropies of primordial universe and its evolution towards current observed isotropy [166,167,168,169]. The list includes standard FLRW model in the limit of isotropization; Bianchi III isotropizing to open FLRW models and Bianchi I isotropizing to flat FLRW models. Hubble parameter H is always monotonic for Bianchi I and Bianchi III. For Bianchi I anisotropy decays on time for $H>0$ and isotropization occurs [170].

There is an interesting hierarchy in Bianchi models [121, 171,172,173]. In particular, LRS Bianchi I model naturally appears as a boundary subset of LRS Bianchi III model. The last one is an invariant boundary of the LRS Bianchi type VIII model as well. Additionally, LRS Bianchi type VIII can be viewed as an invariant boundary of LRS Bianchi type IX model [174,175,176,177,178,179,180]. Bianchi spacetimes in presence of a scalar field were studied in [181]. It was proved that an initial anisotropic universe isotropizes into a FLRW universe for specific initial conditions if the scalar field potential has a large positive value. An exact solution of field equations for an exponential potential in some particular Bianchi spacetimes has been found in [182,183,184]. These exact solutions lead to isotropic homogeneous spacetimes as it was found in [185, 186]. An anisotropic solution of special interest is Kasner spacetime. Kasner solution is essential for the description of BKL singularity when the contribution of Ricci scalar of three-dimensional spatial hypersurface in the field equations is negligible [187]. For other applications of Kasner universe and Bianchi I spacetimes in gravitational physics see [188,189,190,191,192,193,194,195] and references therein. In [196] the conformal algebra of Bianchi III and Bianchi V spacetimes which admit a proper conformal Killing vector were studied. In [197] method of Lie symmetries was applied for the Wheeler–De Witt equation in Bianchi class A cosmologies for minimally coupled scalar field gravity and hybrid gravity in GR. Using these symmetries several invariant solutions were determined and classified according to the form of scalar field potential.

3.1 LRS Bianchi III, Bianchi I and Kantowski–Sachs models

Due to

$$\begin{aligned} \lim _{k\rightarrow -1} k^{-1} \sin ^2 (\sqrt{k} \vartheta )&=\sinh ^2 (\vartheta ), \end{aligned}$$

(6)

$$\begin{aligned} \lim _{k\rightarrow 0} k^{-1} \sin ^2 (\sqrt{k} \vartheta )&= \vartheta ^2, \end{aligned}$$

(7)

$$\begin{aligned} \lim _{k\rightarrow 1} k^{-1} \sin ^2 (\sqrt{k} \vartheta )&=\sin ^2 (\vartheta ), \end{aligned}$$

(8)

the metric element for LRS Bianchi III, Bianchi I and KS models can be written as [198]

$$\begin{aligned} ds^2&= - dt^2 + \left[ {e_1}^1(t)\right] ^{-2} dr^2 \nonumber \\&\quad + \left[ {e_2}^2(t)\right] ^{-2} \left[ d \vartheta ^2 + k^{-1} \sin ^2 (\sqrt{k} \vartheta )d \zeta ^2\right] , \end{aligned}$$

(9)

where ${e_1}^1$, ${e_2}^2$ and ${e_3}^3= \sqrt{k} {e_2}^2/\sin (\sqrt{k} \vartheta )$ are functions of t which are components of the frame vectors [200]: ${\mathbf {e}}_0= \partial _t, \quad {\mathbf {e}}_1 = {e_1}^1\partial _r, \quad {\mathbf {e}}_2={e_2}^2 \partial _\vartheta , \quad {\mathbf {e}}_3={e_3}^3 \partial _\zeta$. That is, we obtain LRS Bianchi III for $k=-1$, Bianchi I for $k=0$ and KS for $k=+1$ [62]. Comparing with reference [198] we have settled parameters $a=f=0$ and ${e_1}^1(t)=D_2(t)^{-1}, \; {e_2}^2(t)=D_2(t)^{-1}$ in their metric and we have used the identifications $(\vartheta , \zeta )=(y, z)$. The line elements for spatially selfsimilar LRS models have been given by Wu in [199]. We only focus on SH but anisotropic class with the exception of SH LRS Bianchi V, that is: LRS Bianchi III, Bianchi I and KS.

It is useful to define a representative length along worldlines of the 4-velocity vector ${\mathbf {u}}=\partial _t$ describing the volume expansion (contraction) of the congruence, denoted $\ell (t)$ and defined by

$$\begin{aligned} \frac{{\dot{\ell }}(t)}{\ell (t)}= H(t):= -\frac{1}{3}\frac{d}{d t} \ln \left[ {e_1}^1(t) ( {e_2}^2(t))^2\right] , \end{aligned}$$

(10)

where the Hubble parameter H(t) and the anisotropic parameter $\sigma _{+}(t)$ are given by

$$\begin{aligned} \sigma _+ = \frac{1}{3}\frac{d}{d t} \ln \left[ {e_1}^1(t) ( {e_2}^2(t))^{-1}\right] . \end{aligned}$$

(11)

Taking variation of (1) for the 1-parameter family of metrics (9) leads to [62]:

$$\begin{aligned}&3 H^2 + k K = 3 {\sigma _+}^2+ \rho _m + \frac{1}{2}{\dot{\phi }}^2 +V(\phi ), \end{aligned}$$

(12)

$$\begin{aligned}&-3 ({\sigma _+}+H)^2 -2 \dot{\sigma _+}- 2 {\dot{H}} - k K \nonumber \\&\quad = (\gamma -1)\rho _m + \frac{1}{2}{\dot{\phi }}^2-V(\phi ), \end{aligned}$$

(13)

$$\begin{aligned}&-3 {\sigma _+}^2 +3 {\sigma _+} H-3 H^2 + \dot{\sigma _+}- 2 {\dot{H}} \nonumber \\&\quad = (\gamma -1)\rho _m + \frac{1}{2}{\dot{\phi }}^2-V(\phi ). \end{aligned}$$

(14)

For modeling matter in our model we use a perfect fluid with a barotropic EoS $p_m=(\gamma -1)\rho _m$ with pressure $p_{m}$, energy density $\rho _{m}$ and barotropic index $\gamma \in [0,2]$.

The Gauss curvature of spatial 2-space and 3-curvature scalar are

$$\begin{aligned} K= ( {e_2}^2(t))^{2}, \quad {}^3\!R= 2 k K. \end{aligned}$$

(15)

Furthermore, evolution of K is

$$\begin{aligned} {\dot{K}}= -2 ({\sigma _+}+ H)K, \end{aligned}$$

(16)

while evolution for ${e_1}^1$ is given by [200]:

$$\begin{aligned} \dot{{e_1}^1}= - (H-2 \sigma _+){e_1}^1. \end{aligned}$$

(17)

From Eqs. (13), (14) the shear equation is obtained:

$$\begin{aligned} \dot{\sigma _+}= -3 H {\sigma _+} -\frac{k K}{3}. \end{aligned}$$

(18)

Equations (12), (13), (14), (18) give the Raychaudhuri equation:

$$\begin{aligned} {\dot{H}}=- H^2 -2 {\sigma _+}^2 -\frac{1}{6}(3 \gamma -2) \rho _m -\frac{1}{3}\dot{\phi }^2+\frac{1}{3} V(\phi ). \end{aligned}$$

(19)

Finally, the matter and KG equations are:

$$\begin{aligned} \dot{\rho _m}&=-3 \gamma H \rho _m, \end{aligned}$$

(20)

$$\begin{aligned} \ddot{\phi }&= -3 H \dot{\phi }- \frac{d V(\phi )}{d \phi }. \end{aligned}$$

(21)

In this paper we will study LRS Bianchi III model. By convenience we write

$$\begin{aligned}&ds^2= - dt^2 + A(t)^2 dr^2 + B(t)^2 {\mathbf {g}}_{H^2}. \end{aligned}$$

(22)

where ${\mathbf {g}}_{H^2}= d \vartheta ^2 + \sinh ^2 (\vartheta )d \zeta ^2$ denotes the 2-metric of negative constant curvature on hyperbolic 2-space. The functions A(t) and B(t), interpreted as scale factors, are defined as $A(t)= {e_1}^1(t)^{-1}$ and $B(t)^2= K(t)^{-1}$.

3.2 FLRW models

The general line element for spherically symmetric (SS) models can be written as [200]

$$\begin{aligned} ds^2&= - dt^2 + \left[ {e_1}^1(t,r)\right] ^{-2} dr^2 \nonumber \\&\quad + \left[ {e_2}^2(t,r)\right] ^{-2} (d\vartheta ^2 + \sin ^2 \vartheta \, d\zeta ^2). \end{aligned}$$

(23)

SH-SS models that are not Kantowski–Sachs are FLRW models where the metric can be written as

$$\begin{aligned}&ds^2 = - dt^2 + a^2(t) \Big [ dr^2+ f^2(r) (d\vartheta ^2 + \sin ^2 \vartheta \, d\zeta ^2)\Big ], \end{aligned}$$

(24)

$$\begin{aligned}&\text {with}\; f(r) = \sin r,\ r,\ \sinh r \end{aligned}$$

(25)

for closed, flat and open FLRW models, respectively. In comparison with metric (23), frame coefficients here are given by $e_1{}^1= a^{-1}(t)$ and $e_2{}^2= a^{-1}(t) f^{-1}(r)$ where a(t) is the scale factor. Anisotropic parameter $\sigma _{+}= \frac{1}{3}\frac{\partial }{\partial t} \ln (e_1{}^1/e_2{}^2)$ vanishes and Hubble parameter (10) can be written as $H = \frac{d}{d t} \ln \left[ a(t)\right]$. Furthermore, ${}^3\!R$ is

$$\begin{aligned} {}^3\!R= \frac{6k}{a^2},\quad k = 1,0,-1, \end{aligned}$$

(26)

for closed, flat and open FLRW models, respectively. Therefore, evolution/constraint equations are reduced to

$$\begin{aligned} \ddot{\phi }&= -3 H \dot{\phi }-V'(\phi ) \end{aligned}$$

(27a)

$$\begin{aligned} \dot{\rho _m}&=- 3\gamma H\rho _m, \end{aligned}$$

(27b)

$$\begin{aligned} {\dot{a}}&= a H, \end{aligned}$$

(27c)

$$\begin{aligned} {\dot{H}}&=-\frac{1}{2}\left( \gamma \rho _m+{{\dot{\phi }}}^2\right) +\frac{k}{a^2}, \end{aligned}$$

(27d)

$$\begin{aligned} 3H^2&=\rho _m+\frac{1}{2}{\dot{\phi }}^2+V(\phi )-\frac{3 k}{a^2}. \end{aligned}$$

(27e)

By setting ${\dot{\phi }}=\rho _m=0$ and $V(\phi )=\varLambda$ we obtain vacuum cases (with or without cosmological constant $\varLambda$), which are de Sitter model ($\varLambda >0$, $k=0$), the model with $\varLambda >0$, $k=1$, the model with $\varLambda >0$, $k=-1$, Milne model ($\varLambda =0$, $k=-1$) and Minkowski spacetime ($\varLambda =0$, $k=0$), which is also static. The model with $\varLambda >0$, $k=1$ is past asymptotic to de Sitter model with negative H, and, is future asympotic to de Sitter model with positive H. The model with $\varLambda >0$, $k=-1$ (and positive H) is past asymptotic to Milne model and it is future asympotic to de Sitter model with positive H.

In this paper we will study open FLRW model. By convenience we write the metric (28) for $k=-1$ as

$$\begin{aligned}&ds^2= - dt^2 + a(t)^2 dr^2 + a(t)^2 S_{-1}(r)^2 d\varOmega ^2. \end{aligned}$$

(28)

where $S_{-1}(r)=\sinh (r), d\varOmega ^2= d\vartheta ^2 + \sin ^2 \vartheta \, d\zeta ^2$.

4 Averaging scalar field cosmologies

Given the differential equation $\dot{{\mathbf {x}}}= {\mathbf {f}}(t, {\mathbf {x}},\varepsilon )$ with ${\mathbf {f}}$ periodic in t. One approximation scheme which can be used to solve the full problem is solving the unperturbed problem $\dot{{\mathbf {x}}}= {\mathbf {f}}(t, {\mathbf {x}},0)$ by setting $\varepsilon =0$ and then use the approximated unperturbed solution to formulate variational equations in standard form which can be averaged. The term averaging is related to approximation of initial value problems in ordinary differential equations which involves perturbations [161, chapter 11].

4.1 Simple example

For example, consider this simple equation

$$\begin{aligned} {\ddot{\phi }} + \omega ^2 \phi = \varepsilon (-2 {\dot{\phi }}) \end{aligned}$$

(29)

with $\phi (0)$ and ${\dot{\phi }}(0)$ given. The unperturbed problem ${\ddot{\phi }} +\omega ^2 \phi = 0$ admits solution ${\dot{\phi }}(t)= r_0 \omega \cos (\omega t-\varPhi _0), \; \phi (t)= r_0 \sin (\omega t-\varPhi _0)$, where $r_0$ and $\varPhi _0$ are constants depending on the initial conditions. Let be defined the amplitude-phase transformation [161, chapter 11]:

$$\begin{aligned} \dot{\phi }(t)= r(t) \omega \cos (\omega t-\varPhi (t)), \; \phi (t) = r(t) \sin (\omega t-\varPhi (t)),\nonumber \\ \end{aligned}$$

(30)

such that

$$\begin{aligned} r=\frac{\sqrt{\dot{\phi }^2(t)+\omega ^2 \phi ^2(t)}}{\omega }, \; \varPhi =\omega t-\tan ^{-1}\left( \frac{\omega \phi (t)}{{\dot{\phi }}(t)}\right) . \end{aligned}$$

(31)

Then, Eq. (29) becomes

$$\begin{aligned} \dot{r}= -2 r \varepsilon \cos ^2(t-\varPhi ), \; {\dot{\varPhi }} = - \varepsilon \sin (2 (t-\varPhi )). \end{aligned}$$

(32)

From (32) it follows that r and $\varPhi$ are slowly varying with time, and the system takes the form $\dot{y}= \varepsilon f(y)$. The idea is consider only nonzero average of right-hand-sides keeping r and $\varPhi$ fixed and leaving out terms with average zero and ignoring slow-varying dependence of r and $\varPhi$ on t through averaging process:

$$\begin{aligned} \bar{{\mathbf {f}}}(\cdot ):=\frac{1}{L} \int _{0}^L {\mathbf {f}}(\cdot , t) dt, \quad L=\frac{2 \pi }{\omega }. \end{aligned}$$

(33)

Replacing r and $\varPhi$ by their averaged approximations ${\bar{r}}$ and ${\bar{\varPhi }}$ we obtain the system

$$\begin{aligned}&\dot{{\bar{r}}} = - \varepsilon \omega {\bar{r}}, \quad \dot{{\bar{\varPhi }}} = 0. \end{aligned}$$

(34)

Solving (34) with initial conditions ${\bar{r}}(0)=r_0$ and ${\bar{\varPhi }}(0)= \varPhi _0$, we obtain ${\bar{\phi }}= r_0 e^{-\varepsilon \omega t} \sin (\omega t-\varPhi _0)$, which is an accurate approximation of the exact solution

$$\begin{aligned} \phi (t)&= -r_0 e^{-t \varepsilon } \sin (\varPhi _0) \cos \left( t \sqrt{\omega ^2-\varepsilon ^2}\right) \\&\quad -\frac{r_0 e^{-t \varepsilon } \sin \left( t \sqrt{\omega ^2-\varepsilon ^2}\right) (\varepsilon \sin (\varPhi _0)-\omega \cos (\varPhi _0))}{\sqrt{\omega ^2-\varepsilon ^2}}, \end{aligned}$$

due to

$$\begin{aligned} {\bar{\phi }}(t) - \phi (t) = \frac{r_0 \varepsilon e^{-t \varepsilon } \sin (\varPhi _0) \sin (t \omega )}{\omega } + {\mathscr {O}}\left( \varepsilon e^{-t \varepsilon }\right) \end{aligned}$$

as $\varepsilon \rightarrow 0^+$.

4.2 General class of systems with a time-dependent perturbation parameter

Generalizing (29), now let us consider the KG system

$$\begin{aligned} {\ddot{\phi }} + \omega ^2 \phi&= -3 H {\dot{\phi }}, \end{aligned}$$

(35)

$$\begin{aligned} {\dot{H}}&= -\frac{1}{2}{\dot{\phi }}^2. \end{aligned}$$

(36)

The similarity between (29) and (35) suggests treating the latter as a perturbed harmonic oscillator as well, and applying averaging in an analogous way; taking into consideration that, in contrast to $\varepsilon$, H is time-dependent and itself is governed by evolution Eq. (36). If it is valid, then a surprising feature of such approach is the possibility of exploiting the fact that H is strictly decreasing and goes to zero, therefore, it can be promoted to a time-dependent perturbation parameter in (35); controlling the magnitude of the error between solutions of full and time-averaged problems. Hence, with strictly decreasing H the error should decrease as well. Therefore, it is possible to obtain information about large-time behaviour of more complicated full system via an analysis of simpler averaged system equations.

With this in mind, in [153] the long-term behavior of solutions of a general class of systems in standard form

$$\begin{aligned} \left( \begin{array}{c} {\dot{H}} \\ \dot{{\mathbf {x}}} \end{array}\right) = H \left( \begin{array}{c} 0 \\ {\mathbf {f}}^1 ({\mathbf {x}}, t) \end{array}\right) + H^2\left( \begin{array}{c} f^{[2]} ({\mathbf {x}}, t) \\ {\mathbf {0}} \end{array}\right) , \end{aligned}$$

(37)

was studied; where $H>0$ is strictly decreasing in t and $\lim _{t\rightarrow \infty }H(t)=0$.

The following Theorem by [153] gives local-in-time asymptotics for system (37). Let the norm $\Vert \cdot \Vert$ denotes the standard discrete $\ell ^1$- norm $\Vert {\mathbf {u}}\Vert := \sum _i^n |u_i|$ for ${\mathbf {u}}\in {\mathbb {R}}^n$. Let also $L_{{\mathbf {x}}, t}^\infty$ denotes the standard $L^{\infty }$ space in both t and ${\mathbf {x}}$ variables with norm defined as $\Vert {\mathbf {f}}\Vert _{L_{{\mathbf {x}}, t}^\infty }:= \sup _{{\mathbf {x}}, t}|{\mathbf {f}}({\mathbf {x}}, t)|.$

Theorem 1

(Theorem 3.1 of [153]) Suppose $H(t)>0$ is strictly decreasing in t and $\lim _{t\rightarrow \infty } H(t)=0.$ Fix any $\epsilon >0$ with $\epsilon <H(0)$ and define $t_*>0$ such that $\epsilon =H(t_*).$ Suppose that $\Vert {\mathbf {f}}^1\Vert _{L_{{\mathbf {x}}, t}^\infty },\quad \Vert f^{[2]}\Vert _{L_{{\mathbf {x}}, t}^\infty }<\infty$ and that ${\mathbf {f}}^1({\mathbf {x}}, t)$ is Lipschitz continuous and $f^{[2]}$ is continuous with respect to x for all $t\ge t_*.$ Also, assume that ${\mathbf {f}}^1$ and $f^{[2]}$ are T-periodic for some $T>0.$ Then for all $t>t_*$ with $t=t_*+{\mathscr {O}}\Big (H(t_*)^{-\delta }\Big )$ for any given $\delta \in (0,1)$ we have

$$\begin{aligned} {\mathbf {x}}(t)-{\mathbf {z}}(t)={\mathscr {O}}\Big (H(t_*)^{\min \{1,2-2\delta \}}\Big ), \end{aligned}$$

where ${\mathbf {x}}$ is the solution of system (37) with initial condition ${\mathbf {x}}(0)={\mathbf {x}}_0$ and ${\mathbf {z}}(t)$ is the solution of the time-averaged system

$$\begin{aligned} \dot{{\mathbf {z}}}=H(t_*)\bar{{\mathbf {f}}}^1({\mathbf {z}}),\quad \text {for} \quad t>t_*, \end{aligned}$$

with initial condition ${\mathbf {z}}(t_*)={\mathbf {x}}(t_*)$ where the time-averaged vector $\bar{{\mathbf {f}}}^1$ is defined as

$$\begin{aligned} \bar{{\mathbf {f}}}^1({\mathbf {z}})=\frac{1}{T}\int _{t_*}^{t_*+T}{\mathbf {f}}^1({\mathbf {z}},s)ds. \end{aligned}$$

Therefore, Hubble parameter H can be used as a time-dependent perturbation parameter.

In this paper we study systems which are not in the standard form (37) but can be expressed as a series with center in $H=0$ according to the equation

$$\begin{aligned} \left( \begin{array}{c} {\dot{H}} \\ \dot{{\mathbf {x}}} \end{array}\right)&= \left( \begin{array}{c} 0 \\ {\mathbf {f}}^0 ({\mathbf {x}}, t) \end{array}\right) + H \left( \begin{array}{c} 0 \\ {\mathbf {f}}^1 ({\mathbf {x}}, t) \end{array}\right) \nonumber \\&\quad + H^2\left( \begin{array}{c} f^{[2]} ({\mathbf {x}}, t) \\ {\mathbf {0}} \end{array}\right) + {\mathscr {O}}(H^3), \end{aligned}$$

(38)

depending on a parameter $\omega$ which is a free frequency that can be tuned to make ${\mathbf {f}}^0 ({\mathbf {x}}, t)= {\mathbf {0}}$. Therefore, systems can be expressed in the standard form (37).

4.3 LRS Bianchi III

Firstly, we consider LRS Bianchi III metrics for the generalized harmonic potential (2) minimally coupled to matter with field equations:

$$\begin{aligned} \ddot{\phi }&= -3 H \dot{\phi } - V'(\phi ), \end{aligned}$$

(39)

$$\begin{aligned} \dot{\rho _m}&= -3 \gamma H \rho _m, \end{aligned}$$

(40)

$$\begin{aligned} {\dot{K}}&= -2 ({\sigma _+} +H) K, \end{aligned}$$

(41)

$$\begin{aligned} {\dot{H}}&= -H^2 -2 {\sigma _+}^2 -\frac{1}{6} (3 \gamma -2) \rho _m -\frac{1}{3} {\dot{\phi }^2} +\frac{1}{3} V(\phi ), \end{aligned}$$

(42)

$$\begin{aligned} \dot{{\sigma _+}}&= -3 H {\sigma _+} +\frac{K}{3}, \end{aligned}$$

(43)

$$\begin{aligned} 3 H^2&= 3 {\sigma _+}^2 +\rho _m+\frac{1}{2}{\dot{\phi }}^2 +V(\phi )+K. \end{aligned}$$

(44)

Defining

$$\begin{aligned}&\varOmega =\sqrt{\frac{\omega ^2 \phi ^2+{{\dot{\phi }}}^2}{6 H^2}}, \; \varSigma =\frac{{\sigma _+}}{H}, \; \varOmega _k=\frac{K}{3 H^2}, \nonumber \\&\varPhi = t \omega -\tan ^{-1}\left( \frac{\omega \phi }{{\dot{\phi }}}\right) , \end{aligned}$$

(45)

we obtain the full system

$$\begin{aligned}&\dot{\varOmega }= -\frac{b \mu ^3}{\sqrt{6} H } \cos (t \omega -\varPhi ) \sin \left( \frac{\sqrt{6} H \sin (t \omega -\varPhi ) \varOmega }{f \omega }\right) \nonumber \\&\quad -\frac{b f \gamma \varOmega \mu ^3}{H } \sin ^2 \left( \frac{\sqrt{\frac{3}{2}} H \sin (t \omega -\varPhi ) \varOmega }{f \omega }\right) \nonumber \\&\quad +\frac{\left( \omega ^2-2 \mu ^2\right) \varOmega }{2 \omega } \sin (2 t \omega -2 \varPhi ) \nonumber \\&\quad + 3 H \left( \left( \gamma \left( \frac{ \mu ^2}{\omega ^2}-\frac{1}{2}\right) +1\right) \varOmega ^3- \varOmega \right) \cos ^2(t \omega -\varPhi ) \nonumber \\&\quad +\frac{1}{2} H \varOmega \Big (-3 (\gamma -2) \varSigma ^2-\frac{6 \gamma \mu ^2 \varOmega ^2}{\omega ^2} +3 \gamma +(2-3 \gamma ) {\varOmega _k} \Big ), \end{aligned}$$

(46a)

$$\begin{aligned} \dot{\varSigma }&= -\frac{b f \gamma \varSigma \mu ^3}{H } \sin ^2\left( \frac{\sqrt{\frac{3}{2}} H \sin (t \omega -\varPhi ) \varOmega }{f \omega }\right) \nonumber \\&\quad -\frac{3}{2} (\gamma -2) H \varSigma \varOmega ^2 \cos ^2(t \omega -\varPhi ) \nonumber \\&\quad +\frac{1}{4} H \Bigg (4 {\varOmega _k}-6 (\gamma -2) \varSigma ^3 +2 \Big (-\frac{6 \gamma \mu ^2 \varOmega ^2}{\omega ^2} \sin ^2(t \omega -\varPhi ) \nonumber \\&\quad +3 \gamma -3 \gamma {\varOmega _k} +2 {\varOmega _k} -6\Big ) \varSigma \Bigg ), \end{aligned}$$

(46b)

$$\begin{aligned} \dot{\varOmega _k}&= \frac{b f \gamma {\varOmega _k} \mu ^3}{H } \left( -1+\cos \left( \frac{\sqrt{6} H \sin (t \omega -\varPhi ) \varOmega }{f \omega }\right) \right) \nonumber \\&\quad -3 (\gamma -2) H \varOmega ^2 {\varOmega _k} \cos ^2(t \omega -\varPhi ) \nonumber \\&\quad +\frac{1}{2} H \Big (-6 (\gamma -2) \varSigma ^2-4 \varSigma -2 (3 \gamma -2) ( {\varOmega _k} -1) \nonumber \\&\quad -\frac{12 \gamma \mu ^2 \varOmega ^2}{\omega ^2} \sin ^2(t \omega -\varPhi ) \Big ) {\varOmega _k} , \end{aligned}$$

(46c)

$$\begin{aligned} \dot{\varPhi }&= -\frac{b \mu ^3}{\sqrt{6} H \varOmega } \sin (t \omega -\varPhi ) \sin \left( \frac{\sqrt{6} H \sin (t \omega -\varPhi ) \varOmega }{f \omega }\right) \nonumber \\&\quad +\frac{\left( \omega ^2-2 \mu ^2\right) }{\omega } \sin ^2(t \omega -\varPhi ) -3 \cos (t \omega -\varPhi ) H \sin (t \omega -\varPhi ), \end{aligned}$$

(46d)

and the Raychauhuri equation is

$$\begin{aligned}&{\dot{H}}= -(1+q) H^2, \end{aligned}$$

(46e)

where the deceleration parameter is given by

$$\begin{aligned} q&= -\frac{b f \gamma \mu ^3}{H ^2} \sin ^2 \scriptscriptstyle \left( \frac{\sqrt{\frac{3}{2}} H \sin (t \omega -\varPhi ) \varOmega }{f \omega }\right) \nonumber \\&\quad -\frac{3}{2} (\gamma -2) \cos ^2(t \omega -\varPhi ) \varOmega ^2 -\frac{3}{2} (\gamma -2) \varSigma ^2 \nonumber \\&\quad -\frac{3 \gamma \mu ^2 \varOmega ^2}{\omega ^2} \sin ^2(t \omega -\varPhi ) - \frac{1}{2} (3 \gamma -2) ( {\varOmega _k} -1). \end{aligned}$$

(47)

Defining ${\mathbf {x}}= \left( \varOmega , \varSigma , \varOmega _k, \varPhi \right) ^T$, the system (46) can be symbolically written as a Taylor series of the form (38). Notice that the term

$$\begin{aligned} {\mathbf {f}}^0 (t, {\mathbf {x}})= & {} \left( \begin{array}{c} \frac{\varOmega (t) \left( f \omega ^2-\mu ^2 (b \mu +2 f)\right) \sin (2 t \omega -2 \varPhi (t))}{2 f \omega } \\ 0 \\ \frac{\left( -b \mu ^3-2 f \mu ^2+f \omega ^2\right) \sin ^2(t \omega -\varPhi (t))}{f \omega } \\ 0 \\ \end{array} \right) \end{aligned}$$

(48)

in expression (38) is eliminated imposing the condition $b \mu ^3+2 f \mu ^2-f \omega ^2=0$, which defines an angular frequency $\omega \in {\mathbb {R}}$. Then, order zero terms in the series expansion around $H=0$ are eliminated assuming $\omega ^2>2 \mu ^2$ and setting $f=\frac{b \mu ^3}{\omega ^2-2 \mu ^2}$, which is equivalent to tune $\omega$. Hence, we obtain:

$$\begin{aligned} \dot{{\mathbf {x}}}&= H {\mathbf {f}}(t, {\mathbf {x}})+ {\mathscr {O}}(H^2), \end{aligned}$$

(49)

$$\begin{aligned} {\dot{H}}&= -\frac{3}{2} H^2 \Big (\gamma (1- \varSigma ^2- {\varOmega _k}-\varOmega ^2) +2 \varSigma ^2 +\frac{2}{3}{\varOmega _k} \nonumber \\&\quad + 2 \varOmega ^2 \cos ^2(t \omega -\varPhi ) \Big ) +{\mathscr {O}}(H^3), \end{aligned}$$

(50)

where

$$\begin{aligned} {\mathbf {f}}(t, {\mathbf {x}})&= \left( \begin{array}{c} \frac{1}{2} \varOmega \Big (-3 (\gamma -2) \varSigma ^2+(2-3 \gamma ) {\varOmega _k} +3 \left( \varOmega ^2-1\right) (-\gamma +2 \cos ^2(t \omega -\varPhi ))\Big ) \\ \\ \frac{1}{2} \Bigg ( {\varOmega _k} ((2-3 \gamma ) \varSigma +2) +3 \varSigma \Big (-(\gamma -2) \varSigma ^2+\gamma +\varOmega ^2 (-\gamma +2 \cos ^2(t \omega -\varPhi ))-2\Big )\Bigg )\\ \\ {\varOmega _k} \Big (-3 \gamma \left( \varSigma ^2+\varOmega ^2+ {\varOmega _k}-1\right) +6 \varSigma ^2-2 \varSigma + 6 \varOmega ^2 \cos ^2(t \omega -\varPhi ) +2 {\varOmega _k}-2\Big ) \\ \\ -\frac{3}{2} \sin (2 t \omega -2\varPhi ) \end{array} \right) . \end{aligned}$$

(51)

Replacing $\dot{{\mathbf {x}}}= H {\mathbf {f}}(t, {\mathbf {x}})$ where ${\mathbf {f}}(t, {\mathbf {x}})$ is defined by (51) with $\dot{{\mathbf {y}}}= H \bar{{\mathbf {f}}}({\mathbf {y}})$, ${\mathbf {y}}= \left( {\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k, {\bar{\varPhi }} \right) ^T$ and $\bar{{\mathbf {f}}}({\mathbf {y}})$ given by time-averaging (33) we obtain:

$$\begin{aligned} \dot{{\bar{\varOmega }}}&=\frac{1}{2} H {\bar{\varOmega }} \Big (-3 \gamma \left( {\bar{\varSigma }} ^2+{\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}-1\right) \nonumber \\&\quad +6 {\bar{\varSigma }} ^2+3 {\bar{\varOmega }} ^2+2 {\bar{\varOmega }}_{k}-3\Big ), \end{aligned}$$

(52)

$$\begin{aligned} \dot{{\bar{\varSigma }}}&=\frac{1}{2} H \Bigg ({\bar{\varSigma }} \Big (-3 \gamma \left( {\bar{\varSigma }} ^2+{\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}-1\right) \nonumber \\&\quad +6 {\bar{\varSigma }} ^2+3 {\bar{\varOmega }} ^2+2 {\bar{\varOmega }}_{k}-6\Big )+2 {\bar{\varOmega }}_{k}\Bigg ), \end{aligned}$$

(53)

$$\begin{aligned} \dot{{\bar{\varOmega }}}_{k}&= -H {\bar{\varOmega }}_{k} \Big (3 \gamma \left( {\bar{\varSigma }} ^2+{\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}-1\right) \nonumber \\&\quad -6 {\bar{\varSigma }} ^2+2 {\bar{\varSigma }} -3 {\bar{\varOmega }} ^2-2 {\bar{\varOmega }}_{k}+2\Big ), \end{aligned}$$

(54)

$$\begin{aligned} \dot{{\bar{\varPhi }}}&=0, \end{aligned}$$

(55)

$$\begin{aligned} {\dot{H}}&= -\frac{1}{2} H^2 \Big (3 \gamma \left( 1-{{\bar{\varSigma }}}^2-{\bar{\varOmega }} ^2-{\bar{\varOmega }}_k\right) \nonumber \\&\quad + 6 {{\bar{\varSigma }}}^2+ 3 {\bar{\varOmega }}^2+ 2 {\bar{\varOmega }}_k\Big ) . \end{aligned}$$

(56)

Proceeding in analogous way as in references [128, 137] we implement a local nonlinear transformation:

$$\begin{aligned}&{\mathbf {x}}_0:=\left( \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}\right) ^T \mapsto {\mathbf {x}}:=\left( \varOmega , \varSigma , \varOmega , \varPhi \right) ^T \nonumber \\&\quad {\mathbf {x}}=\psi ({\mathbf {x}}_0):={\mathbf {x}}_0 + H {\mathbf {g}}(H, {\mathbf {x}}_0,t), \end{aligned}$$

(57)

$$\begin{aligned}&{\mathbf {g}}(H, {\mathbf {x}}_0,t)= \left( \begin{array}{c} g_1(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)\\ g_2(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)\\ g_3(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)\\ g_4(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)\\ \end{array}\right) . \end{aligned}$$

(58)

Taking time derivative in both sides of (57) with respect to t we obtain

$$\begin{aligned}&\dot{{\mathbf {x}}_0}+ {\dot{H}} {\mathbf {g}}(H, {\mathbf {x}}_0,t)+ H \Bigg (\frac{\partial }{\partial t} {\mathbf {g}}(H, {\mathbf {x}}_0,t) \nonumber \\&\qquad + {\dot{H}} \frac{\partial }{\partial H} {\mathbf {g}}(H, {\mathbf {x}}_0,t) + D_{{\mathbf {x}}_0} {\mathbf {g}}(H, {\mathbf {x}}_0,t) \cdot \dot{{\mathbf {x}}_0}\Bigg ) = \dot{{\mathbf {x}}}, \end{aligned}$$

(59)

where

$$\begin{aligned} D_{{\mathbf {x}}_0} {\mathbf {g}}(H, {\mathbf {x}}_0,t)= \left( \begin{array}{cccc} \frac{\partial g_1}{\partial \varOmega _0}&{} \frac{\partial g_1}{\partial \varSigma _0} &{} \frac{\partial g_1}{\partial \varOmega _k}&{} \frac{\partial g_1}{\partial \varPhi _0}\\ \frac{\partial g_2}{\partial \varOmega _0}&{} \frac{\partial g_2}{\partial \varSigma _0} &{} \frac{\partial g_2}{\partial \varOmega _k} &{} \frac{\partial g_2}{\partial \varPhi _0}\\ \frac{\partial g_3}{\partial \varOmega _0}&{} \frac{\partial g_3}{\partial \varSigma _0} &{} \frac{\partial g_3}{\partial \varOmega _k} &{} \frac{\partial g_3}{\partial \varPhi _0}\\ \frac{\partial g_4}{\partial \varOmega _0}&{} \frac{\partial g_4}{\partial \varSigma _0} &{} \frac{\partial g_4}{\partial \varOmega _k} &{} \frac{\partial g_4}{\partial \varPhi _0}\\ \end{array} \right) \end{aligned}$$

(60)

is the Jacobian matrix of ${\mathbf {g}}(H, {\mathbf {x}}_0,t)$ for the vector ${\mathbf {x}}_0$. The function ${\mathbf {g}}(H, {\mathbf {x}}_0,t)$ is conveniently chosen.

By substituting (49) and (57) in (59) we obtain

$$\begin{aligned}&\Bigg ({\mathbf {I}}_4 + H D_{{\mathbf {x}}_0} {\mathbf {g}}(H, {\mathbf {x}}_0,t)\Bigg ) \cdot \dot{{\mathbf {x}}_0}= H {\mathbf {f}}({\mathbf {x}}_0 + H {\mathbf {g}}(H, {\mathbf {x}}_0,t),t) \nonumber \\&\quad -H \frac{\partial }{\partial t} {\mathbf {g}}(H, {\mathbf {x}}_0,t) -{\dot{H}} {\mathbf {g}}(H, {\mathbf {x}}_0,t) -H {\dot{H}} \frac{\partial }{\partial H} {\mathbf {g}}(H, {\mathbf {x}}_0,t), \end{aligned}$$

(61)

where ${\mathbf {I}}_4= \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right)$ is the $4\times 4$ identity matrix.

Then we obtain

$$\begin{aligned} \dot{{\mathbf {x}}_0}&= \Bigg ({\mathbf {I}}_4 {+} H D_{{\mathbf {x}}_0} {\mathbf {g}}(H, {\mathbf {x}}_0,t)\Bigg )^{-1} \cdot \Bigg (H {\mathbf {f}}({\mathbf {x}}_0 {+} H {\mathbf {g}}(H, {\mathbf {x}}_0,t),t)\nonumber \\&\quad -H \frac{\partial }{\partial t} {\mathbf {g}}(H, {\mathbf {x}}_0,t) {-}{\dot{H}} {\mathbf {g}}(H, {\mathbf {x}}_0,t) {-}H {\dot{H}} \frac{\partial }{\partial H} {\mathbf {g}}(H, {\mathbf {x}}_0,t)\Bigg ). \end{aligned}$$

(62)

Using Eq. (50), we have ${\dot{H}}= {\mathscr {O}}(H^2)$. Hence,

$$\begin{aligned} \dot{{\mathbf {x}}_0}&= \underbrace{\Bigg ({\mathbf {I}}_4 - H D_{{\mathbf {x}}_0} {\mathbf {g}}(0, {\mathbf {x}}_0,t) + {\mathscr {O}}(H^2)\Bigg )}_{4\times 4 \, \text {matrix}} \nonumber \\&\qquad \cdot \underbrace{\Bigg (H {\mathbf {f}}({\mathbf {x}}_0, t) -H \frac{\partial }{\partial t} {\mathbf {g}}(0, {\mathbf {x}}_0,t) + {\mathscr {O}}(H^2)\Bigg )}_{4\times 1 \; \text {vector}}\nonumber \\&\quad = \underbrace{H {\mathbf {f}}({\mathbf {x}}_0, t)-H \frac{\partial }{\partial t} {\mathbf {g}}(0, {\mathbf {x}}_0,t) + {\mathscr {O}}(H^2)}_{4\times 1 \; \text {vector}}. \end{aligned}$$

(63)

The strategy is to use Eq. (63) for choosing conveniently $\frac{\partial }{\partial t} {\mathbf {g}}(0, {\mathbf {x}}_0,t)$ to prove that

$$\begin{aligned}&\dot{\varDelta {\mathbf {x}}_0}= -H G({\mathbf {x}}_0, \bar{{\mathbf {x}}}) + {\mathscr {O}}(H^2), \end{aligned}$$

(64)

where $\bar{{\mathbf {x}}}=({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varPhi }})^T$ and $\varDelta {\mathbf {x}}_0={\mathbf {x}}_0 - \bar{{\mathbf {x}}}$. The function $G({\mathbf {x}}_0, \bar{{\mathbf {x}}})$ is unknown at this stage.

By construction we neglect dependence of $\partial g_i/ \partial t$ and $g_i$ on H, i.e., assume ${\mathbf {g}}={\mathbf {g}}({\mathbf {x}}_0,t)$ because dependence of H is dropped out along with higher order terms Eq. (63). Next, we solve a partial differential equation for ${\mathbf {g}}({\mathbf {x}}_0,t)$ given by:

$$\begin{aligned}&\frac{\partial }{\partial t} {\mathbf {g}}({\mathbf {x}}_0,t) = {\mathbf {f}}({\mathbf {x}}_0, t) - \bar{{\mathbf {f}}}(\bar{{\mathbf {x}}}) + G({\mathbf {x}}_0, \bar{{\mathbf {x}}}). \end{aligned}$$

(65)

where we have considered ${\mathbf {x}}_0$, and t as independent variables. The right hand side of (65) is almost periodic of period $L=\frac{2\pi }{\omega }$ for large times. Then, implementing the average process (33) on right hand side of (65), where slow-varying dependence of quantities $\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _0$ and ${\bar{\varOmega }}, {\bar{\varSigma }}, \bar{\varOmega _k}, {\bar{\varPhi }}$ on t are ignored through averaging process, we obtain

$$\begin{aligned}&\frac{1}{L}\int _0^{L} \Bigg [{\mathbf {f}}({\mathbf {x}}_0, s) - \bar{{\mathbf {f}}}(\bar{{\mathbf {x}}}) +G({\mathbf {x}}_0, \bar{{\mathbf {x}}}) \Bigg ] ds \nonumber \\&\quad = \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}} )+G({\mathbf {x}}_0, \bar{{\mathbf {x}}}). \end{aligned}$$

(66)

Defining

$$\begin{aligned} G({\mathbf {x}}_0, \bar{{\mathbf {x}}}):= -\left( \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}})\right) \end{aligned}$$

(67)

the average (66) is zero so that ${\mathbf {g}}({\mathbf {x}}_0,t)$ is bounded.

Finally, Eq. (64) transforms to

$$\begin{aligned}&\dot{\varDelta {\mathbf {x}}_0}= H \left( \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}})\right) + {\mathscr {O}}(H^2) \end{aligned}$$

(68)

and Eq. (65) is simplified to

$$\begin{aligned}&\frac{\partial }{\partial t} {\mathbf {g}}({\mathbf {x}}_0,t) = {\mathbf {f}}({\mathbf {x}}_0, t) - \bar{{\mathbf {f}}}( {\mathbf {x}}_0). \end{aligned}$$

(69)

Theorem 2 establish the existence of the vector (58).

Theorem 2

Let ${\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k, {\bar{\varPhi }}$ and H be defined functions that satisfy averaged Eqs. (52), (53), (54), (55), (56). Then, there exist continuously differentiable functions $g_1, g_2, g_3$ and $g_4$, such that $\varOmega , \varSigma , \varOmega _k$ and $\varPhi$ are locally given by (57), where $\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _0$ are order zero approximations of them as $H\rightarrow 0$. Then, functions $\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _0$ and averaged solution ${\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k, {\bar{\varPhi }}$ have the same limit as $t\rightarrow \infty$. Setting $\varSigma =\varSigma _0=0$ are derived the analogous results for negatively curved FLRW model.

4.4 FLRW metric with $k=-1$

Secondly, we consider FLRW metric (24) with $k=-1$ for generalized harmonic potential (2) minimally coupled to matter with field equations (27) with the substitution $k=-1$. Defining

$$\begin{aligned} \varOmega&=\sqrt{\frac{\omega ^2 \phi ^2+{\dot{\phi }}^2}{6 H^2}}, \quad \varOmega _k=-\frac{k}{a^2 H^2}, \nonumber \\ \varPhi&= t \omega -\tan ^{-1}\left( \frac{\omega \phi }{\dot{\phi }}\right) , \end{aligned}$$

(70)

the full system is deduced from (46) by setting $\varSigma =0$. Then,

$$\begin{aligned} \dot{\varOmega }&= -\frac{b \gamma f \mu ^3 \varOmega }{H} \sin ^2 \left( \frac{\sqrt{\frac{3}{2}} H \varOmega \sin (t \omega -\varPhi )}{f \omega }\right) \nonumber \\&\quad -\frac{b \mu ^3 }{\sqrt{6} H} \cos (t \omega -\varPhi ) \sin \left( \frac{\sqrt{6} H \varOmega \sin (t \omega -\varPhi )}{f \omega }\right) \nonumber \\&\quad +H \cos ^2(t \omega -\varPhi ) \left( \varOmega ^3 \left( \gamma \left( \frac{3 \mu ^2}{\omega ^2}-\frac{3}{2}\right) +3\right) -3 \varOmega \right) \nonumber \\&\quad +\frac{1}{2} H \varOmega \left( 3 \gamma -\frac{6 \gamma \mu ^2 \varOmega ^2}{\omega ^2}+(2-3 \gamma ) \varOmega _{k}\right) \nonumber \\&\quad +\frac{\left( \omega ^2-2 \mu ^2\right) \varOmega \sin (2 t \omega -2 \varPhi )}{2 \omega }, \end{aligned}$$

(71a)

$$\begin{aligned} \dot{\varOmega _k}&=\frac{b \gamma f \mu ^3 \varOmega _{k}}{H} \left( -1+\cos \left( \frac{\sqrt{6} H \varOmega \sin (t \omega -\varPhi )}{f \omega }\right) \right) \nonumber \\&\quad -H \varOmega _{k} \left( \frac{6 \gamma \mu ^2 \varOmega ^2 \sin ^2(t \omega -\varPhi )}{\omega ^2}+(3 \gamma -2) (\varOmega _{k}-1)\right) \nonumber \\&\quad -3 (\gamma -2) H \varOmega ^2 \varOmega _{k} \cos ^2(t \omega -\varPhi ), \end{aligned}$$

(71b)

$$\begin{aligned} {\dot{\varPhi }}&= -3 H \sin (t \omega -\varPhi ) \cos (t \omega -\varPhi )\nonumber \\&\quad +\frac{\left( \omega ^2-2 \mu ^2\right) }{\omega } \sin ^2(t \omega -\varPhi ) \nonumber \\&\quad -\frac{b \mu ^3}{\sqrt{6} H \varOmega } \sin (t \omega -\varPhi ) \sin \left( \frac{\sqrt{6} H \varOmega \sin (t \omega -\varPhi )}{f \omega }\right) , \end{aligned}$$

(71c)

$$\begin{aligned} {\dot{H}}&= -(1+q)H^2, \end{aligned}$$

(71d)

with deceleration parameter

$$\begin{aligned} q&=-1+\frac{3 \gamma }{2} -\frac{3 \gamma \mu ^2 \varOmega ^2 \sin ^2(t \omega -\varPhi )}{\omega ^2} \nonumber \\&\quad -\frac{3}{2} (\gamma -2) \varOmega ^2 \cos ^2(t \omega -\varPhi ) -\frac{3}{2} \gamma \varOmega _{k}+\varOmega _{k} \nonumber \\&\quad -\frac{b \gamma f \mu ^3}{H^2} \sin ^2 \left( \frac{\sqrt{\frac{3}{2}} H \varOmega \sin (t \omega -\varPhi )}{f \omega }\right) . \end{aligned}$$

(71e)

Setting $f=\frac{b \mu ^3}{\omega ^2-2 \mu ^2}>0$, we obtain:

$$\begin{aligned} \dot{{\mathbf {x}}}&= H {\mathbf {f}}(t, {\mathbf {x}}) + {\mathscr {O}}(H^2), \; \nonumber \\ {\mathbf {x}}&= \left( \varOmega , \varOmega _k, \varPhi \right) ^T, \end{aligned}$$

(72)

$$\begin{aligned} {\dot{H}}&= -\frac{1}{2} \left( 3 \gamma \left( 1-\varOmega ^2- \varOmega _{k}\right) +2 \varOmega _{k}\right) \nonumber \\&\quad -3 \varOmega ^2 \cos ^2(t \omega -\varPhi )+ {\mathscr {O}}(H^3), \end{aligned}$$

(73)

where

$$\begin{aligned}&f(t, {\mathbf {x}})\nonumber \\&\quad = \left( \begin{array}{l} \frac{1}{2} \varOmega \left( 3 \gamma -3 \gamma \left( \varOmega ^2+\varOmega _{k}\right) +2 \varOmega _{k}\right) +3 \varOmega \left( \varOmega ^2-1\right) \cos ^2(t \omega -\varPhi ) \\ \\ - \varOmega _{k} \left( 3 \gamma \varOmega ^2+(3 \gamma -2) (\varOmega _{k}-1)\right) +6 \varOmega ^2 \varOmega _{k} \cos ^2(t \omega -\varPhi )\\ \\ -\frac{3}{2} \sin (2 t \omega -2 \varPhi ) \end{array} \right) . \end{aligned}$$

(74)

Replacing $\dot{{\mathbf {x}}}= H {\mathbf {f}}(t, {\mathbf {x}})$ with ${\mathbf {f}}(t, {\mathbf {x}})$ defined by (74) with $\dot{{\mathbf {y}}}= H {\bar{f}}({\mathbf {y}})$, ${\mathbf {y}}= \left( {\bar{\varOmega }}, {{\bar{\varOmega }}_{k}}, {\bar{\varPhi }} \right) ^T$ and using the time averaging (33) we obtain the time-averaged system:

$$\begin{aligned}&\dot{{\bar{\varOmega }}}=-\frac{1}{2} H \; {\bar{\varOmega }} \left( 3 (\gamma -1) \left( {\bar{\varOmega }} ^2-1\right) +(3 \gamma -2) {{{\bar{\varOmega }}_{k}}}\right) , \end{aligned}$$

(75)

$$\begin{aligned}&\dot{{\bar{\varOmega }}} _k=-H \; {{{\bar{\varOmega }}_{k}}} \left( 3 (\gamma -1) {\bar{\varOmega }} ^2-3 \gamma +(3 \gamma -2) {{{\bar{\varOmega }}_{k}}}+2\right) , \end{aligned}$$

(76)

$$\begin{aligned}&\dot{{\bar{\varPhi }}}=0. \end{aligned}$$

(77)

Theorem 2 applies to Bianchi III, and the invariant set $\varSigma =0$ corresponds to negatively curved FLRW models.

5 Qualitative analysis of averaged systems

Theorem 2 proved in  Appendix A implies that $\varOmega , \varSigma , \varOmega _k$ and $\varPhi$ evolve according to time-averaged system (52), (53), (54), (55) as $H\rightarrow 0$. Hence, the full equations of time-dependent system (46) and their corresponding time-averaged versions have the same late-time dynamics as $H\rightarrow 0$. Therefore, the simplest time-averaged system determines the future asymptotic of full system. In particular, depending on values of barotropic index $\gamma$, the generic late-time attractors of physical interests are found. With this approach, the oscillations entering full system through KG equation can be controlled and smoothed out as Hubble factor H – acting as a time-dependent perturbation parameter – tends monotonically to zero. These results are supported by numerical simulations given in Appendix C.

5.1 LRS Bianchi III

From the averaged system (52), (53), (54) and (55) we obtain Hubble normalized averaged system

$$\begin{aligned} \frac{d{\bar{\varOmega }}}{d\tau }&= \frac{1}{2} {\bar{\varOmega }} \Big (3 \gamma \left( 1-{\bar{\varSigma }} ^2-{\bar{\varOmega }} ^2-{\bar{\varOmega }}_{k}\right) \nonumber \\&\quad +6 {\bar{\varSigma }} ^2+3 {\bar{\varOmega }} ^2+2 {\bar{\varOmega }}_{k}-3\Big ), \end{aligned}$$

(78a)

$$\begin{aligned} \frac{d{\bar{\varSigma }}}{d\tau }&= \frac{1}{2} \Bigg ({\bar{\varSigma }} \Big (3 \gamma \left( 1-{\bar{\varSigma }} ^2-{\bar{\varOmega }} ^2-{\bar{\varOmega }}_{k}\right) \nonumber \\&\quad +6 {\bar{\varSigma }} ^2+3 {\bar{\varOmega }} ^2+2 {\bar{\varOmega }}_{k}-6\Big )+2 {\bar{\varOmega }}_{k}\Bigg ), \end{aligned}$$

(78b)

$$\begin{aligned} \frac{d{{\bar{\varOmega }}_k}}{d\tau }&= {\bar{\varOmega }}_{k} \Big (3 \gamma \left( 1-{\bar{\varSigma }} ^2-{\bar{\varOmega }} ^2-{\bar{\varOmega }}_{k}\right) \nonumber \\&\quad +6 {\bar{\varSigma }} ^2-2 {\bar{\varSigma }} +3 {\bar{\varOmega }} ^2+2 {\bar{\varOmega }}_{k}-2\Big ), \end{aligned}$$

(78c)

$$\begin{aligned} \frac{d{{{\bar{\varPhi }}}}}{d\tau }&=0, \end{aligned}$$

(78d)

$$\begin{aligned} \frac{d{H}}{d\tau }&= -\frac{1}{2} H \Big (3 \gamma \left( 1-{{\bar{\varSigma }}}^2-{\bar{\varOmega }} ^2-{\bar{\varOmega }}_k\right) \nonumber \\&\quad + 6 {{\bar{\varSigma }}}^2+ 3 {\bar{\varOmega }}^2+ 2 {\bar{\varOmega }}_k\Big ), \end{aligned}$$

(78e)

where $\frac{dt}{d\tau }= 1/H$. We have ${\bar{\varSigma }} ^2+{\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}+ {\bar{\varOmega }}_{m}=1$. Therefore, from energy condition ${\bar{\varOmega }}_{m}\ge 0$ the phase space is:

$$\begin{aligned} \left\{ ({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_{k})\in {\mathbb {R}}^3: {\bar{\varSigma }} ^2+{\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}\le 1, {\bar{\varOmega }}_{k}\ge 0\right\} . \end{aligned}$$

(79)

The equilibrium points of the guiding system (78a), (78b), (78c) are:

• 1. $T: ({\bar{\varOmega }},{\bar{\varSigma }},{\bar{\varOmega }}_k)=(0,-1,0)$ with eigenvalues $\left\{ 6,\frac{3}{2},6-3 \gamma \right\}$.

  • (i) It is a source for $0\le \gamma <2.$

  • (ii) It is nonhyperbolic for $\gamma =2.$

  Defining a representative length along worldlines of the 4-velocity field as

  $$\begin{aligned} \frac{\ell (t)}{\ell _0}= \left[ {e_1}^1(t) ( {e_2}^2(t))^2\right] ^{-\frac{1}{3}}, \; \tau = \ln \left( \frac{\ell (t)}{\ell _0}\right) , \end{aligned}$$

  (80)

  such that

  $$\begin{aligned} H=\frac{{\dot{\ell }}}{\ell }. \end{aligned}$$

  (81)

  We denote by convention $t=0$ the current time where $\left( \frac{\ell (0)}{\ell _0}\right) ^3= \frac{1}{{e_1}^1(0) ( {e_2}^2(0))^2} =1$ and $\tau (0)=0$ and evaluating Raychaudhuri equation (46e) at T we obtain:

  $$\begin{aligned} \left\{ \begin{array}{c} {\dot{H}}= -3 H^2 \\ \\ \dot{\ell }=\ell H \end{array}\right. \implies \left\{ \begin{array}{c} H(t)= \frac{H_{0}}{3 H_{0} t+1} \\ \\ \ell (t)= {\ell _0} \root 3 \of {3 H_{0} t+1} \end{array}\right. . \end{aligned}$$

  (82)

  $\varSigma =-1$ implies $\sigma _{+}=-H=- \frac{H_{0}}{3 H_{0} t+1}$. This implies that K is constant. Indeed, from

  $$\begin{aligned} \dot{K} = -2 ({\sigma _+} +H) K, \end{aligned}$$

  (83)

  it follows $K=( {e_2}^2(t))^{2}=c_2^{-1}$. Substituting back in Eq. (17) is obtained:

  $$\begin{aligned}&\dot{{e_1}^1}=-\frac{3H_{0}}{3 H_{0} t+1} {e_1}^1, \; {e_1}^1(0)=c_2. \end{aligned}$$

  (84)

  Hence,

  $$\begin{aligned}&{{e_1}^1}(t)=\frac{c_2}{3 H_{0} t+1}. \end{aligned}$$

  (85)

  That is, line element (22) becomes

  $$\begin{aligned}&ds^2= - dt^2 + \frac{\left( 3 H_{0} t+1\right) ^2}{c_2^2} dr^2 + c_2 {\mathbf {g}}_{H^2}. \end{aligned}$$

  (86)

  Therefore, the corresponding solution can be expressed in form of Taub–Kasner solution ($p_1=1, p_2= 0, p_3= 0$) where the scale factors of Kasner solution are $t^{p_i}, i=1,2,3$ with $p_1+p_2+p_3=1, p_1^2+p_2^2+p_3^2=1$ [173, Sect 6.2.2 and p 193, Eq. (9.6)].

• 2. $Q: ({\bar{\varOmega }},{\bar{\varSigma }},{\bar{\varOmega }}_k)=(0,1,0)$ with eigenvalues $\big \{2,\frac{3}{2}, 6-3 \gamma \big \}.$

  • (i) It is a source for $0\le \gamma <2.$

  • (ii) It is nonhyperbolic for $\gamma =2.$

  Evaluating Raychaudhuri equation (46e) at Q and solving it we obtain

  $$\begin{aligned} H(t)= \frac{H_{0}}{3 H_{0} t+1}. \end{aligned}$$

  (87)

  $\varSigma =1$ implies $\sigma _{+}=H=\frac{H_{0}}{3 H_{0} t+1}$. Hence, Gauss equation (16) and evolution equation (17) become

  $$\begin{aligned} {\dot{K}}= -\frac{4 H_{0} K}{3 H_{0} t+1}, \; K(0)=c_1^{-1} \end{aligned}$$

  (88)

  and

  $$\begin{aligned} \dot{{e_1}^1}=\frac{H_{0}}{3 H_{0} t+1}{e_1}^1, \; {e_1}^1(0)=c_1. \end{aligned}$$

  (89)

  Then, by integration,

  $$\begin{aligned} {e_1}^1(t)&= c_1 \root 3 \of {3 H_{0} t+1}, \end{aligned}$$

  (90)
  $$\begin{aligned} K(t)&= \frac{1}{c_1\left( 3 H_{0} t+1\right) ^{4/3}}. \end{aligned}$$

  (91)

  That is, line element (22) becomes

  $$\begin{aligned} ds^2&= - dt^2 + c_1^{-2}\left( {3 H_{0} t+1}\right) ^{-\frac{2}{3}} dr^2 \nonumber \\&\quad + {c_1^{-1}}{\left( 3 H_{0} t+1\right) ^{4/3}} {\mathbf {g}}_{H^2}. \end{aligned}$$

  (92)

  Therefore, the corresponding solution can be expressed in form of non-flat LRS Kasner ($p_1=-\frac{1}{3}, p_2= \frac{2}{3}, p_3= \frac{2}{3}$) Bianchi I solution ( [173] Sect. 6.2.2 and Sect. 9.1.1 (2)).

• 3. $D: ({\bar{\varOmega }},{\bar{\varSigma }},{\bar{\varOmega }}_k)=(0,\frac{1}{2},\frac{3}{4})$ with eigenvalues $\left\{ -\frac{3}{2},0,3-3 \gamma \right\} .$ It is a nonhyperbolic saddle for $0\le \gamma <1.$

  • (i) For $\gamma =1$ the eigenvalues are $\{-\frac{3}{2},0,0\}$

  • (ii) For $\gamma >1$ two eigenvalues are negative.

  Evaluating Raychaudhuri equation (46e) at D we obtain

  $$\begin{aligned} \left\{ \begin{array}{c} {\dot{H}}= -\frac{3}{2} H^2 \\ \\ \dot{\ell }=\ell H \end{array}\right. \implies \left\{ \begin{array}{c} H(t)= \frac{2 H_{0}}{3 H_{0} t+2}\\ \\ \ell (t)= {\ell _0} \left( \frac{3 H_{0} t}{2}+1\right) ^{2/3} \end{array}\right. . \end{aligned}$$

  (93)

  $\varSigma =1/2$ implies $\sigma _{+}=\frac{1}{2}H=\frac{H_{0}}{3 H_{0} t+2}$. Hence, Gauss equation (16) and evolution equation (17) become

  $$\begin{aligned} \dot{{e_1}^1}&=0, \; {e_1}^1(0)=c_1, \end{aligned}$$

  (94)
  $$\begin{aligned} {\dot{K}}&=-\frac{6 H_{0} K }{3 H_{0} t+2}, \; K(0)=\frac{1}{c_1}. \end{aligned}$$

  (95)

  Hence,

  $$\begin{aligned} {e_1}^1=c_1, \; K= \frac{4}{c_1 (3 H_{0} t+2)^2}. \end{aligned}$$

  (96)

  That is, line element (22) becomes

  $$\begin{aligned}&ds^2= - dt^2 + c_1^{-2} dr^2 + \frac{(3 H_{0} t+2)^2}{4 c_1} {\mathbf {g}}_{H^2}. \end{aligned}$$

  (97)

  Therefore, the corresponding solution can be expressed in form of Bianchi III form of flat spacetime ( [173] p 193, Eq. (9.7)).

• 4. $F: ({\bar{\varOmega }},{\bar{\varSigma }},{\bar{\varOmega }}_k)=(1,0,0)$ with eigenvalues $\big \{-\frac{3}{2},1, 3-3 \gamma \big \}.$ This point is always a saddle because it has a negative and a positive eigenvalue. For $\gamma =1$ it is a nonhyperbolic saddle. Setting $\psi (t)= t \omega -\varPhi (t)$ and evaluating Raychaudhuri equation (46e) at F we obtain

  $$\begin{aligned} {\dot{H}}&= \frac{b^2 \gamma \mu ^6 \left( \cos \left( \frac{\sqrt{6} H \left( 2 \mu ^2-\omega ^2\right) \sin (\psi )}{b \mu ^3 \omega }\right) -1\right) }{2(2 \mu ^2-\omega ^2)} \nonumber \\&\quad +\frac{3 H^2 \left( 2 \gamma \mu ^2 \sin ^2(\psi )+\omega ^2 \left( (\gamma -2) \cos ^2(\psi )-\gamma \right) \right) }{2 \omega ^2}. \end{aligned}$$

  (98)

  Therefore,

  $$\begin{aligned} {\dot{H}} \sim -3 H^2 \cos ^2(t \omega -\varPhi ), \end{aligned}$$

  (99)

  for large t. In average, $\varPhi$ is constant, setting for simplicity $\varPhi =0$ and integrating we obtain

  $$\begin{aligned} H(t)=\frac{4 H_{0} \omega }{6 H_{0} t \omega +3 H_{0} \sin (2 t \omega )+4 \omega }, \end{aligned}$$

  (100)

  where $H_{0}$ is the current value of H(t). Finally, $H(t)\sim \frac{2}{3 t}$ for large t. Gauss equation (16) and evolution equation (17) become

  $$\begin{aligned} \dot{e_1^1}=-\frac{2 {e_1^1}}{3 t}, \; {\dot{K}}=-\frac{4 K}{3 t}, \end{aligned}$$

  (101)

  with general solution

  $$\begin{aligned} \dot{e_1^1}(t)= \frac{c_1}{t^{2/3}}, \; K(t)= \frac{c_2}{t^{4/3}}. \end{aligned}$$

  (102)

  That is, line element (22) becomes

  $$\begin{aligned}&ds^2= - dt^2 + c_1^{-2} {t^{4/3}} dr^2 + {c_2^{-1}}{t^{4/3}} {\mathbf {g}}_{H^2}. \end{aligned}$$

  (103)

  Hence for large t the equilibrium point can be associated with Einstein-de-Sitter solution ( [173], Sec 9.1.1 (1)) with $\gamma = 1$.

• 5. $F_0: ({\bar{\varOmega }},{\bar{\varSigma }},{\bar{\varOmega }}_k)=(0,0,0)$ with eigenvalues $\left\{ \frac{3 (\gamma -2)}{2},\frac{3 (\gamma -1)}{2},3 \gamma -2\right\} .$

  • (i) It is a sink for $0\le \gamma <\frac{2}{3}.$

  • (ii) It is a saddle for $\frac{2}{3}<\gamma <1$ or $1<\gamma <2.$

  • (iii) It is nonhyperbolic for $\gamma =\frac{2}{3}$ or $\gamma =1$ or $\gamma =2.$

  Evaluating Raychaudhuri equation (46e) at $F_0$ we obtain

  $$\begin{aligned} \left\{ \begin{array}{c} {\dot{H}}= -\frac{3}{2} \gamma H^2\\ \\ \dot{\ell }=\ell H \end{array} \right. \implies \left\{ \begin{array}{c} H(t)= \frac{2 H_{0}}{3 \gamma H_{0} t+2} \\ \\ \ell (t)= \ell _{0} \left( \frac{3 \gamma H_{0} t}{2}+1\right) ^{\frac{2}{3 \gamma }} \end{array}\right. .\nonumber \\ \end{aligned}$$

  (104)

  That is, line element (22) becomes

  $$\begin{aligned}&ds^2= - dt^2 + \ell _{0}^2 \left( \frac{3 \gamma H_{0} t}{2}+1\right) ^{\frac{4}{3 \gamma }} \left( dr^2 + {\mathbf {g}}_{H^2}\right) . \end{aligned}$$

  (105)

  The corresponding solution is a matter dominated FLRW universe with ${\bar{\varOmega }}_m=1$.

• 6. $MC: ({\bar{\varOmega }},{\bar{\varSigma }},{\bar{\varOmega }}_k)=(0,\frac{3 \gamma }{2}-1,-\frac{9 \gamma ^2}{4}+6 \gamma -3)$ with eigenvalues $\left\{ \frac{3 (\gamma -1)}{2},\frac{3}{4} \left( \gamma +\sqrt{2-\gamma } \sqrt{\gamma (24 \gamma -41)+18}-2\right) , \right.$ $\left. \frac{3}{4} \left( \gamma -\sqrt{2-\gamma } \sqrt{\gamma (24 \gamma -41)+18}-2\right) \right\} .$ By definition $\varOmega _k\ge 0$, therefore, we impose restriction $\frac{2}{3}\le \gamma \le 2$.

  • (i) It is a sink for $\frac{2}{3}<\gamma <1.$

  • (ii) It is a saddle for $1<\gamma <2.$

  • (iii) It is nonhyperbolic for $\gamma =\frac{2}{3}$ or $\gamma =1$ or $\gamma =2.$

  The corresponding solution is a matter-curvature scaling solution with ${\bar{\varOmega }}_m=3(1-\gamma )$. We obtain same expressions in (104) for $\ell , H$ and for $ds^2$ we obtain the expression:

  $$\begin{aligned}&ds^2= - dt^2 + \ell _{0}^2 \left( \frac{3 \gamma H_{0} t}{2}+1\right) ^{\frac{4}{3 \gamma }} \left( dr^2 + {\mathbf {g}}_{H^2}\right) . \end{aligned}$$

  (106)

Fig. 2

Phase space of the guiding system (78a), (78b), (78c) for $\gamma =0, \frac{2}{3}$

In Fig. 2a some orbits in the phase space of the guiding system (78a), (78b), (78c) for $\gamma =0$ corresponding to cosmological constant are presented. The attractor is $F_0$ where scalar field mimics a cosmological constant. The equilibrium point D is a saddle.

In Fig. 2b some orbits of the phase space of the guiding system (78a), (78b), (78c) for $\gamma =\frac{2}{3}$ are presented. The point $F_0$ coincides with MC; it is asymptotically stable as proved in Appendix B.1 by means of Center Manifold theory. The equilibrium point D is a saddle.

Fig. 3

Phase space of the guiding system (78a), (78b), (78c) for some values of $\gamma =0.8, 0.9$

In Fig. 3a, b some orbits in the phase space of the guiding system (78a), (78b), (78c) for $\gamma =0.8$ and $\gamma =0.9$ are presented. In both cases MC is a stable node and D is a saddle.

Fig. 4

Phase space of the guiding system (78a), (78b), (78c) for $\gamma =1$

It is worth to notice that for $\gamma =1$ the system admits the lines of equilibrium points $({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k)= ({\bar{\varOmega }}^*, 0, 0)$ and $D^*:= ({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k)= ({\bar{\varOmega }}^*, \frac{1}{2}, \frac{3}{4})$, where ${\bar{\varOmega }}^*$ is an arbitrary number which satisfies ${\bar{\varOmega }}^*\in [0,1]$. Therefore, the Bianchi III flat spacetime D, and $F_0$ are not isolated fixed points anymore. Additionally, MC coincides with D. In Fig. 4 some orbits in the phase space of the guiding system (78a), (78b), (78c) for $\gamma =1$ which corresponds to dust are presented. The attractor on the invariant set ${\bar{\varOmega }}_k=0$ is the line that contains $F_0$ and F.

According to the center manifold analysis in Appendix B.2 and supported by Fig. 10 for $\gamma =1$, it is shown that D is unstable (saddle type) for $\frac{1}{8} (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_{k}-5)\ne 0$. However, if we restrict the analysis to $\frac{1}{8} (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_{k}-5)<0$ which is the physical region of the phase space, D is asymptotically stable and behaves as a local attractor.

Fig. 5

Phase space of the guiding system (78a), (78b), (78c) for $\gamma =\frac{4}{3}, 2$

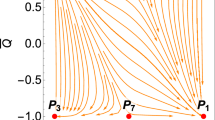
In Fig. 5a some orbits in the phase space of guiding system (78a), (78b), (78c) for $\gamma =\frac{4}{3}$ corresponding to radiation are presented. In Fig. 5b some orbits in the phase space of guiding system (78a), (78b), (78c) for $\gamma =2$ which corresponds to stiff matter are presented. In both figures, the attractor on the invariant set ${\bar{\varOmega }}_k=0$ is F. For $\gamma >1$, D is locally asymptotically stable according to the center manifold analysis in Appendix B.2. For $\gamma =2$ the line connecting $T, F_0, Q$ is invariant and unstable.

In Table 1 exact solutions associated with the equilibrium points of reduced averaged system (78a), (78b) and (78c) are summarized. A(t) and B(t) denote scale factors of the metric (22) where $c_1, c_2, a_0 \in {\mathbb {R}}^+$.

Table 1 Exact solutions associated with equilibrium points of reduced averaged system (78a), (78b) and (78c). A(t) and B(t) denote scale factors of metric (22). $c_1, c_2, \ell _0 \in \mathbb {R}^+$

Table 2 Exact solutions associated with equilibrium points of reduced averaged system (107a)–(107b). a(t) denotes a scale factor of metric (28) and $a_0 \in \mathbb {R}^+$

5.1.1 Late-time behavior

The results from the linear stability analysis, the Center Manifold calculations in  Appendix B and combined with Theorem 2 lead to:

Theorem 3

The late time attractors of full system (46) and averaged system (78) for Bianchi III line element are:

• (i) The matter dominated FLRW universe $F_0$ with line element (105) if $0< \gamma \le \frac{2}{3}$. $F_0$ represents a quintessence fluid for $0<\gamma <\frac{2}{3}$ or a zero-acceleration model for $\gamma =\frac{2}{3}$. In the limit $\gamma =0$ we have de Sitter solution.

• (ii) The matter-curvature scaling solution MC with ${\bar{\varOmega }}_m=3(1-\gamma )$ and line element (106) if $\frac{2}{3}<\gamma <1.$

• (iii) The Bianchi III flat spacetime D with metric (97) if $1\le \gamma \le 2$.

5.2 FLRW metric with $k=-1$

In this case the time-averaged system (75), (76), (77) transforms to:

$$\begin{aligned}&\frac{d {\bar{\varOmega }}}{d \tau }=-\frac{1}{2} {\bar{\varOmega }} \left( 3 (\gamma -1) \left( {\bar{\varOmega }} ^2-1\right) +(3 \gamma -2) {{{\bar{\varOmega }}_{k}}}\right) , \end{aligned}$$

(107a)

$$\begin{aligned}&\frac{d {{{\bar{\varOmega }}_{k}}}}{d \tau }=- {{{\bar{\varOmega }}_{k}}} \left( 3 (\gamma -1) {\bar{\varOmega }} ^2-3 \gamma +(3 \gamma -2) {{{\bar{\varOmega }}_{k}}}+2\right) , \end{aligned}$$

(107b)

$$\begin{aligned}&\frac{d{{{\bar{\varPhi }}}}}{d\tau }=0, \end{aligned}$$

(107c)

$$\begin{aligned}&\frac{d{H}}{d\tau } = -\frac{1}{2} H \left[ 3 \gamma (1- \varOmega _k- \varOmega ^2) + 3 \varOmega ^2 + 2 \varOmega _k \right] , \end{aligned}$$

(107d)

where $\frac{d{ {t}}}{d\tau } = 1/{ {H}}.$ We have ${\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}+ {\bar{\varOmega }}_{m}=1$. Therefore, from condition ${\bar{\varOmega }}_{m}\ge 0$ the phase space is

$$\begin{aligned} \left\{ ({\bar{\varOmega }}, {\bar{\varOmega }}_{k})\in {\mathbb {R}}^2: {\bar{\varOmega }} ^2+{\bar{\varOmega }}_{k}\le 1, {\bar{\varOmega }}_{k}\ge 0\right\} . \end{aligned}$$

(108)

For $\gamma =1$, guiding system (107a)–(107b) is reduced to

$$\begin{aligned}&\frac{d {\bar{\varOmega }}}{d \tau }=-\frac{1}{2} {\bar{\varOmega }} \; {{{\bar{\varOmega }}_{k}}}, \; \frac{d {{{\bar{\varOmega }}_{k}}}}{d \tau }= {{{\bar{\varOmega }}_{k}}} \left( 1- {{{\bar{\varOmega }}_{k}}}\right) . \end{aligned}$$

(109)

The solution is

$$\begin{aligned} {{\bar{\varOmega }}}(\tau )&=\frac{\varOmega _0 }{\sqrt{{e^\tau \varOmega _{k0}-\varOmega _{k0}+1}}}, \nonumber \\ {{{\bar{\varOmega }}_{k}}}(\tau )&=\frac{e^\tau \varOmega _{k0}}{e^\tau \varOmega _{k0}-\varOmega _{k0}+1}. \end{aligned}$$

(110)

Fig. 6

Phase plane of system (109) for $\gamma =1$

Fig. 7

Phase plane for system (107a), (107b) for different choices of $\gamma$

where ${\bar{\varOmega }}(0)=\varOmega _0$, ${{\bar{\varOmega }}_{k}}(0)=\varOmega _{k0}$.

The equilibrium point $C: ({\bar{\varOmega }}, {{\bar{\varOmega }}_{k}})= (0,1)$ with eigenvalues $\{-1,-\frac{1}{2}\}$ is the late-time attractor.

The line of equilibrium points ${\bar{\varOmega }}(\varOmega _0)=\varOmega _0, \; {{\bar{\varOmega }}_{k}}(\varOmega _0)=0$ where $\varOmega _0 \in {\mathbb {R}}$ with eigenvalues $\{1,0\}$ is normally hyperbolic. Therefore, by considering eigenvalues with non zero real parts, it is found that the line is unstable. This line contains the points $F_0, F$. In Fig. 6 the phase plane of system (109) for $\gamma =1$ where the unstable line is ${{\bar{\varOmega }}_{k}}= 0$ and the attractor is C is presented. For $\gamma \ne 1$, the 2D guiding system (107a), (107b) has the following equilibrium points:

• 1. $F_0: ({\bar{\varOmega }}, {{\bar{\varOmega }}_{k}})=(0,0)$ with eigenvalues

  $\left\{ \frac{3 (\gamma -1)}{2},3 \gamma -2\right\}$.

  • (i) It is a sink for $0<\gamma <\frac{2}{3}$.

  • (ii) It is nonhyperbolic for $\gamma =\frac{2}{3}$.

  • (iii) It is a saddle for $\frac{2}{3}<\gamma <1$.

  • (iv) It is source for $1<\gamma <2$.

  Evaluating Eq. (107d) at $F_0$ we obtain

  $$\begin{aligned} \left\{ \begin{array}{c} {\dot{H}}= -\frac{3}{2} \gamma H^2\\ \\ {\dot{a}}=a H \end{array} \right. \implies \left\{ \begin{array}{c} H(t)= \frac{2 H_{0}}{3 \gamma H_{0} t+2} \\ \\ a(t)= a_{0} \left( \frac{3 \gamma H_{0} t}{2}+1\right) ^{\frac{2}{3 \gamma }} \end{array}\right. .\nonumber \\ \end{aligned}$$

  (111)

  That is, line element (28) becomes

  $$\begin{aligned} ds^2&= - dt^2 + a_{0}^2 \left( \frac{3 \gamma H_{0} t}{2}+1\right) ^{\frac{4}{3 \gamma }} \left( dr^2 +\sinh ^2 r d\varOmega ^2 \right) , \end{aligned}$$

  (112)

  where $d\varOmega ^2 = d\vartheta ^2 + \sin ^2 \vartheta \, d\zeta ^2$ is the metric for a two-sphere. The corresponding solution is a matter dominated FLRW universe, i.e., ${\bar{\varOmega }}_m=1$.

• 2. $F: ({\bar{\varOmega }}, {{\bar{\varOmega }}_{k}})=(1,0)$ with eigenvalues

  $\{1,-3 (\gamma -1)\}$.

  • (i) It is a source for $0<\gamma <1$,

  • (ii) It is a saddle for $1<\gamma <2$.

  Evaluating Eq. (107d) at $F_1$ we obtain

  $$\begin{aligned} \left\{ \begin{array}{c} {\dot{H}}= -\frac{3}{2} H^2\\ \\ {\dot{a}}=a H \end{array} \right. \implies \left\{ \begin{array}{c} H(t)= \frac{2 H_{0}}{3 H_{0} t+2} \\ \\ a(t)= a_{0} \left( \frac{3 H_{0} t}{2}+1\right) ^{\frac{2}{3 }} \end{array}\right. . \end{aligned}$$

  (113)

  Then, line element (28) becomes

  $$\begin{aligned} ds^2&= - dt^2 + a_{0}^2 \left( \frac{3 H_{0} t}{2}+1\right) ^{\frac{4}{3 }} dr^2 \nonumber \\&\quad + a_{0}^2 \left( \frac{3 H_{0} t}{2}+1\right) ^{\frac{4}{3 }} \left( dr^2+ \sinh ^2 r d\varOmega ^2 \right) . \end{aligned}$$

  (114)

  Hence for large t the equilibrium point can be associated with Einstein-de-Sitter solution.

• 3. $C: ({\bar{\varOmega }}, {{\bar{\varOmega }}_{k}})=(0,1)$ with eigenvalues $\left\{ -\frac{1}{2},2-3 \gamma \right\}$.

  • (i) It is a saddle for $0<\gamma <\frac{2}{3}$.

  • (ii) It is nonhyperbolic for $\gamma =\frac{2}{3}$.

  • (iii) It is a sink for $\frac{2}{3}<\gamma <2$.

  Evaluating the deceleration parameter (71e) at C we have $q=0$. Then,

  $$\begin{aligned} \left\{ \begin{array}{c} {\dot{H}}= - H^2 \\ \\ {\dot{a}}=a H \end{array}\right. \implies \left\{ \begin{array}{c} H(t)= \frac{H_{0}}{ H_{0} t+1}\\ \\ a(t)= a_0 (H_0 t+1) \end{array}\right. . \end{aligned}$$

  (115)

  The line element (28) becomes

  $$\begin{aligned} ds^2&= - dt^2 + a_{0}^2 \left( H_0 t+1\right) ^{2} \left( dr^2+ \sinh ^2 r d\varOmega ^2 \right) \end{aligned}$$

  (116)

  This is a curvature dominated Milne solution ($\varOmega =\varOmega _m=0, \varOmega _k=1, k=-1$) [173, Sect. 9.1.6, Eq. (9.8)], [209,210,211,212]).

In Table 2 exact solutions associated with equilibrium points of the reduced averaged system (107a)–(107b) where a(t) denote scale factors of metric (28) and $a_0 \in {\mathbb {R}}^+$ are presented.

In Fig. 7 the phase plane of the system (107a), (107b) for $\gamma =0, \frac{2}{3}, 0.8$ and $\gamma =\frac{4}{3}$ is portrayed.

5.2.1 Late-time behaviour

The results from the linear stability analysis combined with Theorem 2 (for $\varSigma =0$) lead to:

Theorem 4

The late time attractors of the full system (71) and the averaged system (107) are:

• (i) The matter dominated FLRW universe $F_0$ with line element (112) for $0< \gamma \le \frac{2}{3}$. $F_0$ represents a quintessence fluid or a zero-acceleration model for $\gamma =\frac{2}{3}$. In the limit $\gamma =0$ we have de Sitter solution.

• (ii) The Milne solution C with ${\bar{\varOmega }}_k=1, k=-1$ with line element (116) for $\frac{2}{3}<\gamma <2$.

6 Conclusions

In this paper we have used asymptotic methods and averaging theory to explore the solution’s space of scalar field cosmologies with generalized harmonic potential (2) in vacuum or minimally coupled to matter. We have studied systems that can be expressed in the standard form (37), where H is the Hubble parameter and is positive strictly decreasing in t and $\lim _{t\rightarrow \infty }H(t)=0$. Defining $Z= 1-\varSigma ^2-\varOmega ^2- \varOmega _{k}$ which is monotonic as $H\rightarrow 0$, due to there is a continuous function $\alpha$ such that ${\dot{Z}}= -H Z \alpha +{\mathscr {O}}\left( H^2\right)$ it was proved that sign of $1-\varSigma ^2-\varOmega ^2- \varOmega _{k}$ is invariant as $H\rightarrow 0$. Then, from Eq. (50) it was proved that H is a monotonic decreasing function of t if $0<\varOmega ^2+\varSigma ^2+{\varOmega _k}<1$. This implies $\lim _{t\rightarrow \infty } H(t)=0$ based on the invariance of initial surface for large t. Hence, from Theorem 2 was deduced that $\varOmega , \varSigma , \varOmega _k$, and $\varPhi$ evolve according to the time-averaged system (52), (53), (54), (55) as $H\rightarrow 0$. Then, the stability of a periodic solution can be established as it matches exactly the stability of stationary solution of time-averaged system. We have given a rigorous demonstration of Theorem  2 in Appendix A based on the construction of a smooth local near-identity nonlinear transformation, well-defined as H tends to zero. We have used properties of the sup norm, and the theorem of the mean values for a vector function $\bar{{\mathbf {f}}}: {\mathbb {R}}^3\longrightarrow {\mathbb {R}}^3$. We have explained preliminaries of the method in Sect. 4.3.

In particular, in LRS Bianchi III late time attractors of full system (46) and averaged system (78) for Bianchi III line element are:

• (i) The matter dominated FLRW universe $F_0$ with line element (105) if $0<\gamma \le \frac{2}{3}$. $F_0$ represents a quintessence fluid or a zero-acceleration model for $\gamma =\frac{2}{3}$. In the limit $\gamma =0$ we have de Sitter solution.

• (ii) The matter-curvature scaling solution CS with ${\bar{\varOmega }}_m=3(1-\gamma )$ and line element (106) if $\frac{2}{3}<\gamma <1.$

• (iii) The Bianchi III flat spacetime D with line element (97) if $1<\gamma \le 2$.

For FLRW metric with $k=-1$, late time attractors of full system (71) and averaged system are:

• (i) The matter dominated FLRW universe $F_0$ with line element (112) for $0<\gamma \le \frac{2}{3}$. $F_0$ represents a quintessence fluid or a zero-acceleration model for $\gamma =\frac{2}{3}$. In the limit $\gamma =0$ we have de Sitter solution.

• (ii) The Milne solution C with line element (116) for $\frac{2}{3}<\gamma <2$.

Summarizing, in LRS Bianchi III late-time attractors are: a matter dominated flat FLRW universe if $0\le \gamma \le \frac{2}{3}$ (mimicking de Sitter, quintessence or zero acceleration solutions), a matter-curvature scaling solution if $\frac{2}{3}<\gamma <1$ and Bianchi III flat spacetime for $1\le \gamma \le 2$. For FLRW metric with $k=-1$ late time attractors are: the matter dominated FLRW universe if $0\le \gamma \le \frac{2}{3}$ (mimicking de Sitter, quintessence or zero acceleration solutions) and Milne solution if $\frac{2}{3}<\gamma <2$. In all metrics, matter dominated flat FLRW universe represents quintessence fluid if $0< \gamma < \frac{2}{3}$.

Continuing the program “Averaging generalized scalar field cosmologies”, the cases: (II) Bianchi I and flat FLRW model and (III) KS and closed FLRW are studied in two companion papers [164, 165], respectively. In [164] using the same approach used here we found the oscillations entering the full system through KG equation can be controlled and smoothed out when the Hubble factor H is used as a time-dependent parameter since it tends monotonically to zero and preserves its sign during the evolution. However, in case (III) this approach is not valid given that H is not necessarily monotonically decreasing to zero, and it can change its sign. Therefore, we have developed an alternative procedure in [165]. For LRS Bianchi I and flat FLRW metrics as well as for LRS Bianchi III and open FLRW, we use Taylor expansion with respect to H near $H=0$ such that the resulting system can be expressed in standard form (37) after selecting a convenient angular frequency $\omega$ in the transformation (31). Next, we have taken the time-averaged of previous system, obtaining a system that can be easily studied using dynamical systems tools. Using the last approach, we have formulated Theorems 3 and  4 about late-time behavior of our model, whose proofs are based on Theorem 2 center manifold calculations and linear stability analysis.

As in paper [152], our analytical results were strongly supported by numerics in Appendix C as well. We showed that asymptotic methods and averaging theory are powerful tools to investigate scalar field cosmologies with generalized harmonic potential, which have evident advantages, e.g., it is not needed to analyze the full dynamics to determine the stability of the full oscillation, but only the late-time behavior of the time-averaged (simpler) system has to be analyzed. Interestingly, for LRS Bianchi III and open FLRW model, when matter fluid corresponds to a cosmological constant, H tends asymptotically to constant values depending on the initial conditions which is consistent to de Sitter expansion (see Figs. 13a, 21a). In addition, for open FLRW and any $\gamma <\frac{2}{3}$ and $\varOmega _k>0$, $\varOmega _k \rightarrow 0$. On the other hand, when $\gamma >\frac{2}{3}$ and $\varOmega _k>0$ the universe becomes curvature dominated asymptotically ($\varOmega _k \rightarrow 1$). In Appendix C, evidences that the main theorem of Sect. 4 is valid for LRS Bianchi III and for FLRW metrics with negative curvature are presented.

Appendices

Appendix A: Proof of Theorem 2

Lemma 5

(Gronwall’s Lemma (Integral form)) Let be $\xi (t)$ a nonnegative function, summable over [0, T] which satisfies almost everywhere the integral inequality

$$\begin{aligned} \xi (t)\le C_1 \int _0^t \xi (s)ds +C_2, \; C_1, C_2\ge 0. \end{aligned}$$

Then,

$$\begin{aligned} \xi (t)\le C_2 e^{C_1 t}, \end{aligned}$$

almost everywhere for t in $0\le t\le T$. In particular, if

$$\begin{aligned} \xi (t)\le C_1 \int _0^t \xi (s)ds, \; C_1\ge 0 \end{aligned}$$

almost everywhere for t in $0\le t\le T$. Then, $\xi \equiv 0$ almost everywhere for t in $0\le t\le T$.

Lemma 6

(Mean value theorem) Let $U \subset {\mathbb {R}}^n$ be open, ${\mathbf {f}}: U \rightarrow {\mathbb {R}}^m$ continuously differentiable, and ${\mathbf {x}}\in U$, ${\mathbf {h}}\in {\mathbb {R}}^m$ vectors such that the line segment ${\mathbf {x}}+z \; {\mathbf {h}}$, $0 \le z \le 1$ remains in U. Then we have:

$$\begin{aligned} {\mathbf {f}}({\mathbf {x}}+{\mathbf {h}})-{\mathbf {f}}({\mathbf {x}}) = \left( \int _0^1 D{\mathbf {f}}({\mathbf {x}}+z \; {\mathbf {h}})\,dz\right) \cdot {\mathbf {h}}, \end{aligned}$$

(A.1)

where $D {\mathbf {f}}$ denotes the Jacobian matrix of ${\mathbf {f}}$ and the integral of a matrix is understood as componentwise.

Proof of Theorem 2

Defining $Z= 1-\varSigma ^2-\varOmega ^2- \varOmega _{k}$ it follows from

$$\begin{aligned} {\dot{Z}}&= -H Z \Big (3 (\gamma -2) \varSigma ^2+3 (\gamma -1) \varOmega ^2 +(3 \gamma -2) \varOmega _{k} \\&\quad -3 \varOmega ^2 \cos (2 (\varPhi -t \omega ))\Big )+{\mathscr {O}}\left( H^2\right) \end{aligned}$$

that the sign of $1-\varSigma ^2-\varOmega ^2- \varOmega _{k}$ is invariant as $H\rightarrow 0$. From Eq. (50) it follows that H is a monotonic decreasing function of t if $0<\varOmega ^2+\varSigma ^2+{\varOmega _k}<1$. These allow to define recursively bootstrapping sequences

$$\begin{aligned}&\left\{ \begin{array}{c} t_0=t_{*} \\ \\ H_0=H(t_{*}) \end{array}\right. , \nonumber \\&\left\{ \begin{array}{c} {t_{n+1}}= {t_{n}} +\frac{1}{H_n} \\ \\ H_{n+1}= H(t_{n+1}) \end{array}\right. , \end{aligned}$$

(A.2)

such that $\lim _{n\rightarrow \infty }H_n=0$ y $\lim _{n\rightarrow \infty } t_n=\infty$. $\square$

Given expansions (57), Eq. (63) become

$$\begin{aligned} \dot{\varOmega _0}&= \frac{1}{2} \Bigg ({\varOmega _0} \Big (6 {\varSigma _{0}}^2+3 {\varOmega _0}^2+2 {\varOmega _{k0}} \\&\quad -3 \gamma \left( {\varSigma _{0}}^2+{\varOmega _0}^2+{\varOmega _{k0}}-1\right) \\&\quad +3 \left( {\varOmega _0}^2-1\right) \cos (2 (t \omega -\varPhi _{0}))-3\Big )\Bigg ) H \\&\quad - \frac{\partial g_1}{\partial t}H +{\mathscr {O}}\left( H^2\right) ,\\ \dot{\varSigma _0}&= \frac{1}{2} \Bigg (3 {\varSigma _{0}} \cos (2 (t \omega -\varPhi _{0})) {\varOmega _0}^2 +2 {\varOmega _{k0}}\\&\quad +{\varSigma _{0}} \Big (6 {\varSigma _{0}}^2+3 {\varOmega _0}^2+2 {\varOmega _{k0}} -6 \\&\quad -3 \gamma \left( {\varSigma _{0}}^2+{\varOmega _0}^2+{\varOmega _{k0}}-1\right) \Big )\Bigg ) H \\&\quad - \frac{\partial g_2}{\partial t}H +{\mathscr {O}}\left( H^2\right) ,\\ \dot{\varOmega _{k0}}&=\Bigg ({\varOmega _{k0}} \Big (6 {\varSigma _{0}}^2-2 {\varSigma _{0}}+3 {\varOmega _0}^2+2 {\varOmega _{k0}} \\&\quad -3 \gamma \left( {\varSigma _{0}}^2+{\varOmega _0}^2+{\varOmega _{k0}}-1\right) \\&\quad +3 {\varOmega _0}^2 \cos (2 (t \omega -\varPhi _{0}))-2\Big ) \Bigg ) H \\&\quad - \frac{\partial g_3}{\partial t}H +{\mathscr {O}}\left( H^2\right) ,\\ \dot{\varPhi _0}&=-\left( \frac{3}{2} \sin (2 (t \omega - \varPhi _{0}))+\frac{\partial g_4}{\partial t}\right) H+{\mathscr {O}}\left( H^2\right) . \end{aligned}$$

Furthermore, Eq. (69) becomes

$$\begin{aligned} \frac{\partial g_1}{\partial t}&= \frac{3}{2} {\varOmega _0} \left( {\varOmega _0}^2-1\right) \cos (2 ({\varPhi _0}-t \omega )), \end{aligned}$$

(A.3a)

$$\begin{aligned} \frac{\partial g_2}{\partial t}&=\frac{3}{2} {\varSigma _0} {\varOmega _0}^2 \cos (2 (\varPhi _{0}-t \omega )), \end{aligned}$$

(A.3b)

$$\begin{aligned} \frac{\partial g_3}{\partial t}&= 3 {\varOmega _0}^2 {\varOmega _{k0}} \cos (2 ({\varPhi _0}-t \omega )), \end{aligned}$$

(A.3c)

$$\begin{aligned} \frac{\partial g_4}{\partial t}&=-\frac{3}{2} \sin (2 ({\varPhi _0}-t \omega )). \end{aligned}$$

(A.3d)

Then, explicit expressions of the $g_i, i=1, \ldots , 4$ are straightforwardly found by integration of (A.3):

$$\begin{aligned} g_1(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)&= \frac{3 {\varOmega _0} \left( 1-{\varOmega _0}^2\right) \sin (2 (\varPhi _0-t \omega ))}{4 \omega } \nonumber \\&\quad +C_1(\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}), \end{aligned}$$

(A.4)

$$\begin{aligned} g_2(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)&= -\frac{3 {\varSigma _0} {\varOmega _0}^2 \sin (2 ({\varPhi _{0}}-t \omega ))}{4 \omega }\nonumber \\&\quad +C_2(\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}), \end{aligned}$$

(A.5)

$$\begin{aligned} g_3(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)&= -\frac{3 {\varOmega _0}^2 {\varOmega _{k0}} \sin (2 ({\varPhi _{0}}-t \omega ))}{2 \omega } \nonumber \\&\quad +C_3(\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}), \end{aligned}$$

(A.6)

$$\begin{aligned} g_4(H , \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}, t)&= \frac{3 \cos (2 (\varPhi _0-t \omega ))}{4 \omega } \nonumber \\&\quad +C_4(\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}), \end{aligned}$$

(A.7)

where we can set four integration functions $C_i(\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _{0}), i = 1,2,3,4$ to zero. Functions $g_i, i=1, \ldots , 4$ are continuously differentiable, such that their partial derivatives are bounded on $t\in [t_n, t_{n+1}]$.

Let $\varDelta \varOmega _0= \varOmega _0 - {\bar{\varOmega }}, \; \varDelta \varSigma _0= \varSigma _0 - {\bar{\varSigma }}, \; \varDelta \varOmega _{k0}= \varOmega _{k0}- {{\bar{\varOmega }}_k},\; \varDelta \varPhi _0= \varPhi _0 - {\bar{\varPhi }}$ be defined such that $\varOmega _0(t_n)={\bar{\varOmega }}(t_n)= {\varOmega _{n}}, \; \varSigma _0(t_n)={\bar{\varSigma }}(t_n)= {\varSigma }_{n}, \; \varOmega _{k0}(t_n)={{\bar{\varOmega }}_k}(t_n)= {\varOmega _k}_{n}, \; \varPhi _0(t_n)={\bar{\varPhi }}(t_n)= {\varPhi }_{n},$ with $0<\varOmega (t_n)+\varSigma (t_n)^2+{\varOmega _k}(t_n)^2 <1.$

Keeping the terms of second order in H, system (68) becomes

$$\begin{aligned} \dot{\varDelta \varOmega _0}&= \frac{1}{2} H \left( {\bar{\varOmega }} \left( 3 (\gamma -2) {\bar{\varSigma }}^2+3 (\gamma -1) \left( {\bar{\varOmega }}^2-1\right) +(3 \gamma -2) {\bar{\varOmega }}_k\right) \nonumber \right. \\&\left. \quad +\varOmega _0 \left( 3 \gamma \left( 1-\varSigma _{0}^2-\varOmega _0^2-\varOmega _{k0}\right) +6 \varSigma _0^2+3 \varOmega _0^2+2 \varOmega _{k0}-3\right) \right) \nonumber \\&\quad +H^2 \sin (2 (\varPhi _0-t \omega )) \Bigg (\frac{\varOmega _0^3 \left( 2 \mu ^2-\omega ^2\right) ^3}{4 b^2 \mu ^6 \omega ^3}\nonumber \\&\quad +\frac{\varOmega _0 \left( 9 b^2 \mu ^6 \omega ^2 \left( -4 \varOmega _0^4+3 \varOmega _0^2+1\right) -2 \varOmega _0^2 \left( 2 \mu ^2-\omega ^2\right) ^3\right) \cos (2 (\varPhi _0-t \omega ))}{8 b^2 \mu ^6 \omega ^3} \nonumber \\&\quad +\!\frac{3 \left( \varOmega _0^2-1\right) \varOmega _0 \left( 3 \gamma \left( \varSigma _0^2+\varOmega _0^2\!+\!\varOmega _{k0}-1\right) \!-6 \varSigma _0^2\!-\!3 \varOmega _0^2-2 \varOmega _{k0}\right) }{8 \omega }\Bigg ), \end{aligned}$$

(A.8a)

$$\begin{aligned} \dot{\varDelta \varSigma _0}&= \frac{1}{2} H \left( 3 {\bar{\varSigma }} \left( (\gamma -2) \left( {\bar{\varSigma }}^2-1\right) +(\gamma -1) \bar{\varOmega }^2\right) +{\bar{\varOmega }}_k \left( (3 \gamma -2) {\bar{\varSigma }}-2\right) \nonumber \right. \\&\left. \quad +\varSigma _0 \left( -3 \gamma \left( \varSigma _0^2+\varOmega _0^2+\varOmega _{k0}-1\right) +6 \varSigma _0^2+3 \varOmega _0^2+2 \varOmega _{k0}-6\right) +2 \varOmega _{k0}\right) \nonumber \\&\quad +H^2 \sin (2 (\varPhi _0-t \omega )) \nonumber \\&\quad \left( \frac{3 \varOmega _0^2 \left( 3 \gamma \varSigma _0 \left( \varSigma _0^2+ \varOmega _{0}^2+\varOmega _{k0}-1\right) -3 \varSigma _0 \left( 2 \varSigma _0^2+\varOmega _0^2\right) -2 (\varSigma _0+1) \varOmega _{k0}\right) }{8 \omega }\nonumber \right. \\&\left. \quad -\frac{9 \varSigma _0 \varOmega _0^4 \cos (2 (\varPhi _0-t \omega ))}{2 \omega }\right) , \end{aligned}$$

(A.8b)

$$\begin{aligned} \dot{\varDelta \varOmega _{k0}}&= H \left( {\bar{\varOmega }}_k \left( 3 (\gamma -2) {\bar{\varSigma }}^2+3 (\gamma -1) {\bar{\varOmega }}^2+(3 \gamma -2) \left( {\bar{\varOmega }}_k-1\right) +2 \bar{\varSigma }\right) \nonumber \right. \\&\left. \quad +\varOmega _{k0} \left( -3 \gamma \left( \varSigma _0^2+\varOmega _0^2+\varOmega _{k0}-1\right) +6 \varSigma _0^2-2 \varSigma _0+3 \varOmega _0^2+2 \varOmega _{k0}-2\right) \right) \nonumber \\&\quad +H^2 \sin (2 (\varPhi _0-t \omega )) \nonumber \\&\quad \left( \frac{3 \varOmega _0^2 \varOmega _{k0} \left( 3 \gamma \left( \varSigma _0^2+\varOmega _0^2+\varOmega _{k0}-1\right) -6 \varSigma _0^2+2 \varSigma _0-3 \varOmega _0^2-2 \varOmega _{k0}\right) }{4 \omega }\nonumber \right. \\&\quad \left. -\frac{45 \varOmega _0^4 \varOmega _{k0} \cos (2 (\varPhi _0-t \omega ))}{4 \omega }\right) , \end{aligned}$$

(A.8c)

$$\begin{aligned}&\dot{\varDelta \varPhi _0}= H^2 \Bigg (\frac{3 {\bar{\varOmega }}^2 \left( 2 \mu ^2-\omega ^2\right) ^3}{8 b^2 \mu ^6 \omega ^3}\nonumber \\&\quad -\frac{\varOmega _0^2 \left( 2 \mu ^2-\omega ^2\right) ^3 \sin ^4(\varPhi _0-t \omega )}{b^2 \mu ^6 \omega ^3} \nonumber \\&\quad +\frac{3 \cos (2 (\varPhi _0-t \omega ))}{8 \omega } \left( -3 \gamma \left( \varSigma _0^2+\varOmega _{0}^2+\varOmega _{k0}-1\right) \nonumber \right. \\&\left. \quad +6 \varSigma _0^2+3 \varOmega _0^2+2 \varOmega _{k0} + 3\left( \varOmega _0^2+2\right) \cos (2 (\varPhi _0-t \omega ))\right) \Bigg ). \end{aligned}$$

(A.8d)

Denoting ${\mathbf {x}}_0=(\varOmega _0, \varSigma _0, \varOmega _{k0})^T$, $\bar{{\mathbf {x}}}=({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_{k})^T$ the system (A.8) can be written as a 3-dimensional system:

$$\begin{aligned}&\dot{\varDelta {\mathbf {x}}_0}= H \left( \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}})\right) + {\mathscr {O}}(H^2), \end{aligned}$$

plus Eq. (A.8d), where the vector function $\bar{{\mathbf {f}}}$ is explicitly given (last row corresponding to $\dot{\varDelta } {\varPhi _0}$ was omitted) by:

$$\begin{aligned}&\bar{{\mathbf {f}}}(y_1, y_2, y_3)\\&= \left( \begin{array}{c} -\frac{1}{2} y_1 \left( -3 \gamma +3 (\gamma -1) y_1^2+3 (\gamma -2) y_2^2+3 \gamma y_3-2 y_3+3\right) \\ \frac{1}{2} \left( y_2 \left( 3 \gamma -3 (\gamma -1) y_1^2-3 \gamma y_3+2 y_3-6\right) -3 (\gamma -2) y_2^3+2 y_3\right) \\ y_3 \left( -3 (\gamma -1) y_1^2-3 (\gamma -2) y_2^2-2 y_2-(3 \gamma -2) (y_3-1)\right) \\ \end{array} \right) . \end{aligned}$$

It is a vector function with polynomial components in variables $(y_1, y_2, y_3)$. Therefore, it is continuously differentiable in all its components.

Let be $\varDelta {\mathbf {x}}_0(t)= (\varOmega _0-{\bar{\varOmega }},{\varSigma _0}- {\bar{\varSigma }}, {\bar{\varOmega }}_k - \varOmega _{k0})^T$ with $0\le |\varDelta {\mathbf {x}}_0|:=\max \left\{ |\varOmega _0-{\bar{\varOmega }}|, |{\varSigma _0}- {\bar{\varSigma }}|, |\varOmega _{k0} - {\bar{\varOmega }}_k| \right\}$ finite in the closed interval $[t_n,t]$. Using same initial conditions for ${\mathbf {x}}_0$ and $\bar{{\mathbf {x}}}$ we obtain by integration:

$$\begin{aligned} \varDelta {\mathbf {x}}_0(t)&= \int _{t_n}^t \dot{\varDelta {\mathbf {x}}_0} d s \\&= \int _{t_n}^t \left( H \left( \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}})\right) + {\mathscr {O}}(H^2)\right) ds. \end{aligned}$$

Using Lemma 6 we have

$$\begin{aligned}&\bar{{\mathbf {f}}}( {{\mathbf {x}}}_0(s))-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}}(s)) \nonumber \\&\quad = \underbrace{\left( \int _0^1 D \bar{{\mathbf {f}}}\left( \bar{{\mathbf {x}}}(s)+ z \; \left( {{\mathbf {x}}}_0(s) - \bar{{\mathbf {x}}}(s)\right) \right) \,d z\right) }_{{\mathbf {A}}(s)}\cdot \left( {{\mathbf {x}}}_0(s) - \bar{{\mathbf {x}}}(s)\right) ,\nonumber \\ \end{aligned}$$

(A.9)

where $D\bar{{\mathbf {f}}}$ denotes the Jacobian matrix of $\bar{{\mathbf {f}}}$ and the integral of a matrix is understood as componentwise. Omitting the dependence on s we calculate the components of

$$\begin{aligned} {\mathbf {A}}= \left( \begin{array}{ccc} a_{11} &{} a_{12} &{} a_{13} \\ a_{21} &{} a_{22} &{} a_{23} \\ a_{31} &{} a_{32} &{} a_{33} \\ \end{array} \right) , \end{aligned}$$

(A.10)

which are

$$\begin{aligned} a_{11}&=\frac{1}{4} \Bigg ( -2 (\gamma -2) {\bar{\varSigma }}^2-2 (\gamma -2) \varSigma _0 {\bar{\varSigma }}\nonumber \\&\quad -6 (\gamma -1) {\bar{\varOmega }}^2+6 \varOmega _0^2-6 (\gamma -1) {\bar{\varOmega }} \varOmega _0 \nonumber \\&\quad +2 \left( 2 \varSigma _0^2+3 \gamma +{\bar{\varOmega }}_k+\varOmega _{k0}-3\right) \nonumber \\&\quad -\gamma \left( 2 \varSigma _0^2+6 \varOmega _0^2+3 {\bar{\varOmega }}_k+3 \varOmega _{k0}\right) \Bigg ), \end{aligned}$$

(A.11a)

$$\begin{aligned} a_{12}&=-\frac{1}{2} (\gamma -2) \left( {\bar{\varSigma }} \left( 2 {\bar{\varOmega }}+\varOmega _0\right) +\varSigma _0 \left( {\bar{\varOmega }}+2 \varOmega _0\right) \right) ,\ \end{aligned}$$

(A.11b)

$$\begin{aligned} a_{13}&= -\frac{1}{4} (3 \gamma -2) \left( {\bar{\varOmega }}+\varOmega _0\right) , \end{aligned}$$

(A.11c)

$$\begin{aligned} a_{21}&= -\frac{1}{2} (\gamma -1) \left( {\bar{\varSigma }} \left( 2 {\bar{\varOmega }}+\varOmega _0\right) +\varSigma _0 \left( {\bar{\varOmega }}+2 \varOmega _0\right) \right) , \end{aligned}$$

(A.11d)

$$\begin{aligned} a_{22}&= \frac{1}{2} \Bigg (-\gamma {\bar{\varOmega }}^2+{\bar{\varOmega }}^2-\gamma \varOmega _0 {\bar{\varOmega }}\nonumber \\&\quad +\varOmega _0 {\bar{\varOmega }}-\gamma \varOmega _0^2+\varOmega _0^2+3 \gamma -\frac{3 \gamma {\bar{\varOmega }}_k}{2}+{\bar{\varOmega }}_k \nonumber \\&\quad -3 (\gamma -2) \left( {\bar{\varSigma }}^2 +\varSigma _0 \bar{\varSigma }+\varSigma _0^2\right) -\frac{3 \gamma \varOmega _{k0}}{2}+\varOmega _{k0}-6\Bigg ), \end{aligned}$$

(A.11e)

$$\begin{aligned} a_{23}&= \frac{1}{4} \left( (2-3 \gamma ) {\bar{\varSigma }}+(2-3 \gamma ) \varSigma _0+4\right) , \end{aligned}$$

(A.11f)

$$\begin{aligned} a_{31}&= -(\gamma -1) \left( {\bar{\varOmega }} \left( 2 {\bar{\varOmega }}_k+\varOmega _{k0}\right) +\varOmega _0 \left( {\bar{\varOmega }}_k+2 \varOmega _{k0}\right) \right) , \end{aligned}$$

(A.11g)

$$\begin{aligned} a_{32}&= -{\bar{\varOmega }}_k \left( (\gamma -2) \left( 2 {\bar{\varSigma }}+\varSigma _0\right) +1\right) \nonumber \\&\quad -\left( (\gamma -2) \left( {\bar{\varSigma }}+2 \varSigma _0\right) +1\right) \varOmega _{k0}, \end{aligned}$$

(A.11h)

$$\begin{aligned} a_{33}&= -(\gamma -2) {\bar{\varSigma }}^2-\left( (\gamma -2) \varSigma _0+1\right) {\bar{\varSigma }}-(\gamma -1) {\bar{\varOmega }}^2+\varOmega _0^2\nonumber \\&\quad +3 \gamma +2 {\bar{\varOmega }}_k+\varSigma _0 \left( 2 \varSigma _0-1\right) -(\gamma -1) {\bar{\varOmega }} \varOmega _0+2 \varOmega _{k0}\nonumber \\&\quad -\gamma \left( \varSigma _0^2+\varOmega _0^2+3 {\bar{\varOmega }}_k+3 \varOmega _{k0}\right) -2. \end{aligned}$$

(A.11i)

Taking sup norm $|\varDelta {\mathbf {x}}_0|=\max \left\{ |\varOmega _0-{\bar{\varOmega }}|, |{\varSigma _0}- {\bar{\varSigma }}|, |\varOmega _{k0}-{\bar{\varOmega }}_k| \right\}$ and the sup norm of a matrix ${|} {\mathbf {A}} {|}$ defined by $\max \{|a_{ij}|: i=1,2,3, j=1,2,3\}$, where $a_{ij}$ are given in (A.11) we have

$$\begin{aligned} | {\mathbf {A}}(s) \cdot \varDelta {\mathbf {x}}_0(s) |\le 3 | {\mathbf {A}}(s) | |\varDelta {\mathbf {x}}_0(s)|, \quad \forall s\in [t_n, t_{n+1}]. \end{aligned}$$

By continuity of polynomials $a_{i j} \left( \varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _0, {\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k, {\bar{\varPhi }}\right)$ given in (A.11) and by continuity of functions $\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _0$ and ${\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k, {\bar{\varPhi }}$ in $[t_n, t_{n+1}]$ the following finite constants are found:

$$\begin{aligned} L_1&= 3 \max _{t\in [t_n,t_{n+1}]} | {\mathbf {A}} (t)|,\\ M_1&= \max _{t\in [t_{n},t_{n+1}]} \Bigg \{ \Bigg | \frac{\varOmega _0^3 \left( 2 \mu ^2-\omega ^2\right) ^3}{4 b^2 \mu ^6 \omega ^3}\\&\quad +\frac{\varOmega _0 \left( 9 b^2 \mu ^6 \omega ^2 \left( -4 \varOmega _0^4+3 \varOmega _0^2+1\right) -2 \varOmega _0^2 \left( 2 \mu ^2-\omega ^2\right) ^3\right) \cos (2 (\varPhi _0-t \omega ))}{8 b^2 \mu ^6 \omega ^3}\\&\quad +\frac{3 \left( \varOmega _0^2-1\right) \varOmega _0 \left( 3 \gamma \left( \varSigma _0^2+\varOmega _0^2+\varOmega _{k0}-1\right) -6 \varSigma _0^2-3 \varOmega _0^2-2 \varOmega _{k0}\right) }{8 \omega }\Bigg |,\\&\quad \Bigg | \frac{3 \varOmega _0^2 \left( 3 \gamma \varSigma _0 \left( \varSigma _0^2+ \varOmega _{0}^2+\varOmega _{k0}-1\right) -3 \varSigma _0 \left( 2 \varSigma _0^2+\varOmega _0^2\right) -2 (\varSigma _0+1) \varOmega _{k0}\right) }{8 \omega }\\&\quad -\frac{9 \varSigma _0 \varOmega _0^4 \cos (2 (\varPhi _0-t \omega ))}{2 \omega }\Bigg |,\\&\Bigg | \frac{3 \varOmega _0^2 \varOmega _{k0} \left( 3 \gamma \left( \varSigma _0^2+\varOmega _0^2+\varOmega _{k0}-1\right) -6 \varSigma _0^2+2 \varSigma _0-3 \varOmega _0^2-2 \varOmega _{k0}\right) }{4 \omega }\\&\quad -\frac{45 \varOmega _0^4 \varOmega _{k0} \cos (2 (\varPhi _0-t \omega ))}{4 \omega }\Bigg | \Bigg \}, \end{aligned}$$

and

$$\begin{aligned} M_2&= \max _{t\in [t_{n},t_{n+1}]}\Bigg | \frac{3 {\bar{\varOmega }}^2 \left( 2 \mu ^2-\omega ^2\right) ^3}{8 b^2 \mu ^6 \omega ^3}\\&\quad -\frac{\varOmega _0^2 \left( 2 \mu ^2-\omega ^2\right) ^3 \sin ^4(\varPhi _0-t \omega )}{b^2 \mu ^6 \omega ^3} \\&\quad +\frac{3 \cos (2 (\varPhi _0-t \omega ))}{8 \omega } \left( -3 \gamma \left( \varSigma _0^2+\varOmega _{0}^2+\varOmega _{k0}-1\right) \right. \\&\left. \quad +6 \varSigma _0^2+3 \varOmega _0^2+2 \varOmega _{k0}\right. \\&\quad \left. + 3\left( \varOmega _0^2+2\right) \cos (2 (\varPhi _0-t \omega ))\right) \Bigg | \end{aligned}$$

such that for all $t\in [t_n, t_{n+1}]$:

$$\begin{aligned} |\varDelta {\mathbf {x}}_0(t) |&= \Bigg | \int _{t_n}^t \dot{\varDelta {\mathbf {x}}_0} d s \Bigg | \\&= \Bigg | \int _{t_n}^t \Bigg (H \left( \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}})\right) + {\mathscr {O}}(H^2)\Bigg ) ds \Bigg |\\&\le H_n \int _{t_n}^t | \bar{{\mathbf {f}}}( {{\mathbf {x}}}_0)-\bar{{\mathbf {f}}}(\bar{{\mathbf {x}}}) | ds + M_1 H_n^2 (t-t_n)\\&\le H_n \int _{t_n}^t | {\mathbf {A}}(s) \cdot \varDelta {\mathbf {x}}_0(s) | ds + M_1 H_n^2 (t-t_n)\\&\le L_1 H_n \int _{t_n}^t | \varDelta {\mathbf {x}}_0(s) | ds + M_1 H_n^2 (t-t_n) \\&\quad \le L_1 H_n \int _{t_n}^t |\varDelta \mathbf {x}_0 (s)| ds + M_1 H_n\\&\text {due to}\; t-t_n\le {t_{n+1}}- {t_{n}} =\frac{1}{H_n}. \end{aligned}$$

Using Gronwall’s Lemma 5, we have for $t \in [t_n, t_{n+1}]$:

$$\begin{aligned} \Big {|} \varDelta \mathbf {x}_0(t) \Big {|} \le M_1 H_n e^{L_1 H_n(t-t_n)} \le M_1 {H_n}e^{L_1}, \end{aligned}$$

due to $t-t_n\le {t_{n+1}}- {t_{n}} =\frac{1}{H_n}$. Then,

$$\begin{aligned}&\Big {|} \varDelta \varOmega _0(t) \Big {|} \le M_1 e^{L_1} {H_n}, \\&\Big {|} \varDelta \varSigma _0(t) \Big {|} \le M_1 e^{L_1} {H_n},\,\, \Big {|} \varDelta \varOmega _{k0}(t) \Big {|} \le M_1 e^{L_1} {H_n}. \end{aligned}$$

Furthermore, from eq. (A.8d) we have

Finally, taking limit as $n\rightarrow \infty$, we obtain $H_n\rightarrow 0$. Then, as $H_n \rightarrow 0$, functions $\varOmega _{0}, \varSigma _{0}, \varOmega _{k0}, \varPhi _0$ and ${\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k, {\bar{\varPhi }}$ have the same limit as $\tau \rightarrow \infty$.

Setting $\varSigma =\varSigma _0=0$ are derived analogous results for negatively curved FLRW model. $\square$

Fig. 8

One dimensional flow for (B.27) for $z\in [-1,1]$ the origin is stable if $z\ge 0$. Note that $z\ge 0$ corresponds to ${\bar{\varOmega }}_k\ge 0$

Fig. 9

One dimensional flow for (B.67) for $z\in [-2,2]$. The origin is stable

Fig. 10

Two dimensional flow for (B.82), (B.83). The physical region of the phase space is $y:=\frac{1}{8} (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_{k}-5)<0$, $z:= {\bar{\varOmega }}>0$

Fig. 11

Two dimensional flow for (B.101), (B.102). The origin is unstable

Appendix B: center manifold calculations

1.1 Appendix B.1: center manifold of $F_0$ for $\gamma =\frac{2}{3}$

Letting $\gamma =\frac{2}{3}$ and defining new variables

$$\begin{aligned}&x={\bar{\varSigma }} -\frac{{\bar{\varOmega }}_{k}}{2}, \; y={\bar{\varOmega }}, \; z={\bar{\varOmega }}_k, \end{aligned}$$

(B.12)

we obtain new equations

$$\begin{aligned} x'&=A x+f_1(x,y,z), \end{aligned}$$

(B.13)

$$\begin{aligned} y'&=B y+f_2(x,y,z), \end{aligned}$$

(B.14)

$$\begin{aligned} z'&=C z +f_3(x,y,z), \end{aligned}$$

(B.15)

with

$$\begin{aligned} A&= - 2, \; B= -\frac{1}{2}, \; C= 0, \end{aligned}$$

(B.16)

$$\begin{aligned} f_1(x,y,z)&=2 x^3+x^2 z+\frac{x y^2}{2}-\frac{x z^2}{2} \nonumber \\&\quad +x z-\frac{y^2 z}{4}-\frac{z^3}{4}+\frac{z ^2}{2}, \end{aligned}$$

(B.17)

$$\begin{aligned} f_2(x,y,z)&= 2 x^2 y+2 x y z+\frac{y^3}{2}+\frac{y z^2}{2}, \end{aligned}$$

(B.18)

$$\begin{aligned} f_3(x,y,z)&=4 x^2 z+4 x z^2-2 x z+y^2 z+z^3-z^2. \end{aligned}$$

(B.19)

Note that if $J_1$ is the linearization matrix of system (B.13), (B.14), (B.15) then the eigensystem of $J_1(0,0,0)$ is

$$\begin{aligned} \left( \begin{array}{ccc} -2 &{} -\frac{1}{2} &{} 0 \\ \{1,0,0\} &{} \{0,1,0\} &{} \{0,0,1\} \\ \end{array} \right) . \end{aligned}$$

This implies that the local center manifold of the origin for (B.13), (B.14), (B.15) is given by the graph

$$\begin{aligned} W^{c}_{loc}({\mathbf {0}})&= \Bigg \{(x,y,z)\in {\mathbb {R}}^3: x=h_1(z), y= h_2(z), \nonumber \\ h_1(0)&=h_2(0)=0, \nonumber \\ h_1'(0)&=h_2'(0)=0, |z|<\delta \Bigg \} \end{aligned}$$

(B.20)

for some $\delta >0$.

Therefore, we can use Taylor series to define

$$\begin{aligned}&h_1(z)=a_1 z^2+a_2 z^3+a_3 z^4+a_4 z^5+a_5 z^6+{\mathscr {O}}\left( z^7\right) , \end{aligned}$$

(B.21)

$$\begin{aligned}&h_2(z)=b_1 z^2+b_2 z^3+b_3 z^4+b_4 z^5+b_5 z^6+{\mathscr {O}}\left( z^7\right) . \end{aligned}$$

(B.22)

The following quasilinear differential equations

$$\begin{aligned} {\mathscr {N}}(h_1(z))&\equiv h_1'(z)(C z+f_3(h_1(z),h_2(z),z)) \nonumber \\&\quad -A h_1(z)-f_1(h_1(z),h_2(z),z), \end{aligned}$$

(B.23)

$$\begin{aligned} {\mathscr {N}}(h_2(z))&\equiv h_2'(z)(C z+f_3(h_1(z),h_2(z),z)) \nonumber \\&\quad -B h_2(z)-f_2(h_1(z),h_2(z),z), \end{aligned}$$

(B.24)

must be solved for $a_i, b_i , i=1, \ldots 5$ up to order six to approximate the center manifold. We notice that $b_i, i=1, \ldots 5$ are zero and $a_1= \frac{1}{4}, \; a_2= \frac{1}{4}, \; a_3=\frac{5}{16}, \; a_4=\frac{7}{16}$. Hence, we obtain

$$\begin{aligned} h_1(z)&=\frac{z^2}{4}+\frac{z^3}{4}+\frac{5 z^4}{16}+\frac{7 z^5}{16} +\frac{21 z^6}{32}+ {\mathscr {O}}(z^7), \end{aligned}$$

(B.25)

$$\begin{aligned} h_2(z)&= {\mathscr {O}}(z^7), \end{aligned}$$

(B.26)

and the dynamics on the center manifold is given by:

$$\begin{aligned} z'=-z^2+\frac{z^3}{2}+\frac{z^4}{ 2}+\frac{5 z^5}{8}+\frac{7 z^6}{8}+{\mathscr {O}}\left( z^7\right) . \end{aligned}$$

(B.27)

Then, $F_0$ is locally asymptotically stable for $z\ge 0$. Note that $z\ge 0$ corresponds to ${\bar{\varOmega }}_k\ge 0$ given that $z={\bar{\varOmega }}_k.$

In Fig. 8 a one dimensional flow of (B.27) for $z\in [-1,1]$ is represented. The origin is locally asymptotically stable if $z\ge 0$.

1.2 Appendix B.2: center manifold of D for $\gamma \ge 1$

Letting $\gamma \notin \left\{ \frac{4}{3}, \frac{3}{2}\right\}$ and defining new variables

$$\begin{aligned} x&=\frac{\gamma (12 {\bar{\varSigma }} -4 {\bar{\varOmega }}_k -3)-16 {\bar{\varSigma }} +8 {\bar{\varOmega }}_k+2}{24-16 \gamma }, \end{aligned}$$

(B.28)

$$\begin{aligned} y&=\frac{(3 \gamma -4) (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_k-5)}{8 (2 \gamma -3)}, \end{aligned}$$

(B.29)

$$\begin{aligned} z&={\bar{\varOmega }}, \end{aligned}$$

(B.30)

we obtain new equations

$$\begin{aligned} x'&=A x+f_1(x,y,z,\gamma ), \end{aligned}$$

(B.31)

$$\begin{aligned} y'&=B y+f_2(x,y,z,\gamma ), \end{aligned}$$

(B.32)

$$\begin{aligned} z'&=C z +f_3(x,y,z,\gamma ), \end{aligned}$$

(B.33)

with

$$\begin{aligned} A&= - \frac{3}{2}, \; B= 3(1-\gamma ), \; C= 0, \end{aligned}$$

(B.34)

$$\begin{aligned} f_1(x,y,z,\gamma )&=\frac{3 (5 \gamma -8) (\gamma -2) x^3}{12-8 \gamma } \nonumber \\&\quad +x^2 \left( \frac{18-13 \gamma }{8 \gamma -12}+\frac{3 (7 \gamma -12) (\gamma -2)^2 y}{4 (2 \gamma -3) (3 \gamma -4)}\right) \nonumber \\&\quad +x \Bigg (\frac{3 \gamma (\gamma -2)^3 y^2}{4 (4-3 \gamma )^2 (2 \gamma -3)} \nonumber \\&\quad +\frac{1}{4} \left( -10 \gamma +\frac{3}{3-2 \gamma }+\frac{8}{3 \gamma -4}+11\right) y\Bigg ) \nonumber \\&\quad +z^2 \Bigg (\frac{3 (\gamma -1)}{8 \gamma -12}+\frac{3 (5 \gamma -8) (\gamma -1) x}{12-8 \gamma } \nonumber \\&\quad +\frac{3 (\gamma -2) (\gamma -1) y}{12-8 \gamma }\Bigg ) -\frac{3 (\gamma -2)^4 y^3}{4 (4-3 \gamma )^2 (2 \gamma -3)} \nonumber \\&\quad -\frac{(\gamma (3 \gamma (12 \gamma -43)+152)-60) (\gamma -2) y^2}{4 (4-3 \gamma )^2 (2 \gamma -3)}, \end{aligned}$$

(B.35)

$$\begin{aligned} f_2(x,y,z,\gamma )&= \frac{3 (\gamma -2) (3 \gamma -4) x^3}{12-8 \gamma } \nonumber \\&\quad +x^2 \Bigg (\frac{3}{8} \left( -6 \gamma +\frac{1}{2 \gamma -3}+11\right) \nonumber \\&\quad +\frac{3 (\gamma -2) (5 \gamma -6) y}{12-8 \gamma }\Bigg ) \nonumber \\&\quad +x \left( \frac{3 (13 \gamma -18) (\gamma -2)^2 y^2}{4 (2 \gamma -3) (3 \gamma -4)}\nonumber \right. \\&\quad \left. +\frac{(30-19 \gamma ) y}{4 \gamma -6}\right) \nonumber \\&\quad +z^2 \Bigg (\frac{3 (\gamma -1) (3 \gamma -4)}{6-4 \gamma }\nonumber \\&\quad +\frac{3 (\gamma -1) (3 \gamma -4) x}{12-8 \gamma } \nonumber \\&\quad +\frac{3 (\gamma -1) (7 \gamma -10) y}{12-8 \gamma }\Bigg )\nonumber \\&\quad -\frac{3 (\gamma -2)^3 (7 \gamma -10) y^3}{4 (4-3 \gamma )^2 (2 \gamma -3)} \nonumber \\&\quad +\frac{1}{8} \left( -30 \gamma +\frac{16}{4-3 \gamma }\nonumber \right. \\&\quad \left. +\frac{3}{2 \gamma -3}+33\right) y^2-6 \gamma y, \end{aligned}$$

(B.36)

$$\begin{aligned} f_3(x,y,z,\gamma )&=z \Bigg (\left( 3-\frac{3 \gamma }{2}\right) x^2 \nonumber \\&\quad +x \left( \frac{3 (\gamma -2)^2 y}{3 \gamma -4}-2\right) \nonumber \\&\quad -\frac{3 (\gamma -2)^3 y^2}{2 (4-3 \gamma )^2} \nonumber \\&\quad +\left( -2 \gamma +\frac{2}{12-9 \gamma }+\frac{7}{3}\right) y\Bigg ) \nonumber \\&\quad -\frac{3}{2} (\gamma -1) z^3. \end{aligned}$$

(B.37)

Note that if $J_1$ is the linearization matrix of system (B.31), (B.32), (B.33) then the eigensystem of $J_1(0,0,0)$ is

$$\begin{aligned} \left( \begin{array}{ccc} -\frac{3}{2} &{} 3-3 \gamma &{} 0 \\ (1,0,0) &{} (0,1,0) &{} (0,0,1) \\ \end{array} \right) . \end{aligned}$$

This implies that the local center manifold of the origin for (B.31), (B.32), (B.33) is given by the graph

$$\begin{aligned} W^{c}_{loc}({\mathbf {0}})&= \Bigg \{(x,y,z)\in {\mathbb {R}}^3: x=h_1(z), y= h_2(z), \nonumber \\ h_1(0)&=h_2(0)=0, \nonumber \\ h_1'(0)&=h_2'(0)=0, |z|<\delta \Bigg \} \end{aligned}$$

(B.38)

for some $\delta >0$.

Table 3 Seven initial data sets for simulation of full system (46) and time-averaged system (78). All initial conditions are chosen in order to fulfill equality ${\bar{\varSigma }}^2(0)+{\bar{\varOmega }}^2(0)+{\bar{\varOmega }}_{k}(0)+{\bar{\varOmega }}_{m}(0)=1$

Fig. 12

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange), corresponding to LRS Bianchi III metric, when $\gamma =b=f=0$, $\omega ^2=2$, $\mu =1$, $\varOmega _m=0$ and $\varOmega _k=1-\varSigma ^2-\varOmega ^2$, with the identification $\varOmega ^2 \mapsto \varOmega$, for which the results of [152] are recovered. We have used initial data sets presented in the Table 3

Fig. 13

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =0$, in the projection $\varOmega _{k}=0$. We have used for both systems initial data sets presented in the Table 3

Fig. 14

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =0$, in the projection $\varSigma =0$. We have used for both systems initial data sets presented in the Table 3

Fig. 15

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =1$, in the projection $\varOmega _{k}=0$. We have used for both systems initial data sets presented in the Table 3

Fig. 16

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =1$, in the projection $\varSigma =0$. We have used for both systems initial data sets presented in the Table 3

Fig. 17

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =4/3$, in the projection $\varOmega _{k}=0$. We have used for both systems initial data sets presented in the Table 3

Fig. 18

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =4/3$, in the projection $\varSigma =0$. We have used for both systems initial data sets presented in the Table 3

Fig. 19

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =2$, in the projection $\varOmega _{k}=0$. We have used for both systems initial data sets presented in the Table 3

Fig. 20

Some solutions of the full system (46) (blue) and time-averaged system (78) (orange) for the LRS Bianchi III metric when $\gamma =2$, in the projection $\varSigma =0$. We have used for both systems initial data sets presented in the Table 3

Table 4 Seven initial data sets for simulation of full system (71) and time-averaged system (107). All the conditions are chosen in order to fulfill equality ${\bar{\varOmega }}^{2}(0)+{\bar{\varOmega }}_{k}(0)+{\bar{\varOmega }}_{m}(0)=1$

Fig. 21

Some solutions of the full system (71) (blue) and time-averaged system (107) (orange) for the FLRW metric with negative curvature ($k=-1$) when $\gamma =0$. We have used for both systems initial data sets presented in the Table 4

Fig. 22

Some solutions of the full system (71) (blue) and time-averaged system (107) (orange) for the FLRW metric with negative curvature ($k=-1$) when $\gamma =1$. We have used for both systems initial data sets presented in the Table 4

Fig. 23

Some solutions of the full system (71) (blue) and time-averaged system (107) (orange) for the FLRW metric with negative curvature ($k=-1$) when $\gamma =4/3$. We have used for both systems initial data sets presented in the Table 4

Fig. 24

Some solutions of the full system (71) (blue) and time-averaged system (107) (orange) for the FLRW metric with negative curvature ($k=-1$) when $\gamma =2$. We have used for both systems initial data sets presented in the Table 4

Therefore, we can use Taylor series to define

$$\begin{aligned} h_1(z)&=a_1 z^2+a_2 z^3+a_3 z^4+a_4 z^5+a_5 z^6+O(z^7), \end{aligned}$$

(B.39)

$$\begin{aligned} h_2(z)&=b_1 z^2+b_2 z^3+b_3 b^4+b_4 z^5+b_5 z^6+O(z^7). \end{aligned}$$

(B.40)

The following quasilinear differential equations

$$\begin{aligned} {\mathscr {N}}(h_1(z))&\equiv h_1'(z)(C z+f_3(h_1(z),h_2(z),z,\gamma )) \nonumber \\&\quad -A h_1(z)-f_1(h_1(z),h_2(z),z,\gamma ), \end{aligned}$$

(B.41)

$$\begin{aligned} {\mathscr {N}}(h_2(z))&\equiv h_2'(z)(C z+f_3(h_1(z),h_2(z),z,\gamma )) \nonumber \\&\quad -B h_2(z)-f_2(h_1(z),h_2(z),z,\gamma ), \end{aligned}$$

(B.42)

must be solved for $a_i,b_i$ up to order six to approximate the center manifold. We notice that the even terms are zero and $a_1= \frac{\gamma -1}{4 \gamma -6}, \; a_3= \frac{5 \gamma -6}{48 \gamma -72}, \; a_5=\frac{5 \gamma -6}{72 \gamma -108}, b_1=\frac{4-3 \gamma }{2 (2 \gamma -3)}, \; b_3= \frac{4-3 \gamma }{8 (2 \gamma -3)}, \; b_5=\frac{4-3 \gamma }{12 (2 \gamma -3)}$. Hence, we obtain

$$\begin{aligned} h_1(z)&=\frac{(5 \gamma -6) z^6}{72 \gamma -108}+\frac{(5 \gamma -6) z^4}{48 \gamma -72}+\frac{(\gamma -1) z^2}{4 \gamma -6}, \end{aligned}$$

(B.43)

$$\begin{aligned} h_2(z)&=\frac{(4-3 \gamma ) z^6}{12 (2 \gamma -3)}+\frac{(4-3 \gamma ) z^4}{8 (2 \gamma -3)}+\frac{(4-3 \gamma ) z^2}{2 (2 \gamma -3)}. \end{aligned}$$

(B.44)

Letting $\gamma =\frac{4}{3}$ and defining new variables

$$\begin{aligned}&x={\bar{\varOmega }}_k-\frac{3}{4}, \; y={\bar{\varSigma }} +\bar{\varOmega _k}-\frac{5}{4}, \; z={\bar{\varOmega }}, \end{aligned}$$

(B.45)

we obtain new equations

$$\begin{aligned} x'&=A x+f_1(x,y,z), \end{aligned}$$

(B.46)

$$\begin{aligned} y'&=B y+f_2(x,y,z), \end{aligned}$$

(B.47)

$$\begin{aligned} z'&=C z +f_3(x,y,z), \end{aligned}$$

(B.48)

where

$$\begin{aligned} A&= - \frac{3}{2}, \; B= -1, \; C= 0, \end{aligned}$$

(B.49)

$$\begin{aligned} f_1(x,y,z)&=2 x^3-4 x^2 y-\frac{x^2}{2}+2 x y^2-3 x y \nonumber \\&\quad -x z^2+\frac{3 y^2}{2}-\frac{3 z^2}{4}, \end{aligned}$$

(B.50)

$$\begin{aligned} f_2(x,y,z)&=x^3-x^2 y+2 x^2-x y^2-7 x y \nonumber \\&\quad -\frac{x z^2}{2}+y^3+3 y^2-\frac{y z^2}{2}-z^2 , \end{aligned}$$

(B.51)

$$\begin{aligned} f_3(x,y,z)&= x^2 z-2 x y z-2 x z+y^2 z+y z-\frac{z^3}{2}. \end{aligned}$$

(B.52)

Note that if $J_1$ is the linearization matrix of system (B.46), (B.47), (B.48) then the eigensystem of $J_1(0,0,0)$ is

$$\begin{aligned} \left( \begin{array}{ccc} -\frac{3}{2} &{} -1 &{} 0 \\ \{1,0,0\} &{} \{0,1,0\} &{} \{0,0,1\} \\ \end{array} \right) . \end{aligned}$$

Then, using Taylor series, the local center manifold of the origin for (B.46), (B.47), (B.48) is given by the graph (B.38) where

$$\begin{aligned} h_1(z)&= -\frac{z^6}{18}-\frac{z^4}{12}-\frac{z^2}{2}, \end{aligned}$$

(B.53)

$$\begin{aligned} h_2(z)&=-\frac{z^6}{6}-\frac{z^4}{4}-z^2. \end{aligned}$$

(B.54)

Letting $\gamma =\frac{3}{2}$ and defining new variables

$$\begin{aligned} x&={\bar{\varOmega }} _k-\frac{3}{4}, \end{aligned}$$

(B.55)

$$\begin{aligned} y&=-\frac{3}{32} (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_k-5), \end{aligned}$$

(B.56)

$$\begin{aligned} z&={\bar{\varOmega }}, \end{aligned}$$

(B.57)

we obtain new equations

$$\begin{aligned} x'&=A_1 x + A_2 y+f_1(x,y,z),\ \end{aligned}$$

(B.58)

$$\begin{aligned} y'&=B y+f_2(x,y,z), \end{aligned}$$

(B.59)

$$\begin{aligned} z'&=C z +f_3(x,y,z), \end{aligned}$$

(B.60)

where

$$\begin{aligned} A_1&= - \frac{3}{2}, \; A_2=1, \; B= - \frac{3}{2}, \; C= 0, \end{aligned}$$

(B.61)

$$\begin{aligned} f_1(x,y,z)&=\frac{3 x^3}{2}+8 x^2 y-\frac{7 x^2}{8}+\frac{32 x y^2}{3}\nonumber \\&\quad +\frac{22 x y}{3}-\frac{3 x z^2}{2}+8 y^2-\frac{9 z^2}{8}, \end{aligned}$$

(B.62)

$$\begin{aligned} f_2(x,y,z)&=-\frac{9 x^3}{32}-\frac{3 x^2 y}{4}-\frac{9 x^2}{16}+2 x y^2-\frac{25 x y}{4}\nonumber \\&\quad +\frac{9 x z^2}{32}+\frac{16 y^3}{3}-6 y^2-\frac{3 y z^2}{4}+\frac{9 z^2}{16} , \end{aligned}$$

(B.63)

$$\begin{aligned} f_3(x,y,z)&=\frac{3 x^2 z}{4}+4 x y z-2 x z+\frac{16 y^2 z}{3}-2 y z-\frac{3 z^3}{4}. \end{aligned}$$

(B.64)

Note that if $J_1$ is the linearization matrix of system (B.58), (B.59), (B.60) then the eigensystem of $J_1(0,0,0)$ is

$$\begin{aligned} \left( \begin{array}{ccc} -\frac{3}{2} &{} -\frac{3}{2} &{} 0 \\ \{1,0,0\} &{} \{0,0,0\} &{} \{0,0,1\} \\ \end{array} \right) . \end{aligned}$$

Then, using Taylor series, the local center manifold of the origin of (B.58), (B.59), (B.60) is given by the graph (B.38) where

$$\begin{aligned} h_1(z)&= -\frac{z^6}{18}-\frac{z^4}{12}-\frac{z^2}{2}, \end{aligned}$$

(B.65)

$$\begin{aligned} h_2(z)&=\frac{z^6}{16}+\frac{3 z^4}{32}+\frac{3 z^2}{8}. \end{aligned}$$

(B.66)

Finally, in these three cases (which correspond to $\gamma >1$), the dynamics on the center manifold is given by the following equation

$$\begin{aligned} z'=-\frac{z^3}{2}+\frac{z^5}{6}+O(z^7). \end{aligned}$$

(B.67)

This is a gradient-like equation

$$\begin{aligned} z'=-\nabla U(z), \quad U(z)= \frac{z^4}{8} - \frac{z^6}{36}, \end{aligned}$$

(B.68)

for which the origin is a degenerate minimum of second order, i.e., $U'(0)=U''(0)=U'''(0)=0, U^{(iv)}(0)=3>0$. Therefore, the origin is locally asymptotically stable as shown in Fig. 9.

Letting $\gamma =1$, we deduce that the center manifold of D is 2-dimensional. On the other hand, the system admits the lines of equilibrium points $({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k)= ({\bar{\varOmega }}^*, 0, 0)$ and $({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k)= ({\bar{\varOmega }}^*, \frac{1}{2}, \frac{3}{4})$ where ${\bar{\varOmega }}^*$ is an arbitrary number which satisfies ${\bar{\varOmega }}^*\in [0,1]$. Therefore, D as well as $F_0$ are not isolated fixed points anymore.

To analyze the stability of $D: ({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k)=(0, \frac{1}{2}, \frac{3}{4})$ we define new variables

$$\begin{aligned} x&=\frac{1}{8} (4 {\bar{\varSigma }} -4 {\bar{\varOmega }}_{k}+1), \; y=\frac{1}{8} (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_{k}-5), \nonumber \\ z&= {\bar{\varOmega }}, \end{aligned}$$

(B.69)

to obtain new equations

$$\begin{aligned} x'&=A x +f_1(x,y,z), \end{aligned}$$

(B.70)

$$\begin{aligned} y'&=C_1 y +f_2(x,y,z), \end{aligned}$$

(B.71)

$$\begin{aligned} z'&=C_2 z +f_3(x,y,z), \end{aligned}$$

(B.72)

where

$$\begin{aligned} A&= - \frac{3}{2}, \; C_1= 0, \; C_2= 0, \end{aligned}$$

(B.73)

$$\begin{aligned} f_1(x,y,z)&=\frac{9 x^3}{4}+x^2 \left( \frac{15 y}{4}+\frac{5}{4}\right) \nonumber \\&\quad +x \left( \frac{3 y^2}{4}-y\right) -\frac{3 y^3}{4}-\frac{y^2}{4}, \end{aligned}$$

(B.74)

$$\begin{aligned} f_2(x,y,z)&=-\frac{3 x^3}{4}+x^2 \left( \frac{3 y}{4}+\frac{3}{2}\right) \nonumber \\&\quad +x \left( \frac{15 y^2}{4}+\frac{11 y}{2}\right) +\frac{9 y^3}{4}+2 y^2, \end{aligned}$$

(B.75)

$$\begin{aligned} f_3(x,y,z)&=z \left( \frac{3 x^2}{2}+x (3 y+2)+\frac{3 y^2}{2}+y\right) . \end{aligned}$$

(B.76)

The local center manifold of the origin for (B.70), (B.71), (B.72) is given by the graph

$$\begin{aligned} W^{c}_{loc}({\mathbf {0}})&= \Bigg \{(x,y,z)\in {\mathbb {R}}^3: x=h(y, z), \; h(0,0)=0, \nonumber \\ \frac{\partial h}{\partial y}(0,0)&=\frac{\partial h}{\partial z}(0,0)=0, |(y,z)^T|<\delta \Bigg \}, \end{aligned}$$

(B.77)

for some $\delta >0$.

h(y, z) satisfies the quasilinear partial differential equation

$$\begin{aligned}&\Bigg (\frac{3}{4} h^3-\frac{3}{4} (y+2) h^2-\frac{1}{4} y (15 y+22) h \nonumber \\&\quad -\frac{1}{4} y^2 (9 y+8)\Bigg ) \frac{\partial h}{\partial y} \nonumber \\&\quad +\left( -\frac{3}{2} z h^2-(3 y+2) z h-\frac{1}{2} y (3 y+2) z\right) \frac{\partial h}{\partial z} \nonumber \\&\quad +\frac{9}{4} h^3+\frac{5}{4} (3 y+1) h^2+\frac{1}{4} (y (3 y-4)-6) h \nonumber \\&\quad -\frac{1}{4} y^2 (3 y+1)=0. \end{aligned}$$

(B.78)

We propose the Taylor expansion

$$\begin{aligned} h(y,z)&= {a_1} y^2+{a_2} y z+{a_3} z^2 \nonumber \\&\quad +{b_1} y^3+{b_2} y^2 z+{b_3} y z^2+{b_4} z^3 + {\mathscr {O}}(4), \end{aligned}$$

(B.79)

where ${\mathscr {O}}(4)$ denotes terms of fourth order in the vector norm. Therefore, Eq. (B.78) can be expressed as

$$\begin{aligned}&\frac{1}{4} (-6 a_1-1) y^2+y^2 z \left( -4 a_2-\frac{3 b_2}{2}\right) \nonumber \\&\quad -\frac{3 a_2 y z}{2}-\frac{3}{2} y z^2 (2 a_3+b_3) -\frac{3 a_3 z^2}{2}-\frac{3 b_4 z^3}{2} = {\mathscr {O}}(4). \end{aligned}$$

(B.80)

Equating the terms of the same power in y, z we have a solution $a_1= -\frac{1}{6}, \; a_2= 0, \; a_3= 0, b_1\; \text {arbitrary}, \; b_2= 0, \; b_3=0, \; b_4=0$. Then, we obtain

$$\begin{aligned} h(y, z)= -\frac{y^2}{6}+ b_1 y^3 + {\mathscr {O}}(4). \end{aligned}$$

(B.81)

The dynamics at the center manifold is given by

$$\begin{aligned}&y'=2 y^2 +\frac{4 y^3}{3}, \end{aligned}$$

(B.82)

$$\begin{aligned}&z'=y z + \frac{7 y^2 z}{6}. \end{aligned}$$

(B.83)

In Fig. 10 a two dimensional flow for (B.82) and (B.83) where is shown that the origin is unstable (saddle type) for $y\ne 0$ is presented. However, if we restrict the analysis to $y<0$, D is asymptotically stable and behaves as a local attractor.

To analyze the stability of an arbitrary point $D^*: ({\bar{\varOmega }}, {\bar{\varSigma }}, {\bar{\varOmega }}_k)=({\bar{\varOmega }}^*, \frac{1}{2}, \frac{3}{4})$ with ${\bar{\varOmega }}^*\ne 0$ we define new variables

$$\begin{aligned} x&=\frac{1}{8} (4 {\bar{\varSigma }} -4 {\bar{\varOmega }}_k+1) \end{aligned}$$

(B.84)

$$\begin{aligned} y&=\frac{1}{6} ({\bar{\varOmega }}^* (-4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_k-7)+6 {\bar{\varOmega }}) \end{aligned}$$

(B.85)

$$\begin{aligned} z&=\frac{1}{8} {\bar{\varOmega }}^* (4 {\bar{\varSigma }} +4 {\bar{\varOmega }}_k-5), \end{aligned}$$

(B.86)

to obtain new equations

$$\begin{aligned} x'&=A x +f_1(x,y,z), \end{aligned}$$

(B.87)

$$\begin{aligned} y'&=C_1 y + B_1 x+ B_2 z+f_2(x,y,z), \end{aligned}$$

(B.88)

$$\begin{aligned} z'&=C_2 z +f_3(x,y,z), \end{aligned}$$

(B.89)

where

$$\begin{aligned} A&= - \frac{3}{2}, \; B_1=4 {\bar{\varOmega }}^*, \; B_2=1, \; C_1= 0, \; C_2= 0, \end{aligned}$$

(B.90)

$$\begin{aligned} f_1(x,y,z)&=\frac{9 x^3}{4}+z \left( \frac{15 x^2}{4 {{\bar{\varOmega }}^*}}-\frac{x}{{{\bar{\varOmega }}^*}}\right) +\frac{5 x^2}{4}\nonumber \\&\quad +z^2 \left( \frac{3 x}{4 {\bar{\varOmega }}^*{}^2}-\frac{1}{4 {\bar{\varOmega }}^*{}^2}\right) -\frac{3 z^3}{4 {\bar{\varOmega }}^*{}^3}, \end{aligned}$$

(B.91)

$$\begin{aligned} f_2(x,y,z)&=-x^3 {\bar{\varOmega }}^*+x^2 \left( \frac{3 y}{2}+\frac{5 {\bar{\varOmega }}^*}{2}\right) \nonumber \\&\quad +z \left( -x^2+x \left( \frac{3 y}{{\bar{\varOmega }}^*}+\frac{17}{3}\right) +\frac{y}{{\bar{\varOmega }}^*}\right) \nonumber \\&\quad +z^2 \left( \frac{x}{{\bar{\varOmega }}^*}+\frac{3 y}{2 {\bar{\varOmega }}^*{}^2}+\frac{11}{6 {\bar{\varOmega }}^*}\right) +2 x y+\frac{z^3}{{\bar{\varOmega }}^*{}^2}, \end{aligned}$$

(B.92)

$$\begin{aligned} f_3(x,y,z)&=-\frac{3 x^3 {\bar{\varOmega }}^*{}}{4}+\frac{3 x^2 {\bar{\varOmega }}^*}{2} \nonumber \\&\quad +\left( \frac{3 x^2}{4}+\frac{11 x}{2}\right) z+z^2 \left( \frac{15 x}{4 {\bar{\varOmega }}^*}+\frac{2}{{\bar{\varOmega }}^*}\right) +\frac{9 z^3}{4 {\bar{\varOmega }}^*{}^2}. \end{aligned}$$

(B.93)

The local center manifold of the origin for (B.87), (B.88), (B.89) is given by the graph

$$\begin{aligned} W^{c}_{loc}({\mathbf {0}})&= \Bigg \{(x,y,z)\in {\mathbb {R}}^3: x=h(y, z), h(0,0)=0, \nonumber \\ \frac{\partial h}{\partial y}(0,0)&=\frac{\partial h}{\partial z}(0,0)=0, |(y,z)^T|<\delta \Bigg \}, \end{aligned}$$

(B.94)

for some $\delta >0$.

h(y, z) satisfies the quasilinear partial differential equation

$$\begin{aligned}&\frac{\partial h}{\partial z} \Bigg (\frac{3}{4} {\bar{\varOmega }}^*{} h^3-\frac{3}{4} \left( 2 {\bar{\varOmega }}^*{}+z\right) h^2 \nonumber \\&\quad -\frac{z \left( 22 {\bar{\varOmega }}^*{}+15 z\right) h}{4 {\bar{\varOmega }}^*}-\frac{z^2 \left( 8 {\bar{\varOmega }}^*{}+9 z\right) }{4 {\bar{\varOmega }}^*{}^2}\Bigg ) \nonumber \\&\quad +\frac{\partial h}{\partial y} \Bigg ({\bar{\varOmega }}^*h^3+\left( -\frac{5 \tilde{\varOmega }}{2}-\frac{3 y}{2}+z\right) h^2 \nonumber \\&\quad -\frac{\left( 6 y {\bar{\varOmega }}^*+12 {\bar{\varOmega }}^*{}^2+17 z {\bar{\varOmega }}^*{}+9 y z+3 z^2\right) h}{3 \tilde{\varOmega }} \nonumber \\&\quad -\frac{z \left( 6 y {\bar{\varOmega }}^*+6 {\bar{\varOmega }}^*{}^2+11 z {\bar{\varOmega }}^*{}+9 y z+6 z^2\right) }{6 {\bar{\varOmega }}^*{}^2}\Bigg ) \nonumber \\&\quad +\frac{5 \left( {\bar{\varOmega }}^*+3 z\right) h^2}{4 {\bar{\varOmega }}^*}+\frac{1}{4} \left( \frac{z \left( 3 z-4 \tilde{\varOmega }\right) }{{\bar{\varOmega }}^*{}^2}-6\right) h \nonumber \\&\quad -\frac{z^2 \left( {\bar{\varOmega }}^*+3 z\right) }{4 {\bar{\varOmega }}^*{}^3}+\frac{9}{4} h^3=0. \end{aligned}$$

(B.95)

We propose the Taylor expansion

$$\begin{aligned} h(y,z)&= {a_1} y^2+{a_2} y z+{a_3} z^2 \nonumber \\&\quad +{b_1} y^3+{b_2} y^2 z+{b_3} y z^2+{b_4} z^3 + {\mathscr {O}}(4), \end{aligned}$$

(B.96)

where ${\mathscr {O}}(4)$ denotes terms of fourth order in the vector norm. Therefore, Eq. (B.95) can be expressed as

$$\begin{aligned}&y z^2 \left( -4 {\bar{\varOmega }}^*{} \left( 2 {a_1} {a_3}+{a_2}^2\right) -\frac{11 {a_1}+12 {a_2}}{3 {\bar{\varOmega }}^*{}}-2 {b_2}-\frac{3 {b_3}}{2}\right) \nonumber \\&\quad +y^2 z \left( -12 {a_1} {a_2} {\bar{\varOmega }}^*{}-\frac{3 {a_1}}{{\bar{\varOmega }}^*{}}-3 {b_1}-\frac{3 {b_2}}{2}\right) \nonumber \\&\quad +y z \left( -2 {a_1}-\frac{3 {a_2}}{2}\right) -\frac{3 {a_1} y^2}{2} \nonumber \\&\quad -\frac{z^3 \left( 2 {\bar{\varOmega }}^*{}^2 \left( {a_2} \left( 24 {a_3} {\bar{\varOmega }}^*{}^2+11\right) +30 {a_3}+6 {b_3} {\bar{\varOmega }}^*{}+9 {b_4} {\bar{\varOmega }}^*{}\right) +9\right) }{12 {\bar{\varOmega }}^*{}^3} \nonumber \\&\quad +z^2 \left( -{a_2}-\frac{3 {a_3}}{2}-\frac{1}{4 \varOmega 1^2}\right) = {\mathscr {O}}(4). \end{aligned}$$

(B.97)

Equating the terms of the same power in y, z we have a solution $a_1= 0, \; a_2= 0, \; a_3= -\frac{1}{6 {\bar{\varOmega }}^*{}^2}, b_1= \frac{3 b_3}{8}, \; b_2= -\frac{3 b_3}{4}, \; b_4= \frac{1}{18} \left( \frac{1}{{\bar{\varOmega }}^*{}^3}-12 b_3\right)$. For simplicity, we set $b_3=\frac{1}{12{\bar{\varOmega }}^*{}^3}, b_4=0$. Then, we obtain

$$\begin{aligned} h(y, z)= \frac{y^3}{32 {\bar{\varOmega }}^*{}^3}-\frac{y^2 z}{16 {\bar{\varOmega }}^*{}^3}+\frac{y z^2}{12 {\bar{\varOmega }}^*{}^3}-\frac{z^2}{6 {\bar{\varOmega }}^*{}^2} + {\mathscr {O}}(4).\nonumber \\ \end{aligned}$$

(B.98)

The dynamics at the center manifold is given by

$$\begin{aligned} y'&= z +\frac{y z}{{\bar{\varOmega }}^*{}}+\frac{7 z^2}{6 {\bar{\varOmega }}^*{}}+ \frac{y^3}{8 {\bar{\varOmega }}^*{}^2}-\frac{y^2 z}{4 {\bar{\varOmega }}^*{}^2} \nonumber \\&\quad +\frac{3 y z^2}{2 {\bar{\varOmega }}^*{}^2} +\frac{z^3}{18 {\bar{\varOmega }}^*{}^2}, \end{aligned}$$

(B.99)

$$\begin{aligned} z'&= \frac{4 z^3}{3 {\bar{\varOmega }}^*{}^2}+\frac{2 z^2}{{\bar{\varOmega }}^*{}}. \end{aligned}$$

(B.100)

Using a re-scaling $(T, Y, Z)= ( {\bar{\varOmega }}^* \tau , \frac{y}{{\bar{\varOmega }}^*}, \frac{z}{{\bar{\varOmega }}^*}), \; {\bar{\varOmega }}^*>0$, we obtain a topologically equivalent system

$$\begin{aligned} \frac{d Y}{d T}&= Z + Y Z +\frac{7 Z^2}{6} + \frac{Y^3}{8}-\frac{Y^2 Z}{4}+\frac{3 Y Z^2}{2} +\frac{Z^3}{18}, \end{aligned}$$

(B.101)

$$\begin{aligned} \frac{d Z}{d T}&=2 Z^2 + \frac{4 Z^3}{3}. \end{aligned}$$

(B.102)

In Fig. 11 a two dimensional flow of (B.101), (B.102) where it is shown that the origin is unstable (saddle type) for $Z\ne 0$ is presented.

Appendix C: Numerical simulation

In this section we present numerical evidence that supports the main Theorem of Sect. 4 by solving numerically full and time-averaged systems obtained for each metric, namely LRS Bianchi III and open FLRW. For this purpose an algorithm in the programming language Python was implemented. The systems of differential equations were solved using the solve_ivp code provided by the SciPy open-source Python-based ecosystem. The integration method used was Radau that is an implicit Runge–Kutta method of the Radau IIa family of order 5 with a relative and absolute tolerances of $10^{-4}$ and $10^{-7}$, respectively. All systems of differential equations were integrated with respect to $\tau$, instead of t, with the range of integration $-40\le \tau \le 10$ for original systems and $-40\le \tau \le 100$ for averaged systems. All of them partitioned in 10000 data points. Furthermore, each full and time-averaged systems were solved considering only one matter component, these are cosmological constant ($\gamma =0$), non relativistic matter or dust ($\gamma =1$), radiation ($\gamma =4/3$) and stiff fluid ($\gamma =2$). Thereby the vacuum solutions corresponds to those where $\varOmega =\varOmega _m\equiv 0$ and the solutions without matter component corresponds to $\varOmega _m\equiv 0$. Finally we have considered fixed constants $\mu =\sqrt{2}/2$, $b=\sqrt{2}/5$ and $\omega =\sqrt{2}$, that leads to a value of $f=\frac{b \mu ^3}{\omega ^2-2 \mu ^2}=1/10$, that fulfills condition $f\ge 0$. With these values a generalized harmonic potential of the form

$$\begin{aligned} V(\phi )=\frac{\phi ^2}{2}+\frac{1}{100}(1-\cos (10\phi )) \end{aligned}$$

(C.103)

is obtained.

1.1 Appendix C.1: LRS Bianchi III

For the LRS Bianchi III metric we integrate:

• 1. The full system given by (46).

• 2. The time-averaged system (78).

As initial conditions we use seven data set presented in Table 3 as initial conditions for a better comparison of both systems. For data set vii current values of $\varOmega _{m}(0)=0.315$ and $\varOmega _{k}(0)=0.001$ according to [213] were considered.

It is important to mention that the first six initial conditions correspond to initial conditions presented in Table 2 of [152] and the additional data set vii is obtained considering current values of $\varOmega _m(0)=0.315$ and $\varOmega _k(0)=0.001$ according to [213]. Even more, the model presented in [152] is contained in our model when $\gamma =b=f=0$, $\omega ^2=2$, $\mu =1$, $\varOmega _m=0$ and $\varOmega _k=1-\varSigma ^2-\varOmega ^2$ (then $\gamma$ does not appear in the model presented in [152]) with the identification $\varOmega ^2\mapsto \varOmega$. As can be seen in Fig. 12a, b where some solutions of the full system (46) and time-averaged system (78) are presented, showing that our results are in complete agreement with results presented in [152] for the limiting case.

In Figs. 13, 14, 15, 16, 17, 18, 19, 20 projections of some solutions of the full system (46) and time-averaged system (78) in the $(\varSigma , H, \varOmega ^{2})$ and $(\varOmega _{k}, H, \varOmega ^{2})$ space with their respective projection when $H=0$ considering for both systems the same initial data sets from Table 3 are presented. Figures 13, 14 shows solutions for matter fluid corresponding to cosmological constant ($\gamma =0$). Figures 15, 16 shows solutions for matter fluid corresponding to dust ($\gamma =1$). Figures 17, 18 shows solutions for matter fluid corresponding to radiation ($\gamma =\frac{4}{3}$). Figures 19, 20 shows solutions for matter fluid corresponding to a stiff fluid ($\gamma =2$). These figures are evidence that the main Theorem presented in Sect. 4 is fulfilled for LRS Bianchi III metric.

1.2 Appendix C.2: FLRW $k=-1$

For the FLRW metric with negative curvature ($k=-1$, $\varOmega _{k}>0$) we integrate:

• 1. The full system given by (71).

• 2. The time-averaged system (107).

Seven data set presented in Table  4 were used as initial conditions. For data set vii current values of $\varOmega _{m}(0)=0.315$ and $\varOmega _{k}(0)=0.001$ according to [213] were considered.

In Figs. 21, 22, 23 and 24 projections of some solutions of the full system (71) and time-averaged system (107) for the FLRW metric with negative curvature ($k=-1$) in the $(\varOmega _{k}, H, \varOmega ^{2})$ space with their respective projection when $H=0$ and considering in both systems the same initial data sets from Table 4 are presented. Figure 21 show solutions for matter fluid corresponding to cosmological constant ($\gamma =0$). Figure 22 show solutions for matter fluid corresponding to dust ($\gamma =1$). Figure 23 show solutions for matter fluid corresponding to radiation ($\gamma =4/3$). Figure 24 show solutions for matter fluid corresponding to stiff fluid ($\gamma =2$). It is interesting to note that in the FLRW with negative curvature case, when the matter fluid corresponds to a cosmological constant, H tends asymptotically to constant values depending on the initial conditions which is consistent to de Sitter expansion. In addition, for any $\gamma <\frac{2}{3}$ and $\varOmega _k>0$, $\varOmega _k \rightarrow 0$. On the other hand, when $\gamma >\frac{2}{3}$ and $\varOmega _k>0$ the universe becomes curvature dominated asymptotically ($\varOmega _k \rightarrow 1$). These figures are evidence that the main Theorem presented in Sect. 4 is fulfilled for FLRW metric with negative curvature.