Exploring new physics contributions to CP violation in $\tau ^- \rightarrow K^-\pi ^0\nu _{\tau }$

Abstract

A general analysis of possible violation of CP in processes like $\tau \rightarrow K\pi \nu$, for unpolarized $\tau$ is presented. In this paper, we derive the new contributions to the effective Hamiltonian governs $\vert \Delta S \vert =1$ semileptonic tau decays in the framework of two Higgs doublet model with generic Yukawa structure and Leptoquarks models. Within these models, we list all operators, in the effective Hamiltonian and provide analytical expression for their corresponding Wilson coefficients. Moreover, we analyze the role of the different contributions, originating from the scalar, vecor and tensor hadronic currents, in generating direct CP asymmetry in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$. We show that non vanishing direct CP asymmetry in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ can be generated due to the presence of both, the weak phase in the Wilson coefficient corresponding to the tensor operator and the strong phase difference resulting from the interference between the form factors expressing the matrix elements of the vector and tensor hadronic currents. After taking into account all relevant constraints, we find that the generated direct CP asymmetry is of order $10^{-8}$ which is several orders of magnitude larger than the standard model prediction. We show also that, in two Higgs doublet model with generic Yukawa structure , direct local or non integrated CP violation can be as large as 0.3 % not far from experimental possibilities. This kind of asymmetry can be generated due to the interference between vector and scalar contributions with different weak phases which is not the case in the SM.

1 Introduction

Probably the most evident fail of the Standard Model (SM) is the absence of a mechanism to explain baryogenesis, even if all CP violation (CPV) processes measured by now are consistent with SM predictions [1,2,3,4,5,6,7,8,9,10]. At the moment CPV has been observed only in non leptonic decays of kaons, B and $B_s$ and recently in D [11]. In the leptonic sector, the quantum mixing of neutrinos yields a source for generating a complex phase [12, 13]. This phase is necessary for having CPV that can be measured in $\nu _\mu -\nu _e$ and $\bar{\nu }_\mu -{\bar{\nu }}_e$ oscillations which are experimentally accessible with the Tokai-to-Kamioka (T2K) experiment [14]. Recently, in Ref. [15], the T2K collaboration has reported a measurement that shows an indication of CPV in the neutrino sector at $3\sigma$ confidence level. Particularly, at this confidence level, the reported measurement are in favor of large enhancement of the neutrino oscillation probability. The measurement also excludes values of a complex phase that can lead to a large enhancement of the observed anti-neutrino oscillation probability at $3\sigma$ confidence level. Decays involving leptons like $K_L^0\rightarrow \pi ^- l^+ \nu _l,\ \pi ^+\pi ^- e^+e^-$, where CPV has been measured can be understood as CPV in the meson sector. SM predictions for direct CPV in the leptonic sector tell us that it should be very small so its observation would be a clear signal of new physics.

Decays like $\tau \rightarrow K\pi \nu$ involve at least two kinds of CPV contributions: direct CPV and the ‘known’ CPV if neutral kaons are involved. Direct CPV is the same for $\tau ^-\rightarrow {\bar{K}}^0 \pi ^-\nu _\tau$, $\tau ^-\rightarrow K^-\pi ^0 \nu _\tau$ and so on, because the transition $\tau \rightarrow s{\bar{u}} \nu _\tau$ is the same. Notice that if additional neutral pions are present the conclusions are identical.

Earlier searches by CLEO [16] and Belle Collaborations [17] for local or nonintegrated CPV in the decay $\tau ^-\rightarrow K_S\pi ^-\nu _\tau$ didn’t find any CPV signal (see the corresponding section in this article). The integrated CPV has been searched by the BaBar collaboration with the result

$$\begin{aligned} A_{\mathrm{CP}}^{\mathrm{exp.}}= & {} {\Gamma (\tau ^+\rightarrow K_S\pi ^+ {\bar{\nu }}_\tau )- \Gamma (\tau ^-\rightarrow K_S\pi ^- \nu _\tau ) \over \Gamma (\tau ^+\rightarrow K_S\pi ^+ {\bar{\nu }}_\tau )+\Gamma (\tau ^-\rightarrow K_S\pi ^- \nu _\tau ) }\nonumber \\= & {} -(0.36 \pm 0.23 \pm 0.11)\% \end{aligned}$$

(1)

According to the Standard Model (SM) this process occurs via the $\tau ^- \rightarrow s \bar{u}\nu _{\tau }$ transition and no direct CPV signal is expected. However due to the CPV in mixing in $K^0-\bar{K}^0$ the total signal should be [18,19,20]

$$\begin{aligned} A_{\mathrm{CP}}^{\mathrm{theo.}} \simeq 2\mathrm{Re}\ \epsilon _K =2\cdot (0.166(2))\%= 0.332(2) \% \end{aligned}$$

(2)

There is a 2.8 sigma discrepancy that may indicate the presence of direct CPV, absent in the SM. However experimental details as the efficiency in the $K_S$ detection has to be taken into account properly as was pointed out by Grossman and Nir in [18]. Any real discrepancy is direct CPV and therefore is new physics (NP) and it should be present in related channels like $\tau ^-\rightarrow K^- \pi ^0 \nu _\tau$ and so on. Possible direct angular integrated CP violation in the modes $\tau ^-\rightarrow K_S\pi ^-\nu _\tau$ and $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ has been studied in the literature in Refs. [19,20,21,22,23,24,25,26,27,28,29,30,31] respectively.

In Ref. [21], it was shown that angular integrated direct CPV asymmetry can not be produced by a simple new scalar interactions, even if they provide new weak phases. As it is well known, to have direct CPV one needs two interfering contributions with different weak and strong phases. In these decays once the angular integral is done the interfering signal vanish. However a direct CPV signal may remain if the angular integration is partial or no integration is done (local CPV) at all.

Moreover, as shown in Ref. [21], another possibility is to have nonstandard tensor interactions with non vanishing weak phases. In this case the interfering vector and tensor interactions remain after the full angular integration and a CPV signal is obtained. However in a recent study, it was shown that this interference is severely suppressed due to the bounds from the neutron electric dipole moment and $D-{\bar{D}}$ mixing constrains [22].

An estimation of the direct CPV in $\tau ^- \rightarrow K^- \pi ^0\nu _{\tau }$, within SM framework showed that the calculated asymmetry is negligibly small of order $10^{-12}$ [27]. This result motivated further studies of CP violation in this decay mode within the framework of supersymmetric extension of the SM [29, 30]. In minimal supersymmetric extension of the SM with R parity conservation, direct CP asymmetry of order $O(10^{-7})$ can be generated through the interference between the vector and tensor interactions [29]. On the other hand, within supersymmetric extensions of SM with allowed R parity violating terms, no direct CP asymmetry in the decay rate can be generated at tree-level due to the absence of tensor interactions [30]. In Refs. [26, 28, 31], it was pointed out that CP violation in $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ can arise in multi Higgs models with complex couplings in the quark sector due to the interference of the vector and scalar quark currents.

The aim of this paper is to analyze how to generate a CP violation in the semileptonic $\vert \Delta S \vert =1$ tau decays in the integrated and nonintegrated CP asymmetries. We shall apply these considerations to specific models of New Physics (NP) such as 2HDM III and in the SM extensions with scalar leptoquarks. With the presence of new weak phases and new tensor operator, we analyze the direct CP violating effects in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$.

This paper is organized as follows. In Sect. 2, we present the effective Hamiltonian describing semileptonic $\vert \Delta S \vert =1$ tau decays, $\tau ^- \rightarrow s \bar{u}\nu _{\tau }$ transition, in the presence of NP beyond SM. Based on this Hamiltonian, we derive the general expression of the differential decay width of the decay process $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$. Switching off NP contributions to the differential decay width, we show in Sects. 3 and 4 that no direct CP asymmetry in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ can be generated in the SM at tree-level.

In Sect. 3.1, we derive the analytic expressions of the Wilson coefficients up to one loop level originating from the charged Higgs mediation in 2HDM III. Leptoquarks contributions to these processes are presented in Sect. 3.2. In Sect. 3.1 also, we give our estimation of the direct CP asymmetry in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$. In Sect. 4 we give our prediction for the local CP violation in the same decay mode. Finally, in Sect. 5, we give our conclusion.

2 Effective Hamiltonian and the differential decay width of $\vert \Delta S \vert =1$ $\tau$ decays

In the presence of NP beyond SM, the effective Hamiltonian governs $\vert \Delta S \vert =1$ $\tau$ decays transition, taking into consideration the parity conservation in the $k\rightarrow \pi$ matrix elements, can be expressed as

$$\begin{aligned} {{\mathcal {H}}}_{eff} = -\frac{G_F}{\sqrt{2}}V^\star _{us}\sum _{i=V, A,S,P,T} C_i(\mu )\,Q_i(\mu ), \end{aligned}$$

(3)

where $V_{us}$ is the us Cabibbo–Kobayashi–Maskawa (CKM) matrix element and $Q_i$ represent the four-fermion local operators at low energy scale $\mu \simeq m_\tau$ where

$$\begin{aligned} Q_{V}= & {} \big (\bar{\nu }_\tau \gamma _\mu \tau \big )\big (\bar{s} \gamma ^\mu u\big ) ,\nonumber \\ Q_{A}= & {} \big (\bar{\nu }_\tau \gamma _\mu \gamma _5 \tau \big )\big (\bar{s} \gamma ^\mu u\big ) ,\nonumber \\ Q_{S}= & {} \big (\bar{\nu }_\tau \tau \big )\big (\bar{s} u\big ) ,\nonumber \\ Q_{P}= & {} \big (\bar{\nu }_\tau \gamma _5 \tau \big )\big (\bar{s} u\big ) ,\nonumber \\ Q_{T}= & {} \big (\bar{\nu }_\tau \sigma _{\mu \nu } (1+ \gamma _5) \tau \big )\big (\bar{s}\sigma ^{\mu \nu } u\big ) , \end{aligned}$$

(4)

with $\sigma _{\mu \nu }= \frac{i}{2} [\gamma _\mu , \gamma _\nu ]$. The Wilson coefficients, $C_i$, corresponding to the operators $Q_i$ can be expressed as

$$\begin{aligned} C_i = C^{SM}_i+C^{NP}_i, \end{aligned}$$

(5)

where $C^{SM}_i$ and $C^{NP}_i$ represent SM and NP contributions to the Wilson coefficients respectively. In order to proceed to write the amplitude we need to calculate the matrix elements of the operators in the effective Hamiltonian. For this, we need to assign the momenta of the particles involved in the decay process. We express the momenta as

$$\begin{aligned} \tau ^-(p_\tau )\rightarrow K^- (p_k) + \pi ^0 (p_\pi ) + \nu _\tau (p_\nu ). \end{aligned}$$

(6)

The matrix elements of the hadronic currents in the $Q_i$ operators, in Eq. (4), are usually parameterized in terms of particles momenta and form factors. Due to parity conservation in the $K\rightarrow \pi$ matrix elements we need only to calculate the matrix element of the vector, scalar and tensor quarks currents only. The matrix element of the vector quark current can be expressed as

$$\begin{aligned} \langle K^- \pi ^0|{\bar{s}}\gamma ^\mu u|0\rangle = \frac{1}{\sqrt{2}} \bigg ((p_K-p_\pi )^\mu f_+(s)+(p_K+p_\pi )^\mu f_-(s)\bigg ), \end{aligned}$$

(7)

and

$$\begin{aligned} f_-(s)=\frac{\Delta ^2_{K\pi }}{s}\big (f_0(s)-f_+(s)\big ), \end{aligned}$$

(8)

here s is the invariant mass defined as $s=(p_K+p_\pi )^2$ of the $\pi K$ system and we have defined $\Delta ^2_{K\pi } = M_K^2-M_{\pi }^2$. The matrix element of the scalar quark current can be obtained from Eq. (7) by taking the divergence in the usual form and hence we get

$$\begin{aligned} \langle K^- \pi ^0|{\bar{s}} u|0\rangle= & {} \frac{(M_K^2-M_{\pi }^2)}{\sqrt{2}(m_s-m_u)}f_0(s) \nonumber \\= & {} \frac{\Delta ^2_{K\pi }}{\sqrt{2}(m_s-m_u)}f_0(s), \end{aligned}$$

(9)

$m_{s,u}$ denote s, u current quark masses. Finally, the matrix element of the tensor quarks current, $\langle K^- \pi ^0|\bar{s}\sigma ^{\mu \nu } u|0\rangle$, can be expressed as [22]

$$\begin{aligned} \langle K^- \pi ^0|{\bar{s}}\sigma ^{\mu \nu } u|0\rangle&=\frac{i(p_K^\mu p_\pi ^\nu -p_K^\nu p_\pi ^\mu )}{\sqrt{2}M_K}B_T(s). \end{aligned}$$

(10)

For specific models, like the ones under investigation in this study, the Wilson coefficients $C_i$ can be expressed in terms of only three independent coefficients. Particularly, in these models, we have $C_A = - C_V$ and $C_P = C_S$ and hence we are left with only three independent Wilson coefficients, namely $C_V$, $C_S$ and $C_T$. This indicates that, the set of the operators in Eq. (4), within these models, can be rewritten in terms of just three independent operators as $\big (\bar{\nu }_\tau \gamma _\mu L \tau \big )\big (\bar{s} \gamma ^\mu u\big )$, $\big (\bar{\nu }_\tau R \tau \big )\big (\bar{s} u\big )$ and $\big (\bar{\nu }_\tau \sigma _{\mu \nu } R \tau \big )\big (\bar{s}\sigma ^{\mu \nu } u\big )$ where $L,R=1\mp \gamma _5$. The total amplitude, $\mathcal {A}$, of $\tau ^- \rightarrow K^-\pi ^0 \nu _\tau$ decay can be expressed as

$$\begin{aligned} \mathcal {A}= & {} -\frac{G_{F}V_{us} C_V}{\sqrt{ 2}}\bigg \{ \bigg ((p_K-p_\pi )^\mu f_+(s)+(p_K+p_\pi )^\mu f_-(s)\bigg )\\&\times \Big (\bar{u}(p_\nu )\gamma _{\mu }Lu(p_\tau )\Big )\\&+ \frac{C_S\,\Delta ^2_{K\pi }}{(m_s-m_u)\, C_V}f_0(s)\Big (\bar{u}(p_\nu )R u(p_\tau )\Big ) \\&+ i\frac{(p_K^\mu p_\pi ^\nu -p_K^\nu p_\pi ^\mu )\, C_{T}}{M_KC_V}B_T(s)\Big (\bar{u}(p_\nu )\sigma _{\mu \nu } R u(p_\tau ) \Big )\bigg \} \ . \end{aligned}$$

The differential decay width is given as

$$\begin{aligned} \frac{\text {d}\Gamma }{\text {d}s}= & {} G_F^2|V_{us}|^2 |C_V|^2 S_\text {EW} \frac{\lambda ^{1/2}(s,M_{\pi }^2,M_K^2)(m_\tau ^2-s)^2 \Delta ^4_{K\pi } }{1024\pi ^3m_\tau s^3}\nonumber \\&\times \bigg [\frac{(m_\tau ^2+2s)\lambda (s,M_{\pi }^2,M_K^2)}{3m_\tau ^2 \Delta ^4_{K\pi } }\bigg (|f_+(s) -T(s)|^2\nonumber \\&+\frac{2(m_\tau ^2-s)^2}{9sm_\tau ^2}|T(s)|^2\bigg )+|S(s)|^2\bigg ], \end{aligned}$$

(11)

where $\lambda (x,y,z)$ is given by $\lambda (x,y,z) = x^2+y^2 +z^2 -2 xy -2 xz -2 yz$, $S_\text {EW}=1.0194$ [32,33,34] accounts for the electroweak running down to $m_\tau$ and

$$\begin{aligned} S(s)= & {} f_0(s)\bigg (1+\frac{s\, C_S}{m_\tau (m_s-m_u)\, C_V} \bigg ),\nonumber \\ T(s)= & {} \frac{3s}{m_\tau ^2+2s}\frac{m_\tau \, C_{T}}{M_KC_V} \, B_T(s). \end{aligned}$$

(12)

It should be noted that Eq. (11) above and Eq. (12) of Ref. [22] are inconsistent only by a factor 1/2 due to the presence of extra factor $1/\sqrt{2}$ in the hadronic matrix elements, Eqs. (7, 9, 10), compared to their corresponding ones listed in Eq. (10) in Ref. [22]. This is due to the difference of the final states $K^-\pi ^0$ and ${\bar{K}}^0\pi ^-$ in our work and in Ref. [11] respectively. In the isospin symmetry limit, the form factors of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ are not equal to their corresponding ones in the decay mode $\tau ^-\rightarrow \bar{K}^0\pi ^-\nu _\tau$ [35]. Rather, they are related by a simple Clebsch–Gordan factor $1/\sqrt{2}$ as given in Eqs. (4, 8) in Ref. [35]. These parameterizations had been adopted in our previous studies in Refs. [29, 36].

Non vanishing direct CP asymmetry in the decay rate requires the presence of two types of phases, the weak CP violating phases and the strong CP conserving phases. The weak CP violating phases can be generated in the Wilson coefficients upon existence of complex couplings. On the other hand, the strong CP conserving phases originate from the phases in the form factors expressing the matrix elements of the hadronic currents.

Breit–Wigner forms are used to parameterize the contributions of the different resonances dominating the scalar and vector hadronic currents. As a consequence, form factors originating from these currents can be expressed as a summation of Breit–Wigner forms. Previous studies of CP asymmetries in $\tau \rightarrow K \pi \nu _\tau$ decays, for instances Refs. [21, 29], adopted the assumption that the form factor $B_T(s)$ has no strong phases. However, this assumption is incorrect as argued in Ref. [22]. As shown in Refs. [37, 38], spin-1 resonances can be described equivalently by vector or antisymmetric tensor fields . Hence the same resonances $K^*(892)$ and the $K^*(1410)$ that dominate the Breit–Wigner forms in $f_+(s)$ will appear in $B_T(s)$ as well [22]. It should be noted that, this conclusion can be derived by analyzing the unitarity relation for the form factors as shown in details in Ref. [22]. Thus, we conclude that $B_T(s)$ has a strong phase that should be taken into account in the calculations of the CP asymmetry.

In the SM, at tree-level, the Wilson coefficients $C_i$ reduces to

$$\begin{aligned} C^{SM}_{V} = -C^{SM}_{A} = 1,\,\,\,\,\,\,\,\,\,\,\,\,\,C^{SM}_{S,P,T} =0, \end{aligned}$$

(13)

This accounts for the fact that $\tau ^{-}\rightarrow K^{-}\pi ^{0}\nu _{\tau }$, at tree-level, can be generated as a result of exchanging single $W^-$ boson which contributes only to $Q_V$ operator. Consequently, the quantities S(s) and T(s) in Eq. (12) reduce to

$$\begin{aligned} S(s) \rightarrow f_0(s),\,\,\,\,\,\,\, T(s) \rightarrow 0, \end{aligned}$$

(14)

and upon substation in Eq. (11) we get

$$\begin{aligned} \frac{\text {d}\Gamma }{\text {d}s}\bigg |_{\text {SM}}&=G_F^2|V_{us}|^2 S_\text {EW} \frac{\lambda ^{1/2}(s,M_{\pi }^2,M_K^2)(m_\tau ^2-s)^2 \Delta ^4_{K\pi }}{1024\pi ^3m_\tau s^3}\nonumber \\&\quad \times \bigg [\frac{(m_\tau ^2+2s)\lambda (s,M_{\pi }^2,M_K^2)}{3m_\tau ^2 \Delta ^4_{K\pi }}|f_+(s)|^2 +|f_0(s)|^2\bigg ], \end{aligned}$$

(15)

The decay rate of the process $\tau \rightarrow K^- \pi ^0 \nu _{\tau }$ in the SM, $\Gamma _{SM}$, can be then obtained upon integrating the previous equation with respect to the kinematic variable s. Thus we get

$$\begin{aligned} \Gamma _{SM}&=\frac{G_F^2|V_{us}|^2 S_\text {EW} \Delta ^4_{K\pi } }{1024\pi ^3m_\tau }\nonumber \\&\quad \times \int ^{m^2_\tau }_{(M_K+M_{\pi })^2} ds \bigg (\frac{\lambda ^{1/2}(s,M_{\pi }^2,M_K^2)(m_\tau ^2-s)^2}{ s^3}\nonumber \\&\quad \times \bigg [\frac{(m_\tau ^2+2s)\lambda (s,M_{\pi }^2,M_K^2)}{3m_\tau ^2 \Delta ^4_{K\pi } }|f_+(s)|^2 +|f_0(s)|^2\bigg ]\bigg ), \end{aligned}$$

(16)

The CP asymmetry in total decay rate of $\tau ^{-}\rightarrow K^{-}\pi ^{0}\nu _{\tau }$ is given by:

$$\begin{aligned} A_{CP}= & {} \frac{\Gamma (\tau ^{-}\rightarrow K^{-}\pi ^{0}\nu _{\tau })-\Gamma (\tau ^{+}\rightarrow K^{+}\pi ^{0}\nu _{\tau })}{\Gamma (\tau ^{-}\rightarrow K^{-}\pi ^{0}\nu _{\tau })+\Gamma (\tau ^{+}\rightarrow K^{+}\pi ^{0}\nu _{\tau })}. \end{aligned}$$

(17)

Clearly, from the expression of $\Gamma _{SM}$, direct CP asymmetry in the decay rate will vanish due to the absence of the weak phase, $C^{SM}_V$ is real, and also due to the remark that the form factors $f_+(s)$ and $f_0(s)$ do not interfere and hence the relative strong phase essential for CP asymmetry vanishes. Thus, to generate no vanishing CP asymmetry in the decay rate within SM, it is essential to consider higher order terms contributing to the amplitude as done in Ref. [27]. These terms can be generated from diagrams with exchanging two W bosons. Thus, the generated asymmetry is expected to be very small. As shown in Ref. [27], the resulting CP asymmetry is suppressed by the CKM factor $V_{td} \simeq 10^{-3}$ and also by a higher order suppression factor $g^2/4\pi M^2_W \simeq 10^{-8}$. As a consequence, the resulting CP rate asymmetry is expected to be negligible. In fact the asymmetry is of order $10^{-12}$ as estimated in Ref. [27].

Integrated direct or local CP violation has been discussed above. However having somehow the ability to measure angular distribution one can extract the local CPV signal [31] and $|f_0|$. The CPV signal is produced due to the interference between the vector and the scalar contributions, as long as they contribute with different weak phases. Additional CPV observables are provided by triple products, but in that case polarized taus are needed [25, 26, 28]. Without considering the exotic tensor interactions, one finds that the local distribution is given as

$$\begin{aligned} {\mathrm{d}^2\Gamma ^- \over \mathrm{d}s \mathrm{d}x}= & {} { G^2_F V^2_{us} m_\tau \over 64\pi ^3 s^{3/2}} |\mathbf{p}_K| |\mathbf{q}|^2 \left\{ \left[ {s\over m_\tau ^2} +\left( 1-{s\over m_\tau ^2}\right) x^2 \right] \right. \nonumber \\&\times \left| \mathbf{p}_K C_V f_+\right| ^2 + {\Delta _{K\pi }^4\over 4s} \left| C_Sf_0\right| ^2 \nonumber \\&\left. +{\Delta _{K\pi }^2\over \sqrt{s}}|\mathbf{p}_K|\mathrm{Re}\left[ C_VC_S^*f_+f_0^* \right] x \right\} , \end{aligned}$$

(18)

where the negative sign in $\Gamma ^-$ corresponds to the QED charge of $\tau ^-$ lepton, $x= \cos \theta$ and $|\mathbf{q}|=m_\tau (1-s/m_\tau ^2)/2$   is the momentum of the $K-\pi$ system (and of the neutrino) in the $\tau$ center of mass. Similarly $|\mathbf{p}_K|=\lambda ^{1/2}(s,\ m_K^2,\ m_\pi ^2)/2\sqrt{s}$ is the kaon (and of the pion) momentum in the $K-\pi$ center of mass. The angle $\theta$ is the scattering angle of kaon with respect to the incoming $\tau$, or equivalently the angle between $\overrightarrow{p}_\pi$ and $\overrightarrow{p}_\nu$, in the hadronic rest frame. The Local CPV is defined as

$$\begin{aligned} A_{\mathrm{CP}}(s,\ x)= & {} { \mathrm{d^2}\Gamma ^+/\mathrm{d}s \mathrm{d}x - \mathrm{d^2}\Gamma ^-/\mathrm{d}s \mathrm{d}x \over \mathrm{d^2}\Gamma ^+/\mathrm{d}s \mathrm{d}x +\mathrm{d^2}\Gamma ^-/\mathrm{d}s \mathrm{d}x }\nonumber \\= & {} {4m_\tau ^2\Delta _{K\pi }^2 \sqrt{s}\ |\mathbf{p}_K| x\ \mathrm{Im}[C_VC_S^*]\ \mathrm{Im}(f_+ (s) f_0^*(s)) \over 4s\left( s+ 2m_\tau |\mathbf{q}|x^2 \right) \left| \mathbf{p}_K C_V f_+(s)\right| ^2 +m_\tau ^2\Delta _{K\pi }^4 \left| C_S f_0(s)\right| ^2 +4 m_\tau ^2 \Delta _{K\pi }^2\sqrt{s}\ |\mathbf{p}_K| x \ \mathrm{Re}(C_V C_S^*) \ \mathrm{Re}(f_+(s)f_0^*(s)) }, \nonumber \\ \end{aligned}$$

(19)

Similarly to the sign convention in $\Gamma ^-$, the positive sign in $\Gamma ^+$ corresponds to the QED charge of $\tau ^+$. Finally, it should be remarked that the local CPV, defined in Eq. (19), is different than the forward–backward asymmetry, ${{\mathcal {A}}}_{FB}(s)$, that can be obtained upon integrating ${\mathrm{d}^2\Gamma \over \mathrm{d}s \mathrm{d}x}$ over x. Explicitly, it is defined as [39]

$$\begin{aligned} {{\mathcal {A}}}_{FB}(s)=\frac{\int ^1_0 \mathrm{d}x \frac{\mathrm{d}^2\Gamma ^- }{\mathrm{d}s \mathrm{d}x} -\int ^0_{-1} \mathrm{d}x \frac{\mathrm{d}^2\Gamma ^- }{\mathrm{d}s \mathrm{d}x} }{\int ^1_0 \mathrm{d}x \frac{\mathrm{d}^2\Gamma ^- }{\mathrm{d}s \mathrm{d}x} +\int ^0_{-1} \mathrm{d}x \frac{\mathrm{d}^2\Gamma ^- }{\mathrm{d}s \mathrm{d}x} } \end{aligned}$$

(20)

It is clear that within SM at tree-level, from Eq. (19), the local CPV is vanishing due to the remark that $C^{SM}_S=0$. This is not the case of the forward–backward asymmetry ${\mathcal A}_{FB}(s)$ that has non-vanishing term independent of $C^{SM}_S$ and $C^{SM}_T$ [39]. Thus, non-vanishing values of the local CPV can be used as a probe of physics beyond the SM as we will discuss in Sect. 4.

3 Integrated CP violation asymmetries

We investigate now the direct CP asymmetry for a general new physics model that can contribute to the effective Hamiltonian in Eq. (3) with Wilson coefficients denoted by $C^{NP}_i$. As can be seen from Eqs. (11, 12), the hadronic form factor $f_0(s)$, in S(s), does not interfere with the form factor $f_+(s)$. The absence of this interference leads to the absence of the strong phase difference between their contributions to the decay rate. This phase difference is essential for generating non vanishing direct CP asymmetry. As a consequence, and for having non-vanishing direct CP asymmetry in the decay rate, we are left only with the interference between $B_T(s)$, in T(s), and $f_0(s)$ as a possible source for the required strong phase difference. However, this interference was estimated to be small due to Watson’s final-state-interaction theorem [22, 40]. Assuming that NP contributions are obtained via integrating out heavy particles, above the electroweak breaking scale, we can set $C^{NP}_V=0$. In this case, the direct CP asymmetry in total decay rate of $\tau ^{-}\rightarrow K^{-}\pi ^{0}\nu _{\tau }$ is given by:

$$\begin{aligned} A^{NP}_{CP}= & {} -\frac{ G_F^2|V_{us}|^2 S_\text {EW}\, Im\,C^{NP}_T}{512\pi ^3m_\tau ^2M_K\Gamma _\tau \text {BR}(\tau \rightarrow K\pi \nu _\tau )} \nonumber \\&\times \int _{(M_{\pi }+M_K)^2}^{m_\tau ^2}\text {d}s \frac{\lambda ^{3/2}(s,M_{\pi }^2,M_K^2)(m_\tau ^2-s)^2}{ s^2}\nonumber \\&\times |f_+(s)||B_T(s)| \sin \big (\delta _+(s)-\delta _T(s)\big ), \end{aligned}$$

(21)

where $\delta _+(s)$, $\delta _T(s)$ are the phases of $f_+(s)$ and $B_T(s)$. Estimation of the CP asymmetry in the previous equation requires information on the form factor $f_+(s)$ and $B_T(s)$. Empirically, $\tau \rightarrow \pi K_S\nu _\tau$ spectrum can give information on the form factor $f_+(s)$ which is mainly dominated by the $K^*(892)$ resonance [41]. As discussed in Refs. [22, 37, 38], spin-1 resonances can be described equivalently by vector or antisymmetric tensor fields. Thus, both of $f_+(s)$ and $B_T(s)$ can receive contributions from the same resonances, mainly $K^*(892)$ resonance. Considering the moduli of the form factors $f_+(s)$ and $B_T(s)$, inelastic corrections turns to be negligible and the elastic solution of the unitarity relation for the form factors can be used [22]

$$\begin{aligned} f_+(s)=f_+(0)\Omega (s),\qquad B_T(s)=B_T(0)\Omega (s), \end{aligned}$$

(22)

in terms of the Omnès factor [42]

$$\begin{aligned} \Omega (s)=\exp \bigg \{\frac{s}{\pi }\int _{s_{\pi K}}^\infty \frac{\delta (s')}{s'(s'-s)}\bigg \}. \end{aligned}$$

(23)

In the previous equation, the phase shift $\delta (s)$ can be approximated by a BW phase [22] with parameters as determined in [41]. As shown in Ref. [22], the modulus of $f_+(s)$, given in Eq. (22), can reproduce well the experimental fit below the $K^*(1410)$ resonance done in Ref. [41].

We turn now to the phase of the form factor $f_+(s)$, namely $\delta _+(s)$. Experiments are only sensitive to the modulus of the form factor. Thus $\delta _+(s)$ cannot be directly estimated from experiments. Rather, its extraction can be done with the help of a fit function that preserves the analytic structure of the form factor [22]. As a consequence, the fit function used in [41] cannot be helpful for extracting $\delta _+(s)$. However, as argued in Ref. [22], still this fit can be useful in extracting $\delta _+(s)$. This can be achieved through comparing the phase from the experimental fit [41] with $\delta _+(s)$ computed using a BW approximation for the $K^*(892)$. To account for the inelastic contribution $\delta ^\text {inel}_+(s)$ to $\delta _+(s)$, the authors of Ref. [22] have added the BW phase for $K^*(1410)\rightarrow K^*(892)\pi$ with a coefficient that allows for a similar phase motion in the vicinity of the $K^*(1410)$. This leads to the band shown in Fig. 2, in Ref. [22], which represents a simple estimation of inelastic effects. The result is consistent with more refined estimates along the lines of [43,44,45,46,47]. Up on the assumption that the inelastic contributions in $\delta _T(s)$ are of similar size with an opposite sign, one can take $\delta _+(s) - \delta _T(s) \sim 2 \delta _+^\text {inel}(s)$ [22].

With the estimation of the form factors following the discussion above and using $\text {BR}(\tau \rightarrow K^- \pi ^0\nu _\tau )= (4.33\pm 0.15)\times 10^{-3}$ [48], $f_+(0)|V_{us}|=0.2165(4)$ [48], $B_T(0)/ f_+(0)=0.676(27)$ from lattice QCD [49], particle masses and couplings from [48], we find that the CP asymmetry can be estimated as

$$\begin{aligned} \big |A^{NP}_{CP}\big |\lesssim 1.4\times 10^{-2}\, Im \, C^{NP}_T, \end{aligned}$$

(24)

An investigation of the limits on $\text {Im}\,C_T$ for general NP models follow from electric dipole moment (EDM) of the neutron and D–$\bar{D}$ mixing was carried in Ref. [22]. In the following we present the derivation of such limits as carried out in Ref. [22]. At an energy scale $\Lambda \gg v$, the decay processes $\tau ^- \rightarrow K^- \pi ^0 \nu _\tau$ receive contribution from a tensor operator. The operator is originating from the $SU(3) \times SU(2) \times U(1)$ gauge-invariant Lagrangian that can be expressed as [22]

$$\begin{aligned} \mathcal {L}_T = C_{abcd} \ \bar{L}_{La}^i \sigma _{\mu \nu } e_{Rb} \, \epsilon ^{ij} \, \bar{q}_{L c}^j \sigma ^{\mu \nu } u_{Rd} \ + \ \text {h.c.}, \end{aligned}$$

(25)

here a, b, c, d are generation indices and i, j are $SU(2)_L$ indices. In the preceding equation $q_L$ and $L_L$ stand for the quark and lepton $SU(2)_L$ doublets while $u_R$ and $e_R$ represent the charged up-quark and lepton $SU(2)_L$ singlets respectively. The tensor operator $Q_T$ listed in Eq. (4) is generated from [22]

$$\begin{aligned} \mathcal {L}_T&= C_{3321}\Big [ (\bar{\nu }_{\tau } \sigma _{\mu \nu }R \tau )(\bar{s} \sigma ^{\mu \nu } R u) \nonumber \\&\quad - V_{us} (\bar{\tau } \sigma _{\mu \nu }R \tau )(\bar{u} \sigma ^{\mu \nu } R u) \Big ] \ + \ \text {h.c.}, \end{aligned}$$

(26)

where $R=(1+\gamma _5)/2$ and other terms that involve the charm and top quark have been omitted. Comparing Eq. (4) and Eq. (26) one finds that

$$\begin{aligned} C_{3321} = - \sqrt{2} G_F V_{us} C_T. \end{aligned}$$

(27)

The renormalization group evolution [50] of the operator $(\bar{\tau } \sigma _{\mu \nu }R \tau )(\bar{u} \sigma ^{\mu \nu } R u)$, second term in the square bracket in Eq. (26), can produce via insertion an up-quark EDM $d_u (\mu )$ [22]

$$\begin{aligned} \mathcal {L}_\text {D}=- \frac{i}{2} d_u (\mu ) \bar{u} \sigma ^{\mu \nu } \gamma _5 u F_{\mu \nu }, \end{aligned}$$

(28)

Upon solving the RG following [51,52,53] one obtains [22]

$$\begin{aligned} d_u (\mu )&= \frac{e m_\tau }{v^2} \frac{V_{us}^2}{\pi ^2} \ \text {Im}\,C_T (\mu ) \ \log \frac{\Lambda }{\mu }. \end{aligned}$$

(29)

The last equation above together with the $90\%$ C.L. bound $d_n = g_T^{u} (\mu ) d_u (\mu ) < 2.9 \times 10^{-26}\,e\,\text {cm}$ [54, 55] can be used to obtain a strong bound on $\text {Im}\,C_T$. Thus, for a value $\Lambda > rsim 100$ GeV and using and the recent lattice result [56] $g_T^{u} (\mu = \mu _\tau = 2\,\mathrm {GeV}) = - 0.233(28)$ one finds the constraint [22]

$$\begin{aligned} | \text {Im}\,C_T (\mu _\tau ) | \lesssim 10^{-5}, \end{aligned}$$

(30)

It should be noted that, the above constraint is based on the assumption that there are no other contributions to $d_n$ that can cancel the effect of $C_T$.

Applying the derived constraint on $\text {Im}\,C_T(\mu _\tau )$, we get a model independent prediction of the direct CP asymmetry as

$$\begin{aligned} \big |A^{NP}_{CP}\big |\lesssim {{\mathcal {O}}} (10^{-7}). \end{aligned}$$

(31)

Clearly, from the above discussion, NP contributions to the phases of $C^{NP}_5$ are needed to have non-vanishing direct CP asymmetry. These contributions will be evaluated below for several NP models.

Fig. 1

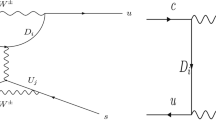
Diagrams contributing to the effective Hamiltonian, ${{\mathcal {H}}}_{eff}$, in Eq. (3) up to one loop-level due to charged Higgs mediation. In the figures, V can be Z boson or photon or both of them depending on the fermions A and B. In the case that A and B are $\tau$ and $\nu _\tau$, the other external lines, in the figures, to be understood as representing up and strange quarks. On the other hand when A and B are up and strange quarks, the other external lines in the figures are simply representing $\tau$ and $\nu _\tau$

3.1 CP asymmetry of $\tau ^{-}\rightarrow K^{-}\pi ^{0}\nu _{\tau }$ in 2HDM III.

Two Higgs doublet models(2HDM) are simple extensions of the SM in which the scalar sector of the SM is enlarged to contain new scalars [57,58,59,60,61,62]. Based on the couplings of the new scalars to quarks and leptons we can classify these models to several types such as type I, II or III [63]. In the two Higgs doublet model with generic Yukawa structure or simply type III (2HDM III), the couplings of the new scalars to quarks and leptons can be complex [64,65,66]. As a consequence, these couplings can serve as the source of the weak CP violating phases essential for generating non vanishing CP asymmetries. The effect of these new weak phases on the CP asymmetry in D meson sector have been investigated in Refs. [67,68,69]. The resultant direct CP asymmetry in this model can be enhanced several orders of magnitudes larger than SM predictions. For instances, a large direct CP asymmetry of order $10^{-3}$ can be achieved in the decay mode $D^0 \rightarrow K^+ \pi ^-$ after taking into account all constraints on the parameter space of the model [69]. This value is 6 orders of magnitude larger than the standard model prediction. The 2HDM III is also motivated by its ability to explain some anomalies in B decays. As shown in Ref. [66], a 2HDM of type II (like the MSSM at tree-level) cannot explain the deviations from the SM in tauonic B decays, while 2HDM III can account for $B\rightarrow D\tau \nu$ and $B\rightarrow D^*\tau \nu$ simultaneously  [65, 70].

The scalar sector of the 2HDM III consists of two Higgs doublets. The mass eigenstates constructed from these doublets are $H_0$ (heavy CP-even Higgs), $h_0$ (light CP-even Higgs) and $A_0$ (CP-odd Higgs) and $H^{\pm }$. In 2HDM III, the charged Higgs couplings to quarks and leptons can be expressed as [64, 65]

$$\begin{aligned} \mathcal {L}^{eff}_{H^\pm }= & {} \bar{u} {\Gamma _{u s }^{H^\pm \,LR\,\mathrm {eff} } }P_R s + \bar{u} {\Gamma _{u s }^{H^\pm \,RL\,\mathrm {eff} } }P_L s\nonumber \\&+\frac{m_\tau \tan \beta }{v} ({\bar{\nu }}_\tau P_R\tau )+h.c.\, ,\nonumber \\ \end{aligned}$$

(32)

where

$$\begin{aligned} {\Gamma _{u s }^{H^\pm \,LR\,\mathrm {eff} } }= & {} {\sin \beta \left( V_{12}\frac{m_{s }}{v_d} - \sum \limits _{j = 1}^3 \, V_{1j} \epsilon ^{ d}_{j2}\tan \beta \right) , } \nonumber \\ {\Gamma _{u s }^{H^ \pm \,RL\,\mathrm {eff} } }= & {} \cos \beta \, \left( \frac{m_{u }}{v_u} V_{12}-\sum \limits _{j = 1}^3 V_{j2} \epsilon ^{ u\star }_{j1}\tan \beta \right) , \end{aligned}$$

(33)

Here $v_u$ and $v_d$ stand for the vacuum expectations values of the neutral component of the Higgs doublets, tan $\beta = v_u/v_d$ and finally V is the CKM matrix. Using the Feynman-rules given in Eq. (32), we can proceed to derive the relevant Wilson coefficients to our investigation. Working in the unitary gauge and after integrating out the charged Higgs in the diagrams in Fig. 1, we find that the relevant Wilson coefficients at $\mu = m_H$ scale can be expressed as

$$\begin{aligned} C^{H^\pm }_{V }= & {} -\frac{ m^2_W m_s m^2_\tau \tan \beta \sin \beta }{2 \pi ^2 m^4_H\, v\, V^\star _{us}\,c^2_w} \nonumber \\&\times \bigg (\bigg (-\frac{1}{2}+ s^2_w\bigg )\bigg (-\frac{1}{2}+\frac{1}{3}s^2_w\bigg ) \, g(x_s,x_\tau ,x_Z) \nonumber \\&+ \frac{ 4 v^2\,\pi \alpha \, m_u c^2_w }{ 3 m^2_W m_s } k(x_u,x_\tau ) \bigg )\nonumber \\&\times \bigg ( \frac{m_s V^\star _{us}}{v_d} - \sum \limits _{j = 1}^3 V^\star _{1j} \epsilon ^{ d \star }_{j2}\tan \beta \bigg )\nonumber \\&-\frac{ 8 m^2_W m_s m^2_\tau \sin \beta s^2_w}{3 v\, V^\star _{us}\,c^2_w} \bigg (\bigg (-\frac{1}{2}+ s^2_w\bigg )\, g(x_s,x_\tau ,x_Z)\nonumber \\&+ \frac{ 4 v^2\,\pi \alpha \, m_u c^2_w }{ m^2_W m_s s^2_w } k(x_u,x_\tau ) \bigg )\nonumber \\&\times \bigg (\frac{m_u V^\star _{us} }{v_u} - \sum \limits _{j = 1}^3 V^\star _{j2} \epsilon ^{ u}_{j1}\tan \beta \bigg ),\nonumber \\ C^{H^\pm }_S= & {} \frac{ v\, m_\tau \sin \beta }{ 4\pi ^2 m^2_H V^\star _{us}}\bigg (16 \pi ^2 + \frac{ 8\,\pi \alpha }{3 } f(x_u,x_\tau ) \nonumber \\&+\frac{ 2 m^2_W s^2_w }{3\,v^2\,c^2_w} f(x_u,x_Z) + \frac{ 4 \pi \alpha }{3 } f(x_s,x_\tau )\nonumber \\&- \frac{ 2 m^2_W s^2_w }{\,v^2\, c^2_w} \bigg (-\frac{1}{2}+\frac{1}{3}s^2_w\bigg ) h(x_s,x_\tau ,x_Z)\bigg )\nonumber \\&\times \bigg (\frac{m_u V^\star _{us} }{v_u} - \sum \limits _{j = 1}^3 V^\star _{j2} \epsilon ^{ u}_{j1}\tan \beta \bigg )\nonumber \\&+ \frac{ v\, m_\tau \sin \beta \,\tan \beta }{ 4\pi ^2 m^2_H V^\star _{us} }\bigg (16 \pi ^2 + \frac{ 8\,\pi \alpha }{3 } f(x_u,x_\tau )\nonumber \\&-\frac{ m^2_W }{\,v^2\,c^2_w} \bigg (\frac{1}{2}-\frac{2}{3}s^2_w\bigg ) f(x_u,x_Z) + \frac{ 4 \pi \alpha }{3 } f(x_s,x_\tau )\nonumber \\&- \frac{ 2 m^2_W s^4_w }{3\,v^2\, c^2_w} h(x_s,x_\tau ,x_Z) \bigg )\bigg ( \frac{m_s V^\star _{us}}{v_d} - \sum \limits _{j = 1}^3 V^\star _{1j} \epsilon ^{ d\star }_{j2}\tan \beta \bigg )\nonumber \\&+\triangle _Z+\triangle _\gamma ,\nonumber \\ C^{H^\pm }_T= & {} \frac{ v\, m_\tau \sin \beta }{ 4\pi ^2 m^2_H V^\star _{us}}\bigg (\frac{ 2 m^2_W s^2_w }{3 v^2 c^2_w} f(x_u,x_Z)\nonumber \\&- \frac{ m^2_W \bigg (-\frac{1}{2}+\frac{1}{3}s^2_w\bigg ) }{ v^2 c^2_w} f(x_s,x_Z) + \frac{ 4 \pi \alpha }{3 } f(x_s,x_\tau )\nonumber \\&- \frac{ 2 m^2_W \, s^2_w }{\,v^2\, c^2_w} \bigg (-\frac{1}{2}+\frac{1}{3}s^2_w\bigg ) h(x_s,x_\tau ,x_Z)\nonumber \\&+\frac{ 8\pi \alpha }{3} f(x_u,x_\tau )\bigg ) \bigg (\frac{m_u V^\star _{us} }{v_u} - \sum \limits _{j = 1}^3 V^\star _{j2} \epsilon ^{ u}_{j1}\tan \beta \bigg )\nonumber \\&- \frac{ v\, m_\tau \sin \beta \,\tan \beta }{ 4\pi ^2 m^2_H V^\star _{us} }\bigg (\frac{ m^2_W }{\,v^2\,c^2_w} \bigg (\frac{1}{2}-\frac{2}{3}s^2_w\bigg ) f(x_u,x_Z)\nonumber \\&+ \frac{ m^2_W s^2_w}{3\,v^2\,c^2_w} f(x_s,x_Z) - \frac{ 4 \pi \alpha }{3 } f(x_s,x_\tau )\nonumber \\&+\frac{ 2 m^2_W s^4_w }{3\,v^2\, c^2_w} h(x_s,x_\tau ,x_Z)- \frac{ 8\,\pi \alpha }{3} f(x_u,x_\tau )\bigg )\nonumber \\&\times \bigg ( \frac{m_s V^\star _{us}}{v_d} - \sum \limits _{j = 1}^3 V^\star _{1j} \epsilon ^{ d\star }_{j2}\tan \beta \bigg ), \end{aligned}$$

(34)

where v denotes the Higgs vacuum expectation value which is defined as $v=\sqrt{v^2_u+v^2_d}=\sqrt{\frac{2 m^2_W}{g^2}}\simeq 174$ GeV. The terms $\triangle _Z$ and $\triangle _\gamma$ represent the contributions to $C^{H^\pm }_S$ originating from the exchange of $V=Z,\gamma$ boson between allowed two lines, A and B, at each vertex of the tree-level diagram mediated by $H^\pm$ exchange. Together, with the box contributions, the gauge independence results is guaranteed at one loop-level considered here. The explicit expressions of $\triangle _Z$ and $\triangle _\gamma$ are listed in the Appendix. The integration loop functions are given, in terms of $x_i =\frac{m_i^2}{m^2_H}$, as

$$\begin{aligned} g(x_i,x_j,x_k)= & {} \frac{x_i log x_i}{(x_i-1)(x_i-x_j)(x_i-x_k)}\nonumber \\&+\frac{x_j log x_j}{(x_j-1)(x_j-x_i)(x_j-x_k)}\nonumber \\&+\frac{x_k log x_k}{(x_k-1)(x_k-x_i)(x_k-x_j)},\nonumber \\ k(x_i,x_j)= & {} \frac{-1}{(x_i-x_j)}\Big (\frac{1}{1-x_i}log x_i-(x_i\leftrightarrow x_j)\Big ),\nonumber \\ f(x_i,x_j)= & {} \frac{1}{(x_i-x_j)}\Big (\frac{x_i}{1-x_i}log x_i-(x_i\leftrightarrow x_j)\Big ),\nonumber \\ h(x_i,x_j,x_k)= & {} \frac{x^2_i log x_i}{(x_i-1)(x_i-x_j)(x_i-x_k)}\nonumber \\&+\frac{x^2_j log x_j}{(x_j-1)(x_j-x_i)(x_j-x_k)}\nonumber \\&+\frac{x^2_k log x_k}{(x_k-1)(x_k-x_i)(x_k-x_j)}, \end{aligned}$$

(35)

It should be noted that an investigation of the dependency of the matrix elements of $H\rightarrow \gamma \gamma$ through one $W^\pm$ loop in SM on the choice of the gauge was done in Ref. [71]. The results showed that the calculated matrix elements using $R_\zeta$ gauge and the unitary gauge are explicitly verified to be different. However, in a subsequent study, it was found that the unitary gauge is consistent and equivalent to the $R_\zeta$ gauge at the level of $\beta$-functions [72]. At higher loops, their is a possibility that the observed consistency between the two gauges may breaks down. In this case, their is a demand of a better understanding of the quantum internal structure of spontaneously broken gauge theories [72]. In Ref. [73], the mismatch which was pointed out by S. L. Wu and T. T. Wu group is resolved by a dedicated calculation of the unitary gauge. In a recent study in Ref. [74], it was shown that the unitary gauge is the default gauge for massive gauge bosons.

In order to estimate the contributions of the charged Higgs to the amplitude of the decay process under consideration we need to discuss the constraints imposed on the couplings $\epsilon ^{u,d}_{ij}$ appear in the expressions of $C^{H^\pm }_i$ above. The couplings $\epsilon ^{d}_{12}$, and $\epsilon ^{d}_{32}$ are stringently constrained from flavor changing neutral current processes, in the down quark sector, due to the tree-level neutral Higgs exchange [65, 66]. On the other hand, the coupling $\epsilon ^{d}_{22}$ can be strongly constrained upon applying the naturalness criterion of ’t Hooft to the quark masses that reads [66]

$$\begin{aligned} |v_{u(d)} \epsilon ^{d(u)}_{ij}|\le & {} \left| V^{CKM}_{ij}\right| \,\mathrm{max }\left[ m_{d_i(u_i)},m_{d_j(u_j)}\right] \,\,\,\,\,\,\,\, for\, i < j,\nonumber \\ |v_{u(d)} \epsilon ^{d(u)}_{ij}|\le & {} \mathrm{max }\left[ m_{d_i(u_i)},m_{d_j(u_j)}\right] \, \,\,\,\,\,\,\,\, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, \,\,\,\,\, for\, i \ge j,\nonumber \\ \end{aligned}$$

(36)

Clearly, from this bound, $\epsilon ^d_{22}$ is severely constrained by the smallness of the s quark mass. As a result, we can safely neglect the contributions of the couplings $\epsilon ^{d}_{ij}$ to $C^{H^\pm }_1,C^{H^\pm }_4$. Other terms, in these Wilson coefficients are real and thus are not relevant for generating CP asymmetries. Thus to a good approximation we can write

$$\begin{aligned} C^{H^\pm }_{V}\simeq & {} \frac{ 8 m^2_W m_s m^2_\tau \sin ^2\beta s^2_w }{3 v\, V^\star _{us}\,c^2_w \cos \beta } \bigg (\bigg (-\frac{1}{2}+ s^2_w\bigg )\, g(x_s,x_\tau ,x_Z) \nonumber \\&+ \frac{ 4 v^2\,\pi \alpha \, m_u c^2_w }{ m^2_W m_s s^2_w } k(x_u,x_\tau ) \bigg )\big (V^*_{cs}\, \epsilon ^{ u}_{21} + V^*_{ts}\, \epsilon ^{ u}_{31}\big ),\nonumber \\ C^{H^\pm }_S\simeq & {} -\frac{4 v\, m_\tau \sin ^2\beta }{V^\star _{us}\,m^2_H \cos \beta }\big (V^*_{cs}\, \epsilon ^{ u}_{21} + V^*_{ts}\, \epsilon ^{ u}_{31}\big ), \nonumber \\ C^{H^\pm }_T\simeq & {} -\frac{4 v m_\tau \sin ^2\beta }{V^\star _{us} m^2_H \cos \beta }\bigg (\frac{ 2 m^2_W m^2_H s^2_w }{3 v^2 c^2_w} f(x_u,x_Z)\nonumber \\&- \frac{ 2 m^2_W m^2_H s^2_w }{v^2\, c^2_w} \bigg (-\frac{1}{2}+\frac{1}{3}s^2_w\bigg ) h(x_s,x_\tau ,x_Z)\nonumber \\&+\frac{ 8\pi \alpha \,m^2_H}{3} f(x_u,x_\tau )+ \frac{ 4 \pi \alpha m^2_H}{3 } f(x_s,x_\tau )\nonumber \\&- \frac{ m^2_W m^2_H \bigg (-\frac{1}{2}+\frac{1}{3}s^2_w\bigg ) }{ v^2 c^2_w} f(x_s,x_Z) \bigg )\nonumber \\&\quad \big (V^*_{cs}\, \epsilon ^{ u}_{21} + V^*_{ts} \epsilon ^{ u}_{31}\big ). \end{aligned}$$

(37)

It should be noted that, in the above expressions, we neglected non relevant real terms. In addition we neglected terms proportional to $\epsilon ^{u}_{11}$ which is severely constrained from the bound in Eq. (36) due to the smallness of the up quark mass.

Recently, a lower bound $m_{H^\pm } > rsim 600$ GeV, independent of $\tan \beta$, has been obtained in 2HDM II after taking into account all relevant results from direct charged and neutral Higgs boson searches at LEP and the LHC, as well as the most recent constraints from flavour physics [57]. This bound should be also respected in 2HDM III [65]. Thus, for $m_{H^\pm } = 600$ GeV and $\tan \beta = 50$ we find that

$$\begin{aligned} C^{H^\pm }_{V}\simeq & {} - 5.23\times 10^{-6} \big (V^*_{cs}\, \epsilon ^{u}_{21} + V^*_{ts}\, \epsilon ^{ u}_{31}\big ),\nonumber \\ C^{H^\pm }_S\simeq & {} - 0.76 \big (V^*_{cs}\, \epsilon ^{ u}_{21} + V^*_{ts}\, \epsilon ^{ u}_{31}\big ),\nonumber \\ C^{H^\pm }_T\simeq & {} 7.49 \,\times 10^{-3} \big (V^*_{cs}\, \epsilon ^{ u}_{21} + V^*_{ts}\, \epsilon ^{ u}_{31}\big ), \end{aligned}$$

(38)

Clearly, to a good approximation, we can neglect contribution of $C^{H^\pm }_{V}$ to the amplitude as it is very small. The previous equation shows that $C^{H^\pm }_S$ is much larger than $C^{H^\pm }_T$. However, as we discussed before, only $C^{H^\pm }_T$ can generate non vanishing direct CP asymmetry.

The ’t Hooft naturalness criterion leading to the bounds in Eq.  (36) implies different bounds for $\epsilon ^u_{ij}$ and $\epsilon ^u_{ji}$ due to the presence of the CKM element in the first line of Eq. (36) corresponding to the case $i < j$. Thus one expects different bounds for $\epsilon ^u_{12}$ and $\epsilon ^u_{21}$ as can be seen from Eq. (16) in Ref. [66]. The authors of Ref. [66] set a bound on $\epsilon ^u_{21}$ after considering all constraints listed in their Tables VII and VIII. This bound can be read from the first matrix in Eq. (75) as $\mid \epsilon ^u_{21}\mid \le 3.0\times 10^{-2}$. However, the strong bound $\mid \epsilon ^u_{12}\epsilon ^{u\,*}_{21}\mid \ < 2\times 10^{-8}$ from considering $D-{\bar{D}}$ mixing [66] implies that $\mid \epsilon ^u_{12,21}\mid < \sqrt{2}\times 10^{-4}$. This can be understood as in the absence of a symmetry that protect $\mid \epsilon ^u_{12}\mid$ from being much smaller than $\mid \epsilon ^u_{21}\mid$ and using the same merit of the ’t Hooft naturalness criterion it is unnatural to have $\mid \epsilon ^u_{12}\mid$ much suppressed than $\mid \epsilon ^u_{21}\mid$. Thus we obtain

$$\begin{aligned} C^{H^\pm }_S\simeq & {} - 0.76 V^*_{ts}\, \epsilon ^{ u}_{31}, \nonumber \\ C^{H^\pm }_T\simeq & {} 7.49 \,\times 10^{-3} V^*_{ts}\, \epsilon ^{ u}_{31}. \end{aligned}$$

(39)

Knowing that $Re(V_{ts})\simeq {{\mathcal {O}}} (10^{-2})$ and the bound $2.7\times 10^{-3} \le \mid \epsilon ^u_{31}\mid \le 2.0\times 10^{-2}$ from the process $B\rightarrow \tau \nu$ [66], it is clearly trivial that the $B\rightarrow \tau \nu$ process sets more severe bound on $\epsilon ^u_{31}$ compared to the model-independent EDM bound. Consequently, one expects a strong bound $Im \, C^{H^\pm }_T < 10^{-6}$ and after using CKM matrix elements from Ref. [75], we obtain from Eq. (24)

$$\begin{aligned} \big |A^{H^\pm }_{CP}\big |\lesssim {{\mathcal {O}}} (10^{-8}), \end{aligned}$$

(40)

Clearly, the charged Higgs contributions can enhance the direct CP asymmetry several orders of magnitude larger than the standard model prediction. However, the estimated CP asymmetry is still so small to be detected by current or near future experiments.

3.2 $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ in Leptoquarks models

Leptoquark particles are scalars or vectors bosons that have both baryon and lepton number [76, 77]. They appear for instance in grand unified theories (GUTs) [78,79,80], technicolor models [81, 82] and SUSY models with R-parity violation. At low energy, Leptoquarks can be described as an effective four fermion interaction induced by leptoquark exchange. Several observables have been used to set bounds on these effective couplings as is the case of D meson decays [83,84,85] and K mesons.

Scalar leptoquarks S may couple to both left or right handed quark chiralities. Let us consider the exchange of the following scalar leptoquarks:

• $S_{1/2}$ with charge 2/3 and SU(3)$_\mathrm{C}\times$SU(2)$_{\mathrm{L}}\times$U(1)$_{\mathrm{Y}}$ gauge numbers given as (3, 2, 7/3); and

• the $S_{0}$ with charge $-1/3$ and $(3,1,-2/3)$ gauge numbers.

Their Yukawa couplings with SM fermions are given by

$$\begin{aligned}&{{\mathcal {L}}}_{S_{1/2}}=[\kappa ^L_{ij}\bar{U}_{R_i}L_{L_j} -\kappa ^R_{ij}\bar{Q}_{L_i}i\tau _2 E_{R_j}] S_{1/2}+\mathrm{h.c.},\nonumber \\&{{\mathcal {L}}}_{S_{0}}=[\xi ^L_{ij}\bar{Q}_{L_i}i\tau _2L^c_{L_j} +\xi ^R_{ij}\bar{U}_{R_i}E^c_{R_j}] S_{0}+\mathrm{h.c.}, \end{aligned}$$

(41)

Here, $\tau _i$ ($i=1,2,3$) are the Pauli matrices, $\bar{Q}_{L_i}=(\bar{u}_i,\bar{d}_i)_L$ and $L_{L_i}=(\bar{\nu }_i,\bar{e}_i)_L$ and for a spinor field $\psi$, the charge conjugation $\psi ^c$ is defined as $\psi ^c_{R,L}=i\gamma ^0\gamma ^2\bar{\psi }^T_{R,L}$. The coupling constants $\kappa ^{L,R}_{ij}$ and $\xi ^{L,R}_{ij}$ can be in general complex numbers. The Yukawa couplings, in Eq. (41), lead to the Lagrangians

$$\begin{aligned}&{{\mathcal {L}}}^{I}=\left[ \kappa ^L_{1i} \bar{u}_{R}\nu _{i_L}+\kappa ^R_{23}\bar{s}_{L}\tau _{R}\right] S_{1/2} +\mathrm{h.c.},\nonumber \\&{{\mathcal {L}}}^{II}=\left[ -\xi ^L_{13}\bar{u}_{L}\tau ^c_{L} +\xi ^L_{2i}\bar{s}_{L}\nu ^c_{i_L} + \xi ^R_{13}\bar{u}_R\tau ^c_{R}\right] S_0 + \mathrm{h.c.}, \end{aligned}$$

(42)

which is relevant to $\tau \rightarrow K^-\pi ^0\nu$ decay with $i=1,2,3$. These Lagrangians result in diagrams similar to the one mediated by the charged Higgs in which the Higgs boson is replaced with the scalar leptoquarks $S_{1/2}$ and $S_{0}$. After integrating out the leptoquarks, we can obtain the Wilson coefficients $C^{I,II}_i$, corresponding to the operators $Q_i$ in Eq. (4), as

$$\begin{aligned} C_{V}^{I}= & {} 0,\quad C_{S}^{I}=\frac{\kappa ^R_{23} \kappa ^{L*}_{1i}}{4 \sqrt{2}\, G_F V^* _{us}\,M^2_{S_{1/2}}},\nonumber \\ C_{T}^{I}= & {} \frac{1}{4} C_{3}^{I},\nonumber \\ C_{V}^{II}= & {} \frac{\xi ^L_{2i} \xi ^{L *}_{13}}{4 \sqrt{2}\, G_F V^* _{us} M^2_{S_{0}}},\quad C_{S}^{II}=\frac{ \xi ^L_{2i} \xi ^{R *}_{13}}{4 \sqrt{2}\, G_F V^* _{us} M^2_{S_{0}}}\nonumber \\ C_{T}^{II}= & {} \frac{1}{4} C_{S}^{II}. \end{aligned}$$

(43)

We now discuss the constraints imposed on the leptoquark couplings. For model II, the couplings $|\xi ^L_{2i} \xi ^{L *}_{13}|$, appears in $C_{V}^{II}$, can be severely constrained from the process $K\rightarrow \pi {\bar{\nu }}\nu$ [83]. From the results of the analysis carried in Ref. [83], the bound reads $|\xi ^L_{2i} \xi ^{L *}_{13}|< 2\times 10^{-5}\times (M_{S_{0}}/[100 \,\mathrm {GeV}])^2$. Thus, in model II, we have $C_V= C^{SM}_V + C_{V}^{II}\simeq C^{SM}_V$.

Turning now to the couplings $\xi ^L_{2i} \xi ^{R *}_{13}$ and setting $i=3$, we find that possible constraints can be derived from the observable $\tau \rightarrow K\nu _\tau$. The expected bound on $\xi ^L_{23} \xi ^{R *}_{13}\equiv \xi ^L_{s \nu _\tau } \xi ^{R *}_{u \tau }$, which corresponds to the Wilson coefficients of the four fermion operator that contributes to both $\tau \rightarrow K\nu _\tau$ and $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$, read $Re(\xi ^L_{23} \xi ^{R *}_{13})\sim [-0.07,0.04]$ and $|Im(\xi ^L_{23} \xi ^{R *}_{13})|\sim [0.0,0.7]$ for $M_{S_{0}}=1$ TeV [86]. Thus, for $i=3$ in model II, we have $|Im(C_T)|=|Im( C_{T}^{II})|\sim [0.0,0.01]$. It should be noted that a strong constraint on $|Im( C_{T}^{II})|$ can be obtained from the EDM of the neutron noticing that the coupling $\xi ^L_{23} \xi ^{R *}_{13}$ can be linked to $C_{3321}\equiv C_{\nu _\tau \tau s u}$, defined in Eq. (26), and using the bound given in Eq. (30). As a consequence,

$$\begin{aligned} \big |A^{II}_{CP}\big |\lesssim {{\mathcal {O}}} (10^{-7}), \end{aligned}$$

(44)

similarly to the obtained value in the charged Higgs model.

Regarding model I, we find that the predicted CP asymmetry will be the same as in model II. This can be explained as similar constraints can be imposed on the couplings $\kappa ^R_{23} \kappa ^{L*}_{13}$ from the observable $\tau ^-\rightarrow K^-\nu _\tau$ [86] and from the electric dipole moment (EDM) of the neutron in Eq. (30).

In the scalar leptoquark models discussed above, the amplitudes of the processes $\tau ^-\rightarrow K^-\pi ^0\nu _{e}$ and $\tau ^-\rightarrow K^-\pi ^0\nu _{\mu }$ receive contributions from the couplings $\xi ^L_{21} \xi ^{R *}_{13} \equiv \xi ^L_{s \nu _e} \xi ^{R *}_{u \tau }$ and $\xi ^L_{22} \xi ^{R *}_{13} \equiv \xi ^L_{s \nu _\mu } \xi ^{R *}_{u \tau }$ respectively. These couplings can be also constrained using the observable $\tau \rightarrow K\nu$ [87]. However, the obtained bounds turns to be one order of magnitude weaker than the bound on $\xi ^L_{23} \xi ^{R *}_{13}\equiv \xi ^L_{s \nu _\tau } \xi ^{R *}_{u \tau }$. Moreover, the couplings $\xi ^L_{21} \xi ^{R *}_{13} \equiv \xi ^L_{s \nu _e} \xi ^{R *}_{u \tau }$ and $\xi ^L_{22} \xi ^{R *}_{13} \equiv \xi ^L_{s \nu _\mu } \xi ^{R *}_{u \tau }$ cannot be linked to $C_{3321}\equiv C_{\nu _\tau \tau s u}$, defined in Eq. (26), and thus evade the strong bound given in Eq. (30). Consequently, we expect a somehow large branching ratios and CP asymmetries for the channels $\tau ^-\rightarrow K^-\pi ^0\nu _e$ and $\tau ^-\rightarrow K^-\pi ^0\nu _\mu$ compared to their corresponding ones of $\tau ^-\rightarrow K^-\pi ^0\nu _{\tau }$. Since these couplings contribute to $C_{S,T}$ one expects that the effect on the branching ratios is not much while a large effect is expected to be seen in the CP asymmetries. With the only constraints from $\tau \rightarrow K\nu$ and in the absence of much stronger constraints, the predicted direct CP asymmetry of $\tau ^-\rightarrow K^-\pi ^0\nu _e$ and $\tau ^-\rightarrow K^-\pi ^0\nu _\mu$ can be of order $10^{-3}$.

Finally, we discuss the possibility of having constraint on the $Im\, C_T$, in the leptoquark models discussed in this work, from the process $B \rightarrow \tau \nu$. Recall that, the process $B\rightarrow \tau \nu$ can be generated through $b\rightarrow u \tau \nu$ transition. In model II, the transition originates at tree-level from the exchanging of the scalar leptoquark $S_0$. The relevant product of the leptoquark couplings to the amplitude of $B\rightarrow \tau \nu$ decay is $\xi ^{L*}_{3i}\, \xi ^{R}_{13}$. Consequently, the constraints from $B\rightarrow \tau \nu$ process are expected to be imposed on $\xi ^{L*}_{3i}\, \xi ^{R}_{13}$ which is irrelevant to $\tau \rightarrow K^-\pi ^0\nu$ process that receives contributions from $\xi ^L_{2i} \xi ^{R *}_{13}$ as we have shown above. Regarding model I, first line in Eq. (42), the $b\rightarrow u \tau \nu$ transition can be generated at tree-level from the exchanging of the scalar leptoquark $S_{1/2}$. In this case, the relevant leptoquark couplings to the amplitude of $B\rightarrow \tau \nu$ decay are $\kappa ^{R*}_{33} \kappa ^L_{1i}$. Again, the expected constraints from $B\rightarrow \tau \nu$ process on $\kappa ^{R*}_{33} \kappa ^L_{1i}$ are irrelevant to $\tau \rightarrow K^-\pi ^0\nu$ process that receives contributions from $\kappa ^R_{23} \kappa ^{L*}_{1i}$.

4 Nonintegrated CP violation asymmetries

Searches for local CPV signal have been done by Cleo [16] and Belle [17] collaborations to obtain bounds on new generic scalar mediators like the ones considered here. Belle collaboration is one order of magnitude more precise. They parameterized new physics with $\eta _S\simeq C_S$ by doing the replacement $f_0\rightarrow [1-\eta _S s/(m_\tau (m_s-m_u))]f_0$. No local CPV signal was found and a bound of $|\mathrm{Im}\ (\eta _S)|\simeq |\mathrm{Im}\ (C_S)|<0.013$ was obtained. Recall that within SM, at tree-level, $C^{SM}_S=0$ which is not the case in some beyond SM physics that have been investigated in the previous section. In the case of 2HDM III, and using Eq. (34), this bound results in the constraints $|\mathrm{Im}\ (\epsilon ^{ u}_{31})|<0.4$. On the other hand and in the case of scalar Leptoquark, the bound $|\mathrm{Im}\ (\eta _S)|\simeq |\mathrm{Im}\ (C_S)|<0.013$ will lead to a weaker bound on $|\mathrm{Im}\ (C^{I,II}_S)|$ compared to that one obtained from the electric dipole moment (EDM) of the neutron in Eq. (30) as, from Eqs. (30, 43), we have $|\mathrm{Im}\ (C^{I,II}_S)|\lesssim 4\times 10^{-5}$.

Fig. 2

Local CPV, in units of $10^{-3}$ as a function of s and $x=\cos \theta$ and the same but for $x=-1$

We proceed now to calculate the local CPV given in Eq. (19) within 2HDM III discussed above. Including charged Higgs contributions to the Wilson coefficients $C_V$ and $C_S$ in Eq. (19) can be done via the replacement $C_V\rightarrow C^{SM}_1\simeq 1$, $C_S \rightarrow 1+C^{H^\pm }_S s/(m_\tau m_s)\simeq 1- 0.76 V^*_{ts}\, \epsilon ^{ u}_{31} s/(m_\tau m_s)$. For a value of $Im(\epsilon ^{ u}_{31})\le 2 \times 10^{-2}$ that satisfies the strongest bound from $B \rightarrow \tau \nu$ process we find that $Im(C_S)\lesssim 3.6\times 10^{-3}\times s$.

We turn now to the form factors $f_+(s)$ and $f_0(s)$ required to the calculation of the local CPV. Recall that a discussion about the form factor $f_+(s)$ has been presented in the preceding section. So we are left here to discuss the scalar form factor $f_0$. While the phase of $f_0$ was measured by the LASS collaboration [88, 89] its magnitude can be obtained by using dispersion relations [43] but uncertainties in the input information avoid a precise prediction. In fact decays as the one we are interested in here should provide experimental information about $f_0$, once the angular distribution can be measured [31]. For our purpose of an estimation of the local CPV the form factor $f_0$ can be parameterized, in terms of a superposition of Breit–Wigner resonances following Refs. [23, 41] as

$$\begin{aligned} f_0(s)= & {} \chi {s\over m_{K_0^*(700)}^2 } BW(K^*(700)) \nonumber \\&+ \gamma {s\over m_{K_0^*(1430)}^2 } BW(K^*(1430)) \nonumber \\ BW(R)= & {} {m_R^2 \over m_R^2-s+i \sqrt{s}\ \Gamma _R(s) },\nonumber \\ \Gamma _R(s)= & {} \Gamma _{0R} {m_R^2\over s} \left( {p(s)\over p(m_R^2)} \right) ^{2J+1} \end{aligned}$$

(45)

with $p=|\mathbf{p}_K|$, $\chi =2.28$ and $\gamma =1.92\mathrm{e}^{4.03\cdot i}$. Breit–Wigner parameters are $m_{K_0^*(700)}=878(23)^{+64}_{-51}$, $\Gamma _{K_0^*(700)}=499(52)^{+55}_{-87}$, $m_{K_0^*(1430)}=1425$ and $\Gamma _{K_0^*(1430)}=270$. The spin of the resonance is J and all masses and widths are expressed in MeV [8,9,10]. With all this in hand, we present a typical graphical representation of the local CPV in Fig. 2. Clearly, from Fig. 2, values as large as 0.3 % can be obtained. Due to the strong constraints

5 Conclusion

In this paper we have derived the contributions to the effective Hamiltonian governing the semileptonic $\vert \Delta S \vert =1$ tau decays in 2HDM III and models with scalar Leptoquarks. We have discussed the imposed constraints on the elements in the parameter space of the model relevant to the decay channel $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$. In addition, we have analyzed the role of the different contributions, originating from the scalar, vector and tensor hadronic currents, in generating direct CP asymmetry in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$.

We have shown that non vanishing direct CP asymmetry in the decay rate of $\tau ^-\rightarrow K^-\pi ^0\nu _\tau$ can be generated in the model due to the presence of the weak phase in the Wilson coefficient $C^{NP}_T$ and due to the strong phase difference resulting from the interference between the form factors $B_T(s)$, and $f_+(s)$. After taking into account the relevant constraints we found that the resultant CP asymmetry can be of order $10^{-8}$ in both models. The asymmetry is so tiny to be probed even in near future experiments.

In this work we have also studied another observable related to the CP violation, namely the local CPV. This kind of asymmetry can be generated if there is interference between vector and scalar contributions, as long as they contribute with different weak phases which is not the case in the SM. In the 2HDM III we studied in this work, we have found that, direct local CPV can be as large as 0.3 % not far from experimental possibilities.

Appendix A

The quantities $\triangle _Z$ and $\triangle _\gamma$ can be expressed as

$$\begin{aligned} \triangle _Z= & {} a^{u s }_Z+a^{u H }_Z+ a^{s H }_Z +a^{\tau \nu _\tau }_Z +a^{\tau H}_Z +a^{\nu _\tau H}_Z,\nonumber \\ \triangle _\gamma= & {} a^{u s }_\gamma +a^{u H }_\gamma + a^{s H }_\gamma +a^{\tau H}_\gamma , \end{aligned}$$

(A1)

Here, $a^{AB}_V$ denotes the contribution from Feynman diagram where the gauge boson $V=Z,\gamma$ connect the two lines A and B at one vertex of the tree-level diagram mediated by $H^\pm$ exchange. The results of each $a^{AB}_V$ can be written in terms of Passarino–Veltman (PV) functions where the sum of the divergent parts, of some of these functions, in the total amplitude vanishes. In the following we show only dominant terms where, in the coefficients of each PV functions, terms proportional to $m_u$, $m_s$, s and $m_\tau$ can be neglected compared to the terms proportional to $m_Z$ and $m_H$. Defining $g^H_L=\big (\Gamma _{u s }^{H^\pm \,LR\,\mathrm {eff} } \big )^*$, $g^H_R=\big (\Gamma _{u s }^{H^ \pm \,RL\,\mathrm {eff} } \big )^*$, $g^\tau _L=-\frac{1}{2}+s^2_w$, $g^\tau _R=s^2_w$, $g^u_L=\frac{1}{2}-\frac{2}{3} s^2_w$, $g^u_R=-\frac{2}{3}s^2_w$, $g^s_L=-\frac{1}{2}+\frac{1}{3}s^2_w$ and $g^s_R=\frac{1}{3}s^2_w$ we find that the different contributions to $\triangle _Z$ can be expressed as

$$\begin{aligned} a^{u s }_Z\simeq & {} - \frac{m_\tau \,m^2_Z\tan \beta }{16 \pi ^2 \, s \,v\, V^\star _{us}\left( s-m_{H^\pm }^2\right) }\bigg ( 4 m_s^2\bigg [ g_L{}^H g_L{}^s g_L{}^u\nonumber \\&+g_R{}^H g_R{}^s g_R{}^u\bigg ] B_0\left( m_s^2+m_u^2-s,m_s^2,m_u^2\right) \nonumber \\&+ \bigg [g_L{}^H g_L{}^u \left( 3\, s \, g_R{}^s-4 m_s^2 g_L{}^s\right) \nonumber \\&+g_R{}^H g_R{}^u \left( 3 \,s\, g_L{}^s-4 m_s^2\, g_R{}^s\right) \bigg ]B_0\left( m_s^2,m_s^2,m_Z^2\right) \nonumber \\&+4s\big [g_L{}^H g_L{}^u g_R{}^s+g_R{}^H g_L{}^s g_R{}^u\big ] B_0\left( 0,m_u^2,m_Z^2\right) \nonumber \\&+ s \big (g_R{}^H g_R{}^u-g_L{}^H g_L{}^u\big )\big (g_L{}^s-g_R{}^s\big ) B_0\left( 0,m_s^2,m_Z^2\right) \nonumber \\&- \frac{2 s}{m_Z^2} \big (g_L{}^H g_L{}^u g_R{}^s+g_R{}^H g_L{}^s g_R{}^u\big ) A_0 (m_Z^2) \nonumber \\&+\bigg [4 m_s^2 m_Z^2\big ( g_L{}^H g_L{}^s g_L{}^u+g_R{}^H g_R{}^s g_R{}^u\big )\nonumber \\&+ 4 s^2 \big (g_L{}^H g_L{}^u g_R{}^s+g_R{}^H g_L{}^s g_R{}^u\big )\bigg ]\nonumber \\&\times C_0\left( m_s^2,m_u^2,m_s^2+m_u^2-s,m_s^2,m_Z^2,m_u^2\right) \bigg ), \nonumber \\ a^{u H }_Z\simeq & {} -\frac{ m_\tau \,m_Z\tan \beta (1-2 s^2_w) (g_L{}^H g_L{}^u+g_R{}^H g_R{}^u)}{16 \pi ^2 V^\star _{us} \left( s-m_{H^\pm }^2\right) }\nonumber \\&\times \bigg (-4 B_0\left( m_s^2+4 m_u^2+2 s,m_H^2,m_u^2\right) -\frac{1}{m_Z^2} \text {A}_0\left( m_Z^2\right) \nonumber \\&+ \frac{3}{2} B_0\left( m_u^2,m_u^2,m_Z^2\right) +\left( 2 m_H^2 -4 m_Z^2\right) \nonumber \\&\times \text {C}_0\left( m_u^2,m_s^2+m_u^2+s,m_s^2+4 m_u^2+2 s,m_u^2,m_Z^2,m_H^2\right) \nonumber \\&+ \left( 3 - \frac{m_H^2}{m_Z^2} \right) B_0\left( m_s^2+m_u^2+s,m_H^2,m_Z^2\right) \nonumber \\&+\frac{1}{2} B_0\left( 0,m_u^2,m_Z^2\right) \bigg ), \nonumber \\ a^{s H }_Z\simeq & {} -\frac{ m_\tau \,m_Z \tan \beta (1-2 s^2_w) \left( g_L{}^H g_R{}^s +g_R{}^H g_L{}^s \right) }{16 \pi ^2 V^\star _{us}\left( s-m_{H^\pm }^2\right) }\nonumber \\&\times \bigg (-2 m_H^2 \text {C}_0\left( m_s^2,m_u^2,m_s^2+m_u^2+s,m_Z^2,m_s^2,m_H^2\right) \nonumber \\&+\left( 1+\frac{m_H^2}{m_Z^2 }\right) B_0\left( m^2_u+m^2_s+s,m_H^2,m_Z^2\right) \nonumber \\&-\frac{1}{2} B_0\left( 0,m_s^2,m_Z^2\right) -\frac{m_H^2 m_s^2}{s} B_0\left( m_s^2,m_s^2,m_Z^2\right) \nonumber \\&+\frac{1}{m_Z^2}\text {A}_0\left( m_Z^2\right) \bigg ), \nonumber \\ a^{\tau \nu _\tau }_Z\simeq & {} \frac{ m_\tau \,m^2_Z\tan \beta \left( g_L{}^H +g_R{}^H \right) }{32 \pi ^2\,\,v\,V^\star _{us} \left( s-m_{\tau }^2\right) \left( s-m_{H^\pm }^2\right) } \nonumber \\&\times \bigg ( 4 \bigg [m_{\tau }^2 m_Z^2 g_L{}^{\tau }+\left( m_{\tau }^2-s\right) {}^2 g_R{}^{\tau }\bigg ]\text {C}_0\big (0,s,m_{\tau }^2,m_Z^2,0,m_{\tau }^2\big )\nonumber \\&+ 4 m_{\tau }^2 g_L{}^{\tau } B_0\left( s,0,m_{\tau }^2\right) \nonumber \\&+\frac{1}{2}\big (3 m_{\tau }^2+s-8\, s\, g_R{}^{\tau }\big ) B_0\big (m_{\tau }^2,m_Z^2,m_{\tau }^2\big ) \nonumber \\&+\frac{2\big (s-m_{\tau }^2\big ) }{ m_Z^2}g_R{}^{\tau } \text {A}_0\left( m_Z^2\right) \nonumber \\&- 4 \big (s-m_{\tau }^2\big ) g_R{}^{\tau } B_0\left( 0,0,m_Z^2\right) \nonumber \\&-\frac{1}{2}\big (s-m_{\tau }^2\big )B_0\left( 0,m_Z^2,m_{\tau }^2\right) \bigg ), \nonumber \\ a^{\tau H}_Z\simeq & {} \frac{m_\tau \,m_Z \tan \beta (1-2 s^2_w) \left( g_L{}^H +g_R{}^H \right) }{32 \pi ^2\,V^\star _{us} m_Z^2 \left( s-m_{H^\pm }^2\right) (s-m_{\tau }^2)} \nonumber \\&\times \bigg ( \bigg [m_{\tau }^2 m_H^2 -\frac{1}{2}m_Z^2 \left( m_{\tau }^2 + s \right) \bigg ]B_0\left( m_{\tau }^2,m_Z^2,m_{\tau }^2\right) \nonumber \\&+ 2\bigg [m_{\tau }^2 \left( m_H^2-m_Z^2\right) g_L{}^{\tau }-s \left( m_H^2+m_Z^2\right) g_R{}^{\tau }\bigg ]\nonumber \\&\times B_0\left( s,m_H^2,m_Z^2\right) -\frac{1}{2} \big (s-m_{\tau }^2\big )\nonumber \\&\times \bigg [ m^2_Z B_0\left( 0,m_Z^2,m_{\tau }^2\right) -4 g_R{}^{\tau } \text {A}_0\left( m_Z^2\right) \bigg ] \nonumber \\&+ m_{\tau }^2 m_H^2(m_H^2-m_Z^2) \text {C}_0\left( 0,s,m_{\tau }^2,m_{\tau }^2,m_H^2,m_Z^2\right) \bigg ),\nonumber \\ \end{aligned}$$

(A2)

$$\begin{aligned} a^{\nu _\tau H}_Z\simeq & {} \frac{m_\tau \, m^2_Z \tan \beta (1-2 s^2_w)\left( g_L{}^H +g_R{}^H \right) }{8\sqrt{2}\, \pi ^2\,v \,V^\star _{us} \left( s-m_{\tau }^2\right) \left( s-m_{H^\pm }^2\right) } \nonumber \\&\times \bigg (2 \bigg [m_{\tau }^2 B_0\left( m_{\tau }^2,0,m_H^2\right) +\big (s\, m_H^2 -m_{\tau }^2 m_H^2+m_{\tau }^2 m_Z^2\big )\nonumber \\&\times \text {C}_0\left( 0,s,m_{\tau }^2,0,m_Z^2,m_H^2\right) \bigg ]\nonumber \\&-\frac{1}{m_Z^2}\bigg [m_{\tau }^2 \left( m_Z^2-m_H^2\right) +s \left( m_H^2+m_Z^2\right) \bigg ] B_0\left( s,m_H^2,m_Z^2\right) \nonumber \\&+ \frac{1}{m_Z^2}\left( s-m_{\tau }^2\right) \text {A}_0\left( m_Z^2\right) \bigg ), \end{aligned}$$

(A3)

where we have used $g^\tau _L-g^\tau _R=-\frac{1}{2}$. Turning now to the contributions to $\triangle _\gamma$ we find that

$$\begin{aligned} a^{s H}_\gamma= & {} \frac{ \alpha _e m_\tau \,v\tan \beta \left( g_L{}^H +g_R{}^H \right) }{12 \pi \,V^\star _{us} \left( s-m_{H^\pm }^2\right) }\nonumber \\&\times \bigg (B_0\left( s,0,m_H^2\right) -2 B_0\left( m_s^2,0,m_s^2\right) \nonumber \\&- 2 m_H^2 \text {C}_0 \left( m_s^2,m_u^2,s,0,m_s^2,m_H^2\right) \bigg ),\nonumber \\ a^{u s}_\gamma= & {} \frac{ \alpha _e m_\tau \,v\tan \beta \left( g_L{}^H +g_R{}^H \right) }{9 \pi \,V^\star _{us} \left( s-m_{H^\pm }^2\right) }\nonumber \\&\times \bigg ( s\text {C}_0\left( m_s^2,m_u^2,-s,m_s^2,0,m_u^2\right) +B_0\left( m_s^2,0,m_s^2\right) \nonumber \\&+B_0\left( m_u^2,0,m_u^2\right) \bigg ),\nonumber \\ a^{u H}_\gamma= & {} -\frac{ \alpha _e m_\tau \,v\tan \beta \left( g_L{}^H +g_R{}^H \right) }{6 \pi \,V^\star _{us}\left( s-m_{H^\pm }^2\right) }\nonumber \\&\times \bigg ( 2 m_H^2\text {C}_0\left( m_u^2,s,2 s,m_u^2,0,m_H^2\right) + 3 B_0\left( s,0,m_H^2\right) \nonumber \\&- 4 B_0\left( 2 s ,m_H^2,m_u^2\right) +2 B_0\left( m_u^2,0,m_u^2\right) \bigg ),\nonumber \\ a^{\tau H}_\gamma\simeq & {} \frac{ \alpha _e m_\tau \,v\tan \beta \left( g_L{}^H +g_R{}^H \right) }{4 \pi \,V^\star _{us} \left( s-m_{\tau }^2\right) \left( s-m_{H^\pm }^2\right) } \nonumber \\&\times \bigg (2\big (m_{\tau }^4- s \, m_H^2\big ) \text {C}_0\left( 0,s,m_{\tau }^2,m_{\tau }^2,m_H^2,0\right) \nonumber \\&+\left( m_{\tau }^2+s\right) B_0\left( s,0,m_H^2\right) \nonumber \\&- 2 s\, B_0\left( m_{\tau }^2,0,m_{\tau }^2\right) \bigg ). \end{aligned}$$

(A4)

The loop function $A_0(m^2)$ is defined as

$$\begin{aligned} A_0(m^2)= & {} \frac{16\pi ^2 \mu ^{4-d}}{i}\int \frac{d^d k}{(2\pi )^d}\frac{1}{k^2-\bar{m}^2}\nonumber \\= & {} m^2\bigg [D+1-\ln \bigg (\frac{m^2}{\mu ^2}\bigg )\bigg ], \end{aligned}$$

(A5)

where $\mu$ is the renormalization scale, ${\bar{m}}^2= m^2- i\epsilon$ and $D=2/(4-d)-\gamma _E+\ln (4\pi )$. Concerning the loop function $B_0(\ell ^2,m^2,n^2)$, it is defined as

$$\begin{aligned} B_0(p^2,m^2,n^2)= & {} \frac{16\pi ^2 \mu ^{4-d}}{i} \int \frac{d^d k}{(2\pi )^d}\frac{1}{(k^2-{\bar{m}}^2)\big [(k+p)^2-\bar{n}^2\big ]}\bigg ]\nonumber \\= & {} D-\int ^1_0 dx\, \ln \bigg [\frac{-x(1-x) p^2+x n^2+(1-x) m^2}{\mu ^2}\bigg ],\nonumber \\ \end{aligned}$$

(A6)

Defining $m^2_\ell =\frac{m^2}{\ell ^2}$ and $n^2_\ell =\frac{n^2}{\ell ^2}$ we find that

$$\begin{aligned} B_0(\ell ^2,m^2,n^2)= & {} D -\ln \bigg (\frac{m^2}{\mu ^2}\bigg )+2\nonumber \\&-\sqrt{-\lambda (1,m^2_\ell ,n^2_\ell )}\bigg \{\sin ^{-1}\bigg [\sqrt{{\frac{1}{4 m^2_\ell }}}\big (1+m^2_\ell -n^2_\ell \big )\bigg ]\nonumber \\&+ \sin ^{-1}\bigg [\sqrt{{\frac{1}{4 n^2_\ell }}}\big (1+n^2_\ell -m^2_\ell \big )\bigg ]\bigg \}\nonumber \\&+\frac{1}{2}\big (1+n^2_\ell - m^2_\ell \big )\ln \bigg (\frac{n^2_\ell }{m^2_\ell }\bigg ), \end{aligned}$$

(A7)

when $\lambda (1,m^2_\ell ,n^2_\ell )< 0$. On the other hand, when $\lambda (1,m^2_\ell ,n^2_\ell ) \ge 0$ we have

$$\begin{aligned} B_0(\ell ^2,m^2,n^2)= & {} D -\ln \bigg (\frac{m^2}{\mu ^2}\bigg )+2\nonumber \\&-\sqrt{\lambda (1,m^2_\ell ,n^2_\ell )}\bigg \{\ln \bigg [\sqrt{\frac{1}{4 m^2_\ell }}\big (1+m^2_\ell -n^2_\ell \big )\nonumber \\&+\sqrt{\frac{1}{4 m^2_\ell }\lambda (1,m^2_\ell ,n^2_\ell )}\bigg ]\nonumber \\&+ \ln \bigg [\sqrt{\frac{1}{4 n^2_\ell }}\big (1+n^2_\ell -m^2_\ell \big )\nonumber \\&+\sqrt{\frac{1}{4 n^2_\ell }\lambda (1,n^2_\ell ,m^2_\ell )}\bigg ]-i\pi \bigg \}\nonumber \\&+\frac{1}{2}\big (1+n^2_\ell - m^2_\ell \big )\ln \bigg (\frac{n^2_\ell }{m^2_\ell }\bigg ),\nonumber \\ \end{aligned}$$

(A8)

For some special cases of $B_0(\ell ^2,m^2,n^2)$, we find that

$$\begin{aligned} B_0(m^2,0,n^2)= & {} D -\ln \bigg (\frac{n^2}{\mu ^2}\bigg )+2\nonumber \\&+\bigg (\frac{n^2}{m^2}-1\bigg )\ln \bigg (1-\frac{m^2}{n^2}\bigg ) \,\,\,\, if\,\, m^2< n^2, \nonumber \\ B_0(m^2,0,n^2)= & {} D -\ln \bigg (\frac{n^2}{\mu ^2}\bigg )+2\nonumber \\&+\bigg (\frac{n^2}{m^2}-1\bigg )\bigg [\ln \bigg (\frac{m^2}{n^2}-1\bigg )-i \pi \bigg ] \,\,\,\, if\,\, m^2 \ge n^2, \nonumber \\ B_0(0,m^2,n^2)= & {} D -\ln \bigg (\frac{m^2}{\mu ^2}\bigg )+1\nonumber \\&+\frac{n^2}{m^2-n^2}\ln \bigg (\frac{n^2}{m^2}\bigg ), \nonumber \\ B_0(0,m^2,n^2)= & {} \frac{A_0(m^2)-A_0(n^2)}{m^2-n^2}, \nonumber \\ B_0(m^2,0,m^2)= & {} 1+\frac{A_0(m^2)}{m^2}. \end{aligned}$$

(A9)

Finally, the loop function $C_0(m^2_1,\kappa ^2,m^2_2,\ell ^2,m^2,n^2)$ can be defined as

$$\begin{aligned}&C_0(p^2_1,(p_1+p_2)^2,p^2_2,\ell ^2,m^2,n^2)\nonumber \\&\quad = \frac{16\pi ^2 \mu ^{4-d}}{i}\int \frac{d^d k}{(2\pi )^d}\nonumber \\&\qquad \times \frac{1}{(k^2-{\bar{\ell }}^2)((k+p_1)^2-\bar{m}^2)\big [(k-p)^2-{\bar{n}}^2\big ]}\bigg ],\nonumber \\ \end{aligned}$$

(A10)

where $p^2_1= m^2_1$, $p^2_2= m^2_2$ and $(p_1+p_2)^2= \kappa ^2$. After Feynman parameterization and shifting the loop momentum k to absorb the terms linear in k one can proceed to obtain the final result of the integration.