Cross sections for 2-to-1 meson–meson scattering

Abstract

We study the processes $K{\bar{K}} \rightarrow \phi$, $\pi D \rightarrow D^*$, $\pi {\bar{D}} \rightarrow {\bar{D}}^*$, and the production of $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons in collisions of charmed mesons or charmed strange mesons. The process of 2-to-1 meson–meson scattering involves a quark and an antiquark from the two initial mesons annihilating into a gluon and subsequently the gluon being absorbed by the spectator quark or antiquark. Transition amplitudes for the scattering process derive from the transition potential in conjunction with mesonic quark–antiquark wave functions and the relative-motion wave function of the two initial mesons. We derive these transition amplitudes in the partial wave expansion of the relative-motion wave function of the two initial mesons so that parity and total-angular-momentum conservation are maintained. We calculate flavor and spin matrix elements in accordance with the transition potential and unpolarized cross sections for the reactions using the transition amplitudes. Cross sections for the production of $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ relate to nodes in their radial wave functions. We suggest the production of $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ as probes of hadronic matter that results from the quark–gluon plasma created in ultrarelativistic heavy-ion collisions.

1 Introduction

Elastic meson–meson scattering produces many resonances. Starting from meson–meson scattering amplitudes obtained in chiral perturbation theory [1,2,3,4,5,6,7], elastic scattering has been studied within nonperturbative schemes, for example, the inverse amplitude method [8,9,10,11,12,13,14,15] and the coupled-channel unitary approaches [16,17,18,19,20]. Elastic meson–meson scattering has also been studied with quark interchange in the first Born approximation in Refs. [21,22,23,24] and with quark–antiquark annihilation and creation in Ref. [25]. Elastic scattering reported in the literature includes $\pi \pi$ [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], $\pi K$ [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], $K{{\bar{K}}}$ [26,27,28,29], $\pi \eta$ [26, 27, 30,31,32,33], $K \eta$ [26], $\eta \eta$ [28], $\pi \rho$ [34, 35], $\pi D$ [36], ${\bar{K}} D$ [37, 38], ${\bar{K}} D^*$ [37], and $D D^*$ [37]. We know that resonances observed in the elastic scattering are usually produced by a process where two mesons scatter into one meson. The 2-to-1 meson–meson scattering includes $\pi \pi \rightarrow \rho$, $\pi \pi \rightarrow f_0(980)$, $\pi K \rightarrow K^*$, $K{\bar{K}} \rightarrow \phi$, $\pi \eta \rightarrow a_0(980)$, $\pi \rho \rightarrow a_1(1260)$, $\pi D \rightarrow D^*$, and so on. Since some resonances like $f_0(980)$, $a_0(980)$, and $a_1(1260)$ are not quark–antiquark states, we do not study $\pi \pi \rightarrow f_0(980)$, $\pi \eta \rightarrow a_0(980)$, $\pi \rho \rightarrow a_1(1260)$, etc. in the present work. The reactions $\pi \pi \rightarrow \rho$ and $\pi K \rightarrow K^*$ have been studied in Ref. [39] via a process where a quark in an initial meson and an antiquark in another initial meson annihilate into a gluon and subsequently the gluon is absorbed by the other antiquark or quark. The resulting cross sections in vacuum agree with the empirical data. Since these two reactions also take place in hadronic matter that is created in ultrarelativistic heavy-ion collisions at the Relativistic Heavy Ion Collider and at the Large Hadron Collider, the dependence of cross sections for the two reactions on the temperature of hadronic matter has also been investigated. With increasing temperature the cross sections decrease. In the present work we consider the reactions: $K{\bar{K}} \rightarrow \phi$, $\pi D \rightarrow D^*$, $\pi {\bar{D}} \rightarrow {\bar{D}}^*$, $D{\bar{D}} \rightarrow \psi (3770)$, $D{\bar{D}} \rightarrow \psi (4040)$, $D^*{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}}^* \rightarrow \psi (4040)$, $D^*{\bar{D}}^* \rightarrow \psi (4040)$, $D_s^+D_s^- \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, $D^*{\bar{D}} \rightarrow \psi (4160)$, $D{\bar{D}}^* \rightarrow \psi (4160)$, $D^*{\bar{D}}^* \rightarrow \psi (4160)$, $D_s^+D_s^- \rightarrow \psi (4160)$, $D_s^{*+}D_s^- \rightarrow \psi (4160)$, $D_s^+D_s^{*-} \rightarrow \psi (4160)$, $D{\bar{D}} \rightarrow \psi (4415)$, $D^*{\bar{D}} \rightarrow \psi (4415)$, $D{\bar{D}}^* \rightarrow \psi (4415)$, $D^*{\bar{D}}^* \rightarrow \psi (4415)$, $D_s^+D_s^- \rightarrow \psi (4415)$, $D_s^{*+}D_s^- \rightarrow \psi (4415)$, $D_s^+D_s^{*-} \rightarrow \psi (4415)$, and $D_s^{*+}D_s^{*-} \rightarrow \psi (4415)$. The $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons consist of a quark and an antiquark [40,41,42,43,44]. All these reactions are governed by the strong interaction. The reaction $K{\bar{K}} \rightarrow \phi$ was studied in Refs. [45, 46] in a mesonic model. The twenty-one reactions that lead to $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, or $\psi (4415)$ as a final state have not been studied theoretically. We now study $K{\bar{K}} \rightarrow \phi$, $\pi D \rightarrow D^*$, $\pi {\bar{D}} \rightarrow {\bar{D}}^*$, and the twenty-one reactions using quark degrees of freedom. The production of $J/\psi$ is a subject intensively studied in relativistic heavy-ion collisions. The $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons may decay into the $J/\psi$ meson. Through this decay the twenty-one reactions add a contribution to the $J/\psi$ production in relativistic heavy-ion collisions. This is another reason why we study the twenty-one reactions here.

This paper is organized as follows. In Sect. 2 we consider four Feynman diagrams and the S-matrix element for 2-to-1 meson–meson scattering, derive transition amplitudes and provide cross-section formulas. In Sect. 3 we present transition potentials corresponding to the Feynman diagrams and calculate flavor matrix elements and spin matrix elements. In Sect. 4 we calculate cross sections, present numerical results and give relevant discussions. In Sect. 5 we summarize the present work. In an Appendix we study decays of the $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons to charmed mesons or charmed strange mesons.

2 Formalism

Fig. 1

Reaction $A+B \rightarrow H$. Solid lines with right (left) triangles stand for quarks (antiquarks). Wavy lines stand for gluons

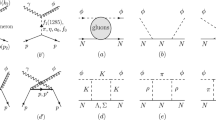
Lowest-order Feynman diagrams are shown in Fig. 1 for the reaction $A(q_1{\bar{q}}_1)+B(q_2{\bar{q}}_2) \rightarrow H(q_2{\bar{q}}_1~\mathrm{or}~q_1{\bar{q}}_2)$. A quark in an initial meson and an antiquark in the other initial meson annihilate into a gluon, and the gluon is then absorbed by a spectator quark or antiquark. The four processes $q_1+{\bar{q}}_2+{\bar{q}}_1 \rightarrow {\bar{q}}_1$, $q_1+{\bar{q}}_2+q_2 \rightarrow q_2$, $q_2+{\bar{q}}_1+q_1 \rightarrow q_1$, and $q_2+{\bar{q}}_1+{\bar{q}}_2 \rightarrow {\bar{q}}_2$ in Fig. 1 give rise to the four transition potentials $V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$, $V_{\mathrm{r}q_1{\bar{q}}_2q_2}$, $V_{\mathrm{r}q_2{\bar{q}}_1q_1}$, and $V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2}$, respectively. Denote by $E_{\mathrm{i}}$ and $\vec {P}_{\mathrm{i}}$ ($E_{\mathrm{f}}$ and $\vec {P}_{\mathrm{f}}$) the total energy and the total momentum of the two initial (final) mesons, respectively; let $E_A$ ($E_B$, $E_H$) be the energy of meson A (B, H), and V the volume where every meson wave function is normalized. The S-matrix element for $A+B \rightarrow H$ is

$$\begin{aligned} S_{\mathrm{fi}}= & {} \delta _{\mathrm{fi}} - 2\pi i \delta (E_{\mathrm{f}} - E_{\mathrm{i}}) (<H \mid V_{\mathrm{r}q_1{\bar{q}}_2 {\bar{q}}_1}\mid A,B>\nonumber \\&+ {<}H \mid V_{\mathrm{r} q_1{\bar{q}}_2 q_2}\mid A,B> \nonumber \\&+ {<}H \mid V_{\mathrm{r}q_2 {\bar{q}}_1 q_1}\mid A,B> + <H \mid V_{\mathrm{r} q_2 {\bar{q}}_1 {\bar{q}}_2}\mid A,B>) \nonumber \\= & {} \delta _{\mathrm{fi}} -(2\pi )^4 i \delta (E_{\mathrm{f}} - E_{\mathrm{i}}) \delta ^3 (\vec {P}_{\mathrm{f}} - \vec {P}_{\mathrm{i}}) \nonumber \\&\times \frac{{{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 {\bar{q}}_1}+ {{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 q_2}+{{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 q_1} +{{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 {\bar{q}}_2}}{V^{\frac{3}{2}}\sqrt{2E_A2E_B2E_H}}, \end{aligned}$$

(1)

where in the four processes mesons A and B go from the state vector $\mid A,B>$ to the state vector $\mid H>$ of meson H, and ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 {\bar{q}}_1}$, ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 q_2}$, ${{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 q_1}$, and ${{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 {\bar{q}}_2}$ are the transition amplitudes given by

$$\begin{aligned}&{{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 {\bar{q}}_1} = \sqrt{2E_A2E_B2E_H} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _H^+ \nonumber \\&\quad \times V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1} \psi _{AB} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(2)

$$\begin{aligned}&{{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 q_2}= \sqrt{2E_A2E_B2E_H} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _H^+\nonumber \\&\quad \times V_{\mathrm{r}q_1{\bar{q}}_2 q_2} \psi _{AB} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(3)

$$\begin{aligned}&{{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 q_1}= \sqrt{2E_A2E_B2E_H} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _H^+\nonumber \\&\quad \times V_{\mathrm{r}q_2{\bar{q}}_1 q_1} \psi _{AB} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(4)

$$\begin{aligned}&{{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 {\bar{q}}_2}= \sqrt{2E_A2E_B2E_H} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _H^+ \nonumber \\&\quad \times V_{\mathrm{r}q_2 {\bar{q}}_1 {\bar{q}}_2} \psi _{AB} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(5)

where $\vec {r}_{ab}$ is the relative coordinate of constituents a and b; $\vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}$ the relative coordinate of $q_1{\bar{q}}_1$ and $q_2{\bar{q}}_2$; $\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}$ the relative momentum of $q_1{\bar{q}}_1$ and $q_2{\bar{q}}_2$; $\psi _H^+$ the Hermitean conjugate of $\psi _H$.

The wave function of mesons A and B is

$$\begin{aligned} \psi _{AB} =\phi _{A\mathrm{rel}} \phi _{B\mathrm{rel}} \phi _{A\mathrm{color}} \phi _{B\mathrm{color}} \chi _{S_A S_{Az}} \chi _{S_B S_{Bz}} \varphi _{AB\mathrm{flavor}}, \end{aligned}$$

(6)

and the wave function of meson H is

$$\begin{aligned} \psi _H =\phi _{J_HJ_{Hz}} \phi _{H\mathrm{color}} \phi _{H\mathrm{flavor}}, \end{aligned}$$

(7)

where $S_A$ ($S_B$) is the spin of meson A (B) with its magnetic projection quantum number $S_{Az}$ ($S_{Bz}$); $\phi _{A\mathrm{rel}}$ ($\phi _{B\mathrm{rel}}$), $\phi _{A\mathrm{color}}$ ($\phi _{B\mathrm{color}}$), and $\chi _{S_A S_{Az}}$ ($\chi _{S_B S_{Bz}}$) are the quark–antiquark relative-motion wave function, the color wave function, and the spin wave function of meson A (B), respectively; $\phi _{H\mathrm{flavor}}$ and $\varphi _{AB\mathrm{flavor}}$ are the flavor wave functions of meson H and of mesons A and B, respectively; $\phi _{H\mathrm{color}}$ is the color wave function of meson H; $\phi _{J_HJ_{Hz}}$ is the space-spin wave function of meson H with the total angular momentum $J_H$ and its z component $J_{Hz}$.

The development in spherical harmonics of the relative-motion wave function of mesons A and B (aside from a normalization constant) is given by

$$\begin{aligned}&e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}} \nonumber \\&\quad = 4\pi \sum \limits _{L_{\mathrm{i}}=0}^{\infty } \sum \limits _{M_{\mathrm{i}}=-L_{\mathrm{i}}}^{L_{\mathrm{i}}} i^{L_{\mathrm{i}}} j_{L_{\mathrm{i}}} (\mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid r_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) \nonumber \\&\qquad \times Y_{L_{\mathrm{i}}M_{\mathrm{i}}}^*({\hat{p}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) Y_{L_{\mathrm{i}}M_{\mathrm{i}}} ({\hat{r}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}), \end{aligned}$$

(8)

where $Y_{L_{\mathrm{i}}M_{\mathrm{i}}}$ are the spherical harmonics with the orbital-angular-momentum quantum number $L_{\mathrm{i}}$ and the magnetic projection quantum number $M_{\mathrm{i}}$, $j_{L_{\mathrm{i}}}$ are the spherical Bessel functions, and ${\hat{p}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}$ (${\hat{r}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}$) denote the polar angles of $\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}$ ($\vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}$). Let $\chi _{SS_{z}}$ stand for the spin wave function of mesons A and B, which has the total spin S and its z component $S_z$. The Clebsch–Gordan coefficients $(S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})$ couple $\chi _{SS_z}$ to $\chi _{S_AS_{Az}}\chi _{S_BS_{Bz}}$,

$$\begin{aligned} \chi _{S_{A}S_{A_{z}}}\chi _{S_{B}S_{B_{z}}}= \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\sum ^{S}_{S_{z}=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\chi _{SS_{z}}, \end{aligned}$$

(9)

where $S_{\mathrm{min}}=\mid S_A-S_B \mid$ and $S_{\mathrm{max}}=S_A+S_B$. $Y_{L_{\mathrm{i}}M_{\mathrm{i}}}$ and $\chi _{SS_{z}}$ are coupled to the wave function $\phi ^{\mathrm{in}}_{JJ_z}$ which has the total angular momentum J of mesons A and B and its z component $J_z$,

$$\begin{aligned} Y_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}\chi _{SS_{z}}= \sum ^{J_{\mathrm{max}}}_{J=J_{\mathrm{min}}}\sum ^J_{J_z=-J} (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|JJ_{z})\phi ^{\mathrm{{in}}}_{JJ_{z}}, \end{aligned}$$

(10)

where $J_{\mathrm{min}}=\mid L_{\mathrm{i}}-S \mid$, $J_{\mathrm{max}}=L_{\mathrm{i}}+S$, and $(L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|JJ_{z})$ are the Clebsch–Gordan coefficients. It follows from Eqs. (8)–(10) that the transition amplitude given in Eq. (2) becomes

$$\begin{aligned}&{{\mathcal {M}}}_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}}4\pi \sum ^{\infty }_{L_{\mathrm{{i}}}=0} \nonumber \\&\qquad \times \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}i^{L_{\mathrm{{i}}}} Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) \phi ^+_{H\mathrm {color}}\phi ^+_{H\mathrm {flavor}}\nonumber \\&\qquad \times \int {d^{3}r_{q_{1}{\bar{q}}_{1}}d^{3}r_{q_{2}{\bar{q}}_{2}}} \phi ^+_{J_{H}J_{Hz}}V_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1} \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_{z}=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\nonumber \\&\qquad \times \sum ^{J_{\mathrm{max}}}_{J=J_{\mathrm{min}}}\sum ^J_{J_z=-J} (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|JJ_{z}) \phi ^{\mathrm{{in}}}_{JJ_{z}}j_{L_{\mathrm{{i}}}}(|\vec {p}_{q_{1}{\bar{q}}_{1}, q_{2}{\bar{q}}_{2}}|r_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}})\nonumber \\&\qquad \times \phi _{A\mathrm {rel}}\phi _{B\mathrm {rel}}\phi _{A\mathrm {color}}\phi _{B\mathrm {color}} \varphi _{AB\mathrm {flavor}}, \end{aligned}$$

(11)

Denote by $L_H$ and $S_H$ the orbital angular momentum and the spin of meson H, respectively, and by $M_H$ and $S_{Hz}$ the magnetic projection quantum number of $L_H$ and $S_H$. In Eq. (11) $\phi _{J_{H}J_{Hz}}=R_{L_H}(r_{q_2{\bar{q}}_1})$ $\sum ^{L_H}_{M_H=-L_H} \sum ^{S_H}_{S_{Hz}=-S_H} (L_HM_HS_HS_{Hz} \mid J_HJ_{Hz}) Y_{L_HM_H} \chi _{S_HS_{Hz}}$ where $R_{L_H}(r_{q_2{\bar{q}}_1})$ is the radial wave function of the relative motion of $q_2$ and ${\bar{q}}_1$, and $(L_H M_H S_H S_{Hz} \mid J_H J_{Hz})$ are the Clebsch–Gordan coefficients. Conservation of total angular momentum implies that J equals $J_H$ and $J_z$ equals $J_{Hz}$. This leads to

$$\begin{aligned}&{{\mathcal {M}}}_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}}4 \pi \sum ^\infty _{L_{\mathrm{{i}}}=0} \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}i^{L_{\mathrm{{i}}}} Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}\nonumber \\&\qquad \times ({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) \phi ^+_{H\mathrm {color}}\phi ^+_{H\mathrm {flavor}}\nonumber \\&\qquad \times \int {d^{3}r_{q_{1}{\bar{q}}_{1}}d^{3}r_{q_{2}{\bar{q}}_{2}}} \phi ^+_{J_HJ_{Hz}}V_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1} \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_{z}=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\nonumber \\&\qquad \times (L_{\mathrm{i}}M_{\mathrm{i}}SS_{z}|J_{H}J_{H_{z}})\phi ^{\mathrm{{in}}}_{J_{H}J_{Hz}} j_{L_{\mathrm{{i}}}}(|\vec {p}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}} |r_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}})\nonumber \\&\qquad \times \phi _{A\mathrm {rel}}\phi _{B\mathrm {rel}}\phi _{A\mathrm {color}} \phi _{B\mathrm {color}}\varphi _{AB\mathrm {flavor}}. \end{aligned}$$

(12)

Using the relation

$$\begin{aligned} \phi ^{\mathrm{{in}}}_{J_{H}J_{Hz}}= \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz}) Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}}\chi _{S{\bar{S}}_{z}}, \end{aligned}$$

(13)

where $(L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})$ are the Clebsch–Gordan coefficients, we get

$$\begin{aligned}&{{\mathcal {M}}}_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}}4\pi \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\sum ^{S}_{S_{z}=-S} (S_{A}S_{Az}S_{B}S_{Bz} |SS_{z})\nonumber \\&\qquad \times \sum ^\infty _{L_{\mathrm{{i}}}=0}\sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}} =-L_{\mathrm{{i}}}}i^{L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|J_{H}J_{Hz}) \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\nonumber \\&\qquad \times \sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})\nonumber \\&\qquad \times \phi ^+_{H\mathrm {color}}\phi ^+_{H\mathrm {flavor}}\int {d^{3}r_{q_{1} {\bar{q}}_{1}}d^{3}r_{q_{2}{\bar{q}}_{2}}}\phi ^+_{J_HJ_{Hz}} V_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1}j_{L_{\mathrm{{i}}}}\nonumber \\&\qquad \times (|\vec {p}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}|r_{q_{1}{\bar{q}}_{1}, q_{2}{\bar{q}}_{2}})\nonumber \\&\qquad \times Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}}({\hat{r}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) \phi _{A\mathrm {rel}}\phi _{B\mathrm {rel}}\chi _{S{\bar{S}}_{z}}\phi _{A\mathrm {color}} \phi _{B\mathrm {color}}\varphi _{AB\mathrm {flavor}}.\nonumber \\ \end{aligned}$$

(14)

Furthermore, we need the identity

$$\begin{aligned} j_l(pr)Y_{lm}({\hat{r}})=\int \frac{d^3p^\prime }{(2\pi )^3}\frac{2\pi ^2}{p^2} \delta (p-p^\prime ) i^l (-1)^l Y_{lm}({\hat{p}}^\prime ) e^{i\vec {p}^{~\prime } \cdot \vec {r}} ,\nonumber \\ \end{aligned}$$

(15)

which is obtained with the help of $\int _0^\infty j_l(pr)j_l(p^\prime r)r^2dr=\frac{\pi }{2p^2} \delta (p-p^\prime )$ [47, 48]. Substituting Eq. (15) in Eq. (14), we get

$$\begin{aligned}&{{\mathcal {M}}}_{rq_{1}{\bar{q}}_{2}{\bar{q}}_1}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}}4\pi \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_{z}=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\sum ^\infty _{L_{\mathrm{{i}}}=0} \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}i^{L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|J_{H}J_{Hz}) \nonumber \\&\qquad \times \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})\nonumber \\&\qquad \times \phi ^+_{H\mathrm {color}}\phi ^+_{H\mathrm {flavor}}\int {\frac{d^{3}p_{\mathrm{{irm}}}}{(2\pi )^3}}\frac{2\pi ^2}{\vec {p}^{~2}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}} \delta (|\vec {p}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}|\nonumber \\&\qquad -|\vec {p}_{\mathrm{{irm}}}|) i^{L_{\mathrm{{i}}}}(-1)^{L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}}({\hat{p}}_{\mathrm{{irm}}})\int {d^{3}r_{q_{1} {\bar{q}}_{1}}d^{3}r_{q_{2}{\bar{q}}_{2}}}\phi ^+_{J_{H}J_{Hz}}V_{rq_{1}{\bar{q}}_{2} {\bar{q}}_{1}}e^{i\vec {p}_{\mathrm{{irm}}}\cdot \vec {r}_{q_{1}{\bar{q}}_{1},q_{2} {\bar{q}}_{2}}}\nonumber \\&\qquad \times \phi _{A\mathrm {rel}} \phi _{B\mathrm {rel}}\chi _{S{\bar{S}}_{z}}\phi _{A\mathrm {color}}\phi _{B\mathrm {color}} \varphi _{AB\mathrm {flavor}}. \end{aligned}$$

(16)

Let $\vec {r}_c$ and $m_c$ be the position vector and the mass of constituent c, respectively. Then $\phi _{A\mathrm {rel}}$, $\phi _{B\mathrm {rel}}$, and $R_{L_H}$ are functions of the relative coordinate of the quark and the antiquark. We take the Fourier transform of $V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$ and the mesonic quark–antiquark relative-motion wave functions:

$$\begin{aligned} V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}(\vec {r}_{{\bar{q}}_1}-\vec {r}_{q_1})= & {} \int \frac{d^3k}{(2\pi )^3} V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1} (\vec {k}) e^{i\vec {k} \cdot (\vec {r}_{{\bar{q}}_1}-\vec {r}_{q_1})}, \end{aligned}$$

(17)

$$\begin{aligned} \phi _{A\mathrm{rel}}(\vec {r}_{q_1{\bar{q}}_1})= & {} \int \frac{d^3p_{q_1{\bar{q}}_1}}{(2\pi )^3} \phi _{A\mathrm{rel}} (\vec {p}_{q_1{\bar{q}}_1}) e^{i\vec {p}_{q_1{\bar{q}}_1} \cdot \vec {r}_{q_1{\bar{q}}_1}}, \end{aligned}$$

(18)

$$\begin{aligned} \phi _{B\mathrm{rel}}(\vec {r}_{q_2{\bar{q}}_2})= & {} \int \frac{d^3p_{q_2{\bar{q}}_2}}{(2\pi )^3} \phi _{B\mathrm{rel}} (\vec {p}_{q_2{\bar{q}}_2}) e^{i\vec {p}_{q_2{\bar{q}}_2} \cdot \vec {r}_{q_2{\bar{q}}_2}}, \end{aligned}$$

(19)

$$\begin{aligned} \phi _{J_HJ_{Hz}}(\vec {r}_{q_2{\bar{q}}_1})= & {} \int \frac{d^3p_{q_2{\bar{q}}_1}}{(2\pi )^3} \phi _{J_HJ_{Hz}} (\vec {p}_{q_2{\bar{q}}_1}) e^{i\vec {p}_{q_2{\bar{q}}_1} \cdot \vec {r}_{q_2{\bar{q}}_1}},\nonumber \\ \end{aligned}$$

(20)

for the two upper diagrams in Fig. 1, and

$$\begin{aligned} \phi _{J_HJ_{Hz}}(\vec {r}_{q_1{\bar{q}}_2}) = \int \frac{d^3p_{q_1{\bar{q}}_2}}{(2\pi )^3} \phi _{J_HJ_{Hz}} (\vec {p}_{q_1{\bar{q}}_2}) e^{i\vec {p}_{q_1{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_2}},\nonumber \\ \end{aligned}$$

(21)

for the two lower diagrams. In Eq. (17) $\vec k$ is the gluon momentum, and in Eqs. (18)–(21) $\vec {p}_{ab}$ is the relative momentum of constituents a and b. The spherical polar coordinates of $\vec {p}_{\mathrm{irm}}$ are expressed as $(\mid \vec {p}_{\mathrm{irm}} \mid , \theta _{\mathrm{irm}}, \phi _{\mathrm{irm}})$. In momentum space the normalizations are

$$\begin{aligned}&\int \frac{d^3p_{q_1{\bar{q}}_1}}{(2\pi )^3} \phi _{A\mathrm{rel}}^+(\vec {p}_{q_1{\bar{q}}_1}) \phi _{A\mathrm{rel}}(\vec {p}_{q_1{\bar{q}}_1})=1, \\&\int \frac{d^3p_{q_2{\bar{q}}_2}}{(2\pi )^3} \phi _{B\mathrm{rel}}^+(\vec {p}_{q_2{\bar{q}}_2}) \phi _{B\mathrm{rel}}(\vec {p}_{q_2{\bar{q}}_2})=1,\\&\int \frac{d^3p_{q_2{\bar{q}}_1}}{(2\pi )^3} \phi _{J_HJ_{Hz}}^+(\vec {p}_{q_2{\bar{q}}_1}) \phi _{J_HJ_{Hz}}(\vec {p}_{q_2{\bar{q}}_1})=1,\\&\int \frac{d^3p_{q_1{\bar{q}}_2}}{(2\pi )^3} \phi _{J_HJ_{Hz}}^+(\vec {p}_{q_1{\bar{q}}_2}) \phi _{J_HJ_{Hz}}(\vec {p}_{q_1{\bar{q}}_2})=1. \end{aligned}$$

Integration over $\mid \vec {p}_{\mathrm{irm}} \mid$, $\vec {r}_{q_1{\bar{q}}_1}$, and $\vec {r}_{q_2{\bar{q}}_2}$ yields

$$\begin{aligned}&{{\mathcal {M}}}_{rq_1{\bar{q}}_2{\bar{q}}_1}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}} \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_z=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\sum ^\infty _{L_{\mathrm{{i}}}=0} \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|J_{H}J_{Hz}) \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\nonumber \\&\qquad \times \sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})\nonumber \\&\qquad \times \phi ^{+}_{H\mathrm {color}}\phi ^{+}_{H\mathrm {flavor}}\int {d\theta _{\mathrm{{irm}}} d\phi _{\mathrm{{irm}}}\sin \theta _{\mathrm{{irm}}}}Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}} ({\hat{p}}_{\mathrm{{irm}}})\nonumber \\&\qquad \times \int {\frac{d^{3}p_{q_{1}{\bar{q}}_{1}}}{(2\pi )^3}} \int {\frac{d^{3}p_{q_{2}{\bar{q}}_{2}}}{(2\pi )^3}}\phi ^+_{J_{H}J_{Hz}} \left( \vec {p}_{q_{2}{\bar{q}}_{2}}\right. \nonumber \\&\qquad \left. -\frac{m_{q_{2}}}{m_{q_2}+m_{{\bar{q}}_{2}}} \vec {p}_{\mathrm{{irm}}}\right) V_{rq_1{\bar{q}}_2{\bar{q}}_1}\nonumber \\&\qquad \times \left[ \vec {p}_{q_{1}{\bar{q}}_{1}}-\vec {p}_{q_{2}{\bar{q}}_{2}}+ \left( \frac{m_{q_{2}}}{m_{q_{2}}+m_{{\bar{q}}_{2}}}-\frac{m_{{\bar{q}}_{1}}}{m_{q_{1}}+m_{{\bar{q}}_{1}}}\right) \vec {p}_{\mathrm{{irm}}}\right] \nonumber \\&\qquad \times \phi _{A\mathrm {rel}}(\vec {p}_{q_{1}{\bar{q}}_{1}})\phi _{B\mathrm {rel}} (\vec {p}_{q_{2}{\bar{q}}_{2}})\chi _{S{\bar{S}}_{z}} \phi _{A\mathrm {color}}\phi _{B\mathrm {color}}\varphi _{AB\mathrm {flavor}}, \end{aligned}$$

(22)

in which $\mid \vec {p}_{\mathrm{irm}} \mid = \mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid$. So far, we have obtained a new expression of the transition amplitude from Eq. (2).

Making use of the Fourier transform of $V_{\mathrm{r}q_1{\bar{q}}_2q_2}$, $V_{\mathrm{r}q_2{\bar{q}}_1q_1}$, and $V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2}$,

$$\begin{aligned}&V_{\mathrm{r}q_1{\bar{q}}_2q_2}(\vec {r}_{q_2}-\vec {r}_{{\bar{q}}_2}) = \int \frac{d^3k}{(2\pi )^3} V_{\mathrm{r}q_1{\bar{q}}_2q_2} (\vec {k}) e^{i\vec {k} \cdot (\vec {r}_{q_2}-\vec {r}_{{\bar{q}}_2})}, \end{aligned}$$

(23)

$$\begin{aligned}&V_{\mathrm{r}q_2{\bar{q}}_1q_1}(\vec {r}_{q_1}-\vec {r}_{{\bar{q}}_1}) = \int \frac{d^3k}{(2\pi )^3} V_{\mathrm{r}q_2{\bar{q}}_1q_1} (\vec {k}) e^{i\vec {k} \cdot (\vec {r}_{q_1}-\vec {r}_{{\bar{q}}_1})}, \end{aligned}$$

(24)

$$\begin{aligned}&V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2}(\vec {r}_{{\bar{q}}_2}-\vec {r}_{q_2}) = \int \frac{d^3k}{(2\pi )^3} V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2} (\vec {k}) e^{i\vec {k} \cdot (\vec {r}_{{\bar{q}}_2}-\vec {r}_{q_2})},\nonumber \\ \end{aligned}$$

(25)

from Eqs. (3)–(5) we obtain

$$\begin{aligned}&{{\mathcal {M}}}_{rq_1{\bar{q}}_2q_2}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}} \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_z=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\sum ^\infty _{L_{\mathrm{{i}}}=0} \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|J_{H}J_{Hz}) \nonumber \\&\qquad \times \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})\nonumber \\&\qquad \times \phi ^{+}_{H\mathrm {color}}\phi ^{+}_{H\mathrm {flavor}}\int {d\theta _{\mathrm{{irm}}} d\phi _{\mathrm{{irm}}}\sin \theta _{\mathrm{{irm}}}}Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}} ({\hat{p}}_{\mathrm{{irm}}})\nonumber \\&\qquad \times \int {\frac{d^{3}p_{q_{1}{\bar{q}}_{1}}}{(2\pi )^3}} \int {\frac{d^{3}p_{q_{2}{\bar{q}}_{2}}}{(2\pi )^3}}\phi ^+_{J_{H}J_{Hz}} \left( \vec {p}_{q_1{\bar{q}}_1}\right. \nonumber \\&\qquad \left. -\frac{m_{{\bar{q}}_1}}{m_{q_1}+m_{{\bar{q}}_1}} \vec {p}_{\mathrm{{irm}}}\right) V_{rq_1{\bar{q}}_2q_2}\nonumber \\&\qquad \times \left[ \vec {p}_{q_{1}{\bar{q}}_{1}}-\vec {p}_{q_{2}{\bar{q}}_{2}}+ \left( \frac{m_{q_{2}}}{m_{q_{2}}+m_{{\bar{q}}_{2}}}-\frac{m_{{\bar{q}}_{1}}}{m_{q_{1}}+m_{{\bar{q}}_{1}}}\right) \vec {p}_{\mathrm{{irm}}}\right] \nonumber \\&\qquad \times \phi _{A\mathrm {rel}}(\vec {p}_{q_{1}{\bar{q}}_{1}})\phi _{B\mathrm {rel}} (\vec {p}_{q_{2}{\bar{q}}_{2}})\chi _{S{\bar{S}}_{z}} \phi _{A\mathrm {color}}\phi _{B\mathrm {color}}\varphi _{AB\mathrm {flavor}}, \end{aligned}$$

(26)

$$\begin{aligned}&{{\mathcal {M}}}_{rq_2{\bar{q}}_1q_1}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}} \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_z=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\sum ^\infty _{L_{\mathrm{{i}}}=0} \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|J_{H}J_{Hz}) \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\nonumber \\&\qquad \times \sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})\nonumber \\&\qquad \times \phi ^{+}_{H\mathrm {color}}\phi ^{+}_{H\mathrm {flavor}}\int {d\theta _{\mathrm{{irm}}} d\phi _{\mathrm{{irm}}}\sin \theta _{\mathrm{{irm}}}}Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}} ({\hat{p}}_{\mathrm{{irm}}})\nonumber \\&\qquad \times \int {\frac{d^{3}p_{q_{1}{\bar{q}}_{1}}}{(2\pi )^3}} \int {\frac{d^{3}p_{q_{2}{\bar{q}}_{2}}}{(2\pi )^3}}\phi ^+_{J_{H}J_{Hz}} \left( \vec {p}_{q_{2}{\bar{q}}_{2}}\right. \nonumber \\&\qquad \left. +\frac{m_{{\bar{q}}_2}}{m_{q_2}+m_{{\bar{q}}_2}} \vec {p}_{\mathrm{{irm}}}\right) V_{rq_2{\bar{q}}_1q_1}\nonumber \\&\qquad \times \left[ -\vec {p}_{q_{1}{\bar{q}}_1}+\vec {p}_{q_{2}{\bar{q}}_2}+ \left( \frac{m_{{\bar{q}}_2}}{m_{q_2}+m_{{\bar{q}}_2}}-\frac{m_{q_1}}{m_{q_1}+m_{{\bar{q}}_1}}\right) \vec {p}_{\mathrm{{irm}}}\right] \nonumber \\&\qquad \times \phi _{A\mathrm {rel}}(\vec {p}_{q_{1}{\bar{q}}_{1}})\phi _{B\mathrm {rel}} (\vec {p}_{q_{2}{\bar{q}}_{2}})\chi _{S{\bar{S}}_{z}} \phi _{A\mathrm {color}}\phi _{B\mathrm {color}}\varphi _{AB\mathrm {flavor}}, \nonumber \\ \end{aligned}$$

(27)

$$\begin{aligned}&{{\mathcal {M}}}_{rq_2{\bar{q}}_1{\bar{q}}_2}\nonumber \\&\quad =\sqrt{2E_{A}2E_{B}2E_{H}} \sum ^{S_{\mathrm{max}}}_{S=S_{\mathrm{min}}}\nonumber \\&\qquad \times \sum ^{S}_{S_z=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\sum ^\infty _{L_{\mathrm{{i}}}=0} \sum ^{L_{\mathrm{{i}}}}_{M_{\mathrm{{i}}}=-L_{\mathrm{{i}}}}\nonumber \\&\qquad \times Y^*_{L_{\mathrm{{i}}}M_{\mathrm{{i}}}}({\hat{p}}_{q_{1}{\bar{q}}_{1},q_{2}{\bar{q}}_{2}}) (L_{\mathrm{{i}}}M_{\mathrm{{i}}}SS_{z}|J_{H}J_{Hz}) \nonumber \\&\qquad \times \sum ^{L_{\mathrm{i}}}_{{\bar{M}}_{\mathrm{i}}=-L_{\mathrm{i}}}\sum ^S_{{\bar{S}}_{z}=-S} (L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}S{\bar{S}}_{z}|J_{H}J_{Hz})\nonumber \\&\qquad \times \phi ^{+}_{H\mathrm {color}}\phi ^{+}_{H\mathrm {flavor}}\int {d\theta _{\mathrm{{irm}}} d\phi _{\mathrm{{irm}}}\sin \theta _{\mathrm{{irm}}}}Y_{L_{\mathrm{{i}}}{\bar{M}}_{\mathrm{{i}}}} ({\hat{p}}_{\mathrm{{irm}}})\nonumber \\&\qquad \times \int {\frac{d^{3}p_{q_{1}{\bar{q}}_{1}}}{(2\pi )^3}} \int {\frac{d^{3}p_{q_{2}{\bar{q}}_{2}}}{(2\pi )^3}}\phi ^+_{J_{H}J_{Hz}} \left( \vec {p}_{q_1{\bar{q}}_1}\right. \nonumber \\&\qquad \left. +\frac{m_{q_1}}{m_{q_1}+m_{{\bar{q}}_1}} \vec {p}_{\mathrm{{irm}}}\right) V_{rq_2{\bar{q}}_1{\bar{q}}_2}\nonumber \\&\qquad \times \left[ -\vec {p}_{q_{1}{\bar{q}}_1}+\vec {p}_{q_{2}{\bar{q}}_2}+ \left( \frac{m_{{\bar{q}}_2}}{m_{q_2}+m_{{\bar{q}}_2}}-\frac{m_{q_1}}{m_{q_1}+m_{{\bar{q}}_1}}\right) \vec {p}_{\mathrm{{irm}}}\right] \nonumber \\&\qquad \times \phi _{A\mathrm {rel}}(\vec {p}_{q_{1}{\bar{q}}_{1}})\phi _{B\mathrm {rel}} (\vec {p}_{q_{2}{\bar{q}}_{2}})\chi _{S{\bar{S}}_{z}} \phi _{A\mathrm {color}}\phi _{B\mathrm {color}}\varphi _{AB\mathrm {flavor}}. \end{aligned}$$

(28)

With these transition amplitudes the unpolarized cross section for $A+B \rightarrow H$ is

$$\begin{aligned} \sigma ^{\mathrm{unpol}}= & {} \frac{\pi \delta (E_{\mathrm{f}}-E_{\mathrm{i}})}{4\sqrt{(P_A \cdot P_B)^2 - m_A^2m_B^2}E_H}\frac{1}{(2J_A+1)(2J_B+1)} \nonumber \\&\times \sum \limits _{J_{Az}J_{Bz}J_{Hz}} \mid {{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 {\bar{q}}_1}+{{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2q_2} +{{\mathcal {M}}}_{\mathrm{r}q_2{\bar{q}}_1 q_1}\nonumber \\&+{{{\mathcal {M}}}_{\mathrm{r}q_2{\bar{q}}_1 {\bar{q}}_2}}\mid ^2 , \end{aligned}$$

(29)

where $P_A$, $m_A$, $J_A$, and $J_{Az}$ ($P_B$, $m_B$, $J_B$, and $J_{Bz}$) of meson A (B) are the four-momentum, the mass, the total angular momentum, and its z component, respectively. We calculate the cross section in the center-of-mass frame of the two initial mesons, i.e., with meson H at rest.

3 Flavor and spin matrix elements

Let $p_c$ be the four-momentum of constituent c. The two upper diagrams give $q_1(p_{q_1})+{\bar{q}}_1(p_{{\bar{q}}_1})+q_2(p_{q_2}) +{\bar{q}}_2(p_{{\bar{q}}_2}) \rightarrow {\bar{q}}_1(p_{{\bar{q}}_1}^\prime ) +q_2(p_{q_2}^\prime )$, and the two lower diagrams $q_1(p_{q_1})+{\bar{q}}_1(p_{{\bar{q}}_1})+q_2(p_{q_2}) +{\bar{q}}_2(p_{{\bar{q}}_2}) \rightarrow q_1(p_{q_1}^\prime ) +{\bar{q}}_2(p_{{\bar{q}}_2}^\prime )$. The transition potentials $V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$, $V_{\mathrm{r}q_1{\bar{q}}_2q_2}$, $V_{\mathrm{r}q_2{\bar{q}}_1q_1}$, and $V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2}$ are expressed as

$$\begin{aligned}&V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}(\vec {k}) \nonumber \\&\quad = - \frac{\vec {\lambda }(1)}{2}\cdot \frac{\vec {\lambda }(21)}{2} \frac{g_{\mathrm{s}}^2}{k^2} \left( \frac{\vec {\sigma }(21)\cdot \vec {k}}{2m_{q_1}} \right. \nonumber \\&\qquad \left. -\frac{\vec {\sigma }(1)\cdot \vec {p}_{{\bar{q}}_1} \vec {\sigma }(1)\cdot \vec {\sigma }(21) +\vec {\sigma }(1)\cdot \vec {\sigma }(21) \vec {\sigma }(1)\cdot \vec {p}_{{\bar{q}}_1}^{~\prime } }{2m_{{\bar{q}}_1}}\right) , \end{aligned}$$

(30)

$$\begin{aligned}&V_{\mathrm{r}q_1{\bar{q}}_2q_2}(\vec {k}) \nonumber \\&\quad = \frac{\vec {\lambda }(2)}{2}\cdot \frac{\vec {\lambda }(21)}{2} \frac{g_{\mathrm{s}}^2}{k^2} \left( \frac{\vec {\sigma }(21)\cdot \vec {k}}{2m_{q_1}} \right. \nonumber \\&\qquad \left. - \frac{\vec {\sigma }(2)\cdot \vec {\sigma }(21)\vec {\sigma }(2)\cdot \vec {p}_{q_2}+ \vec {\sigma }(2)\cdot \vec {p}_{q_2}^{~\prime } \vec {\sigma }(2)\cdot \vec {\sigma }(21)}{2m_{q_2}}\right) , \end{aligned}$$

(31)

$$\begin{aligned}&V_{\mathrm{r}q_2{\bar{q}}_1q_1}(\vec {k}) \nonumber \\&\quad = \frac{\vec {\lambda }(1)}{2}\cdot \frac{\vec {\lambda }(12)}{2} \frac{g_{\mathrm{s}}^2}{k^2} \left( \frac{\vec {\sigma }(12)\cdot \vec {k}}{2m_{q_2}} \right. \nonumber \\&\qquad \left. - \frac{\vec {\sigma }(1)\cdot \vec {\sigma }(12)\vec {\sigma }(1)\cdot \vec {p}_{q_1}+ \vec {\sigma }(1)\cdot \vec {p}_{q_1}^{~\prime } \vec {\sigma }(1)\cdot \vec {\sigma }(12)}{2m_{q_1}}\right) , \end{aligned}$$

(32)

$$\begin{aligned}&V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2}(\vec {k}) \nonumber \\&\quad = - \frac{\vec {\lambda }(2)}{2}\cdot \frac{\vec {\lambda }(12)}{2} \frac{g_{\mathrm{s}}^2}{k^2} \left( \frac{\vec {\sigma }(12)\cdot \vec {k}}{2m_{q_2}} \right. \nonumber \\&\qquad \left. - \frac{\vec {\sigma }(2)\cdot \vec {p}_{{\bar{q}}_2} \vec {\sigma }(2)\cdot \vec {\sigma }(12) +\vec {\sigma }(2)\cdot \vec {\sigma }(12) \vec {\sigma }(2)\cdot \vec {p}_{{\bar{q}}_2}^{~\prime } }{2m_{{\bar{q}}_2}}\right) ,\nonumber \\ \end{aligned}$$

(33)

where $g_{\mathrm{s}}$ is the gauge coupling constant, k the gluon four-momentum, $\vec \lambda$ the Gell-Mann matrices, and $\vec \sigma$ the Pauli matrices. In Eqs. (30) and (31), $\vec {\lambda }(21)$ ($\vec {\sigma }(21)$) mean that they have matrix elements between the color (spin) wave functions of initial antiquark ${\bar{q}}_2$ and initial quark $q_1$. In Eqs. (32) and (33), $\vec {\lambda }(12)$ ($\vec {\sigma }(12)$) mean that they have matrix elements between the color (spin) wave functions of initial antiquark ${\bar{q}}_1$ and initial quark $q_2$. In Eqs. (30) and (33), $\vec {\lambda }(1)$ and $\vec {\lambda }(2)$ ($\vec {\sigma }(1)$ and $\vec {\sigma }(2)$) mean that they have matrix elements between the color (spin) wave functions of the initial antiquark and the final antiquark. In Eqs. (31) and (32), $\vec {\lambda }(2)$ and $\vec {\lambda }(1)$ ($\vec {\sigma }(2)$ and $\vec {\sigma }(1)$) mean that they have matrix elements between the color (spin) wave functions of the final quark and the initial quark.

Table 1 Flavor matrix elements

It is shown in Refs. [41,42,43,44] that $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ can be individually interpreted as the $1 ^3D_1$, $3 ^3S_1$, $2 ^3D_1$, and $4 ^3S_1$ quark–antiquark states. We use the notation $K= \left( \begin{array}{c} K^+ \\ K^0 \end{array} \right)$, ${\bar{K}}= \left( \begin{array}{c} {\bar{K}}^0 \\ K^- \end{array} \right)$, $K^*= \left( \begin{array}{c} K^{*+} \\ K^{*0} \end{array} \right)$, ${\bar{K}}^*= \left( \begin{array}{c} {\bar{K}}^{*0} \\ K^{*-} \end{array} \right)$, $D= \left( \begin{array}{c} D^+ \\ D^0 \end{array} \right)$, ${\bar{D}}= \left( \begin{array}{c} {\bar{D}}^0 \\ D^- \end{array} \right)$, $D^*= \left( \begin{array}{c} D^{*+} \\ D^{*0} \end{array} \right)$, and ${\bar{D}}^*= \left( \begin{array}{c} {\bar{D}}^{*0} \\ D^{*-} \end{array} \right)$. Based on the formulas in Sect. 2, we study the following reactions:

$$\begin{aligned}&K{\bar{K}} \rightarrow \phi ,~\pi D \rightarrow D^*,~\pi {\bar{D}} \rightarrow {\bar{D}}^*, \\&D{\bar{D}} \rightarrow \psi (3770),~D{\bar{D}} \rightarrow \psi (4040), \\&D^*{\bar{D}} \rightarrow \psi (4040),~D{\bar{D}}^* \rightarrow \psi (4040),\\&\quad D^*{\bar{D}}^* \rightarrow \psi (4040),~D_s^+D_s^- \rightarrow \psi (4040), \\&D{\bar{D}} \rightarrow \psi (4160),~D^*{\bar{D}} \rightarrow \psi (4160),\\&\quad D{\bar{D}}^* \rightarrow \psi (4160),~D^*{\bar{D}}^* \rightarrow \psi (4160), \\&D_s^+D_s^- \rightarrow \psi (4160),~D_s^{*+}D_s^- \rightarrow \psi (4160),\\&\quad D_s^+D_s^{*-} \rightarrow \psi (4160), \\&D{\bar{D}} \rightarrow \psi (4415),~D^*{\bar{D}} \rightarrow \psi (4415),\\&\quad D{\bar{D}}^* \rightarrow \psi (4415),~D^*{\bar{D}}^* \rightarrow \psi (4415), \\&D_s^+D_s^- \rightarrow \psi (4415),~D_s^{*+}D_s^- \rightarrow \psi (4415),\\&\quad D_s^+D_s^{*-} \rightarrow \psi (4415),~D_s^{*+}D_s^{*-} \rightarrow \psi (4415). \end{aligned}$$

From the Gell–Mann matrices and the Pauli matrices in the transition potentials, the expressions of the transition amplitudes in Eqs. (22) and (26)–(28) involve color matrix elements, flavor matrix elements, and spin matrix elements for the above reactions. The color matrix elements in ${{\mathcal {M}}}_{rq_1{\bar{q}}_2{\bar{q}}_1}$, ${{\mathcal {M}}}_{rq_1{\bar{q}}_2q_2}$, ${{\mathcal {M}}}_{rq_2{\bar{q}}_1q_1}$, and ${{\mathcal {M}}}_{rq_2{\bar{q}}_1{\bar{q}}_2}$ are $-\frac{4}{3\sqrt{3}}$, $\frac{4}{3\sqrt{3}}$, $\frac{4}{3\sqrt{3}}$, and $-\frac{4}{3\sqrt{3}}$, respectively. While we calculate the flavor matrix elements, we keep the total isospin of the two initial mesons the same as the isospin of the final meson. The flavor wave functions of charmed mesons and charmed strange mesons are $\mid D^+>=-\mid c{\bar{d}}>$, $\mid D^0>=\mid c{\bar{u}}>$, $\mid {\bar{D}}^0>=\mid u{\bar{c}}>$, $\mid D^->=\mid d{\bar{c}}>$, $\mid D^{*+}>=-\mid c{\bar{d}}>$, $\mid D^{*0}>=\mid c{\bar{u}}>$, $\mid {\bar{D}}^{*0}>=\mid u{\bar{c}}>$, and $\mid D^{*-}>=\mid d{\bar{c}}>$. The flavor matrix element ${{\mathcal {M}}}_{\mathrm{f}K{\bar{K}} \rightarrow \phi }$ (${{\mathcal {M}}}_{\mathrm{f}\pi D \rightarrow D^*}$, ${{\mathcal {M}}}_{\mathrm{f}D{\bar{D}} \rightarrow \psi (3770)}$, ${{\mathcal {M}}}_{\mathrm{f}D_s^+D_s^- \rightarrow \psi (4040)}$) for $K{\bar{K}} \rightarrow \phi$ ($\pi D \rightarrow D^*$, $D{\bar{D}} \rightarrow \psi (3770)$, $D_s^+D_s^- \rightarrow \psi (4040)$) is shown in Table 1. The flavor matrix element for $\pi {\bar{D}} \rightarrow {\bar{D}}^*$ equals ${{\mathcal {M}}}_{\mathrm{f}\pi D \rightarrow D^*}$. The flavor matrix elements for $D{\bar{D}} \rightarrow \psi (4040)$, $D^*{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}}^* \rightarrow \psi (4040)$, $D^*{\bar{D}}^* \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, $D^*{\bar{D}} \rightarrow \psi (4160)$, $D{\bar{D}}^* \rightarrow \psi (4160)$, $D^*{\bar{D}}^* \rightarrow \psi (4160)$, $D{\bar{D}} \rightarrow \psi (4415)$, $D^*{\bar{D}} \rightarrow \psi (4415)$, $D{\bar{D}}^* \rightarrow \psi (4415)$, and $D^*{\bar{D}}^* \rightarrow \psi (4415)$ are the same as ${{\mathcal {M}}}_{\mathrm{f}D{\bar{D}} \rightarrow \psi (3770)}$. The flavor matrix elements for $D_s^+D_s^- \rightarrow \psi (4160)$, $D_s^{*+}D_s^- \rightarrow \psi (4160)$, $D_s^+D_s^{*-} \rightarrow \psi (4160)$, $D_s^+D_s^- \rightarrow \psi (4415)$, $D_s^{*+}D_s^- \rightarrow \psi (4415)$, $D_s^+D_s^{*-} \rightarrow \psi (4415)$, and $D_s^{*+}D_s^{*-} \rightarrow \psi (4415)$ equal ${{\mathcal {M}}}_{\mathrm{f}D_s^+D_s^- \rightarrow \psi (4040)}$. The flavor matrix elements for $K{\bar{K}} \rightarrow \phi$, $\pi D \rightarrow D^*$, and $\pi {\bar{D}} \rightarrow {\bar{D}}^*$ are zero for the two lower diagrams, and those for the production of $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ are zero for the two upper diagrams. Hence, every reaction receives contributions only from two Feynman diagrams.

Now we give the spin matrix elements. Let $P_{rq_1{\bar{q}}_2{\bar{q}}_1i}$ with $i=0$, $\ldots$, and 15 stand for 1, $\sigma _1(21)$, $\sigma _2(21)$, $\sigma _3(21)$, $\sigma _1(1)$, $\sigma _2(1)$, $\sigma _3(1)$, $\sigma _1(21) \sigma _1(1)$, $\sigma _1(21) \sigma _2(1)$, $\sigma _1(21) \sigma _3(1)$, $\sigma _2(21) \sigma _1(1)$, $\sigma _2(21) \sigma _2(1)$, $\sigma _2(21) \sigma _3(1)$, $\sigma _3(21) \sigma _1(1)$, $\sigma _3(21) \sigma _2(1)$, and $\sigma _3(21) \sigma _3(1)$, respectively. Let $P_{rq_1{\bar{q}}_2q_2i}$ with $i=0$, $\ldots$, and 15 correspond to 1, $\sigma _1(21)$, $\sigma _2(21)$, $\sigma _3(21)$, $\sigma _1(2)$, $\sigma _2(2)$, $\sigma _3(2)$, $\sigma _1(21) \sigma _1(2)$, $\sigma _1(21) \sigma _2(2)$, $\sigma _1(21) \sigma _3(2)$, $\sigma _2(21) \sigma _1(2)$, $\sigma _2(21) \sigma _2(2)$, $\sigma _2(21) \sigma _3(2)$, $\sigma _3(21) \sigma _1(2)$, $\sigma _3(21) \sigma _2(2)$, and $\sigma _3(21) \sigma _3(2)$, respectively. Let $P_{rq_2{\bar{q}}_1q_1i}$ with $i=0$, $\ldots$, and 15 represent 1, $\sigma _1(12)$, $\sigma _2(12)$, $\sigma _3(12)$, $\sigma _1(1)$, $\sigma _2(1)$, $\sigma _3(1)$, $\sigma _1(12) \sigma _1(1)$, $\sigma _1(12) \sigma _2(1)$, $\sigma _1(12) \sigma _3(1)$, $\sigma _2(12) \sigma _1(1)$, $\sigma _2(12) \sigma _2(1)$, $\sigma _2(12) \sigma _3(1)$, $\sigma _3(12) \sigma _1(1)$, $\sigma _3(12) \sigma _2(1)$, and $\sigma _3(12)$ $\sigma _3(1)$, respectively. Let $P_{rq_2{\bar{q}}_1{\bar{q}}_2i}$ with $i=0$, $\ldots$, and 15 denote 1, $\sigma _1(12)$, $\sigma _2(12)$, $\sigma _3(12)$, $\sigma _1(2)$, $\sigma _2(2)$, $\sigma _3(2)$, $\sigma _1(12) \sigma _1(2)$, $\sigma _1(12) \sigma _2(2)$, $\sigma _1(12) \sigma _3(2)$, $\sigma _2(12) \sigma _1(2)$, $\sigma _2(12) \sigma _2(2)$, $\sigma _2(12)$ $\sigma _3(2)$, $\sigma _3(12) \sigma _1(2)$, $\sigma _3(12) \sigma _2(2)$, and $\sigma _3(12) \sigma _3(2)$, respectively. Set $n_A$ as -1, 0, or 1, and $n_B$ as -1, 0, or 1. In order to easily tabulate values of the spin matrix elements, we define $\phi _{\mathrm{iss}} (S_A,S_{Az};S_B,S_{Bz}) \equiv \chi _{S_AS_{Az}}\chi _{S_BS_{Bz}}$ and $\phi _{\mathrm{fss}}(S_H,S_{Hz})\equiv \chi _{S_HS_{Hz}}$. The spin matrix elements $\phi ^+_{\mathrm{fss}}(S_H,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i} \phi _{\mathrm{iss}} (S_A,S_{Az};S_B,S_{Bz})$ are shown in Tables 2, 3, 4, 5 and 6. Other spin matrix elements, $\phi ^+_{\mathrm{fss}} (S_H, S_{Hz}) P_{rq_1{\bar{q}}_2q_2i} \phi _{\mathrm{iss}} (S_A, S_{Az}; S_B,$ $S_{Bz})$, $\phi ^+_{\mathrm{fss}} (S_H, S_{Hz})$ $P_{rq_2{\bar{q}}_1q_1i}$ $\phi _{\mathrm{iss}} (S_A, S_{Az}; S_B, S_{Bz})$, and $\phi ^+_{\mathrm{fss}} (S_H, S_{Hz})$ $P_{rq_2{\bar{q}}_1{\bar{q}}_2i}$ $\phi _{\mathrm{iss}} (S_A, S_{Az};$ $S_B, S_{Bz})$, are related to $\phi ^+_{\mathrm{fss}} (S_H, S_{Hz}) P_{rq_1{\bar{q}}_2{\bar{q}}_1i} \phi _{\mathrm{iss}} (S_A, S_{Az}; S_B, S_{Bz})$ by the following equations:

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2q_2i}\phi _{\mathrm{iss}} (S_A=1,S_{Az}\nonumber \\&\quad =n_A; S_B=0,S_{Bz}=0) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A=0,S_{Az}\nonumber \\&\quad =0; S_B=1,S_{Bz}=n_A) , \end{aligned}$$

(34)

with $i=2$, 5, 8, 10, 12, and 14;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2q_2i}\phi _{\mathrm{iss}} (S_A=1,S_{Az}\nonumber \\&\quad =n_A; S_B=0,S_{Bz}=0) \nonumber \\&\quad = -\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A=0,S_{Az}\nonumber \\&\quad =0; S_B=1,S_{Bz}=n_A) , \end{aligned}$$

(35)

with $i=0$, 1, 3, 4, 6, 7, 9, 11, 13, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2q_2i}\phi _{\mathrm{iss}} (S_A=0,S_{Az}\nonumber \\&\quad =0; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_B; S_B=0,S_{Bz}=0) , \end{aligned}$$

(36)

with $i=2$, 5, 8, 10, 12, and 14;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2q_2i}\phi _{\mathrm{iss}} (S_A=0,S_{Az}\nonumber \\&\quad =0; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = -\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_B; S_B=0,S_{Bz}=0) , \end{aligned}$$

(37)

with $i=0$, 1, 3, 4, 6, 7, 9, 11, 13, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2q_2i}\phi _{\mathrm{iss}} (S_A=1,S_{Az}\nonumber \\&\quad =n_A; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_B; S_B=1,S_{Bz}=n_A) , \end{aligned}$$

(38)

with $i=0$, 1, 3, 4, 6, 7, 9, 11, 13, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2q_2i}\phi _{\mathrm{iss}} (S_A=1,S_{Az}\nonumber \\&\quad =n_A; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = -\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_B; S_B=1,S_{Bz}=n_A) , \end{aligned}$$

(39)

with $i=2$, 5, 8, 10, 12, and 14;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1q_1i}\phi _{\mathrm{iss}} (S_A=1,S_{Az}\nonumber \\&\quad =n_A; S_B=0,S_{Bz}=0) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=0,S_{Bz}=0) , \end{aligned}$$

(40)

with $i=2$, 5, 8, 10, 12, and 14;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1q_1i}\phi _{\mathrm{iss}} (S_A=1,S_{Az}\nonumber \\&\quad =n_A; S_B=0,S_{Bz}=0) \nonumber \\&\quad = -\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=0,S_{Bz}=0) , \end{aligned}$$

(41)

with $i=0$, 1, 3, 4, 6, 7, 9, 11, 13, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1q_1i}\phi _{\mathrm{iss}} (S_A=0,S_{Az}\nonumber \\&\quad =0; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =0,S_{Az}=0; S_B=1,S_{Bz}=n_B) , \end{aligned}$$

(42)

with $i=2$, 5, 8, 10, 12, and 14;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1q_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =0,S_{Az}=0; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = -\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =0,S_{Az}=0; S_B=1,S_{Bz}=n_B) , \end{aligned}$$

(43)

with $i=0$, 1, 3, 4, 6, 7, 9, 11, 13, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1q_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=1,S_{Bz}=n_B) , \end{aligned}$$

(44)

with $i=0$, 1, 3, 4, 6, 7, 9, 11, 13, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1q_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = -\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=1,S_{Bz}=n_B) , \end{aligned}$$

(45)

with $i=2$, 5, 8, 10, 12, and 14;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1{\bar{q}}_2i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=0,S_{Bz}=0) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =0,S_{Az}=0; S_B=1,S_{Bz}=n_A) , \end{aligned}$$

(46)

with $i=0$, $\ldots$, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1{\bar{q}}_2i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =0,S_{Az}=0; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_B; S_B=0,S_{Bz}=0) , \end{aligned}$$

(47)

with $i=0$, $\ldots$, and 15;

$$\begin{aligned}&\phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_2{\bar{q}}_1{\bar{q}}_2i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_A; S_B=1,S_{Bz}=n_B) \nonumber \\&\quad = \phi ^+_{\mathrm{fss}}(S_H=1,S_{Hz})P_{rq_1{\bar{q}}_2{\bar{q}}_1i}\phi _{\mathrm{iss}} (S_A\nonumber \\&\quad =1,S_{Az}=n_B; S_B=1,S_{Bz}=n_A) , \end{aligned}$$

(48)

with $i=0$, $\ldots$, and 15.

Table 2 Spin matrix elements in ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$ for $A(S_A=1)+B(S_B=0) \rightarrow H(S_H=1)$

Table 3 Spin matrix elements in ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$ for $A(S_A=0)+B(S_B=1) \rightarrow H(S_H=1)$

Table 4 Spin matrix elements in ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$ for $A(S_A=1)+B(S_B=1) \rightarrow H(S_H=1)$ with $S_{Hz}=-1$

Table 5 Spin matrix elements in ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$ for $A(S_A=1)+B(S_B=1) \rightarrow H(S_H=1)$ with $S_{Hz}=0$

Table 6 Spin matrix elements in ${{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$ for $A(S_A=1)+B(S_B=1) \rightarrow H(S_H=1)$ with $S_{Hz}=1$

4 Numerical cross sections and discussions

The mesonic quark–antiquark relative-motion wave functions $\phi _{A\mathrm{rel}}$, $\phi _{B\mathrm{rel}}$, and $\phi _{J_HJ_{Hz}}$ in Eqs. (6) and (7) are solutions of the Schrödinger equation with the potential between constituents a and b in coordinate space [49],

$$\begin{aligned} V_{ab}(\vec {r}_{ab})= & {} - \frac{\vec {\lambda }_a}{2} \cdot \frac{\vec {\lambda }_b}{2} \xi _1 \left[ 1.3- \left( \frac{T}{T_{\mathrm{c}}} \right) ^4 \right] \tanh (\xi _2 r_{ab}) \nonumber \\&+ \frac{\vec {\lambda }_a}{2} \cdot \frac{\vec {\lambda }_b}{2} \frac{6\pi }{25} \frac{v(\lambda r_{ab})}{r_{ab}} \exp (-\xi _3 r_{ab}) \nonumber \\&-\frac{\vec {\lambda }_a}{2} \cdot \frac{\vec {\lambda }_b}{2} \frac{16\pi ^2}{25}\frac{d^3}{\pi ^{3/2}}\exp (-d^2r^2_{ab}) \frac{\vec {s}_a \cdot \vec {s}_b}{m_am_b} \nonumber \\&+\frac{\vec {\lambda }_a}{2} \cdot \frac{\vec {\lambda }_b}{2}\frac{4\pi }{25} \frac{1}{r_{ab}} \frac{d^2v(\lambda r_{ab})}{dr_{ab}^2} \frac{\vec {s}_a \cdot \vec {s}_b}{m_am_b} \nonumber \\&-\frac{\vec {\lambda }_a}{2} \cdot \frac{\vec {\lambda }_b}{2} \frac{6\pi }{25m_am_b}\left[ v(\lambda r_{ab}) -r_{ab}\frac{dv(\lambda r_{ab})}{dr_{ab}} \right. \nonumber \\&\left. +\frac{r_{ab}^2}{3} \frac{d^2v(\lambda r_{ab})}{dr_{ab}^2} \right] \nonumber \\&\times \left( \frac{3\vec {s}_a \cdot \vec {r}_{ab}\vec {s}_b \cdot \vec {r}_{ab}}{r_{ab}^5} -\frac{\vec {s}_a \cdot \vec {s}_b}{r_{ab}^3} \right) , \end{aligned}$$

(49)

where $\xi _1=0.525$ GeV, $\xi _3=0.6$ GeV, $T_{\mathrm{c}}=0.175$ GeV, $\xi _2=1.5[0.75+0.25 (T/{T_{\mathrm{c}}})^{10}]^6$ GeV, and $\lambda =\sqrt{25/16\pi ^2 \alpha '}$ with $\alpha '=1.04$ $\hbox {GeV}^{-2}$; T is the temperature; $\vec {s}_a$ is the spin of constituent a; the quantity d is given in Ref. [49]; the function v is given by Buchmüller and Tye in Ref. [40]. The potential is obtained from perturbative QCD [40] and lattice QCD [50]. The masses of the up quark, the down quark, the strange quark, and the charm quark are 0.32 GeV, 0.32 GeV, 0.5 GeV, and 1.51 GeV, respectively. Solving the Schrödinger equation with the potential at zero temperature, we obtain meson masses that are close to the experimental masses of $\pi$, $\rho$, K, $K^*$, $J/\psi$, $\chi _{c}$, $\psi '$, $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, $\psi (4415)$, D, $D^*$, $D_s$, and $D^*_s$ mesons [51]. Moreover, the experimental data of S-wave and P-wave elastic phase shifts for $\pi \pi$ scattering in vacuum [52,53,54,55,56,57,58,59,60,61,62,63,64] are reproduced in the Born approximation [25, 49].

Gluon, quark, and antiquark fields in the thermal medium depend on its temperature. The interaction between two constituents is influenced by gluons, quarks, and antiquarks in the thermal medium, and thus depends on the temperature. The quark–antiquark potential is related to the Polyakov loop correlation function defined from the gluon field, the quark field, and the antiquark field, and has been obtained in lattice gauge calculations. When the temperature is low, the potential at large distances is modified by the medium. When the temperature is near the critical temperature $T_{\mathrm{c}}$, the potential at intermediate distances is also modified. The lattice gauge calculations [50] only provide a numerical spin-independent and temperature-dependent potential at intermediate and large distances. When the distance increases from zero, the numerical potential increases, and obviously becomes a distance-independent value (exhibits a plateau) at large distances at $T>0.55T_{\mathrm{c}}$. The plateau height decreases with increasing temperature. This means that confinement becomes weaker and weaker. The short-distance part of the first two terms in Eq. (49) originates from one-gluon exchange plus perturbative one- and two-loop corrections, and the intermediate-distance and large-distance part fits well the numerical potential. The third and fourth terms indicate the spin–spin interaction with relativistic effects, and the fifth term is the tensor interaction, which are obtained from an application of the Foldy–Wouthuysen canonical transformation to the gluon propagator with perturbative one- and two-loop corrections [65]. The potential in Eq. (49) is valid when the temperature is below the critical temperature.

In Eq. (49) $\xi _1$ is fixed, but the values of $\xi _2$ and $\xi _3$ are not unique; $\xi _2$ is allowed to change by at most 5%, and $\xi _3$ by at most 10% while the numerical potential obtained in the lattice gauge calculations can be well fitted. However, an increase (decrease) of $\xi _2$ must be accompanied by a decrease (increase) of $\xi _3$. The uncertainties of $\xi _2$ and $\xi _3$ cause a change less than 2.7% in meson mass, a change less than 3.6% in cross section, and a change less than 4.3% in decay width.

From the transition potentials, the color matrix elements, the flavor matrix elements, the spin matrix elements, and the mesonic quark–antiquark relative-motion wave functions, we calculate the transition amplitudes. As seen in Eq. (8), the development in spherical harmonics contains the summation over the orbital-angular-momentum quantum number $L_{\mathrm{i}}$ that labels the relative motion between mesons A and B. However, not all orbital-angular-momentum quantum numbers are allowed. The orbital-angular-momentum quantum numbers are selected to satisfy parity conservation and $J=J_H$, i.e., the total angular momentum of the two initial mesons equals the total angular momentum of meson H. The choice of $L_{\mathrm{i}}$ thus depends on the total spin S of the two initial mesons. From the transition amplitudes we get unpolarized cross sections at zero temperature. The selected orbital-angular-momentum quantum numbers and the cross sections are shown in Tables 7 and 8. The processes $D^*{\bar{D}}^*\rightarrow \psi (4040)$, $D^*{\bar{D}}^*\rightarrow \psi (4160)$, $D^*{\bar{D}}^*\rightarrow \psi (4415)$, and $D^{*+}_s D^{*-}_s \rightarrow \psi (4415)$ allow $S=0$, $S=1$, and $S=2$. Including contributions from $S=0$, $S=1$, and $S=2$, the cross sections for the four reactions are 0.42 mb, 0.57 mb, 1.39 mb, and 0.11 mb, respectively. When $L_{\mathrm{i}}=1$ is selected, the partial wave for $L_{\mathrm{i}}=1$ in Eq. (8) is normalized as

$$\begin{aligned} 4\pi \mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid i j_1 (\mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid r_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) Y_{1M_{\mathrm{i}}} ({\hat{r}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}). \end{aligned}$$

When $L_{\mathrm{i}}=1$ and $L_{\mathrm{i}}=3$ are selected together, the partial waves for $L_{\mathrm{i}}=1$ and $L_{\mathrm{i}}=3$ are normalized as

$$\begin{aligned}&4\pi \mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid i j_1 (\mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid r_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) \\&\quad \times \sum \limits _{M_{\mathrm{i}}=-1}^1 Y_{1M_{\mathrm{i}}} ({\hat{r}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) \sqrt{\frac{4\pi }{10}} Y_{1M_{\mathrm{i}}}^*({\hat{p}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) \\&\quad +4\pi \mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid i^3 j_3 (\mid \vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \mid r_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) \\&\quad \times \sum \limits _{M_{\mathrm{i}}=-3}^3 Y_{3M_{\mathrm{i}}} ({\hat{r}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}) \sqrt{\frac{4\pi }{10}} Y_{3M_{\mathrm{i}}}^*({\hat{p}}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}). \end{aligned}$$

In Table 7 the cross section for $K{\bar{K}} \rightarrow \phi$ equals 8.05 mb. The magnitude 8.05 mb is larger than the peak cross section of $K{\bar{K}} \rightarrow K^*{\bar{K}}^*$ for total isospin $I=0$ at zero temperature, and is roughly 8 times the peak cross section of $K{\bar{K}} \rightarrow K^*{\bar{K}}^*$ for $I=1$ in Ref. [25]. The case $K{\bar{K}} \rightarrow K^*{\bar{K}}^*$ may be caused by a process where a quark in an initial meson and an antiquark in another initial meson annihilate into a gluon and subsequently the gluon creates another quark–antiquark pair. The magnitude is much larger than the peak cross sections of $K{\bar{K}} \rightarrow \pi K {{\bar{K}}}$ for I=1 and $I_{\pi {{\bar{K}}}}^{\mathrm{f}}=3/2$ and for I=1 and $I_{\pi {{\bar{K}}}}^{\mathrm{f}}=1/2$ at zero temperature in Refs. [66, 67], where $I_{\pi {{\bar{K}}}}^{\mathrm{f}}$ is the total isospin of the final $\pi$ and ${{\bar{K}}}$ mesons. The case $K{\bar{K}} \rightarrow \pi K {{\bar{K}}}$ is governed by a process where a gluon is emitted by a constituent quark or antiquark in the initial mesons and subsequently the gluon creates a quark–antiquark pair. The magnitude is also much larger than the peak cross section of $KK \rightarrow K^*K^*$ for $I=1$ at zero temperature in Ref. [68]. The case $KK \rightarrow K^*K^*$ for $I=1$ can be caused by quark interchange between the two colliding mesons. The cross section for $\pi D \rightarrow D^*$ is particularly large. This means that the reaction easily happens. The large cross section is caused by the very small difference between the $D^*$ mass and the sum of the $\pi$ and D masses.

Table 7 Total spin, orbital-angular-momentum quantum number, and cross section

Table 8 The same as Table 7

The transition potentials involve quark masses. The charm-quark mass is larger than the strange-quark mass, and the transition potentials with the charm quark are smaller than the ones with the strange quark. The cross sections for $D{\bar{D}} \rightarrow \psi (3770)$, $D{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, and $D{\bar{D}} \rightarrow \psi (4415)$ are thus smaller than the one for $K{\bar{K}} \rightarrow \phi$. Because the $D^*$ radius is larger than the D radius, the cross sections for $D^*{\bar{D}} \rightarrow \psi (4040)$, $D^*{\bar{D}} \rightarrow \psi (4160)$, and $D^*{\bar{D}} \rightarrow \psi (4415)$ are larger than those for $D{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, and $D{\bar{D}} \rightarrow \psi (4415)$, respectively. However, the cross sections for $D^*{\bar{D}}^* \rightarrow \psi (4040)$, $D^*{\bar{D}}^* \rightarrow \psi (4160)$, and $D^*{\bar{D}}^* \rightarrow \psi (4415)$ are smaller than those for $D^*{\bar{D}} \rightarrow \psi (4040)$, $D^*{\bar{D}} \rightarrow \psi (4160)$, and $D^*{\bar{D}} \rightarrow \psi (4415)$, respectively. This is caused by the two nodes of $\psi (4040)$, the node of $\psi (4160)$, and the three nodes of $\psi (4415)$ in the radial part of the quark–antiquark relative-motion wave function. The radial wave function on the left of a node has a sign different from the one on the right of the node. The nodes lead to cancellation between the positive radial wave function and the negative radial wave function in the integration involved in the transition amplitudes. Since $D^+_s$ (the antiparticle of $D^-_s$) consists of a charm quark and a strange antiquark, the cross sections for $D^+_s D^-_s \rightarrow \psi (4040)$, $D^+_s D^-_s \rightarrow \psi (4160)$, and $D^+_s D^-_s \rightarrow \psi (4415)$ are smaller than the ones for $D{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, and $D{\bar{D}} \rightarrow \psi (4415)$, respectively.

Fig. 2

K and $\phi$ masses as functions of $T/T_{\mathrm{c}}$

In the present work the $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons come from fusion of D, ${{\bar{D}}}$, $D^*$, ${\bar{D}}^*$, $D_s$, and $D^*_s$ mesons. The reason why we are interested in these reactions is that $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ may decay into $J/\psi ,$ which is an important probe of the quark–gluon plasma produced in ultrarelativistic heavy-ion collisions. We do not investigate the $\chi _{c0}(2P)$ and $\chi _{c2}(2P)$ mesons because they cannot decay into the $J/\psi$ meson. The $\chi _{c1}(2P)$ meson may decay into the $J/\psi$ meson, but $D {\bar{D}} \rightarrow \chi _{c1}(2P)$ allowed by energy conservation does not simultaneously satisfy the parity conservation and the conservation of the total angular momentum. Therefore, we do not consider $D {\bar{D}} \rightarrow \chi _{c1}(2P)$. The production of $\chi _{c1}(2P)$ from fusion of other charmed mesons is forbidden by energy conservation. Also $\pi D^{\pm }_s \rightarrow D^{*\pm }_s$ is not allowed because of violation of isospin conservation, and $K D \rightarrow D^{*+}_s$ and ${\bar{K}} {\bar{D}} \rightarrow D^{*-}_s$ because of violation of energy conservation.

Fig. 3

$\pi$, D, and $D^*$ masses as functions of $T/T_{\mathrm{c}}$

As seen in Eq. (49), the potential between two constituents depends on temperature. The meson mass obtained from the Schrödinger equation with the potential thus depends on temperature. The temperature dependence of meson masses is shown in Figs. 2, 3, 4 and 5. In vacuum the $\phi$ mass is larger than two times the kaon mass, and so the reaction $K{\bar{K}} \rightarrow \phi$ takes place. Since the $\phi$ mass in Fig. 2 decreases faster than the kaon mass with increasing temperature, the $\phi$ mass turns smaller than two times the kaon mass. The reaction thus no longer occurs in the temperature region $0.6T_{\mathrm{c}}\le T <T_{\mathrm{c}}$. In Fig. 3 the $D^*$ mass decreases faster than the pion and D masses, and the $D^*$ mass is smaller than the sum of the pion mass and the D mass. The processes $\pi D \rightarrow D^*$ and $\pi {\bar{D}} \rightarrow {\bar{D}}^*$ also do not occur for $0.6T_{\mathrm{c}}\le T <T_{\mathrm{c}}$. The mesons $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ are dissolved in hadronic matter when the temperature is larger than $0.97T_{\mathrm{c}}$, $0.95T_{\mathrm{c}}$, and $0.87T_{\mathrm{c}}$, respectively [69]. Their masses are thus plotted only for $0.6T_{\mathrm{c}}\le T < 0.97T_{\mathrm{c}}$, for $0.6T_{\mathrm{c}}\le T < 0.95T_{\mathrm{c}}$, and for $0.6T_{\mathrm{c}}\le T < 0.87T_{\mathrm{c}}$ in Figs. 4 and 5, and are smaller than the sum of the masses of the two initial mesons that yield them. Therefore, in hadronic matter where the temperature is constrained by $0.6T_{\mathrm{c}}\le T < T_{\mathrm{c}}$, we cannot see the production of $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ from the fusion of two charmed mesons and of two charmed strange mesons. Here $T_{\mathrm{c}}$ is the critical temperature at which the phase transition between the quark–gluon plasma and hadronic matter takes place. Since $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ are dissolved in hadronic matter when the temperature is larger than $0.97T_{\mathrm{c}}$, $0.95T_{\mathrm{c}}$, and $0.87T_{\mathrm{c}}$, respectively, they cannot be produced in the phase transition, but they can be produced in the following reactions in hadronic matter:

$$\begin{aligned}&D {\bar{D}} \rightarrow \rho R; ~D {\bar{D}}^* \rightarrow \pi R,~\rho R, \eta R;\\&\quad D^* {\bar{D}} \rightarrow \pi R, \rho R, \eta R; ~D^* {\bar{D}}^* \rightarrow \pi R, \rho R, \eta R; \\&D_s^+ {\bar{D}} \rightarrow K^*R; ~D_s^- D \rightarrow {\bar{K}}^*R; ~D_s^+ {\bar{D}}^* \rightarrow K R, K^*R; \\&\quad D_s^- D^* \rightarrow {\bar{K}} R, {\bar{K}}^*R; \\&D_s^{*+} {\bar{D}} \rightarrow K R, K^*R; ~D_s^{*-} D \rightarrow {\bar{K}} R, {\bar{K}}^*R; \\&\quad D_s^{*+} {\bar{D}}^* \rightarrow K R, K^*R; ~D_s^{*-} D^* \rightarrow {\bar{K}} R, {\bar{K}}^*R; \\&D_s^+ D_s^- \rightarrow \phi R; ~D_s^+ D_s^{*-} \rightarrow \eta R, \phi R;\\&\quad D_s^{*+} D_s^- \rightarrow \eta R, \phi R; ~D_s^{*+} D_s^{*-} \rightarrow \eta R, \phi R. \end{aligned}$$

In these reactions R stands for $\psi (4040)$, $\psi (4160)$, or $\psi (4415)$. Hadronic matter undergoes expansion, and its temperature decreases until kinetic freeze-out occurs. Every kind of hadron in hadronic matter satisfies a momentum distribution function. The temperature, the expansion, and the momentum distribution functions are needed for a full description of hadronic matter. The $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons produced from hadronic matter depend on the temperature, the expansion, and the distribution functions. Inversely, from the production we know the temperature, the expansion, and the distribution functions. Therefore, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ may provide us with information on hadronic matter, and are a probe of hadronic matter that results from the quark–gluon plasma.

No experimental data on $K{\bar{K}} \rightarrow \phi$ are available. Our cross section for $K{\bar{K}} \rightarrow \phi$ is about 8 mb, which is smaller than the experimental cross section 80 mb for $\pi \pi \rightarrow \rho$ [70]. Assuming pointlike hadron vertices, the mesonic model in Refs. [45, 46] leads to a large value of 260 mb.

From Tables 7 and 8 we get ratios of the cross sections,

$$\begin{aligned}&\sigma _{D{\bar{D}} \rightarrow \psi (4040)}: \sigma _{D^*{\bar{D}}+D{\bar{D}}^* \rightarrow \psi (4040)}:\nonumber \\&\qquad \sigma _{D^*{\bar{D}}^* \rightarrow \psi (4040)}: \sigma _{D_s^+D_s^- \rightarrow \psi (4040)} \nonumber \\&\quad = 1:4.6:0.12:0.33 , \end{aligned}$$

(50)

$$\begin{aligned}&\sigma _{D{\bar{D}} \rightarrow \psi (4160)}: \sigma _{D^*{\bar{D}}+D{\bar{D}}^* \rightarrow \psi (4160)}: \sigma _{D^*{\bar{D}}^* \rightarrow \psi (4160)}: \nonumber \\&\sigma _{D_s^+D_s^- \rightarrow \psi (4160)}: \sigma _{D_s^{*+}D_s^- + D_s^+D_s^{*-} \rightarrow \psi (4160)} \nonumber \\&\quad = 1:4.2:0.17:0.15:0.14 . \end{aligned}$$

(51)

Fig. 4

D, $D^*$, $D_s$, $D_s^*$, $\psi (3770)$, and $\psi (4160)$ masses as functions of $T/T_{\mathrm{c}}$

Fig. 5

D, $D^*$, $D_s$, $D_s^*$, $\psi (4040)$, and $\psi (4415)$ masses as functions of $T/T_{\mathrm{c}}$

In an analysis of the production of charmed mesons and charmed strange mesons in the region of $\psi (4040)$ and $\psi (4160)$ resonances in $e^+e^-$ collisions in Ref. [71], the couplings of $\psi (4040)$ and $\psi (4160)$ to two charmed mesons and charmed strange mesons are factorized. The couplings are assumed to be proportional to a coefficient (denoted as $\mathrm{g}_{Ri}$ in the reference), the values of which are listed in Table 1 of the reference. If it is assumed that cross sections for the production of $\psi (4040)$ and $\psi (4160)$ from $D{\bar{D}}$, $D^*{\bar{D}}$, $D{\bar{D}}^*$, $D^*{\bar{D}}^*$, $D_s^+D_s^-$, $D_s^{*+}D_s^-$, $D_s^+D_s^{*-}$, and $D_s^{*+}D_s^{*-}$ differ from each other only by the coefficient, then ratios of the cross sections are,

$$\begin{aligned}&\sigma _{D{\bar{D}} \rightarrow \psi (4040)}: \sigma _{D^*{\bar{D}}+D{\bar{D}}^* \rightarrow \psi (4040)}: \sigma _{D^*{\bar{D}}^* \rightarrow \psi (4040)}:\nonumber \\&\qquad \sigma _{D_s^+D_s^- \rightarrow \psi (4040)} \nonumber \\&\quad = 1:4:7:1 , \end{aligned}$$

(52)

$$\begin{aligned}&\sigma _{D{\bar{D}} \rightarrow \psi (4160)}: \sigma _{D^*{\bar{D}}+D{\bar{D}}^* \rightarrow \psi (4160)}: \sigma _{D^*{\bar{D}}^* \rightarrow \psi (4160)}: \nonumber \\&\sigma _{D_s^+D_s^- \rightarrow \psi (4160)}: \sigma _{D_s^{*+}D_s^- + D_s^+D_s^{*-} \rightarrow \psi (4160)} \nonumber \\&\quad = 1:1:7.7:1:1 . \end{aligned}$$

(53)

This assumption is correct when the $D^*$ (${\bar{D}}^*$, $D_s^{*+}$, $D_s^{*-}$) mass equals the D (${\bar{D}}$, $D_s^+$, $D_s^-$) mass. Regarding the ratios given in Eq. (52) we mention a study of production of charmed mesons in $e^+ e^-$ collisions in Ref. [72]. An electron and a positron annihilate into a photon. The photon directly produces a pair of charmed quarks, each of which becomes a charmed meson in combination with a subsequently produced u or d quark. Neglecting the difference between the D and $D^*$ masses and the spin–spin interaction between the charmed quark and the light quark, the final states $D{{\bar{D}}}$, $D^*{\bar{D}} + D{\bar{D}}^*$, and $D^*{\bar{D}}^*$ are populated in ratios 1:4:7, which agree with those given in Eq. (52). Nevertheless, the agreement does not surprise us in view of heavy quark symmetry [72,73,74,75,76]. Heavy quark symmetry is that, in the limit of very large quark mass, strong interactions of the heavy quark become independent of its mass and spin. A consequence of heavy quark symmetry is that $m_{D^*}=m_D$, $m_{{\bar{D}}^*}=m_{{{\bar{D}}}}$, and $m_{D_s^{*\pm }}=m_{D_s^{\pm }}$. Therefore, heavy quark symmetry is assumed in obtaining the ratios in Eq. (52) and in Ref. [72], and the ratios 1:4:7 are general in the transition between charmed mesons and $c{{\bar{c}}}$ in heavy quark symmetry.

Cross sections for the production of $\psi (4040)$ from the fusion of two charmed mesons are proportional to not only the couplings squared but also the factor $\frac{1}{\sqrt{(P_A \cdot P_B)^2 -m_A^2m_B^2}}$ as seen in Eq. (29). When the colliding mesons go through the cases of $D{\bar{D}}$, $D^*{\bar{D}}$, and $D^*{\bar{D}}^*$, the factor does not change in heavy quark symmetry, but changes if the $D^*$ mass is not the same as the D mass. The latter causes $\sigma _{D{\bar{D}} \rightarrow \psi (4040)}: \sigma _{D^*{\bar{D}}+D{\bar{D}}^* \rightarrow \psi (4040)}: \sigma _{D^*{\bar{D}}^* \rightarrow \psi (4040)}$ to deviate from the general ratios 1:4:7.

We have obtained cross sections for the production of $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ from the fusion of two charmed mesons and of two charmed strange mesons. As seen from the Review of Particle Physics in Ref. [51], time reversal of these reactions dominate decays of the four $c{{\bar{c}}}$ mesons. We study the decays in terms of the process where a gluon is emitted by a constituent quark or antiquark in the initial mesons and subsequently the gluon creates a quark–antiquark pair. This part is given in the Appendix.

5 Summary

Using the process where one quark annihilates with one antiquark to create a gluon and subsequently the gluon is absorbed by a spectator quark or antiquark, we have studied 2-to-1 meson–meson scattering. In the partial wave expansion of the relative-motion wave function of the two initial mesons, we have obtained the new expressions of the transition amplitudes. The orbital-angular-momentum quantum number corresponding to the total spin of the two initial mesons is selected to satisfy parity conservation and conservation of the total angular momentum. The flavor and spin matrix elements have been calculated. The spin matrix elements corresponding to the four transition potentials are presented. The mesonic quark–antiquark relative-motion wave functions are given by the Schrödinger equation with the temperature-dependent potential. From the transition amplitudes we have obtained the cross sections for the reactions: $K{\bar{K}} \rightarrow \phi$, $\pi D \rightarrow D^*$, $\pi {\bar{D}} \rightarrow {\bar{D}}^*$, $D{\bar{D}} \rightarrow \psi (3770)$, $D{\bar{D}} \rightarrow \psi (4040)$, $D^*{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}}^* \rightarrow \psi (4040)$, $D^*{\bar{D}}^* \rightarrow \psi (4040)$, $D_s^+D_s^- \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, $D^*{\bar{D}} \rightarrow \psi (4160)$, $D{\bar{D}}^* \rightarrow \psi (4160)$, $D^*{\bar{D}}^* \rightarrow \psi (4160)$, $D_s^+D_s^- \rightarrow \psi (4160)$, $D_s^{*+}D_s^- \rightarrow \psi (4160)$, $D_s^+D_s^{*-} \rightarrow \psi (4160)$, $D{\bar{D}} \rightarrow \psi (4415)$, $D^*{\bar{D}} \rightarrow \psi (4415)$, $D{\bar{D}}^* \rightarrow \psi (4415)$, $D^*{\bar{D}}^* \rightarrow \psi (4415)$, $D_s^+D_s^- \rightarrow \psi (4415)$, $D_s^{*+}D_s^- \rightarrow \psi (4415)$, $D_s^+D_s^{*-} \rightarrow \psi (4415)$, and $D_s^{*+}D_s^{*-} \rightarrow \psi (4415)$. The cross sections are affected by radii of initial mesons and quark masses that enter the transition potentials. The cross section for $K{\bar{K}} \rightarrow \phi$ is larger than the ones for $D{\bar{D}} \rightarrow \psi (3770)$, $D{\bar{D}} \rightarrow \psi (4040)$, $D{\bar{D}} \rightarrow \psi (4160)$, and $D{\bar{D}} \rightarrow \psi (4415)$, but smaller than the one for $\pi D \rightarrow D^*$. The $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ mesons resulting from ultrarelativistic heavy-ion collisions have been shown to be a probe of hadronic matter that is produced in the phase transition of the quark–gluon plasma.

Appendix

Fig. 6

Decay $Z \rightarrow X+Y$. Solid lines with right (left) triangles stand for quarks (antiquarks). Wavy lines stand for gluons

We calculate widths of the $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ decays, which produce two charmed mesons or two charmed strange mesons. Four Feynman diagrams at tree level are involved in $Z \rightarrow X+Y$, and are shown in Fig. 6. The two upper diagrams correspond to $Z(q_2{\bar{q}}_1) \rightarrow X(q_1{\bar{q}}_1)+Y(q_2{\bar{q}}_2)$, and the two lower diagrams $Z(q_1{\bar{q}}_2) \rightarrow X(q_1{\bar{q}}_1)+Y(q_2{\bar{q}}_2)$. Denote by $\psi _Z$ and $\psi _{XY}$ the mesonic quark–antiquark wave functions of meson Z and of mesons X and Y, respectively. Let $(E_X, \vec {p}_X)$, $(E_Y, \vec {p}_Y)$, and $(E_Z, \vec {p}_Z)$ be the four-momenta of mesons X, Y, and Z, respectively. The transition amplitudes corresponding to the left upper diagram, the right upper diagram, the left lower diagram, and the right lower diagram are given by

$$\begin{aligned} {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_1}= & {} \sqrt{2E_Z2E_X2E_Y} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _{XY}^+\nonumber \\&\times V_{\mathrm{c}{\bar{q}}_1} \psi _Z e^{-i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(54)

$$\begin{aligned} {{\mathcal {M}}}_{\mathrm{c}q_2}= & {} \sqrt{2E_Z2E_X2E_Y} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _{XY}^+\nonumber \\&\times V_{\mathrm{c}q_2} \psi _Z e^{-i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(55)

$$\begin{aligned} {{\mathcal {M}}}_{\mathrm{c}q_1}= & {} \sqrt{2E_Z2E_X2E_Y} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _{XY}^+\nonumber \\&\times V_{\mathrm{c}q_1} \psi _Z e^{-i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(56)

$$\begin{aligned} {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_2}= & {} \sqrt{2E_Z2E_X2E_Y} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _{XY}^+\nonumber \\&\times V_{\mathrm{c}{\bar{q}}_2} \psi _Z e^{-i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}}, \end{aligned}$$

(57)

where $V_{\mathrm{c}{\bar{q}}_1}$, $V_{\mathrm{c}q_2}$, $V_{\mathrm{c}q_1}$, and $V_{\mathrm{c}{\bar{q}}_2}$ are the transition potentials for the processes where a gluon is emitted by a constiutent quark or antiquark in the initial mesons and subsequently the gluon creates a quark–antiquark pair, and are given in Eqs. (51) and (52) of Ref. [66]. The two upper diagrams give ${\bar{q}}_1(p_{{\bar{q}}_1}^\prime ) +q_2(p_{q_2}^\prime ) \rightarrow q_1(p_{q_1})+{\bar{q}}_1(p_{{\bar{q}}_1})+q_2(p_{q_2}) +{\bar{q}}_2(p_{{\bar{q}}_2})$, and the two lower diagrams $q_1(p_{q_1}^\prime ) +{\bar{q}}_2(p_{{\bar{q}}_2}^\prime ) \rightarrow q_1(p_{q_1})+{\bar{q}}_1(p_{{\bar{q}}_1})+q_2(p_{q_2}) +{\bar{q}}_2(p_{{\bar{q}}_2})$. We have $V_{\mathrm{c}{\bar{q}}_1}=V_{\mathrm{r}q_1{\bar{q}}_2{\bar{q}}_1}$, $V_{\mathrm{c}q_2}=V_{\mathrm{r}q_1{\bar{q}}_2q_2}$, $V_{\mathrm{c}q_1}=V_{\mathrm{r}q_2{\bar{q}}_1q_1}$, and $V_{\mathrm{c}{\bar{q}}_2}=V_{\mathrm{r}q_2{\bar{q}}_1{\bar{q}}_2}$.

Table 9 Decay modes and decay widths of $\psi (3770)$, $\psi (4040)$, and $\psi (4160)$

Table 10 $\psi (4415)$ decay modes and decay widths

The transition amplitudes squared are given by

$$\begin{aligned} \mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_1} \mid ^2= & {} \mid \sqrt{2E_X2E_Y2E_Z} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _Z^+ \nonumber \\&V_{\mathrm{c}{\bar{q}}_1} \psi _{XY} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}} \mid ^2, \end{aligned}$$

(58)

$$\begin{aligned} \mid {{\mathcal {M}}}_{\mathrm{c}q_2} \mid ^2= & {} \mid \sqrt{2E_X2E_Y2E_Z} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _Z^+\nonumber \\&V_{\mathrm{c}q_2} \psi _{XY} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}} \mid ^2, \end{aligned}$$

(59)

$$\begin{aligned} \mid {{\mathcal {M}}}_{\mathrm{c}q_1} \mid ^2= & {} \mid \sqrt{2E_X2E_Y2E_Z} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _Z^+\nonumber \\&V_{\mathrm{c}q_1} \psi _{XY} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}} \mid ^2, \end{aligned}$$

(60)

$$\begin{aligned} \mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_2} \mid ^2= & {} \mid \sqrt{2E_X2E_Y2E_Z} \int d\vec {r}_{q_1{\bar{q}}_1} d\vec {r}_{q_2{\bar{q}}_2} \psi _Z^+\nonumber \\&V_{\mathrm{c}{\bar{q}}_2} \psi _{XY} e^{i\vec {p}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2} \cdot \vec {r}_{q_1{\bar{q}}_1,q_2{\bar{q}}_2}} \mid ^2. \end{aligned}$$

(61)

It is obvious that $\mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_1} \mid ^2$, $\mid {{\mathcal {M}}}_{\mathrm{c}q_2} \mid ^2$, $\mid {{\mathcal {M}}}_{\mathrm{c}q_1} \mid ^2$, and $\mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_2} \mid ^2$ equal $\mid {{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 {\bar{q}}_1} \mid ^2$, $\mid {{\mathcal {M}}}_{\mathrm{r}q_1{\bar{q}}_2 q_2} \mid ^2$, $\mid {{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 q_1} \mid ^2$, and $\mid {{\mathcal {M}}}_{\mathrm{r}q_2 {\bar{q}}_1 {\bar{q}}_2} \mid ^2$, respectively. Therefore, Eqs. (22) and (26)-(28) can be used to calculate $\mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_1} \mid ^2$, $\mid {{\mathcal {M}}}_{\mathrm{c}q_2} \mid ^2$, $\mid {{\mathcal {M}}}_{\mathrm{c}q_1} \mid ^2$, and $\mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_2} \mid ^2$.

The transition amplitudes lead to the decay width for $Z \rightarrow X+Y$:

$$\begin{aligned} W= & {} \frac{1}{2J_Z+1}\int \frac{d^3p_X}{(2\pi )^3}\frac{d^3p_Y}{(2\pi )^3} \frac{(2\pi )^4\delta (E_X+E_Y-E_Z)\delta ^3 (\vec {p}_X+\vec {p}_Y-\vec {p}_Z)}{2E_X2E_Y2E_Z} \nonumber \\&\times \sum \limits _{J_{Zz}J_{Xz}J_{Yz}} \mid {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_1} + {{\mathcal {M}}}_{\mathrm{c}q_2} + {{\mathcal {M}}}_{\mathrm{c}q_1} + {{\mathcal {M}}}_{\mathrm{c}{\bar{q}}_2} \mid ^2 . \end{aligned}$$

(62)

where $J_i$ ($i=Z$, X, Y) is the total angular momentum of meson i with its magnetic projection quantum number $J_{iz}$. In Tables 9, 10 decay widths are shown for the $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ decays that produce charmed mesons or charmed strange mesons. The decay width for $\psi (3770) \rightarrow D{\bar{D}}$ is 18 MeV compared to the experimental value $25.3\pm 0.09$ MeV. The total widths of the $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ decays listed in the Review of Particle Physics [51] are $80\pm 10$ MeV, $70\pm 10$ MeV, and $62\pm 20$ MeV, respectively, but the partial widths for the $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ decays to charmed mesons or charmed strange mesons have not been given. However, since the $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ decays mainly produce charmed mesons and charmed strange mesons, the measured total widths of the $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$ decays may be compared to 70.2 MeV as the sum of the five $\psi (4040)$ partial widths, 63.3 MeV as the sum of the seven $\psi (4160)$ partial widths, and 61 MeV as the sum of the eight $\psi (4415)$ partial widths. We note that our partial widths differ from those obtained in the $^3P_0$ model in Ref. [42].