Is X(7200) the heavy anti-quark diquark symmetry partner of X(3872)?

Abstract

The $D^{(*)}\Xi _{cc}^{(*)}$ system and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system can be related to the $D^{(*)}{\bar{D}}^{(*)}$ system via heavy anti-quark di-quark symmetry (HADS). In this work, we employ a contact-range effective field theory to systematically investigate the likely existence of molecules in these systems in terms of the hypothesis that X(3872) is a $1^{++}~D{\bar{D}}^{*}$ bound state in the isospin symmetry limit, with some of the unknown low energy constants estimated using the light-meson saturation approximation. In the meson–meson system, a $J^{PC}=2^{++}~{\bar{D}}^{*}D^{*}$ molecule commonly referred to as X(4013) is reproduced, which is the heavy quark spin partner of X(3872). In the meson-baryon system, we predict two triply charmed pentaquark molecules, $J^{P}=1/2^{-}~D^{*}\Xi _{cc}$ and $J^{P}=5/2^{-}~D^{*}\Xi _{cc}^{*}$. In the baryon-baryon system, there exist seven di-baryon molecules, $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$, $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}$, $J^{PC}=1^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=2^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=2^{-+}~{\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$, and $J^{PC}=3^{--}~{\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$. Among them, the $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$ molecule may contribute to the X(7200) state recently observed by the LHCb Collaboration, which implies that X(7200) can be related to X(3872) via HADS. As a byproduct, with the heavy quark flavor symmetry we also study likely existence of molecular states in the $B^{(*)}{\bar{B}}^{(*)}$, ${\bar{B}}^{(*)}\Xi _{bb}^{(*)}$, and ${\bar{\Xi }}_{bb}^{(*)}\Xi _{bb}^{(*)}$ systems.

1 Introduction

Hadrons can be classified either as mesons made of a pair of quark and antiquark or as baryons made of three quarks in the conventional quark model, which has been rather successful at least up to 2003. According to the quark model [1], more complicated quark configurations, such as multiquark states, should also exist, which are also allowed by Quantum Chromodynamics(QCD). In recent years a lot of XYZ and $P_{c}$ states that can not easily fit into the conventional quark model were discovered by many collaborations all over the world, which not only challenges the conventional quark model but also opens a new era for hadron physics [2,3,4,5,6].

In 2003, the Belle Collaboration reported a resonant state, X(3872), in the $J/\psi \pi ^{+}\pi ^{-}$ invariant mass spectrum of the $B\rightarrow J/\psi \pi ^{+}\pi ^{-} K$ decay [7], which has later been confirmed by other collaborations [8,9,10,11,12,13]. Its spin-parity was determined by the LHCb Collaboration in 2013 [14]. Being close to the mass threshold of $D{\bar{D}}^{*}$, it is naturally considered to be a hadronic molecule. In addition, another convincing evidence of the molecular nature of X(3872) is its isospin breaking decays into $J/\Psi \pi \pi$ and $J/\Psi \pi \pi \pi$ [15, 16]. A series of theoretical works interpreted X(3872) as a $J^{PC}=1^{++}~{\bar{D}}D^{*}$ molecule [17,18,19,20,21,22,23,24,25]. Although the molecular interpretation seems to be the most popular, its nature has not been completely unveiled.¹ Nonetheless, given current experimental and theoretical results, one may conclude that the molecule components of X(3872) must play a relevant (if not dominant) role. In our previous work [25], assuming that X(3872) is a $J^{PC}=1^{++}~{\bar{D}}D^{*}$ molecule, we have used the one boson exchange model to predict the binding energies and scattering lengths of the heavy quark spin symmetry (HQSS) partners of X(3872).

HQSS plays an important role in describing the spectra of heavy hadrons including both conventional and exotic ones. The D and $D^{*}$ mesons as well as $\Sigma _{c}$ and $\Sigma _{c}^{*}$ baryons can be regarded as doublets of HQSS. Applying HQSS to their bottom partners, the mass splittings of doublets become small, which indicates that HQSS works well in the heavy quark limit. The interactions between heavy hadrons are also constrained by HQSS, which can further decrease the number of unknown couplings and increase the predictive power of effective field theories (EFT) as well. In the meson–meson system, $D_{s0}^*(2317)$ and $D_{s1}(2460)$ are assigned as DK and $D^{*}K$ hadronic molecules, respectively, belonging to a HQSS doublet [35,36,37,38,39,40,41,42]. A lot of theoretical works described $Z_{c}(3900)$ and $Z_{c}(4020)$ as isovector resonances generated by the ${\bar{D}}D^{*}$ and ${\bar{D}}^{*}D^{*}$ interactions, respectively, which indicates that $Z_{c}(3900)$ can be related to $Z_{c}(4020)$ via HQSS [23, 43, 44]. Very recently $Z_{cs}(3985)$ was proposed to be the SU(3)-flavor partner of $Z_{c}(3900)$ [45,46,47]. In the heavy meson and baryon systems, $P_{c}(4312)$, $P_{c}(4440)$, and $P_{c}(4457)$ are nicely arranged into a multiplet of ${\bar{D}}^{(*)}\Sigma _{c}^{(*)}$ hadronic molecules [48,49,50,51,52,53,54,55], and in terms of HQSS there should exist other four states which need to be confirmed by future experiments.

Heavy quark flavor symmetry has already shown its power in constructing the spectra of charmed and bottom hadrons. In short, if there exists a charmed hadron there should also exist the corresponding bottom partner. Heavy anti-quark di-quark symmetry (HADS) dictates that in terms of color degree of freedom a pair of heavy quarks can be related to a heavy antiquark in the heavy quark limit [56]. From this symmetry we can derive the following mass relation: $m_{\Xi _{cc}^{*}}-m_{\Xi _{cc}}=\frac{3}{4}(m_{D^{*}}-m_{D})$ [57]. Although this relation has not been confirmed by experiments so far, it is consistent with lattice QCD calculations and phenomenological studies [58,59,60,61]. In our previous work, we have employed HADS to extend the ${\bar{D}}^{(*)}\Sigma _{c}^{(*)}$ system to the $\Xi _{cc}^{(*)}\Sigma _{c}^{(*)}$ system, and predicted the likely existence of $\Xi _{cc}^{(*)}\Sigma _{c}^{(*)}$ bound states according to the hypothesis that $P_{c}(4440)$ and $P_{c}(4457)$ are ${\bar{D}}^{*}\Sigma _{c}$ bound states [62, 63].

Fig. 1

HADS related hidden charm tetraquark states, triply charmed pentaquark states, and hidden charmed hexaquark states

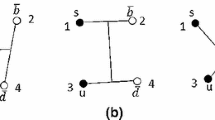
Along the line of Ref. [62], we can extend the $D^{(*)}{\bar{D}}^{(*)}$ system to the $D^{(*)}\Xi _{cc}^{(*)}$ system and then to the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system via HADS as shown in Fig. 1, and systematically investigate the likely existence of bound states in these systems using a contact-range EFT. In Refs. [23, 64] the authors have already studied the $D^{(*)}{\bar{D}}^{(*)}$ and $D^{(*)}\Xi _{cc}^{(*)}$ systems in the contact-range EFT. However, because of the existence of two unknown couplings and only one effective input, the full spectra of these two systems could not be determined. In this work we employ the light-meson saturation approach to estimate the ratio of the two couplings [65]. In our previous work [55], we found that the two couplings of the ${\bar{D}}^{(*)}\Sigma _{c}^{(*)}$ system determined by the contact-range EFT and the light-meson saturation approach are quite similar. In Ref. [66], Peng. et al used the light-meson saturation approach to estimate the contact-range potential between ${\bar{D}}\Xi _{c}$ and ${\bar{D}}\Xi _{c}^{\prime }$, yielding results consistent with the local hidden gauge approach [67, 68]. Therefore, in this work, to fully determine the mass spectra of these systems, we will combine the hypothesis that X(3872) is a $J^{PC}=1^{++}$ bound state and the light-meson saturation approach to determine the values of the only two unknown couplings $C_{a}$ and $C_{b}$, and then calculate the binding energies (if bound states exist) and scattering lengths of the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ systems.

Recently, the LHCb Collaboration reported one resonant state with a mass of 6.9 GeV in the $J/\psi$-$J/\psi$ invariant mass spectrum, labelled as X(6900). In addition, there exist two more structures, a broad one from 6.2 to 6.8 GeV and a vague structure around 7.2 GeV [69]. These tetraquark states containing fully charmed quarks undoubtedly open another new era for hadron physics since the discovery of X(3872), which has motivated a lot of theoretical studies [70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89]. Two popular interpretations of these structures are resonances generated by several coupled channels of charmonium pairs and compact tetraquark states of diquark and anti-diquark. In this work we mainly focus on the structure near 7.2 GeV, namely X(7200), whose mass is close to the mass threshold of ${\bar{\Xi }}_{cc}\Xi _{cc}$. Since the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system can be related to the ${\bar{D}}^{(*)}D^{(*)}$ system via HADS, we further explore whether there exist ${\bar{\Xi }}_{cc}\Xi _{cc}$ molecules from the hypothesis that X(3872) is a $J^{PC}=1^{++}$ bound state, in other words, whether X(7200) can be related to X(3872) via HADS.

The manuscript is structured as follows. In Sect. 2 we present the contact-range potentials of the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ systems. In Sect. 3 we introduce the light-meson saturation approach to help determine the unknown couplings. Then we calculate the binding energies (if bound states exist) and scattering lengths of the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ systems. Finally we present the conclusions in Sect. 4

Table 1 Contact-range potentials for the heavy meson-heavy anti-meson, heavy meson-doubly heavy baryon, and doubly heavy baryon-doubly heavy anti-baryon systems depending on two unknown coupling constants, $C_{a}$ and $C_{b}$. These coupling constants can be determined from the sum of $C_{a}$ and $C_{b}$ by reproducing the mass of X(3872) and the ratio of $C_{a}$ and $C_{b}$ by the light-meson saturation approach

2 Formalism

Generically, the interaction between two heavy hadrons can be decomposed into a long- and a short-range piece within the EFT. The long-range piece corresponds to the one-pion-exchange potential, while the short-range piece can be described by a series of contact-range potentials with unknown couplings. In the present context, the short-range interaction between two heavy hadrons is constrained by heavy quark symmetry. In the following we explain how to derive the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ interactions. In the line of Refs. [62, 90], their interactions can be determined in the EFT approach. One should note that we just consider the leading order contact-range potentials because our previous studies indicated that the pion exchanges are perturbative in the charm sector [91, 92]. The short-range interaction of the meson–meson system can be written as

$$\begin{aligned} {\mathcal {L}}_{HH}= & {} C_{a}Tr[H^{\dag }H]Tr[H^{\prime \dag } H^{\prime }]\nonumber \\&+ C_{b}Tr[H^{\dag }\sigma _{i}H]Tr[H^{\prime \dag }\sigma _{i} H^{\prime }], \end{aligned}$$

(1)

where $C_{a}$ and $C_{b}$ are two unknown couplings and H is a non-relativistic superfield with $H=\frac{1}{\sqrt{2}}[P+\vec {P}^{*}\cdot \vec {\sigma }]$, and P and $P^{*}$ denote pseuoscalar and vector charmed meson fields. The $D^{(*)}\Xi _{cc}^{(*)}$ system can be related to the $D^{(*)}{\bar{D}}^{(*)}$ system through HADS, resulting in the following Lagrangian

$$\begin{aligned} {\mathcal {L}}_{HT}= & {} C_{a}Tr[H^{\dag }H]Tr[T^{\prime \dag } T^{\prime }]\nonumber \\&+ C_{b}Tr[H^{\dag }\sigma _{i}H]Tr[T^{\prime \dag }\sigma _{i} T^{\prime }], \end{aligned}$$

(2)

where $T=\frac{1}{\sqrt{3}}\vec {\sigma }\Xi _{cc}+\vec {\Xi }_{cc}^{*}$ is a non-relativistic superfield of $\Xi _{cc}$ and $\Xi _{cc}^{*}$ respecting HQSS. The Lagrangian of the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system have the same form as those of the $D^{(*)}{\bar{D}}^{(*)}$ and $D^{(*)}\Xi _{cc}^{(*)}$ systems

$$\begin{aligned} {\mathcal {L}}_{TT}= & {} C_{a}Tr[T^{\dag }T]Tr[T^{\prime \dag } T^{\prime }]\nonumber \\&+ C_{b}Tr[T^{\dag }\sigma _{i}T]Tr[T^{\prime \dag }\sigma _{i} T^{\prime }]. \end{aligned}$$

(3)

The term $C_{a}$ is independent of the spin, while $C_{b}$ accounts for the spin spin interaction. Using the same approach of Ref. [62], the contact potentials of the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ systems can be easily constructed and are shown in Table 1.

To make concrete predictions for likely existence of molecular states we have to solve a non-relativistic bound state equation with the contact-range potentials of Table 1. In the momentum space, we can solve the Lippmann-Schwinger equation to find (virtual) bound states as

$$\begin{aligned} \phi (k)+\int \frac{d^{3}p}{(2\pi )^3}\langle k|V|p\rangle \frac{\phi (p)}{B+\frac{p^2}{2\mu }}=0, \end{aligned}$$

(4)

where $\phi (k)$ is the vertex function, B the binding energy, and $\mu$ the reduced mass. To solve the equation we regularize the contact potential in the following way

$$\begin{aligned} \langle p| V_{\Lambda }| p^{\prime }\rangle =C(\Lambda )f\left( \frac{p}{\Lambda }\right) f\left( \frac{p^{\prime }}{\Lambda }\right) , \end{aligned}$$

(5)

with $\Lambda$ the cutoff, f(x) a regular function, and $C({\Lambda })$ the running coupling constant. A typical choice of the cutoff is $\Lambda =0.5-1$ GeV, while for the regulator we choose a Gaussian type $f(x)=e^{-x^2}$. In this work, to be consistent with the cutoff adopted in the light-meson saturation approach, we use a cutoff of $\Lambda =0.7$ GeV. Considering only S-wave contact interactions, the integral equation simplifies to

$$\begin{aligned} 1+C(\Lambda )\frac{\mu }{\pi ^2}\int _{0}^{\infty }dqe^{-2\frac{q^2}{\Lambda ^{2}}}\frac{q^2}{B+\frac{\vec {q}^{2}}{2\mu }}=0. \end{aligned}$$

(6)

3 Numerical results and discussions

In this section we study the likely existence of molecular states in the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and $\Xi _{cc}^{(*)}{\bar{\Xi }}_{cc}^{(*)}$ systems. The contact-range potentials of these systems are only dependent on two couplings, $C_{a}$ and $C_{b}$. To determine these couplings, the best approach is to fit to the experimental data. However, there exists only one molecular candidate X(3872) to determine the sum of $C_{a}$ and $C_{b}$. We, therefore, resort to the light-meson saturation approach to estimate the ratio of $C_{a}$ and $C_{b}$.

The assumption of light-meson saturation implies that the values of the EFT couplings are saturated by light meson exchanges. Following the formalism of Ref. [65], we estimate the couplings of $C_{a}$ and $C_{b}$ by the sigma and vector meson exchange saturation,

$$\begin{aligned} C_{a}^{sat}(\Lambda \sim m_{\sigma },m_{V})\propto & {} C_{a}^{S}+ C_{a}^{V}, \nonumber \\ C_{b}^{sat}(\Lambda \sim m_{\sigma },m_{V})\propto & {} C_{b}^{V}, \end{aligned}$$

(7)

where the cutoff $\Lambda \sim m_{\sigma },m_{V}$ implies that the saturation works at an EFT cutoff close to the masses of exchanged mesons, i.e., $0.6\sim 0.8$ GeV. The values of saturated couplings are expected to be proportional to the potentials of light meson exchanges in the OBE model once we have removed the spurious Dirac-delta potential [55]. Thus $C_{a}$ and $C_{b}$ can be written as

$$\begin{aligned} C_{a}^{sat(\sigma )}(\Lambda \sim m_{\sigma })\propto & {} -\frac{g_{\sigma }^2}{m_{\sigma }^2}, \nonumber \\ C_{a}^{sat (V)}(\Lambda \sim m_{V})\propto & {} -\frac{g_{v}^2}{m_{v}^2}(1+\vec {\tau }_{1}\cdot \vec {\tau }_{2}), \nonumber \\ C_{b}^{sat (V)}(\Lambda \sim m_{V})\propto & {} -\frac{f_{v}^2}{4 M^2}(1+\vec {\tau }_{1}\cdot \vec {\tau }_{2}), \end{aligned}$$

(8)

where $g_{\sigma _{1}}$ denotes the charm meson coupling to sigma meson, $g_{v1}$ and $f_{v1}$ denote electric-type and magnetic-type couplings between charm mesons and light vector mesons, and M is a mass scale to render $f_{v1}$ dimensionless, see, e.g., Table 2. The proportionality constant is unknown and depends on the details of the renormalization procedure. However, assuming that the constant is the same for $C_{a}^{sat}$ and $C_{b}^{sat}$, we can calculate their ratio.

Table 2 Masses of light mesons, heavy mesons, and heavy baryons as well as couplings of the heavy mesons to the light mesons. The magnetic couplings of vector mesons are defined as $f_{v}=\kappa _{v}g_{v}$, and M refers to the mass scale (in MeV) involved in the magnetic-type couplings

In the following, we explain how to determine the values of $C_{a}$ and $C_{b}$ in detail. Assuming that X(3872) is a $J^{PC}=1^{++}$  $D^{*}{\bar{D}}$ bound state with the contact potential $C_{a}+C_{b}$, we can determine the sum of $C_{a}$ and $C_{b}$ as 31.4 $\hbox {GeV}^{-2}$ by Eq. (4),² where the cutoff is fixed at 0.7 GeV. With this sum we can only predict the binding energies of states for which the contact potentials are $C_{a}+C_{b}$. Fortunately, combining the ratio of $C_{a}$ and $C_{b}$ determined by the light-meson saturation, we can determine the values of $C_{a}$ and $C_{b}$. The ratio is

$$\begin{aligned} \frac{C_{b}^{sat}}{C_{a}^{sat}}=\frac{C_{b}^{sat (V)}}{C_{a}^{sat(V+\sigma )}}\approx 0.35. \end{aligned}$$

(9)

Comparing it with the ratio $C_{b}/C_{a}\approx 0.134$ for the meson–baryon system of Ref. [55], we find that the spin-spin term plays a more important role in the meson–meson system, which could be the main reason why we can not obtain a complete multiplet of hadronic molecules in the heavy meson–meson system. Using the ratio determined by the light-meson saturation we finally obtain $C_{a}=-23.3$ $\hbox {GeV}^{-2}$ and $C_{b}=-8.1$ $\hbox {GeV}^{-2}$, which can help us compute the full spectra of the $D^{(*)}{\bar{D}}^{(*)}$, $D^{(*)}\Xi _{cc}^{(*)}$, and ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ systems in the EFT approach. According to the EFT, the breaking of HADS is of the order of $\Lambda _{QCD}/(m_{Q}v)$ [56], where $\Lambda _{QCD}\sim 200-300$ MeV and $m_{Q}$ and v are the mass and velocity of the di-quark. From the estimation of Ref. [94], $m_{Q}v\sim$0.8 GeV for a charm quark pair. In this work we take $30\%$ uncertainty for HADS. The breaking of HQSS is taken to be $15\%$ [62].

3.1 Meson–meson system

Table 3 Scattering lengths (a in fm), binding energies (B in MeV if bound states exist) and mass spectra (M in MeV) of prospective isoscalar heavy antimeson–meson molecules. The $\dag$ symbol indicates that there is no bound state. The subscript V denotes the existence of a virtual state. The c and b subscripts denote the charm and bottom sector, respectively. The uncertainties originate from the HQSS breaking of the order $15\%$

The binding energies (if bound states exist) and scattering lengths of the $D^{(*)}{\bar{D}}^{(*)}$ system are shown in Table 3. For the $D^{(*)}{\bar{D}}^{(*)}$ system, we obtain a $J^{PC}=2^{++}~D^{*}{\bar{D}}^{*}$ bound state with a binding energy of 5 MeV, namely X(4013), which has already been predicted by many theoretical studies [22, 23, 95]. However, its existence has not been confirmed by experiments. Except for X(3872) and X(4013) there are no other bound states in this system, which is consistent with the conclusion of the OBE model [25]. The potential between ${\bar{D}}$ and D is only weakly attractive, and does not support a bound state. We find a pole in the second Riemann sheet, which is located 0.1 MeV below the ${\bar{D}}D$ mass threshold and with a particularly small width, and we conclude that it is a virtual state. Our result is consistent with the results of Ref. [96]. Recently a Lattice QCD study obtained a shallow bound state located 4 MeV below the $D{\bar{D}}$ mass threshold [97]. If we use the OBE model to reproduce the 4 MeV binding energy, the cutoff needed is about $\Lambda =1.4$ GeV, whose value is close to but larger than that obtained in our previous work to reproduce X(3872), i.e., $\Lambda =1.01$ GeV. We note that several theoretical works have predicted the existence of a bound state in the $D{\bar{D}}$ channel [21, 38, 98,99,100,101,102]. The scattering lengths of $J^{PC}=1^{+-}$ ${\bar{D}}^{*}D$ and ${\bar{D}}^{*}D^{*}$ are also relatively large, and using the same approach we find that two poles are located 7.9 and 6.3 MeV below the ${\bar{D}}^{*}D$ and ${\bar{D}}^{*}D^{*}$ mass thresholds, respectively, in the second Riemann sheet, which can be regarded as virtual states

With heavy quark flavor symmetry we can also study the $B^{(*)}{\bar{B}}^{(*)}$ system. We find five bound states, $J^{PC}=0^{++}~{\bar{B}}B$, $J^{PC}=1^{++}$  ${\bar{B}}B^{*}$, $J^{PC}=1^{+-}~{\bar{B}}B^{*}$, $J^{PC}=1^{+-}~{\bar{B}}^{*}B^{*}$, and $J^{PC}=2^{++}~{\bar{B}}^{*}B^{*}$, consistent with the results of the OBE model [25]. Among them we can regard the $J^{PC}=1^{++}~{\bar{B}}B^{*}$ and $J^{PC}=2^{++}~{\bar{B}}^{*}B^{*}$ states, referred to as $X_{b}$ and $X_{b}^{\prime }$, as the hidden bottom partners of X(3872) and X(4013), respectively. We note that Törnqvist has already predicted two deuteron-like ${\bar{B}}B^{*}$ and ${\bar{B}}^{*}B^{*}$ bound states in the one pion exchange model [103], but its existence has not been confirmed by experiments. In addition, a virtual state is found 0.6 MeV below the ${\bar{B}}^{*}B^{*}$ mass threshold.

3.2 Meson–baryon system

Using HADS we can extend the $D^{(*)}{\bar{D}}^{(*)}$ system to the $D^{(*)}\Xi _{cc}^{(*)}$ system as shown in Fig. 1, where a HQSS multiplet of meson–baryon molecules can be expected. The contact-range potentials of the $D^{(*)}\Xi _{cc}^{(*)}$ system are expressed as combinations of $C_{a}$ and $C_{b}$, which can be related to the couplings arising in the $D^{(*)}{\bar{D}}^{(*)}$ system by HADS. Therefore, we take the same inputs to calculate the binding energies and scattering lengths of the $D^{(*)}\Xi _{cc}^{(*)}$ system, and the results are given in Table 4. Although most $D^{(*)}\Xi _{cc}^{(*)}$ systems are bound with the central values of $C_a$ and $C_b$, they may become unbound once the breaking of HADS is taken into account. Only two systems, $J^{P}=1/2^{-}~D^{*}\Xi _{cc}$ and $J^{P}=5/2^{-}~D^{*}\Xi _{cc}^{*}$, always remain bound. Thus in this work we predict the existence of two triply charmed pentaquark molecules. It is to be noted that in our previous study, we also predicted a $J^{P}=1/2^{-}~D^{*}\Xi _{cc}$ bound state in the OBE model [104], while in Ref. [64] a $J^{P}=5/2^{-}~D^{*}\Xi _{cc}^{*}$ bound state is predicted using a contact-range potential. These two molecules can decay into $\Omega _{ccc}\omega$ via triangle diagrams, and we expect that they can be detected in future experiments.

With heavy quark flavor symmetry we also study the ${\bar{B}}^{(*)}\Xi _{bb}^{(*)}$ system, and find that bound states exist in all the channels within uncertainties induced by heavy quark symmetry breaking, which indicates that we obtain a complete HQSS multiplet of hadronic molecules. Comparing the results with those of the meson–meson system, we find that the meson–baryon molecular states are more bound, in agreement with naive expectations because of the larger reduced masses in the latter system.

Table 4 Scattering lengths (a in fm), binding energies (B in MeV, if bound states exist) and mass spectra (M in MeV) of prospective isoscalar heavy meson–baryon molecules. The superscript V denotes the existence of virtual states, the $\dag$ symbol denotes that the system is unbound, and the ? symbol indicates that the system is bound with the central value of the potential, and can become unbound if the potential is made less attractive within the range specified in the text. The c and b subscript denote the charm and bottom sector, respectively. The uncertainties originate from the HADS breaking of the order $30\%$

Table 5 Scattering lengths (a in fm), binding energies (B in MeV, if bound states exist) and mass spectra (M in MeV) of prospective isoscalar heavy baryon-baryon molecules. The superscript V denotes the existence of virtual states, the $\dag$ symbol denotes that the system is unbound, and the ? symbol indicates that the system is bound with the central value of the potential, and can become unbound if the potential is made less attractive within the range specified in the text. The c and b subscript denote the charm and bottom sector, respectively. The uncertainties originate from the HADS breaking of the order $30\%$

3.3 Baryon-anti-baryon system

In this section, we further extend the $D^{(*)}\Xi _{cc}^{(*)}$ system to the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system as shown in Fig. 1. This baryon-antibaryon system contains 10 channels related by HQSS. The contact-range potentials of the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system can also be written in terms of $C_{a}$ and $C_{b}$ dictated by HQSS. We compute the binding energies and scattering lengths of the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system, and show the results in Table 5. We find seven bound states, i.e., $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$, $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}$, $J^{PC}=1^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=2^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=2^{-+}~{\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$, and $J^{PC}=3^{--}~{\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$. The ${\bar{\Xi }}_{cc}\Xi _{cc}$ system [105] and the ${\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$ system [106] have been studied in the OBE model, where it is shown that all of these systems are bound. Assuming heavy quark flavor symmetry, we further investigate their hidden bottom partners ${\bar{\Xi }}_{bb}^{(*)}\Xi _{bb}^{(*)}$, and all the states are found to be bound as shown in Table 5, suggesting the emergence of a complete multiplet of hadronic molecules.

Among these molecules, we note that there are two molecules, $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$ and $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}$ , located close to 7200 MeV, the former one of which could contribute to the structure X(7200) observed by the LHCb Collaboration recently. The $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$ molecule is predicted in terms of the hypothesis that X(3872) is a $J^{PC}=1^{++}~{\bar{D}}D^{*}$ bound state and utilyzing the HADS. It is well known that the heavy meson–anti meson channel affects the spectra of conventional charmonia. According to the relationship between X(7200) and X(3872) proposed by the present work it is rather likely that the two doubly charmed baryon-antibaryon channel would affect the spectra of fully charmed tetraquark states as shown in Fig. 2, which indicates that X(7200) might contain both ${\bar{\Xi }}_{cc}\Xi _{cc}$ molecular and charmed diquark-anti diquark tetraquark components. It is interesting to note that our current study shows that X(7200) might contain $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$ molecular components.

Fig. 2

Left: the two charmed meson channel heavily affects the mass spectra of charmonia close to their mass thresholds. Right: HADS implies that the two doubly charmed baryon channel could also affect the mass spectra of fully charmed tetraquark states close to their mass thresholds

4 Summary

In this work we extended the $D^{(*)}{\bar{D}}^{(*)}$ system to the $D^{(*)}\Xi _{cc}^{(*)}$ system then to the ${\bar{\Xi }}_{cc}^{(*)}\Xi _{cc}^{(*)}$ system utilyzing the heavy antiquark diquark symmetry (HADS). The contact-range potentials of these systems respecting heavy quark spin symmetry (HQSS) are constrained to two couplings at the leading order, $C_{a}$ and $C_{b}$. Assuming that X(3872) is a $J^{PC}=1^{++}~{\bar{D}}D^{*}$ bound state, we determined the sum of $C_{a}$ and $C_{b}$. To fully determine the value of $C_{a}$ and $C_{b}$, we used the light-meson saturation approach to determine its ratio. With the so-determined $C_{a}$ and $C_{b}$ we calculated the binding energies (if bound states exist) and scattering lengths of all these systems as well as their heavy quark flavor partners.

In the ${\bar{D}}^{(*)}D^{(*)}$ system, we obtained a $J^{PC}=2^{++}~{\bar{D}}^{*}D^{*}$ molecule with a mass of 4013 MeV referred to as X(4013), which can be regarded as the heavy quark spin symmetry partner of X(3872). Moreover, in the bottom sector we predicted the existence of five molecules. We extended the ${\bar{D}}^{(*)}D^{(*)}$ to the $D^{(*)}\Xi _{cc}^{(*)}$ system by HADS. Two molecules, $J^{P}=1/2^{-}~D^{*}\Xi _{cc}$ and $J^{P}=5/2^{-}~D^{*}\Xi _{cc}^{*}$, are obtained. There exist a complete multiplet of hadronic molecules in the corresponding bottom sector. Using HADS again we studied the ${\bar{\Xi }}_{cc}^{(*)}{\Xi }_{cc}^{(*)}$ system, and found 7 bound states, $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$, $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}$, $J^{PC}=1^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=1^{--}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=2^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}^{*}$, $J^{PC}=2^{-+}~{\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$, and $J^{PC}=3^{--}~{\bar{\Xi }}_{cc}^{*}\Xi _{cc}^{*}$. There also exist a complete multiplet of hadronic molecules in the bottom sector. Among them, the $J^{PC}=0^{-+}~{\bar{\Xi }}_{cc}\Xi _{cc}$ molecule may contribute to X(7200) recently observed by the LHCb Collaboration, which is related to X(3872) via HADS.