1 Introduction

The Schwinger–Dyson equations [1, 2] of quantum field theory can be derived [3, 4] from the invariance of the functional integration under field translations. The structure of the Schwinger–Dyson equations is determined by the action functional, which is involved in the computation of the vacuum expectation values of the fields. Let the action \(S[\phi ]\) be a function of a set of fields denoted by \(\phi (x) \). The basic Schwinger–Dyson equation takes the form

$$\begin{aligned}&\left\langle \frac{\delta S[\phi ]}{\delta \phi (x)} \, \phi (y_1) \phi (y_2) \cdots \phi (y_n) \right\rangle \nonumber \\&\quad = i \sum _{j=1}^n \, \delta (x-y_j) \langle \phi (y_1) \cdots \phi (y_{j-1}) \phi (y_{j+1}) \cdots \phi (y_n) \rangle ,\nonumber \\ \end{aligned}$$
(1.1)

where the vacuum expectation value \(\langle {{\mathscr {P}}} [\phi ] \rangle \) of a field operator \({{\mathscr {P}}} [\phi ] \) is given by

$$\begin{aligned}&\langle {\mathscr {P}} [\phi ] \rangle = \frac{\int D \phi \; e^{iS[\phi ]} \; {{\mathscr {P}}} [\phi ] }{\int D \phi \; e^{iS[\phi ]}}. \end{aligned}$$
(1.2)

Recently, developments of the Schwinger–Dyson equations have been applied in the study of various subjects like, for instance, the renormalization theory [5, 6], condensed matter investigations [7, 8], and bound states and strong interactions [9,10,11,12,13,14,15,16,17,18]. Standard Schwinger–Dyson equations have been used also in the case of topological quantum field theories with and without matter [19,20,21].

We are interested in a particular generalisation of Eq. (1.1) which concerns the computation of the expectation values of the products of the composite operator \(\delta S [\phi ] / \delta \phi (x)\),

$$\begin{aligned}&F(x_1,x_2,\ldots , x_n) = \left\langle \frac{\delta S[\phi ]}{\delta \phi (x_1)} \frac{\delta S[\phi ]}{\delta \phi (x_2)} \cdots \frac{\delta S[\phi ]}{\delta \phi (x_n)} \right\rangle . \end{aligned}$$
(1.3)

The generating functional \(Z_{SD}[B] \) of the expectation values (1.3) is called the Schwinger–Dyson functional and is defined by

$$\begin{aligned} Z_{SD}[B] = \langle e^{i \int dx \, B(x) \, \delta S[\phi ] / \delta \phi (x) } \rangle , \end{aligned}$$
(1.4)

where B(x) denotes a classical source.

The functional (1.4) plays an important role in the low-dimensional gauge field theories of topological type, like the Chern–Simons and BF quantum field theories [22,23,24]. In these models, the derivative of the action with respect to the components of the connection is proportional to the curvature (plus possible additional contributions which are related to the gauge-fixing lagrangian terms), that combined with the topology of 3-manifolds determines the values of the Wilson line observables [22].

In facts, when the gauge structure group of these topological models is abelian, the Schwinger–Dyson functional provides the complete solution for the gauge invariant observables [22, 25].

For instance, when the first homology group [25] \(H_1(M)\) of the 3-manifold M is trivial, one can compute [22] the observables of the abelian Chern–Simons theory defined in M by means of perturbation theory. The action for the connection A is given by \(2 \pi k \int A \wedge dA \) and the variation of the action with respect to the fields is proportional to the curvature \(F_A= dA\). By introducing the coupling \(\int B \wedge dA \) of the curvature with an external classical source \(B = B_\mu (x) dx^\mu \), one finds

$$\begin{aligned} {\widetilde{Z}}_{SD} [B] \equiv \langle e^{ 2 \pi i \int B \wedge dA } \rangle = e^{ -i \, \pi / 2 k \int B\wedge B}, \end{aligned}$$
(1.5)

that specifies the expectation values of the Wilson lines associated with links in M. Quite remarkably, an appropriate generalization [22] of this procedure furnishes the solution of the abelian Chern–Simons theory in a generic closed and oriented 3-manifold M. Indeed, when the first homology group \(H_1(M)\) is not trivial, for each element of the torsion subgroup [25] of \(H_1(M)\) one can introduce a corresponding classical background connection. Then one needs to take the sum of the Schwinger–Dyson functionals that are computed in the presence of each background connection. Somehow, in the functional integration, the values of the curvature correspond to the local degrees of freedom – which do not depend on the topology of the manifold M – whereas the effects of topology are taken into account by the background connections.

In the case of the non-abelian SU(N) Chern–Simons theory, the structure of the gauge orbits, which are associated with the SU(N) connections, does not admit [26] a simple description based on the homology group \(H_1(M)\). Yet, in the characterization of the local degrees of freedom which are not related with the manifold topology, the non-abelian curvature \(F_A = 2 dA + i [A, A]\) appears to play a fundamental role. In fact, the value \(F_A(x)\) of the curvature in the point x is specified [4, 27] by the value of the gauge holonomy associated an infinitesimal loop centered in x, and each infinitesimal loop does not depend on the topology of M. Let us present a rough sketch of a possible argument that can be used to make this statement more precise.

SU(N) gauge connections can be described by one-forms defined in M with values in the SU(N) Lie algebra. The local value \(\{ A(x) \} \) of each configuration A can also be specified by the set \( \{ H_\gamma [A] \}\) of the holonomies,

$$\begin{aligned} H_\gamma [A] = \mathrm{P} e^{i \int _\gamma A}, \end{aligned}$$

which are associated with all the possible closed oriented paths \(\{ \gamma \} \) in M with a given base-point \(x_0 \in M\), which represents the starting/final point of each closed path \(\gamma \). This correspondence is denoted by

$$\begin{aligned} \{ A (x) \} \; \leftrightarrow \; \{ H_\gamma [A] \}. \end{aligned}$$
(1.6)

In turn, the value of the holonomies \(H_\gamma [A]\) as a function of the paths can be determined by combining the local values \(\{ F_A (x) \} \) of the curvature with smooth deformations of the paths. In order to illustrate this point, let us consider a nontrivial reference path \(\gamma _0\), with parametrization \(x^\mu (\tau )\) in which \(0 \le \tau \le 1\). Let the holonomy \(\widehat{H}_{\gamma _0}(s) \) with \(0 \le s \le 1\) be defined by

$$\begin{aligned} {\widehat{H}}_{\gamma _0}(s) = \mathrm{P} e^{i \int _0^s d\tau \, A(\tau ) }, \end{aligned}$$
(1.7)

in which \(A(\tau ) = A_\mu (x (\tau )) (d x^\mu (\tau ) / d \tau ) \). Note that \(H_{ \gamma _0} [A] = {\widehat{H}}_{\gamma _0}(1) \). An infinitesimal deformation \(\gamma _0 + \delta \gamma \) of the path \(\gamma _0\) can be described by the parametrization \(x^\mu (\tau )+ \varepsilon ^\mu (\tau )\) with \(\varepsilon ^\mu (\tau ) \ll 1 \). At first order in \( \varepsilon ^\mu \), one has \(H_{\gamma _0 + \delta \gamma } \simeq H_{\gamma _0} + \varDelta H_{\gamma _0} \), where the infinitesimal modification \( \varDelta H_{\gamma _0}\) of the holonomy,

$$\begin{aligned} \varDelta H_{\gamma _0}= & {} i \int _0^1 ds \, \widehat{H}_{\gamma _0}(s) \, \varepsilon ^\mu (s) \nonumber \\&\quad \times \dot{x}^\nu (s) F_{\mu \nu } (x(s)) \, {\widehat{H}}^{-1}_{\gamma _0}(s) \, H_{\gamma _0} [A], \end{aligned}$$
(1.8)

is specified by \(\widehat{H}_{\gamma _0}(s)\) and by the values \(\{ F_A (x) \} \) of the curvature. If the path \(\gamma \) is homotopically equivalent to \(\gamma _0\), the value of the associate holonomy \(H_\gamma [A]\) is expected to be determined by \( H_{\gamma _0} [A] \) with the help of a set of infinitesimal transformations of the path. As shown in Eq. (1.8), the corresponding infinitesimal modifications of the holonomy can be fixed by means of \(\widehat{H}_{\gamma _0}(s) \) and the local values \(\{ F_A (x) \} \) of the curvature. If the 3-manifold M is simply connected, any closed path \(\gamma \) is homotopic with \(\gamma _0\). If M is not simply connected, for each generator g of the fundamental group \(\pi _1 (M)\) one can choose a representative path \(\gamma _g\) and, in agreement with Eq. (1.7), one can compute the corresponding holonomy \({\widehat{H}}_{\gamma _g} (s)\). For each set of homotopic paths, the associated holonomies can be determined by combining \({\widehat{H}}_{\gamma _g} (s)\) with the local values \(\{ F_A (x) \} \) of the curvature. Thus relation (1.6) should develop into

$$\begin{aligned}&\{ A (x) \} \; \leftrightarrow \; \{ H_\gamma [A] \} \nonumber \\&\quad \leftrightarrow \; \{ {\widehat{H}}_{\gamma _1}(s) , {\widehat{H}}_{\gamma _2}(s),\ldots , {\widehat{H}}_{\gamma _g}(s) , \ldots ; F_A (x)\}. \end{aligned}$$
(1.9)

Consequently, in the computation of the functional integration, the sum over the configurations \(\{ A (x) \}\) can then be envisaged to be decomposed into a sum over the values \(\{ F_A (x) \} \) of the curvature and a sum over the values of the holonomies associated with the paths which represent the generators of the fundamental group \(\pi _1 (M)\). The values of the curvature should correspond to the “purely local” degrees of freedom which are independent of the topology of the manifold M. Whereas the values of the holonomies \(\{ {\widehat{H}}_{\gamma _1}(s) , {\widehat{H}}_{\gamma _2}(s), \ldots , {\widehat{H}}_{\gamma _g}(s) \} \) should describe the effects of the nontrivial topology of M.

How to carry out the precise disentanglement of the “purely local” degrees of freedom – described by the curvature – and the “topology dependent” degrees of freedom in the functional integration is an open problem. In order to investigate this issue in the case of the nonabelian Chern–Simons and BF theories, in the present article we analyze a preliminary question which is related to the perturbative computation of the renormalized generating functional of the vacuum expectation values of the products of the nonabelian curvature \(F_A (x)\) in different points of spacetime. Indeed, for the topological abelian gauge theories the renormalization is trivial, whereas in the non-abelian case the renormalization task is not trivial. The main purposes of our article is to show how the renormalization of the corresponding Schwinger–Dyson functional \(Z_{SD}[B] \) is canonically determined by the standard renormalization procedure [28, 29] for the correlation functions of the gauge connections.

We demonstrate that, in the Chern–Simons and BF theories, the renormalized Schwinger–Dyson functional is related with the generating functional Z[J] of the correlation functions of the gauge connections by some kind of duality transformation. Therefore the standard perturbative procedure called “renormalized perturbation theory” [4] provides a canonical renormalization for \(Z_{SD}[B] \). Note that we are not interested in the matrix elements the composite operator \(\delta S[\phi ] / \delta \phi (x) \) between generic states; this issue can be studied by means of standard techniques [4, 29, 30]. Motivated by the results of the topological models with an abelian gauge group, we shall concentrate on the vacuum expectation values of products of operators \(\delta S[\phi ] / \delta \phi (x) \). In this case, the relationship that we derive between \(Z_{SD}[B] \) and Z[J] shows that the standard technique [4, 29, 30] for the study of the renormalization properties of the composite operator \(\delta S[\phi ] / \delta \phi (x) \) greatly simplifies.

Let us remember that the renormalization of the lagrangian field theory models is expected [31, 32] to be independent of the global aspects of the manifold that do not modify the short-distance behaviour of the theory. Therefore, since the nonabelian curvature \(F_A(x)\) describes degrees of freedom which do not depend on the topology of the manifold, we shall consider the renormalization properties of \(Z_{SD}[B] \) in flat spacetime.

The combinatoric structure of the Feynman diagrams – entering the perturbative computation of \(Z_{SD}[B]\) – is illustrated in the simple case of the field theory models \(\phi ^3\) and \(\phi ^4\) in four dimensions in Sect. 2. By means of the Wick contractions [3, 4] of the field operators, we examine the Feynman diagrams which are associated with the expectation values (1.3). We demonstrate that the short distance behaviour of the products of the composite operator \(\delta S [\phi ] / \delta \phi (x)\) – that in d dimensional spacetime has dimension \((d-1)\) – is really determined by the ultraviolet properties of operators of dimensions \((d-2)\) and/or \((d-3)\). For instance, when the interacting lagrangian entering the action \(S[\phi ]\) is a cubic function of a scalar field \(\phi (x)\), \(Z_{SD}[B]\) can be related to the ordinary generating functional Z[J] of correlation functions of the field \(\phi (x)\). In general, it turns out that the connected component of \(Z_{SD}[B]\) is the union of a local functional of B(x) and a non-local part which is specified by the expectation values of field components \(\phi (x)\) and possibly \(\phi ^2(x)\).

Applications and extensions of the results of Sect. 2 are presented in Sect. 3, where low dimensional gauge theories of topological type are considered. For the nonabelian SU(N) Chern–Simons model and the ISU(2) BF gauge theory in \({\mathbb R}^3\), the relationship between the renormalized Schwinger–Dyson functional and the generating functional of the correlation functions of the gauge fields is produced. Section 4 contains the conclusions.

2 Structure of the Feynman diagrams

The case of a cubic interaction lagrangian is relevant for the topological gauge theories in low dimensions. So, let us first consider the field theory model which is defined by the action

$$\begin{aligned} S [\phi ] = \int d^4 x \, \left( \frac{1}{/}2 \partial _\mu \phi \, \partial ^\mu \phi - \frac{1}{/}2 m^2 \phi ^2 + \frac{1}{/}3g \phi ^3 \right) , \end{aligned}$$
(2.1)

where \(\phi (x) \) is a real scalar field and the real parameter g denotes the coupling constant. The generating functional Z[J] of the correlation functions of the field \(\phi (x)\) is defined by

$$\begin{aligned} Z[J] = \langle e^{i \int d^4x \, J(x) \, \phi (x) } \rangle . \end{aligned}$$
(2.2)

The renormalization of Z[J] is obtained by means of the standard procedure denominated “renormalized perturbation theory” [4]. In this scheme, the lagrangian parameters assume their renormalized values and, in order to maintain the validity of the normalization conditions at each order of perturbation theory, local counterterms are introduced, which cancel exactly all the contributions to these parameters which are obtained in the loop expansion. The normalization conditions for the model defined be the action (2.1) concern the values of the mass, of the coupling constant and the wave function normalization. Finally, in order to complete the list of the normalization conditions, one needs to require the absence of a proper vertex which is linear in the field. Let \(\varGamma [\varphi ]\) be the effective action which corresponds to the sum of the one-particle-irreducible diagrams with external legs represented by \(\varphi (x)\). In agreement with the structure of the lagrangian (2.1), the additional normalization condition is given by \( \left( \delta \varGamma / \delta \varphi (x) \right) |_{\varphi =0} = 0 \). Note that, in the case of the \(\phi ^4\) model, the vanishing of the proper vertices which are linear and cubic in powers of the fields is a consequence of the symmetry \( \varphi \rightarrow - \varphi \) which is imposed to the effective action. In the case of gauge fields, the analogue of the condition \( \left( \delta \varGamma / \delta \varphi (x) \right) |_{\varphi =0} = 0 \) is automatically satisfied.

Let us now consider the perturbative computation of the mean values (1.3). The perturbative expansion [3, 4] of a generic expectation value (1.2) can be written as

$$\begin{aligned} \langle {{\mathscr {P}}} [\phi ] \rangle = \frac{ \langle \, {{\mathscr {P}}} [\phi ] \, e^{i S_I [\phi ]} \, \rangle _0 }{\langle \, e^{i S_I [\phi ] } \, \rangle _0 }, \end{aligned}$$
(2.3)

where \(S_I [\phi ]\) denotes the integral of the interaction lagrangian

$$\begin{aligned} S_I [\phi ] = \frac{1}{/}3g \int d^4x \, \phi ^3 (x), \end{aligned}$$
(2.4)

and the vacuum expectation value of the time-ordered product of the fields

$$\begin{aligned} \langle \, {{\mathscr {P}}} [\phi ] \, e^{i S_I [\phi ]} \, \rangle _0 \equiv \langle 0 | \, \mathrm{T} \left( {\mathscr {P}} [\phi ] \, e^{i S_I [\phi ]} \right) | 0 \rangle \end{aligned}$$
(2.5)

corresponds to the sum of the Feynman diagrams which are obtained by means of the Wick contractions [32] of the fields. The set of the connected diagrams is denoted by \(\langle \, {{\mathscr {P}}} [\phi ] \, e^{i S_I [\phi ]} \, \rangle _0^c\). The Feynman propagator reads

(2.6)

The composite operator \(\delta S [\phi ] / \delta \phi (x)\) takes the form

$$\begin{aligned}&\frac{\delta S}{\delta \phi (x)} \equiv E_\phi (x) = [ -\partial ^2 - m^2] \phi (x) + g \phi ^2 (x)\nonumber \\&\quad = \nabla \phi (x) + g \phi ^2(x), \end{aligned}$$
(2.7)

where we have introduced the simplifying notation \(\nabla \phi (x) \equiv [ -\partial ^2 - m^2] \phi (x) \). The Schwinger–Dyson functional (1.4) can be written as \(Z_{SD}[B] = \exp (i W_{SD} [B]) \) where \(i W_{SD} [B]\) is given by the sum of the connected diagrams

$$\begin{aligned} i W_{SD}[B]= & {} \sum _n \frac{i^n}{n!} \int d^4x_1 \cdots d^4x_n B(x_1) \nonumber \\&\quad \cdots B(x_n) \, \langle E_\phi (x_1) \cdots E_\phi (x_n) \, e^{i S_I [\phi ]} \, \rangle ^c_0. \end{aligned}$$
(2.8)

Note that the overall multiplying factor, which is given by the sum of the vacuum-to-vacuum diagrams, is not included in the set of the connected diagrams (2.8) contributing to \(Z_{SD}[B]\). Indeed, as a consequence of the normalisation – shown in Eqs. (1.2) and (2.3) – of the generating functional (1.4), the multiplying factor of the numerator simplifies – or cancels – with the same factor of the denominator.

Let us examine the perturbative evaluation of \(\langle E_\phi (x_1) \cdots \) \(E_\phi (x_n) \, e^{i S_I [\phi ]} \, \rangle ^c_0\). In agreement with the Wick Theorem, let us first consider all the possible Wick contractions of the operator \(\nabla \phi (x)\). Since , the Wick contraction of \(\nabla \phi (x) \) with the fields contained in \(e^{i S_I [\phi ]}\) gives

(2.9)

and consequently

$$\begin{aligned}&\langle E_\phi (x) \, e^{i S_I [\phi ] } \, \rangle ^c_0\nonumber \\&\quad = \langle ( \nabla \phi (x) + g \phi ^2(x) ) \, e^{i S_I [\phi ] } \, \rangle ^c_0 = 0. \end{aligned}$$
(2.10)

Let us now consider \( \langle E_\phi (x_1) E_\phi (x_2) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \). Because of Eq. (2.9), the contraction of \(\nabla \phi (x_1)\) with the fields contained in \(e^{i S_I [\phi ]}\) gives a vanishing result as a consequence of the sum with the term \(g \phi ^2 (x_1)\), as shown in Eq. (2.10) for the case of \( \langle E_\phi (x) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \). So we must consider the contraction of \(\nabla \phi (x_1)\) with \(E_\phi (x_2)\), which produces

(2.11)

Thus one finds

$$\begin{aligned}&\langle E_\phi (x_1) E_\phi (x_2) \, e^{i S_I [\phi ] } \, \rangle ^c_0 = i [ -\partial ^2 - m^2 ] \, \delta ^4 (x_1-x_2) \nonumber \\&\quad + 2 i g \delta ^4 (x_1 - x_2) \langle \phi (x_2) \, e^{i S_I [\phi ]} \rangle _0^c. \end{aligned}$$
(2.12)

The normalization condition \( \left( \delta \varGamma / \delta \varphi (x) \right) |_{\varphi =0} = 0 \) on the absence of the tadpole implies \(\langle \phi (x_2) \, e^{i S_I [\phi ]} \rangle _0^c = 0\). Therefore

$$\begin{aligned} \langle E_\phi (x_1) E_\phi (x_2) \, e^{i S_I [\phi ] } \, \rangle ^c_0 = i [ -\partial ^2 - m^2 ] \, \delta ^4 (x_1-x_2). \end{aligned}$$
(2.13)

The same arguments illustrated above give

$$\begin{aligned}&\langle E_\phi (x_1) E_\phi (x_2) E_\phi (x_3) \, e^{i S_I [\phi ] } \, \rangle ^c_0\nonumber \\&\quad = - 4 \, g\, \delta ^4 (x_1-x_2) \, \delta ^4 (x_2 - x_3). \end{aligned}$$
(2.14)

The structure of the diagrams associated with \(\langle E_\phi (x_1)\)\(E_\phi (x_2) \cdots E_\phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \), for generic \(n \ge 4\), can be obtained by first considering all the Wick contractions of the field operators of the type \(\nabla \phi \). The combinatoric of these contractions can easily be obtained by taking into account the symmetric role of the operators \(E_\phi (x_1) E_\phi (x_2) \cdots E_\phi (x_n)\) in the computation of \(W_{SD} [B]\), as shown in Eq. (2.8). For the connected diagrams, we find

$$\begin{aligned} \langle E_\phi (x_1) E_\phi (x_2) \cdots E_\phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 = 0, \quad \hbox {if }n\hbox { is odd}, \end{aligned}$$
(2.15)

and

$$\begin{aligned}&\langle E_\phi (x_1) E_\phi (x_2) \cdots E_\phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \nonumber \\&\quad = \langle \phi (x_2) \, \phi (x_4) \cdots \phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \nonumber \\&\qquad \times (n-1)!! \, (2 i g )^{n/2} \, \delta ^4 (x_1 - x_2) \cdots \delta ^4 (x_{n-1} - x_n),\nonumber \\&\qquad \hbox {if }n\hbox { is even}. \end{aligned}$$
(2.16)

Equations (2.15) and (2.16) show that the expectation value \(\langle E_\phi (x_1) E_\phi (x_2) \cdots E_\phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \) is completely specified by the expectation value \(\langle \phi (x_2) \, \phi (x_4) \cdots \phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0\). Therefore the standard renormalization procedure for the correlation functions of the field \(\phi (x)\) canonically defines the renormalization for \(\langle E_\phi (x_1) E_\phi (x_2) \cdots E_\phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \). Equation (2.10) implies

$$\begin{aligned} i \int d^4x \, B(x) \, \langle E_\phi (x) \, e^{i S_I [\phi ]} \, \rangle ^c_0 = 0, \end{aligned}$$
(2.17)

The contact terms (2.13) and (2.14) give origin to a local contribution to \(W_{SD}[B]\). In particular, we find

$$\begin{aligned}&\frac{i^2}{2!} \int d^4x_1 d^4x_2 \, B(x_1) B(x_2) \, \langle E_\phi (x_1) E_\phi (x_2) \, e^{i S_I [\phi ]} \, \rangle ^c_0 \nonumber \\&\quad = i \int d^4x \, \left\{ - \frac{1}{/}2 \partial _\mu B \partial ^\mu B + \frac{1}{/}2 m^2 B^2 \right\} , \end{aligned}$$
(2.18)
$$\begin{aligned}&\frac{i^3}{3!} \int d^4x_1 d^4x_2 d^4x_3 \, B(x_1) B(x_2) B(x_3)\nonumber \\&\quad \quad \times \langle E_\phi (x_1) E_\phi (x_2) E_\phi (x_3) \, e^{i S_I [\phi ]} \, \rangle ^c_0 \nonumber \\&\quad = i \int d^4 x \, \left[ \frac{2}{/}3g B^3 \right] . \end{aligned}$$
(2.19)

The expectation values \(\langle \phi (x_2) \, \phi (x_4) \cdots \phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0\), with \(n \ge 4\), correspond to non-local amplitudes. By collecting all the results on \(\langle E_\phi (x_1) E_\phi (x_2) \cdots E_\phi (x_n) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \) with \(n\ge 4\), we get

$$\begin{aligned}&\sum _{n=4}^\infty \frac{i^n}{n!} \int d^4x_1 \cdots d^4x_n B(x_1) \cdots B(x_n)\nonumber \\&\qquad \times \langle E_\phi (x_1) \cdots E_\phi (x_n) \, e^{i S_I [\phi ]} \, \rangle ^c_0\nonumber \\&\quad =\sum _{p=2}^\infty \frac{i^{(2p)} (2p -1)!! \, (2 i g )^{p} }{(2p)!} \int d^4x_1 \cdots d^4x_{2p}\nonumber \\&\qquad \times B(x_1) \cdots B(x_{2p}) \nonumber \\&\qquad \times \langle \phi (x_2) \, \phi (x_4) \cdots \phi (x_{2p}) \, e^{i S_I [\phi ] } \, \rangle ^c_0\nonumber \\&\qquad \times \delta ^4 (x_1 - x_2) \cdots \delta ^4 (x_{2p-1} - x_{2p}) \nonumber \\&\quad = \sum _{p=2}^\infty \frac{(- i g )^{p} }{p!} \int d^4x_1 \cdots d^4x_{p} B^2(x_1) \cdots B^2(x_p)\nonumber \\&\qquad \times \langle \phi (x_1) \, \phi (x_2) \cdots \phi (x_p) \, e^{i S_I [\phi ] } \, \rangle ^c_0 \nonumber \\&\quad = \langle e^{i \int d^4x (-g) B^2 (x) \phi (x)} \, e^{i S_I [\phi ] } \> \rangle ^c_0 = Z [(J= - g B^2 )]. \quad \end{aligned}$$
(2.20)

The sum of the contributions (2.17)–(2.20) shows that the renormalized Schwinger–Dyson functional for the \(\phi ^3\) model satisfies

$$\begin{aligned} Z_{SD}[B ] = e^{iR[ B ]} \, Z[\widetilde{J}[B] ], \end{aligned}$$
(2.21)

where

(2.22)

and

$$\begin{aligned} {\widetilde{J}}[B](x) = - g B^2(x). \end{aligned}$$
(2.23)

The expectation values (2.13) and (2.14) determine the local functional R[B] of Eq. (2.22). As shown in Eq. (2.21), the renormalization of \(Z_{SD}[B ] \) is specified by the standard renormalization of Z[J].

The structure of the results for the \(\phi ^3\) model admits appropriate generalizations which depend on the form of the lagrangian of each field theory. Let us consider for instance the \(\phi ^4\) model which is specified by the action

(2.24)

One has

$$\begin{aligned} \frac{\delta S}{\delta \phi (x)} = [ -\partial ^2 - m^2 ] \phi (x) - g \phi ^3 (x). \end{aligned}$$
(2.25)

The perturbative expansion of the Schwinger–Dyson functional \(Z_{SD} [B]\) can be examined by means of the method described above. We find

$$\begin{aligned}&Z_{SD}[B ] = e^{iQ[ B ]}\nonumber \\&\quad \times \left\langle \exp \left\{ i \int d^4 x \, \left[ -2 g B^3(x) \, \phi (x) + \frac{3}{/}2 g B^2(x) \, \phi ^2 (x) \right] \right\} \right\rangle ,\nonumber \\ \end{aligned}$$
(2.26)

in which

(2.27)

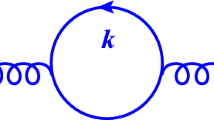
In this case, \(Z_{SD}[B ] \) is related to the expectation value of a term in which, in addition to a coupling with the field operator \(\phi (x)\), a coupling with the operator \(\phi ^2(x)\) is also present. Note that the short distance behaviour of the composite operator \(\phi ^2 (x)\) is taken into account by the standard renormalization of the generating functional Z[J] of the correlation functions because \(\phi ^2 (x)\) has canonical dimension 2. For instance, the one-loop correlation \(\langle \phi ^2 (x) \phi ^2 (y) \rangle \) is described by the diagram of Fig. 1 (with removed external legs), which enters the ordinary renormalization of the \(\phi ^4\) theory. Thus, for this model also, the renormalization of \(Z_{SD}[B ] \) can be specified by the standard renormalization procedure.

Fig. 1
figure 1

One loop diagram of the \(\phi ^4\) model contributing to \(\langle \phi ^2 (x) \phi ^2 (y) \rangle \)

Full size image

As these examples have shown, the connected component \(W_{SD} [B]\) of the renormalized Schwinger–Dyson functional contains a local part, expressions (2.22) and (2.27), which is determined by the form of the lagrangian of each specific model, and a non-local contribution which is related to the vacuum expectation values of field operators of dimension 1 or 2, i.e. the fields \(\phi (x)\) and \(\phi ^2 (x)\). This universal feature can be used to specify the renormalized values of the parameters of each model by the introduction of appropriate normalization conditions written in terms of the operator \(\left[ \delta S / \delta \phi (x) \right] \). Equivalently, some of the vacuum expectations values of the products of \(\left[ \delta S / \delta \phi (x) \right] \) are uniquely specified and do not receive perturbative changes. For example, in the \(\phi ^3\) model, relations (2.13) and (2.14) are exact and are not modified by loop corrections.

3 Topological models

In this section we consider gauge theories of topological type in \({{\mathbb {R}}}^3\). The action of the SU(N) quantum Chern–Simons theory [24, 33, 34] in the Landau gauge is given by

(3.1)

and then

(3.2)

The Schwinger–Dyson functional \(Z_{SD} [L^a_\mu ]\) is defined by

$$\begin{aligned} Z_{SD}[L^a_\mu ] = \left\langle \exp \left( i \int d^3x \, L^a_\mu (x) \left[ \delta S / \delta A_\mu ^a(x) \right] \right) \right\rangle , \end{aligned}$$
(3.3)

and the generating functional \(Z[J^a_\mu ]\) of the correlation functions for the gauge field \(A^a_\mu (x)\) is given by

$$\begin{aligned} Z[J^a_\mu ] = \langle \exp \left( i \int d^3x \, J^{ a \mu } (x) A_\mu ^a(x) \right) \rangle . \end{aligned}$$
(3.4)

In order to examine the diagrams entering the vacuum expectation values of the product of fields \(\delta S / \delta A^a_\mu (x_1) \cdots \delta S / \delta A^b_\nu (x_n) \), one needs to use the following relationship between the propagators of the fields

(3.5)

which can be derived from the action (3.1), or it can be checked directly by means of the expressions

(3.6)
(3.7)

The presence of the operator \( \partial ^\mu {{\overline{c}}}^b (x) f^{abd} c^d (x) \) in the Eq. (3.2) does not modify the perturbative relations between the expectation values of the operators \(\delta S / \delta A^a_\mu (x_1) \cdots \delta S / \delta A^b_\nu (x_n) \) – that have been derived in Sect. 2 by using the Wick contractions of the fields – because this additional term has no contractions with the gauge fields \(A^a_\mu (x)\) and the auxiliary field \(M^a(x)\). Thus, by means of the arguments presented in Sect. 2, one gets

$$\begin{aligned} Z_{SD}[L^a_\mu ] = e^{iF[L^a_\mu ]} \, Z[{\widehat{J}}[ L]^a_ \mu ], \end{aligned}$$
(3.8)

where

(3.9)

and

$$\begin{aligned} \widehat{J}[L]^a_\mu (x) = {k \over 8 \pi } \varepsilon ^{\mu \nu \tau } \, f^{abc} L_\nu ^b(x) L^c_\tau (x). \end{aligned}$$
(3.10)

In addition to the local component which is described the function \( F[L^a_\mu ]\) of Eq. (3.9), the connected component of \(Z_{SD}[L^a_\mu ] \) contains powers of \(L^a_\mu \) greater than (or equal to) four. In particular, for each connected diagram D contributing to \(Z[J^a_\mu ]\) there is a corresponding connected diagram \( D^\prime \) contributing to \(Z_{SD}[L^a_\mu ]\). In agreement with Eq. (3.8), \( D^\prime \) can be obtained from D by the introduction of the “effective classical vertex” (3.10) in each external leg of D, as depicted in Fig. 2. Clearly, the renormalization of the amplitude associated with each diagram D defines a canonical renormalization of the amplitude corresponding to \(D^\prime \). So, Eq. (3.8) provides a definition of the renormalized Schwinger–Dyson functional \(Z_{SD} [L^a_\mu ]\).

Fig. 2
figure 2

Diagram D and the associated diagram \(D^\prime \) contributing to \(Z_{SD}\)

Full size image

Equation (3.8) also specifies the leading term of the operator product expansion [4]

$$\begin{aligned}{}[\delta S / \delta A^a_\mu (0) ] \, [ \delta S / \delta A^b_\nu (x) ] \rightarrow \sum _n C_n(x) \, {{\mathscr {O}}}_n. \end{aligned}$$
(3.11)

Indeed the value of the coefficient function \(C_1(x)\) for the identity operator \({{\mathscr {O}}}_1 = 1\) is determined by expression (3.9)

$$\begin{aligned} C_1(x) = \left( \frac{k}{4 \pi } \right) \delta ^{ab} \varepsilon ^{\mu \nu \lambda } \partial _\lambda \delta ^3 (x), \end{aligned}$$
(3.12)

and it does not receive perturbative corrections.

The Schwinger–Dyson functional for the abelian Chern–Simons theory can be obtained in the \(f^{abc} \rightarrow 0 \) limit. In this case, Eq. (3.8) becomes

(3.13)

When \(L_\mu (x)\) coincides with the de Rham–Federer current [35,36,37,38] associated with a link \({\mathscr {L}}\) (with support on a Seifert surface [25] which bounds the link \({\mathscr {L}}\, \)), expression (3.13) represents precisely the exponent of the linking matrix corresponding to \({\mathscr {L}}\). For this reason, in the abelian Chern–Simons theory the Schwinger–Dyson functional provides the solution [22] for the link observables.

Finally, let us consider the ISU(2) BF theory [39,40,41,42,43] in \({{\mathbb {R}}}^3\), with fields \(A^a_\mu (x)\) and \(B^a_\mu (s)\) and gauge-fixed action in the Landau gauge

(3.14)

where the real parameter g denotes a coupling constant and

$$\begin{aligned} F^a_{\mu \nu }(A) = \partial _\mu A_\nu ^a - \partial _\nu A_\mu ^a - \varepsilon ^{abc} A^b_\mu A^c_\nu . \end{aligned}$$
(3.15)

The non-vanishing propagators for the components of the connection and the auxiliary fields are given by [43]

(3.16)

and

(3.17)

In this model one has

$$\begin{aligned}&\frac{\delta S}{\delta A^a_\mu (x)} = \varepsilon ^{\mu \nu \lambda } \left[ \left( \partial _\nu B^a_\lambda - \varepsilon ^{abc} A^b_\nu B_c^c \right) + \frac{g}{/}2 F^a_{\nu \lambda } (A) \right] \nonumber \\&\quad - \partial ^\mu M^a - \varepsilon ^{abc} \left[ \partial ^\mu {{\overline{c}}}^a c^c - \partial ^\mu {\overline{\xi }}^a \xi ^c \right] , \end{aligned}$$
(3.18)

and

(3.19)

The Schwinger–Dyson functional \(Z_{SD} [L^a_\mu , H^a_\mu ]\) is defined by

$$\begin{aligned} Z_{SD}[L^a_\mu , H^a_\mu ] = \left\langle e^{i \int d^3x \left[ L^a_\mu \left( \delta S / \delta A_\mu ^a \right) + H^a_\mu \left( \delta S / \delta B_\mu ^a \right) \right] }\right\rangle , \end{aligned}$$
(3.20)

where \(L^a_\mu (x)\) and \(H^a_\mu (x)\) are classical sources. The generating functional \(Z[J^a_\mu , K^a_\mu ]\) of the correlation functions for the gauge field \(A^a_\mu (x)\) and \(B_\mu ^a(x)\) is given by

$$\begin{aligned} Z[J^a_\mu , k^a_\mu ] = \langle e^{ i \int d^3x \left[ J^a_ \mu A_\mu ^a + K^a_\mu B^a_\mu \right] } \rangle . \end{aligned}$$
(3.21)

With several field components, the construction and the sum of the Feynman diagrams becomes rather laborious. We get

$$\begin{aligned} Z_{SD}[L^a_\mu , H^a_\mu ] = e^{i G[ L^a_\mu , H^a_\mu ]} \, Z[{\widetilde{J}}^a_\mu , {\widetilde{K}}^a_\mu ], \end{aligned}$$
(3.22)

in which

$$\begin{aligned}&G[ L^a_\mu , H^a_\mu ] = - \int d^3x \, \varepsilon ^{\mu \nu \lambda } \Bigl \{ H^a_\mu \partial _\nu L^a_\lambda + \varepsilon ^{abc} H^a_\mu L^b_\nu L^c_\lambda \nonumber \\&\quad + \frac{g}{/}2 L^a_\mu \partial _\nu L^a_\lambda + \frac{g}{/}3 \varepsilon ^{abc} L^a_\mu L^b_\nu L^c_\lambda \Bigr \} , \end{aligned}$$
(3.23)

and

(3.24)

In addition to the contact terms, which are specified by the local functional \(G[ L^a_\mu , H^a_\mu ] \), in the BF theory there are additional expectation values that can be displayed in their exact form. For instance, since the vacuum polarization vanishes, from Eq. (3.22) one derives the following relation for the connected mean value

$$\begin{aligned}&\int d^3x d^3y d^3z d^3t \, L^a_\mu (x) L^b_\nu (y) L^c_\lambda (z) H^d_\rho (t) \nonumber \\&\qquad \times \left\langle \frac{\delta S}{A^a_\mu (x)} \frac{\delta S}{A^b_\nu (y)} \frac{\delta S}{A^c_\lambda (z)} \frac{\delta S}{B^d_\rho (t)} \right\rangle ^c \nonumber \\&\quad = -i \frac{3}{4 \pi } \int d^3x \, d^3y \, \frac{(x-y)^\lambda }{|x-y|^3} \varepsilon _{\lambda \mu \nu } \varepsilon ^{\mu \rho \tau } \varepsilon ^{\nu \sigma \xi } \varepsilon ^{abc} \varepsilon ^{ade}\nonumber \\&\qquad \times H^b_\rho (x) L^c_\tau (x) L^d_\sigma (y) L^e_\xi (y). \end{aligned}$$
(3.25)

Actually in both the Chern–Simons and the BF theories, the connected components of the Schwinger–Dyson functional containing up to six powers of the external classical sources are exhibited in closed form because of the vanishing of the loop corrections to the two-points and three-points correlation functions of the gauge fields [29, 34, 43].

4 Conclusions

For renormalizable quantum field theories we have shown that, in the perturbative computation of the corresponding Schwinger–Dyson functional \(Z_{SD}\), the use of standard renormalized perturbation theory provides a canonical renormalization procedure for \(Z_{SD}\). In facts, the short distance behaviour of the products of the composite operator \(\delta S [\phi ] / \delta \phi (x)\) turns out to be determined by the ultraviolet properties of the field operators of dimensions 1 (and possibly 2). The explicit combinatoric of the Wick contractions of the field operators and the resulting structure of the Feynman diagrams have been illustrated in the simple cases of the \(\phi ^3\) and \(\phi ^4\) models. We have shown that the connected component of \(Z_{SD}\) is the union of a local functional of the classical source and a non-local part which is specified by the expectation values of field components. The arguments that have been presented in these scalar models naturally extend to a generic theory.

In order to study possible applications of the Schwinger–Dyson functional in gauge field theories of topological type, for the non-abelian Chern–Simons and BF gauge theories, the relationship between the renormalized Schwinger–Dyson functional and the generating functional of the correlation functions of the gauge fields has been derived. In these cases, the vanishing of the loop corrections for the two-points and three-points correlation functions implies that the connected components of the renormalized Schwinger–Dyson functional containing up to six powers of the external classical sources have been produced in closed form. In these topological models, the derivative of the action with respect of the gauge fields is proportional to the curvature of the connection (plus gauge-fixing contributions). So relations (3.8) and (3.22) could possibly be used for the introduction of appropriate field variables – similar to the local gauge invariant variables decomposition [44] – which simplify the functional integration when the theory is defined in topological non-trivial manifolds.