Radiative $p_{\perp }$-broadening of fast partons in an expanding quark–gluon plasma

Abstract

We study contribution of radiative processes to $p_{\perp }$-broadening of fast partons in an expanding quark–gluon plasma. It is shown that the radiative correction to $\langle p_{\perp }^2\rangle$ for the QGP produced in AA-collisions at RHIC and LHC may be negative, and comparable in absolute value with the non-radiative contribution. We have found that the QGP expansion enhances the radiative suppression of $p_\perp$-broadening as compared to the static medium.

1 Introduction

One of the major signals of the quark–gluon plasma (QGP) formation in heavy ion collisions at RHIC and LHC is the strong suppression of particle spectra at high transverse momenta. It is believed that this effect (usually called the jet quenching) is a consequence of parton energy loss in the QGP, which softens the jet fragmentation functions. The parton energy loss is dominated by the radiative mechanism through induced gluon emission [1,2,3,4,5,6,7]. The induced gluon emission is caused by multiple scattering of fast partons in the QGP. The induced gluon spectrum can be expressed via the Green function of a 2D Schrödinger equation with an imaginary potential [2, 4], which is proportional to the product $n\sigma _{q\bar{q}}(\rho )$, where n is the QGP number density and $\sigma _{q\bar{q}}(\rho )$ is the dipole cross section of scattering of a $q\bar{q}$ pair off the QGP constituent (here, $\rho$ is the size of the $q\bar{q}$-pair). In the quadratic approximation $\sigma _{q\bar{q}}(\rho )\approx C\rho ^2$, the Hamiltonian of the Schrödinger equation takes the oscillator form with a complex frequency. The square of the frequency is proportional to the transport coefficient $\hat{q}$ [2, 3] defined by the relation $\hat{q}=2Cn$.

Besides the modification of the longitudinal jet structure due to the parton energy loss, multiple parton scattering in the QGP can also modify the transverse structure of the jet. For a single fast parton the mean squared transverse momentum (relative to its initial velocity) in a uniform medium is given by [3]

$$\begin{aligned} \langle p_{\perp }^2\rangle =\hat{q}L\,, \end{aligned}$$

(1)

where L is the path length in the medium. One could expect that the $p_\perp$-broadening of the leading parton in the jet should lead to an increase of azimuthal jet decorrelation in the di-jet events (or in decorrelation of a photon and the jet in the photon-jet events) in AA-collisions [8]. For a better understanding of the in-medium jet evolution, it would be interesting to compare the values of $\hat{q}$ extracted from the $R_{AA}$ data with that obtained from the jet $p_\perp$-broadening. However, due to a considerable background from the azimuthal jet decorrelation in pp collisions related to the Sudakov formfactors [8], experimental detection of the jet $p_\perp$-broadening is a difficult problem. This background is especially large for LHC energies. However, even at RHIC in Au + Au collisions at $\sqrt{s}=0.2$ TeV, where the effect of Sudakov formfactors are weaker, the STAR Collaboration has not detected a statistically significant effect of the jet deflection in the QGP [9]. The first data from ALICE [10] for Pb + Pb collisions at $\sqrt{s}=5.02$ TeV also do not allow to draw a definite conclusion on the jet $p_\perp$-broadening. But the new preliminary ALICE results [11] indicate that the jet $p_\perp$ distribution in 5.02 TeV Pb + Pb collisions may be somewhat narrower than that in pp collisions. The situation with detecting the jet $p_\perp$-broadening can become better after improving the accuracy of the data [12, 13].

On the theoretical side, it would be interesting to understand the role of the radiative contribution to $p_\perp$-broadening. The radiative correction to $p_\perp$-broadening can come from the real and virtual induced gluon emission [14,15,16]. It was expected that, due to smallness of the formation length for dominating soft gluon emission, this effect can be viewed as a local renormalization of $\hat{q}$. In [15], within the oscillator approximation in the soft gluon limit, it was found that the radiative contribution to the mean $p_\perp ^2$, $\langle p_{\perp }^2\rangle _r$, in a homogeneous QGP has a double logarithmic form

$$\begin{aligned} \langle p_{\perp }^2\rangle _r\sim \frac{\alpha _sN_c\hat{q}L}{\pi }\ln ^2(L/l_0)\,, \end{aligned}$$

(2)

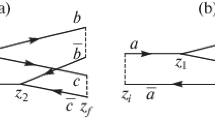
where $l_0$ is the size on the order of the Debye radius in the QGP. For central AA-collisions ($L\sim 5$ fm) the radiative contribution to $\langle p_{\perp }^2\rangle$ turns out to be comparable with that from ordinary multiple scattering [15]. In [15] the authors used the light-cone path integral (LCPI) formalism developed in [4]. The case of the transverse spectra has been addressed within the LCPI technique in our earlier work [17] (see also [5, 18]). In the formulation of [17], for $a\rightarrow bc$ transition the distribution of the particle b in the Feynman variable x and the transverse momentum is described by the diagram of Fig. 1a. The contribution from the virtual process $a\rightarrow bc\rightarrow a$ to the distribution of the final particle a is described by the diagram of Fig. 1b. In the case of $a=b$ both the diagrams contribute to the radiative correction to $p_\perp$-broadening. The parallel lines for two-body parts in Fig. 1 correspond to the Glauber factors, that describe the initial and final state interaction for real and virtual processes, and the three-body part describes dynamics of the transverse motion of the $bc\bar{a}$-state. The analytical expressions for the diagrams of Fig. 1 will be discussed below. Calculations of [15] correspond to the diagrams of Fig. 1, but the authors have not accounted for the effect of the Glauber factors for the initial and final states. In [19, 20] (as in [15] for a static medium), we have addressed the radiative correction to $p_\perp$-broadening with an accurate treatment of the Glauber factors. It was found that the effect of the final state Glauber factors on $\langle p_{\perp }^2\rangle _r$ vanishes for the sum of the real and virtual diagrams. However, the initial state Glauber factors give a considerable negative contribution to $\langle p_{\perp }^2\rangle _r$, and its absolute magnitude turns out to be bigger than the positive contribution from the diagrams of Fig. 1 evaluated without the Glauber factors. As a result, the radiative contribution to the mean $p_\perp ^2$ turns out to be negative, and comparable to the ordinary non-radiative mean $p_\perp ^2$ given by (1) (below we denote it by $\langle p_{\perp }^2\rangle _0$). If this really occurs, then the absence of a signal of the jet deflection in the data [9, 10] may be due to a considerable compensation between the radiative and non-radiative contributions to $p_\perp$-broadening. To understand better whether or not this scenario is possible it is highly desirable to study the radiative $p_\perp$-broadening for a more realistic model with an expanding QGP. This is the purpose of the present paper. The case of the expanding QGP has been addressed previously in [21]. But there the effect of the Glauber factors has not been accounted for.

For an expanding QGP the transport coefficient decreases with the proper time $\tau$. In the Bjorken model [22] without the transverse expansion $\hat{q}(\tau )=\hat{q}(\tau _0)(\tau _0/\tau )$ [23], where $\tau _0$ is the QGP formation time. In this case, in the oscillator approximation, the induced gluon spectrum can be expressed through the Green function for the oscillator frequency $\propto 1/\sqrt{\tau }$. The induced gluon emission in the oscillator approximation, in an expanding QGP has been addressed in [24]. There it was shown that for the transport coefficient $\hat{q}(\tau )=\hat{q}(\tau _0)(\tau _0/\tau )^{\alpha }$ the resulting total radiative energy loss coincides with that for a static medium with an effective transport coefficient given by

$$\begin{aligned} \hat{q}_{st}=\frac{2}{L^2}\int _{\tau _0}^{L} d\tau \tau \hat{q}(\tau )\approx \frac{2}{2-\alpha }\hat{q}(L)\,. \end{aligned}$$

(3)

In [25] it was demonstrated by numerical calculations that for $\alpha \sim$ 0–1.5 this scaling law works very well for the induced gluon spectrum as well. This means that for decreasing with $\tau$ $\hat{q}(\tau )$ the reduction of the radiation rate in the region of large $\tau$, where $\hat{q}(\tau )<\hat{q}_{st}$, is almost compensated by its excess from the region of small $\tau$, where $\hat{q}(\tau )>\hat{q}_{st}$. Of course, this scaling law is not valid for the non-radiative contribution to the mean $p_\perp ^2$, which for an expanding medium reads

$$\begin{aligned} \langle p_{\perp }^2\rangle _{0}=\int _0^L d \tau \hat{q}(\tau )\,. \end{aligned}$$

(4)

One could expect that it does not hold for the radiative contribution $\langle p_{\perp }^2\rangle _r$ as well. Because there is no reason for the delicate compensation between the regions of large and small $\tau$, even if it occurs for the gluon spectrum. However, from the point of view of the jet $p_\perp$-broadening the most interesting quantity is the ratio $\langle p_{\perp }^2\rangle _r/\langle p_{\perp }^2\rangle _{0}$, (which characterizes the relative effect of the radiative correction). For this ratio the violation of the dynamical scaling potentially could be smaller than that for $\langle p_{\perp }^2\rangle _r$ and $\langle p_{\perp }^2\rangle _{0}$ separately. Intuitively, one can expect that for the expanding scenario the ratio $\langle p_{\perp }^2\rangle _r/\langle p_{\perp }^2\rangle _{0}$ should be negative and bigger, in absolute value, than that for the static case. Because, the effect of the negative contribution from the initial parton rescatterings (which is mostly sensitive to the region of small $\tau$) should be more pronounced for the decreasing $\hat{q}(\tau )$. Our numerical calculations confirm this.

Fig. 1

a Diagram representation for the spectrum of the particle b for the $a\rightarrow bc$ process. b Diagram representation for the radiative correction to the spectrum of the particle a from the virtual process $a\rightarrow bc\rightarrow a$. There are also similar diagrams with transposition of vertices between the upper and lower parts of diagrams a and b

The paper is organized as follows. In Sect. 2, we discuss the method for evaluation of the radiative contribution to the mean $p_\perp ^2$ within the LCPI approach. In Sect. 3, we present the results of numerical calculations. Conclusions are contained in Sect. 4. In appendix, we give formulas necessary for numerical calculations of $\langle p_{\perp }^2\rangle _r$ in the oscillator approximation.

2 Theoretical framework for evaluation of $p_\perp$-broadening in LCPI approach

We will consider $p_\perp$-broadening for a fast quark, when the real process is $q\rightarrow q g$ splitting (i.e., $a=b=q$ and $c=g$), and the virtual one is $q\rightarrow qg\rightarrow q$. We assume that the initial quark with energy E is produced at $z=0$ (we choose the z-axis along the initial quark momentum) in the QGP of thickness L. The radiative correction to the distribution of the final quark in x and $p_\perp$ from the real process $q\rightarrow qg$ is described by the diagram of the type shown in Fig. 1a. And the virtual contribution is described by the diagram of the type of shown in Fig. 1b. If one disregards the collisional parton energy loss, the total energy of the two-parton state and the energy of the one-parton state are identical at $z\rightarrow \infty$. However, the medium changes the relative weight of the one-parton and two-parton states, and their transverse momentum distributions. As in [15], we consider the medium effect on the transverse momentum distribution for the final quark, which is integrated over its energy. For the virtual contribution the energy remains unchanged, but rescatterings in the medium of the intermediate two-particle state differ from rescatterings of a single quark. The radiative contribution to the mean quark $p_\perp ^2$ due to the real and virtual process, associated with the interaction with the medium can be written as [15]

$$\begin{aligned} \langle p_\perp ^2\rangle _r=\int dx d{\mathbf{p}}_\perp {\mathbf{p}}_\perp ^2 \left[ \frac{dP}{dxd{\mathbf{p}}_\perp }+\frac{d \tilde{P}}{dxd{\mathbf{p}}_\perp }\right] _{ind}\,, \end{aligned}$$

(5)

where $\frac{d P}{dxd{\mathbf{p}}_\perp }$ is the distribution in the Feynman variable $x=x_q$ and the transverse momentum of the quark for real process $q\rightarrow qg$, and $\frac{d\tilde{P}}{dxd{\mathbf{p}}_\perp }$ is the distribution for the virtual process $q\rightarrow qg \rightarrow q$. The subscript “ind” indicates that the purely vacuum contribution is subtracted. For the virtual process, x is determined by the Feynman variable of the quark in the intermediate qg state. The variable $p_\perp$ in (5) for the real and virtual terms corresponds to the final quarks. Of course, formula (5) can be written in terms of the Feynman variable for the gluon, $x_g=E_g/E$, which is connected with $x_q$ by the relation $x_q+x_g=1$.

Let us consider first the real splitting. For $a\rightarrow bc$ splitting the distribution on the transverse momentum and the longitudinal fractional momentum of the particle b (which includes both the vacuum and the induced contributions) can be written in the form [17] (see also [20])

$$\begin{aligned} \frac{dP}{dx_b d{\mathbf{p}}_\perp }=\frac{1}{(2\pi )^{2}} \int \!\! d{{\varvec{\tau }}}_f\,\exp (-i{\mathbf{p}}_\perp {{\varvec{\tau }}}_f)F({{\varvec{\tau }}}_f)\,, \end{aligned}$$

(6)

where

$$\begin{aligned} F({{\varvec{\tau }}}_f)= & {} 2\hbox {Re}\!\! \left. \int _{0}^{\infty }\!\!dz_{1}\!\!\int _{z_{1}}^{\infty }\!\!dz_{2} \Phi _{f}({{\varvec{\tau }}}_f,z_{2}) \hat{g}\right. \nonumber \\&\times \left. {\mathcal {K}}({{\varvec{\rho }}}_{2},z_{2}|{{\varvec{\rho }}}_1,z_{1}) \Phi _{i}({{\varvec{\tau }}}_i,z_{1})\right| _{{{\varvec{\rho }}}_2={{\varvec{\tau }}}_f, {{\varvec{\rho }}}_1=0} \,, \end{aligned}$$

(7)

$$\begin{aligned} \Phi _{i}({{\varvec{\tau }}}_i,z_{1})= & {} \exp \left[ -\frac{\sigma _{a\bar{a}}({{\varvec{\tau }}}_i)}{2} \int _{0}^{z_{1}}\!dz n(z)\right] \,, \end{aligned}$$

(8)

$$\begin{aligned} \Phi _{f}({{\varvec{\tau }}}_f,z_{2})= & {} \exp \left[ -\frac{\sigma _{b\bar{b}}({{\varvec{\tau }}}_f)}{2} \int _{z_{2}}^{\infty }\!dz n(z)\right] \,, \end{aligned}$$

(9)

${{\varvec{\tau }}}_i=x_b{{\varvec{\tau }}}_f$, n(z) is the number density of the medium, $\sigma _{a\bar{a}}$ and $\sigma _{b\bar{b}}$ are the dipole cross sections for the $a\bar{a}$ and $b\bar{b}$ pairs, $\hat{g}$ is the vertex operator, ${\mathcal {K}}$ is the Green function for the Hamiltonian

$$\begin{aligned} H=\frac{{\mathbf{q}}^2+\epsilon ^2}{2M} -\frac{in(z)\sigma _{\bar{a}bc}({{\varvec{\tau }}}_i,{{\varvec{\rho }}})}{2}\,, \end{aligned}$$

(10)

where ${\mathbf{q}}=-i\partial /\partial {{\varvec{\rho }}}$, $M=E_{a}x_bx_c$, $\epsilon ^2=m_{b}^{2}x_c+m_{c}^{2}x_b-m_{a}^{2}x_bx_c$ with $x_c=1-x_b$, and $\sigma _{\bar{a}bc}$ is the cross section for the three-body $\bar{a}bc$ system. The relative transverse parton coordinates for the $\bar{a}bc$ state are given by ${{\varvec{\rho }}}_{b}-{{\varvec{\rho }}}_{\bar{a}} ={{\varvec{\tau }}}_i+x_c{{\varvec{\rho }}}$, ${{\varvec{\rho }}}_{c}-{{\varvec{\rho }}}_{\bar{a}} ={{\varvec{\tau }}}_i-x_b{{\varvec{\rho }}}$. The vertex operator in (7) reads

$$\begin{aligned} \hat{g} =\frac{P^b_a(x_b)g(z_1)g(z_2)}{8\pi M^2} \frac{\partial }{\partial {{\varvec{\rho }}}_1} \frac{\partial }{\partial {{\varvec{\rho }}}_2} \,, \end{aligned}$$

(11)

where $P^b_a(x_b)$ is the standard $a\rightarrow b$ splitting function. Differentiation with respect to ${{\varvec{\rho }}}_1$ and ${{\varvec{\rho }}}_2$ on the right-hand side of (7) should be performed at a fixed ${{\varvec{\tau }}}_i$, i.e. for a fixed position of the center mass of the bc pair. The Glauber factors $\Phi _i$ and $\Phi _f$ in (7) correspond to the parallel lines in Fig. 1 for the initial ($z<z_1$) and final ($z>z_2$) particles, and the Green function ${\mathcal K}$ describes evolution of the three-body system in Fig. 1 between $z_1$ and $z_2$. The factor 2 in (3) accounts for the contribution from the diagram that can be obtained by inter-exchange of the vertices between the upper and lower lines in Fig. 1.

For $q\rightarrow qg$ splitting the three-body cross section reads [26]

$$\begin{aligned} \sigma _{\bar{q}qg}= \frac{9}{8}\left[ \sigma _{q\bar{q}}({{\varvec{\rho }}}_{qg})+\sigma _{q\bar{q}}({{\varvec{\rho }}}_{g\bar{q}})\right] -\frac{1}{8}\sigma _{q\bar{q}}({{\varvec{\rho }}}_{q\bar{q}})\,, \end{aligned}$$

(12)

where

$$\begin{aligned} \sigma _{q\bar{q}}(\rho )= & {} C_{F}C_{T}\int d{\mathbf{q}}\alpha _{s}^{2}(q^2) \frac{[1-\exp (i{\mathbf{q}}{{\varvec{\rho }}})]}{(q^{2}+m_{D}^{2})^{2}}\nonumber \\= & {} \frac{2}{\pi }\int d{\mathbf{q}}[1-\exp (i{\mathbf{q}}{{\varvec{\rho }}})]\frac{d\sigma }{dq^2}\,, \end{aligned}$$

(13)

is the dipole cross section for the $q\bar{q}$ system, $m_D$ is the Debye mass, $C_F$ and $C_T$ are the color Casimir operators for quark and the QGP constituent, $d\sigma /dq^2$ is the differential cross section for quark scattering off the QGP constituent. The ratio $C(\rho )=\sigma _{q\bar{q}}(\rho )/\rho ^2$ is a smooth function of $\rho$. For the quadratic approximation

$$\begin{aligned} \sigma _{q\bar{q}}(\rho )=C\rho ^2,\quad C=\hat{q}C_F/2C_An\,, \end{aligned}$$

(14)

the Hamiltonian (10) can be written in the oscillator form. For an expanding medium the oscillator frequency depends on z.

The purely vacuum contribution to $a\rightarrow bc$ splitting in (7) comes from the region of large $z_{1,2}$ up to $z_f=\infty$. For an accurate treatment of the contribution of this region, an adiabatically switching off coupling should be used in the vertex factor (11). To separate the vacuum contribution it is convenient to write the product $\Phi _{f} \hat{g} {\mathcal {K}}\Phi _{i}$ on the right-hand side of (7) as (we omit arguments for clarity)

$$\begin{aligned} \Phi _f\hat{g}{\mathcal K}\Phi _i= & {} \Phi _f\hat{g}({\mathcal {K}}-{\mathcal {K}}_v)\Phi _i+ (\Phi _f-1)\hat{g}{\mathcal K}_v\Phi _i\nonumber \\&+{\hat{g}\mathcal {K}}_v(\Phi _i-1)+\hat{g}{\mathcal K}_v\,. \end{aligned}$$

(15)

Here ${\mathcal K}_v$ is the vacuum Green function, and the last term on the right-hand side of (15) corresponds to the ordinary vacuum splitting. Its contribution can be calculated using the adiabatically switching off coupling $g(z)=g\exp (-\delta z)$ and taking the limit $\delta \rightarrow 0$ (see [20] for details). This leads to the vacuum spectrum

$$\begin{aligned} \frac{dP_{v}}{dx d{\mathbf{p}}_\perp }=\frac{\alpha _sP_{ba}(x)}{2\pi ^2} \frac{{\mathbf{p}}_\perp ^2}{({\mathbf{p}}_\perp ^2+\epsilon ^2)^2}\,, \end{aligned}$$

(16)

where $P_{ba}$ is the conventional $a\rightarrow b$ splitting function. Note that calculation of the medium dependent contribution to the spectrum of the last but one term in (15) also requires using the adiabatically switching off coupling. The region of very large $z_{1,2}$ is not important for the first two terms on the right hand side of (15), and they can be calculated with a z-independent coupling.

The distribution $\frac{d \tilde{P}}{dxd{\mathbf{p}}_\perp }$ for the virtual process $a\rightarrow bc \rightarrow a$, which is described by the diagram of Fig. 1b, can be written in the form similar to that for the real process by replacing F by its virtual counterpart $\tilde{F}$, given by

$$\begin{aligned} \tilde{F}({{\varvec{\tau }}}_f)= & {} -2\hbox {Re}\!\! \int _{0}^{\infty }\!\!dz_{1}\!\!\int _{z_{1}}^{\infty }\!\!dz_{2} \Phi _{f}({{\varvec{\tau }}}_f,z_{2}) \nonumber \\&\left. \times \hat{g} \tilde{\mathcal {K}}({{\varvec{\rho }}}_{2},z_{2}|{{\varvec{\rho }}}_1,z_{1}) \Phi _{i}({{\varvec{\tau }}}_i,z_{1})\right| _{{{\varvec{\rho }}}_2={{\varvec{\rho }}}_1=0} \,. \end{aligned}$$

(17)

Except for the opposite sign, the functional form of $\tilde{F}$ is similar to that for F, given by (7), but now we have ${{\varvec{\tau }}}_i={{\varvec{\tau }}}_f$, and the Green function (we denote it $\tilde{\mathcal {K}}$), for the three-body part between $z_1$ and $z_2$, should be calculated at ${{\varvec{\rho }}}_1={{\varvec{\rho }}}_2=0$. The change of the sign in (17) as compared to (7) occurs due to the fact that for the virtual process both the vertices, for parton splitting and merging, belong to the amplitude (upper part of the graph of Fig. 1b), which changes the sign of the vertex operator (11). Note that, similarly to the Green function $\mathcal {K}$ entering the formula (7) for F, the Green function $\tilde{\mathcal {K}}$ in (17) has a hidden dependence on ${{\varvec{\tau }}}_f$ coming from the ${{\varvec{\tau }}}_f$-dependence of its Hamiltonian. For $\tilde{\mathcal {K}}$ the Hamiltonian is also given by (10), but now with ${{\varvec{\tau }}}_i={{\varvec{\tau }}}_f$. It is important that due to different relations between ${{\varvec{\tau }}}_i$ and ${{\varvec{\tau }}}_f$ for the real and virtual diagrams, the initial Glauber factors $\Phi _i({{\varvec{\tau }}}_i)$ in (7) and (17) differ as well.

It is evident that $\langle p_\perp ^2\rangle _r$ can be expressed in terms of the Laplacian of function $F+\tilde{F}$ with respect to ${{\varvec{\tau }}}_f$ at ${{\varvec{\tau }}}_f=0$ as¹

$$\begin{aligned} \langle p_\perp ^2\rangle _r= -\int dx \left. [\nabla ^2F({{\varvec{\tau }}}_f)+\nabla ^2\tilde{F}({{\varvec{\tau }}}_f)] \right| _{{{\varvec{\tau }}}_f=0}\,. \end{aligned}$$

(18)

We stress that calculation of the Laplacians in (18) should be performed treating the functions F and $\tilde{F}$ as functions of ${{\varvec{\tau }}}_f$ only, i.e., using the rigid connections ${{\varvec{\rho }}}_2={{\varvec{\tau }}}_f$, ${{\varvec{\tau }}}_i=x{{\varvec{\tau }}}_f$ for F and ${{\varvec{\tau }}}_i={{\varvec{\tau }}}_f$ for $\tilde{F}$ in calculating the initial Glauber factors $\Phi _i$ and the Green functions $\mathcal {K}$ and $\tilde{\mathcal {K}}$. A simple calculation using the identity (15), after subtraction of the purely vacuum contributions, allows to represent $\langle p_\perp ^2\rangle _r$ as a sum of three terms

$$\begin{aligned} \langle p_\perp ^2\rangle _r=I_1+I_2+I_3\,, \end{aligned}$$

(19)

where $I_i$ are given by

$$\begin{aligned} I_1= & {} -2\int dx\int _{0}^L dz_1 \int _{0}^{\infty } d\Delta z \hbox {Re}\Big \{\nabla ^2\hat{g}\nonumber \\&\times [{\mathcal { K}} ({{\varvec{\rho }}}_2 , z_2 | {{\varvec{\rho }}}_1 , z_1)- {\mathcal { K}}_v ({{\varvec{\rho }}}_2 , z_2 | {{\varvec{\rho }}}_1 , z_1)]\nonumber \\&\times \Big |_{{{\varvec{\rho }}}_2={{\varvec{\tau }}}_f,{{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0} \nonumber \\&-\nabla ^2\hat{g} [\tilde{\mathcal { K}} ({{\varvec{\rho }}}_2 , z_2 | {{\varvec{\rho }}}_1 , z_1) \nonumber \\&- \tilde{\mathcal { K}}_v ({{\varvec{\rho }}}_2 , z_2 | {{\varvec{\rho }}}_1 , z_1)]\Big |_{{{\varvec{\rho }}}_2={{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0}\Big \}\,, \end{aligned}$$

(20)

$$\begin{aligned} I_2= & {} -2\int dx \int _{0}^L dz_1 \int _{0}^{\infty } d\Delta z \hbox {Re}\Big \{\hat{g}\nonumber \\&\times [{\mathcal K}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)-{\mathcal K}_v({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)]\nonumber \\&\times \nabla ^2\Phi _i(x{{\varvec{\tau }}}_f,z_1)\Big |_{{{\varvec{\rho }}}_2={{\varvec{\tau }}}_f,{{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0} \nonumber \\&-\hat{g}[\tilde{{\mathcal K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1) -\tilde{{\mathcal K}}_v ({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)]\nonumber \\&\times \nabla ^2\Phi _i({{\varvec{\tau }}}_f,z_1)\Big |_{{{\varvec{\rho }}}_2={{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0}\Big \} \nonumber \\= & {} -2 \!\int \!dx f(x)\!\!\int _{0}^L\!\!\! dz_1 \langle p_\perp ^2(z_1)\rangle _0 \int _{0}^{\infty }d\Delta z \hbox {Re}\hat{g}\nonumber \\&\times \left[ {\mathcal K}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)-{\mathcal K}_v({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)\right] \Big |_{{{\varvec{\rho }}}_2={{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0}\,, \end{aligned}$$

(21)

$$\begin{aligned} I_3= & {} \int dx \nabla ^2[\Phi _i({{\varvec{\tau }}}_f,L) -\Phi _i(x{{\varvec{\tau }}}_f,L)]\Big |_{{{\varvec{\tau }}}_f=0} \frac{dP_v}{dx}\nonumber \\= & {} -\langle p_\perp ^2\rangle _0 \int dx f(x)\frac{dP_v}{dx}\,, \end{aligned}$$

(22)

Here $\langle p_\perp ^2(z_1)\rangle _0=\int _0^{z_1}\hat{q}(z)dz$, $f(x)=1-x^2$, $\Delta z=z_2-z_1$, and $dP_v/dx$ is the x-spectrum for vacuum given by

$$\begin{aligned} \frac{dP_v}{dx}=\int d{\mathbf{p}}_\perp \frac{dP_v}{dx d{\mathbf{p}}_\perp }\,. \end{aligned}$$

(23)

In the expressions for $I_{2,3}$, we have used that

$$\begin{aligned}&\hat{g} [{\mathcal K}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)-{\mathcal K}_v({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)]\Big |_{{{\varvec{\rho }}}_2={{\varvec{\tau }}}_f,{{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0}\nonumber \\&\quad =\hat{g}[\tilde{{\mathcal K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1) -\tilde{{\mathcal K}}_v ({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)]\Big |_{{{\varvec{\rho }}}_2={{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0}\,,\nonumber \\ \end{aligned}$$

(24)

and the equalities

$$\begin{aligned}&\nabla ^2\Phi _i(x{{\varvec{\tau }}}_f,z_1)\Big |_{{{\varvec{\tau }}}_f=0}=x^2\nabla ^2\Phi _i({{\varvec{\tau }}}_f,z_1)\Big |_{{{\varvec{\tau }}}_f=0}, \nonumber \\&\nabla ^2\Phi _i({{\varvec{\tau }}}_f,z_1)\Big |_{{{\varvec{\tau }}}_f=0}=-\langle p_\perp ^2(z_1)\rangle _0. \end{aligned}$$

(25)

The terms $I_{1,2}$ in (19) arise from calculating the Laplacian in ${{\varvec{\tau }}}_f$ of the first term on the right hand side of (15), and $I_3$ of the third term. The second term on the right hand side of (15) does not contribute to $\langle p_\perp ^2\rangle _r$) because its Laplacian (for sum of the real and virtual terms) vanishes at ${{\varvec{\tau }}}_f=0$. The integral over $p_\perp$ in (23) diverges logarithmically for large $p_{\perp }$. In numerical calculations, we regularized it by limiting the integration region to $p_\perp <p_\perp ^{max}$ with $p_\perp ^{max}=E\hbox {min}(x,(1-x))$. We use expressions (19)–(22) for numerical calculations. The formulas required for calculating $I_{1,2}$ in the oscillator approximation are given in Appendix.

The integrand in the formula (20) for $I_1$ behaves as $1/\Delta z$ for $\Delta z\rightarrow 0$, which leads to the logarithmic divergence of $I_1$. In the LCPI approach it is assumed that the typical $|z_2-z_1|$ (i.e., the formation length $L_f$) is bigger than the correlation radius of the medium. For the QGP it is the Debye radius. For this reason, it is reasonable to regularize the integration over $\Delta z$ taking the lower limit in (20) at $\Delta z\sim 1/m_D$. This prescription was used in [15] in calculating with a logarithmic accuracy the analogue of our contribution $I_1$. As we mentioned in the Introduction, in [15] the Glauber factors $\Phi _{i,f}$ have not been accounted for. For this reason, the terms $I_{2,3}$ which contain $\nabla ^2 \Phi _i$ have been missed. It will be seen from the numerical calculations that these terms give a negative contribution which is larger in magnitude than $I_1$.

One remark should be made about the application of the above formulas to the $p_\perp$-broadening in the real QGP. Formally, in the oscillator approximation, one can use a unique transport coefficient for calculating the Green function and the Glauber factors. However, physically it is clear that the values of the transport coefficient that enters the Hamiltonian (via the oscillator frequency (A7)) and the Laplacian of the Glauber factor $\Phi _i$ (25) (via $\langle p_\perp ^2\rangle _{0}$) may differ due to the Coulomb effects. The transport coefficient of the fast quark (we will denote it $\hat{q}'$, and leave the notation $\hat{q}$ for the transport coefficient that enters the oscillator frequency) that controls $\langle p_\perp ^2\rangle _{0}$ can be written in a simple probabilistic form [3, 23, 27]

$$\begin{aligned} \hat{q}'=n\int _{0}^{p_{\perp max}^2} dp_\perp ^2 p_\perp ^2\frac{d\sigma }{d p_\perp ^2} \end{aligned}$$

(26)

with $p^2_{\perp max}\sim 3E T$, T the QGP temperature, $d\sigma /d p_\perp ^2$ the differential cross section for quark scattering off the thermal parton. The transport coefficient for the Hamiltonian for the induced gluon emission it is reasonable to define as $\hat{q}=2nC(\rho _{eff})$ [4, 28], where $\rho _{eff}$ is the typical size of the gq-state. From the Schrödinger diffusion relation one obtains for soft gluons $\rho _{eff}\sim \sqrt{2L_{f}^{eff}/\omega }$. Here $L_f^{eff}$ is the effective in-medium gluon formation length, which in the oscillator approximation is given by the inverse oscillator frequency $1/|\Omega |$.² For the relevant region $\rho _{eff}\lesssim 1/m_D$, with the help of the double gluon formula (13), one can show that the product $2nC(\rho _{eff})$ coincides with (26) but with $p_{max}^2\sim 10/\rho _{eff}^2$ (see, e.g. [29]). This prescription gives the value of the transport coefficient $\hat{q}$ about $\hat{q}'$ calculated for the quark energy $\sim \omega$. For RHIC and LHC conditions, for gluon emission from a quark with $E\sim 30-100$ GeV the typical gluon energy $\bar{\omega }\sim 3-5$ GeV, i.e., $\bar{\omega }/E\ll 1$. Although, $\hat{q}'$ has a smooth (logarithmic) dependence on E, the ratio $r=\hat{q}'/\hat{q}$ may differ significantly from unity due to the fact that $E\gg \bar{\omega }$. As will be seen below this gives a considerable effect on the magnitude of $\langle p_\perp ^2\rangle _r$.

Finally, we would like to make a remark on the physical interpretation of the $I_3$ term, which, as will be seen below, may dominate in the sum (19). From (22) one sees that $I_3$ contains $\langle p_\perp ^2\rangle _0$ for the whole medium, and the vacuum spectrum $dP_v/dx$ without medium modification. At first glance, this says that the $I_3$ is connected with real and virtual gluon emission outside the medium from the initial parton which has undergone multiple scattering in the whole medium. However, this interpretation is completely wrong. In reality the vacuum like gluon emission occurs at the longitudinal distances which may be much smaller than the QGP size. Say, for jets with $E\lesssim 100$ GeV the typical z-scale for the vacuum like gluon emission is $\lesssim 1$ fm [30], and the typical jet path length in the QGP is $\sim 5$ fm. For this reason, it is clear that typically for the vacuum like gluon emission we have a situation with multiple scattering in the QGP of the final partons (say, if the QGP is formed at $\tau _0 > rsim 1$ fm, the contribution of the initial parton rescatterings will be very small). The form of the $I_3$ term is just a nontrivial consequence of the representation of the product $\Phi _f\hat{g}{\mathcal K}\Phi _i$ in the rearranged form on the right hand side of (15), and of the fact that the color charge of the final quark equals to that for the initial quark. But one should bear in mind that the decomposition on the right hand side of (15) by adding and subtracting the terms with the vacuum Green function is an artificial procedure, and only the full sum, given on the left hand side of (15), matters. For this reason, all the terms in (19) have the same status, and it does not make sense to say that the $I_3$ is connected with a specific mechanism due to rescatterings of the initial quark in the whole medium and its subsequent splitting into gq state outside the QGP. Of course, such processes are possible, but their contribution to $p_\perp$-broadening becomes very small at $L\gg 1$ fm.

3 Numerical results

We will consider $p_\perp$-broadening for conditions of central heavy ion collisions at RHIC and LHC. We assume that the plasma fireball is produced at the proper time $\tau =0.5$ fm. For the fast parton path length in the QGP we take $L=5$ fm, which is the typical jet path length in the QGP for for Au + Au (Pb + Pb) collisions at RHIC(LHC). We neglect the variation of the initial QGP temperature in the impact parameter. In this case, z-dependence of the transport coefficient along the fast parton path coincide with its $\tau$-dependence. We describe the QGP evolution at $\tau >\tau _0$ within Bjorken’s model [22] without the transverse expansion that leads to the entropy density $s\propto 1/\tau$. Within the ideal gas model it gives $\hat{q}(z)=\hat{q}_0(\tau _0/z)$ at $z>\tau _0$, where $\hat{q}_0$ is the value of the transport coefficient at $\tau =\tau _0$. To account for qualitatively the fact that the QGP formation is not instantaneous we take $\hat{q}(z)=\hat{q}_0(z/\tau _0)$ for $z<\tau _0$.

For main variant we use the quasiparticle masses $m_{q}=300$ MeV and $m_{g}=400$ MeV, which were obtained within quasiparticle model from the lattice data in [31] for temperatures relevant for RHIC and LHC conditions. With these values of the quasiparticle masses, in [32, 33], we successfully described the RHIC and LHC data on the nuclear modification factor $R_{AA}$. To understand the uncertainties associated with the parton masses, we also perform calculations for masses $m_{q}=150$ MeV and $m_{g}=200$ MeV. As in [15], we take $\alpha _s=1/3$ at the vertex of the $q\rightarrow qg$ transition. Also, like in [15], we regularize the $1/\Delta z$ divergence in (20) by truncating the integration at $\Delta z_{min}=1/m$ with $m=300$ MeV. In (20)–(22) we integrate over x from $x_{min}=m_q/E$ up to $x_{max}=1-m_g/E$ (recall that we define x as $x_q$; in terms of $x_g$, our integration region corresponds to the variation of $x_g$ from $m_g/E$ to $1-m_q/E$).

To fix the value of the parameter $\hat{q}_0$ in the above parametrization of $\hat{q}(z)$ we use the results of our previous analyses of jet quenching beyond the oscillator approximation. In [32, 33] we have performed calculations of $R_{AA}$ with running $\alpha _s$ beyond the the oscillator approximation with accurate treatment of the Coulomb effects. To make our analysis as accurate as possible we adjusted the value of $\hat{q}_0$ to reproduce the quark energy loss $\Delta E$ for the running $\alpha _s$ in the model of [33] with the Debye mass from the lattice calculations [34]. This procedure gives $\hat{q}_0\approx 0.551$ GeV$^3$ at $E=30$ GeV for Au + Au collisions at $\sqrt{s}=0.2$ TeV and $\hat{q}_0\approx 0.719$ GeV$^3$ at $E=100$ GeV for Pb + Pb collisions at $\sqrt{s}=2.76$ TeV³ (we call these variants the RHIC(LHC) versions). In terms of the $\hat{q}_{st}$ for the static scenario given by (3) our RHIC(LHC) versions correspond to $\hat{q}_{st} \approx 0.103(0.134)$ GeV$^3$. We have used a similar running $\alpha _s$ and the Debye mass to determine the introduced in section 2 the coefficient r describing the enhancement of the transport coefficient entering the Glauber factor. We obtained for the RHIC(LHC) versions $r\approx 2(2.3)$. We are fully aware that the errors in the factor r may be rather large. But the fact that $\hat{q}'/\hat{q}$ should be $\sim 2$ seems to be fairly reliable.

Table 1 The results for $m_q=300$ MeV, $m_g=400$ MeV obtained with $\hat{q}'=\hat{q}$ and with $\hat{q}'=r\hat{q}$ (the numbers in brackets)

Table 2 The same as in Table 1, but for $m_q=150$ MeV, $m_g=200$ MeV

In Table 1 we present the results for the ratio of the terms $I_{1,2,3}$ and of the total $\langle p_\perp ^2\rangle _r$ to the $\langle p_\perp ^2\rangle _{0}$ for our main variant of the parton masses ($m_q=300$ MeV and $m_g=400$ MeV). We also give $\langle p_\perp ^2\rangle _{0}$. We present the results both for the expanding and for static models. For the static case the calculations are performed using $\hat{q}_{st}$. The results for the set $m_q=150$ MeV and $m_g=200$ MeV are given in Table 2. The comparison of the results from Tables 1 and 2, shows that the sensitivity of the predictions to the parton masses turns out to be not very strong. Note that the sensitivity of the induced gluon emission to the mass of the light quark is generally low (except for the emission of hard gluons with $x_g\sim 1$), and the change in the predictions is mainly due to variation of $m_g$.

From Tables 1 and 2, one can see that in all the cases $\langle p_\perp ^2\rangle _r<0$. This occurs because the negative contribution from the $I_{2,3}$ terms turns out to be larger in magnitude than the positive contribution of the $I_1$. Note that, as we expected, the relative effect of the negative contribution to the mean $p_\perp ^2$ from the Glauber factors becomes bigger for the expanding QGP. The negative $\langle p_\perp ^2\rangle _r$ can lead to a sizable reduction of the total (non-radiative plus radiative) mean $p_\perp ^2$. For the version with $\hat{q}'=\hat{q}$ the reduction is approximately by half for the expanding scenario. For the version with $\hat{q}'>\hat{q}$ the magnitude of the negative radiative contribution is comparable to that from the non-radiative mechanism, and the total mean $p_\perp ^2$ may be very small. However, one should bear in mind that this conclusion may depend on the value of the $I_1$ term, which requires the $\Delta z$-regularization. To understand the sensitivity of the results to the lower limit of the $\Delta z$-integration in (20), we have performed calculations for $\Delta z_{min}=1/m$ with $m=600$ MeV. In this case $I_1$ becomes bigger by a factor of $\sim 2.5(2)$ for RHIC(LHC). This gives $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0\approx 0.01(-0.47)$ for $\hat{q}'/\hat{q}=1(r)$ for RHIC, and $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0\approx 0.37(-0.5)$ for $\hat{q}'/\hat{q}=1(r)$ for LHC. Thus, we see that, for the clearly more realistic version with $\hat{q}'>\hat{q}$, the radiative correction to the mean $p_\perp ^2$ is negative, and may suppress the mean $p_\perp ^2$ by a factor of $\sim 2$.

In the above, we presented results of the fixed coupling computations within the oscillator approximation for the dipole cross section. Accurate calculations of the $I_{1,2}$ terms for the running coupling and the double gluon $\sigma _{q\bar{q}}(\rho )$ (13) is a complicated problem. However, for the ratio $I_3/\langle p_\perp ^2\rangle _0$ the form of $\sigma _{q\bar{q}}(\rho )$ is unimportant, and the generalization to the running $\alpha _s$ can be easily done by replacing in $dP_{v}/dx$ the fixed $\alpha _s$ by the running one [20]. We performed such calculations with the one-loop $\alpha _s$ frozen for small momenta at the value $\alpha _{s}^{fr}=0.7$, which was obtained earlier from analysis of the low-x structure functions within the dipole BFKL equation [36]. This value is also supported by the analysis of heavy quark energy loss in vacuum [37]. For expanding scenario (and parton masses as in Table 1), this procedure, while keeping $I_{1,2}/\langle p_\perp ^2\rangle _0$ unchanged, gives $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0\approx -0.76(-0.97)$ for $\hat{q}'/\hat{q}=1(r)$ for RHIC, and $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0\approx -0.5(-0.92)$ for $\hat{q}'/\hat{q}=1(r)$ for LHC. These numbers are for the $\Delta z$-regularization of $I_1$ with $m=300$ MeV. For $m=600$ MeV we obtained $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0\approx -0.19(-0.59)$ for $\hat{q}'/\hat{q}=1(r)$ for RHIC, and $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0\approx 0.29(-0.58)$ for $\hat{q}'/\hat{q}=1(r)$ for LHC. As one can see, for the running $\alpha _s$, the effect of the initial state rescatterings becomes somewhat stronger. As far as the accurate predictions for $I_{1,2}/\langle p_\perp ^2\rangle _0$ are concerned, intuitively, one can expect that the accurate calculations should give smaller values of $I_{1,2}/\langle p_\perp ^2\rangle _0$ than obtained in the present analysis. Indeed, for the Green functions in the formulas (20) and (21) the typical size of the intermediate three-body state (in the sense of their path integral representations) should be, more or less, similar to that for the induced gluon emission. But we adjusted $\hat{q}$ (i.e. $2nC(\rho _{eff})$) to reproduce the induced gluon emission energy loss obtained with the running coupling and accurate $\sigma _{q\bar{q}}(\rho )$. This means that the variation of the $I_{1,2}/\langle p_\perp ^2\rangle _0$ should be approximately similar to the variation of of the ratio $C(\rho _{eff})/C(1/p_{\perp \,max})$ (because $\langle p_\perp ^2\rangle _0\propto C(1/p_{\perp \,max})$. However, for the accurate $C(\rho )$ this ratio will be smaller than that in the oscillator approximation (see e.g. [38]). Note that this occurs even without the logarithmic growth of $C(\rho )$ at $\rho \rightarrow 0$. Thus, one can expect that the accurate calculations should give smaller $I_{1,2}/\langle p_\perp ^2\rangle _0$. As a results, the effect of the negative contribution from the $I_3$ term on the $\langle p_\perp ^2\rangle _r/\langle p_\perp ^2\rangle _0$ will be more pronounced.

4 Conclusions

We have studied the radiative $p_\perp$-broadening of fast partons in an expanding QGP for conditions of central Au + Au (Pb + Pb) collisions at RHIC(LHC). The analysis has been performed within the LCPI formalism [4, 17] in the oscillator approximation, accounting for the initial state rescatterings. Similarly to the case of the static QGP, addressed in [19, 20], we have found that the radiative correction may be negative, i.e., it may lead to reduction of $p_\perp$-broadening. The negative contribution to $\langle p_\perp ^2\rangle _r$ comes mostly from the difference of the initial state Glauber factors for the real and virtual processes. This effect appears naturally beyond the soft gluon approximation. Formally, this phenomenon is due to rescatterings of the initial parton for the vacuum like gluon emission. However, we argue that this interpretation is wrong, and the effect is dominated by rescatterings of the final fast parton.

We have found that the QGP expansion leads to a sizeable increase of the effect of the initial state rescatterings, as compared to the static QGP. Our numerical results show that for the RHIC and LHC conditions, due to the negative $\langle p_\perp ^2\rangle _r$ the total (non-radiative plus radiative) mean $p_\perp ^2$ may be quite small. In light of this, it is possible that the negative experimental searches for the jet rescatterings in the QGP [9,10,11] may be due to a considerable reduction of $p_\perp$-broadening by the radiative contribution.

Appendix A: Formulas necessary for calculating the factors \(I_i\)

In this appendix, we give formulas necessary for numerical calculations of the contributions $I_i$ in (19) with the help of (20)–(22) in the oscillator approximation. For quadratic parameterization of the dipole cross section $\sigma _{q\bar{q}}(\rho )=C\rho ^2$ (in terms of quark transport coefficient $C=\hat{q}/2n$), the three-body cross section $\sigma _{\bar{a}bc}$ can be written as

$$\begin{aligned} \sigma _{\bar{a}bc}({{\varvec{\rho }}}, {\mathbf{R}})= C_{b\bar{a}}({{\varvec{\rho }}}_{b}-{{\varvec{\rho }}}_{\bar{a}})^2+C_{c\bar{a}}({{\varvec{\rho }}}_{c}-{{\varvec{\rho }}}_{\bar{a}})^2 +C_{bc}({{\varvec{\rho }}}_{b}-{{\varvec{\rho }}}_{c})^2\,, \end{aligned}$$

(A1)

where, ${{\varvec{\rho }}}={{\varvec{\rho }}}_{b}-{{\varvec{\rho }}}_c$, ${\mathbf{R}}=x_c{{\varvec{\rho }}}_b+x_b{{\varvec{\rho }}}_c-{{\varvec{\rho }}}_{\bar{a}}$, ${{\varvec{\rho }}}_{b}-{{\varvec{\rho }}}_{\bar{a}}={\mathbf{R}}+x_c{{\varvec{\rho }}}$, and ${{\varvec{\rho }}}_{c}-{{\varvec{\rho }}}_{\bar{a}}={\mathbf{R}}-x_b{{\varvec{\rho }}}$. For process $q\rightarrow qg$ ($a=b=q$, $c=g$)

$$\begin{aligned} C_{bc}=C_{c\bar{a}}=\frac{9C}{8}\,,\,\,\, C_{b\bar{a}}=-\frac{C}{8}\,. \end{aligned}$$

(A2)

For diagrams in Fig. 1a, ${\mathbf{R}}={{\varvec{\tau }}}_i$. It is convenient to write $\sigma _{\bar{a}bc}$ as

$$\begin{aligned} \sigma _{\bar{a}bc}({{\varvec{\rho }}}, {\mathbf{R}})= Cp{\mathbf{R}}^2+C_3{\mathbf{u}}^2\,, \end{aligned}$$

(A3)

where $C_3=C_{b\bar{a}}x_c^2+C_{c\bar{a}}x_b^2+C_{bc}$, $p=[C_{b\bar{a}}C_{c\bar{a}}+C_{b\bar{a}}C_{bc}+C_{c\bar{a}}C_{bc}]/CC_3$, and the new variable ${\mathbf{u}}$ is given by

$$\begin{aligned} {\mathbf{u}}={{\varvec{\rho }}}+ {{\varvec{\tau }}}_iV \end{aligned}$$

(A4)

with $V=(x_cC_{b\bar{a}}-x_bC_{c\bar{a}})/C_3$. The Hamiltonian (10) can be written in terms of the variable ${\mathbf{u}}$ in the form

$$\begin{aligned} H=H_{osc}-\frac{i \hat{q}(z)p{{\varvec{\tau }}}_i^2}{4}+\frac{\epsilon ^2}{2M}\,, \end{aligned}$$

(A5)

where $\hat{q}(z)=2n(z)C$ is the local transport coefficient, and $H_{osc}$ is the harmonic oscillator Hamiltonian

$$\begin{aligned} H_{osc}= -\frac{1}{2M}\, \left( \frac{\partial }{\partial {\mathbf{u}}}\right) ^{2} +\frac{M\Omega ^2{\mathbf{u}}^2}{2} \end{aligned}$$

(A6)

with the complex z-dependent frequency

$$\begin{aligned} \Omega =\sqrt{\frac{-i\hat{q}(z)C_3}{2CM}}\,. \end{aligned}$$

(A7)

The Green function ${\mathcal {K}}$ for the Hamiltonian (A5) can be written as

$$\begin{aligned} {\mathcal {K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)= & {} K_{osc}({\mathbf{u}}_2,z_2|{\mathbf{u}}_1,z_1)\nonumber \\&\times \exp {\left[ -\frac{p{{\varvec{\tau }}}_i^2}{4}\int _{z_1}^{z_2}q(z) -\frac{i(z_2-z_1)\epsilon ^2}{2M}\right] },\nonumber \\ \end{aligned}$$

(A8)

where $K_{osc}$ is the Green function for the oscillator Hamiltonian (A6). In general, for arbitrary $\Omega (z)$ the oscillator Green function can be written in the form [24, 35]

$$\begin{aligned} K_{osc}({\mathbf{u}}_2,z_2|{\mathbf{u}}_1,z_1)=\frac{\gamma }{2\pi i} \exp {\left[ i(\alpha {\mathbf{u}}_2^2+\beta {\mathbf{u}}_1^2-\gamma {\mathbf{u}}_1\cdot {\mathbf{u}}_2)\right] }\,. \end{aligned}$$

(A9)

The numerical method for evaluation of $\alpha$, $\beta$, and $\gamma$ will be discussed below.

In our formulas (20)–(22), the differential operator $\hat{g}$ (11) is acting on the Green function ${\mathcal {K}}$ at fixed ${{\varvec{\tau }}}_i$. Therefore, in $\hat{g}$, we can replace $\frac{\partial }{\partial {{\varvec{\rho }}}_2}\cdot \frac{\partial }{\partial {{\varvec{\rho }}}_1}$ by $\frac{\partial }{\partial {\mathbf{u}}_2}\cdot \frac{\partial }{\partial {\mathbf{u}}_1}$. Then, from (A9) one obtains

$$\begin{aligned}&\frac{\partial }{\partial {{\varvec{\rho }}}_2}\cdot \frac{\partial }{\partial {{\varvec{\rho }}}_1} {\mathcal {K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)\nonumber \\&\quad = -\left[ 2i\gamma + (2\alpha {\mathbf{u}}_2-\gamma {\mathbf{u}}_1)\cdot (2\beta {\mathbf{u}}_1-\gamma {\mathbf{u}}_2)\right] \nonumber \\&\qquad \times {\mathcal {K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)\,. \end{aligned}$$

(A10)

For the diagram in Fig. 1a, ${{\varvec{\rho }}}_1=0$, ${{\varvec{\rho }}}_2={{\varvec{\tau }}}_f={{\varvec{\tau }}}_i/x_b$, and

$$\begin{aligned} {\mathbf{u}}_{1,2}={{\varvec{\tau }}}_f k_{1,2}\,,\,\,\, k_1=x_bV\,,\,\,\, k_2=1+x_bV\,. \end{aligned}$$

(A11)

Then from (11) we obtain

$$\begin{aligned}&\hat{g}{\mathcal {K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)\Big |_{{{\varvec{\rho }}}_{1,2}={{\varvec{\tau }}}_f=0}\nonumber \\&\quad =-\left( \frac{\alpha _sP_{ba}}{2M^2}\right) \cdot \frac{\gamma ^2}{\pi }\exp {\left[ -\frac{i(z_2-z_1)\epsilon ^2}{2M}\right] }. \end{aligned}$$

(A12)

For calculating $I_1$ (20), we need the Laplacian in ${{\varvec{\tau }}}_f$ for ${{\varvec{\tau }}}_f=0$ of $\hat{g}{\mathcal {K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)$ at ${{\varvec{\rho }}}_{2}={{\varvec{\tau }}}_f$ and ${{\varvec{\rho }}}_1=0$. A simple calculation gives

$$\begin{aligned}&\nabla _{{{\varvec{\tau }}}_f}^2 \hat{g}{\mathcal {K}}({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1)\Big |_{{{\varvec{\rho }}}_2={{\varvec{\tau }}}_f,{{\varvec{\rho }}}_1=0,{{\varvec{\tau }}}_f=0}\nonumber \\&\quad =\left( \frac{\alpha _sP_{ba}}{2M^2}\right) \cdot \frac{2\gamma (2\gamma D-G)}{i\pi } \exp {\left[ -\frac{i(z_2-z_1)\epsilon ^2}{2M}\right] },\nonumber \\ \end{aligned}$$

(A13)

where

$$\begin{aligned} D= & {} \alpha k_2^2+\beta k_1^2-\gamma k_1k_2+ \frac{ix_bp}{4}\int _{z_1}^{z_2}dz \hat{q}(z)\,, \end{aligned}$$

(A14)

$$\begin{aligned} G= & {} (2\alpha k_2-\gamma k_1)(2\beta k_1-\gamma k_2)\,. \end{aligned}$$

(A15)

For the vacuum Green function, one just has to replace in formulas (A12) and (A13) the functions $\alpha$, $\beta$, and $\gamma$ by their vacuum analogues

$$\begin{aligned} \alpha _0=\beta _0=\gamma _0/2=\frac{M}{2(z_2-z_1)}\,. \end{aligned}$$

(A16)

and to set $\hat{q}(z)=0$. In this case one obtains $D_0=\alpha _0$, $G_0=0$.

The formula (A12) holds for the Green function $\tilde{\mathcal {K}}$ for the virtual diagram in Fig. 1b as well. In the virtual counterparts of the formulas (A14) and (A15) $\tilde{k}_{1,2}=V$, and in the last term on the right-hand side of (A14) the factor $x_b$ is absent. For the virtual vacuum contribution $\tilde{D}_0=\tilde{G}_0=0$.

Let us finally discuss evaluation of the functions $\alpha$, $\beta$, and $\gamma$. For a harmonic oscillator with a z-independent frequency $\Omega$

$$\begin{aligned} \alpha =\beta =\frac{M\Omega }{2\tan {(\Omega (z_2-z_1))}}\,,\,\,\,\,\, \gamma =\frac{M\Omega }{\sin {(\Omega (z_2-z_1))}}\,. \end{aligned}$$

(A17)

For numerical calculations in the case of z-dependent frequency $\Omega (z)$ we use the z-slicing method based on the recurrent relations [35]

$$\begin{aligned} \alpha (z_{n+1},z_1)= & {} \alpha (z_{n+1},z_n)- \frac{\gamma ^2(z_{n+1},z_n)}{4[\alpha (z_n,z_1)+\beta (z_{n+1},z_n)]}\,, \nonumber \\ \beta (z_{n+1},z_1)= & {} \beta (z_{n},z_1)- \frac{\gamma ^2(z_{n},z_1)}{4[\alpha (z_n,z_1)+\beta (z_{n+1},z_n)]}\,,\nonumber \\ \gamma (z_{n+1},z_1)= & {} \frac{\gamma (z_{n},z_1)\gamma (z_{n+1},z_n)}{2[\alpha (z_n,z_1) +\beta (z_{n+1},z_n)]}\,. \end{aligned}$$

(A18)

These relation can be readily obtained using (A9) and the convolution formula for the Green functions

$$\begin{aligned} K({{\varvec{\rho }}}_3,z_3|{{\varvec{\rho }}}_1,z_1)=\int d{{\varvec{\rho }}}_2 K({{\varvec{\rho }}}_3,z_3|{{\varvec{\rho }}}_2,z_2) K({{\varvec{\rho }}}_2,z_2|{{\varvec{\rho }}}_1,z_1). \end{aligned}$$

(A19)