NLO QCD corrections to exclusive quarkonium-pair production in photon–photon collision

Abstract

We calculate the next-to-leading order (NLO) quantum chromodynamics (QCD) corrections to the exclusive processes $\gamma +\gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}}$, with ${\mathcal {Q}}=J/\psi ,\ \eta _c,\ \Upsilon$, or $\eta _b$, in the framework of non-relativistic QCD (NRQCD) factorization formalism. The cross sections at the SuperKEKB electron–positron collider, as well as at the future colliders, like the circular electron positron collider (CEPC) and the international linear collider (ILC), are evaluated. Numerical result indicates that the processes for $J/\psi$-pair production and $\eta _c$-pair production are hopefully observable at the Belle II detector within the next decade.

1 Introduction

The $J/\psi$ meson is thought of an ideal laboratory to investigate the perturbative and non-perturbative properties of quantum chromodynamics (QCD) since its discovery in 1974. The non-relativistic QCD (NRQCD) factorization formalism [1], which proposed by Bodwin, Braaten, and Lepage, provide a systematic framework for the theoretical study of quarkonium physics. In the NRQCD factorization formalism, the quarkonium production and decay rates can be factorized as process dependent, but perturbative calculable, short distance coefficients and universal long distance matrix elements (LDMEs). The relative importance between the LDMEs can be estimated by means of velocity scaling rules. In this way, the theoretical prediction takes the form of a double expansion in the strong coupling constant $\alpha _s$ and the heavy quark relative velocity v.

Quarkonium production in photon–photon collision is an interesting topic to study, where the signals are relatively clean. At present, the inclusive $J/\psi$ production via photon–photon scattering was studied extensively [2,3,4,5,6,7]. These researches indicate that the color-singlet (CS) sectors are inadequate to explain the experimental data [2, 7], while the color-octet (CO) contributions based on different LDME sets diverse quite a lot, which even lead to opposite conclusions in some cases [2, 6]. Besides the inclusive single $J/\psi$ production, the exclusive $J/\psi$-pair production, where the CO contributions are suppressed by $v^8$, also provides a test to the NRQCD factorization formalism at photon–photon colliders. In Ref. [8], the leading order (LO) calculation of exclusive $J/\psi$-pair production via photon–photon fusion was performed within the NRQCD factorization framework, while the $J/\psi$-pair diffractive production was investigated in the pomeron exchange scheme [9,10,11,12]. Considering the fact that the next-to-leading order (NLO) QCD corrections to physical processes in quarknoium energy regime are normally significant [13,14,15,16], in this work we calculate $\gamma +\gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}}$ processes, where ${\mathcal {Q}}=J/\psi$, $\eta _c$, $\Upsilon$, or $\eta _b$, at the NLO accuracy.

The rest of the paper is organized as follows. In Sect. 2, we present the primary formulae employed in the calculation. In Sect. 3, we elucidate some technical details for the analytical calculation. In Sect. 4, the corresponding numerical evaluation is performed. The last section is reserved for summary and conclusions.

Fig. 1

Typical LO Feynman diagrams for quarkonium-pair production via photon–photon fusion

2 Formulation

In this work, we investigate the photon–photon scattering at $e^+e^-$ colliders. The initial photons are assumed to be generated by the bremsstrahlung or the laser back scattering (LBS) effects. The energy spectrum of bremsstrahlung photon can be well formulated in Weizsacker–Williams approximation (WWA) [17] as

$$\begin{aligned} f_{\gamma }(x)= & {} \frac{\alpha }{2\pi }\left( \frac{1+(1-x)^2}{x}\log \left( \frac{Q^{2}_{\mathrm{max}}}{Q^{2}_{{\mathrm{min}}}}\right) \right. \nonumber \\&\left. +2m^2_{e}x\left( \frac{1}{Q^{2}_{\mathrm{max}}}-\frac{1}{Q^{2}_{{\mathrm{min}}}}\right) \right) , \end{aligned}$$

(1)

where $Q^{2}_{{\mathrm{min}}}=m^{2}_{e}x^{2}/(1-x)$ and $Q^{2}_{\mathrm{max}}=(\theta _{c}\sqrt{s}/2)^2(1-x)+Q^{2}_{{\mathrm{min}}}$, $m_e$ is the electron mass, $x=\frac{E_{\gamma }}{E_{e}}$ is the energy fraction of photon, $\sqrt{s}$ is the collision energy for $e^+e^-$ collider, $\theta _{c}$ is the maximum scattering angle of the electron or positron.

The energy spectrum of LBS photon is [18]

$$\begin{aligned} f_{\gamma }(x)=\frac{1}{N}\left( 1-x+\frac{1}{1-x}-4r(1-r)\right) , \end{aligned}$$

(2)

where $r=\frac{x}{x_{m}(1-x)}$ and N is the normalization factor:

$$\begin{aligned} N= & {} \left( 1-\frac{4}{x_{m}}-\frac{8}{x^{2}_{m}}\right) \log (1+x_{m})+\frac{1}{2}+\frac{8}{x_{m}}\nonumber \\&-\frac{1}{2(1+x_{m})^2}. \end{aligned}$$

(3)

Here $x_{m} \approx 4.83$ [19] and the maximum energy fraction of LBS photon is restricted by $0 \le x \le \frac{x_m}{1+x_m}\approx 0.83$.

The total cross sections can be expressed as the convolution of the $\gamma + \gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}}$ cross sections with the photon distribution functions,

$$\begin{aligned} d\sigma =\int dx_{1}dx_{2} f_{\gamma }(x_{1})f_{\gamma }(x_{2})d {\hat{\sigma }}( \gamma + \gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}})\ , \end{aligned}$$

(4)

where the $d {\hat{\sigma }}$ will be calculated perturbatively up to the NLO level,

$$\begin{aligned} d{\hat{\sigma }}( \gamma + \gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}})=d{\hat{\sigma }}_{\mathrm{born}}+d{\hat{\sigma }}_{\mathrm{NLO}}+{\mathcal {O}}(\alpha ^{2}\alpha ^{4}_{s})\ . \end{aligned}$$

(5)

The Born level cross section and the NLO correction take the following forms:

$$\begin{aligned} \begin{aligned} d{\hat{\sigma }}_{\mathrm{born}}&=\frac{1}{2}\frac{1}{2{\hat{s}}}{\overline{\sum }}|{\mathcal {M}}_{\mathrm{tree}}|^{2}d{\mathrm{PS}}_{2}\ ,\\ d{\hat{\sigma }}_{\mathrm{NLO}}&=\frac{1}{2}\frac{1}{2{\hat{s}}}{\overline{\sum }}2\mathrm{Re}({\mathcal {M}}^{*}_{{\mathrm{tree}}}{\mathcal {M}}_{\mathrm{oneloop}})d{\mathrm{PS}}_{2}\ , \end{aligned} \end{aligned}$$

(6)

where $\frac{1}{2}$ is a statistical factor for identical particles in the final state, ${\hat{s}}$ is the center-of-mass energy square for the two photons, ${\overline{\sum }}$ means sum (average) over the polarizations and colors of final (initial) state particles, $d{\mathrm{PS}}_{2}$ denotes two-body phase space.

The standard form of quarkonium spin and color projection operator is adopted in our calculation [20]:

$$\begin{aligned} v(p^{}_{{\bar{Q}}}){\bar{u}}(p^{}_Q)= & {} \frac{1}{4\sqrt{2}E(E+m^{}_Q)}(\not \! p^{}_{{\bar{Q}}}-m^{}_Q)\not \! \epsilon ^{*}_{S}(\not \!P+2E)\nonumber \\&\times (\not \!p^{}_Q+m^{}_Q)\otimes \left( \frac{{\mathbf{1}}_{c}}{\sqrt{N_{c}}}\right) . \end{aligned}$$

(7)

Here, $p^{}_Q$ and $p^{}_{{\bar{Q}}}$ are the momenta of heavy quark and antiquark respectively, $P=p^{}_Q+p^{}_{{\bar{Q}}}$ is the momentum of quarkonium, $E=\sqrt{P^{2}/4}$ is the energy of heavy (anti)quark in quarkonium rest frame, $\epsilon ^{*}_{S}$ denotes the polarization vector of the spin-triplet state, $\mathbf{1}_{c}$ represents the unit color matrix, and $N_c=3$ is the number of colors in QCD. At the leading order of the relative velocity expansion, it is legitimate to take $p^{}_Q=p^{}_{{\bar{Q}}}=P/2$ and $E=m^{}_Q$. The projection operator for spin-singlet state can be readily obtained by replacing the $\not \! \epsilon ^{*}_{S}$ with $\gamma _5$ in Eq. (7).

Fig. 2

Typical NLO Feynman diagrams for quarkonium-pair production via photon–photon fusion

3 Analytical calculation

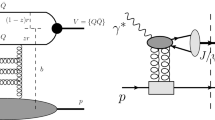
At the LO, there are twenty Feynman diagrams contributing to the $\gamma +\gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}}$ processes. Four of them are shown is Fig. 1. The LO calculation is straightforward and the result is pretty simple. We reproduce the Eq. (4) of Ref. [8], where the analytical expression for LO differential cross section was presented.

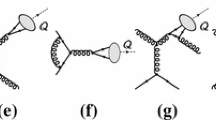
The typical Feynman diagrams for the NLO QCD corrections are shown in Fig. 2. According to their topologies, all diagrams can be classified into four groups:

• Corrections to the tree-level Feynman diagrams, which are schematically shown in Fig. 2a–e.

• Two-gluon exchange mechanism, as representatively shown in Fig. 2f–h. This mechanism is essential in vector quarkonium-pair diffractive production, while forbidden in pseudo-scalar quarkonium-pair production due to the requirement of charge-parity (C-parity) conservation.

• One of the quarkonia is produced through the two-gluon intermediate state, as schematically shown in Fig. 2i–k. This topology is excluded in the calculation of vector quarkonium-pair production also due to the C-parity conservation.

• Fermion box diagrams, as representatively shown in Fig. 2l.

Due to the fact that the C-parity selection rule excludes different topologies of vector and pseudo-scalar quarkonium-pair productions respectively, their NLO behaviors can be quite different.

Table 1 The LO (in brackets) and NLO total cross sections for $J/\psi$-pair and $\eta _c$-pair productions via photon–photon fusion at the SuperKEKB collider. Here, the transverse momentum cut $p_{t}\ge 0.01\,\hbox {GeV}$ is imposed on every single quarkonium

In the calculation of NLO corrections, the ultraviolet (UV) and infrared (IR) singularities are regularized by the dimensional regularization with $D=4-2\epsilon$. According to Ref. [1], the soft IR singularities are canceled with each other. Since the final charm quarks are massive, there is no collinear IR singularity in the hard-collinear region. The Coulomb IR singularities, which appears when a potential gluon is exchanged between the constituent quarks of a quarkonium, vanish in the dimensional regularization since we set $p^{}_Q=p^{}_{{\bar{Q}}}$ before calculating the Feynman integrals [21]. The UV singularities are removed by the standard renormalization procedure. The relevant renormalization constants include $Z_{2}, Z_{3}, Z_{m}$ and $Z_{g}$, which correspond to the heavy quark field, gluon field, heavy quark mass and strong coupling constant, respectively. Among them, $Z_{2}$ and $Z_{m}$ are defined in the on-mass-shell (OS) scheme, while others are defined in the modified minimal-subtraction ($\overline{\mathrm{MS}}$) scheme. The counter terms are written as

$$\begin{aligned} \begin{aligned} \delta Z^{\mathrm{OS}}_{2}&=-C_{F}\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{\mathrm{UV}}}+\frac{2}{\epsilon _{\mathrm{IR}}}-3\gamma _{E}+3\ln \frac{4\pi \mu ^{2}}{m_Q^{2}}+4\right] ,\\ \delta Z^{\mathrm{OS}}_{m}&=-3C_{F}\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{\mathrm{UV}}}-\gamma _{E}+\ln \frac{4\pi \mu ^{2}}{m_Q^{2}}+\frac{4}{3}\right] ,\\ \delta Z^{\overline{\mathrm{MS}}}_{3}&=(\beta _{0}-2C_{A})\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{\mathrm{UV}}}-\gamma _{E}+\ln (4\pi )\right] ,\\ \delta Z^{\overline{\mathrm{MS}}}_{g}&=-\frac{\beta _{0}}{2}\frac{\alpha _{s}}{4\pi }\left[ \frac{1}{\epsilon _{\mathrm{UV}}}-\gamma _{E}+\ln (4\pi )\right] . \end{aligned} \end{aligned}$$

(8)

Here $\mu$ is the renormalization scale, $\gamma _{E}$ is the Euler’s constant, $\beta _{0}=\frac{11}{3}C_{A}-\frac{4}{3}T_{F}n_{f}$ is the one-loop coefficient of the QCD $\beta$-function, and $n_{f}$ denotes the active quark flavor numbers. The color factors $C_{A}=3, C_{F}=\frac{4}{3}$ and $T_{F}=\frac{1}{2}$.

In the calculation, the Mathematica package FeynArts [22] is used to generate Feynman diagrams; FeynCalc [23] and FeynCalcFormLink [24] are used to handle the algebraic calculation; The package FIRE [25] is employed to reduce all the one-loop integrals into typical master intergrals $A_{0}, B_{0}, C_{0}, D_{0}$, which can be numerically evaluated by the LoopTools [26]. The overall phase space integrals are performed numerically by using the package CUBA [27].

4 Numerical results

In the numerical calculation, the input parameters are taken as

$$\begin{aligned}&\alpha =1/137.065,\ m_e=0.511\ {\mathrm{MeV}},\ m_c=1.5\ {\mathrm{GeV}},\nonumber \\&m_b=4.8\ {\mathrm{GeV}};\nonumber \\&|R_{J/\psi }^{{\mathrm{LO}}}(0)|^2=0.528\ {\mathrm{GeV}}^3,\ |R_{J/\psi }^{\mathrm{NLO}}(0)|^2=0.907\ {\mathrm{GeV}}^3,\nonumber \\&R_{\eta _c}(0)=R_{J/\psi }(0); \nonumber \\&|R_{\Upsilon }^{{\mathrm{LO}}}(0)|^2=5.22\ {\mathrm{GeV}}^3,\ |R_{\Upsilon }^{{\mathrm{NLO}}}(0)|^2=7.48\ {\mathrm{GeV}}^3,\nonumber \\&R_{\eta _b}(0)=R_{\Upsilon }(0). \end{aligned}$$

(9)

Here, the $J/\psi$ and $\Upsilon$ radial wave functions at the origin are extracted from their leptonic widths

$$\begin{aligned}&\Gamma ({\mathcal {Q}}\rightarrow e^+e^-)=\frac{\alpha ^2e_Q^2}{m_Q^2}|R_H(0)|^2\left( 1-4C_F\frac{\alpha _s(\mu _0)}{\pi }\right) ,\nonumber \\&e^{}_Q={\left\{ \begin{array}{ll}\frac{2}{3},\ {\mathrm{if}}\ {\mathcal {Q}}=J/\psi \\ \frac{1}{3},\ {\mathrm{if}}\ {\mathcal {Q}}=\Upsilon \end{array}\right. }, \end{aligned}$$

(10)

with $\mu _0=2m^{}_Q$, $\Gamma (J/\psi \rightarrow e^+e^-)=5.55$ keV, and $\Gamma (\Upsilon \rightarrow e^+e^-)=1.34\,\hbox {keV}$ [28]. Note, the LO and NLO extractions are employed in the LO and NLO calculation respectively. According to the heavy quark spin symmetry of NRQCD at the leading order in relative velocity expansion [1], here we take $R_{\eta _c}(0)=R_{J/\psi }(0)$ and $R_{\eta _b}(0)=R_{\Upsilon }(0)$.

The two-loop formula

$$\begin{aligned} \frac{\alpha _{s}(\mu )}{4\pi }=\frac{1}{\beta _{0}L}-\frac{\beta _{1}\ln L}{\beta ^{3}_{0}L^{2}}, \end{aligned}$$

(11)

for the running coupling constant is employed in the NLO calculation, in which, $L=\ln (\mu ^{2}/\Lambda ^{2}_{{\mathrm{QCD}}})$, $\beta _0=\tfrac{11}{3}C_A-\tfrac{4}{3}T_Fn_f$, $\beta _{1}=\frac{34}{3}C^{2}_{A}-4C_{F}T_{F}n_{f}-\frac{20}{3}C_{A}T_{F}n_{f}$, with $n_f=4$, $\Lambda _{{\mathrm{QCD}}}=297$ MeV for charmonium production, and $n_f=5$, $\Lambda _{{\mathrm{QCD}}}=214$ MeV for bottomonium production. For LO calculation, the one-loop formula for the running coupling constant is used.

According to our calculation, it turns out the charmonium-pair production process is hopeful to be observed by Belle II detector at the SuperKEKB electron–positron collider due to its high luminosity, where the beam energies of the positron and electron are 4 GeV and 7 GeV respectively, yielding a center-of-mass energy of 10.6 GeV. The corresponding LO and NLO cross sections for $J/\psi$-pair and $\eta _c$-pair productions with the WWA photon as the initial state are shown in Table 1. The angular cut $\theta _c$ of the WWA is set to be 83 mrad, the crossing angle between the positron and electron beams [29]. The transverse momentum cut $p_{t}\ge 0.01\,\hbox {GeV}$ is imposed on each individual quarkonium. In order to estimate the theoretical uncertainty, four reasonable choices for the renormalization scale [30], i.e. $\mu =2m_c$, $\mu =\sqrt{4m_c^2+p_t^2}$, $\mu =\sqrt{{\hat{s}}}/2$ and $\mu =\sqrt{{\hat{s}}}$ are taken, where $\sqrt{{\hat{s}}}$ is the center-of-mass energy of the photon–photon system. It can be seen that, for $J/\psi$-pair production, the total cross section are generally suppressed by the NLO corrections, and the theoretical uncertainty induced by renormalization scale is even larger at NLO than that at the LO, which seems a little counterintuitive and needs a further investigation. While for $\eta _c$-pair production, after including the NLO corrections, the total cross sections are enhanced by a factor of about 2, and the theoretical uncertainty is reduced evidently.

Fig. 3

The differential cross sections for charmonium-pair production. a $J/\psi$-pair production in bins of $\mathrm{cos}\theta$; b $J/\psi$-pair production in bins of $M_{J/\psi J/\psi }$; c $\eta _c$-pair production in bins of ${\mathrm{cos}}\theta$; d $\eta _c$-pair production in bins of $M_{\eta _c \eta _c}$. Here the renormalization scale $\mu =\sqrt{4m_{c}^2+p^{2}_{t}}$. The transverse momentum cut $p_{t}\ge 0.01\,\hbox {GeV}$ is imposed on each single quarkonium

Table 2 The LO (in brackets) and NLO total cross sections for quarkonium pair production via photon–photon fusion at future $e^+e^-$ colliders. The renormalization scale $\mu =\sqrt{4m_{c}^{2}+p_{t}^{2}}$. The kinematic cuts $2 \le p_{t} \le 40\,\hbox {GeV}$ and $|y|<2$ are imposed on each single quarkonium

Since the instantaneous luminosity of the SuperKEKB collider may reach $8\times 10^{35}\ {\mathrm{cm}}^{-2}\,{\mathrm{s}}^{-1}\approx 2.52\times 10^4\ {\mathrm{fb}}^{-1}{\mathrm{year}}^{-1}$ in 2025 [31], we will obtain (2.52–10.05) $\times 10^3$ $J/\psi$-pair events and (6.80–9.27) $\times 10^3$ $\eta _c$-pair events per year. In experiment, $J/\psi$ can be reconstructed through its leptonic decays, and $\eta _c$ can be reconstructed through its $K{\bar{K}}\pi$ decay channel. According to Ref. [28], the branching ratios ${\mathrm{Br}}(J/\psi \rightarrow l^+l^-(l=e,\mu ))=12\%$ and ${\mathrm{Br}}(\eta _c\rightarrow K{\bar{K}}\pi )=7.3\%$, and hence the numbers of reconstructed candidates per year would reach $36\sim 145$ for $J/\psi$-pair production and 36–49 for $\eta _c$-pair production.

The differential cross sections $d\sigma /d{\mathrm{cos}}\theta$ for $J/\psi$-pair and $\eta _c$-pair productions at the SuperKEKB collider are shown in Fig. 3a, c respectively, where $\theta$ is the scattering angle. It can be seen that the events are more likely to be produced along the electron beam line, which is one of the consequences of the asymmetric beam energies of the SuperKEKB collider. The differential cross sections $d\sigma /dM_{{\mathcal {Q}}{\mathcal {Q}}}$ for $J/\psi$-pair and $\eta _c$-pair productions are shown in Fig. 3b, d respectively, where $M_{{\mathcal {Q}}{\mathcal {Q}}}=\sqrt{{\hat{s}}}$ is invariant mass of the quarkonium-pair. The invariant mass distribution reaches the maximum around threshold energy.

Of the future high energy $e^+e^-$ colliders, like the Circular electron positron collider (CEPC) [32] and the international linear collider (ILC) [33], the collision energy may reach 250 GeV or 500 GeV. And the LBS photon collision can be realized by imposing a laser beam to each e beam. Therefore, we investigate the $J/\psi$-pair and $\eta _c$-pair productions under both WWA and LBS photon collisions with $\sqrt{s}=250\,\hbox {GeV}$ and $\sqrt{s}=500\,\hbox {GeV}$. The corresponding LO and NLO total cross sections are presented in Table 2. The angular cut $\theta _c$ in WWA is set to be 32 mrad, as at the Large Electron–positron Collider (LEP) [2]. Due to the fact, that the LBS photon are more likely to be produced with large momentum fraction x, while the partonic cross section ${\hat{\sigma }}(\gamma +\gamma \rightarrow {\mathcal {Q}}+{\mathcal {Q}})$ arrives at the peak around the threshold energy, the total cross sections for charmonium-pair production in the LBS photon case are only 1/10 to 1/2 the total cross sections in the WWA photon case. Given a typical collider luminosity $10^{34}\ {\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\approx 315\ \mathrm{fb}^{-1}{\mathrm{year}}^{-1}$, the event numbers of $J/\psi$-pair production and $\eta _c$-pair production through WWA photon collision at $\sqrt{s}=500\,\hbox {GeV}$ are about 532 and 913 respectively. Assuming $J/\psi$ is reconstructed through $J/\psi \rightarrow l^+l^-(l=e,\mu )$, and $\eta _c$ is reconstructed through $\eta _c\rightarrow K{\bar{K}}\pi$, several events might be observed per year in each case.

For completeness, we also calculate the total cross sections of $\Upsilon$-pair and $\eta _b$-pair productions, as shown in Table 2. It can be seen that the bottomonium-pair production rates are two to three orders of magnitude smaller than the charmonium-pair production rates. Hence the bottomonium-pair production via photon–photon is invisible in the foreseeable future.

5 Summary and conclusions

In this work, we investigate the quarkonium-pair production in photon–photon fusion at the NLO QCD accuracy in the framework of NRQCD factorization formalism. The total cross sections and the differential cross sections in bins of $\cos \theta$ and $M_{{\mathcal {Q}} {\mathcal {Q}}}$ for charmonium-pair production at the SuperKEBK collider are given. The total cross sections for charmonium-pair and bottomonium-pair productions at the CEPC and the ILC are also estimated.

Numerical results shows that, for $J/\psi$-pair production, after including the radiative correction, the total cross sections are generally decreased and their renormalization scale dependence is increased. This is a bit counterintuitive and needs a further investigation. For $\eta _c$-pair production, with the NLO corrections, the total cross sections are enhanced by a factor of about 2, and their renormalization scale dependence is reduced. The total cross sections for $J/\psi$-pair production and $\eta _c$-pair production via photon–photon fusion at the SuperKEBK collider are 0.100–0.399 fb and 0.270–0.368 fb respectively. Considering $J/\psi$ may be reconstructed via $J/\psi \rightarrow l^+l^-(l=e,\mu )$ processes, $\eta _c$ may be reconstructed via $\eta _c\rightarrow K{\bar{K}}\pi$, the double $J/\psi$ and double $\eta _c$ events may in the end reach 36–145 and 36–49 a year, respectively. Since the signals are significant in experiment, the possibility of observing double quarkonium in future experiments still exists. Finally, it is remarkable that the successful application of the NRQCD factorization formalism to the NLO calculation of double quarkonium production poses another independent check on its validity at the next-to-leading order.