Electroweak physics in inclusive deep inelastic scattering at the LHeC

Abstract

At the proposed electron-proton collider LHeC electroweak interactions can be uniquely studied in a largely unexplored kinematic region of spacelike momentum transfer. We simulate inclusive neutral- and charged-current deep-inelastic lepton proton scattering cross section data at center-of-mass energies of 1.2 and 1.3 TeV, and estimate the uncertainties of Standard Model parameters as well as of parameters describing physics beyond the Standard Model. A precision at sub-percent level is expected for the measurement of the weak neutral-current couplings of the light-quarks to the Z boson, $g_{A/V}^{u/d}$, improving their present precision by more than an order of magnitude. The weak mixing angle can be determined with a precision of about $\Delta \sin ^2\theta _\text {W}=\pm \,0.00015$, and its scale dependence can be studied in the range between about 25 and 700 GeV. An indirect determination of the W-boson mass in the on-shell scheme is possible with an experimental uncertainty down to $\Delta m_{W}=\pm \,6\,\text {MeV}$. We discuss how measurements in deep-inelastic scattering compare with those in the timelike domain, and which aspects are unique, for instance electroweak parameters in charged-current interactions. We conclude that the LHeC will determine electroweak physics parameters, in the spacelike region, with unprecedented precision leading to thorough tests of the Standard Model and possibly beyond.

1 Introduction

With the discovery of the Standard Model (SM) Higgs boson at the CERN Large Hadron Collider (LHC) experiments and subsequent measurements of its parameters, the fundamental parameters of the SM have been measured directly and with remarkable precision. To further map out the validity of the theory of electroweak interactions, more and higher precision electroweak measurements have to be performed. Such high-precision measurements can also be considered as a portal to new physics, since non-SM contributions may lead to significant deviations for some precisely measurable and calculable observables.

The Large Hadron-electron Collider (LHeC) [1,2,3], planned at the LHC, may complement the proton ring with an electron beam, allowing to perform deep inelastic scattering (DIS) with electrons and protons at TeV energies. Its electron beam energy may be chosen to be 60 or 50 GeV. Considerations in this choice, as for example cost reasons, are discussed in the forthcoming thorough update of the physics and conceptual accelerator and detector design report  [3]. In both cases its kinematic reach extends to much higher scales in comparison to HERA, which together with the huge increase of the expected integrated luminosity will allow to perform high-precision electroweak measurements at high scales in DIS for the first time.

Since the discovery of weak neutral currents in 1973 [4, 5] and the formulation of the Glashow-Weinberg-Salam model [6,7,8,9,10,11,12,13], deep-inelastic lepton nucleon scattering has played an important role in testing the Standard Model. One of the first measurements of the electroweak mixing angle, $\sin ^2 \theta _W$, was obtained from polarized electron-deuteron scattering at SLAC [14, 15]. With the advent of HERA, the first electron-proton collider, a much larger range of momentum transfers squared, $Q^2$, became accessible – an important prerequisite for probing electroweak interactions in DIS. First measurements of electroweak effects at HERA were undertaken in Refs. [16, 17], and more thorough electroweak analyses have been performed recently, for example with the complete set of H1 data in Ref. [18].

Apart from the LHeC, other options for electron-hadron colliders are presently considered. A DIS option is studied as part of the possible Future Circular Collider (FCC) at CERN, the FCC-eh [19], and will reach center-of-mass energies still higher than at the LHeC. At Brookhaven, the Electron Ion Collider (EIC) [20,21,22] is under development to perform DIS measurements at lower energies but with higher luminosities than were achieved at HERA. For comparison, in Fig. 1 we show single-differential neutral- and charged-current (NC and CC) inclusive DIS cross sections for polarized electron-proton scattering as a function of $Q^2$ comparing the future facilities LHeC, FCC-eh, and EIC, with H1 data from the past HERA collider [23]. For studies of electroweak effects, data at higher values of $Q^2$ will be particularly suitable. However, it is expected, that also the EIC may contribute to electroweak physics [24]. The LHeC might be realized during the lifetime of the LHC and could start taking data in the 2030s, and it has recently been described as a realistic option in the EPPSU deliberation document [25]. The newly proposed energy-recovery linac (ERL) for a high-quality electron beam, together with the high-luminosity upgrade of the LHC (HL-LHC), are expected to provide more than an order of magnitude increase in the reach towards higher $Q^2$ compared to HERA and furthermore an extraordinary increase of the integrated luminosity compared to what was assumed in all previous studies. This motivates us to perform a novel exploratory study for the LHeC investigating new possibilities for the measurement of electroweak physics effects. Previously, studies of electroweak effects for similar energies have been performed for the LHeC [1] and earlier, to some extent, for the LEP$\otimes$LHC proposal [26].

Fig. 1

Single differential inclusive DIS cross sections for neutral- and charged-current $e^-p$ DIS with longitudinally polarized electrons ($P_e=-0.8$) at LHeC, EIC, FCC-eh, and HERA. For HERA, unpolarized cross sections are displayed together with data from the H1 experiment

We will put the focus on the measurement prospects of inclusive NC and CC cross sections at the LHeC with the aim to determine parameters of the electroweak interaction by analysing pseudo-data which we simulated with different assumptions on the experimental uncertainties or the center-of-mass energy. Measurements in the regime of space-like momentum transfer, where the interaction is mediated by gauge boson exchange in the t-channel, are essentially complementary to other experiments, such as proton-proton collisions or electron-positron annihilation, or experiments at lower energies, like neutrino or muon scattering. The potential of experiments at the LHeC with exclusive final states, for example W- or Z-boson production, or production of the Higgs boson, has been studied elsewhere [27,28,29,30]; the possible improvement in our knowledge of parton distribution functions due to LHeC experiments was described in Refs. [31, 32] (see also Refs. [1, 3, 19] and references therein).

Our goal is to study tests of the electroweak SM. We therefore start with laying out the theoretical framework and summarize the SM predictions for NC and CC DIS cross sections, including higher-order electroweak corrections in the following Sect. 2. In subsequent sections we describe the main features of the cross section predictions (Sect. 3), the simulated data that we use (Sect. 4), and the methodology for fitting these data to extract electroweak physics parameters (Sect. 5). Then we present a first group of results in Sect. 6 for the determination of mass parameters, i.e. the masses of the W and Z bosons and in Sect. 7 for the weak mixing angle. The expected high precision of measurements at the LHeC motivates to also envisage an indirect determination of the top-quark mass through higher-order corrections (Sect. 8). These studies will allow one to perform tests of the SM by comparing different determinations of the electroweak physics parameters.

A high precision measurement of parameters of the SM is important in order to study the validity of the theory of electroweak interactions. In addition, we will study a number of possible ways to generically parameterize new physics beyond the SM In Sect. 9 we study the well-known STU-parameters which describe new physics entering through loop insertions in the self energy corrections of the gauge bosons. Then we follow the wide-spread convention to generalize the SM gauge-boson fermion couplings by introducing $\rho$ and $\kappa$ parameters, both for NC (Sect. 10) and for CC (Sect. 11), or, eventually, allowing the vector and axial-vector coupling constants to be independent free parameters, not obeying any restriction as imposed by the SM (Sect. 12). We will be able to show that in particular the quark coupling constants, separately for up- and down-type quarks, can be determined with a precision at the sub-percent level. The large kinematic reach of the LHeC will also allow us to study the scale-, i.e. $Q^2$-dependence of coupling parameters. This opportunity is in fact unique to the LHeC. Finally, we conclude and summarize the most important results in Sect. 13. The impact of the LHeC measurements on possible future global fits of the electroweak SM parameters is discussed in an appendix (A).

A summary of our results is also part of the description of the electroweak physics potential within the forthcoming publication of the update [3] of the 2012 Conceptual Design Report on the LHeC.

2 Electroweak effects in inclusive NC and CC DIS

In this section we lay out the general properties of DIS cross sections, first at leading order, taking into account single boson exchange diagrams at tree level.

Inclusive NC DIS cross sections are expressed in terms of generalized structure functions $\tilde{F}_2^\pm$, $x\tilde{F}_3^\pm$ and $\tilde{F}_\mathrm{L}^\pm$ at electroweak (EW) leading order (LO) as

$$\begin{aligned}&\frac{d^2\sigma ^\mathrm{NC}(e^\pm \, p)}{dxdQ^2} = \frac{2\pi \alpha ^2}{xQ^4} \nonumber \\&\quad \times \left[ Y_+\tilde{F}_2^\pm \,(x,Q^2) \mp Y_{-} x\tilde{F}_3^\pm \,(x,Q^2) - y^2 \tilde{F}_\mathrm{L}^\pm \,(x,Q^2) \right] ~, \nonumber \\ \end{aligned}$$

(1)

where $\alpha$ denotes the fine structure constant, x is the Bjorken scaling variable, and y the inelasticity. The factors $Y_\pm \, = 1\pm \,(1-y)^2$ encode the helicity dependence of the underlying lepton quark hard-scattering process. The generalized structure functions can be separated into contributions from pure $\gamma$- and Z-exchange, and their interference [33]:

$$\begin{aligned} \tilde{F}_2^\pm \,= & {} F_2 -(g_V^e\pm \, P_eg_A^e)\varkappa _ZF_2^{\gamma Z}\nonumber \\&+\left[ (g_V^eg_V^e+g_A^eg_A^e)\pm \,2P_eg_V^eg_A^e\right] \varkappa _Z^2F_2^Z~, \end{aligned}$$

(2)

$$\begin{aligned} \tilde{F}_3^\pm \,= & {} -(g_A^e\pm \, P_eg_V^e)\varkappa _ZF_3^{\gamma Z}\nonumber \\&+\left[ 2g_V^eg_A^e\pm \, P_e(g_V^eg_V^e+g_A^eg_A^e)\right] \varkappa _Z^2F_3^Z~, \end{aligned}$$

(3)

where $P_e$ is the degree of longitudinal polarization ($P_e = -1$ for a purely left-handed polarized electron beam). A similar decomposition exists for $\tilde{F}_L$. The naive quark-parton model corresponds to the LO approximation of Quantum Chromodynamics (QCD). In this approximation the structure functions are calculated from quark and anti-quark parton distribution functions, q(x) and $\bar{q}(x)$:

$$\begin{aligned} \left[ F_2,F_2^{\gamma Z},F_2^Z\right]= & {} x\sum _q\left[ Q_q^2,2Q_qg_V^q,g_V^qg_V^q+g_A^qg_A^q\right] \{q+\bar{q}\}~, \end{aligned}$$

(4)

$$\begin{aligned} x\left[ F_3^{\gamma Z},F_3^Z\right]= & {} x\sum _q\left[ 2Q_qg_A^q,2g_V^qg_A^q\right] \{q-\bar{q}\}~. \end{aligned}$$

(5)

In Eqs. (2) and (3), the coefficient $\varkappa _Z$ accounts for the Z-boson propagator and the normalization of the weak, relative to the electromagnetic, interaction. It is calculated, at LO, as

$$\begin{aligned} \varkappa _Z(Q^2)&= \frac{Q^2}{Q^2 +m^2_Z} \frac{1}{4\sin ^2\theta _W\cos ^2\theta _W} \nonumber \\&= \frac{Q^2}{Q^2 +m^2_Z} \frac{G_\mathrm{F}m_Z^2}{2\sqrt{2}\pi \alpha }~. \end{aligned}$$

(6)

Thus, depending on the choice of independent theory parameters, the normalization of $\varkappa _Z$ is fixed by an input value for $\sin ^2\theta _W$, or, alternatively, using the Fermi coupling constant $G_\mathrm{F}$. The first option where $\sin ^2\theta _W= 1 - \cos ^2\theta _W = 1 - m_W^2/m_Z^2$ is fixed, is called the on-shell scheme, while the second option with $G_\mathrm{F}$ as input parameter is known as the modified on-shell scheme.

The vector and axial-vector coupling constants of the lepton or quark to the Z-boson, $g_V^f$ and $g_A^f$ (with $f = e$, q and $q = u$, d) in Eqs. (2) and (3), are given by the SM electroweak theory. They depend on the electric charge, $Q_f$, in units of the positron charge, and on the third component of the weak-isospin of the fermion, $I^3_{\mathrm{L},f}$. They are given, at LO, by

$$\begin{aligned} g_A^{f}= & {} I^3_{\mathrm{L},f} \,, \end{aligned}$$

(7)

$$\begin{aligned} g_V^{f}= & {} I^3_{\mathrm{L},f} - 2 Q_{f} \sin ^2\theta _W\, . \end{aligned}$$

(8)

The CC DIS cross section is written, in the LO approximation, as

$$\begin{aligned}&\frac{d^2\sigma ^\mathrm{CC}(e^\pm \, p)}{dxdQ^2} = \frac{1 \pm \, P_e}{2} \frac{\pi \alpha ^2}{4\sin ^4\theta _W} \frac{1}{x} \left[ \frac{1}{Q^2 +m_W^2}\right] ^2 \nonumber \\&\quad \times \left( Y_+ W_2^\pm \,(x,Q^2) \mp Y_{-} xW_3^\pm \,(x,Q^2) - y^2 W_\mathrm{L}^\pm \,(x,Q^2)\right) ~. \nonumber \\ \end{aligned}$$

(9)

Here, an incoming electron can scatter only with positively charged quarks. Therefore, in the naive quark-parton model the structure functions $W_2^\pm \,$ and $xW_3^\pm \,$ are obtained from parton distribution functions for up-type quarks and down-type anti-quarks as

$$\begin{aligned} W_2^- = x \left( U + \overline{D} \right) \, , \quad xW_3^- = x \left( U - \overline{D} \right) , \end{aligned}$$

(10)

where $U = u+c$ and $\overline{D} = \bar{d} + \bar{s}$. For positron scattering, the combinations $\overline{U} = \bar{u} + \bar{c}$ and $D = d+s$ are needed and one has

$$\begin{aligned} W_2^+ = x \left( \overline{U} + D \right) , \quad xW_3^+ = x \left( D - \overline{U} \right) . \end{aligned}$$

(11)

At LO of QCD, one has for the longitudinal structure function $W_\mathrm{L}^\pm \, = 0$.

Higher-order perturbative corrections of QCD are included in the $\overline{\mathrm{MS}}$ scheme by using $Q^2$-dependent parton distribution functions, $q(x, Q^2)$ and $\bar{q}(x, Q^2)$, evolved according to the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi equations. In addition, there are corrections of order $O(\alpha _s)$ to the relations (4, 5) and (10, 11) between PDFs and structure functions, and the longitudinal structure functions for NC and CC are predictions of perturbative QCD.

We will see below that the precision of LHeC measurements is expected to be at a level which makes the inclusion of higher-order electroweak corrections indispensable. In particular, QED radiative corrections (bremsstrahlung) have to be taken into account. We assume that these corrections will be removed from the data at the required level of precision. One-loop EW corrections have been calculated in Refs. [34,35,36] for NC and in Refs. [37, 38] for CC scattering (see also ref. [39] for a study of numerical results). We have adapted the implementation in the program EPRC [40] for our present study.

The dominating universal higher-order EW corrections can be described by a modification of the fermion gauge-boson couplings. For NC scattering, vacuum polarization leads to the running of the fine structure constant. The NC couplings are affected by $\gamma Z$ mixing and Z self energy corrections. These corrections are taken into account by replacing Eqs. (7, 8) with corrected couplings

$$\begin{aligned} g_A^{f}= & {} \sqrt{\rho _{\text {NC}, f}} \, I^3_{\mathrm{L},f} \,, \end{aligned}$$

(12)

$$\begin{aligned} g_V^{f}= & {} \sqrt{\rho _{\text {NC}, f}} \, \left( I^3_{\mathrm{L},f} - 2 Q_{f} \, \kappa _{f} \, \sin ^2\theta _W\right) \,. \end{aligned}$$

(13)

At LO, the coefficients $\rho _{\text {NC}, f}$ and $\kappa _{f}$ are unity, but at NLO they are promoted to form factors which are flavor and scale dependent. Since they depend on $Q^2$, they render the coupling constants ‘effective’ running couplings. The coefficient $\kappa _{f}$ can be combined with $\sin ^2\theta _W$ to define an effective, flavor and scale-dependent ($\mu ^2$) weak mixing angle,

$$\begin{aligned} \sin ^2 \theta _{W,f}^\mathrm{eff} (\mu ^2) = \kappa _{f}(\mu ^2) \sin ^2\theta _W\, . \end{aligned}$$

(14)

The leptonic weak mixing angle, $\sin ^2\theta _{\text {W},\ell }^\text {eff}(m_Z^2)$, has been used to describe LEP/SLD observables at the Z-pole (see e.g. [41]). We emphasize that the $\mu ^2$ dependence of the effective weak mixing angle is not negligible for LHeC physics ($\mu ^2 = - Q^2$), while only its value at and close to $\mu ^2 = +m_Z^2$ was relevant for Z-pole observables.

For CC scattering, a corresponding correction factor $\rho _{\text {CC}, eq}$ is introduced for $e^- q$ and $e^+ \bar{q}$ scattering, and $\rho _{\text {CC}, e\bar{q}}$ for $e^- \bar{q}$ and $e^+ q$ scattering, by the replacement of Eqs. (10, 11) with

$$\begin{aligned} W_2^-&= x \left( \rho _{\text {CC}, eq}^2 U + \rho _{\text {CC},e\bar{q}}^2 \overline{D} \right) \, , \nonumber \\&\quad xW_3^- = x \left( \rho _{\text {CC}, eq}^2 U - \rho _{\text {CC},e\bar{q}}^2 \overline{D} \right) \, , \end{aligned}$$

(15)

and

$$\begin{aligned} W_2^+&= x \left( \rho _{\text {CC},e\bar{q}}^2 \overline{U} + \rho _{\text {CC}, eq}^2 D \right) \, , \nonumber \\&\quad xW_3^+ = x \left( \rho _{\text {CC},e\bar{q}}^2 D - \overline{U} \rho _{\text {CC}, eq}^2 \right) \, . \end{aligned}$$

(16)

In addition, box graph corrections, which are $Q^2$- and energy-dependent, are added as separate correction terms to the NC and CC cross sections. Higher-order EW corrections are defined in the on-shell scheme [42, 43], using $m_Z$ and $m_W$ as independent parameters (see also Refs. [44, 45]).

In order to calculate predictions in the SM electroweak theory at LO, only two independent parameters are needed in addition to $\alpha$. At higher orders, loop corrections involve a non-negligible dependence on the complete set of SM parameters, where the most important ones are the top-quark mass, $m_t$, and the Higgs-boson mass, $m_H$. In addition, hadronic contributions to the running of the effective couplings have to be provided as independent input [46, 47], since the corresponding higher-order corrections can not be calculated in perturbation theory.

In the on-shell scheme, the masses of all particles are taken as independent input parameters. The weak mixing angle is defined by the masses of the W and Z bosons, $\sin ^2\theta _W= 1-m_W^2/m_Z^2$, also at NLO. Since the Fermi constant $G_\mathrm{F}$ has been measured with a very high precision in muon-decay experiments [48] it is often preferred to calculate the less well-known W-boson mass from the relation

$$\begin{aligned} G_\mathrm{F}= \frac{\pi \alpha }{\sqrt{2} m_W^2} \frac{1}{\sin ^2\theta _W} \frac{1}{1 - \Delta r} \, , \end{aligned}$$

(17)

where higher-order corrections enter through the quantity $\Delta r=$ $\Delta r(\alpha ,$ $m_W$, $m_Z$, $m_t$, $m_H, \ldots )$ [42], which depends on all mass parameters of the EW SM. The correction $\Delta r$ has also to be taken into account when the propagator factor $\varkappa _Z(Q^2)$ (see Eq. (6)) is calculated, using either $\alpha$, $m_W$ and $m_Z$ (the naive on-shell scheme), or $\alpha$, $G_\mathrm{F}$ and $m_Z$ (the modified on-shell scheme) to fix input parameters. The choice of a scheme for input parameters is important since it leads to very different sensitivities to parameter variations.

3 Inclusive DIS cross sections at the LHeC

The contribution of the weak interaction to inclusive NC and CC DIS cross sections becomes large at high momentum transfers squared and competes with the purely electromagnetic neutral current interaction. This is most clearly illustrated in Fig. 2 where we show predictions for the single-differential cross sections for polarized $e^-p$ scattering as a function of $Q^2$. Here, LHeC electron beam energies of $E_e=50~\mathrm {GeV}$ and 60 $\mathrm {GeV}$, and a proton beam energy of $E_p=7000~\mathrm {GeV}$ are chosen. The LHeC predictions are compared to data for unpolarized scattering measured at HERA, where the electron and proton beam energies had been $E_e = 27.6$ GeV and $E_p = 920$ GeV, respectively.

Fig. 2

Single differential inclusive DIS cross sections for polarized $e^-p$ NC and CC DIS at the LHeC for two different electron beam energies ($E_e=50$ and 60 $\mathrm {GeV}$). Cross sections for longitudinal electron beam polarizations of $P_e=-0.8$ and $+0.8$ are displayed. For comparison also data measured by H1 at HERA [23] at center-of-mass energies of $\sqrt{s}=920~\mathrm {GeV}$ with unpolarized ($P=0$) electron beams are displayed

At lower values of $Q^2$, the NC cross section is dominated by the photon-exchange contribution, determined by the structure function $F_2$ (cf. Eqs. (2, 3)), and much larger than the cross section for CC scattering. At values of $Q^2$ below the mass of the W boson, $Q^2 \ll m_W^2$, the propagator term in the CC cross section becomes $m_W^2 / (m_W^2+Q^2) \simeq 1$ and, therefore, the CC cross section depends only little on $Q^2$.

Weak contributions to the NC cross section become important at $Q^2$ values around the electroweak scale, $Q^2 \approx m_Z^2$. As a consequence, the dependence of the NC cross section on the longitudinal beam polarization, $P_e$, becomes strong, and the cross sections for positive and negative helicities differ significantly. Since CC scattering is purely left-handed, the dependence on the longitudinal beam polarization is strongest in this case: the CC cross section scales linearly with the fraction of left-handed electrons in the beam, i.e. with $1 - P_e$ (cf.  Eq. (9)). Note that, since DIS is mediated by gauge boson exchange with spacelike momentum transfer, $\mu ^2=-Q^2$, no resonance of a weak boson is present in the $Q^2$-dependent cross section.

The cross sections increase slowly with the center-of-mass energy, mainly because the reach towards smaller values of the Bjorken variable x gets larger. For an electron beam energy of $E_e=60~\mathrm {GeV}$, the cross sections for NC or CC scattering in the typical range of $Q^2$ in $10,000< Q^2 < 100,000~\mathrm {GeV}^2$ are larger by about 10 to 15 %, compared to the case of $E_e=50~\mathrm {GeV}$. The difference of cross sections between $E_e=50$ and 60 $\mathrm {GeV}$ increases with $Q^2$.

4 LHeC pseudo data

In this section, details of the simulation of LHeC pseudo-data ¹ used subsequently for an extraction of electroweak parameters are described.

In the present analysis simulated double-differential inclusive NC and CC DIS cross section data are exploited. The data have been simulated based on a numerical procedure [49] for the purpose of the LHeC CDR update [3]. The data are briefly described in the following.

The data sets include electron and positron scattering, different lepton beam polarization settings, and different proton beam energies. Since a decision about the actual layout of the LHeC energy-recovery linac for the lepton beam has not yet been taken, we will study scenarios for two lepton beam energies, i.e. $E_e = 50$ and 60 $\mathrm {GeV}$. Most of the data were generated with the nominal LHC proton beam energy of $E_p = 7000\,\mathrm {GeV}$, but in addition, a small sample with reduced proton energy of $E_p = 1000$ GeV is also considered. A summary of the data sets is given in Table 1.

Table 1 Summary of data sets used in our analysis. Each set is simulated for the two electron beam energies $E_e=50~\mathrm {GeV}$ and 60 $\mathrm {GeV}$

The majority of the data will be collected with an electron beam ($Q_e=-1$) and with a longitudinal beam polarization of $P_e=-0.8$, expected to reach an integrated luminosity of about $\mathcal {L}\simeq 1000~\text {fb}^{-1}$. This will allow us to consider measurements of NC and CC DIS cross sections up to values of $Q^2 \simeq 1,000,000\,\mathrm {GeV}^2$. A considerably smaller data sample will be collected with a positive electron beam polarization of $P_e=+0.8$, i.e. with right-handed electrons. For this sample, an integrated luminosity of 10 fb$^{-1}$ was assumed. Another data sample may be collected with a positron beam, where it is assumed that polarization will not be available. Technical limitations for the positron source put constraints on the achievable beam current and thus on the instantaneous luminosity. Therefore, an integrated luminosity of 10 fb$^{-1}$ is assumed for this sample.² Such reduced luminosity values still allow to consider measurements with positrons reaching up to $Q^2$ values of 500,000 $\mathrm {GeV}^2$. Finally, another data sample will be collected with a reduced proton beam energy. This will be important for a determination of $F_L$ and to access higher values of x at fixed medium $Q^2$. For this low-energy sample an integrated luminosity of 1 fb$^{-1}$ was assumed.

The analysis of all data sets is restricted to $Q^2 \ge 5\,\mathrm {GeV}^2$ in order to avoid regions where non-perturbative QCD effects are important, which could deteriorate the determinations of parton distribution functions. For our purpose, the low-$Q^2$ region is anyway of less interest since it does not contribute much to the sensitivity to EW parameters. CC DIS data are simulated only for $Q^2 \ge 100\,\mathrm {GeV}^2$, since CC scattering events with significantly lower $Q^2$ may be difficult to measure due to limitations of the trigger system.

The data simulation accounts for the acceptance of the LHeC detector, the kinematic reconstruction, and trigger restrictions. The resulting coverage of the kinematic plane can be found, for instance, in Ref. [32].

Table 2 Summary of the assumptions for uncertainties from various sources used in the simulation of the NC and CC cross sections. The first three items are calibration uncertainties and affect the event reconstruction. The last four items are uncertainties which can be assigned directly to the cross section

The data include a full set of systematic uncertainties and the individual sources are summarized in Table 2. For the bulk of the phase space, the ‘electron’ reconstruction method is used where the kinematic variables x and $Q^2$ are determined from the energy and polar angle of the scattered electron. Important uncertainties originate from the electron energy scale and polar angle measurement, and uncertainties of $\Delta E_e^\prime / E_e^\prime = 0.1~\%$ and $\Delta \theta ^\prime _e = 0.1$ mrad are assumed. However, at lower values of y the electron method leads to a deterioration of the measurement resolution $\propto 1/y$. Thus one has to exploit the hadronic final state in the determination of the inelasticity. The present simulation accounts for this by using a simple ‘mixed’ (i.e. $Q^2_e,~y_h$) reconstruction method [49] to determine $x=Q^2/(sy)$. For the measurement of the hadronic final state, an uncertainty on the hadronic energy scale of $\Delta E_h/E_h = 0.5~\%$ is imposed. As discussed in Sect. 2, for the analysis of inclusive DIS data, we expect that these data are corrected for QED radiative corrections, including QED bremsstrahlung off the lepton, photonic lepton-vertex corrections, self-energy contributions at the external lepton lines, and fermionic contributions to the running of the finestructure constant. An uncertainty of 0.3 % on the cross sections due to these corrections is expected and the resulting experimental uncertainties will therefore comprise a corresponding contribution. An uncertainty due to the background from photoproduction events of $1.0~\%$ in the high-y region is assumed. The statistical uncertainty of each data point is taken to be at least 0.1 %. A global normalization uncertainty of 1 % is taken into account, which includes the luminosity uncertainty.

Finally, potential additional sources of measurement errors are combined in an uncorrelated uncertainty component of 0.5 %. These may comprise unfolding and model uncertainties, efficiency uncertainties, beam background related uncertainties, possible small stochastic uncertainties related to the calibration procedure, or uncorrelated components of any of the above sources. In fact, the actual size of this uncorrelated uncertainty is very difficult to estimate for the future LHeC, but we consider the assumption of 0.5 % to be rather conservative. In order to address the effect of the unknown size of the uncorrelated uncertainty in some detail, we consider in the following two alternative scenarios, one with an uncorrelated uncertainty of 0.5 %, as well as one with a more optimistic value of 0.25 %. These will be denoted in the following as the ‘a’ or ’b’ scenarios, respectively. Our data samples have been simulated for simplicity with an ad hoc and rather coarse x-$Q^2$ grid (see Table 1). Yet, real data may allow a much finer binning, in particular at medium x values or at higher $Q^2$, depending on the actual detector performance and its resolution. In fact, the effect of a possibly finer binning may be simulated to a very good approximation by changing the size of the uncorrelated uncertainty, which would then be equivalent by comparing the ‘a’ and ‘b’ scenarios. The properties of the generated four sets of data samples are summarized in Table 3.

Table 3 Summary of the LHeC measurement scenarios. The LHeC data scenarios differ by the assumption on the electron beam energy, $E_e$, and the assumptions made for the uncorrelated uncertainty (see text). They will be referred to by the names shown in the first column

In previous similar studies (see, e.g. [50, 51]) it was often assumed that cross section ratios are measured. These are for example the ratio of CC over NC cross sections, $R_\mathrm{CC/NC}$, the polarization asymmetry $A_\mathrm{LR}$, or the charge asymmetry $B_{\pm \,}$ measuring the difference between cross sections for electron and positron scattering. In fact, our inclusive DIS data implicitly comprise such a collection of cross section ratios, but while we do not construct these ratios explicitly we instead leave it to the parameter extraction procedure to exploit the corresponding information. In the following, however, it is often informative to consider these ratios for the purpose of exposing the parameter dependence and estimate the potential impact of data on the parameter determinations. In such ratios, we can then expect that most of the correlated uncertainties, such as normalization errors, become largely constrained by the fit while uncorrelated uncertainties are reduced by taking the properly weighted average of all data. As a consequence, due to the large number of data points, in the order of a few hundred, uncertainties at the per mille level can be expected for the observables which we are going to study in the following. The two measurement scenarios labeled with ‘a’ and ‘b’ described above will help us to verify this estimate of expected parameter uncertainties and its dependence on our assumption for correlated measurement errors.

5 Methodology of a combined EW+PDF fit

By the time when the LHeC is realized, one should expect that the determination of PDFs will be dominated by NC and CC DIS data obtained with it. The uncertainties of PDF parameterizations will mainly represent the propagated uncertainties of these inclusive LHeC data. The uncertainties of EW parameters determined from cross section data will therefore be correlated with PDF uncertainties. In order to account for these correlations, EW parameters have to be determined in a combined fit simultaneously with PDFs. This allows the complete set of statistical, as well as correlated and uncorrelated systematic uncertainties to be taken into account. We denote such an approach in the following by ‘EW’+PDF fit, while ‘EW’ may be replaced by the parameter of interest.

The x-dependence of the PDFs is parameterized at a starting scale of $\mu _0 = 1.3784~\mathrm {GeV}$, i.e. below the charm threshold. The NC and CC DIS inclusive cross sections determine four independent combinations of quark distributions, besides the gluon. Here the following five PDFs are chosen as independent input at this scale: the u and d valence quark distributions (xu and xd), the up-type and down-type anti-quark distributions ($x\overline{U}$ and $x\overline{D}$), and the gluon distribution (xg). The choice of the parameterization follows previous LHeC PDF studies [1, 31], which are closely related to HERAPDF-style PDFs [52,53,54]. The following functional form is used:

$$\begin{aligned} xf&= f_A x^{f_B} (1-x)^{f_C} (1+f_Dx+f_Ex^2) \nonumber \\&\quad - f_{A^\prime }x^{f_{B^\prime }}(1-x)^{0.25}\,, \end{aligned}$$

(18)

where f denotes any of the five input PDFs, $f = u$, d, $\overline{U}$, $\overline{D}$, g. The second term in this ansatz is taken into account only for the gluon distribution,³ i.e. $u_{A^\prime } = d_{A^\prime } = \overline{U}_{A^\prime } = \overline{D}_{A^\prime } = 0$. The normalization of each PDF is determined by the quark number sum-rule ($u_A$, $d_A$) or the momentum sum-rules ($g_A$). For the anti-quark PDF, we fix $\overline{U}_A = \overline{D}_A(1-0.4)$. Furthermore, we use $\overline{D}_B = \overline{U}_B$. Altogether, 13 independent PDF parameters are determined in each fit ($g_B$, $g_C$, $g_{A^\prime }$, $g_{B^\prime }$, $u_B$, $u_C$, $u_E$, $d_B$, $d_C$, $\overline{U}_C$, $\overline{D}_A$, $\overline{D}_B$, $\overline{D}_C$). The values of the PDF parameters used for the generation of pseudo data are not of particular relevance here. They have been obtained from a private fit to HERA data, similar to Refs. [23, 54].

QCD higher-order corrections are taken into account at NNLO in the zero-mass variable flavor number scheme. They are implemented for the evolution of the PDFs and the calculation of the structure functions using QCDNUM [55]. The strong coupling is fixed, $\alpha _s^{\overline{\text {MS}},N_f=5}(m_Z) = 0.118$. We do not consider QED or EW corrections for the PDF evolution [56,57,58,59], since their impact on the determination of EW parameters is expected to be small and does not change the uncertainties estimated in the present study. EW effects are, however, included in the calculation of cross sections, as described above in Sect. 2.

The $\chi ^2$ quantity which is subject to the minimization and error propagation is based on normal-distributed relative uncertainties,

$$\begin{aligned} \chi ^2 =\sum _{ij} \log {\frac{\varsigma _i}{\sigma _i}}V^{-1}_{ij} \log {\frac{\varsigma _j}{\sigma _j}} \end{aligned}$$

(19)

where the sum runs over all data points, $\varsigma _i$ are the measured cross section values and $\sigma _i$ their corresponding theory predictions (cf. Eqs. (1) and (9)), which incorporate the dependence on the fit parameters. The covariance matrix V represents the relative uncertainties of the data points. The Minuit library is employed, and the resulting uncertainties of the fit parameters are calculated using the HESSE or MINOS algorithm [60]. For our study, we set the data values equal to the predictions, i.e. our data represent an Asimov data set [61] and resulting uncertainties refer to expected uncertainties. It is important to note that with the above definition of $\chi ^2$ the actual value of the cross section at a given point does not enter the calculation of the uncertainties, but only the relative size of the uncertainties is of relevance. A very similar methodology has previously been used by H1 for the determination of the expected uncertainties in their electroweak analysis of inclusive DIS data [18]. We have validated that the uncertainties on the PDFs from a pure PDF fit, i.e. with fixed electroweak parameters, are in good agreement with dedicated PDF studies based on the same LHeC data samples [3, 32].

6 Weak boson masses

First, we investigate the possibility to determine the fundamental parameters of the EW theory from LHeC inclusive DIS data. In this initial part of our study we are further interested to understand how the uncertainty estimates depend on the assumptions of the simulated data.

Since our analysis is based on theory predictions derived in the on-shell scheme, the free parameters at the LO are only the masses of the weak gauge bosons, $m_W$ and $m_Z$, and the fine structure constant $\alpha$. The latter is fixed in the analysis, i.e. it is considered to be known with ultimate precision. The weak mixing angle is defined by the ratio of the gauge boson masses and thus not independent. At higher orders, there is in addition a sensitivity to the top-quark and the Higgs-boson mass, which will be studied in a subsequent section.

We determine the expected uncertainties for $m_W$ in an $m_W$+PDF fit, where the value of $m_Z$ is considered as an external input, e.g. taken from the LEP+SLD combined measurement [62]. For the W-boson mass parameter, we then find expected uncertainties of

$$\begin{aligned} \Delta m_W(\text {LHeC-60a})= & {} \pm \,8_{(\mathrm{exp})}\pm \,5_{(\mathrm{PDF})}\,\mathrm {MeV} \nonumber \\= & {} \, \pm \,10_{\text {(tot)}}\,\mathrm {MeV} \mathrm{~~~~and~~} \\ \Delta m_W(\text {LHeC-50a})= & {} \pm \,9_{(\mathrm{exp})}\pm \,8_{(\mathrm{PDF})}\,\mathrm {MeV} \nonumber \\= & {} \, \pm \,12_{\text {(tot)}}\,\mathrm {MeV} \nonumber \end{aligned}$$

(20)

for the scenarios LHeC-60a and LHeC-50a (cf. Sect. 4), and

$$\begin{aligned} \Delta m_W(\text {LHeC-60b})= & {} \pm \,5_{(\mathrm{exp})}\pm \,6_{(\mathrm{PDF})}\,\mathrm {MeV} \nonumber \\= & {} \, \pm \,6_{\text {(tot)}}\,\mathrm {MeV} \mathrm{~~~~and~~} \\ \Delta m_W(\text {LHeC-50b})= & {} \pm \,6_{(\mathrm{exp})}\pm \,6_{(\mathrm{PDF})}\,\mathrm {MeV} \nonumber \\= & {} \, \pm \,8_{\text {(tot)}}\,\mathrm {MeV} \nonumber \end{aligned}$$

(21)

for LHeC-60b and LHeC-50b, respectively. The breakdown of the uncertainty into contributions due to systematic experimental and PDF uncertainties was obtained by repeating the fit with PDF parameters kept fixed, which yields the exp uncertainty, while the PDF uncertainty is then calculated as the quadratic difference from the total uncertainty. The size of the uncertainty component associated to the PDFs is found to be of similar size as the exp uncertainty.

Fig. 3

Left: The total uncertainty $\Delta m_W$ as a function of the size of the uncorrelated uncertainty. The horizontal line marks the uncertainty of the present world average. The ‘a’ scenarios LHeC-60a and LHeC-50a (uncorrelated uncertainty of 0.5 %) and the ‘b’ scenarios LHeC-60b and LHeC-50b (0.25 %) are indicated by vertical lines. Right: The uncertainty $\Delta m_W$ as a function of the size of the normalization uncertainty of the DIS cross sections. The nominal assumption of 1 % is indicated by a vertical line. All other systematic uncertainties are kept as listed in Table 2

Altogether, we find a relative uncertainty for $m_W$ of the order of $10^{-4}$, which is compatible with our rough initial estimate for cross section ratios.⁴. The two scenarios (‘a’ and ‘b’) differ by the assumption for the size of the single-bin uncorrelated uncertainty, but have otherwise the same experimental uncertainties. The dependence of $\Delta m_W$ on this uncertainty component is displayed in the left panel of Fig. 3. Obviously, a good control of the uncorrelated uncertainty component will help to improve the precision of a potential W-boson mass determination. We re-iterate that a smaller uncorrelated uncertainty can be achieved through a higher resolution which allows one to choose finer binning of the data. In the right panel of Fig. 3 we show how the uncertainty of $m_W$ depends on the cross section normalization uncertainty for the different LHeC scenarios. Obviously this component of the uncertainty for the cross section measurement cancels to a large extent, as already discussed in the previous section. Other (correlated) systematic uncertainty components behave similar as the normalization uncertainty.

The expected uncertainties $\Delta m_W$ are displayed in Fig. 4 and compared with the measurements ⁵ by LEP2 [64], Tevatron [63], ATLAS [65] and the PDG [41]. We conclude that the LHeC can be expected to yield a W-boson mass determination with the smallest experimental uncertainty from a single experiment. It will even be superior to the current world average. Therefore, when real data are available, a detailed assessment of associated theoretical uncertainties will be needed to determine the accurate central value of the W-boson mass. For example, a theoretical uncertainty due to the top-quark mass dependence entering through radiative corrections in $\Delta r$ (see Eq. (17)) will have to be taken into account. Assuming $\Delta m_t = 0.5~\mathrm {GeV}$, one should expect an additional uncertainty of $\Delta m_W=2.5\,\mathrm {MeV}$. The estimate of experimental and PDF uncertainties given above, is, however, not sensitive by itself to higher-order corrections beyond NLO, while the actual values would be.

The high precision of the W-boson mass parameter requires an in-depth discussion of its interpretation and the relation to other, more direct, measurements. We find, that the sensitivity of the DIS cross sections to $m_W$ arises mainly from the weak mixing angle in the NC vector couplings $g_V^f$, Eqs. (13) (cf. also next section), whereas the contribution from the NC and CC normalization, Eqs. (6) and (9), and from the W-boson propagator term in CC DIS, $(1/(Q^2 +m_W^2))^2$, cf. Eq. (9), is only small.⁶ Therefore, the precise measurement of DIS cross sections yields primarily (only) an indirect determination of the SM mass parameters. In fact, the philosophy of this indirect parameter determination is similar to the one of the so-called ‘global EW fits’ [66,67,68] where a collection of observables is fitted to SM predictions calculated as a function of properly chosen free theory parameters. The ‘measurement’ of $m_W$ from inclusive DIS cross sections at the LHeC, therefore, provides a consistency check of the SM and is complementary to direct, true, mass measurements of the W-boson mass.

Fig. 4

Determination of the W-boson mass from a combined $m_W$+PDF fit, assuming fixed values for all other EW parameters. Different LHeC scenarios with beam energies of $E_e=60~\mathrm {GeV}$ and 50 $\mathrm {GeV}$ as described in the text are considered and compared with existing measurements [63,64,65] and with the world average value (PDG2020) [41]

A determination of the Z-boson mass from an $m_Z$+PDF fit yields expected experimental uncertainties of $\Delta m_Z=11$ MeV (13 MeV) for LHeC-60a (LHeC-50a), respectively. These uncertainties are of a similar size as those for $m_W$. However, they cannot compete with the high precision measurements at the Z-pole by LEP+SLD [62]. Moreover, future $e^+e^-$ colliders are expected to provide a substantial improvement of the precision of $m_Z$ [19, 69, 70].

Fig. 5

Simultaneous determination of the Z-boson and W-boson masses $m_Z$ and $m_W$ from LHeC-60a or LHeC-50a data. The additional precision measurement of $G_\mathrm{F}$ yields a strong constraint and its combination with the $m_Z$ and $m_W$ determination leads to a very shallow ellipse

Finally we investigate the possibility to perform a combined determination of $m_W$ and $m_Z$. The result is shown in Fig. 5, where the 68 % confidence level contours are displayed. The precision of $m_W$ and $m_Z$ if taken from the projections of these contours, is only moderate. However, the observed strong correlation provides a test of the high-energy behavior of the EW SM theory. Indeed, the 68 % C.L.-contour is aligned along the line of a constant value of $\sin ^2\theta _W$ (dotted line in Fig. 5). Imposing the additional constraint for the very precisely known value of $G_F$ [48] (dashed line, see Refs. [51, 71]) results in a very shallow ellipse (yellow). Real data would have to lead to a consistent picture of the different constraints shown in this figure. Their comparison provides a test for the consistency of high-energy data from the LHeC with low-energy input from $\alpha$, $G_F$ and $\sin ^2\theta _W$.

7 The weak mixing angle $\sin ^2\theta _W$

In the SM, the weak neutral-current couplings of the fermions are fixed by one single parameter, i.e. through the weak mixing angle $\theta _\text {W}$. High-precision measurements of $\sin ^2\theta _W$ in as many as possible different processes are therefore considered as a key to test and to restrict extensions of the SM. Therefore, we study in this section the prospects for a determination of $\sin ^2\theta _W$ from DIS data at the LHeC, i.e. we assume the weak mixing angle in the fermion neutral-current couplings as a free fit parameter while all other parameters are fixed. This way we allow the weak neutral-current couplings to deviate from their SM values, however only in a correlated way, instead of allowing independent, flavor-dependent variations for vector and axial-vector couplings as we will do in a subsequent section.

The highest precision on $\sin ^2\theta _W$ so far has been obtained from interpretations of dedicated measurements in $e^+e^-$ collisions at the Z pole [62]. The results are conventionally expressed in terms of a leptonic effective weak mixing angle which is related to the on-shell definition of $\sin ^2\theta _W$ by a well-known correction factor,

$$\begin{aligned} \sin ^2\theta _{\text {W},\ell }^\text {eff}= \kappa _{\ell }(m_Z^2) \sin ^2\theta _W\,. \end{aligned}$$

(22)

A determination of $\sin ^2\theta _W$ from DIS data can be compared with Z-pole measurements, provided its value is mapped to the definition of the leptonic weak mixing angle. Also in DIS one can define an effective, scale- and flavor-dependent weak mixing angle, cf. Eq. (14),

$$\begin{aligned} \sin ^2\theta _{\text {W},f}^\text {eff}(\mu ^2) = \kappa _{f}(\mu ^2) \sin ^2\theta _W\,. \end{aligned}$$

(23)

We will now consider $\sin ^2\theta _W$ as a free parameter which is allowed to vary in a $\sin ^2\theta _W$+PDF fit. Note that we consider in this fit only the $\sin ^2\theta _W$-dependence in the vector couplings, taken the same for leptons and quarks. SM higher-order corrections are taken into account as described in Sect. 2 by keeping the $Q^2$- and flavor-dependent form factors $\kappa _{f}$ (see Eq. (13)). Our estimate for the uncertainties in the different LHeC scenarios are

$$\begin{aligned} \Delta \sin ^2\theta _W\ (\text {LHeC-60a})= & {} \pm \,0.00023_{(\mathrm{exp})}\pm \,0.00009_{(\mathrm{PDF})} \nonumber \\= & {} \, \pm \,0.00025_{\text {(tot)}} \, , \\ \Delta \sin ^2\theta _W\ (\text {LHeC-50a})= & {} \pm \,0.00028_{(\mathrm{exp})}\pm \,0.00019_{(\mathrm{PDF})} \nonumber \\= & {} \, \pm \,0.00034_{\text {(tot)}} \nonumber \end{aligned}$$

(24)

and

$$\begin{aligned} \Delta \sin ^2\theta _W\ (\text {LHeC-60b})= & {} \pm \,0.00014_{(\mathrm{exp})}\pm \,0.00006_{(\mathrm{PDF})} \nonumber \\= & {} \, \pm \,0.00015_{\text {(tot)}} \, , \\ \Delta \sin ^2\theta _W\ (\text {LHeC-50b})= & {} \pm \,0.00017_{(\mathrm{exp})}\pm \,0.00014_{(\mathrm{PDF})} \nonumber \\= & {} \, \pm \,0.00022_{\text {(tot)}} \, . \nonumber \end{aligned}$$

(25)

Fig. 6

Comparison of determinations of the weak mixing angle. The results from LEP+SLD [62], Tevatron [72], LHC [73,74,75,76] and the SM value refer to the leptonic weak mixing angle, $\sin ^2\theta _{\text {W},\ell }^\text {eff}$, and include the information about the W- and Z-boson masses [76]. They are all obtained from a combination of various separate measurements (not shown individually) (see also Ref. [68] for additional information). Two scenarios for the simulation of LHeC inclusive NC/CC DIS data are considered. Here, the estimated uncertainties refer to the fermionic effective weak mixing angle, $\sin ^2\theta _{\text {W},f}^\text {eff}$. With real data, the central values will have to be mapped to each other by taking into account the proper $\kappa$-factors, see Eqs. (22, 23)

These results are collected in Fig. 6 where we compare with presently available determinations of the leptonic weak mixing angle. Here we have neglected additional parametric uncertainties that may enter when the LHeC measurements are mapped to the leptonic effective weak mixing angle. The determination at the LHeC is superior to any current single measurement and of similar size as the LEP+SLD combination. Even measurements in a spacelike region of momentum transfers, i.e. for a non-resonant process, turns out to be competitive with Z-pole measurements, despite of the fact that the cross section receives large contributions from pure photon exchange at lower $Q^2$, which is independent of the weak mixing angle.

In the on-shell scheme, $\sin ^2\theta _W$ and $m_W$ are related to each other and a measurement of one parameter can be interpreted as a determination of the other. The uncertainty for $\sin ^2\theta _W$ in scenario LHeC-60b, $\Delta \sin ^2\theta _W\ = \pm \, 0.00015$ would result in an uncertainty for the W-boson mass of $\Delta m_W= \pm \, 8$ MeV or, vice versa, $\Delta m_W= \pm \, 6$ MeV from the $m_W$+PDF fit (Sect. 6) would correspond to $\Delta \sin ^2\theta _W\ = \pm \, 0.00012$. Comparing these numbers we can conclude that most of the sensitivity to $m_W$ is due to the weak NC couplings; the additional $m_W$-dependence from the CC propagator mass provides little extra information for the determination of $m_W$.

Fig. 7

Expected uncertainties of the weak mixing angle determined in sub-regions of $Q^2$. Two scenarios for the simulation of LHeC inclusive NC/CC DIS data are displayed, LHeC-50a and LHeC-60b. The SM expectation is displayed as a dotted line

Table 4 Expected relative uncertainties for the determination of $\sin ^2\theta _W$ as a function of $Q^2$ for the four LHeC scenarios. The uncertainties are obtained in a simultaneous fit of 12 parameters $\sin ^2\theta _{\text {W}}(\mu ^2_i)$ with $\mu _i^2 = - Q_i^2$ ($i=1,\dots ,12$) together with the PDF parameters. Absolute uncertainties $\Delta \sin ^2\theta _W$ can be calculated by multiplication with the value of $\sin ^2\theta _W$

The measurement of $\sin ^2\theta _W$ can be performed in sub-regions of the wide kinematic range of $Q^2$ accessible at the LHeC. The results for twelve $Q^2$ values obtained from bin-width and bin-center corrected cross section data are shown in Fig. 7 and Table 4. We find that $\sin ^2\theta _W$ can be determined in the range of about $25< \sqrt{Q^2} < 700\,\mathrm {GeV}$ with a precision better than 0.1 % and everywhere better than 1 %. We emphasize that DIS is complementary to other measurements since the scattering process is mediated by boson exchange with spacelike momenta, i.e. the scale is given by $\mu ^2 = - Q^2$ (cf. Sect. 7). If a calculation of DIS cross sections including higher-order EW corrections in the $\overline{\mathrm{MS}}$ scheme is available, the uncertainty of this $Q^2$-dependent $\sin ^2\theta _W$-determination can be translated into a test of the running of the weak mixing angle.

8 Mass parameters through higher-order corrections

The sensitivity to the weak boson masses $m_W$ and $m_Z$ is high since these parameters enter at tree level through the cross section normalization and through the boson propagators. Other SM mass parameters enter only at higher orders. Cross sections are therefore only weakly dependent on them. However, measurements with a high precision may still exhibit some sensitivity. Their investigation is interesting since this provides a test of the SM at the level of quantum corrections which is complementary to direct determinations.

The dominant corrections to the gauge boson self energies depend on the top-quark mass $m_t$.⁷ In the on-shell scheme they enter in the NC coupling parameters $\rho _\text {NC}$ and $\kappa$ and in the CC correction factor $\Delta r$ through the quantity $\rho _t = (3\alpha /16\pi \sin ^2\theta _W) (m_t^2/m_W^2)$. Therefore, inclusive DIS cross sections depend quadratically on $m_t$ and since $\rho _t$ is in the order of 1 %, one can expect to observe a sizeable effect on the DIS cross sections.

We have determined the uncertainties of the top-quark mass $m_t$ through DIS cross section measurements for the four scenarios in an $m_t$+PDF fit. For LHeC-50a and LHeC-50b we find $\Delta m_t= \pm \,2.2\,\mathrm {GeV}$ and $\pm \, 1.8\,\mathrm {GeV}$, respectively. For the LHeC scenarios with $E_e=60\,\mathrm {GeV}$, the top-quark mass can be determined with an uncertainty of $\Delta m_t= \pm \,1.4\,\mathrm {GeV}$ (LHeC-60a) and

$$\begin{aligned} \Delta m_t\,\text {(LHeC-60b)} = \pm \,1.1\,\mathrm {GeV} \,. \end{aligned}$$

(26)

The size of the PDF-related uncertainty amounts to about 0.6 $\mathrm {GeV}$ and is already included in the values above. In these studies, the value of $m_W$ is considered as an external, i.e. fixed, parameter. However, the dominant theoretical uncertainty for an $m_t$ determination arises in fact from the uncertainty of $m_W$. At present, the W mass is known with an uncertainty of $\Delta m_W= \pm \, 12\,\mathrm {MeV}$ [41]. This corresponds to a theory uncertainty of $m_t$ of about $\pm \,2\,\mathrm {GeV}$.

The size of the LHeC experimental uncertainty compares well with uncertainties from recent LHC measurements, which are typically in the range between $\Delta m_t= \pm \,0.3$ and $\pm \,2.0$ $\mathrm {GeV}$  [77] (see also Ref. [41] and references therein). One should note, however, that the uncertainty of $m_t$ at the LHC experiments is dominated by Monte Carlo modelling and theoretical uncertainties related to the proper definition of the top-quark mass. These theoretical uncertainties are shared between different LHC measurements and it is expected that they limit the precision of the $m_t$ determination also in the future. In contrast, the definition of the top-quark mass entering in higher-order EW corrections to DIS cross sections is theoretically very clean and free from QCD-related ambiguities. In fact, the definition of $m_t$ corresponds to the one used in the calculation of observables in the SM framework, as it is also done in the global EW fits. It will therefore be justified to include possible future data from the LHeC in a determination of a world average of $m_t$. We study this possibility briefly in appendix A. Our results indicate that LHeC data will not improve the present uncertainty of $\Delta m_t= \pm \,2.1\,\mathrm {GeV}$ from global fits [41, 66, 67] once direct measurements of $m_t$ and $m_W$ are taken into account.

Fig. 8

Simultaneous determination of the W-boson and top-quark masses from LHeC-60a or LHeC-50a data. Results from the Z-pole fit using LEP+SLD data [62] and from a global EW fit, where direct measurements of $m_W$ and $m_t$ have been excluded [66] are also shown

We also consider the possibility to determine the W-boson mass $m_W$ simultaneously together with $m_t$. Prospects for such a simultaneous determination of $m_t$, $m_W$, and the PDFs are displayed for selected LHeC scenarios in Fig. 8 and compared with results from the LEP+SLD combination of Z-pole measurements [62]. The figure shows also results from a global EW fit [66], for which the direct $m_t$ and $m_W$ measurements have been excluded. We find that the uncertainties of the LHeC are better than those obtained from the LEP+SLD combined data. For the scenario LHeC-60b, the uncertainty contour is very similar in size as the global EW fit. It is not surprising that both the global EW fit and the LHeC fit exhibit the same type of correlation since they exploit the same $m_t^2/m_W^2$-dependent terms of the radiative corrections.

One may also attempt to determine the Higgs-boson mass $m_H$ from inclusive DIS data. $m_H$ also enters through the self-energy corrections in the SM, however, the $m_H$ dependence is only logarithmic, $\propto \log (m_H^2/m_W^2)$, i.e. very weak. An $m_H$+PDF fit leads to an uncertainty of $\Delta m_H=^{+28}_{-23}$ and $^{+14}_{-13}~\mathrm {GeV}$ for the scenarios LHeC-50a and LHeC-60b, respectively. This compares well with the precision found for the indirect $m_H$ determinations from LEP+SLD combined data [62, 66, 67], but is, of course, much less precise than the direct determination from the LHC experiments nowadays [78, 79]. From Higgs boson production and its decays into fermion pairs, the LHeC has a direct Higgs mass measurement potential as well, which surely is much better than the indirect one but unlikely competitive to that at the LHC through the 4-lepton and 2-photon decays.

Fig. 9

Results of 2-parameter fits to pairs of S, T, and U where $m_Z$ and $m_W$ are fixed SM input parameters. For each choice of two of the three parameters S, T, or U, the third oblique parameter is kept equal to zero. $1\sigma$ contours are shown for three LHeC scenarios. The relation how a direct measurement of $G_\mathrm{F}$ would constrain the parameters is indicated in addition

9 Oblique parameters S, T, and U

Many theories beyond the SM predict additional heavy particles. While these may be too heavy for a direct detection in present or future experiments, they may contribute through effective low-energy operators or through higher-order loop corrections to observables. High-precision measurements provide an opportunity to observe in an indirect way their presence.

Loop insertions with particle-antiparticle pairs in gauge boson self energies, $\Sigma ^{ij}(q^2)$, are particularly important since they are universal. If the masses of the non-SM particles are large, a low-$q^2$ expansion of the self-energy corrections,

$$\begin{aligned} \Sigma ^{ij}(q^2)&= \Sigma ^{ij}(0) + q^2 F^{ij}(q^2) \, , \nonumber \\&\quad \quad (ij) = (\gamma \gamma ),~(\gamma Z),~(ZZ),~(WW) \, , \end{aligned}$$

(27)

and neglecting the $q^2$-dependence of $F^{ij}(q^2)$, can provide a sufficiently precise approximation by constant parameters. Taking into account that the electromagnetic U(1) gauge symmetry has to stay intact and that some of these constants can be absorbed into renormalization constants, there are three free parameters, usually called S, T and U [80]. A suitable definition is described in Ref. [41] which we adopt in the following, while their relation to alternative definitions [81, 82] is described in Ref. [51].

Results for various STU+PDF fits are presented in Fig. 9 and Table 5. These fits are performed in the on-shell scheme and the SM masses are fixed at their PDG values, in particular the values of $m_Z$ and $m_W$. Single-parameter fits of S, T or U can provide uncertainties that are better by a factor of 2 to 5 compared to the present PDG values [41]. In 2- and 3-parameter fits we observe a very strong correlation of the parameters. This can be traced back to the fact that only certain linear combinations of S, T and U contribute to the NC and CC scattering cross sections and the $\gamma Z$ interference contribution. For instance, the values of T and U can be disentangled only if their contributions to NC and CC DIS are combined, but not from NC DIS alone. By implication, however, these linear combinations can be determined with very high precision – a fact which makes the DIS measurement particularly useful since it is complementary to determinations of S, T and U from Z-pole data (see, for example, Refs. [41, 66, 67]).

Table 5 Results of the STU+PDF fits with fixed SM gauge boson masses. From top to bottom we show the expected uncertainties for 1-, 2- and 3-parameter fits as indicated in the first column for all four LHeC scenarios. In the case of 2- and 3-parameter fits, the last columns show the correlation matrices

The STU+PDF fit to LHeC DIS data in the on-shell scheme can be combined with the constraint from the $G_F$ measurement, cf. Fig. 9. Since $G_F$ is known with very high precision, this constraint amounts essentially to fixing one linear combination of the STU parameters, the one that enters in $\Delta r$ (see Eq. (17)).

Fig. 10

Same as Fig. 9, but the calculations are performed in the modified on-shell scheme, i.e. the value for $m_Z$ is fixed, but the W boson mass is calculated from its relation to the Fermi constant $G_\mathrm{F}$. The relations how direct measurements of $m_W$ or $\sin ^2\theta _{\text {W},\ell }^\text {eff}$ at the Z-pole would constrain the two oblique parameters are additionally indicated by dashed and dotted lines, respectively. In the modified on-shell scheme, the measurement of $m_W$ would constrain the same relation as a measurement of $1-m_W^2/m_Z^2$ (dashed line)

Table 6 Same as Table 5, but in the modified on-shell scheme with $m_Z$ and $G_F$ as fixed input parameters, i.e. $m_W$ is calculated

New physics parameterized with the help of S, T and U will also affect the $G_\mathrm{F}$-$m_W$ relation, Eq. (17), through the W-boson self energy correction to the muon decay. In the modified on-shell scheme [83], where $m_W$ is calculated from $G_F$, new physics will therefore not only contribute by corrections to the measured cross sections, but also through a modification of the input parameters. As a consequence, the sensitivity to S, T and U is modified. Results of a STU+PDF fit in the modified on-shell scheme are collected in Fig. 10 and Table 6. The uncertainties determined from single-parameter fits are slightly less favorable in this case. However, the 2- and 3-parameter fits exhibit weaker correlations leading to smaller uncertainties for their corresponding 1-parameter projections. In the modified on-shell scheme, additional constraints on the STU parameters may be obtained by adding further direct measurements of $m_W$ or $\sin ^2\theta _{\text {W},\ell }^\text {eff}$, e.g. from measurements in $e^+e^-$ or hadron-hadron collisions. The parameter relations of such measurements are also indicated in Fig. 10 and in particular external measurements sensitive to $\sin ^2\theta _{\text {W},\ell }^\text {eff}$ would be useful for further improvements.

10 Weak neutral-current couplings beyond the SM: $\rho _{\text {NC}}$ and $\kappa$

In the following we consider the option that modifications of the EW interaction by new physics can be parameterized directly with the help of the NC weak coupling constants. A systematic approach is based on using anomalous parameters $\rho ^{\prime }_{\text {NC}\ }$and $\kappa ^{\prime }_{}$. The first, $\rho ^{\prime }_{\text {NC}}$, affects the SU(2) component of NC couplings, while the second, $\kappa ^{\prime }_{}$, represents a modification of the weak mixing with the U(1) gauge field. These parameters can be chosen flavor-specific and are introduced by writing [18]

$$\begin{aligned} g_A^f= & {} \sqrt{\rho ^{\prime }_{\text {NC},f}\rho _{\text {NC}, f}} \, I^3_{\mathrm{L},f}\, , \end{aligned}$$

(28)

$$\begin{aligned} g_V^f= & {} \sqrt{\rho ^{\prime }_{\text {NC},f}\rho _{\text {NC}, f}} \, \left( I^3_{\mathrm{L},f}- 2 Q_f \kappa ^{\prime }_{f}\kappa _{f}\sin ^2\theta _W\right) \, . \end{aligned}$$

(29)

Here, the un-primed form factors $\rho _\text {NC}$ and $\kappa _f$ take higher-order SM corrections into account, as described in Sect. 2. In the SM, the anomalous parameters $\rho ^{\prime }_{\text {NC}\ }$and $\kappa ^{\prime }_{}$ are unity. In the presence of physics beyond the SM, they can deviate from unity and be $Q^2$-dependent. In particular, a value of $\rho ^{\prime }_{\text {NC}\ }\ne 1$ corresponds to a modification of the ratio of the strengths of NC and CC weak interactions. A similar study of a generalization of the CC form factor $\rho _\text {CC}$ will be discussed below in Sect. 11. The parameter $\kappa ^{\prime }_{}$ can also be interpreted as a modification of the weak mixing angle $\sin ^2\theta _W$ (see Sect. 7), i.e. the definition of the effective weak mixing angle, Eq. (23), is replaced by

$$\begin{aligned} \sin ^2\theta _{\text {W},f}^\text {eff}(\mu ^2) = \kappa ^{\prime }_{f}(\mu ^2) \kappa _{f}(\mu ^2) \sin ^2\theta _W\,. \end{aligned}$$

(30)

Fig. 11

Expectation for a determination of $\rho ^{\prime }_{\text {NC},f}$ and $\kappa ^{\prime }_{f}$ at the 68 % confidence level, assuming one common anomalous factor for each fermion type. The results for three different LHeC scenarios are compared with the relative uncertainties obtained from an analysis of LEP+SLD combined data [62] for leptonic couplings

We determine the uncertainties of the anomalous form factors $\rho _\text {NC}^\prime$ and $\kappa ^\prime$ in a simultaneous fit together with the PDFs, using the simulated LHeC inclusive NC and CC DIS data. First, we consider universal, i.e. flavor-independent, $\rho _\text {NC}^\prime$ and $\kappa ^\prime$ parameters for both the quark and electron couplings. The results are displayed in Fig. 11. In this figure, we compare the expected LHeC uncertainties with corresponding results that have been obtained from combined LEP+SLD data for leptonic couplings.⁸ At the LHeC, uncertainties are expected at the level of a few per mille, i.e. of similar size as those of the LEP+SLD combination. As expected, the scenario LHeC-60b yields the smallest uncertainties, while from the LHeC-50a scenario one should expect the largest ones.

The $\rho _\text {NC}^\prime$-$\kappa ^\prime$ fit can be interpreted as a simultaneous determination of $\sin ^2\theta _{\text {W},f}^\text {eff}$ and a universal modification of the normalization of NC weak couplings by $\rho ^{\prime }_{\text {NC}.}$ We find an uncertainty of $\Delta \sin ^2\theta _{\text {W},f}^\text {eff} = \pm \, 0.00023$ ($\pm \,0.00071$) for LHeC-60b (LHeC-50a).

Next, we allow the anomalous form factors to be different for up- and down-type quarks, but assume the couplings of the electron as predicted by the SM. A precise knowledge of the up- and down-type couplings is particularly interesting since this may help to narrow down possible explanations of the flavor-structure of the SM. We perform a fit of the four anomalous parameters ($\rho _{\text {NC},u}^\prime$, $\kappa _{u}^\prime$, $\rho _{\text {NC},d}^\prime$, and $\kappa _{d}^\prime$). The resulting contours at 68 % C.L. for a combination of two of the free parameters is shown in Fig. 12 (left panel for up-type, right panel for down-type quarks). The high-precision data from LEP+SLD did not allow for a full flavor-separated determination of quark couplings; however there are determinations of the couplings of the second- and third-generation quarks, charm and bottom, based on a data analysis using flavor tagging. It is interesting to compare the LHeC analysis, which is dominated by light-quark couplings, with these LEP+SLD results for heavy quarks. This is shown in Fig. 12 and we find that the uncertainties for up-type quarks are superior to those from LEP+SLD and comparable in the case of down-type quarks. The results for different LHeC scenarios are summarized in Table 7.

Fig. 12

Expectations at the 68 % confidence level for the simultaneous determination of anomalous up- and down-type quark couplings, assuming electron couplings fixed at their SM value. In the left panel, for up-type quarks, the results are compared with uncertainties from LEP+SLD for charm-quark anomalous couplings. The right panel for down-type quarks shows a comparison of LHeC results with LEP+SLD [62] determinations of bottom-quark couplings

Table 7 Overview of results for the $\rho ^{\prime }_{\text {NC}}$ and $\kappa ^{\prime }_{}$ fits in different LHeC scenarios. From top to bottom we list results for 4-, 2- and 1-parameter+PDF fits

Fig. 13

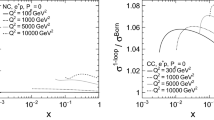
Scale dependence of the anomalous form factors $\rho ^{\prime }_{\text {NC},f}(\mu ^2)$ (left) and $\kappa ^{\prime }_f(\mu ^2)$ (right) with $\mu ^2 = - Q^2$ for the scenarios LHeC-50a and LHeC-60b. The highest precision is obtained in the region of about $Q^2 \approx 20,000\,\mathrm {GeV}^2$ for scenario LHeC-60b. The expected uncertainties are compared to measured values by H1 [18]

The fact that DIS at the LHeC covers a huge range of $Q^2$ values allows us to perform a test of SM couplings which is not feasible at other experiments: one can determine the scale dependence of the anomalous form factors. Indeed, many models predict flavor-specific and $Q^2$-dependent modifications. In order to study such a test, we perform fits of $\rho _\text {NC}^\prime$ and $\kappa ^\prime$ to LHeC data split into twelve subsets with different $Q^2$ ranges. Our findings are shown in Fig. 13 for the scenarios LHeC-60a and LHeC-50a, where we include, for comparison, results obtained from H1 data [18]. At the LHeC we expect highest precision in the region of about $Q^2 \approx 20,000~\mathrm {GeV}^2$. In the worst case, for scenario LHeC-50a, we can expect uncertainties $\Delta \rho ^{\prime }_{\text {NC}\ }= \pm \, 0.0029$ and $\Delta \kappa ^{\prime }_{\ }= \pm \, 0.0023$, while the best-case scenario LHeC-60b can provide a determination of the non-standard parameters with $\Delta \rho ^{\prime }_{\text {NC}\ }= \pm \, 0.0015$ and $\Delta \kappa ^{\prime }_{\ }= \pm \, 0.0011$, i.e. in this case, the uncertainties obtained in the two extreme LHeC scenarios differ by a factor of 2.

11 Electroweak effects in charged-current scattering

The LHeC provides a unique opportunity to investigate charged-current scattering processes over many orders of magnitude in the momentum transfer $Q^2$ in a single experiment. This is a consequence not only of the excellent detector performance like precise tracking, highly granular calorimetry and high-bandwidth triggers; particularly important is the fact that in CC DIS the event kinematics can be fully reconstructed from the measurement of the hadronic final state and the incoming electron beam four-momentum.

Higher-order EW corrections to the CC DIS cross sections are collected in the effective couplings of the fermions to the W boson as shown in Eqs. (15, 16). To allow for physics beyond the SM, we introduce new anomalous, primed parameters, $\rho ^\prime _{\text {CC},\, eq}$ and $\rho ^\prime _{\text {CC},\, e\bar{q}}$ [18], in a similar way as for the case of NC scattering. The modified CC structure functions then become

$$\begin{aligned} W_2^-= & {} x \left( (\rho _{\text {CC}, eq}\rho ^{\prime }_{\text {CC},eq})^2 U + (\rho _{\text {CC},e\bar{q}}\rho ^{\prime }_{\text {CC},e\bar{q}})^2 \overline{D} \right) , \end{aligned}$$

(31)

$$\begin{aligned} xW_3^-= & {} x \left( (\rho _{\text {CC},eq}\rho ^{\prime }_{\text {CC},eq})^2 U - (\rho _{\text {CC},e\bar{q}}\rho ^{\prime }_{\text {CC},e\bar{q}})^2 \overline{D} \right) , \end{aligned}$$

(32)

$$\begin{aligned} W_2^+= & {} x \left( (\rho _{\text {CC},eq}\rho ^{\prime }_{\text {CC},eq})^2 \overline{U}+ (\rho _{\text {CC},e\bar{q}}\rho ^{\prime }_{\text {CC},e\bar{q}})^2 D \right) , \end{aligned}$$

(33)

$$\begin{aligned} xW_3^+= & {} x \left( (\rho _{\text {CC},e\bar{q}}\rho ^{\prime }_{\text {CC},e\bar{q}})^2 D - (\rho _{\text {CC},eq}\rho ^{\prime }_{\text {CC},eq})^2 \overline{U} \right) . \end{aligned}$$

(34)

Fig. 14

Expected uncertainties of anomalous CC coupling parameters $\rho ^{\prime }_{\text {CC},eq}$ and $\rho ^{\prime }_{\text {CC},e\bar{q}}$ for three different LHeC scenarios compared with results from the H1 measurement [18]

Table 8 Expected uncertainties of anomalous CC coupling parameters $\rho ^{\prime }_{\text {CC},eq}$ and $\rho ^{\prime }_{\text {CC},e\bar{q}}$ from 2-parameter (upper part) and 1-parameter fits (lower part). The last two lines show the results from a fit combining the CC parameter $\rho ^{\prime }_{\text {CC}}$ with the NC $\kappa ^\prime$ parameter (see Eq. (30))

The prospects for a determination of these anomalous couplings with LHeC data are obtained by performing a fit of the two parameters $\rho ^\prime _{\text {CC},eq}$ and $\rho ^\prime _{\text {CC},e\bar{q}}$ together with the PDFs. The expected uncertainties for the LHeC-50a and LHeC-60a scenarios are displayed in Fig. 14 and collected in Table 8. We find that these parameters can be determined with a relative uncertainty of better than 0.3 %. For the LHeC-60b scenario, even smaller uncertainties can be achieved and we find in 1-parameter+PDF fits relative uncertainties below one per mille. We can also consider a fit combining the CC parameters $\rho ^\prime _{\text {CC},eq} = \rho ^\prime _{\text {CC},e\bar{q}} =: \rho ^\prime _{\text {CC},f}$ with the anomalous NC parameter $\kappa ^\prime$ (see Eq. (30)). Results for this case are also shown in Table 8. Since the determination of the $\rho ^\prime _{\text {CC}}$ parameters are strongly correlated with the normalization uncertainty of the data, the study benefits from the simultaneous analysis of NC and CC DIS data. By doing so, not only the PDFs are constrained, but also systematic uncertainties that are common to NC and CC DIS data, mainly the luminosity uncertainty, are reduced by the NC DIS data, and therefore smaller uncertainties are obtained in this analysis than in a fit with CC DIS data alone.

Event rates at the LHeC are expected to be large and will cover a large $Q^2$ range between $10^2$ GeV$^2$ and almost $1000^2$ GeV$^2$. It is therefore possible to determine the anomalous CC couplings in different $Q^2$ ranges. Our results are shown in Fig. 15, assuming one flavor-independent parameter $\rho ^\prime _{\text {CC},f} = \rho ^\prime _{\text {CC},eq} = \rho ^\prime _{\text {CC},e\bar{q}}$. The $Q^2$ range is split into twelve bins, and for each bin the coupling parameter $\rho ^\prime _{\text {CC},f}$ was allowed to vary independently in a EW+PDF fit. We find uncertainties below 0.3 % in the $Q^2$ bins up to about $500^2$ GeV$^2$. They are dominated by the normalization uncertainties of the data. Higher center-of-mass energies, i.e. with $E_e=60~\mathrm {GeV}$ instead of 50 $\mathrm {GeV}$, has therefore only a moderate impact on the size of the uncertainties in the central $Q^2$ region. However, a larger beam energy allows one to extend the measurement to higher $Q^2$ values.

12 SM weak neutral-current couplings

The NC DIS cross sections are determined by products of the weak neutral-current coupling constants of the quarks. They enter through the $\gamma Z$ interference and Z exchange terms in the generalized structure functions defined in Eqs. (4, 5). Here we focus on the inclusive measurement of DIS cross sections and do not discuss the possibility that individual quark flavors might be identified in the final state (e.g. for charm and bottom). Therefore a full flavor separation of quark couplings will not be possible. However, mainly two effects allow us to separate the up-type and the down-type quark contributions to the cross section: first, they carry different electric charge and contribute with different weights to the $\gamma Z$ interference terms; second, they affect, through $\tilde{F}_3^\pm$, the dependence on the polarization and the lepton charge. In fact, these effects due to the weak interaction are important predominantly at higher values of $Q^2$, corresponding to large x, where the up- and down-valence quark PDFs dominate. A determination of vector and axial-vector couplings of up-type and down-type quarks can therefore be interpreted, with high precision, as a determination of the coupling constants of the up- and down-quarks, i.e. of light quarks only. Only for the down-type couplings, a contribution from strange quarks has some relevant size.

We perform an EW+PDF fit where the vector and axial-vector couplings of up-type (u and c) and down-type quarks (d, s and b), denoted as $g_V^{u}$, $g_V^{d}$ and $g_A^{u}$, $g_A^{d}$, are free parameters in one single fit. Other parameters, in particular the lepton couplings, are fixed.⁹ The fit parameters are identified with the coupling constants defined in the Born approximation, and $Q^2$ dependent higher-order corrections are calculated in the SM formalism in the 1-loop approximation. We have verified that the results of this analysis is consistent with those of the anomalous form factors described above in Sect. 10 (cf. Fig. 12). The resulting uncertainties of the fits are summarized in Table 9 for different LHeC scenarios. Figure 16 shows the results for the LHeC-50a scenario, compared with the current most precise measurements. All other LHeC scenarios result in even smaller uncertainties.

Fig. 15

Scale dependent determination of the anomalous CC coupling parameters, assuming $\rho ^\prime _{\text {CC},eq} = \rho ^\prime _{\text {CC},e\bar{q}} = \rho ^\prime _{\text {CC},f}$. For comparison, values from H1 [18] are also displayed

Table 9 Present values and uncertainties of the light-quark ($g_A^u$, $g_A^d$, $g_V^u$, $g_V^d$) and electron ($g_A^e$, $g_V^e$) weak neutral-current couplings from the PDG [41] and the uncertainties expected for inclusive DIS measurements in different LHeC scenarios, obtained in a simultaneous EW+PDF fit. The upper section shows results of a fit where all 4 couplings are free fit parameters, the lower three sections are results from two-parameter+PDF fits

Fig. 16

Weak-neutral-current vector and axial-vector couplings of up-type quarks to the Z-boson (left), and those of the down-type quarks (right) at 68 % confidence level for simulated LHeC data with $E_e=50\,\mathrm {GeV}$ (scenario LHeC-50a). The LHeC expectations are compared with results from the combined LEP+SLD experiments [62] and single measurements by D0 [84] and H1 [18]. The standard model expectations are at the crossing of the horizontal and vertical lines

Current determinations of light-quark couplings from $e^+e^-$, ep or $p\bar{p}$ collisions all appear with a similar precision. Future measurements at the LHeC, however, will greatly improve the measurement of these EW parameters. The scenario with $E_e = 60~\mathrm {GeV}$ and the optimistic assumptions for systematic uncertainties is particularly promising, see Table 9. In this table we also show results from fits where only two couplings are free fit parameters while the other couplings are fixed at their SM value. We find that the uncertainties of light-quark couplings can be improved by more than an order of magnitude through LHeC data.

At the LHeC, the vector and axial-vector couplings can be disentangled without any sign-ambiguity, since the DIS cross sections receive important contributions from the interference of photon and Z-boson exchange diagrams. This is in contrast with Z-pole observables where only squares of the couplings are accessible. The determination of quark NC couplings will provide a unique possibility for testing the EW SM theory. Such a measurement cannot be performed with a comparably high precision in other experiments.

13 Summary and conclusion

The proposed LHeC experiment at CERN’s HL-LHC will provide a unique opportunity for high precision electroweak physics in neutral- and charged-current interactions in a yet completely unexplored kinematic regime of spacelike momentum transfer.

In this article we have simulated inclusive NC and CC deep-inelastic scattering cross section data at electron-proton center-of-mass energies of 1.2 and 1.3 TeV, and assessed their sensitivity to a number of parameters of the electroweak theory and the sensitivity to possible generic extensions beyond the SM. Our theoretical calculations include next-to-next-to-leading order QCD corrections to the DGLAP evolution of PDFs and their relation to the structure functions and the full set of one-loop electroweak corrections to electron–(anti-)quark t-channel scattering in the on-shell renormalization scheme. Our simulated pseudo-data comprise a full set of experimental systematic uncertainties and have been used also elsewhere to study the prospects for a determination of parton distribution functions. The latter are implicitly also included in our analysis framework, while we extend the phenomenological analysis towards electroweak parameters.

Table 10 Prospects for the determination of Standard Model parameters from simulated inclusive NC and CC DIS data at the LHeC. Scenarios for electron beam energies of $E_e=50$ and 60 $\mathrm {GeV}$, and with two assumptions for experimental uncertainties, denoted scenarios ‘a’ and ‘b’, are studied

The sensitivity of inclusive NC/CC DIS data at the LHeC to important independent parameters of the electroweak Standard Model are summarized in Table 10. At the LHeC, the high experimental precision for SM parameters is due to the fact that a large kinematic range of space-like momentum transfer can be used to obtain a large amount of DIS data points that all contribute to the sensitivity. For our prospects, we perform combined fits of EW parameters and PDFs to simulated NC and CC DIS data. The large number of cross section data in different $Q^2$ bins and including both NC and CC scattering, as well as scattering with positrons and with polarized electrons, is equivalent to a large number ratios of bin cross sections. In particular, the ratios of NC cross sections at large and small $Q^2$ carry information about electroweak parameters. Therefore, correlated (normalization) uncertainties cancel to a large extent and play a minor role, while uncorrelated uncertainties are reduced by the implicit averaging over a set of several hundreds of independent measurements. This explains why we observe that the uncertainties for most of the electroweak parameters are found at the per mille level while the uncertainties for individual cross section data points are in the order of percent. For instance the weak mixing angle can be determined with a high experimental uncertainty of down to $\pm \,1.5\cdot 10^{-4}$ which corresponds to 0.65 per mille, as shown in Table 10. The large number of data points at different $Q^2$ will also allow a determination of the scale dependence of the weak mixing angle in the spacelike regime of about $25<\sqrt{Q^2}<700\,\mathrm {GeV}$. Experimental uncertainties below $\pm \,20\cdot 10^{-4}$ will be possible in the range $60\lesssim \sqrt{Q^2}\lesssim 450\,\mathrm {GeV}$. This analysis will be equivalent to a determination of the running of the weak mixing angle, an opportunity which is unique to the LHeC. Only small and well-known correction factors from theory will be needed to turn the result of such measurements into a determination of the effective weak mixing angle, or the weak mixing angle in the $\overline{\mathrm{MS}}$ scheme, which then can be compared with other measurements.

In the on-shell scheme, the weak mixing angle is defined by the ratio of the weak boson masses, $m_W$ and $m_Z$. The measurement of inclusive DIS cross sections can therefore be interpreted as an indirect determination of the W-boson mass. We find from our combined $m_W$+PDF fit an experimental uncertainty down to $\pm \,6\,\mathrm {MeV}$. This is compatible with a rough estimate, based on simple error propagation, of an expected relative uncertainty at the level of $10^{-4}$. This high precision will improve all present measurements and provide a highly valuable validation of future improved direct $m_W$ measurements with $\mathcal {O}(\mathrm {MeV})$ accuracy.

The high precision of the Born-level parameters of the EW theory also suggests a determination of the dominant parameters of the higher-order EW corrections, most notably the top-quark mass $m_t$. The value of $m_t$ can be determined with an uncertainty down to $\pm \, 1.1\,\mathrm {GeV}$. This provides a precise indirect determination which is complementary to direct measurements, since it is theoretically clean and free from ambiguities due to unknown QCD corrections. The dependence of higher-order corrections on the Higgs-boson mass, $m_H$, is logarithmic only, i.e. sub-dominant. Therefore, its uncertainty is fairly large and compares in size with the indirect determinations from the LEP+SLD data. Non-Standard Model contributions to one-loop weak boson self energy corrections, usually described by the so-called oblique parameters S, T and U, can also be determined independently when NC and CC DIS data are considered together, and uncertainties of a few percent are expected.

A simultaneous determination of the weak boson masses, $m_W$ and $m_Z$, or a simultaneous determination of $m_W$ together with $m_t$, yield moderate uncertainties. These, however, compare well with the uncertainties that can be achieved nowadays in global EW fits. We have studied in a simplified formalism the potential impact of LHeC NC/CC DIS data to such a global EW fit and found only small improvements; the correlation between $m_W$ and $m_t$ or $m_W$ and $m_Z$ are not very different in DIS than in other observables.

The $\text {SU}(2) \times \text {U}(1)$ gauge symmetry predicts the weak NC couplings of fermions, $g_V^f$ and $g_A^f$, in a unique way. Modifications of the SM can be studied in a rather model-independent manner by considering these coupling constants as free parameters, or alternatively, by introducing multiplicative anomalous factors to the $\rho _{\text {NC},f}$ and $\kappa _f$ form factors, which can be considered to be flavor and $Q^2$ dependent. While the NC coupling parameters have been measured at the Z-pole with high precision, in particular for leptons and b quarks, the couplings of the light quarks, u and d, are experimentally measured only with a rather poor precision. The LHeC, in contrast, has a high sensitivity to the NC couplings of light quarks, and DIS data will provide the unique opportunity to determine the light-quark couplings with per mille accuracy, either for the vector and axial-vector coupling constants ($g_V^u$, $g_A^u$, $g_V^d$ and $g_A^d$), or for the anomalous form factors, $\rho ^{\prime }_{\text {NC}f}$ and $\kappa ^{\prime }_{f}$. In addition, their $Q^2$ dependence can be determined with percent precision in the range $60\lesssim \sqrt{Q^2}\lesssim 600\,\mathrm {GeV}$.

Many precise data for parameters of the NC sector of the EW theory can be found in the literature, based on measurements extending to highest energies. In contrast, high-precision measurements of CC interactions are often restricted to low energies. Here, the LHeC will offer once more unique opportunities. Anomalous electron–quark and electron–anti-quark form factors can be determined with an accuracy in the order of $\mathcal {O}(0.1\,\%)$, and their potential $Q^2$ dependence can be measured with per mille uncertainties in a $Q^2$ range up to about $400^2\,\mathrm {GeV}^2$.

We have compared LHeC inclusive DIS pseudo data at two different center-of-mass energies, $\sqrt{s}=1.2$ and 1.3 $\mathrm {TeV}$, corresponding to an electron beam energy of 50 or 60 $\mathrm {GeV}$, respectively. Our studies confirm the presumption that higher center-of-mass energies would be quite valuable for the precise determination of EW parameters. Of course, with higher $\sqrt{s}$, also the range of $Q^2$ dependent studies can be extended to some extent. Further improvements will be obtained by higher resolution of the detector, which would allow us to obtain measurements for a larger set of independent data points. Altogether, the expected uncertainties from the four LHeC scenarios studied in this article differ by about a factor of 2 to 3. Such an improvement is indeed interesting in view of the fact that many parameters are measured with comparable uncertainties in $e^+e^-$ or hadron-hadron interactions.

In this study, we employed calculations in the on-shell renormalization scheme including the full set of one-loop EW corrections. For our main purpose, i.e. to investigate prospects for the uncertainties of EW parameters, this provides a valid framework. However, once real LHeC data are available, a more careful study of higher-order corrections will be necessary. On the one hand, one has to match the high experimental precision of the data with correspondingly accurate theoretical predictions. On the other hand, a conclusive test of the SM can only be achieved by comparing as many as possible different measurements, i.e. also observables in processes other than DIS. Therefore, a consistent framework for the calculation of higher-order corrections to all observables in question will be needed. For example, different definitions of the effective weak mixing angle have to be matched to each other. We believe that our study provides a motivation for the investigation and calculation of higher-order corrections to DIS observables beyond the 1-loop level, and in different renormalization schemes.

In conclusion, the high center-of-mass energy, the large kinematic range, and the large integrated luminosity at the LHeC will allow for the first time to perform precision electroweak measurement at high momentum transfer in NC and CC DIS. Rich aspects of the electroweak theory can be probed with highest precision without being limited by uncertainties from parton distribution functions. Instead, electroweak parameters and PDFs can be determined in simultaneous fits taking into account their mutual correlations. In many cases, the results are complementary to direct measurements in $e^+e^-$ or hadron-hadron collisions, such as the indirect determination of the W-boson mass or the top-quark mass. A unique measurement can be expected for the scale-dependence of the weak mixing angle, as well as of non-SM coupling parameters. A particularly important and outstanding precision is expected for the determination of weak neutral-current couplings of the light quarks.

A simplified global EW fit including LHeC data

The validity of the Standard Model is frequently studied in so-called ‘global EW fits’ [41, 66, 67]. A large number of precision measurements are simultaneously fitted and compared within a consistent theoretical framework. On the one hand, such a general approach allows one to perform a comprehensive consistency test of the SM; on the other hand one can expect to obtain the most precise determination of SM parameters. In this appendix, we are interested in estimating the potential impact of LHeC inclusive NC/CC DIS data on the parameter determination within such a global fit. We describe in the following a simplified approach which is suited for our purpose.

Fig. 17

Left: Expected uncertainties from a simplified global EW fit including LHeC-60b inclusive NC/CC DIS data. The results are compared with expected uncertainties from the simplified global EW fit without LHeC data and to the direct measurements of $m_W$ and $m_t$. Right: A magnified view of the left figure

Table 11 Results for expected uncertainties of $m_W$ and $m_t$ from a simplified global fit, with and without NC/CC DIS data using the LHeC-60b scenario

It is common to consider a set of data as input for a global EW fit comprising $\alpha$ and $G_\mathrm{F}$, the mass parameters $m_Z$, $m_W$, $m_H$, and $m_t$, partial decay widths of the gauge bosons, $\Gamma _W$ and $\Gamma _Z$, the effective weak mixing angle $\sin ^2\theta _{\text {W},\ell }^\text {eff}$, partial decay widths and asymmetry observables in $e^+e^-$ collisions [62] $R_\ell ^0$, $R_b^0$, $R_c^0$, $A_\ell$, $A_c$, $A_b$, $A_\text {FB}^{0,\ell }$, $A_\text {FB}^{0,c}$, $A_\text {FB}^{0,b}$, QCD contributions to the QED vacuum polarization $\Delta \alpha _\text {had}^5$, and sometimes also measurements of $\alpha _\text {s}$, $m_b$, and $m_c$. With the assumption that $\alpha$ and $G_\mathrm{F}$ are known with ultimate precision, the fit parameters are chosen as $m_Z$, $m_H$, $m_t$, $\Delta \alpha _\text {had}^5$ and $\alpha _\text {s}$. Sometimes also $m_b$ and $m_c$ are taken as parameters to be determined by the fit.

Since we are interested only in estimating uncertainties and how these are affected by LHeC data, rather than in the actual fit values, some simplifications can be made in the following. One can observe that some of the fit parameters are determined with a high precision directly from measurements. This is the case for $m_Z$, $m_H$, $m_b$, $m_c$, $\Delta \alpha _\text {had}^5$ and $\alpha _\text {s}$. If these direct data were not taken into account in the global fit, these parameters could be determined only with a much larger uncertainty. We do not expect that this will change if LHeC data are taken into account. Many other observables, like the Z-pole cross section ratios and asymmetries have much larger experimental uncertainties than predicted by the global fit. However, in the case of $m_W$ and $m_t$, the uncertainties from direct measurements is of a similar size as those from a global fit. These parameters are therefore of special interest since for them one might expect a significant impact from LHeC data.

Therefore, we perform a simplified global EW fit, where we consider only the determination of the SM parameters $m_Z$, $m_W$, $m_H$ and $m_t$. All other parameters do not provide additional constraints or are known with good precision. The calculations are performed in the on-shell scheme. The fit parameters are chosen as $m_W$, $m_t$ and $m_H$. When using input data for $\alpha$, $G_\mathrm{F}$ and the SM masses from PDG16 [85] we obtain uncertainties of $\Delta m_W=\pm \,5.6\,\mathrm {MeV}$ ($\pm \,6.2\,\mathrm {MeV}$) and $\Delta m_t=\pm \,0.87\,\mathrm {GeV}$ ($\pm \,2.3\,\mathrm {GeV}$) when the data for $m_W$ and $m_t$ are included (excluded) in the fit. This result is very similar to the one of the general global EW fit [66,67,68] and confirms that the simplifications of our approach are justified for our purpose.

We can therefore proceed and include LHeC-60b inclusive NC/CC DIS data into the fit. Moreover, we include the PDF parameters as well, and we use recent values for $m_W$, $m_t$, and $m_H$ from PDG20 [41]. When including LHeC-60b NC/CC DIS data, we obtain a very moderate improvement for $m_W$: $\Delta m_W=\pm \,4.6\,\mathrm {MeV}$ changes to $\Delta m_W= \pm \, 4.5\,\mathrm {MeV}$. The 68 % C.L. contours in the $m_W$-$m_t$–plane are displayed in Fig. 17. Numerical values of the validation fits, and the study including LHeC-60b data are collected in Table 11. No significant improvement of $\Delta m_t$ is seen. This was to be expected, since $m_t$ contributes to NC/CC DIS only through higher-order corrections. Obviously, already other than the LHeC NC/CC DIS data are sufficient to provide good constraints on $m_W$ and $m_t$. LHeC DIS data probe essentially the same relation of $m_W$ and $m_t$ and they cannot compete with direct measurements of these mass parameters.

Therefore, the strength of the LHeC EW analysis is its complementary with measurements in $e^+e^-$ or pp collisions, in particular the fact that the dominant uncertainty in the W-boson mass determination is due to its correlation with the PDF determination. The impact of the latter may be considerably reduced if measurements at the LHeC will become available [86]. Commonly, the global fit is repeated with direct measurements of the parameters of interest excluded, i.e. without $m_W$ and $m_t$. This was studied in Sect. 8.