SMART U(1)$_X$: standard model with axion, right handed neutrinos, two Higgs doublets and U(1)$_X$ gauge symmetry

Abstract

To address five fundamental shortcomings of the Standard Model (SM) of particle physics and cosmology, we propose a phenomenologically viable framework based on a $U(1)_X \times U(1)_{PQ}$ extension of the SM, that we call “SMART U(1)$_X$”. The $U(1)_X$ gauge symmetry is a well-known generalization of the $U(1)_{B-L}$ symmetry and $U(1)_{PQ}$ is the global Peccei–Quinn (PQ) symmetry. Three right handed neutrinos are added to cancel $U(1)_X$ related anomalies, and they play a crucial role in understanding the observed neutrino oscillations and explaining the observed baryon asymmetry in the universe via leptogenesis. Implementation of PQ symmetry helps resolve the strong CP problem and also provides axion as a compelling dark matter (DM) candidate. The $U(1)_X$ gauge symmetry enables us to implement the inflection-point inflation scenario with $H_{inf} \lesssim 2 \times 10^{7}$ GeV, where $H_{inf}$ is the value of Hubble parameter during inflation. This is crucial to overcome a potential axion domain wall problem as well as the axion isocurvature problem. The SMART U(1)$_X$ framework can be successfully implemented in the presence of SU(5) grand unification, as we briefly show.

1 Introduction

A variety of cosmological and particle physics observations have demonstrated some shortcomings of the Standard Model (SM) of particle physics. Cosmological and astrophysical observations strongly support, indeed require, the existence of dark matter (DM) which accounts for about 25% of the total (critical) energy density in the universe [1]. However, no viable non-baryonic DM candidate exists in the SM. Experimental observations of neutrino oscillations and flavor mixings indicate that neutrinos have a tiny but non-zero mass [2]. But neutrinos are massless to all orders in perturbation theory in the SM. Cosmological and astrophysical observations have also confirmed that ordinary baryonic matter dominates over the anti-baryons in the universe [2]. The SM fails to generate this so-called baryon asymmetry in the universe (BAU) [3]. Experimental measurement of the electric dipole moment of neutron require that the effective dimensionless parameter ${\bar{\theta }}_{QCD}$ of the SM must be tiny, ${\bar{\theta }}_{QCD} \simeq 0.7 \times 10^{-11}$ [4]. This is the so-called strong CP problem [5] of the SM. Finally, according to the current cosmological paradigm, the universe experienced cosmic inflation, a period of accelerated expansion in the early stages of its evolution. Inflation solves two major problems of standard big bang cosmology [6], namely the origin of the observed spatial flatness of the universe and the observed uniformity of the cosmic microwave background radiation with $\delta T/T \simeq 10^{-5}$ [7]. Moreover, the primordial density fluctuations generated during inflation can seed these tiny fluctuations which are essential to reproduce the observed large scale structures of the universe. The SM needs to be extended to accommodate a realistic inflationary scenario.

It is clear that these five fundamental shortcomings of the SM are at the frontiers of high energy physics and cosmology research and crucial to understand the origin and evolution of our universe. Equivalently, it implies that the SM is at best an effective theory description of nature and needs to be supplemented with new physics beyond the SM. In this paper, we propose a phenomenologically viable framework based on a gauged $U(1)_X$ extension of the SM which addresses all these shortcomings and also offer some testable predictions.¹

We augment the SM with $U(1)_X \times U(1)_{PQ}$ symmetry, where $U(1)_{PQ}$ is the well-known global Peccei–Quinn (PQ) symmetry [10], and $U(1)_X$ [11] is a well-known generalization of the $U(1)_{B-L}$ gauge symmetry [12,13,14,15,16,17,18]. The generalized $U(1)_X$ charge of each field is defined as a linear combination of its hypercharge and $B-L$ charge, and is determined by a single free parameter $x_H$ [19]. The $B-L$ charges for the particles are reproduced in the limit $x_H \rightarrow 0$. To cancel the $U(1)_X$ associated anomalies, three generations of SM singlet (Majorana) right handed neutrinos (RHNs) are added. These SM singlet RHNs explain the origin of observed neutrino masses via type-I seesaw mechanism [20,21,22,23,24,25]. Furthermore, the RHNs can generate the observed BAU via leptogenesis [26]. In addition to a SM singlet Higgs field which breaks $U(1)_X$ symmetry, the model also contains a SM and $U(1)_{X}$ singlet Higgs field which breaks $U(1)_{PQ}$ symmetry and a pair of SM doublet Higgs fields which are crucial to implement the PQ symmetry. In this regard, our model is a $U(1)_X$ extension of the well-known Dine–Fischler–Srednicki–Zhitnitsky (DFSZ) model [27, 28].

The PQ symmetry solves the strong CP problem and also provides axion as a compelling DM candidate [29, 30]. The axion models can potentially encounter two major cosmological problems, namely, the axion domain wall problem and the isocurvature problem. For a review, see, for example, Ref. [31]. The topological defects (strings and domain walls) associated with PQ symmetry breaking can potentially dominate the energy density of the universe which is inconsistent with the cosmological observation. In addition, if inflation takes place after PQ symmetry breaking, it can induce isocurvature fluctuations which are severely constrained by observations [32]. Both of these problems can be resolved in an inflation scenario² with a Hubble parameter during inflation $H_{inf} \lesssim 2 \times 10^{7}$ GeV. Such a low value for the Hubble parameter cannot be realized in a simple inflation scenario based, say, on a Coleman-Weinberg or Higgs potential with a minimal coupling to gravity [34], or a quartic potential with non-minimal coupling to gravity [35]; both scenarios predict $H_{inf} \simeq 10^{13-14}$ GeV [36]. This leads us to consider the inflection-point inflation (IPI) scenario [37, 38] (see also Ref. [39, 40]). To realize this, it is crucial that the inflaton field which drives inflation has both gauge and Yukawa interactions. The Higgs field which breaks the $U(1)_X$ gauge symmetry is a unique candidate in our model for the inflaton field. We will refer to this framework as SMART U(1)$_X$: SM with Axion, Right handed neutrinos, Two Higgs doublets and U(1)$_X$ gauge symmetry.

We also consider a merger of the SMART U(1)$_X$ with grand unification. It was previously demonstrated in Ref. [41] that the SM quark and lepton representations in a $U(1)_X$ extended SM can be embedded inside SU(5) for a fixed $x_H = -4/5$. Therefore this grand unified theory (GUT) scenario, the $U(1)_X$ symmetry explains the origin of charge quantization. By incorporating the PQ symmetry, the model we consider is $SU(5)\times U(1)_X \times U(1)_{PQ}$. With the addition of suitable new vector-like fermions, the three SM gauge couplings successfully unify at $M_{GUT} \simeq 9.8 \times 10^{15}$ GeV. These new fermions are also essential for a successful implementation of the IPI scenario, which plays an important role in solving both the axion domain wall and isocurvature problems. In addition, we show that the SM Higgs potential can also be stabilized in the presence of the new vector-like fermions.

The recently proposed Trans-Planckian Censorship Conjecture (TCC) [42], when applied to slow-roll inflation, significantly lowers the bound on the value of Hubble parameter during inflation, $H_{inf} \lesssim 1$ GeV [43]. An IPI inflation scenario consistent with TCC was recently examined by the authors of this paper [44] in a model whose particle content matches that of the SMART U(1)$_X$ with $x_H =0$. Therefore, the model in Ref. [44] is the $B-L$ version of the SMART U(1)$_X$.

This paper is organized as follows: In Sect. 2 we describe the SMART U(1)$_X$ framework. We discuss the axion DM scenario in Sect. 3 and show that both the axion domain wall and isocurvature problems can be solved if $H_{inf} \lesssim 2 \times 10^{7}$ GeV. An IPI scenario with this constraint is discussed in Sect. 4, where we consider reheating after inflation and identify the model parameters required for successful leptogenesis. In Sect. 5 we consider the merger of SU(5) with the SMART U(1)$_X$. Our results are summarized in Sect. 6.

Table 1 Particle content of the SMART U(1)$_X$ model where all fermions fields are left-handed. In addition to the three generations of SM fermions ($i=1,2,3$), we have three Majorana neutrinos, $(N^c)^{i}$, and the scalar sector has two SM doublet Higgs, $H_{u,d}$, and two SM singlet Higgs, $\Phi$ and S

2 SMART U(1)$_X$

The particle content of our model is listed in Table 1, where all fermion fields are left-handed. The $U(1)_X$ charge of each particle is defined as $Q_X = x_{H} Q_{Y} + x_{\Phi } Q_{B-L}$, where $Q_Y$ and $Q_{B-L}$ are their SM hypercharge and $B-L$ (baryon minus lepton) number, respectively. We fix $x_\Phi = 1$ without loss of generality so that the $U(1)_X$ charges of all the particles are uniquely determined by a single free parameter $x_H$. The $B-L$ charges are reproduced in the limit $x_H \rightarrow 0$. In addition to three generations of SM quarks and leptons ($i = 1,2,3$), there are three SM singlet Majorana neutrinos, $(N^c)^{i}$, which cancel all the $U(1)_X$ related gauge and mixed gauge-gravitational anomalies. The scalar sector includes four complex scalar fields, namely the two SM doublet Higgs fields, $H_{u,d}$, and two SM singlet Higgs fields, $\Phi$ and S.

The gauge $U(1)_X$ and global $U(1)_{PQ}$ invariant Higgs potential is given by

$$\begin{aligned} V= & {} - \sum _{i = u,d} \mu _i^2 \left( H_i^{\dagger }H_i \right) +\sum _{i = u,d}\lambda _i \left( H_i^{\dagger }H_i \right) ^2\nonumber \\&+ \left( \sqrt{2}\Lambda _{s}\left( H_u \cdot H_d \right) S + \mathrm{h.c.}\right) \nonumber \\&+\lambda _{\phi } \left( \Phi ^\dagger \Phi - \frac{v_{BL}^2}{2}\right) ^2 +\lambda _{S} \left( S^\dagger S - \frac{v_{PQ}^2}{2}\right) ^2\nonumber \\&+ \text {mixed quartic terms}, \end{aligned}$$

(2.1)

where the couplings parameters are all chosen to be positive, the dot represents contraction of SU(2) indices by epsilon tensor, and the vacuum expectation values (VEVs) of $\Phi$ and S are given by $\langle \Phi \rangle = v_X/\sqrt{2}$ and $\langle S \rangle = v_{PQ}/\sqrt{2}$, respectively. The mixed quartic interactions includes terms such as $(H_i^\dagger H_i)(\Phi ^\dagger \Phi )$, $(H_i^\dagger H_i)(S^\dagger S)$, etc. For simplicity, we assume these mixed quartic couplings to be adequately small, and they do not alter our results. We also assume that both $U(1)_X$ and $U(1)_{PQ}$ symmetry are broken at a scale much higher than the electroweak scale as well as $\Lambda _s$.

We parameterize S and $\Phi$ in terms of real fields as follows:

$$\begin{aligned} \Phi (x)= & {} \frac{1}{\sqrt{2}}\left( \phi (x) + v_{X}\right) e^{i \chi (x)/ v_{X}}, \nonumber \\ S(x)= & {} \frac{1}{\sqrt{2}}\left( s(x) + v_{PQ}\right) e^{i a(x)/ v_{PQ}}. \end{aligned}$$

(2.2)

Note that the Higgs field $\Phi$ is charged under both $U(1)_X$ and $U(1)_{PQ}$, whereas S is charged only under $U(1)_{PQ}$. After S and $\Phi$ fields acquire their VEVs, the would-be Nambu–Goldstone (NG) boson $\chi (x)$ is absorbed by the $U(1)_X$ gauge boson ($Z^\prime$) and a(x) is identified with the axion. After the $U(1)_X \times U(1)_{PQ}$ symmetry breaking, the masses of $\phi$, s and $Z^\prime$ gauge boson are respectively given by

$$\begin{aligned} m_\phi = \sqrt{2 \lambda _\phi } v_{X}, \; \; m_s = \sqrt{2 \lambda _s} v_{PQ}, \;\; m_{Z^\prime } = 2 g v_{X}, \end{aligned}$$

(2.3)

where g is the $U(1)_X$ gauge coupling.

Our assumption of negligible mixed quartic couplings allows us to separately analyze the SM doublet Higgs potential at low energies from the singlet Higgs sector. In Eq. (2.1), the PQ symmetry breaking Higgs field S generates the mixing mass term between the two doublet Higgs fields, $m_{mix}^2 (H_u. H_d)$, where $m_{mix}^2 = \Lambda _{s} v_{PQ}$. Because of their charge assignments, $H_u$ ($H_d$) only couple with up-type (down-type) SM fermions (see Eqs. (2.4) and (2.5) below). The doublet Higgs potential at low energies in this case is the same as that of the type-II two Higgs doublet extension of the SM. Since the two Higgs doublet model is well studied in the literature [45, 46], we will skip the detailed phenomenology of the Higgs potential at low energies.

In addition to the Yukawa interactions for the SM quarks,

$$\begin{aligned} \mathcal{L} \supset \sum _{i,j=1}^{3} Y_u^{ij} \left( q^i . H_u\right) (u^{c})^j + \sum _{i,j=1}^{3} Y_d^{ij} \left( q^{i}. H_d\right) (d^{c})^j,\nonumber \\ \end{aligned}$$

(2.4)

the Lagrangian includes the following new Yukawa interactions involving the Majorana neutrinos:

$$\begin{aligned}&\mathcal{L} \supset \sum _{i,j=1}^{3}Y_\ell ^{ij} \left( \ell ^{i}. H_d\right) (e^{c})^j -\frac{1}{2} \sum _{i,j=1}^{3} Y_D^{ij}\left( \ell ^{i}. H_u\right) \left( N^c\right) ^{j}\nonumber \\&\quad - \left( \frac{1}{2} \sum _{i=1}^{3} Y_i \Phi {\left( N^c\right) }^{i} \left( N^c\right) ^{i} +\text {h.c.}\right) , \end{aligned}$$

(2.5)

where $Y_D$ ($Y_i$) is the Dirac (Majorana) Yukawa coupling, and we have chosen a flavor-diagonal basis for $Y_i$. After the $U(1)_X$ and electroweak symmetry breakings, the Dirac and the Majorana masses for the neutrinos are generated,

$$\begin{aligned} m_D^{ij}= \frac{Y_D^{ij}}{\sqrt{2}} v_{u},\quad m_{N^i}= \frac{1}{\sqrt{2}} Y_i v_{X}, \end{aligned}$$

(2.6)

where $\langle H_u^0 \rangle = v_u/\sqrt{2}$ is the VEV of the charge neutral component of $H_u$.

3 Axion dark matter

As discussed before, the axion DM scenario possibly suffers from two major cosmological problems, namely, the axion domain wall problem and the axion DM isocurvature problem. This domain wall problem can be solved if inflation takes places after the PQ symmetry breaking, or equivalently, $H_{inf} < F_a=v_{PQ}/N_{DW}$, where $F_a$ is the axion decay constant and $N_{DW}$ is the domain wall number. In our case, $N_{DW} = 12$. The measurement of supernova SN 1987A pulse duration provides a model-independent constraint on the axion decay constant $F_a \gtrsim 4 \times 10^8$ GeV [47]. We will shortly show that the resolution of the isocurvature problem leads to an even stronger constraint on $H_{inf}$ than the one required to solve the axion domain wall problem, $H_{inf} < F_a$.

3.1 Relic abundance of axion dark matter

The PQ symmetry breaking produces cosmic strings, which can efficiently decay into axions [31]. Because inflation takes place after the PQ symmetry breaking in our setup, the axions produced from cosmic string decay contribute negligibly to the relic abundance. Although QCD interactions can also produce axions in the thermal plasma, their relic abundance from such processes was shown to be negligible compared to the observed abundance of DM in Ref. [48]. At the end of QCD phase transition, the coherently oscillating axion field behaves like cold DM and contribute dominantly to the relic abundance of the axion [31],

$$\begin{aligned} \Omega _a^\mathrm{mis} h^2\simeq & {} 0.18 \; \left( \theta _m^2 +\delta {\theta _m}^2\right) \; \left( \frac{F_a}{10^{12}\; \mathrm{GeV}}\right) ^{1.19}\nonumber \\\simeq & {} 0.18 \; \theta _m^2 \left( \frac{F_a}{10^{12}\; \mathrm{GeV}}\right) ^{1.19}. \end{aligned}$$

(3.1)

Here, the misalignment angle $\theta _m$ is the initial displacement of axion field from the potential minima at the onset of oscillations, and $\delta {\theta _m} = H_{inf}/(2\pi F_a)$ is the fluctuation of $\theta _m$ generated by inflation. A natural choice for the misalignment angle is $\theta _a \simeq 1$, and we have used $H_{inf} < F_a$ to obtain the final expression in Eq. (3.1). Requiring that the axion fully account for the DM in the universe, $\Omega _{a} h^2 = 0.120 \pm 0.0012$ [1], the axion decay constant $F_a$ is determined as a function of $\theta _m$,

$$\begin{aligned} F_a \simeq 7.11 \times 10^{11} \; \mathrm{GeV} \; \theta _m^{-1.68}. \end{aligned}$$

(3.2)

3.2 Axion dark matter isocurvature fluctuations

If inflation takes place after the PQ symmetry breaking, it induces isocurvature fluctuation in the axion DM power spectrum [49],

$$\begin{aligned} \mathcal{P}_\mathrm{iso} =\left( \frac{H_{inf}}{\pi \theta _m F_a }\right) ^2, \end{aligned}$$

(3.3)

which is constrained by Planck measurements [32], namely

$$\begin{aligned} \beta _\mathrm{iso} \equiv \frac{\mathcal{P}_\mathrm{iso}(k_*)}{\mathcal{P}_\mathrm{iso}(k_*)+ \mathcal{P}_\mathrm{adi}(k_*)} < 0.038, \end{aligned}$$

(3.4)

where $\mathcal{P}_\mathrm{adi} (k_*) \simeq 2.2 \times 10^{-9}$ [32] is the adiabatic power spectrum and $k_* = 0.05$ Mpc$^{-1}$ is the pivot scale. Combining Eqs. (3.2) and (3.4) yields an upper bound on $H_{inf}$,

$$\begin{aligned} H_{inf} < 2.08 \times 10^7\,\mathrm{GeV} \left( \frac{F_a}{7.11 \times 10^{11}\,\mathrm{GeV}}\right) ^{0.405}. \end{aligned}$$

(3.5)

Together with Eq. (3.2), we find that $\delta \theta _m^2/ \theta _m^2 \simeq 10^{-11}$, or equivalently, $H_{inf}/{F_a} \lesssim 3.0\times 10^{-5}\; \theta _m$. This shows that the axion DM isocurvature constraint imposes a much stronger restriction on $H_{inf}$ than the one required to solve the axion domain wall problem, $H_{inf} < F_a$.

Let us set $\theta _m$ to be $\mathcal{O} (1)$ and $F_a = 7.11 \times 10^{11}$ GeV such that the axion saturates the observed DM abundance. We therefore obtain an upper bound on the Hubble parameter during inflation, $H_{inf} < 2.08 \times 10^{7}$ GeV. In the next section, we discuss an IPI scenario with the Hubble parameter value of this magnitude which also solves both the axion domain wall and axion DM isocurvature problems.

4 Inflection-point inflation

Let us begin by highlighting the key results of the inflection-point inflation (IPI) scenario driven by a real scalar field $\phi$. See Refs. [37, 38] for details. An inflaton potential which exhibits an approximate inflection-point around $\phi = M$ can be expressed as

$$\begin{aligned} V(\phi )\simeq V_0 +\ V_1 (\phi -M) + \frac{V_2}{2} (\phi -M)^2 + \frac{V_3}{6} (\phi -M)^3,\nonumber \\ \end{aligned}$$

(4.1)

where $V_0 = V(M)$, $V_n \equiv \mathrm{d}^{n}V/\mathrm{d} \phi ^n |_{\phi =M}$, and we identify $\phi = M$ to be the horizon exit scale that corresponds to the pivot scale $k_* = 0.05$ Mpc$^{-1}$ used in Planck measurements [32].

With the potential in Eq. (4.1), the inflationary slow-roll parameters are given by

$$\begin{aligned} \epsilon \simeq \frac{M_P^2}{2} \left( \frac{V_1}{V_0}\right) ^2, \quad \eta \simeq M_P^2 \left( \frac{V_2}{V_0}\right) ,\quad \zeta \simeq M_P^4 \frac{V_1 V_3}{V_0^2},\nonumber \\ \end{aligned}$$

(4.2)

where $M_P = 2.43\times 10^{18}$ GeV is the reduced Planck mass. In terms of the slow-roll parameters, the inflationary predictions for the scalar spectral index ($n_s$), the tensor-to-scalar ratio (r), and the running of the spectral index ($\alpha$) are respectively given by

$$\begin{aligned} n_s=1- 6\epsilon +2 \eta ,\quad r=16 \epsilon ,\quad \alpha = 16 \epsilon \eta -24 \epsilon ^2 -2 \zeta ^2.\nonumber \\ \end{aligned}$$

(4.3)

The amplitude of the curvature perturbation $\Delta _{\mathcal {R}}^2$ is expressed as

$$\begin{aligned} \Delta _{\mathcal {R}}^2 \simeq \frac{1}{24 \pi ^2} \frac{V_0}{ M_P^4 \;\epsilon }. \end{aligned}$$

(4.4)

The central values from the Planck 2018 results [32], $\Delta _{\mathcal {R}}^2= 2.099 \times 10^{-9}$ and $n_s = 0.965$, can be used to express $V_{1,2}$ in terms of $V_0$ and M:

$$\begin{aligned} \frac{V_1}{M^3}\simeq & {} 2.01 \times 10^3 \left( \frac{M}{M_P}\right) ^3\left( \frac{V_0}{M^4}\right) ^{3/2}, \nonumber \\ \frac{V_2}{M^2}\simeq & {} -1.73 \times 10^{-2} \left( \frac{M}{M_P} \right) ^2 \left( \frac{V_0}{M^4}\right) , \end{aligned}$$

(4.5)

The following expression for the number of e-folds has been derived in Ref. [37, 38]:

$$\begin{aligned} N = \frac{1}{M_P^2} \int _{\phi _e}^M \, d\phi \, \frac{V}{(dV/d\phi )} \simeq \pi \frac{V_0}{M_P^2 \sqrt{2V_1V_3}}. \end{aligned}$$

(4.6)

Combining Eqs. (4.5) and (4.6) we obtain

$$\begin{aligned} \frac{V_3}{M}\simeq & {} 6.83 \times 10^{-7} \; \left( \frac{60}{N} \right) ^2 \left( \frac{M}{M_P} \right) \left( \frac{V_0}{M^4} \right) ^{1/2}. \end{aligned}$$

(4.7)

In the following analysis, we set $N=60$ to solve the horizon problem of big bang cosmology. Using Eqs. (4.3), (4.5), and (4.7), the prediction for the running of spectral index is obtained as $\alpha = -2.74 \times 10^{-3}$. This is consistent with the Planck 2018 measurements, $\alpha = - 0.0045\pm 0.0067$, and can be tested in the future [50].

Next we identify the inflaton field used in the IPI analysis with the real component of the $U(1)_X$ Higgs field, $\phi = \sqrt{2} \mathrm{Re} [\Phi ]$. The inflaton potential in Eq. (4.1) is identified with the renormalization group improved $U(1)_X$ Higgs potential,

$$\begin{aligned} V( \phi ) = \lambda _\phi (\phi ) \left( \Phi ^\dagger \Phi - \frac{v_X^2}{2} \right) ^2 \simeq \frac{1}{4} \lambda _\phi ( \phi )\; \phi ^4. \end{aligned}$$

(4.8)

To obtain the second expression, we have assumed that during inflation $\phi \gg v_{PQ}$ and $\lambda _\phi (\phi )$ is determined by solving the following renormalization group equations (RGEs):

$$\begin{aligned} \phi \frac{d g}{d \phi }= & {} \frac{1}{16 \pi ^2} \left( \frac{72 + 64 x_H + 41 x_H^2}{6}\right) g^3, \nonumber \\ \phi \frac{d Y_{i}}{d \phi }= & {} \frac{1}{16 \pi ^2}\left( Y_i^2+\frac{1}{2} \sum _{j=1}^3 Y_j^2-6 g^2 \right) Y_i, \nonumber \\ \phi \frac{d \lambda _\phi }{d \phi }= & {} \beta _{\lambda _\phi }. \end{aligned}$$

(4.9)

Here, the beta-function of ${\lambda _\phi }$ and is given by

$$\begin{aligned} \beta _{\lambda _\phi } \!=\! \frac{1}{16 \pi ^2}\! \left( \!20 \lambda _\phi ^2 \!- 48\lambda _\phi g^2\!+2 \lambda _\phi \sum _{i=1}^3 Y_i^2 +96 g^4 - \sum _{i=1}^3 Y_i^4\!\right) .\nonumber \\ \end{aligned}$$

(4.10)

The renormalization group improved Higgs potential together with the RGE for $\lambda _\phi$ can be used to express $V_{1,2,3}$ in Eq. (4.1) as

$$\begin{aligned} \frac{V_1}{M^3}= & {} \left. \frac{1}{4} (4 \lambda _\phi + \beta _{\lambda _\phi })\right| _{ \phi = M},\nonumber \\ \frac{V_2}{M^2}= & {} \left. \frac{1}{4} (12\lambda _\phi + 7\beta _{\lambda _\phi }+M \beta _{\lambda _\phi }^\prime )\right| _{ \phi = M}, \nonumber \\ \frac{V_3}{M}= & {} \left. \frac{1}{4} (24\lambda _\phi + 26\beta _{\lambda _\phi }+10M \beta _{\lambda _\phi }^\prime +M^2 \beta _{\lambda _\phi }^{\prime \prime })\right| _{ \phi = M}, \end{aligned}$$

(4.11)

where the prime denotes derivatives with respect to $\phi$. To realize an approximate inflection-point at M, we impose $V_1/M^3\simeq 0$ and $V_2/M^2\simeq 0$, which yields the following relations: $\beta _{\lambda _\phi } (M)\simeq -4\lambda _\phi (M)$ and $M\beta _{\lambda _\phi }^{\prime }(M) \simeq 16 \lambda _\phi (M)$ which requires $g, Y_i, \lambda _\phi \ll 1$. For such small coupling values, we can approximate $M^2 \beta _{\lambda _\phi }^{\prime \prime }(M) = - M \beta _{\lambda _\phi }^{\prime }(M) +\phi \frac{{ d} }{{d}\phi } ( \phi \beta _{\lambda _\phi }^{\prime } ) |_{\phi = M} \simeq - M \beta _{\lambda _\phi }^{\prime }(M) \simeq -16 \lambda _\phi (M)$. The dominant terms in the total derivative involve products of g and $Y_i$ which is a polynomial of degree 8 while $M \beta _{\lambda _\phi }^{\prime }(M)$ is a polynomial of degree 6. Therefore, the last expression in Eq. (4.11) is simplified to $V_3/M \simeq 16 \;\lambda _\phi (M)$. Comparison with the expression for $V_3/M$ in Eq. (4.7), with $V_0 \simeq (1/4) \lambda _\phi (M) M^4$, leads to the following expression for $\lambda _\phi$ at the inflation scale $\phi = M$:

$$\begin{aligned} \lambda _\phi (M)\simeq 4.56 \times 10^{-16} \left( \frac{M}{M_{P}}\right) ^2. \end{aligned}$$

(4.12)

Using this expression for $\lambda _\phi (M)$, both the tensor-to-scalar ratio (r) in Eq. (4.3) and the Hubble parameter during the inflation ($H_{inf}$) are uniquely determined as a function of only the single parameter,

$$\begin{aligned} r\simeq & {} 3.7 \times 10^{-9} \left( \frac{M}{M_{P}}\right) ^6, \nonumber \\ H_{inf}\simeq & {} \sqrt{\frac{V_0}{M_P^4}} \simeq 1.5\times 10^{10} \;\mathrm{GeV} \;\left( \frac{M}{M_P}\right) ^3. \end{aligned}$$

(4.13)

Recall that we obtained an upper bound on $H_{inf}$ in Eq. (3.5) to solve the axion domain wall and isocurvature problems. Combined with Eq. (4.13), this leads to an upper-bound on M:

$$\begin{aligned} \frac{M}{M_P} < 0.11 \left( \frac{F_a}{7.11 \times 10^{11} \;\mathrm{GeV}}\right) ^{0.135}. \end{aligned}$$

(4.14)

For the benchmark values $\theta _m \approx 1$ and $F_a = 7.11 \times 10^{11}$ GeV, we obtain an upper bound $M < 0.11 \; M_P$. Therefore, the tensor-to-scalar ratio is predicted to be tiny, $r < 6.55 \times 10^{-15}$, well below the reach of any foreseeable experiments.

4.1 Low energy predictions

In the following analysis, we will estimate the low energy values for the gauge coupling (g), the Yukawa couplings ($Y_i$), and the quartic coupling ($\lambda _\phi$), to determine the masses of the gauge boson $Z^\prime$, Majorana neutrinos, and the inflaton. Let us fix the mass ratio between $Z^\prime$ and $(N^c)^1$ at the inflation scale $\phi = M$ to be $m_{Z^\prime }/m_{N^1} = 10$, or equivalently, $Y_1 (M)/g(M) = \sqrt{2}/5$. The two remaining Yukawa couplings are assumed to be degenerate, $Y_{2,3} (M) = Y$. As we have obtained in Eq. (4.12), IPI requires $\lambda _\phi (M)$ to be extremely small. Assuming $g, Y_{1,2,3} \gg \lambda _\phi$, the condition $\beta _{\lambda _\phi }(M) \simeq 0$ for the inflection-point leads to

$$\begin{aligned} Y(M)\simeq 2.63\;g(M). \end{aligned}$$

(4.15)

Explicitly evaluating another inflection-point condition, $M\beta _{\lambda _\phi }^{\prime }(M) \simeq 16 \lambda _\phi (M)$, using the RGEs in Eq. (4.9) and the relation in Eq. (4.15), we obtain

$$\begin{aligned} \lambda _\phi (M) \simeq 3.95\times 10^{-5} \left( 100+260 x_H+166 {x_H}^2\right) \, g(M)^6.\nonumber \\ \end{aligned}$$

(4.16)

Substituting this $\lambda _\phi (M)$ to Eq. (4.12), the gauge coupling at the inflation scale $\phi = M$ is given by

$$\begin{aligned} g(M)\simeq \frac{ 1.51\times 10^{-2}}{\left( 100+260 x_H+166 {x_H}^2\right) ^{1/6}} \left( \frac{M}{M_{P}}\right) ^{1/3}. \end{aligned}$$

(4.17)

Let us first evaluate the low-energy values of $g(\varphi )$ and $Y(\varphi )$. Since $g(M), Y(M) \ll 1$, we can approximate their low energy values as follows:

$$\begin{aligned} g(\phi )\simeq & {} g(M) +\beta _{g}(M) \ln \left[ \frac{\phi }{M}\right] ,\nonumber \\ Y(\phi )\simeq & {} Y(M)+ \beta _{Y}(M) \ln \left[ \frac{\phi }{M}\right] , \end{aligned}$$

(4.18)

where $\beta _{g}(M)$ ($\beta _{Y}(M)$) is g (Y) beta-function in Eq. (4.9). We evaluate Eq. (4.10) using Eq. (4.18) to approximate $\beta _{\lambda }(\phi )$ as

$$\begin{aligned} 16\pi ^2 \beta _{\lambda }(\phi )\simeq & {} 16 \lambda _\phi (M) \ln \left[ \frac{\phi }{M}\right] , \end{aligned}$$

(4.19)

where we used $\beta _{\lambda _\phi } (M) \simeq 0$ and $M\beta _{\lambda _\phi }^{\prime }(M) \simeq 16 \lambda _\phi (M)$. Using Eq. (4.19) the solution of $\lambda _\phi$ RG equation in Eq. (4.9) is given by

$$\begin{aligned} \lambda _\phi ( \phi )= & {} \lambda _\phi (M) + 8 \lambda _\phi (M) \left( \ln \left[ \frac{ \phi }{M}\right] \right) ^2 \nonumber \\\simeq & {} 3.81 \times 10^{-15}\left( \frac{M}{M_P}\right) ^2\left( \ln \left[ \frac{ \phi }{M}\right] \right) ^2. \end{aligned}$$

(4.20)

The masses of the particles in Eq. (2.3), evaluated at $\phi =v_X$, are then given by

$$\begin{aligned} m_\phi\simeq & {} 8.54 \times 10^{-8} v_X \left| \mathrm{ln}\left[ \frac{v_X}{M}\right] \right| \left( \frac{M}{M_P}\right) , \nonumber \\ m_{Z^\prime }\simeq & {} \frac{ 3.03\times 10^{-2} v_X}{\left( 100+260 x_H+166 {x_H}^2\right) ^{1/6}} \left( \frac{M}{M_{P}}\right) ^{\!\!1/3}, \nonumber \\ m_{N^{1}}\simeq & {} \frac{m_{Z^\prime }}{10}, \nonumber \\ m_{N^{2,3}}\simeq & {} 0.93 \; m_{Z^\prime }. \end{aligned}$$

(4.21)

Fig. 1

With $M = 0.11 M_{P}$, the left panel shows the RG running of the inflaton quartic coupling as a function of $\phi /M$, where the dashed horizontal line corresponds to $\lambda _\phi =0$. The right panel shows the RG improved effective inflaton potential with an approximate inflection-point at $\phi \simeq M$ (vertical dashed-dotted line)

In Fig. 1, we plot the RG running of the inflaton quartic coupling (left) and the corresponding RG improved effective inflaton potential (right) which exhibits an approximate inflection-point at $\phi \simeq M$ (vertical dashed-dotted line). The dashed horizontal line in the left panel depicts $\lambda _\phi =0$. Here, we have set $M = 0.11 M_{P}$ and $x_H = 0$ such that $g (M) \simeq 3.37 \times 10^{-3}$, $Y (M) \simeq 8.86 \times 10^{-3}$, and $\lambda _\phi (M) \simeq 5.52 \times 10^{-18}$. The left panel shows that the running quartic coupling (solid curve) exhibits a minimum with almost vanishing value near $\phi \simeq M$, namely, $\lambda _\phi (M)\simeq 0$ and $\beta _{\lambda _\phi } (M) \simeq 0$.³ This behavior for the RG running of $\lambda _\phi$ is a key to realize an approximate inflection-point behavior for the inflaton potential at $\phi = M$.

4.2 Thermal leptogenesis and reheating

Leptogenesis [26] is a relatively simple mechanism to generate the observed baryon asymmetry in a model with the type-I seesaw mechanism. If Majorana neutrinos are non-degenerate in mass, a successful thermal leptogenesis scenario requires the lightest Majorana neutrino mass ($m_{N^1}$) to be heavier than $10^{9-10}$ GeV and the reheat temperature $T_R > m_{N^1}$ [52, 53]. In our setup, the $U(1)_X$ gauge interactions [54] and Yukawa interactions [55] of the Majorana neutrinos can keep these neutrinos in thermal equilibrium with the SM particles. These processes will suppress the generation of lepton asymmetry until they freeze out. By requiring these processes to decouple before the temperature of the thermal plasma drops to $T \sim m_{N^1}$, we now derive the conditions necessary to prevent such a suppression.

We first consider the $Z^\prime$ mediated process, ${(N^c)^1} (N^c)^1 \rightarrow Z^\prime \rightarrow \overline{f_{SM}} f_{SM}$, where $f_{SM}$ are the SM fermions. Since $m_{Z^\prime } > m_{N^{1}}$, the $Z^\prime$ mediated process is effectively a four-Fermi interaction, and its thermal-averaged cross section for $T \gtrsim m_{N^1}$ can be approximated as [37, 38]

$$\begin{aligned} \langle \sigma v\rangle \simeq \frac{F(x_H)}{768\pi } \frac{T^2}{v_X^4} , \end{aligned}$$

(4.22)

where $F(x_H) = 13 + 16 x_H + 10x_H^2$. The process decouples at $T\sim m_{N^1}$, if $\left. \Gamma /H\right| _{T=m_{N^1}}< 1$, where $\Gamma (T) = n_{eq}(T) \langle \sigma v\rangle$ is the annihilation/creation rate of $(N^c)^1$ with an equilibrium number density $n_{eq}(T) \simeq 2 T^3/\pi ^2$, and $H(T) \simeq \pi T^2/M_P$ is the corresponding value of the Hubble parameter. This leads to a lower bound

$$\begin{aligned} v_{X} > 2.17 \times 10^{10} \;\mathrm{GeV} \left( F(x_H)\right) ^{1/4}\left( \frac{m_{N^1}}{10^{9} \; \mathrm{GeV}}\right) ^{3/4}. \end{aligned}$$

(4.23)

Because we require $M<0.11 M_P$ to solve the axion domain wall and isocurvature problems, it follows from Eq. (4.21) that $m_{N^1} > m_\phi$. In this case, another process, ${N_R}^{1,2} N_R^{1,2} \leftrightarrow \phi \phi$, can suppress the generation of lepton asymmetry as investigated in Ref. [55]. The thermal-averaged cross section of this process is roughly given by [56]

$$\begin{aligned} \langle \sigma v \rangle \simeq \frac{1}{4 \pi } \frac{{m_{N^1}}^2}{v_{BL}^4}. \end{aligned}$$

(4.24)

Requiring $\Gamma /H < 1$ at $T=m_{N^1}$ to avoid the suppression of the generation of lepton asymmetry, we obtain

$$\begin{aligned} v_{X} > 5.95 \times 10^{10} \;\mathrm{GeV} \left( \frac{m_{N^1}}{10^{9} \; \mathrm{GeV}}\right) ^{3/4}. \end{aligned}$$

(4.25)

For the remainder of this section, let us fix $x_H = 0$, $M = 0.05M_P$ and $m_{N^1} = 10^9$ GeV to be our benchmark values, and we find $v_X \simeq 1.93 \times 10^{12}$ GeV, $m_\phi \simeq 9.11 \times 10^4$ GeV and $m_{N^{2,3}} \simeq 9.30 \times 10^9$ GeV from Eq. (4.21). This value of $v_X$ is consistent with Eq. (4.25), which is stronger than condition in Eq. (4.23) for $x_H = 0$. The observed baryon asymmetry therefore can be produced by thermal leptogenesis if the reheat temperature $T_R>m_{N^1}$.

The SM particles produced from the decay of the inflation reheat the universe, thereby connecting inflation to the standard hot big bang cosmology. To estimate the reheat temperature, we assume an instantaneous inflaton decay, which yields the standard formula

$$\begin{aligned} T_R \simeq \left( \frac{90}{\pi ^2 g_*}\right) ^{1/4} \sqrt{\Gamma _\phi M_P}, \end{aligned}$$

(4.26)

where $g_* \simeq 100$ and $\Gamma _\phi$ is the total decay width of the inflaton. To estimate the inflaton decay width, we consider the following interactions between $\Phi$ and the SM doublet Higgs fields,

$$\begin{aligned} V&\supset&2 \lambda ^\prime \left( \Phi ^\dagger \Phi \right) \left( H_u^\dagger H_u + H_d^\dagger H_d\right) \nonumber \\&\supset&2 \lambda ^\prime v_{X} \phi \left( H_u^\dagger H_u + H_d^\dagger H_d\right) . \end{aligned}$$

(4.27)

The decay width of $\phi$ can be approximated as

$$\begin{aligned} \Gamma _\phi \simeq \frac{{\lambda ^\prime }^2 v_X^2 }{\pi \, m_ \phi }, \end{aligned}$$

(4.28)

where we have neglected the mass of Higgs bosons in the final state. The reheat temperature is given by

$$\begin{aligned} T_R \simeq 10^{10} \;\mathrm{GeV} \left( \frac{\lambda ^\prime }{2.29 \times 10^{-9}}\right) . \end{aligned}$$

(4.29)

Thus, an adequate reheat temperature for successful thermal leptogenesis, $T_R >m_{N^1}$ can be achieved with $\lambda ^\prime \gtrsim 2.29\times 10^{-9}$. Such a small value of $\lambda ^\prime$ has a negligible effect on the effective potential of the inflaton and can be safely ignored as far as the inflationary phase is concerned.

5 SU(5) grand unification and SMART U(1)$_X$

In this section we discuss how the SMART U(1)$_X$ framework can be merged with SU(5) grand unification. In Table 1, for $x_H=-4/5$, the SM quarks and leptons are unified in $SU(5)\times U(1)_X \times U(1)_{PQ}$ multiplets: ${(F_{5}^*)}^i$ $(\mathbf{5^*}, -3/5, -1) \supset (d^c)^{i} \oplus \ell ^{i}$ and $F_{10}^i$ of $(\mathbf{10}, 1/5, 1) \supset q^{i} \oplus (d^c)^{i} \oplus (e^c)^{i}$. The Higgs multiplets in $\mathbf{5}$ and $\mathbf{5}^*$ representation of SU(5) contain the SM doublet Higgs fields $H_{u,d}$, namely, $(\mathbf{2}, +1/2,-2) \supset H_u$ and $(\mathbf{2}, -1/2,-2) \supset H_d$. A simple scenario realizing the unification of the SM gauge couplings at around $M_{GUT} \simeq 4.0 \times 10^{16}$ can be achieved in the presence of a pair of vector-like quarks with mass of $\mathcal{O}$(TeV) [57,58,59,60,61,62,63]. To implement this, we include two sets of new vector-like fermions, namely, $V_5+{V_5}^*=(\mathbf{5}, 3/5, 1)+(\mathbf{5^*}, -3/5, -1)$ and $V_{10}+{V_{10}}^*=(\mathbf{10}, 1/5, 1)+(\mathbf{10^*}, -1/5, -1)$. Furthermore, a $U(1)_X$ and $U(1)_{PQ}$ charge neutral Higgs field in the adjoint representation of SU(5), which breaks SU(5) symmetry to the SM, is used to generate a mass-splitting between the triplet and doublet components of the new fermions [41]. We fix the model parameters such that only a pair of vector-like quarks, $D+D^c$ and $Q+Q^c$, remain light at low energies whose representation under the SM gauge group is the same as $(d^c)^{i}$ and $q^{i}$, respectively.

The presence of the new quarks can also stabilize the SM Higgs potential⁴ at high energies [62, 63]. We shall work in the so-called alignment limit for the two Higgs doublet model with $\tan \beta = v_u/v_d \gg 1$, such that $H_u \supset h \sin \beta$ and the quartic self-coupling $\lambda _u$ can be effectively identified with the SM Higgs (h) and its quartic self-coupling ($\lambda _h$), respectively [45, 46]. We fixed the mixed quartic coupling between $H_u$ and $H_d$ to be negligible in our analysis. Following Refs. [62, 63], we numerically solve the RGEs. We set two vector-like quark pairs and the new Higgs doublet mass to be 2.5 TeV.

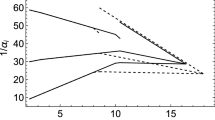
In the left panel of Fig. 2, we plot the RG running of the SM gauge couplings as a function of the energy scale $\mu$. The diagonal solid lines labeled $\alpha _i = g_i^2/4\pi$ ($i=1,2,3$) depict the SM gauge couplings for $U(1)_Y$, $SU(2)_L$ and $SU(3)_c$, respectively. The SM gauge couplings successfully unify at around $M_\mathrm{GUT} \simeq 9.8 \times 10^{15}$ GeV, with $\alpha _{GUT} \simeq 1/35$. With these values, the gauge boson mediated proton lifetime⁵ is estimated to be [65]

$$\begin{aligned} \tau _p \approx \frac{1}{\alpha _{GUT}^2} \frac{M_{GUT}^4}{m_p^5} \approx 2.6 \times 10^{35} \; \mathrm{years}, \end{aligned}$$

(5.1)

where $m_p= 0.983$ GeV is the proton mass. This is consistent with the experimental lower bound obtained by the Super-Kamiokande, $\tau _p(p \rightarrow \pi ^0 e^+) \gtrsim 10^{34}$ year [66]. The predicted lifetime is close to the sensitivity limit of future Hyper-Kamiokande, $\tau _p \lesssim 1.3 \times 10^{35}$ year [67].

In the right panel, the solid (dotted) curve depicts the RG running of the SM Higgs quartic coupling with (without) the new vector-like quarks and a the new Higgs doublet contributions, and the horizontal dashed line depicts $\lambda _h = 0$. In the presence of the new vector-like fields, $\lambda _h(\mu ) > 0$, and thus the SM Higgs potential is stabilized.

Fig. 2

Renormalization group running of the SM couplings including vector-like quarks with degenerate masses of 1 TeV. Top panel: the diagonal solid lines labeled $\alpha _i = g_i^2/4\pi$ ($i=1,2,3$) depict the SM $U(1)_Y$, $SU(2)_L$ and $SU(3)_c$ gauge coupling, respectively, which are unified at $M_\mathrm{GUT} \simeq 9.8 \times 10^{15}$ GeV. Bottom panel: the solid (dotted) curve depicts the RG running of the SM Higgs quartic coupling with (without) the inclusion of the new vector-like quarks, and the horizontal dashed line depicts $\lambda _h = 0$

Next we study the IPI scenario. Note that in the SMART U(1)$_X$ case and we have $\lambda _\phi (M) < 0$ for $-0.87 \lesssim x_H \lesssim -0.69$ from Eq. (4.16), which implies that the inflaton potential is unstable. With the inclusion of the new vector-like quarks ($D+D^c$ and $Q+Q^c$), which is essential for the unification of the SM gauge couplings, we now show that the inflaton potential remains stable for any value of $x_H$. As in the SMART U(1)$_X$ case, we fix $Y_1 (M)/g(M) = \sqrt{2}/5$ and $Y_{2,3} (M)= Y(M)$, such that the conditions $\beta _{\lambda _\phi } (M) = 0$ leads to $Y(M) \simeq 2.63\; g(M)$, which is the same relation as before. However, in the presence of the new vector-like quarks and the extra Higgs doublet, which are also charged under the $U(1)_X$ symmetry, the $U(1)_X$ gauge coupling RG equation in Eq. (4.9) is modified to

$$\begin{aligned} \phi \frac{d g}{d \phi }= & {} \frac{1}{16 \pi ^2} \left( \frac{40 + 32 x_H + 23 x_H^2}{6}\right) g^3. \end{aligned}$$

(5.2)

This leads to a new relation between the quartic and gauge couplings at the inflation scale $\phi = M$,

$$\begin{aligned} \lambda _\phi (M) \!\simeq \! 5.23\times 10^{-5}\! \left( 100+196x_H+141 {x_H}^2\right) \! g(M)^6.\nonumber \\ \end{aligned}$$

(5.3)

which is positive for any value of $x_H$. Therefore the inflaton potential is stable and we can realize a successful IPI scenario for $x_H = -4/5$.

To discuss reheating and leptogenesis, we next consider the low energy predictions for the masses and couplings. Since the quartic coupling at low energies only depends on $\lambda _\phi (M)$, its low energy value is still determined by Eq. (4.20). Comparing Eq. (5.3) with $\lambda _\phi (M)$ value given by Eq. (4.12), the $U(1)_X$ gauge coupling at the inflation scale $\phi = M$ is given by

$$\begin{aligned} g(M)\simeq \frac{1.43\times 10^{-3}}{\left( 100+196x_H+141 {x_H}^2\right) ^{1/6}} \;\left( \frac{M}{M_{P}}\right) ^{1/3}. \end{aligned}$$

(5.4)

The low energy values of the gauge and Yukawa couplings are well approximated by their values at $\phi =M$, $g(v_X) \simeq g(M)$ and $Y_i (v_X) \simeq Y_i (M)$. For a benchmark value $M= 0.05 M_P$, with the lightest Majorana neutrino mass $m_{N^1} = 10^{10} \; \mathrm{GeV}= m_{Z^\prime }/10$, we obtain $v_X \simeq 1.70 \times 10^{12}$ GeV, and the particle masses are given by $m_\phi \simeq 8.10 \times 10^4$ GeV, and $m_{N^{2,3}} \simeq 9.30 \times 10^9$ GeV. The conditions for preventing a suppression of lepton asymmetry from the gauge (Yukwa) interactions of the lightest Majorana neutrino leads to a lower bound of $v_X >3.48\;(7.92) \times 10^{10}$ GeV. This is consistent with the $v_X$ value obtained for the benchmark. The observed baryon asymmetry can be generated by thermal leptogenesis for $T_R \simeq 10^{10} > m_{N^1}$ GeV and this can be realized with $\lambda ^\prime \gtrsim 2.45\times 10^{-6}$ as shown in Eq. (4.29).

6 Summary

We have proposed a phenomenologically viable SMART U(1)$_X$ framework which is an anomaly free $U(1)_X$ extension of the SM supplemented by a $U(1)_{PQ}$ symmetry. The $U(1)_X$ charge of each particle is defined as a linear combination of its hypercharge and $B-L$ charge and is determined by a single free parameter $x_H$. Three right handed neutrinos (RNHs) are added to cancel all $U(1)_X$ related anomalies. These neutrinos, as is well-known, also explain the origin of the observed neutrino oscillations via the type-I seesaw mechanism and generate the observed baryon asymmetry via leptogenesis. Implementation of the $U(1)_{PQ}$ symmetry solves the strong CP problem and also provides the axion as a compelling dark matter (DM) candidate. By identifying a $U(1)_X$ breaking Higgs field as the inflaton, we have implemented a low-scale inflection-point inflation (IPI) scenario in our model to realize a Hubble parameter during inflation $H_{inf} \lesssim 2 \times 10^{7}$ GeV. The $U(1)_X$ gauge symmetry is crucial for the implementation of the IPI scenario. This low-scale inflation is a key for resolving the axion domain wall and the axion DM isocurvature problems. After the end of inflation, we have shown that the inflaton decay adequately reheats the universe to allow for a successful implementation of the leptogenesis scenario.

We have also examined another possibility to merge the SMART U(1)$_X$ framework with SU(5) grand unification. For $x_H=-4/5$, all the SM quarks and leptons are embedded within the $SU(5)\times U(1)_X \times U(1)_{PQ}$ representations. We extended the particle content of the SMART U(1)$_X$ with a pair of new vector-like fermions and a new Higgs doublet with $\mathcal{O}(1)$ TeV mass to realize successful unification of the three SM gauge couplings at $M_{GUT}=9.8 \times 10^{15}$ GeV. This leads to proton lifetime estimate of $2.6 \times 10^{35}$ year, which is close to the sensitivity limit of the future Hyper-Kamiokande experiment. These new fermions also help stabilize the SM Higgs potential as well as the inflaton potential. The latter is crucial for successful implementation of the IPI scenario which is a key for solving the two cosmological problems encountered in the axion DM scenario. The leptogenesis scenario is also implementable in the SU(5) model.