The effective field theory of low scale see-saw at colliders

Abstract

We study the Standard Model effective field theory ($\nu$SMEFT) extended with operators involving right-handed neutrinos, focussing on the regime where the right-handed neutrinos decay promptly on collider scales to a photon and a Standard Model neutrino. This scenario arises naturally for right-handed neutrinos with masses of the order $m_N \sim 0.1 \dots 10\, \,\text {GeV}$. We limit the relevant dimension-six operator coefficients using LEP and LHC searches with photons and missing energy in the final state as well as pion and tau decays. While bounds on new physics contributions are generally in the TeV scale for order one operator coefficients, some coefficients, however, remain very poorly constrained or even entirely evade bounds from current data. Consequently, we identify such weakly constrained scenarios and propose new searches for rare top and tau decays involving photons to probe potential new physics in the $\nu$SMEFT parameter space. Our analysis highlights the importance of performing dedicated searches for new rare tau and top decays.

1 Introduction

The discovery that neutrinos are massive [1,2,3,4,5,6,7] is direct evidence of physics beyond the Standard Model (SM). One of the most appealing explanations of neutrino masses is the so called type I see-saw mechanism [8,9,10,11]. In its most simple incarnation, it extends the SM with three right-handed (RH) neutrinos N with very large lepton-number violating (LNV) Majorana mass terms $\sim m_N \overline{N^c}N$ and ${\mathcal {O}}(1)$ Yukawa couplings y for the SM neutrinos $\nu$; so that the mass of the latter is $m_\nu \sim y^2 v^2/m_N\lesssim$ eV with $v\sim 246$ GeV being the Higgs vacuum expectation value (VEV).

There are however two big modifications of this simplistic setup, both of which can hold simultaneously: (i) a priori, at least one field N can be at the electroweak (EW) scale¹ [13, 14]. (ii) N can be part of a bigger sector with further heavy particles not related to LNV; this is in general the case in left-right symmetric inspired models [15], GUTs [16] and others [17]. If both (i) and (ii) hold simultaneously, the physics at the EW scale can be described by an effective field theory (EFT) involving not only the SM degrees of freedom but also light sterile neutrinos. This EFT is known as $\nu$SMEFT.

$\nu$SMEFT was first considered in Refs. [18, 19]; see also Ref. [20]. The first complete and non-redundant basis of operators of up to dimension six was provided in Ref. [21]. $\nu$SMEFT-operators relevant at energies below the EW scale, where the top and the W, Z and Higgs bosons are integrated out, have been recently studied, including partial renormalization group equations, in Ref. [22]. The corresponding chiral EFT valid at energies below the QCD scale has been considered in Ref. [23] for operators relevant for neutrinoless double beta decay.

The collider phenomenology of $\nu$SMEFT has been explored in a variety of studies, which can be classified depending on the interactions which are assumed to trigger the production and decay of N. Most works have focused on the decay of N via active-sterile neutrino mixing, but in general both production and decay can be mediated and even dominated by effective operators [24]. The parameter space in which they both occur via tree-level generated contact interactions has been studied in Refs. [18, 25]. This regime arises naturally when there are no electrically charged particles in the UV. The parameter space in which effective bosonic operators dominate both production and decay has been considered in Ref. [26]. This regime is inherent to models in which the new physics undergoes a ${\mathbb {Z}}_2$ symmetry that forbids tree-level operators in the EFT; see Ref. [22] for an example including a thorough calculation of all operators arising in the one-loop matching.

However, the most general scenario is that in which both tree-level as well as loop-induced operators are generated when integrating out the new physics that manifests itself as particles in the UV. In that case, four-fermion operators trigger the production of N at colliders, which subsequently decays to $N\rightarrow \nu \gamma$ via bosonic operators. No systematic study of $\nu$SMEFT in this more likely regime has been performed, beyond some preliminary exploration of potential displaced vertex signals [25, 27]. We intend to fill this gap in this article.

In Sect. 2 we define and discuss the parameter space of $\nu$SMEFT that we are interested in. In Sect. 3, we present limits on the bosonic operators of our $\nu$SMEFT Lagrangian. In Sect. 4, we study the impact of four-fermion operators in $\nu$SMEFT on different experimental signatures, focussing on LHC searches for one lepton, one photon and missing energy at CMS in Sect. 4.1. In Sect. 4.2, we discuss searches for two photons and missing energy at the same experiment. In Sects. 4.3 and 4.4 we explore the implications of the EFT on pion and tau decays, respectively. Finally, in Sect. 4.5, we investigate the $\nu$SMEFT contributions to processes with one or multiple photons and missing energy in the final state as studied by the LEP experiments.

On the basis of these results, in Sect. 5 we summarise the obtained limits on the $\nu$SMEFT operators, thereby unravelling which directions in parameter space are less or not yet constrained and therefore identifying where new physics is more likely to be found. In Sect. 7, we develop new search strategies to explore these not yet constrained directions, which include operators triggering $\tau$ decays via the $\tau \rightarrow \ell \gamma \gamma \nu (\nu )$ channel and the rare top decay $t\rightarrow \gamma b\ell \nu$. We conclude in Sect. 8.

2 Relevant parameter space

Table 1 Lepton number conserving operators containing a RH neutrino N [21]

The renormalizable Lagrangian of $\nu$SMEFT reads

$$\begin{aligned} L_{SM+N}&= K - V - \left\{ {\overline{Q}} \mathbf {Y_d} H d +{\overline{Q}}\mathbf {Y_u}{\tilde{H}}u +{\overline{L}} \mathbf {Y_e} H e \right. \nonumber \\&\quad \left. +\, {\overline{L}} \mathbf {Y_N} {\tilde{H}} N + \frac{1}{2} \overline{N^c} \mathbf {M_N}N \right\} , \end{aligned}$$

(2.1)

where K and V are the kinetic terms and the scalar potential, respectively, while L and Q represent the left-handed (LH) lepton and quark doublets, respectively. Accordingly, e and u and d stand for the RH leptons and the up and down quarks. We use the symbol H to denote the Higgs doublet, while ${\tilde{H}} = \epsilon H^*$ with $\epsilon$ being the fully antisymmetric tensor in two dimensions. $B_{\mu \nu }$ and $W^I_{\mu \nu }$ represent the weak field strength tensors. Flavour indices are not shown explicitly. Without loss of generality, we work on the basis in which the Yukawa matrices $\mathbf {Y_e}$ and $\mathbf {Y_d}$ are diagonal.

The effective Lagrangian can be parameterised as

$$\begin{aligned} L_{EFT}= & {} \frac{1}{\Lambda }(\alpha _{NNH} \, \mathcal {O}_{NNH} + \alpha _{NNB}\, \mathcal {O}_{NNB})\nonumber \\&+\frac{1}{\Lambda ^2} \sum _i\alpha _i \, \mathcal {O}^6_i, \end{aligned}$$

(2.2)

where $\mathcal {O}_{NNH} = \overline{N^c} N H^\dagger H$ and $\mathcal {O}_{NNB} =\overline{N^c}\sigma _{\mu \nu } N B^{\mu \nu }$ are the (LNV) dimension-five operators, and $\mathcal {O}^6$ represent the dimension-six operators in Table 1.

Following the line of thought of Ref. [28], we assume that the RH neutrino mass term $\mathbf {M_N}$ is the only source of LNV. Likewise, in order to reduce the plethora of independent Wilson coefficients in the EFT, we assume universality in N and no off-diagonal couplings. We also assume universality and no flavour violation in the light lepton sector. Finally, we require flavour universality in the light quark sector and no flavour-violating transitions between any of the three quark families. Most of these assumptions, if not all, can be enforced by symmetries; e.g. $e\leftrightarrow \mu$ for light lepton flavour universality. We refer the reader to the Appendix A for the explicit expressions of the Lagrangian, including all flavour indices.

As an example, let us show the full structure of the operators ${\mathcal {O}}_{eN}$ and ${\mathcal {O}}_{uN}$

$$\begin{aligned} \alpha _{eN} \, \mathcal {O}_{eN}= & {} \, \alpha _{eN}^{\ell \ell }\, (\mathcal {O}_{eN}^{11ii}+\mathcal {O}_{eN}^{22ii}) +\alpha _{eN}^{\ell \tau } \, (\mathcal {O}_{eN}^{13ii}+\mathcal {O}_{eN}^{23ii}\nonumber \\&+\mathcal {O}_{eN}^{31ii}+\mathcal {O}_{eN}^{32ii}) + \alpha _{eN}^{\tau \tau } \, \mathcal {O}_{eN}^{33ii}, \nonumber \\ \alpha _{uN} \, \mathcal {O}_{uN}= & {} \alpha _{uN}^{qq}\, (\mathcal {O}_{uN}^{11ii}+\mathcal {O}_{uN}^{22ii}) + \alpha _{uN}^{tt} \, \mathcal {O}_{uN}^{33ii}, \end{aligned}$$

(2.3)

where the index $i = \{1, \, 2,\, 3\}$ specifies the RH neutrino flavour.

As a consequence of the above conditions, $\mathbf {M_N}$ must be proportional to the identity matrix, $\mathbf {M_N} = m_N\mathbb {1}$, and $\alpha _{NNH}$ and $\alpha _{NNB}$ must vanish ² (likewise for the Weinberg operator). The strong constraints from SM neutrino dipole moments [29, 30], that would arise upon active-sterile neutrino mixing if $\alpha _{NB}$ was not vanishing, are therefore evaded.

Without loss of generality, we can make the redefinition

$$\begin{aligned} (\mathbf {Y_N})_{ij}\rightarrow (\mathbf {Y_N})_{ij} + \frac{v^2}{2\Lambda ^2}\alpha _{LNH}^{ij}. \end{aligned}$$

(2.4)

Therefore, the effects of the operator $\mathcal {O}_{LNH}$ manifest themselves only in rare decays of the Higgs boson; see Ref. [26]. The neutrino mass matrix then reads

$$\begin{aligned} {\mathbf {M}} = \Bigg ( \begin{array}{cc} 0 &{}\quad \frac{v}{\sqrt{2}}\mathbf {Y_N}\\ \frac{v}{\sqrt{2}}\mathbf {Y_N}^T &{}\quad \mathbf {M_N} \end{array}\Bigg ). \end{aligned}$$

(2.5)

Upon diagonalization, for the active-sterile neutrino mixing matrix one finds

$$\begin{aligned} \mathbf {\Theta } = \frac{v}{\sqrt{2}} \mathbf {M_N}^{-1}\mathbf {Y_N}. \end{aligned}$$

(2.6)

Using the Casas–Ibarra parameterization [31], $\mathbf {Y_N}$ can be expressed (remember that we work in the basis in which the charged lepton Yukawa is diagonal), as

$$\begin{aligned} \mathbf {Y_N}= & {} \frac{\sqrt{2m_N}}{v}\, \mathbf {U_{\text {PMNS}}}\, \sqrt{\text {diag}}(m_{\nu _1},m_{\nu _2},m_{\nu _3}) \,{\mathbf {R}}\,\nonumber \\\approx & {} \frac{\sqrt{m_\nu m_N}}{v}\mathbf {U_{PMNS}} , \end{aligned}$$

(2.7)

where $\mathbf {U_{PMNS}}$ is the Pontecorvo–Maki–Nakagawa–Nasaka matrix, $m_{\nu _i}$ is the mass of the i-th SM neutrino and ${\mathbf {R}}$ is an orthogonal matrix. In the last step of Eq. 2.7 we have conservatively assumed that ${\mathbf {R}}_{ij}\sim \mathcal {O}(1)$ as well as $m_{\nu _1}\approx 0$ and $m_{\nu _2}\approx m_{\nu _3}=m_\nu$.

In the following we will show that our model naturally leads to a RH neutrino mass-range in which the neutrino decays almost exclusively via the $N\rightarrow \nu \gamma$ channel and the decay is prompt on collider scales. Under the conservative approximation that $\mathbf {U_{PMNS}}_{ij}\sim \mathcal {O}(1)$, the decay $N\rightarrow \ell \ell \nu$ is driven by an off-shell Z boson due to the active-sterile neutrino mixing. It is approximately given by

$$\begin{aligned} \Gamma _\text {mix}(N\rightarrow \ell \ell \nu )\approx \frac{1}{64\pi ^3}\frac{m_\nu }{m_N}\left( \frac{m_N}{v}\right) ^4 m_N, \end{aligned}$$

(2.8)

valid for arbitrarily small $m_N$.

On the other hand, tree-level generated contact interactions, e.g. $\mathcal {O}_{LNQd}$, drive the decays $N\rightarrow qq\nu$, $N\rightarrow q q' \ell$ as well as purely leptonic decays. The dominant of these modes for the mass range $m_N > rsim 1$ GeV is

$$\begin{aligned} \Gamma _\text {tree}(N\rightarrow q q' \ell ) \approx \frac{N_c\,\alpha _{LNQd}^2}{3072\pi ^3}\left( \frac{m_N}{\Lambda }\right) ^4 m_N, \end{aligned}$$

(2.9)

and likewise for other four-fermion operators.

Finally, the decay $N\rightarrow \nu \gamma$ triggered by the loop-suppressed $\mathcal {O}_{NA}=c_W\, \mathcal {O}_{NB}+s_W \, \mathcal {O}_{NW}$ is

$$\begin{aligned} \Gamma _\text {loop}(N\rightarrow \nu \gamma ) = \frac{\alpha _{NA}^2}{4\pi } \frac{m_N^2 v^2}{\Lambda ^4}m_N. \end{aligned}$$

(2.10)

For $m_\nu \sim 1$ eV, even for $\Lambda \sim 10$ TeV, if $\alpha _{NA}\sim 1/(4\pi )$ due to the loop-suppression and $\alpha _{LNQd}\sim 1$, we obtain respectively

$$\begin{aligned} \frac{\Gamma _\text {mix}}{\text {GeV}}\approx & {} 10^{-21} \left( \frac{m_N}{\text {GeV}}\right) ^4, \quad \frac{\Gamma _\text {tree}}{\text {GeV}}\approx 10^{-20} \left( \frac{m_N}{\text {GeV}}\right) ^5, \quad \nonumber \\ \frac{\Gamma _\text {loop}}{\text {GeV}}\approx & {} 10^{-15}\left( \frac{m_N}{\text {GeV}}\right) ^3. \end{aligned}$$

(2.11)

Due to the suppression with the LH neutrino mass $\Gamma _\text {mix}$ will remain subdominant throughout the whole RH neutrino mass range. We therefore obtain the hierarchy $\Gamma _\text {mix} \ll \,\Gamma _\text {tree}<\Gamma _\text {loop}$ provided $m_N\lesssim 10$ GeV, where for the tree-level decay we take into account contributions from multiple four-fermion operators.³

Moreover, to assure that N decays promptly at colliders like the LHC, we require the decay length of N to be $c\tau \lesssim 4 \,\text {cm}$. Using Eq. (2.10), we find that this is the case for $m_N > rsim 0.04$ GeV and $\alpha _{NA} /\Lambda ^2 \lesssim 4\pi /(10 \,\text {TeV})^{2}$.

While the assumption that the RH neutrino decays almost exclusively via the $N \rightarrow \nu \gamma$ channel sets an upper bound on the RH neutrino mass, the requirement of a prompt decay bounds $m_N$ from below, leaving us with the regime $m_N \in [0.04, \, 10]\,\,\text {GeV}$ and $\alpha _{NA}\sim \mathcal {O}(1)$ for $\Lambda =10$ TeV. We focus on this region of the parameter space hereafter and discuss to what extent the coefficients of $\nu$SMEFT are constrained by current data in this regime.

3 Constraints on bosonic operators

While most of our study focusses on constraints on four-fermion operators, (see Sect. 4), in this section we want to summarise limits on the bosonic operators in Table 1.

For convenience, we will trade the operators $\mathcal {O}_{NB}$ and $\mathcal {O}_{NW}$ by $\mathcal {O}_{NA} = c_W\mathcal {O}_{NB}+s_W\mathcal {O}_{NW}$ and $\mathcal {O}_{NZ}=-s_W\mathcal {O}_{NB}+c_W\mathcal {O}_{NW}$. As we anticipated above, $\alpha _{NA}=c_W\alpha _{NB}+s_W\alpha _{NW}$, while $\alpha _{NZ}=c_W\alpha _{NW}-s_W\alpha _{NB}$. We also have the relation $\alpha _{NW}=\alpha _{NB}t_W$ with $t_W=s_W/c_W$.

The operator ${\mathcal {O}}_{NZ}$ triggers the decay $Z \rightarrow \nu N$. Accounting for the three RH neutrinos, we find

$$\begin{aligned} \Gamma (Z \rightarrow \nu N) = \frac{3 m_Z^3 v^2}{12 \pi \Lambda ^4} \, \left[ 2(\alpha _{NZ}^{\ell })^2 + (\alpha _{NZ}^{\tau })^2 \right] . \end{aligned}$$

(3.1)

This process leads to the signal $Z\rightarrow \nu \nu \gamma$. The corresponding branching ratio is experimentally bounded to $\mathcal {B}(Z\rightarrow \nu \nu \gamma )<3.2\times 10^{-6}$ [33]. Using that the total Z width is $\sim 2.5$ GeV [34], we obtain the bounds $|\alpha _{NZ}^{\ell }|< 0.37$ and $|\alpha _{NZ}^{\tau }|< 0.52$ for $\Lambda =1$ TeV.

Z decays are also triggered by $\mathcal {O}_{HN}$

$$\begin{aligned} \Gamma (Z \rightarrow N N) = \frac{m_Z^3 v^2}{8 \pi \Lambda ^4} \, \alpha _{HN}^2, \end{aligned}$$

(3.2)

which leads to $Z\rightarrow \nu \nu \gamma \gamma$. The experimental upper bound on the corresponding branching ratio is $\mathcal {B}(Z\rightarrow \nu \nu \gamma \gamma ) < 3.1\times 10^{-6}$ [34]. This translates into a bound on $|\alpha _{HN}| < 0.065$ for $\Lambda = 1$ TeV.

The coefficient of the operator ${\mathcal {O}}_{HNe}$ can be constrained by measurements of the W boson width:

$$\begin{aligned} \Gamma (W \rightarrow \ell N )= & {} \frac{3m_W^3 v^2}{48 \pi \Lambda ^4} \bigg \lbrace 2(\alpha _{HNe}^\ell )^2 + (\alpha _{HNe}^{\tau })^2 \nonumber \\&+ s_W^2 \bigg [2(\alpha _{NA}^\ell )^2 +(\alpha _{NA}^\tau )^2 \bigg ] \bigg \rbrace +\cdots , \end{aligned}$$

(3.3)

where the ellipsis involve terms proportional to the very constrained $\alpha _{NZ}$.

To the best of our knowledge, there is no measurement of this branching ratio, while the bounds on $\alpha _{HNe}$ and $\alpha _{NA}$ from the measurement of the total W width are very weak ⁴. The best bounds on $\alpha _{NA}$ were actually obtained in Ref. [26] using LHC searches for one photon and missing energy. Given our flavour assumptions, this is about $\alpha _{NA}^{\ell }/\Lambda ^2<0.3$ TeV$^{-2}$, and hence consistent with our range for $m_N$; see Sect. 2.

4 Searches limiting four-fermion operators

The four-fermion operators listed in Table 1 can have observable consequences for searches at pp as well as $e^+e^-$ colliders. In the following, we will use LHC and LEP searches as well as $\tau$ and $\pi$ decay measurements to constrain the coefficients of the $\nu$SMEFT Lagrangian. As a first overview, we list the considered experiments and the coefficients which they are sensitive to in Table 2. We generally neglect contributions from bosonic operators, since the processes we consider in the following will not provide competitive bounds on bosonic operators compared to the ones presented in Sect. 3. Furthermore, within their bounds the bosonic operators will not have a meaningful impact on the derivation of the limits on four-fermion operators in multi-parameter fits, so we can safely neglect them.

Table 2 Overview of the considered processes as well as the parameters of four-fermion operators which they constrain. The notation (XX) means that the parameter $\alpha ^{XX}$ can be bound by a given process. For instance, the entry (qq) for ${\mathcal {O}}_{uN}$ and $pp \rightarrow NN$ stands for the process $pp \rightarrow NN$ setting a bound on $\alpha _{uN}^{(qq)}$. We use “Mult” if a process is able to constrain multiple coefficients of an operator

To constrain the $\nu$SMEFT parameter space, we will recast existing LEP and LHC searches. Event generation for these studies is performed with MadGraph-v2.6.7 [36] at leading order, using the NNPDF30_nlo_as_0118 PDFs from the LHAPDF set [37] for proton collisions. We use the default MadGraph dynamical renormalization and factorization scales. Parton showering, fragmentation and hadronization is performed with Pythia v8 [38]. To recast the cuts employed in the experimental analyses, we use routines from HepMC v2 [39] and Fastjet v3 [40]. Detector effects are generally neglected, but we include factors to account for the detector efficiencies.

Some of the considered analyses allow for jets in the final state. We have explicitly checked that generating our signal process with additional hard jets does not significantly increase the number of events.

4.1 LHC searches for one lepton plus one photon plus missing transverse energy

Operators which generate four-point interactions of two light quarks, a lepton and a RH neutrino, ${\mathcal {O}}_{duNe}$, ${\mathcal {O}}_{LdQN}$, ${\mathcal {O}}_{LNQd}$ and ${\mathcal {O}}_{QuNL}$, contribute to the $pp\rightarrow \ell N$ process, where N can be any of the three RH neutrinos. After the decay of the RH neutrino this leads to an $\ell \gamma E_T^\text {miss}$ signature. We neglect contributions from the bosonic operators ${\mathcal {O}}_{NW}$ and ${\mathcal {O}}_{HNe}$.

Given the different helicity structures of the dimension-six operators involved in this process, only the operators ${\mathcal {O}}_{LdQN}$ and ${\mathcal {O}}_{LNQd}$ interfere with each other. We can therefore express the number of events in different signal regions as (compare also Eqs. (2.1) and (2.2) of Ref. [41])

$$\begin{aligned} \begin{aligned} N&= \frac{1}{\Lambda ^4} \bigg \{ \left[ (\alpha _{QuNL}^{qq\ell })^2 + 4 (\alpha _{duNe}^{qq\ell })^2 + (\alpha _{LNQd}^{\ell qq})^2 \right] \mathcal{A}_1\\&\quad + \left[ 4 (\alpha _{duNe}^{qq\ell })^2 + (\alpha _{LdQN}^{\ell qq})^2 \right] \mathcal{A}_2 \\&\quad +2\left[ 4 (\alpha _{duNe}^{qq\ell })^2 - \alpha _{LNQd}^{\ell qq} \, \alpha _{LdQN}^{\ell qq} \right] \mathcal{A}_3 \bigg \}. \end{aligned} \end{aligned}$$

(4.1)

CMS has carried out a search for the one lepton (e or $\mu$) plus one photon plus large missing energy (and jets) signature based on $35.9\text { fb}^{-1}$ of data collected at 13 TeV in Ref. [42]. The search demands at least one photon with $p_T^\gamma > 35\,\text {GeV}$ and at least one lepton with $p_T^\ell > 25 \,\text {GeV}$. Signal events are required to fulfil $E_T^\text {miss}> 120$ GeV and $m_T>100$ GeV⁵ and are classified into different signal regions according to their $H_T$, $p_T^\gamma$ and $E_T^\text {miss}$. As we do not expect any jets in our signal final state, we concentrate on the lowest-$H_T$ signal regions, i.e. we consider $H_T < 100\, \,\text {GeV}$ only. We also neglect overflow bins in which an EFT description would not be valid for $\Lambda \sim \mathcal {O}( 1)$ TeV. Since the momentum flow through the four-fermion vertex can reach $\sqrt{{\hat{s}}} > rsim 1 \,\text {TeV}$, the validity of an EFT expansion is limited by the choice of the new physics scale $\Lambda$. We find that for the LHC processes studied in this and the next section, only $1\%$ of the events exceed a momentum flow of $4\,\text {TeV}$ through the four-fermion vertex. Therefore, we will present our limits for $\Lambda = 4 \,\text {TeV}$ in this and the following sections. The definition of the four remaining signal regions in terms of $p_T^\gamma$ and $E_T^\text {miss}$ is presented in Table 3, along with the number of data events in each region as well as the SM prediction including its uncertainty. The numerical values are directly taken from Fig. 5 of Ref. [42], as a HepData entry for this analysis was not available.

Table 3 CMS lepton plus photon plus missing energy: Number of expected SM events and data in different bins of the $E_T^\text {miss}$ distribution in Fig. 5 of [42] for the $e\gamma$ ($\mu \gamma$) case, excluding the overflow bins

The numerical values for the coefficients $\mathcal{A}_i$ of Eq. (4.1), which represent the different beyond the SM (BSM) contributions to the signal region, are also presented in Table 3. They include a factor of 0.59 to account for detector effects.⁶

Using the information in Table 3, we set limits on the relevant coefficients of $\alpha _{duNe}$, $\alpha _{LdQN}$, $\alpha _{LNQd}$, $\alpha _{QuNL}$ in one-parameter fits. We allow the BSM contribution to produce $s_\text {max}$ events, where $s_\text {max}$ is the maximum number of allowed additional signal events, determined using the CL$_s$ technique [44], that we quote in Table 3 too. Assuming a new physics (NP) scale of $\Lambda = 4\,\text {TeV}$, the resulting one-parameter fit limits in the electron (muon) channel are $|\alpha _{duNe}^{qq\ell }|<0.75 \, (0.66)$, $|\alpha _{LdQN}^{\ell qq}|<1.4 \, (1.2)$, $|\alpha _{LNQd}^{\ell qq}|, \,|\alpha _{QuNL}^{qq\ell }| < 0.78 \, (0.67)$. These limits come from the last bin of Table 3 only, $p_T^\gamma >200 \,\text {GeV}$ and $E_T^\text {miss}\in [200, \, 400] \,\text {GeV}$, where there is a small underfluctuation in the muon data. The limits from the muon channel are hence stronger than those from the electron channel. For the limits on $\alpha _{LdQN}$ and $\alpha _{LNQd}$, we should take into account that the corresponding operators have a negative interference. We therefore marginalise over $\alpha _{LdQN}$ when constraining $\alpha _{LNQd}$ (and vice versa). The marginalization weakens the limits on these operators to $|\alpha _{LdQN}^{\ell qq}|< 3.7 \, (3.2)$, $|\alpha _{LNQd}^{\ell qq}| < 1.9 \,(1.6)$ in the electron (muon) channel. Limits for lower values of $\Lambda$ could be obtained by imposing a cut on the momentum flow through the four-fermion vertex. As an example, more than $50\%$ of the events have a momentum flow through the four-fermion vertex of less than $1\,\text {TeV}$. This allows us to set a limit of, for instance, $|\alpha _{duNe}^{qq\ell }|< \sqrt{2} \cdot 0.66 \cdot (1 \,\text {TeV})^2/(4\,\text {TeV})^2 = 0.058$ for $\Lambda = 1 \,\text {TeV}$ in the muon channel.

In principle, the presented CMS search is also sensitive to $pp \rightarrow t t, \, t \rightarrow b \ell N$, as it allows for jets in the final state. However, the resulting limits are very weak, $\alpha /\Lambda ^2 \sim {\mathcal {O}}(50 )\, \,\text {TeV}^{-2}$.

4.2 LHC searches for two photons plus missing transverse energy

Four-fermion operators containing two light quarks and two RH neutrinos can contribute to a diphoton plus missing energy signature at the LHC via the process $pp\rightarrow N N \rightarrow \gamma \gamma \nu \nu$, where the NN can be any pair of the three RH neutrinos $NN = N_1 N_1 + N_2 N_2 + N_3 N_3$. The operators contributing to the considered signature are ${\mathcal {O}}_{uN}$, ${\mathcal {O}}_{dN}$, ${\mathcal {O}}_{QN}$. The interference between either of the operators ${\mathcal {O}}_{uN}$ and ${\mathcal {O}}_{dN}$ with the operator ${\mathcal {O}}_{QN}$ is helicity suppressed. We can therefore parametrise the number of events in different signal regions as

$$\begin{aligned} N = \frac{1}{\Lambda ^4} \left[ (\alpha ^{qq}_{uN})^2 \, \mathcal{C}_1 + (\alpha ^{qq}_{dN})^2 \, \mathcal{C}_2 + (\alpha ^{qq}_{QN})^2 \, \mathcal{C}_3 \right] . \end{aligned}$$

(4.2)

CMS has carried out a search for two photons plus missing energy in Ref. [45], based on $35.9\text { fb}^{-1}$ of data at $\sqrt{s}=13\,\text {TeV}$. The main signal specifications are two photons with $p_T^\gamma >40\,\text {GeV}$ in the central detector region $|\eta ^\gamma |<1.44$ and a significant amount of missing transverse energy $E_T^\text {miss}>100\,\text {GeV}$. The analysis further vetoes events with leptons with $p_T^\ell > 25\,\text {GeV}$ and the two photons are required to have an invariant mass $m_{\gamma \gamma } >105\,\text {GeV}$ and to be separated by $\Delta R > 0.6$. The predicted number of SM events as well as the observed data in different $E_T^\text {miss}$ bins as provided in Tab. 2 of Ref. [45] is given in Table 4, together with the values of $s_{\mathrm{max}}$.

Table 4 CMS diphoton plus missing energy: Number of expected events and data in different bins of the $E_T^\text {miss}$ distribution in Tab. 3 (post-fit) of Ref. [45]. We neglect the overflow bin

We validate our implementation of the CMS signal region definition using the $Z\gamma \gamma$ background. This background is subdominant, accounting for between $1\%$ and $20\%$ of the total background only (depending on the missing energy bin). For the analysis validation, however, it has the advantage that it comes purely from Monte Carlo simulation and no data-driven correction factors were applied. Moreover, this background is the only one with a genuine $\gamma \gamma E_T^{miss}$ signature from $\nu \nu \gamma \gamma$ and therefore the detector effects relevant for it will best represent the detector effects on our signal. We find that using a global scale factor of 0.59 to account for detector efficiencies, we can reproduce the $E_T^\text {miss}$ distribution of the $Z\gamma \gamma$ background within $5\%$.

Recasting the CMS analysis for our heavy neutrino pair production signal, we find the parametrization of the event numbers in different $E_T^\text {miss}$ bins in terms of the parameters $\mathcal{C}_i$ of Eq. (4.2) displayed in Table 4. Translating the parametrization into limits on the $\nu$SMEFT coefficients, we observe that the highest bin provides the best sensitivity, as expected. The resulting limits from the last bin only are $|\alpha _{uN}^{qq}| < 0.93$, $|\alpha _{dN}^{qq}|<1.2$, $|\alpha _{QN}^{qq}|<0.77$, where we again use $\Lambda = 4 \,\text {TeV}$ to stay within the range of validity of the EFT description. As expected from the PDFs, the limits on up-quark couplings to NN are stronger than the ones from down-quark couplings and the strongest limits arise for the operator influencing both up-quark and down-quark couplings. Limits for lower new physics scales $\Lambda$ could be obtained by imposing a cut on the momentum flow through the four-fermion vertex. About $40 \%$ of all events have a momentum flow of $\sqrt{{\hat{s}}} < 1 \,\text {TeV}$, for $\sqrt{{\hat{s}}} < 2 \,\text {TeV}$ the fraction rises up to $80\%$. Taking these values into account, one can rescale the above limits for lower values of $\Lambda$.

4.3 Pion decays

Given low RH neutrino masses $m_N \lesssim m_\pi$, operators which generate four-point interactions of two light quarks, a lepton and a RH neutrino, ${\mathcal {O}}_{duNe}$, ${\mathcal {O}}_{LdQN}$, ${\mathcal {O}}_{LNQd}$ and ${\mathcal {O}}_{QuNL}$, do not only contribute to the $pp\rightarrow \ell N$ process as discussed in Sect. 4.1, but they also trigger the pion decay $\pi \rightarrow \ell \gamma \nu$. In the following, we will neglect the operator ${\mathcal {O}}_{LdQN}$, for which the pion form factor is hard to estimate.

The pion decay width, including all fermion masses and a factor of 3 to account for the three RH neutrino flavours, is described by (see also Ref. [46])

$$\begin{aligned} \begin{aligned}&\Gamma (\pi \rightarrow \ell N) = \frac{3 f_\pi ^2 k}{16\pi m_\pi ^2 \Lambda ^4} \, \Bigg \{ \alpha _V^2 \left[ (m_\ell ^2 + m_N^2) (m_\pi ^2 \right. \\&\quad \left. -m_N^2 - m_\ell ^2)+ 4 m_\ell ^2 m_N^2 \right] \\&\quad + 2 \, \alpha _V \, \alpha _P \, m_\ell \, \frac{m_\pi ^2}{m_u+m_d} \, \left[ m_\pi ^2 + m_N^2 - m_\ell ^2 \right] \\&\quad + \alpha _P^2 \, \left( \frac{m_\pi ^2}{m_u+m_d} \right) ^2 \, (m_\pi ^2 -m_N^2 - m_\ell ^2) \Bigg \}, \end{aligned} \end{aligned}$$

(4.3)

with $f_\pi \sim 131 \,\text {MeV}$. Here, $\alpha _V= \alpha _{duNe}^{qq\ell }$ and $\alpha _P = ( \alpha _{QuNL}^{qq \ell } - \alpha _{LNQd}^{\ell qq} )$ denote the contributions from operators with vector couplings and pseudo-scalar couplings respectively, and k is the magnitude of the three-momenta of the lepton and neutrino in the center-of-mass (c.o.m) frame⁷:

$$\begin{aligned}&k = \frac{1}{2m_\pi } \sqrt{\left( m_\pi ^2 - (m_l +m_N)^2 \right) \, \left( m_\pi ^2 - (m_l - m_N)^2 \right) } \, \nonumber \\&\quad \overset{m_N = 0}{=} \, \frac{m_\pi ^2 - m_\ell ^2}{2m_\pi } \, . \end{aligned}$$

(4.4)

Due to the helicity suppression for vector couplings, $\alpha _{duNe}^{qq\ell }$ will be much less constrained than the combination $(\alpha _{QuNL}^{qq\ell } - \alpha _{LNQd}^{\ell qq})$.

We compare the BSM pion decay width to the experimental measurements of the $\pi \rightarrow \ell \gamma \nu$ branching ratio which we list in Table 5. We also cite the corresponding theory prediction and determine the maximally allowed BSM contribution to the decay width $\Delta \Gamma ^\text {BSM}$ which we define as

$$\begin{aligned}&\Delta \Gamma ^\text {BSM} \nonumber \\&\quad = \left\{ ~~ \begin{matrix} \, \Gamma _\text {exp} - \Gamma _\text {theo} + 2 \sigma _{\Gamma _\text {exp}} \\ 2 \sigma _{\Gamma _\text {exp}}, ~\text {where no measurement/prediction is available.} \end{matrix} \right. \nonumber \\ \end{aligned}$$

(4.5)

Table 5 Measured values and theoretical predictions of branching ratios for different $\pi$ decays. The theory predictions are taken from the corresponding experimental references. For convenience, we also translate the measured branching ratio into decay width and list the allowed contribution from BSM processes according to Eq. (4.5)

The resulting bounds in a one-parameter fit in the limit $m_N=0$ are $|\alpha _{duNe}^{qq\ell }| < 73 \, (0.04)$, and $|\alpha _{QuNL}^{qq\ell } - \alpha _{LNQd}^{\ell qq}| < 1.3 \times 10^{-5}$ (0.002) in the electron (muon) channel respectively, for $\Lambda = 1\,\,\text {TeV}$. As $\alpha _{QuNL}^{qq\ell }$ and $\alpha _{LNQd}^{\ell qq}$ interfere negatively, we should note, however, that any BSM contributions for one operator can in principle be cancelled exactly by the other one. We can only constrain the difference between the two coefficients, but each individual coefficient is unconstrained. For $m_N=0.1 \,\text {GeV}$, only the electron decay channel is kinematically open. The limits from this channel are $|\alpha _{duNe}^{qq \ell }| <7.7\times 10^{-4}$ and $|\alpha _{QuNL}^{qq \ell } -\alpha _{LNQd}^{\ell qq}| < 2.7\times 10^{-5}$.

4.4 Tau decays

The four-fermion operators in Table 1 can contribute to $\tau$ decays with a photon in the $\tau \rightarrow \ell \nu N \rightarrow \ell \nu \nu \gamma$ and $\tau \rightarrow \pi N \rightarrow \pi \gamma \nu$ channels. Each of these processes is sensitive to a different set of operator coefficients; see Table 2. In Table 6, we list the experimentally measured branching ratios of the considered decay channels along with their theory prediction.

Table 6 Measured values and theoretical predictions of branching ratios for different $\tau$ decays. All experimental values are taken from the PDG [34]. For convenience, we also translate the measured branching ratio into decay width and list the allowed contribution from BSM processes according to Eq. (4.5). Note the discrepancy between theory and experiment in the $\tau \rightarrow e \nu N$ channel

4.4.1 Tau decays to $\tau \rightarrow \ell \nu N$

The $\tau \rightarrow \ell \nu N$ process is sensitive to different coefficients of the operator ${\mathcal {O}}_{LNLe}$. Neglecting the mass of the RH neutrino, they contribute to the decay width through

$$\begin{aligned} \Gamma (\tau \rightarrow \ell _i N \nu _i)= & {} \frac{m_\tau ^5}{2048 \pi ^3 \Lambda ^4} (\alpha _{LNLe}^{\ell \ell \tau })^2\,\, \nonumber \\ \Gamma (\tau \rightarrow \ell _i \bar{\nu _i} N)= & {} \frac{m_\tau ^5}{2048 \pi ^3 \Lambda ^4}\nonumber \\&\left[ (\alpha _{LNLe}^{\ell \tau \ell })^2 + (\alpha _{LNLe}^{\tau \ell \ell })^2 - \alpha _{LNLe}^{\ell \tau \ell } \alpha _{LNLe}^{\tau \ell \ell } \right] ~, \nonumber \\ \Gamma (\tau \rightarrow \ell _i N \nu _\tau )= & {} \frac{m_\tau ^5}{2048 \pi ^3 \Lambda ^4}\nonumber \\&\left[ (\alpha _{LNLe}^{\ell \tau \tau })^2 + (\alpha _{LNLe}^{\tau \ell \tau })^2 - \alpha _{LNLe}^{\ell \tau \tau } \alpha _{LNLe}^{\tau \ell \tau } \right] ,\nonumber \\ \Gamma (\tau \rightarrow \ell _i \bar{\nu _\tau } N)= & {} \frac{m_\tau ^5}{2048 \pi ^3 \Lambda ^4} (\alpha _{LNLe}^{\tau \tau \ell })^2. \end{aligned}$$

(4.6)

The correction factor to include the mass of the RH neutrinos reads⁸

$$\begin{aligned} \frac{\Gamma (x = \frac{m_N}{m_\pi })}{\Gamma (m_N=0)} = 1 - 8 x^2 + 8 x^6 - x^8 - 24 x^4 \log x. \end{aligned}$$

(4.7)

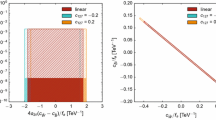
We set limits on the components of $\alpha _{LNLe}$ by letting the EFT contribution account for $\Delta \Gamma ^\text {BSM}$ as given in Eq. (4.5). Assuming that only one of the $\alpha _{LNLe}$ components is non-zero, we can set a limit of $|\alpha _{LNLe}| < 4.9$ (1.5) for the decay into an electron (muon) and relatively light RH neutrinos $m_N=0.1\, \,\text {GeV}$. The difference between the limits in the electron and muon channels results entirely from $\Delta \Gamma ^\text {BSM}_{\tau \rightarrow e \gamma \nu } > \Delta \Gamma ^\text {BSM}_{\tau \rightarrow \mu \gamma \nu }$; we do not include the mass of the charged leptons in our calculations. The obtained limits for $m_N=0.1 \,\,\text {GeV}$ are already quite weak and are further diluted when we consider heavier RH neutrinos; see the left panel of Fig. 1. At $m_N = 1\, \,\text {GeV}$, for instance, the limits become $\alpha _{LNLe} < 16$ (4.8) in the electron (muon) channel, respectively, assuming $\Lambda = 1 \,\text {TeV}$.

For those components with negative interferences, we marginalise over the other relevant components when setting limits. The obtained bounds in the muon decay channel for $m_N = 0.1 \,\text {GeV}$ are $|\alpha _{LNLe}^{\ell \ell \tau }|, \, |\alpha _{LNLe}^{\tau \tau \ell }|< 1.5$ (no interference) and $|\alpha _{LNLe}^{\ell \tau \ell }|, \, |\alpha _{LNLe}^{\tau \ell \ell }|, \,$ $|\alpha _{LNLe}^{\ell \tau \tau }|, \, |\alpha _{LNLe}^{\tau \tau \ell }| < 1.7$.

Fig. 1

RH neutrino mass dependence of the one-parameter fit limits from $\tau$ decays. Left: limits on $\alpha _{LNLe}$ from the process $\tau \rightarrow \ell \nu N$. The mass on the charged leptons has been neglected. Right: limits on $\alpha _V= \alpha _{duNe}^{qq\tau }$ and $\alpha _P = ( \alpha _{QuNL}^{qq\tau } - \alpha _{LNQd}^{\tau qq} )$ from $\tau \rightarrow \pi N$

4.4.2 Tau decays to $\tau \rightarrow \pi N$

The same operators that contribute to leptonic pion decays (see Sect. 4.3) will also add to $\tau$ decays to pions (with different coefficients). We can therefore use the search for $\tau$ decays in the $\tau \rightarrow \pi \gamma \nu$ channel, to constrain the coefficients $\alpha _{duNe}^{qq\tau }$, $\alpha _{QuNL}^{qq\tau }$ and $\alpha _{LNQd}^{\tau qq}$. The observed branching ratio in this channel is given in Table 6.

The decay width of the $\tau$ lepton into a pion and a RH neutrino is structurally very similar to the pion decay width in Eq. (4.3):

$$\begin{aligned} \begin{aligned} \Gamma _{\tau \rightarrow \pi N }&= \frac{3 f_\pi ^2 k}{16\pi m_\tau ^2 \Lambda ^4} \, \Bigg \{ \alpha _V^2 \left[ (m_\tau ^2 + m_N^2) (m_\tau ^2 +m_N^2 - m_\pi ^2)\right. \\&\quad \left. + 4 m_\tau ^2 m_N^2 \right] \\&\quad + 2 \, \alpha _V \, \alpha _P \, m_N \, \frac{m_\pi ^2}{m_u+m_d} \, ( 3 m_\tau ^2 + m_N^2 - m_\pi ^2 ) \\&\quad + \alpha _P^2 \, \left( \frac{m_\pi ^2}{m_u+m_d} \right) ^2 \, (m_\tau ^2 +m_N^2 - m_\pi ^2) \Bigg \}, \end{aligned} \end{aligned}$$

(4.8)

where $\alpha _V= \alpha _{duNe}^{qq\tau }$ and $\alpha _P = ( \alpha _{QuNL}^{qq\tau } - \alpha _{LNQd}^{\tau qq} )$ denote the contributions from the operators with vector couplings and pseudo-scalar couplings respectively and we use $f_\pi \sim 131 \,\text {MeV}$ again for the pion form factor. k is the magnitude of the three-momenta of the pion and neutrino in the c.o.m frame⁹

$$\begin{aligned}&k = \frac{1}{2m_\tau } \sqrt{\left( m_\tau ^2 - (m_\pi +m_N)^2 \right) \, \left( m_\tau ^2 - (m_\pi - m_N)^2 \right) } \, \nonumber \\&\quad \overset{m_N = 0}{=} \, \frac{m_\tau ^2 - m_\pi ^2}{2m_\tau }. \end{aligned}$$

(4.9)

As expected for a two-body decay, the decay width does not drop as quickly with $m_N$ as for the three-body decays considered before.

To the best of our knowledge, there is no SM estimate for the width $\Gamma _{\tau \rightarrow \pi \gamma \nu }$. We therefore set conservative limits on the dimension-six operators involved by letting the BSM contribution account for twice the uncertainty of the experimental measurement, see Table 6. For $m_N = 0.1 \,\,\text {GeV}$ and $\Lambda = 1\, \,\text {TeV}$, we obtain limits of $|\alpha _{duNe}^{qq\tau }| < 0.49$ and $|( \alpha _{QuNL}^{qq\tau } - \alpha _{LNQd}^{\tau qq} ) | < 0.30$. These limits are rather insensitive to the RH neutrino mass (see the right panel of Fig. 1), as long as $m_N < m_\tau - m_\pi$ of course.

4.5 LEP searches for single and multiple photons

LEP searches for a single high-energy photon or multiple photons and missing energy can be used to constrain the interactions of (first family) leptons to RH as well as LH neutrinos via the $e e \rightarrow NN \rightarrow \gamma \gamma \nu \nu$ and $e e \rightarrow \nu N \rightarrow \gamma \nu \nu$ channels. The LEP L3 analysis for single and multi-photon events with missing energy [50] provides $\mathcal {L} = 619.1 \text { pb}^{-1}$ of data at an average c.o.m energy of $\sqrt{s} = 197.6 \,\text {GeV}$. In the following, we will use this experimental analysis to constrain the coefficients $\alpha _{eN}^{\ell \ell }$, $\alpha _{LN}^{\ell \ell }$ in $ee \rightarrow NN$ and $\alpha _{LNLe}$ in $ee \rightarrow \nu N$.

4.5.1 LEP search for multiple photons and missing energy

The coefficients $\alpha _{eN}^{\ell \ell }$, $\alpha _{LN}^{\ell \ell }$ contribute to the process $ee \rightarrow NN \rightarrow \gamma \gamma \nu \nu$, where again the NN can be any pair of the three RH neutrinos $NN = N_1 N_1 + N_2 N_2 + N_3 N_3$. The interference of the operators contributing to $ee \rightarrow NN \rightarrow \gamma \gamma \nu \nu$ is helicity suppressed and we parametrise the number of events in terms of the $\nu$SMEFT coefficients as

$$\begin{aligned} N = \frac{1}{\Lambda ^4} \left[ (\alpha ^{\ell \ell }_{eN})^2 + (\alpha ^{\ell \ell }_{lN})^2 \right] \, \mathcal{D}, \end{aligned}$$

(4.10)

where the numerical value for ${\mathcal {D}}$ is given in Table 7 for two overlapping signal regions.

The considered LEP L3 analysis in the multi-photon channel focuses on events with (at least) two photons with $E_\gamma > 1 \,\,\text {GeV}$ and a transverse momentum of the diphoton system of $p_T^\gamma > 0.02 \sqrt{s} \approx 4 \,\text {GeV}$. The hardest photon has to be inside the range $\theta _{\gamma _1} \in [14^\circ , \, 166^\circ ]$. A cut on the acoplanarity $| | \phi _{\gamma _1} - \phi _{\gamma _2} | - \pi |> 2.5^\circ$ severely reduces the sensitivity on our signal process, where the photons are mostly back-to-back. However, we can still deduce meaningful results from the LEP analysis.

We base our limits on the missing mass $m_\text {miss}$ distribution in the LEP analysis, where $m_\text {miss}$ is defined as the invariant mass of the missing momentum. Given the fact that $m_\text {miss}$ is expected to peak around the Z boson mass $m_Z=91\, \,\text {GeV}$ for the SM background, we will only consider the range $m_\text {miss} \in [120, \, 210]\,\,\text {GeV}$. We analyse two non-exclusive signal regions: the full region contains all events with both photons in the full detector region, defined in Table 7, whereas the central region only accepts events with both photons in the central detector area.

In Table 7, we present the LEP data in the full and central signal regions along with their SM prediction and uncertainties, the experimental efficiencies and the resulting upper $95\%$ CL limit on additional contributions to these regions. We also list the numerical values of the parameters $\mathcal{D}_i$ for the BSM contributions according to Eq. (4.10). Systematic uncertainties are very small compared to the statistical ones in this analysis and can hence safely be neglected.

Table 7 LEP data, expected number of events and corresponding CLs limit for the multi-photon selection for the two considered angular ranges for the photons. We also list the considered average detector efficiencies

We have validated our analysis using the SM $ee \rightarrow \gamma \gamma (\gamma ) \nu \nu$ process. We can reproduce the total cross sections for the full and central regions using the respective detector efficiencies as given in Table 7.

The resulting limits on the $\nu$SMEFT coefficients are $|\alpha _{eN}^{\ell \ell }|, \, |\alpha _{LN}^{\ell \ell }| < 0.97\, (0.93)$ in the full (central) detector region, for $\Lambda = 1 \,\text {TeV}$.

4.5.2 LEP search for a single photon and missing energy

The coefficients $\alpha _{LNLe}^{\ell \ell \ell }$, $\alpha _{LNLe}^{\tau \ell \ell }$, $\alpha _{LNLe}^{\ell \tau \ell }$ can be constrained using the process $ee \rightarrow \nu N \rightarrow \gamma \nu \nu$, where N is any of the three RH neutrinos. We parametrise the $\nu$SMEFT contributions to the number of events in this channel as

$$\begin{aligned} N&= \frac{1}{\Lambda ^4} \left[ (\alpha ^{\ell \ell \ell }_{LNLe})^2 + (\alpha ^{\tau \ell \ell }_{LNLe})^2 + (\alpha ^{\ell \tau \ell }_{LNLe})^2 \right. \nonumber \\&\quad \left. - (\alpha ^{\tau \ell \ell }_{LNLe}) (\alpha ^{\ell \tau \ell }_{LNLe}) \right] \, \mathcal{E}, \end{aligned}$$

(4.11)

where the numerical value of $\mathcal{E}$ is listed in Table 8.

We now make use of the single high-energy photon events region of the LEP L3 analysis discussed above [50]. For this signature, the analysis requires exactly one photon with $p_T^{\gamma } > 0.02 \sqrt{s} \approx 4 \,\text {GeV}$ in the region $\theta _{\gamma } \in [14^\circ , \, 166^\circ ]$.

We again restrict ourselves to the missing mass range $m_\text {miss} \in [120, \, 210]\,\text {GeV}$ to exclude the main peak of the SM background from our signal regions and list the number of events, the SM prediction and its uncertainty in Table 8. Systematic uncertainties can again safely be neglected.

Table 8 LEP data, expected number of events and corresponding CLs limit for the single high-energy photon selection for the two considered angular ranges of the photon. We also list the considered average detector efficiencies

We have again validated our analysis using the SM background, $ee \rightarrow \gamma (\gamma ) \nu \nu$. We can reproduce the total cross section in the full and central signal regions within $5 \%$ when including the detector efficiencies listed in Table 8.

The resulting limits on the coefficients of $\alpha _{LNLe}$ are $|\alpha _{LNLe}^{\ell \ell \ell }| < 0.52\, (0.53)$ in the full (central) detector region, assuming $\Lambda = 1 \,\,\text {TeV}$. For $\alpha _{LNLe}^{\tau \ell \ell }$ and $\alpha _{LNLe}^{\ell \tau \ell }$, for which the corresponding operators interfere negatively, the limit is diluted to $|\alpha _{LNLe}^{\tau \ell \ell }|, \, |\alpha _{LNLe}^{\ell \tau \ell }| <0.60$ (0.61). These limits are much stronger than the corresponding limits from $\tau$ decays; see Sect. 4.4. Note also that these limits are less dependent on the mass of the RH neutrinos.

5 Limits on contact interactions

Let us start our discussion of the limits on contact interactions from those which are independent of the RH neutrino mass. This is definitely the case of bounds from the LHC, $pp \rightarrow \ell N$ and $pp \rightarrow NN$, and LEP, $ee \rightarrow NN$ and $ee \rightarrow \nu N$, where $m_N$ is negligible compared to the large c.o.m energies. The only mass dependence stems from the RH neutrino branching ratio which we assume to be $100\%$ for the $N \rightarrow \gamma \nu$ channel throughout. At masses approaching $m_N = 10 \,\text {GeV}$, the branching ratio can be slightly reduced by new tree-level decay modes of N opening up, which we neglect in our analysis.

Table 9 Summary of limits on four-fermion operators from LHC processes and observables they result from. Note that $\Lambda = 4 \,\text {TeV}$ is assumed for the limits on $\alpha$ to stay within the range of validity of the EFT

Table 10 Summary of limits on RRRR and LLRR operators and observables they result from, assuming $m_N = 0.1 \,\text {GeV}$

Table 11 Summary of limits on LRRL operators and observables they result from, assuming $m_N = 0.1 \,\text {GeV}$

For the $pp \rightarrow NN$, for which none of the contributing operators interfere, limits on the relevant coefficients $\alpha _{uN}^{qq}$, $\alpha _{dN}^{qq}$ and $\alpha _{QN}^{qq}$ can be extracted from one-parameter fits. The resulting bounds are presented in Table 9, where we assume $\Lambda = 4 \,\text {TeV}$ to stay within the range of validity of the EFT description.

As already pointed out in Sect. 4.1, in the $pp \rightarrow \ell N$ channel, the limits on $\alpha _{duNe}$ and $\alpha _{QuNL}$ can be extracted from one-parameter fits as well, as the corresponding operators do not interfere with any other operator contributing to this channel. For the limits on $\alpha _{LdQN}$ and $\alpha _{LNQd}$, on the other hand, we account for the negative interference of the corresponding operators by marginalizing over one parameter when constraining the other. The resulting limits are displayed in Table 9. Since we assume e-$\mu$ universality, we only present the limits from the $\mu \gamma$ channel which gives the stronger constraints.

The LEP searches for a single photon or multiple photons accompanied by missing energy provide constraints on the parameters $\alpha _{eN}^{\ell \ell }, \,\alpha _{LN}^{\ell \ell }$ and multiple coefficients of $\alpha _{LNLe}$ respectively. In multi-photon production, there are no negative interferences between different operators and we can directly copy the limits obtained in Sect. 4.5 into Table 10. The fact that these bounds are more than an order of magnitude weaker than the bounds on the structurally similar operators $\alpha _{uN}^{qq}$, $\alpha _{dN}^{qq}$ and $\alpha _{QN}^{qq}$ from $pp \rightarrow NN$ is a result not only of lower energy at LEP, but also of the strong acoplanarity cut applied by LEP which reduces the sensitivity to BSM contributions with back-to-back photons. For the single high-energy photon analysis we marginalise over the contributing coefficients of $\alpha _{LNLe}$. The constraints on $\alpha _{LNLe}^{\tau \ell \ell }$ and $\alpha _{LNLe}^{\ell \tau \ell }$ are much stronger than those derived from $\tau$ decays in the $\tau \rightarrow \ell N$ channel.

Limits from tau and pion decays are a lot more sensitive to the RH neutrino masses than the limits from direct production at colliders discussed so far. However, for low RH neutrino masses, especially pion decays provide very strong constraints. For $\tau$ decays in the $\tau \rightarrow \ell \gamma \nu$ channel, the limits from the muon channel are stronger than the ones from the electron channel due to their different experimental uncertainties. For a RH neutrino mass of $m_N \le 0.1 \,\text {GeV}$ and $\Lambda = 1 \,\text {TeV}$, we can set a limit of $|\alpha _{LNLe}| < 1.5$ on those components of $\alpha _{LNLe}$ which do not interfere, i.e. $\alpha _{LNLe}^{\ell \ell \tau }$ and $\alpha _{LNLe}^{\tau \tau \ell }$. For those components with negative interferences, we marginalise over the relevant other components when setting limits. We obtain a limit of $|\alpha _{LNLe}^{\ell \tau \ell }|, \, |\alpha _{LNLe}^{\tau \ell \ell }|, \, |\alpha _{LNLe}^{\ell \tau \tau }|, \, |\alpha _{LNLe}^{\tau \tau \ell }| < 1.7$.

The $\tau$ decay channel $\tau \rightarrow \pi N$ lets us constrain the coefficients $\alpha _{duNe}^{qq\tau }$ as well as the difference $|( \alpha _{QuNL}^{qq\tau } - \alpha _{LNQd}^{\tau qq} ) |$. The limits, which are largely independent of $m_N$ are presented in Tables 10 and 11.

Limits from pion decays can only be derived for low RH neutrino masses. In the region $m_N < m_\pi$, however, pion decays can set strong bounds. At $m_N < 0.1 \,\text {GeV}$, we find limits of $|\alpha _{duNe}^{qq\ell }|<7.7\times 10^{-4}$ and $|\alpha _{QuNL}^{qq\ell } -\alpha _{LNQd}^{\ell qq}| < 2.7\times 10^{-5}$, assuming $\Lambda = 1 \,\text {TeV}$. Combining the limit on the $|\alpha _{QuNL}^{qq\ell } -\alpha _{LNQd}^{\ell qq}|$ difference with the constraints from $pp \rightarrow \ell N$, allows us to reduce the limit on $|\alpha _{LNQd}^{\ell qq}| < 0.042$.

Overall, many of the Wilson coefficients of the $\nu$SMEFT parameter space can already be constrained to $\alpha /\Lambda ^2 \lesssim 1/\,\text {TeV}^2$. Our bounds are comparable to those obtained for very light RH neutrinos effectively stable at detector scales, from both LHC searches [41] as well as beta decay experiments [51]. (Note however that this latter reference uses a slightly different operator basis, so the comparison is not inmediate.) We should be aware, however, that some of these constraints are only valid for relatively small RH neutrino masses, e.g. $m_N < m_\tau$ or even $m_N < m_\pi$. Moreover, we note that out of the 37 independent coefficients in our $\nu$SMEFT four-fermion Lagrangian, 17 are still entirely unconstrained after our analyses in Sect. 4, namely

$$\begin{aligned} \begin{aligned}&\alpha _{NN}, \, \alpha _{eN}^{\ell \tau }, \, \alpha _{LN}^{\ell \tau }, \, \alpha _{eN}^{\tau \tau }, \, \alpha _{LN}^{\tau \tau }, \, \alpha _{LNLe}^{\tau \tau \tau }, \, \alpha _{LdQN}^{\tau qq} \\&\quad \alpha _{duNe}^{bt\tau }, \, \alpha _{LNQd}^{\tau 3b}, \, \alpha _{LdQN}^{\tau b3}, \, \alpha _{LNQd}^{ 3b\tau } \\&\quad \alpha _{uN}^{tt}, \, \alpha _{QN}^{33}, \, \alpha _{duNe}^{bt\ell }, \, \alpha _{LNQd}^{\ell 3b}, \, \alpha _{LdQN}^{\ell b3}, \, \alpha _{QuNL}^{3t\ell }. \end{aligned} \end{aligned}$$

(5.1)

While some of these operator coefficients, for instance those involving only the RH neutrinos and $\tau$ leptons, will be difficult to constrain, dedicated searches will be able to probe further directions of our parameter space. In the next sections, we will point out further possibilities to probe NP triggered by some of the coefficients in Eq. (5.1) using rare tau and top decays.

6 Projections for rare tau decays

The operators ${\mathcal {O}}_{eN}$ and ${\mathcal {O}}_{lN}$ contribute to the $\tau$ decay width in the $\tau \rightarrow \ell N N \rightarrow \ell \gamma \gamma \nu \nu$ channel:

$$\begin{aligned}&\Gamma (\tau \rightarrow \ell N N \rightarrow \ell \gamma \gamma \nu \nu )|_{m_N=0} \nonumber \\&\quad = \frac{m_\tau ^5}{512 \pi ^3 \Lambda ^4} \left[ (\alpha _{eN}^{\ell \tau })^2 + (\alpha _{lN}^{\ell \tau })^2 \right] . \end{aligned}$$

(6.1)

The decay width includes a factor 3 to account for the RH neutrino flavours. The mass dependence of this decay channel is given by¹⁰

$$\begin{aligned}&\left. \frac{\Gamma (x = \frac{m_N}{m_\tau })}{\Gamma (m_N=0)} \right| _{\tau \rightarrow \ell N N} = \sqrt{1-4x^2} (1 -14 x^2 - 2 x^4 - 12 x^6) \nonumber \\&\quad + 48 x^4 (1-x^4) {{\,\mathrm{arcCoth}\,}}\left( \frac{1}{\sqrt{1-4x^2}} \right) . \end{aligned}$$

(6.2)

To the best of our knowledge, there are no experimental bounds on $\tau \rightarrow \ell \gamma \gamma \nu (\nu )$. In the SM, the contribution to this channel comes from $\tau \rightarrow \ell \nu \nu \gamma \gamma$, i.e. two extra photons radiated in the decay $\tau \rightarrow \ell \nu \nu$. We expect the main backgrounds to this channel to come from mistags and fakes, compare Ref. [52], and will leave a dedicated study of this signature to experimentalists. To estimate the experimental sensitivity for this channel we can compare the uncertainties on the branching ratio of other $\tau$ decay channels in Ref. [34], see also Table 6. We find that the uncertainties on $\text {BR}(\tau \rightarrow e \nu \nu )$ and $\text {BR}(\tau \rightarrow e \gamma \nu \nu )$ are $\sigma _\text {BR}=0.04\%$ and $\sigma _\text {BR}=0.05\%$, respectively. For decays to a muon, $\text {BR}(\tau \rightarrow \mu \nu \nu )$ with or without an extra photon, as well as for decays to a $\pi ^0$ with subsequent decays to photons, the uncertainty on the branching ratio is (well) below $4\times 10^{-4}$. Therefore, we will conservatively assume an absolute experimental uncertainty of $\sigma _\text {BR}= 0.05\%$ on the channel $\tau \rightarrow \ell \gamma \gamma \nu (\nu )$ which translates into a $\pm 1.1 \times 10^{-15} \,\text {GeV}$ uncertainty on the experimental decay width.

For the limit setting, we allow the BSM contribution to the decay width to reach twice the assumed experimental uncertainty, i.e. $\Delta \Gamma ^\text {BSM} = 2.3 \times 10^{-15} \,\text {GeV}$. For $m_N=0.1\,\text {GeV}$ and $\Lambda =1\,\text {TeV}$, the Wilson coefficients $\alpha _{eN}^{\ell \tau }$ and $\alpha _{LN}^{\ell \tau }$ can be constrained to $|\alpha _{eN}^{\ell \tau }|, \, |\alpha _{L N}^{\ell \tau }| <~1.5$. If the experimental uncertainty on the branching ratio can be reduced to $10^{-5}$, the resulting limit is $|\alpha _{eN}^{\ell \tau }|, \, |\alpha _{LN}^{\ell \tau }| < 0.21$. The mass dependence of these limits is shown in the right panel of Fig. 2.

Fig. 2

RH neutrino mass dependence of the projected limits on $\alpha _{eN}^{\ell \tau }$ and $\alpha _{LN}^{\ell \tau }$ from $\tau$ decays in the $\tau \rightarrow \ell N N$ channel. We show the limits for two different assumptions on the experimental uncertainty of the branching ratio. The mass on the charged leptons has been neglected

Fig. 3

Normalised distribution of different observables in $t {\bar{t}}$ production. Top left: reconstructed W mass after the basic cuts. Top right: reconstructed mass of the SM-decaying top after the cut on $m_W^\text {rec}$. Bottom left: reconstructed mass of the rare decaying top after the cut on $m_{t_1}^\text {rec}$. Bottom right: angular separation between the lepton and the photon after the cut on $m_{t_1}^\text {rec}$. In all cases, the signal (background) appears in green (orange)

7 Projections for rare top decays

The weak sensitivity of current analyses to operators involving the top quark (see the end of Sect. 4.1) suggests that dedicated searches for signals triggered by these operators must be developed. We propose one such search strategy in top pair production, with one of the top quarks decaying as $t\rightarrow b\ell N, N\rightarrow \gamma \nu$, and the other via the dominant SM channel, $t\rightarrow bW$. We focus on the signal ensuing from the hadronic decay of the W.

The background is dominated by the process $t{\overline{t}}\gamma$. For event simulation, we employ the same tool chain as above, compare Sect. 4. We simulate the corresponding samples at $\sqrt{s}=13$ TeV with no parton level cuts for the signal and enforcing $p_T^\gamma > 10$ GeV for the background. The tree-level cross section of the signal, up to the rare top branching ratio, is $\sigma _s \approx 240$ pb for a top mass $m_t = 172.5$ GeV. For the background we obtain $\sigma _b \approx 0.68$ pb. We rescale both cross sections by an approximated NLO $\alpha _s$ K-factor of 1.5 [36] and we neglect detector effects. We implement the following search strategy: First, we require events to have exactly one (light) lepton with $p_T^\ell > 25$ GeV and $|\eta _\ell | < 2.5$, exactly one isolated photon with $p_T>12$ GeV and at least three jets with $p_T > 30$ GeV, of which exactly two must be b-tagged.¹¹ In addition, we require $E_T^\text {miss}> 30$ GeV. We will refer to this set of restrictions as basic cuts.

In a second step, we reconstruct the W boson from the two leading light jets. The normalised distribution of its invariant mass $m_W^\text {rec}$ is shown in the upper left panel of Fig. 3 in both the signal and the background. We require $m_W^\text {rec}$ to lie in the window $m_W^\text {rec} \in [50, 120]$ GeV.

We subsequently reconstruct the SM top from the W and the b-tagged jet closer to it in $\Delta R$. The normalised distribution of the corresponding mass $m_{t_1}^\text {rec}$ in both the signal and the background is depicted in the upper right panel of the Fig. 3. We require this observable to lie in the window [100, 200] GeV.

Finally, we reconstruct two variables that can discriminate well signal from background. The first one is the invariant mass of the reconstructed leptonic top, $m_{t_2}^\text {rec}$. This top is built from the lepton, the remaining b-tagged jet, the photon and the neutrino. (The x and y components of the neutrino are identified with the respective components of the missing energy; the longitudinal component is obtained under the collinear assumption by which the neutrino and the photon three-momenta are aligned because they are the two decay products of a very light particle, N.) This observable peaks around the top quark mass $\sim 172$ GeV in the signal while it is more spread in the background; see the bottom left panel of Fig. 3.

The second discriminating variable is the $\Delta R$ separation between the lepton and the photon, $\Delta R(\ell ,\gamma )$. Because these two objects originate from the decay of the same top quark in the signal, this variable is peaked to smaller values in the signal than in the background, where it is flatter; see the bottom right panel of the aforementioned Fig. 3.

Fig. 4

Left: LHC sensitivity to $t\rightarrow b\ell N$ as a function of the branching ratio for two values of the collected luminosity. Right: Luminosity required to probe $t\rightarrow b\ell N$ to $2\sigma$ and $5\sigma$ as a function of the branching ratio. In both cases we rely on the analysis based on the asymmetry defined in Eq. (7.1)

These two variables are however highly correlated. Thus, for example, a cut on $m_{t_2}^\text {rec} < 200$ GeV reduces significantly the difference between signal and background in $\Delta (\ell ,\gamma )$. For this reason, we propose two different statistical analyses, each using just one of these variables at a time. First, we just count the number of events passing the cut on $150\,\, \text {GeV}< m_{t_2}^\text {rec}<200$ GeV. The efficiencies for selecting signal and background events in this region are $\sim 0.013$ and $\sim 0.0073$, respectively. (The small difference between signal and background is mostly due to the different parton-level cuts.) Thus, for a luminosity of $\mathcal{L}=3$ ab$^{-1}$ and assuming a 10% uncertainty on the background, we obtain that $\mathcal {B}(t\rightarrow b\ell N) > 1.6\times 10^{-4}$ can be probed at the 95% CL upon using the CL$_s$ method.

A potentially more robust analysis relies on the asymmetry

$$\begin{aligned} A= & {} \frac{N_+ - N_-}{N_+ + N_-} \nonumber \\= & {} \frac{N(\Delta R(\ell , \gamma )> 2) - N(\Delta R(\ell , \gamma ) < 2)}{N(\Delta R(\ell , \gamma )> 2) + N(\Delta R(\ell , \gamma ) > 2)}. \end{aligned}$$

(7.1)

Systematic uncertainties are expected to cancel in this ratio. The efficiency for selecting events in the region $N_+ (N_-)$ (defined as the ratio of events that pass all cuts in each region over the total number of events before the basic cuts) is of about 0.0055 (0.014) in the signal and 0.028 (0.021) in the background.

In the left panel of Fig. 4 we show the CL (in number of standard deviations) to which the signal can be probed depending on $\mathcal {B}(t\rightarrow b\ell N)$ and for two different assumptions on the collected luminosity. In the right panel, we plot the luminosity required to test the signal at two different levels of confidence, again as a function of the top’s rare decay branching ratio.

For $\mathcal{L} = 3$ ab$^{-1}$, the value of A in the signal departs by more than two sigmas from the SM, i.e. $A_s < A_b - 2\sigma (A_b)$, for $\mathcal {B}(t\rightarrow b\ell N) > 6.6\times 10^{-5}$. Under the flavour-universality assumption (the top decays into both $eN_i$ and $\mu N_i$, with $i=1,2,3$), and using Eq. (2.27) in Ref. [41], the expected limit on $\mathcal {B}(t\rightarrow b\ell N)$ translates into $|\alpha _{duNe}^{bt\ell }|<2.3$, $|\alpha _{QuNL}^{3t\ell }|<4.5$ and $|\alpha _{LdQN}^{\ell b3}|$, $|\alpha _{LNQd}^{\ell 3b}|<5.1$, for $\Lambda =1$ TeV. For setting bounds on the last two operators we have marginalised over the interfering one.

8 Conclusions

In this paper we have studied the phenomenology of the low-scale see-saw EFT, in the regime in which the sterile neutrinos N decay as $N\rightarrow \nu \gamma$. With the aim of unravelling in which directions of the parameter space new physics can hide, we have derived constraints on the different Wilson coefficients, with special attention to four-fermion operators as they can arise at tree level in UV completions of the see-saw model.

For this goal we have relied on data from LHC searches for one lepton, one photon and missing energy and two photons and missing energy; on measurements of different pion and tau decays; as well as on LEP data from analyses of one or multiple photons and missing energy. The strongest limits result from LHC searches and, in the low-$m_N$ regime, also from pion decays. Operator coefficients constrained from these processes obtain bounds of $\alpha /\Lambda ^2 \lesssim 0.2 \,\text {TeV}^{-2}$. LEP limits are below $\alpha /\Lambda ^2 \lesssim 1 \,\text {TeV}^{-2}$.

We note that, in deriving these bounds, we have assumed flavour universality in N as well as in the light fermions and quarks; and we allowed LFV only in tau-to-light-lepton transitions. Nonetheless, our results can trivially be interpreted under different assumptions. For example, if the three N flavours couple differently to the SM fermions, then the bound on $\alpha _{uN}^{1111}$ is just $\sqrt{3} \approx 1.73$ times weaker than the one we provide on $\alpha _{uN}^{qq}$. Likewise, if moreover flavour-universality in the light quarks is abandoned, the bound on $\alpha _{uN}^{2211}$ can be estimated from $c{\bar{c}} \rightarrow NN$ versus $u{\bar{u}}\rightarrow NN$ as 4.6 times the limit on $\alpha _{uN}^{qq}$ due to the PDF suppression.

Applying our results to UV models where several operators arise simultaneously (and therefore the bounds are strengthened) is also straightforward, as we have provided master equations to straightforwardly predict the number of signal events in the different signal regions as well as quoted the upper limit on the latter in each case.

Still, there are operators coefficients that current data do not bound. These include the parameters $\alpha _{eN}^{\ell \tau }$ and $\alpha _{LN}^{\ell \tau }$ which trigger the tau decay $\tau \rightarrow \ell \gamma \gamma \nu \nu$. The resulting limits very much depend on the estimated experimental sensitivity of the branching ratio, which we conservatively assume to be $\sim 0.05\%$. The emerging bounds are $|\alpha _{eN}^{\ell \tau }|, \, |\alpha _{L N}^{\ell \tau }| <~1.5$ for $\Lambda = 1 \,\text {TeV}$. To push these limits below $\alpha /\Lambda ^2 \lesssim 1 \,\text {TeV}^{-2}$, an experimental sensitivity on the branching ratio below $\sigma _\text {BR} \lesssim 0.023 \%$ has to be reached. Other operator coefficients that are very weakly constrained by current data are $\alpha _{duNe}^{bt\ell }$, $\alpha _{LdQN}^{\ell b 3}$, $\alpha _{LNQd}^{\ell 3 b}$ and $\alpha _{QuNL}^{3t\ell }$, which drive the top decay $t\rightarrow b\ell \gamma \nu$. We have provided a dedicated analysis to test this channel in top pair production at the LHC, and found that branching ratios as small as $6.6\times 10^{-5}$ could be probed at the 95% CL in the high-luminosity phase. This in turn translates to a potential upper bound on $\alpha _{duNe}^{bt\ell }$ of $\sim 2.3$ for $\Lambda = 1$ TeV; and about twice weaker for the others.

In total, 11 out of 37 four-fermion operator coefficients in our $\nu$SMEFT Lagrangian remain unconstrained even after our additional analyses. In particular, this concerns operator coefficients describing couplings of tau leptons to the third quark generation, which could potentially be bounded by analyses of top decays to tau leptons, photons and missing energy ¹². Coefficients describing $\tau \tau NN$, $\tau \tau tt$ and $\tau \tau bb$ couplings are not constrained either. We leave studies to bound these directions of the parameter space for future work.

Altogether, our work highlights in particular the importance of performing dedicated searches for new rare tau and top decays.

Appendices

A Explicit Lagrangian

In order to further clarify our notation, we write here explicitly the full $\nu$SMEFT dimension-six Lagrangian indicating all independent Wilson coefficients according to our flavour assumptions.

The relevant bosonic Lagrangian is

$$\begin{aligned} L&= {\alpha _{HN}} \, \mathcal {O}_{HN}^{ii} +{\alpha _{HNe}^{\ell }}\, (\mathcal {O}_{HNe}^{i1}+\mathcal {O}_{HNe}^{i2}) +{\alpha _{HNe}^{\tau }}\, \mathcal {O}_{HNe}^{i3}\\&\quad +{\alpha _{NA}^{\ell }}\, (\mathcal {O}_{NA}^{1i}+\mathcal {O}_{NA}^{2i}) +{\alpha _{NA}^{\tau }}\, \mathcal {O}_{NA}^{3i}\\&\quad +{\alpha _{NZ}^{\ell }}\, (\mathcal {O}_{NZ}^{1i}+\mathcal {O}_{NZ}^{2i}) +{\alpha _{NZ}^{\tau }}\, \mathcal {O}_{NZ}^{3i}, \end{aligned}$$

with $i=1,2,3$.

Fig. 5

Dependence of the pion decay width on the neutrino mass $m_N$ for operators with axial (left) and pseudo-scalar (right) couplings

Fig. 6

RH neutrino mass dependence of the $\tau$ decay width in different decay channels. Left: decay width of $\tau \rightarrow \ell \nu N$ and $\tau \rightarrow \ell N N$ (rescaled) where the mass on the charged leptons has been neglected. Right: decay width of $\tau \rightarrow \pi N$ for operators with axial and pseudo-scalar structures

And for the relevant four-fermion operators we have:

$$\begin{aligned} L&= {\alpha _{NN}}\, \mathcal {O}_{NN}^{iijj} + {\alpha _{eN}^{\ell \ell }}\, (\mathcal {O}_{eN}^{11ii}+\mathcal {O}_{eN}^{22ii}) \\&\quad + {\alpha _{eN}^{\ell \tau }}\, (\mathcal {O}_{eN}^{13ii}+\mathcal {O}_{eN}^{23ii}+\mathcal {O}_{eN}^{31ii}+\mathcal {O}_{eN}^{32ii}) + {\alpha _{eN}^{\tau \tau }}\, \mathcal {O}_{eN}^{33ii}\\&\quad +{\alpha _{uN}^{qq}}\, (\mathcal {O}_{uN}^{11ii}+\mathcal {O}_{uN}^{22ii}) + {\alpha _{uN}^{tt}}\, \mathcal {O}_{uN}^{33ii} \\&\quad + {\alpha _{dN}^{qq}}\, (\mathcal {O}_{dN}^{11ii}+\mathcal {O}_{dN}^{22ii}) + {\alpha _{dN}^{bb}}\, \mathcal {O}_{dN}^{33ii}\\&\quad +\bigg [{\alpha _{duNe}^{qq\ell }}\, (\mathcal {O}_{duNe}^{11i1} + \mathcal {O}_{duNe}^{11i2} + \mathcal {O}_{duNe}^{22i1} + \mathcal {O}_{duNe}^{22i2}) \\&\quad + {\alpha _{duNe}^{qq\tau }}\, (\mathcal {O}_{duNe}^{11i3} + \mathcal {O}_{duNe}^{22i3})+ {\alpha _{duNe}^{bt\ell }}\, (\mathcal {O}_{duNe}^{33i1} + \mathcal {O}_{duNe}^{33i2}) \\&\quad + {\alpha _{duNe}^{bt\tau }}\, (\mathcal {O}_{duNe}^{33i3} + \mathcal {O}_{duNe}^{33i3}) + \text {h.c.}\bigg ] \\&\quad +{\alpha _{LN}^{\ell \ell }}\, (\mathcal {O}_{LN}^{11ii}+\mathcal {O}_{LN}^{22ii})\\&\quad + {\alpha _{LN}^{\ell \tau }}\, (\mathcal {O}_{LN}^{13ii}+\mathcal {O}_{LN}^{23ii}+\mathcal {O}_{LN}^{31ii}+\mathcal {O}_{LN}^{32ii}) + {\alpha _{LN}^{\tau \tau }}\, \mathcal {O}_{LN}^{33ii} \\&\quad + {\alpha _{QN}^{qq}}\, (\mathcal {O}_{QN}^{11ii}+\mathcal {O}_{uN}^{22ii}) + {\alpha _{QN}^{33}}\, \mathcal {O}_{QN}^{33ii}\\&\quad + \bigg [{\alpha _{LNLe}^{\ell \ell \ell }}\, (\mathcal {O}_{LNLe}^{1i11} + \mathcal {O}_{LNLe}^{2i22})\\&\quad + {\alpha _{LNLe}^{\ell \ell \tau }}\, (\mathcal {O}_{LNLe}^{1i13} + \mathcal {O}_{LNLe}^{2i23})\\&\quad + {\alpha _{LNLe}^{\ell \tau \ell }}\, (\mathcal {O}_{LNLe}^{1i31} + \mathcal {O}_{LNLe}^{2i32})\\&\quad + {\alpha _{LNLe}^{\ell \tau \tau }}\, (\mathcal {O}_{LNLe}^{1i33} + \mathcal {O}_{LNLe}^{2i33})\\&\quad + {\alpha _{LNLe}^{\tau \ell \ell }}\, (\mathcal {O}_{LNLe}^{3i11} + \mathcal {O}_{LNLe}^{3i22})\\&\quad + {\alpha _{LNLe}^{\tau \ell \tau }}\, (\mathcal {O}_{LNLe}^{3i13} + \mathcal {O}_{LNLe}^{3i23}) + {\alpha _{LNLe}^{\tau \tau \ell }}\, (\mathcal {O}_{LNLe}^{3i31} \\&\quad + \mathcal {O}_{LNLe}^{3i32})+ {\alpha _{LNLe}^{\tau \tau \tau }}\, \mathcal {O}_{LNLe}^{3i33}\\&\quad + {\alpha _{LNQd}^{\ell qq}}\, (\mathcal {O}_{LNQd}^{1i11} + \mathcal {O}_{LNQd}^{1i22} + \mathcal {O}_{LNQd}^{2i11} + \mathcal {O}_{LNQd}^{2i22})\\&\quad +{\alpha _{LNQd}^{\ell 3b}}\, (\mathcal {O}_{LNQd}^{1i33} + \mathcal {O}_{LNQd}^{2i33})\\&\quad +{\alpha _{LNQd}^{\tau qq}}\, (\mathcal {O}_{LNQd}^{3i11} + \mathcal {O}_{LNQd}^{3i22}) +{\alpha _{LNQd}^{\tau 3b}}\, \mathcal {O}_{LNQd}^{3i33}\\&\quad +{\alpha _{LdQN}^{\ell qq}}\, (\mathcal {O}_{LdQN}^{111i} + \mathcal {O}_{LdQN}^{122i} + \mathcal {O}_{LdQN}^{211i} + \mathcal {O}_{LdQN}^{22i})\\&\quad +{\alpha _{LdQN}^{\ell b3}}\, (\mathcal {O}_{LdQN}^{133i} + \mathcal {O}_{LdQN}^{233i})\\&\quad +{\alpha _{LdQN}^{\tau qq}}\, (\mathcal {O}_{LdQN}^{311i} + \mathcal {O}_{LdQN}^{322i})+{\alpha _{LdQN}^{\tau b3}}\, \mathcal {O}_{LdQN}^{333i}\\&\quad +{\alpha _{QuNL}^{qq\ell }}\, (\mathcal {O}_{QuNL}^{11i1} + \mathcal {O}_{QuNL}^{11i2} + \mathcal {O}_{QuNL}^{22i1} + \mathcal {O}_{QuNL}^{22i2})\\&\quad +{\alpha _{QuNL}^{qq\tau }}\, (\mathcal {O}_{QuNL}^{11i3} + \mathcal {O}_{QuNL}^{22i3})\\&\quad +{\alpha _{QuNL}^{3t\ell }}\, (\mathcal {O}_{QuNL}^{33i1} + \mathcal {O}_{QuNL}^{33i2})\\&\quad +{\alpha _{QuNL}^{3t\tau }}\, \mathcal {O}_{QuNL}^{33ie} + \text {h.c.}\bigg ]~. \end{aligned}$$

B Mass dependence of pion and tau decay widths

In Fig. 5, we explicitly show the mass dependence of the pion decay width in the $\pi \rightarrow \ell N$ channel for operators with vector and pseudo-scalar couplings.

In Fig. 6, we explicitly show the mass dependence of the $\tau$ decay width in the $\tau \rightarrow \ell N$, $\tau \rightarrow N N$ and $\tau \rightarrow \pi N$ channels.