Abstract
In the paper we develop, in the CGC approach, a new mechanism for quarkonia production in events with high multiplicity of the soft produced particles. In this mechanism both \(J/\varPsi \) and soft hadrons are produced at short distances \(r\, \propto \,1/Q_s\), where \(Q_s\) is the saturation scale, which is considered to be proportional to the multiplicity of soft hadrons. Using this approach, we analyze the vigorously growing multiplicity dependence of quarkonia production, which was recently discovered by the STAR and ALICE collaborations. We demonstrate that this result presents a strong evidence in favor of multigluon fusion mechanisms of the quarkonia states. We analyze in detail the contribution of the 3-gluon fusion mechanism and demonstrate that it describes correctly all the available experimental data on the multiplicity dependence of \(J/\psi \) meson production. We also make predictions for other quarkonia states, such as \(\psi (2S)\) and \(\varUpsilon (1S)\), and find that the multiplicity dependence of these states should be similar to that of the \(J/\psi \) meson. Finally, we discuss an experimental setup in which the very strong multiplicity dependence could be observed. This observation would be a strong evidence in favor of the CGC approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The production mechanisms of hadrons which contain heavy quarks, especially charmonia states, remains one of the long-standing puzzles of high energy particle physics. The conventional paradigm considers that the dominant contribution comes from gluon-gluon fusion, and that the heavy quarks formed in the process emit soft gluons in order to hadronize into quarkonia states [1,2,3,4,5,6]. This picture gives reasonable estimates for the total and differential cross-sections, within uncertainty of Long Distance Matrix Elements (LDMEs) of quarkonia states [7,8,9,10,11,12,13,14].
Nevertheless, the above described picture was challenged by recent measurements of the multiplicity dependence of certain heavy mesons. As was found recently by the STAR [15, 16] and ALICE [17, 18] collaborations, the \(J/\psi \) yields grow rapidly as function of the multiplicity of co-produced charged particles. Since these charged hadrons are predominantly soft, the description of their production presents in general a complicated theoretical problem in the realm of non-perturbative QCD. For this reason up to now there have been few attempts to describe theoretically the multiplicity dependence of quarkonia production [19, 20]. This problem has also been addressed by using Monte Carlo event generators [21,22,23,24], which combine perturbative QCD with a phenomenological treatment of the hadronization processes. However, recent data [18] clearly demonstrated that none of the above-mentioned approaches could predict correctly the observed yields of \(J/\psi \) mesons at large multiplicities. As we will show below, the large multiplicity data present also a challenge for all the approaches based on the gluon-gluon fusion mechanism.
Recently, in [25], we suggested that the experimentally observed multiplicity dependence of quarkonia production [18, 26] could indicate a sizable contribution of the multipomeron mechanisms.Footnote 1 This claim was inspired by the observation that each pomeron on the average gives the same contribution to the observed multiplicity, and for this reason the events with large multiplicities potentially might get enhanced contributions from configurations with additional pomerons. While it is expected that such higher-order contributions should be suppressed in the heavy quark mass limit, for the 3-pomeron term such suppression does not work due to quantum numbers of the S-wave quarkonia [25, 27, 28]. Indeed, as we can see from Fig. 1, formally the two-pomeron and three-pomeron mechanisms contribute at the same order in the strong coupling \(\alpha _{s}\). For a long time it was believed that the two-pomeron mechanism dominates, since the softness of the emitted gluons in the two-pomeron mechanism implies that the suppression in the heavy quark mass limit is milder than expected, from \({\mathcal {O}}(\alpha _{s})\)-counting. However, the contribution of the three-pomeron mechanism is also enhanced at high energies, due to the additional t-channel pomeron and the associated increase of gluon density. As was illustrated in [25, 27, 28], the latter mechanism provides a reasonable description of the rapidity and the \(p_{T}\)-dependence of produced charmonia,Footnote 2 as well as describes qualitatively the main features of the multiplicity dependence.
The goal of this paper is to analyze in detail the multiplicity dependence in the framework of the CGC/saturation approach, compare its predictions with available experimental data and make predictions for the forthcoming measurements.
As we have mentioned, the relation between the production of quarkonia, which comes from short distances, and of soft hadrons, which originates from long distances, is a very complicated problem for theoretical approaches due to the present embryonic state of non-perturbative QCD. One possible solution is the building of Monte Carlo programs, which are based on perturbative QCD and on the phenomenological experience in the treatment of the hadronization processes. In this paper we suggest an alternative approximation, based on the CGC approach, which being an effective QCD theory at high energies, states that a new phase of QCD: a dense system of partons (gluons and quarks) is produced in collisions with a new characteristic scale: the saturation momentum \(Q_s(W)\), which increases as a function of energy W [37,38,39,40,41]. At LHC energies, the scale \(Q_{s}(W)\) is much larger than the scale of soft physics \(\mu _{\mathrm{soft}}\), and therefore the dynamics of the events at those energies can be treated theoretically in the framework of the CGC approach. Nevertheless, the transition from this system of partons to the measured state of hadrons is still an unsolved problem, and for this reason at the moment we need to use a pure phenomenological input for the long distance non-perturbative physics. Hence, our model for multi-particle production at high energies consists of a two stage scenario. The first stage is the production of a gluon with transverse momentum \(p_T \,\sim \,Q_s(W) \), which is much larger than the scale of soft physics \(\mu _\mathrm{soft}\), and therefore can be treated theoretically in the framework of the CGC approach. The second stage is the hadronization of the produced hard gluons. In what follows we will rely on the widely used hypothesis of Local Parton–Hadron Duality (LPHD) [42,43,44], which assumes that the distributions of observed hadrons differ from the distributions of partonic mini-jets only by a numerical constant. In addition, we will assume that the correlations between hadrons in rapidity are long range in nature and stem from the production of parton showers, described by BFKL Pomerons. The experimental data show that the short range correlations are small [45,46,47], in accord with the expectation from CGC models for high energy scattering [48].
The paper is structured as follows. In the next Sect. 2 we describe a framework for quarkonia production in the CGC/Saturation approach. In Sect. 3 we outline our main theoretical results and make numerical estimates of the multiplicity dependence, compare with available experimental data, and make predictions for the \(\psi (2S)\) and \(\varUpsilon (1S)\) quarkonia. Finally, in Sect. 4 we draw conclusions and discuss some open challenges in our approach.
2 Three-pomeron contribution to charmonia production
The contribution of the three-pomeron mechanism to the cross-section of the S-wave quarkonia production is given by [25]
where y is the rapidity of the produced quarkonia, measured in the center-of-mass frame of the colliding protons; \(\varPsi _{M}(r,\,z)\) is the light-cone wave function of the quarkonium M (\(M=J/\psi ,\,\psi (2S),\,\varUpsilon (1S)\)) with transverse separation between quarks r; and z is the light-cone fraction carried by the quark (see Appendix B for its parametrization). In the heavy quark limit the wave function \(\varPsi _{g}\) of the heavy quark-antiquark pair might be approximated by the perturbative expressions from Ref. [49] (see Appendix B for details). We also use the notation \(N_{G}=2N\,-\,N^{2}\), where \(N\left( y,\,\mathbf {r}\right) \equiv \int d^{2}b\,N\left( y,r,b\right) \) is the dipole scattering amplitude. The factors in the first line of (1) are explained in detail in [25] and are related to the gluon uPDFs and DPDFs in the proton. The nonperturbative factor \(\sim \int d^{2}Q\,S_{h}^{2}\left( Q_{T}\right) \) is important for the study of the absolute cross-sections considered in [25], although eventually it will cancel in the self-normalized observables considered in this paper. The second factor includes the gluon PDF \(\,x_{1}G\left( x_{1},\mu _{F}\right) ,\) which we take at the scale \(\mu _{F}\,\approx 2\,m_{c}\). In LHC kinematics and at central rapidities (our principal interest) this scale significantly exceeds the saturation scale \(Q_{s}(x)\), which justifies the use of the two-gluon approximation. However, in the kinematics of small-\(x_{g}\) (large energies) there are sizable non-perturbative (nonlinear) corrections to evolution in the CGC/Saturation approach. In this kinematics the corresponding scale \(\mu _{F}\) should be taken at the saturation momentum \(Q_{s}\), while the gluon PDF \(x_{1}G\left( x_{1},\,\mu _{F}\right) \) is in this approach closely related to the dipole scattering amplitude \(N\left( y,r\right) =\int d^{2}b\,N\left( y,r,b\right) \) as [50, 51]
where \(y=\ln (1/x)\). Equation (3) might be inverted and gives the gluon uPDF in terms of the dipole amplitude,
This result allows us to rewrite (1) in a more symmetric form, entirely in terms of the dipole amplitude N,
which will be used for analysis below. While the relations (4, 5) are valid only when both xG and \(\phi \) satisfy the linear evolution equations, Eq. (6) is the correct generalization of Eq. (1) for the BK non-linear evolution (see Refs. [33,34,35,36]). Therefore, Eq. (6) correctly accounts for the diagrams of Fig. 2b, which is the goal of this paper.
3 Multiplicity dependence
3.1 Theoretical framework
3.1.1 Dipole scattering amplitude in CGC approach
In the CGC/saturation approach the dipole amplitude \(N\,\left( y,\mathbf {r},\,\mathbf {b}\right) \) should satisfy the non-linear Balitsky–Kovchegov (BK) equation [52,53,54] for dipoles of small size r. In the saturation region this solution exhibits a geometric scaling, being a function of one variable \(\tau \,=\,r^{2}\,Q_{s}^{2}\), where \(Q_{s}\) is the saturation scale [55,56,57,58].
The main observation of Ref. [25] is that the typical r and \(r'\) in Eq. (6) are in the vicinity of the saturation scale \( r^2\,Q^2_s \,\sim \,1\) (\(r'^2 Q^2_s \,\sim \,1\)), where we know the general solution of the non-linear BK equation [59]. It has the form:
At long distances the scattering amplitude N approaches 1, having the following form [58]:
where \(\kappa \) is a constant (see Refs. [50, 58])
Hence the difference of the amplitude in Eq. 6 at large \(r^2 Q_s^2 \,\gg \,1\) vanishes as
where \(z_{\pm } \,=\,\ln \left( \left( \mathbf {r} \pm \mathbf {r}'\right) ^2 \,Q^2_s/4\right) \). Therefore, one can see that at large \(\tau \) \(\delta N^2 \) vanishes.
However, to find the behavior of \(\delta N^2\) at moderate \(\tau \) we need to solve the non-linear Balitsky–Kovchegov [52,53,54] equation in the entire kinematic region. Generally speaking, the BFKL kernel (\(\chi (\gamma )\) in \(\gamma \)-representation) takes into account all twists contributions. Nevertheless, for our estimates we restrict ourselves to the leading twist term only, which has the form [58] (see also Ref. [48]):
As indicated in Eq. (10) we have two types of logs: \( \Big ({\bar{\alpha }}_S\ln \left( r\,\varLambda _{QCD}\right) \Big )^n\) in the perturbative QCD kinematic region, where \(r\,Q_s\left( Y,b\right) \,\,\equiv \,\,\tau \,\,\ll \,\,1\); and \( \Big ({\bar{\alpha }}_S\ln \left( r \,Q_s\left( Y,b \right) \right) \Big )^n\) inside the saturation domain (\(\tau \,\gg \,1\)), where \(Q_s\left( Y, b \right) \) denotes the saturation scale. To sum these logs it is necessary to modify the BFKL kernel in different ways in the two kinematic regions, as shown in Eq. (10).
In the saturation region \( r^2 \,Q^2_s \,>\,1\) it has been shown [55,56,57,58] that the scattering amplitude manifests geometric scaling behavior and the BK equation with the simplified kernel of Eq. (10) can be re-written in the form [58]:
where \({\widetilde{N}}\left( z \right) \,=\,\int ^z d z' N\left( z'\right) \) and \(z \,=\,\ln \tau ^2\) with \(\tau = r\,Q_s\).
In Ref. [58] it has been shown that the solution of this equation takes the form
for the function \(\phi \) which has been defined as
The value of the constant C has to be found from matching with the region \(\tau \,<\,1\). For study of the small \(\phi \sim \phi _0\) we can see that we should choose \(C=0\). Indeed, in this case the solution at small \(\phi \) has a form
which coincides with the general solution of Eq. (7) for the region \(\tau \,<\,1\) at small \(\phi _0 \,=\,N_0\,\ll \,1\).
\(\varDelta N^2 \equiv \int d \varphi \,\delta N^2\) versus \(\tau = r \,Q_s\) at different value of \(\tau ' = r' Q_s\). \(\varphi \) is the angle between \(\mathbf {r}\) and \(\mathbf {r}'\). For \(N_G\) we use the solution to Eq. (12) with \(N_0\) = 0.05. The red line presents the overlapping integral (see Appendix B) with \(r=r'\) for \(Q^2_s = 9 \,\hbox {GeV}^2\)
In Fig. 2 we plot the solution of Eq. (12). One can see that the function
which enters the master equation (see Eq. (6)),Footnote 3 decreases with growing \(\tau \) and the largest contribution stems from the region \(\tau \sim \tau '\). Therefore, the estimates from Eq. (11) supports our main idea that the typical distances in Eq. (6) are in the vicinity of the saturation scale where both \(\tau \sim 1\) and \(\tau ' \sim 1\). The solid curve in Fig. 2 gives \(\varDelta N^2\) at \(r =r'\) which corresponds to the main contribution to Eq. (6). One can see that at \(\tau = 1 \div 2\) this curve shows \(\tau ^{{{\bar{\gamma }}}}\) behaviour. The red curve presents the behaviour of the overlapping integral which is a function of \(r = \tau /Q_s\) but not of \(\tau \). In the figure we plot this function fixing \(Q^2_s = 9 \,GeV^2 \) which corresponds to large \(n \approx 10\div 12\). One can see that the main contribution stems from the region of \(\tau \), where we can use \(N\,\propto \,\tau ^{\bar{\gamma }}\).
3.1.2 Saturation model
There are different phenomenological parametrizations for N available in the literature. One of such parametrizations, which we will use for our numerical estimates, is the CGC parametrization [60] (for sake of definiteness, we use the first set of parameters from Table I in [60]). As we have shown, the dominant contribution to the integrals over \(r,\,r'\) in (6) comes from the vicinity of the saturation scale, \(|r|\sim |r'|\sim Q_{s}^{-1}\), where the dipole amplitude is given by [59] \(N\left( r,\,x\right) \sim N_{0}\,\tau ^{{\bar{\gamma }}}\), with \(\tau \equiv r\,Q_{s}(x)\). For this reason in what follows we will also use the parametrization
for semi-analytical estimates of multiplicity dependences. Note that in Eq. (16) we restricted \(\tau \, < \,2\) in accord with Fig. 2. As we can see from the structure of the cross-section (6), the contribution of the large \(r\,> \,4\,Q_{s}^{-1}(x)\) (saturated region) is negligible, for this reason the parametrization (16) gives results close to the realistic dipole amplitude [60] (see Appendix C for more details).
3.1.3 Generalities
As was illustrated in [25], the quarkonia production cross-section (6) with CGC dipole parametrization provides a very reasonable description of the shapes of produced charmonia as a function of rapidity and transverse momentum, as well as predicts that the suggested mechanism gives the dominant contribution to \(J/\psi \) yields. The description of the multiplicity dependence presents more challenges at the conceptual level, because there are different mechanisms to produce enhanced number of charged particles \(N_{\mathrm{ch}}\). The probability of multiplicity fluctuations decreases rapidly as a function of the number of produced charged particles \(N_{\mathrm{ch}}\) [61], and for this reason for the study of the multiplicity dependence it is more common to use a normalized ratio [18]
where \(n=N_{\mathrm{ch}}/\langle N_{\mathrm{ch}}\rangle \) is the relative enhancement of the number of charged particles in the bin, \(w\left( N_{J/\psi }\right) /\left\langle w\left( N_{J/\psi }\right) \right\rangle \) and \(w\left( N_{\mathrm{ch}}\right) /\left\langle w\left( N_{\mathrm{ch}}\right) \right\rangle \) are the self-normalized yields of \(J/\psi \) and charged particles (minimal bias events) in a given multiplicity class; \(d\sigma _{J/\psi }(y,\,\sqrt{s},\,n)\) is the production cross-sections for \(J/\psi \) with rapidity y and \(\langle N_{\mathrm{ch}}\rangle =\varDelta \eta \,dN_{\mathrm{ch}}/d\eta \) charged particles in the pseudorapidity window \((\eta -\varDelta \eta /2,\,\,\eta +\varDelta \eta /2)\).
3.1.4 Traditional approach
In our scenario of multi-particle production, described in the introduction, the enhanced multiplicity \(N_{\mathrm{ch}}>\langle N_{\mathrm{ch}}\rangle \) is due to contributions from multigluon (multipomeron) configurations, as shown in Fig. 3. This mechanism leads to the multiplicity dependence
where \({\tilde{P}}\left( N_{{\mathbb {P}}}\right) \) is the probability to produce \(N_{{\mathbb {P}}}\) BFKL cascades (cut pomerons). The latter parameter \(N_{{\mathbb {P}}}\) is proportional to the number of charged particles \(N_{\mathrm{ch}}\), due to the LPHD hypothesis. In the case of inclusive charged particles production in a given multiplicity class, due to the LPHD hypothesis the production cross-section is given by
where c is some numerical coefficient, so the yield \(w\left( N_{\mathrm{ch}}\right) /\left\langle w\left( N_{\mathrm{ch}}\right) \right\rangle \) is given by \({\tilde{P}}\left( N_{{\mathbb {P}}}\right) .\) The ratio (17) evaluated with this mechanism should have a linear dependence on \(n=N_{\mathrm{ch}}/\langle N_{\mathrm{ch}}\rangle \sim N_{{\mathbb {P}}}/\langle N_{{\mathbb {P}}}\rangle \), which reflects the simple physics that \(J/\varPsi \) can be produced by three Pomeron mechanism in each BFKL cascade. The experimental observation [26, 62] that the n-dependence grows faster than linearly implies that other mechanisms must give important contributions.
3.1.5 Dependence of the saturation scale on the multiplicity of the soft hadrons
In the 3-pomeron mechanism analyzed in this paper we expect that the multiplicity dependence is enhanced due to a larger average number of particles produced from each pomeron (see the right panel of the Fig. 3). We expect that each such cascade (“pomeron”) should satisfy the nonlinear Balitsky-Kovchegov equation. The increased multiplicity in individual pomerons leads to a modification of the dipole amplitude and the saturation scale \(Q_{s}\)
As was shown in [37,38,39,40,41, 50, 63,64,65,66], the saturation scale \(Q_{s}\) is closely related to the gluon density of the target,
For high multiplicity events, in view of the LPHD hypothesis, we expect that the density of gluons in the rhs of (22) should grow linearly as a function of multiplicity [50, 63,64,65,66,67,68,69,70], so we expect that the multiplicity dependence of the saturation scale is given by
While at LHC energies it is expected that the typical values of saturation scale \(Q_{s}\left( x,\,b\right) \) fall into the range 0.5–1 \(\mathrm{GeV}\), from (24) we can see that in events with enhanced multiplicity this parameter might exceed the values of heavy quark mass \(m_{Q}\) and lead to an interplay of large-\(Q_{s}\) and large-\(m_{Q}\) limits. Thus the study of the high-multiplicity events gives us access to a new regime which otherwise would require significantly higher energies.
To the best of our knowledge, currently there is no microscopic first-principle evaluation of the dipole amplitude \(N\left( y,\,\mathbf {r},\,\mathbf {b},\,n\right) .\) For this reason in what follows we assume that the modification of the dipole amplitude on n is properly taken into account only by modification of the saturation scale (24).
We can derive Eq. (24) directly from our scenario for multi-particle production in CGC approach (see the introduction). Indeed, the multiplicity of soft hadrons in this scenario stems from the diagrams of Fig. 2, and is equal to
where \(N_{\mathbb {P}}\) is the number of cut pomerons (BFKL cascades), and c is a numerical coefficient of order one. Taking into account that the distribution \(dN_{\mathrm{ch}}/dy\) is almost flat, we may approximate \(n=N_{\mathrm{ch}}/\langle N_{\mathrm{ch}}\rangle \approx (dN_{\mathrm{ch}}/dy)/\langle dN_{\mathrm{ch}}/dy\rangle \), so the assumption (24) agrees with (25) up to possible logarithmic corrections, which stem from the scale dependence of \({\bar{\alpha }}_{S}\) in the denominator of (25). Note that in Eq.24 we replace \( c\frac{d N^{NFKL}_{parton}}{d Y}\) by \( Q^2_s/\alpha _S(Q_s)\) in accord with the KLN formula for hadron-hadron collision. The parametrization of (24) might be interpreted as a choice of a fixed coupling \({\bar{\alpha }}_{S}\) in (25): \({\bar{\alpha }}_S(Q_s)\), where \(Q_s\) is the saturation scale for one BFKL cascade and it does not depend on multiplicity. Such choice of the scale in the argument of \({\bar{\alpha }}_{S}\) makes an essential difference from the KLN formula for the number of participants \(N_{\mathrm{part}}\). It reflects the fact that for proton we replace a solution of BFKL \(\frac{dN_{\mathrm{parton}}^{\mathrm{BFKL}}}{dy}\) in Eq. (25) by \(\frac{dN_{\mathrm{parton}}^{\mathrm{BK}}}{dy}\) and the multiplicity in the BK cascade depends on the number of participants.
Concluding, we would like to emphasize that we suggest a new mechanism for hard particle ( quarkonia) production in events with high multiplicity of soft produced particles. In this mechanism both \(J/\varPsi \) and soft hadrons are produced at short distances \(r\, \propto \,1/Q_s\) and the difference between them is originated in different dependences of the hard cross sections on the saturation scales. This mechanism is quite different from other approaches, such as the percolation approach [19] or the modification of the slope of the elastic amplitude [20]. It can be applied both to the production of soft and hard particles. In the following subsection we will apply this approach to the multiplicity dependence of quarkonia production. It is worthwhile mentioning that the suggested approach has been successfully used for description of the experimental data in Refs. [69, 70].
Contribution of different configurations to the observed multiplicity of charged particles, when quarkonium (\(J/\psi \)) and charged particle bins are well-separated by rapidity. We can clearly attribute the observed enhanced multiplicity (measured in the bin \(\varDelta \eta \)) either to 1-pomeron or two-pomeron ladders
In the case when the quarkonia and charged particle bins overlap, the observed enhanced multiplicity cannot be attributed either to single-pomeron or to double-pomeron yields, for this reason we have to integrate over the rapidity of \(J/\psi \) in the bin and sum over all possible distributions between the upper and lower pomerons, such that \(n_{1}+n_{2}+n_{3}=n\)
3.2 Phenomenological estimates
3.2.1 Charmonia production outside of the rapidity window of produced hadrons
In measuring the multiplicity there are two different situations, when the bins used for collecting charmonia and co-produced charged particles are well-separated by rapidity, and when the bins overlap, as shown in Figs. 4 and 5. In the former case, we may unambiguously assign all the produced particles either to one-gluon or to the two-gluon ladders in the t-channel. Since we assume that each gluon reggeizes independently and gives equal contribution to the observed average yields of charged particles, for the two-pomeron case the enhanced multiplicity should be assigned in equal parts to both pomerons. For this reason, the cross-section (6) for \(n\not =1\) modifies as
where we introduced the shorthand notation
added explicitly the dependence on the relative multiplicity enhancement parameter n, and for the sake of definiteness assumed that the co-produced charged particles are collected at higher rapidity \(\eta \) than the rapidity y of \(J/\psi \), as seen in the Diagram (A) of the Fig. 4 (the opposite case corresponds to an inversion of sign of the rapidity y).
The evaluation of (26) requires knowledge of the probability distribution P(n) for a pomeron to have relative enhancement of multiplicity n. The theoretical evaluation of this quantity is very involved. As was found experimentally [61], the distribution of charged particles in pp collisions for \(n\gtrsim 1\) is close to exponential behavior \(\sim \exp (-\mathrm{const}\,n)\) (modulo logarithmic corrections).Footnote 4 However, we would like to emphasize that this result cannot be applied to single pomerons, because a convolution of any two pomeron parts does not satisfy the convolution identity
On the other hand, it was predicted long ago [72] that the distribution of particles inside a single pomeron P(N) is described by a Poisson distribution, which clearly satisfies (28). However, in order to reproduce the experimentally observed behavior in this approach, we would have to re-sum an infinite number of pomerons with additional model assumptions for hadron-hadron collisions. In view of this ambiguity, in what follows we will assume that the convolution of the distributions \(P\left( n_{i}\right) \) in (26) just cancels in the ratio (17), and in the case when more than one pomeron spans through the region covered by the detector, the multiplicity is shared equally between pomerons, as we would get with Poisson distributions. For this reason, instead of the ratio (17) we will work with a simplified ratio
where we use the notation \(d{\tilde{\sigma }}\) instead of \(d\sigma \) for the cross-section, in order to emphasize that we took out of the normalization the probability distribution of charged particles (factor P(n)). According to our assumption, the integral over \(n_{1}\) in (26) gets the dominant contribution from the region when the enhanced multiplicity is shared equally between pomerons, i.e. \(n_{1}=n/2\), so we can rewrite the normalized cross-section as
In the small-n limit (\(1\lesssim n\ll m_{Q}^{2}/Q_{s}^{2}(x)\)) we may use the dipole amplitude (16) and get for the ratio (17)
Left: multiplicity dependence at forward rapidities (\(2.5<y_{J/\psi }<4\)), when charged particles are collected at central rapidities (\(|\eta |<1\)). Experimental data are from [73]. Right: evaluation at central rapidities (\(|y_{J/\psi }|<0.9\)). Due to overlap of the bins of charmonium and charged particles, we have an additional contribution of the nonlinear term 33, which leads to a more pronounced n-dependence. Experimental data are from [26, 62]. In both plots the dashed curves labeled “Small-n approx.” correspond to evaluation with a dipole amplitude (16). The curves labeled “2-gluon” in both plots correspond to n-dependence of the gluon-gluon fusion mechanism, as explained in the text. In both plots we use the LC Gauss wave function [49] (see Appendix B) for more details
where \(\kappa =Q_{s}^{2{\bar{\gamma }}}\left( x_{2}\right) /Q_{s}^{2{\bar{\gamma }}} \left( x_{1}\right) \) is a numerical coefficient. Footnote 5At the same time, for the gluon-gluon fusion mechanism we expect that in this kinematics the corresponding n-dependence would be simply \(\sim n^{{\bar{\gamma }}}\), since we have only one pomeron which might contribute to charged particles in a given rapidity window. This expectation does not depend on a particular choice of the NRQCD LDMEs for a given quarkonium state. As can be seen from the left panel of Fig. 6, the three-gluon mechanism (26,17) describes the experimental data [73] reasonably well, whereas the 2-gluon contribution clearly underestimates the n-dependence.
3.2.2 Coinciding rapidity windows for charmonia and soft hadrons productions
The situation when the \(J/\psi \) and charged particle bins partially overlap or coincide is certainly more complicated. In the overlap region we cannot attribute the enhanced multiplicity just to a single or double gluon ladder, and instead we have to average over all possible distributions of particles \(n_{1},\,n_{2},\,n_{3}\) among pomerons, such that \(n_{1}+n_{2}+n_{3}=n\). For this reason the cross-section for this case is given by (see Appendix A for more details)
where we integrate over the rapidity of \(J/\psi \) inside the bin, using the variable \(t=(y-\eta _{\mathrm{min}})/\varDelta \eta \), and over relative multiplicities in each pomeron. In the case when the rapidity bins used to collect charged particles and the \(J/\psi \) fully overlap (\(y_{\mathrm{min}}=\eta _{\mathrm{min}}\), \(y_{\mathrm{max}}=\eta _{\mathrm{max}}\)), the variable \(t\in [0,\,1]\). As we discussed earlier, currently we do not have a reliable first-principle parametrization for P(z), and for this reason in what follows we will use the simplified assumption that the full cross-section might be approximated by a sum of three contributions: when the quarkonium is produced at the center of the rapidity bin or when it is produced a either of the borders, as shown in Fig. 5. The contribution of the border regions is given by (30,31). In the center of the bin, we may assume that the observed multiplicity n is shared equally between the pomerons, so the contribution of this region is given by
With the dipole amplitude (16) the expected large-n dependence of this additional term (33) is given by
considerably more pronounced than (31). In the experimentally measured ratio (17) for the cross-section \(d\sigma \) we should take a weighted sum of the cross-sections (30) and (33). We expect that with the parametrization (16) the n-dependence should have a form
Left: dependence of the ratio (17) on the choice of wave function. The solid line corresponds to evaluation with the light-cone Gauss WF. The dashed and dotted lines correspond to evaluations with boosted rest frame wave functions introduced in Appendix B. The experimental data are from [26, 62]. Right: comparison of \(J/\psi \) results with predictions for different quarkonia states, \(\psi (2S)\) and \(\varUpsilon (1S)\). We use Cornell WFs (see Appendix B for details) instead of LC Gauss, because it allows to make predictions for \(J/\psi \) and higher excited states in the same approach. For other parametrizations of the wave functions the results are similar
In the right panel of the Fig. 6 we show the n-dependence, taking into account the additional term, and compare it with experimental data from [26, 62]. As we can see, the model gives a reasonable description of the experimental data, while at the same time the 2-gluon fusion mechanism underestimates the data. In Fig. 7 we show the dependence of our predictions on the choice of the wave function, using for comparison boosted rest frame wave functions described in Appendix B. As expected, this dependence is very mild. In the right panel of the same Fig. 7, we show predictions for other quarkonia states which might be within the reach of experimental searches in the near future. We expect that both the \(\psi (2S)\) and the \(\varUpsilon (1S)\) states should have an n-dependence close to that of the \(J/\psi \) meson. Technically this happens because the typical dipole sizes \(\langle r\rangle \sim \langle r'\,\rangle \sim \mathrm{min}\left( m_{Q}^{{}^{\text{- }}1},\,Q_{s}\left( x,\,n\right) \right) \) in (33) are significantly smaller than the sizes of the quarkonia states (see Appendix C for details), and in this approximation the wave function \(\varPsi _{M}\) of the latter might be approximated with its value at \(r=0\). This leads to an independence on quarkonium size or mass for the self-normalized ratio (17,29) . The residual dependence seen in the data is due to corrections beyond the heavy quark mass limit.
In Fig. 8 we have shown results for the \(J/\psi \) multiplicity dependence, in the RHIC kinematics, which are in a very good agreement with experimental data [15, 16]. We also show predictions for \(\varUpsilon (1S)\) and \(\psi (2S)\), which are close to the results for \(J/\psi \). We hope that these predictions will be checked very soon.
3.2.3 Charmonia production outside of the rapidity window of produced hadrons
Finally, we would like to mention that the contribution of the last term of Eq. (32) (see also Eq. (35)) might be singled out if the width of the pseudorapidity bin \(\varDelta y\) used for collection of quarkonia is significantly smaller than the width of the bin \(\varDelta \eta \) used for collection of charged particles and it is included inside \((\varDelta y\ll \varDelta \eta ),\,(y_{\mathrm{min}},\,y_{\mathrm{max}}){\subset }(\eta _{\mathrm{min}},\,\eta _{\mathrm{max}})\). In this case the contribution of the border region is negligible, and we expect that the n-dependence is given only by Eq. (34). We hope that in the future the experimentalists will be able to check this prediction. Also, we would like to remind that the other approaches [19, 74] do not predict such a rapid n-dependence (Eq. (34)), and for this reason its possible observation could be a decisive test in favor of the three-gluon mechanism of quarkonia production.
4 Conclusions
In this paper we have developed, in the framework of the CGC approach, a new mechanism for hard particle ( quarkonia) production in events with high multiplicity of the soft produced particles. In this mechanism both \(J/\varPsi \) and soft pions are produced at short distances \(r\, \propto \,1/Q_s\) and the difference between them originates in different dependences of the hard cross sections on the saturation scale. Based on this formalism we analyzed the multiplicity dependence of the two-gluon and three-gluon fusion mechanisms, assuming that the observed multiplicity dependence is due to an increase of the average number of particles produced from each CGC pomeron. We found that the two-gluon mechanism significantly underestimates the multiplicity dependence, whereas the predictions of the three-gluon mechanism are in reasonable agreement with available experimental data in a wide energy range, from RHIC to LHC. This conclusion does not depend on the particular choice of the NRQCD LDMEs for a given quarkonium. We believe that this argument is a strong evidence that the contribution of the three-gluon mechanism might be substantial in \(J/\psi \) production. We call the experimentalists to measure the multiplicity dependence of other charmonia (e.g. \(\psi (2S)\) and \(\varUpsilon (1S)\)), for which we expect approximately the same multiplicity dependence as for \(J/\psi \). Such measurements would be an important argument in favor of 3-gluon mechanism in the CGC approach. We also predict that the suggested mechanism should provide a strong \(\sim n^{3 {\bar{\gamma }}}\) dependence, in the kinematics when \(J/\psi \) is produced at the center of the charged particle bin, i.e. the width of the bin \(\varDelta y\ll \varDelta \eta \).
Our predictions are sensitive to the large-distance behavior of the dipole amplitude, and going to higher values of n potentially could allow to test the saturation model implemented in a dipole amplitude. However, the experimental study of this regime is challenging due to a rapid decrease of probability (yields) of such high-multiplicity events [61], which puts it out of reach of modern and forthcoming accelerators.
The mechanism of multiplicity dependence suggested in this paper is not unique: multiplicity might also be enhanced due to large number of pomerons, as shown in the left panel of Fig. 3 and in Fig. 9. We should also take into account that each of the ladders (pomerons) shown in Fig. 9 might lead to development of a Balitsky–Kovchegov cascade, as shown in the right panel of Fig. 3. We plan to address these issues in a future publication [75].
Data Availability Statement
Notes
In what follows we call “pomeron” a gluon cascade (“shower”), which in Fig. 1 corresponds to the initial state “cut ladder” and which leads to production of hadrons almost uniformly distributed in the entire region of rapidities. Such parton showers correspond to the cut BFKL Pomeron.
Such an exponential behavior is an inherent feature of the Balitsky–Kovchegov parton cascade, as it has been demonstrated in [71].
We would like to emphasize that we would get a similar dependence from any quarkonium mechanism which proceeds via 3-gluon fusion. E.g., we would get the same n-dependence if we considered that the fusion of three gluons produces a color octet state which later hadronizes into quarkonium.
References
R. Maciula, A. Szczurek, Open charm production at the LHC - \(k_{t}\)-factorization approach. Phys. Rev. D 87(9), 094022 (2013). arXiv:1301.3033
C.H. Chang, Hadronic production of \(J/\psi \) associated with a Gluon. Nucl. Phys. B 172, 425 (1980)
C.H. Chang, Nucl. Phys. B 172, 425 (1980)
R. Baier, R. Ruckl, Hadronic production of \(J/\varPsi \) and upsilon: transverse momentum distributions. Phys. Lett. 102B, 364 (1981)
R. Baier, R. Ruckl, Phys. Lett. 102B, 364 (1981)
E.L. Berger, D.L. Jones, Inelastic photoproduction of \(J/\varPsi \) and upsilon by Gluons. Phys. Rev. D 23, 1521 (1981)
G.T. Bodwin, E. Braaten, G.P. Lepage, Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 51, 1125 (1995). Erratum: [Phys. Rev. D 55, 5853 (1997)] [arXiv:hep-ph/9407339]
F. Maltoni, M.L. Mangano, A. Petrelli, Quarkonium photoproduction at next-to-leading order. Nucl. Phys. B 519, 361 (1998). [arXiv:hep-ph/9708349]
N. Brambilla, E. Mereghetti, A. Vairo, Hadronic quarkonium decays at order \(v^7\). Phys. Rev. D 79, 074002 (2009). Erratum: [Phys. Rev. D 83, 079904 (2011)] arXiv:0810.2259
Y. Feng, J.P. Lansberg, J.X. Wang, Energy dependence of direct-quarkonium production in \(pp\) collisions from fixed-target to LHC energies: complete one-loop analysis. Eur. Phys. J. C 75(7), 313 (2015). arXiv:1504.00317
N. Brambilla et al., Heavy quarkonium: progress, puzzles, and opportunities. Eur. Phys. J. C 71, 1534 (2011)
S.P. Baranov, A.V. Lipatov, N.P. Zotov, Prompt charmonia production and polarization at LHC in the NRQCD with \(k_T\) -factorization. Part I: \(\psi (2S)\) meson. Phys. J. C 75, 455 (2015)
S.P. Baranov, A.V. Lipatov, Prompt charmonia production and polarization at LHC in the NRQCD with \(k_T\)-factorization. Part III: \(J/\psi \) meson. Phys. Rev. D 96(3), 034019 (2017). arXiv:1611.10141
A. Andronic et al., Heavy-flavour and quarkonium production in the LHC era: from proton?proton to heavy-ion collisions. Eur. Phys. J. C 76(3), 107 (2016). arXiv:1506.03981
B. Trzeciak [STAR Collaboration], \(J/\psi \) and \(\psi (2S)\) measurement in p+p collisions \(\sqrt{s} =\) 200 and 500 GeV with the STAR experiment. J. Phys. Conf. Ser. 668(1), 012093 (2016). arXiv:1512.07398
R. Ma [STAR Collaboration], Measurement of \(J/\varPsi \) production in p + p collisions at s=500 GeV at STAR experiment. Nucl. Part. Phys. Proc. 276-278, 261 (2016). arXiv:1509.06440
J. Adam et al. [ALICE Collaboration], Enhanced production of multi-strange hadrons in high-multiplicity proton-proton collisions. Nat. Phys. 13, 535 (2017) arXiv:1606.07424
D. Thakur [ALICE Collaboration], \(J/\psi \) production as a function of charged-particle multiplicity with ALICE at the LHC. arXiv:1811.01535
E.G. Ferreiro, C. Pajares, High multiplicity \(pp\) events and \(J/\psi \) production at LHC. Phys. Rev. C 86, 034903 (2012). arXiv:1203.5936
B.Z. Kopeliovich, H.J. Pirner, I.K. Potashnikova, K. Reygers, I. Schmidt, \(J/\varPsi \) in high-multiplicity pp collisions: lessons from pA collisions. Phys. Rev. D 88(11), 116002 (2013). arXiv:1308.3638
T. Sjöstrand, S. Mrenna, P. Skands, PYTHIA 6.4 physics and manual. JHEP 05 026 (2006)
T. Sjöstrand, S. Mrenna, P. Skands, PYTHIA 6.4 physics and manual. Comput. Phys. Comm. 178, 852 (2008)
J. Bellm et al., Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 76(4), 196 (2016). [arXiv:1512.01178 [hep-ph]]
T. Gleisberg, S. Hoeche, F. Krauss, M. Schonherr, S. Schumann, F. Siegert, J. Winter, Event generation with SHERPA 1.1. JHEP 0902, 007 (2009). [arXiv:0811.4622 [hep-ph]]
E. Levin, M. Siddikov, \(J/\psi \) production in hadron scattering: three-pomeron contribution. Eur. Phys. J. C 79(5), 376 (2019). https://doi.org/10.1140/epjc/s10052-019-6894-1. arXiv:1812.06783
B. Abelev et al. [ALICE Collaboration], \(J/\psi \) production as a function of charged particle multiplicity in pp collisions at \(\sqrt{s}\)=7 TeV. Phys. Lett. B 712 165 (2012)
V.A. Khoze, A.D. Martin, M.G. Ryskin, W.J. Stirling, Inelastic \(J/\psi \) and \(\upsilon \) hadroproduction. Eur. Phys. J. C 39, 163 (2005). arXiv:hep-ph/0410020
L. Motyka, M. Sadzikowski, On relevance of triple gluon fusion in \(J/\psi \) hadroproduction. Eur. Phys. J. C 75(5) (2015). arXiv:1501.04915
D. Kharzeev, K. Tuchin, Signatures of the color glass condensate in \(J/\varPsi \)production off nuclear targets. Nucl. Phys. A 770, 40 (2006). arXiv:hep-ph/0510358
D. Kharzeev, E. Levin, M. Nardi, K. Tuchin, Phys. Rev. Lett. 102, 152301 (2009). arXiv:0808.2954
D. Kharzeev, E. Levin, M. Nardi, K. Tuchin, \(J/\varPsi \) production in heavy ion collisions and gluon saturation. Nucl. Phys. A 826, 230 (2009). arXiv:0809.2933
D. Kharzeev, E. Levin, M. Nardi, K. Tuchin, Nucl. Phys. A 924, 47 (2014). arXiv:1205.1554
F. Dominguez, D.E. Kharzeev, E. Levin, A.H. Mueller, K. Tuchin, Gluon saturation effects on the color singlet J/\(\psi \) production in high energy dA and AA collisions. Phys. Lett. B 710, 182 (2012). arXiv:1109.1250
D.E. Kharzeev, E.M. Levin, K. Tuchin, Nuclear modification of the J/\(\psi \) transverse momentum distributions in high energy pA and AA collisions. Nucl. Phys. A 924, 47 (2014). https://doi.org/10.1016/j.nuclphysa.2014.01.006. arXiv:1205.1554
Z.B. Kang, Y.Q. Ma, R. Venugopalan, Quarkonium production in high energy proton-nucleus collisions: CGC meets NRQCD. JHEP 1401, 056 (2014). arXiv:1309.7337
E. Gotsman, E. Levin, Energy evolution of J/\(\varPsi \) production in DIS on nuclei. Phys. Rev. D 98(3), 034014 (2018). arXiv:1804.02561
L.V. Gribov, E.M. Levin, M.G. Ryskin, Semihard processes in QCD. Phys. Rep. 100, 1 (1983)
A.H. Mueller, J. Qiu, Gluon recombination and shadowing at small values of \(x\). Phys. Nucl. B268, 427 (1986)
L. McLerran, R. Venugopalan, Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 49, 3352 (1994)
L. McLerran, R. Venugopalan, Green’s function in the color field of a large nucleus. Phys. Rev. D 50, 2225 (1994). https://doi.org/10.1103/PhysRevD.50.2225
L. McLerran, R. Venugopalan, Fock space distributions, structure functions, higher twists, and small \(x\). Phys. Rev. D 59, 094002 (1999). https://doi.org/10.1103/PhysRevD.59.094002
Y.L. Dokshitzer, V.A. Khoze, S.I. Troian, On the concept of local parton hadron duality. J. Phys. G17, 1585 (1991)
V.A. Khoze, W. Ochs, J. Wosiek, Analytical QCD and multiparticle production. arXiv:hep-ph/0009298
V.A. Khoze, W. Ochs, Perturbative QCD approach to multiparticle production. Int. J. Mod. Phys. A 12, 2949 (1997). arXiv:hep-ph/9701421 and reference therein
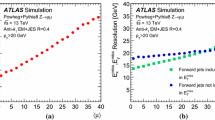
G. Aad et al. [ATLAS Collaboration], Forward-backward correlations and charged-particle azimuthal distributions in pp interactions using the ATLAS detector. JHEP 1207 019 (2012). https://doi.org/10.1007/JHEP07(2012)019. arXiv:1203.3100
V. Khachatryan et al. [CMS Collaboration], Charged Particle Multiplicities in \(pp\) Interactions at \(\sqrt{s}=0.9\), 2.36, and 7 TeV. JHEP 1101 079 (2011). https://doi.org/10.1007/JHEP01(2011)079. arXiv:1011.5531
G. Aad et al. [ATLAS Collaboration], Charged-particle multiplicities in \(pp\) interactions at \(\sqrt{s}=900\) GeV measured with the ATLAS detector at the LHC. Phys. Lett. B 688 21 (2010). https://doi.org/10.1016/j.physletb.2010.03.064. arXiv:1003.3124
E. Gotsman, E. Levin, U. Maor, CGC/saturation approach for soft interactions at high energy: long range rapidity correlations. Eur. Phys. J. C 75(11), 518 (2015). https://doi.org/10.1140/epjc/s10052-015-3727-8. arXiv:1508.04236
J. Nemchik, N.N. Nikolaev, E. Predazzi, B.G. Zakharov, Color dipole phenomenology of diffractive electroproduction of light vector mesons at HERA. Z. Phys. C 75, 71 (1997)
Y.V. Kovchegov, E. Levin, Quantum Chromodynamics at High Energy, vol. 33 (Cambridge University Press, Cambridge, 2012)
R.S. Thorne, Gluon distributions and fits using dipole cross-sections. AIP Conf. Proc. 792(1), 324 (2005)
I. Balitsky, Operator expansion for high-energy scattering. arXiv:hep-ph/9509348
I. Balitsky, Factorization and high-energy effective action. Phys. Rev. D 60, 014020 (1999). arXiv:hep-ph/9812311
Y.V. Kovchegov, Small-x \(F_{2}\) structure function of a nucleus including multiple Pomeron exchanges. Phys. Rev. D 60, 034008 (1999). arXiv:hep-ph/9901281
J. Bartels, E. Levin, Solutions to the Gribov-Levin-Ryskin equation in the nonperturbative region. Nucl. Phys. B 387, 617 (1992). https://doi.org/10.1016/0550-3213(92)90209-T
A.M. Stasto, K.J. Golec-Biernat, J. Kwiecinski, Geometric scaling for the total \(\gamma {*}\) p cross-section in the low x region. Phys. Rev. Lett. 86, 596 (2001). arXiv:hep-ph/0007192
E. Iancu, K. Itakura, L. McLerran, Geometric scaling above the saturation scale. Nucl. Phys. A 708, 327 (2002). arXiv:hep-ph/0203137
E. Levin, K. Tuchin, Solution to the evolution equation for high parton density QCD. Nucl. Phys. B 573, 833 (2000). arXiv:hep-ph/9908317
A.H. Mueller, D.N. Triantafyllopoulos, The Energy dependence of the saturation momentum. Nucl. Phys. B 640, 331 (2002). arXiv:hep-ph/0205167
A.H. Rezaeian, I. Schmidt, Impact-parameter dependent Color Glass Condensate dipole model and new combined HERA data. Phys. Rev. D 88, 074016 (2013). arXiv:1307.0825
B. Abelev et al. [ALICE Collaboration], \(J/\psi \) production as a function of charged particle multiplicity in \(pp\) collisions at \(\sqrt{s} = 7\) TeV. Phys. Lett. B 712, 165 (2012). arXiv:1202.2816
D. Thakur [ALICE Collaboration], \(J/\psi \) production as a function of charged-particle multiplicity with ALICE at the LHC. arXiv:1811.01535
D. Kharzeev, M. Nardi, Hadron production in nuclear collisions at RHIC and high density QCD. Phys. Lett. B 507, 121 (2001). arXiv:nucl-th/0012025
D. Kharzeev, E. Levin, ‘Manifestations of high density QCD in the first RHIC data. Phys. Lett. B 523, 79 (2001). arXiv:nucl-th/0108006
D. Kharzeev, E. Levin, M. Nardi, The Onset of classical QCD dynamics in relativistic heavy ion collisions. Phys. Rev. C 71, 054903 (2005). arXiv:hep-ph/0111315
D. Kharzeev, E. Levin, M. Nardi, Hadron multiplicities at the LHC. J. Phys. G 35(5), 054001.38 (2008). arXiv:0707.0811
A. Dumitru, D.E. Kharzeev, E.M. Levin, Y. Nara, Gluon saturation in \(pA\) collisions at the LHC: KLN model predictions for Hadron multiplicities. Phys. Rev. C 85, 044920 (2012). arXiv:1111.3031
Y.V. Kovchegov, Classical initial conditions for ultrarelativistic heavy ion collisions. Nucl. Phys. A 692, 557 (2001). arXiv:hep-ph/0011252
E. Levin, A.H. Rezaeian, Gluon saturation and inclusive hadron production at LHC. Phys. Rev. D 82, 014022 (2010). arXiv:1005.0631
T. Lappi, Energy dependence of the saturation scale and the charged multiplicity in pp and AA collisions. Eur. Phys. J. C 71, 1699 (2011). arXiv:1104.3725
D.E. Kharzeev, E.M. Levin, Deep inelastic scattering as a probe of entanglement. Phys. Rev. D 95(11), 114008 (2017). arXiv:1702.03489
E. Levin, ’Hard’ pomeron approach to ’soft’ processes at high-energy. Phys. Rev. D 49, 4469 (1994)
A. Khatun [ALICE Collaboration], J/\(\psi \) production as a function of charged-particle multiplicity in pp collisions at \(\sqrt{s}\) = 5.02 TeV with ALICE. arXiv:1906.09877
A. Khatun [ALICE Collaboration], J/\(\psi \) production as a function of charged-particle multiplicity in pp collisions at \(\sqrt{s}\) = 5.02 TeV with ALICE. arXiv:1906.09877
M. Siddikov et alin preparation
J. Hufner, Y.P. Ivanov, B.Z. Kopeliovich, A.V. Tarosov, Photoproduction of charmonia and total charmonium proton cross-sections. Phys. Rev. D 62, 094022 (2000). [arXiv:hep-ph/0007111]
E. Eichten, K. Gottfried, T. Kinoshita, K.D. Lane, T.M. Yan, Charmonium: the model. Phys. Rev. D 17 (1978) 3090 Erratum: [Phys. Rev. D 21 (1980) 313]
E. Eichten, K. Gottfried, T. Kinoshita, K.D. Lane, T.M. Yan, Charmonium: comparison with experiment. Phys. Rev. D 21, 203 (1980)
C. Quigg, J.L. Rosner, Quarkonium level spacings. Phys. Lett. 71B, 153 (1977)
A. Martin, A FIT of upsilon and charmonium spectra. Phys. Lett. 93B, 338 (1980)
Acknowledgements
We thank our colleagues at Tel Aviv university and UTFSM for encouraging discussions. This research was supported by Proyecto Basal FB 0821(Chile), and by Fondecyt (Chile) Grants 1180118 and 1180232.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of the Eq. (32)
In this section we will evaluate the cross-section of the pion production case, when the bins used for collection of quarkonia and charged particles overlap. In this setup we cannot attribute the observed increase of multiplicity to any of the pomerons and have to evaluate probability-weighted sum over all possible partitions of the number of charged particles \(N_{\mathrm{ch}}\) into three integers. Since the quarkonium might be produced at any rapidity y (not necessarily at the center of the bin), this implies that the average contribution of each pomeron to the enhanced multiplicity seen in the bin \(\varDelta \eta \) will also depend on y. In what follows it is convenient to work with a variable \(t=(y-\eta _{\mathrm{min}})/\varDelta \eta \), which for the case of the full overlap (\(y_{\mathrm{min}}=\eta _{\mathrm{min}}\), \(y_{\mathrm{max}}=\eta _{\mathrm{max}}\)) remains in the interval \(t\in [0,\,1]\).
In what follows we will use the notations \(N_{\mathrm{ch}}^{(1)},\,N_{\mathrm{ch}}^{(2)}\) and \(N_{\mathrm{ch}}^{(3)}\) for the number of charged particles produced from each of the pomerons, with
where \(N_{\mathrm{ch}}^{(\Delta \eta )}\) is the total number of charged particles produced inside the bin \(\varDelta \eta \). The probability that a given pomeron of length \(\eta _{\mathrm{tot}}\) units of rapidity produces \(N_{\mathrm{ch}}^{(\mathrm{tot})}\) particles is given by \(P\left( N_{\mathrm{ch}}^{(\mathrm{tot})}/\left\langle N_{\mathrm{ch}}^{(\mathrm{tot})}\right\rangle \right) \), where \(\left\langle N_{\mathrm{ch}}^{(\mathrm{tot})}\right\rangle \) is the average number of particles produced by the whole pomeron. Since the distribution \(dN_{\mathrm{ch}}/d\eta \) almost does not depend on rapidity, we may assume that inside each interval \(\varDelta \eta _{i}\) (\(i=1,2,3\)) the distribution of produced charged particles is given by the same function, \(P\left( N_{\mathrm{ch}}^{(i)}/\left\langle N_{\mathrm{ch}}^{(i)}\right\rangle \right) \), where the average number \(\left\langle N_{\mathrm{ch}}^{(i)}\right\rangle =\left\langle N_{\mathrm{ch}}^{(\mathrm{tot})}\right\rangle \varDelta \eta _{i}/\eta _{\mathrm{tot}},\) and the length of the pomeron is given by
According to (A.1), the probability that the three pomerons contribute to the observed multiplicity enhancement is given by
where we introduced the variables \(n_{i}=N_{\mathrm{ch}}^{(1)}/\left\langle N_{\mathrm{ch}}^{(\varDelta \eta )}\right\rangle ,\) and \(n=N_{\mathrm{ch}}^{(\varDelta \eta )}/\left\langle N_{\mathrm{ch}}^{(\varDelta \eta )}\right\rangle \). The experimentally observable cross-section \(d\sigma \left( M+N_{\mathrm{ch}}^{(\varDelta \eta )}\right) \) to produce heavy quarkonium M and \(N_{\mathrm{ch}}^{(\varDelta \eta )}\) particles in the bin \(\varDelta \eta \) can be related to the cross-sections to produce quarkonium M and \(N_{\mathrm{ch}}^{(1)},\,N_{\mathrm{ch}}^{(2)},\,N_{\mathrm{ch}}^{(3)}\) charged particles in the rapidity interval \(\varDelta \eta \) from each of the three pomerons as
If the width of the bin \(\varDelta \eta \) is sufficiently large (so that \(\left\langle N_{\mathrm{ch}}^{(\varDelta \eta )}\right\rangle \gg 1\)), we may replace the summation over \(N_{\mathrm{ch}}^{(1)},\,N_{\mathrm{ch}}^{(2)}\) with an integral over \(n_{1},\,n_{2}\) and obtain the Eq. (32).
Left: Function \(K\left( r,\,\,r'\right) \sim \left\langle \varPsi _{g}\cdot \varPsi _{M}(r)\right\rangle \left\langle \varPsi _{g}\cdot \varPsi _{M}(r')\right\rangle \int d\phi \,\varDelta N\left( {\varvec{r}},\,{\varvec{r}}'\right) \) which appears in the integrand of (32,33) for \(x=10^{-3}\) and \(n=8\). Right: The same integrand for the hypothetic case of light meson production, with wave function (B.6) with parameter (meson size) \({\mathcal {R}}\sim 1\,\mathrm{fm}\) and light quark mass \(m_{q}\approx 0.3\,\mathrm{GeV}\). In both plots the semitransparent pink surface corresponds to evaluation with CGC parametrization, and the semitransparent green surface corresponds to evaluation with parametrization (16). The latter has a visible cusp due to the discontinuity of the dipole amplitude (16)
Appendix B: Wave functions
In our evaluations, unless stated otherwise, we use the so-called light-cone wave functions of 1S quarkonia states [49],
where \({\mathcal {N}}\) and \({\mathcal {R}}\) are some numerical constants. In the heavy quark mass limit, as well as in the deeply saturated regime, we expect that the results should not depend at all on the choice of the wave function, since only small dipole configurations in (6) give the dominant result. In the small-r approximation we may replace the wave function \(\varPsi _{M}(z,\,r)\) with its value at the point \(r=0\), which eventually cancels in the ratio (17). However, in order to assess the accuracy of this approximation, as well as to have the wave functions of other quarkonia (primarily \(\psi (2S)\) and \(\varUpsilon (1S)\) are of interest for experimental searches), we also used wave functions evaluated in rest frame potential models and boosted them to a moving frame in momentum space. Technically, this prescription is given by the relation [49, 76]
where \(\psi _{\mathrm{RF}}\) is the Fourier image of the eigenfunction of the corresponding Schroedinger equation. For comparison we considered three different choices of the potential:
The linearly growing Cornell potential
$$\begin{aligned} V_{\mathrm{Cornell}}(r)=-\frac{\alpha }{r}+\sigma \,r, \end{aligned}$$(B.8)The potential with logarithmic large-r behaviour suggested in [79],
$$\begin{aligned} V_{\mathrm{Log}}(r)=\alpha +\beta \,\ln r. \end{aligned}$$(B.9)The power-like potential introduced in [80],
$$\begin{aligned} V_{\mathrm{pow}}(r)=a+b\,r^{\alpha }. \end{aligned}$$(B.10)
We checked that the wave functions obtained with all three potentials have similar shapes, and in the case of \(J/\psi \) are close to the light-cone Gauss potential (B.6). In the heavy quark mass limit the wave functions of the gluon \(\varPsi _{g}\) in (1) can be approximated with the perturbative expressions from [49]. Their overlap with the wave function of quarkonium are given by
Appendix C: Small-n approximation
As was illustrated in Sect. 3.1.1, the approximation (16), which was derived for r in the vicinity of the saturation scale (\(r\,Q_{s}\,\sim \,1\)), works up to surprisingly large values of n. In this section we would like to discuss briefly the technical reasons why this happens.
In LHC kinematics, we expect that the typical sizes of r and \(r'\) in the integrand of (26) are controlled by the wave functions \(\varPsi _{g}\), for events with normal multiplicity (\(n\approx 1\)). In the heavy quark mass limit this gives an estimate \(\langle r\rangle \sim \langle r'\,\rangle \sim m_{Q}^{-1}\). However, the situation changes for events with elevated multiplicity (\(n\gg 1\)), because the saturation scale \(Q_{s}\left( x,\,n\right) \) increases and at some point becomes comparable and even exceeds the heavy quark mass \(m_{Q}\). In the deeply saturated regime \(Q_{s}\left( x,\,n\right) \gg m_{Q}\), so the factor \(\varDelta N\) defined in (27) leads to a strong suppression of dipoles with a size larger than \(Q_{s}^{-1}\left( x,\,n\right) \). For this reason we can see that the integrand of (6,26) always gets the dominant contribution from the region \(r\lesssim Q_{s}\), which explains why the predictions of (16) for self-normalized ratios are close to the more realistic CGC parametrization [60].
In order to illustrate these findings numerically, in the left panel of Fig. 10 we have plotted the function \(K\left( r,\,\,r'\right) \sim \left\langle \varPsi _{g}\cdot \varPsi _{M}(r)\right\rangle \) \(\times \left\langle \varPsi _{g}\cdot \varPsi _{M}(r')\right\rangle \int d\phi \,\varDelta N\left( {\varvec{r}},\,{\varvec{r}}'\right) \), which appears in the integrand of (32,33). For the sake of definiteness we have chosen the point \(n\approx 8\), where the expected deviations of the parametrization (16) from CGC are the largest. We can see that for charmonia the difference between the integrands is of order \(10\%\), in agreement with our earlier results. For the sake of comparison, in the right panel of the Fig. 10 we have also plotted a similar integrand for the hypothetic case of light meson (e.g. \(\rho \)-meson) production, assuming that its wave function is given by (B.6) with an adjusted parameter \({\mathcal {R}}\sim 1\,\mathrm{fm}\) (size) and using the light quark mass \(m_{q}\approx 0.3\,\mathrm{GeV}\). We can see that in this case the discrepancy is significantly larger, i.e, the small-n approximation (parametrization (16)) cannot be used for estimates of multiplicity dependence.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Levin, E., Schmidt, I. & Siddikov, M. Multiplicity dependence of quarkonia production in the CGC approach. Eur. Phys. J. C 80, 560 (2020). https://doi.org/10.1140/epjc/s10052-020-8086-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8086-4