1 Introduction

Since the first observation of the fast radio transient phenomenon in the universe [1], the astronomy of fast radio bursts (FRBs) has attracted broad interests from both the observational and the theoretical perspectives [2, 3]. Due to their large dispersion measure and bright pulses, many researchers attempt to investigate these mysterious signals from cosmological interpretations. A major effort has been made to establish the broad-band, wide-field surveys for the purpose of hunting for FRB events from the perspective of observational astronomy, such as Parkes [4,5,6,7], Arecibo [8, 9], Green Bank Telescope (GBT) [10], Square Kilometre Array (SKA) [11, 12], Molonglo Observatory Synthesis Telescope (MOST) [13, 14], and Canadian Hydrogen Intensity Mapping Experiment (CHIME) [15]. Meanwhile, different theoretical models have been proposed to understand the possible origin of these FRB signals [16], namely, synchrotron maser emission from young magnetars in supernova remnants [17], radiation from cosmic string cusps [18], charged primordial black hole binaries coalescence [19], and many other possible models [20,21,22,23]. Finding the origin of FRBs has become one of the most important tasks for understanding them.

Cosmic strings [24], being one-dimensional topological defects, formed during the early evolution of the universe [25]. It might be possible that cosmic strings are superconducting wires if they carry electric charge [26]. These so-called superconducting cosmic strings (SCSs) can be achieved by introducing a charged scalar field whose flux is trapped inside strings with the electromagnetic gauge invariance broken, and hence can yield electromagnetic effects [24]. These primordial relics, if they exist in the sky, could behave as giant wires that may release electromagnetic signals in a wide range of frequencies [27, 28]. Thus, it is natural to explore the hypothetical possibility for SCSs to explain the observed FRB events, namely, due to the oscillations of string loops [29], dynamics of string cusps and kinks [30,31,32], and effects of the magnetic field upon string loops [33].

The parameters of SCSs (string tension \(G\mu \) and current on the string I) have been constrained by different types of astronomical observations. Namely, the CMB analyses based on the Wilkinson Microwave Anisotropy Probe (WMAP) and the South Pole Telescope can lead to an upper bound on the string tension of \(G\mu < 1.7 \times 10^{-7}\) [34], and this bound was later improved to \(G\mu < 1.3 \times 10^{-7}\) with the data from the Planck satellite [35]. Both CMB and the pulsar timing measurements put a robust bound on the string tension in the same order [36,37,38,39,40,41]. The spectral distortions of the CMB photons [42,43,44] suggested some additional constraints on parameter space i.e. \(10^{-19}< G\mu < 10^{-7}\) and \(I > 10^4 ~ \mathrm{GeV}\) would be excluded [45]. In most of the previous work, it has been assumed that all SCSs take the exact same value of the current, which would greatly simplify the analysis while one could grasp the basic picture of the underlying physics. However, in a much realistic situation, one would expect a probability distribution for the currents inside various strings in the universe. To explore this possibility, in this article we put forward a novel parameterization for SCSs, in which the currents are assumed to follow the exponential distribution. For this type of distribution, the probability of electric neutral strings is the highest, which corresponds to uncharged cosmic strings. The probability for cosmic strings with larger current becomes lower, which indicates that SCSs can hardly be formed at extremely high-energy scales. Such an exponential distribution as considered in the present work is not based on a particular fundamental theory, but generally from the intuitive observation that the lifetime of a string with the fixed tension should be shorter if it would carry a larger current due to the energy loss of both gravitational and electromagnetic radiations. We also update the constraints on the parameter space of SCSs using the latest published data.

This article is organized as follows. In Sect. 2 we describe the parameterized model of SCSs and the associated radiation mechanism. In Sect. 3 we present the numerical estimation based on the newly proposed parametrization and report the updated constraint on the parameter space of these cosmic strings. Section 4 is devoted to a summary of our results accompanied by a discussion. In the theoretical derivations, we used the natural units with \(\hbar = c = 1\). In the numerical calculations, we followed the setups of the Parkes multi-beam receiver and ASKAP survey.Footnote 1

2 Characteristics of cosmic strings

Cosmic strings could form via phase transitions of the very early universe when the manifold of the vacuum background has nontrivial topology for symmetry breaking. These cosmic relics reveal crucial information about fundamental physics at extremely high-energy scales. In particular, these strings could carry a current, i.e. SCSs, which could be achieved by a charged scalar field whose flux is trapped in normal cosmic strings with the electromagnetic gauge invariance broken inside the strings, and hence would give rise to electromagnetic effects. Namely, as described in [32], radiations can be emitted from various structures of SCSs. In the following, we briefly review the radiation mechanism of SCSs and put forward a parametrized distribution function for SCSs.

2.1 Parametrization of SCSs

Recall that a cosmic string in general can emit both gravitational and electromagnetic radiation if there is a current. In the following context, we consider a string with the initial length \(L_i\) at the initial time \(t_i\). Its length evolves as [24]

$$\begin{aligned} L(t) = L_i - \Gamma G{\mu }(t-t_i) , \end{aligned}$$
(1)

where \(\Gamma \) is a scaling factor for the total radiation power P from SCSs. It takes the form [32]

$$\begin{aligned} \Gamma = \frac{P}{G\mu ^2} \simeq \frac{P_g+P^{c}_{\gamma }}{G\mu ^2} , \end{aligned}$$
(2)

where \(P_g\) and \(P^{c}_{\gamma }\) denote the powers of gravitational and the cusp-sourced electromagnetic radiations, respectively.

As cosmic strings yield both gravitational and electromagnetic radiations, the lifetime of a typical string loop can be estimated by [24]

$$\begin{aligned} \tau = \frac{L_i}{\Gamma G \mu } . \end{aligned}$$
(3)

Note that, in the literature on the electromagnetic effects of cosmic string, it was often assumed that all strings carry the same value of the current. However, this assumption could be relaxed by adopting a probability distribution for the currents inside various strings that may exist in the universe. Accordingly, the number density of SCSs can be expressed as

$$\begin{aligned} dn_{SCS}=\Phi (I) ~ dn_{CS} ~ dI , \end{aligned}$$
(4)

where \(dn_{SCS}\) is the number density of SCSs and \(dn_{CS}\) is that of non-superconducting cosmic strings, while \(\Phi (I)\) is the probability distribution for the current. In the following context, we discuss a toy model where \(\Phi (I)\) is an exponential distribution:

$$\begin{aligned} \Phi (I)=\frac{1}{I_c}e^{-I/I_c} , \end{aligned}$$
(5)

with \(I_c\) being a positively valued parameter. The choice of the exponential distribution is based on an intuitive picture that strings with smaller currents emit lower electromagnetic radiation power and hence will exist longer.

We comment that, as these topological defects have formed at different energy scales, the value of the corresponding current inside the strings varies along with the relevant energy scales for phase transitions. For an infinite current, the probability approaches zero, which is in agreement with the description of the exponential distribution function. Note that a truncated Gaussian distribution could be another attractive candidate for parametrization, in particular if one takes into account the possible correlation between the current and the string tension. In this case, there is automatically a theoretical bound on the maximal value of current for a fixed \(G\mu \) when the current is uniformly distributed around a mean value for different strings. However, this case would be sensitive to the underlying theoretical models. As the present work focuses on the development of the analysis method on confronting the SCSs with FRB data, we wish to leave more detailed discussions on the parametrization of the distribution function for a future study.

2.2 Radiations from string loops

The gravitational radiation from cosmic strings can be expressed as [24]

$$\begin{aligned} P_{g} = \Gamma _g G\mu ^2~, \end{aligned}$$
(6)

where \(\Gamma _g\sim 100\). For electromagnetic radiation, the case becomes complicated. Note that it is crucial to study the energy emitted from SCSs by taking into account the effect of the charge carriers upon the motion of the string itself, which has been exactly examined in the case of the chiral current in [46]. For a generic case, the electromagnetic backreaction becomes important when it is comparable with the string tension itself, and thus, this leads to a cutoff on the frequency of the emitted radiation as addressed in [31], which is typically above the observational region for the FRB astronomy. The electromagnetic radiation power of SCS loops with length L mainly comes from cusps and kinks regions, which can be estimated as [27, 31, 32]

$$\begin{aligned} P_\gamma ^c&\sim \kappa I \sqrt{\mu } , \end{aligned}$$
(7)
$$\begin{aligned} P_\gamma ^k&\sim I^2 N \Psi \ln \biggl ( \frac{\omega _{max}}{\omega _{min}} \biggr ) , \end{aligned}$$
(8)

where the superscripts c and k stand for cusps and kinks, respectively. Here \(\kappa \sim 10\) is a numerical coefficient, \(\omega _{max}\) and \(\omega _{min}\) denote the highest and lowest frequency cutoffs for kinks, which are estimated as \(\omega _{max} \sim \sqrt{\mu }\), and \(\omega _{min} \sim (L/N)\sim 1\). We assume that neither the numbers of kinks per loop N nor sharpness of discontinuity \(\Psi \) would induce an order-of-magnitude change to the radiations from kinks; hence we take \(N\Psi =1\) in this work.

2.3 Event rate of burst

We consider the event rate of radio signals from string loops that reach scaling in the matter-dominated epoch. Assuming the spatially flat Friedmann–Lemaitre–Robertson–Walker (FLRW) universe, the number density of these string loops can be expressed in terms of the redshift z and the length L as [24, 31],

$$\begin{aligned} dn_{SCS}(z,L,I) \simeq \frac{C_L(z)(1+z)^6 \Phi (I)}{t_0^{2}[(1+z)^{3/2} L + \Gamma G\mu t_0 ]^2} dL dI ~, \end{aligned}$$
(9)

where the exponential distribution has already been considered and \(t_0\) denotes the age of the universe at present. Moreover,

$$\begin{aligned} C_L(z)=1+{\frac{t_{eq}^{1/2}(1+z)^{3/4}}{\sqrt{(1+z)^{3/2}L+ \Gamma G\mu t_0}}} ~. \end{aligned}$$
(10)

The burst event rate in terms of string loop length L, redshift z, and kink sharpness \(\Psi \), with the beam width \(\Theta _w=(L \omega )^{-1/3}\) per unit volume is [31]

$$\begin{aligned} d \dot{\mathcal {N}}(z,L,I) \simeq \frac{N^p \Theta _{\nu _0}^{-3m}}{L (1+z)} dn_{SCS}(z,L,I) dV(z) , \end{aligned}$$
(11)

where we have (\(p = 0\), \(m = -\frac{2}{3}\)) for cusps and (\(p = 1, m = -\frac{1}{3}\)) for kinks. Additionally, \(\Theta _{\nu _0} = [\nu _0 (1+z) L]^{-1/3}\) with \(\nu _0\) being the observed frequency of the bursts. The physical volume element is given by

$$\begin{aligned} dV(z)= {4\pi }\frac{r_0(z)^2}{(1+z)^3}dz , \end{aligned}$$
(12)

where

$$\begin{aligned} r_0(z)=3t_0\biggl (1-\frac{1}{\sqrt{1+z}}\biggr ) \end{aligned}$$
(13)

is the comoving distance.

So far, we have demonstrated the burst event rate in terms of loop length and redshift. From an observational point of view, it is rather peculiar that we can relate the burst event rate to measured variables, namely, the energy flux per frequency interval S and the observed duration \(\Delta \) of the burst. The burst event rate in terms of measured parameters then takes the form [32]

$$\begin{aligned} d \dot{\mathcal {N}}(S,z,I)=\tilde{A}\frac{[ {\nu }_0 L(S,z,I)]^m}{S}f_m(z,S,I) \Phi (I) dz dS dI , \end{aligned}$$
(14)

where

$$\begin{aligned}&\tilde{A}=\frac{3 A N^p t_0}{2(1-3m)} ~, \end{aligned}$$
(15)
$$\begin{aligned}&L(z,S,I) = \biggl [ \frac{r_0(z)^2(1+z)^2 S \Delta }{I^2 \Psi ^p} \biggr ]^{\frac{3}{2(1-3m)}} \big [ \nu _0(1+z) \big ]^{\frac{2+3m}{1-3m}} ~, \end{aligned}$$
(16)
$$\begin{aligned}&f_m(z,S,I)=\frac{C_L(z)(1+z)^{m-\frac{1}{2}}(\sqrt{1+z}-1)^2}{[(1+z)^{\frac{3}{2}}L + \Gamma G\mu t_0]^2} , \end{aligned}$$
(17)

with \(A\sim 50\). [47,48,49]

A radio signal, all the way from source to receiver, experiences scattering effects in various ways. For the observed width \(\Delta \) of the FRB signal, we considered both intrinsic and scattering duration caused by astrophysical medium given by [50]

$$\begin{aligned} \Delta ^2=\Delta t_{ISM}^2+\Delta t_{IGM}^2+\Delta t_{int}^2 , \end{aligned}$$
(18)

where \(\Delta t_{ISM}\) and \(\Delta t_{IGM}\) are the scattering duration due to the interstellar medium (ISM) and the intergalactic medium (IGM), respectively. Note that the ISM and IGM mainly affect the propagations of photons but not the sources when they are extra-galactic. However, it is interesting to examine SCSs within the IGM environment, such as involving certain intergalactic magnetic fields [51]. This may give rise to novel phenomena of experimental interest at different observational windows.

Due to ISM, the time broadening effects (scattering) for the radio pulse, therefore yield [50, 52]

$$\begin{aligned} \log _{10}(\Delta t_{ISM}) =&-6.5+0.15\log _{10}(DM_{ISM})\nonumber \\&+ 1.1\log _{10}(DM_{ISM})^2 - 3.9 \log _{10}(\nu _0) , \end{aligned}$$
(19)

where \(DM_{ISM}\) is a constant equivalent to \(95pc/\mathrm{cm}^3\). Likewise, the rescaling of the time broadening effect through IGM gives [50, 53]

$$\begin{aligned} \log _{10}(\Delta t_{IGM}) =&-9.5+0.15\log _{10}(DM_{IGM}) \nonumber \\&+ 1.1\log _{10}(DM_{IGM})^2 - 3.9 \log _{10}(\nu _0) . \end{aligned}$$
(20)

The observed FRBs are all from extra-galactic sources. Then one finds that the dispersion measure of the IGM takes [54,55,56]

$$\begin{aligned} DM_{IGM}(z)=\frac{3cH_0\Omega _bf_{IGM}}{8\pi Gm_p}\int _{0}^{z}\frac{(1+z^\prime )dz^\prime }{E(z^\prime )} , \end{aligned}$$
(21)

with

$$\begin{aligned} E(z)=\sqrt{\Omega _m(1+z)^3+\Omega _\Lambda } , \end{aligned}$$
(22)

where we have introduced the Hubble parameter \(H_0\), the density parameter of matter \(\Omega _m\) and that of dark energy \(\Omega _\Lambda \) of the present universe; \(\Omega _b\) is the baryon mass fraction of the universe, \(f_{IGM}\) the fraction of the baryon mass in the intergalactic medium, and \(m_p\) is the mass of the proton.

To deal with time dilation at observation point for cusps, one needs to consider the cosmological expansion factor. Therefore, the intrinsic duration at the point of the observer is [27, 31, 32]

$$\begin{aligned} (\Delta _{int})_{cusp} \approx \frac{(1+z)L^{2/3}}{\nu _e^{1/3}} , \end{aligned}$$
(23)

where \(\nu _e=\nu _0(1+z)\) is the emitted frequency of the radiation and \({\nu }_0\) is the observed one. The intrinsic duration of kinks is very short and is given by

$$\begin{aligned} (\Delta _{int})_{kink}\approx \frac{1+z}{\nu _e} \sim 0 . \end{aligned}$$
(24)

Hence only the scattering effect will be considered.

3 Numerical results

At this stage, we have tackled the theoretical predictions of SCSs according to observational data of FRB. In this regard, there are five parameters in total that describe the FRB data: \(G\mu \), \(I_c\), \(\nu _0\), \(\Delta \) and S. We fit the event burst rate to the normalized observed data, hence for each \((G\mu ,I_c)\), we express the event burst rate in terms of the redshift. As a result, we infer values for the pairs \((G\mu , I_c)\) according to the FRB signals. For each \(I_c\), the range of the current I is chosen to be \((0, 10^4]\)GeV; based on the previous work [32], we need to integrate Eq. (14) over respective bandwidth and energy flux for different receivers to get the burst event rates for cusps and kinks. For Parkes and ASKAP receivers, using the radiometer equation, the threshold flux is [50, 57]

$$\begin{aligned} S_*=\frac{SNR\times T_{sys}}{G_{sys}\sqrt{\Delta BN_{pol}}} , \end{aligned}$$
(25)

where \(T_{sys}\) is the temperature of the system, \(G_{sys}\) is the system gain, B is the bandwidth, \(N_{pol}\) is the polarization number and SNR is the signal-to-noise ratio. Following Table 1, one can get threshold flux for Parkes and ASKAP.

Table 1 Parameters of Parkes multi-beam and ASKAP recivers. The values of system parameters including the system gain \(G_{sys}\), the bandwidth B, the polarization number \(N_{pol}\), the system temperature \(T_{sys}\) and the signal-to-noise ratio SNR are listed
Full size table
Table 2 Observational parameters including redshift, energy flux and observed frequency for Parkes and ASKAP are listed
Full size table

The observational parameters are displayed in Table 2. For the event rate of the bursts, the contribution of the flux has been suppressed outside the given range and is consistent with the detected events [32]. We put a few limitations on the loop length for cusps. Given the tension of the string, from Eq. (7) we can get the upper bound on L, i.e. \(L<\mu ^{\frac{3}{2}}/(I^3\omega _{max})\). Also, for the given \(G\mu \), one expects that the current through strings greater than a critical value, i.e. \(I_*\simeq 10^{20}\times (G \mu )^{3/2}\) GeV, yields a major contribution in the form of electromagnetic radiation [32]. For statistical analysis, we divide each data set into 6 bins. Note that we normalize the data as

$$\begin{aligned} \sum y_{obs}\Delta z_{bin} = 1 , \end{aligned}$$
(26)

with \(y_{obs}\) being the normalized event number per redshift. To examine the compatibility of theoretical data with the observed ones, we create different values of the normalized event burst rate in terms of (\(G\mu , I_c\)) so that

$$\begin{aligned} \int y_\mathbf{i} dz=1 . \end{aligned}$$
(27)

In order to quantify the ability of FRB observations to constrain the parameter space for SCSs, we perform the following \(\chi ^2\) fit:

$$\begin{aligned} \chi ^2=\sum _i^n \frac{(y_{obs}-\mathbf{y} _i)^2}{e_{obs}^2} , \end{aligned}$$
(28)

where n is the number of bins, \(e_{obs}\) is the respective error bar of observational data for each redshift bin, and \(y_i\) is the theoretical event rate at the center of redshift bin. We are interested in the regime with burst event rates per year between \(10^2\) to \(10^6\).

Fig. 1
figure 1

The \(\chi ^2\) distribution with \(2\sigma \) significance for Parkes (red shadow) and ASKAP (purple shadow), respectively

Full size image
Fig. 2
figure 2

The contour for the burst event rate distribution with \(2\sigma \) significance for Parkes (red shadow) and ASKAP (purple shadow). The lighter to darker shadows of each color correspond to the regimes with \(\dot{\mathcal {N}}(\mathrm{year}^{-1})\) from \(10^2\) to \(10^6\), respectively

Full size image

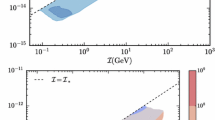
We investigate two observational data sets consisting of 25 signals from Parkes and 26 from ASKAP. In our analysis, we examine a \(2\sigma \) significance level to scrutinize the parameter space for each experiment. For both instruments, the significance of \(2\sigma \) demonstrates the contour with \(\chi ^2<11\). This is shown in Fig. 1. The red shaded region corresponds to Parkes and the purple region is for ASKAP. Both data sets allow us to constrain the parameter space to \(G\mu \sim [10^{-17}, 10^{-12}]\) and \(I_c \sim [10^{-1}, 10^2]\) GeV. Further observations reveal that, for Parkes, the range of the parameter space is slightly broadened as calculated by [32], which could be due to the increase in both data points and redshift range.

For the aforementioned estimated parameter space, we can infer the distribution of burst event rates per year. Figure 2 displays the findings of our analysis. We have calculated the event burst rate per year for each observational data set. The results of our analysis are compatible with the ones of [58]. We calculate that \(\dot{\mathcal {N}}\) per year varies within the regime \(10^2\) to \(10^6\) and show that the parameter space with string tension \(G\mu \sim 10^{-14}\) gives the highest event rate per year. If SCSs radiate bursts with observable frequency \(\nu _0\) and energy flux mentioned in Table 3, the burst production rate is of the order of \(10^3\)–\(10^5\) per year. Our results suggest that current and future radio experiments can probe SCS properties in this promising parameter space. For each instrument, we notice that, when \(I_c>10^2\) GeV, the event number becomes stable for the corresponding string tension.

Table 3 Best fits for Parkes and ASKAP with corresponding parameter values, \(\dot{\mathcal {N}}\) per year and \(\chi ^{2}_{min}\) are provided
Full size table
Fig. 3
figure 3

The normalized observed event rate per redshift from Parkes (red) and ASKAP (orange), and theoretical fitting curve using SCSs model are shown with dashed lines. The observational parameters are listed in Table 2. The \(\chi ^2_{min}\) are 0.77 for Parkes and 4.34 for ASKAP. The corresponding parameter values with event rates per year are listed in Table 3

Full size image

For the best-fitting contours for each data set in the estimated regime, we examine the best fits shown in Fig. 3. In this figure, we compare the normalized observed event rate to our theoretical prediction. The model parameters corresponding to \(\chi ^{2}_{min}\) are given in Table 3. The best-fitting spot corresponding to \(\dot{\mathcal {N}}\) per year for ASKAP is approximately consistent with the analysis done by [59]. However, for Parkes, it might be quite lower than the estimated rate. In order to get insight in further details, one may refer to [50].

4 Conclusion and discussion

To summarize, in the present article we have derived the updated constraints on the parameter space for SCS by confronting the theoretically predicted event rate with observational data of FRBs. We have analyzed the observed data from two telescopes, the Parkes and ASKAP telescopes.

Note that we have assumed all cosmic strings to be superconducting and the currents through the string loops following the exponential distribution. We put forward a model in which the number density for SCSs can be defined in terms of the number density for cosmic strings and the distribution of strings’ currents. We notice the parameter space suggested by Parkes data for SCS suggested by [32] is slightly broadened, demonstrated by Fig. 1.

Another important finding is that the combination of Parkes and ASKAP constrained the parameter space well enough. Figure 1 shows that the updated parameter space, allowed by FRB data from two radio experiments, can be constrained within \(G\mu \sim [10^{-17}, 10^{-12}]\) and \(I_c \sim [10^{-1}, 10^2]\) GeV. For each data set, our detailed analysis declared a best-fitting contour estimated by \(\chi ^{2}_{min}\). The burst event rate per year for the aforementioned constrained parameter space ranges approximately between \(10^2\) to \(10^6\), which is consistent with the analysis conducted by [50, 59].

The current studies have been conducted under some simplifying assumptions that can be reconsidered in the future research. The string tension might rely on the current distribution, i.e. \(\tilde{G\mu }=G\mu \times \Phi (I)\), while we have taken \(G\mu \) to be the averaged tension along the string length in our work. Also, we have ignored the cosmological expansion for the number density defined in the dark energy era. As our universe has entered into a dark energy epoch, it is challenging to probe the radiation mechanism. The lack of convincing theoretical arguments to determine the number density in the dark energy era has given rise to a discrepancy for this approach.

In addition, from all the detected FRBs, six repeated bursts from FRB180814.J0422\(+\)73 have been reported in [60]. We intend to look at two aspects for repeated bursts; one is observational and the other theoretical. For the observational aspect, we expect more data, and along the theoretical line, we need more in-depth knowledge to explore these signals. In this regard, the precise measurement of energy released from our proposed parameterization could help to identify the theoretical origin for repeated FRBs.

Because of the precise constraints from FRBs, SCSs can be treated as the possible source for FRBs. In this perspective, the current in the string loops could be in the range of the GeV scale which makes the SCS a useful tool to investigate the high-energy paradigm along with collider experiments, for instance, the International Linear Collider and the Large Hadron Collider.