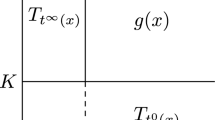This letter is an attempt to describe a meaning of the new parameter, the rank of the tensor, which can be arbitrary in generic string theory, and which has been finally brought to light in modern theory of tensor models. As usual with the free parameters, the crucial point is to understand what happens to the theory when the parameter is changed. Since so far the tensor rank is discrete, the changes are also discrete and imply some mapping between theories with different field content. If one wants the rank to be a true free parameter, this mapping should be functorial, at least w.r.t. embedding morphisms, i.e. if one restricts the symmetry or the gauge content in one theory, the same should happen to its image. Potentially the intertwined morphisms should be more involved and concern both kinematics and dynamics of the theory. In this paper, we provide such a map, which looks quite universal and thus promising. At the moment, it is restricted to a pure combinatorial problem of classification of states (which is by itself quite complicated in tensor models), but it clearly has a good potential for much more: in fact, already at this level, it relates kinematics of one model with dynamics of another one. To emphasize the universal meaning of this functor, wherever possible we present a discussion in generic terms of quantum field theory, and restrict consideration to the simplest tensor models only at the points where sample calculations are needed to illustrate a power of the method.

In modern quantum field theory, through functional integrals or operator products (see [1], for example), Gaussian averages of a set of operators, invariant under a given symmetry, can serve as a starting point of the perturbative consideration. In the case of four spacetime dimensions, the criterion of perturbative renormalizability to tame UV divergences selects the list of such operators to consist of a few ones, and we can start full-fledged perturbation theory based on the action in accord with the list. Physical S-matrix can be extracted by resorting to the state/operator correspondence.

Over the years, we have, however, occasionally seen cases in the study of (supersymmetric) low energy effective actions where we may even enumerate the whole set of such singlet operators and lift our considerations to all possible vacua and perturbation theory thereon. This phenomenon is known to be handled by the matrix model in general [2, 4, 5] and the structure of chiral ring [6] is responsible for the reduction in the degrees of freedom from four dimensional quantum fields to zero dimensional matrices. In this letter, we point out a novel functorial relationship that lies in Feynman diagrams (FD) having no external line in one theory \(\mathbf{Th}_1\) and singlet operators in another one \(\mathbf{Th}_2\) having an additional \(U(\mathcal{N})\) symmetry. We will refer to this as FD functor from now on.

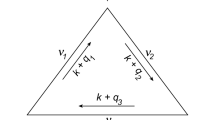
We will present the FD functor in the rank r complex tensor model which has been studied in [7, 10, 11, 13, 14]. The symmetry group is \({\prod _{i=1}^r} U({N}_i)\) (as opposed to U(N)) and the rank r implies r different colorings in the diagrams representing the operators. The cases with lower r are the vector model for \(r=1\), the rectangular complex matrix model for \(r=2\), and the Aristotelian tensor model for \(r=3\), and so on. The FD functor relates Feynman diagrams (FD) in \(\mathbf{Th}_1 =\varvec{\mathcal{T}}_{r-1} \) with singlet operators in \(\mathbf{Th}_2 =\varvec{\mathcal{T}}_r\). Accordingly, the number of entries of the former coincides with that of the latter:

$$\begin{aligned} \boxed {\begin{array}{cc} &{}\# ({\text { Feynman diagrams in}}\ \varvec{\mathcal{T}}_{r-1}) \\ &{}= \# ({\text {singlet operators in}}\ \varvec{\mathcal{T}}_r) \end{array}} \end{aligned}$$
(1)

This equality holds at each level, i.e. the number of Feynman diagrams with n propagators in \(\varvec{\mathcal{T}}_{r-1}\) is equal to the number of singlet operators with 2n vertices in \( \varvec{\mathcal{T}}_{r}\). Moreover, at the large \(\mathcal{N}\) limit, values of the Feynman diagrams coincide with the Gaussian averages of the singlet operators. That Eq. (1) holds in the case of \(r=3\) was first observed in [15]. The purpose of this letter is to demonstrate this operator/FD correspondence fully.

Restricting ourselves to rank 2–rank 3 correspondence, we will discuss that the above FD functor can be combined with the geometrical pictures of the dual of the original FD, namely, the equilateral triangulations (Grothendieck’s dessins d’enfant) [16] to form a triality. In particular, we will relate directly any rank 3 tensor operator with a dessin and the map associated with it and this triality provides a higher-rank point of view for the two different approaches to non-critical string theory (two-dimensional system coupled to 2d gravity), which are the continuum one based on the direct integration over 2d metric [17] and the discretized one given by the matrix model [18].

In Feynman diagram calculations of local quantum field theory in d dimensions, expressions for the values take a (somewhat trivial) factorized form of the part containing tensorial structure associated with the internal symmetry and the well-known part of the spacetime propagator. This is a consequence of the theorem [19] in cases where the symmetry of fields are reflected in the symmetry of S-matrix. We will, in fact, see easily that the above FD functor can act on the d dimensional QFT generalization of the tensor model as well and this uplift should hold in a more general setup as long as the theorem applies.

Let us now consider the \(\varvec{\mathcal {T}}_r/\varvec{\mathcal {T}}_{r-1}\) correspondence. The level n operators in the rank r model are obtained by contracting all indices of n tensors \(M_{a_1a_2\ldots a_r}\) with those of n complex conjugates \(\bar{M}^{a_1a_2\ldots a_r}\):

$$\begin{aligned} K_{\vec {\sigma }^{(r)}} = \prod _{p=1}^n M_{a_1^p\ldots a_r^p} \bar{M}^{a_1^{\sigma _1(p)}\ldots a_r^{\sigma _r(p)}}, \end{aligned}$$
(2)

where the contraction is specified by an r-ple of permutations \(\vec {\sigma }^{(r)} = (\sigma _1,\ldots ,\sigma _r) \in S_n^{\otimes r}\). The i-th index runs over \(1, \ldots , N_i\).

On the other hand, any Feynman diagram (no external line) with n propagators is given by the Wick contractions of a level n operator. Let us consider the Wick contractions of a rank \(r-1\) operator designated \(K^{(n)}_{\vec {\sigma }^{(r-1)}}\) in \(\varvec{\mathcal {T}}_{r-1}\). The corresponding Feynman diagram is specified by a permutation \(\sigma \in S_n\),

(3)

where

(4)

is the Wick contractions of the p-th M and the q-th \(\bar{M}\) in \(K_{\vec {\sigma }^{(r-1)}}\).

Now let us form an r-component vector \((\vec {\sigma }^{(r-1)}, \sigma ) \in S_n^{\otimes r}\). Recall that the operator (2) is labeled by an r-ple of permutations and, therefore, there is always a rank r operator labeled by \((\vec {\sigma }^{(r-1)}, \sigma )\).

Conversely, for any rank r operator, by interpreting the contraction of any one of r indices as a symbol specifying the Wick contraction pair, we can also obtain the corresponding rank \(r-1\) Feynman diagram.

Hence the following correspondence is established,

$$\begin{aligned} \mathbf{FD }_{\sigma } \left( K_{\vec {\sigma }^{(r-1)}}\right) ~~ \leftrightarrow ~~ K_{(\vec {\sigma }^{(r-1)}, \sigma )}. \end{aligned}$$
(5)

This correspondence is one to one and we obtain the relation (1).

Let \({{\text {Op}}}^{(r)}\) be the set of all operators in the rank r tensor model and \({\text {FD}}^{(r-1)}\) be the set of all Feynman diagrams in the rank \(r-1\) tensor model. For any operator K, we define \(FD_{i}\) \((i=1,\ldots r)\) by \({\text {Op}}^{(r)} \ni K \mapsto FD_{i}(K) \in {\text {FD}}^{(r-1)}\), mapping K to the corresponding Feynman diagram. Here, the subscript i means that the contraction by the i-th index \(a_i\) is interpreted as the Wick contraction symbol. One may pick any i as that does not change the nature or category of our functor and we may denote \(N_i\) by \({\mathcal {N}}\).

Let us consider the Gaussian average \(\langle K \rangle \) for an operator \(K \in \text {Op}^{(r)}\) at level n. The leading term in \(N_i\) is order n and comes from the case where all of the Wick contractions of M and \(\bar{M}\) are accompanied with the \(a_i\) index loops:

$$\begin{aligned} \langle K \rangle = N_i^n \prod _{j \ne i} N_j^{P_j} + {\mathcal {O}}(N_i^{n-1}). \end{aligned}$$
(6)

Here, the exponent \(P_j\) is some integer less than or equal to n. On the other hand, \(FD_i (K)\) has the following contribution to the Gaussian average of the rank \(r-1\) operator,

$$\begin{aligned} \text {value}\left\{ FD_i (K)\right\} = \prod _{j \ne i} N_j^{P_j}. \end{aligned}$$
(7)

We obtain

$$\begin{aligned} \text {value}\left\{ FD_i (K)\right\} = \lim _{N_i \rightarrow \infty } \frac{1}{N_i^n} \langle K \rangle , \end{aligned}$$
(8)

demonstrating that the Op/FD correspondence is realized as the relation between the Gaussian averages as well. For any rank \(r-1\) operators \(O^{(r-1)}\), there is a linear combination of the operators \(O^{(r)}\) in the rank r model such that

(9)

For example, one can check the \(\varvec{\mathcal {T}}_3/\varvec{\mathcal {T}}_2\) correspondence

(10)
(11)

See [10] for evaluating the averages. Here the rank 2 tensors (rectangular matrices) are denoted by A and \(\bar{A}\) and

figure a
figure b

Let us specifically consider the \(\varvec{\mathcal {T}}_3/\varvec{\mathcal {T}}_2\) correspondence. We will see that the correspondence in this case extends to the triality including a relation with dessin. A dessin D is a graph embedded into a compact orientable surface X satisfying the following conditions:

  • It is constructed by bicolored (red and green in this letter) vertices and edges.

  • Each edge connects the vertices which have the different color.

  • Multiple edges can end on a vertex.

  • The complement \(X\backslash D\) is a disjoint union of the connected components which are called faces. Each face is homeomorphic to an open disk.

The dessins are closely related to the so-called Belyi functions. The Belyi function is a meromorphic function \(\beta : X \rightarrow \mathbb {C}P^1\) unramified outside \(\{0,1,\infty \}\). The pair \((\beta ,X) \) is called Belyi map. It is well-known that there is one to one correspondence between dessins and Belyi maps up to an automorphism of X. For any dessin D, there exists a Belyi function \(\beta \) on X and \(D = \beta ^{-1} ([0,1])\). the concrete relations are as follows:

  • the red vertices are \(\beta ^{-1}(0).\)

  • the green vertices are \(\beta ^{-1}(1).\)

  • the edges are \(\beta ^{-1} ([0,1])\)

The number of edges ending on each vertex is equal to the ramification index and there is only one pole on each face.

The operator/dessin correspondence is as follows: Every operator of level n contains n blue lines. Let us choose one of the blue lines. There are a red-blue cycle and a green-blue cycle which share the blue line as the common boundary. In particular, these two faces can have the same orientation. Therefore, when we paint the regions surrounded by the red-blue (resp. green-blue) cycles in red (resp. green) for any connected rank 3 operator, the diagram representing the operator becomes an orientable surface painted in two colors. The blue lines are the common boundaries of two adjacent regions. In order to obtain the corresponding dessin, the following replacements should be made:

figure c

For example,

figure d

where the function \(\beta : {\mathbb {C}P}^1 \rightarrow {\mathbb {C}P}^1\) is the Belyi function associated to the dessin. Similarly,

figure e
figure f
figure g
figure h
figure i
figure j
figure k
figure l
figure m
figure n

The dessin corresponding to \(K_{3W}\) is non-planar and can be embedded in a two-torus as shown in Fig. 1. The Belyi function is given by \(\beta = \frac{1}{2} (1+y)\) on X: \(y^2 = x^3+1\), \(x,y \in \mathbb {C}\) [20].

Fig. 1
figure 1

The dessin embedded in a two-torus

Full size image

We have checked the correspondence up to level 4. The numbers of the connected operators at each level are \(1,3,7,26,\ldots \). Here 6 of 26 operators at level 4 correspond to dessins on torus. The operators of genus \(g \ge 2\) appear at level 5 or higher. These are, of course, in accord with the Riemann–Hurwitz formula

$$\begin{aligned} 2g-2 = n - { V_R} - { V_G} - { F}, \end{aligned}$$
(26)

where n is the number of edges (the level of the operator), \(V_R\) and \(V_G\) are the numbers of red and green vertices respectively and F is the number of faces [21] .

The dessins and the rank two Feynman diagrams are dual to each other, namely,

(27)

The centers of faces are the poles of the Belyi function and each face contains only one pole.

For example,

figure o

where the center of the face is denoted by \(\otimes \). This dessin is embedded in a sphere and there exists, therefore, one face. Note that the exponents of and are equal to the numbers of red and green vertices respectively. This is because the vertices in a dessin correspond to the faces in the corresponding Feynman diagram.

The above discussion provides the following bulk-boundary correspondence at the range (“the target space”) of the Belyi function and its uplift to the rank 3 operators. The vertices of each FD lie at infinity, namely, at the “boundary” of the complex plane. As for the propagators, they start and end at infinity where the vertices lie. They must also cross the segment [0, 1] as they are dual to the edges, and, therefore, extends over the entire complex plane. See [22] for a similar discussion.

Finally, it is straightforward to extend the Op/FD correspondence to the d dimensional field theory described by the spacetime dependent tensors \(M_{a_1a_2\ldots }(x)\) and \(\bar{M}^{a_1a_2\ldots }(x)\) . Let us consider the large \({\mathcal {N}}\) limit of the average of a singlet operator in the rank r theory:

$$\begin{aligned} \lim _{{\mathcal {N}} \rightarrow \infty } \frac{1}{{\mathcal {N}}^n} \int dx \langle O_{r,n}(x) \rangle , \end{aligned}$$
(29)

where \(O_{r,n}(x)\) is a level n operator. Following the discussion leading to (9), it is easy to see that (29) has the corresponding Feynman diagram in the rank \(r-1\) d dimensional QFT. The average (29) of level n operator includes n propagators, each of which contains a momentum dependent factor. As discussed above, the tensorial structure determines the corresponding Feynman diagram which has no external line and, therefore, all momenta have to be integrated.

For example, the level 3 operator \(K_{3W}(x)\) in the rank 3 theory corresponds to a non planar graph:

(30)

Here G(p) is the momentum part of the propagator.