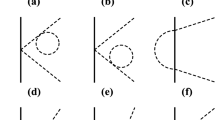1 Introduction

Understanding meson–baryon scattering processes at low and intermediate energies involving strangeness is a non-trivial problem. One often uses the so-called chiral unitary approach (see e.g. Ref. [1] for an early review), which involves a non-perturbative resummation of the chiral amplitude to extend the range of applicability of low-energy effective field theory (EFT) into the resonance region. This, however, comes with certain shortcomings as discussed below. So far, a variety of unitarization methods have been proposed. In the pioneering work by the Munich group [2,3,4], the Lippmann-Schwinger equation in coupled channels were used to iterate the leading order (LO) kernel in the region of the \(\Lambda (1405)\) and \(N^*(1535)\) resonances, employing Gaussian regulators to tame the UV behaviour of the chiral potential. In Refs. [5, 6], the relativistic counterpart of the scattering equation, the Bethe–Salpeter equation, was employed to sum up the iterations of the covariant interaction kernel. Besides, different frameworks were subsequently developed based on the inverse amplitude method (IAM) [7,8,9], the N/D method (based on dispersion relations) [10, 11] and the Bethe–Salpeter equation supplemented by large-\(N_C\) constraints [12], to name a few. Clearly, having such a variety of unitarization schemes introduces some model-dependence in the chiral unitary approach, which can be minimized if one enforces a matching to the perturbative amplitudes, as suggested in [11].

Chiral unitary approaches have been used to describe hadron scattering amplitudes and interpret the molecular components of resonances. Arguably the most striking result of this method is the interpretation of the \(\Lambda (1405)\) resonance as a superposition of two states [11, 13]. To identify the nature of resonances, one has to carefully derive the kernel of the meson–baryon scattering amplitude order by order in chiral perturbation theory (ChPT). At lowest order, one has to take into account the Weinberg-Tomozawa (WT) contact term as well as the Born and crossed-Born term contributions. Often considered as the most important piece of the LO kernel, the WT term has been mostly employed in the initial studies of meson–baryon scattering, see e.g. Ref. [5]. This approximation should, however, not be performed any more. First, one cannot expect that this is suitable for all the meson–baryon scattering channels, because the WT term does not contribute to e.g. the \(K^- p \rightarrow K^+\Xi ^-, K^0\Xi ^0\) reactions. Second, and most importantly, such an approach violates the counting rules of the underlying effective field theory, which states that one has to include all terms at a given order, not just picking the presumably dominant one(s). Thus, beyond the WT term, the Born and crossed-Born terms in the lowest order and the higher order contributions are necessary to improve the description of the rich information available for meson–baryon scattering.

Along this line, in Ref. [8], the scattering amplitudes up to next-to-next-to-leading order (NNLO) in the heavy baryon (HB) ChPT [14, 15] have been employed in the chiral unitary approach. The obtained results turned out to provide a reasonably good description of the scattering data up to around 1.3 GeV, including the region of the \(\Delta (1232)\) resonance in the \(P_{33}\) partial wave. A further step in this direction was the Bethe–Salpeter approach in Ref. [16] (see also Ref. [17]) used to investigate pion-nucleon scattering in the \(S_{11}\) partial wave, showing that both the \(N^*(1535)\) and the \(N^*(1650)\) can be dynamically generated. Also, it should be pointed out that state-of-the-art investigations of the \(\Lambda (1405)\) employ kernels at least to NLO accuracy, see e.g. Ref. [18] for a comparison of different approaches and Ref. [19] for a recent study including also P-waves. Extending these results beyond NLO accuracy can indeed lead to distortions of the analytic structure, as exemplified in Ref. [20].

In recent years, covariant ChPT with the extended-on-mass-shell (EOMS) scheme [21,22,23] was utilized because of the somewhat faster convergence than HB scheme in the one-baryon sector [24,25,26,27]. Hence, in the chiral unitary approach, one might also want to use the relativistic meson–baryon interaction from covariant ChPT. Thus, the relativistic integral equation, e.g. the Bethe–Salpeter equation (\(T=V+ VGT\)), has to be employed to obtain the unitarized amplitude in such a Lorentz-invariant framework. This is, in general, a technically very demanding task. In practice, the approximation of on-shell factorization, which takes V and T on shell to factor out the four-dimensional integral, is often used to solve the Bethe–Salpeter equation [5, 28].

Due to the resummation of the interaction kernel in the unitarization procedure, not all the ultraviolet divergent terms of the meson–baryon scattering amplitude can be absorbed in the low-energy constants (LECs) of the effective Lagrangians. Therefore, in chiral unitary approaches, the amplitudes depend on the cutoff parameter (\(\Lambda \)) or the subtraction constant(s) [11, 29, 30]. To obtain an explicitly renormalizable approach we apply the rules of time-ordered perturbation theory (TOPT) [31] to the effective Lagrangian of mesons, baryons and vector mesons as dynamical degrees of freedom. The inclusion of vector mesons leads to a softer UV-behaviour as will be discussed below. We define the effective meson–baryon potential as the sum of the two-particle irreducible TOPT diagrams contributing to the meson–baryon scattering amplitudes. The scattering amplitudes are obtained by solving the corresponding integral equations. The advantage of this formulation as compared to the alternative approaches mentioned above is that the leading-order scattering amplitude is renormalizable. This guarantees that all divergences can be removed by renormalizing the coupling constants available at a given order, provided that the higher-order corrections to the effective potential are taken into account perturbatively. To demonstrate how this formalism can be applied to a meson–baryon scattering problem, we apply it to elastic pion-nucleon (\(\pi N\)) scattering, where we use the parameterization of fields specified in Ref. [32] (this parametrization is only suitable for the two-flavor case).

Our paper is organized as follows: In Sect. 2 we specify the effective Lagrangian for meson–baryon scattering in the three-flavor case. An integral equation for the meson–baryon scattering amplitude using TOPT is derived in Sect. 3. In Sect. 4, we discuss the application of the developed formalism to the LO pion-nucleon scattering amplitude and the results of our work are summarized in Sect. 5. Some technicalities are relegated to the appendices.

2 Effective Lagrangian

We start with the effective Lagrangian of the interacting SU(3) octet fields of pseudoscalar mesons P, baryons B, and the vector mesons \(V_\mu \) in the vector field representation of Ref. [33] (corresonding to model II of Ref. [34]) invariant under the symmetries of QCD, in particular the non-linearly realized spontaneously broken chiral symmetry. We include vector mesons as explicit degrees of freedom because this improves the ultraviolet behaviour of meson–baryon integral equations without altering the low-energy scattering amplitudes. However, care has to be taken to avoid double counting, exemplified for the WT term in different effective Lagrangians in Ref. [33].

Our lowest-order Lagrangian is given by

$$\begin{aligned} \mathcal{L}_0= & {} \frac{F_0^2}{4}\, \text{ Tr }\left\{ u_\mu u^\mu +\chi _+\right\} + \text{ Tr } \left\{ \bar{\mathrm{B}} \left( i\gamma _\mu D^\mu -m \right) \mathrm{B} \right\} \nonumber \\&- \frac{1}{4} \, \mathrm{Tr} \left( V_{\mu \nu } V^{\mu \nu } - 2 M_V^2 \,V_{\mu } V^{\mu } \right) \nonumber \\&+ \frac{D/F}{2} \text{ Tr } \left\{ \bar{\mathrm{B}} \gamma _\mu \gamma _5 [u^\mu ,\mathrm{B}]_{\pm }\right\} \nonumber \\&+\left( G_D/G_F\right) \text{ Tr } \left\{ \bar{\mathrm{B}} \gamma _\mu [V^\mu ,\mathrm{B}]_{\pm }\right\} , \end{aligned}$$
(1)

where

$$\begin{aligned}&V_{\mu \nu }= D_\mu V_\nu - D_\nu V_\mu , \ D_\mu \mathrm{X} = \partial _\mu \mathrm{X}+[\Gamma _\mu , \mathrm{X}], \nonumber \\&\quad \Gamma _\mu =\frac{1}{2} \left( u^{\dagger } \partial _\mu u + u \partial _\mu u^\dagger \right) , \nonumber \\&u_\mu =iu^{\dagger } \partial _\mu U u^{\dagger },\ u^2=U=\exp \left( \sqrt{2} i P/ F_0 \right) ,\nonumber \\&\quad \chi _{\pm }= u^\dagger \chi u^\dagger \pm u \chi ^\dagger u, \ \chi = 2 B_0 \mathcal{M}~. \end{aligned}$$
(2)

Here, \(F_0\) is the pion decay constant in the three-flavor chiral limit, while D, F, \(G_D\) and \(G_F\) are coupling constants, \(\mathcal{M}\) denotes the quark mass matrix and \(B_0\) is related to the scalar quark condensate. The SU(3) matrix U is parametrized in terms of the pseudoscalar meson octet.

We take into account the results of Ref. [35] obtained from the analysis of constraints imposed on the interactions of vector meson fields leading to \(G_D=0\) and \(G_F=g\), with g the coupling of the vector-field self-interactions, corresponding to a massive Yang-Mills theory [36, 37]. Analogously to Ref. [34], we introduce new vector fields by substituting \(V_\mu = {\bar{V}}_\mu -(i/g) \Gamma _\mu \) and obtain, modulo terms of higher order in the chiral expansion and/or with more than two vector fields, the following Lagrangian

$$\begin{aligned} \mathcal{L}_0= & {} \frac{F_0^2}{4}\, \text{ Tr }\left\{ u_\mu u^\mu +\chi _+\right\} + \text{ Tr } \left\{ \bar{\mathrm{B}} \left( i\gamma _\mu \partial ^\mu -m \right) \mathrm{B} \right\} \nonumber \\&- \frac{1}{4} \, \mathrm{Tr} \left( {\bar{V}}_{\mu \nu } {\bar{V}}^{\mu \nu } - 2 M_V^2 \,\left( {\bar{V}}_{\mu } -\frac{i}{g} \, \Gamma _\mu \right) \left( {\bar{V}}^{\mu } -\frac{i}{g} \, \Gamma ^\mu \right) \right) \nonumber \\&+ \frac{D/F}{2} \text{ Tr } \left\{ \bar{\mathrm{B}} \gamma _\mu \gamma _5 [u^\mu ,\mathrm{B}]_{\pm }\right\} + g \, \text{ Tr } \left\{ \bar{\mathrm{B}} \gamma _\mu [{\bar{V}}^\mu ,\mathrm{B}]\right\} , \end{aligned}$$
(3)

where \({\bar{V}}_{\mu \nu } = \partial _\mu {\bar{V}}_\nu - \partial _\nu {\bar{V}}_\mu -i g[{\bar{V}}_\mu , {\bar{V}}_\nu ]\). Notice that the covariant derivatives have been replaced by ordinary ones in Eq. (3), similar to the two-flavor parameterization of Ref. [32]. To calculate the meson–baryon scattering amplitudes, we apply the diagrammatic rules of TOPT [31] corresponding to the effective Lagrangian of Eq. (3).

We should mention here that this approach still lacks some physics, namely the explicit inclusion of the \(\Delta (1232)\) resonance, see e.g. Ref. [10] (or, more generally, the inclusion of the spin-3/2 decuplet). The \(\Delta (1232)\) can not be generated dynamically if one insists on a matching to chiral amplitudes at low energies or in the unphysical region as done in Refs. [38,39,40]. In particular, very large dimension-two and dimension-three LECs incompatible with the above mentioned determinations were found to be necessary in order to generate a resonance in the \(P_{33}\)-wave using the IAM in Ref. [8].

3 Integral equations for meson–baryon scattering

The meson–baryon scattering amplitude \(T_{MB}\) is obtained from the four-point vertex function \({\tilde{\Gamma }}_{4}\) by applying the standard LSZ formula

$$\begin{aligned} T_{MB}= & {} Z_{B_i}^{1/2} Z_{B_f}^{1/2} Z_{M_i}^{1/2}Z_{M_f}^{1/2}\, {\bar{u}}(p_f)\,{\tilde{\Gamma }}_{4}^{}\,u(p_i) \nonumber \\\equiv & {} Z_{B_i}^{1/2} Z_{B_f}^{1/2} Z_{M_i}^{1/2}Z_{M_f}^{1/2}\, {\tilde{T}}~, \end{aligned}$$
(4)

where \(Z_{M_i}\) (\(Z_{M_f}\)) and \(Z_{B_i}\) (\(Z_{B_f}\)) are the residues of the propagators corresponding to the initial (final) meson and baryon, respectively and u, \({\bar{u}}\) are Dirac spinors corresponding to the incoming and outgoing baryons, in order. The on-shell amplitude \({\tilde{T}}\) is given as a sum of an infinite number of TOPT diagrams. Notice that it does not include diagrams with corrections on the external legs. Let us discuss this in more detail. It is convenient to define the effective meson–baryon potential as a sum of all possible meson–baryon irreducible TOPT diagrams. The amplitude \({\tilde{T}}\) is then given by an infinite series

$$\begin{aligned} {\tilde{T}}= & {} {\tilde{V}}+{\bar{V}} G\, {\bar{V}} +{\bar{V}} G\, V G\, {\bar{V}}+ {\bar{V}} G\, V G\, V G\, {\bar{V}} +\cdots \nonumber \\= & {} {\tilde{V}}+{\bar{V}} G\, {\bar{V}} +{\bar{V}} G\, \left[ V + V G\, V +\cdots \ \right] G\, {\bar{V}}\nonumber \\= & {} {\tilde{V}}+{\bar{V}} G\, {\bar{V}} +{\bar{V}} G\, T G\, {\bar{V}}, \end{aligned}$$
(5)

where G is the meson–baryon Green function and \({\tilde{T}}\), T, \({\tilde{V}}\), \({\bar{V}}\) and V are the on-shell amplitude, the off-shell amplitude, the on-shell potential, the half-off-shell potential and the off-shell potential, respectively. The on-shell potential \({\tilde{V}}\) does not include diagrams with corrections on the external legs. The half-off-shell potential \({\bar{V}}\) does not include diagrams with corrections on the external legs with on-shell momenta while the off-shell potential V also includes diagrams with corrections on the external legs. The off-shell amplitude T satisfies the following equation:

$$\begin{aligned} T=V+ V G\,T. \end{aligned}$$
(6)

To cover all processes with different strangeness, Eq. (6) has to be understood as a matrix equation, i.e. one has to deal with coupled channels.

The meson–baryon scattering amplitude can be conveniently calculated in the center-of-mass system (CMS). We denote the relative three-momenta of the incoming and outgoing particles in the CMS by \(\vec {p}\) and \(\vec {p}\,'\), respectively. In the partial wave basis, Eq. (6) leads to the following coupled equations with the potentials \(V^{M_fB_f,M_iB_i}\left( \vec {p}\,', \vec {p}\right) \),

$$\begin{aligned}&T^{M_fB_f,M_iB_i}\left( E; {\vec {p}\,'} ,\vec {p}\right) \nonumber \\&\quad = V^{M_fB_f,M_iB_i}\left( E;\vec {p}\,',\vec {p}\right) \nonumber \\&\qquad + \sum _{M,B} \int \frac{d ^3\vec {k} }{(2 \pi )^3} V^{M_fB_f,MB}(E;\vec {p}\,',\vec {k})\nonumber \\&\qquad \quad \times G^{MB}(E) \, T^{MB,M_iB_i} (E; \vec {k} ,\vec {p}), \end{aligned}$$
(7)

where \(M_iB_i,M_fB_f\) and MB denote initial, final and intermediate particle channels. Further, the two-body Green functions read

$$\begin{aligned} G^{MB}(E)= \frac{1}{2\, \omega _M \omega _B}\, \frac{-m_B}{E - \omega _M-\omega _B+i \epsilon } , \end{aligned}$$
(8)

where \(m_I\) and \(\omega _I\equiv \omega _I(q,m_I):=\left( \vec {q}\,{ }^2+m_I^2\right) ^{1/2}\) are the mass and energy of the \(I^{\mathrm{th}}\) hadron.

To calculate the meson–baryon scattering amplitudes, we apply the standard power counting to the effective potential for its expansion in powers of a small parameter and solve the leading order equation for the amplitude

$$\begin{aligned} T_0 = V_0 + V_0 \, G \ T_0 . \end{aligned}$$
(9)

Higher order corrections to the effective potential can be taken into account perturbatively, or alternatively, subtractive renormalization, analogous to the one outlined in Ref. [41], can be applied. For the next-to-leading order correction \(T_1\) we have

$$\begin{aligned} T_1=V_1+ T_0\,{ G}\, V_1+ V_1\,{ G}\, T_0+ T_0\,{ G}\,V_1\,{ G}\,T_0, \end{aligned}$$
(10)

and higher order corrections can be obtained analogously. In practice, we will solve the half-on-shell equation and then put the solution fully on-shell.

In the next section we apply this formalism to \(\pi N\) scattering as an example. Applications in SU(3) BChPT will be considered in forthcoming publications.

4 Application to pion-nucleon scattering

In the limit of exact isospin symmetry, the on-shell amplitude of the elastic \(\pi N\) scattering reaction \(\pi ^a(q_1)+N(p_1)\rightarrow \pi ^{b}(q_2)+N(p_2)\), with Cartesian isospin indices a and b, can be parameterized as

$$\begin{aligned} T_{\pi N}^{b a}(s,t,u)= & {} \chi _{N^\prime }^\dagger \left\{ \delta _{b a}T^+(s,t,u) \right. \nonumber \\&\left. +\frac{1}{2}[\tau _{b},\tau _a]T^-(s,t,u)\right\} \chi _N\ , \end{aligned}$$
(11)

where the \(\tau _i\) are the Pauli matrices and \(\chi _{N}\), \(\chi _{N^\prime }\) denote nucleon iso-spinors. The conventional Mandelstam variables are defined as \(s=(p_1+q_1)^2,\ t=(p_1-p_2)^2,\ u=(p_1-q_2)^2\), subject to the constraint \(s+t+u= 2(m_N^2+M_\pi ^2)\).

The Lorentz decomposition of the invariant amplitudes \(T^{\pm }\) reads (we use here the D-B representation instead of the more common A-B one, see e.g. [42]),

(12)

with the superscripts \(\lambda ^\prime \), \(\lambda \) denoting the spins of the Dirac spinors \(\bar{u}\), u, respectively.

We use Dirac spinors u(p) with four-momentum p:

$$\begin{aligned} u(p) = \left( \frac{\omega (p,m)+m}{2m}\right) ^{1/2} \left( \begin{array}{c} \chi \\ \frac{\vec {\sigma }\cdot \vec {p} \ \chi }{\omega (p,m)+m} \end{array}\right) , \end{aligned}$$
(13)

where m is the mass of the corresponding baryon and \(\chi \) a two-component spinor, and decompose

$$\begin{aligned} u(p)= & {} u_0 +\left[ u(p)-u_0\right] \equiv u_0 + u_{\mathrm{ho}}. \end{aligned}$$
(14)

Here \(u_0= \left( \chi \; 0 \right) ^T \) is the leading order contribution and \( u_{\mathrm{ho}}\) stands for the higher order part. The leading order contribution satisfies

(15)

with \(v=(1,0,0,0)\) in the rest-frame of the particle. For the reduced amplitude we use the following parameterization [43]

$$\begin{aligned} T^{ba}_{\pi N}= & {} \delta ^{ba} \left[ g^+ + i \,\vec \sigma \cdot (\vec q_2\times \vec {q}_1) h^+ \right] \nonumber \\&+ i\,\epsilon ^{bac} \tau ^c \left[ g^- + i \,\vec \sigma \cdot (\vec {q}_2\times \vec {q}_1) h^- \right] . \end{aligned}$$
(16)

The partial wave projection of the isospin amplitudes is given by

$$\begin{aligned}&f_{\ell \pm }^\pm (s) = \frac{m_N}{8\pi \sqrt{s}} \int _{-1}^{+1} dz\nonumber \\&\quad \times \left[ g^\pm \,P_\ell (z) +q(s)^2 h^\pm \,\left( P_{\ell \pm 1}(z) -z P_\ell (z)\right) \right] , \quad z\equiv \cos \theta ,\nonumber \\ \end{aligned}$$
(17)

where \(\theta \) is the scatting angle in the CMS frame, the \(P_\ell (z)\) are the Legendre polynomials and \(q(s)^2=((s-m_N^2-M_\pi ^2)^2-4 m_N^2 M_\pi ^2)/({4\,s})\). A commonly used parametrization of the partial wave amplitudes is

$$\begin{aligned} f_{\ell \pm }^I(s)= & {} \frac{1}{2iq(s)}\left\{ e^{2i\delta _{\ell \pm }^I(s)}-1\right\} . \end{aligned}$$
(18)

Here, the phase shifts \(\delta _{\ell \pm }^I(s)\) are real-valued functions.

4.1 LO pion-nucleon potential

We take the effective Lagrangian of pions, nucleons and the \(\rho \)-meson contributing to the LO \(\pi N\) potential in the form given by Weinberg in Ref. [32], where we also use the universality of the \(\rho \)-meson coupling [44]:

$$\begin{aligned} \mathcal{L}= & {} \frac{1}{2}\,\partial _\mu \pi ^a \partial ^\mu \pi ^a -\frac{M^2}{2}\, \pi ^a \pi ^a \nonumber \\&+{\bar{\Psi }} \left( i\gamma _\mu \partial ^\mu -m + \frac{g}{2} \, \gamma ^\mu \tau ^a \, \rho _\mu ^a +\frac{1}{2} {\mathop {g_A}\limits ^{\circ }}\gamma _\mu \gamma _5 u^\mu \right) \Psi , \nonumber \\&- \frac{1}{4} \, F^a_{\mu \nu } F^{a \mu \nu } + \frac{M_\rho ^2}{2}\,\rho _\mu ^a \rho ^{a\mu } + g \, \epsilon ^{abc} \pi ^a \partial _\mu \pi ^b \rho ^{c\mu }. \nonumber \\ \end{aligned}$$
(19)

Here, \(\pi ^a\) and \(\rho ^a_\mu \) are iso-triplets of the pion and \(\rho \)-meson fields with masses M and \(M_\rho \), respectively, and \(M_\rho ^2=2 g^2 F_\pi ^2\) (KSFR relation).Footnote 1 Further, \(F^a_{\mu \nu } =\partial _\mu \rho _\nu ^a-\partial _\nu \rho _\mu ^a+ g\, \epsilon ^{abc} \rho _\mu ^b \rho _\nu ^c\), \(\Psi \) is the doublet of the nucleon fields, m and \({\mathop {g_A}\limits ^{\circ }}\) are the chiral limit values of the nucleon mass and the axial-vector coupling constant, respectively. Notice that by integrating out the vector mesons from EFT defined by the Lagrangian of Eq. (19), one generates the standard chiral effective Lagrangian of pions and nucleons alone, including the Weinberg-Tomozawa term. As mentioned above, we prefer to work with dynamical vector mesons because the vector meson exchange diagram, which at low energies is equivalent to Weinberg-Tomozawa term, has a better ultraviolet behaviour.

Fig. 1
figure 1

Time-ordered diagrams contributing to the LO meson–baryon potential. The solid, wiggled and dashed lines correspond to baryons, vector mesons and pseudoscalar mesons, respectively

Full size image

The LO \(\pi N\) potential is given by time-ordered diagrams shown in Fig. 1. Notice that while we include the vector mesons as explicit degrees of freedom, for pion-nucleon scattering for small Mandelstam t all four components of the momenta \(q^\mu \) carried by vector meson lines are small compared to their masses.Footnote 2 Therefore, in the propagator of the vector meson \(\sim g^{\mu \nu }-q^\mu q^\nu /M_\rho ^2\), the contribution of the second term is suppressed compared to the first one. Thus, we include only the first term in the leading order potential by treating the second term as a higher order correction. This issue is discussed in more detail in Appendix A. In TOPT, this leads to the standard rules (i.e. similar to the ones for scalar particles) for intermediate states containing vector meson lines. Let us emphasize that this is completely different from processes involving external vector mesons, where such an approximation is not justified [45, 46].

By taking into account the projectors \(P_+\) which reduce the expressions corresponding to the diagrams of Fig. 1 to the LO contributions to the effective potential, we have (to obtain the amplitude/potential, one factor of i is dropped in the expressions of the diagrams):

$$\begin{aligned} V^{ba}_{\pi N}= & {} \delta ^{ba} \left[ g_V^+ + i \,\vec \sigma \cdot (\vec {q}_2\times \vec {q}_1) h_V^+ \right] + i\,\epsilon ^{bac} \tau ^c \nonumber \\&\times \left[ g_V^- + i \,\vec \sigma \cdot (\vec {q}_2\times \vec {q}_1) h_V^- \right] , \end{aligned}$$
(20)

with

$$\begin{aligned} g_V^{\pm }= & {} g_{V_a}^{\pm }+g_{V_b}^{\pm }+g_{V_{c+d}}^{\pm }, \quad h_V^{\pm } = h_{V_a}^{\pm }+h_{V_b}^{\pm }+h_{V_{c+d}}^{\pm }, \end{aligned}$$
(21)
$$\begin{aligned} g_{V_a}^{\pm }= & {} \vec {q}_1\cdot \vec {q}_2 \, h_{V_a}^{\pm }\nonumber \\= & {} \frac{ g_A^2 m_N}{4 F_\pi ^2} \frac{\vec {q}_1 \cdot \vec {q}_2 }{\omega \left( p_1 + q_1,m_N\right) \left( \omega \left( p_1 + q_1,m_N\right) - E -i\,\epsilon \right) },\nonumber \\ g_{V_b}^+= & {} - g_{V_b}^- \,=\, - \vec {q}_1 \cdot \vec {q}_2\, h_{V_b}^+ = \vec {q}_1 \cdot \vec {q}_2\, h_{V_b}^- \nonumber \\= & {} \frac{ g_A^2 m_N}{4 F_\pi ^2} \frac{\vec {q}_1\cdot \vec q_2}{\omega \left( p_1-q_2,m_N\right) \left( \omega \left( p_1-q_2,m_N\right) +\omega (q_1,M_\pi )+\omega (q_2,M_\pi )-E -i\,\epsilon \right) },\nonumber \\ g_{V_{c+d}}^+= & {} h_{V_{c+d}}^\pm = 0,\nonumber \\ g_{V_{c+d}}^-= & {} \frac{M_{\rho }^2\left( \omega (q_1,M_\pi )+\omega (q_2,M_\pi )\right) }{8F_\pi ^2\,\omega (q_1-q_2,M_\rho )}\nonumber \\&\times \left( \frac{1}{\omega \left( p_2,m_N\right) +\omega \left( q_1-q_2,M_{\rho }\right) +\omega \left( q_1,M_{\pi }\right) -E-i\,\epsilon } \right. \nonumber \\&\left. + \frac{1}{\omega \left( p_1,m_N\right) +\omega \left( q_1-q_2,M_{\rho }\right) +\omega \left( q_2,M_{\pi }\right) -E-i\,\epsilon }\right) . \end{aligned}$$
(22)

The actual calculations described below are performed in the CMS with \(\vec {p}_1 = - \vec {q}_1 = \vec {p}\) and \(\vec {p}_2 = - \vec {q}_2 = \vec {p}\, '\).

4.2 Renormalization

We work in the partial wave basis and write the leading order potential as the sum of the one-nucleon reducible and irreducible parts,

$$\begin{aligned} V _0 = V_{R} + V_I , \end{aligned}$$
(23)

where \(V_{R} =V_a\) and \(V_I=V_b + V_{c+d}\). For the above potential it is possible to write the solution to the LO equation in a form (analogously to Ref. [47]), that allows one to carry out a subtractive renormalization. To that end, we write the solution to the LO equation as [48]

$$\begin{aligned} T_0=T_I+(1+T_I\,G)\,T_R (1+G\,T_I). \end{aligned}$$
(24)

Here and in what follows, we use a symbolic notation and do not explicitly write the momentum integrations. The amplitudes \(T_I\) and \(T_R\) satisfy the equations

$$\begin{aligned} T_I=V_I+V_I\,G\,T_I, \end{aligned}$$
(25)

and

$$\begin{aligned} T_R=V_R+V_R\,G\, (1 + T_I G) \, T_R. \end{aligned}$$
(26)

Notice that while the amplitude \(T_I\) is finite in the removed regulator limit, it gets large finite contributions. For example, the one-loop diagram with the iterated rho-meson-exchange potential contains pieces which violate the chiral power counting. Such large power-counting-breaking contributions can (and must) be systematically removed by additional finite subtractions. We choose the subtraction scheme such that our iterated amplitude matches the perturbative one obtained in chiral EFT with the EOMS renormalization scheme [23]. To implement such subtractions, we apply a subtractive renormalization scheme analogous to the one of Ref. [41], adjusted to the pion-nucleon system. In particular, working in the CMS, we replace the pion-nucleon propagator G(E) with the subtracted propagator \(G_S(E)=G(E)-G(m_N)\). As discussed in Ref. [41], this corresponds to taking into account contributions of an infinite number of pion-nucleon counterterms. Notice that such extra subtractions have no influence on the dynamical generation of resonances or bound states, see Appendix B for details. Thus, instead of Eq. (24), we have

$$\begin{aligned} T_0^S=T_I^S+\left( 1+T_I^S\,G_S\right) \,T_R \left( 1+G_S\,T_I^S\right) , \end{aligned}$$
(27)

where the subtracted amplitude \(T_I^S\) satisfies the equation

$$\begin{aligned} T_I^S=V_I+V_I\,G_S\,T_I^S. \end{aligned}$$
(28)

The reducible potential \(V_R\) can, in the partial wave basis, be written as

$$\begin{aligned} V_R(E,p',p)= \xi ^T(p')\, \mathcal{C}(E)\xi (p)~, \end{aligned}$$
(29)

where \(\xi ^T(q) : = (1, q)\) with \(q \equiv | \vec {q} \,|\) and the \(2 \times 2\) matrix \(\mathcal{C}(E)\) is obtained from the partial wave reduction of Eq. (22). Then, the amplitude \(T_R\) is also given in a separable form

$$\begin{aligned} T_R(E,p',p)= \xi ^T(p') \mathcal{X}(E)\xi (p), \end{aligned}$$
(30)

with

$$\begin{aligned} \mathcal{X}(E)= \left[ \mathcal{C}^{-1}-\xi \,G_R\,\xi ^T - \xi \,G_R\,T_I^S G_R\, \xi ^T \,\right] ^{-1}. \end{aligned}$$
(31)

Thus the final expression for the amplitude T has the form

$$\begin{aligned} T_0^S=T_I^S+(\xi ^T+T_I^S\,G_R\,\xi ^T)\,\mathcal{X} (\xi + \xi \,G_R\,T_I^S)~. \end{aligned}$$
(32)

In a close analogy to Ref. [48], we apply subtractive renormalization, i.e. all divergences in all loop diagrams are subtracted and the coupling constants are substituted by their renormalized, finite values. For the amplitude of Eq. (32) this amounts to the procedure outlined below. A straightforward ultraviolet power counting demonstrates that the amplitude \(T_I^S\) as well as \(\Xi ^T (q') \equiv \xi ^T +T_I^S\,G_S\,\xi ^T\) and \(\Xi (q) \equiv \xi +\xi \, G_S\,T_I^S\) are finite while \(\mathcal{X}(E)\) is divergent. Renormalization is carried out by performing subtractions that correspond to taking into account counterterms generated by the renormalization of the nucleon mass and the pion-nucleon coupling constant. That is, the dreesed nucleon propagator is enforced to have a pole at the physical mass of the nucleon \(m_N\), and the renormalized pion-nucleon coupling is required to take its physical value \(g_A\).

Our results for the pion-nucleon phase shifts based on the renormalized amplitude are shown in Fig. 2 in comparison with the ones obtained from a perturbative tree-order calculation using the effective Lagrangiang with vector mesons and the results from the Roy–Steiner equation analysis [49] and the partial wave analysis of the George Washington University group (GWU) [50]. As expected for low-energies in the non-strange sector, the results for the renormalized resummed amplitudes are only slightly different from the ones of the perturbative approach. Notice that the \(P_{33}\)-wave can not be described properly as long as the \(\Delta (1232)\) is not included as an explicit degree of freedom, as it was already pointed out in Sect. 2. An extension to the delta-full case will be reported in a separate publication.

Fig. 2
figure 2

Pion-nucleon scattering phase shifts in standard partial-wave notation. Blue (dashed) lines are the LO perturbative results (tree-order result), red (solid) lines represent the results of the resummed LO potential, while the dots and circles correspond to the Roy–Steiner analysis [49] and GWU [50] phase shifts, respectively

Full size image

5 Summary

In this paper we considered the meson–baryon scattering problem starting with a manifestly Lorentz-invariant formulation of BChPT and applying time-ordered perturbation theory.

We defined the effective potential as a sum of two-particle irreducible time ordered diagrams contributing to the meson–baryon scattering amplitude. The full scattering amplitudes can be obtained by solving the corresponding integral equations. By considering an effective field theory of pseudoscalar and vector mesons and baryons, we obtained the integral equation for LO scattering amplitudes which is renormalizable. By treating higher-order terms in the effective potential as perturbative corrections one can maintain renormalizability also at higher orders.

The proposed approach for meson–baryon scattering in terms of the integral equations can provide quantitative information on the convergence of ChPT in the single-baryon sector [51,52,53]. ChPT provides a framework to perform perturbative calculation of the scattering amplitude order by order. It is, therefore, important to investigate the applicability of the chiral expansion, especially in the SU(3) sector, where the perturbative expansion parameter is \(m_K/\Lambda _\chi \sim 0.5\), with \(m_K\) denoting the kaon mass and \(\Lambda _\chi \) the chiral symmetry breaking scale. In the chiral unitary approach proposed in this paper, iterations of the meson–baryon scattering kernel within the integral equation result in the nonperturbative resummation of a certain class of renormalized contributions to the scattering amplitude which are of higher orders according to the chiral power counting. Thus, by comparing the non-perturbative amplitude with its perturbative expansion, one can get insights into the energy region of the applicability of the chiral expansion. Similarly, since the scattering amplitude is a function of the light-quark masses, we can also investigate the range of quark masses for which the chiral extrapolation of the lattice QCD data for meson–baryon scattering, see e.g. Refs. [54,55,56,57,58,59], can be trusted.

As a first but still somewhat simplistic application we considered here the pion-nucleon scattering amplitude and compared the phase shifts obtained by solving the leading order integral equation to those of chiral EFT. While the LO amplitude is finite in the removed cutoff limit, it gets large contributions that violate the chiral power counting in the low-energy region and therefore requires finite subtractions. After performing additional finite renormalization, the resummation of an infinite number of higher order contributions is found to yield small corrections to the phase shifts at low energies. We note again that this approach is not applicable to all partial waves since we have not included the \(\Delta (1232)\) as an explicit degree of freedom. This can be done straightforwardly as it merely amounts to the corresponding extension of the effective Lagrangian with no need to modify the approach to calculate the scattering amplitudes described in this work.

In view of the existing data on and the upcoming experiments of strangeness production, applying our renormalizable framework to study the meson–baryon scattering in the SU(3) sector will help to further understand the dynamics of hadrons with strangeness. In particular, antikaon-proton scattering plays an important role in the study of the two-pole nature of the \(\Lambda (1405)\) [11, 13, 18] and the properties of dense nuclear matter, see [60] for a recent review. Along this lines, we will carry out the leading- and next-to-leading order studies of the meson–baryon scattering amplitudes in the strangeness \(S=-1\) sector.