1 Introduction

In the past, the conventional quark model has successfully explained structures of numerous hadronic states observed in a large number of experiments. However, not all predicted particles by the quark model have been experimentally established. In particular, doubly heavy baryons, that is baryonic states made of two heavy quarks, are of this type. After pursuing the \(\Xi _{cc}\) for many years, the LHCb collaboration finally announced in 2017 the observation of \(\Xi _{cc}^{++}\), a lowest-lying doubly-charmed baryon whose mass is give as [1]

$$\begin{aligned} m_{\Xi _{cc}^{++}}=(3621.40\pm 0.72\pm 0.27\pm 0.14)\ \mathrm{MeV}. \end{aligned}$$
(1)

This inspiring observation follows an earlier prediction Ref. [2], where the \(\Xi _{cc}^{++}\) is expected to be reconstructed from the decay channel \(\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}\). One year later, LHCb has also successfully measured the \(\Xi _{cc}^{++}\)’s lifetime [3], and reconstructed this resonance from the \(\Xi _{c}^{+}\pi ^{+}\) final state [4]. Thus, the existence of the \(\Xi _{cc}^{++}\) is unambiguously established. We believe that through continuous experimental efforts [5,6,7], other heavier doubly heavy baryons could be discovered in the future. In addition, there have been numerous theoretical studies aiming to understand the dynamical and spectroscopical properties of the doubly-heavy baryon states, see e.g. Refs. [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. However, a comprehensive description of the decay mechanism of doubly heavy baryons is not established yet.

Generally, an ideal platform for studying hadrons is through semi-leptonic weak decays. The main advantage of a semi-leptonic process is its naturalness in separating the QCD relevant and the QCD irrelevant dynamics in the weak decays. All the QCD dynamics is encapsulated in the hadron transition matrix element, which is independent from the leptonic part and can be parametrized by several form factors. However, as a three-body system, a doubly heavy baryon possess a much more complicated dynamics than a heavy meson.

A straightforward way to consider this problem is to reduce a doubly heavy baryon into a two-body system, where two of the three quarks are treated as a point-like diquarks. Generally, each two quarks in a baryon form a color antitriplet so that they might be bound by an attractive potential. However, for a doubly heavy baryon, it is more reasonable to treat the two heavy quarks behave as static color sources and thus as a diquark. According to Refs. [36, 37, 43], there are three different momentum scales display in the dynamics of a doubly heavy baryon: the heavy quark mass \(m_Q\), its typical 3-momentum \(m_Qv\) in the rest frame of baryon, and its typical kinetic energy \(m_Qv^2\). The spatial size of the two heavy quarks can be estimated to be \(r_{QQ}\sim 1/{m_Qv}\), while the distance between one of the heavy quarks and the light quark is approximately \(r_{Qq}\sim 1/{\Lambda _{QCD}}\). As argued by Ref. [44], when \(m_Q\) is heavy enough the heavy quark velocity v is proportional to the running coupling constant \(\alpha _s(m_Q)\sim 1/\mathrm{{log}}(m_Q)\). Thus, for doubly bottom baryons, one can deduce that \(v_b\ll 1\) and \(m_bv_b^2\ll m_bv_b\ll m_b\). Particularly, quark potential model calculations indicate that for charm quark \(v_c^2\sim 0.3\) and for bottom quark \(v_b^2\sim 0.1\) [45]. This implies that \(m_b v_b^2\sim m_c v_c^2\sim \Lambda _{QCD}\sim 350-500\) MeV, while \(m_bv_b\sim 1.5\) GeV and \(m_cv_c\sim 800\) MeV. Thus, \(r_{bb}/r_{bq}\sim 1/m_{b}v_b \ll 1\) is perfectly satisfied and \(r_{cc}/r_{cq}\sim 1/m_{c}v_c\) is also suppressed. Accordingly, one can conclude that in a doubly bottom baryon, the two bottom quarks can be safely combined to be a point-like diquark, while the same treatment for the two charm quarks in a doubly charmed baryon is approximately reasonable. In the heavy diquark limit, the heavy diquark is a static color source in the \({\bar{3}}\) representation, just like a heavy anti-quark. Some earlier papers [46,47,48,49] have used the heavy quark-diquark symmetry to simplify the transition form factors.

In this work, we will try to develop a heavy diquark effective theory (HDiET), whose Lagrangian is expanded in powers of \(r_{QQ}/r_{Qq}\). At leading-order, the diquark appears as a point-like scalar or axial-vector particle described by a scalar or axial-vector field in the color \({\bar{3}}\) representation. The scalar HDiET has been developed in [50], where the leading order (LO) effective Lagrangian coupling two scalar diquarks and two light quarks was obtained. In this work, we will first construct HDiET for both scalar and axial-vector diquarks. For the transition form factors we will assume the applicability of HDiET, and by assuming the diquark to be a point-like particle, we can construct the weak and electromagnetic transition currents of the diquarks according to the \(\mathrm SU(2)\) heavy flavor symmetry and \(\mathrm U(1)\) symmetry. On the other hand, in the large recoil region, the diquark currents will be derived through the matching between QCD and HDiET at tree level. We then show that the six transition form factors of doubly heavy baryon semi-leptonic decay can be reduced into only one soft function. Furthermore, it will be shown that this soft function is an universal quantity which is nothing but the well known Isgur–Wise function in HQET for heavy meson decays. These results can be used in the phenomenology studies.

This article is organized as follows: In Sect. 2, we construct the LO diquark effective theory (DiET) Lagrangian including the kinetic part as well as the terms coupling with weak and electromagnetic fields. The DiET is also transformed to HDiET in the heavy diquark limit. In Sect. 3, we derive the diquark transition currents both from symmetry and tree level matching. Section 4 focuses on the semi-leptonic decays of doubly heavy baryons. We perform a reduction of the transition matrix element, where a universal soft function is factorized out and the \(q^2\) distributions of all the six form factors are completely determined from it. The resulting form factors are used to predict the semi-leptonic decay widths. Section 5 contains our conclusions.

2 Heavy diquark effective theory

2.1 Effective Lagrangian for scalar and axial-vector diquark

In this section we will construct the DiET at leading order. The first step is to write down the diquark effective Lagrangian. We denote the scalar and axial-vector diquark field as \(S^i\) and \(X^i_{\mu }\), where i is the \({\bar{3}}\) color index. The free scalar diquark Lagrangian is simply

$$\begin{aligned} {{\mathcal {L}}}_S={1\over 2}\partial _{\mu }S^{i\dagger }\partial ^{\mu }S^i-{1\over 2}m_X^2S^{i\dagger }S^i. \end{aligned}$$
(2)

Here we have assumed that both the scalar and axial-vector diquark have the same mass \(m_X\). On the other hand, to construct the axial-vector diquark Lagrangian, one should be aware of that \(X^i_{\mu }\) is a matter field in the color fundamental representation \({\bar{3}}\), instead of the adjoint representation which belongs to the standard gauge fields. Therefore, the axial-vector diquark field is not required to couple with any conserved current, and it seems not necessary to construct the effective Lagrangian with the building blocks of the strength tensor \(F_{\mu \nu }^i=\partial _{\mu }X^i_{\nu }-\partial _{\nu }X^i_{\mu }\) as is done for Yang-Mills theory. Instead, one can write down a general form

$$\begin{aligned} {{\mathcal {L}}}_{X}=a\ \partial _{\mu }X^i_{\nu } \partial ^{\mu }X^{\nu }_i+b\ \partial _{\mu }X^i_{\nu } \partial ^{\nu }X^{\mu }_i +c\ X^i_{\mu }X^{\mu }_i. \end{aligned}$$
(3)

However, note that \(X_{\mu }\) has four components while a spin-1 particle has only three physical degrees of freedom. According to the canonical theory, one needs to introduce two second-class constraints for the Hamiltonian to remove one redundant canonical variable as well as its conjugate momentum. As a result, one still arrives at a gauge-field-like Lagrangian

$$\begin{aligned} {{\mathcal {L}}}_{X}&=-\frac{1}{4}F_{\mu \nu }^{i\dagger }F^{\mu \nu i}+\frac{1}{2}m_{X}^{2}X_{\mu }^{i\dagger }X^{\mu i}, \end{aligned}$$
(4)

with an on-shell constraint condition \(\partial _{\mu }X^{i\mu }=0\).

Since the diquark is composed of two flavored heavy quarks, it is natural to dress the diquark fields with certain representation in the flavor space. Notice that in QCD, heavy quarks include bottom and charm. If we approximately assume \(m_b\sim m_c\rightarrow \infty \), the mass matrix for \((b, c)^T\) is almost diagonal so that there exists a flavor \(\mathrm {SU}(2)\) symmetry for the heavy quark sector of the QCD Lagrangian. Furthermore, in HQET, the leading power Lagrangian \({{\bar{Q}}}_v i v\cdot D Q_v\) is exactly invariant under the flavor \(\mathrm {SU}(2)\) transformation. Such a transformation on a multiplet \(Q=(b,c)^T\) is denoted as \(Q=(b,c)^T\), \(Q\rightarrow UQ,\ U\in \mathrm {SU}(2)\). Besides the \(\mathrm {SU}(2)\) flavor symmetry, there is also a \(\mathrm U(1)\) symmetry which corresponds to the electromagnetic (EM) interaction, \(Q\rightarrow U_c Q,\ U_c\in \mathrm {U}(1)\), where

$$\begin{aligned} U_{c}=\mathrm{exp\left[ i{{\mathcal {Q}}}\ \theta \right] }\in \mathrm{U}(1),\quad {{\mathcal {Q}}}=\begin{pmatrix}-1/3&{}0\\ 0&{} 2/3 \end{pmatrix}. \end{aligned}$$
(5)

As an effective theory of QCD, DiET should also reflect the \(\mathrm {SU}(2)\times \mathrm U(1)\) symmetry. In the flavor space, a diquark field can be considered to have the structure \(q^i q^j\), where \(i,\ j=b\ \mathrm {or} \ c\) are flavor indexes. Thus a diquark field should be represented by a \(2\times 2\) matrix

$$\begin{aligned} S=\begin{pmatrix} 0&{} S_{bc}\\ -S_{bc} &{}0 \end{pmatrix},\quad X_{\mu }=\begin{pmatrix}X_{bb\mu } &{} X_{bc\mu }\\ X_{bc\mu } &{} X_{cc\mu } \end{pmatrix}. \end{aligned}$$
(6)

Note that the representation for a scalar diquark is anti-symmetric while the representation for an axial-vector diquark is symmetric. Under \(\mathrm {SU}(2)\times \mathrm U(1)\), they transform as

$$\begin{aligned}&S \rightarrow U_{(c)} S U_{(c)}^T,\quad X_{\mu } \rightarrow U_{(c)} X_{\mu } U_{(c)}^T,\quad \nonumber \\&U_{(c)}\in \mathrm {SU}(2) \ or\ \mathrm {U}(1). \end{aligned}$$
(7)

With these matrixes as basic building blocks, one can construct a \(\mathrm {SU}(2)\times \mathrm U(1)\) invariant diquark Lagrangian. An efficient way to realize these symmetries is to apply the spinor representation for the diquark fields. Following Ref. [51], one firstly combines the spin-1 and spin-0 diquarks to be a multiplet, which is described by a bilinear spinor field \(\Sigma \)

$$\begin{aligned} \Sigma =(X_{\mu }\gamma ^{\mu }+S\gamma _{5})C, \end{aligned}$$
(8)

where C is the charge conjugating matrix. A reason to choose such form is due to the Lorentz covariance. Under a general Lorentz transformation \(X^{\mu }\rightarrow \Lambda ^{\mu }_{\nu }X^{\nu }\), one can show that \(\Sigma \) does transform in the expected manner, \(\Sigma \rightarrow \Lambda _{1/2}\ \Sigma \ \Lambda ^T_{1/2}\). In addition, in momentum space the equation of motion of the two constituent heavy quarks yakes the form . Note that since the diquark is treated as a point-like particle, both the two constituent heavy quarks and the diquark itself share a common velocity \(v_d\), so that it is reasonable to operate with the same slash on the both sides of \(\Sigma \). Therefore, we can define \(\Sigma ^{\prime }\)

(9)

To obtain the second equality we have used the on-shell constraint \(v_{d}\cdot X(v_d)=0\). After transforming \(\Sigma ^{\prime }(v_d)\) into coordinates space, we can define a multiplet field K(x) as

(10)

where \({{\bar{\Sigma }}}(x)=\gamma ^0 \Sigma ^{\dagger }(x) \gamma ^0\). According to Eq. (7), under \(\mathrm {SU}(2)\times \mathrm U(1)\) transformation, K and \({\bar{K}}\) transform in the same manner as \(S, X^{\mu }\) and \(S^{\dagger }, X^{\mu \dagger }\). Therefore the kinematic Lagrangian of DiET is just the simplest globally \(\mathrm {SU}(2)\times \mathrm U(1)\) invariant Lagrangian constructed by K, \({\bar{K}}\), \(m_X\) and one derivative operator

(11)

where the trace acts in both flavor and spinor spaces. Expressed in terms of \(X_{\mu }\) and S, the kinematic Lagrangian takes the form of a combination of a spin-1 part and a spin-0 part

$$\begin{aligned} {{\mathcal {L}}}_{DiET}^{kin}&=-{1\over 2}\mathrm{Tr}^f\left[ \partial _{\nu }X_{\mu }^{\dagger }\partial ^{\nu }X^{\mu }-m_X^2X_{\mu }^{\dagger }X^{\mu }\right] \nonumber \\&\quad +{1\over 2}\mathrm{Tr}^f\left[ \partial _{\mu }S^{\dagger }\partial ^{\mu }S-m_X^2S^{\dagger }S\right] , \end{aligned}$$
(12)

where \(\mathrm{Tr}^f\) only acts in the flavor space. Compared with Eq. (4), this equation has no \(\partial _{\mu }X_{\nu }^{\dagger }\partial ^{\nu }X^{\mu }\) term. The reason is that in the heavy quark limit, the diquark field is a very massive field, which is approximately on shell and satisfies the constraint \(\partial _{\mu }X^{\mu }=0\).

Next, let us consider how the diquark field couples to external sources. At the quark level, the weak and the EM coupling come from the coupling terms in QCD

$$\begin{aligned} {{\mathcal {L}}}_{QCD}^{cou}={\bar{Q}}_j \left[ V^{\mu }\gamma _{\mu }(1-\gamma _5)+A^{\mu }\gamma _{\mu }\right] _{ji} Q_i = \mathrm{Tr}\left[ Q{\bar{Q}} J\right] , \end{aligned}$$
(13)

where \(i, j=b\ \mathrm{or} \ c\) are flavor indexes, \(V_{\mu }=V_{\mu }^{a}T^{a}\), \(A_{\mu }=A^{em}_{\mu }{\mathcal {Q}}\) and \(J_{ij}=V_{ij}^{\mu }\gamma _{\mu }(1-\gamma _5)+A_{ij}^{\mu }\gamma _{\mu }=L_{ij}+A_{ij}\). The trace acts in both flavor and spinor spaces. Note that this coupling term is invariant under \(\mathrm {SU}(2)\times \mathrm U(1)\) transformations if J is assumed to transform as \(J\rightarrow U_{(c)} J U_{(c)}^{\dagger }\). Therefore, at the diquark level, the simplest global \(\mathrm {SU}(2)\times \mathrm U(1)\) invariant coupling terms with external source J transforming in this way are

$$\begin{aligned} {{\mathcal {L}}}_{DiET}^{cou}=\frac{\lambda _1}{2} m_X \mathrm{Tr}[{\bar{K}} J K]+\frac{\lambda _2}{2} m_X \mathrm{Tr}[{\bar{K}} K J^T]. \end{aligned}$$
(14)

Here, \(\lambda _1\) and \(\lambda _2\) are two independent coupling constants. After being expressed in terms of \(X_{\mu }\) and S, the coupling Lagrangians of the X-J-X, S-J-X, X-J-S and S-J-S types are given by

$$\begin{aligned} {{\mathcal {L}}}_{XJX}&=-i\ \mathrm{Tr}^{f}\left[ F_{\nu \mu }^{\dagger }\langle J^{\mu },X^{\nu }\rangle _{+}-X_{\nu }^{\dagger }\langle J_{\mu },F^{\nu \mu }\rangle _{+}\right. \nonumber \\&\quad \left. +i\ {\tilde{F}}_{\mu \nu }^{\dagger }\langle V^{\mu },X^{\nu }\rangle _{+}-i\ X_{\nu }^{\dagger } \langle V_{\mu },{\tilde{F}}^{\nu \mu }\rangle _{+}\right] , \end{aligned}$$
(15)
$$\begin{aligned} {{\mathcal {L}}}_{SJX}&=\frac{1}{m_{X}}\mathrm{Tr}^{f}\left[ \partial _{\nu }S^{\dagger }\langle V_{\mu },F^{\nu \mu }\rangle _{-}\right. \nonumber \\&\quad \left. +i\ \partial _{\nu }S^{\dagger }\langle J_{\mu },{\tilde{F}}^{\nu \mu }\rangle _{-}+m_{X}^{2}S^{\dagger }\langle V_{\mu },X^{\mu } \rangle _{-}\right] , \end{aligned}$$
(16)
$$\begin{aligned} {{\mathcal {L}}}_{XJS}&=\frac{1}{m_{X}}\mathrm{Tr}^{f}\left[ F_{\nu \mu }^{\dagger }\langle V^{\mu },\partial ^{\nu }S\rangle _{-}\right. \nonumber \\&\quad \left. -i\ {\tilde{F}}_{\mu \nu }^{\dagger }\langle J^{\mu },\partial ^{\nu }S\rangle _{-}+m_{X}^{2}X^{\dagger \mu }\langle V_{\mu }, S\rangle _{-}\right] , \end{aligned}$$
(17)
$$\begin{aligned} {{\mathcal {L}}}_{SJS}&=-i\ \mathrm{Tr}^{f}\left[ \partial _{\mu }S^{\dagger }\langle J^{\mu },S\rangle _{+} -S^{\dagger }\langle J^{\mu },\partial _{\mu }S\rangle _{+}\right] , \end{aligned}$$
(18)
$$\begin{aligned} {{\mathcal {L}}}_{DiET}^{cou}&={{\mathcal {L}}}_{XJX} +{{\mathcal {L}}}_{SJX} +\mathcal{L}_{XJS} +{{\mathcal {L}}}_{SJS}, \end{aligned}$$
(19)

where \(\mathrm{Tr}^{f}\) only acts in the flavor space and \(J_{\mu }=V_{\mu }+A_{\mu }\). \({{{\tilde{F}}}}_{\mu \nu }= \frac{1}{2}\epsilon _{\mu \nu \alpha \beta }F^{\alpha \beta }\) is the dual field strength tensor. We have also defined two kinds of commutators in the flavor space

$$\begin{aligned} \langle A,B\rangle _{\pm }=\frac{\lambda _1}{2}A\ B\pm \frac{\lambda _2}{2}B\ A^{T}. \end{aligned}$$
(20)

2.2 Heavy diquark effective theory (HDiET)

A diquark in the color \({\bar{3}}\) representation interacts with gluons in a similar way as a an anti-quark. Replacing the ordinary derivatives in Eqs. (2) and (4) with covariant derivatives, one can introduce the coupling of a diquark and a gluon

$$\begin{aligned} {{\mathcal {L}}}_S&={1\over 2}(D_{\mu }S)^{i\dagger }(D^{\mu }S)^i-{1\over 2}m_X^2S^{i\dagger }S^i, \end{aligned}$$
(21)
$$\begin{aligned} {{\mathcal {L}}}_{X}&=-\frac{1}{2}\left[ (D_{\mu }X_{\nu })^{i\dagger }(D^{\mu }X^{\nu })^i-(D_{\mu }X_{\nu })^{i\dagger }(D^{\nu }X^{\mu })^i\right] \nonumber \\&\quad +\frac{1}{2}m_{X}^{2}X_{\mu }^{i\dagger }X^{\mu i}, \end{aligned}$$
(22)

where \(D_{\mu }=\partial _{\mu }-i g_d A^a_\mu {{\bar{t}}}^a\), \(g_d\) is the effective coupling constant between the diquark and the gluon. In the heavy diquark limit, to expand the Lagrangian in power of \(1/m_{X}^{2}\), one has to separate the diquark field into a static part and a residual part as is done in with the heavy quark in HQET.

For the case of scalar diquark, the \(1/m_{X}^{2}\) expansion is trivial. By factorizing out an exponential phase \(S=\mathrm{exp}[-im_X v\cdot x]S_v\), with v the four velocity of the baryon, Eq. (21) becomes

$$\begin{aligned} {{\mathcal {L}}}_S=im_X S^{\dagger }_v v\cdot D S_v-\frac{1}{2}S^{\dagger }_v D^{2}S_v. \end{aligned}$$
(23)

Note that each covariant derivative scales as \(\Lambda _{QCD}\). Thus in the heavy diquark limit, the second term in Eq. (23) is suppressed by \(\Lambda _{QCD}/m_X\) compared with the first term. Furthermore, at the leading order, \(S_v\) is massless and its propagator is simply

$$\begin{aligned} D_S(k)=\frac{i}{m_X v\cdot k}. \end{aligned}$$
(24)

In case of an axial-vector diquark, just factorizing out an exponential phase is not enough. In the heavy diquark limit, one has to separate \(X^{\mu }\) into a static part \(\mathrm{exp}[-im_X v\cdot x]X_v^{\mu }\) which satisfies \(v\cdot X_v=0\) instead of \(v_d\cdot X_v=0\), as well as a residual part \(\mathrm{exp}[-im_X v\cdot x] Y_v^{\mu }\), which is suppressed as \(Y_v^{\mu }\sim (\Lambda _{QCD}/m_X)X_v^{\mu }\). Also note that both \(X_v^{\mu }\) and \(Y_v^{\mu }\) are dominated by the small momentum \(k\sim \Lambda _{QCD}\). Let us introduce two projection operators \(P^{\mu }_{~\nu }\) and \(T^{\mu }_{~\nu }\),

$$\begin{aligned} P^{\mu }_{~\nu }&=\delta ^{\mu }_{~\nu }-v^{\mu }v_{\nu },\quad T^{\mu }_{~\nu }=v^{\mu }v_{\nu },\nonumber \\ P^{\mu }_{~\nu }+T^{\mu }_{~\nu }&=\delta ^{\mu }_{~\nu },\quad P^{\mu }_{~\nu }P^{\nu }_{~\sigma }=P^{\mu }_{~\sigma },\quad T^{\mu }_{~\nu }T^{\nu }_{~\sigma }=T^{\mu }_{~\sigma },\nonumber \\ P^{\mu }_{~\nu }T^{\nu }_{~\sigma }&=v_{\mu }P^{\mu }_{~\nu }=0. \end{aligned}$$
(25)

Using the projection operators, one can project out the static part \(X_v^{\mu }\) and the residual part \(Y_v^{\mu }\) of the heavy axial-vector diquark field \(X^{\mu }\)

$$\begin{aligned} X_v^{\mu }=e^{im_X v\cdot x}\ P^{\mu }_{~\nu }X^{\nu },\quad Y_v^{\mu }=e^{im_X v\cdot x}\ T^{\mu }_{~\nu }X^{\nu }, \end{aligned}$$
(26)

which satisfy \(v\cdot X_v=0~\text {and}~(\cdots X_v^{\mu })^{\dagger }(\cdots Y_{v\mu })=(\cdots Y_v^{\mu })^{\dagger } (\cdots X_{v\mu })=0\), where the dots represent any possible insertion of covariant derivatives. Then the full diquark field can be separated as

$$\begin{aligned} X^{\mu }=e^{-im_X v\cdot x}(X_v^{\mu }+Y_v^{\mu }). \end{aligned}$$
(27)

Inserting Eq. (27) into Eq. (22), and using integration by part \(\overleftarrow{D}=-D\) to make all the covariant derivatives act on the X, Y fields instead of the \(X^{\dagger }, Y^{\dagger }\) fields, one finally arrives at

$$\begin{aligned} {{\mathcal {L}}}_{X}&=-im_{X}X_{v\mu }^{\dagger }v\cdot D X_{v}^{\mu }\nonumber \\&\quad +\frac{1}{2}X_{v\mu }^{\dagger }\left( D^{2}g^{\mu \nu }-D^{\nu }D^{\mu }\right) X_{v\nu } -im_{X}Y_{v\mu }^{\dagger }\left[ g^{\mu \nu }(v\cdot D)\right. \nonumber \\&\quad -\frac{1}{2}\left( v^{\nu }D^{\mu }+v^{\mu }D^{\nu }-im_{X}v^{\mu }v^{\nu }\right) \nonumber \\&\quad \left. +\frac{i}{2m_{X}}\left( D^{2}g^{\mu \nu }-D^{\nu }D^{\mu }\right) \right] Y_{v\nu }\nonumber \\&\quad +\frac{i}{2}m_{X}X_{v\nu }^{\dagger }\left( v^{\mu }D^{\nu }+\frac{i}{m_{X}}D^{\mu }D^{\nu }\right) Y_{v\mu }\nonumber \\&\quad +\frac{i}{2}m_{X}Y_{v\nu }^{\dagger }\left( v^{\nu }D^{\mu } +\frac{i}{m_{X}}D^{\mu }D^{\nu }\right) X_{v\mu }. \end{aligned}$$
(28)

From the Lagrangian Eq. (28), one finds that \(X_v^{\mu }\) is a massless field, while \(Y_v^{\mu }\) is massive due to the non-diagonal mass term \(-(m_X^2/2)v^{\mu }v^{\nu }Y_{v\mu }^{\dagger }Y_{v\nu }\). To obtain an effective theory containing only the massless field \(X_v^{\mu }\), one needs to integrate out the heavy degree of freedom \(Y_v^{\mu }\). One way to realize this is to use the saddle point approximation, where one first solves the equation of motion of the heavier field \(Y_v^{\mu }\) while keeping \(X_v^{\mu }\) fixed. The solution is

$$\begin{aligned}&\left[ g^{\mu \nu }(v\cdot D)-\frac{1}{2}\left( v^{\nu }D^{\mu }+v^{\mu }D^{\nu }-im_{X}v^{\mu }v^{\nu }\right) \right. \nonumber \\&\qquad \left. +\frac{i}{2m_{X}}(D^{2}g^{\mu \nu }-D^{\nu }D^{\mu })\right] Y_{v\nu }\nonumber \\&\quad =\frac{1}{2}\left( v^{\mu }D^{\nu }+\frac{i}{m_{X}}D^{\nu }D^{\mu }\right) X_{v\nu }. \end{aligned}$$
(29)

It is not simple to solve this matrix equation directly. To simplify it, we can multiply with \(v_{\mu }\) on both sides of the equation

$$\begin{aligned}&\left[ iv^{\mu }+\frac{v^{\mu }(v\cdot D)-D^{\mu }}{m_{X}}+i\frac{D^{2}v^{\mu }-D^{\mu }(v\cdot D)}{m_{X}^{2}}\right] Y_{v\mu }\nonumber \\&\quad =\left[ \frac{D^{\mu }}{m_{X}}+i\frac{D^{\mu }(v\cdot D)}{m_{X}^{2}}\right] X_{v\mu }, \end{aligned}$$
(30)

and introduce a power counting scheme to solve this equation perturbatively. Note that each covariant derivative D scales as \(\Lambda _{QCD}\) which is small compared to \(m_X\). So by counting the number of \({\kappa }=D/{m_X}\), we can conclude that

$$\begin{aligned}&v^{\mu }\sim {{\mathcal {O}}}(1);\ \ \ \frac{v^{\mu }(v\cdot D)-D^{\mu }}{m_{X}},\ \frac{D^{\mu }}{m_{X}}\sim {{\mathcal {O}}}(\kappa ); \ \ \ \nonumber \\&\frac{D^{2}v^{\mu }-D^{\mu }(v\cdot D)}{m_{X}^{2}},\ \frac{D^{\mu }(v\cdot D)}{m_{X}^{2}}\sim {{\mathcal {O}}}(\kappa ^2). \end{aligned}$$
(31)

Since \(Y_v^{\mu }\) is orthogonal to \(X_v^{\mu }\), \(Y_v^{\mu }\) cannot involve a term like \(\text {const}\times X_v^{\mu }\). The solution of Eq. (30) up to \({{\mathcal {O}}}(\kappa ^3)\) is given as:

$$\begin{aligned} Y_v^{\mu }= -\frac{i}{m_X}v^{\mu }D_{\nu }X_v^{\nu }+\frac{1}{m_X^2} D_{\nu }D^{\mu }X_v^{\nu } +{{\mathcal {O}}}(\kappa ^3). \end{aligned}$$
(32)

After inserting this solution of \(Y_v^{\mu }\) back to Eq. (28), one finally obtains the effective Lagrangian in the form of a power expansion

$$\begin{aligned} {{\mathcal {L}}}_{X}&=-im_{X}X_{v\mu }^{\dagger } v\cdot D X_{v}^{\mu }+\frac{1}{2}X_{v\mu }^{\dagger }D^{2}X_{v}^{\mu }+\frac{i}{2}g_d X_{v\mu }^{\dagger }{{\bar{G}}}^{\mu \nu }X_{v\nu }\nonumber \\&\quad +\frac{i}{2 m_X}X_{v\mu }^{\dagger }\left\{ D^{\mu }D^{\nu },v\cdot D\right\} X_{v\nu }+{{\mathcal {O}}}\left( 1/m_X^2\right) , \end{aligned}$$
(33)

where \({{\bar{G}}}_{\mu \nu }=G^a_{\mu \nu }{{\bar{t}}}^a\) is the gluon tensor. In the Eq. (33), the second term represents the heavy diquark kinetic energy while the third term corresponds to the chromomagnetic coupling. These two terms are consistent with those given in Refs. [43, 52,53,54], where a non-relativistic approach is used. The propagator of the massless heavy axial-vector diquark is

$$\begin{aligned} D_X^{\mu \nu }(k)=\frac{-i}{m_X v\cdot k}(g^{\mu \nu }-v^{\mu }v^{\nu }). \end{aligned}$$
(34)

The heavy diquark can only couple to soft gluons. Through the following field redefinition, one can decouple the diquark field from gluon field:

$$\begin{aligned}&X_{v\mu }=P\Big \{\mathrm{exp}\Big [ig\int _{-\infty }^{v\cdot x}ds\ v\cdot A(s)\Big ]\Big \}\tilde{X_v}_{\mu } = W\Big [\begin{array}{c} x\\ v \end{array}\Big ]{{{\tilde{X}}}}_{v\mu },\nonumber \\&S_{v}=W\Big [\begin{array}{c} x\\ v \end{array}\Big ]{{{\tilde{S}}}}_{v}. \end{aligned}$$
(35)
$$\begin{aligned}&(v\cdot D)X_v^{\mu }=W\Big [\begin{array}{c} x\\ v \end{array}\Big ](v\cdot \partial ){{{\tilde{X}}}}_v^{\mu },\quad (v\cdot D)S_v=W\Big [\begin{array}{c} x\\ v \end{array}\Big ](v\cdot \partial ){{{\tilde{S}}}}_v.\nonumber \\ \end{aligned}$$
(36)

Using the decoupling transformation, one can replace all the covariant derivatives in Eq. (33) by ordinary derivatives, while the X field should be replaced by the dressed field \({{\tilde{X}}}\).

3 Heavy to heavy baryonic transitions

3.1 Diquark transition currents from symmetry

When using DiET to study doubly heavy baryon decays \(\mathcal{B}_{bQ}\rightarrow {{\mathcal {B}}}_{cQ} l\nu \), for instance when the bb diquark turns into the bc diquark through the \(V-A\) current \(\bar{c}\gamma _{\mu }(1-\gamma _5)b\), or electromagnetic transitions \({{\mathcal {B}}}_{Q_1Q_2}\rightarrow {{\mathcal {B}}}_{Q_1Q_2} \gamma ^{*}\) induced by the vector current \(\bar{Q}\gamma _{\mu }Q\), one needs to express the corresponding currents in terms of the diquark fields instead of the heavy quark fields. Particularly, if we approximate the diquark as a point like particle, we require the four most general kinds of diquark currents

$$\begin{aligned}&X_{\alpha }^{\dagger }\Gamma _{\mu }^{\alpha \beta }[\overleftarrow{\partial },\partial ]X_{\beta }, \quad S^{\dagger }\Gamma _{\mu }^{\beta }[\overleftarrow{\partial },\partial ]X_{\beta },\nonumber \\&X_{\beta }^{\dagger }\Gamma _{\mu }^{\beta }[\overleftarrow{\partial },\partial ]S\quad \text {and} \quad S^{\dagger }\Gamma _{\mu }[\overleftarrow{\partial },\partial ]S, \end{aligned}$$
(37)

which correspond to pure axial-vector, axial-vector to scalar, scalar to axial-vector and pure scalar transitions. Note that \(\Gamma _{\mu }^{\alpha \beta }, \Gamma _{\mu }^{\beta }\) and \(\Gamma _{\mu }\) depend on the momentum of the initial and final diquarks. In the heavy diquark limit we can simply replace the \(\overleftarrow{\partial },\ \partial \) with the four-velocities of the final and initial baryons \(im_Xv_2\), \(-im_Xv_1\), with \(w=v_1\cdot v_2~ \text {close to}~ 1\) for the low recoil region.

Consider first the case of \(V-A\) weak current \(\bar{c}\gamma _{\mu }(1-\gamma _5)b\). According to Eq. (13), it is just a current coupling to the external source \(V_{\mu }^{1}+iV_{\mu }^{2}\), which can be found from the expansion

$$\begin{aligned} \mathrm{Tr}\left[ Q{\bar{Q}} L\right]&=\ \bar{c}\gamma ^{\mu }(1-\gamma _5)b\ (V_{\mu }^{1}+iV_{\mu }^{2})\nonumber \\&\quad +\bar{b}\gamma ^{\mu } (1-\gamma _5)c\ (V_{\mu }^{1} -iV_{\mu }^{2})\nonumber \\&\quad +\left[ \bar{b}\gamma ^{\mu }(1-\gamma _5)b-\bar{c}\gamma ^{\mu }(1-\gamma _5)c\right] \ V_{\mu }^{3}. \end{aligned}$$
(38)

Straightforwardly, one can conclude that the \(\bar{c}\gamma _{\mu }(1-\gamma _5)b\) current can be produced by operating with a derivative on the part of the Lagrangian of QCD that contains the couplings to the external fields

$$\begin{aligned} \bar{c}\gamma _{\mu }(1-\gamma _5)b=\frac{\partial }{\partial (V^{\mu }_{1}+iV^{\mu }_{2})}\mathcal{L}^{\mathrm{coup}}_{QCD}. \end{aligned}$$
(39)

On the other hand, on the diquark level, if one performs the same derivative operation on the DiET Lagrangian Eq. (15–19), one arrives at the \(V-A\) currents in the DiET form

$$\begin{aligned} J_{\mu }^{Transition}= \frac{\partial }{\partial (V^{\mu }_{1}+iV^{\mu }_{2})}\left[ \mathcal{L}_{XJX}+{{\mathcal {L}}}_{SJX} +{{\mathcal {L}}}_{XJS}+{{\mathcal {L}}}_{SJS}\right] . \end{aligned}$$
(40)

Explicitly for \(X\rightarrow X\), \(X\rightarrow S\) and \(S\rightarrow S\) transitions, one has

$$\begin{aligned} J_{\mu }^{X\rightarrow X}&= -\frac{1}{2}(\lambda _{1}+\lambda _{2})\Big [i\left( \partial _{\nu }X_{bc\mu }^{\dagger }X_{bb}^{\nu }-\partial _{\mu }X_{bc\nu }^{\dagger }X_{bb}^{\nu }\right. \nonumber \\&\quad \left. -X_{bc\nu }^{\dagger }\partial ^{\nu }X_{bb\mu }+X_{bc\nu }^{\dagger }\partial _{\mu }X_{bb}^{\nu }\right) \nonumber \\&\quad -\epsilon _{\alpha \beta \mu \rho }\left( \partial ^{\rho }X_{bc}^{\dagger \alpha }X_{bb}^{\beta }-X_{bc}^{\dagger \alpha }\partial ^{\rho }X_{bb}^{\beta }\right) +(bc \rightarrow cc)\Big ], \end{aligned}$$
(41)
$$\begin{aligned} J_{\mu }^{X\rightarrow S}&=-\frac{1}{2m_{X}}(\lambda _{1}+\lambda _{2})\left( \partial _{\nu }S_{bc}^{\dagger }\partial ^{\nu }X_{bb\mu }\right. \nonumber \\&\quad \left. -\partial _{\nu }S_{bc}^{\dagger }\partial _{\mu }X_{bb}^{\nu }+m_{X}^{2}S_{bc}^{\dagger }X_{bb\mu }\right) \nonumber \\&\quad +\frac{i}{2m_{X}}(\lambda _{1}+\lambda _{2})\epsilon _{\rho \mu \sigma \beta }\partial ^{\rho }S_{bc}^{\dagger }\partial ^{\sigma }X_{bb}^{\beta }, \end{aligned}$$
(42)
$$\begin{aligned} J_{\mu }^{S\rightarrow X}&= -\frac{1}{2m_{X}}(\lambda _{1}+\lambda _{2})\left( \partial _{\mu }X_{cc\nu }^{\dagger }\partial ^{\nu }S_{bc}\right. \nonumber \\&\quad \left. -\partial _{\nu }X_{cc\mu }^{\dagger }\partial ^{\nu }S_{bc}-m_{X}^{2}X_{cc\mu }^{\dagger }S_{bc}\right) \nonumber \\&\quad -\frac{i}{2m_{X}}(\lambda _{1}+\lambda _{2})\epsilon _{\alpha \rho \mu \sigma }\partial ^{\rho }X_{cc}^{\dagger \alpha }\partial ^{\sigma }S_{bc}. \end{aligned}$$
(43)

Note that the antisymmetric S has only one non-vanishing component \(S_{bc}\), for flavor changing processes \(b\rightarrow c\) there is no \(S\rightarrow S\) transition. Similarly, the electromagnetic currents \(I_{\mu }^\mathrm{Transition}\) can be derived by acting with a derivative on \(A_{em}^{\mu }\),

Fig. 1
figure 1

Diquark transition at the quark level. Single gluon exchanges between the two heavy quarks are explicitly shown, with the quantum numbers of the quarks are denoted as (spinor index, color index)

Full size image
$$\begin{aligned} I_{\mu }^{\mathrm{Transition}}&= \frac{\partial }{\partial A_{em}^{\mu }}\left[ {{\mathcal {L}}}_{XJX}+{{\mathcal {L}}}_{SJX} +{{\mathcal {L}}}_{XJS}+{{\mathcal {L}}}_{SJS}\right] , \end{aligned}$$
(44)
$$\begin{aligned} I_{\mu }^{X\rightarrow X}&=-\frac{i}{4}C_{X}(\lambda _1+\lambda _2)\left( \partial ^{\dagger \nu }X_{\mu }X_{\nu }-\partial _{\mu }X_{\nu }^{\dagger }X^{\nu }\right. \nonumber \\&\quad \left. -X_{\nu }^{\dagger }\partial ^{\nu }X_{\mu }+X_{\nu }^{\dagger }\partial _{\mu }X^{\nu }\right) , \end{aligned}$$
(45)
$$\begin{aligned} I_{\mu }^{X\rightarrow S}&=-\frac{i}{2m_X}\epsilon _{\rho \mu \alpha \beta }(\lambda _1+\lambda _2)\partial ^{\rho }S_{bc}^{\dagger }\partial ^{\alpha }X_{bc}^{\beta }, \end{aligned}$$
(46)
$$\begin{aligned} I_{\mu }^{S\rightarrow V}&=-\frac{i}{2m_X}\epsilon _{\alpha \rho \mu \beta }(\lambda _1+\lambda _2)\partial ^{\rho }X_{bc}^{\dagger \alpha }\partial ^{\beta }S_{bc}, \end{aligned}$$
(47)
$$\begin{aligned} I_{\mu }^{S\rightarrow S}&=-\frac{i}{6}(\lambda _1+\lambda _2)\left( \partial _{\mu }S_{bc}^{\dagger }S_{bc}-S_{bc}^{\dagger }\partial _{\mu }S_{bc}\right) , \end{aligned}$$
(48)

where \(C_X\) is the total electric charge of X. It should be mentioned that all the currents in Eqs. (41–43, 45–48) are expressed by the full diquark fields. These expressions are simpler in the heavy diquark limit. According to Eqs. (27) and (32), the full diquark fields X, S are related with the effective ones \(X_v, S_v\) in HDiET as

$$\begin{aligned} S=e^{-im_X v\cdot x}S_v,\quad X^{\mu }=e^{-im_X v\cdot x}\left( X_v^{\mu }-\frac{i}{m_X}v^{\mu }D_{\nu }X_{v}^{\nu }\right) .\nonumber \\ \end{aligned}$$
(49)

Inserting Eq. (49) into Eqs. (41–43, 45–48), at leading order, all the derivative operators are simply replaced by the corresponding four velocities

$$\begin{aligned} J_{\mu }^{X\rightarrow X}&=\Lambda \ X_{(v)cQ}^{\dagger \alpha }\left[ g_{\mu \alpha }v_{2\beta }+v_{1\alpha }g_{\mu \beta }-(v_{1\mu }+v_{2\mu })g_{\alpha \beta }\right. \nonumber \\&\quad \left. +i\epsilon _{\alpha \beta \mu \rho }(v_{2}^{\rho } +v_{1}^{\rho })\right] X_{(v)bQ}^{\beta }, \end{aligned}$$
(50)
$$\begin{aligned} J_{\mu }^{X\rightarrow S}&=-\Lambda \ S_{(v)bc}^{\dagger }\left[ (1+w)g_{\mu \beta }\right. \nonumber \\&\quad \left. -v_{1\mu }v_{2\beta }-i\epsilon _{\rho \mu \sigma \beta }v_{2}^{\rho }v_{1}^{\sigma }\right] X_{(v)bb}^{\beta }, \end{aligned}$$
(51)
$$\begin{aligned} J_{\mu }^{S\rightarrow X}&=-\Lambda \ X_{(v)cc}^{\dagger \alpha }\left[ -(1+w)g_{\mu \alpha }+v_{2\mu }v_{1\alpha }\right. \nonumber \\&\quad \left. -i\epsilon _{\rho \mu \sigma \alpha }v_{2}^{\rho }v_{1}^{\sigma }\right] S_{(v)bc}, \end{aligned}$$
(52)
$$\begin{aligned} I_{\mu }^{X\rightarrow X}&=\frac{1}{2}C_{X}\Lambda \ X_{(v)}^{\dagger \alpha }\left[ g_{\mu \alpha }v_{2\beta }-v_{2\mu }g_{\alpha \beta }\right. \nonumber \\&\quad \left. +v_{1\alpha }g_{\mu \beta }-v_{1\mu }g_{\alpha \beta }\right] X_{(v)}^{\beta }, \end{aligned}$$
(53)
$$\begin{aligned} I_{\mu }^{X\rightarrow S}&=\Lambda \ S_{(v)bc}^{\dagger }\left[ -i\epsilon _{\rho \mu \sigma \beta }v_{2}^{\rho }v_{1}^{\sigma }\right] X_{(v)bc}^{\beta }, \end{aligned}$$
(54)
$$\begin{aligned} I_{\mu }^{S\rightarrow X}&=\Lambda \ X_{(v)bc}^{\dagger \alpha }\left[ i\epsilon _{\rho \mu \sigma \alpha }v_{2}^{\rho }v_{1}^{\sigma }\right] S_{(v)bc}, \end{aligned}$$
(55)
$$\begin{aligned} I_{\mu }^{S\rightarrow S}&=\frac{1}{3}\Lambda \ S_{(v)bc}^{\dagger }\left[ v_{2\mu }+v_{1\mu }\right] S_{(v)bc}, \end{aligned}$$
(56)

where \(\Lambda =(\lambda _{1}+\lambda _{2})m_{X}\). Similarly one can obtain the currents at next-to-leading order if the second expansion term of \(X^{\mu }\) in Eq. (49) is used, but the results will not be shown explicitly here.

It should be mentioned that like the chromomagnetic coupling in the Eq. (33), one can also introduce the magnetic couplings of the axial-vector diquark as those given in Ref. [43] by NRQCD. Such a term will contribute an extra EM current suppressed by \(1/m_X\) in Eqs. (53–56).

3.2 Diquark transition currents from matching

When the recoil is small, to derive the diquark transition currents from symmetries we can assume the diquark as a point-like particle without any internal structure. Therefore, the currents we get in Eqs. (41–43, 45–48) are only proportional to the constant couplings \(\lambda _1, \lambda _2\). On the other hand, if the recoil is large, we should consider finite sized diquarks where the transition is dominated by hard internal gluon exchange which can be factorized into short distance coefficients. One way to obtain these short distance coefficients is to perform a matching between DiET and QCD in the large recoil region, where at the quark level one may factorize out a hard kernel, with its tree level form shown in Fig. 1. A hard gluon is exchanged between the two heavy quarks so that the recoil is large, \(q^2~\text {close to zero}\), and \({{\mathcal {V}}}_{\mu }=\gamma _{\mu }\ \text {or}\ \gamma _{\mu }\gamma _{5}\) is the current vertex.

The calculation of the two diagrams in Fig. 1 is straightforward. However, although at tree level we can set the initial and final quarks to be free, the two quark spins are coupled so that the total spin should match with the corresponding diquark spin. Particularly, to match with a scalar or axial-vector diquark, the spinor indexes of the two quarks should be symmetrical or anti-symmetrical. Consider first the \(X\rightarrow X\) transition. By equating the velocities of the initial and final two quarks to be \(v_1\) and \(v_2\) respectively, the amplitude of the two diagrams in Fig. 1 reads

(57)

where a, b, c, d are spinor indices, and i, j, m, n are color indices. Further, \(\xi _1=m_Q/(m_Q+m_b)\) and \(\xi _2=m_Q/(m_Q+m_c)\). For the finite-sized diquark, the corresponding weak transition amplitude is

$$\begin{aligned} {{\mathcal {M}}}_{\mathrm{DiET}}&=X_{\alpha }^{\dagger }(v_2)\Gamma _{\mu }^{\alpha \beta }\left[ v_1,v_2\right] X_{\beta }(v_1). \end{aligned}$$
(58)

Here, \(X^{\dagger }(v_2), X(v_1)\) should be treated as the polarization vectors of the final and initial diquarks, and \(\Gamma _{\mu }^{\alpha \beta }\left[ v_1,v_2\right] \) represents the hard kernel. Explicitly, the diquark wave function can be composed of two heavy quark spinors as

where i, j, k and \(\beta , \gamma \) are color and spinor indices, respectively, and \(N_S, N_X\) are normalization factors. Inserting Eq. (59) into Eq. (58) and factorizing an independent color factor \(C\ \delta _{l}^{k}\), one arrives at

(59)

The tree level matching demands the equivalence of the amplitudes at the quark and the diquark level \({{\mathcal {M}}}_{\mathrm{QCD}} ={{\mathcal {M}}}_\mathrm{DiET}\), thus we can determine the hard kernel as

(60)

and the color factor is \(C=-1/3\). Similarly, for \(X\rightarrow S\) and \(S\rightarrow X\) transitions, we have

(61)
(62)

Particularly, for the \(V-A\) currents, where \(\mathcal{V}_{\mu }=\gamma _{\mu }\ \text {or}\ \gamma _{\mu }\gamma _{5}\), the hard kernels are

$$\begin{aligned}&\Gamma _{\mu (V)}^{\alpha \beta }= -\frac{g_{d}^{2}}{8N_{X_{bQ}}N_{X_{cQ}}m_{Q}^{3}(1-w)^{2}}\Big [(\xi _{1}+1)v_{2}^{\beta } g_{\mu }^{\alpha }\nonumber \\&\quad +(\xi _{1}-1)v_{2\mu }g^{\alpha \beta }-(\xi _{1}+1)v_{2}^{\alpha }g_{\mu }^{\beta }\nonumber \\&\quad -(\xi _{2}+1)v_{1}^{\beta }g_{\mu }^{\alpha }+(\xi _{2}-1)v_{1\mu }g^{\alpha \beta }+(\xi _{2}+1)v_{1}^{\alpha } g_{\mu }^{\beta }\Big ], \end{aligned}$$
(63)
$$\begin{aligned}&\Gamma _{\mu (A)}^{\alpha \beta }=-\frac{g_{d}^{2}}{8N_{X_{bQ}}N_{X_{cQ}}m_{Q}^{3}(1-w)^{2}}i \epsilon _{~~\mu \sigma }^{\alpha \beta }\nonumber \\&\qquad \qquad \times \left[ (\xi _{1}-1)v_{2}^{\sigma }+(\xi _{2}-1)v_{1}^{\sigma }\right] , \end{aligned}$$
(64)
$$\begin{aligned}&\Gamma _{\mu (V)}^{\beta }[X\rightarrow S]= \Gamma _{\mu (V)}^{\beta }[S\rightarrow X]=0, \end{aligned}$$
(65)
$$\begin{aligned}&\Gamma _{\mu (A)}^{\beta }[X\rightarrow S] \nonumber \\&\quad = -\frac{g_{d}^{2}}{8N_{X_{bQ}}N_{S_{cQ}}m_{Q}^{3}(1-w)^{2}}\left( 2-\xi _1-\xi _2\right) g_{\mu }^\beta , \end{aligned}$$
(66)
$$\begin{aligned}&\Gamma _{\mu (A)}^{\beta }[S\rightarrow X]\nonumber \\&\quad = \frac{g_{d}^{2}}{8N_{S_{bQ}}N_{X_{cQ}}m_{Q}^{3}(1-w)^{2}}\left( 2-\xi _1-\xi _2\right) g_{\mu }^\alpha . \end{aligned}$$
(67)

For the EM currents, the \(X\rightarrow X\), \(X\rightarrow S\) and \(S\rightarrow X\) currents have the same hard kernel as those of the \(V-A\) currents except for the replacements \(m_b\rightarrow m_{Q^{\prime }}, m_c\rightarrow m_{Q^{\prime }}\). However, the \(S\rightarrow S\) EM current is

$$\begin{aligned} \Gamma _{\mu (\mathrm EM)}[S\rightarrow S]&= -\frac{g_{d}^{2}}{8N_{S_{bQ}}N_{S_{cQ}}m_{Q}^{3}(1-w)^{2}}\nonumber \\&\quad \times \left[ (\xi _1-1)v_{2\mu }+(\xi _2-1) v_{1\mu }\right] . \end{aligned}$$
(68)

Note that the structures shown in Eqs. (63–68) are different from those in Eqs. (41–48). Such differences can be understood because the singular point \(w=1\) appearing in the Eqs. (63–68) implies that they are only valid in the large recoil region \(w\rightarrow w_{max}\).

4 Semi-leptonic decays of doubly heavy baryons

4.1 Interpolating fields

In this section we will focus on semi-leptonic decays of doubly heavy baryons, \({{\mathcal {B}}}_{bQ}\rightarrow {{\mathcal {B}}}_{cQ}\ell {{\bar{\nu }}}\). The transition matrix element of the doubly heavy baryon can be calculated by the reduction formula

$$\begin{aligned}&\langle {{\mathcal {B}}}_{cQ}(P_c)|J_{\mu }(0)|{{\mathcal {B}}}_{bQ}(P_b)\rangle = L(P_{b},P_{c})\nonumber \\&\quad \times \int d^{4}xd^{4}y\ e^{iP_{c}\cdot x} e^{-iP_{b}\cdot y}\langle 0|\mathrm {T}\Phi _{cQ}(x)J_{\mu }(0)\Phi _{bQ}^{\dagger }(y)|0\rangle , \end{aligned}$$
(69)

where \(J_{\mu }\) is the current inducing the weak decay. \(L(P_{b},P_{c})\) is the operator to pick out the initial and final mass pole residues

$$\begin{aligned} L(P_{b},P_{c})=\lim _{P_{b}^{2}\rightarrow M_{b}^{2}}(P_{b}^{2}-M_{b}^{2})\lim _{P_{c}^{2}\rightarrow M_{c}^{2}}(P_{c}^{2}-M_{c}^{2}). \end{aligned}$$
(70)

\(\Phi _{cQ}(x)\) and \(\Phi _{bQ}(x)\) are the interpolating fields of the final and initial baryon. Equation (69) can be expressed both at the quark level and the diquark level. At the quark level, \(J_{\mu }={\bar{c}}\gamma _{\mu }(1-\gamma _5)b\), and

$$\begin{aligned} \Phi _{Q_{1}Q_{2}}(x)&=N_{Q_1Q_2}\epsilon ^{ijk}{\bar{\chi }}^{\alpha \beta \gamma }q_{i\alpha }(x)Q_{1}{}_{j\beta }(x) Q_{2}{}_{k\gamma }(x),\nonumber \\ \Phi _{Q_{1}Q_{2}}^{\dagger }(x)&=N_{Q_1Q_2}\epsilon _{ijk}\chi _{\alpha \beta \gamma }\bar{Q}_{2}^{i\gamma }(x)\bar{Q}_{1}^{j\beta }(x) \bar{q}^{k\alpha }(x), \end{aligned}$$
(71)

where \(\chi \) are the Bargmann-Wigner wave functions [55], where the total spin contributed by the two heavy quarks is j. For a spin-1/2 doubly heavy baryon with \(j=0\) or \(j=1\), and a spin-3/2 baryon with \(j=1\), they are

(72)

The symmetry indices \(\beta ,\ \gamma \) project out the spin-1 configuration of the two heavy quarks. The conjugate forms are defined as \({\bar{\chi }}^{\alpha \beta \gamma }=(\gamma _{0})^{\alpha \alpha ^{\prime }}(\gamma _{0})^{\beta \beta ^{\prime }} (\gamma _{0})^{\gamma \gamma ^{\prime }}\chi _{\alpha \beta \gamma }\). \(\chi _{\alpha \beta \gamma }\) satisfies

(73)

On the other hand, we can equivalently express Eq. (69) at diquark level, with the assumption that the spin-0 and spin-1 heavy diquark field is composed of two heavy quark fields

(74)
(75)

Thus the interpolating field of a doubly heavy baryon can be expressed by the combination of a diquark field and a light quark field

$$\begin{aligned} \Phi ^{1/2(0)}_{Q_{1}Q_{2}}(x)&=\frac{N^{1/2(0)}_{Q_1Q_2}}{N_{S_{Q_1Q_2}}}\frac{1}{2}\bar{u}^{\alpha }q_{i\alpha }(x)S^{i}(x), \end{aligned}$$
(76)
$$\begin{aligned} \Phi ^{1/2(1)}_{Q_{1}Q_{2}}(x)&=\frac{N^{1/2(1)}_{Q_1Q_2}}{N_{X_{Q_1Q_2}}}\frac{1}{2}[\bar{u}\gamma _{5}(\gamma ^{\mu } +v^{\mu })]^{\alpha }q_{i\alpha }(x)X_{\mu }^{i}(x), \end{aligned}$$
(77)
$$\begin{aligned} \Phi ^{3/2}_{Q_{1}Q_{2}}(x)&=\frac{N^{3/2}_{Q_1Q_2}}{N_{X_{Q_1Q_2}}}{{\bar{u}}}^{\mu , \alpha }q_{i\alpha }(x)X_{\mu }^{i}(x). \end{aligned}$$
(78)

In fact, these normalization factors are related by the heavy flavor symmetry, which leads to

$$\begin{aligned}&N_{Q_{1}Q_{2}}^{1/2(1)}\rightarrow N^{1/2(1)},~~N_{Q_{1}Q_{2}}^{1/2(0)}\rightarrow N^{1/2(0)},~~N_{Q_{1}Q_{2}}^{3/2}\rightarrow N^{3/2},\nonumber \\&N_{X_{Q_{1}Q_{2}}}\rightarrow N_X,~~N_{S_{Q_{1}Q_{2}}}\rightarrow N_S. \end{aligned}$$
(79)

However, the relation between \(N_X\) and \(N_S\) as well as the relation among \(N^{1/2}, N^{1/2(0)}\ \text {and}\ N^{3/2}\) are not obvious. According to Eqs. (74) and (75), we can write the spinor structure of the scalar and axial-vector diquarks in momentum space as

(80)

Here, we have omitted the color indices. \(s, s^{\prime }\) denote the helicity of the spinors \(u_1, u_2\), in order. Since \(X_{\mu }^{ss^{\prime }}\) has three independent degrees of freedom, while \(S^{ss^{\prime }}\) has only one degree of freedom, we can derive the following relation

$$\begin{aligned} \sum _{ss^{\prime }}S^{\dagger ss^{\prime }}(v)S^{ss^{\prime }}(v)=\frac{1}{3}\sum _{ss^{\prime }}g^{\mu \nu } X_{\mu }^{\dagger ss^{\prime }}(v)X_{\nu }^{ss^{\prime }}(v), \end{aligned}$$
(81)

where the sum of all the helicity indices is equivalent to counting the total degrees of freedom. The relations among \(N^{1/2(1)}, N^{1/2(0)}\ \text {and}\ N^{3/2}\) can be determined by a similar approach. We transform Eqs. (76–78) into the spinor structure in momentum space

$$\begin{aligned} \Phi _{rlss^{\prime }}^{1/2(0)}(v)&=\frac{N^{1/2(0)}}{N_{S}}\frac{1}{2}\bar{u}^{r}(v)u^{l}(v)S^{ss^{\prime }}(v), \end{aligned}$$
(82)
$$\begin{aligned} \Phi _{rlss^{\prime }}^{1/2(1)}(v)&=\frac{N^{1/2(1)}}{N_{X}}\frac{1}{2}\bar{u}^{r}(v)\gamma _{5}(\gamma ^{\mu }+v^{\mu }) q^{l}(v)X_{\mu }^{ss^{\prime }}(v), \end{aligned}$$
(83)
$$\begin{aligned} \Phi _{rlss^{\prime }}^{3/2}(v)&=\frac{N^{3/2}}{N_{X}}\bar{u}^{\mu ,r}(v)u^{l}(v)X_{\mu }^{ss^{\prime }}(v), \end{aligned}$$
(84)

where \(r, l, s, s^{\prime }\) denote the helicities. Since a spin-1/2 particle has two degrees of freedom while a spin-3/2 particle has four, we require the following relations

$$\begin{aligned} \sum _{rlss^{\prime }}\Phi _{rlss^{\prime }}^{1/2(0)\dagger }(v)\Phi _{rlss^{\prime }}^{1/2(0)}(v)= & {} \sum _{rlss^{\prime }} \Phi _{rlss^{\prime }}^{1/2\dagger }(v)\Phi _{rlss^{\prime }}^{1/2}(v)\nonumber \\= & {} \frac{1}{2}\sum _{rlss^{\prime }}\Phi _{rlss^{\prime }}^{3/2\dagger }(v) \Phi _{rlss^{\prime }}^{3/2}(v).\nonumber \\ \end{aligned}$$
(85)

Finally, according to Eqs. (81) and (85) we arrive at

$$\begin{aligned} N_S= & {} \sqrt{2}N_X,\quad N^{1/2(0)}=\sqrt{6}N^{1/2(1)},\nonumber \\ N^{3/2}= & {} \frac{\sqrt{3}}{2}N^{1/2(1)}, \end{aligned}$$
(86)

where the following properties have been used

(87)

It should be mentioned that the spinors used here are rescaled from the standard ones as \({\sqrt{m}_Q}u=u_{\mathrm{QCD}}\). However, as long as we also choose rescaled states as \({\sqrt{m}_Q}|\cdots \rangle = |\cdots \rangle _{\mathrm{QCD}}\), this will never affect our calculations.

4.2 Transition matrix element

With DiET, the transition matrix element defined in Eq. (69) can be calculated at the diquark level. Further, in the heavy diquark limit, utilizing the technique given in Ref. [56], we can reduce the transition matrix element so that it will depend on less unknown form factors. Consider first the case of \({{\mathcal {B}}}_{bQ}^{1/2(1)}\rightarrow \mathcal{B}_{cQ}^{1/2(1)}\). The flavor changing current is

$$\begin{aligned} J^{b\rightarrow c}_{\mu }= X_{\rho ,j}^{\dagger (c)}[\Gamma _{\mu }^{\rho \sigma }(\overleftarrow{\partial },\partial )]_{k}^{j} X_{\sigma }^{(b)k}, \end{aligned}$$
(88)

where \(j,\ k\) are color indices. \([\Gamma _{\mu }^{\rho \sigma }]_{k}^{j}\) can be factorized as \(\Gamma _{\mu }^{\rho \sigma } \times C \delta _{k}^{j}\), and \(C=-1/3\) is given in the last section from matching. To leading power of \(1/m_{X}^{2}\), one can approximate the \(X_{\mu }\) field as \({X}_{v\mu }\), so that the \(\overleftarrow{\partial },\ \partial \) in Eq. (88) can be replaced with \(im_Xv_2\), \(-im_Xv_1\). According to the reduction formula Eq. (69), the transition matrix element in DiET is

$$\begin{aligned}&\langle {{\mathcal {B}}}_{cQ}^{1/2(1)}(P_c)|J^{b\rightarrow c}_{\mu }(0)|{{\mathcal {B}}}_{bQ}^{1/2(1)}(P_b)\rangle \nonumber \\&= \frac{(N^{1/2(1)})^2}{N_{X}^2}L(P_{b},P_{c})\int d^{4}xd^{4}y\ e^{i(P_{c}-m_{X_c}v_{2})\cdot x}e^{-i(P_{b}-m_{X_b}v_{1})\cdot y}\nonumber \\&\quad \times {\bar{\chi }}_{\alpha ,a}^{(c)}\chi _{\beta ,b}^{(b)}C\langle 0|T\big \{X_{v_{2}(c)}^{\alpha ,i}(x)q_{i}^{a}(x)\nonumber \\&\quad X_{v_2\rho ,j}^{\dagger (c)}(0)\Gamma _{\mu }^{\rho \sigma }X_{v_1\sigma }^{(b)j}(0)\ X_{v_1(b)l}^{\dagger \beta }(y)\bar{q}^{l,b}(y)\big \}|0\rangle , \end{aligned}$$
(89)

where \(a,\ b\) are Dirac indices, while \(i,\ j,\ k,\ l\) are color indices. \(v_1\) and \(v_2\) are is four-velocity of the initial and the final baryon, respectively. Using the decoupling transformation defined in Eq. (35), and noting that the \(\tilde{X}_{v\mu }\) fields are totally decoupled from the soft gluons and also the light quarks, one can factorize the time-ordered matrix element in Eq. (89) to be

$$\begin{aligned}&\langle 0|T\Big \{W\Big [\begin{array}{c} x\\ v_{2} \end{array}\Big ]_{i^{\prime }}^{i}W^{-1}\Big [\begin{array}{c} 0\\ v_{2} \end{array}\Big ]_{j}^{j^{\prime }}W\Big [\begin{array}{c} 0\\ v_{1} \end{array}\Big ]_{k^{\prime }}^{j}W^{-1}\Big [\begin{array}{c} y\\ v_{1} \end{array}\Big ]_{l}^{l^{\prime }}q_{i}^{a}(x)\bar{q}^{l,b}(y)\Big \}|0\rangle \nonumber \\&\times \langle 0|T\big \{{\tilde{X}}_{v_2(c)}^{\alpha ,i^{\prime }}(x){\tilde{X}}_{v_2\rho ,j^{\prime }}^{\dagger (c)}(0)\big \}|0\rangle \Gamma _{\mu }^{\rho \sigma }\langle 0|T\big \{{\tilde{X}}_{v_1\sigma (b)}^{k^{\prime }}(0){\tilde{X}}_{v_1l^{\prime }}^{\dagger \beta (b)}(y)\big \}|0\rangle . \end{aligned}$$
(90)

The last two matrix elements in Eq. (90) can be calculated directly from the free diquark propagator Eq. (34). Using the fact that \({\bar{\chi }}_{\alpha ,a}^{(c)}v_2^{\alpha }=\chi _{\beta ,b}^{(b)}v_1^{\beta }=0\), one has

$$\begin{aligned}&\langle {{\mathcal {B}}}_{cQ}(P_c)^{1/2(1)}|J^{b\rightarrow c}_{\mu }(0)|{{\mathcal {B}}}_{bQ}^{1/2(1)}(P_b)\rangle \nonumber \\&\quad = -C\frac{(N^{1/2(1)})^2}{N_{X}^2}\frac{1}{4m_{X_c}m_{X_b}}L(P_{b},P_{c})\int d^{4}kd^{4}q[\bar{u}\gamma _{5}(\gamma _{\alpha }\nonumber \\&\qquad +v_{2\alpha })]_{a}\Gamma _{\mu }^{\alpha \beta }[(\gamma _{\beta }+v_{1\beta })\gamma _{5}u]_{b}\nonumber \\&\qquad \times M(k,q;v_{2},v_{1})^{ab}\frac{1}{v_{2}\cdot (P_{c}-m_{X}v_{2}-k)}\nonumber \\&\qquad \times \frac{1}{v_{1}\cdot (P_{b}-m_{X}v_{1}+q)}. \end{aligned}$$
(91)

The dynamics of the light degrees of freedom is completely encapsulated in the following Fourier transformed soft function

$$\begin{aligned}&M(k,q;v_{2},v_{1})^{ab} =\int \frac{d^{4}k}{(2\pi )^{4}}\frac{d^{4}q}{(2\pi )^{4}}e^{-ik\cdot x}e^{-iq\cdot y}\nonumber \\&\times \Bigg \langle 0|T\Big \{W\Big [\begin{array}{c} x\\ v_{2} \end{array}\Big ]_{i^{\prime }}^{i}W^{-1}\Big [\begin{array}{c} 0\\ v_{2} \end{array}\Big ]_{j}^{i^{\prime }}W\Big [\begin{array}{c} 0\\ v_{1} \end{array}\Big ]_{k^{\prime }}^{j}W^{-1}\Big [\begin{array}{c} y\\ v_{1} \end{array}\Big ]_{l}^{k^{\prime }}q_{i}^{a}(x)\bar{q}^{l,b}(y)\Big \}|0\Bigg \rangle . \end{aligned}$$
(92)

Next, we need to extract the residues of the mass poles by applying the operator \(L(P_{b},P_{c})\) on the correlation function. Near the mass shell, the external momenta \(P_{Q}\) can be parameterized as

$$\begin{aligned} P_{Q}&=M_{Q}(1+\epsilon _{Q})v_{Q}+M_{Q}\epsilon _{\perp },\ \ \ (\epsilon _{\perp }\cdot v_Q=0)\nonumber \\ L(P_{Q})&=\lim _{\epsilon \rightarrow 0}(P_{Q}^{2}-M_{Q}^{2})=\lim _{\epsilon \rightarrow 0}(2\epsilon _{Q}+\epsilon _{\perp }^2)M_{Q}^{2}. \end{aligned}$$
(93)

Although the decoupling transformation Eq. (35) realizes the factorization as shown in Eq. (90), there still exist non-perturbative interactions between the heavy and light degrees of freedom due to confinement. Such effects have been absorbed into the momentum distribution of \(M(k,q;v_{2},v_{1})\). In other words, the light particles in the baryon always “know” that they are bound with a heavy diquark. To reflect the confinement, \(M(k,q;v_{2},v_{1})\) is assumed to peak at \(v_{2}\cdot k={\bar{\Lambda }}_{c},\ v_{1}\cdot q=-{\bar{\Lambda }}_{b}\), where \({\bar{\Lambda }}_{Q}=M_{Q}-m_{X_{Q}}\). Operating with \(L(P_{Q})\) on the denominators, taking the limit \(\epsilon _Q, \epsilon _{\perp } \rightarrow 0\), and noting that there are no poles of \(1/\epsilon _{\perp }^2\), one gets

$$\begin{aligned} L(P_{c})\frac{1}{v_{2}\cdot (P_{c}-m_{X_c}v_2-k)}&= 2M_c,\nonumber \\ L(P_{b})\frac{1}{v_{1}\cdot (P_{b}-m_{X_b}v_1+q)}&=2M_b. \end{aligned}$$
(94)

On the other hand, the soft function can be generally parametrized as

(95)

However, the \(B(w),\ C(w),\ D(w)\) form factors can be totally absorbed into the the form factor A(w) since and , which leaves only one w-dependent form factor denoted as \(A^{\prime }(w)\). Explicitly they are related by \(A^{\prime }(w)=\mathcal{F}[A(w),B(w),C(w),D(w)]\). Thus we have

$$\begin{aligned}&\langle {{\mathcal {B}}}_{cQ}^{1/2(1)}(P_c)|J^{b\rightarrow c}_{\mu }(0)|{{\mathcal {B}}}_{bQ}^{1/2(1)}(P_b)\rangle \nonumber \\&\quad = -C\frac{(N^{1/2(1)})^2 M^2}{N_{X}^2m_X^2}\nonumber \\ {}&\qquad \times A^{\prime }(w)[\bar{u}\gamma _{5}(\gamma _{\alpha } +v_{2\alpha })]\Gamma _{\mu }^{\alpha \beta }[(\gamma _{\beta }+v_{1\beta })\gamma _{5}u], \end{aligned}$$
(96)

where the masses are blind to the flavors so that \(M_b=M_c=M\) and \(m_{X_{b}}=m_{X_{c}}=m_X\). Similarly, for the 1/2(1) \(\rightarrow \) 1/2(0), 1/2(0) \(\rightarrow \) 1/2(1) and 1/2(1) \(\rightarrow \) 3/2(1) transitions, we have

$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(0)}_{cQ}(P_c)|J^{b\rightarrow vcc}_{\mu }(0)|{{\mathcal {B}}}^{1/2(1)}_{bQ}(P_b)\rangle \nonumber \\&\quad = \sqrt{3}C\frac{(N^{1/2(1)})^2 M^2}{N_{X}^2m_X^2}A^{\prime }(w)\ \bar{u}\Gamma _{\mu }^{\beta }(\gamma _{\beta }+v_{1\beta })\gamma _{5}u, \end{aligned}$$
(97)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(1)}_{cQ}(P_c)|J^{b\rightarrow c}_{\mu }(0)|{{\mathcal {B}}}^{1/2(0)}_{bQ}(P_b)\rangle \nonumber \\&\quad = \sqrt{3}C\frac{(N^{1/2(1)})^2 M^2}{N_{X}^2m_X^2}A^{\prime }(w)\ \bar{u}\gamma _{5}(\gamma _{\alpha }+v_{2\alpha })\Gamma _{\mu }^{\alpha }u, \end{aligned}$$
(98)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{3/2(1)}_{cQ}(P_c)|J^{b\rightarrow c}_{\mu }(0)|\mathcal{B}^{1/2(1)}_{bQ}(P_b)\rangle \nonumber \\&\quad = -\sqrt{3}C\frac{(N^{1/2(1)})^2 M^2}{N_{X}^2 m_X^2}A^{\prime }(w)\ \bar{u}_{\alpha }\Gamma _{\mu }^{\alpha \beta }(\gamma _{\beta }+v_{1\beta })\gamma _{5}u, \end{aligned}$$
(99)

where Eq. (86) has been used. The unknown function \(A^{\prime }(w)\) contains all the dynamics of light degrees of freedom, and it describes the response of the light particles to the changing of heavy diquark velocity. Furthermore, \(A^{\prime }(w)\) is totally determined by the soft function Eq. (92). In fact, this soft function is a universal quantity which also appears in the HQET analysis of \(B\rightarrow D\) transition [56], where the Isgur–Wise function \(\xi (w)\) is derived from it in the same way as done here for \(A^{\prime }(w)\). Explicitly, \({\xi }(w)\propto {{\mathcal {F}}}[A(w),B(w),C(w),D(w)]\). Thus one can conclude that \(A^{\prime }(w)\) is related to \(\xi (w)\) up to some constant coefficients.

4.3 Phenomenological results for reduced form factors

Generally, the doubly heavy baryon transition matrix element induced by the \(V-A\) current is parametrized by several independent form factors. For \({{\mathcal {B}}}_{bQ}^{1/2}\rightarrow {{\mathcal {B}}}_{cQ}^{1/2}\) it reads

$$\begin{aligned}&\langle \mathcal{B}_{cQ}^{1/2}(P_c)|\left( J_{\mu }^{V}(0)-J_{\mu }^{A}(0)\right) |\mathcal{B}_{bQ}^{1/2}(P_b)\rangle \nonumber \\&\quad = \bar{u}_{cQ}(P_{c})\bigg [F_{1}(q^{2})\gamma ^{\mu }+F_{2}(q^{2})P_{c}^{\mu }+F_{3}(q^{2}) P_{b}^{\mu }\bigg ]u_{bQ}(P_{b})\nonumber \\&\qquad - \bar{u}_{cQ}(P_{c})\bigg [G_{1}(q^{2})\gamma ^{\mu }+G_{2}(q^{2})P_{c}^{\mu }+G_{3}(q^{2})P_{b}^{\mu }\bigg ] \gamma _{5}u_{bQ}(P_{b}), \nonumber \\ \end{aligned}$$
(100)

while for \({{\mathcal {B}}}_{bQ}^{1/2}\rightarrow {{\mathcal {B}}}_{cQ}^{3/2}\) the parametrization takes the form

Fig. 2
figure 2

\(q^2\)-dependence of the \({{\mathcal {B}}}_{bQ}^{1/2}\rightarrow \mathcal{B}_{cQ}^{1/2}\) form factors, where \(Q=b,c\)

Full size image
$$\begin{aligned}&\langle \mathcal{B}_{cQ}^{3/2}(P_{c})|\left( J_{\mu }^{V}(0)-J_{\mu }^{A}(0)\right) |\mathcal{B}_{bQ}^{1/2}(P_{b})\rangle \nonumber \\&\quad = \bar{u}_{cQ}^{\alpha }(P_{c})\bigg [\frac{f_{1}^{\prime }(q^{2})}{M_{b}}\gamma ^{\mu }P_{b\alpha } \nonumber \\&\qquad +\frac{f_{2}^{\prime }(q^{2})}{M_{b}^{2}}P_{b\alpha }P_{b\mu } +\frac{f_{3}^{\prime }(q^{2})}{M_{b}M_{c}}P_{b\alpha }P_{c\mu } \nonumber \\&\qquad +f_{4}^{\prime }(q^{2})g_{\mu \alpha }\bigg ]\gamma _{5}u_{bQ}(P_{b})-\bar{u}_{cQ}^{\alpha }(P_{c})\bigg [\frac{g_{1}^{\prime }(q^{2})}{M_{b}}\gamma ^{\mu }P_{b\alpha } \nonumber \\&\qquad +\frac{g_{2}^{\prime }(q^{2})}{M_{b}^{2}}P_{b\alpha }P_{b\mu } +\frac{g_{3}^{\prime }(q^{2})}{M_{b}M_{c}}P_{b\alpha } P_{c\mu }+g_{4}^{\prime }(q^{2})g_{\mu \alpha }\bigg ]u_{bQ}(P_{b}). \end{aligned}$$
(101)

However, if we treat such process by HDiET considering also the heavy flavor symmetry, the number of independent form factors can be greatly reduced. Especially, by combining Eqs. (41–43) and Eqs. (96–99), one arrives at

$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(1)}_{cQ}|J^{V}_{\mu }(0)|{{\mathcal {B}}}^{1/2(1)}_{bQ}\rangle \nonumber \\&\quad = \eta (w)\bar{u}\big [2(1+w)\gamma _{\mu }+v_{b\mu }+v_{c\mu }\big ]u, \end{aligned}$$
(102)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(1)}_{cQ}|J^{A}_{\mu }(0)|{{\mathcal {B}}}^{1/2(1)}_{bQ}\rangle \nonumber \\&\quad = \eta (w)\bar{u}\big [2(1+w)\gamma _{\mu }\big ]\gamma _{5}u, \end{aligned}$$
(103)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(0)}_{cQ}|J^{V}_{\mu }(0)|{{\mathcal {B}}}^{1/2(1)}_{bQ}\rangle \nonumber \\&\quad = -\sqrt{3}\eta (w)\bar{u}\big [(1+w)\gamma _{\mu }-v_{b\mu }-v_{c\mu }\big ]u, \end{aligned}$$
(104)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(0)}_{cQ}|J^{A}_{\mu }(0)|{{\mathcal {B}}}^{1/2(1)}_{bQ}\rangle \nonumber \\&\quad = \sqrt{3}\eta (w)\bar{u}\big [(1+w)\gamma _{\mu }\big ]\gamma _5 u, \end{aligned}$$
(105)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(1)}_{cQ}|J^{V}_{\mu }(0)|{{\mathcal {B}}}^{1/2(0)}_{bQ}\rangle \nonumber \\&\quad = \sqrt{3}\eta (w)\bar{u}\big [(1+w)\gamma _{\mu }-v_{b\mu }-v_{c\mu }\big ]u, \end{aligned}$$
(106)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{1/2(1)}_{cQ}|J^{A}_{\mu }(0)|{{\mathcal {B}}}^{1/2(0)}_{bQ}\rangle \nonumber \\&\quad = \sqrt{3}\eta (w)\bar{u}\big [(1+w)\gamma _{\mu }\big ]\gamma _5 u, \end{aligned}$$
(107)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{3/2(1)}_{cQ}|J_{\mu }^{V}(0)|{{\mathcal {B}}}^{1/2(1)}_{bQ}\rangle \nonumber \\&\quad =-\sqrt{3}\eta (w)\bar{u}_{\alpha }\big [(1+w)g^{\alpha }_{\mu }-v_{c\mu }v_{b}^{\alpha }+\gamma _{\mu }v_{b}^{\alpha }\big ]\gamma _{5}u, \end{aligned}$$
(108)
$$\begin{aligned}&\langle {{\mathcal {B}}}^{3/2(1)}_{cQ}|J_{\mu }^{A}(0)|\mathcal{B}^{1/2(1)}_{bQ}\rangle \nonumber \\&\quad =\sqrt{3}\eta (w)\bar{u}_{\alpha }\big [(1+w)g^{\alpha }_{\mu }-v_{c\mu }v_{b}^{\alpha }\big ]u, \end{aligned}$$
(109)

where only one form factor \(\eta (w)\) is left. This is shared by all the six matrix elements and \(\eta (w)\) is proportional to the soft function \(A^{\prime }(w)\)

$$\begin{aligned} \eta (w)=C\Lambda \frac{(N^{1/2})^2 M^2}{N_{X}^2m_X^2}A^{\prime }(w). \end{aligned}$$
(110)

The vector transition shown in Eq. (102) is exactly the same as that given in [47], where the transition matrix element was derived based on heavy quark-diquark symmetry. However, Ref. [47] did not give the result for the axial-current transition. In terms of the complicated factors in Eq. (110), this is determined through the normalization at the zero-recoil point \(w=1\). From Eq. (41), one can find that the vector current \(J_{\mu (V)}^{X\rightarrow X}\) is conserved \(\partial ^{\mu }J_{\mu (V)}^{X\rightarrow X}=0\). This implies the conservation of diquark number. Thus we can conclude that

$$\begin{aligned}&\langle {{\mathcal {B}}}_{cQ}(v)|\int d^3\vec x\ J_{0(V)}^{X\rightarrow X}(\vec x)|{{\mathcal {B}}}_{bQ}(v)\rangle \nonumber \\&\quad = \langle \mathcal{B}_{cQ}(v)|{\mathbf {1}}|{{\mathcal {B}}}_{bQ}(v) \rangle =2v^0(2\pi )^3\delta ^3(0), \end{aligned}$$
(111)

where \({\mathbf {1}}\) means the diquark number is one. On the other hand, using Eq. (102), and choosing the rest-frame of \({{\mathcal {B}}}_{bQ}(v)\), \(v=(1,\vec {0})\), the same matrix element becomes

$$\begin{aligned}&\langle {{\mathcal {B}}}_{cQ}(v)|\int d^3\vec x\ J_{0(V)}^{X\rightarrow X}(\vec x)|{{\mathcal {B}}}_{bQ}(v)\rangle \nonumber \\&\quad =(2\pi )^3\delta ^3(0)\eta (1)\bar{u}(v)\big [4\gamma _{0}+2v_{0}\big ]u(v)\nonumber \\&\quad =12\eta (1)v^0(2\pi )^3\delta ^3(0), \end{aligned}$$
(112)

where we have used and . Comparing the above two equations, one can conclude that \(\eta (1)=1/6\). At the end of last subsection, we have argued that \(A^{\prime }(w) \propto \xi (w)\). Since \(\xi (1)=1\), it thus follows that \(\eta (1)=(1/6)\xi (1)\).

However, it is necessary to point out that the reduced matrix elements Eqs. (102–109) are only applicable in the region \(w\sim 1\) or equivalently \(q^2\sim q_{max}^2=(M_b-M_c)^2\). In the smaller-\(q^2\) region, the large recoil may invalidate the static dynamics of HDiET. As a result, one cannot argue that for any w we have \(\eta (w)=(1/6)\xi (w)\), and an appropriate extension of the form factors from \(q^2=q_{max}^2\) to \(q^2=0\) is necessary. Since the transition matrix elements Eqs. (102–109) are expected to have a lowest-\(q^2\) pole at the mass of \(B_c\) meson, it is appropriate to multiply \(\eta (w)\) with single pole function B(w) with a suitable normalization \(B(1)=1\),

$$\begin{aligned} B\left( w=\frac{M_b^2+M_c^2-q^2}{2M_bM_c}\right) =\frac{1-q_{max}^2/m_{B_c}^2}{1-q^2/m_{B_c}^2}. \end{aligned}$$
(113)

Finally, we arrive at an explicit expression of the \(\eta \) function

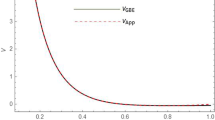
$$\begin{aligned} \eta (q^2)=\frac{1}{6}\xi \left( \frac{M_b^2+M_c^2-q^2}{2M_bM_c}\right) \frac{1-q_{max}^2/m_{B_c}^2}{1-q^2/m_{B_c}^2}. \end{aligned}$$
(114)

Note that for the practical calculation we have to distinguish between the different masses \(M_b, M_c\). The Isgur–Wise function was calculated e.g. in Ref. [57], which has the expression

$$\begin{aligned} \xi (w)&=\int \limits _0^{\beta _0/w} d\rho \exp \left( \frac{{\bar{\Lambda }}-\rho w}{\tau }\right) \nonumber \\&\quad \times \Big [\frac{1}{2w}\phi _{-}^B(\rho )+ \big (1-\frac{1}{2w}\big )\phi _{+}^B(\rho ) \Big ], \end{aligned}$$
(115)
$$\begin{aligned} s_0^D&=\kappa ^2 m_Q^2+2\kappa m_Q\beta _0,\quad M^2=2\kappa m_Q\tau , \end{aligned}$$
(116)

where \({{\bar{\Lambda }}}=m_B-m_b\), \(m_Q=m_b\), \(\kappa =m_c/m_b\), \(s_0^D=6\ \mathrm {GeV}^2\) is the effective threshold, while \(M^2=3-6\) GeV\(^2\) is the Borel parameter. In this work, we simply use its center value \(M^2=4.5\) GeV\(^2\). \(\phi _{\pm }^B\) are the B meson light-cone distribution amplitudes, which have the form

Fig. 3
figure 3

\(q^2\)-dependence of the \({{\mathcal {B}}}_{bQ}^{1/2(1)}\rightarrow \mathcal{B}_{cQ}^{3/2(1)}\) form factors, where \(Q=b,c\)

Full size image
$$\begin{aligned} \phi _+^B(\omega ) = \dfrac{\omega }{\omega _0^2}\,e^{-\frac{\omega }{\omega _0}},\quad \phi _-^B(\omega ) = \dfrac{1}{\omega _0}\,e^{-\frac{\omega }{\omega _0}}, \end{aligned}$$
(117)

where \(\omega _0=(2/3){{\bar{\Lambda }}}\) [58]. The mass parameters are set as \(m_b=4.18\) GeV, \(m_c=1.27\) GeV, \(m_B=5.279\) GeV, \(m_D=1.869\) GeV and \(m_{Bc}=6.275\) GeV. Fig. 2 shows \(q^2\)-dependence of the \(\mathcal{B}_{bQ}^{1/2(1)}\rightarrow {{\mathcal {B}}}_{cQ}^{1/2(1)}, {{\mathcal {B}}}_{cQ}^{1/2(0)}\) form factors, where we have redefined the six form factors as

$$\begin{aligned}&\langle \mathcal{B}_{cQ}(P_c)|\left( J_{\mu }^{V}(0)-J_{\mu }^{A}(0)\right) |\mathcal{B}_{bQ}(P_b)\rangle \nonumber \\&\quad = \bar{u}_{cQ}(P_{c})\bigg [\gamma ^{\mu }f_{1}(q^{2})+i\sigma ^{\mu \nu }\frac{q_{\nu }}{M_b}f_{2}(q^{2})\nonumber \\&\qquad +\frac{q^{\mu }}{M_b} f_{3}(q^{2})\bigg ]u_{bQ}(P_{b})\nonumber \\&\qquad - \bar{u}_{cQ}(P_{c})\bigg [\gamma ^{\mu }g_{1}(q^{2})+i\sigma ^{\mu \nu }\frac{q_{\nu }}{M_b}g_{2}(q^{2})\nonumber \\&\qquad +\frac{q^{\mu }}{M_b}g_{3}(q^{2})\bigg ] \gamma _{5}u_{b}(P_{b}), \end{aligned}$$
(118)

with \(q^{\mu }=P_{b}^{\mu }-P_{c}^{\mu }\) the transferred momentum. The \(f_i\) and \(g_i\) are related to the \(F_i\) and \(G_i\) as

$$\begin{aligned} f_1(q^2)= & {} F_1(q^2)+\frac{1}{2}(M_b+M_c)(F_2(q^2)+F_3(q^2)), \nonumber \\ f_2(q^2)= & {} \frac{1}{2}M_b(F_2(q^2)+F_3(q^2)), \nonumber \\ f_3(q^2)= & {} \frac{1}{2}M_b(F_3(q^2)-F_2(q^2)), \nonumber \\ g_1(q^2)= & {} G_1(q^2)-\frac{1}{2}(M_b-M_c)(G_2(q^2)+G_3(q^2)), \nonumber \\ g_2(q^2)= & {} \frac{1}{2}M_b(G_2(q^2)+G_3(q^2)), \nonumber \\ g_3(q^2)= & {} \frac{1}{2}M_b(G_3(q^2)-G_2(q^2)), \end{aligned}$$
(119)

and here we have \(g_2(q^2)=g_3(q^2)=0\). The masses of the baryons are \(m_{{{\mathcal {B}}}_{bb}}=10.143\) GeV, \(m_{\mathcal{B}_{bc}^{1/2}}=6.943\) GeV, \(m_{{{\mathcal {B}}}_{bc}^{3/2}}=6.985\) GeV, \(m_{{{\mathcal {B}}}_{cc}^{1/2}}=3.621\) GeV and \(m_{\mathcal{B}_{cc}^{3/2}}=3.69\) GeV. Figure 3 shows the \(q^2\)-dependence of the \({{\mathcal {B}}}_{bQ}^{1/2(1)}\rightarrow \mathcal{B}_{cQ}^{3/2(1)}\) form factors, where \(f_2^{\prime }(q^2)=g_1^{\prime }(q^2) =g_2^{\prime }(q^2)=0\).

4.4 Semi-leptonic decay widths

Next, using the form factors given in the last section, we will calculate the semi-leptonic decay widths of \(\mathcal{B}_{bQ}^{1/2(1)}\rightarrow {{\mathcal {B}}}_{cQ}^{1/2(1)}, \mathcal{B}_{cQ}^{1/2(0)}~\text {and}~{{\mathcal {B}}}_{cQ}^{3/2(1)}\). For the case of \({{\mathcal {B}}}_{bQ}^{1/2(1)}\rightarrow {{\mathcal {B}}}_{cQ}^{1/2(1)}, \mathcal{B}_{cQ}^{1/2(0)}\), the formula of the differential decay width is given in [9, 34]

$$\begin{aligned} \frac{d\Gamma _{L}}{dq^{2}}&=\ \frac{G_{F}^{2}|V_{\mathrm{CKM}}|^{2}q^{2}\ p\ (1-{\hat{m}}_{l}^{2})^{2}}{384\pi ^{3} M_{1}^{2}}\nonumber \\&\quad \times \left( (2+{\hat{m}}_{l}^{2})(|H_{-\frac{1}{2},0}|^{2}+|H_{\frac{1}{2},0}|^{2})\right. \nonumber \\&\quad \left. +3{\hat{m}}_{l}^{2}(|H_{-\frac{1}{2},t}|^{2} +|H_{\frac{1}{2},t}|^{2})\right) , \end{aligned}$$
(120)
$$\begin{aligned} \frac{d\Gamma _{T}}{dq^{2}}&= \frac{G_{F}^{2}|V_{\mathrm{CKM}}|^{2}q^{2}\ p (1-{\hat{m}}_{l}^{2})^{2}(2+{\hat{m}}_{l}^{2})}{384\pi ^{3}M_{1}^{2}} \nonumber \\&\quad \times (|H_{\frac{1}{2},1}|^{2}+|H_{-\frac{1}{2},-1}|^{2}), \end{aligned}$$
(121)

with the helicity amplitudes given as \(H_{\lambda _{2},\lambda _{W}}=H_{\lambda _{2},\lambda _{W}}^{V}-H_{\lambda _{2},\lambda _{W}}^{A}\),

$$\begin{aligned}&H_{\frac{1}{2},0}^{V} = -i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M_{1}+M_{2})f_{1}-\frac{q^{2}}{M_{1}}f_{2}\right) ,\nonumber \\&H_{\frac{1}{2},0}^{A} = -i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}}\left( (M_{1}-M_{2})g_{1}+\frac{q^{2}}{M_1}g_{2}\right) ,\nonumber \\&H_{\frac{1}{2},1}^{V} = i\sqrt{2Q_{-}}\left( -f_{1}+\frac{M_{1}+M_{2}}{M_{1}}f_{2}\right) ,\nonumber \\&H_{\frac{1}{2},1}^{A} = i\sqrt{2Q_{+}}\left( -g_{1}-\frac{M_{1}-M_{2}}{M_{1}}g_{2}\right) ,\nonumber \\&H_{\frac{1}{2},t}^{V} = -i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}}\left( (M_{1}-M_{2})f_{1}+\frac{q^{2}}{M_{1}}f_{3}\right) ,\nonumber \\&H_{\frac{1}{2},t}^{A} = -i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M_{1}+M_{2})g_{1}-\frac{q^{2}}{M_{1}}g_{3}\right) , \nonumber \\&H_{-\lambda _{2},-\lambda _{W}}^{V}=H_{\lambda _{2},\lambda _{W}}^{V},\nonumber \\&H_{-\lambda _{2},-\lambda _{W}}^{A}=-H_{\lambda _{2},\lambda _{W}}^{A},\quad \text {and}\quad Q_{\pm }=(M_1\pm M_2)^{2}-q^{2}, \end{aligned}$$
(122)

where \(p=M_2\sqrt{w^2-1}\) with \(w=(M_1^2+M_2^2-q^2)/2M_1M_2\), while \(M_1(M_2)\) is the initial(final) baryon mass, \({\hat{m}}_{l}\equiv m_{l}/\sqrt{q^{2}}\) and \(m_l\) is the lepton mass. For the case of \({{\mathcal {B}}}_{bQ}^{1/2(1)} \rightarrow {{\mathcal {B}}}_{cQ}^{3/2(1)}\), the formula for the differential decay width is given in [23]

Table 1 Decay widths of \({{{\mathcal {B}}}}_{bb}\rightarrow {\mathcal{B}}_{bc}(l/\tau )\nu \). Comparison between the results in this work and those derived in Ref. [9] using the LFQM
Full size table
$$\begin{aligned} \frac{d\Gamma _{T}}{dw}&= \frac{G_{F}^{2}}{(2\pi )^{3}}|V_{\mathrm{CKM}}|^{2}\frac{q^{2}M_1^{\prime 2}\sqrt{w^{2}-1}}{12M}\nonumber \\&\quad \times \left( |{{\bar{H}}}_{{1\over 2},1}|^{2}+|{{\bar{H}}}_{-{1\over 2},-1}|^{2}+|{{\bar{H}}}_{{3\over 2},1}|^{2}+|{{\bar{H}}}_{-{3\over 2},-1}|^{2}\right) , \end{aligned}$$
(123)
$$\begin{aligned} \frac{d\Gamma _{L}}{dw}&= \frac{G_{F}^{2}}{(2\pi )^{3}}|V_{\mathrm{CKM}}|^{2}\frac{q^{2}M_1^{\prime 2}\sqrt{w^{2}-1}}{12M}\nonumber \\&\quad \times \left( |{\bar{H}}_{{1\over 2},0}|^{2}+|{{\bar{H}}}_{-{1\over 2},0}|^{2}\right) , \end{aligned}$$
(124)

with the helicity amplitudes given as

$$\begin{aligned} {{\bar{H}}}_{3/2,1}^{V,A}= & {} \mp i\sqrt{2M_1M_2(w\mp 1)}f_{4}^{\prime V,A}, \end{aligned}$$
(125)
$$\begin{aligned} {{\bar{H}}}_{1/2,1}^{V,A}= & {} i\sqrt{\frac{2}{3}}\sqrt{M_1M_2(w\mp 1)}\left[ f_{4}^{\prime V,A}-2(w\pm 1)f_{1}^{\prime V,A}\right] ,\nonumber \\ \end{aligned}$$
(126)
$$\begin{aligned} {{\bar{H}}}_{1/2,0}^{V,A}= & {} \pm i\frac{1}{\sqrt{q^{2}}}\frac{2}{\sqrt{3}}\sqrt{M_1M_2(w\mp 1)}\nonumber \\&\times \Big [(M_1w-M_2)f_{4}^{\prime V,A}\mp (M_1\mp M_2)(w\pm 1)f_{1}^{\prime V,A}\nonumber \\&+M^{\prime }(w^{2}-1)f_{2}^{\prime V,A}+M(w^{2}-1)f_{3}^{\prime V,A}\Big ], \end{aligned}$$
(127)

where the upper (lower) sign denotes V (A), \(f_{i}^{V}=f_{i}\) (\(f_{i}^{A}=g_{i}\)). The total decay width is the sum of the longitudinal and the transversal parts

$$\begin{aligned} \Gamma =\int _{m_l^2}^{(M_{1}-M_{2})^{2}}dq^{2}\left( \frac{d\Gamma _{L}}{dq^{2}}+\frac{d\Gamma _{T}}{dq^{2}}\right) . \end{aligned}$$
(128)

The masses of \(e, \mu \) are neglected here and \(m_{\tau }=1.78\) GeV. Table 1 gives the resulting decay widths and also a comparison with those derived in Ref. [9] within light-front quark model (LFQM). It appears that the two sets of decay width results are consistent.

5 Conclusions

In summary, we have constructed a heavy diquark effective theory (HDiET), which satisfies the global heavy quark flavor SU(2) symmetry and electromagnetic U(1) symmetry. Imposing these symmetries, we constructed the coupling terms where the diquark fields interact with the external weak and electromagnetic sources. Such coupling terms enable us to obtain the effective diquark transition currents in the small recoil region. On the other hand, for large recoil, the diquark transition currents are derived from the matching between QCD and DiET at tree level. Furthermore, we simpilfied DiET as HDiET in the heavy diquark limit, from which we reduced the form factors of the doubly heavy baryon transition to only one function \(\eta (w)\). The reduced vector matrix element is the same as those derived by heavy quark-diquark symmetry in earlier works. In addition, we pointed out that \(\eta (w)\) is related with the universal soft function which is proportional to the Isgur-Wise function of heavy meson decays. Thus we obtained the \(q^2\)-dependence of \(\eta (q^2)\) by assuming a monopole structure. Finally, the obtained form factors are used to predict the semi-leptonic decay widths of doubly heavy baryons, and the results are consistent with those derived by LFQM in the earlier works.