Revisiting the B-physics anomalies in R-parity violating MSSM

Abstract

In recent years, several deviations from the Standard Model predictions in semileptonic decays of B-meson might suggest the existence of new physics which would break the lepton-flavour universality. In this work, we have explored the possibility of using muon sneutrinos and right-handed sbottoms to solve these B-physics anomalies simultaneously in R-parity violating minimal supersymmetric standard model. We find that the photonic penguin induced by exchanging sneutrino can provide sizable lepton flavour universal contribution due to the existence of logarithmic enhancement for the first time. This prompts us to use the two-parameter scenario $(C^\mathrm{V}_9, \, C^\mathrm{U}_9)$ to explain $b \rightarrow s \ell ^+ \ell ^-$ anomaly. Finally, the numerical analyses show that the muon sneutrinos and right-handed sbottoms can explain $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies simultaneously, and satisfy the constraints of other related processes, such as $B \rightarrow K^{(*)} \nu \bar{\nu }$ decays, $B_s-\bar{B}_s$ mixing, Z decays, as well as $D^0 \rightarrow \mu ^+ \mu ^-$, $\tau \rightarrow \mu \rho ^0$, $B \rightarrow \tau \nu$, $D_s \rightarrow \tau \nu$, $\tau \rightarrow K \nu$, $\tau \rightarrow \mu \gamma$, and $\tau \rightarrow \mu \mu \mu$ decays.

1 Introduction

Recently, several flavour anomalies in semileptonic B-decays have been reported, which have been attracting great interest. Among them, the observables $R_{K^{(*)}} = \mathcal{B}(B \rightarrow K^{(*)} \mu ^+ \mu ^-) / \mathcal{B}(B \rightarrow K^{(*)} e^+ e^-)$ in flavour-changing neutral current $b \rightarrow s \ell ^+ \ell ^-$ ($\ell = e,\, \mu$) transition and the observables $R(D^{(*)}) = \mathcal{B}(B \rightarrow D^{(*)} \tau \nu ) / \mathcal{B}(B \rightarrow D^{(*)} \ell \nu )$ in flavour-changing charged current $b \rightarrow c \tau \nu$ transition are particularly striking. The advantage of considering the ratios $R_{K^{(*)}}$ and $R(D^{(*)})$ instead of the branching fractions themselves is that, apart from the significant reduction of the experimental systematic uncertainties, the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements cancel out and the dependence on the transition form factors become much weaker. These observables can be good probes to test the lepton-flavour universality (LFU) held in the Standard Model (SM).

The latest measurement of $R_K$ by LHCb collaboration gives [1, 2]

$$\begin{aligned} R_K = 0.846^{+0.060+0.016}_{-0.054-0.014}, \, 1.1< q^2 < 6 ~\mathrm{GeV}^2 , \end{aligned}$$

(1)

but the SM prediction is around 1 with $\mathcal{O}(1\%)$ uncertainty [3], there is $2.5\sigma$ discrepancy. Moreover, the measurement of $R_{K^{*}}$ by LHCb at low and high $q^2$ are [4]

$$\begin{aligned} R_{K^*} = {\left\{ \begin{array}{ll} 0.66^{+0.11}_{-0.07} \pm 0.03 , &{} 0.045< q^2< 1.1\, \mathrm{GeV}^2 \\ 0.69^{+0.11}_{-0.07} \pm 0.05 , &{} 1.1< q^2 < 6.0 \,\mathrm{GeV}^2 \end{array}\right. } , \end{aligned}$$

(2)

while the SM predictions are $R_{K^*}^{[0.045,\,1.1]} = 0.906 \pm 0.028$ and $R_{K^*}^{[1.1,\,6.0]} = 1.00 \pm 0.01$ [3]. The measurements show $2.1\sigma$ discrepancy in the low $q^2$ region and $2.5 \sigma$ discrepancy in the high $q^2$ region, respectively. The Belle collaboration also reported their measurements of $R_{K^{(*)}}$ [5, 6], which are consistent with the SM predictions within their quite large error bars. In addition to $R_{K^{(*)}}$, there are also some other deviations in $b \rightarrow s \mu ^+ \mu ^-$ transition, such as the angular observable $P_5'$ [7,8,9] of $B \rightarrow K^*\mu ^+ \mu ^-$ decay with $2.6 \sigma$ discrepancy [10,11,12,13,14,15] and the differential branching fraction of $B_s \rightarrow \phi \mu ^+ \mu ^-$ decay with $3.3 \sigma$ discrepancy [16, 17].

These deviations indicate the possible existence of new physics (NP) beyond the SM in $b \rightarrow s \ell ^+ \ell ^-$ transition. This NP may break LFU. Many recent model-independent analyses [18,19,20,21,22,23,24,25] show that some scenarios can explain the $b\rightarrow s\ell ^+\ell ^-$ anomaly well. To express the fit results, we consider the low-energy effective weak Lagrangian governing the $b\rightarrow s\ell ^+\ell ^-$ transition

$$\begin{aligned} \mathcal{L}_\mathrm{eff} = \frac{4 G_F}{\sqrt{2}} \eta _t \sum _{i}C_i\mathcal{O}_i + \mathrm{H.c.} , \end{aligned}$$

(3)

where CKM factor $\eta _t \equiv V_{tb} V_{ts}^{*}$. We mainly concern the semileptonic operators

$$\begin{aligned} \mathcal{O}_9&= \frac{e^2}{16\pi ^2}(\bar{s}\gamma _\mu P_{L} b)(\bar{\ell }\gamma ^\mu \ell ), \end{aligned}$$

(4)

$$\begin{aligned} \mathcal{O}_{10}&= \frac{e^2}{16\pi ^2}(\bar{s}\gamma _\mu P_{L} b)(\bar{\ell }\gamma ^\mu \gamma _5 \ell ), \end{aligned}$$

(5)

where $P_L=(1-\gamma _5)/2$ is the left-handed chirality projector. The Wilson coefficients $C_{9,10} = C_{9,10}^\mathrm{SM} + C_{9,10}^\mathrm{NP}$. In this work, we try to explain the anomaly through a two-parameter scenario where the total NP effects are given by [26]

$$\begin{aligned}&C^\mathrm{NP}_{9,\mu } = C^\mathrm{V}_9 + C^\mathrm{U}_9,\quad C^\mathrm{NP}_{10,\mu } = - C^\mathrm{V}_9, \end{aligned}$$

(6)

$$\begin{aligned}&C^\mathrm{NP}_{9,e} = C^\mathrm{U}_9,\quad C^\mathrm{NP}_{10,e} = 0. \end{aligned}$$

(7)

The global analyses show that this scenario has the largest pull-value. The best-fit point performed by Ref. [20] is $(C^\mathrm{V}_9,\,C^\mathrm{U}_9) = (-0.30,\,-0.74)$, with the $2\sigma$ range being

$$\begin{aligned} -0.53< C^\mathrm{V}_9< -0.10,\quad -1.15< C^\mathrm{U}_9 < -0.25. \end{aligned}$$

(8)

As we will see in the following discussion, this scenario can be implemented naturally in the R-parity violating minimal supersymmetric standard model (MSSM) [27].

The combined measurements of $R(D^*)$ and R(D) are from BaBar [28, 29] and Belle [30, 31], and Belle [32, 33] and LHCb [34,35,36] only give the measurements of $R(D^*)$. After being averaged by the Heavy Flavor Averaging Group (HFLAV) [37], they give the results as follows [38]

$$\begin{aligned} R(D)_\mathrm{avg}&= 0.340 \pm 0.027 \pm 0.013, \end{aligned}$$

(9)

$$\begin{aligned} R(D^*)_\mathrm{avg}&= 0.295 \pm 0.011 \pm 0.008, \end{aligned}$$

(10)

with a correlation of $-0.38$. Comparing these with the arithmetic average of the SM predictions [38,39,40,41,42],

$$\begin{aligned} R(D)_\mathrm{SM}=0.299 \pm 0.003,\quad R(D^*)_\mathrm{SM}=0.258 \pm 0.005, \end{aligned}$$

(11)

one can see that the difference between experiment and theory is at about $3.08\sigma$, implying the existence of LFU violating NP in the charged-current B-decays. Global analyses [43,44,45,46,47] show that the NP contributing to the left-handed operator $(\bar{c} \gamma _\mu P_L b)(\bar{\tau }\gamma ^\mu P_L \nu )$ can solve the $R(D^{(*)})$ anomaly. Such operator can be generated in R-parity violating MSSM by exchanging the right-handed down type squarks at tree level.

There have been attempts to explain the $b \rightarrow s \ell ^+ \ell ^-$ anomaly [48,49,50,51,52] or $R(D^{(*)})$ anomaly [53,54,55,56,57] or both of them [58,59,60] by R-parity violating interactions in the supersymmetric (SUSY) models. For example, based on the inspiration from the paper by Bauer and Neubert [61], the authors in Ref. [58] investigated the possibility of using right-handed down type squarks to explain the $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies simultaneously, and found that this was impossible due to the severe constraints from $B\rightarrow K^{(*)} \nu \bar{\nu }$ decays. Considering that the parameter space obtained by using squarks to explain $b \rightarrow s \ell ^+ \ell ^-$ anomaly is very small [49, 50, 58] due to the strict constraints from other related processes, such as $B\rightarrow K^{(*)} \nu \bar{\nu }$ decays and $B_s-\bar{B}_s$ mixing, the authors in Ref. [52] used sneutrinos to explain it and found that it is almost unconstrained by other related processes. Based on this knowledge, in this work, we will explore the possibility of using muon sneutrinos $\tilde{\nu }_\mu$ and right-handed sbottoms $\tilde{b}_R$ to explain the $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies simultaneously within the context of R-parity violating MSSM.

Our paper is organized as follows. In Sect. 2, we scrutinize all the one-loop contributions of terms $\lambda '_{ijk} L_i Q_j D_k^c$ to $b\rightarrow s\ell ^+\ell ^-$ processes in the framework of R-parity violating MSSM, and then give our scenario to explain the $b \rightarrow s \ell ^+ \ell ^-$ anomaly. Discussions of $R(D^{(*)})$ anomaly and other related processes are included in Sect. 3. The numerical analyses and results are shown in Sect. 4. Our conclusions are finally made in Sect. 5.

2 $b\rightarrow s\ell ^+\ell ^-$ processes in R-parity violating MSSM

The superpotential terms violating R-parity in the MSSM are [27]

$$\begin{aligned} W_\mathrm{RPV}&= \, \mu _i L_i H_u + \frac{1}{2} \lambda _{ijk} L_i L_j E_k^c + \lambda '_{ijk} L_i Q_j D_k^c\nonumber \\&\quad + \frac{1}{2} \lambda ''_{ijk} U_i^c D_j^c D_k^c\, , \end{aligned}$$

(12)

where the generation indices are denoted by $i,j,k=1,2,3$ and the colour indices are suppressed. All repeated indices are assumed to be summed over throughout this paper unless otherwise stated (For example, repeated indices in both numerator and denominator are not automatically summed). $H_u$, L and Q are SU(2) doublet chiral superfields while $E^c$, $D^c$ and $U^c$ are SU(2) singlet chiral superfields.

In this work, we are mainly interested in the terms $\lambda '_{ijk} L_i Q_j D_k^c$ which related to both quarks and leptons. This choice can also alleviate the constraint of sneutrino masses on the collider, because the lower limit of sneutrino masses will be as high as TeV scale [62,63,64,65] when there are non-zero $\lambda$ and $\lambda '$ at the same time. The corresponding Lagrangian can be obtained by the chiral superfields composing of the fermions and sfermions as follows

$$\begin{aligned} \mathcal{L}&= \, \lambda '_{ijk}\big (\tilde{\nu }_{Li} \bar{d}_{Rk} d_{Lj} + \tilde{d}_{Lj} \bar{d}_{Rk} \nu _{Li} + \tilde{d}_{Rk}^*\bar{\nu }_{Li}^c d_{Lj}\nonumber \\&\quad - \tilde{l}_{Li} \bar{d}_{Rk} u_{Lj} - \tilde{u}_{Lj} \bar{d}_{Rk} l_{Li} - \tilde{d}_{Rk}^*\bar{l}_{Li}^c u_{Lj}\big ) + \mathrm{H.c.} , \end{aligned}$$

(13)

where the sparticles are denoted by “$\tilde{\ }$”, and “c” indicates charge conjugated fields. Working in the mass eigenstates for the down type quarks and assuming sfermions are in their mass eigenstates, one replaces $u_{Lj}$ by $(V^\dagger u_L)_j$ in Eq. (13).

These R-parity violating interactions can induce $b \rightarrow s \ell ^+ \ell ^-$ processes by exchanging left-handed up squarks $\tilde{u}_{Lj}$ at tree level, but resulting in the operators with right-handed quark current, which are unable to explain the $b \rightarrow s \ell ^+ \ell ^-$ anomaly. This unwanted effect can be eliminated by assuming that the masses of $\tilde{u}_{Lj}$ are very large or/and by assuming that $\lambda '_{ij2} = 0$. Assuming that $\lambda '_{ij2} = 0$ also forbids the exchange of $\tilde{l}_{Li}$ or/and $\tilde{d}_{Lj}$ in one loop level to affect the $b \rightarrow s \ell ^+ \ell ^-$ processes.¹ In the following discussion, we should assume that $\lambda '_{ij1} = \lambda '_{ij2} = 0$.

Fig. 1

Box diagrams for $b \rightarrow s \mu ^+ \mu ^-$ transition in our scenario. a Shows an example $\tilde{W} - b$ box diagram, b shows an example $W - \tilde{b}_R$ box diagram, c shows the $H^\pm - \tilde{b}_R$ box diagram, and d shows an example $4\lambda '$ box diagram

Fig. 2

Photonic penguin diagrams studied in our scenario

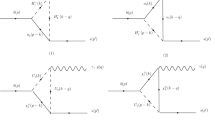
Next, we will show the contributions of R-parity violating MSSM to $b\rightarrow s\ell ^+\ell ^-$ processes. All the Feynman diagrams include four $\tilde{W} - b$ box diagrams (Fig. 1a), five $W - \tilde{b}_R$ box diagrams (one of which is Goldstone$- \tilde{b}_R$ box diagram) (Fig. 1b), one $H^\pm - \tilde{b}_R$ box diagram (Fig. 1c), two $4\lambda '$ box diagrams (Fig. 1d) and two $\gamma$-penguin diagrams (Fig. 2). Most of these results can be found in Refs. [49, 50, 52, 58], however, to our knowledge, the results of the diagram induced by exchanging charged Higgs $H^\pm$ and right-handed sbottom $\tilde{b}_R$ in loop are the first to be given in this paper. The photonic penguin diagrams, which have been neglected in previous work, play an important role in our discussion, as we will explain in more detail later. We do not find sizable Z-penguin contributions to $b\rightarrow s\ell ^+\ell ^-$ processes. In this work, the contributions of $\gamma /Z$-penguin diagrams always include their supersymmetric counterparts unless otherwise specified. For convenience, the following Passarino–Veltman functions [67] $D_0$ and $D_2$ are defined as

$$\begin{aligned}&D_0[m_1^2,m_2^2,m_3^2,m_4^2] \nonumber \\&\equiv \int \frac{d^4 k}{(2\pi )^4}\frac{1}{(k^2-m_1^2)(k^2-m_2^2)(k^2-m_3^2)(k^2-m_4^2)} \nonumber \\&= -\frac{i}{16\pi ^2} \biggl [\frac{m_1^2 \log (m_1^2)}{(m_1^2-m_2^2)(m_1^2-m_3^2)(m_1^2-m_4^2)} \nonumber \\&\quad +\, (m_1 \leftrightarrow m_2) + (m_1 \leftrightarrow m_3) + (m_1 \leftrightarrow m_4)\biggr ], \end{aligned}$$

(14)

$$\begin{aligned}&D_2[m_1^2,m_2^2,m_3^2,m_4^2] \nonumber \\&\equiv \int \frac{d^4 k}{(2\pi )^4}\frac{k^2}{(k^2-m_1^2)(k^2-m_2^2)(k^2-m_3^2)(k^2-m_4^2)} \nonumber \\&= -\frac{i}{16\pi ^2} \biggl [\frac{m_1^4 \log (m_1^2)}{(m_1^2-m_2^2)(m_1^2-m_3^2)(m_1^2-m_4^2)} \nonumber \\&\quad +\, (m_1 \leftrightarrow m_2) + (m_1 \leftrightarrow m_3) + (m_1 \leftrightarrow m_4)\biggr ]. \end{aligned}$$

(15)

The contributions of box diagram are listed below. We eliminate the contributions of all box diagrams to $b \rightarrow s e^+ e^-$ processes by assuming $\lambda '_{1j3} = 0$.

• The contributions of $\tilde{W} - b$ box diagram to $b \rightarrow s \mu ^+ \mu ^-$ processes are given by

  $$\begin{aligned} C_9^{\mathrm{V}(\tilde{W})}&= \frac{- i \pi ^2}{\sqrt{2} G_F \sin ^2\theta _W \eta _t} \nonumber \\&\quad \times \Bigl ( \lambda '_{2i3}\lambda '^*_{223}V_{ib} D_2[m^2_{\tilde{W}},m^2_{\tilde{u}_{Li}},m^2_{\tilde{\nu }_{\mu }},m^2_b] \nonumber \\&\quad - \lambda '_{2i3}\lambda '^*_{2j3}V_{ib}V^*_{js} D_2[m^2_{\tilde{W}},m^2_{\tilde{u}_{Li}},m^2_{\tilde{u}_{Lj}},m^2_b] \nonumber \\&\quad + \lambda '_{233}\lambda '^*_{2j3}V^*_{js} D_2[m^2_{\tilde{W}},m^2_{\tilde{u}_{Lj}},m^2_{\tilde{\nu }_{\mu }},m^2_b] \nonumber \\&\quad - \lambda '_{233}\lambda '^*_{223} D_2[m^2_{\tilde{W}},m^2_{\tilde{\nu }_{\mu }},m^2_{\tilde{\nu }_{\mu }},m^2_b] \Bigr ), \end{aligned}$$

  (16)

  where the winos engage these interactions with left-hand up type squarks and muon sneutrinos. The last term plays an important role in numerical analysis [52].

• The contributions of $W - \tilde{b}_R$ box diagram to $b \rightarrow s \mu ^+ \mu ^-$ processes are given by

  $$\begin{aligned} C_9^{\mathrm{V}(W)}&= \frac{-i \pi ^2}{\sqrt{2}G_F \sin ^2\theta _W \eta _t} \nonumber \\&\quad \times \Bigl ( \tilde{\lambda }'_{2i3}\lambda '^*_{223}V_{ib} D_2[m^2_{\tilde{b}_{R}},m^2_{u_i},m^2_{W},0] \nonumber \\&\quad - \tilde{\lambda }'_{2i3}\tilde{\lambda }'^*_{2j3}V_{ib}V^*_{js} D_2[m^2_{\tilde{b}_{R}},m^2_{u_i},m^2_{u_j},m^2_W] \nonumber \\&\quad + \lambda '_{233}\tilde{\lambda }'^*_{2j3}V^*_{js} D_2[m^2_{\tilde{b}_{R}},m^2_{u_j},m^2_{W},0] \nonumber \\&\quad - \lambda '_{233}\lambda '^*_{223} D_2[m^2_{\tilde{b}_{R}},m^2_W,0,0] \nonumber \\&\quad + \tilde{\lambda }'_{2i3}\tilde{\lambda }'^*_{2j3}V_{ib}V^*_{js} \frac{m^2_{u_i}m^2_{u_j}}{m_W^2}\nonumber \\&\quad \times D_0[m^2_{\tilde{b}_{R}},m^2_{u_i},m^2_{u_j},m^2_W] \Bigr ), \end{aligned}$$

  (17)

  where $\tilde{\lambda }'_{ijk} \equiv \lambda '_{ilk}V^{*}_{jl}$. The right-hand sbottom $\tilde{b}_{R}$ is the only NP particle here. In the limit $m_{\tilde{b}_R} \gg m_t$, one has $C_9^{\mathrm{V}(W)}= \frac{m_t^2}{16\pi \alpha m^2_{\tilde{b}_{R}}}|\lambda '_{233}|^2$ [49, 50, 61] which is obviously positive.

• The contributions of $H^\pm - \tilde{b}_R$ box diagram to $b \rightarrow s \mu ^+ \mu ^-$ processes are given by

  $$\begin{aligned} C_9^{\mathrm{V}(H^\pm )}&= \frac{-i\pi ^2 V_{ib}V_{js}^* \tilde{\lambda }'_{2i3}\tilde{\lambda }'^*_{2j3}}{\sqrt{2} G_F \sin ^2\theta _W \tan ^2\beta \eta _t}\frac{m_{u_i}^2 m_{u_j}^2}{m_W^2}\nonumber \\&\quad \times D_0[m^2_{H^\pm },m_{u_i}^2,m_{u_j}^2,m^2_{\tilde{b}_{R}}], \end{aligned}$$

  (18)

  which should be considered in the following numerical analysis. The $\tan \beta =v_u/v_d$ where $v_u$ and $v_d$ are the vacuum expectation values of two Higgs doublets respectively.

• The contributions of $4\lambda '$ box diagram to $b \rightarrow s \mu ^+ \mu ^-$ processes are given by

  $$\begin{aligned} C_9^{\mathrm{V}(4\lambda ')}&= \frac{-i\pi \lambda '_{i33} \lambda '^*_{i23}}{4\sqrt{2}G_F \alpha \eta _t} \Bigl (|\tilde{\lambda }'_{2j3}|^2 D_2[m^2_{\tilde{b}_{R}},m^2_{\tilde{b}_{R}},m^2_{u_j},0] \nonumber \\&\quad + |\lambda '_{2j3}|^2 D_2[m^2_{\tilde{u}_{Lj}},m^2_{\tilde{\nu }_i},m^2_b,m^2_b]\Bigr ). \end{aligned}$$

  (19)

The contributions of photonic penguin diagrams are lepton flavour universal which naturally gives us a nonzero $C_9^\mathrm{U}$

$$\begin{aligned} C_9^\mathrm{U} = \frac{\sqrt{2}\lambda '_{i33}\lambda '^*_{i23}}{36 G_F \eta _t}\biggl [ \frac{1}{6 m_{\tilde{b}_{R}}^2} -\biggl (\frac{4}{3} + \log \frac{m_b^2}{m_{\tilde{\nu }_i}^2} \biggr )\frac{1}{m_{\tilde{\nu }_i}^2}\biggr ]. \end{aligned}$$

(20)

As stated in Ref. [52], this result is consistent with that in Ref. [68], but it has a negative sign different from that in Ref. [50]. The first term in Eq. (20) comes from the contribution of Fig. 2b, like the photonic penguin induced by scalar leptoquark. We find this term gives a negligible contribution, which is in agreement with Refs. [61, 69]. However the second term in Eq. (20) has a significant contribution because of the logarithmic enhancement, which has never been addressed before. These photonic penguins also contribute new electromagnetic dipole operator $\mathcal{O}_7=\frac{m_b}{e}(\bar{s} \sigma ^{\alpha \beta } P_R b)F_{\alpha \beta }$, which is strictly constrained by $B \rightarrow X_s \gamma$ decay [9]. Fortunately, we find that the corresponding contribution can be ignored numerically because there such logarithmic enhancement is absent [50, 52, 68].

We will discuss the possibility of using muon sneutrinos $\tilde{\nu }_\mu$ and right-handed sbottoms $\tilde{b}_R$ to explain $b \rightarrow s \ell ^+ \ell ^-$ anomaly, for which we set the mass of tau sneutrinos $\tilde{\nu }_\tau$ and three left-handed up type squarks $\tilde{u}_{Lj}$ sufficiently large that the contributions of the loop diagrams containing them are ignored.² The contribution from $H^\pm - \tilde{b}_R$ box diagram is usually positive, and we find that it is numerically negligible when $\tan \beta >2$. Thus, the contributions to only muon channel are

$$\begin{aligned} C_9^\mathrm{V}&= -\frac{\sqrt{2} \lambda '_{233}\lambda '^*_{223}f(x_{\tilde{\nu }_\mu })}{32 G_F \sin ^2\theta _W \eta _t m^2_{\tilde{\nu }_\mu }} + \frac{|\lambda '_{233}|^2 x_{\tilde{b}_R}}{16\pi \alpha }\nonumber \\&\quad -\frac{\lambda '_{i33}\lambda ^{\prime *}_{i23} \left[ |\tilde{\lambda }'_{213}|^2 + |\tilde{\lambda }'_{223}|^2 - |\tilde{\lambda }'_{233}|^2 f\left( 1/x_{\tilde{b}_R}\right) \right] }{64\sqrt{2}\pi G_F \alpha \eta _t m^2_{\tilde{b}_R}}, \end{aligned}$$

(21)

where $x_{\tilde{\nu }_\mu } \equiv m^2_{\tilde{\nu }_\mu }/m^2_{\tilde{W}}$, $x_{\tilde{b}_R} \equiv m^2_t/m^2_{\tilde{b}_R}$, and the loop function $f(x) \equiv \frac{x (1-x+\log {x}) }{(1-x)^2}$.

3 $R(D^{(*)})$ anomaly and other constraints

In this section, we discuss the interpretation of $R(D^{(*)})$ anomaly and consider the constraints imposed by other related processes from $B,\,D,\,K,\,\tau$, and Z decays.

3.1 $R(D^{(*)})$ anomaly

In R-parity violating MSSM, the charged current processes $d_j \rightarrow u_n l_l\nu _i$ are induced by exchanging $\tilde{b}_R$ at tree level. The effective Lagrangian of these processes are given by

$$\begin{aligned} \mathcal{L}_\mathrm{eff} = -\frac{4G_F}{\sqrt{2}} V_{nj} (\delta _{li}+C_{njli}) \bar{u}_n \gamma _{\mu } P_L d_j \bar{l}_l \gamma ^{\mu } P_L \nu _i + \mathrm{H.c.}, \end{aligned}$$

(22)

where the Wilson coefficient $C_{njli}$ is

$$\begin{aligned} C_{njli} = \frac{\lambda '_{ij3} \tilde{\lambda }^{\prime *}_{ln3}}{4 \sqrt{2} G_F V_{nj} m_{\tilde{b}_{R}}^2} . \end{aligned}$$

(23)

Because taking $\lambda '_{1j3}=0$ to eliminate the contributions of box diagrams to $b \rightarrow s e^+ e^-$ processes,³ we have $C_{nj1i} = C_{njl1} = 0$. It is useful to define the ratio

$$\begin{aligned} R_{njl}\equiv \frac{\mathcal{B}(d_j\rightarrow u_n l_l \nu )}{\mathcal{B}(d_j\rightarrow u_n l_l \nu )_\mathrm{SM}} =\sum _{i=1}^3 \left| \delta _{li}+C_{njli}\right| ^2, \end{aligned}$$

(24)

and we have

$$\begin{aligned} \frac{R(D)}{R(D)_\mathrm{SM}} =\frac{R(D^*)}{R(D^*)_\mathrm{SM}} = \frac{2R_{233}}{R_{232} + 1}. \end{aligned}$$

(25)

To obtain the allowed parameter region, we use the following best fit value in the R-parity violating scenario

$$\begin{aligned} \frac{R(D)}{R(D)_\mathrm{SM}} =\frac{R(D^*)}{R(D^*)_\mathrm{SM}} = 1.14 \pm 0.04. \end{aligned}$$

(26)

3.2 Constraints from the tree-level processes

In the scenario we set up, some other processes receive tree level R-parity violating contributions. Here we mainly discuss the constraints from neutral current processes $B \rightarrow K^{(*)} \nu \bar{\nu }$, $B \rightarrow \pi \nu \bar{\nu }$, $K \rightarrow \pi \nu \bar{\nu }$, $D^0 \rightarrow \mu ^+ \mu ^-$ and $\tau \rightarrow \mu \rho ^0$, as well as charged current processes $B \rightarrow \tau \nu$, $D_s \rightarrow \tau \nu$ and $\tau \rightarrow K \nu$. These decays relate to

$$\begin{aligned}&\frac{\lambda '_{ij3}\lambda ^{\prime *}_{lm3}}{2 m^2_{\tilde{b}_R}} \bar{d}_m \gamma ^\mu P_L d_j \bar{\nu }_l\gamma _\mu P_L \nu _i, \end{aligned}$$

(27)

$$\begin{aligned}&\frac{\tilde{\lambda }'_{ij3}\tilde{\lambda }^{\prime *}_{lm3}}{2 m^2_{\tilde{b}_R}} \bar{u}_m \gamma ^\mu P_L u_j \bar{l}_l\gamma _\mu P_L l_i, \end{aligned}$$

(28)

$$\begin{aligned}&-\frac{\lambda '_{ij3}\tilde{\lambda }^{\prime *}_{lm3}}{2 m^2_{\tilde{b}_R}} \bar{u}_m \gamma ^\mu P_L d_j \bar{l}_l \gamma _\mu P_L \nu _i. \end{aligned}$$

(29)

The effective Lagrangian for $B \rightarrow K^{(*)} \nu \bar{\nu }$, $B \rightarrow \pi \nu \bar{\nu }$ and $K \rightarrow \pi \nu \bar{\nu }$ decays are defined by

$$\begin{aligned} \mathcal{L}_\mathrm{eff} = (C_{mj}^\mathrm{SM} \delta _{li} + C_{mj}^{\nu _l \bar{\nu }_i }) ({\bar{d}}_m \gamma ^\mu P_L d_j)({\bar{\nu }}_l \gamma _\mu P_L \nu _i) + \mathrm{H.c.}, \end{aligned}$$

(30)

where [71]

$$\begin{aligned} C_{mj}^\mathrm{SM} = - \frac{\sqrt{2}G_F \alpha X(x_t)}{\pi \sin ^2\theta _W} V_{tj} V^*_{tm}, \end{aligned}$$

(31)

is the SM one. The loop function $X(x_t)\equiv \frac{x_t(x_t+2)}{8(x_t-1)}+\frac{3 x_t (x_t-2)}{8(x_t-1)^2}\log (x_t)$ with $x_t \equiv m^2_t/m^2_W$. The R-parity violating contributions are given by

$$\begin{aligned} C_{mj}^{\nu _l \bar{\nu }_i } = \frac{\lambda '_{ij3}\lambda ^{\prime *}_{lm3}}{2 m^2_{\tilde{b}_R}}. \end{aligned}$$

(32)

It is useful to define the ratio

$$\begin{aligned} R^{\nu \bar{\nu }}_{mj }&\equiv \frac{\mathcal{B}(d_j\rightarrow d_m \nu \bar{\nu })}{\mathcal{B}(d_j\rightarrow d_m \nu \bar{\nu })_\mathrm{SM}} \nonumber \\&= \frac{\sum \nolimits _{i=1}^3 \left| C_{mj}^\mathrm{SM} + C_{mj}^{\nu _i \bar{\nu }_i }\right| ^2 + \sum \nolimits _{i \ne l}^3 \left| C_{mj}^{\nu _l \bar{\nu }_i } \right| ^2}{3 \left| C_{mj}^\mathrm{SM} \right| ^2}. \end{aligned}$$

(33)

The upper limit of $B \rightarrow K^{(*)} \nu \bar{\nu }$ decay corresponds to $R^{\nu \bar{\nu }}_{23} < 2.7$ [71,72,73] at 90% confidence level (CL), and the upper limit of $B \rightarrow \pi \nu \bar{\nu }$ decay is related to $R^{\nu \bar{\nu }}_{13} < 830.5$ [74, 75] at 90% CL. By combining the SM prediction $\mathcal{B}(K^+ \rightarrow \pi ^+\nu \bar{\nu })_\mathrm{SM} = (9.24 \pm 0.83) \times 10^{-11}$ [76] with experimental measurement $\mathcal{B}(K^+ \rightarrow \pi ^+\nu \bar{\nu })_\mathrm{exp} = (1.7 \pm 1.1) \times 10^{-10}$ [77], we obtain a stringent constraint from $K \rightarrow \pi \nu \bar{\nu }$ decay that makes

$$\begin{aligned} |\lambda '_{i23}\lambda ^{\prime *}_{l13}| < 7.4\times 10^{-4}(m_{\tilde{b}_R}/1\,\mathrm{TeV})^2. \end{aligned}$$

(34)

Therefore, we will assume $\lambda '_{i1k} =0$ to satisfy this constraint. At the same time, under this assumption, $B \rightarrow \pi \nu \bar{\nu }$ decay is unaffected by the NP.

The branching fraction for $D^0 \rightarrow \mu ^+ \mu ^-$ decay is given by [58]

$$\begin{aligned} \mathcal{B}(D^0 \rightarrow \mu ^+ \mu ^-) = \frac{\tau _D f^2_D m_D m^2_\mu }{32\pi } \left| \frac{\tilde{\lambda }'_{223}\tilde{\lambda }^{\prime *}_{213}}{2 m^2_{\tilde{b}_R}}\right| ^2 \sqrt{1-\frac{4 m^2_\mu }{m^2_D}}, \end{aligned}$$

(35)

where decay constant of $D^0$ is $f_D = 209.0 \pm 2.4$  MeV [78]. The mean life $\tau _D= 410.1\pm 1.5$ fs [77] and the upper limit of branching fraction of $D^0 \rightarrow \mu ^+ \mu ^-$ decay is $6.2 \times 10^{-9}$ at 90% CL [77]. The corresponding constraint is $|\lambda '_{223}|^2 < 0.31(m_{\tilde{b}_R}/1\,\mathrm{TeV})^2$.

The branching fraction for $\tau \rightarrow \mu \rho ^0$ decay is given by [79]

$$\begin{aligned} \mathcal{B}(\tau \rightarrow \mu \rho ^0)&= \frac{\tau _\tau f^2_\rho m^3_\tau }{128\pi }\left| \frac{\tilde{\lambda }'_{313}\tilde{\lambda }^{\prime *}_{213}}{2 m^2_{\tilde{b}_R}}\right| ^2 \left( 1-\frac{m^2_\rho }{m^2_\tau }\right) \nonumber \\&\quad \times \left( 1+ \frac{m^2_\rho }{m^2_\tau } - 2\frac{m^4_\rho }{m^4_\tau }\right) , \end{aligned}$$

(36)

where $\tau _\tau = 290.3 \pm 0.5$ fs and the decay constant $f_\rho = 153$ MeV [50]. The current experimental upper limit on the branching fraction for this process is $\mathcal{B}(\tau \rightarrow \mu \rho ^0) < 1.2\times 10^{-8}$ at 90% CL [77]. The corresponding constraint is $|\lambda '_{323}\lambda '^*_{223}| < 0.38(m_{\tilde{b}_R}/1\,\mathrm{TeV})^2$.

The formulas for charged current processes are given, respectively, by

$$\begin{aligned}&\frac{\mathcal{B}(B \rightarrow \tau \nu )}{\mathcal{B}(B \rightarrow \tau \nu )_\mathrm{SM}} = R_{133}, \end{aligned}$$

(37)

$$\begin{aligned}&\frac{\mathcal{B}(D_s \rightarrow \tau \nu )}{\mathcal{B}(D_s \rightarrow \tau \nu )_\mathrm{SM}} = R_{223}, \end{aligned}$$

(38)

$$\begin{aligned}&\frac{\mathcal{B}(\tau \rightarrow K \nu )}{\mathcal{B}(\tau \rightarrow K \nu )_\mathrm{SM}} = R_{123}. \end{aligned}$$

(39)

The corresponding experimental and theoretical values are listed, respectively, as follows: $\mathcal{B}(B \rightarrow \tau \nu )_\mathrm{exp} = (1.09\pm 0.24) \times 10^{-4}$ [77], $\mathcal{B}(B \rightarrow \tau \nu )_\mathrm{SM} = (9.47\pm 1.82) \times 10^{-5}$ [80]; $\mathcal{B}(D_s \rightarrow \tau \nu )_\mathrm{exp} = (5.48 \pm 0.23)\%$ [77], $\mathcal{B}(D_s \rightarrow \tau \nu )_\mathrm{SM} = (5.40 \pm 0.30)\%$; $\mathcal{B}(\tau \rightarrow K \nu )_\mathrm{exp} = (6.96 \pm 0.10)\times 10^{-3}$ [77], $\mathcal{B}(\tau \rightarrow K \nu )_\mathrm{SM} = (7.15 \pm 0.026)\times 10^{-3}$ [56].

3.3 Constraints from the loop-level processes

First of all, the most important one-loop constraint comes from $B_s-\bar{B}_s$ mixing, which is governed by

$$\begin{aligned} \mathcal{L}_\mathrm{eff} = (C_{B_s}^\mathrm{SM} + C_{B_s}^\mathrm{NP})(\bar{s}\gamma _{\mu }P_L b)(\bar{s}\gamma ^{\mu } P_L b) + \mathrm{H.c.}, \end{aligned}$$

(40)

where the SM and NP Wilson coefficients are given respectively by

$$\begin{aligned} C_{B_s}^\mathrm{SM}&= -\frac{1}{4 \pi ^2} G_F^2 m_W^2 \eta _t^2 S(x_t), \end{aligned}$$

(41)

$$\begin{aligned} C_{B_s}^\mathrm{NP}&= -\frac{1}{128 \pi ^2}\biggl [\frac{(\lambda ^{\prime }_{i33} \lambda ^{\prime *}_{i23})^2 }{m_{\tilde{b}_R}^2} +\frac{ (\lambda ^{\prime }_{233} \lambda ^{\prime *}_{223})^2 }{m_{\tilde{\nu }_{\mu }}^2}\biggr ], \end{aligned}$$

(42)

where loop function $S(x_t)=\frac{x_t(4-11x_t+x_t^2)}{4(x_t-1)^2}+\frac{3x_t^3\log (x_t)}{2(x_t-1)^3}$. At $2\sigma$ level, the UTfit collaboration [81] gives the bound $0.93< |1+ C_{B_s}^\mathrm{NP}/C_{B_s}^\mathrm{SM}| < 1.29$.

Next, we investigate a series of Z decaying to two charged leptons with the same flavour like $Z\rightarrow \mu \mu (\tau \tau )$ and the different one like $Z\rightarrow \mu \tau$. The amplitude of these diagrams is $i \mathcal M =i \frac{g}{32\pi ^2 \cos \theta _W} B_{ij} \epsilon ^\alpha \bar{u}_{\ell _i}\gamma _\alpha P_L v_{\ell _j}$ [50], where $B_{ij} = B^1_{ij} + B^2_{ij}$ and [50, 82]

$$\begin{aligned} B^1_{ij}&= \ \sum _{l=1}^2 \tilde{\lambda }'_{jl3} \tilde{\lambda }'^{*}_{il3} \frac{m_Z^2}{m^2_{\tilde{b}_R}} \biggl [\biggl (1 - \frac{4}{3} \sin ^2\theta _W \biggr )\nonumber \\&\quad \times \biggl (\log \frac{m_Z^2}{m^2_{\tilde{b}_R}} - i \pi - \frac{1}{3} \biggr ) + \frac{\sin ^2\theta _W}{9} \biggr ], \end{aligned}$$

(43)

$$\begin{aligned} B^2_{ij}&= \ 3 \tilde{\lambda }'_{j33} \tilde{\lambda }'^{*}_{i33} \biggl \{-x_{\tilde{b}_R}(1 + \log x_{\tilde{b}_R}) \nonumber \\&\quad + \frac{m_Z^2}{18 m^2_{\tilde{b}_R}}\biggl [(11 - 10 \sin ^2\theta _W) + (6 - 8 \sin ^2\theta _W)\log x_{\tilde{b}_R}\nonumber \\&\quad + \frac{1}{10}(-9 + 16 \sin ^2\theta _W)\frac{m_Z^2}{m_t^2} \biggr ] \biggl \}, \end{aligned}$$

(44)

here $B^1_{ij}$ is the contribution from the diagram induced by exchanging $\tilde{b}_R-u-u$ or $\tilde{b}_R-c-c$ in triangular loop and $B^2_{ij}$ is the contribution from the diagram induced by exchanging $\tilde{b}_R-t-t$ in triangular loop. As shown in Ref. [50], for $Z\rightarrow \mu \mu (\tau \tau )$, demanding the interference term in the partial width between the SM tree-level contribution and the NP one-loop level ones is less than twice the experimental uncertainty on the partial width [77], there are the bounds $|\mathfrak {R}(B_{22})| < 0.32$ and $|\mathfrak {R}(B_{33})| < 0.39$ [50]. And the experimental upper limit ${\mathcal B}(Z\rightarrow \mu \tau )<1.2\times 10^{-5}$ [77] makes the bound $\sqrt{|B_{23}|^2 + |B_{32}|^2} < 2.1$ [50].

Finally, we discuss the lepton-flavour violating decay of $\tau$ lepton, including $\tau \rightarrow \mu \gamma$ and $\tau \rightarrow \mu \mu \mu$. In the limit $m^2_\mu /m^2_\tau \rightarrow 0$, the branching fraction for $\tau \rightarrow \mu \gamma$ is given by [68, 83, 84]

$$\begin{aligned} \mathcal{B}(\tau \rightarrow \mu \gamma ) = \frac{\tau _\tau \alpha m^5_\tau }{4}(|A^L_2|^2 + |A^R_2|^2), \end{aligned}$$

(45)

where the effective couplings $A^{L,R}_2$ come from on shell photon penguin diagrams [68],

$$\begin{aligned} A^L_2 = -\frac{\lambda '_{2j3}\lambda '^*_{3j3}}{64 \pi ^2 m^2_{\tilde{b}_R}}, \quad A^R_2 = 0. \end{aligned}$$

(46)

The current experimental upper limit is $\mathcal{B}(\tau \rightarrow \mu \gamma ) < 4.4 \times 10^{-8}$ at 90% CL [77].

In general, the effective Lagrangian leading to $\tau \rightarrow \mu \mu \mu$ decay is given by [83, 84]

$$\begin{aligned} \mathcal{L}_\mathrm{eff}&= -\frac{B_1}{2}(\bar{\tau } \gamma ^\nu P_L \mu )( \bar{\mu } \gamma _\nu P_R \mu )-\frac{B_2}{2}(\bar{\tau } \gamma ^\nu P_R \mu )(\bar{\mu } \gamma _\nu P_L \mu ) \nonumber \\&\quad + C_1 (\bar{\tau } P_R \mu )(\bar{\mu } P_R \mu )+ C_2 (\bar{\tau } P_L \mu )(\bar{\mu } P_L \mu ) \nonumber \\&\quad + G_1 (\bar{\tau } \gamma ^\nu P_R \mu )(\bar{\mu } \gamma _\nu P_R \mu )+ G_2 (\bar{\tau } \gamma ^\nu P_L \mu )(\bar{\mu } \gamma _\nu P_L \mu ) \nonumber \\&\quad -A_R (\bar{\tau } [\gamma _\mu ,\gamma _\nu ]\frac{q^\nu }{q^2} P_R \mu ) (\bar{\mu } \gamma ^\mu \mu )\nonumber \\&\quad -A_L (\bar{\tau } [\gamma _\mu ,\gamma _\nu ] \frac{q^\nu }{q^2} P_L \mu )(\bar{\mu }\gamma ^\mu \mu )+ \mathrm{H.c.}. \end{aligned}$$

(47)

This Lagrangian leads to  [83, 84]

$$\begin{aligned}&\mathcal{B}(\tau \rightarrow 3\mu ) = \frac{\tau _\tau m^5_\tau }{6144 \pi ^3} \biggl [ |B_1|^2+|B_2|^2+8(|G_1|^2+|G_2|^2) \nonumber \\&\quad +\frac{|C_1|^2+|C_2|^2}{2}+32\biggl (4\log \frac{m_\tau ^2}{ m_\mu ^2} - 11\biggr )\frac{|A_R|^2+|A_L|^2 }{ m_\tau ^2} \nonumber \\&\quad -64 \frac{\mathfrak {R}(A_L G_2^*+A_R G_1^*)}{ m_\tau }+32\frac{\mathfrak {R}(A_L B_1^*+A_R B_2^*)}{m_\tau } \biggr ]. \end{aligned}$$

(48)

In our scenario, there are three different types of contributions, the photonic and Z penguins as well as box diagrams with four $\lambda '$ couplings, that can contribute to $\tau \rightarrow \mu \mu \mu$ decay. The nonzero Wilson coefficients are [50, 68]

$$\begin{aligned} B_1&= -2 \bigl (4\pi \alpha A^L_1 + \sin ^2\theta _W B' \bigr ), \end{aligned}$$

(49)

$$\begin{aligned} G_2&= 4\pi \alpha A^L_1 + \biggl (-\frac{1}{2} + \sin ^2\theta _W\biggr ) B' + C_\tau , \end{aligned}$$

(50)

$$\begin{aligned} A_L&= 2\pi \alpha m_\tau A^L_2, \end{aligned}$$

(51)

where

$$\begin{aligned} B'&= -\frac{3\alpha \tilde{\lambda }'_{233} \tilde{\lambda }'^{*}_{333} x_{\tilde{b}_R}(1 + \log x_{\tilde{b}_R})}{8\pi \cos ^2\theta _W \sin ^2\theta _W m^2_Z}, \end{aligned}$$

(52)

$$\begin{aligned} C_\tau&= \frac{i}{4} \tilde{\lambda }'_{2i3} \tilde{\lambda }^{'*}_{2i3} \tilde{\lambda }'_{2j3} \tilde{\lambda }^{'*}_{3j3} D_2[m^2_{\tilde{b}_R},m^2_{\tilde{b}_R},m^2_{u_i},m^2_{u_j}], \end{aligned}$$

(53)

and the off-shell effective coupling $A^L_1$ is [68]

$$\begin{aligned} A^L_1 = \frac{\lambda '_{2j3}\lambda '^*_{3j3}}{16 \pi ^2 m^2_{\tilde{b}_R}} \biggl [ \frac{1}{18} -\frac{2}{3}\biggl (\frac{4}{3} + \log \frac{m^2_{u_j}}{m^2_{\tilde{b}_R}}\biggr )\biggr ]. \end{aligned}$$

(54)

The current experimental upper limit on the branching fraction for this decay is $\mathcal{B}(\tau \rightarrow \mu \mu \mu ) < 2.1\times 10^{-8}$ at 90% CL [77].

Fig. 3

Numerical analysis in which $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies are solved and other constraints are satisfied. The masses $m_{\tilde{b}_R}$ and $m_{\tilde{\nu }_{\mu }}$ are given in units of GeV. The $2\sigma$ favored regions from the $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ measurements are shown in blue and green, respectively. The hatched areas filled with black-vertical, black-horizontal, red-horizontal, and red-vertical lines are excluded by $B \rightarrow K^{(*)} \nu \bar{\nu }$ decays, $B_s-\bar{B}_s$ mixing, Z decays, and $\tau \rightarrow \mu \mu \mu$ decay, respectively. The overlaps are marked in purple

4 Numerical results and discussions

In this section, we discuss how to interpret both $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies and satisfy all these potential constraints simultaneously. The relevant model parameters in our scenario are the wino mass $m_{\tilde{W}}$, the mass of muon sneutrino $m_{\tilde{\nu }_\mu }$, the mass of right-handed sbottom $m_{\tilde{b}_R}$, as well as four nonzero couplings $\lambda '_{223}$, $\lambda '_{233}$, $\lambda '_{323}$, and $\lambda '_{333}$. We set $m_{\tilde{W}} = 250$ GeV. It can be seen from Ref. [52] that a positive product $\lambda '_{233} \lambda '^*_{223}$ is needed to explain the $b \rightarrow s \ell ^+ \ell ^-$ anomaly mainly through muon sneutrinos (the $C_9^\mathrm{V}$ part). Both $\lambda '_{323}$ and $\lambda '_{333}$ are positive to help solve $R(D^{(*)})$ anomaly by exchanging $\tilde{b}_R$ at tree level [56]. The combination of the choice of above couplings will naturally produce a negative $C_9^\mathrm{U}$, which is in line with the conclusion of the global analysis [20]. Our numerical results are shown in Fig. 3. These results show that it is possible to explain $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies simultaneously at $2\sigma$ level.⁴ The regions of NP parameters that can solve B-physics anomalies are most constrained by $B \rightarrow K^{(*)} \nu \bar{\nu }$ decays, $B_s-\bar{B}_s$ mixing and Z decays. In addition, the $\tau \rightarrow \mu \mu \mu$ decay can provide a weak constraint. We find that other related processes, such as $D^0 \rightarrow \mu ^+ \mu ^-$, $\tau \rightarrow \mu \rho ^0$, $B \rightarrow \tau \nu$, $D_s \rightarrow \tau \nu$, $\tau \rightarrow K \nu$, and $\tau \rightarrow \mu \gamma$ decays, do not provide available constraints.

We show in Fig. 3a, b the allowed regions in the planes of coupling parameters $(\lambda '_{233},\, \lambda '_{333})$ and $(\lambda '_{223},\, \lambda '_{323})$ respectively when other parameters are fixed. These two subfigures show that in order to explain the B-physics anomalies, the coupling parameters need to satisfy the relation $\lambda '_{333}>\lambda '_{233}>\lambda '_{323}\simeq \lambda '_{223}$, and the required $\lambda '_{223}$ and $\lambda '_{323}$ are very small. Therefore, the next four subfigures in Fig. 3 mainly discuss the relationships between the coupling parameters $\lambda '_{333}$ and $\lambda '_{233}$ and the masses $m_{\tilde{b}_R}$ and $m_{\tilde{\nu }_{\mu }}$. From Fig. 3a, we can see that $\lambda '_{333}$ is more constrained by $R(D^{(*)})$, $B \rightarrow K^{(*)} \nu \bar{\nu }$ and Z decays, but less affected by $b \rightarrow s \ell ^+\ell ^-$ processes and $B_s - \bar{B}_s$ mixing. On the contrary, $\lambda '_{233}$ is greatly constrained by $b \rightarrow s \ell ^+\ell ^-$ processes and $B_s - \bar{B}_s$ mixing, but has little influence on $R(D^{(*)})$, $B \rightarrow K^{(*)} \nu \bar{\nu }$ and Z decays. As shown in Fig. 3c, after the variable parameter $m_{\tilde{b}_R}$ is added, the constraints of $\lambda '_{333}$ from $R(D^{(*)})$, $B \rightarrow K^{(*)} \nu \bar{\nu }$ and Z decays will be relaxed a lot. The parameters $\lambda '_{333}$ and $m_{\tilde{b}_R}$ are highly correlated. Because we choose a smaller mass of muon sneutrino, the $B_s - \bar{B}_s$ mixing is more sensitive to $m_{\tilde{\nu }_{\mu }}$ than to $m_{\tilde{b}_R}$, which can be seen by comparing Fig. 3d with Fig. 3f. All subfigures contain parameter spaces (marked in purple) that can resolve $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies, and satisfy the constraints from other related processes simultaneously.

5 Conclusions

The recent measurements on semileptonic decays of B-meson suggest the existence of NP which breaks the LFU. Among them, the observables $R_{K^{(*)}}$ and $P'_5$ in $b \rightarrow s \ell ^+ \ell ^-$ processes and the $R(D^{(*)})$ in $B \rightarrow D^{(*)} \tau \nu$ decays are more striking. They are collectively called B-physics anomalies. In this work, we have explored the possibility of using muon sneutrinos $\tilde{\nu }_\mu$ and right-handed sbottoms $\tilde{b}_R$ to solve these B-physics anomalies simultaneously in R-parity violating MSSM.

To explain the anomalies in $b \rightarrow s \ell ^+ \ell ^-$ processes, we use a two-parameter scenario, where the total Wilson coefficients of NP are divided into two parts, one is the $C^\mathrm{V}_9$ (Noting $C^\mathrm{NP}_{10,\mu } = - C^\mathrm{V}_9$) that only contributes the muon channel and the other is the $C^\mathrm{U}_9$ that contributes both the electron and the muon channels. First, we scrutinize all the one-loop contributions of the superpotential terms $\lambda '_{ijk} L_i Q_j D_k^c$ to the $b \rightarrow s \ell ^+ \ell ^-$ processes under the assumptions $\lambda '_{ij1} = \lambda '_{ij2} = 0$ and $\lambda '_{1j3} = 0$. We find that the contribution from the $H^\pm - \tilde{b}_R$ box diagram (Fig. 1c) is missed in the literature, this contribution is usually positive, and we find that it is numerically negligible when $\tan \beta >2$. The photonic penguin induced by exchanging sneutrino can provide important contribution due to the existence of logarithmic enhancement, which has never been addressed before. This contribution is lepton flavour universal due to the SM photon, so it is natural to contribute a nonzero $C^\mathrm{U}_9$.

Global analyses show that the sizable magnitude of $C^\mathrm{V}_9$ is needed to explain $b \rightarrow s \ell ^+ \ell ^-$ anomaly. However, $C^\mathrm{V}_9$ in the scenario with nonzero $C^\mathrm{U}_9$ is smaller than the one in the scenario without $C^\mathrm{U}_9$. With the addition of the latest measurements from the Belle collaboration, the world averages of $R(D^{(*)})$ are closer to the predicted values of the SM. These changes make it possible to use $\tilde{\nu }_\mu$ and $\tilde{b}_R$ to explain $b \rightarrow s \ell ^+ \ell ^-$ and $R(D^{(*)})$ anomalies, simultaneously. We also consider the constraints of other related processes in our scenario. The strongest constraints come from $B \rightarrow K^{(*)} \nu \bar{\nu }$ decays, $B_s-\bar{B}_s$ mixing, and the processes of Z decays. Besides, $\tau \rightarrow \mu \mu \mu$ decay can provide a few constraints. The other decays, such as $D^0 \rightarrow \mu ^+ \mu ^-$, $\tau \rightarrow \mu \rho ^0$, $B \rightarrow \tau \nu$, $D_s \rightarrow \tau \nu$, $\tau \rightarrow K \nu$, and $\tau \rightarrow \mu \gamma$, do not provide available constraints.