1 Introduction

Topological techniques in General Relativity [1,2,3], developed mainly by Penrose, Hawking and Geroch, reveal their power in the celebrated singularity theorems (see, for example, [2]). Among the most important ingredients of these theorems are the energy conditions and topological considerations on certain three dimensional hypersurfaces. Interestingly, the interplay between topology and energy conditions also appear in Hawking’s first black hole topology theorem [4], which asserts that the event horizon of an asymptotically flat stationary four-dimensional black hole obeying the dominant energy condition is a two-sphere. Of the various ways to escape this theorem, we can mention going to higher dimensions [5] or considering matter sources that violate the dominant energy condition.

When considering five-dimensional spacetimes, the event horizon can be, in principle, any compact orientable three-dimensional manifold. However, due to the Thurston geometrization conjecture proved by Perelman [6], the event horizon can be endowed with a metric locally isometric to one of the eight Thurston geometries [7]. Within these geometries, the simples one are the Euclidean space \({\mathbb {E}}^3\), the three-sphere \({\mathbb {S}}^3\), the hyperbolic space \({\mathbb {H}}^3\) and the products \({\mathbb {S}}^1\times {\mathbb {S}}^2\) and \({\mathbb {S}}^1\times {\mathbb {H}}^2\). There are also three non-trivial geometries called the Solv geometry, the Nil geometry and the geometry of the universal cover of \(\hbox {SL}_2({\mathbb {R}})\).

In Ref. [8], the authors catalogued solutions to the five-dimensional vacuum Einstein equations which were modelled on three-dimensional geometries of spherical, hyperbolic, flat or product type. In addition, they found two families of new black hole solutions modelled by the Solv and the Nil geometries. Some of these results were generalized in Ref. [9], where new Nil black holes with hyperscaling violation were studied. Even more, in the context of AdS/CMT, thermoelectric transport coefficients form charged Solv and Nil black holes have been recently reported [10]. In addition, DC conductivities have been computed for Solv, Nil and \(\hbox {SL}_2({\mathbb {R}})\) black branes [11]. Finally, we note that Solv and Nil solutions electromagnetically charged through a dilatonic source have been considered in Ref. [12].

Interestingly, all these five-dimensional black hole solutions have been found, to the best of our knowledge, only within classical General Relativity. Therefore, it is our interest to model, if possible, the event horizon of certain black holes beyond General Relativity by some of the eight Thurston three-geometries. As a preliminary step in order to attack more general cases, in this work we will consider black hole solutions embedded in the so-called scale-dependent gravity [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] which, as it is well known, has become an alternative tool to introduce semiclassical corrections in black hole solutions in \(2+1\) and \(3+1\) dimensional space-times.

The main idea in which the scale-dependent scenario is inspired can be summarized as follows: following the lessons of Weinberg’s Asymptotic Safety program, we consider that the effective action (i.e., a modified version of the classical action, which includes quantum-mechanical corrections) is the fundamental object and, therefore, the corresponding equations of motion should be derived using this action. Irrespectively of how complicated these effective actions could be, a common feature between them is always present: the couplings involved acquire a scale-dependence. Taking this statement seriously, we shall analyse how the aforementioned black holes suffer deviations with respect to their classical counterparts.

The manuscript is organized as follows: Sect. 2 summarizes the main points of the scale-dependent gravitational theory. In Sect. 3, some classical black holes in five dimensions with constant curvature and Solv horizons are reviewed in order to extend them, in Sect. 4, into the scale-dependent theory. In Sect. 5 we discuss the consistency of the scale-dependent model with the asymptotic safety program, and concluding remarks and some comments are given in Sect. 6.

2 Scale-dependent gravity

In order to be able to include any quantum correction in certain black hole solutions, it is mandatory to specify the object which describes the “fundamental theory”. Analogously to standard gravity (where the classical action is taken to be the main object), scale-dependent gravity takes advantage of the idea provided by the Asymptotic Safety program in which the gravitational effective action, \({\varGamma }[{\tilde{k}},g_{\mu \nu }, \ldots ]\), where \({\tilde{k}}\) is a scale field, describes the theory. One of the most remarkable features in quantum field theories is that the effective action for the gravitational field, indeed at low-energy, acquires a scale dependence. This effect appears at the level of the couplings which means that it runs according to certain energy scale, this fact being a generic result of quantum field theory.

The Asymptotic Safety program, which is based on a non-trivial ultra-violet fixed point for the leading dimensionless gravitational couplings is, by far, where these ideas have been best implemented. Let us point out that it was Weinberg, in his seminal work [30], who introduced this program. Substantial improvement has been made up to now [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53].

During the last years, scale-dependent gravity has been used to construct black hole backgrounds both by improving classical solutions with the scale dependent couplings from Asymptotic Safety [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73] and by solving the gap equations of a generic scale-dependent action [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. This last approach has revealed certain non-trivial features regarding the black hole entropy and the energy conditions. Even more, more recently, scale-dependent regular black holes [28] and traversable (vacuum) scale-dependent wormholes [26] have been found, showing that, in some sense and in particular situations, scale-dependent gravity might shed light on how to cure, in an effective way, some of the classical problems related to singularities and the appearance of exotic matter inside wormholes. From the cosmological point of view, the impact of scale dependence has been studied in Refs. [74,75,76,77,78,79,80,81,82,83,84,85,86].

The simplest formulation of scale-dependent gravity is given by the scale-dependent version of the Einstein–Hilbert action as follows

$$\begin{aligned} {\varGamma }[g_{\mu \nu },{\tilde{k}}]=\int \mathrm {d}^{n}x\sqrt{-g} \bigg [\frac{1}{2 \kappa _{{\tilde{k}}}} \bigg (R-2{\varLambda }_{{\tilde{k}}}\bigg )\bigg ], \end{aligned}$$
(1)

where \({\tilde{k}}\) is a scale-dependent field related to a renormalization scale, \(\kappa _{{\tilde{k}}} \equiv 8 \pi G_{{\tilde{k}}}\) is the Einstein coupling, and \(G_{{\tilde{k}}}\) and \({\varLambda }_{{\tilde{k}}}\) refer to the scale-dependent gravitational and cosmological couplings, respectively. The modified Einstein’s equations are obtained by taking variations with respect to the metric field \(g_{\mu \nu }\):

$$\begin{aligned} G_{\mu \nu }+g_{\mu \nu }{\varLambda }_{{\tilde{k}}}=-{\varDelta }t_{\mu \nu }, \end{aligned}$$
(2)

where the so-called non-matter energy-momentum tensor, \({\varDelta }t_{\mu \nu }\), is defined according to [79, 87]

$$\begin{aligned} {\varDelta }t_{\mu \nu }=G_{{\tilde{k}}}\Bigl (g_{\mu \nu }\square -\nabla _{\mu }\nabla _{\nu }\Bigl )G_{{\tilde{k}}}^{-1}. \end{aligned}$$
(3)

By taking the variation of the effective action with respect to the scale field, \({\tilde{k}}(x)\), one imposes [88]

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d} {\tilde{k}}} {\varGamma }[g_{\mu \nu }, {\tilde{k}}] =0, \end{aligned}$$
(4)

which can be seen as an a posteriori condition towards background independence [87, 89,90,91,92,93,94]. The \(\beta \)-functions describe the renormalization group running of both Newton’s constant and the cosmological coupling. These \(\beta \)-functions are, in general, unknown because they depend of how we solve the problem. Given that we do not want to compute them, we do not have enough information in order to find both the metric and the scale field. In order to bypass this issue, here we consider that the couplings \(G_{{\tilde{k}}}\) and \({\varLambda }_{{\tilde{k}}}\) inherit the dependence on the space-time coordinates from the space-time dependence of the scale field, \({\tilde{k}}(x)\). Therefore, these couplings are written as G(x) and \({\varLambda }(x)\) [18, 88]. This idea, together with an appropriate choice for the line element, allows, in principle, to solve the problem in situations with a high degree of symmetry.

At this point, a couple of important points are in order. First, let us note that, after variations of the scale field, Eq. (4) turns out to be

$$\begin{aligned} \left( R\nabla _{\mu }\left( \frac{1}{G_{{{\tilde{k}}}}} \right) -2\nabla _{\mu }\left( \frac{{\varLambda }_{{{\tilde{k}}}}}{G_{{{\tilde{k}}}}} \right) \right) \partial ^{\mu }{{\tilde{k}}}=0. \end{aligned}$$
(5)

And second, this equation, together with Eq. (2), are consistent with diffeomorphism invariance, as expressed by the conserved covariance of the Einstein tensor, as explicitly shown in [88].

3 Some classical five dimensional black hole solutions

In this section we will briefly review some of the five-dimensional black holes obtained within Einstein’s theory in Ref. [8]. This choice of solutions is related to those which we have been able to generalize into the scale-dependent theory, as subsequent sections will show.

The classical Einstein–Hilbert action is, in five dimensions, given by

$$\begin{aligned} I_0[g_{\mu \nu }]&= \int \mathrm {d}^{5}x \sqrt{-g} \bigg [ \frac{1}{2 \kappa _0} \bigg (R - 2{\varLambda }_0 \bigg ) \bigg ], \end{aligned}$$
(6)

where \(\kappa _0 \equiv 8 \pi G_0\) is the gravitational coupling, \(G_0\) is Newton’s constant and \({\varLambda }_0\) is the cosmological coupling. Varying the classical action (6) yields the equations of motion, i.e.,

$$\begin{aligned} R_{\mu \nu } - \frac{1}{2}R g_{\mu \nu }&= -{\varLambda }_0 g_{\mu \nu }, \end{aligned}$$
(7)

which can be expressed as

$$\begin{aligned} R_{ab}=\frac{2 {\varLambda }_{0}}{3}g_{ab}. \end{aligned}$$
(8)

If the metric is written as

$$\begin{aligned} ds^2 = -V(r)dt^2 + V(r)^{-1}dr^2 + f^2(r)dx^{i}dx^{j}, \end{aligned}$$
(9)

where \(d{{\tilde{s}}}^2= dx^{i}dx^{j}\) is the metric induced on the \(t=\) constant, \(r=\) constant surfaces, two type of solutions are obtained, depending on the integration of \(f''(r)\) (see [8] for details). The first set of the solutions are given by [8]

$$\begin{aligned} f(r)= & {} r \nonumber \\ V(r)= & {} k-\frac{2G_{0}M}{r^2}-\frac{r^2{\varLambda }_{0}}{6}, \end{aligned}$$
(10)

and

$$\begin{aligned} d{{\tilde{s}}}^2= & {} d\xi ^2+ \sin ^{2}\xi d{\varOmega }^2 \; (k =1) \nonumber \\ d{{\tilde{s}}}^2= & {} d\xi ^2+ \sinh ^{2}\xi d{\varOmega }^2 \; (k = - 1) \nonumber \\ d{{\tilde{s}}}^2= & {} d\xi ^2+ d\theta ^2 + d \phi ^2 \; (k = 0) . \end{aligned}$$
(11)

These solutions are a warped product between a certain two-dimensional spacetime and a three-dimensional Riemannian manifold of constant curvature (spherical, hyperbolic or flat). Interestingly, there is also a second set of solutions which are products of a two-dimensional spacetime with an Einstein three-manifold, with no warping. The interested reader can consult the specific form of these solutions in [8]. In adition to these constant-curvature black hole solutions, Solv and Nil geometries were found in Ref. [8]. In particular, the Solv black hole is found for \({\varLambda }_{0}<0\) and it has a metric given by

$$\begin{aligned} \mathrm {d}s^2 = - B(r) \mathrm {d}t^2 + B(r)^{-1} \mathrm {d}r^2 + \frac{3}{(-{\varLambda }_0)}\mathrm {d}{\tilde{s}}^2, \end{aligned}$$
(12)

assuming the following definitions:

$$\begin{aligned}&B(r) \equiv -\frac{2}{9}{\varLambda }_{0} r^2 - \frac{2\sqrt{G_{0}M}}{r} \end{aligned}$$
(13)
$$\begin{aligned}&d{{\tilde{s}}}^2 = r^2\left( e^{2 z}dx^2+e^{-2 z}dy^2\right) +dz^2. \end{aligned}$$
(14)

As previously commented, we are interested in the generalization of some classical black hole solutions. Specifically, the solutions given by Eqs. (10) and (12) will be generalized in the next section when certain effective deformation of the classical theory is incorporated in terms of scale-dependent gravity.

4 Five-dimensional scale-dependent AdS black holes

Due to the symmetries we want to explore, let us make the choice \(G=G(r)\) and \({\varLambda }={\varLambda }(r)\) for the quasi-dynamical Newton and cosmological couplings, respectively. It is remarkable that, in non-trivial situations, for instance with the Kerr black hole, the functional dependence of the coupling could be more complex. In our particular case, we arrive to the following vacuum equations:

$$\begin{aligned} G_{\mu \nu } + g_{\mu \nu }{\varLambda }(r) + {\varDelta }t_{\mu \nu }(r) =0. \end{aligned}$$
(15)

Let us note that the Einstein tensor is covarianty conserved and, therefore, \(\nabla ^{\mu } \left( g_{\mu \nu }{\varLambda }(r) + {\varDelta }t_{\mu \nu }(r)\right) \) vanishes on shell, as can be explicitly shown. Specifically, the consistency condition, which can be explicitly stated in this case as

$$\begin{aligned} {\varLambda }' -\frac{G'}{G}\bigg ({\varLambda }- \frac{1}{2}R \bigg )=0, \end{aligned}$$
(16)

where the prime denotes derivative with respect to the r coordinate, is automatically satistified. Interestingly, there are other non-\({\varLambda }\)-vacuum cases where the same phenomenon occurs and the consistency condition is satisfied by construction [87].

In the next subsections we shall consider several horizon geometries.

4.1 Black holes with spherical and hyperbolic horizons

Here we consider line elements parametrized as

$$\begin{aligned} ds^2= & {} -V(r)dt^2+\frac{dr^2}{V(r)}+ f(r)^2\left( d\xi ^2+ \sin ^2 \xi d{\varOmega }^2\right) \nonumber \\ ds^2= & {} -V(r)dt^2+\frac{dr^2}{V(r)}+ f(r)^2\left( d\xi ^2+ \sinh ^2 \xi d{\varOmega }^2\right) ,\nonumber \\ \end{aligned}$$
(17)

where \(d{\varOmega }^2\) is the round metric for the two-sphere.

We get the following solutions:

$$\begin{aligned} f(r)= & {} r \nonumber \\ V(r)= & {} k-\frac{2 G_{0} M}{r^2}-\frac{r^2 {\varLambda }_{0}}{6}+ \frac{8 G_{0} M \epsilon }{3 r}-k\frac{2 r \epsilon }{3}-4 G_{0} M \epsilon ^2 \nonumber \\&+k\frac{5 r^2 \epsilon ^2}{9}+8 G_{0} M r \epsilon ^3\nonumber \\&-\left( -\frac{2}{3}k r^2 \epsilon ^2+8 G_{0} M r^2 \epsilon ^4\right) \log \left( 1+\frac{1}{\epsilon r}\right) \nonumber \\ G(r)= & {} \frac{G_{0}}{1+\epsilon r} \nonumber \\ {\varLambda }(r)= & {} \frac{1}{9 r^2 (1+r \epsilon )^2}\left( -12 G_{0} M \epsilon ^2 (-1+2 r \epsilon (4\nonumber \right. \\&\left. +3 r \epsilon (11+10 r \epsilon ))) \right) \nonumber \\&+\frac{1}{9 r^2 (1+r \epsilon )^2}r^2 \left( \epsilon ^2 k (27-10 r \epsilon (2+5 r \epsilon ))\right. \nonumber \\&\left. +3 (1+r \epsilon ) (3+5 r \epsilon ) {\varLambda }_{0}\right) \nonumber \\&+\frac{1}{9 r^2 (1+r \epsilon )^2} \left( 12 r^2 \epsilon ^2 (1+r \epsilon ) (3\right. \nonumber \\&\left. +5 r \epsilon ) \left( -k+12 G_{0} M \epsilon ^2\right) \right) \left( \log \left( 1+\frac{1}{\epsilon r}\right) \right) \end{aligned}$$
(18)

where \(k=\pm 1\) stands for the curvature of the horizon.

It is worth mentioning that the scale-dependent system can be integrated without providing some extra information, in contrast to which occurs in lower dimensional cases [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. To be more precice, in \(2+1\) and \(3+1\)-dimensional space-times, the scale-dependent system is undeterminated: we have more unknowns that equations to be solved, so decreasing the degrees of freedom is mandatory. In all of these cases, the null energy condition plays an important role in the sense that it allows to decrease these number of degrees of freedom. In particular, this condition leads to a differential equation for the Newton coupling, G(r), which is finally written as \(G(r) = G_{0}/(1 + \epsilon r)\).

The fact that the Newton coupling obtained for the five-dimensional solutions here presented coincides with that of lower-dimensional cases is not a coincidence. It was proved that, after a suitable choice of certain null vector, higher-dimensional solutions are forced to obtain the same gravitational coupling [95]. This is true indeed without invoking the null energy condition or another suitable constraint. Therefore, the information encoded into the null energy condition is contained into the modified Einstein field equations. Such a statement, indeed, was pointed out in [17], where the authors shown that the classical null energy condition is also satisfied when we take advantage of the Schwarzschild ansatz. Thus, although in this work we are not explicitly using such a condition, it is already satisfied.

Finally, we note that in the limit \(\epsilon \rightarrow 0\) the classical (non-running) solution is recovered. Specifically,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}f(r)= & {} r \nonumber \\ \lim _{\epsilon \rightarrow 0}V(r)= & {} k-\frac{2 G_{0} M}{r^2}-\frac{r^2 {\varLambda }_{0}}{6} \nonumber \\ \lim _{\epsilon \rightarrow 0} G(r)= & {} G_{0} \nonumber \\ \lim _{\epsilon \rightarrow 0}{\varLambda }(r)= & {} {\varLambda }_{0}. \end{aligned}$$
(19)

4.1.1 Asymptotics

In order to both interpretate the results and evaluate the differences in some thermodynamics quantities between the classical and the running solutions, here we show the asymptotic expansion, for small \(\epsilon \) and large r, for both the Ricci curvature and the lapse function. They read

$$\begin{aligned} R= & {} \frac{10 {\varLambda }_0}{3}+\left( -\frac{16 G_0 M}{3 r^3}+k \frac{8}{r}\right) \epsilon \nonumber \\&+\frac{2}{9} \left( -k 23+\frac{108 G_0 M}{r^2}+k 60 \log (r \epsilon )\right) \epsilon ^2+{\mathcal {O}}[\epsilon ]^3 \nonumber \\ R= & {} \frac{10}{9} \left( -k 10 \epsilon ^2+3 {\varLambda }_0\right) +k\frac{2}{r^2}+{\mathcal {O}}\left[ \frac{1}{r}\right] ^3, \end{aligned}$$
(20)

and

$$\begin{aligned} V(r)= & {} \left( k-\frac{2 G_0 M}{r^2}-\frac{r^2 {\varLambda }_0}{6}\right) +\left( \frac{8 G_0 M}{3 r}-k\frac{2 r}{3}\right) \epsilon \nonumber \\&+\frac{1}{9} \left( -36 G_0 M+k 5 r^2-k 6 r^2 \log [\epsilon r]\right) \epsilon ^2+{\mathcal {O}}[\epsilon ]^3\nonumber \\ V(r)= & {} \left( \frac{k 5 \epsilon ^2}{9}-\frac{{\varLambda }_0}{6}\right) r^2+ \frac{2 k}{3}+\frac{2k}{9 \epsilon r} -\frac{k}{6 \epsilon ^2 r^2}\nonumber \\&-\frac{2 \left( -k+12 G_0 M \epsilon ^2\right) }{15 \epsilon ^3 r^3}+\frac{-k+12 G_0 M \epsilon ^2}{9 \epsilon ^4 r^4} \nonumber \\&+{\mathcal {O}}\left[ \frac{1}{r}\right] ^5. \end{aligned}$$
(21)

From these results, a couple of comments are in order. (i) Both the spherical (\(k=1)\) and hyperbolic (\(k=-1\)) solutions give place to an effective cosmological constant given by

$$\begin{aligned} {\varLambda }_{\mathrm {eff}}=\frac{5 k}{9}\epsilon ^2-\frac{{\varLambda }_{0}}{6}. \end{aligned}$$
(22)

Interestingly, only in the spherical case, this \({\varLambda }_{\mathrm {eff}}\) can be turned off for certain values of the running parameter. (ii) A mass-like term appears only in the spherical case. Specifically,

$$\begin{aligned} G_{0}M_{\mathrm {eff}}=\frac{1}{12\epsilon ^2}. \end{aligned}$$
(23)

(iii) A charge-like term appears in both cases. Specifically

$$\begin{aligned} G_{0}Q^2_{\mathrm {eff}}=\frac{12G_{0}M\epsilon ^2-k}{9\epsilon ^4}. \end{aligned}$$
(24)

As for the effective cosmological constant, this \(Q_{\mathrm {eff}}\) can be turned off for certain values of the running parameter. And (iv), both the spherical and hyperbolic solutions incorporate a defect-like term (monopole-like [96]) with an effective deficit angle \(\delta _{\mathrm {eff}}\) given by the term

$$\begin{aligned} \delta _{\mathrm {eff}}\sim \frac{2}{3}k. \end{aligned}$$
(25)

We note that this deficit angle does not depend on the running parameter. It is worth mentioning that this is not a surprising finding in the context of scale-dependent gravity. In fact, in Ref. [16] the authors reported an \(\epsilon \)-independent deficit angle in the asymptotic behaviour of the line element at infinity in the scale-dependent Einstein–Maxwell system.

Even more, it is noticeable that all these effective quantities which emerge at infinity do not turn off when the running parameter goes to zero. As commented in [16], we ascribe this behaviour to the fact all dimensionless terms of the form \(\epsilon r\) are incompatible with first taking the limit \(r \rightarrow \infty \) and then \(\epsilon \rightarrow 0\). Clearly, if the limit of small \(\epsilon \) is taken first, the classical results are recovered, as shown in Eq. (19).

4.2 Black holes with planar horizon

For a line element parametrized as

$$\begin{aligned} ds^2=-V(r)dt^2+\frac{dr^2}{V(r)}+ f(r)^2\left( d\xi ^2+ d\theta ^2 + d\phi ^2 \right) , \end{aligned}$$
(26)

we get the following solution:

$$\begin{aligned} f(r)= & {} r \\ V(r)= & {} -\frac{2 G_{0} M}{r^2}-\frac{r^2 {\varLambda }_{0}}{6}+ \frac{8 G_{0} M \epsilon }{3 r}-4 G_{0} M \epsilon ^2 \\&-\frac{5 r^2 \epsilon ^2}{9}+8 G_{0} M r \epsilon ^3 \\&-8 G_{0} M r^2 \epsilon ^4 \log \left( 1+\frac{1}{\epsilon r}\right) \\ G(r)= & {} \frac{G_{0}}{1+\epsilon r} \\ {\varLambda }(r)= & {} \frac{1}{3 r^2 (1+r \epsilon )^2}\left( -4 G_0 M \epsilon ^2 (-1+2 r \epsilon (4\right. \\&\left. +3 r \epsilon (11+10 r \epsilon )))\right) \\&+\frac{1}{3 r^2 (1+r \epsilon )^2}\left( r^2 (1+r \epsilon ) (3+5 r \epsilon ) {\varLambda }_0\right) \\&+\frac{1}{3 r^2 (1+r \epsilon )^2}\left( +48 G_0 M r^2 \epsilon ^4 (1+r \epsilon ) (3\right. \\&\left. +5 r \epsilon ) \log \left[ 1+\frac{1}{\epsilon r }\right] \right) , \end{aligned}$$

Also in this case the classical (non-running) solution is recovered when the running parameter is turned off. That is,

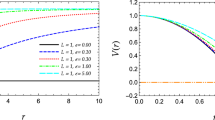
$$\begin{aligned} \lim _{\epsilon \rightarrow 0}f(r)= & {} r \nonumber \\ \lim _{\epsilon \rightarrow 0}V(r)= & {} -\frac{2 G_{0} M}{r^2}-\frac{r^2 {\varLambda }_{0}}{6} \nonumber \\ \lim _{\epsilon \rightarrow 0}G(r)= & {} G_{0} \nonumber \\ \lim _{\epsilon \rightarrow 0}{\varLambda }(r)= & {} {\varLambda }_{0}. \end{aligned}$$
(27)

4.2.1 Asymptotics

In this planar case, the expansions of both R and V(r) are given by

$$\begin{aligned} R= & {} \frac{10 {\varLambda }_0}{3}-\frac{16 (G_0 M) \epsilon }{3 r^3}+\frac{24 G_0 M \epsilon ^2}{r^2}+{\mathcal {O}}[\epsilon ]^3\nonumber \\ R= & {} \frac{10 {\varLambda }_0}{3}-\frac{8 (G_0 M)}{3 \epsilon ^2 r^6}+{\mathcal {O}}\left[ \frac{1}{r}\right] ^7, \end{aligned}$$
(28)

and

$$\begin{aligned} V(r)= & {} \left( -\frac{2 G_0 M}{r^2}-\frac{r^2 {\varLambda }_0}{6}\right) +\frac{8 G_0 M \epsilon }{3 r} \nonumber \\&-4 (G_0 M) \epsilon ^2+{\mathcal {O}}[\epsilon ]^3\nonumber \\ V(r)= & {} -\frac{{\varLambda }_0 r^2}{6}-\frac{8 (G_0 M)}{5 \epsilon r^3}+\frac{4 G_0 M}{3 \epsilon ^2 r^4} +{\mathcal {O}}\left[ \frac{1}{r}\right] ^5, \end{aligned}$$
(29)

showing that the rule of the running parameter can be interpreted in this case as related to an effective charge, which is given by

$$\begin{aligned} Q^2_{\mathrm {eff}}=\frac{4 M}{3 \epsilon ^2}. \end{aligned}$$
(30)

4.3 Solv black holes

When appropriate units are used, a five-dimensional metric with three-dimensional Solv geometry can be parametrized as [8]

$$\begin{aligned} ds^2= & {} -V(r)dt^2+\frac{dr^2}{V(r)}+ A e^{2 z} r^2 dx^2 \nonumber \\&+ A e^{-2 z} r^2 dy^2 + A dz^2. \end{aligned}$$
(31)

Using this ansatz, we get the following solution:

$$\begin{aligned} A= & {} -\frac{3}{{\varLambda }_{0}} \nonumber \\ V(r)= & {} -\frac{2 \sqrt{G_0 M}}{r}+3 \sqrt{G_0 M} \epsilon -6 \sqrt{G_0 M} r \epsilon ^2-\frac{2 r^2 {\varLambda }_0}{9} \nonumber \\&+6 \sqrt{G_0 M} r^2 \epsilon ^3 \log \left[ 1+\frac{1}{r \epsilon }\right] \nonumber \\ G(r)= & {} \frac{G_{0}}{1+\epsilon r} \nonumber \\ {\varLambda }(r)= & {} \frac{1}{3 A r (1+r \epsilon )^2}\left( 9 A \sqrt{G_0 M} \epsilon ^2+108 A \sqrt{G_0 M} r \epsilon ^3 \right) \nonumber \\&+\frac{1}{3 A r (1+r \epsilon )^2}\left( 108 A \sqrt{G_0 M} r^2 \epsilon ^4 \right) \nonumber \\&+ \frac{1}{3 A r (1+r \epsilon )^2}\left( r (1+r \epsilon ) (-3+2 A {\varLambda }_0\right. \nonumber \\&\left. +r \epsilon (-3+4 A {\varLambda }_0))\right) \nonumber \\&-\frac{1}{3 A r (1+r \epsilon )^2} \left( 54 A \sqrt{G_0 M} r \epsilon ^3 (1+r \epsilon ) (1+2 r \epsilon ) \right) \nonumber \\&-\frac{1}{3 A r (1+r \epsilon )^2} \left( \log \left[ 1+\frac{1}{r\epsilon }\right] \right) . \end{aligned}$$
(32)

We note that in the limit \(\epsilon \rightarrow 0\) the classical (non-running) solution is recovered:

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}A= & {} -\frac{3}{{\varLambda }_{0}} \nonumber \\ \lim _{\epsilon \rightarrow 0}V(r)= & {} -\frac{2 \sqrt{G_{0} M}}{r}-\frac{2 r^2 {\varLambda }_{0}}{9}\equiv V_{0}(r)\nonumber \\ \lim _{\epsilon \rightarrow 0}G(r)= & {} G_{0} \nonumber \\ \lim _{\epsilon \rightarrow 0}{\varLambda }(r)= & {} {\varLambda }_{0}. \end{aligned}$$
(33)

4.3.1 Asymptotics

In the Solv case, the corresponding expansions are written as

$$\begin{aligned} R= & {} \frac{10 {\varLambda }_0}{3}-\frac{6 \sqrt{G_0} M \epsilon }{r^2}+\frac{36 \sqrt{G_0 M} \epsilon ^2}{r} +{\mathcal {O}}[\epsilon ]^3 \nonumber \\ R= & {} \frac{10{\varLambda }_0}{3}-\frac{12 \sqrt{G_0 M}}{5 \epsilon ^2 r^5}+{\mathcal {O}}\left[ \frac{1}{r}\right] ^6. \end{aligned}$$
(34)
$$\begin{aligned} V(r)= & {} -\frac{2 \left( 9 \sqrt{G_0 M}+r^3 {\varLambda }_0\right) }{9 r}+3 \sqrt{G_0 M} \epsilon \nonumber \\&-6 \left( \sqrt{G_0 M} r\right) \epsilon ^2+{\mathcal {O}}[\epsilon ]^3\nonumber \\ V(r)= & {} -\frac{2 {\varLambda }_0 r^2}{9}-\frac{3 \sqrt{G_0 M}}{2 \epsilon r^2} +\frac{6 \sqrt{G_0 M}}{5 \epsilon ^2 r^3}\nonumber \\&-\frac{\sqrt{G_0 M}}{\epsilon ^3 r^4}+{\mathcal {O}}\left[ \frac{1}{r}\right] ^5. \end{aligned}$$
(35)

In this case, the running parameter gives place asymptotically to an effective charge given by

$$\begin{aligned} Q_{\mathrm {eff}}=\frac{3}{2}\frac{\sqrt{G_{0}M}}{\epsilon }. \end{aligned}$$
(36)

Interestingly, due to the sign of the term which goes with \(r^{-4}\), this interpetation is only valid when \(\epsilon <0\) (see eq. (2.3) of Ref. [10] for charged Solv black holes).

Therefore, the combination of the running parameter, \(\epsilon \), together with the considered topology (\({\mathbb {E}}^3\), \({\mathbb {S}}^3\), \({\mathbb {H}}^3\) and Solv), give place to different asymptotic structures for the solutions here reported. Specifically, as shown in this section and summarized in Table 1, an effective cosmological constant (different to \({\varLambda }_{0}\)) is obtained for non-planar constant curvature horizons. On the contrary, both planar and Solv-geometries retain the classical cosmological constant. Even more, although effective Maxwellian charges appear in all the solutions here reported, only the scale-dependent Solv black hole contains a Reissner–Nordström-like structure without gravitational monopoles, which are, on the contrary, included, in both the \({\mathbb {S}}^3\) and \({\mathbb {H}}^3\) cases. Finally, we have noted that the planar case is the only type which does not give place to a mass-like term. It is important to remark that the asymptotic structure here outlined has not to be taken literally. In fact, the asymptotic limits of the solutions here presented include other terms which are difficult to interpretate and which typically fall-off slower than those we have given an interpretation in terms of an effective mass, charge, monopole or cosmological constant.

Table 1 Asymptotics of classical and improved (scale-dependent) black holes
Full size table

In order to evaluate the differences in some thermodynamical quantities introduced by the scale-dependence procedure, only the more exotic scale-dependent Solv black holes will be considered. The extension of these results to scale-dependent black holes with constant curvature horizons it is straightforward and it will no be treated in this work.

Let us define the volume element of the compact Solv spacetime as

$$\begin{aligned} {\varOmega }_{\mathrm {Solv}}=\int _{{\varOmega }_{x}\times {\varOmega }_{y}\times {\varOmega }_{x}}\sqrt{A} dx\, dy\, dz, \end{aligned}$$
(37)

where the \({\varOmega }_{I}\)’s for \(I=(x,y,z)\) stand for the compact ranges of the horizon coordinates, \(x_{I}\).

On one hand, as shown in Refs. [10, 12], the Bekenstein–Hawking entropy for classical (non-running) Solv black holes is given by

$$\begin{aligned} S_{0}=\frac{2\pi }{\kappa } |{\varOmega }_{\mathrm {solv}}|\sqrt{\frac{2}{3}}r_{h}^2, \end{aligned}$$
(38)

where we remind the reader that \(\kappa =8 \pi G_{0}\) and \(r_{h}\) stands for the event horizon corresponding to Eq. (12).

On the other hand, although the scale-dependent Solv black hole has a different event horizon compared to its non-running counterpart, we arrive to an improved entropy very similar to that given by Eq. (38) given by

$$\begin{aligned} S=\frac{2\pi }{8\pi G(r_{H})} |{\varOmega }_{\mathrm {solv}}|\sqrt{\frac{2}{3}}r_{H}^2, \end{aligned}$$
(39)

where \(r_{H}\) stands for the event horizon corresponding to Eq. (32).

A simple expression which permits to compare the entropies in both the classical and the running situations is

$$\begin{aligned} S= S_{0}(1+ \epsilon r_{H})\left( \frac{r_{H}}{r_{h}}\right) ^2. \end{aligned}$$
(40)

Concerning the temperature, after employing the well-known formula

$$\begin{aligned} T=\frac{1}{4\pi }\left| \lim _{r\rightarrow r_{+}}\frac{\partial _{r} g_{tt}}{\sqrt{-g_{tt}g_{rr}}}\right| , \end{aligned}$$
(41)

where \(r_{+}\) refers to the event horizon for the classical or the running solution, we get that

$$\begin{aligned} T=T_{0}\frac{V'(r_{H})}{V_{0}'(r_{h})}. \end{aligned}$$
(42)

As commented in previous works [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], the running parameter has to be smaller than the other scales entering the problem. Therefore, taking the asymptotic expansion for V(r) obtained in Eq. (35) up to second order in \(\epsilon \), we get that the new event horizon lies at

$$\begin{aligned} r_{H}=r_{h}-\frac{1}{2}\epsilon r_{h}^2 -\epsilon ^2 r_{h}^3+ {\mathcal {O}}[\epsilon ]^3. \end{aligned}$$
(43)

Within this approximation, the corrections to both the temperature and the entropy are found to be

$$\begin{aligned} T = T_{0}\left[ 1-2 \epsilon r_{h}-\frac{7}{4}\epsilon ^2 r_{h}^2 \right] + {\mathcal {O}}[\epsilon ]^3, \end{aligned}$$
(44)

and

$$\begin{aligned} S=S_{0}\left[ 1-\frac{13}{4}r_{h}^2\epsilon ^2\right] + {\mathcal {O}}[\epsilon ]^3. \end{aligned}$$
(45)

Finally, it is interesting to note that the corrected temperature includes a term linear in \(\epsilon \) which is absent in the corresponding correction for the entropy. In this sense, the entropy remains more robust with respect to the scale-dependence corrections than the temperature, which responds faster to the effects of the running.

5 Is the scale-dependent scenario consistent with the Asymptotic Safety program?

The Asymptotic Safety program for quantum gravity (for details, see the seminal review [37]) establishes that a fundamental theory should be divergence free, which means that the theory is well-defined in all the energy spectrum. It is important to notice that the crucial point is the existence of non-gaussian fixed points (NGFPs hereafter), which is required for a good behavior of the theory. Certainly, the existence of NGFPs is not ensured; however, in cases where they exist, one should be able to obtain a full description of the problem for any value of \({\tilde{k}}\).

In some circumstances it is useful to link the arbitrary scale, \({\tilde{k}}\), with some coordinate of the spacetime. Usually, in black hole physics, the connection is established via the condition \({\tilde{k}}r = \text {constant}\) (for instance in spherical symmetry) but different parametrizations are still possible. The “renormalization group improvement” technique is precisely one in which, solving the \(\beta \) function for the gravitational coupling, one can improve the classical background (see for example [55]) and where one uses the link between the renormalization scale and some physical parameter. As we previously said, in black holes with spherical symmetry, the relation between \({\tilde{k}}\) and the radial coordinate is taken to be reciprocal. This choice ensures that (i) quantum effects appear in the “correct” sector (i.e., in the UV sector) and (ii) the standard sector reamain unchanged (i.e., the IR sector).

Regarding the scale-dependent scenario, we remark that the formalism allows to obtain generalized black hole solutions for several symmetries [13, 14, 16,17,18,19,20,21,22,23,24,25,26,27,28,29]. These solutions, however, introduce relevant correction for small values of \({\tilde{k}}\) (i.e. in the IR region). In this sense, the scale-dependent scenario introduces changes in the opposite sector compared with that expected from the approaches based on the Asymptotic Safety program. At this point, one could consider that the scale-dependent and the Asymptotic Safety programs are not compatible. However, recent studies within the asymptotic safety program reported relevant corrections for small \({\tilde{k}}\) [86, 97, 98]. This relevant feature, who was not anticipated, could reconcile both formalisms (in the corresponding sector).

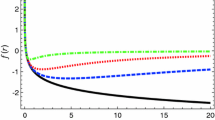
In Fig. 1 we show a comparison between the dimensionful gravitational coupling, as given by [97], and our solution for G(r), showing encouraging similarities in the IR regime.

Fig. 1
figure 1

Left panel: gravitational running coupling \(G({\tilde{k}})\) extracted from [97]. An unusual feature in the IR sector is observed. This was called “IR instability” and reveals that some deviation in such sector could appear. Right panel: gravitational running coupling \(G({\tilde{k}})\) obtained in our model assuming the replacement \({\tilde{k}} r=1\). We observe that our solution mimics the same IR instability for small values of \({\tilde{k}}\). In addition, \(G({\tilde{k}})\) tends to be constant for intermediate values of \({\tilde{k}}\) and, finally, for large values of \({\tilde{k}}\) our solution seems to miss the behavior predicted by the Asymptotic Safety approach

Full size image

Before concluding this section, we would like to point out the difference between the method here employed and other alternative formalism largely inspired in Asymptotic Safety, i.e., the RG-improvement method. With respect to the RG-improvement method, the strategy consists in taking advantage of the computation of \(\beta \)-functions to obtain the gravitational coupling. Thus, Newton’s coupling (in terms of the radial coordinate) is obtained just after considering a specific relation between the renormalization scale, \({\tilde{k}}\) and the radial coordinate, r. After doing so, the relation \(G_0 \rightarrow G(r)\) is replaced into the classical BH solution in order to incorporate the corresponding quantum features. Our formalism, however, follows an alternative route. Given that scale-dependent gravity modifies classical gravity starting from the action, we have an additional term, \({\varDelta }t_{\mu \nu }\), to be considered into the equations of motion. This term codifies the quantum features and can be interpreted as an additional contribution to the energy-momentum tensor (as was previously shown). It is precisely such an interpretation which is crucial for us. Notice that in scale-dependent gravity the precise relation between \({\tilde{k}}\) and r is not specified. In this respect, an unusual feature appears following this idea: the Newton’s coupling now has a correction at large distance (apparently) absent in the Asymptotic Safety solutions. However, such feature was also recently reported within this framework, as commented before.

6 Concluding remarks

In this work we have constructed, for the first time, five dimensional scale-dependent black holes. Although we have been able to generalize some of the classical (non-running) solutions presented in Ref. [8], it remains to be seen if all the classical black holes with Thurston geometries have their scale-dependent counterparts. Interestingly, all the solutions found incorporate the same running for the Newton coupling without invoking the null energy condition, in contrast with some previous works [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. It is remarkable that, at lower dimensions, the null energy condition supplements the set of equations to be solved. However, at higher dimensions, this requirement is not mandatory. Despite of that, given the symmetry of the problem, the Schwarzschild ansatz is consistent with the null energy condition as was previously reported in [17, 95]. Interestingly, after comparing the result here obtained for the running gravitational coupling with the corresponding results provided by the Asymptotic Safety program [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] one finds that a matching is straightforward for the scale setting choice \({\tilde{k}}(r)\sim r\). As noted in [27], this choice seems peculiar, since in a naive scale setting one usually expects \({\tilde{k}} \sim 1/r\) for dimensional reasons. However, it is important to note that this finding is not in contradiction with the Asymptotic Safety paradigm itself but with the naive scale setting \({\tilde{k}}\sim 1/r\), which is only an educated guess applied a posteriori, when one tries to improve classical solutions with the running couplings found in Asymptotic Safety. After briefly discussing the effects due to the combination of both the topology of the horizon and the scale-dependence, we have computed the corrections to the temperature and the entropy for the scale-dependent Solv black hole, finding linear and quadratic growing behaviours with the running parameter and recovering the classical results when the theory reduces to General Relativity. Finally, an IR instability similar to that found in the Asymptotic Safety approach has been found in the scale-dependent setting here employed by comparing the running of the Newton coupling in both cases, suggesting interesting similarities between these approaches. To conclude, we would like to mention that this work is, to the best of our knowledge, the first attempt to construct black holes with Thurston horizons in theories beyond General Relativity.