Abstract
In this paper, we discuss the theoretical framework and the experimental measurements of the magnetic moment of the charmed baryons. We first review the theoretical predictions of the \(\varLambda _c^{+}\) magnetic moment and show that the measurements of the magnetic moments of other charmed baryons, such as \(\varXi _{c}\), allow to perform detailed spectroscopy studies. The magnetic moment of the charm quark can be determined using radiative charmonium decay, which can be compared to the \(\varLambda _c^{+}\) magnetic moment within theoretical models. The present results show a tension with majority of theoretical predictions. The magnetic moment of the charmed baryons could potentially be measured directly, using bent-crystal experiments at LHC. The possibility to measure precisely the magnetic moments of charmed baryons needs precise measurement of their polarisation and weak decay parameters. In this paper, we revisit the formalism of the angular analysis needed for these measurements and make a detailed evaluation of initial polarisation of deflected \(\varLambda _c\) baryons as a function of crystal orientation. We found a special orientation of the crystal that gives the opportunity to measure the \(\varLambda _c\) dimensionless electric dipole moment almost with the same precision as its g-factor, which is more than an order of magnitude more efficient than suggested before.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 The magnetic dipole moment of charmed baryon
The spin 1/2 particles, such as leptons, proton, quarks, have intrinsic magnetic dipole moment (MDM), of the form:
where Q is the electric charge in units of the positron charge e, and m is the mass of a particle.Footnote 1 Factor g is called gyromagnetic factor, or g-factor, which is equal to 2 for a Dirac point-like fermion, while the quantum effects modify this value. As this deviation, anomalous MDM \(\kappa \equiv (g -2)/2 \), comes from the loop effects, it is known to be sensitive to the contributions from new physics: a heavy particle from new physics can propagate in the loop.
The MDM of electron and muon are one of the most precisely measured quantities in particle physics: \(g_e=2.002 319 304 361 82 (52)\) [1] and \(g_\mu =2.002 331 841 78 (126)\) [2]. The theoretical predictions for these quantities are also computed at a very high accuracy, for example, for the muon to the order \((\alpha /\pi )^5\) in QED [3]. Intriguingly, deviation of the theoretical prediction from experiment at a level (3.5–4)\(\sigma \) is observed in the muon anomalous MDM, which is one of most significant hints of new physics observed today (see, e.g., [4,5,6,7]).
The proton MDM is also measured very precisely, \(g_p=5.585 694 689 24 (164)\) [8]. This corresponds to using the proton charge and mass in Eq. (1), i.e. \(Q=1\) and \(m=m_p\). The value of \(g_p\) being far from 2 is an indication of the proton substructure.
Thus, let us take into account the fact that proton is made of three quarks. Within the quark model description, the MDM of proton can be computed as a sum of the MDMs of the three constituent quarks. It is important here to take into account the spin configuration of the three quarks. As a result one finds
where \(\mu _{u, d}\) is the MDM of up and down quarks given as
where \(Q_{q}\) and \(m_{q}\) are the electric charge and the mass, and \(g_q\) is the g-factor of the quark \(q = (u, \, d)\).
In the limit of isospin symmetry, \(m_u=m_d\equiv m_q\) and \(g_u=g_d \equiv g_q\), we find
One can immediately recognise that the result suffers from the uncertainty coming from the quark mass. In the quark model, the constituent quark mass \(m_q=m_p/3\) can be used. Using this, a comparison of Eqs. (1) and (4) leads to the value \(g_q = g_p/3 \simeq 1.862\). This result being close to 2 indicates that the light quarks \(u, \, d\) have little substructure. Note that this argument can be reversed: by going to the case of a Dirac point-like particle, \(g_q=2\), one can determine the u and d quark mass, \(m_q= 0.336\) GeV.
The difficulties for concluding whether the quark g-factor is SM-like or not are the two-fold:
- (i)
the result heavily depends on the quark mass, in fact from the experiment one can only determine the ratio \(g_q / m_q= g_p / m_p \simeq 5.95\,\)GeV\(^{-1}\);
- (ii)
different from the lepton case, the anomalous MDM is induced by the strong interaction and it can be very large and also scale dependent.
Having said this, the agreement of this experimental result does not seem to be just an accident. The computation of the MDM of neutron in the same model leads to
where the relation between \(\mu _n\) and \(\mu _p\) is quark mass and g-factor independent. It is very well satisfied in the experiment.
In this article, we discuss a possible new measurement of charmed baryons MDM using bent crystal. These MDMs have never been measured because of a very short lifetime of charmed baryons, \(\tau \sim 10^{-13}\,\)s. From theoretical point of view the charmed baryon MDM has similarities with the proton MDM. Contrary to the muon, which is an elementary particle, the charmed baryon is a bound system of strongly interacting quarks. Therefore prediction of its MDM suffers from uncertainties, related to the choice of masses of constituent (“dressed”) quarks, and to model description of the baryon structure. In the following, as an example, we summarise the current status of the theory predictions of the \(\varLambda _c^+\) magnetic moment.
Let us first compute the MDM of \(\varLambda _c^+\) in the constituent quark model as before, i.e. \(\varLambda _c^+\) MDM is sum of the MDMs of up, down and charm quarks in the configuration antisymmetric in spin of the light quarks (see Appendix A). In this case the \(\varLambda _c^+\) MDM is equal to the charm quark MDM:
For example, using the constituent quark mass
with \(m_q=m_p/3\), we find
where \(\mu _N\) is the nuclear magneton.
It is curious that the g-factor of \(\varLambda _c^+\), which is defined via
is actually close to the charm quark g-factor, i.e.
although \(\varLambda _c^+\) has a substructure.
There are various models to compute the MDM beyond the quark model. For example, the so-called Heavy Hadron Chiral Perturbation Theory (HHCPT) is developed [9,10,11,12], which combines the heavy quark effective theory and the chiral perturbation theory of light hadrons. It allows to improve theoretical prediction in a systematic manner.
The next to leading order Lagrangian for the MDM of triplet and sextet baryons was given in [13, 14]. At the order \({\mathcal {O}}(1/m_Q)\) (\(m_Q\) is the heavy quark mass), we have two extra contributions. First, it is the heavy quark MDM, i.e. the interaction of the photons and the heavy quark constituent inside of the hadrons, which also induces M1 transition. This term induces the contribution of the quark model. The second contribution is the photon interaction with the light “brown mock” inside of the heavy hadrons. However, the baryon \(\varLambda _c^+\), whose light degrees of freedom are in the spinless state, does not receive contribution to the MDM from this interaction. As a result, even at this order, the quark model limit results given above hold. The lack of contributions from the light degrees of freedom seems to be generic and theoretical predictions using different models show that the MDM of \(\varLambda _c\) is close to the one predicted by the constituent quark model.
MDM predictions using various theoretical models can be summarized as [15,16,17,18,19,20,21,22,23,24,25,26,27,28]:
although there are exceptions falling out of these bounds. In particular, Ref. [29], using the QCD spectral sum rule approach, gives \(\mu _{\varLambda _c} =( 0.15\pm 0.05)\, \mu _N\), while Ref. [20] in the Dirac point-form dynamics obtains \(\mu _{\varLambda _c} = 0.52 \, \mu _N\), and Ref. [30] in the next-to-next-to-leading order in the HHCPT gives \(\mu _{\varLambda _c} = (0.24\pm 0.02) \, \mu _N\). It should be noted that each theoretical model fits the charm quark mass with various observables. In this sense, the charm quark mass uncertainty is included in this value.
Recently, a magnetic dipole moment measurement of charmed baryons using bent crystal is proposed [31, 32]. In the present paper, we investigate possible theoretical impact of such measurement and achievable experimental precision. In Sect. 2, we discuss the extraction of the \(\varLambda _c^+\) magnetic moment from the radiative charmonium decays, which provides its most precise information as of today. In Sect. 3, we discuss the impact of the charmed baryon magnetic moment measurements for a better understanding of the charmed baryon spectroscopy. In Sect. 4, we introduce the charmed baryon magnetic dipole measurement with bent crystal and further investigate its achievable precision. We briefly discuss the charmed baryon electric dipole moment measurement as well. For the \(\varLambda _c^+\) magnetic moment measurement, it turned out that the initial polarisation and the weak decay parameter have to be pre-measured. We discuss what observable can provide such information in Sect. 5 and give conclusions in Sect. 6.
2 The prediction of the magnetic dipole moment of \(\varLambda _c^+\) using the radiative charmonium decays
It turned out that the charm quark MDM is most precisely measured by the quarkonium radiative decays as of today. In this section, using this result, we estimate the \(\varLambda _c\) MDM.
The process used by the CLEO [33] and BESIII [34] collaboration is the cascade radiative decay,
where the initial \(\psi (2S)\) is produced from the \(e^+e^-\) collision.
Using the non-relativistic model, this cascade radiative decay is computed (see [35, 36] for detail). We have 5 observable angles: \(\chi _{c1,2}\) the angle between \(\gamma _1\) and \(\gamma _2\) in the rest frame of \(\chi _{c1,2}\) (\(\theta _{\gamma _1\gamma _2}\)) and the directions of the initial positron (\(\theta _1, \phi _1\)) and of the final lepton (\(\theta _2, \phi _2\)), which characterise the \(\psi ^{\prime }\) and \(J/\psi \) polarisation, respectively. The angular distribution can be expressed in terms of the Wigner-D function with associated helicity amplitudes \(A_\nu ^{J_\chi }\) which characterise the decay \(\chi _{c1,2} ({\nu })\rightarrow \gamma _{2}(\mu )\psi ({\lambda })\) and \(B_{\nu ^{\prime }}^{J_\chi }\) does \(\psi ^{\prime }({\lambda ^{\prime }})\rightarrow \gamma _{1 }(\mu )\chi _{c1,2}(\nu ^{\prime })\) where \(\nu ^{(\prime )}, \mu ^{(\prime )}, \lambda ^{(\prime )}\) are the helicity of each particle.
In the following discussion, we use the so-called multipole amplitudes \(a_i^J\) and \(b^J_i\) which are related to the helicity amplitudes \(A_\nu ^{J_\chi }\) and \(B_{\nu ^{\prime }}^{J_\chi }\), by Clebsch–Gordan coefficients as
where \(0 \le \nu ^{(\prime )}\le J_\chi \) and \(1 \le J_\gamma \le J_\chi +1\). \(J_\gamma =1, 2, 3\) corresponds to the E1, M1 and E3 transitions.
The normalised M2 contributions, \(b^{1,2}_2\) and \(a^{1,2}_2\) from the \(\psi (2S) \rightarrow \gamma _1 \chi _{c1,2}\) and \(\chi _{c1,2} \rightarrow \gamma _2 J/\psi \), respectively, are related to the mass of the charm quark \(m_c\) and its anomalous magnetic moment \(\kappa \) (see [33] for detail). In the ratios \(\beta = b^1_2 / b^2_2\) and \(\alpha = a^1_2 / a^2_2\), the \(m_c\) and \(\kappa \) cancel to first order in \(E_\gamma / m_c\). The ratios thus receive clear numerical predictions of \(\beta = 1.000 \pm 0.015\) and \(\alpha = 0.676 \pm 0.071\), respectively [33]. Recently, the BES III experiment reported [34] the measurement of the M2 amplitudes and the determination of the two ratios \(\beta = 1.35 \pm 0.72\) and \(\alpha = 0.617 \pm 0.083\), in agreement with the theory prediction.
The precision of the \(b^{1,2}_2\) and \(a^{1,2}_2\) measurements reported by BES III is dominated by the available statistical sample, and is expected to be improved by future experiments with larger collected data samples. Among important systematic uncertainties are photon detection, efficiency estimates with the simulation assuming the phase space, kinematic fit and fitting technique. With improved electromagnetic calorimeter and the efficiency determined in bins of relevant angular variables, systematic uncertainty is also expected to be significantly improved in the next-generation experiments. In the BES III analysis [34], the \((1 + \kappa _c)\) measurement, which can be related to \(g_c\) by
was performed:
where the last systematic error is coming from the charm quark mass ambiguity \(m_c = 1.5 \pm 0.3\,\hbox {GeV}\).
What would be the implication of this result? Indeed, the obtained value of \(g_c\) is close to 2 but the precision is limited by the uncertainty from the charm quark mass. In fact, the charm quark would receive a radiative correction, from the strong interaction, which would also induce uncertainty. As in the case of the muon anomalous magnetic moment, there is a chance that the charm quark anomalous magnetic moment is non-SM like. However, the SM prediction of the \(g_c\) contains an ambiguity as a concept. This problem can be solved only when we chose a theoretical model which allows to consistently calculate the charm quark anomalous magnetic moment effect inside of hadrons. In the following we prefer to write the result in Eq. (11) in terms of ratio between \(g_c\) and the charm quark mass as
Since the magnetic moment of charm quark is proportional to \(g_c/{2 m_c}\), the experimental results given in Eq. (11), can provide a prediction of the \(\varLambda _c\) magnetic moment in the constituent quark model without any charm quark mass uncertainty
If we compare this with the theoretical predictions in the end of the previous Section, we can conclude that there is a tension with the majority of theoretical predictions. In particular, the deviation with calculation [29] is 5.7 \(\sigma \), with the NNLO HHCPT [30] the deviation is 6.7 \(\sigma \). On the other hand, there are theoretical models which do not contradict to Eq. (13); for example, the calculation in [19] agrees with the value in Eq. (13) on the level of 1.4 \(\sigma \).
In order to increase the significance of this discrepancy what would be needed are: (i) to achieve a better precision of the measurement given in (12) by further improving radiative charmonium decay at BES III and a possible future charm factory, (ii) to achieve a direct measurement of \(\varLambda _c^+\) magnetic moment at an equivalent precision. We will briefly discuss on (i) in the following, while (ii) will be discussed in Sects. 5 and 6. In both cases we should aim to have an experimental precision at 5\(\%\) or better.
Theory calculations of \(b^{0,1,2}_2\) and \(a^{0,1,2}_2\) to the next order in \(E_\gamma / m_c\) are therefore of primary importance. A dependence of the corrections on \(E_\gamma \) and \(m_c\) is expected to be different, so that the experimental determination of different amplitudes will provide truly complementary information. This can be possible by BES III and also at the future tau-charm factories.
Another path can be the measurement of the absolute values of \(b^{1,2}_2\) and \(a^{1,2}_2\) instead of the ratios. While part of the systematic uncertainties will not cancel in the absolute measurements, the system can be over-constrained to verify model assumptions. Comparison of the all four values of \(b^{1,2}_2\) and \(a^{1,2}_2\) measured experimentally to theory predictions will provide complementary information. Taking into account correlations of experimental measurements and retaining only variables that yield identical theoretical interpretations, the extracted values for \(\kappa \) or \(\kappa \oplus m_c\) can be averaged. Involving measurements with intermediate \(\chi _{c0}\) and \(\eta _c (2S)\) states would allow a simultaneous fit to the \(m_c\) and \(\kappa \) variables to be performed using the eight quasi-independent measurements.
Higher-order multipole amplitudes can be extracted from the angular distributions of the final-state particles. They were first considered in Ref. [34] by the BES III experiment, who performed a simultaneous unbinned maximum likelihood fit according to the procedure from Refs. [35, 36]. The relevant angular variables are the polar angle of \(\gamma _1\) with respect to the beam axis, in the \(\psi (2S)\) rest frame, \(\theta _1\); the polar, \(\theta _2\), and azimuthal, \(\phi _2\), angles of \(\gamma _1\) with respect to the direction of \(\gamma _1\), in the \(\chi _{cJ}\) rest frame (\(\phi _2 = 0\) in the electron-beam direction); the polar, \(\theta _3\), and azimuthal, \(\phi _3\), angles of \(l^+\) from the \(J/\psi \) decay with respect to the direction of \(\gamma _2\), in the \(J/\psi \) rest frame (\(\phi _3 = 0\) in the \(\gamma _1\) direction).
3 The charmed baryon spectroscopy and the magnetic dipole moment
Recently LHCb experiment as well as \(e^+e^-\) machine, such as BES III and Belle II are making a great progresses in the charmed baryon spectroscopy. The first observation of the doubly charmed baryon at LHCb [37] has triggered various theoretical investigation of charmed baryon weak decays as well. In this section, we show that the MDM which reflects the spin configuration of the internal degree of freedom of baryon can be a powerful tool for identification of charmed baryons.
Let us first derive the MDM of different charmed baryons.
First of all, it turns out that the two remaining triplet (spin 1/2, anti-symmetric) charmed baryons, \(\varXi _c^0\) and \(\varXi _c^+\) have the same MDM as \(\varLambda _c^+\) in the quark model:
A confirmation of this relation plays an important role to test the quark model description.
In [17, 38], higher order corrections to this relation are discussed. The reference [17] discusses the so-called spin-symmetry breaking effect, which typically induces the \(\varSigma _c^*-\varSigma _c\) mass splitting. It comes form a loop diagram with \(\varSigma _c^{(*)}\) and \(\pi , K\) in the loop. This contribution leads to a sub-leading effect (order \(1/m_Q^2\)) to the MDM of \(\varXi _c^{+, 0}\). There are two input parameters to this computation: the mass splitting \(\varDelta m\) and the sextet-anti-triplet axial vector coupling \(g_2\)Footnote 2 in the Chiral Lagrangian. \(\varDelta m\) can be obtained by \(\varDelta m=m_{\varSigma _c^*}-m_{\varSigma _c}\), which is equal to \(m_{\varXi ^{\prime *}_c}-m_{\varXi ^{\prime }_c}\) at the SU(3) limit, while the coupling \(g_2\) must be fixed by the charmed baryon strong decays. In recent years, there have been a lot of progress in determination of \(g_2\): the latest fit to the experimental data gives \(0.989^{+0.019}_{-0.042}\) [39] and the lattice QCD result shows \(0.71\pm 0.13\) [40]. Using the former result, to be conservative, we can find that the relation (14) would be modified slightly:
Note that this result does not depend on the charm quark mass. In [38], the SU(3) breaking effect was further included. In this case, we cannot obtain all the parameters from other experiments, which causes additional theoretical uncertainty. However, this contribution is typically of order \(1/m_Q\varLambda _\chi ^2\) and can be small.
For the sextet (spin 1/2, symmetric) charmed baryons, the situation is very different. We find (Appendix A):
which leads to the values
(with \(m_c=m_{\varSigma _c}-2 \, m_q =1.8 \,\mathrm{GeV}\)). Even though these numerical values suffer from the quark mass uncertainty, the sign of MDM for \(\varSigma _c^0\) seems to be opposite to the one of \(\varLambda _c^+\), and the MDM of doubly-charged \(\varSigma ^{++}_c\) is much larger than MDM of \(\varLambda _c^+\), which would be also interesting to be tested. Note that the main decay channel of \(\varSigma _c\) is \(\varLambda _c^+ \, \pi \).
Finally, let us discuss other sextet (spin 1/2, symmetric) charmed baryons \(\varXi _{c}^{\prime +, 0}\). These baryons have the same quark content as \(\varXi _c^{+, 0}\) but their wave functions are SU(3) flavour symmetric. Since these states have the same quark contents and the same spin, they can mix with the triplet \(\varXi _c^{+, 0}\) states. In the infinite mass limit, though, this mixing is zero, i.e. \(\varXi _c^{+, 0}\) is the pure anti-symmetric and \(\varXi _{c}^{\prime +, 0}\) is the pure symmetric state. Indeed, two states are observed, one at \(\sim 2468 \,\) MeV and the other at \(\sim 2578 \,\) MeV. The latter decays radiatively to the former. Whether these observed two states (mass eigenstates) are the pure anti-symmetric and symmetric states (flavour eigenstates) is not known though it can offer an excellent test of the heavy quark limit. In the following, we show that the MDM measurements, which are the most sensitive to the flavour symmetry of the constituent quarks, can be used to answer this question.
The MDM of \(\varXi _{c}^{\prime +, 0}\) yields:
which leads to \(\mu _{\varXi ^{\prime +}_{c}}=\mu _{\varSigma _c^+}, \ \mu _{\varXi ^{\prime 0}_{c}}=\mu _{\varSigma _c^0}\) in the SU(3) limit. The theoretical uncertainty might be larger than the case of \(\varSigma _c^{0, +}\) due to SU(3) violation, however, we would still expect the MDM of the \(\varXi _{c}^{\prime 0}\) to have an opposite sign comparing to the one of \(\varXi _{c}^{0}\). This result implies that the MDM measurements are very sensitive to resolve the deviation between the flavour and the mass eigenstate of \(\varXi _c\)’s. In particular, the equality of the MDM of \(\varXi _c^{+, 0}\) and \(\varLambda _c^+\) in Eq. (14) does not depend on the quark masses and the most precise test can be performed. It should be noted that, contrary to the triplet (anti-symmetric) baryons, the sextet (symmetric) baryons receive the next to leading order long-distance contributions (the photon interacting with light degrees of freedom), which are quite sizeable. Nevertheless, most of the theoretical predictions (see, e.g., [22]) confirm the negative MDM for \(\varXi _c^{\prime 0}\), which can be used to clarify the issue of the \(\varXi _c-\varXi _c^{\prime }\) mixing as discussed earlier.
In summary, measurement of \(\mu _{\varLambda _c}\) as well as \(\mu _{\varXi _c}\) at a high precision will be highly appreciated to distinguish different spin configurations of the charmed baryon states.
4 Magnetic dipole moment measurement of charmed baryons using bent crystal
The MDMs of baryons containing u, d and s quarks have been extensively studied and measured. The experimental results are all obtained by using the conventional methods, namely the measurement of the precession angle of the polarisation vector when particle is travelling through an intense magnetic field by analysing the angular distribution of the decay products.
No measurement of MDMs of charmed or beauty baryons has been performed so far. A reason of the non-availability of experimental information is because the lifetimes of charmed/beauty baryons are too short to measure the MDM by standard techniques.
One proposal to meet the challenge of measuring the MDMs of baryons with heavy flavoured quarks is to use the strong effective magnetic field inside the channels of a bent crystal instead of the conventional magnetic field to precess the polarisation vector and measure the MDM. The detailed precession theory has been developed by [41,42,43,44,45].
Shortly, in a curved crystal the electrostatic field of the atomic planes deflecting the particle transforms into a magnetic field in the particle’s rest frame. Thus the spin precession angle \(\phi \) is
where \(\gamma \) is the Lorentz factor, g is the g-factor or dimensionless MDM of baryon, and \(\omega \) is the deflection angle of the channelled particle. From a measurement of \(\gamma \), \(\phi \) and \(\omega \) of the channeled particles, we can determine g and hence the particle’s MDM. We expect that channeling can provide the equivalent magnetic fields up to several hundreds of Tesla, thus offering the potential of significant precession angles even when the length of the bent crystal is of order of cm.
\(\varLambda _c\) initial polarisation as a function of transverse momentum (red curves) on top of its distribution over transverse momentum (histograms). Red solid curve – theoretical prediction [51], red crosses – experimental data [52], red dashed curve – experimental data fit by Eq. (23); blue histogram (left plot) – distribution over transverse momentum of all \(\varLambda _c\) produced in a fixed target by \(6.5\,\)TeV protons, histograms (right plot) – same for specific energies of \(\varLambda _c\) indicated on the right. Here the polarisation is projected on the \(\mathbf {p}_{\varLambda _c}\times \mathbf {p}_\mathrm{beam}\) direction
Selection of \(\varLambda _c\) initial polarisation by the crystal, and spin precession in a bent crystal (for the case \(\phi =\pi /2\)). (Middle) the distribution of the \(\varLambda _c\) polarisation in the phase space \(\vartheta _x\vartheta _y\), here \(\vartheta =\sqrt{\vartheta _x^2+\vartheta _y^2}\) is the angle between the proton and the \(\varLambda _c\) momenta. Red arrows show the \(\varLambda _c\) polarisation. The distribution is symmetric with respect to the direction of proton momentum. The blue rectangular areas close to \(\vartheta _y\) axis and at the bottom of the plot show the phase spaces of initially captured and deflected \(\varLambda _c\) baryons, respectively. The layout of the target-crystal setup (left) in the yz plane and (right) in the zx plane
E761 Collaboration (1992) demonstrated the feasibility of this idea by measuring the MDM of the strange \(\varSigma ^+\) baryon [46, 47] using the decay into p\(\pi ^0\).
Recently a few papers have appeared [31, 32] proposing experiments to measure the MDM of the \(\varLambda _c\) and other charmed charged baryons at LHC top energies. In [48] the method for measuring the electromagnetic dipole moments of the \(\tau \) lepton using double or triple crystal setups at LHC was proposed. The clear advantages of the use of LHC are the much larger boost and the possibility of using well-known detectors. The unavoidable drawback is the complex integration of the crystals into the LHC vacuum pipe in the respect of the machine protection requirements. However, the recent success of crystal-collimation tests of the UA9 Collaboration [49, 50], may provide the necessary technical know-how for such a complex task.
The experiment foresees the installation of a bent crystal in the halo of the LHC to obtain an intense collimated proton beam. Polarised heavy baryons are produced by strong interaction of this proton beam impinging into a few mm (tungsten) target. A large angle bent crystal, located downstream of the target will induce the rotation of the polarisation vector of the heavy baryons. The change of the polarisation is studied by performing an angular analysis of the decay products of the heavy baryons using either one of the LHC existing detectors or a dedicated new one.
Our goal is to measure the \(\varLambda _c\) magnetic moment at a few % level. As presented in [32], the sensitivity depends on two factors. The first is to have an experimental setup capable to collect enough statistic. This studies have been made in details using the LHCb detector [53]. In [54] two possible layouts of such a setup are reported, together with a thorough evaluation on their expected performance and impact on LHC operations. The second factor is to know precisely the initial polarisation of \(\varLambda _c\) and to use the most suitable \(\varLambda _c\) decay channels giving the greatest sensitivity to the polarisation measurements. Let us elaborate this second point and discuss on our strategy.
The sensitivity depends on the precision of \(\phi \) in Eq. (21), which represents the spin precession of \(\varLambda _c\), \(\mathrm{i.e.}\) the change of the polarisation. The polarisation of \(\varLambda _c\) can be measured, in general, by the angular distribution of its decay \(\varLambda _c\rightarrow BP\) (B is a baryon and P is pseudoscalar meson, namely pion or kaon)
where the \(\xi \) is the polarisation projection of \(\varLambda _c\), and the \(\theta \) is the angle between \(\varLambda _c\) polarisation axis and the final baryon direction \(\mathbf {n}_\mathrm{baryon}=\mathbf {p}_\mathrm{baryon}/|p_\mathrm{baryon}|\). The \(\alpha \) is called asymmetry parameter, which represents the forward–backward asymmetry of the final state baryon with respect to the initial \(\varLambda _c\) polarisation direction. This asymmetry is non-zero only when the decay is induced by a parity violating interaction.
4.1 Initial polarisation
The experimental data [52, 55] together with theoretical predictions [51, 56, 57] show that \(\varLambda _c\) baryons produced in a fixed target are polarised, the polarisation vector is orthogonal to production plane, directed opposite to \(\mathbf {p}_\mathrm{beam}\times \mathbf {p}_{\varLambda _c}\), and the absolute value of polarisation grows with transverse momentum (see Fig. 1). In [32] the analysis of these data together with \(\varLambda _c\) spectra angular distribution obtained from Pythia [58] shows that the average absolute value of polarisation of \(\varLambda _c\) produced in the fixed target is \(|\xi |=0.40(5)\). In the current paper we would like to estimate initial polarisation more accurately.
We extrapolate experimental data with the following expression for polarisation as a function of transverse momentum:
where \(\langle p_\mathrm{t}^2\rangle =1.26(20)\,\mathrm{GeV}^2\) is the square of the typical transverse momentum of produced \(\varLambda _c\) baryons.
The distribution over transverse momentum of \(\varLambda _c\) produced in a fixed target by \(6.5\,\)TeV protons is obtained using Pythia v.8.240 accounting all soft QCD processes. Using this data we obtain the root mean square of initial polarisation \(\xi ^\mathrm{rms}=0.46(6)\). We assume that polarisation is a function of transverse momentum and does not depend on \(\varLambda _c\) energy. On the other hand, the distribution over the transverse momentum varies with \(\varLambda _c\) energy (see Fig. 1, right). Thus, the average polarisation depends on the energy: \(\xi ^\mathrm{rms}\approx 0.50(6)\) for \(\varLambda _c\) energy \(\varepsilon =50\,\)GeV, and \(\xi ^\mathrm{rms}\approx 0.34(6)\) for \(\varepsilon =4\,\)TeV.
Same as in Fig. 2. The areas highlighted with red and green show the phase spaces of \(\varLambda _c\) baryons with spin precession in crystal caused mainly by MDM and EDM, respectively
We propose to place a crystal immediately after the target, to deflect as many \(\varLambda _c\) baryons as possible before they decay (see Fig. 2, left and right). Note that the crystal selects by channeling only a small fraction of produced baryons, that have a small angle with respect to the crystallographic plane, \(\vartheta _x\in (\vartheta _\mathrm{crys}-\vartheta _\mathrm{acc}, \vartheta _\mathrm{crys}+\vartheta _\mathrm{acc})\). Here \(\vartheta _\mathrm{acc}\) is the acceptance angle to channeling [32, 59], the axis Oz is chosen in the direction of impinging protons, the axis Oy lies in the crystal plane, the initial direction of crystal plane normal is shifted from Ox by a small angle \(\vartheta _\mathrm{crys}\) around Oy axis, and the crystal is bent around the Oy direction (see Fig. 2).
For the MDM measurement the optimal orientation is when the crystallographic plane is aligned with the impinging proton beam (\(\vartheta _\mathrm{crys}=0\)), as in this case the x-component of polarisation, \(\mathrm{i.e.}\) orthogonal to spin precession axis, is maximal. Note that with this orientation \(\varLambda _c\) initial polarisation is almost parallel to the \(\mathbf {n}_x\) axis, with two fractions that are positively or negatively polarised and can be separated experimentally by reconstructing \(\vartheta _y\) (see Fig. 3 left). This feature was used to cancel the systematic uncertainty connected with the acceptance of the apparatus in Fermilab experiment E761 [47].
In the current study we considered two setup configurations proposed in [54], that are (IR3) at momentum cleaning area of LHC and (IR8) in front of interaction point at the LHCb detector. In both cases the target and the crystal materials are tungsten and silicon, respectively, and the target length is \(5\,\)mm. The other parameters of the setup are presented in Table 1.
Root mean square of initial polarisation projection of \(\varLambda _c\) deflected by the crystal (\(\xi _x\) and \(\xi _y\) – projections on axes Ox and Oy, respectively) and \(N_\mathrm{defl}\) – the integral number of deflected \(\varLambda _c\) baryons after 10 hour LHC fill as functions of initial crystal orientation \(\vartheta _\mathrm{crys}\). (Left) and (right) for configurations at IR3 and IR8, respectively
As the \(\varLambda _c\) production is a rare event, it is important to avoid channeling of initial protons, \(\mathrm{i.e.}\) ones that pass through the target with negligible interaction. In the case of experiment at the extraction line this can be done by slight (\(\vartheta _\mathrm{crys}=100\)–\(200\, \mu \)rad) misalignment of the crystal. As we show latter, this misalignment would have no effect on the measurement efficiency (see Fig. 5). For the circulating machine the risk of accidental deflection of the initial protons to the beam pipe is not tolerable, so the bending radius of the crystal is chosen in order to avoid channeling at the top energy [54].
The \(\varLambda _c\) electric dipole moment (EDM) can be obtained by measuring the spin precession caused by interaction of particle EDM with the electric field of crystal planes [60]. For this measurement the initial polarisation should have considerable component perpendicular to crystal electric field [61], \(\mathrm{i.e.}\) y-component. Note that to achieve this condition the crystal should be rotated by a small angle \(\vartheta _\mathrm{crys}\) around Oy axis, as shown in Fig. 3, but not by \(90^\circ \) around Oz axis. Here we present a simplified scheme just to demonstrate the main direction of spin precession caused by interaction of \(\varLambda _c\) MDM and EDM with electric field of bent crystal. One can see that by orienting the crystal with respect to the initial proton beam we can select deflected \(\varLambda _c\) baryons with a certain (parallel or perpendicular to crystallographic plane) initial polarisation.
Thus there are three possible initial crystal orientations optimised for MDM, EDM and simultaneous measurement, presented in Fig. 3 left, centre and right, respectively. The phase space in the blue rectangles at the bottom represent the deflected \(\varLambda _c\) baryons. To simplify the picture we suppose that the precession angle is \(\pi /2\) and the final polarisation has only z-component. We consider this in more details in the following section. In [32] it was shown that it should be easy to separate experimentally deflected \(\varLambda _c\) baryons events since the deflection angle is greater than the typical production angle of the deflected part of \(\varLambda _c\) baryons. Note that it is also very important to reconstruct \(\vartheta _y\) especially for MDM measurement.
To calculate the average initial polarisation of deflected \(\varLambda _c\) baryons and to verify the optimal crystal orientation, we performed computer simulations of \(\varLambda _c\) propagation though a crystal using the approach described in [32, 62]. The integral number of \(\varLambda _c\) baryons deflected by the crystal within 10 h LHC fill can be written as
where \(N_\mathrm{PoT}\) is the integral number of protons on target that can be obtained during 10 hour LHC fill [54], and \(N_\mathrm{tar+crys}\) is the number of deflected \(\varLambda _c^+\) per proton (see Eq. (3.2) in [32]).
In Fig. 4 we present \(N_\mathrm{defl}\) as functions of initial crystal orientation \(\vartheta _\mathrm{crys}\) (blue curve), and on top of it the root mean square of initial polarisation of deflected \(\varLambda _c\). Red and green curves labeled \(\xi _x\) and \(\xi _y\) correspond to root mean squares of polarisation projections on axes Ox and Oy, respectively:
where \(\xi _x\) and \(\xi _y\) are the \(\varLambda _c\) initial polarisation projections.
4.2 Final polarisation
Precession efficiency (left) of MDM and (right) of EDM measurements as a function of crystal orientation \(\vartheta _\mathrm{crys}\). The same configurations as in Fig. 4
Due to the MDM, the spin precession takes place in the xz plane. We first choose the polarisation axis to be perpendicular to the production plane, \(\mathrm{i.e.}\)
In this case, supposing \(\vartheta _\mathrm{crys}=0\), we can write the polarisation of the \(\varLambda _c\) before going through the crystal by the absolute value of the polarisation:
Two signs correspond to two fractions of \(\varLambda _c\) baryons of positive and negative initial polarisations (see Fig. 3 left). After passing through the crystal, the \(\varLambda _c\) spin precesses in the plane perpendicular to the effective magnetic field \(\mathbf {B}\). As a result, the polarisation of \(\varLambda _c\) after the crystal is modified as:
If we choose another polarisation axis (let us call it \(\mathbf {n}_z\)), that is perpendicular to \(\mathbf {n}_x\) and to the effective magnetic field \(\mathbf {B}\) the polarisation after crystal is modified as
If we rotate the crystal by a small angle \(\vartheta _\mathrm{crys}\) around Oy axis, we would capture the fraction of \(\varLambda _c\) baryons polarised along Oy axis (see Fig. 3 centre) and hence the root mean square of y-component of initial polarisation \(\xi _y^\mathrm{rms}\) will appear (see Fig. 4). This would provide a better efficiency for the EDM measurement with respect to the setup considered in [60]. Indeed, using spin precession equation [63, 64] one can show that, if the particle possesses an EDM, its interaction with the average electric field of bent crystal will cause the spin precession around Ox axis. Assuming \(\gamma \gg 1\ \mathrm{and}\ g\approx 2\)
where \(\xi _y\) is the y-component of initial polarisation, \(\phi ^\prime \) is the precession angle around Ox axis, and f is a dimensionless EDM.
In case \(g\ne 2\), there might be a significant spin rotation around Oy which would be important to take into account. By taking a theoretical prediction of g-factor \(g=1.92\) and other parameters from the Table 1 and pluging them into Eq. (21), we get the values for spin rotation angle around Oy axis: \(8.5^\circ \) and \(16.3^\circ \) for configurations at IR3 and IR8, respectively. This can be translated to a 5–9\(\,\%\) correction to the Eqs. (26)–(29) due to interaction of precessions caused by MDM and EDM. Note that this effect can be mitigated by comparing two fractions of \(\varLambda _c\) with positive and negative \(\vartheta _y\).
4.3 MDM and EDM measurement accuracy
Analysing the angular distribution (22) and considering(21), (26)–(29) one can obtain the expressions for the uncertainty to the \(\varLambda _c\) baryon g-factor and dimensionless EDM:
where \(\alpha _j\), \(Br_j\) and \(\eta _j^\mathrm{det}\) are the weak decay parameter, the branching ratio and the detector efficiency for j decay channel, \(\eta _\mathrm{MDM}\) and \(\eta _\mathrm{EDM}\) are the efficiencies of crystal-target setup for MDM and EDM measurement, respectively,
First three terms depend only on the \(\varLambda _c\) decay channel and on the detector efficiency. Last two terms are defined mainly by channeling efficiency and properties of the accelerator. We call the product of these two parameters the precession efficiency. Its maximum corresponds to the optimal crystal configuration for the measurement.
Absolute error of g-factor (left) as a function of its expected value \(\overline{g}\), and (right) as a function of error on alpha parameter \(\varDelta \alpha \). (Left) for different numbers of registered events and (right) for various expected values of g-factor \(\overline{g}\), stated in the plot. Calculation results for IR3 configuration, considering \(\varLambda _c^+\rightarrow \varDelta ^{++}K^-\) decay channel, assuming \(\alpha =-0.67\)
The results of computer simulations show that for MDM measurement the optimal initial orientation of the crystal is \(|\vartheta _\mathrm{crys}|\le 0.15\,\)mrad and \(|\vartheta _\mathrm{crys}|\le 0.3\,\)mrad for configurations at IR3 and IR8, respectively; and for EDM measurement: \(\vartheta _\mathrm{crys}\approx 0.4\,\)mrad and \(\vartheta _\mathrm{crys}\approx 0.9\,\)mrad (see Fig. 5). The difference between last two angles is due to a softer spectra of deflected \(\varLambda _c\) baryons at IR8. The baryons with the same transverse momentum \(p_t\) (same polarisation \(\xi \)) but with smaller energy would have a greater production angle \(\vartheta \).
The precession efficiencies of MDM and EDM measurements at IR3 are \(\sim 5.3\) times better. This is because the setup at IR8 is limited by the properties of LHCb detector, whereas for IR3 the optimal parameters of the detector (acceptance angle, energy range, etc.) were obtained in order to maximise the double crystal efficiency. The obvious downside of the IR3 configuration is that it requires building a new detector, but on the other hand, as it would be dedicated to this measurement, the detecting efficiency of the particular events could be much better than at LHCb. The values of precession efficiencies and properties of deflected \(\varLambda _c\) baryons are listed in the Table 1.
Note that the \(\varLambda _c\) baryons with different directions of polarisation can be separated by reconstructing \(\vartheta _y\). \(\mathrm{E.g.}\) at \(\vartheta _y=0\) and \(\vartheta _x\ne 0\) polarisation has only y-component (see Fig. 2, middle), which makes it the optimal region for EDM measurement. At the same time, with the same crystal orientation \(\vartheta _\mathrm{crys}\) but with \(\vartheta _y\ge \vartheta _x\) the polarisation has also a considerable x-component which is essential for MDM measurement (see Fig. 3, left). Thus the measurement of MDM and EDM can be done at the same time with a small \(\sim 20\,\%\) drop of efficiency, with respect to the optimal one for each of them (see Fig. 5). In this case the crystal should be oriented at \(\vartheta _\mathrm{crys}=0.25\,\)mrad and \(\vartheta _\mathrm{crys}=0.6\,\)mrad for measurement at IR3 and IR8, respectively.
Absolute error of g-factor as a function of reconstructed events number \(N_j\) (left) for \(\varLambda _c^+\rightarrow \varLambda ^0\pi ^+\) and (right) for \(\varLambda _c^+\rightarrow \varDelta ^{++}K^-\) decay channels. Red curves labeled with \(\varDelta \alpha \) value are obtained using the pre-measured values of \(\alpha \,\xi _x^\mathrm{rms}\) factor, black line corresponds to the case when we measure \(\alpha \xi \) and g-factor simultaneously at current experiment. Calculation results for IR3 configuration. Margins represents the current uncertainly on a weak decay parameter value
Another very important parameter for reconstruction of final polarisation is the weak decay parameter. Below, we consider only the MDM measurement, but the approach can be extended also to the EDM measurement. In Fig. 6, we demonstrate the sensitivity of g-factor precision on the weak decay parameter uncertainty \(\varDelta \alpha \). One can see that the poor knowledge of \(\varDelta \alpha = 0.3\) essentially limits the precision of the MDM as it adds a significant systematical uncertainty.
On the other hand, this problem can be solved by measuring the \(\alpha \,\xi _x^\mathrm{rms}\) factor and the MDM at the same time. If we neglect EDM, the spin precession modifies the polarisation projection on both axes, \(\mathbf {n}_z\) and \(\mathbf {n}_x\), which can be measured independently [47],
where \(\cos \theta _x = \mathbf {n}_x\cdot \mathbf {n}_\mathrm{baryon}\) and \(\cos \theta _z = \mathbf {n}_z\cdot \mathbf {n}_\mathrm{baryon}\). Thus, we can have two observables: two angular coefficients,
that can provide both \(\alpha \,\xi _x^\mathrm{rms}\) and the \(\phi \) angle via
The uncertainty of g-factor in this case is
where \(N_j\) is the number of reconstructed events,
The expression in parentheses represents the increase of error on g-factor due to simultaneous measurement of \(\alpha \,\xi _x^\mathrm{rms}\). For \(|\overline{g}-2|/2=0.05\) this factor is about 1.4 and 1.6 for IR3 and IR8 configurations, respectively.
The Fig. 7 presents the evolution of uncertainty on the g-factor with number of reconstructed events, \(\mathrm{i.e.}\) when \(\varLambda _c\) baryon is deflected by a full bending angle of the crystal and then decays by a certain channel stated in the figure. Here we compare two cases: when g-factor is measured while the value \(\alpha \,\xi _x^\mathrm{rms}\) is taken from the another experiment (red curves labeled with \(\varDelta \alpha \) values) and when g-factor and \(\alpha \,\xi _x^\mathrm{rms}\) are measured simultaneously (black curves). Each point in the red curves is calculated using the method described in the Appendix B with the Gaussian distributions for the input parameters \(\alpha _j\), \(\xi \) and \(\gamma \). For the bold solid red curve the central values and standard deviations of the input parameters are taken from the Table 1 and Table 2, the energy resolution \(\varDelta \gamma \) is taken \(100\,\mathrm{GeV}/m_{\varLambda _c}\) and the expected value \(|\overline{g}-2|/2=0.05\). The margins of the solid curve are calculated in the same way, but the central values for \(\alpha \) and \(\xi \) distributions were taken \(\alpha \pm \varDelta \alpha \) and \(\xi \pm \varDelta \xi \), respectively. In Fig. 7 the curves labeled \(\varDelta \alpha =0.15\) and \(\varDelta \alpha =0.30\) correspond to the current knowledge of weak decay parameters of corresponding decays. To motivate the new measurements of \(\alpha \) parameters we plot the dashed curve labeled \(\varDelta \alpha =0.05\). The only difference between the dashed and solid red curves is the uncertainty of weak-decay parameter \(\varDelta \alpha \). The black curves are calculated in the analogous way but the fixed values of \(\alpha \) and \(\xi \) were taken instead of the distributions over these parameters.
One can see that using the external value of \(\alpha \,\xi _x^\mathrm{rms}\) improves the precision to g-factor while \(\varDelta g\gtrsim 0.1\), or at low statistics (\(10^3\)–\(10^4\) events), and after collecting more data the systematical error from \(\varDelta \alpha \) becomes dominant and it is more efficient to measure two factors at the same time.
The other potential source of systematic error is expected from \(\varLambda _c\) energy reconstruction. Our calculations show that this impact is quite small, \(\mathrm{e.g.}\) even for the energy error as big as \(\varDelta \varepsilon =100\,\)GeV we start to see the effect on \(\varDelta g\) only after \(10^5\) events (see the bend of black curves in Fig. 7). With respect to that, the ionisation energy losses of \(\varLambda _c\) in the target and crystal are negligible. Indeed, according to [65], the mean energy loss rate of relativistic charged particles in tungsten is \(<2\,\)MeV cm\(^2\)g\(^{-1}\) and in silicon or germanium \(<2.4\,\)MeV cm\(^2\)g\(^{-1}\). Thus, even for 4 cm tungsten target and 8 cm silicon or germanium crystal energy losses would be less than 160, 50 or 100 MeV, respectively. In addition, the energy losses of channeled particles are smaller comparing to their losses in the amorphous matter [59].
The multiple scattering of \(\varLambda _c\) in the target leads to a small deflection of the baryon (20–200\(\,\mu \)rad). This angle is much smaller than the crystal bending angle, so its contribution to the spin precession of \(\varLambda _c\) is negligible. At the same time, the deflection in the target affects the distribution of initial polarisation of \(\varLambda _c\) captured and deflected by the crystal. As a reference scale it is convenient to use the characteristic angular width of the \(\varLambda _c\) production \(\gamma ^{-1}\). In a relativistic case, the ratio of multiple scattering angle [65] to \(\gamma ^{-1}\) is
where \(x/X_0\) is the thickness of the scattering medium in radiation lengths. Thus, even for a very thick (\(4\,\)cm) tungsten target this ratio is \(\sim 1\,\%\), i.e. smaller than the uncertainty of polarisation \(\sim 15\,\%\) (see Fig. 1 left, horizontal error bars with respect to \(m_{\varLambda _c}\)).
Absolute statistical error of g-factor as a function of number of fills (left) for IR3 and (right) for IR8 configurations. Black curves for \(5\,\)mm tungsten target attached to silicon crystal, red curves for \(40\,\)mm tungsten target attached to germanium crystal. Margins represents the current uncertainly of the weak decay parameters and the initial polarisation
In any case it is very important to know \(\alpha \,\xi _x^\mathrm{rms}\) as the current precisions for \(\varLambda _c\rightarrow p\ \bar{K}^*\) and \(\varLambda _c\rightarrow \varDelta (1232)K\) channels give almost one order of magnitude uncertainty on data taking time needed to reach a certain \(\varDelta g\). The factor \(\alpha \,\xi _x^\mathrm{rms}\) could be pre-measured if we can have exactly the same setup for the \(\varLambda _c\) production: using the fixed-target data sample collected at the LHCb experiment with the SMOG system [66] might be an interesting possibility. On the other hand, to reach a higher precision, we may need to obtain this factor from other experiments, such as LHCb which has a much higher statistics. As the \(\alpha \) value is the same in any environment, this can be measured precisely by LHCb. Per contra, the \(\xi _x^\mathrm{rms}\) value depends on \(p_\mathrm{t}\) and \(\varLambda _c\) energy \(\varepsilon \), so we need a theoretical extrapolation, which leads to some uncertainties. In any case, if we use the LHCb data, the \(\alpha \) parameters should be reconstructed separately.
We discuss how we can achieve that in the next section, considering two decay processes,
The first decay is intermediated by the \(\varLambda _c\rightarrow \varLambda \pi \) whose \(\alpha \) value has been measured as \(\alpha = 0.91 \pm 0.15 \).
The second decay is more complex since there are three intermediate channels,
which introduce three different \(\theta \) angles (c.f. \(\theta \) is defined by the direction of these intermediate baryons). Despite of this complexity, the second decay may be able to determine MDM more precisely since it has a larger branching ratio compared to the first one, which occurs via successive weak decays.
Another drawback of the first decay is the presence of relatively long-living \(\varLambda ^0\) baryon in the intermediate state, that significantly reduces the detecting efficiency at LHCb detector (by about 47 times, according to [53]). At IR3 this problem could be partially solved by building a longer detector, but as the average energy of deflected \(\varLambda _c\) baryons is twice greater with respect to IR8, we do not expect the gain of more than 5 times with respect to IR8.
In Table 2 we list the properties of the most useful \(\varLambda _c\) decay channels in terms of polarisation reconstruction together with their detection efficiencies. Using these values in Eq. (30) we obtain the weights of these channels at MDM reconstruction (see Table 2 last column). One can see that about \(95\,\%\) of information for MDM reconstruction comes from the first two channels: \(\varLambda _c\rightarrow p \bar{K}^*(892)\) and \(\varLambda _c \rightarrow \varDelta (1232) K\).
Finally, in Fig. 8 we present the absolute statistical error of the g-factor as a function of number of 10 h LHC fills. Two vertical lines correspond to 1 and 10 years of data taking based on LHC 2018 operation, for the consistency with [54]. Due to a poor current knowledge of weak decay parameters and polarisation, the spread in resulting values of the data taking time needed to reach the same \(\varDelta g\) with a probability of \(68\,\%\) (within 1 standard deviation), is from \(\sim 1\,\)year to \(\sim 10\,\)years. The central values of \(\varDelta g\) for this time stamps are listed in the Table 3.
Our calculations show that in order to reach the error on g-factor at a few percents, the target length should be enlarged at least to \(40\,\)mm and the silicon crystal should be replaced with germanium, like it was suggested in [32]. The length and the bending radius of germanium crystal for IR3 were chosen \(7\,\)cm and \(10\,\)m to avoid channeling of impinging protons, and for IR8 (\(3.3\,\)cm and \(5\,\)m) were taken from [53]. Going from 5 to \(40\,\)mm target and switching to germanium reduces the data taking time by factors 6 and 2.4, respectively. Further enlargement of the target should not essentially increase the efficiency because of the decay of \(\varLambda _c\) and the shower productions inside of the target.
Using a dedicated detector in IR3 would give an additional reduction of data taking time by a factor of about 7.5 with respect to measurement at LHCb detector.
With the optimal orientation for EDM measurement obtained in this paper the error on dimensionless EDM \(\varDelta f\) is about \(22\,\%\) greater than \(\varDelta g\). Thus the EDM of \(\varLambda _c\) baryon could be measured with an error \(\sim 2.6\,\times \,10^{-16}\,e\,\)cmFootnote 3 using \(40\,\)mm tungsten target and germanium crystal after 10 years of data taking at IR8 or less than 2 years at IR3. Note that in [53] the estimation of error on EDM is two orders of magnitude lower, but there the expected number of protons on target is 1400 greater, the estimated initial polarisation is 2.3 times greater and g-factor value is 1.4 whereas we consider more conservative prediction \(g=1.92\). Considering all this, the method proposed in [53] is \(\sim 13\) times less efficient by precision or requires \(\sim 170\) times longer data taking time to reach the same precision, and also depends on the value of g-factor.
5 Improving the precision on weak asymmetry parameters of charmed baryons at LHCb
Equation (22) shows that in the decay \(\varLambda _c \rightarrow B \, P\), the \(\varLambda _c\) polarisation \(\xi \) can not be measured separately from the parameter \(\alpha \). This problem can be solved if there are more observables (than just \(\cos \theta \) dependence), which provides independent information allowing to fit both \(\alpha \) and \(\xi \). In the following we introduce two such examples.
5.1 The case of \(\varLambda _c \rightarrow \varLambda \pi \) followed by \({\varLambda } \rightarrow p \pi \)
Let us start with computing the first decay chain,
The parity violating interaction is induced by a weak interaction in the form
where \(p_{\varLambda _c}\) (\(p_{\varLambda }\)) is the 4-momentum, and the constants A and B represent parity conserving and violating contributions, respectively. The helicity \(\lambda _{\varLambda _c}\) (\(\lambda _{\varLambda }\)) is the projection of the baryon spin in its momentum direction.
We next consider the subsequent decay,
The transition amplitude can be written similarly to the \(\varLambda _c\) decay:
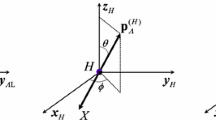
To describe the cascade decay \(\varLambda _c^+\rightarrow \varLambda \, \pi ^+\rightarrow p \, \pi ^- \, \pi ^+\) of the polarised \(\varLambda _c^+\) we choose the rest frame of \(\varLambda _c^+\). In this frame the momentum of \(\varLambda \) is directed along the Oz axis, and we assume that the polarisation vector \(\mathbf {\xi }_{\varLambda _c}\) lies in the xz plane with positive x-component (see Fig. 9). \(\theta _\varLambda \) is the angle between \(\mathbf {\xi }_{\varLambda _c}\) and \(\varLambda \) momentum. The polar angle \(\theta _p\) is defined in the rest frame of \(\varLambda \) baryon, and it is the angle between the proton momentum and the Oz axis. The azimuthal angle \(\phi _p\) is the angle between the decay plane \(\varLambda \rightarrow p \pi ^-\) and xz plane.
The differential decay rate for \(\varLambda _c^+\rightarrow \varLambda \pi ^+\rightarrow p\pi ^-\pi ^+\) in this frame can be written as
Here
is the full angular distribution of this decay, \(\xi _{\varLambda _c}=|\mathbf {\xi }_{\varLambda _c}|\) and decay parameters for \(\varLambda _c^+\rightarrow \varLambda \,\pi ^+ \) and \(\varLambda \rightarrow p \,\pi ^- \) are defined as
Here
where \(A_{\lambda \, 0 }\) (\(a_{\lambda \, 0 }\)) are helicity amplitudes for the decay \(\varLambda _c^+\rightarrow \varLambda \pi ^+\) (\(\varLambda \rightarrow p \pi ^-\)), and \(A_S\) (\(a_S\)) and \(A_P\) (\(a_P\)) are the S- and P-wave amplitudes. In addition
The parameters \(\alpha _{\varLambda _c}\), \(\beta _{\varLambda _c}\), and \(\gamma _{\varLambda _c}\) satisfy
It is useful to introduce additional parameter \(\Phi _{\varLambda _c}\)
Note that a formula similar to Eqs. (40), (41) for differential decay rate was written in Ref. [69], however the corresponding equation (20) in [69] has inaccuracies or misprints.
Having a sufficient number of events of the decay \(\varLambda _c^+\rightarrow \varLambda \,\pi ^+ \rightarrow p \,\pi ^- \, \pi ^+\), and knowing the parameter \(\alpha _\varLambda = 0.642\pm 0.013\) [65], one can use Eq. (41) for estimation of the decay parameters \(\alpha _{\varLambda _c}\), \(\beta _{\varLambda _c}\), \(\gamma _{\varLambda _c}\) and \(\varLambda _c^+\) polarisation using, for example, the method of maximum likelihood.
From the general three-dimensional angular distribution, Eq. (41), one can obtain simpler distributions. For example, by integrating Eq. (41) over the azimuthal angle, we get the two-dimensional distribution
This equation does not include parameters \(\beta _{\varLambda _c}\) and \(\gamma _{\varLambda _c}\) and its analysis allows one to extract the asymmetry \(\alpha _{\varLambda _c}\) and \(\varLambda _c^+\) polarisation \(\xi _{\varLambda _c}\).
If the number of events of \(\varLambda _c^+\rightarrow \varLambda \,\pi ^+ \rightarrow p \,\pi ^- \, \pi ^+\) is not sufficient, then for extraction of the unknown parameters in Eq. (41) one can use one-dimensional angular distributions which are obtained by integration of (41) over two angles. In this way we obtain one-dimensional angular distributions in \(\cos \theta _\varLambda \), \(\cos \theta _p\) and \(\phi _p\),
The product \(\alpha _{\varLambda _c} \xi _{\varLambda _c}\) can be found from the distribution in Eq. (49) by measuring the forward–backward asymmetry of \(\varLambda \) baryon in the rest frame of \(\varLambda _c^+\)
where
The study of the distribution in Eq. (50) in the rest frame of baryon \(\varLambda \), with a known value of \(\alpha _{\varLambda }\), will allow one to measure the parameter \(\alpha _{\varLambda _c}\). Indeed,
where
As a result we can find the magnitude of \(\varLambda _c^+\) polarisation
In order to find the remaining parameters \(\beta _{\varLambda _c}\) and \(\gamma _{\varLambda _c}\) one can apply the angular distribution Eq. (51) in the azimuthal angle \(\phi _p\) in the rest frame of \(\varLambda \). For example, by measuring the following asymmetries:
Then it follows from Eqs. (57) and (58) that
Therefore by studying one-dimensional angular distributions, the information on the \(\varLambda _c^+\) polarisation and parameters of the decay \(\varLambda _c^+\rightarrow \varLambda \,\pi ^+ \) can be obtained.
Another way of measuring the \(\varLambda _c^+\) polarisation in the decay \(\varLambda _c^+\rightarrow \varLambda \pi ^+\) is based on relation between polarisations of \(\varLambda _c^+\) and \(\varLambda \) (see, e.g., [65]):
where \(\mathbf {n}_\varLambda \) is a unit vector in the direction of the \(\varLambda \) hyperon, \(\mathbf {\xi }_{\varLambda _c}\) is polarisation of the \(\varLambda _c^+\) in the \(\varLambda _c^+\) rest frame. \(\mathbf {\xi }_{\varLambda }\) is the polarisation of the \(\varLambda \) hyperon in the \(\varLambda \) rest frame obtained by a Lorentz transformation along \(\mathbf {n}_\varLambda \) from the \(\varLambda _c^+\) baryon rest frame.
Note that if time-reversal invariance is valid and final-state interactions are ignored, then the parameter \(\beta _{\varLambda _c} =0\).
The spin direction of \(\varLambda \) baryon could be determined by measuring the decay asymmetry in the \(\varLambda \) rest frame through the relation
where \(\hat{\mathbf {p}}\) is a unit vector along the daughter-proton direction and \(\mathbf {\xi }_{\varLambda }\) is given by Eq.(60). If parameters \(\alpha _{\varLambda _c}\), \(\beta _{\varLambda _c}\), and \(\gamma _{\varLambda _c}\) are known, by projection of Eq. (60) on three orthogonal axes, one can find the components of the polarisation vector of \(\mathbf {\xi }_{\varLambda _c}\) for each event. Thus, in this way all the information about polarisation of \(\varLambda _c^+\) can be obtained from the decay of \(\varLambda \) baryon, without the need to refer to asymmetries or distributions in the rest frame of the \(\varLambda _c^+\). Note that methods based on relation between polarisation of parent baryon and daughter baryon have been applied in studies of hyperon decays (see, e.g., Refs. [70, 71]).
Then using the very well measured value of \(\alpha _\varLambda =0.642\pm 0.013\) [65] we could achieve to obtain \(\alpha _{\varLambda _c}\) and \(\xi _{\varLambda _c}\) separately, for example, using Eqs. (52) and (54). So far \(\alpha _{\varLambda _c}\) is measured with less precision, \(\alpha _{\varLambda _c}=-0.91\pm 0.15\) [65]. Measuring \(\alpha _{\varLambda _c}\) and \(\xi _{\varLambda _c}\) with much higher statistics data of LHCb will be very interesting in the future. In particular, in view of results of \(\varLambda _b\) polarisation measurement at LHCb [72], \(\xi _b = 0.06 \pm 0.07 \pm 0.02, \, \alpha _b=0.05 \pm 0.17 \pm 0.07\), and at CMS [73], \(\xi _b = 0.00 \pm 0.06 \pm 0.06, \, \alpha _b=0.14 \pm 0.14 \pm 0.10\), which show that \(\varLambda _b\) is little polarised, it is most important to measure the \(\varLambda _c\) polarisation. In the case of \(\varLambda _c\), the large value of \(\alpha _{\varLambda _c} \) would help to measure both \(\alpha _{\varLambda _c}\) and \(\xi _{\varLambda _c}\) at a much higher precision.
5.2 The case of \(\varLambda _c \rightarrow p \, K \, \pi \)
The use of the \(\varLambda _c \rightarrow p \, K \, \pi \) decays is also interesting because it has the largest branching fraction, \(6.23\pm 0.33\,\%\). E791 experiment [52] studied three main intermediate states:
In this analysis, this decay is parametrised by 4 (2) complex helicity amplitudes. Those are given as 8 (4) real parameters
Furthermore, the continuum background is modelled by the S-wave amplitude which introduce another 8 real parameters. Including the polarisation parameter \(\xi _{\varLambda _c}\) (denoted as \(\mathbf{P}\) in the paper [52]), a total of 25 parameters are fitted by using the full angular and Dalitz variables.
From the amplitude parameters, we can also obtain \(\alpha \) for each resonance
Note that we find a different value for \(\alpha _{K^*p}\) with respect to [60]. The higher values of \(\alpha _{K^*p}\) and \(\alpha _{\varDelta K}\) make the use of these channels interesting for polarisation studies, though the error is still too large to be able to conclude.
It would be interesting to repeat this analysis at LHCb, which has much higher rate of the \(\varLambda _c^+\) production. The crucial point of this measurement lies on the value of the polarisation of \(\varLambda _c^+\) produced at LHCb.
6 Conclusions
Recently a new experiment for measuring the magnetic moment of the \(\varLambda _c\) baryon using a bent crystal was proposed [32, 60]. Although the magnetic moment of charm quark is a fundamental property, which enters to various QCD computations, it has never been determined precisely. This experimental proposal can provide us its very first measurement.
The theoretical predictions of the magnetic moment of charmed baryons suffer from the hadronic uncertainties. These theoretical predictions are summarised in Sect. 1. We have introduced relations among magnetic moments of different charmed baryons, which could cancel the charm quark mass ambiguity. We have also related the \(\varLambda _c\) magnetic moment to the charm quark magnetic moment measurement by the radiative quarkonium decays, using angular distribution of successive decays
which were performed by the CLEO and the BESIII collaborations. Interestingly, we observed a slight tension: the obtained value is higher than most of the theoretical predictions of the \(\varLambda _c\) magnetic moment. Further improvement of quarkonium radiative decay is very important.
It was shown that when measuring the g-factor of \(\varLambda _c\) directly, \(\mathrm{i.e.}\) through spin precession, the knowledge of weak decay parameter \(\alpha \) and initial polarisation \(\xi \) could reduce the data taking time needed to reach the error of \(\varDelta g=0.1\). The \(\alpha \) parameter can be pre-measured in another experiment which has the same experimental setting (\(\mathrm{i.e.}\) \(p_\mathrm{t}\) and \(\xi \)), \(\mathrm{e.g.}\) using SMOG system, though the statistics are limited. Alternatively, we may use the very high statistic data of LHCb to extract separately \(\alpha \) and \(\xi \) values and we can extrapolate the \(\xi \) to the required \(p_\mathrm{t}\) range by using theory. The error on g-factor at a few percent level could be reached after reconstructing \(10^4\) decays of deflected \(\varLambda _c\) baryons, and in this case it is more efficient to measure g-factor and \(\alpha \,\xi \) simultaneously.
We estimated the error on g-factor using these two approaches and compared the measurement efficiencies at two places: at LHCb detector and at momentum cleaning area of LHC (IR3), proposed in [54]. The latter case requires building a new dedicated detector but it would need about 7.5 times less data taking time in order to reach the same precision.
We found a special orientation of the crystal that gives the opportunity to measure the \(\varLambda _c\) dimensionless electric dipole moment almost with the same precision as its g-factor. Our calculations show that this method is about 170 times more efficient in terms of data taking time with respect to the one proposed in [53].
The estimated error on g-factor after 10 years of data taking using the setup of \(40\,\)mm tungsten target and germanium crystal at LHCb and IR3 is \(\varDelta g=0.100\) and \(\varDelta g=0.037\), respectively. With a slight adjustment of the crystal orientation (rotating the crystal by a few milliradians) the \(\varLambda _c\) EDM could be measured with an error \(\varDelta d = 2.6 \times 10^{-16} e\,\)cm at LHCb and \(\varDelta d = 1.0 \times 10^{-16} e\,\)cm at IR3.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This manuscript does not presents any new experimental data.]
References
B.C. Odom et al., Phys. Rev. Lett. 97, 030801 (2006). [Erratum: Phys. Rev. Lett.99,039902(2007)]
Muon g-2, G.W. Bennett et al., Phys. Rev. D 73 (2006) 072003, arXiv:hep-ex/0602035
T. Aoyama et al., Phys. Rev. Lett. 109, 111808 (2012). arXiv:1205.5370
F. Jegerlehner, A. Nyffeler, Phys. Rept. 477, 1 (2009). arXiv:0902.3360
M. Davier et al., Eur. Phys. J. C77, 827 (2017). arXiv:1706.09436
I.B. Logashenko, S.I. Eidelman, Phys. Usp. 61, 480 (2018)
A. Keshavarzi, D. Nomura, T. Teubner, Phys. Rev. D 97, 114025 (2018). arXiv:1802.02995
G. Schneider et al., Science 358, 1081 (2017)
M.B. Wise, Phys. Rev. D 45, R2188 (1992)
G. Burdman, J.F. Donoghue, Phys. Lett. B 280, 287 (1992)
T.M. Yan et al., Phys. Rev. D 46, 1148 (1992). [Erratum: Phys. Rev.D55,5851(1997)]
P.L. Cho, Phys. Lett. B 285, 145 (1992). arXiv:hep-ph/9203225
P.L. Cho, H. Georgi, Phys. Lett. B 296, 408 (1992). arXiv:hep-ph/9209239, [Erratum: Phys. Lett. B300, 410 (1993)]
P.L. Cho, Phys. Rev. D 50, 3295 (1994). arXiv:hep-ph/9401276
J. Franklin et al., Phys. Rev. D 24, 2910 (1981)
N. Barik, M. Das, Phys. Rev. D 28, 2823 (1983)
M.J. Savage, Phys. Lett. B 326, 303 (1994). arXiv:hep-ph/9401345
B. Silvestre-Brac, Few Body Syst. 20, 1 (1996)
T.M. Aliev, A. Ozpineci, M. Savci, Phys. Rev. D 65, 056008 (2002). arXiv:hep-ph/0107196
B. Julia-Diaz, D.O. Riska, Nucl. Phys. A 739, 69 (2004). arXiv:hep-ph/0401096
S. Kumar, R. Dhir, R.C. Verma, J. Phys. G 31, 141 (2005)
A. Faessler et al., Phys. Rev. D 73, 094013 (2006). arXiv:hep-ph/0602193
M. Karliner, H.J. Lipkin, Phys. Lett. B 660, 539 (2008). arXiv:hep-ph/0611306
A. Majethiya, B. Patel, P.C. Vinodkumar, Eur. Phys. J. A 38, 307 (2008). arXiv:0805.3439
B. Patel, A.K. Rai, P.C. Vinodkumar, J. Phys. G 35, 065001 (2008). arXiv:0710.3828
B. Patel, A.K. Rai, P.C. Vinodkumar, J. Phys. Conf. Ser. 110, 122010 (2008)
N. Sharma et al., Phys. Rev. D 81, 073001 (2010). arXiv:1003.4338
A. Bernotas, V. Simonis, Lith. J. Phys. Tech. Sci. 53, 84 (2013)
S.L. Zhu, W.Y.P. Hwang, Z.S. Yang, Phys. Rev. D 56, 7273 (1997). arXiv:hep-ph/9708411
G.J. Wang et al., Phys. Rev. D 98, 054026 (2018). arXiv:1803.00229
V.G. Baryshevsky, Phys. Lett. B 757, 426 (2016)
A.S. Fomin et al., JHEP 08, 120 (2017). arXiv:1705.03382
CLEO, M. Artuso et al., Phys. Rev. D, 80 112003 (2009). arXiv:0910.0046
M. Ablikim et al., Phys. Rev. D 95, 072004 (2017). arXiv:1701.01197
G. Karl, S. Meshkov, J.L. Rosner, Phys. Rev. D 13, 1203 (1976)
G. Karl, S. Meshkov, J.L. Rosner, Phys. Rev. Lett. 45, 215 (1980)
LHCb, R. Aaij et al., Phys. Rev. Lett. 119, 112001 (2017). arXiv:1707.01621
M.C. Banuls et al., Phys. Rev. D 61, 074007 (2000). arXiv:hep-ph/9905488
H.Y. Cheng, C.K. Chua, Phys. Rev. D 92, 074014 (2015). arXiv:1508.05653
W. Detmold, C.J.D. Lin, S. Meinel, Phys. Rev. D 85, 114508 (2012). arXiv:1203.3378
V. Baryshevsky, Sov. Tech. Phys. Lett. 5, 73 (1979)
V. Baryshevsky, Zh. Tekh. Fiz. 5, 182 (1979)
V. Lyuboshits, Sov. J. Nucl. Phys. 31, 509 (1980)
V. Lyuboshits, Yad. Fiz. 31, 986 (1980)
I. Kim, Nucl. Phys. B 229, 251 (1983)
E761, D. Chen et al., Phys. Rev. Lett. 69, 3286 (1992)
D. Chen, The Measurement of the Magnetic Moment of \(\Sigma ^{+}\) Using Channeling in Bent Crystals (SUNY, Albany, 1992). PhD thesis
A.S. Fomin et al., JHEP 03, 156 (2019). arXiv:1810.06699
W. Scandale et al., Phys. Lett. B 748, 451 (2015). [Erratum: Phys. Lett. B750, 666 (2015)]
W. Scandale et al., Phys. Lett. B 758, 129 (2016)
G.R. Goldstein, Hyperon physics symposium : Hyperon 99, September 27-29, 1999, Fermi National Accelerator Laboratory, Batavia, Illinois, pp. 132–136, 1999, arXiv:hep-ph/0001187
E791, E.M. Aitala et al., Phys. Lett. B 471 449, (2000). arXiv:hep-ex/9912003
E. Bagli et al., Eur. Phys. J. C 77, 828 (2017). arXiv:1708.08483
D. Mirarchi et al., (2019), arXiv:1906.08551
J.G. Korner, G. Kramer, J. Willrodt, Z. Phys. C 2, 117 (1979)
W.G.D. Dharmaratna, G.R. Goldstein, Phys. Rev. D 53, 1073 (1996)
G.R. Goldstein, (1999). arXiv:hep-ph/9907573
T. Sjostrand, S. Mrenna, P.Z. Skands, Comput. Phys. Commun. 178, 852 (2008). arXiv:0710.3820
J. Lindhard, Mat. Fys. Medd. Dan. Vid. Selsk. 34, 1 (1965)
F.J. Botella et al., Eur. Phys. J. C 77, 181 (2017). arXiv:1612.06769
V.G. Baryshevsky, Eur. Phys. J. C 79, 350 (2019)
A. Fomin, Multiple scattering effects on the dynamics and radiation of fast charged particles in crystals. Transients in the nuclear burning wave reactor., PhD thesis, Paris-Sud University: PHENIICS, Orsay, France, (2017)
V. Bargmann, L. Michel, V.L. Telegdi, Phys. Rev. Lett. 2, 435 (1959)
E.M. Metodiev, (2015), arXiv:1507.04440
Particle Data Group, M. Tanabashi et al., Phys. Rev. D 98 030001, (2018)
LHCb, R. Aaij et al., JINST 9 P12005, (2014). arXiv:1410.0149
F. Sala, JHEP 03, 061 (2014). arXiv:1312.2589
H. Gisbert, J. Ruiz Vidal, (2019), arXiv:1905.02513
J.G. Korner, H.W. Siebert, Ann. Rev. Nucl. Part. Sci. 41, 511 (1991)
R. Handler et al., Phys. Rev. D 25, 639 (1982)
D. Aston et al., Phys. Rev. D 32, 2270 (1985)
LHCb, R. Aaij et al., Phys. Lett. B 724 27, (2013). arXiv:1302.5578
CMS, A.M. Sirunyan et al., Phys. Rev. D 97, 072010 (2018). arXiv:1802.04867
V. Simonis, (2018), arXiv:1803.01809
Acknowledgements
This research was partially conducted in the scope of the IDEATE International Associated Laboratory (LIA). A.Yu.K., V.A.K. and A.S.F. acknowledge partial support by the National Academy of Sciences of Ukraine via the program “Support for the development of priority areas of scientific research” (6541230).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Quark model relations
In this Appendix we summarise expressions for the magnetic dipole moments (MDM) of the single and double charmed baryons in non-relativistic constituent quark model. Only baryons with \(J^P=\frac{1}{2}^+\) are considered here. Some properties of these baryons are shown in Table 4. For a review of the charm baryons see Ref. [69].
In the 2nd column of Table 4 the flavour wave functions of baryons are shown. To construct spin-flavour wave functions of the baryons with total spin \(J =\tfrac{1}{2}\) and its projection \(J_z = +\tfrac{1}{2}\) the flavour functions are to be combined with either antisymmetric spin function
or symmetric one
with respect to interchange of particles 1 and 2.
The magnetic dipole moment of baryon B is calculated from the definition
where \(\mu _i = \tfrac{g_i}{2} \tfrac{e Q_i}{2m_i} \) is the magnetic moment of the i-th quark.
Below we list wave functions of the baryons from \(SU(3)_f\) anti-triplet from Table 4:
Wave functions for the \(SU(3)_f\) sextet read
and
Finally, the double-charmed baryons from \(SU(3)_f\) triplet have wave functions
These wave functions are normalised to unity.
The magnetic moments of the charmed baryons are shown in Table 5.
Important modification included in Table 5 is the effect of mixing which was first addressed in [15] and studied in detail in Refs. [28, 74]. The mixing appears between the states \(\varXi _c^+\) and \(\varXi _c^{\prime +}\), and between the states \(\varXi _c^0\) and \(\varXi _c^{\prime 0}\). According to [28], the mixing is of little importance for the neutral baryons \(\varXi _c^0\) and \(\varXi _c^{\prime 0}\), while it is essential for the charged ones \(\varXi _c^+\) and \(\varXi _c^{\prime +}\). This is related to different magnitude of the transition operators in Table 5, namely \( \tfrac{1}{\sqrt{3}}|\mu _s - \mu _u| \gg \tfrac{1}{\sqrt{3}}|\mu _s - \mu _d|\). The transition magnetic moments between \(\varXi _c^+\) and \(\varXi _c^{\prime +}\), and between \(\varXi _c^0\) and \(\varXi _c^{\prime 0}\) are
and one also finds that \( |\mu _{\, \varXi _c^{\prime +} \rightarrow \varXi _c^{+}}| \gg |\mu _{\, \varXi _c^{\prime 0} \rightarrow \varXi _c^{0}}|\). The mixing for the baryons \(\varXi _c^+\) and \(\varXi _c^{\prime +}\) may complicate interpretation of \(\varXi _c^+\) MDM as being entirely due to the charm quark.
Appendix B: Taking into account the uncertainties of \(\alpha _j\), \(\xi \) and \(\gamma \)
By measuring the slopes of the angular distributions of \(\varLambda _c\) decay products (22) and considering (21), (26) and (27) one can obtain the following parameter (observable)
that has a Gaussian probability density function (PDF) with the standard deviation
and the central value
where \(\overline{\alpha }_j\), \(\overline{\xi }\) and \(\overline{\gamma }\) are the central values of \(\alpha _j\), \(\xi \) and \(\gamma \), and \(\overline{g}\) is the expected value of g-factor. Here we assumed that the expected value of precession angle \(\phi \) is small (see Table 1). From Eq. (68) one can express g-factor as a function of known parameters and the observable
The PDF of g-factor can be calculated as an integral of the delta function with PDFs of input parameters and the observable
and finally the uncertainty of g-factor can be estimated in the following way
where the values \(g_1\) and \(g_2\) correspond to the cumulative distribution function values \(N(g_1)=0.159\) and \(N(g_2)=0.841\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Fomin, A.S., Barsuk, S., Korchin, A.Y. et al. The prospect of charm quark magnetic moment determination. Eur. Phys. J. C 80, 358 (2020). https://doi.org/10.1140/epjc/s10052-020-7891-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-7891-0