Double parton scattering in pA collisions at the LHC revisited

Abstract

We consider the production of W-boson plus dijet, W-boson plus b-jets and same sign WW via double parton scattering (DPS) in pA collisions at the LHC and evaluate the corresponding cross sections. The impact of a novel DPS contribution pertinent to pA collisions is quantified. Exploiting the experimental capability of performing measurements differential in the impact parameter in pA collisions, we discuss a method to single out this novel DPS contribution. The method allows the subtraction of the leading twist (LT) single parton scattering background and it gives access in a very clean way to double parton distribution functions in the proton. We calculate leading twist and DPS cross sections and study the dependence of the observables on the cuts in the jets phase space. In the Wjj channel the observation of DPS is possible with data already accumulated in pA runs and the situation will greatly improve for the next high luminosity runs. For the $Wb{\bar{b}}$ final state, the statistics within the current data is too low, but there is possibility to observe DPS in this channel in future runs, albeit with much reduced sensitivity than in Wjj final state. Finally the DPS observation in the same sign WW channel will require either significant increase of integrated luminosity beyond that foreseen in next pA runs or improved methods for W reconstruction, along with its charge, in hadronic decay channels.

1 Introduction

The flux of incoming partons in hadron-induced reactions increases with the collision energy so that multiple parton interactions (MPI) take place, both in pp and pA collisions. The study of MPIs started in eighties in Tevatron era [1, 2], both experimentally and theoretically. Recently a significant progress was achieved in the study of MPI, in particular of double parton scattering (DPS). From the theoretical point of view a new self consistent pQCD based formalism was developed both for pp [3,4,5,6,7,8,9,10,11,12] and pA DPS collisions [13] (see [14] for recent reviews). From the experimental point of view, among many DPS measurements performed recently, the one in the W+dijet final state is of particular relevance for the present analysis. The corresponding cross section was measured in pp collisions both by ATLAS and CMS [15, 16]. Moreover recent observations of double open charm  [17,18,19,20] and same sign WW (ssWW) production [21] clearly show the existence of DPS interactions in pp collisions.

The MPI interactions play a major role in the Underlying Event (UE) and thus are taken into account in all MC generators developed for the LHC [22, 23]. On the other hand the study of DPS will lead to understanding of two parton correlations in the nucleon. In particular the DPS cross sections involve new non-perturbative two-body quantities, the so-called two particle Generalised Parton Distribution Functions ($_2$GPDs), which encode novel features of the non-perturbative nucleon structure. Such distributions have the potential to unveil two-parton correlations in the nucleon structure [24, 25] and to give access to information complementary to the one obtained from nucleon one-body distributions.

The study of MPI and in particular of the DPS reactions in pA collisions is important for our understanding of MPI in pp collisions and it constitutes a benchmark of the theoretical formalism available for these processes. On the other hand the MPI in pA collisions may play an important role in underlying event (UE) and high multiplicity events in pA collisions. Moreover it was argued in Ref. [13] that they are directly related to longitudinal parton correlations in the nucleon.

Fig. 1

Pictorial representation of DPS process in pA collisions via a DPS1 and b DPS2 mechanisms. The light grey blobs indicate nucleons, darker grey ones the nucleus and black ones the hard interactions

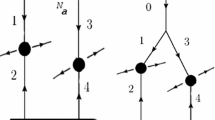
The theory of MPI and in particular DPS in pA collisions was first developed in [26], where it was shown that there are two DPS contributions at work in such a case. First, there is the so-called DPS1 contribution, depicted in the left panel of Fig. (1), in which two partons from the incoming nucleon interact with two partons in the target nucleon in the nucleus, making such a process formally identical to DPS in the pp collisions. Next there is a new type of contribution, depicted in the right panel of Fig. (1) and often called DPS2, in which two partons from the incoming nucleon interact with two partons each of them belonging to the distinct nucleons in the target nucleus located at the same impact parameter. Such a contribution is parametrically enhanced by a factor $A^{1/3}$ over the DPS1 contribution, A being the atomic number of the nucleus.

The basic challenge in observing and making precision studies of DPS both in pp and pA collisions is the tackling the large leading twist (LT), single parton scattering (SPS) background. This problem is especially acute in pA collisions where, due to several orders of magnitude lower luminosity relative to pp collisions, rare DPS cross sections will suffer serious deficit in statistics [27, 28].

Recently a new method was suggested [29] which could allow the observation of DPS2 in pA collisions. It was pointed out that the DPS2 has a different dependence on impact parameter than SPS and DPS1 contributions. Namely while the latter contributions are proportional to the nuclear thickness function T(B), B being the pA impact parameter, the DPS2 contribution is proportional to the square of T(B). Therefore the cross section producing a given final state can be schematically written as:

$$\begin{aligned} \frac{d^2\sigma _{pA}}{d^2B}= \Big (\sigma ^{LT}_{pA}+\sigma ^{DPS1}_{pA}\Big ) \frac{T(B)}{A} +\sigma _{pA}^{DPS2} \frac{T^2(B)}{\int d^2 B \, T^2(B)}\,, \nonumber \\ \end{aligned}$$

(1)

where T(B) is normalized to the atomic number A of the nucleus. This observation gives the possibility to distinguish the DPS2 contribution in pA collisions from both the LT SPS and DPS1 contributions that are instead linear in T(B). This approach was used in Ref. [29] to study two-dijets processes in pA collisions.

The purpose of the present paper is to investigate whether the latter approach can be used to observe the DPS2 process in pA collisions for the following final states, ordered by decreasing cross sections:

$$\begin{aligned} pA\rightarrow & {} W^\pm + dijets +X\,, \\ pA\rightarrow & {} W^\pm + b {\bar{b}}-jets +X\,, \\ pA\rightarrow & {} W^\pm + W^\pm +X\,. \end{aligned}$$

In all considered channels one electroweak boson ($W^\pm$) is produced in one of the scatterings, which then leptonically decays into muon and a neutrino. A second scattering in the same pA collision produces the remaining part of the final state ($jj,b{\bar{b}},W^\pm$). The first process, as it emerges from our simulations, has the advantage of higher statistics which could allow the characterization of the DPS cross section. The second one has been discussed in detail in Ref. [30] in pp collisions and, despite the lower rate, its study is relevant since DPS contribution is an important background to new physics searches with the same final state. The third one is a gold channel DPS reaction but suffer from very low cross sections [31,32,33].

In this paper we present the numerical estimates both for the DPS cross sections and for the background LT contributions, the impact of the latter driving the experimental capability to discover the DPS2 mechanisms in the current and in the future pA runs at the LHC.

We show that in the Wjj final state there is rather large number of events that allows to determine DPS2 already from data already recorded in pA runs in 2016 at the LHC. The situation will improve even more for the next runs for pA runs at LHC scheduled for 2024. For the $Wb{\bar{b}}$ final state the statistics is too low to determine DPS2 in the current run, but this may be possible in the future high luminosity runs, albeit with much reduced sensitivity than in Wjj final state. On the other hand, ssWW process suffers from a rather low statistics, even for the next runs. Nevertheless we expect we shall be able to observe it in the future runs if W reconstruction techniques will allow to establish the W charge from its hadronic decays.

The paper is organised as follows. In Sect. 2 we review the theoretical framework on which are based our calculations. In the following three Sections we present our results for each considered final state, Wjj, $Wb{\bar{b}}$ and ssWW, respectively, and discuss the corresponding results. Our findings are summarised in the conclusion.

2 Theoretical framework

The cross section for the production of final states C and D in pA collisions via double parton scattering can be written as the convolution of the double $_2$GPDs of the proton and the nucleus, $G_p$ and $G_A$, respectively [13, 26]:

$$\begin{aligned} \frac{d \sigma ^{CD}_{DPS} }{d\Omega _C d\Omega _D}= & {} \int \frac{d^2\vec \Delta }{(2\pi )^2}\frac{d {{\hat{\sigma }}}_{ik}^C(x_1, x_3)}{d\Omega _C}\frac{d {\hat{\sigma }}_{jl}^{D}(x_2,x_4)}{d\Omega _D}\nonumber \\&G_p^{ij}(x_1,x_2, \vec \Delta )G_A^{kl}(x_3,x_4, -\vec \Delta )\,. \end{aligned}$$

(2)

Two parton GPDs depend on the transverse momentum imbalance momentum $\vec \Delta$. The structure and relative weight of different contributions to the nuclei $_2GPD$ was studied in detail in Ref. [13], where it was shown that only two contributions survive: the one that corresponds to DPS1 mechanism and an other corresponding to DPS2.

Since our analysis will especially deal with impact parameter B dependence of the cross section, we find natural to rewrite Eq. (2) in coordinate space, introducing the double distributions $D_{p,A}$ which are the Fourier conjugated of $G_{p,A}$ with respect to $\vec \Delta$. In such a representation these distributions admit a probabilistic interpretation and represent the number density of parton pairs with longitudinal fractional momenta $x_1,x_2$, at a relative transverse distance ${\vec {b}_\perp }$, the latter being the Fourier conjugated to $\vec \Delta$.

In the impulse approximation for the nuclei, neglecting possible corrections to factorisation due to the shadowing for large nuclei, and taking into account that $R_A \gg R_p$ for heavy nuclei, we can rewrite the cross section as [13, 26]

$$\begin{aligned} \frac{d \sigma ^{CD}_{DPS}}{d\Omega _1 d\Omega _2}= & {} \frac{m}{2} \sum _{i,j,k,l} \sum _{N=p,n} \int d \vec {b}_\perp \int d^2 B \,\nonumber \\&\quad D^{ij}_{p}(x_1,x_2;\vec {b}_\perp ) D^{kl}_{N}(x_3,x_4;\vec {b}_\perp ) T_N(B) \frac{d {{\hat{\sigma }}}_{ik}^C}{d\Omega _C} \frac{d {{\hat{\sigma }}}_{jl}^D}{d\Omega _D}\,,\nonumber \\&+ \frac{m}{2} \sum _{i,j,k,l} \sum _{N_3, N_4=p,n} \int d \vec {b}_\perp D^{ij}_{p}(x_1,x_2;\vec {b}_\perp ) \nonumber \\&\quad \int d^2 B \, f^{k}_{N_3}(x_3) f^{l}_{N_4}(x_4) T_{N_3}(B) T_{N_4}(B) \frac{d {{\hat{\sigma }}}_{ik}^C}{d\Omega _C} \frac{d {{\hat{\sigma }}}_{jl}^D}{d\Omega _D}. \nonumber \\ \end{aligned}$$

(3)

Here $m=1$ if C and D are identical final states and $m=2$ otherwise, $i,j,k,l = \{q, {{\bar{q}}}, g \}$ are the parton species contributing to the final states C(D). In Eq. (3) and in the following, $d {\hat{\sigma }}$ indicates the partonic cross section for producing the final state C(D), differential in the relevant set of variables, $\Omega _C$ and $\Omega _D$, respectively. The functions $f^i$ appearing in Eq. (3) are single parton densities and the subscript N indicates nuclear parton distributions. The double parton distribution $D_N$ is the double GPD for the nucleon bound in the nuclei, once again calculated in the mean field approximation.

Partonic cross sections and parton densities do additionally depend on factorization and renormalization scales whose values are set to appropriate combination of the large scales occuring in final state C and D.

The nuclear thickness function $T_{p,n}(B)$, mentioned in the Introduction and appearing in Eq. (3), is obtained integrating the proton and neutron densities $\rho _0^{(p,n)}$ in the nucleus over the longitudinal component z

$$\begin{aligned} T_{p,n}(B)=\int dz \rho ^{(p,n)}(B,z)\,, \end{aligned}$$

(4)

where we have defined r, the distance of a given nucleon from nucleus center, in terms of the impact parameter B between the colliding proton and nucleus, $r=\sqrt{B^2+z^2}$. Following Ref. [34], for the ${}^{208} P_b$ nucleus, the density of proton and neutron is described by a Wood-Saxon distribution

$$\begin{aligned} \rho ^{(p,n)}(r)=\frac{\rho _0^{(p,n)}}{1+e^{(r-R_0^{(p,n)})/a_{(p,n)}}}\,. \end{aligned}$$

(5)

For the neutron density we use $R_0^n=6.7$ fm and $a_n=0.55$ fm [35]. For the proton density we use $R_0^p=6.68$ fm and $a_p=0.447$ fm [36]. The $\rho _0^{(p,n)}$ parameters are fixed by requiring that the proton and neutron density, integrated over all distance r, are normalized to the number of the protons and neutrons in the lead nucleus, respectively.

As already anticipated, the DPS1 contribution, the first term in Eq. (3), stands for the contribution already at work in pp collisions. It depends linearly on the nuclear thickness function T and therefore scales as the number of nucleon in the nucleus, A.

The second term, the DPS2 contribution, contains in principle two-body nuclear distributions. We work here in the impulse approximation, neglecting short range correlations in the nuclei since their contribution may change the results by several percent only [29]. The latter term is therefore proportional to the product of one-body nucleonic densities in the nucleus, i.e. it depends quadratically on T and parametrically scales as $A^{4/3}$.

As we already stated above we shall work here for simplicity in the mean field approximation for the nucleon. In such approximation double GPD has a factorized form:

$$\begin{aligned} D^{ij}_p(x_1,x_2,\mu _A,\mu _B,\vec {b}_\perp ) \simeq f^{i}_p (x_{1},\mu _{A}) f^{j}_p (x_{2},\mu _{B})\, {\mathcal {T}}(\vec {b}_\perp ),\nonumber \\ \end{aligned}$$

(6)

where the function ${\mathcal {T}}(\vec {b}_\perp )$ describes the probability to find two partons at a relative transverse distance $\vec b_\perp$ in the nucleon and is normalized to unity. In such a simple approximation, this function does not depend on parton flavour and fractional momenta. Then one may define the so-called effective cross section as

$$\begin{aligned} \sigma _{eff}^{-1} = \int d \vec {b}_\perp [{\mathcal {T}}(\vec {b}_\perp )]^2~, \end{aligned}$$

(7)

which controls the double parton interaction rate. Under all these approximations the DPS cross section in pA collision can be rewritten as

$$\begin{aligned} \frac{d \sigma ^{CD}_{DPS}}{d\Omega _1 d\Omega _2}= & {} \frac{m}{2} \sum _{i,j,k,l} \sum _{N=p,n} \sigma _{eff}^{-1} f^{i}_{p}(x_1) \nonumber \\&\times f^{j}_{p}(x_2) f^{k}_{N}(x_3) f^{l}_{N}(x_4) \frac{d {{\hat{\sigma }}}_{ik}^C}{d\Omega _C} \frac{d {{\hat{\sigma }}}_{jl}^D}{d\Omega _D} \int d^2 B \, T_N(B)\,,\nonumber \\&+ \frac{m}{2} \sum _{i,j,k,l} \sum _{N_3, N_4=p,n} f^{i}_{p}(x_1) f^{j}_{p}(x_2) f^{k}_{N_3}(x_3) \nonumber \\&\times f^{l}_{N_4}(x_4) \frac{d {{\hat{\sigma }}}_{ik}^C}{d\Omega _C} \frac{d {{\hat{\sigma }}}_{jl}^D}{d\Omega _D}\, \int d^2 B \, T_{N_3}(B) T_{N_4}(B)\,. \end{aligned}$$

(8)

We find important to remark the key observation that leads to the second term of Eq. (3): namely that the b and B integrals practically decouple since the nuclear density does not vary on subnuclear scale [13, 26, 37]. As a result this term depends on $_2$GPDs integrated over transverse distance $b_\perp$, i.e. at $\vec \Delta =0$, for which we assume again mean field approximation:

$$\begin{aligned} \int d \vec {b}_\perp D^{ij}_{p}(x_1,x_2;\vec {b}_\perp ) \simeq f^{i}_p (x_{1}) f^{j}_p (x_{2})\,. \end{aligned}$$

(9)

In the DPS1 term, deviations from the mean field approximation for $_2$GPDs are taken into account at least partially by using in our calculations the experimental value of $\sigma _{eff}$ measured in pp collisions. Additional corrections of order $10-20\%$ to Eq. (8) due to longitudinal correlations in the nucleon [13] and beyond mean field approximation will be neglected in the following. Note that after integration in $b_\perp$, this will be the only non-perturbative parameter characterising the DPS cross section. We shall neglect small possible dependence of $\sigma _{eff}$ on energy. Indeed while there is some dependence on energy in pQCD and mean field approach, it is at least partly compensated by non-perturbative contributions to $\sigma _{eff}$ [38].

In this last part of the Section we specify the kinematics and additional settings with which we evaluate Eq. (8). We consider proton lead collisions at a centre-of-mass energy $\sqrt{s_{pN}}$ = 8.16 TeV. Due to the different energies of the proton and lead beams ($E_p = 6.5$ TeV and $E_{Pb} = 2.56$ TeV per nucleon), the resulting proton-nucleon centre-of-mass is boosted with respect to the laboratory frame by $\Delta y = 1/2 \, \ln E_p/E_N$ = 0.465 in the proton direction, assumed to be at positive rapidity. Therefore the muon and jets rapidities, in this frame, are given by $y_{CM}=y_{lab}-\Delta y$. By assuming a rapidity coverage in the laboratory system $|y_{lab}|<2.4$, this bound translates into the range $-2.865<y_{CM}<1.935$. In all calculations, we have always considered proton-nucleon centre-of-mass rapidities.

The relevant partonic cross sections have been evaluated at leading order [39] in the respective coupling differential in muon and/or jets transverse momenta and rapidities in order to be able to implement realistic kinematical cuts used in experimental analyses. For cross sections involving jets, final state partons are identified as jets, as appropriate for a leading order calculation.

We use CTEQ6L1 free proton parton distributions  [40] and EPS09 nuclear parton distributions [43]. Consistently with the cross section calculations, both distributions and strong coupling constant have been evaluated at leading order. We have successfully benchmarked our codes against DYNNLO [41] and ALPGEN [42]. The latter has also been used to obtain leading order, parton level, estimates of the SPS Wjj and $Wb{\bar{b}}$ cross sections.

In order to determine the DPS2 contribution we shall use the strategy devised in Ref. [29] . The latter exploits the experimental capabilities to accurately relate centrality with the impact parameter B of the pA collision. The procedure for the determination of centrality in pA collisions was developed e.g. by ATLAS [46]. It makes use of the transverse energy $E_T$ deposited in the pseudorapidity interval $-3.2\ge \eta \ge -4.9$ (i.e. along the nucleus direction) as a measure of centrality. It was shown in Ref. [47] that $E_T$ in this kinematics is not sensitive to production of hadrons at forward rapidities. The $E_T$ distribution as a function of the number of collisions $\nu$ (and thus on the impact parameter B) is presented in Refs. [45,46,47] (see also the related discussion in Ref. [29]).

We close this Section discussing the uncertainties related to our theoretical predictions. As already stated, aside from uncertainties related to the mean field approximation for double PDFs, the DPS2 term is largely free of unknowns. On the contrary, the DPS1 contribution needs, as input, a value for $\sigma _{eff}$ whose value and the associated error we borrow from available experimental analyses and which we propagate to our theoretical predictions. Theoretical errors due to missing higher orders can be kept under control by using higher order calculations, which are known for all processes considered in the present paper and are available in the literature. Uncertainties related to PDFs and nuclear effects are by far subleading in the present context. Finally, when appropriate, we will show statistical errors on the predictions within a given luminosity scenario, assuming in such a case a Poissonian distribution.

3 Results : Wjj

3.1 Kinematics

In this Section we present results for the associated production of one electroweak boson in one of the scatterings, which then decays leptonically into a muon and a neutrino, and of a dijet system produced in the other. This process has been already analyzed in pp collisions at $\sqrt{s}=7\hbox { TeV}$ by ATLAS [15] and CMS [16] whose results constitute therefore a useful baseline for this analysis. For this channel we define the fiducial phase space in terms of muon transverse momentum and rapidity by requiring that $p_{T}^{\mu }>25$ GeV and $|y^{\mu }_{lab}|<2.4$. Additionally the missing transverse energy is required to satisfy . These sets of cuts are the same as those used in the analysis of Ref. [44]. The fiducial phase space for jets is defined by $p_{T}^{jets}>20$ GeV and $|y^{jets}_{lab}|<2.4$. As already mentioned, both ATLAS [15] and CMS [16] have measured the DPS contribution to the Wjj final state in pp collisions at $\sqrt{s}=7$ TeV and found $\sigma _{eff}$ to be:

$$\begin{aligned} \sigma _{eff}^{ATLAS}= & {} 15 \pm 3 \,(\text {stat.}) ^{+5} _{-3} \,(\text {syst.}) \,\text {mb}\,, \end{aligned}$$

(10)

$$\begin{aligned} \sigma _{eff}^{CMS}= & {} 20.7 \pm 0.8 \, (\text {stat.}) \pm 6.6 \,(\text {syst.}) \,\text {mb}\,. \end{aligned}$$

(11)

Table 1 Predictions for Wjj DPS and SPS cross sections in pA collisions in fiducial phase space, for different cuts on jets transverse momenta. These numbers refer to charged summed W cross sections accounting for the W boson decaying into muons as well as electrons. The quoted error is entirely due to the propagation of ${\bar{\sigma }}_{eff}$ uncertainty

Fig. 2

Wjj DPS cross section as a function of impact parameter B (left panel) and normalized to the nuclear thickness function $T_A(B)$ (right panel)

Fig. 3

Number of events in Wjj final state in bins of B assuming $\int {\mathcal {L}}dt=0.1 \text{ pb }^{-1}$ and for $p_T^j>30$ GeV (left). The ratio $R_W$ as a function of $T_A$ for different cuts on jet transverse momenta (right)

We combine these numbers into ${\bar{\sigma }}_{eff} = 18 \pm 6$ mb. Since we simulate pA collisions at $\sqrt{s_{pN}}=8.16\hbox { TeV}$, a centre-of-mass energy close to the energies at which those values of $\sigma _{eff}$ have been extracted, we use such an average in our numerical simulations for the Wjj and $Wb{\bar{b}}$ final states, neglecting any possible dependence of $\sigma _{eff}$ on energy. For the DPS contributions, the W cross section has been evaluated with factorization and renormalization scales fixed to the W boson mass, $\mu _F=\mu _R=M_W$, while for the dijet cross section to $\mu _F=\mu _R=\sqrt{p_{T,j1}^{2}+p_{T,j2}^{2}}$. The cross section for the SPS Wjj background was evaluated with ALPGEN [42] with the same selection cuts described above and $\mu _F=\mu _R=\sqrt{M_W^2+p_{T,j1}^{2}+p_{T,j2}^{2}}$.

3.2 DPS calculation results

We are now in position to discuss our results. First we are interested to quantify at the integrated level the DPS2 contribution to DPS in pA collisions, which, despite having been predicted theoretically [26], has not been yet observed experimentally.

For this purpose we first report in Table 1 the various contributions to the Wjj fiducial cross section. These numbers account for W charged summed cross sections considered in both the muon and electron decay channels. From the table it appears that the DPS2 contribution is more than two times larger with respect to DPS1 one.

With these numbers at our disposal we may use the strategy put forward in Ref. [29] to separate the DPS2 contribution.

We present in the left panel of Fig. (2) the various contributions to the Wjj cross section differential in impact parameter B for $p_T^j>30$ GeV. In the right panel of the same plot the same differential distribution is normalized to the nuclear thickness functions. With such a normalization, the DPS1 contribution will contribute a constant value to the cross section, as well as the SPS background, while DPS2 will show a B dependence driven by T(B). The DPS2 observation will essentially rely on the experimental ability to distinguish a non-constant behaviour of such a normalized distribution.

The efficiency of this discrimination method will depend on the accumulated integrated luminosity. Here we choose a value in line with data recorded in 2016 pA runs of $\int {\mathcal {L}} \text{ dt }= 0.1 \, \text{ pb }^{-1}$.

For this purpose we present in the left panel of Fig. (3) the number of events for the Wjj final state integrated in bins of B. The distribution presents a kinematic zero at $B=0$ due to the jacobian arising from Eq. (3) when the cross section is kept differential in B. On the same plot is also superimposed the uncertainty on the predictions coming from the propagation of the error on ${\bar{\sigma }}_{eff}$.

The method can be applied to subtract the overwhelming LT SPS contribution, or, at least to complement the subtraction techniques already developed in experimental analyses of DPS cross sections. For this purpose we consider the ratio $R_W$ between the total number (DPS+SPS) of Wjj events over those for inclusive W production as a function of $T_A(B)$:

$$\begin{aligned} R_W(T) = N_{Wjj} (T)/ N_W(T). \end{aligned}$$

(12)

In such a ratio, $N_W(T)$ is linear in $T_A(B)$, as well as the SPS background and DPS1 contribution. Therefore, in absence of the quadratic DPS2 contribution, it would be a constant. Its deviation from such a behaviour will be just due to DPS2 contribution, which will determine the slope of its linear increase.

It is worth mentioning that such ratio is directly measurable in experiments since $T_A(B)$ is proportional to the number of collisions $\nu$  [48] and that many of the systematics related to W reconstruction simplify. We present the physical observables as a function of $T_A(B)$ since they are measured in terms of $T_A(B)$ (or equivalently in terms of a number of collisions) in the real experimental setup  [48].

The resulting distribution is presented in the right panel of Fig. (3) for different values of jet transverse momenta cut off. The rise of the slope is related to fast rise of the dijet cross sections entering the DPS2 estimation as the cuts on jet transverse momenta are decreased.

Fig. 4

Wjj DPS cross sections in pA collisions as a function of the charged muon rapidity in the proton-nucleon centre-of-mass frame (left) and the corresponding muon charge asymmetry (right)

Given the large number of signal DPS events in the Wjj channel, after proper subtraction of the SPS contribution, the characterization of the DPS cross section could be attempted by inspecting the charged lepton rapidity distributions. The latter are presented in the left panel of Fig. (4) for all different charge contribution and DPS mechanism and are obtained integrating over impact parameter B and over dijet phase space.

Correlations beyond mean field approximation could be appreciated by considering the lepton charge asymmetry, a generalization of the familiar observable defined in SPS:

$$\begin{aligned} {\mathcal {A}}(y^\mu _{CM})=\frac{d\sigma _{DPS}(W^+jj)-d\sigma _{DPS}(W^-jj)}{d\sigma _{DPS}(W^+jj)+d\sigma _{DPS}(W^-jj)}\,. \end{aligned}$$

(13)

The corresponding distribution is presented in the right panel of Fig. (4). Given the factorized ansatz for double PDFs and that the dijet system is completely integrated over, its line shape is the same as the lepton charge asymmetry measured in SPS production of $W^\pm$ in pA collisions, see for example Fig. (4) of Ref. [44]. Therefore, after proper subtraction of SPS and DPS1 contribution, the observation in data of any departure from the predicted line shape might be an indication of parton correlations not accounted for in the mean field approximation.

3.3 Leading twist background versus DPS2

The main experimental impediment to the observation of the DPS2 contribution is the large LT background. We have calculated the latter in the leading order (LO) approximation by using the ALPGEN generator.

Fig. 5

The ratio $R_W$ as a function of T for Wjj integrated in bins of $T_A$ for two values of the integrated luminosity and different cuts on jet transverse momenta

We display in the Fig. (5) the ratio $R_W$, defined by Eq. (12) in the previous Subsection, and integrated in the interval of the thickness function to better facilitate the connection with centrality dependence. The bin widths are chosen as to evenly distribute the number of events across the various $T_A$ bin.

Table 2 Predictions for $Wb{\bar{b}}$ DPS and SPS cross sections in pA collisions in fiducial phase space, for different cuts on jets transverse momenta. These numbers refer to charged summed W cross sections accounting for the W boson decaying into muons as well as electrons. The quoted error is entirely due to the propagation of $\sigma _{eff}$ uncertainty

Fig. 6

Number of events in $Wb{\bar{b}}$ final state in bins of B assuming $\int {\mathcal {L}}dt=0.1 \text{ pb }^{-1}$ and for $p_T^j>20$ GeV (left). The ratio $R_W$ as a function of $T_A$ for different cuts on jet transverse momenta (right)

The error band associated to the ratio is obtained assuming a Poissonian distribution of statistical errors, obtained from the number of total $N_{Wjj}$ and $N_W$ events expected for two values of $\int {\mathcal {L}} \, dt = 0.1$ and 1 $pb^{-1}$. Large (small) values of $T_A$ correspond to central (peripheral) events, with the ratio increasing going from peripheral to central collisions. The errors associated to the distribution determine a marked sensitivity to DPS2 mechanism which is responsible for the non zero slope of the distribution.

4 Results : $Wb{\bar{b}}$

We consider in this Section a special case of the former process in which the second scattering produces a $b{\bar{b}}$ heavy-quark pair. This particular final state has been analyzed in detail in pp collisions in [30] where a number of kinematic variables have been proposed to disentangle the signal DPS process from the SPS background. It is worth noticing that this final state is particularly important for new physics searches in pp collisions so that the DPS component needs to be properly modelled. For this final state we use ${\bar{\sigma }}_{eff} = 18 \pm 6$ mb as for the Wjj case.

For this channel we define the fiducial phase space in terms of muon transverse momentum and rapidity by requiring that $p_{T}^{\mu }>25$ GeV and $|y^{\mu }_{lab}|<2.4$. Additionally the missing transverse energy is required to satisfy . The fiducial phase space for b-jets is given by $p_{T}^{b-jets}>20$ GeV and $|y^{b-jets}_{lab}|<2.4$. For the DPS contributions, the W cross section has been evaluated with factorization and renormalization scales fixed to the W boson mass, $\mu _F=\mu _R=M_W$, while for the $b{\bar{b}}$ dijet cross section to $\mu _F=\mu _R=\sqrt{m_{T,j1}^{2}+m_{T,j2}^{2}}$, being $m_T$ the transverse mass of the b-jet. The cross section for the SPS $Wb{\bar{b}}$ background was evaluated with ALPGEN [42] with the same selection cuts described above and $\mu _F=\mu _R=\sqrt{M_W^2+m_{T,j1}^{2}+m_{T,j2}^{2}}$.

Fig. 7

The ratio $R_W$ as a function of T for $Wb{\bar{b}}$ final state integrated in bins of $T_A$ for two values of the integrated luminosity and different cuts on jet transverse momenta

The various contributions to the $Wb{\bar{b}}$ cross sections are reported in Table 2. As expected, they are reduced by several order of magnitude with respect to the Wjj case. Assuming again a rather conservative scenario in which the integrated luminosity is $\int {\mathcal {L}} \text{ dt }= 0.1 \, \text{ pb }^{-1}$, we present in the left panel of Fig. (6) the expected number of events for the various contributions integrated in bins of B.

In the right panel of Fig. (6) we present, for this particular final state, the ratio $R_W$ between the total number (SPS+DPS) of $Wb{{\bar{b}}}$ events over those for inclusive W production

$$\begin{aligned} R_W(T) = N_{Wb{{\bar{b}}}} (T)/ N_W(T), \end{aligned}$$

(14)

as a function of $T_A(B)$ for different transverse momenta cut off on the b-jets.

In Fig. (7) we present the ratio $R_W$ defined by Eq. (14) integrated in two ranges of $T_A$ and assuming $\int {\mathcal {L}} \text{ dt }=$ 0.1 and 1 $\text{ pb }^{-1}$. The bin widths were determined from the condition that the events are evenly distributed in each bins.

According to our error estimates, the result is not conclusive for the current integrated luminosity scenario, while a sufficient discrimination power is achievable in the future runs, although even in the latter case this channel is much less sensitive to DPS2 than the Wjj one.

As already observed in the Wjj case, lowering the cut on the transverse momenta of b-jet increases the sensitivity to a non constant behaviour of $R_W$.

From the latter plot it is clear that for this final state, given the lower number of events, the identification of a non-constant behaviour in data will be difficult. Nevertheless, since at the B-integrated level, the DPS2 contribution is more than twice the DPS1 one, this channel has anyway the potential to allow the observation of the DPS2 mechanism.

5 Results : ssWW

Double Drell-Yan like processes have been recognized as an ideal laboratory to investigate DPS [2, 49] and its factorization property [50]. Among this class of process, the production of a same sign W boson pair (ssWW), where each W-boson is produced in a distinct hard scattering, has received special attention [31, 33, 51,52,53,54], since single parton scattering (SPS) at tree-level starts contributing to higher order in the strong coupling and can be suppressed by additional jet veto requirements. This process has been investigated in pA collisions in Ref. [55].

A measurement of the ssWW DPS cross section in pp collisions at $\sqrt{s}=$13 TeV has been recently reported by the CMS collaboration [21]. In that analysis a value of $\sigma _{eff} = 12.7^{+5.0}_{-2.9}$ mb has been extracted and which will be used in our predictions, assuming that such a value is valid also at $\sqrt{s_{pN}}=$8.16 TeV, the nominal energy at which we simulate pA collisions in this analysis. Again we assumed that its value is the same in both charged channels and the same across the fiducial phase space. Both W’s are required to decay into same sign muons and we adopt the fiducial phase space from the analysis of Ref. [44]: it is given by $p_{T}^{\mu }>25$ GeV for the leading muon, $p_{T}^{\mu }>20$ GeV for the subleading one and $|y^{\mu }_{lab}|<2.4$ for muons’ rapidities. Additionally the missing transverse energies are required to satisfy and 20 GeV. We report the cross sections results in Table 3 for various DPS mechanisms and for separate dimuon charge configurations. In Fig. 8 we present the differential cross sections and the number of expected events for $\int {\mathcal {L}}dt= 1\hbox { pb}^{-1}$, a value within reach at future pA runs at LHC.

Table 3 Fiducial cross sections for ssWW DPS cross sections for the positive (left), negative (central) and charged summed (right) dimuon final state for all DPS contributions. The quoted errors follow from the propagation of $\sigma _{eff}$ uncertainty

Fig. 8

DPS cross sections as a function of B (left) and expected number of events with $\int {\mathcal {L}}dt=1\hbox { pb}^{-1}$ in the charged summed dimuon channel (right). The error band represents the propagation of the ${\bar{\sigma }}_{eff}$ uncertainty

Considering all leptonic channels ($\mu ^\pm \mu ^\pm , e^\pm \mu ^\pm , e^\pm e^\pm$), the resulting fiducial cross section is four times larger than that reported in Table 3 and it is of order 1 pb. These results are consistent with the ones reported in Ref. [55] after noting that those have been obtained at higher $\sqrt{s_{pN}}=8.8$ TeV with respect to the one used here and that cross sections have been calculated there at next to leading order. Given these numbers we conclude that the observation of DPS in this channel will not only depend on the integrated luminosity accumulated in future pA runs but also on the experimental ability to reconstruct W’s and its charge via its hadronic decays.

6 Conclusions

In this paper we have calculated DPS cross sections for a variety of final states produced in pA collisions at the LHC, as well as the corresponding SPS backgrounds. We have discussed a strategy to separate the so-called DPS2 contributions, pertinent to pA collisions, which relies on the experimental capabilities to correlate centrality with impact parameter B of the proton-nucleus collision. With this respect the Wjj final state has large enough cross sections to allow the method to be used already with 2016 recorded data. Moreover the distribution in lepton charge asymmetry has the potential to uncover correlations in double $_2$GPD of the nucleon beyond the mean field approximation. The $Wb{\bar{b}}$ final state, having lower rate, can still be used at the inclusive level to search for the DPS2 contribution in the future runs, albeit with reduced sensitivity relative to Wjj final state. The observation of the ssWW final state, being a clean but a rare process, will depend crucially on the running conditions of the future pA runs and upon the W-reconstruction experimental capabilities.