1 Introduction

The research of thermal properties of black holes (BH) is one of the topics in which theoretical physicists were interest. In recent years, the study of AdS space-time’s thermodynamic property has gained intensive attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. When the cosmological constant in AdS space-time corresponds to the pressure of the general thermodynamic system, the extended first law of thermodynamics for the black hole can be obtained. Then we compare BH state parameter to the Van der Waal’s equation of state to study several kinds of critical phenomenon in AdS space-time. The critical point and critical exponent can also be obtained in AdS space-time, and the effect of various parameters in space-time on phase transition is discussed. As to de Sitter (dS) space-time, the black hole horizon and cosmological horizon have different radiation temperature in general, the dS space-time does not satisfy the requirements of thermodynamic equilibrium stability , and it limits the study of dS space-time’s thermodynamic property. However, with the in-depth study of dark energy, the study of the thermodynamic properties of dS space-time has attracted more attention [27,28,29,30,31,32,33,34,35,36,37,38,39]. Because in the early period of inflation, the universe is a quasi-dS space-time, and the cosmological constant introduced in the study of dS space-time plays the role of vacuum energy. If the cosmological constant corresponds to dark energy, the universe will evolve into a new dS phase. In order to construct the whole history of universe evolution, we should have a clear understanding of classical and quantum properties in dS space-time. dS space-time’s entropy and temperature are two important parameters to study its property, but both of them are not conclusive at present. There are currently two kinds of viewpoints. In references [35, 36, 41,42,43,44,45], the authors think that dS space-time’s entropy is the sum of the two horizons’ \(S=S_{+}+S_{c} \) (\(S_{+}\) and \(S_{c}\) represent the entropy of black hole horizon and cosmological horizon, respectively), but, in references [40, 45], they think that it is the difference of two horizons’ \(S=S_{c}-S_{+}\). Different effective temperatures are obtained for the same de Sitter space-time due to different values of entropy. Different effective temperature’s special property in higher-dimensional Schwarzschild-de Sitter space-time were analyzed in paper [40] in which, on the basis of dimensional consistency, we assume that dS space-time’s entropy is a function in the form of \(F_{n}(x)\), with \(x=r_{+} / r_{c}\) (\(r_{+, c}\) is the position of black hole horizon and cosmological horizon namely). Using space-time’s thermodynamic parameter satisfy the first law of thermodynamic and the relation of it’s effective temperature with two horizon’s radiation temperature to build a differential equation that \(F_{n}(x)\) is satisfied. Using the initial condition that dS space-time tend to be pure dS space-time when space-time’s black hole horizon tend to be zero, we solve the differential equation that \(F_{n}(x)\) must be satisfied, then obtain the entropy of ds space-time. Further we obtain other thermodynamic parameters such as equivalent temperature and pressure in dS space-time. To make our discussion more universality, for instance, we take higher-dimensional dS black holes in dRGT massive gravity space-time for example to discuss.

Einstein’s general relativity predicts that gravity is a spin-2 mass-free particle [46,47,48]. This prediction is also the latest expression of modern physics, which is of great significance to the study of astrophysics. But whether the graviton has mass or not and the problems such as cosmological constants and the late acceleration of the origin of the universe are challenges in relativity. Generally speaking, adding mass terms to gravitational background will bring various instabilities to gravitational theory. De Rham, Gabadadze and Tolley (dRGT) propose a non-linear theory of mass gravity [49,50,51], which eliminates Boulware-Deser ghost [52] by adding higher-order interaction terms. Vegh had constructed a non-trivial black hole solution in a Ricci flat horizon under 4-dimensional dRGT gravity [53, 54]. Later, spherically symmetric solutions [55,56,57], charged black hole solutions [58], including its bi-gravity extension were also proposed [59, 60]. In addition, in [4, 61,62,63], the solution of charged ADS black hole in high-dimensional DRGT gravity and its corresponding thermodynamics and phase structure in large canonical ensembles and canonical ensembles were also introduced. Ge and Zou studied the relationship between dynamic instability and thermodynamic instability in dRGT gravitation[62, 64].

For charged de Sitter space-time and complex space-time, taking space-time entropy as the sum of two horizons’ entropy, some progresses had been made in the study of space-time effective temperature [32, 35, 65,66,67,68]. However, the entropy correction term caused by the interaction between two horizons has not been taken into account in the discussion. In this paper, the thermodynamic characteristics of de Sitter space-time are discussed on the basis of considering the correlation between black hole horizon and cosmological horizon. Effective temperature and entropy of higher-dimensional dS black holes in dRGT massive gravity (HBHRGT) space-time are obtained and the influence of coupling coefficients \(c_{i} m^{2}\) on the effective temperature and entropy is analyzed. By studying, we know that the space-time entropy of de Sitter is the sum of two horizon entropies and the entropy correction term of the system caused by the interaction of two horizons. The total entropy of the system does not show the coupling coefficients \(c_{i} m^{2}\) term, but it is just a function of the horizon position, which is consistent with that of the black hole horizon and the cosmological horizon. The determination of the space-time entropy and the effective temperature of de Sitter lays a foundation for further study of the thermodynamic characteristics of the universality of de Sitter space-time.

This paper is arranged as follows, in Sect. 2, we will briefly introduce the black hole horizon and cosmological horizon corresponding thermodynamic parameter in the HBHRGT space-time. The conditions for space-time charges to be satisfied when the radiation temperatures of the two horizons are equal are given. In the third part, the total space-time entropy and effective temperature of HBHRGT satisfying the first law of thermodynamics are given on the basis of considering the correlation between the two horizons. In the forth part, we give discussion about the conclusion (We use the units \(G=\hbar =k_{B}=c=1\)).

2 Higher-dimensional dS black holes in dRGT massive gravity

The form of (\(n+2\))-dimensional Einstein space-time metric is

$$\begin{aligned} d s^{2}=-f(r) d t^{2}+f^{-1}(r) d r^{2}+r^{2} h_{ij} d x^{i} d x^{j}, \end{aligned}$$
(1)

where \(h_{ij} d x^{i} d x^{j}\) is the line element including constant curvature \(\frac{n(n-1)}{k}\). \(k=0\) represents a flat universe, however, if \(k= \pm 1\), the universe is non-flat, \(k=1\) for positive curvature and \(k=-1\) for negative curvature respectively.

By using the reference metric

$$\begin{aligned} f_{\mu \nu }={\text {diag}} \left( 0,0,c_{0}^{2}h_{ij}\right) , \end{aligned}$$
(2)

the metric function f(r) is obtained as [61, 64],

$$\begin{aligned} f(r)= & {} k+c_{0}^{2} c_{2} m^{2}-\frac{m_{0}}{r^{n-1}}-\frac{2 \Lambda r^{2}}{n(n+1)}+\frac{(n-1) c_{0}^{3} c_{3} m^{2}}{r} \nonumber \\&+\frac{c_{0} c_{1} m^{2}}{n} r+\frac{(n-1)(n-2) c_{0}^{4} c_{4} m^{2}}{r^{2}}\nonumber \\&+\frac{q^{2}}{2 n(n-1) r^{2(n-1)}}. \end{aligned}$$
(3)

where \(\Sigma _{n}\) is the volume of space spanned by coordinates \(x^{i}\), \(c_{0}\) is a positive constant, and here m is the black hole mass. It is worth noting that the terms \(c_{3} m^{2}\) and \(c_{4} m^{2}\) only appear for \(n \ge 3\) and \(n \ge 4\) in the black hole solutions, respectively [61]. When \(m \rightarrow 0\), namely there is no mass, Eq. (3) goes back to the \((n+2)\)-dimensional Schwarzschild dS (AdS) black hole solution.

When cosmological constants \(\Lambda <0\), the spacetime is named AdS and there is only one black hole horizon. As shown in reference [61, 64] there are some discussions about black hole phase translation and critical phenomena. When \(\Lambda >0\), it is dS space-time, there are not only black hole horizon \(r_{+}\), but also cosmological horizon \(r_{c}\). The thermodynamic parameters of the two horizon satisfy the first law of thermodynamics [27, 32, 33, 69].

Some thermodynamic quantities associated with the cosmological horizon are

$$\begin{aligned} Q= & {} \frac{\Sigma _{n}q}{16 \pi },S_{c}=\frac{\Sigma _{n}}{4} r_{c}^{n}, V_{c}=\frac{\Sigma _{n}}{n+1} r_{c}^{n+1}, P=-\frac{\Lambda }{8 \pi }<0, \nonumber \\ T_{c}= & {} -\frac{1}{4 \pi r_{c}}\left[ (n-1) k-\frac{2 r_{c}^{2} \Lambda }{n}-\frac{q^{2}}{2 n r_{c}^{2(n-1)}}\right. \nonumber \\&+(n-1) c_{2} c_{0}^{2} m^{2}+\frac{(n-1)(n-2) c_{3} c_{0}^{3} m^{2}}{r_{c}}\nonumber \\&\left. +c_{1} c_{0} m^{2} r_{c}+\frac{(n-1)(n-2)(n-3) c_{4} c_{0}^{4} m^{2}}{r_{c}^{2}}\right] . \end{aligned}$$
(4)

Furthermore, the first law of thermodynamics of the cosmological horizon is [27, 32, 33]

$$\begin{aligned} d M= & {} -T_{c} d S_{c}+U_{c} d Q+V_{c} d P \nonumber \\&+C_{1 c} d c_{1}+C_{2 c} d c_{2}+ C_{3 c} d c_{3}+C_{4 c} d c_{4}, \end{aligned}$$
(5)

where \(M=\frac{n \Sigma _{n}}{16 \pi } m_{0}\).

The corresponding potentials are

$$\begin{aligned} U_{c}= & {} \frac{q}{(n-1) r_{c}^{n-1}}, \quad C_{1c}=\frac{c_{0} m^{2} \Sigma _{n} r_{c}^{n}}{16 \pi },\nonumber \\ C_{2c}= & {} \frac{n c_{0}^{2} m^{2} \Sigma _{n} r_{c}^{n-1}}{16 \pi }, \quad C_{3 c}=\frac{n(n-1) c_{0}^{3} m^{2} \Sigma _{n} r_{c}^{n-2}}{16 \pi },\nonumber \\ C_{4 c}= & {} \frac{n(n-1)(n-2) c_{0}^{4} m^{2} \sum _{n} r_{c}^{n-3}}{16 \pi }. \end{aligned}$$
(6)

For the black hole horizon, the associated thermodynamic quantities are

$$\begin{aligned} S_{+}= & {} \frac{\Sigma _{n}}{4} r_{+}^{n}, \quad V_{+}=\frac{\sum _{n}}{n+1} r_{+}^{n+1}, \nonumber \\ T_{+}= & {} \frac{1}{4 \pi r_{+}}\left[ (n-1) k-\frac{2 r_{+}^{2} \Lambda }{n}-\frac{q^{2}}{2 n r_{+}^{2(n-1)}}+c_{1} c_{0} m^{2} r_{+}\right. \nonumber \\&\left. +(n-1) c_{2} c_{0}^{2} m^{2}+\frac{(n-1)(n-2) c_{3} c_{0}^{3} m^{2}}{r_{+}}\right. \nonumber \\&\left. +\frac{(n-1)(n-2)(n-3) c_{4} c_{0}^{4} m^{2}}{r_{+}^{2}}\right] . \end{aligned}$$
(7)

The thermodynamic quantities of black hole horizon satisfy the first law,

$$\begin{aligned} d M= & {} T_{+} d S_{+}+U_{+} d Q+V_{+} d P\nonumber \\&+C_{1+} d c_{1}+C_{2+} d c_{2}+C_{3+} d c_{3}+C_{4+} d c_{4}, \end{aligned}$$
(8)

where the corresponding potential and parameter \(C_{i}\) respectively are

$$\begin{aligned} U_{+}= & {} \frac{q}{(n-1) r_{+}^{n-1}},\quad C_{1+}=\frac{c_{0} m^{2} \Sigma _{n} r_{+}^{n}}{16 \pi },\nonumber \\ C_{2+}= & {} \frac{n c_{0}^{2} m^{2} \Sigma _{n} r_{+}^{n-1}}{16 \pi }, \quad C_{3+}=\frac{n(n-1) c_{0}^{3} m^{2} \Sigma _{n} r_{+}^{n-2}}{16 \pi },\nonumber \\ C_{4+}= & {} \frac{n(n-1)(n-2) c_{0}^{4} m^{2} \Sigma _{n} r_{+}^{n-3}}{16 \pi }, \end{aligned}$$
(9)

from horizon’s equation \(f\left( r_{+, c}\right) =0\), we get that

$$\begin{aligned} \frac{2 \Lambda }{n(n+1)}= & {} -\frac{q^{2}\left( 1-x^{n-1}\right) }{2 n(n-1) r_{c}^{2 n} x^{n-1}\left( 1-x^{n+1}\right) }\nonumber \\&+\frac{c_{0} c_{1} m^{2}}{n} \frac{\left( 1-x^{n}\right) }{r_{c}\left( 1-x^{n+1}\right) }\nonumber \\&+\left( k+c_{0}^{2} c_{2} m^{2}\right) \frac{\left( 1-x^{n-1}\right) }{r_{c}^{2}\left( 1-x^{n+1}\right) }\nonumber \\&+(n-1)c_{0}^{3} c_{3} m^{2} \frac{\left( 1-x^{n-2}\right) }{r_{c}^{3}\left( 1-x^{n+1}\right) }\nonumber \\&+(n-1)(n-2) c_{0}^{4} c_{4} m^{2} \frac{\left( 1-x^{n-3}\right) }{r_{c}^{4}\left( 1-x^{n+1}\right) }, \end{aligned}$$
(10)
$$\begin{aligned} \frac{16\pi M}{n \Sigma _n}= & {} \left( k+c_{0}^{2} c_{2} m^{2}\right) r_{c}^{n-1} x^{n-1} \frac{\left( 1-x^{2}\right) }{\left( 1-x^{n+1}\right) }\nonumber \\&+\frac{q^{2}\left( 1-x^{2 n}\right) }{2 n(n-1) r_{c}^{n-1} x^{n-1}\left( 1-x^{n+1}\right) }\nonumber \\&+\frac{c_{0} c_{1} m^{2}}{n} r_{c}^{n} x^{n} \frac{(1-x)}{\left( 1-x^{n+1}\right) }\nonumber \\&+(n-1) c_{0}^{3} c_{3} m^{2} r_{c}^{n-2} x^{n-2} \frac{\left( 1-x^{3}\right) }{\left( 1-x^{n+1}\right) } \nonumber \\&+(n-1)(n-2) c_{0}^{4} c_{4} m^{2} r_{c}^{n-3} x^{n-3}\nonumber \\&\times \frac{\left( 1-x^{4}\right) }{\left( 1-x^{n+1}\right) }. \end{aligned}$$
(11)

where \(x=r_{+}/r_{c}\).

When \({\tilde{T}}_{+}={\tilde{T}}_{c}=T\), from Eqs. (4) and (7) we get

$$\begin{aligned} \frac{2 \Lambda }{n}&=\frac{(n-1)}{r_{c}^{2} x}\left( k+c_{2} c_{0}^{2} m^{2}\right) \nonumber \\&\quad -\frac{q^{2}}{2 n r_{c}^{2 n} x^{2 n-1}} \frac{1+x^{2 n-1}}{(1+x)}+2 \frac{c_{1} c_{0} m^{2}}{r_{c}(1+x)}\nonumber \\&\quad +(n-1)(n-2) c_{3} c_{0}^{3} m^{2} \frac{\left( 1+x^{2}\right) }{r_{c}^{3}x^{2}(1+x)}\nonumber \\&\quad +\frac{(n-1)(n-2)(n-3) c_{4} c_{0}^{4} m^{2}}{r_{c}^{4} x^{3}} \frac{\left( 1+x^{3}\right) }{(1+x)}, \end{aligned}$$
(12)

From Eqs. (10) and (12), we get a relevant expression among the parameters of \(\frac{q^{2}}{r_{c}^{2 n-2}}, \left( k+c_{0}^{2} c_{2} m^{2}\right) , c_{0} c_{1} m^{2} r_{c}, \frac{c_{0}^{3} c_{3} m^{2}}{r_{c}}\) and \(\frac{c_{0}^{4} c_{4} m^{2}}{r_{c}^{2}}\), when black hole horizon and cosmological horizon have the same radiation temperature.

$$\begin{aligned} \frac{q^{2}}{r_{c}^{2 n-2}} K(x, n)= & {} \left( k+c_{0}^{2} c_{2} m^{2}\right) A(x, n)+c_{0} c_{1} m^{2} r_{c} B(x, n)\nonumber \\&+\frac{c_{0}^{3} c_{3} m^{2}}{r_{c}} C(x, n)+\frac{c_{0}^{4} c_{4} m^{2}}{r_{c}^{2}} D(x, n),\nonumber \\ \end{aligned}$$
(13)

where

$$\begin{aligned} K(x,n)= & {} \left( 1+x^{n}\right) \left( 1-x^{2n}\right) -n(1-x^{n})\nonumber \\&\times \left[ 1+x^{2n}+2n x^{n+1}\left( 1-x^{n-2}\right) \right] , \nonumber \\ A(x,n)= & {} 2n(n-1)x^{2n-2}\nonumber \\&\times \left[ (1+x)^{2}\left( 1-x^{n}\right) -n\left( 1-x^{2}\right) \left( 1+x^{n}\right) \right] ,\nonumber \\ B(x, n)= & {} 2(n-1) x^{2n-1}\nonumber \\&\times \left[ \left( 1-x^{n}\right) (1+x)-n(1-x)\left( 1+x^{n}\right) \right] , \nonumber \\ C(x, n)= & {} 2n(n-1)^{2} x^{2 n-3}\left[ 2+3 x^{2}-x^{n}+x^{3}\right. \nonumber \\&\left. -3 x^{n+1}-2x^{n+3}-n\left( 1+x^{n}\right) \left( 1-x^{3}\right) \right] , \nonumber \\ D(x, n)= & {} 2n(n-1)^{2}(n-2) x^{2 n-4}\left[ 3+4 x^{3}-x^{n}+x^{4}\right. \nonumber \\&\left. -4 x^{n+1}-3x^{n+4}-n\left( 1+x^{n}\right) \left( 1-x^{4}\right) \right] .\nonumber \\ \end{aligned}$$
(14)

From Eq. (13) we know \(\left( k+c_{0}^{2} c_{2} m^{2}\right) \), \(\frac{ q^{2}}{r_{c}^{2 n-2}}\), \(\frac{c_{0}^{3} c_{3} m^{2}}{r_{c}}\), \(\frac{ c_{0}^{4} c_{4} m^{2}}{r_{c}^{2}}\) and \(c_{0} c_{1} m^{2} r_{c}\) are not completely independent, when black hole horizon and cosmological horizon have the same radiation temperature, any of these variables can be expressed as functions of other variables. When we use \(\frac{q^{2}}{r_{c}^{2 n-2}}\) as other variables’ function, substituting Eqs. (12) and (13) into Eqs. (4) or (7), we obtain the temperature when two horizons have same radiation temperature.

$$\begin{aligned} T_{K}= & {} T_{+, k}=T_{c, k} \nonumber \\= & {} \frac{2\left( k+c_{2} c_{0}^{2} m^{2}\right) }{4 \pi r_{c} K(x, n)}\nonumber \\&\times \left[ n^{2} x^{n-1}(1-x)\left( 1-x^{n-1}\right) -n\left( 1-x^{n+1}\right) \right. \nonumber \\&\left. \times \left( 1-x^{2 n-2}\right) +\left( 1-x^{2 n}\right) \left( 1-x^{n-1}\right) \right] \nonumber \\&+\frac{c_{1} c_{0} m^{2}}{4 \pi n K(x, n)}\nonumber \\&\times \left[ 2 n^{2} x^{n}(1-x)\left( 1-x^{n-1}\right) -n\left( 1-x^{2 n}\right) \right. \nonumber \\&\times \left. \left( 1-x^{n}\right) +\left( 1-x^{2 n}\right) \left( 1-x^{n}\right) \right] \nonumber \\&+\frac{(n-1) c_{3} c_{0}^{3} m^{2}}{4 \pi r_{c}^{2} K(x, n)}\nonumber \\&\times \left[ 2n^{2}x^{n-2}\left( 1-x^{3}\right) (1-x^{n-1})\right. \nonumber \\&\left. +3\left( 1-x^{n-2}\right) \left( 1-x^{2n}\right) -n\right. \nonumber \\&\left. \times (3+3 x^{3 n-2}-4 x^{n+1}-4 x^{2 n-3}+x^{n-2}+x^{2 n})\right] \nonumber \\&+\frac{2(n-1)(n-2) c_{4} c_{0}^{4} m^{2}}{4 \pi r_{c}^{3} K(x, n)}\nonumber \\&\times \left[ 2\left( 1-x^{n-3}\right) \left( 1-x^{2 n}\right) \right. \nonumber \\&\left. +n^{2}x^{n-3}\left( 1-x^{n-1}\right) \left( 1-x^{4}\right) -n\right. \nonumber \\&\left. \times (2+x^{n-3}+x^{2 n}+2 x^{3 n-3}-3 x^{2 n-4}-3 x^{n+1})\right] .\nonumber \\ \end{aligned}$$
(15)

When we select \(c_{0} c_{1} m^{2} r_{c}\) as the function of other variables, we substitute Eqs. (12) and (13) into Eqs. (4) or (7) to obtain the temperature when the radiation temperature of two horizons is equal.

$$\begin{aligned}&4 \pi r_{c} B(x, n) T_{B}=4 \pi r_{c} B(x, n) T_{+, B}=4 \pi r_{c} B(x, n) T_{c, B}\nonumber \\&=-2(n-1)\left( k+c_{2} c_{0}^{2} m^{2}\right) x^{2 n-2}(1-x)\nonumber \\&\qquad \times \left[ \left( 1-x^{n}\right) (1+x)-n(1-x)\left( 1+x^{n}\right) \right] \nonumber \\&\qquad - 2 \frac{c_{4} c_{0}^{4} m^{2}}{r_{c}^{2}}(n-1)^{2}(n-2) x^{2 n-4}\nonumber \\&\qquad \times \left[ 3\left( 1-x^{4}\right) \left( 1-x^{n}\right) -n\right. \nonumber \\&\qquad \times \left. \left( 1+3 x^{n}+3 x^{4}-4 x^{3}-4 x^{n+1}+x^{n+4}\right) \right] \nonumber \\&\qquad +\frac{q^{2}}{n r_{c}^{2 n-2}} \left[ \left( 1-x^{n}\right) \left( 1-x^{2 n}\right) -n\left( 1-x^{n}\right) \right. \nonumber \\&\left. \qquad \times \left( 1-x^{2 n}\right) +2 n^{2} x^{n}(1-x)\left( 1+x^{n-1}\right) \right] \nonumber \\&\qquad -\frac{2 c_{3} c_{0}^{3} m^{2}}{r_{c}}(n-1)^{2} x^{2n-3}(1-x)\nonumber \\&\qquad \times \left[ 2\left( 1+x+x^{2}\right) \left( 1-x^{n}\right) \right. \nonumber \\&\left. \qquad -n(1-x)\left( 1+2 x+2 x^{n}+x^{n+1}\right) \right] , \end{aligned}$$
(16)

when we take \(\left( k+c_{0}^{2} c_{2} m^{2}\right) \) as other functions, from Eqs. (4), (7), (12) and (13), we can obtain the temperature when two horizons have same radiation temperature.

$$\begin{aligned}&4\pi r_{c} A(x, n) T_{A}= 4 \pi r_{c} A(x, n) T_{+, A}=4 \pi r_{c} A(x, n) T_{c, A} \nonumber \\&=-\frac{q^{2}}{r_{c}^{2 n-2}} 2(n-1)\nonumber \\&\qquad \times \left[ \left( 1-x^{n-1}\right) \left( 1-x^{2 n}\right) -n x^{n-1}(1-x)\left( 1-x^{n}\right) \right] \nonumber \\&\qquad +2 c_{1} c_{0} m^{2} r_{c}(n-1)(1-x) x^{2 n-2}\nonumber \\&\qquad \times \left[ \left( 1-x^{n}\right) (1+x)-n(1-x)\left( 1+x^{n}\right) \right] \nonumber \\&\qquad -2 \frac{c_{0}^{3} c_{3} m^{2}}{r_{c}} n(n-1)^{2} x^{2 n-3}\nonumber \\&\qquad \times \left[ \left( 4-3 x-x^{3}-x^{n-1}-3 x^{n+1}+4 x^{n+2}\right) -n\right. \nonumber \\&\qquad \times \left. \left( 2-3 x+x^{3}+x^{n-1}-3 x^{n+1}+2 x^{n+2}\right) \right] \nonumber \\&\qquad -2 \frac{c_{0}^{4} c_{4} m^{2}}{r_{c}^{2}} n(n-1)^{2}(n-2) x^{2 n-5}\nonumber \\&\qquad \times \left[ x\left( 6-4 x^{2}-2 x^{4}-2 x^{n-1}-4 x^{n+1}+6 x^{n+3}\right) +n \right. \nonumber \\&\qquad \times \left. (2+4 x^{3}-3 x^{4}-x^{5}-4 x^{n}-2 x^{n+1}+4 x^{n+2}\right. \nonumber \\&\left. \qquad -3 x^{n+4}+3 x^{n+5})\right] , \end{aligned}$$
(17)

when we take \(\frac{c_{0}^{3} c_{3} m^{2}}{r_{c}}\) as other functions, substituting Eqs. (12) and (13) into Eqs. (4) or (7), when two horizons have same radiation temperature, the temperature is as following .

$$\begin{aligned}&4\pi r_{c} C(x, n) T_{c}=4 \pi r_{c} C(x, n) T_{+, c}=4 \pi r_{c} C(x, n) T_{c, c} \nonumber \\&\quad =2 n(n-1)^{2}\left( k+c_{2} c_{0}^{2} m^{2}\right) x^{2 n-3}\nonumber \\&\qquad \times \left[ \left( 4-3 x-x^{3}-x^{n-1}-3 x^{n+1}+4 x^{n+2}\right) -n\right. \nonumber \\&\qquad \times \left. (2-3 x+x^{3}+x^{n+1}-3 x^{n+1}+2 x^{n+2})\right] \nonumber \\&\qquad -\frac{q^{2}(n-1)}{r_{c}^{2 n-2} x^{2}} \left[ -3 x^{2}\left( 1-x^{2n}\right) \left( 1-3 x^{n-2}\right) +n \right. \nonumber \\&\qquad \times \left. \left( 3 x^{2}+x^{n}+3 x^{3n}+x^{2 n+2}-4 x^{n+3}-4 x^{2 n-1}\right) \right. \nonumber \\&\qquad \left. -2 n^{2}x^{n}\left( 1-x^{3}\right) \left( 1-x^{n-1}\right) \right] \nonumber \\&\qquad +2 c_{1} c_{0}m^{2} r_{c}(n-1)^{2} x^{2 n-3} \left[ 2\left( 1-x^{3}\right) \left( 1-x^{n}\right) +n\right. \nonumber \\&\qquad \left. \times \left( -1+3x^{2}-2 x^{3}-2 x^{n}+3 x^{n+1}-x^{n+3}\right) \right] \nonumber \\&\qquad +\frac{c_{4}c_{0}^{4} m^{2}}{r_{c}^{2}} 2 n(n-1)^{3}(n-2) x^{2 n-6}\nonumber \\&\qquad \times \left[ \left( x^{n}-9 x^{2}+8 x^{3}+x^{6}+8 x^{n+3}-9 x^{n+4}\right) +n \right. \nonumber \\&\qquad \left. \times \left( x^{n}+x^{6}-4 x^{3}+3 x^{2}-4 x^{n+3}+3 x^{n+4}\right) \right] , \end{aligned}$$
(18)

When we take \(\frac{c_{0}^{4} c_{4} m^{2}}{r_{c}^{2}}\) as other functions, we substitute Eqs. (12) and (13) into Eqs. (4 ) or (7) to obtain the temperature when the radiation temperature of two horizons is equal.

$$\begin{aligned}&4\pi r_{c} D(x, n) T_{d}=4 \pi r_{c} D(x, n) T_{+, d}=4 \pi r_{c} D(x, n) T_{c, d} \nonumber \\&\quad =\left( k+c_{2} c_{0}^{2} m^{2}\right) 2n(n-1)^{3} (n-2) x^{2 n-5}\nonumber \\&\qquad \times \left[ \left( 6-6 x^{4}+4 x^{3}-4 x^{n}-6 x^{n+1}-6 x^{5}+4 x^{n+2}\right. \right. \nonumber \\&\qquad \left. \left. +6 x^{n+6}\right) -n\left( 1-x^{4}\right) \left( 5-3 x+3 x^{n}-5 x^{n+1}\right) \right. \nonumber \\&\qquad \left. +n^{2}\left( 1-x^{4}\right) (1-x)\left( 1+x^{n}\right) \right] \nonumber \\&\qquad -\frac{q^{2}}{r_{c}^{2 n-2}} 2(n-1)(n-2)\left[ -2\left( 1-x^{2 n}\right) \left( 1-x^{n}\right) \right. \nonumber \\&\qquad \left. +n x\left( 1+x^{n-4}-3 x^{n}-3 x^{2n-5}+x^{2 n-1}+2 x^{3 n-4}\right) \right. \nonumber \\&\qquad \left. -n^{2}x^{n-3}\left( 1-x^{4}\right) \left( 1-x^{n-1}\right) \right] \nonumber \\&\qquad +2(n-1)^2(n-2)c_1c_0m^2r_c^2x^{2n-4}\left[ 3(1-x^4)(1-x^n)\right. \nonumber \\&\qquad \left. +n\left( -1+4 x^{3}-3 x^{4}+4 x^{n+1}-3 x^{n}-x^{n+4}\right) \right] \nonumber \\&\qquad +2 n(n-1)^{3}(n-2) \frac{c_{3} c_{0}^{3} m^{2}}{r_{c}} x^{2 n-6}\nonumber \\&\qquad \times \left[ \left( 9 x^{2}-8 x^{3}-6 x^{6}-8 x^{n+3}+9 x^{n+4}\right) +n \right. \nonumber \\&\qquad \times \left. \left( -3 x^{2}-4 x^{3}-x^{n}-x^{6}+4 x^{n+3}-3 x^{n+4}\right) \right] . \end{aligned}$$
(19)

The temperature of two horizons with the same radiation temperature expressed by different independent variables is given by Eqs. (15)–(19).

3 Effective thermodynamic quantity

We regard the HBHRGT space-time as a thermodynamic system, for which the state parameters satisfy the first law of thermodynamics, Considering the connection between the black hole horizon and the cosmological horizon, we can derive the effective thermodynamic quantities and the corresponding first law of black hole thermodynamics

$$\begin{aligned} d M= & {} T_{eff} d S-P_{eff} d V+\phi _{eff} d Q \nonumber \\&+C_{1} d c_{1}+ C_{2} d c_{2}+C_{3} d c_{3}+C_{4} d c_{4}, \end{aligned}$$
(20)

Here the thermodynamic volume is that between the black hole horizon and the cosmological horizon, namely [27]

$$\begin{aligned} V=V_{c}-V_{+}=\frac{\sum _{n}}{n+1}r_{c}^{n+1}\left( 1-x^{n+1}\right) , \end{aligned}$$
(21)

Considering that black hole horizon and cosmological horizon are not independent, the entropy is [44, 70]

$$\begin{aligned} S= & {} S_{c}+S_{+}+S_{t}=\frac{\Sigma _{n}}{4} r_{c}^{n}\left( 1+x^{n}+f_{n}(x)\right) \nonumber \\= & {} \frac{\Sigma _{n}}{4} r_{c}^{n} F_{n}(x), \end{aligned}$$
(22)

Here the undefined function \(f_{n}(x)\) represents the extra contribution from the correlations of the two horizons. From (20), the system’s effective temperature \(T_{eff}\), pressure \(p_{eff}\) and potential \(\phi _{eff}\), respectively can be represented as

$$\begin{aligned} T_{eff}= & {} \left( \frac{\partial M}{\partial S}\right) _{Q,V, c_{i}}\nonumber \\= & {} \frac{\left( \frac{\partial M}{\partial x}\right) _{r_{c}}\left( \frac{\partial V}{\partial r_{c}}\right) _{x} -(\frac{\partial V}{\partial x})_{r_c}(\frac{\partial M}{\partial r_{c}})_{x}}{(\frac{\partial S}{\partial x})_{r_{c}}(\frac{\partial V}{\partial r_{c}})_{x}-(\frac{\partial V}{\partial x})_{r_{c}}(\frac{\partial {S}}{\partial r_{c}})_{x}}, \end{aligned}$$
(23)
$$\begin{aligned} P_{eff}= & {} -\left( \frac{\partial M}{\partial V}\right) _{Q,S, c_{i}}\nonumber \\= & {} \frac{\left( \frac{\partial S}{\partial x}\right) _{r_{c}}\left( \frac{\partial M}{\partial r_{c}}\right) _{x}-\left( \frac{\partial M}{\partial x}\right) _{r_{c}}\left( \frac{\partial S}{\partial r_{c}}\right) _{x}}{\left( \frac{\partial V}{\partial x}\right) _{r_{c}}\left( \frac{\partial S}{\partial r_{c}}\right) _{x} -\left( \frac{\partial S}{\partial x}\right) _{r_{c}}\left( \frac{\partial V}{\partial r_{c}}\right) _{x}}, \end{aligned}$$
(24)

From Eq. (11), Eqs. (21) and (22), \(T_{eff}\) can be expressed as

$$\begin{aligned} T_{eff}=\frac{n B(x, q)}{4 \pi r_{c} A(x)}, \end{aligned}$$
(25)

where

$$\begin{aligned} B(x, q)= & {} \left( k+c_{0}^{2} c_{2} m^{2}\right) x^{n-2}\nonumber \\&\times \frac{n\left( 1-x^{2}\right) \left( 1+x^{n+1}\right) -\left( 1+x^{2} \right) \left( 1-x^{n+1}\right) }{\left( 1-x^{n+1}\right) }\nonumber \\&+\frac{q^{2}\left[ \left( 1-x^{2n}\right) \left( 1+x^{n+1}\right) -n \left( 1+x^{2n}\right) \left( 1-x^{n+1}\right) \right] }{2 n(n-1) r_{c}^{2 n-2} x^{n}\left( 1-x^{n+1}\right) }\nonumber \\&+\frac{c_{0} c_{1} m^{2}}{n} r_{c} x^{n-1} \frac{n(1-x)\left( 1+x^{n+1}\right) -x\left( 1-x^{n}\right) }{\left( 1-x^{n+1} \right) }\nonumber \\&+(n-1)c_0^3c_3m^2x^(n-4)\nonumber \\&\times \frac{n(1-x^3)(1+x^{n+1})-(2+x^3-x^{n+1}-2x^{n+4})}{r_c(1-x^{n+1})}\nonumber \\&+(n-1)(n-2)c_0^4c_4m^2x^{n-4}\nonumber \\&\times \frac{n(1-x^4)(1+x^{n+1})-(3+x^4-x^{n+1})-3x^{n+5}}{r_c^2(1-x^{n+1})}, \nonumber \\\end{aligned}$$
(26)
$$\begin{aligned} A(x)= & {} \left[ n x^{n-1}+f_{n}^{\prime }(x)\right] \left[ 1-x^{n+1}\right] \nonumber \\&+n x^{n}\left[ 1+x^{n}+f_{n}(x)\right] \nonumber \\= & {} \left[ 1-x^{n+1}\right] F_{n}^{\prime }(x)+n x^{n} F_{n}(x). \end{aligned}$$
(27)

The space-time’s effective temperature should equal to radiation temperature, when the two horizons have the same radiation temperatures, that is

$$\begin{aligned} {\tilde{T}}_{eff}=T={\tilde{T}}_{+}={\tilde{T}}_{c}, \end{aligned}$$
(28)

Substituting (13) into (26), from (25) we get

$$\begin{aligned} A(x)=\frac{n {\tilde{B}}(x)}{4 \pi r_{c} {\tilde{T}}_{eff}}, \end{aligned}$$
(29)

when \(\frac{q^{2}}{r_{c}^{2 n-2}}\) is other variables’ function , the \( {\tilde{T}}_{eff}=T_{k}\) can be obtained from Eq. (15), and \({\tilde{B}}(x)\) can be shown

$$\begin{aligned}&{\tilde{B}}(x) \left( 1-x^{n+1}\right) =\frac{2(k+c_{0}^{2} c_{2} m^{2})}{K(x, n)}x^{n-1}(1+x^{n+2})\nonumber \nonumber \\&\quad \times [n^{2}x^{n-1}(1-x^{2})(1-x^{n-1})-n(1-x^{n+1})\nonumber \\&\quad \times (1-x^{2 n-2})+(1-x^{2 n})(1-x^{n-1})]\nonumber \\&\quad +\frac{c_{0} c_{1} m^{2} r_{c}}{n K(x, n)} x^{n-1}\left( 1+x^{n+2}\right) \nonumber \\&\qquad \times [2 n^{2} x^{n}(1-x)\left( 1-x^{n-1}\right) -n\left( 1-x^{n}\right) \nonumber \\&\quad \times \left( 1-x^{2 n}\right) +\left( 1-x^{n}\right) \left( 1-x^{2 n}\right) ]\nonumber \\&\quad +(n-1) c_{0}^{3} c_{3} m^{2} x^{n-1} \frac{\left( 1+x^{n+2}\right) }{r_{c} K(x, n)}\nonumber \\&\quad \times \left[ 2 n^{2} x^{n-2}\left( 1-x^{3}\right) \left( 1-x^{n-1}\right) \right. \nonumber \\&\quad +3\left( 1-x^{2 n}\right) \left( 1-x^{n-2}\right) -n\nonumber \\&\quad \times \left( 3+3 x^{3 n-2}-4 x^{n+1}-4 x^{2 n-3}-x^{n-2}+x^{2 n}\right) ]\nonumber \\&\quad +\frac{2(n-1)(n-2) c_{0}^{4} c_{4} m^{2} x^{n-1}\left( 1+x^{n+2}\right) }{r_{c}^{2} K(x, n)}\nonumber \\&\quad \times [2(1-x^{2 n})(1-x^{n-3})-n\nonumber \\&\quad \times (2+x^{n-3}+x^{2 n}+2 x^{3 n-3}-3 x^{2 n-4}-3 x^{n+1})\nonumber \\&\quad +n^{2} x^{n-3}(1-x^{n-1})(1-x^{4})]. \end{aligned}$$
(30)

Putting Eqs. (15) and (30) into Eq. (29) we get

$$\begin{aligned} A(x)=\frac{n x^{n-1}\left( 1+x^{n+2}\right) }{\left( 1-x^{n+1}\right) }. \end{aligned}$$
(31)

The different results of \({\tilde{B}}(x)\) are obtained when we select different state parameters. By substituting \({\tilde{B}}(x)\) and the corresponding radiation temperature \(T={\tilde{T}}_{+}={\tilde{T}}_{c}\) into Eq. (29), the same results are obtained as Eq. (31). It is shown that Eq. (31) has nothing to do with the selected variables and is a universal relationship between space and time. Solving Eq. (31), we get

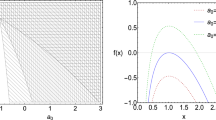
$$\begin{aligned} F_{n}(x)= & {} \frac{3 n+2}{2 n+1}\left( 1-x^{n+1}\right) ^{\frac{n}{n+1}}\nonumber \\&-\frac{(n+1)\left( 1+x^{2 n+1}\right) -(2 n+1) x^{n}(1+x)}{(2 n+1)\left( 1-x^{n+1}\right) }\nonumber \\= & {} \frac{3 n+2}{2 n+1}\left( 1-x^{n+1}\right) ^{\frac{n}{n+1}}-\frac{(n+1)\left( 1+x^{2 n+1}\right) }{(2 n+1)\left( 1-x^{n+1}\right) }\nonumber \\&-\frac{\left( 1-2 x^{n+1}-x^{2 n+1}\right) }{\left( 1-x^{n+1}\right) }+1+x^{n}\nonumber \\= & {} f_{n}(x)+1+x^{n}, \end{aligned}$$
(32)

when we solve Eq. (31), we take \(F_{n}(0)=1\) and \(f_{n}(0)=0\). It is considering that when \(x \rightarrow 0\), \(r_{+}<<r_{c}\) is just that space-time tends to be pure dS space-time. As for different space dimension \( n=2\), \(n=3\), and \(n=4\), Eq. (32) can be written as

$$\begin{aligned} F_{n=2}(x)= & {} \frac{8}{5}(1-\varvec{x}^{\varvec{3}})^{\frac{2}{3}}-\frac{3\left( 1+x^{5}\right) -5 x^{2}(1+x)}{5\left( 1-x^{3}\right) }\nonumber \\= & {} \frac{8}{5}(1-\varvec{x}^{\varvec{3}})^{\frac{2}{3}}-\frac{2\left( 4-5 x^{3}-x^{5}\right) }{5\left( 1-x^{3}\right) }+1+x^{2}\nonumber \\= & {} f_{n=2}(x)+1+x^{2},\nonumber \\ F_{n=3}(x)= & {} \frac{11}{7}\left( 1-x^{4}\right) ^{\frac{3}{4}}-\frac{4 \left( 1+x^{7}\right) -7 x^{3}(1+x)}{7\left( 1-x^{4}\right) } \nonumber \\= & {} \frac{11}{7}\left( 1-x^{4}\right) ^{3 / 4}-\frac{11-14 x^{4}-3 x^{7}}{7\left( 1-x^{4}\right) }+1+x^{3}\nonumber \\= & {} f_{n=3}(x)+1+x^{3},\nonumber \\ F_{n=4}(x)= & {} \frac{14}{9}\left( 1-x^{5}\right) ^{\frac{4}{5}}-\frac{5\left( 1+x^{9} \right) -9 x^{4}(1+x)}{9\left( 1-x^{5}\right) } \nonumber \\= & {} \frac{14}{9}\left( 1-x^{5}\right) ^{\frac{4}{5}}-\frac{2\left( 7-9 x^{5}-2 x^{9}\right) }{9\left( 1-x^{5}\right) }+1+x^{4}\nonumber \\= & {} f_{n-4}(x)+1+x^{4}. \end{aligned}$$
(33)
Fig. 1
figure 1

\( f(x)-x \) diagram for diffrent n

Full size image

Meanwhile, we can find the zero position of \(f_{n}(x)-x\), and the \(x_0\) when \(f_{n}\left( x_{0}\right) =0\). According to Eq. (32), the interaction terms \(f_{n}(x)\) are different in different dimensions, but the general trend is the same. At the point \(x=x_0\), the correction term of entropy is vanished. When \(x_{0}<x<1\), the correction term of entropy has the positive value and is increases with the increasing of x. At that time, it tends to be infinite when \(x \rightarrow 1\). When the correction term of interval entropy is negative in the region \(0<x<x_{0}\) and has a minimum value \(x=x_{m}\), From Fig. 1 we know that both \(x_{0}\) and \(x_{m}\) increase as the dimension n increases. The results show that with the increase of dimension n, the region in which the corrected entropy increases, will decrease, while the other region in which the corrected entropy decreases, will increase. Meanwhile the modified value of entropy is a function of dimension.

In the same way, we choose other independent variables to discuss, we all get the differential Eq. (31) that space-time entropy must be satisfied in different independent variables. From Eq. (31) we know that the space-time entropy’s correction term f(x) only relate to black hole horizon and cosmological horizon’s place. This point matchs to black hole horizon and cosmological horizon corresponding entropy. So the entropy is just a function of the event horizon.

When putting Eq. (31) into Eq. (25), we get the effective temperature of higher-dimensional dS black holes in dRGT massive gravity

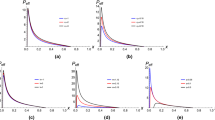
$$\begin{aligned} T_{eff}=\frac{B(x, q)\left( 1-x^{n+1}\right) }{4 \pi r_{c} x^{n-1}\left( 1+x^{n+2}\right) }. \end{aligned}$$
(34)

From Eq. (34), we can draw the \(T_{eff}-x\) curve of effective temperature by using dimension \(n=4,5,6\), certain k, and different q taking the same or different \(c_{0}^{2} c_{2} m^{2}\), \(c_{0} c_{1} m^{2}\), \( c_{0}^{3} c_{3} m^{2}\), \(c_{0}^{4} c_{4} m^{2}\) when \(r_{c}=1\), the maximum of \(T_{eff}\) is signed as \(T_{eff}^{c}\), corresponding \(x=x_{c}\); \(T_{eff}=0\) corresponding \(x_{min}=x_{0}^{T}\) as listed in Table 1.

Table 1 When n takes different values, the maximum values \(T_{eff}\) under different parameters are denoted as \(T_{eff}^c\) corresponding \(x=x_c\), and the corresponding values \(T_{eff}=0\) under different parameters are denoted as corresponding \({\varvec{x}}_{\varvec{min}}=\varvec{x}_{\varvec{0}}^{\varvec{T}}\)
Full size table

In order to clearly see the effect of relevant parameters on the effective temperature, we illustrate an example of the \(T_{eff}-x\) diagram with different value of \(c_0-c_4\) and m, n, q. which are explicitly shown in Fig. 3a–e. More specifically, the maximum value of the effective temperature \(T_{eff}\) of the system increase with \(c_0-c_4\), while the allowed region with \(T_{eff}\) lager than zero is also increased. Such tendency can also be seen from the behavior of the effective temperature as a function of x, in term of different m which is presented in Fig. 3f. In Fig. 3g, we can clearly see that the maximum value of the effective temperature of the system will decrease with n, however the variable x of maximum value of the effective temperature is increasing. Meanwhile the whole interval with \(T_{eff}\) lager than zero moves to the right. More specifically, the maximum value of the effective temperature of the system decreases with q, while the allowed region with \(T_{eff} > 0\) is also reduced in Fig.  3h.

From Eq. (11), Eqs. (22) and (24), we get

$$\begin{aligned} P_{eff}= & {} \frac{n x^{n-1} g(x, q)}{2 k^{2} r_{c}^{2} A(x)\left( 1-x^{n+1}\right) ^{2}}\nonumber \\= & {} \frac{g(x, q)}{2 k^{2} r_{c}^{2}\left( 1+x^{n+2}\right) \left( 1-x^{n+1}\right) }, \end{aligned}$$
(35)

where

$$\begin{aligned} g(x, q)= & {} \left[ \left( k+c_{0}^{2} c_{2} m^{2}\right) \frac{n \left( 1-x^{2}\right) -\left( 1-2 x^{n+1}+x^{2}\right) }{x}\right. \nonumber \\&+\frac{q^{2}\left[ \left( 1-x^{2 n}\right) -n\left( 1+x^{2 n}-2 x^{n+1}\right) \right] }{2 n(n-1) r_{c}^{2 n-2} x^{2 n-1}}\nonumber \\&+\frac{c_{0} c_{1} m^{2}}{n} r_{c}\left[ n(1-x)-x\left( 1-x^{n}\right) \right] \nonumber \\&+(n-1) c_{0}^{3} c_{3} m^{2} \frac{n\left( 1-x^{3}\right) -\left( 2+x^{3}-3 x^{n+1}\right) }{r_{c} x^{2}}\nonumber \\&+(n-1)(n-2) c_{0}^{4} c_{4} m^{2} \nonumber \\&\quad \left. \times \frac{n\left( 1-x^{4}\right) -\left( 3+x^{4}-4 x^{n+1}\right) }{r_{c}^{2} x^{3}}\right] n F_{n}(x)\nonumber \\&-\left[ \frac{n x^{n-1}\left( 1+x^{n+2}\right) }{\left( 1-x^{n+1}\right) }-n x^{n} F_{n}(x)\right] \nonumber \\&\quad \times \left[ (n-1)\left( k+c_{0}^{2} c_{2} m^{2}\right) \left( 1-x^{2}\right) \right. \nonumber \\&\quad -\frac{q^{2}\left( 1-x^{2 n}\right) }{2 n_{c}^{2 n-2} x^{2 n-2}}+c_{0} c_{1} m^{2} r_{c} x(1-x)\nonumber \\&\quad +(n-1)(n-2) c_{0}^{3} c_{3} m^{2} \frac{\left( 1-x^{3}\right) }{r_{c} x}\nonumber \\&\quad \left. +(n-1)(n-2)(n-3) c_{0}^{4} c_{4} m^{2} \frac{\left( 1-x^{4}\right) }{r_{c}^{2} x^{2}}\right] .\nonumber \\ \end{aligned}$$
(36)

From Eq. (35), we can draw the \(P_{eff}-x\) curve parameters when \(r_{c}=1\), after being determined, and when \(c_{0}^{2} c_{2} m^{2}\), \(c_{0} c_{1} m^{2}\), \(c_{0}^{3} c_{3} m^{2}\), \(c_{0}^{4} c_{4} m^{2}\), and any parameter change in dimension and other parameters remain unchanged. We can analyze the effect of parameters on the effective pressure \(P_{eff}\). The effect on the effective pressure with different \(c_{0}^{2} c_{2} m^{2}\), \(c_{0} c_{1} m^{2}\), \(c_{0}^{3} c_{3} m^{2}\), \(c_{0}^{4} c_{4} m^{2}\).

We also analyze the behavior of the effective pressure \(P_{eff}\) with different value \(c_0-c_4\), m, n, q in Fig. 4, from which one could clearly see the effect of these parameters on the effective pressure \(P_{eff} \). Notice that it is the same behavior as that of the effective temperature shown in Fig. 3a–e and Fig. 3h. Figure 4 shows the curve of the effective pressure of the system changing with the parameters. Although the values of the curves vary with the parameters, the shapes of the curves are very similar. The curve has a maximum value \(P_{eff}^c\) with the change of x, marked as \(x_c\) and the effective pressure increases monotonously as x increasing when \(x_0^T<x<x_c\), while the effective pressure decreases monotonously as x increasing the range of \(x_c<x<1\), the maximum value of the effective pressure \(P_{eff}\) and its positive region (\(P_{eff}>0\)) increase with \(c_0-c_4\) and m, but decreases with q. Differently, When n is the largest, \(P_{eff}\) is also the largest, but \(P_{eff}\) is not the smallest when n is the smallest. When only n increases, the x corresponding to the largest \(P_{eff}\) increases.

Fig. 2
figure 2

\( F(x)-x \) diagram for diffrent n

Full size image
Fig. 3
figure 3

\(T_{eff}-x \) diagrams when the parameters change respectively

Full size image
Fig. 4
figure 4

\(P_{eff}-x\) diagrams when the parameters change respectively

Full size image

4 Critical phenomena

From Fig. 3, we can see that the curves of the effective temperature of the system change with the parameters. Although the values of the curves vary with the parameters, the shapes of the curves are basically the same. The curve has a maximum value \(T_{eff}^c\) with the change of x, marked as \(x_c\) and the effective temperature increases monotonously with the increase of x when \(x_0^T<x<x_c\), but decreases monotonously with the increase x at the range of \(x_c<x<1\). From the Fig. 2, we know that the entropy increases monotonously with x, so the heat capacity of the system is positive in the \(x_0^T<x<x_c\) interval, which satisfies the requirement of equilibrium stability of the thermodynamic system, while the thermal capacity of the interval system is negative at \(x_c<x<1\) ranges, which does not satisfy the requirement of qualitative thermodynamic equilibrium.

The expression of the heat capacity of a thermodynamic system

$$\begin{aligned} C=T_{eff}\left( \frac{\partial S}{\partial T_{eff}}\right) , \end{aligned}$$
(37)

when \(r_{c}=1 \), we put Eqs. (22) and (34) into Eq. (37), one can get curve \(C-x\) .

Fig. 5
figure 5

\( C-x \) diagram for \(k=1, m=3, c_1=-3, c_2=1, c_3=1, c_4=1, r_c=1, q=0.1\)

Full size image

In Fig. 5, Phase 1 is a steady-state interval, while phase 2 is a non-steady-state interval. From the \(C-x\) curve, the system diverges at the point of \(x=x_c\). From the Fig. 2 and Eq. (21), the entropy and volume are continuous at the points \(x=x_c\). According to Ehrenfest’s classification of phase transitions, the phase transitions occurring in the system are second-order at the point \(x=x_c\). In order to further discuss the critical phenomena of the system, we discuss the Gibbs free energy of the system, where \(G=M-T_{eff}S\) [4, 64], and draw the curves under isobaric conditions, as shown in Fig. 6.

Fig. 6
figure 6

\( G-T_{eff}\) diagram for \(n=5, k=1, m=3, c_1=-3, c_2=1, c_3=1, c_4=1, r_c=1, q=0.1\)

Full size image

From the Fig. 6, we know that the effective temperature of the system corresponds to two different Gibbs free energy values. According to the irreversible process of the ordinary thermodynamic system under isothermal and isobaric conditions, the Gibbs function always decreases. Therefore, the actual process of the system follows the process of that the Gibbs function takes a small value. From the \(C-x\) curve, in the increasing process of Gibbs’ function the heat capacity is negative, which means the system is thermodynamically unstable. So the black hole satisfying this \(x_c<x<1\) condition is unstable, and there is no black hole satisfying the condition in the universe. When the effective temperature \(T_{eff}\) of the black hole remains unchanged and the black hole is in the unsteady state region \(x_c<x<1\) under external disturbance, the black hole reaches the steady state region \(x_0^T<x<x_c\) through the first-order phase transition black hole. Therefore, the first-order phase transition occurring in de Sitter space-time is a process from unstable region to stable region, which is different from the first-order phase transition of vdW system and AdS black hole, because the first-order phase transition of vdW system and AdS black hole are the transition between two states which meet the requirements of thermodynamic equilibrium stability.

5 Conclusion and discussion

Early studies on the effective temperature of de Sitter space-time were based on the assumption that the space-time entropy is known [35, 40, 65,66,67,68], and the effective temperature of de Sitter space-time was obtained by using the space-time thermodynamic quantity to satisfy the first law of thermodynamics. When the radiation temperature \(T_{+}\) of the black hole horizon is equal to that of the cosmological horizon: \(T=T_{+}=T_{c}\), the effective temperature \(T_{eff}\) obtained is not equal to that of the two horizons in general, that is \(T_{eff}\ne T\), it is hard to be accepted by people. In addition, the hypothetical entropy in studying the effective temperature of de Sitter space-time has not been proved theoretically.

In this paper we obtain the entropy equation Eq. (31) in HBHRGT space-time using the relationship of the thermodynamic first law, and the condition of \(T=T_{eff}\) when black hole horizon radiation temperature is equal to cosmological space-time horizon’s, that’s \(T=T_{+}=T_{c}\). In addition, we know that all parameters are not independent for multi-parameter space-time, because the radiation temperature of two horizons is equal, the space-time parameters need to satisfy equation Eq. (13). However, When different independent parameters are taken, we all get the equation Eq. (31) that the space-time entropy satisfies, which is independent of the parameters selected, and it is the universal relationship between space-time. When \(x\rightarrow 0\), space-time tends to be pure dS space-time (it only has the cosmological horizon), we get the HBHRGT space-time entropy function Eq. (32) and the HBHRGT space-time effective temperature Eq. (34) through solving differential equation. If we divide the HBHRGT space-time entropy S into two horizons’ sum \(S_c+S_+\) and add interaction term \(S_{t}\), we know that interaction is negative and positive value at \(0<x<x_{0}\) and \(x_{0}<x<1\), respectively, from Fig. 1 and the HBHRGT space-time entropy is an increasing function of x, which is raising with x as Fig. 2. The trend of curve changing is independent of space-time dimension, but the entropy is a function of dimensions of space-time. The curve of \(S-x\), \(T_{eff}\) and \(P_{eff}\) are presented in Figs. 2, 3 and 4 respectively.

The curves also show the effect of the effective temperature \(T_{eff}\) and the pressure of each parameter \(P_{eff}\). From Fig. 3 of the curve, we can see that no matter how the parameters change, the effective temperature \(T_{eff}\) of the system has a maximum \(T_{eff}^{c}\), which is also the second-order phase transition temperature of the system. This characteristic is different from AdS black hole. From Figs. 3 and 4, the maximum value of the effective pressure \(P_{eff}\) and the effective temperature \(T_{eff}\), as well as its positive region (\(T_{eff}>0, P_{eff} >0\)) increase with \(c_0-c_4\) and m but decrease with q. Differently, In Fig. 3g, we can clearly see that the maximum value of the effective temperature of the system decrease with n, however the variable x of maximum value of the effective temperature is increasing. Meanwhile the whole interval with \(T_{eff}\) lager than zero moves to the right. While in Fig. 4g, When only n increases, the x corresponding to the largest \(P_{eff}\) increases.

The \(C-x\) curve shows that the heat capacity has the positive value in the region \(0<x<x_{c}\), which is satisfied with the requirements of thermodynamic system equilibrium stability. However it is negative in the region \(x_{c}<x<1\), it does not satisfy the requirements of equilibrium stability. At \(x=x_{c}\) point, the heat capacity is emanative, and the system satisfies the requirements of the secondary phase change in thermodynamic system, so that \(x=x_{c}\) is the second point of phase change. Therefore dS space-time is unstable in universe when x is in range from \(x_c\) to 1 (\(x_{c}<x<1\)). And there is only black hole that satisfies the points of \(0<x<x_{c}\) possibly, which provides theoretical basis for one to investigate black hole. From the \(C-x\) curve, the effects of space-time dimension on the heat capacity and phase transition can be observed. When the parameters describing the space-time are fixed, the position of the phase transition point increases with the increase of the space-time dimension. Therefore the scope of the thermodynamically stable region increases correspondingly, which will lay the foundation for studying the thermodynamic properties of space-time in higher dimensional.