Light quark masses in ${N_\mathrm{f}=2+1}$ lattice QCD with Wilson fermions

Abstract

We present a lattice QCD determination of light quark masses with three sea-quark flavours ($N_\mathrm{f}=2+1$). Bare quark masses are known from PCAC relations in the framework of CLS lattice computations with a non-perturbatively improved Wilson-Clover action and a tree-level Symanzik improved gauge action. They are fully non-perturbatively improved, including the recently computed Symanzik counter-term $b_{\mathrm{A}} - b_{\mathrm{P}}$. The mass renormalisation at hadronic scales and the renormalisation group running over a wide range of scales are known non-perturbatively in the Schrödinger functional scheme. In the present paper we perform detailed extrapolations to the physical point, obtaining (for the four-flavour theory) $m_{\mathrm{u}/\mathrm{d}}(2~\mathrm{GeV})= 3.54(12)(9)~\mathrm{MeV}$ and $m_{\mathrm{s}}(2~\mathrm{GeV}) = 95.7(2.5)(2.4)~\mathrm{MeV}$ in the $\overline{\mathrm{MS}}$ scheme. For the mass ratio we have $m_{\mathrm{s}}/m_{\mathrm{u}/\mathrm{d}}= 27.0(1.0)(0.4)$. The RGI values in the three-flavour theory are $M_{\mathrm{u}/\mathrm{d}}= 4.70(15)(12)~\mathrm{MeV}$ and $M_{\mathrm{s}}= 127.0(3.1)(3.2)~\mathrm{MeV}$.

1 Introduction

The lattice regularisation of QCD provides a well-defined procedure for the determination of the fundamental parameters of the theory (i.e. the gauge coupling and the quark masses) from first principles. The aim of the present work is the determination of the three lightest quark masses (i.e. those of the up, down and strange flavours), in a framework in which the up and down quarks are degenerate and all heavier flavours (i.e. charm and above), if present in the theory, would be quenched (valence) degrees of freedom. This is known as $N_\mathrm{f}=2+1$ lattice QCD. Moreover, QED effects are ignored.

The three-flavour theory adopted in this paper is presumably sufficient for determining light quark masses due to the decoupling of heavier quarks [1,2,3,4]. Indeed, lattice world averages of light quark masses $m_{\mathrm{u}/\mathrm{d}}$, $m_{\mathrm{s}}$ do not show a significant dependence on the number of flavours at low energies for $N_\mathrm{f}\ge 2$ within present-day errors [5]. This also holds for the more accurately known renormalisation group independent ratio $m_{\mathrm{u}/\mathrm{d}}/m_{\mathrm{s}}$. Recently, heavy-flavour decoupling has been substantiated also non-perturbatively [6].

This paper is based on large-scale $N_\mathrm{f}=2+1$ flavour ensembles produced by the Coordinated Lattice Simulation (CLS) effort [7, 8]. The simulations employ a tree-level Symanzik-improved gauge action and a non-perturbatively improved Wilson fermion action; see references [9,10,11,12]. The sea quark content is made of a doublet of light degenerate quarks $m_{\mathrm {q},1} = m_{\mathrm {q},2}$, plus a heavier one $m_{\mathrm {q},3}$. At the physical point $m_{\mathrm {q},1}, m_{\mathrm {q},2} = m_{\mathrm{u}/\mathrm{d}}\equiv \tfrac{1}{2}(m_{\mathrm{u}}+m_{\mathrm{d}})$ and $m_{\mathrm {q},3} = m_{\mathrm{s}}$.

The bare quark masses produced by CLS [7, 8] need to be combined with renormalisation and improvement coefficients in order to obtain renormalised quantities with $\mathrm{O}(a^2)$ discretisation effects. We use ALPHA collaboration results for the quark mass renormalisation and Renormalisation Group (RG) running [13] in the Schrödinger functional (SF) scheme. Symanzik improvement is implemented for the removal of discretisation effects from correlation functions, leaving us with $\mathrm{O}(a^2)$ uncertainties in the bulk and $\mathrm{O}(g_0^4 a)$ ones at the time boundaries. We find that correlation functions extrapolations to the continuum limit are compatible with an $\mathrm{O}(a^2)$ overall behaviour. The counter-terms required for the improvement of the axial current are known from refs. [14,15,16]. The present work has combined all these elements, obtaining estimates of the up/down and strange quark masses, as well as their ratio. These are expressed as renormalisation scheme-independent and scale-independent quantities, known as Renormalisation Group Invariant (RGI) quark masses. Of course we also give the same results in the $\overline{\mathrm{MS}}$ scheme at scale $\mu = 2$ GeV.

The bare dimensionless parameters of the lattice theory are the strong coupling $g_0^2 \equiv 6/\beta$ and the quark masses expressed in lattice units $a m_{\mathrm {q},1} = a m_{\mathrm {q},2}$ and $a m_{\mathrm {q},3}$, with a the lattice spacing. They can be varied freely in simulations. Having chosen a specific discretisation of the QCD action, its parameters must be calibrated so that three “input” hadronic quantities (one for each bare mass parameter and one for the lattice spacing) attain their physical values. Other physical quantities can subsequently be predicted. Such input quantities are typically very well-known from experiment, but they also need to be precisely computed on the lattice; examples are ground state hadron masses and decay constants $(m_{\pi },f_{\pi },m_\mathrm{K},f_\mathrm{K},\ldots )$. Since the majority of numerical large-scale simulations do not yet include the small strong-isospin breaking and electromagnetic effects, the physical input quantities have to be corrected accordingly. Following Ref. [8], we use the values of Ref. [17]

$$\begin{aligned} m_{\pi }^{\scriptscriptstyle \mathrm phys}&= 134.8(3)\,\mathrm{MeV}, \quad m_\mathrm{K}^{\scriptscriptstyle \mathrm phys}= 494.2(3)\,\mathrm{MeV}, \nonumber \\ f_{\pi }^{\scriptscriptstyle \mathrm phys}&= 130.4(2)\,\mathrm{MeV}, \quad f_\mathrm{K}^{\scriptscriptstyle \mathrm phys}= 156.2(7)\,\mathrm{MeV}. \end{aligned}$$

(1.1)

The calibration of the lattice spacing, referred to as scale setting, usually singles out a dimensionful quantity as reference scale $f_\mathrm{ref}\,[\mathrm{MeV}]$. Its dimensionless counterpart $af_\mathrm{ref}$ is computed on the lattice for fixed values of the bare coupling at the point where the physical spectrum, such as $[am_{\pi }/(af_\mathrm{ref})]_{g_0^2}\equiv m_{\pi }/f_\mathrm{ref}$, is reproduced in the bare parameter space $(g_0^2,am_{\mathrm{q},i})$ of the lattice theory. In this way, the lattice spacings $a(g_0^2)=[af_\mathrm{ref}]_{g_0^2}/f_\mathrm{ref}$, and consequently all computed observables, are obtained in physical units. When simulations approach the point of physical mass parameters while the lattice spacing is lowered, computational demands rapidly increase. In the present work results are obtained at non-zero lattice spacings and at quark masses which correspond to unphysical meson and decay constant values. Thus our data need to be extrapolated to the continuum limit and extra/interpolated to the physical quark mass values. This is achieved with a joint chiral and continuum extrapolation. The present work pays particular attention to these extrapolations and interpolations and the ensuing sources of systematic error.

So far we did not specify the reference scale $f_\mathrm{ref}$. In Ref. [8] the three-flavor symmetric combination $f_{\pi \mathrm K}^{{\scriptscriptstyle \mathrm phys}}=\tfrac{2}{3}(f_\mathrm{K}^{{\scriptscriptstyle \mathrm phys}}+\tfrac{1}{2}f_{\pi }^{{\scriptscriptstyle \mathrm phys}})=147.6(5)~\mathrm{MeV}$, (obtained from the physical input of Eqs. (1.1)) was used for calibration, and for the determination of the hadronic gradient flow scale $t_0$ [18].¹ An artificial (theoretical) hadronic scale with mass dimension $-2$, $t_0$ is precisely computable with small systematic effects [19, 20], and thus well-suited as intermediate scale on the lattice. Its physical value determined from CLS ensembles [8] reads

$$\begin{aligned} \sqrt{8t_{0}^{{\scriptscriptstyle \mathrm phys}}} = 0.415(4)(2) \,\mathrm{fm}, \end{aligned}$$

(1.2)

at fixed

$$\begin{aligned} \phi _4 \equiv \Big [8t_0 (m_\mathrm{K}^2+\tfrac{1}{2}m_{\pi }^2)\Big ]^{{\scriptscriptstyle \mathrm phys}} = 1.119(21), \end{aligned}$$

(1.3)

where the first error of $\sqrt{8t_{0}^{{\scriptscriptstyle \mathrm phys}}}$ is statistical and the second systematic.

The theoretical framework of our work is explained in Sect. 2. The definitions of bare current quark masses, their renormalisation parameters and the $\mathrm{O}(a)$-improvement counter-terms are provided in standard ALPHA-collaboration fashion. There is also a fairly detailed exposition of how the so-called “chiral trajectory” (a line of constant physics – LCP) is traced by $N_\mathrm{f}=2+1$ CLS simulations. In Sect. 3 we outline the computations leading to renormalised current quark masses as functions of the pion squared mass. These are computed in the SF renormalisation scheme at a hadronic (low energy) scale. In Sect. 4 we perform the combined chiral and continuum limit extrapolations in order to obtain estimates of the physical up/down and strange quark masses. Details of the ansätze we have used are provided in Appendix A and in Appendix B. Our final results are gathered in Sect. 5. Preliminary results have been presented in [21].

2 Theoretical framework

We review our strategy for computing light quark masses with improved Wilson fermions. In what follows equations are often written for a general number of flavours $N_\mathrm{f}$. In practice $N_\mathrm{f}= 2+1$. Flavours 1 and 2 indicate the lighter fermion fields, which are degenerate; at the physical point their mass is the average up/down quark mass. Flavour 3 stands for the heavier fermion, corresponding to the strange quark at the physical point.

2.1 Quark masses, renormalisation, and improvement

The starting point is the definition of bare correlation functions on a lattice with spacing is a and physical extension $L^3 \times T$:

$$\begin{aligned} f_{\mathrm {P}}^{ij}(x_0,y_0) \,\,\equiv & {} \,\, - \dfrac{a^6}{L^3} \, \sum _{\mathbf {x}, \mathbf {y}} \langle P^{ij}(x_0,\mathbf {x}) P^{ji}(y_0,\mathbf {y}) \rangle , \nonumber \\ f_{\mathrm {A}}^{ij}(x_0,y_0) \,\,\equiv & {} \,\, - \dfrac{a^6}{L^3} \, \sum _{\mathbf {x}, \mathbf {y}} \langle A_0^{ij}(x_0,\mathbf {x}) P^{ji}(y_0,\mathbf {y}) \rangle , \end{aligned}$$

(2.1)

where the pseudoscalar density and axial current are

$$\begin{aligned} P^{ij}(x) \,\,\equiv & {} \,\, {{\bar{\psi }}}^i(x) \gamma _5 \psi ^j(x) \,\, , \end{aligned}$$

(2.2)

$$\begin{aligned} A_0^{ij}(x) \,\,\equiv & {} \,\, {{\bar{\psi }}}^i(x) \gamma _0 \gamma _5 \psi ^j(x). \end{aligned}$$

(2.3)

The indices $i,j =1,2,3$ label quark flavours, which are always distinct ($i \ne j$).

The bare current (or PCAC) quark mass is defined via the axial Ward identity at zero momentum and a plateau average between suitable initial and final time-slices $t_{\mathrm{i}} < t_{\mathrm{f}}$,

$$\begin{aligned} m_{ij}&\equiv \dfrac{a}{t_{\mathrm{f}} - t_{\mathrm{i}}+a} \nonumber \\&\quad \times \sum _{x_0 = t_{\mathrm{i}}}^{t_{\mathrm{f}}}\dfrac{\left[ \tfrac{1}{2} ({\partial _{0}}+\partial ^{*}_{0}) \, f_{\mathrm {A_0}}^{ij} + c_\mathrm{A}a{\partial _{0}}\partial ^{*}_{0} f_{\mathrm {P}}^{ij}\right] (x_0,y_0)}{2 \, f_{\mathrm {P}}^{ij}(x_0,y_0)}, \end{aligned}$$

(2.4)

with the source $P^{ji}$ positioned either at $y_0=a$ or $y_0=T-a$.² The mass-independent improvement coefficient $c_\mathrm{A}$ is determined non-perturbatively [14]. The average of two renormalised quark masses is then expressed in terms of the PCAC mass $m_{ij}$ as follows:

$$\begin{aligned}&\dfrac{m_{i\mathrm R} + m_{j\mathrm R}}{2} \,\, \equiv \,\, m_{ij\mathrm R} \,\, = \dfrac{Z_\mathrm {A}(g_0^2)}{Z_\mathrm {P}(g_0^2,a\mu )}\,\, m_{ij}\,\, \nonumber \\&\qquad \times \Big [ 1 \, + \, (b_\mathrm{A}-b_\mathrm{P}) am_{\mathrm {q},ij} \, + \, (\bar{b}_{\text {A}} - \bar{b}_{\text {P}}) a \mathrm{Tr}[M_\mathrm{q}] \Big ]\nonumber \\&\qquad + \,\, \mathrm{O}(a^2), \end{aligned}$$

(2.5)

where $M_\mathrm{q}\equiv \mathrm{diag}(m_{\mathrm {q},1},m_{\mathrm {q},2}, \cdots , m_{\mathrm {q},N_\mathrm{f}})$ is the matrix of the sea quark subtracted masses, characteristic of Wilson fermions. Given the bare mass parameter $m_{0,i} \equiv (1/\kappa _i - 8)/(2a)$, with $\kappa _i$ the Wilson hopping parameter, these are defined as

$$\begin{aligned} m_{\mathrm {q},i} = 1/(2a\kappa _i) - 1/(2a\kappa _{\mathrm{cr}}) \equiv m_{0,i}-m_\mathrm {cr}\end{aligned}$$

(2.6)

where $m_\mathrm {cr}\sim 1/a$ is an additive mass renormalisation arising from the loss of chiral symmetry by the regularisation and $\kappa _{\mathrm{cr}}$ is the critical (chiral) point. The average of two subtracted masses is then denoted by $m_{\mathrm {q},ij} \equiv \tfrac{1}{2}(m_{\mathrm {q},i}+m_{\mathrm {q},j})$ in Eq. (2.5).

The axial current normalisation $Z_\mathrm {A}(g_0^2)$ is scale-independent, whereas the current quark mass renormalisation parameter $1/Z_\mathrm {P}(g_0^2,a\mu )$ depends on the renormalisation scale $\mu$. The renormalisation condition imposed on the pseudoscalar density operator $P^{ji}$ defines the renormalisation scheme for the quark masses. The schemes used in the present work (SF and $\overline{\mathrm{MS}}$) are mass-independent. Pertinent details will be discussed in latter sections.

The improvement coefficients $b_\mathrm{A}-b_\mathrm{P}$ and $\bar{b}_{\text {A}} - \bar{b}_{\text {P}}$ of Eq. (2.5) cancel $\mathrm{O}(a)$ mass-dependent cutoff effects; they are functions of the bare gauge coupling $g_0^2$. The corresponding counter-terms of Eq. (2.5) contain the subtracted masses $am_{\mathrm {q},ij}$ and $\mathrm{Tr}[aM_\mathrm{q}]$, which require knowledge on the critical mass $m_\mathrm {cr}$. This can be avoided by substituting these masses with current quark masses and their sum. Their relationship is [22],

$$\begin{aligned} m_{ij}= Z \bigg [ m_{\mathrm {q,}ij} + \left( r_{\mathrm {m}}- 1 \right) \dfrac{\mathrm{Tr}[M_\mathrm{q}]}{N_\mathrm{f}} \bigg ] + \mathrm{O}(a), \end{aligned}$$

(2.7)

where $Z(g_0^2)\equiv Z_\mathrm{P}/(Z_\mathrm{S}Z_\mathrm{A})$ and $r_\text {m}(g_0^2)$ are finite normalisations. $Z_\mathrm{S}$ is the renormalisation parameter of the non-singlet scalar density $S^{ij} \equiv {{\bar{\psi }}}^i \psi ^j$ and $r_{\mathrm {m}}/Z_\mathrm{S}$ is the renormalisation parameter of the singlet scalar density, which indirectly defines $r_{\mathrm {m}}$; cf. Ref. [22]. In the above we neglect $\mathrm{O}(a)$ terms, as they only contribute to $\mathrm{O}(a^2)$ in the b-counter-terms of Eq. (2.5). Substituting $am_{\mathrm {q},ij}\rightarrow am_{ij}$ in the latter expression, we obtain

$$\begin{aligned}&m_{ij\mathrm R}(\mu _{\mathrm{had}}) \,\, = \,\, \dfrac{Z_\mathrm {A}(g_0^2)}{Z_\mathrm {P}(g_0^2,a\mu )} \,\, m_{ij} \,\, \Bigg [ 1 \, + \, (\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}) am_{ij} \nonumber \\&\qquad + \, \Bigg \{ (\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}) \dfrac{1-r_{\mathrm {m}}}{r_{\mathrm {m}}} + (\bar{b}_{\text {A}} - \bar{b}_{\text {P}}) \dfrac{N_\mathrm{f}}{Z r_{\mathrm {m}}} \Bigg \} \dfrac{a M_{\mathrm{sum}}}{N_\mathrm{f}} \Bigg ] \nonumber \\&\qquad + \,\, \mathrm{O}(a^2), \end{aligned}$$

(2.8)

where we define

$$\begin{aligned} \tilde{b}_{\mathrm {A}}- \tilde{b}_{\mathrm {P}}\equiv & {} \dfrac{b_\mathrm{A}- b_\mathrm{P}}{Z}, \nonumber \\ M_{\mathrm{sum}}\equiv & {} m_{12} + m_{23} + \cdots + m_{(N_\mathrm{f}-1)N_\mathrm{f}} + m_{N_\mathrm{f}1} \,\, \nonumber \\= & {} \,\, Z r_{\mathrm {m}}\mathrm{Tr}[M_\mathrm{q}] + \mathrm{O}(a). \end{aligned}$$

(2.9)

To leading order in perturbation theory the difference $b_\mathrm{A}-b_\mathrm{P}$ is $\mathrm{O}(g_0^2)$ and equals $\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}$. However, non-perturbative estimates are likely to differ significantly, especially in the range of couplings $g_0$ considered here ($1.56 \lesssim g_0^2 \lesssim 1.76$). We will employ non-perturbative estimates of $b_\mathrm{A}-b_\mathrm{P}$ and Z; cf. Ref. [23]. The term multiplying $M_{\mathrm{sum}}$ contains $(1-r_{\mathrm {m}})/r_{\mathrm {m}}$ and $(\bar{b}_{\text {A}} - \bar{b}_{\text {P}})$. In perturbation theory $r_{\mathrm {m}}= 1 + 0.001158\,C_\mathrm{F}\,N_\mathrm{f}\,g_0^4$ [24, 25], $(1-r_{\mathrm {m}})/r_{\mathrm {m}}\sim \mathrm{O}(g_0^4)$ and $(\bar{b}_{\text {A}} - \bar{b}_{P}) \sim \mathrm{O}(g_0^4)$ [22]. A first non-perturbative study of the coefficients $\bar{b}_{\text {A}}$ and $\bar{b}_{\text {P}}$ produced noisy results with 100% errors [26]. Given the lack of robust non-perturbative results and the fact that the term in curly brackets is $\mathrm{O}(g_0^4)$ in perturbation theory, it will be dropped in what follows.

Once the quark mass averages $m_{12\mathrm R}$ and $m_{13\mathrm R}$ are computed say, in the SF scheme at a scale $\mu _{\mathrm{had}}$, the three renormalised quark masses can be determined. Since we are working in the isospin limit ($m_{\mathrm {q},1} = m_{\mathrm {q},2}$), the lighter quark mass is given by $m_{12\mathrm R}$. Then one can isolate $m_{13\mathrm R}$ from the ratio $m_{13\mathrm R}/m_{12\mathrm R}$ in which, as seen from Eq. (2.8), the $M_{\mathrm{sum}}$ counter-term cancels out.

The ALPHA Collaboration is devoting considerable resources to the determination of the non-perturbative evolution of the renormalised QCD parameters (strong coupling and quark masses) between a hadronic and a perturbative energy scale ($\mu _{\text {had}} \le \mu \le \mu _{\text {pt}}$). Quark masses are renormalised at $\mu _{\text {had}} \sim \mathrm{O}(\varLambda _{\text {QCD}})$ and evolved to $\mu _{\text {pt}} \sim \mathrm{O}(M_{\text {W}})$ [13, 27,28,29,30,31,32,33,34,35,36] in the SF scheme [37, 38]. Both renormalisation and RG-running are done non-perturbatively. At $\mu _{\text {pt}}$ perturbation theory is believed to be reliably controlled and we may safely switch to the conventionally preferred, albeit inherently perturbative $\overline{\mathrm{MS}}$ scheme.

We will be quoting results also for the scheme- and scale-independent renormalisation group invariant (RGI) quark masses $M_{12}$ and $M_{13}$ (corresponding to the current masses $m_{12}$ and $m_{13}$) as well as the physical RGI quark masses $M_{\mathrm{u}/\mathrm{d}}$ and $M_{\mathrm{s}}$ derived from them. They are conventionally defined in massless schemes [39] by

$$\begin{aligned} M_i \equiv \,&m_{i \mathrm R}(\mu ) \left[ 2b_0 g_{\mathrm{R}}^2(\mu )\right] ^{-\frac{d_0}{2b_0}} \nonumber \\&\times \exp \left\{ -\int _0^{g_{\mathrm{R}}(\mu )}\mathrm{d}g\left[ \dfrac{\tau (g)}{\beta (g)}-\dfrac{d_0}{b_0g}\right] \right\} , \end{aligned}$$

(2.10)

for each quark flavour i. In our opinion, $M_i$ is better suited for comparisons either to experimental results or other theoretical determinations. Equation (2.10) is formally exact and independent of perturbation theory as long as the renormalised parameters $(g_{\mathrm{R}}, m_{i\mathrm R})$ and the continuum renormalisation group functions (i.e. the Callan–Symanzik $\beta$-function and the mass anomalous dimension $\tau$) are known non-perturbatively with satisfacory accuracy [13, 33,34,35,36]. Their computation in the SF scheme with $N_\mathrm{f}=3$ massless quarks has been carried out in Ref. [13].

Our determination of the renormalised quark masses is based on the bare current mass averages $m_{ij\mathrm R}$; cf. Eqs. (2.5) and (2.8). The analogue of these expressions for the RGI mass averages is given by

$$\begin{aligned} M_{ij} \equiv \dfrac{1}{2} ( M_i + M_j) = \dfrac{M}{m_{\mathrm{R}}(\mu _{\text {had}})} \, \, m_{ij\mathrm R}(\mu _{\mathrm{had}}). \end{aligned}$$

(2.11)

Note that the ratio $M/m_{\mathrm{R}}(\mu _{\text {had}})$ is flavour-independent; cf. Eq. (2.10). In Ref. [13] it has been computed in the SF scheme for the $N_\mathrm{f}=3$ massless flavours at $\mu _{\text {had}} = 233(8)~\mathrm{MeV}$.

2.2 The chiral trajectory and scale setting

Our aim is to stay on a line of constant Physics within systematic uncertainties of $\mathrm{O}(a^2)$, as we vary the bare parameters of the theory (i.e. the gauge coupling $g_0$ and the $N_\mathrm{f}= 2+1$ quark masses). In particular, if the improved bare gauge coupling

$$\begin{aligned} {\tilde{g}}_0^2 \equiv g_0^2 \,\, \Big ( 1 \, + \, \dfrac{1}{N_\mathrm{f}} b_g(g_0^2) a \mathrm{Tr}[ M_\mathrm{q}] \Big ) \end{aligned}$$

(2.12)

is kept fixed in the simulations, so does the lattice spacing, with any fluctuations being attributed to $\mathrm{O}(a^2)$-effects. The problem is that $b_\mathrm{g}(g_0^2)$ is only known to one-loop order in perturbation theory [40, 41]; $b_\mathrm{g}^{\mathrm{PT}}=0.012N_\mathrm{f}g_0^2$. Thus, following refs. [42, 43], we vary the quark masses at fixed $g_0^2$, ensuring that the trace of the quark mass matrix remains constant:

$$\begin{aligned} \mathrm{Tr}[ M_\mathrm{q}] \,\, = \,\, 2 m_{\mathrm{q},1} \, + \, m_{\mathrm{q},3} \,\, = \,\, \mathrm{const}. \end{aligned}$$

(2.13)

In this way the improved bare gauge coupling ${\tilde{g}}_0^2$ is kept constant at fixed $\beta$ for any $b_g$.³

This requirement leads to an unusual but unambiguous approach to the physical point, shown in the $(M_{12},M_{13})$-plane in the left panel of Fig. 1. Initially, one starts at the symmetric point ($am_{\mathrm {q},1}=am_{\mathrm {q},2}=am_{\mathrm {q},3}=am_{\mathrm {q}}^{{\scriptscriptstyle \mathrm sym}}$) for some fixed coupling $\beta =6/g_0^2$, and tunes the mass parameter of the simulation in such a way that $\mathrm{Tr}[M_\mathrm{q}]=\mathrm{Tr}[M_\mathrm{q}]_{{\scriptscriptstyle \mathrm phys}}$ to a good approximation.⁴ This is achieved by varying $am_{\mathrm {q}}^{{\scriptscriptstyle \mathrm sym}}$ until $(m_\mathrm{K}^2+\tfrac{1}{2}m_{\pi }^2)/f_\mathrm{ref}$ takes its physical value. Since it is proportional to $\mathrm{Tr}[M_\mathrm{q}]$ at leading order in chiral perturbation theory ($\chi \mathrm {PT}$), it suffices as tuning observable. In subsequent simulations, one successively lifts the mass-degeneracy towards the physical point by decreasing the light quark masses while maintaining the constant-trace condition. By doing so the physical strange quark mass is approached from below as in Fig. 1 (left panel). We call this procedure “the determination of the chiral trajectory”.

Fig. 1

The left panel shows an idealisation of the chiral trajectory for renormalised RGI current quark masses $M_{12}$ and $M_{13}$ in the continuum. The symmetric point (gray box) is defined by the trace of the renormalised RGI quark mass matrix, $M_{12}=M_{13}=M_{{\scriptscriptstyle \mathrm sym}}=\tfrac{1}{3}\mathrm{Tr}[M]$, and the physical point is indicated by red circles, where $M^{{\scriptscriptstyle \mathrm phys}}_{12}=M_{\mathrm{u}/\mathrm{d}}$ and $M^{{\scriptscriptstyle \mathrm phys}}_{13}=\tfrac{1}{2}(M_{\mathrm{u}/\mathrm{d}}+M_{\mathrm{s}})$. The right panel shows our data $\phi _{ij}\equiv \sqrt{8t_0} m_{ij}$ versus $\phi _2\equiv 8t_0m_{\pi }^2 \propto m_{12}$. Coloured (gray) points correspond to mass-shifted (-unshifted) points in parameter space, cf. the discussion in the text

Note that the improved renormalised quark mass matrix $M_{\mathrm{R}}$ is given by [22]

$$\begin{aligned}&\mathrm{Tr}[M_{\mathrm{R}}] \,\, = Z_m r_m \nonumber \\&\quad \times \Big [ (1 + a {{\bar{d}}}_m \mathrm{Tr}[M_\mathrm{q}] ) \mathrm{Tr}[ M_\mathrm{q}] + a d_m \mathrm{Tr}[M_\mathrm{q}^2] \Big ] +\mathrm{O}(a^2). \end{aligned}$$

(2.14)

Since the $d_m$-counter-term is proportional to squared bare masses, a constant $\mathrm{Tr}[M_\mathrm{q}]$ does not correspond to a constant $\mathrm{Tr}[M_{\mathrm{R}}]$; the latter requirement is violated by $\mathrm{O}(a)$ effects. This is an undesirable feature, as it implies that the chiral trajectory is not a line of constant-physics. In practice these violations have been monitored in Ref. [8] (Fig. 4, lowest lhs panel), where $\mathrm{Tr}[M_{\mathrm{R}}]$ has been computed, at constant $\mathrm{Tr}[M_q]$, from the current quark masses with 1-loop perturbative Symanzik b-coefficients. The violations appear to be bigger than what one would expect from $\mathrm{O}(a)$ effects.

These considerations have led the authors of Ref. [8] to redefine the chiral trajectory in terms of $\phi _4 =$ const., where

$$\begin{aligned} \phi _4 \,\, \equiv \,\, 8 \, t_0 \, \Big ( m_\mathrm{K}^2 \, + \, \dfrac{1}{2} m_{\pi }^2 \Big ), \end{aligned}$$

(2.15)

and $t_0$ is the gluonic quantity of the Wilson flow [18]; it has mass dimension $-2$. Here $m_{\pi }$ and $m_\mathrm{K}$ are the lightest and strange pseudoscalar mesons respectively; at the physical point these are the pion $m_{\pi }^{\scriptscriptstyle \mathrm phys}$ and kaon $m_\mathrm{K}^{\scriptscriptstyle \mathrm phys}$. Keeping $\phi _4$ constant is a Symanzik-improved constant physics condition. But $\phi _4$ is proportional to the sum of the three quark masses only in leading-order (LO) chiral perturbation theory ($\chi$PT). Thus, the improved bare coupling ${\tilde{g}}_0^2$ now suffers from $\mathrm{O}(a m_q \mathrm{Tr}[M_q ])$ discretisation effects due to higher-order $\chi$PT contributions. In practice, these turn out to be small, as can be seen from Ref. [8] (Fig. 4, lowest rhs panel), where $\mathrm{Tr}[M_{\mathrm{R}}]$ has been computed, at constant $\phi _4$. The violations appear to be at most 1% and thus the variation of the $\mathrm{O}(a)$ $b_g$-term in ${\tilde{g}}_0^2$ can be ignored.

Obviously, one must also ensure, through careful tuning, that the chosen $\phi _4 =$ const. trajectory passes through the point corresponding to physical up/down and strange renormalised masses (i.e. quark masses that correspond to the physical pseudoscalar mesons $m_{\pi }^{\scriptscriptstyle \mathrm phys}$ and $m_\mathrm{K}^{\scriptscriptstyle \mathrm phys}$). This is done by driving $\phi _4$ to its physical value $\phi _4^{\scriptscriptstyle \mathrm phys}= 8 t_0 [ (m_\mathrm{K}^{\scriptscriptstyle \mathrm phys})^2 \, + \, (m_{\pi }^{\scriptscriptstyle \mathrm phys})^2/2 ]$ through mass shifts [8]. The aim is to express the computed quantities of interest (in our case the quark masses) as functions of

$$\begin{aligned} \phi _2 \,\, \equiv \,\, 8 \, t_0 \,m_{\pi }^2, \end{aligned}$$

(2.16)

with $\phi _4$ held fixed at $\phi _4^{\scriptscriptstyle \mathrm phys}$, and eventually extrapolate them to $\phi _2^{\scriptscriptstyle \mathrm phys}= 8 t_0 (m_{\pi }^{\scriptscriptstyle \mathrm phys})^2$.

The determination of the redefined chiral trajectory is not straightforward. One needs to know the value of $\phi _4^\mathrm{{\scriptscriptstyle \mathrm phys}}$. The latter is obtained from $t_0$ and the pseudoscalar masses (corrected for isospin-breaking effects) quoted in Eq. (1.1). But since the value of $t_0$ is only approximately known, one starts with an initial guess ${\tilde{t}}_0$, which provides an initial guess ${{\tilde{\phi }}}_4$. At each $\beta$, the symmetric point with degenerate masses ($\kappa _1 = \kappa _3$) is tuned so that the computed $t_0/a^2$, $a m_{\pi }$ and $a m_\mathrm{K}$ combine as in Eq. (2.15) to give a value close to ${{\tilde{\phi }}}_4$. The other ensembles at the same $\beta$ have been obtained by decreasing the degenerate (lightest) quark mass $m_{\mathrm{q},1} = m_{\mathrm{q},2}$, while increasing the heavier mass $m_{\mathrm{q},3}$ so as to keep $\mathrm{Tr}[M_\mathrm{q}]$ constant. Thus they do not correspond exactly to the same ${{\tilde{\phi }}}_4$. Small corrections of the subtracted bare quark masses (or hopping parameters) are introduced, using a Taylor expansion discussed in Sect. IV of Ref. [8], in order to shift $\phi _4$ to the reference value ${{\tilde{\phi }}}_4$ and correct analogously the measured PCAC quark masses and other quantities of interest such as the decay constants. The procedure is repeated for each $\beta$ and the same value ${{\tilde{\phi }}}_4$ at the starting symmetric point.

All shifted quantities are now known at ${{\tilde{\phi }}}_4$ as functions of $\phi _2$. Defining the combination of decay constants

$$\begin{aligned} f_{\pi \mathrm{K}} \,\, \equiv \,\, \dfrac{2}{3} \, \Big (f_{\mathrm{K}} + \dfrac{f_\pi }{2} \Big ), \end{aligned}$$

(2.17)

the dimensionless $\sqrt{8 {\tilde{t}}_0} f_{\pi \mathrm{K}}$ is computed for all $\phi _2$ and extrapolated to ${{\tilde{\phi }}}_2 = 8 {\tilde{t}}_0 (m_\pi ^{{\scriptscriptstyle \mathrm phys}})^2$. The extrapolated $\sqrt{{\tilde{t}}_0} f_{\pi \mathrm{K}}$ , combined with the experimentally known $f_{\pi \mathrm{K}}^{{\scriptscriptstyle \mathrm phys}}$, gives a better estimate of ${\tilde{t}}_0$, and thus of ${{\tilde{\phi }}}_4$. As described in Sect. V of Ref. [8], this procedure can be recursively repeated and eventually the physical value of $t_0$ is fixed through $f_{\pi \mathrm{K}}^{{\scriptscriptstyle \mathrm phys}}$; the value in Eq. (1.2) from Ref. [8] leads to

$$\begin{aligned} \phi _4^{{\scriptscriptstyle \mathrm phys}} \,\,= & {} \,\, 1.119(21), \end{aligned}$$

(2.18)

$$\begin{aligned} \phi _2^{{\scriptscriptstyle \mathrm phys}} \,\,= & {} \,\, 0.0804(8). \end{aligned}$$

(2.19)

The main message is that once PCAC quark masses are shifted onto the chiral trajectory defined by the constant $\phi _4^{{\scriptscriptstyle \mathrm phys}}$, they only depend on a single variable, namely $\phi _2$.

In analogy to the definitions (2.15) and (2.16), we also define rescaled dimensionless bare current quark masses and their renormalised counterparts at scale $\mu _{\mathrm{had}}$

$$\begin{aligned} \phi _{ij} \, \equiv \, \sqrt{8 \, t_0} \, m_{ij} , \,\,\, \phi _{ij\mathrm R}(\mu )\, \equiv \, \sqrt{8 \, t_0} \, m_{ij\mathrm R}(\mu ). \end{aligned}$$

(2.20)

The redefined chiral trajectory is shown in Fig. 1 (right panel), where the light-light and heavy-light dimensionless mass averages ($\phi _{12 \mathrm R}$ and $\phi _{13 \mathrm R}$ respectively) are plotted as functions of $\phi _2$. Extrapolating in $\phi _2$ to $\phi _2^{{\scriptscriptstyle \mathrm phys}}$ amounts to the simultaneous approach of the light and heavy quark masses to the corresponding physical up/down and strange values. All other physical quantities are then also at the physical point. Section 4 is dedicated to these extrapolations.

Table 1 Details of CLS configuration ensembles, generated as described in Ref. [7]. In the last column, ensembles are labelled by a letter, denoting the lattice geometry, a first digit for the coupling and a further two digits for the quark mass combination

3 Quark mass computations

We base our determination of quark masses on the CLS ensembles for $N_\mathrm{f}= 2+1$ QCD, listed in Table 1. The bare gauge action is the Lüscher–Weisz one, with tree-level coefficients [11]. The bare quark action is the Wilson, Symanzik-improved [10] one. The Clover term coefficient $c_\mathrm{sw}$ has been tuned non-perturbatively in Ref. [12]. Boundary conditions are periodic in space and open in time, as detailed in Ref. [45].

For details on the generation of these ensembles see Ref. [7]. As seen in Table 1, results have been obtained at four lattice spacings in the range $0.05 \lesssim a/\mathrm{fm}\lesssim 0.086$. For each lattice coupling $\beta = 6/g_0^2$, gauge field ensembles have been generated for a few⁵ values of the Wilson hopping parameters $\kappa _1 = \kappa _2$ and $\kappa _3$. The light pseudoscalar meson (pion) varies between 200 and 420 MeV. The heaviest value corresponds to the symmetric point where the three quark masses and the pseudoscalar mesons are degenerate. The strange meson (kaon) varies between 420 and 470 MeV. Given that our lightest pseudoscalars are relatively heavy (200 MeV), the chiral limit ought to be taken with care.

The bare correlation functions $f_{\mathrm {P}}^{ij}, f_{\mathrm {A}}^{ij}$ of Eqs. (2.1) are estimated with stochastic sources located on time slice $y_0$, with either $y_0 = a$ or $y_0 = T-a$. From them the current quark masses $m_{12}, m_{13}$ are computed as in Eq. (2.4), with the $\mathrm{O}(a)$-improvement coefficient $c_{\mathrm{A}}$ determined non-perturbatively in Ref. [14]. The exact procedure to select the plateaux range in the presence of open boundary conditions has been explained in Refs. [7, 44, 46].

Having obtained the bare current quark masses $m_{12}$, $m_{13}$ at four values of the coupling $g_0^2$, we construct the renormalised dimensionless quantities $m_{12\mathrm R}(\mu _{\text {had}})$ and $m_{13\mathrm R}(\mu _{\text {had}})$; cf. Eq. (2.8). For this we need the ratio $Z_{\mathrm{A}}(g_0^2)/Z_{\mathrm{P}}(g_0^2,\mu _{\mathrm{had}})$ and the Symanzik b-counter-terms. Results for the axial current normalisation $Z_{\mathrm{A}}(g_0^2)$ are available in Ref. [47], from a separate computation based on the chirally rotated Schrödinger Functional setup of Refs. [48,49,50]. The computation of $Z_{\mathrm{P}}(g_0^2,\mu _{\mathrm{had}})$ in the SF scheme, for $\mu _{\mathrm{had}} = 233(8)~\mathrm{MeV}$, was carried out in Ref. [13] for a theory with $N_\mathrm{f}=3$ massless quarks and the lattice action of the present work. The $Z_{\mathrm{P}}$ results, shown in Eqs. (5.2) and (5.3) of Ref. [13], are in a range of inverse gauge couplings which covers the $\beta \in [3.40,3.85]$ interval of the large volume simulations of Ref. [8], from which our bare dimensionless PCAC masses are extracted.

Besides the ratio $Z_{\mathrm{A}}/Z_{\mathrm{P}}$, we also need the improvement coefficient $(\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}})$, which multiplies the $\mathrm{O}(a)$ counter-term proportional to $a m_{ij}$ in Eq. (2.8). To leading order in perturbation theory $\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}= -0.0012 g_0^2$. Non-perturbative estimates based on a coordinate-space renormalisation scheme have been provided for $N_\mathrm{f}=2+1$ lattice QCD in Ref. [26]. More accurate non-perturbative results have been subsequently obtained by the ALPHA Collaboration, using suitable combinations of valence current quark masses, measured on ensembles with $N_\mathrm{f}=3$ nearly-chiral sea quark masses in small physical volumes [16, 23]. Also these simulations have been carried out in an inverse coupling range that spans the interval $\beta \in [3.40,3.85]$ of the large volume CLS results of Ref. [8]. They are expressed in the form of ratios $R_{\mathrm{AP}}$ and $R_{\mathrm{Z}}$, from which $(b_\mathrm {A}- b_\mathrm {P})$ and Z are estimated; thus $(\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}) = R_{\mathrm{AP}}/R_{\mathrm{Z}}$. In Ref. [23], results are quoted for two values of constant Physics, dubbed LCP-0 and LPC-1. In LCP-0, $R_{\mathrm{AP}}$ and $R_{\mathrm{Z}}$ are obtained with all masses in the chiral limit. In LCP-1, one valence flavour is in the chiral limit (so it is equal to the sea quark mass), while a second one is held fixed to a non-zero value. The physical volumes are always kept fixed. In Ref. [23], Eqs. (5.1), (5.2) and (5.3) refer to LCP-0 results, while those in Eqs. (5.1), (5.4) and (5.5) refer to LCP-1; differences are due to $\mathrm{O}(a)$ discretisation effects.

We have opted to use the LCP-0 values of $\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}$ in the present work. The covariance matrices of the fit parameters of $R_{\mathrm{AP}}$ as well as those of $R_{\mathrm{Z}}$ are provided in Ref. [23]. We assume that the covariance matrix between fit parameters of $R_{\mathrm{AP}}$ and $R_{\mathrm{Z}}$ is nil. This is justified a posteriori, by repeating the analysis with LCP-1 values, as a means to estimate the magnitude of systematic errors arising from our choice. Moreover, we have also compared our LCP-0 results to those obtained from different fit functions, used in the preliminary analysis of Ref. [16], as well as from the perturbative estimate $\tilde{b}_{\mathrm {A}}-\tilde{b}_{\mathrm {P}}$. We find that the contribution arising from such variations is below $\sim 1\%$ of the total error on renormalised quark masses at the physical point.

As discussed in Sect. 2, the complicated Symanzik counter-term in curly brackets, multiplying $aM_{\mathrm{sum}}$ in Eq. (2.8), is $\mathrm{O}(g_0^4 a)$ in perturbation theory. As there are no robust non-perturbative estimates of its magnitude at present, we will drop this term, assuming that the $\mathrm{O}(g_0^4 a)$ effects it would remove are subdominant compared to $\mathrm{O}(a^2)$ uncertainties.

Table 2 Rescaled dimensionless current quark masses $\phi _{12}$ and $\phi _{13}$, renormalised in the SF scheme at $\mu _{\mathrm{\scriptscriptstyle had}}$, for each CLS ensemble used in our analysis. Note that for simulation points H102, H105, C101 more than one independent ensembles exist, which have been run with different algorithmic setups; we keep those separate before fits. All points have been shifted to the target chiral trajectory as described in the text, and the quoted errors contain both statistical uncertainties and the contribution from renormalisation and the mass shift

As already explained in Sect. 2.2, our analysis is based on the rescaled dimensionless quantities defined in Eqs. (2.15), (2.16), and (2.20). At each $\beta$ value and for each gauge field configuration, we have results for $t_0/a^2$, $a m_{12}$ and $a m_{13}$ from Refs. [7, 8], from which $\phi _{12}$ and $\phi _{13}$ are obtained. The error analysis is carried out using the Gamma method approach [51,52,53,54] and automatic differentiation for error propagation, using the library described in Ref. [55]. This takes into account all the existing errors and correlations in the data and ancillary quantities (renormalisation constants, improvement coefficients, etc.), and estimates autocorrelation functions (including exponential tails) to rescale the uncertainties correspondingly. Following [8], the estimate of the exponential autocorrelation times $\tau _{\mathrm{\scriptscriptstyle exp}}$ used in the analysis is the one quoted in [7], viz.,

$$\begin{aligned} \tau _{\scriptscriptstyle \mathrm{exp}} = 14(3)\,\dfrac{t_0}{a^2}. \end{aligned}$$

(3.1)

We have checked that without attaching exponential tails statistical errors are 40–70% smaller in our final results. The full analysis has been crosschecked by an independent code based on (appropriately) binned jackknife error estimation. Note that one of the strengths of data analysis based on the Gamma-method is that each Monte Carlo ensemble is treated independently, and the final statistical uncertainty is determined as a sum in quadratures of the statistical fluctuations for each ensemble. This allows to trace back which fraction of the statistical variance comes from each ensemble or ancillary quantities, such as renormalisation constants (see References 5–7 in [55]). This feature will be exploited in the error budgets provided below.

The starting values for $\phi _{12\mathrm R}$ and $\phi _{13 \mathrm R}$ on which the analysis is based are shown in Table 2, where renormalised quark masses are in the SF scheme at a scale $\mu _{\mathrm{\scriptscriptstyle had}} = 233(8)~\mathrm{MeV}$. By suitably fitting these quantities as functions of $\phi _2$, and extrapolating to $\phi _2^{{\scriptscriptstyle \mathrm phys}}$, we obtain the results for physical up/down and strange quarks at scale $\mu _{\mathrm{had}}$, as detailed in Sect. 4. Only then do we convert them to the RGI masses, by multiplying them with the RG-running factor [13]

$$\begin{aligned} \dfrac{M}{m_{\mathrm{R}}(\mu _{\text {had}})}=0.9148(88), \end{aligned}$$

(3.2)

with the error added in quadrature; cf. Eq. (2.11).

Before presenting our chiral fits in Sect. 4, we conclude this section with a comment on finite-volume effects. Current quark masses are not expected to be affected by finite-volume corrections, since their values are fixed by Ward identities. On the other hand, meson masses, decay constants, and the ratio $t_0/a^2$ are expected to suffer from such effects. This can be directly checked in the ensembles H200 and N202, obtained at $\beta = 3.55$ with degenerate masses and corresponding to volumes of about 2 fm and 3 fm respectively. A glance at the relevant entries of Table II of Ref. [8] shows that quark masses do not change as the volume is varied, while meson masses and decay constants vary by about 2.5%, which corresponds to differences of about $2-3.5\sigma$.⁶ Standard $\mathrm{SU}(3)$ $\chi$PT NLO formulae are available for masses and decay constants [56]; $t_0/a^2$ does not suffer from finite-volume effects up to NNLO corrections [20]. In particular, the $\chi$PT-predicted effects for meson masses are below the percent level, since the lattice spatial size in units of the inverse lightest pseudoscalar meson mass is in the range [3.9, 5.8]. On the other hand, by directly comparing the values in Table 2 obtained at the same lattice spacing and sea quark masses but different volumes (cf. Ref. [44]), it is seen that the finite-volume effects on $t_0/a^2$ and $m_\pi ^2$ are comparable and come with opposite signs. As a result, they largely cancel in $\phi _2$, the variable in which chiral fits are performed. Decay constants, which generally suffer from larger finite-volume effects than meson masses, enter our computation indirectly only – firstly through NLO terms in chiral fits, where the finite-volume correction is sub-leading, and secondly through the physical value of $\sqrt{8t_0}$ determined in [8], where these corrections have already been taken into account. We therefore expect that the quantities most affected by finite-volume effects are the rescaled current quark masses $\phi _{12},\phi _{13}$, due to the presence of $\sqrt{8t_0}/a$ in their definition. As mentioned above, these are much smaller than our statistical uncertainty, cf. Table 2. In the rest of our analysis we will therefore neglect this source of uncertainty.

4 Extrapolations to physical quark masses

Having obtained the dimensionless renormalised current mass combinations $\phi _{12 \mathrm R}$ and $\phi _{13 \mathrm R}$ at each $\beta$ as functions of $\phi _2$, we now proceed with the determination of the physical values $\phi _{\mathrm{ud}}$ and $\phi _{\mathrm{s}}$. This is done in fairly standard fashion through fits and extrapolations. To begin with, we note that the two lighter degenerate quark masses are simply given by $\phi _{12}$, whereas the heavier strange one is obtained from the difference⁷

$$\begin{aligned} \phi _{\mathrm{h}} \,\, = \,\, 2 \, \phi _{\mathrm{13}} \,- \, \phi _{\mathrm{12}}. \end{aligned}$$

(4.1)

It is then possible to perform simultaneous fits of $\phi _{12}$ and $\phi _{\mathrm{h}}$ as functions of $\phi _2$ and the lattice spacing, subsequently extrapolating the results to $\phi _2^{{\scriptscriptstyle \mathrm phys}}$ of Eq. (2.19) and the continuum limit, so as to obtain $\phi _{\mathrm{ud}}$ and $\phi _{\mathrm{s}}$. Variants of this method consist in simultaneous fits and extrapolations of either $\phi _{\mathrm{13}}$ or $\phi _{\mathrm{12}}$ on one hand and their ratio $\phi _{\mathrm{12}}/\phi _{\mathrm{13}}$ on the other. These turn out to be advantageous, as does a certain combination of ratios involving $\phi _{12}$, $\phi _{13}$, $\phi _2$, and $\phi _4$, for reasons discussed below. We recall in passing that in the ratio $\phi _{12}/\phi _{13}$ all renormalisation factors cancel.

We use fits based in chiral perturbation theory ($\chi$PT fits) which are expected to model the data well close to the chiral limit $\phi _2 = 0$. Recall that we have performed $N_\mathrm{f}= 2+1$ simulations on a chiral trajectory; starting from a symmetric point where all quark masses are degenerate, we increase the mass of the heavy quark while decreasing that of the light one, until the physical point is reached. Since both masses are varying, it is natural to use $\mathrm SU(3)_L \otimes SU(3)_R$ chiral perturbation theory, which bears explicit dependence on both masses. This works when all three quark masses in the simulations are light enough for say, NLO $\chi$PT with three flavours to provide reliable fits. In Ref. [57] it is stated that this is the case for their data, obtained with domain wall fermions, as long as the average quark mass satisfies $a m_{\mathrm{avg}} < 0.01$. As seen in Table 2 of Ref. [8], our PCAC dimensionless quark masses $a m_{12}$ and $a m_{13}$ also satisfy this empirical constraint. The real test comes about a posteriori, when the $\mathrm SU(3)_L \otimes SU(3)_R$ NLO ansätze are seen to fit our results well.

In Appendix A and Appendix B, ansätze for NLO $\chi$PT and discretisation effects are adapted to our specific parametrisation in terms of $\phi _2$ and $\phi _4$. For the current quark masses these are

$$\begin{aligned} \phi _{12} = \,&\phi _2\left[ p_1 + p_2\phi _2 + p_3 K\left( {\mathcal {L}}_2 - \dfrac{1}{3}{\mathcal {L}}_\eta \right) \right] \nonumber \\&+ \dfrac{a^2}{8t_0}\left[ C_0+C_1\phi _2\right] , \end{aligned}$$

(4.2)

$$\begin{aligned} \phi _{13} =\,&\phi _K \left[ p_1 + p_2\phi _K + \dfrac{2}{3}p_3 K{\mathcal {L}}_\eta \right] \nonumber \\&+ \dfrac{a^2}{8t_0}\left[ {\widetilde{C}}_0+ {\widetilde{C}}_1\phi _2\right] , \end{aligned}$$

(4.3)

where $\phi _K = (2 \phi _4 - \phi _2)/2$. The constants $p_1, p_2, p_3$ and K are related to standard $\chi$PT parameters in Eqs. (A.8)-(A.11), whereas the chiral logarithms ${\mathcal {L}}_2$ and ${\mathcal {L}}_\eta$ are defined in Eq. (A.12). For justification of the ansatz used for the discretisation effects, see comments after Eqs. (B.8) and (B.9). We stress again that $\phi _{12}$ and $\phi _{13}$ are functions of $\phi _2$ only, $\phi _4$ being held constant. They have common fit parameters $p_1$, $p_2$ and $p_3$.

Using the above expressions and consistently neglecting higher orders in the continuum $\chi$PT terms, we obtain the ratio of PCAC masses (cf. Eqs. (A.13) and (B.11))

$$\begin{aligned} \dfrac{\phi _{12}}{\phi _{13}} =&\dfrac{2 \phi _2}{2 \phi _4 - \phi _2}\left[ 1 + \dfrac{p_2}{p_1} \left( \dfrac{3}{2}\phi _2 - \phi _4\right) - {\tilde{K}}\left( {\mathcal {L}}_2-{\mathcal {L}}_\eta \right) \right] \nonumber \\&+ \dfrac{a^2}{8t_0} (2\phi _4 - 3\phi _2) \Big [ D_0 + D_1\phi _2 \Big ]. \end{aligned}$$

(4.4)

As discussed in Appendix B, the form of the cutoff effects respects the constraint $\phi _{12}/\phi _{13}=1$ at the symmetric point $m_{\mathrm{q},1} = m_{\mathrm{q},3}$, which is exact at all lattice spacings by construction.

For the combination defined in Eq. (A.14), we have

$$\begin{aligned} \dfrac{4 \phi _{13}}{2\phi _4 - \phi _2} + \dfrac{\phi _{12}}{\phi _2} =\,&3p_1 + 2p_2\phi _4 + p_3 K\left( {\mathcal {L}}_2+{\mathcal {L}}_\eta \right) \nonumber \\&+ \dfrac{a^2}{8t_0} \Big [ G_0 + G_1\phi _2 \Big ]. \end{aligned}$$

(4.5)

An alternative to NLO $\chi$PT fits is the use of power series, based simply on Taylor expansions around the symmetric point $m_{\mathrm{q},1} = m_{\mathrm{q},2} = m_{\mathrm{q},3}$, for which $\phi _2^{\scriptscriptstyle \mathrm{sym}} = 2\phi _4^{\scriptscriptstyle \mathrm{phys}}/3$:

$$\begin{aligned} \phi _{12}= & {} s_0 + s_1 (\phi _2-\phi _2^{\scriptscriptstyle \mathrm{sym}}) + s_2 (\phi _2-\phi _2^{\scriptscriptstyle \mathrm{sym}})^2 \nonumber \\&+ \dfrac{a^2}{t_0}\left[ S_0 + S_1(\phi _2-\phi _2^{\scriptscriptstyle \mathrm{sym}})\right] , \end{aligned}$$

(4.6)

$$\begin{aligned} \phi _{13}= & {} s_0 + {\tilde{s}}_1(\phi _2-\phi _2^{\scriptscriptstyle \mathrm{sym}}) + {\tilde{s}}_2 (\phi _2-\phi _2^{\scriptscriptstyle \mathrm{sym}})^2 \nonumber \\&+ \dfrac{a^2}{t_0}\left[ S_0 + {\tilde{S}}_1 (\phi _2-\phi _2^{\scriptscriptstyle \mathrm{sym}})\right] . \end{aligned}$$

(4.7)

Note that imposing the constraint $\phi _{12}=\phi _{13}$ at the symmetric point implies that $s_0$ and $S_0$ are common fit parameters. These expansions are expected to give reliable results in the higher end of the $\phi _2$ range, underperforming close to the chiral limit. They are thus complementary to the chiral fits, which are better suited for the small-mass regime. In this sense the two approaches may provide a handle to estimate the systematic uncertainties due to these fits and extrapolations.

We explore various fit variants, in order to unravel the presence of potentially significant systematic effects. They are encoded as follows:

• Fitted quantities and ansätze:

  [chi12] Fit of $\phi _{12}$ data only, using the $\chi$PT ansatz.

  [chi13] Fit of $\phi _{13}$ data only, using the $\chi$PT ansatz.

  [tay12] Fit of $\phi _{12}$ data only, using the Taylor expansion ansatz.

  [tay13] Fit of $\phi _{13}$ data only, using the Taylor expansion ansatz.

  [chipc] Combined fit to $\phi _{12}$ and $\phi _{13}$, using $\chi$PT.

  [chirc] Combined fit to $\phi _{13}$ and $\phi _{12}/\phi _{13}$, using $\chi$PT.

  [chirr] Combined fit to the ratio $\phi _{12}/\phi _{13}$ and the combination $2\phi _{13}/\phi _K+\phi _{12}/\phi _2$ using $\chi$PT.

  [tchir] Combined fit to $\phi _{13}$ and the ratio $\phi _{12}/\phi _{13}$, using the Taylor expansion for $\phi _{13}$ and $\chi$PT for $\phi _{12}/\phi _{13}$.

• Discretisation effects:

  [a1] Fits with terms $\propto a^2/t_0$ only.

  [a2] Fits with terms $\propto a^2/t_0$ and $\propto \phi _2 a^2/t_0$.

• Cuts on pseudoscalar meson masses:

  [420] Fit all available data, including the symmetric point; i.e. data satisfies $m_\pi \lesssim 420~\mathrm{MeV}$.

  [360] Fit excluding the symmetric point; i.e. data satisfies $m_\pi \lesssim 360~\mathrm{MeV}$.

  [300] Fit only points for which $m_\pi \le 300~\mathrm{MeV}$.

Any given fit will thus be labelled as [xxxxx][yy][zzz], using the above tags.

Fig. 2

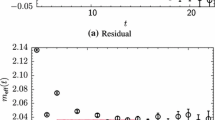
Results for the RGI light ($M_{u/d}$) and averaged ($M_{13}^{{\scriptscriptstyle \mathrm phys}}=(M_{u/d}+M_s)/2$) quark masses from independent fits to either $M_{12}$ or $M_{13}$. Results are converted to $\mathrm{MeV}$ by dividing out with $\sqrt{8t_0^{\scriptscriptstyle {\mathrm{phys}}}}$. Dotted lines indicate the central value of the latest FLAG average [5] for reference

Fig. 3

Results for the RGI light ($M_{\mathrm{u}/\mathrm{d}}$) and strange ($M_{\mathrm{s}}$) quark masses, and their ratio, from the simultaneous fits [chipc], [chirc], [chirr], and [tchir]. Results are converted to $\mathrm{MeV}$ by dividing out with $\sqrt{8t_0^{\scriptscriptstyle {\mathrm{phys}}}}$. Dotted lines indicate the central value of the latest FLAG average [5] for reference

The results obtained with the various fit methods at the physical point (cf. Eq. (2.19)) are expressed in physical units by dividing them out by $\sqrt{8t_0^{\scriptscriptstyle {\mathrm{phys}}}}$. Multiplication by the factor of Eq. (3.2) subsequently gives the RGI mass estimates shown in Figs. 2 and 3. We comment on the various fit ansätze:

Independent fits of $\varvec{\phi }_{12}$ and $\varvec{\phi }_{13}$: comparing light quark masses $M_{\mathrm{u}/\mathrm{d}}$ (upper panel of Fig. 2) from [chi12][a1] and [chi12][a2] we find that they are sensitive to the presence of a discretisation term $\propto a^2/t_0$, albeit within $\sim 1-2\sigma$. This difference is attenuated when the more stringent mass cutoff [chi12][300] is enforced, mainly because the error increases as less points are fitted. The same qualitative conclusions are true for the Taylor expansion fits [tay12] of the light quark mass. On the other hand, the lower panel of Fig. 2 shows that the average quark mass $M_{13}^{{\scriptscriptstyle \mathrm phys}}$ is not sensitive to the details of the fit ansätze. This is not surprising, given that our simulations have been performed in a region of rather heavy pions 220 MeV $\le m_\pi \le$ 420 MeV, with data covering the physical point $M_{13}^{{\scriptscriptstyle \mathrm phys}}$, while $M_{\mathrm{u}/\mathrm{d}}$ requires long extrapolations. The conclusion is that independent fits are reliable for $\phi _{13}$ but less so for $\phi _{12}$, and so we discard their results.

Combined fits to $\varvec{\phi }_{12}$ and $\varvec{\phi }_{13}$: Fig. 3 shows that the fits [chipc][a1] and [chipc][a2] give results which are sensitive to the ansatz employed for the cutoff effects. This is more pronounced for $M_{\mathrm{u}/\mathrm{d}}$ and the ratio $M_{\mathrm{s}}/M_{\mathrm{u}/\mathrm{d}}$, but persists also for $M_{\mathrm{s}}$. Moreover, fits [chipc][a1][420] and [chipc][a1][360] display visible differences when compared to fits of the [chipc][a2] variety; the latter agree with results obtained from different fit ansätze. For these reason we have also discarded results from this analysis.

Combined fits to $\varvec{\phi }_{13}$ and $\varvec{\phi }$-ratios: As previously explained, we have explored three ansätze, namely [chirc], [chirr], and [tchir]. In all cases Fig. 3 shows that there is no significant dependence of the results from the details of these fits, except for a very slight fluctuation of the [tchir][a1][420] results for $M_{\mathrm{s}}$. Preferring to err on the side of caution, we also discard [tchir] fits.

A few general points concerning the fit analysis deserve to be highlighted:

• In all our fits the $\chi ^2$/dof is well below 1. This is partly because our data are correlated – both from the fact that there are common renormalisation factors and improvement coefficients, and because we are including the contribution to the $\chi ^2$ from the fluctuations of the meson masses (horizontal errors). Therefore, while the goodness-of-fit is in general satisfactory, we will refrain from quoting the corresponding p-values, since they are not really meaningful.

• Unsurprisingly, the inclusion of a second discretisation term $\propto \phi _2(a^2/t_0)$ in the fits contributes to an increase of the error. This term is often compatible with zero, and almost always so within $\sim 2\sigma$, suggesting that fits [a1] are safe. As stated previously, exceptions are fits [chi12] and [chipc], where inclusion of this term has a strong effect.

• Within large uncertainties, the coefficients of the leading cutoff effects (i.e. those $\propto a^2/t_0$) depend on the fitted observable, and are larger for $\phi _{13}$ than for $\phi _{12}$.

• The power-series fits [tay12] and [tay13] behave remarkably well. Results from [tay12] vanish within errors in the chiral limit, except for fits going up to the symmetric point, which are sometimes incompatible with naught by 2–3$~\sigma$. This is evidence that our data are not precise enough to capture the impact of chiral logs. Fits [tay13] to $\phi _{lh}$ are very stable, and impressively better than those obtained with the $\chi$PT ansatz. Indeed, if one considers fits [texp1] and [texp2], which are safest from the point of view of error estimation, all the fits considered provide compatible results for $M_{13}$ within one sigma. Notice, furthermore, that the constant terms of [tay12] and [tay13] are generally in good agreement, signalling the consistency of the approach. It is also interesting to note that the coefficient of the quadratic term is very small and always compatible with zero within 1$\sigma$ (save for two cases where it vanishes within 2$\sigma$).

• Fits [chirc] and [chirr] appear to be the stablest.

• NLO $\chi$PT appears to be suffering around and above $400~\mathrm{MeV}$.

Fig. 4

Illustration of the chiral$+$continuum fit from which our central values are obtained. The grey band is the continuum limit of our fit, and the full black point corresponds to our extrapolation to the physical point

5 Final results and discussion

Following the analysis of Sect. 4, we quote as final results those obtained from the following procedure:

• The central values are those of a combined fit to the ratio $\phi _{12}/\phi _{13}$ and the quantity $2\phi _{13}/\phi _K+\phi _{12}/\phi _2$, using NLO $\chi$PT, with pseudoscalar meson masses less than 360 MeV and a discretisation term proportional to $a^2/t_0$ (i.e., fit [chirr][a1][360]). The error from this fit will appear as the first uncertainty in the results below. The fit is illustrated in Fig. 4.

• We estimate systematic errors from the spread of central values of all other [chirr] and [chirc] fits, for all pion mass cutoffs, and for both [a1] and [a2]. The spread is intended to be the difference between the central value, obtained as described in the previous item, and the most distant central value of all other [chirr] and [chirc] fits. This is the second error of the results below. Recall that [chirc] are combined fits to $\phi _{13}$ and the ratio $\phi _{12}/\phi _{13}$, using NLO $\chi$PT.

• Discard other fits, including [chipc], considered too unstable.

• All results have been obtained using the Symanzik ${\tilde{b}}$-parameters computed in the LCP-0 case (see discussion in Sect. 3). Using LPC-1 results instead, has very marginal effects on the error.

• In Sect. 3 we have also argued that for the quantities under consideration finite volume effects are negligible.

The resulting RGI masses are

$$\begin{aligned} M_{\mathrm{s}}&= 127.0(3.1)(3.2)~\mathrm{MeV}, \nonumber \\ M_{\mathrm{u}/\mathrm{d}}&= 4.70(15)(12)~\mathrm{MeV}. \end{aligned}$$

(5.1)

Table 3 Contributions to the squared errors of our final quantities from different sources

The quark mass ratio is obtained from

$$\begin{aligned} \dfrac{M_{\mathrm{s}}}{M_{\mathrm{u}/\mathrm{d}}} = \dfrac{2}{\phi _{ll}/\phi _{lh}}-1. \end{aligned}$$

(5.2)

Dependence on renormalisation is only implicit, from the joint fit with $\phi _{13}$. The same procedures as above yield

$$\begin{aligned} \dfrac{M_{\mathrm{s}}}{M_{\mathrm{u}/\mathrm{d}}} = 27.0(1.0)(0.4). \end{aligned}$$

(5.3)

The above results for RGI masses refer to the $N_\mathrm{f}=2+1$ theory.

Fig. 5

Contributions to the statistical$+$chiral extrapolation$+$continuum limit uncertainties from each ensemble included in our analysis, for our preferred fit [chirr][a1][360]

It is customary in phenomenological studies to report light quark masses measured in the $N_\mathrm{f}=2+1$ lattice theory in the $\overline{\mathrm{MS}}$ scheme at 2 GeV, referred to the more physical QCD with four flavours. This entails using $N_\mathrm{f}=3$ perturbative RG-running from 2 GeV down to the charm threshold, followed by $N_\mathrm{f}=4$ perturbative RG-running back to 2 GeV; see for example Ref. [5]. We use 4-loop perturbative RG-running and the value for the $\varLambda _{\mathrm{QCD}}^{\overline{\mathrm{MS}}}$ parameter computed by the ALPHA Collaboration in Ref. [34] to obtain⁸

$$\begin{aligned} m_{\mathrm s \mathrm R}(2~\mathrm{GeV})&= 95.7(2.5)(2.4)~\mathrm{MeV}, \nonumber \\ m_{\mathrm {u/d} \mathrm R}(2~\mathrm{GeV})&= 3.54(12)(9)~\mathrm{MeV}. \end{aligned}$$

(5.4)

The mass ratio is obviously the same as in Eq. (5.3). We note in passing that switching to the four-flavour theory has a very small effect on $\overline{\mathrm{MS}}$ results, since at $2~\mathrm{GeV}$ the matching factor is $m_{\mathrm{R}}(N_\mathrm{f}=4)/m_{\mathrm{R}}(N_\mathrm{f}=3) =1.002$.

The error budget for our computation is summarised in Table 3 and Fig. 5. Uncertainties are completely dominated by our chiral fits. We have separated these errors into two contributions; see first two lines of Table 3. The first error is that of our best fit [chirr][a1][360], and includes the statistical errors as well as the error from combined fits in $\phi _2$ and a. The second uncertainty is the one arising upon varying the fit ansätze and their $\phi _2$ range. All other errors are clearly seen to be subdominant. It is worth noting that, as expected, the largest contribution to the uncertainty comes from the ensembles with the lightest sea pion masses, especially the one with the finest lattice spacing. It is then clear that decreasing our errors would require more chiral ensembles, and more extensive simulations at light masses.

The current FLAG 2019 [5] world averages from $N_\mathrm{f}=2+1$ simulations, in the $\overline{\mathrm{MS}}$ scheme, reportedly quoted for the $N_\mathrm{f}=4$ theory as explained above, are:

$$\begin{aligned} m_{\mathrm s \mathrm R}(2 \mathrm{GeV})&= 92.03(88) \mathrm{MeV}, \nonumber \\ m_{\mathrm {u/d} \mathrm R}(2 \mathrm{GeV})&= 3.364(41) \mathrm{MeV}. \end{aligned}$$

(5.5)

The strange mass estimate is based on the results of Refs. [58,59,60,61,62,63], while the up/down one is based on Refs. [58,59,60,61, 64]. For the quark mass ratio, based on Refs. [58,59,60, 63], FLAG quotes

$$\begin{aligned} \dfrac{m_{\mathrm s \mathrm R}}{m_{\mathrm {u/d} \mathrm R}} = 27.42(12) \mathrm{MeV}. \end{aligned}$$

(5.6)

Our results for the strange and light quark masses agree with those of FLAG within $1.7\sigma$ and $1.2\sigma$ respectively and thus exhibit good compatibility albeit with bigger errors.

Appendices

Chiral perturbation theory expansions

We adapt standard $\chi$PT expressions to our specific parametrisation of the data, stemming from our choice of chiral trajectory. We start, for example, from Eqs. (B5) and (B6) of Ref. [57], which are NLO chiral expansions of the light and strange pseudoscalar mesons $m_{\pi }$ and $m_{\mathrm{K}}$ in terms of light and strange quark masses $m_1 = m_2$ and $m_3$. These series are inverted, so that quark masses are functions of meson masses. The PCAC quark mass combinations $m_{12} = (m_1 + m_2)/2$ and $m_{13} = (m_1 + m_3)/2$ are then formed and everything is re-expressed in terms of the dimensionless quark masses $\phi _{\mathrm{12}}$, $\phi _{\mathrm{13}}$ and the dimensionless quantities $\phi _2$ and $\phi _4$, so that we arrive at

$$\begin{aligned} \phi _{12}= & {} \dfrac{\phi _2}{2 B_0 \sqrt{8t_0}} \,\cdot \,\Bigg \{\, 1 \, - \, \dfrac{16}{8t_0 f_0^2}(2 L_8 - L_5) \phi _2 \nonumber \\&-\, \dfrac{32}{8t_0 f_0^2}(2L_6-L_4) \phi _4 \, -\, \dfrac{1}{24\pi ^2 8 t_0 f_0^2}\nonumber \\&\, \times \bigg [\dfrac{3}{2} \phi _2\ln \bigg ( \dfrac{\phi _2}{8 t_0 \varLambda _\chi ^2} \bigg ) \, - \,\dfrac{1}{2}\phi _\eta \ln \bigg ( \dfrac{\phi _\eta }{8 t_0 \varLambda _\chi ^2}\bigg ) \bigg ] \,\Bigg \},\nonumber \\ \end{aligned}$$

(A.1)

and

$$\begin{aligned} \phi _{13}= & {} \dfrac{2\phi _4 - \phi _2}{4 B_0 \sqrt{8t_0}} \,\cdot \,\Bigg \{\,1\, -\,\dfrac{8}{8t_0 f_0^2}(- 2 L_8 + L_5) \phi _2\nonumber \\&-\,\dfrac{16}{8t_0 f_0^2}(4L_6 + 2 L_8 -2L_4 - L_5) \phi _4 \nonumber \\&- \dfrac{1}{24\pi ^2 8t_0 f_0^2}\,\phi _\eta \ln \bigg ( \dfrac{\phi _\eta }{8t_0 \varLambda _\chi ^2}\bigg ) \,\Bigg \}, \end{aligned}$$

(A.2)

where $B_0, f_0, L_k (k=4,5,6,8)$ are standard $\chi$PT parameters and

$$\begin{aligned} \phi _\eta \,\, \equiv 8 t_0 \dfrac{4 m_{\mathrm{K}}^2 - m_\pi ^2}{3} \,\, = \,\, \dfrac{4 \phi _4 - 3 \phi _2}{3}. \end{aligned}$$

(A.3)

The NLO LECs $L_i$ and $B_0$ are implicitly renormalised at scale $\varLambda _\chi$. It is also useful to consider the ratio

$$\begin{aligned} \dfrac{\phi _{12}}{\phi _{13}} =&\dfrac{2\phi _2}{2\phi _4 - \phi _2} \left\{ 1 - \dfrac{24}{8t_0f_0^2}(2L_8-L_5)\left[ \phi _2 - \dfrac{2}{3}\phi _4\right] \right. \nonumber \\&- \dfrac{1}{16\pi ^2(8t_0f_0^2)}\left[ \phi _2\ln \left( \dfrac{\phi _2}{8t_0\varLambda _\chi ^2}\right) \right. \nonumber \\&\left. \left. -\, \phi _\eta \ln \left( \dfrac{\phi _\eta }{8t_0\varLambda _\chi ^2}\right) \right] \right\} , \end{aligned}$$

(A.4)

which does not require renormalisation. Note that at the symmetric point ($\phi _2 = 2 \phi _4 /3$) the current quark masses of Eqs. (A.1) and (A.2) respect the constraint $\phi _{12} = \phi _{13}$, while the ratio (A.4) is exactly 1. Note that the sum of ratios

$$\begin{aligned}&\dfrac{4 \phi _{13}}{2\phi _4-\phi _2} + \dfrac{\phi _{12}}{\phi _2} = \dfrac{3}{2B_0\sqrt{8t_0}}\nonumber \\&\qquad \times \left\{ 1 - \dfrac{16}{8t_0f_0^2}\left( \dfrac{4}{3}L_8-\dfrac{2}{3}L_5+4L_6-2L_4\right) \phi _4\right. \nonumber \\&\qquad - \dfrac{1}{48\pi ^2(8t_0f_0^2)}\left[ \phi _2\ln \left( \dfrac{\phi _2}{8t_0\varLambda _\chi ^2}\right) \right. \nonumber \\&\qquad \left. \left. +\, \phi _\eta \ln \left( \dfrac{\phi _\eta }{8t_0\varLambda _\chi ^2}\right) \right] \right\} , \end{aligned}$$

(A.5)

has the remarkable advantages of depending on just one combination of NLO LECs, and of being free of polynomial dependence on $\phi _2$.

We next rewrite Eqs. (A.1) and (A.2) in forms which are suitable for combined fits, with common coefficients for $\phi _{12}$ and $\phi _{13}$, obtaining

$$\begin{aligned} \phi _{12}&= \phi _2\left[ p_1 + p_2\phi _2 + p_3 K\left( {\mathcal {L}}_2 - \dfrac{1}{3}{\mathcal {L}}_\eta \right) \right] , \end{aligned}$$

(A.6)

$$\begin{aligned} \phi _{13}&= \dfrac{2\phi _4 - \phi _2}{2}\left[ p_1 + p_2 \left( \phi _4 - \dfrac{\phi _2}{2} \right) + \dfrac{2}{3}p_3 K{\mathcal {L}}_\eta \right] , \end{aligned}$$

(A.7)

where the coefficients $p_1, p_2$, and $p_3$ relate to LECs as follows:

$$\begin{aligned} p_1&= \dfrac{1}{2B_0\sqrt{8t_0}}\left[ 1-\dfrac{32}{8t_0f_0^2}(2L_6-L_4)\phi _4\right] \nonumber \\&\approx \dfrac{1}{2B_0\sqrt{8t_0}}\left[ 1-\dfrac{32}{8t_0f_{\pi K}^2}(2L_6-L_4)\phi _4\right] , \end{aligned}$$

(A.8)

$$\begin{aligned} p_2&= -\dfrac{1}{2B_0\sqrt{8t_0}}\dfrac{16}{8t_0f_0^2}(2L_8-L_5)\nonumber \\&\approx -\dfrac{1}{2B_0\sqrt{8t_0}}\dfrac{16}{8t_0f_{\pi K}^2}(2L_8-L_5), \end{aligned}$$

(A.9)

$$\begin{aligned} p_3&= -\dfrac{1}{2B_0\sqrt{8t_0}}. \end{aligned}$$

(A.10)

We also define

$$\begin{aligned} K \equiv (8t_016\pi ^2 f_0^2)^{-1} \approx (8t_016\pi ^2f_{\pi K}^2)^{-1}, \end{aligned}$$

(A.11)

with $f_{\mathrm{\pi K}}$ given by Eq. (2.17). The chiral logarithms are

$$\begin{aligned} {\mathcal {L}}_2 \equiv \phi _2\ln \phi _2, \quad {\mathcal {L}}_\eta \equiv \phi _\eta \ln \phi _\eta . \end{aligned}$$

(A.12)

The following points should be kept in mind:

• We are using only configurations along the $\phi _4=\mathrm{constant}$ chiral trajectory. Terms proportional to $\phi _4$ are thus reabsorbed into constant fit terms.

• Our expressions are linear in fit parameters, rather than non-linear factors in which LECs appear explicitly. Determination of LECs is beyond the scope of the present work.

• By replacing $f_0^2$ by $f_{\pi K}^2$ in the above definition of K, the coefficients of chiral logarithms are completely fixed relative to the LO value; cf. Eqs. (A.1) and (A.2). This eliminates one fit parameter, pushing its effect to NNLO LECs. In practice, the fact that terms with $\phi _4$ are reabsorbed into the LO terms nullifies the effect in some fits, e.g., those for $\phi _{12}$ and $\phi _{13}$. A second advantage of this choice is that the resulting ansätze are fully linear in the fit parameters. See also Eq. (2.5) in [8] and comments therein on the reasons that $f_0 \approx f_{\pi K}$ and for preferring $f_{\pi K}$ to $f_0$.

• We conveniently set the renormalisation scale to $\varLambda _\chi =1/\sqrt{8t_0} \simeq 476~\mathrm{MeV}$, simplifying the chiral logs. There is no need to reabsorb $\ln (8t_0\varLambda _\chi ^2)$ terms in fit parameters. This is an unconventional choice, as common practice consists in providing results for LECs at $\varLambda _\chi =m_\rho$ or $\varLambda _\chi =4\pi f_0$. Consequently, NLO LECs eventually obtained with our methodology may only be compared to results in the literature after some extra work.

Using the above expressions and consistently neglecting higher mass orders, we obtain for the ratio (A.4) of PCAC masses

$$\begin{aligned} \dfrac{\phi _{12}}{\phi _{13}}= & {} \dfrac{2\phi _2}{2\phi _4 - \phi _2}\left[ 1 + \dfrac{p_2}{p_1} \left( \dfrac{3}{2}\phi _2 - \phi _4\right) - {\tilde{K}}\left( {\mathcal {L}}_2-{\mathcal {L}}_\eta \right) \right] .\nonumber \\ \end{aligned}$$

(A.13)

For the combination (A.5) we have

$$\begin{aligned} \dfrac{4\phi _{13}}{2\phi _4-\phi _2} + \dfrac{\phi _{12}}{\phi _2} = 3p_1 + 2p_2\phi _4 + p_3 K\left( {\mathcal {L}}_2+{\mathcal {L}}_\eta \right) .\nonumber \\ \end{aligned}$$

(A.14)

With $\phi _4$ held constant, the quantities of Eqs. (A.6), (A.7), (A.13), and (A.14) are functions of $\phi _2$ only. We use these expressions to fit our data, after adding $\mathrm{O}(a^2)$ terms which model leading discretisation effects that have been neglected throughout this “Appendix”.

Discretisation effects

In order to parametrise the discretisation effects of the quantities we fit, we first examine $\phi _{ij}$; cf. Eqs. (2.5) and (2.20). It can be written in the very general form

$$\begin{aligned} \phi _{ij}=\phi _{ij}^{\text {cont}}+f\big (a,\frac{m_i+m_j}{2},\frac{m_i-m_j}{2}, \mathrm{Tr}[ M_\mathrm{q}] \big ), \end{aligned}$$

(B.1)

where $\phi _{ij}^{\text {cont}}$ is the continuum quantity and the function f contains the discretisation effects which in general depend on the lattice spacing a, the quark masses $m_i$, $m_j$, and the trace of the mass matrix $\mathrm{Tr}[M_\mathrm{q}]$. As we have discussed in Sect. 2, we will ignore $\mathrm{O}(g_0^4 \mathrm{Tr}[M_{\mathrm{sum}}])$ discretisation effects and only consider the influence of $\mathrm{O}(a^2)$ uncertainties. Also $\phi _{ij}$ has to be symmetric with respect to the exchange of quarks, $i \leftrightarrow j$. We can thus parametrise f as follows:

$$\begin{aligned}&f\big (a,\frac{m_i+m_j}{2},\frac{m_i-m_j}{2}, \mathrm{Tr}[ M_\mathrm{q}]\big ) \nonumber \\&\quad =c_0\dfrac{a^2}{t_0}+c_1\dfrac{a^2}{t_0}\sqrt{8t_0}\bigg (\dfrac{m_i+m_j}{2}\bigg ) + c_2 \dfrac{a^2}{t_0} \sqrt{8t_0} \mathrm{Tr}[M_{\mathrm{_q}}] \nonumber \\&\qquad +c_3\dfrac{a^2}{t_0}8t_0\bigg (\dfrac{m_i+m_j}{2}\bigg )^2 +c_4\dfrac{a^2}{t_0}8t_0\bigg (\dfrac{m_i-m_j}{2}\bigg )^2 \nonumber \\&\qquad + c_5 \dfrac{a^2}{t_0} 8t_0 \mathrm{Tr}[M_\mathrm{q}^2] + c_6 \dfrac{a^2}{t_0} 8t_0 (\mathrm{Tr}[M_\mathrm{q}])^2 \nonumber \\&\qquad + c_7 \dfrac{a^2}{t_0}\sqrt{8t_0}\bigg (\dfrac{m_i+m_j}{2} \bigg ) \sqrt{8t_0} \mathrm{Tr}[M_\mathrm{q}] + \mathrm{O}(a^3). \end{aligned}$$

(B.2)

A further simplification is brought about by neglecting the dependence of $c_0, \ldots , c_7$ on the bare coupling $g_0^2$.

Next we write the function f in terms of $\phi _2$, recalling that a constant $\phi _4$ constrains the relation between the heavier (strange) and light quark masses. This is done by first expressing the current quark masses on the rhs of the above equation in terms of $\phi _{12}$ and $\phi _{13}$, followed by using their LO $\chi \mathrm {PT}$ relations to $\phi _2$ and $\phi _4$. In particular, with $\beta _0 \equiv 1/(2 B_0 \sqrt{8 t_0})$, we see from Eqs. (A.6), (A.7) that to LO:

$$\begin{aligned}&\phi _{12} {\mathop { =}\limits ^{\small {\mathrm{LO}} }} \beta _0\phi _2, \end{aligned}$$

(B.3)

$$\begin{aligned}&\phi _{13} {\mathop { =}\limits ^{\small {\mathrm{LO}} }} \beta _0\dfrac{1}{2}(2\phi _4-\phi _2), \end{aligned}$$

(B.4)

$$\begin{aligned}&\sqrt{8t_0} \bigg (\dfrac{m_1-m_3}{2}\bigg ) \phi _{12}-\phi _{13} {\mathop { =}\limits ^{\small {\mathrm{LO}} }} \beta _0\bigg (\dfrac{3}{2}\phi _2-\phi _4\bigg ), \end{aligned}$$

(B.5)

$$\begin{aligned}&\sqrt{8t_0} \mathrm{Tr}[M_\mathrm{q}] = \sqrt{8t_0} [ 2 m_1 + m_3] \,\, {\mathop { =}\limits ^{\small {\mathrm{LO}} }} \,\, 2 \beta _0 \phi _4, \end{aligned}$$

(B.6)

$$\begin{aligned}&8t_0 \mathrm{Tr}[M_\mathrm{q}^2] = 8t_0 [ 2 m_1^2 + m_3^2] \,\, = \,\, 2 \phi _{12}^2 + \phi _h^2 \nonumber \\&\qquad \qquad \quad \,\, {\mathop { =}\limits ^{\small {\mathrm{LO}} }} 2 \beta _0^2 [ 3 \phi _2^2 + 2\phi _4^2 - 4 \phi _4 \phi _2]. \end{aligned}$$

(B.7)

Inserting the above LO expressions in Eq. (B.2) we obtain, after some straightforward algebra, that for two light quarks the discretisation function has the form

$$\begin{aligned} f_{12}(a,\phi _2)&\equiv f(a, m_1, 0,\mathrm{Tr}[M_\mathrm{q}]) \nonumber \\&= \dfrac{a^2}{8 t_0} \big [ C_0+C_1 \phi _2+C_2 \phi _2^2 \big ]+\mathrm{O}(a^3), \end{aligned}$$

(B.8)

where $C_k$ (with $k = 0, 1, \dots$) depend on the constants $\beta _0$, $\phi _4$, and the coefficients $c_l$, suitably rescaled by factors of $8 t_0$ (with $l = 0, 1, \dots$). Similarly, for the heavier and a light quark we obtain

$$\begin{aligned} f_{13}(a,\phi _2)&\equiv f(a, m_1, m_3, \mathrm{Tr}[M_\mathrm{q}]) \nonumber \\&= \dfrac{a^2}{8 t_0} \big [ \widetilde{C}_0 +{\widetilde{C}}_1\phi _2+{\widetilde{C}}_2\phi _2^2\big ] +\mathrm{O}(a^3). \end{aligned}$$

(B.9)

Note that, although in general coefficients $C_n$ and ${\widetilde{C}}_n$ are not the same, in the case of $m_3 = m_1$ (symmetric point) $f_{13} = f_{12}$ trivially.

The very fact that we have used LO $\chi$PT to obtain the last two expressions (cf. Eqs. (B.3)–(B.7)) allows us to drop $\mathrm{O}(a^2 \phi _2^2)$ contributions of $f_{12}$ and $f_{13}$. Moreover, standard power-counting schemes in Wilson $\chi$PT [65, 66] suggest that terms of $\mathrm{O}(a^2)$ enter at the same order as $\mathrm{O}(m_\pi ^2)$, which would imply that the terms of $\mathrm{O}(a^2 \phi _2)$ should also be dropped. We will nevertheless keep this term and explore its impact.

For the ratio of $\phi _{12}$ and $\phi _{13}$ we have that

$$\begin{aligned} \dfrac{\phi _{12}}{\phi _{13}}&= \dfrac{\phi _{12}^{\text {cont}}+f_{12}(a,\phi _2)}{\phi _{13}^{\text {cont}} +f_{13}(a,\phi _2)} \nonumber \\&= \dfrac{\phi _{12}^{\text {cont}}}{\phi _{13}^{\text {cont}}} + \dfrac{f_{12}}{\phi _{13}^{\text {cont}}} - \dfrac{f_{13} \phi _{12}^{\text {cont}}}{(\phi _{13}^{\text {cont}})^2} +\cdots . \end{aligned}$$

(B.10)

We write the discretisation functions $f_{12}$ and $f_{13}$ as in Eqs. (B.8) and (B.9) and then express coefficients $C_0, C_1, \widetilde{C}_0, \widetilde{C}_1, \dots$ in terms of the original coefficients $c_i$ of Eq. (B.2). After some algebra we end up with

$$\begin{aligned} \dfrac{\phi _{12}}{\phi _{13}}&= \dfrac{\phi _{12}^{\text {cont}}}{\phi _{13}^{\text {cont}}} + \dfrac{a^2}{8t_0} \dfrac{2\phi _4 - 3\phi _2}{(2 \phi _4- \phi _2)^2} \Big [ D_0 + D_1\phi _2 + D_2 \phi _2^2 \Big ]\nonumber \\&+ \mathrm{O}(a^3). \end{aligned}$$

(B.11)

The coefficients $D_0, D_1, D_2, \dots$ depend on the $c_i$’s. The factor $2 \phi _4 - \phi _2$ in the discretisation term vanishes at the symmetric point $\phi _2= 2 \phi _4/3$. This confirms that at the symmetric point the ratio $\phi _{12}/\phi _{13}$ is 1 by construction, for any lattice spacing. In analogy to the arguments exposed above for $f_{12}$ and $f_{13}$, we drop the $D_2 \phi _2^2$ term in our fits. Moreover, the variation of the denominator $(2\phi _4 - \phi _2)^2$ is relatively mild, ranging between $\sim 2$ and $\sim 4.6$ as $\phi _2$ varies between $\sim 0.1$ and $\sim 0.8$ in our simulations. To simplify matters, we reabsorb this $\mathrm{O}(1)$ term in re-definitions of $D_0$ and $D_1$.

Finally, for the combination of Eq. (A.14), we straightforwardly parametrise the discretisation errors in a way analogous to $f_{12}$ and $f_{13}$; see Eq. (4.5).