1 Introduction

In cosmology, current experimental information appear to show the recent cosmic expansion of the universe. On a broad range, physical cosmology covers the investigation of the description of the universe. From the different recognize cosmological evidence the current cosmic acceleration of the universe disclosed [1,2,3,4,5,6,7], which is measured by certain analyses [8,9,10,11,12]. In the present age current perceptions fully recommend that the cosmic acceleration is experiencing by the universe [13, 14]. The force is generally indicated as dark energy (DE), which is responsible for a development in a specific phase of the universe. To coordinate with later examined data different DE models have been proposed and in this arrangement the most least complex model is the \(\Lambda \)CDM (Cold dark matter) model, which is in great concurrence with the ongoing observational information. In general relativity (GR), this model is obtained by presenting the cosmological constant \(\Lambda ,\) for which equation of state (EoS) parameter is \(w_{\Lambda }=-1\) [15, 16].

To illustrate the entire development history of the universe, a cosmological model needs both an accelerated and a decelerated phase, for this the deceleration parameter plays a vital part [3, 17,18,19,20,21]. A valuable tool against a progressively development history of the universe is the parametrization of the deceleration parameter q. Up until now a few well-known parameterizations for the deceleration parameter have been introduced [22,23,24]. Mamon and Das [25] presented a logarithmic parameterization of the deceleration parameter in the spatially flat FRW metric. They used type Ia supernovae, cosmic microwave background and baryon acoustic oscillation dataset and also they reconstructed the EoS, deceleration parameter and the jerk parameter compared with reconstructed models of parameterized deceleration parameter with other known parameterizations of q. Mamon [26] introduced a generalized parametrization of q to studied the development history of the universe. They used the recent measurement of the Hubble parameter found from the type Ia supernovae and cosmic chronometer model data. Furthermore, the parametric approach likewise improves productivity of the future cosmological overviews. To determine the transition from decelerating phase to an accelerating phase it is reasonable to follow a parametric approach. Inspired by these facts, we have picked a special type of deceleration parameter so that the parameterized deceleration parameter q(z) will give the ideal property for sign flip from a decelerating phase to an accelerating phase.

For the expansion of the universe many theories have represented models, however none of them was totally fruitful. GR was not conformally invariant theory [27], therefore, as an alternative theory of GR modified conformal gravity was proposed [28, 29]. Under the scale transformation the conformal Weyl gravity is the primary gravitational theory which is constant. Hermann Weyl [30, 31] introduced conformal gravity or Weyl gravity, for cosmology conformal gravity is also of concern. Tanhayi et al. [32] shown that the estimated value of cosmological constant and Hubble parameter are close to their measured values. They studied the dependence of Hubble parameter and cosmological constant in Weyl gravity, as a function of t and r. Ghanaatian et al. [33] considered the modified gravity coupled by Weyl tensor in spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric, they described the cosmic expansion of the universe also they checked stability conditions of models. Varieschi and Ault [34] analyzed the classic wormhole geometries in conformal Weyl gravity. They described the main energy condition as well as distinct wormhole solutions.

It is generally trusted that, investigations of the associations among thermodynamics and gravity theories would gives us some understanding into the genuine idea of gravity. For this reason generally many models have been examined, specifically gravity theories for example braneworld [35,36,37], Lovelock and Gauss–Bonnet gravity [38, 39], f(R) [40,41,42,43,44] models. Geng et al. [45] verified the generalized first and second law of thermodynamics with the disformal transformation of the f(R) gravity in the FLRW metric. They studied the equilibrium as well as non-equilibrium picture of the generalized second law of thermodynamics (GSLT). Zubair et al. [46] examined the first law of thermodynamics (FLT) and GSLT at apparent horizon in FRW universe in \(f(R,R_{\alpha \beta } R^{\alpha \beta },\phi )\) gravity, where R is the Ricci invariant, \(R_{\alpha \beta }R^{\alpha \beta }\) is the Ricci tensor and \(\phi \) is the scalar field respectively. They presented the equilibrium as well as non-equilibrium picture of GSLT and to observed the validity of GSLT they choose some specific models.

This paper is structure as follows. In Sect. 2 we discuss the model of the Weyl gravity and construct the cosmological parameters and define the four different models of Hubble parameter. In Sect. 3 we examine the equilibrium picture of thermodynamics and analyze the GSLT. In Sect. 4 we define the observational values from the dataset and observe the behavior of cosmological parameters, validity of GSLT as well as thermal equilibrium condition and in Sect. 5 we conclude our result.

2 Basics of Weyl gravity

The action [47] for Weyl gravity is given as

$$\begin{aligned} S= & {} -\int \sqrt{-g}d^4x\bigg [\frac{C_{\mu \nu \rho \lambda }C^ {\mu \nu \rho \lambda }}{k} \nonumber \\&+\frac{g^{\mu \nu }\partial _ {\mu }\phi \partial _{\nu }\phi }{2}-V(\phi )-f(\phi ) {\mathcal {L}}_m\bigg ], \end{aligned}$$
(1)

where \({\mathcal {L}}_m\) is the matter Lagrangian density, \(V(\phi )\) is the potential term dependent on chameleon scalar field \(\phi ,\) \(f(\phi )\) is an analytical function which is the modification of matter Lagrangian density and \(C_{\mu \nu \rho \lambda }\) is the Weyl tensor, which is given as

$$\begin{aligned} C_{\mu \nu \rho \lambda }= & {} R_{\mu \nu \lambda \rho }-\frac{1}{2} \bigg (g_{\mu \lambda }R_{\nu \rho }-g_{\mu \rho }R_{\nu \lambda }- g_{\nu \lambda }R_{\mu \rho }+g_{\nu \rho }R_{\mu \lambda }\bigg )\nonumber \\&+\frac{R}{6} \bigg (g_{\mu \lambda }g_{\nu \rho }-g_{\mu \rho }g_{\nu \lambda }\bigg ). \end{aligned}$$
(2)

Putting the Weyl tensor in Eq. (1), we get

$$\begin{aligned} S= & {} -\int \sqrt{-g}d^4x\bigg [\frac{1}{k}\bigg (R^{\mu \nu \rho \lambda }R_ {\mu \nu \rho \lambda }-2R^{\mu \nu }R_{\mu \nu }+\frac{R^2}{3}\bigg ) \nonumber \\&+\frac{g^{\mu \nu }\partial _\mu \phi \partial _\nu \phi }{2}-V(\phi ) -f(\phi ){\mathcal {L}}_m\bigg ], \end{aligned}$$
(3)

the term \(\sqrt{-g}(R^{\mu \nu \rho \lambda }R_{\mu \nu \rho \lambda } -4R^{\mu \nu }+R^2)\) is a Gauss–Bonnet term and during the integration of Eq. (3) it disappears. The term \(R^{\mu \nu \rho \lambda }R_{\mu \nu \rho \lambda }\) can be written as \(R^2\) and \(R^{\mu \nu }R_{\mu \nu }.\) Then the action is given as

$$\begin{aligned} S= & {} -\int \sqrt{-g}d^4x\bigg [\frac{2}{k}\bigg (R_{\mu \nu }R^{\mu \nu }-\frac{R^2}{3}\bigg ) \nonumber \\&+\frac{g^{\mu \nu }\partial _\mu \phi \partial _\nu \phi }{2}-V(\phi )-f(\phi ) {\mathcal {L}}_m\bigg ]. \end{aligned}$$
(4)

By solving the Eq. (4) about the metric \(g^{\mu \nu },\) the field equation [48, 49] is define as

$$\begin{aligned} fT^{(m)}_{\mu \nu }+T^{(\phi )}_{\mu \nu }=\frac{4{\mathcal {W}}_{\mu \nu }}{k}, \end{aligned}$$
(5)

where \(T^{(\phi )}_{\mu \nu }\) is the energy-momentum tensor and \(T^{(m)} _{\mu \nu }\) is the energy-momentum tensor in the form of perfect fluid of the non-relativistic matter and

$$\begin{aligned} {\mathcal {W}}_{\mu \nu }= & {} -\frac{g_{\mu \nu }\square R}{2}-\square R_{\mu \nu } +\nabla _\rho \nabla _\mu R^\rho _\nu \nonumber \\&+\nabla _\rho \nabla _\nu R^\rho _\mu - 2R^\rho _\mu R_\nu \rho \nonumber \\&+\frac{g_{\mu \nu }R_{\rho \lambda }R^{\rho \lambda }}{2}-\frac{2\nabla _\mu \nabla _\nu R}{3}+\frac{2g_{\mu \nu }\square R}{3}\nonumber \\&+\frac{2RR_{\mu \nu }}{3} -\frac{g_{\mu \nu }R^2}{6}, \end{aligned}$$
(6)
$$\begin{aligned} T^{(\phi )}_{\mu \nu }= & {} \partial _\mu \phi \partial _\nu \phi -g_{\mu \nu } \bigg (\frac{g^{\alpha \beta }\partial _{\alpha }\phi \partial _\beta \phi }{2}-V(\phi )\bigg ), \end{aligned}$$
(7)
$$\begin{aligned} T^{(m)}_{\mu \nu }= & {} g_{\mu \nu }{\mathcal {L}}_m-\frac{2\Delta {\mathcal {L}}_m}{\Delta g^{\mu \nu }}, \end{aligned}$$
(8)

and \(f=f(\phi )\) and \(R_{\mu \nu }\) is the Ricci tensor.

Now, the flat FRW metric is given by

$$\begin{aligned} ds^2=dt^2-a(t)^2\bigg [dr^2+r^2(d\theta ^2+\sin \theta ^2 d\varphi ^2)\bigg ], \end{aligned}$$
(9)

from Eq. (9) the standard modified FRW equations defined as

$$\begin{aligned} 3H^2= & {} \rho _{eff}, \nonumber \\ {\dot{H}}= & {} -\frac{1}{2}(\rho _{eff}+p_{eff}), \end{aligned}$$
(10)

where \(H\equiv \frac{{\dot{a}}}{a}\) is the expansion rate with respect to the cosmic time, \(\rho _{eff}\) and \(p_{eff}\) are effective energy density and pressure of the system, here \(\rho _{eff}\) and \(p_{eff}\) are

$$\begin{aligned} \rho _{eff}= & {} \rho _R+\rho _mf, \nonumber \\ p_{eff}= & {} p_R+\gamma \rho _mf, \end{aligned}$$
(11)

where \(\gamma =\frac{p_m}{\rho _m}\) and

$$\begin{aligned} \rho _R= & {} V(\phi )+\frac{{\dot{\phi }}^2}{2}+\frac{3H^2}{k}-\frac{48H{\ddot{H}}}{k},\nonumber \\ p_R= & {} V(\phi )-\frac{{\dot{\phi }}^2}{2}-\frac{3H^2}{k}-\frac{2{\dot{H}}}{k} -\frac{72}{k}\bigg (5H^4+\frac{26{\dot{H}}H^2}{3}\nonumber \\&+\frac{4H{\ddot{H}}}{3}+{\dot{H}}^2\bigg ). \end{aligned}$$
(12)

The energy conservation equations are given as

$$\begin{aligned} {\dot{\rho }}_m+3H\rho _m(1+\gamma )= & {} -\frac{\rho _m{\dot{f}}}{f}, \end{aligned}$$
(13)
$$\begin{aligned} {\dot{\rho }}_R+3H\rho _R(1+w)= & {} 0. \end{aligned}$$
(14)

From action (4) the wave equation of motion for chameleon scalar field is obtained as

$$\begin{aligned} \ddot{\phi }+3H{\dot{\phi }}+V_{\phi }+\gamma \rho _mf_{\phi }=0, \end{aligned}$$
(15)

where subscript \(\phi \) denotes the derivative with respect to scalar field. Now from (13), we find

$$\begin{aligned} \rho _m=\frac{A}{a^{3(1+\gamma )}f}, \end{aligned}$$
(16)

where A is the constant term. By using Eqs. (11) and (12) the effective EoS is define as

$$\begin{aligned}&w_{eff}=\frac{p_{eff}}{\rho _{eff}}=\frac{A\gamma a^{-3(1+\gamma )}+V(\phi )-\frac{{\dot{\phi }}^2}{2}-3H^2-2{\dot{H}} -72(H^4+\frac{26{\dot{H}}H^2}{3}+\frac{4H{\ddot{H}}}{3}+{\dot{H}}^2)}{Aa^{-3(1+\gamma )} +V(\phi )+\frac{{\dot{\phi }}^2}{2}+3H^2-48H{\ddot{H}}}, \end{aligned}$$
(17)

from the parameter of EoS we classify the acceleration and deceleration aspects of the universe. By taking the time derivative of Eq. (11) the square speed of sound is given as

$$\begin{aligned} v^2_s=\frac{\frac{dp_{eff}}{dt}}{\frac{d\rho _{eff}}{dt}}, \end{aligned}$$
(18)

where

$$\begin{aligned} \frac{dp_{eff}}{dt}= & {} -3AH\gamma (1+\gamma )a^{-3(1+\gamma )}+V_{\phi }{\dot{\phi }}-{\dot{\phi }}\ddot{\phi } \nonumber \\&-6H{\dot{H}}-2{\ddot{H}}-72\bigg [4{\dot{H}}H^3\nonumber \\&+\frac{26}{3}[2{\dot{H}}^2H+{\ddot{H}}H^2]+\frac{4}{3}[{\dot{H}}{\ddot{H}} +\dddot{H}H]+2{\dot{H}}{\ddot{H}}\bigg ], \nonumber \\ \frac{d\rho _{eff}}{dt}= & {} -3AH\gamma (1+\gamma )a^{-3(1+\gamma )}+V_\phi {\dot{\phi }}+{\dot{\phi }}\ddot{\phi } \nonumber \\&+6H{\dot{H}}-48[H\dddot{H}+{\dot{H}}{\ddot{H}}], \end{aligned}$$
(19)

the square speed of sound tell us about the stability of DE models, the model is stable if \(v^2_s>0\) otherwise it is unstable. The deceleration parameter is define as

$$\begin{aligned} q(z)=-1-\frac{{\dot{H}}}{H^2}=-1+\frac{(H'(z))^2(1+z)}{2H^2(z)}. \end{aligned}$$
(20)

To representing the nature of the universe expansion rate parametrization of the q (deceleration parameter) plays a vital role. For this we choose four different models of parameterized deceleration parameter and find Hubble parameter in terms of redshift.

2.1 Model 1:

The parametrization of this model [25] is given as

$$\begin{aligned} q(z)=q_0+q_1\bigg (\frac{\ln (N+z)}{1+z}-\ln N\bigg ).~N>1 \end{aligned}$$
(21)

We deal with two parameters \(q_0,~q_1\) with their convenient physical analysis, by using the observational data we can efficiently constrain them, so the Eq. (eq21) can clarify the current universe evolution more accurately [25]. By comparing the Eqs. (20) and (21), the Hubble parameter is given by

$$\begin{aligned} H(z)=H_0N^{\frac{Nq_1}{-1+N}}(N+z)^{-\frac{(N+z)q_1}{(1+z)(-1+N)}}(1+z)^ {(1+q_0+\frac{q_1}{-1+N}-q_1\ln N)}, \end{aligned}$$
(22)

where \(q_0,~q_1,~N\) are model parameters and \(H_0\) is the current value of Hubble parameter, which is describe as \(H_0=67.\)

2.2 Model 2:

The linear parametrization of the deceleration parameter is given by [3]

$$\begin{aligned} q(z)=q_0+q_1z. \end{aligned}$$
(23)

The above linear deceleration parameter (which is linear in z (cosmic redshift) and a (scale factor)) utilized to examine the kinematics of the universe [50]. By taking Eqs. (20) and (23) the Hubble parameter is derived as

$$\begin{aligned} H(z)=H_0e^{q_1z}(1+z)^{(1+q_0-q_1)}. \end{aligned}$$
(24)

2.3 Model 3:

Next parametrization of the q is of following the form [21, 51,52,53,54,55]

$$\begin{aligned} q(z)=q_0+\frac{q_1z}{1+z}. \end{aligned}$$
(25)

The motivation of this parametric structure for deceleration parameter q(z) comes from one of the most prominent parametrization of the dark energy EoS [56, 57] and despite extremely basic, is by all accounts adaptable enough to mimic the q(z) behavior of immense class of acceleration models [58].

The expression of H(z) is evolve for this model as

$$\begin{aligned} H(z)=H_0e^{-\frac{q_1z}{1+z}}(1+z)^{(1+q_0+q_1)}. \end{aligned}$$
(26)

2.4 Model 4:

Now we have q(z) for flat \(\Lambda \)CDM model [25] which is obtain as

$$\begin{aligned} q(z)=-1+\frac{3}{2\bigg [1+\frac{\Omega _{\Lambda _0}}{\Omega _{m_0}}(1+z)^{-3}\bigg ]}, \end{aligned}$$
(27)

where \(\Omega _{m_0}+\Omega _{\Lambda _0}=1.\) We use this model to observe the decelerated and accelerated phase of the universe for the best fit values from the observational data. And we chose \(\Omega _{m_0}=0.375\) for flat universe. For this model Hubble parameter is define as

$$\begin{aligned} H(z)=H_0\bigg [\Omega _{m_0}(1+z)^3+(1-\Omega _{m_0})\bigg ]^{\frac{1}{2}}. \end{aligned}$$
(28)

3 Thermodynamics laws in equilibrium characterization

In this section, we analyze the FLT in modified Weyl gravity at Hubble horizon for flat FRW universe. From the condition \(h^{\mu \nu }\partial _\mu R_A \partial _\nu R_A =0\) [59,60,61], Hubble horizon is given as

$$\begin{aligned} R_A = \frac{1}{H}. \end{aligned}$$

By taking the time derivative of Hubble horizon, we have

$$\begin{aligned} dR_A =\frac{HR^3_A}{2}(\rho _{eff} + p_{eff})dt, \end{aligned}$$
(29)

the general Bekenstein–Hawking entropy is defined as \(S=\frac{A}{4G},\) where \(A=4\pi r^2\) is the area of the horizon [62, 63]. Utilizing the entropy, Eq. (29) becomes

$$\begin{aligned} \frac{G}{2\pi R_A}dS=\frac{HR^3_A}{2}(\rho _{eff}+p_{eff})dt. \end{aligned}$$
(30)

The horizon temperature [64] is described as

$$\begin{aligned} T_h = \frac{|k_{sg}|}{2 \pi },~~ k_{sg}&= \frac{1}{2\sqrt{-h}} \partial _\mu (\sqrt{-h} h^{\mu \nu } \partial _\nu R_A)\nonumber \\&= -\frac{1}{R_A} (1 - \frac{{\dot{R}}_A}{2 H R_A})= -\frac{R_A}{2} (2 H^2 {+} {\dot{H}}). \end{aligned}$$
(31)

Multiplying \(T_h = -\frac{1}{2 \pi R_A}(1 - \frac{\dot{R_A}}{2 H R_A})\) on both sides of Eq. (30), we can get

$$\begin{aligned} T_h dS=[4\pi HR^3_A dt-2\pi R^2_A dR_A](\rho _{eff}+p_{eff}). \end{aligned}$$
(32)

The Misner-sharp energy is given as \(E=\frac{R_A}{4G},\) the energy density in terms of the volume represent as \(V=\frac{4\pi R_A^3}{3},\) which is interpret as

$$\begin{aligned} {\tilde{E}}=\frac{3H^2}{8\pi G}V\equiv \rho _{eff} V. \end{aligned}$$
(33)

Taking the differential of Eq. (33), we easily find

$$\begin{aligned} d{\tilde{E}}=-4\pi HR_A^3(\rho _{eff}+p_{eff})dt+4\pi R^2_A\rho _{eff} dR_A. \end{aligned}$$
(34)

Combining the Eqs. (32) and (34), we can acquire

$$\begin{aligned} T_hdS=-d{\tilde{E}}+2\pi R_A^2(\rho _{eff}-p_{eff})dR_A. \end{aligned}$$
(35)

The work density is described as

$$\begin{aligned} {\tilde{W}}= -\frac{1}{2} (T^{(M)\mu \nu } h_{\mu \nu } + {\tilde{T}}^{(de)\mu \nu } h_{\mu \nu })=\frac{1}{2}(\rho _{eff}-p_{eff}), \end{aligned}$$
(36)

using the work density in Eq. (35), we get

$$\begin{aligned} T_hdS=-d{\tilde{E}}+{\tilde{W}}dV. \end{aligned}$$
(37)

3.1 Generalized second law of thermodynamics

To describe the equilibrium picture of the GSLT [46], we can write the Gibbs equation in terms of the density and total pressure which is define as

$$\begin{aligned} TdS_i=d(\rho _{eff}V)+p_{eff}dV, \end{aligned}$$
(38)

by taking the time derivative of Eqs. (37) and (38) it leads to

$$\begin{aligned} {\dot{S}}+{\dot{S}}_i=-\frac{48\pi ^2{\dot{H}}^2}{RH^3}(\rho _{eff}+p_{eff}), \end{aligned}$$
(39)

where \(R=6({\dot{H}}+2H^2),~~{\dot{S}}\) and \({\dot{S}}_i\) represents the horizon entropy and the sum of all entropy components inside the horizon. The condition which satisfy the entropy relation is define as

$$\begin{aligned} {\dot{S}}_{tot}={\dot{S}}+{\dot{S}}_{i}\ge 0. \end{aligned}$$
(40)

From Eq. (39), we can easily get

$$\begin{aligned} {\dot{S}}_{tot}=\frac{12\pi {\dot{H}}^2}{GRH^3}\ge 0. \end{aligned}$$
(41)

4 Power-law correction

By the power-law correction we choose \(\phi =\phi _oa^n\) and \(V(\phi )=\phi ^p.\) By putting the power-law terms the EoS parameter, reads

$$\begin{aligned} w_{eff}= & {} \bigg [A\gamma a^{-3(1+\gamma )}+(\phi _oa^n)^p-\frac{(n{\dot{a}}a^{n-1}\phi )^2}{2}-3H^2 \nonumber \\&-2{\dot{H}} -72\bigg (H^4+\frac{26{\dot{H}}H^2}{3} + \frac{4H{\ddot{H}}}{3}\nonumber \\&+{\dot{H}}^2\bigg )\bigg ]\bigg [ Aa^{-3(1+\gamma )} +(\phi _oa^n)^p+\frac{(n{\dot{a}}a^{n-1}\phi )^2}{2}\nonumber \\&+3H^2 - 48H{\ddot{H}}\bigg ]^{-1}. \end{aligned}$$
(42)

Inserting the power-law terms in Eq. (18) becomes

$$\begin{aligned} v^2_s= & {} \bigg [-3H\gamma A(1+\gamma )a^{-3(1+\gamma )}\nonumber \\&+p(\phi _oa^n)^{p-1}(n{\dot{a}}a^{n-1}\phi )^2- n^2(n-1)a^{2n-3}{\dot{a}}^3\phi _o^2 \nonumber \\&-n^2a^{2n-2}{\dot{a}}\ddot{a}\phi _o^2-6H{\dot{H}} -2{\ddot{H}}\nonumber \\&-72\bigg (20{\dot{H}}H^3+\frac{26}{3}\bigg (2H{\dot{H}}^2+{\ddot{H}}H^2\bigg )\nonumber \\&+\frac{4}{3}\bigg (H\dddot{H}+{\ddot{H}} {\dot{H}}\bigg )+ 2{\dot{H}}{\ddot{H}}\bigg )\bigg ] \nonumber \\&*\bigg [-3HA\gamma (1+\gamma )a^{-3(1+\gamma )}+p(\phi _oa^n)^{p-1}\nonumber \\&*(n{\dot{a}}a^{n-1}\phi )^2 - n^2(n-1)a^{2n-3}{\dot{a}}^3\phi _o^2\nonumber \\&- n^2a^{2n-2}{\dot{a}}\ddot{a}\phi _o^2-6H{\dot{H}} \nonumber \\&-48\bigg (H\dddot{H}+{\dot{H}}{\ddot{H}}\bigg )\bigg ]^{-1}. \end{aligned}$$
(43)

From the power-law terms Eq. (39) can be written as

$$\begin{aligned} {\dot{S}}+{\dot{S}}_i= & {} -\frac{48\pi ^2{\dot{H}}^2}{RH^3}\bigg [\bigg (Aa^{-3(1+\gamma )} +(\phi _oa^n)^p \nonumber \\&+\frac{(n{\dot{a}}a^{n-1}\phi )^2}{2}+3H^2 \nonumber \\&- 48H{\ddot{H}}\bigg )+\bigg (A\gamma a^{-3(1+\gamma )}+(\phi _oa^n)^p \nonumber \\&-\frac{(n{\dot{a}}a^{n-1}\phi )^2}{2}-3H^2-2{\dot{H}} \nonumber \\&-72\bigg (H^4+\frac{26{\dot{H}}H^2}{3} + \frac{4H{\ddot{H}}}{3}+{\dot{H}}^2\bigg )\bigg )\bigg ]. \end{aligned}$$
(44)

Now, by using four different models of Hubble parameter we observe the validity of GSLT and thermal equilibrium condition. We also check the stability of the system and decelerated phase of EoS parameter. For this purpose, we consider the observational values of \(q_0,~q_1\) and \(H_0.\)

5 Observational results

In this section, we express the current Observational dataset and explain the results. We use the observational values from cosmic chronometer (CC) dataset and local value of the Hubble parameter [26]. To measure the Hubble parameter in terms of redshift CC was first established by Jimenez and Loeb [65]. By using CC+\(H_0\) dataset for all models, graphically we observe the stability of GSLT, thermal equilibrium condition, EoS and square speed of sound. The observational values of the model parameter \((q_o,~q_1)\) from CC+\(H_o\) dataset is given in Table 1.

Table 1 For \(q_o,~q_1\) the best fit values from CC+\(H_o\) dataset
Full size table

5.1 Model 1

We plot graphs for model 1 at Hubble horizon with Bekenstein-Hawking entropy for the best fit values of \(q_0, ~q_1\) from the CC+\(H_o\) dataset by taking the values of parameter \(A=1.5,~\phi =6000,~\gamma =-0.3,~p=0.1 ,~n=3,~N=2\) and the observational value of Hubble constant is \(H_o=67.\)

Fig. 1
figure 1

Plot of \(w_{eff}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 2
figure 2

Plot of \(v^2_s\) versus z at Hubble horizon with Bekenstein entropy

Full size image

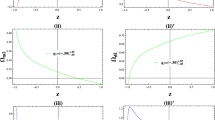
Figure 1 demonstrate that with the observational values of \(q_o,~q_1\) and \(H_o\) the trajectories of Eos parameter remains in quintessence region at early as well as present epoch and it leads to vacuum DE region at later epoch. In Fig. 2 with the same observational values of \(q_o,~q_1\) and \(H_o\) trajectories remains in positive direction at early, present and later epoch which confirms the stability condition i.e. \(v^2_s\ge 0.\)

Fig. 3
figure 3

Plot of \(S'_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 4
figure 4

Plot of \(S''_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image

The trajectories in Fig. 3 remains in positive direction at early and present epoch and for \(z\ge -0.6\) increasing towards positive direction at later epoch which shows that GSLT is valid at early as well as present epoch and at later epoch GSLT only valid for \(z\ge -0.6\). Figure 4 confirms that the thermal equilibrium condition satisfies at early, present as well as later epoch.

5.2 Model 2

By taking the same values of all parameters we plot the graphs and observe the stability of EoS, square speed of sound, GSLT and thermal condition for the best fit values from CC+\(H_o\) dataset..

Fig. 5
figure 5

Plot of \(w_{eff}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 6
figure 6

Plot of \(v^2_s\) versus z at Hubble horizon with Bekenstein entropy

Full size image

At early as well as present epoch the Eos parameter remains in the quintessence region with the observational values of \(q_o,~q_1\) and \(H_o\) and at later epoch it meet the vacuum DE region in Fig. 5. All trajectories in Fig. 6 increasing towards positive direction which shows the stability for the model 1 at Hubble horizon for the best fit values from observational dataset.

Fig. 7
figure 7

Plot of \(S'_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 8
figure 8

Plot of \(S''_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image

The validity of GSLT confirms in the left side figure for all the observational values as all trajectories gradually decreasing in positive direction at early, present as well as later epoch Fig. 7. The thermal equilibrium condition Fig. 8 cannot satisfies at early as well as present epoch but at later epoch blue trajectory fulfills the thermal condition at \(z\ge -0.01,\) red and green trajectory confirms the thermal equilibrium condition at \(z\ge -0.2.\) Thus the thermal equilibrium condition satisfies for \(z\ge -0.01\) (blue trajectory) and for \(z\ge -0.2\) (red and green trajectory) at Hubble horizon.

5.3 Model 3

From the CC+\(H_0\) dataset we plot graphs for best fit values with the same values of parameter \(A,~\phi ,~p,~n, ~\gamma ,~n.\)

Fig. 9
figure 9

Plot of \(w_{eff}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 10
figure 10

Plot of \(v^2_s\) versus z at Hubble horizon with Bekenstein entropy

Full size image

In Fig. 9 EoS parameter displays the quintessence region in early, present as well as later epoch. The right side trajectories Fig. 10 increasing positively which confirms the stability condition at early, present as well as later epoch.

Fig. 11
figure 11

Plot of \(S'_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 12
figure 12

Plot of \(S''_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image

Figure 11 demonstrate the validity of GSLT at early, present as well as later epoch as all trajectories fulfill the condition \(S'_{tot}\ge 0.\) All trajectories (Fig. 12) shows that the thermal equilibrium condition satisfies at early, present as well as later epoch.

5.4 Model 4

In this model we choose the value of \(\Omega _{m0}=0.37\) for flat universe [66] with the same values of all parameters and discuss result at Hubble horizon along with Bekenstein–Hawking entropy.

Fig. 13
figure 13

Plot of \(w_{eff}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 14
figure 14

Plot of \(v^2_s\) versus z at Hubble horizon with Bekenstein entropy

Full size image

At early as well as present epoch the EoS parameter remains in quintessence region and at later epoch it gradually decreasing towards the vacuum DE region Fig. 13. The right side trajectory Fig. 14 fulfills the stability condition \(v^2_s \ge 0\) at early, present as well as later epoch.

Fig. 15
figure 15

Plot of \(S'_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Fig. 16
figure 16

Plot of \(S''_{tot}\) versus z at Hubble horizon with Bekenstein entropy

Full size image
Table 2 Results of the cosmological parameters, GSLT and thermal equilibrium condition
Full size table

GSLT is valid at early, present as well as later epoch in Fig. 15 as the condition \(S'_{tot}\ge 0\) fulfills. The condition of thermal equilibrium satisfies at early as well as present epoch and at later epoch thermal condition cannot satisfies as the trajectory increasing towards positive phase in Fig. 16.

6 Summary

In this work, we observed the validity of GSLT and thermal equilibrium condition in Weyl gravity in a flat FRW universe with chameleon scalar field at Hubble horizon with Bekenstein-Hawking entropy, also we constructed the cosmological parameters. We choose different parameterized deceleration parameter and Hubble parameter models in term of redshift, by using these models of Hubble parameter we discussed the validity of GSLT, thermal equilibrium condition as well as we discussed the stability condition and the behavior of EoS parameter. We explored the behavior of GSLT, thermal equilibrium condition and cosmological parameters by using power-law corrections, in terms of redshift. We graphically plot these constructed models and discussed our results for observational values from CC+\(H_o\) dataset. We also discussed the behavior of constructed models for the \(\Lambda \)CDM model by taking the observational value for flat universe. We used the current measured observational value of the Hubble constant analyzed by Planck. We shown that for the power-law terms the EoS parameter remains in quintessence and vacuum region, the stability condition is valid for all models. The preference of choosing this type of parameterized deceleration parameter is that it organize a wide class of feasible models of cosmic expansion. In cosmology, by choosing some particular evolution situation for a cosmological parameter and after that gauge the estimations of the parameters with the support of various observational dataset, the parametric reconstruction procedure manages an attempt to develop a model. The plan to parameterize deceleration parameter q(z) is a straightforward way to deal with the transition of the universe from decelerated expansion phase to accelerated expansion phase and furthermore establish possibilities for future examination in regards to the nature of the dark energy.

The results we analyzed from the values of the model parameter from CC+\(H_o\) dataset in 1\(\sigma \) confidence level are given in Table 2.