Abstract
Models with non-gravitational interactions between the dark matter and dark energy components are an alternative to the standard cosmological scenario. These models are characterized by an interaction term, and a frequently used parameterization is \(Q = 3\xi H \rho _{x}\), where H is the Hubble parameter and \(\rho _{x}\) is the dark energy density. Although recent analyses have reported that this particular scenario provides a potential solution to the \(H_{0}\) and \(\sigma _{8}\) tensions for negative values of the interaction parameter \(\xi \), we show here that such an interval of values of \(\xi \) leads to a violation of the Weak Energy Condition for the dark matter density, which is accompanied by unphysical instabilities of matter perturbations. Using current observational data we also show that the inclusion of the physical prior \(\xi \ge 0\) in the statistical analysis alters the parameter selection for this model and discards it as a solution for the \(H_{0}\)-tension problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As it is well known, there is no known fundamental principle that prevents a non-minimal coupling between the energy components of the cosmological dark sector. Such a possibility has in fact been explored since the eighties as an alternative to the standard cosmology (see e.g. [1,2,3]), with its theoretical and observational consequences being of great interest nowadays [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. However, in the absence of a natural guidance from fundamental physics on the coupling term, a number of phenomenological models have been proposed and their cosmological consequences investigated in light of the current observational data – we refer the reader to [24] for a recent comparative analysis of different classes of interacting models.
In particular, models in which the coupling or interacting term Q is proportional to the dark energy (DE) density \(\rho _{x}\) [25,26,27,28], \(Q = 3\xi H \rho _{x}\), where H and \(\xi \) are the Hubble and interaction parameters respectively, have become popular in the recent years (see e.g. [29] and references therein). However, as will be shown in this paper, this class of models shows unphysical behavior for the interval of values of its parameters currently constrained by observational data [29]. In particular, the model predicts that the pressureless matter density will eventually become negative, violating the Weak Energy Condition (WEC), with further consequences for the evolution of the dark matter and baryon density perturbations.
2 Background dynamics
Let us first consider the balance equations of the model
where \(\rho _{dm}\) and \(\rho _{b}\) are respectively the densities of dark matter (DM) and conserved baryons, \(\omega _x < 0\) is the DE equation-of-state (EoS) parameter, and a dot means derivative with respect to (w.r.t.) cosmological time. Summing up equations (1) and (2) gives (\( \rho _{m} = \rho _{dm}+ \rho _b\))
for the total pressureless matter. The general solutions of (3) and (4) are
In the spatially flat case, C and \(\rho _{x0}\) obey the additional constraint \(\rho _{m0} + \rho _{x0} = 3H_0^2\), where a subscript 0 denotes the value of the corresponding quantity at present time. That is,
where \(\Omega _{x0} = \rho _{x0}/(3H_0^2)\) is the present DE density parameter.
In order to assess the conditions that lead to the WEC violation, it is convenient to split the analysis into two parts, namely, the past and future WEC. From (5), it is possible to show that the matter energy density becomes negative at
Assuming that \(w_{x}<0\), it is straightforward to obtain the conditions that will provide solutions for Eq. (8) in the intervals \(0<a<1\) (past) and \(a>1\) (future). To ensure that the matter energy density does not assume negative values at early times, the interaction parameter must obey the relation
On the other hand, the second term on the right-hand side of Eq. (5) is negative and it will eventually dominate \(\rho _m\) in the future unless
regardless of the value of \(w_{x}\). Equations (9) and (10), therefore, define the range where the model is physically well-defined for any time scale. In particular, the latter relation will be used in Sect. 4 to define the WEC or physical prior when constraining the cosmological parameters within non-prohibited regions.
For example, if \(\omega _x = -1\), \(\Omega _{x0} = 0.7\) and \(\xi = -0.1\), \(\rho _m\) becomes negative when the scale factor is \(a \approx 1.7\). In Fig. 1 we show the scale factor for WEC violation as a function of the interaction parameter \(\xi \). Figure 2 shows the behavior of the Hubble function, as well as of the DE and matter densities, as functions of the scale factor. The violation of the WEC in this class of interacting models was also pointed out in [6].
Scale factor for WEC violation as a function of the interaction parameter \(\xi \). The solid line corresponds to \(w_{x}=-0.8\) and the dashed line corresponds to \(w_{x}=-1.2\). The DE density parameter was fixed to \(\Omega _{x0} = 0.7\). The result for \(w_{x}=-1\) is in between solid and dashed lines
Background solutions as functions of the scale factor. Left panel: Hubble function \(H/H_0\). Centre panel: DE relative energy density. Right panel: pressureless matter relative energy density. In all panels solid lines correspond to \(\xi = -0.1\), \(\omega _x = -1\) and \(\Omega _{x0} = 0.7\) and dashed lines correspond to the \(\Lambda \)CDM model with the same \(\Omega _{x0}\)
3 Perturbations
In a model with non-gravitational interaction in the dark sector, the conservation equations for conserved baryons, DM and DE are
Combining Eqs. (11) and (12) we obtain
We can decompose the energy-momentum transfer \(Q^{\mu }\) in directions parallel and orthogonal to the fluid 4-velocity \(u^{\mu }\),
with
For comoving observers, Q represents the energy transfer between the components, and \(\bar{Q}^{\mu }\) represents the momentum transfer.
Assuming that both DE and pressureless matter are adiabatic perfect fluids, perturbing (13) and (14) in the longitudinal gauge, and assuming that there is no momentum transfer in the matter rest frame (i.e. matter follows geodesics), we find the balance and Poisson equations
where a prime means derivative w.r.t. conformal time, \({\mathcal {H}} = aH\), \(\rho \) is the total energy density, \(\delta =\delta \rho /\rho \), and \(\theta \) is the fluid velocity potential.
Multiplying (18) by \((1+\omega _x)\) and setting \(\omega _x = -1\), we obtain
The remaining equations lead to the Poisson and matter perturbation equations
where \(\theta = \theta _{m}\) (the DE velocity remains undefined). In the limit of small scales, Eqs. (24)–(26) are reduced to
whereas (22) and (23) are negligible in this limit. For conserved baryons the balance equations are
There is no pressure term in Eqs. (27)–(30). Instabilities are caused by the background interaction term \(Q = 3 \xi H \rho _x\) due to the violation of the WEC discussed earlier. Some authors try to fix this issue by taking \(\omega _x \ne -1\). In this case, the system of perturbation equations (17)–(21) does not close. Then an additional ansatz for \(\delta Q\) is needed, but it should be consistent to a covariant perturbation of the background ansatz \(Q = 3 \xi H \rho _x\). Another possibility is to consider interacting models with a non-adiabatic DE, with sound speed \(c_s^2 = 1\), which on the other hand leads in general to large scale instabilities [4, 30] (see also [31, 32]). In any case, the weak energy condition is still violated by the background in the present model.
Perturbative solutions in subhorizon limit as functions of the scale factor. Top left panel: pressureless matter density contrast. Top right panel: pressureless matter velocity potential. Bottom left panel: Baryon density contrast. Bottom right panel: Baryon velocity potential. In all panels solid lines correspond to \(\xi = -0.1\), \(\omega _x = -1\) and \(\Omega _{x0} = 0.7\), and dashed lines correspond to the \(\Lambda \)CDM model with the same \(\Omega _{x0}\)
In Fig. 3 we plot the evolution of the total matter/baryon density contrasts and velocity potentials, that show an instability at \(a \approx 1.7\), when the matter density becomes negative (for \(\xi = -0.1\) and \(\Omega _{x0}=0.7\)). As can be seen in the top left panel, when \(\rho _m\) reaches values arbitrarily close to zero, \(\delta _{m}\) diverges. On the other hand, the bottom panels show that this instability propagates, via \(\delta \rho _{m}\), to the baryonic component, even though that component does not violate the WEC and remains positive for \(a>1.7\). In order to solve the closed system (27)–(30), we have used \(\xi = -0.1\), \(\omega _x = -1\) and \(\Omega _{x0} = 0.7\), besides the initial conditions \(\delta _{m} = \delta _{b} = 10^{-5}\) and \(\theta _{m} = \theta _{b} = 0\) at \(a = 10^{-3}\).
As we have shown, for \(\omega _x = -1\) the DE component is smooth on sub-horizon scales. This is not true if \(\omega _x > -1\), when DE clusters and contributes to clustering matter [5]. Therefore, one may argue that the weak energy condition must be satisfied by the total clustering energy, not by pressureless matter alone. In order to verify this possibility, let us decompose the dark energy as
where \(\rho _{m'}\) is pressureless and \(\rho _{\Lambda }\) has EoS parameter \(-1\). The total clustering matter (including the fluctuating DE part) is given by
It is easy to verify that \(\rho _c\) is positive definite if, and only if,
When this inequality is saturated, the model is equivalent to a \(\Lambda \)CDM model. It is violated, in particular, by the best-fit values obtained from current observations [29].
With the above decomposition, Eqs. (3) and (4) can be rewritten as
with
If (36) is satisfied, the energy flux is from \(\rho _{\Lambda }\) to \(\rho _c\). With this interaction term, the sub-horizon perturbation equations for the clustering matter are the same as (27) and (28),
with \(\delta _{\Lambda } \ll \delta _c\) and \(\delta Q_c \approx 0\). Under condition (36), there is no instability. Note that the decomposition defined by Eq. (31) was introduced as part of a complementary discussion on the weak energy condition analysis. This approach must be considered only in this context, and there is no relation with the parameter selection presented in Sect. 4.
To conclude this analysis, a discussion on the use of the comoving synchronous gauge is in order. In the synchronous gauge the balance equations are given by
For the metric potential, we obtain from the Einstein’s equations
In the case \(\omega _x = -1\) we can assume, as above, that matter follows geodesics, that is, we can set \(\delta \bar{Q}^i = 0\), \(\theta = \theta _m = 0\), and (41) is identically satisfied. From (42) we see that \(\delta \rho _x = -\delta p_x = 0\) (while \(\theta _x\) remains undefined). Finally, from (44) we have \(\delta Q = 0\) and our system is reduced to
Systems (27) and (28) and (46) and (47) lead to the same second order equation for the matter contrast,
where we have introduced the rate of matter creation \(\Gamma = Q/\rho _m\). It is easy to check that, for \(\omega _x \ne -1\), this is not generally possible. Dark energy is perturbed, there is momentum transfer in the matter rest frame, matter does not follow geodesics, which means that it is not comoving with synchronous observers.
4 Impact of the WEC prior on parameter estimation
We shall now investigate the impact of the physical or WEC prior, \(\xi \ge 0\), on the model parameter estimation. With and without the inclusion of such a prior we perform a Bayesian statistical analysis considering two different data sets. First, we use the full CMB data from Planck alone, which contains information from temperature and polarization maps and the lensing reconstruction, Planck (TT,TE,EE+lowE+lensing) [33]. Second we combine the Planck data with the current sample of the Pantheon catalog of type Ia Supernovae (SNe Ia) [34, 35].Footnote 1
We choose not to use the Baryonic Acoustic Oscillations (BAO) data as there is no evidence that the fiducial model used in the BAO peak extraction would not bias our analysis, contrary to the usual \(\Lambda \)CDM parameters [36]. Furthermore, we emphasize that the parameter estimation itself is not the main goal of the paper, but rather to assess how the inclusion of the WEC prior affects the parameter constraints.
In order to perform the parameter selection we make use of a suitable modified version of the Boltzmann code class [37] for the studied interacting model, combined with MontePython [38, 39] for running the MCMC process. The cosmological parameters considered in our analysis are the six usual ones plus the interaction parameter, i.e., \(\theta =\{ \omega _{b }, \omega _{c }, \ln (10^{10}A_{s}), n_{s }, \tau _{reio }, H_{0}, \xi \}\), with the dark energy EoS parameter \(w_{x}\) = -1. The results of our analysis are presented in Table 1.
Figure 4 shows the posteriors obtained for the interaction parameter \(\xi \) for the cases where no prior (left panel) and the WEC prior (centre panel) are used. As can be seen, the \(\Lambda \)CDM limit (\(\xi =0\)) is obtained within \(1\sigma \) (C.L.) in all cases. For the case with no prior, when only Planck data is used, the best-fit and mean value of \(\xi \) are both positive, which avoid the WEC violation discussed earlier. On the other hand, when the Pantheon data is added to the analysis, the best-fit and mean value of \(\xi \) are slightly smaller than zero, which means that, inevitably, the WEC will be violated in the future. Notwithstanding, when the WEC prior is taken into account, the analysis for \(\xi \) is not drastically affected. When only the Planck data is employed the best-fit and mean values for \(\xi \) are also positive, in agreement with the analysis with no prior. For the combined Planck + Pantheon data set, the constraint on \(\xi \) has the \(\Lambda \)CDM limit as the best-fit, with an upper-bound limit compatible with the previous analysis with the WEC prior. It is worth mentioning that the interval of \(\xi \) derived from the past WEC condition (Eq. (9)) agrees with all analysis, which amounts to saying that the impact on the parameter estimation comes from the future WEC condition, i.e., the positivity of the interacting parameter \(\xi \) defined in Eq. (10).
The posteriors for \(H_{0}\) are shown in the right panel of Fig. 4. Both analyses, with and without the WEC prior, have weak constraints on the Hubble constant when we consider only the Planck data, with best-fit and mean around \(H_{0}\approx 64\ \mathrm{km}\ \mathrm{s}^{-1}\ \mathrm{Mpc}^{-1}\). The wide error bars of \(H_{0}\) in these cases evidence the necessity of adding more data to the analysis. Adding the SNe Ia data from Pantheon, the studied model seems to alleviate the \(H_{0}\) tension, which is related to the negative value of the interacting parameter \(\xi \). The inclusion of the WEC prior moves the constraints towards smaller values of \(H_{0}\), which increases the well-known tension with local measurements of the current expansion rate [40].
Finally, we show the corner plot for the plane \(\Omega _{m0}\) - \(\sigma _{8}\) in Fig. 5. Similarly to the \(H_{0}\) analysis, in the case where only the Planck data is employed, we have weak constraints on \(\Omega _{m0}\) and \(\sigma _{8}\). In particular, the predictions for \(\Omega _{m0}\) and \(\sigma _{8}\) in both analyses are about 0.35 and 0.74 respectively. On the other hand, when the Pantheon data is combined with Planck data, the constraints on \(\Omega _{m0}\) and \(\sigma _{8}\) are considerably improved. Also in this case, the inclusion of the WEC prior alters the parameter constraints, with a slight preference for smaller values of \(\sigma _8\), which somehow seems to alleviate the \(\sigma _{8}\) tension between the Planck primary CMB results and estimates from cosmic shear surveys [41]. For example, a naive comparison between our estimates of the quantity \(S_8 = \sigma _8(\Omega _m/0.3)^{1/2}\) with and without the WEC prior with the one provided by the KiDS weak lensing survey [41] shows a difference of \(1.5\sigma \) and \(1.64\sigma \), respectively. An even better agreement (\(\lesssim 1\sigma \)) is obtained from a comparison using the current clustering and lensing data from the Dark Energy Survey [42].
5 Conclusions
Interacting DE cosmologies are capable of providing a good description of the Universe evolution and constitute an alternative to the standard cosmological model [8]. As recently reported in [29], the current observational data seem to favor the former class of models with an interaction term of the type \(Q = 3\xi H \rho _{x}\). In particular, for negative values of the interacting parameter (\(3\xi \simeq -0.5\)), that study showed that this model is able to provide a solution for the widely discussed \(H_0\) and \(\sigma _8\)-tension problems.
In this paper, we have investigated the theoretical consistency of this class of cosmologies and shown that for negative values of \(\xi \), which physically corresponds to a transfer of energy from dark matter to dark energy, this particular model predicts an eventual violation of the WEC (\(\rho \ge 0\)) for the dark matter density, which results in the instabilities of the matter perturbations discussed in Sect. 3. For completeness, we have also discussed the impact of the physical prior, \(\xi \ge 0\), on the model parameter estimation through a statistical analysis of the latest CMB and type Ia Supernovae data. The results show that the model predictions are in good agreement with current estimates of \(\sigma _8\) but far from providing a possible solution for the \(H_{0}\)-tension problem.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: No data will be made available since all data-sets are publicly available, or can be made available by contacting the authors.]
Notes
The Pantheon data can be downloaded from http://www.github.com/dscolnic/Pantheon. For CMB analysis, all Planck likelihood codes and data can be obtained at http://www.pla.esac.esa.int/pla.
References
M. Ozer, M. Taha, Phys. Lett. B 171, 363 (1986)
M. Ozer, M. Taha, Nucl. Phys. B 287, 776 (1987)
K. Freese, F.C. Adams, J.A. Frieman, E. Mottola, Nucl. Phys. B 287, 797 (1987)
J. Valiviita, E. Majerotto, R. Maartens, JCAP 07, 020 (2008)
S. Carneiro, H. Borges, JCAP 06, 010 (2014)
H.A. Borges, D. Wands, Phys. Rev. D 101, 103519 (2020)
R. von Marttens, L. Casarini, D. Mota, W. Zimdahl, Phys. Dark Univ. 23, 100248 (2019)
M. Benetti, W. Miranda, H.A. Borges, C. Pigozzo, S. Carneiro, J.S. Alcaniz, JCAP 12, 023 (2019)
D.-M. Xia, S. Wang, Mon. Not. R. Astron. Soc. 463, 952 (2016)
E. Di Valentino, A. Melchiorri, O. Mena, Phys. Rev. D 96, 043503 (2017)
S. Kumar, R.C. Nunes, Phys. Rev. D 96, 103511 (2017)
W. Yang, A. Mukherjee, E. Di Valentino, S. Pan, Phys. Rev. D 98, 123527 (2018)
W. Yang, O. Mena, S. Pan, E. Di Valentino, Phys. Rev. D 100, 083509 (2019)
S. Kumar, R.C. Nunes, S.K. Yadav, Eur. Phys. J. C 79, 576 (2019)
E. Di Valentino, A. Melchiorri, J. Silk, JCAP 01, 013 (2020)
S. Pan, W. Yang, C. Singha, E.N. Saridakis, Phys. Rev. D 100, 083539 (2019)
M. Martinelli, N.B. Hogg, S. Peirone, M. Bruni, D. Wands, Mon. Not. R. Astron. Soc. 488, 3423 (2019)
E. Di Valentino, A. Melchiorri, O. Mena, S. Vagnozzi, Phys. Rev. D 101, 063502 (2020)
W. Yang, S. Pan, E. Di Valentino, R.C. Nunes, S. Vagnozzi, D.F. Mota, JCAP 09, 019 (2018)
S. Pan, W. Yang, E. Di Valentino, E.N. Saridakis, S. Chakraborty, Phys. Rev. D 100, 103520 (2019)
W. Yang, S. Pan, D.F. Mota, Phys. Rev. D 96, 123508 (2017)
S. Pan, W. Yang, A. Paliathanasis, Mon. Not. R. Astron. Soc. 493, 3114 (2020)
R. von Marttens, L. Lombriser, M. Kunz, V. Marra, L. Casarini, J. Alcaniz, Phys. Dark Univ. 28, 100490 (2020)
A. Cid, B. Santos, C. Pigozzo, T. Ferreira, J. Alcaniz, JCAP 03, 030 (2019)
W. Zimdahl, D. Pavon, Phys. Lett. B 521, 133 (2001)
L.P. Chimento, A.S. Jakubi, D. Pavon, W. Zimdahl, Phys. Rev. D 67, 083513 (2003)
M.R. Setare, Phys. Lett. B 642, 1 (2006)
H. Sadjadi, M. Alimohammadi, Phys. Rev. D 74, 103007 (2006)
E. Di Valentino, A. Melchiorri, O. Mena, S. Vagnozzi, Phys. Dark Univ. 30, 100666 (2020)
T. Clemson, K. Koyama, G.-B. Zhao, R. Maartens, J. Valiviita, Phys. Rev. D 85, 043007 (2012)
B.M. Jackson, A. Taylor, A. Berera, Phys. Rev. D 79, 043526 (2009)
E. Majerotto, J. Valiviita, R. Maartens, Mon. Not. R. Astron. Soc. 402, 2344 (2010)
N. Aghanim et al. (Planck) (2019)
D. Jones et al., Astrophys. J. 857, 51 (2018)
D. Scolnic et al., Astrophys. J. 859, 101 (2018)
P. Carter, F. Beutler, W.J. Percival, J. DeRose, R.H. Wechsler, C. Zhao, Mon. Not. R. Astron. Soc. 494, 2076 (2020)
D. Blas, J. Lesgourgues, T. Tram, JCAP 07, 034 (2011)
B. Audren, J. Lesgourgues, K. Benabed, S. Prunet, JCAP 02, 001 (2013)
T. Brinckmann, J. Lesgourgues, Phys. Dark Univ. 24, 100260 (2019)
A.G. Riess, S. Casertano, W. Yuan, L.M. Macri, D. Scolnic, Astrophys. J. 876, 85 (2019)
S. Joudaki et al., Mon. Not. R. Astron. Soc. 474, 4894 (2018)
M. Troxel et al., DES. Phys. Rev. D 98, 043528 (2018)
Acknowledgements
RvM acknowledges support from CNPq and from the Federal Commission for Scholarships for Foreign Students for the Swiss Government Excellence Scholarship (ESKAS no. 2018.0443) for the academic year 2018–2019. SC is partially supported by CNPq with Grant no. 307467/2017-1. JSA acknowledges support from CNPq (Grants nos. 310790/2014-0 and 400471/2014-0) and FAPERJ (Grant no. E-26/203.024/2017).
Author information
Authors and Affiliations
Corresponding author
Appendix A: Corner plots
Appendix A: Corner plots
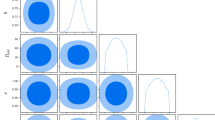
For the sake of completeness, we show the resulting triangle plots with all free cosmological parameters. These plots are particularly useful because they illustrate the correlation between all parameters. In Fig. 6 we show the result for the analyses with no prior, while Fig. 7 shows the result for the case where the WEC prior is taken into account.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
von Marttens, R., Borges, H.A., Carneiro, S. et al. Unphysical properties in a class of interacting dark energy models. Eur. Phys. J. C 80, 1110 (2020). https://doi.org/10.1140/epjc/s10052-020-08682-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08682-5