Earth tomography with atmospheric neutrino oscillations

Abstract

The study of the flux of atmospheric neutrino crossing the Earth can provide useful information not only on the matter density of the different layers that make up the planet but also on their chemical composition. The key phenomenon that makes this possible is flavor oscillations and their dependence on the electron density along the neutrino baseline. To extract the relevant information, we simulate the energy and azimuth angle distribution of events produced in a generic neutrino telescope by atmospheric neutrinos passing through the deepest parts of the Earth. Changes in the densities of the outer core and the mantle are implemented by varying the location of the boundary between these layers so that the restrictions on the mass of and the moment of inertia of the Earth are both satisfied. This allows us to examine the effect of simultaneous changes in composition and density of the outer core, unlikely other works on the subject, where only one of these quantities was varied.

1 Introduction

To understand the internal dynamics and evolution of the Earth we need to know its internal structure and composition. These are essential ingredients for a full comprehension of basic geological phenomena, such as volcanology, earthquakes, plate tectonics and mountain formation [1, 2]. Current knowledge has led to symmetric spherical models consisting of several concentric shells that differ in composition and mechanical behavior [3], of which the main ones are: crust, upper mantle, lower mantle, outer core, and inner core. Characterizing their properties has not been an easy task. Except in the crust, technological difficulties prevent inspecting the deeper layers by drilling holes to take samples. Instead, several type of observations on the surface need to be combined to probe the Earth’s inner parts. Most of our knowledge comes from geophysics, in particular examining how the direction and/or speed of seismic waves generated by earthquakes are affected when they travel through different layers [4,5,6]. Valuable information has also been obtained from measurements of the magnetic and gravitational fields, observations of the moment of inertia and the precession motion of the planet, laboratory experiments at high pressures and temperatures, and physical, chemical and mineralogical analysis of meteorites and xenoliths.

While the distribution of the matter density can be inferred from seismological observations, the compositional structure of the Earth is more difficult to determine. This is particularly true for the lower mantle and the core, whose compositions remain quite uncertain despite significant progress in recent years. According to the most popular model, the core mainly consists of an iron-nickel alloy, with Ni/Fe$\,\sim 0.06$, and is divided into inner and outer regions distinguished by a great density difference at a depth of approximately 5100 km [7]. The inner core is solid, while the outer core is liquid as indicated by the lower density and lack of s-wave propagation in it [3]. The density deficit of $4.5 \%$ in the outer core is too large to be due only to the solid-liquid phase transition and requires elements of lower atomic weight, such as Si, O, S, C, and/or H, to be present in about 5–10 wt% (weight percent) [8,9,10,11]. The nature and content of the light elements has important implications for convection in the outer core, which in turn is closely related to the geodynamo that generates the planetary magnetic field. They are also linked to the scenario of Earth’s differentiation, the rate of core cooling, and the way the core and the mantle interact. It has been challenging (and not free of controversy) to ascertain the identity and concentrations of the light elements. In order to discriminate between the variety of plausible models, the most direct method should be to compare laboratory measurements with the seismically observed density and acoustic velocity of the core. These experiments are difficult to conduct for liquid iron alloys samples at the extreme temperature and pressure conditions of the core [12]; as consequence, the available accurate experimental data are still insufficient to make a direct comparisons with the seismological data. On the other hand, in a recent work, the chemical composition of liquid iron alloys at outer-core pressure and temperature conditions has been constrained by comparing first principle calculations of the density and bulk sound velocity with the PREM profiles [13]. The primary light component was found to be hydrogen when the inner-core boundary temperature $T_{ICB}$ is not high (4800–5400 K) or oxygen if $T_{ICB} = 6000 \, \hbox {K}$. Hence, as the authors conclude, it is still difficult to specify the chemical composition of the outer core based solely on comparing theoretical calculations and seismological observations of the density and speed of sound.

From the above, it is clearly important to develop alternative methods that can provide complementary and independent information about the deep interior of the Earth. In this regard, the use of neutrinos seems to be a promising and viable option. In general, there are two possible ways to perform geophysical investigations with neutrinos: geoneutrinos and neutrino tomography. Geoneutrinos are electron antineutrinos from the $\beta$-decay of long-lived natural isotopes within the Earth. Measurements of their flux provide valuable evidence of the amount and distribution of the radio active elements internally heating the planet [14, 15]. Two experiments, Borexino [16] and KamLAND [17], have currently sensitivity to geoneutrinos. In respect to neutrino tomography, the underlying idea is that the propagation of neutrinos in a medium is affected by their interactions with matter [18]. In neutrino absorption tomography the density profile can be reconstructed from the attenuation of the flux of very high energy ($> rsim 10 \, \hbox {TeV}$) neutrinos, which are absorbed when passing through the Earth. Measuring at large neutrino telescopes the isotropic flux of ultra-high energy cosmic neutrinos seems to be a promising tool to make an independent determination of the Earth’s density profile [19,20,21,22,23,24,25]. On the other hand, neutrino oscillation tomography takes advantage of the matter effect on neutrino oscillations [26,27,28] to probe the Earth’s interior with lower energy (MeV to GeV) neutrinos. In matter the flavor transition probabilities depend on the number density of electrons $n_e$ along the neutrino baseline, which is proportional to the product of the matter density $\rho$ times the average ratio of the atomic number Z to the mass number A [18, 29,30,31,32,33,34,35].

Since the Z/A ratio is a function of the chemical and isotopic composition of the medium, from the determination of the densities of matter and electrons, it might be possible in principle to restrict the different composition models of the Earth. With this in mind, in this work we reexamine the feasibility of studying the internal structure of the planet by means of oscillation tomography with atmospheric neutrinos, namely, those produced in the atmosphere by the interactions of cosmic rays with air nuclei. We pay particular attention to how changes in the content of light elements in the outer core could influence the number density of electrons. At the same time, we allow some variation in the location of the core-mantle boundary (CMB) as an effective way to account for the existence of a transition zone including the D” layer [36, 37]. This is the lowermost $\sim 250 \, \hbox {km}$ thick portion of the mantle directly above the CMB and gaining a better picture of it can help to better understand the dynamics of the entire mantle, as well as how the core and mantle interact. Furthermore, requiring variations in the CMB radius to be consistent with the well-measured Earth’s mass and moment of inertia allows us to change the densities of the outer core and mantle without violating such important constraints.

The paper is organized as follows. In Sect. 2 we present a simplified model of the Earth’s structure with four density layers. In Sect. 3 we briefly review the formalism of neutrino oscillations in matter and present the formulas for the transition probabilities. In Sect. 4 we determine the number of $\mu$-like neutrino events in a generic detector and the effects that changes in the composition and radius of the outer core have on it. Sect. 5 contains our results and final comments. There, we present a Monte Carlo simulation of the number of $\mu$-like events and the application of this observable to test different composition models of the outer core. We included an appendix with details of the derivation of the transition amplitudes between flavor neutrinos in a medium with a symmetric density profile.

2 Model of the Earth’s structure

We want to explore the possibility that neutrino oscillations in matter can provide information on the CMB and its near zone, contributing to a better understanding of some of the mechanism responsible for the phenomena described above. For this purpose, we consider the simplified spherical model for the Earth’s interior shown in Fig. 1, which consists of four layers of constant densities delimited by concentric spheres of different radii: inner core, outer core, mantle, and crust.¹ The radii of the inner core $R_{\mathtt {ic}}$, the mantle $R_{\mathtt {m}}$, and the Earth $R_{_{\oplus }}$ are assumed to have the following fixed values: $R_{\mathtt {ic}} = 1221.5 \, \hbox {km}$, $R_{\mathtt {m}} = 5600 \, \hbox {km}$, and $R_{_{\oplus }} = 6371 \, \hbox {km}$ (Fig. 2).

The primary information on the Earth’s density as a function of the position comes from the total mass of the Earth $M_{_{\oplus }} = 5.9724 \times 10^{27} \mathrm{g}$ and its mean moment of inertia about the polar axis $I_{_{\oplus }} = 8.025 \times 10^{44} \mathrm{g} \mathrm{cm}^2$ [38]. In terms of the radial density distribution they are given by [39]:

$$\begin{aligned} M_{_{\oplus }}= & {} 4\pi \int _0^{R_{_{\oplus }}} \text {d}{r}\, r^2 \rho (r)\,, \end{aligned}$$

(1)

$$\begin{aligned} I_{_{\oplus }}= & {} 4\pi \dfrac{2}{3}\int _0^{R_{_{\oplus }}} \text {d}{r} \, r^4 \rho (r)\,. \end{aligned}$$

(2)

These important conditions alone requires that there be a concentration of mass towards the centre of the planet. Unlike previous works on the subject, we incorporate both constraints into our model. This is done by introducing a scheme for density variations, in which they are caused by changes in the radius of the outer core $R_{\mathtt {oc}}$ around the value $R_{\mathtt {oc}} = 3480 \, \hbox {km}$.

Fig. 1

Diagram (to scale) of the model of the Earth’s interior and baseline for an atmospheric neutrino going to detector D. Note that $L_{1} = L_{7}$, $L_{2} = L_{6}$, and $L_{3} = L_{5}$

Fig. 2

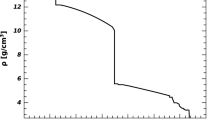
Radial density of the Earth as a function of the distance from the center R divided by the Earth’s radius $R_{_{\oplus }} = 6371 \, \hbox {km}$. The solid line is the PREM profile and the dashed lines are the constant densities of the four-step model used in this work, calculated for three different values of the outer core radius ${\tilde{R}}_{\mathtt {oc}} = \varkappa \,R_{\mathtt {oc}}$, $\varkappa = 0.96, 1, 1.04$, where $R_{\mathtt {oc}} = 3480 \, \hbox {km}$ is the PREM value of the outer core radius

According to the above considerations we require that the sum of the masses and the sum of the inertial moments of the four spherical shells have to be equal to $M_{_{\oplus }}$ and $I_{_{\oplus }}$, respectively:

$$\begin{aligned} \begin{aligned}&\dfrac{4 \pi }{3}\left[ {\rho }_{\mathtt {ic}} R^{3}_{\mathtt {ic}} + \rho _{\mathtt {oc}} ({\tilde{R}}^3_{\mathtt {oc}} - R_{\mathtt {ic}}^3)+\rho _{\mathtt {m}} (R_{\mathtt {m}}^3 - {\tilde{R}}^3_{\mathtt {oc}}) \right. \\&\qquad \left. + \rho _{\mathtt {c}} (R_{_{\oplus }}^3 - R_{\mathtt {m}}^3)\right] = M_{_{\oplus }}\,, \\&\dfrac{8 \pi }{15}\left[ \rho _{\mathtt {ic}} R^{5}_{\mathtt {ic}} + \rho _{\mathtt {oc}} ({\tilde{R}}^5_{\mathtt {oc}} - R^{5}_{\mathtt {ic}})+ \rho _{\mathtt {m}} (R^{5}_{\mathtt {m}} - {\tilde{R}}^{5}_{\mathtt {oc}}) \right. \\&\qquad \left. + \rho _{\mathtt {c}} (R^{5}_{_{\oplus }} - R^{5}_{\mathtt {m}})\right] = I_{_{\oplus }}\,, \end{aligned} \end{aligned}$$

(3)

with ${\tilde{R}}_{\mathtt {oc}} = \varkappa \,R_{\mathtt {oc}}$, where the numerical variable $\varkappa$ takes values close to one. For the densities of the inner core $\rho _{\mathtt {ic}}$ and the crust $\rho _{\mathtt {c}}$ we take the average values of the Preliminary Reference Earth Model (PREM) [3]: $\rho _{\mathtt {ic}} = 12.916\,\mathrm{g/cm}^3$ and $\rho _{\mathtt {c}} = 3.671\,\mathrm{g}\mathrm{/cm}^3$. On the other hand, the (average) densities of the mantle $\rho _{\mathtt {m}}$ and the outer core $\rho _{\mathtt {oc}}$ are variables that depends on $\varkappa$. To determine them, let us rewrite Eq. (3) as

$$\begin{aligned} \begin{aligned} \big (Y^{3}_{\mathtt {oc}}{\varkappa }^{3} - Y^{3}_{\mathtt {ic}}\big ) \rho _{\mathtt {oc}} - \big (Y^{3}_{\mathtt {oc}}{\varkappa }^{3} - Y^{3}_{\mathtt {m}}\big ) \rho _{\mathtt {m}}&= \delta \rho _{\text {M}}, \\ \big (Y^{5}_{\mathtt {oc}}{\varkappa }^{5} - Y^{5}_{\mathtt {ic}}\big ) \rho _{\mathtt {oc}} - \big (Y^{5}_{\mathtt {oc}}{\varkappa }^{5} - Y^{5}_{\mathtt {m}}\big ) \rho _{\mathtt {m}}&= \delta \rho _{\text {I}}, \end{aligned} \end{aligned}$$

(4)

with $Y_{\mathtt {ic},\mathtt {oc},\mathtt {m}} = R_{\mathtt {ic},\mathtt {oc},\mathtt {m}}/ R_{_{\oplus }}$ and

$$\begin{aligned} \begin{aligned} \delta \rho _{\text {M}}&= \rho _{\text {M}} - \rho _{\mathtt {ic}} Y^{3}_{\mathtt {ic}} - \rho _{\mathtt {c}}(1 - Y^{3}_{\mathtt {m}}),\nonumber \\ \delta \rho _{\text {I}}&= \rho _{\text {I}} - \rho _{\mathtt {ic}} Y^{5}_{\mathtt {ic}} - \rho _{\mathtt {c}}(1 - Y^{5}_{\mathtt {m}}), \end{aligned} \end{aligned}$$

where $\rho _{\text {M}}$ and $\rho _{\text {I}}$ denote the average mass density of the Earth calculated by means of the total mass and the total moment of inertia, respectively:

$$\begin{aligned} \rho _{\text {M}} = \frac{3}{4\pi } \frac{M_{\oplus }}{R^3_{_{\oplus }}} , \quad \rho _{\text {I}} = \frac{8}{15 \pi }\frac{I_{\oplus }}{R^5_{_{\oplus }}}. \end{aligned}$$

(5)

Fig. 3

Densities of the outer core and the mantle as functions of $\varkappa = {\tilde{R}}_{\mathtt {oc}}/R_{\mathtt {oc}}$

By solving the linear system given in Eq. (4) we express the densities of the outer core and the mantle as functions of $\varkappa$

$$\begin{aligned} \rho _{\mathtt {oc}} (\varkappa ) = \frac{{{\mathscr {F}}}(\varkappa )}{{{{\mathscr {D}}}}(\varkappa )}, \quad \rho _{\mathtt m}(\varkappa ) = \frac{{{\mathscr {G}}} (\varkappa )}{{{{\mathscr {D}}}}(\varkappa )}, \end{aligned}$$

(6)

with

$$\begin{aligned} {{{\mathscr {F}}}}(\varkappa )= & {} - \delta \rho _{\text {M}} Y^5_{\mathtt { oc}}{\varkappa }^5 + \delta \rho _{\text {I}}Y^3_{\mathtt {oc}}{\varkappa }^3 + \delta \rho _{\text {M}} Y_{\mathtt m}^5 - \delta \rho _{\text {I}}Y_{\mathtt m}^3\,,\nonumber \\ {{{\mathscr {G}}}}(\varkappa )= & {} - \delta \rho _{\text {M}}Y^5_{\mathtt { oc}}{\varkappa }^5 + \delta \rho _{\text {I}}Y^3_{\mathtt {oc}}{\varkappa }^3 + \delta \rho _{\text {M}}Y_{\mathtt {ic}}^5 - \delta \rho _{\text {I}}Y_{\mathtt {ic}}^3,\nonumber \\\end{aligned}$$

(7)

$$\begin{aligned} {{{\mathscr {D}}}}(\varkappa )= & {} - \left( Y^3_{\mathtt m} - Y^3_{\mathtt {ic}}\right) Y^5_{\mathtt {oc}}{\varkappa }^5 + \left( Y^5_{\mathtt m} - Y^5_{\mathtt {ic}}\right) Y^3_{\mathtt {oc}}{\varkappa }^3 \nonumber \\&- \left( Y^2_{\mathtt m} - Y^2_{\mathtt {ic}}\right) Y^3_{\mathtt m} Y^3_{\mathtt {ic}}\,. \end{aligned}$$

(8)

The coefficients of the polynomials ${{{\mathscr {F}}}}(\varkappa )$, ${{{\mathscr {G}}}}(\varkappa )$ and ${{{\mathscr {D}}}}(\varkappa )$ are evaluated in terms of the radii and the average densities given above. The resulting formulas for $\rho _{\mathtt {oc}} (\varkappa )$ and $\rho _{\mathtt m} (\varkappa )$ has been plotted in Fig. 3 in the interval of $\varkappa$ relevant to us. In particular, for $\varkappa =1$ (i.e., ${{{\tilde{R}}}}_{\mathtt {oc}} = R_{\mathtt {oc}}$) we get $\rho _{\mathtt oc} = 11.526 \,\mathrm{g/cm}^3$ and $\rho _{\mathtt m} = 4.742 \, \mathrm{g/cm}^3$. Later, we will allow the radius and the composition of the outer core to vary simultaneously to examine their join effects on the flavor transformations and, in particular, possible cancellations among them that could leave the flow of neutrinos in the detector unaltered.

3 Atmospheric neutrino oscillations

The discovery of flavor oscillations with atmospheric and solar neutrinos, and their subsequent verification using reactor and accelerator neutrinos, has firmly established that neutrinos are massive mixed particles [40]. Except for some unconfirmed anomalies (see Refs. [41, 42] for recent reviews) the current data set can be interpreted in terms of the minimal extension of the Standard Model, where the known flavor states $|{\nu }_{\alpha }\rangle (\alpha = e, \mu , \tau )$ are linear combinations of the states $|{\nu }_i \rangle$ with masses $m_i\,(i= 1,2,3)$: $|{\nu }_{\alpha }\rangle = \sum _i U^*_{\alpha i} |{\nu }_i \rangle$. The coefficients $U_{\alpha i}$ are elements of the unitary mixing matrix U that appears in the leptonic charged current, which can be parametrized as²

$$\begin{aligned} U = {{{\mathscr {O}}}}_{23}\Gamma {{{\mathscr {O}}}}_{13}\Gamma ^\dagger {{{\mathscr {O}}}}_{12}\,, \end{aligned}$$

(9)

where ${{{\mathscr {O}}}}_{ij}$ are orthogonal matrices representing rotations by angles $\theta _{ij}\in [0, \pi /2]$ in the respective planes and $\Gamma = \mathrm{diag} (1, 1, e^{i \delta })$ is a diagonal matrix with $\delta \in [0, 2\pi ]$. Values of the phase $\delta \ne 0, \pi$ imply CP violation in the leptonic sector. Besides these quantities, the oscillations between three neutrinos are parametrized by two mass-squared differences: ${\varDelta }m^2_{21} \equiv m^2_2- m^2_1$, ${\varDelta }m^2_{31} \equiv m^2_3- m^2_1$. The sign of ${\varDelta }m^2_{31}$ is unknown and will be considered in our study. The two possibilities correspond to different array of neutrino masses: the normal ordering (NO) and the inverted ordering (IO), depending on whether $m_3$ is greater or less than $m_{1,2}$.

Neutrinos are produced and detected in flavor eigenstates. Due to slight mass differences, the phases of the mass eigenstate components of the original flavor state change at different rates and, as a consequence, the flavor content of the neutrino beam oscillates along the trajectory. The relevant quantity in connection with neutrino oscillations is the probability $P_{{\nu _\alpha } \rightarrow {\nu _\beta }}(L)$ that a neutrino born as a $\nu _{\alpha }$ can be found in a flavor $\nu _{\beta }$ at a distance L from the source:

$$\begin{aligned} P_{{\nu _\alpha } \rightarrow {\nu _\beta }}(L) = |\,{{{\mathscr {U}}}}_{\beta \alpha }(L)|^2\,, \end{aligned}$$

(10)

where the probability amplitude ${{{\mathscr {U}}}}_{\beta \alpha }(L) = \langle \nu _{\beta }|\,\hat{{{\mathscr {U}}}}(L)|\nu _{\alpha }\rangle$ is an element of the $3 \times 3$ unitary matrix ${{\mathscr {U}}}(L)$ representing the evolution operator in the flavor basis.

When neutrinos propagate in a medium, their dispersion relations are modified due to the coherent forward scattering with electrons and nucleons. This effect can be incorporated by means of a refraction index different for $\nu _e$ and $\nu _{\mu ,\tau }$ and, after subtracting an unobservable overall phase, results in a additional contribution to the Hamiltonian H(L) that governs the evolution of flavor amplitudes. Besides the vacuum part, it now contains a potential term $V(L) = \mp \mathrm {v}(L)\,\mathrm{diag}(1,0,0)$, with $\mathrm {v}(L) = \sqrt{2} G_F n_e(L)$. Here, $G_F$ is the Fermi constant and the signs refer to neutrinos (minus) and antineutrinos (plus). The electron number density $n_e(L)$ is related to the mater density $\rho (L)$ according to

$$\begin{aligned} n_e (L) = \dfrac{Z}{A} \dfrac{{\rho }(L)}{m_{\mathrm{u}}}\,, \end{aligned}$$

(11)

where $m_{\mathrm{u}} = 931.494$ MeV is the atomic mass unit and $Z/A = \sum _{\lambda } r_{\lambda } (Z/A)_{\lambda }$. The summation runs over all the elements present in the medium and $(Z/A)_{\lambda }$ denotes the ratio between the atomic number $Z_{\lambda }$ and the atomic mass $A_{\lambda }$ of the element that contributes a fraction $r_{\lambda }$ to the total mass. Under proper conditions, the pattern of neutrino oscillations in matter can be significantly modified compared to the oscillations in vacuum. New resonance enhancement effects appear, which are sensitive to the density and composition of the medium. Matter effects in long baseline oscillations inside the Earth are strongly dependent on $\sin ^2 \theta _{13}$, which drives the transitions $\nu _e \leftrightarrow \nu _{\mu }$. Since the enhancement features depends on the sign of ${\varDelta }m^2_{23}$, the large measured value of $\theta _{13}$ has opened the possibility to distinguish among the two mass ordering by using atmospheric neutrinos going deeply through the Earth. Atmospheric neutrinos are generated as decay products in hadronic showers resulting from collisions of cosmic rays with nuclei in the upper atmosphere. Due to the isotropic nature of the primary cosmic ray flux, these neutrinos are produced around the world, providing a continuous source of neutrinos spanning a very wide range of energies and travelled distances before detection. On this work, we concentrate on those with long baseline and energies in the range of 2–10 GeV, which also offer the possibility to determine the unknown neutrino mass ordering and also to conduct an oscillation tomographic study of the Earth’s interior.

Table 1 Three-neutrino oscillation parameters obtained by averaging the best-fit values of three recent global fits of the current neutrino oscillation data [45,46,47]

Fig. 4

Survival probability $P_{{\nu _\mu } \rightarrow {\nu _\mu }}$ as a function of the neutrino energy for normal ordering. The outer core radius is 3340.8 km ($\varkappa = 0.96$) in the upper panels and 3619.2 km ($\varkappa = 1.04$) in the lower panels. The values of the azimuthal angle are $\eta = 15^\circ$ (a, c), and $\eta = 25^\circ$ (b, d)

Fig. 5

Transition probability $P_{{\nu _e} \rightarrow {\nu _\mu }}$ as a function of the neutrino energy, for normal ordering (NO) and inverse ordering (IO). The outer core radius is 3340.8 km ($\varkappa = 0.96$) in the upper panels and 3619.2 km ($\varkappa = 1.04$) in the lower panels. The values of the azimuthal angle are $\eta =15^\circ$ (a, c) and $\eta = 25^\circ$ (b, d)

According to Eq. (10), to calculate $P_{\nu _\alpha \rightarrow \nu _\beta }(L)$ we have to determine ${{{\mathscr {U}}}}(L)$ subject to the condition ${{{\mathscr {U}}}}(0) = I$ at $L = 0$. For three flavors the problem cannot be solved analytically in arbitrary density profiles, but a solution can be given for a constant density in terms of the energy eigenvalues in matter. Therefore, for a model like ours in which the planet consist of concentric spherical layers with constant densities, the evolution operator in the Earth ${{{\mathscr {U}}}}_{_{\oplus }}(L)$ can be expressed as the ordered product of the respective operators in the consecutive layers traversed by neutrinos. For the calculations we take advantage of the fact that the density profile is symmetrical with respect to the midpoint of the entire neutrino trajectory. The details are presented in the Appendix. We need the probabilities for the transitions ${\nu _\mu } ({\bar{\nu }}_\mu ) \rightarrow {\nu _\mu } ({\bar{\nu }}_\mu )$ and ${\nu _e} ({\bar{\nu }}_e) \rightarrow {\nu _\mu } ({\bar{\nu }}_\mu )$, which are those that are involved in the computation of the $\mu$-like events produced in a detector by ‘upward’ atmospheric neutrinos. From the results derived in the Appendix, we have

$$\begin{aligned}&P_{{\nu _\mu } \rightarrow {\nu _\mu }}(L_{_{\oplus }}) = |{{{\mathscr {U}}}}^{^{\oplus }}_{\mu \mu }(L_{_{\oplus }})|^2\,, \nonumber \\&P_{{\nu _e} \rightarrow {\nu _\mu }}(L_{_{\oplus }}) = |{{{\mathscr {U}}}}^{^{\oplus }}_{\mu e}(L_{_{\oplus }})|^2\,, \end{aligned}$$

(12)

where $L_{_{\oplus }} = 2 R_{_{\oplus }} \cos \eta$ denotes the length of the neutrino baseline within the Earth and

$$\begin{aligned} \begin{aligned} {{\mathscr {U}}}^{^{\oplus }}_{\mu e} (L_{_{\oplus }})&= \mathrm {c}_{2 3} \,\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ae}(L_{_{\oplus }}) + \mathrm {s}_{2 3} e^{i \delta } \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{be} (L_{_{\oplus }})\,, \\ {{\mathscr {U}}}^{^{\oplus }}_{\mu \mu } (L_{_{\oplus }})&= \mathrm {c}^{2}_{2 3} \,\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{a a} (L_{_{\oplus }}) + \mathrm {s}^{2}_{2 3}\,\tilde{{\mathscr {U}}}^{^{\oplus }}_{b b}(L_{_{\oplus }}) \\&\quad + 2\mathrm {s}_{2 3} \mathrm {c}_{2 3} \cos \delta \,\tilde{{\mathscr {U}}}^{^{\oplus }}_{ab}(L_{_{\oplus }}) \,. \end{aligned} \end{aligned}$$

(13)

The quantities in the right hand side of these equations with a tilde over them are elements of the symmetric matrix in Eq. (A.5). The expressions for antineutrinos are similar but with the replacements $\delta \rightarrow - \delta$ and $\mathrm {v} \rightarrow -\mathrm {v}$. The electron number density depends on both the matter density and Z/A, which is a function of the chemical and isotopic composition of the medium. Then, for neutrinos going through the deepest part of the Earth, $P_{{\nu _\mu }(\nu _e) \rightarrow {\nu _\mu }}(L_{_{\oplus }})$ become sensitive to changes in the composition of the outer core. In this work, additional effects are introduced by allowing variations in the position of the boundary between the outer core and the mantle, which lead to modifications in the matter densities of these layers.

The Earth’s outer core is composed mostly of liquid iron, or iron alloyed with nickel, along with a significant fraction of lighter elements (up to 15%) necessary to meet the density required by seismic wave velocities. Except for hydrogen $((Z/A))_H =1)$, for the components of this alloy $Z/A \cong 0.5$ because they have almost equal numbers of protons and neutrons. To appreciate the effect that changes in composition have on the flavor oscillations probabilities we will take a pure iron core as the standard model with which to compare models that contain a small percentage of hydrogen. In Figs. 5 and 4 we show the $\nu _{\mu } \rightarrow \nu _{\mu }$ and $\nu _{e} \rightarrow \nu _{\mu }$ transition probabilities as a function of the neutrino energy, for different values of $\varkappa$ and weight percent of hydrogen.The values of the oscillations parameters are those given in Table 1. All figures were made both for normal and inverse ordering and $\theta _{2 3}$ in the first octant. The values of the radii and the average densities of the layers are those given in Sect. 2, which were adapted from the PREM model. In the next section, we use these probabilities in the calculation of the $\mu$-like events produced by atmospheric neutrinos after crossing the internal regions of the Earth.

4 Neutrino events and test of Earth’s composition

To examine the feasibility of a tomographic study of the deeper layers of the Earth we look at the mark that variations of the density and composition leave on the flux of atmospheric neutrinos arriving to the detector after experience the effect of flavor oscillations in the terrestrial matter. We concentrate on the outer core, which is believe to play a fundamental role in the creation and behavior of the geomagnetic field, as well as in other important geophysical phenomena, such as plumes and hotspots. For our analysis, we consider a generic detector with a mass of water or ice containing a number of nucleons $n_{{\scriptscriptstyle N}}$ as target. A detector of this type, like for example IceCube, detect efficiently the Cherenkov radiation emitted along the trajectory of the $\mu ^{\pm }$ produced by the interactions of $\nu _{\mu }$ and ${{\bar{\nu }}}_{\mu }$ with the nucleons in the instrumented volume or near it.

We implement a Monte Carlo simulation of neutrino propagation in order to have a data set that simulates real observations, with the inevitable statistical fluctuations. To study the possibility of distinguishing between the different compositions and densities of the outer core, we applied the statistical methods for hypothesis testing considering a large number of pseudo experimental outcomes. To identify the most sensitive regions, we first do a scan dividing the cone under the detector into a series of angular and energy bins and calculate the number of $\mu$-type events ${{{\mathscr {N}}}}_{\mu }$ within given angular and energy intervals. This can be expressed as

$$\begin{aligned} {{{\mathscr {N}}}}_{\mu }= & {} n_{{\scriptscriptstyle N}} T \int _{E_{\text {min}}}^{E_{\text {max}}} \text {d}{E}\, \int _{\eta _{\text {min}}}^{\eta _{\text {max}}} \text {d}{\Omega }\nonumber \\&\times \left[ \sigma ^{cc}_{\nu _{\mu }}(E)\left( P_{\nu _{\mu }\rightarrow \nu _{\mu }} {\dfrac{d\Phi }{dE}}^{\nu _{\mu }} + P_{\nu _{e}\rightarrow \nu _{\mu }}{\dfrac{d\Phi }{dE}}^{\nu _{e}}\right) \right. \nonumber \\&\left. + \sigma ^{cc}_{{{\bar{\nu }}}_{\mu }}(E)\left( P_{{\bar{\nu }}_{\mu }\rightarrow {\bar{\nu }}_{\mu }} {\dfrac{d\Phi }{dE}}^{{\bar{\nu }}_{\mu }} + P_{{\bar{\nu }}_{e}\rightarrow {\bar{\nu }}_{\mu }} {\dfrac{d\Phi }{dE}}^{{\bar{\nu }}_{e}} \right) \right] , \end{aligned}$$

(14)

where T is the detection time. The flux of atmospheric neutrinos and antineutrinos have been taken from Ref. [48], while the charged-current cross sections for the ${\nu }_{\mu }(\bar{\nu }_{\mu })$-nucleon scattering, in the range of neutrino energies considered ($1-10$ GeV), are give approximately by [49]

$$\begin{aligned} \begin{aligned} \sigma ^{cc}_{\nu _{\mu }}(E)&\simeq 0.75 \times 10^{-38} \left( {E}/\mathrm{GeV}\right) \mathrm{cm}^2\,, \\ \sigma ^{cc}_{{\bar{\nu }}_{\mu }}(E)&\simeq 0.35 \times 10^{-38} \left( {E}/\mathrm{GeV}\right) \mathrm{cm}^2\,. \end{aligned} \end{aligned}$$

(15)

In Eq. (14) it is understood that oscillations probabilities are evaluated at $L_{_{\oplus }}$. The dependence of ${{{\mathscr {N}}}}_{\mu }$ on the density and composition of the medium is incorporated through these probabilities, which are calculated from the expressions given in Sect. 3 (see also the Appendix).

Fig. 6

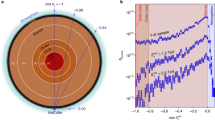
Level surfaces for $\Upsilon (E,\eta )$ (Eq. (16)) with 1 wt% of hydrogen

To find the angular and energy intervals where ${{{\mathscr {N}}}}_{\mu }$ is more sensitive to changes in the upper core composition we introduce the quantity

$$\begin{aligned} {\Upsilon }(E,\eta )= |1 - \dfrac{{{\mathscr {N}}}_{\mu }^{\mathrm{H}}}{{{\mathscr {N}}}_{\mu }^0} | \times 100\,, \end{aligned}$$

(16)

which gives the percentage difference between the number of events for the standard composition ${{\mathscr {N}}}_{\mu }^{0}$, without hydrogen in the outer core, and the number of events for a different composition ${{\mathscr {N}}}_{\mu }^{\mathrm{H}}$. The values for the radii and the average densities of the layers are those given in Sect. 2, which were adapted from the PREM model.

In Fig. 6a and b we represent the level surfaces for $\Upsilon$ in the ($E,\eta$) plane with a hydrogen proportion of 1wt%, both for the normal and inverted hierarchies. From the pictures, it is apparent that in all the cases the most sensitive region corresponds to energies around the 5 GeV and angles compatible with the shadow of the outer core. Deviations in the number of events are considerably more pronounced for NO, mainly because the effects of matter for IO occur for antineutrinos, whose charged cross section is approximately twice as small as for neutrinos. We also examine the change in the radii of the outer core and find that the sensitivity zone do not change appreciably.

Our observable is the number of $\mu$-like events and in what follows we use it to test different hypothesis about the composition and density of the outer core. To this end, we consider events with $4 \,\text {GeV}< E < 6\, \text {GeV}$ and $10^{\circ }<\,\eta \,<30^{\circ }$, and divide each of these intervals into 200 bins. In order to perform the Monte Carlo simulation we consider that each pseudo experiment consists of tossing, in each square bin of the grid, a number of Poisson distributed events with the mean value as given by Eq. (14). Thus, each pseudo experiment consist in 200 $\times$ 200 numbers corresponding to events, one for each bin. This sample of events are then distributed in angle and energy. We call it the true events and suppose that they are distributed according to the probability distribution function (pdf) $f^{i_{exp}}_t(E,\eta )$ for the $i_{exp}$-th experiment. For this pdf we take the normalized histograms constructed by means of the Monte Carlo simulation. Calling ${{{\mathscr {T}}}}^{i_{exp}}_{i,j}$ the number of true events in bin (i, j) for the $i_{exp}$-th experiment, we have

$$\begin{aligned} {{\mathscr {T}}}^{i_{exp}}_{i,j}={{{\mathscr {N}}}}_{tot} \iint _{\text {bin} \, i,j} f^{i_{exp}}_t(E, \eta ) \text {d}{E}\, \text {d}{\eta }, \end{aligned}$$

(17)

where the integral is over the energy and angle intervals of the bin (i, j).

To obtain a realistic distribution of events we must allow for a limited resolution of the detector, both in energy and angle. The net effect is the redistribution of the true events (“smearing”) in the grid bins, which is implemented by folding the true distribution with a resolution function ${{\mathscr {S}}}(E_{\mathtt o}, \eta _{\mathtt o} \vert E, \eta )$. We assume a Gaussian smearing and write

$$\begin{aligned} {{\mathscr {S}}}(E_{\mathtt o}, \eta _{\mathtt o} \vert E, \eta )= & {} \dfrac{1}{2\pi {\varDelta }\eta (E) {\varDelta }E(E)}\exp \left( -\dfrac{(\eta - \eta _{\mathtt o})^2}{2{\varDelta }\eta (E)^2}\right) \nonumber \\&\exp \left( -\dfrac{(E-E_{\mathtt o})^2}{2{\varDelta }E(E)^2}\right) , \end{aligned}$$

(18)

with the detector characterized by the angular and energy resolutions ${\varDelta }\eta (E) = \alpha _{\eta }/\sqrt{E/\text {GeV}}$ and ${\varDelta }E(E) = \alpha _{E} \, E$, respectively. For the values of the parameters $\alpha _{\eta }$ and $\alpha _{E}$ we consider different situations according to the discussion in Ref. [32]. To keep our analysis as simple as possible we assume a detection efficiency of $100\%$.

When convoluted with the true events the kernel in Eq. (18) gives us what we call the observed events. That is, ${S}(E_{\mathtt o}, \eta _{\mathtt o} \vert E, \eta )$ represents the conditional pdf for the measured values $(E_{\mathtt o}, \eta _{\mathtt o})$ given that the true values were $(E, \eta )$ and, since the event is observed somewhere, it is normalized such that

$$\begin{aligned} \iint {{{\mathscr {S}}}}(E_{\mathtt {o}}, \eta _{\mathtt {o}} \vert E, \eta ) \text {d}{E}_{\mathtt {o}} \text {d}{\eta }_{\mathtt {o}} = 1\,. \end{aligned}$$

(19)

In terms of the resolution function, the number of observed events ${{\mathscr {O}}}^{i_{exp}}_{m,n}$ in the bin (m, n) for the $i_{exp}$-th experiment is given by

$$\begin{aligned} {{\mathscr {O}}}^{i_{exp}}_{m,n}= & {} {{{\mathscr {N}}}}_{tot}\sum \limits _{i,j} \iint _{\text {bin} \; m,n} \text {d}{E}_{\mathtt {o}} \, \text {d}{\eta }_{\mathtt {o}} \nonumber \\&\iint _{\text {bin} \; i,j} \text {d}{E} \, \text {d}{\eta }\; {{\mathscr {S}}}(E_{\mathtt o}, \eta _{\mathtt {o}} \vert E, \eta ) f^{i_{exp}}_t(E, \eta )\,. \end{aligned}$$

(20)

As an illustration, in Fig. 7 we show the pdf of the true and observed events as functions of the energy and nadir angle, for a standard Earth (wt%H = 0, $\varkappa =1$) and the normal ordering of neutrino masses. To draw the figures we used the same (large) number of bins for both kind of events, but these numbers generally differ. In what follows, to test how well the hypothesis about different Earth compositions are in agreement with the standard Earth we consider the observed events to be distributed into five angular bins and nine energy bins.

Fig. 7

Probability distribution functions of a true events and b observed events, as functions of energy and nadir angle, for the standard Earth (wt%H = 0, $\varkappa =1$) and normal ordering of neutrino masses. The same number of bines has been used to make the figures, but in the calculations a much small number of bins is used for the observed events

From Eq. (20), for each bin (m, n), with $m = 1, \ldots , 9$ and $n = 1, \ldots , 5$, we determine the number of events ${{\mathscr {O}}}^{0;i_{exp}}_{m,n}$ for a standard Earth and the number of events ${{\mathscr {O}}}^{i_{exp}}_{m,n}(\mathrm{H}, \varkappa )$ for an alternative Earth with a given fraction of hydrogen in the outer core and a ratio $\varkappa = {\tilde{R}}_{\mathtt {oc}}/R_{\mathtt {oc}}$ for each of the $n_{exp}$ pseudo experiment. Thus, for each bin of the observed events we have a sample of the events and determinate the corresponding mean value

$$\begin{aligned} {\bar{{{\mathscr {O}}}}}^{\,0}_{\alpha }= & {} \frac{1}{n_{exp}}\sum _{i_{exp}}{{\mathscr {O}}}^{0;i_{exp}}_{\alpha }\,, \nonumber \\ {\bar{{{\mathscr {O}}}}}_{\alpha }(\mathrm{H}, \varkappa )= & {} \frac{1}{n_{exp}}\sum _{i_{exp}}{{\mathscr {O}}}^{i_{exp}}_{\alpha }(\mathrm{H}, \varkappa )\,, \end{aligned}$$

(21)

where $\alpha$ label the two-dimensional bins (m, n). For Poisson distributed events and for the likelihood function L we construct the negative log-likelihood ratio function as

$$\begin{aligned} \chi ^2_{\lambda }= & {} -2 \ln \frac{L({\bar{{{\mathscr {O}}}}}^{\,0}_{\alpha };{\bar{{{\mathscr {O}}}}}_{\alpha }(\mathrm{H}, \varkappa ))}{L({\bar{{{\mathscr {O}}}}}^{\,0}_{\alpha },{\bar{{{\mathscr {O}}}}}^0_{\alpha })} \nonumber \\= & {} 2\sum _{\alpha } \left[ {\bar{{{\mathscr {O}}}}}_{\alpha }(\mathrm{H} , \varkappa )-{\bar{{{\mathscr {O}}}}}^0_{\alpha } \ln \left( \frac{{\bar{{{\mathscr {O}}}}}^0_{\alpha }}{{\bar{{{\mathscr {O}}}}}_{\alpha }(\mathrm{H} , \varkappa )}\right) \right] \,. \end{aligned}$$

(22)

According to Wilks’ theorem [50] the $\chi ^2_{\lambda }$ distribution can be approximated by the $\chi ^2$ distribution, and from it, the goodness of fit can be established. The statistical significance of the $\chi ^{2}$ test is, as usual, given by the ${{\mathbf {p}}}$-value:

$$\begin{aligned} {{\mathbf {p}}}=\int _{\chi ^2}^\infty f_{\chi }(w,n_{_\mathrm{dof}}) \text {d}{w}\,, \end{aligned}$$

(23)

where $n_{_\mathrm{dof}}$ is the number of degrees of freedom and $f_{\chi }(w,n_{_\mathrm{dof}})$ is the chi-square distribution. In our case, $n_{_\mathrm{dof}} = 9\times 5 -2 = 43$. In this way, we can study the discrepancy level between the standard Earth and different hypothesis about the composition and density of the outer core. This is done in the next section where we present our results and final comments.

5 Results and final comments

As discussed in Sect. 2, we allow some variation in the location of the CMB that, to meet the constraints on the total mass and moment of inertia of the Earth, results in the dependence of the outer core and mantle densities on $\varkappa$ (Fig. 3).

As the quantities to be fitted, in what follows we take the fraction of hydrogen in the outer core and the relative change of its density ${\varDelta }\rho _{\mathtt {oc}}/\rho _{\mathtt {oc}}$, where ${\varDelta }\rho _{\mathtt {oc}} = \rho _{\mathtt {oc}}(\varkappa ) - \rho _{\mathtt {oc}}$ and $\rho _{\mathtt oc} = 11.526 \,\mathrm{g/cm}^3$ is the density for $\varkappa =1$. In order to evaluate the effect that changes on both of these quantities have on our observable, we construct the regions in the (${\varDelta }_{\rho _{\mathtt {oc}}}/\rho _{\mathtt {oc}}$, H) plane where the statistical significance, given by the p-value, for the discrepancy between the standard and the modified Earth is less than $1\sigma$. In Fig. 8 we show these regions for the oscillation parameters given in Table 1, for 10 years operation of a 10 and 100 Mton detector, with resolution parameters $\alpha _{\eta } = \alpha _{E} = 0.1$. As can be seen, the regions for NO are more restricted than for IO. In both cases, a negative correlation is observed between ${\varDelta }\rho _{\mathtt {oc}}/\rho _{\mathtt {oc}}$ and H, which indicates that an increase in the percentage of hydrogen in the outer core can be compensated by a decrease in its density.

Fig. 8

Correlated limits of the hydrogen fraction in the outer core and the relative change of its density at $1 \sigma$ confidence level, for detector resolution parameters $\alpha _{\eta } = \alpha _{E}=0.1$

We also examine the effect that variations of the detector resolutions have on the bounds at $1\, \sigma$ confidence level. Fig. 9 left (right) panel shows the bound for ${\varDelta }\rho _{\mathtt {oc}}/\rho _{\mathtt {oc}}$ as a function of the resolution parameters, when no hydrogen is present in the outer-core (H $= 0$), for normal (inverted) hierarchy. Likewise, the panels in Fig.10 show the corresponding bounds on the hydrogen fraction in the outer-core, when the matter density is that given by the PREM (${\varDelta }\rho _{\mathtt {oc}}/\rho _{\mathtt {oc}}=0$).

Fig. 9

Bounds on the relative change of the outer-core density ${\varDelta }\rho _{\mathtt {oc}}/\rho _{\mathtt {oc}}$ at $1\, \sigma$ confidence level as a function of the detector resolution parameters $\alpha _{\eta }=\alpha _{E}$, for hydrogen fraction H $= 0$

Fig. 10

Bounds on the hydrogen fraction (H) in the outer-core at $1\, \sigma$ confidence level as a function of the detector resolution parameters $\alpha _{\eta }=\alpha _{E}$, for no change in the outer-core density (${\varDelta }\rho _{\mathtt {oc}}/\rho _{\mathtt {oc}} = 0$)

In summary, we have studied the possibility of conducting an oscillation tomography of the Earth based on the matter effects on the flavor oscillations of atmospheric neutrinos propagating through the depths of the planet. Using the $\mu$-like events in a generic large Cherenkov detector as physical observables and making a Monte Carlo simulation of the energy and azimuthal angle distribution of these event, we tested possible variants with respect to a reference geophysical model with the average densities as given by PREM and no hydrogen in the outer core. Unlike previous studies, the procedure we followed in this work allowed us to simultaneously vary the composition and density of the outer core. When one of these quantities was fixed in the value of the reference geophysical model, our results, shown in Figs. 9 and 10, are compatible with those obtained by others authors in an uncorrelated way [33, 35].

The remote located interface between the rocky mantle and iron core is physically the most significant in the Earth’s interior. The phenomena that happens in the region around this interface play an important role in several process that impact he whole Earth and its complete understanding requires a combined effort of different geophysical disciplines. This task could greatly benefit from the use of phenomena of the type described here, normally studied in particle physics, and the arrival of new and improved neutrino telescopes, such as KM3NeT, ORCA, PINGO, and HyperKamiokande [51,52,53,54]. Even though our results were derived considering a simplified PREM model with four layer of constant densities, and without taking into account the systematics related to the experimental device, they exemplify the potentialities of neutrino oscillations as a novel techniques to explore the interior of the Earth.

Appendix A: Flavor neutrino evolution in the Earth

In this appendix we describe in detail the calculation of the flavor transition amplitudes for neutrinos produced in the atmosphere and detected after they go through the Earth. Let denote by $L_{\mathtt D}$ the distance between the detector and the source, then for the ${{{\mathscr {U}}}}(L_{\mathtt D}) = {{{\mathscr {U}}}}_{_{\oplus }} (L_{_{\oplus }})\,{{{\mathscr {U}}}}_{\mathtt A}(L_{\mathtt A})$, where ${{{\mathscr {U}}}}_{_{\oplus }}$ and ${{{\mathscr {U}}}}_{\mathtt A}$ are the matrix representations of the evolution operators in the Earth and the atmosphere, respectively. We have denoted by $L_{_{\oplus }}$ and $L_{\mathtt A}$ the lengths of the neutrino path en each of these media, with $L_{\mathtt D} = L_{_{\oplus }} + L_{\mathtt A}$. The flavor evolution along the atmosphere is well described assuming that neutrinos propagate in vacuum. Thus, in the flavor basis we have

$$\begin{aligned} {{{\mathscr {U}}}}_{\mathtt A}(L_{\mathtt A}) =U\exp \big ({- i L_{\mathtt A} H_0}\big ) U^\dagger , \end{aligned}$$

(A.1)

where U is the mixing matrix in Eq. (9) and $H_0 = \mathrm{diag}\,(E_1, E_2, E_3)$. Here, $E_i = \sqrt{|{\mathbf {p}}|^2 + m_i^2}$ are the energies of the neutrino mass eigenstates described as plane waves with the same momentum ${\mathbf {p}}$. Discarding a global phase, for relativistic neutrinos we have ${{{\mathscr {U}}}}_{\mathtt A}(L_{\mathtt A}) = U D U^\dagger$, where $D = \mathrm{diag} (1, e^{-i \varphi _{21}}, e^{-i \varphi _{31}})$, with $\varphi _{21} = {\varDelta }m^2_{21}L_{\mathtt A}/2E$, $\varphi _{31} = {\varDelta }m^2_{31}L_{\mathtt A}/2E$, and $E\cong |{\mathbf {p}}|$. Typically, $L_{\mathtt A}\sim 10 \, \hbox {km}$ and, for neutrinos with energies $E > rsim 1$ GeV, both $\varphi _{21}$ and $\varphi _{31}$ are small quantities. Therefore, D is almost equal to the identity matrix and ${{{\mathscr {U}}}}_{\mathtt A}(L_{\mathtt A})\simeq U U^\dagger = I$. Consequently, the probabilities $P_{\nu _{\alpha } \rightarrow {\nu _\beta }}$ in the detection volume can be calculated by means of the matrix elements of the evolution operator within the Earth. In what follows we will focus on deriving them.

The $3 \times 3$ matrix ${{{\mathscr {U}}}}_{_{\oplus }}(L)$ is the solution of the differential equation

$$\begin{aligned} i \frac{\partial }{\partial L}\,{ {{\mathscr {U}}}}_{_{\oplus }}(L) = H(L)\,{{{\mathscr {U}}}}_{_{\oplus }}(L)\,, \quad {{{\mathscr {U}}}}_{_{\oplus }}(0) = I, \end{aligned}$$

(A.2)

where L is the distance traveled by neutrinos along the Earth and

$$\begin{aligned} H(L) = U H_0 U^{\dagger } + V(L) \end{aligned}$$

(A.3)

is the effective Hamiltonian that determine the evolution of the flavor amplitudes in the presence of matter. The second term in the last equation is given by $V(L) = \mp \mathrm {v}(L)(1, 0, 0)$ with $\mathrm {v}(L)= \sqrt{2} G_F n_e(L)$, and represents the net effect of the coherent interactions of neutrinos (minus sign) or antineutrinos (plus sign) with the particles (e, p, n) present in the background. Reordering the mixing matrix as $U = {{{\mathscr {O}}}}_{23}\Gamma {{{\mathscr {O}}}} \Gamma ^\dagger$, with ${{{\mathscr {O}}}} = {{{\mathscr {O}}}}_{13}{{{\mathscr {O}}}}_{12}$, we can write

$$\begin{aligned} {{{\mathscr {U}}}}_{_{\oplus }}(L) = {{{{\mathscr {O}}}}_{23}\Gamma }\,\tilde{{{\mathscr {U}}}}_{_{\oplus }}(L){\Gamma }^\dagger {{{\mathscr {O}}}}^{\mathtt T}_{23}\,, \end{aligned}$$

(A.4)

where ${{{\mathscr {O}}}}^{\mathtt T}_{23}$ is the transpose of ${{{\mathscr {O}}}}_{23}$ and $\tilde{{{\mathscr {U}}}}_{_{\oplus }}(L)$ obeys an equation like the one in Eq. (A.2), with H(L) replaced by the real and symmetric Hamiltonian ${{\tilde{H}}}(L) = {{{\mathscr {O}}}} H_{0} {{{\mathscr {O}}}}^{\mathtt T} + V(L)$.

In one-dimensional models of the type we use here, which represent the average properties of the Earth, the density profile seen by neutrinos passing through the terrestrial matter is symmetrical with respect to the midpoint of their entire path. Hence, the effective potential energy satisfies the equality $v(2 {{\bar{L}}} - L) = v(L)$, with ${{\bar{L}}} = L_{_{\oplus }} /2$. This, together with the condition ${\tilde{H}}^*(L) = {\tilde{H}}(L)$, implies that

$$\begin{aligned} \tilde{{{\mathscr {U}}}}_{_{\oplus }}(L_{_{\oplus }}) = \tilde{{{\mathscr {U}}}}_{_{\oplus }} ^{\mathtt T}({{\bar{L}}})\,\tilde{{{\mathscr {U}}}}_{_{\oplus }}({\bar{L}}) = \begin{pmatrix} \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ee} &{}\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ea} &{} \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{eb} \\ \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ae} &{}\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{aa} &{}\tilde{{{\mathscr {U}}}}^{^{\oplus }} _{ab} \\ \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{be} &{}\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ba}&{}\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{bb} \\ \end{pmatrix}, \end{aligned}$$

(A.5)

where for notational brevity we have omitted the dependence of the matrix elements on $L_{_{\oplus }}$. As is evident from the first equality, $\tilde{{{\mathscr {U}}}}_{_{\oplus }}(L_{_{\oplus }} )$ is a symmetric matrix and therefore $\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ae} = \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ea}$, $\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{be} = \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{eb}$ and $\tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ba} = \tilde{{{\mathscr {U}}}}^{^{\oplus }}_{ab}$.

To compute the matrix in Eq. (A.5) we keep in mind that, as described in Sect. (2), we model the Earth as an onion like sphere made of four layers with different constant densities. Consequently, the full evolution operator can be expressed in terms of the product of the evolution operators in each of the successive layers through which the neutrinos pass on their way to the detector. Thus, for neutrinos traversing the inner core we have

$$\begin{aligned} \tilde{{{\mathscr {U}}}}_{_{\oplus }}({\bar{L}})= & {} \prod _{\ell } \tilde{{{\mathscr {U}}}}_{\ell }(L_{\ell })\,, \qquad (\ell = \mathtt {ic}, \mathtt {oc}, \mathtt {m}, \mathtt {c}) \nonumber \\= & {} \tilde{{{\mathscr {U}}}}_{\mathtt {ic}}(L_{\mathtt {ic}})\,\tilde{{{\mathscr {U}}}}_{\mathtt {oc}}(L_{\mathtt {oc}})\, \tilde{{{\mathscr {U}}}}_{\mathtt {m}}(L_{\mathtt {m}})\,\tilde{{{\mathscr {U}}}}_{\mathtt {c}}(L_{\mathtt {c}})\,. \end{aligned}$$

(A.6)

It should be noted that, in general, the matrices of the different layers do not commute between them and the factors must go in the order prescribed. Here, $L_{\ell }$ is equal to half of the whole distance that neutrinos travel in layer $\ell$, so $\sum _{\ell } L_\ell = {\bar{L}}$. These distances can be easily determined as functions of the nadir angle $\eta$ by applying elemental trigonometry (see Fig. 1):

$$\begin{aligned} \begin{aligned} L_{\mathtt c}&= R_{_{\oplus }} \left( \cos {\eta } - \sqrt{Y^{2}_{\mathtt m} - \sin ^{2}{\eta }}\right) ,\\ L_{\mathtt m}&= R_{_{\oplus }} \left( \sqrt{Y^{2}_{\mathtt m} - \sin ^{2}{\eta }} - \sqrt{Y^{2}_{\mathtt {oc}} - \sin ^{2}{\eta }}\right) ,\\ L_{\mathtt {oc}}&= R_{_{\oplus }} \left( \sqrt{Y^{2}_{\mathtt {oc}} - \sin ^{2}{\eta }} - \sqrt{Y^{2}_{\mathtt {ic}} - \sin ^{2}{\eta }}\right) , \\ L_{\mathtt {ic}}&= R_{_{\oplus }} \sqrt{Y^{2}_{\mathtt {ic}} - \sin ^{2}{\eta }}\,, \end{aligned} \end{aligned}$$

(A.7)

with $0 \le \eta \lesssim 11^{\circ }$. If neutrinos goes trough the outer core but not the inner core, then $\ell = \mathtt {oc}, \mathtt {c}, \mathtt {m}$ and $11^{\circ } \lesssim \eta \lesssim 33^{\circ }$. In this case, $L_{\mathtt {ic}} = 0$ and $L_{\mathtt {oc}} = R_{_{\oplus }} \sqrt{Y^{2}_{\mathtt {oc}} - \sin ^{2}{\eta }}$, while the formulas for $L_{\mathtt m}$ and $L_{\mathtt c}$ remain unchanged.

Since the layers are assumed to have a constant electron number density $n^{\ell }_e$, for each factor in Eq. (A.6) we have $\tilde{{{\mathscr {U}}}}_{\ell }(L_{\ell }) = \exp (-i {{\tilde{H}}}_{\ell } L_{\ell })$, where in ${{\tilde{H}}}_{\ell }$ the effective potential takes the fixed value $v_{\ell } = \sqrt{2}G_{F} n^{\ell }_e$. The exponential of a constant matrix can be evaluated by means of the Putzer’s algorithm [55]. For our $3 \times 3$ matrices, discarding in material phases, the results are [56]

$$\begin{aligned} \tilde{{{\mathscr {U}}}}_{\ell }(L_{\ell })= & {} (1 + {{{\mathscr {E}}}}^{\ell }_1{{\mathscr {A}}}_\ell )I - ( {{\mathscr {A}}}_\ell + {{{\mathscr {E}}}}^{\ell }_1 {{\mathscr {B}}}_\ell ){{\tilde{H}}}_{\ell } \nonumber \\&+ {{\mathscr {B}}}_\ell {{\tilde{H}}}_{\ell }^2 \,, \end{aligned}$$

(A.8)

where

$$\begin{aligned} {{\mathscr {A}}}_\ell= & {} \frac{1}{\omega ^{\ell }_{32}}\left( {{{\mathscr {E}}}}^{\ell }_3\frac{1- e^{-i \omega ^{\ell }_{21}L_\ell }}{\omega ^{\ell }_{21}} - {{{\mathscr {E}}}}^{\ell }_2\frac{1- e^{-i \omega ^{\ell }_{31}L_\ell }}{\omega ^{\ell }_{31}}\right) , \end{aligned}$$

(A.9)

$$\begin{aligned} {{\mathscr {B}}}_\ell= & {} \frac{1}{\omega ^{\ell }_{32}}\left( \frac{1- e^{-i \omega ^{\ell }_{21}L_\ell }}{\omega ^{\ell }_{21}} - \frac{1- e^{-i \omega ^{\ell }_{31}L_\ell }}{\omega ^{\ell }_{31}}\right) , \end{aligned}$$

(A.10)

with $\omega ^{\ell }_{21} = {{{\mathscr {E}}}}^{\ell }_2 - {{{\mathscr {E}}}}^{\ell }_1$ and similarly for $\omega ^{\ell }_{31}$ and $\omega ^{\ell }_{32}$. The quantities ${{{\mathscr {E}}}}^{\ell }_k\,(k = 1, 2, 3$) are the energy eigenvalues in matter and are given by the real roots of the characteristic (cubic) equation

$$\begin{aligned} {{{\mathscr {E}}}}^3 - b_{\ell }{{{\mathscr {E}}}}^2 + c_{\ell }{{{\mathscr {E}}}} - d_{\ell } = 0\,, \end{aligned}$$

(A.11)

where

$$\begin{aligned} b_{\ell }= & {} {\varDelta }_{21} + {\varDelta }_{31} + v_{\ell }\,,\nonumber \\ c_{\ell }= & {} {\varDelta }_{31}\,{\varDelta }_{21} + \big [{\varDelta }_{31} c_{13}^2 + {\varDelta }_{21} \big (c_{12}^2 + s_{12}^2\,s_{13}^2\big )\big ] v_{\ell }\,, \nonumber \\ d_{\ell }= & {} {\varDelta }_{31}\,{\varDelta }_{21} c_{12}^2\,c_{13}^2 v_{\ell }\,. \end{aligned}$$

(A.12)

They are the eigenvalues of ${{\tilde{H}}}_{\ell }$ (which coincide with those of $H_{\ell }$), do not depend on $\theta _{23}$ or $\delta$, are positive and unequal, and can be expressed as

$$\begin{aligned} {{{\mathscr {E}}}}^{\ell }_k= & {} \frac{2}{3} \sqrt{b_{\ell }^2 - 3 c_{\ell }} \cos \nonumber \\&\times \left[ \frac{1}{3}\arccos \left( \dfrac{2b_{\ell }^3 + 27d_{\ell } - 9b_{\ell }c_{\ell } }{2(b_{\ell }^2 - 3c_{\ell })^{3/2}}\right) - \frac{2\pi }{3}(3-k)\right] \nonumber \\&+ \dfrac{b_{\ell }}{3}\,, \end{aligned}$$

(A.13)

with ${{{\mathscr {E}}}}^{\ell }_1< {{{\mathscr {E}}}}^{\ell }_2 < {{{\mathscr {E}}}}^{\ell }_3$.

In this way, we have completed the determination of all the ingredients necessary to calculate each factor in Eq. (A.6) using formula (A.8). Once $\tilde{{{\mathscr {U}}}}_{_{\oplus }}({\bar{L}})$ has been obtained by multiplying the required factors, it is immediate to find $\tilde{{{\mathscr {U}}}}_{_{\oplus }}(L_{_{\oplus }})$ by means of Eq. (A.5). The resulting matrix, when substituted into Eq. (A.4), allows us to express the elements of ${{{\mathscr {U}}}}_{_{\oplus }}(L_{_{\oplus }})$ in terms of those of the matrix in (A.5).